Abstract
A peak-tracking algorithm for chromatograms recorded using liquid chromatography and mass spectrometry was developed. Peaks are tracked across chromatograms using the spectrometric information, the statistical moments of the chromatographic peaks, and the relative retention. The algorithm can be applied to pair chromatographic peaks in two very different chromatograms, obtained for different samples using different methods. A fast version of the algorithm was specifically tailored to process chromatograms obtained during method development or optimization, where a few similar mobile-phase-composition gradients (same eluent components, but different ranges and programming rates) are applied to the same sample for the purpose of obtaining model parameters to describe the retention of sample components. Due to the relative similarity between chromatograms, time-saving preselection protocols can be used to locate a candidate peak in another chromatogram. The algorithm was applied to two different samples featuring isomers. The automatically tracked peaks and the resulting retention parameters generally yielded prediction errors of less than 1%.
Liquid chromatography (LC) is one of the most established and useful tools for the analytical chemist. In recent years, developments including ultrahigh-pressure operation, core–shell particles, and monolithic stationary phases have improved the technique further, and hyphenation with powerful detectors, such as mass spectrometers, has rendered LC indispensable in the analytical lab. For very complex samples, for which more resolving power is needed, (comprehensive) two-dimensional (2D) liquid chromatography is a valuable addition. In recent years, this latter technique has been maturing rapidly. Advanced modulation interfaces have significantly reduced the threats of solvent incompatibility1,2 and limited detector sensitivity3 in the comprehensive mode (LC × LC).4 However, these developments are accompanied by an increase in the complexity of the system and, thus, the time required for method development. This is not only important in the case of two-dimensional LC, where essentially two complementary LC methods are required both in heart-cut 2D-LC and in LC × LC.5 Method development is also critical in 1D-LC. For example, in the emerging field of biopharmaceuticals, including biosimilars, many difficult questions arise, and very efficient method development is needed.
The prospect of cumbersome method development looms as a millstone around the neck of chromatographers, and this has spurred the development of computer-aided method-development tools. Research in such tools can roughly be categorized in two major categories, viz., (i) tools that rely on very large sets (>200 experiments) of data to train an algorithm in modeling the data6,7 and (ii) tools that describe component retention with relatively simple (physicochemical interaction or empirical) models. In the first case, no knowledge on the retention mechanism is required. However, the requirement of recording hundreds of experiments tailored to the analytes of interest is daunting. Moreover, the obtained models are not related to the physicochemical interactions that take place in the column. This latter aspect renders the models vulnerable if they are extrapolated to analytes or conditions outside the training set.
In the second case, a thorough understanding of the physicochemical interactions is crucial to derive a robust strategy to address unknown analytes and unexplored conditions. This type of strategy is routinely applied by optimization approaches such as DryLab8 and PEWS9 in 1D-LC and PIOTR10 in both 1D- and 2D-LC. Typically, gradient-scanning techniques are used, where two to three chromatograms are recorded of the same sample using a different gradient slope (and possibly different initial and/or final compositions). The peaks of sample analytes are then matched (or “paired”) across the recorded chromatograms and a physicochemical retention model is derived from the retention times. The retention parameters for all analytes are then used to predict the results of potential methods. Readers interested in this approach are referred to useful works.4,9,10 In the case of the PIOTR program, Pareto optimality analysis is used to identify methods, which meet user-defined optimization objectives. The PIOTR approach allows (LC × LC) method-development times to be reduced from several months to a few days.10
For such approaches to run as automatically as possible, the computer program must be able to efficiently track the different peaks found in all scanned chromatograms, i.e., decide which peaks in the different chromatograms belong to the same analyte. Especially in LC × LC, the number of possible analytes is vast, for example, when protein digest samples are targeted. In such a case manual peak tracking may form a new millstone around the chromatographer’s neck.
In comprehensive two-dimensional gas chromatography (GC × GC) algorithms have been developed to track peaks across chromatograms automatically.11 However, one critical difference between GC × GC and LC × LC is that in the latter case the elution order of peaks is subject to more dramatic changes. As a result, existing algorithms cannot easily be applied. In 1D-LC, already in the late 1980s peak-tracking strategies were developed that exclusively relied on chromatographic band areas12 or spectroscopic data.13 More recently, the group of Bylund proposed and tested an integrated statistical approach for tracking components in liquid chromatography–mass spectrometry (LC–MS) methods.14,15
Seeking an integrated, comprehensive package for both 1D and 2D separations, we initiated the development of a peak-pairing algorithm that would combine chromatographic and spectral information to pair chromatographic signals across a number of chromatograms, while simultaneously allowing us to correctly assign isomer species and to distinguish between true peaks and system/background peaks.
A secondary objective of the algorithm involves cases in which the number of detected peaks is vast and/or analytes might be present at trace concentrations. In such a case a successful algorithm may contribute to the discovery of untargeted analytes in the sample. In practice, signals that barely meet the minimum signal-to-noise ratio may easily be (accidentally) excluded by the user. This is not avoided when a peak-detection algorithm is used, because such a tool mathematically treats all signals that meet the criteria similarly and may also detect peaks which are not of interest (e.g., noise peaks). However, a peak-tracking algorithm which compares chromatographic and spectral features of each detected signal can determine the similarity between these signals across chromatograms. Therefore, in the event that apparent noise or a baseline irregularity can be matched with a similar signal in another chromatogram based on similarity between spectral and chromatographic data, the likelihood of the signal representing a real peak rather than an irregularity increases greatly. Thus, through comparison of all peak features across the chromatograms, the algorithm may discover peaks that would be difficult to find manually.
In this paper, we present a novel combination of algorithms to track untargeted and unidentified peaks across LC–MS separations through comparison of chromatographic and spectral information. The algorithm is described in detail, and it is explored how the available data can be used to reduce the number of possible candidates. The performance of the algorithm is tested on two degraded dye mixtures separated by reversed-phase LC (RPLC) and a mixture of metabolites separated by hydrophilic-interaction LC (HILIC). The dye mixtures contain a number of (coeluting) isomer peaks to obtain insight in the robustness of the algorithms in case of coelution and the presence of isomers. The tracked peaks are used to predict retention times for a new method, and the results are compared with experimental values to assess the accuracy.
Theory
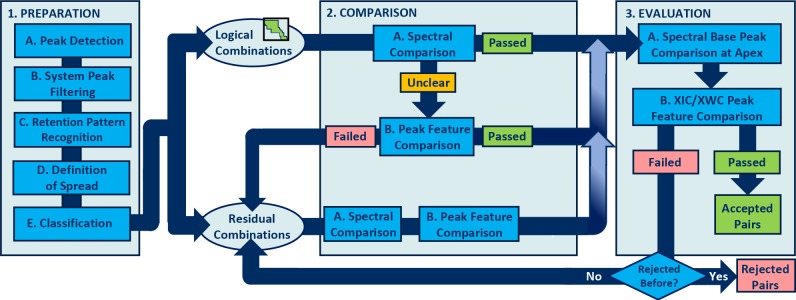
One important aspect of a practical peak-tracking algorithm is efficient use of computational resources. A reasonable balance must be found between the use of computational/time resources and tracking performance. Figure 1 shows a decision flowchart of the overall algorithm. The overall algorithm was composed in several blocks, each targeting different objectives, viz., (1) preparation, (2) comparison, and (3) evaluation. Each block comprises several steps which are denoted with capital characters (A, B, C, etc.) in Figure 1. In this section, the theoretical functionality of each block will be discussed; references to the different steps will be made.
Figure 1.
Scheme depicting the decision flowchart of the peak-tracking algorithm.
Preparation of the Data
The preparation block of the algorithm aims to reliably reduce the number of potential candidates for tracking evaluation. Depending on the sampling frequency a chromatogram of, say, 30 min may easily contain hundreds if not thousands of mathematically identified peaks. Comparing all chromatographic and spectral information on every possible peak pair would require extreme computational power. By excluding system/noise bands (Figure 1, steps 1A/B) and using retention patterns (Figure 1, step 1C) to preselect a logical domain of possible pairs (Figure 1, step 1D), the computational resources required can be significantly reduced.
Peak Detection
The first step (Figure 1, step 1A) is generic peak detection across the chromatogram. The peak-detection algorithm developed by Peters et al. was applied to generate an array of candidate peaks.16 A relatively sensitive detection threshold was typically used in this study, i.e., the maximum observed intensity (Imax) divided by 10 000 (Imax/10 000). This allowed untargeted peaks at very low concentrations to be detected. In cases in which all peaks are of low intensity, such a sensitive setting may generate too many candidates, but this should automatically be corrected in the next step (Figure 1). The above setting worked satisfactory for all examples shown in this publication, but it is one of several overall input parameters that the eventual end-user of the system may tweak.
Filtering of Background Signals
After generating the initial list of candidates, all spurious peaks (i.e., baseline noise or irregularities) must be filtered out (Figure 1, step 1B). The algorithm selects a number of spectrometric information points at minimal intensities across the chromatogram to establish a generic spectrum of the background signal. All spectra are reduced to the most prominent mass (i.e., the intensity of all other masses is set to equal 0). This process is carried out for all chromatograms in which peaks are to be tracked, and the final result is compared. The algorithm defines this as the background signal. Next, all detected peaks of which the spectrum matches the background spectrum are removed from the candidate list. To enhance the accuracy, the background spectrum can easily be extended to include the n most dominant peaks, but no substantial benefit of such an expansion was observed. While, theoretically, all remaining candidates should derive from the sample mixture, there is still a possibility that this is not the case. The existence of erroneous peaks in the remaining pool of candidates does not dramatically affect the algorithm, because they are unlikely to be paired with unique sample components. However, non-sample peaks will increase the number of candidates and thus slow the entire process down.
Reduction of the Number of Candidate Pairs: Recognition of Retention Pattern and Definition of Spread
Having filtered out the background peaks, further reduction of the number of candidate pairs across chromatograms is still required. For example, if both chromatograms contain, say, 30 remaining candidates, then an unbiased algorithm should theoretically assess 900 possible pairs based on both chromatographic and spectral information, which is time-consuming. Indeed, the drain on computational resources may be significantly reduced if the algorithm is equipped with a search function.
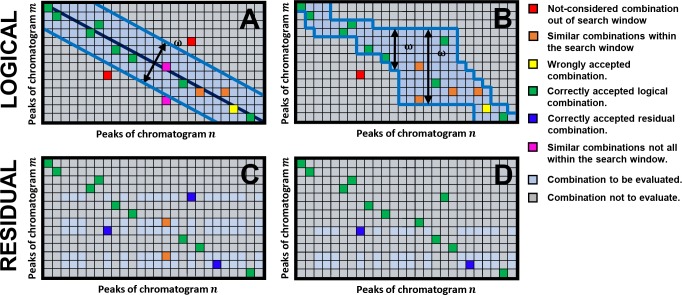
To understand this we regard Figure 2A, which portrays an m-by-n matrix of all possible combinations of peaks for a hypothetical case of two chromatograms. Here, every box represents one possible combination, which—without a search function—would all have to be evaluated. The colored boxes will gradually be introduced in the course of this section. For now we will focus on the size of the search window (highlighted in blue) and how it is established.
Figure 2.
Matrix depicting the selection of logical combinations of peaks between two hypothetical chromatograms m and n, and definition of the required search window (highlighted in blue) using the (A) diagonal and (B) relative retention method. The subsequent residual possible combinations for the evaluation block of the algorithm (Figure 1, block 3) are reflected in panels C and D, respectively. See text for further clarification on the colored boxes.
While the elution order may potentially be altered, it is not likely that the elution order will shift dramatically across two different scanning gradients. Exaggerating, the first-eluting peak in chromatogram m is unlikely to match the last-eluting peak in chromatogram n if only the gradient conditions are changed.
To greatly reduce the number of possible pairs, the algorithm may exclusively evaluate pairs along the diagonal of the matrix within a range, ω; this “diagonal” method is illustrated in Figure 2A. Here, the diagonal represents an identical elution order and the width of the window accounts for shifts in elution order. At this stage, the algorithm will only evaluate combinations within this range and thus ignore combinations depicted as gray boxes. This relatively narrow window can fairly be assumed to allow pairing of a significant fraction of the true peak pairs as is depicted by the green boxes in Figure 2A. Consequently, the remaining possible pairs for later evaluation (Figure 2C, light blue boxes) can also be expected to be small in number, allowing the algorithm to overall swiftly track the residual peaks (Figure 2C, dark blue).
In practice, however, we found the remaining number of detected peaks after preprocessing to be quite variable. The case displayed in Figure 2A assumes that the initially unpaired peaks are spread evenly across the first chromatogram, but in practice this does not have to be true. For example, the red boxes reflect a true combination which fell outside of the search window. Alternative, two peaks in one chromatogram might both be candidates for one peak in the other chromatogram (e.g., resolved isomers) such as depicted by the orange boxes. However, the purple boxes depict a case where one was outside of the window. Consequently, the algorithm might wrongly conclude it found the true peak, requiring more exhaustive computations during the evaluation step to undo this mistake.
The diagonal method described above applies a search
window to
the matrix. It selects boxes on the diagonal plus a number ω
of boxes around it. However, if a candidate peak is nested in a relatively
densely populated area of the chromatogram, more neighbors may be
considered. Therefore, the algorithm was expanded so as to search
for likely mean relative retention times (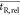 ) between
peaks in two chromatograms (Figure 2B, relative retention
method). Here, the algorithm does not apply a search window to the
matrix, but to the chromatograms (Figure 3).
) between
peaks in two chromatograms (Figure 2B, relative retention
method). Here, the algorithm does not apply a search window to the
matrix, but to the chromatograms (Figure 3).
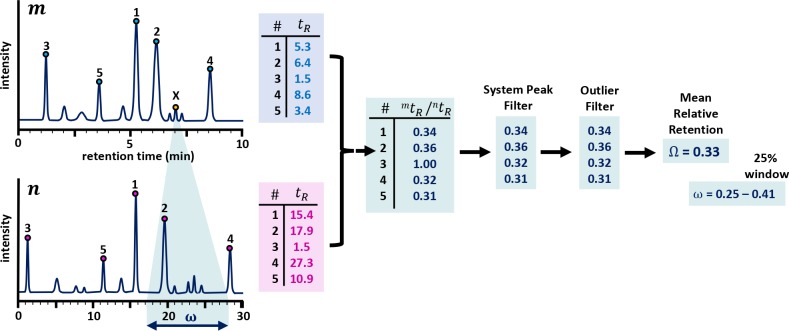
Figure 3.
Example of the determination of the mean relative
retention time
(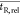 ) between
two chromatograms and the corresponding
search window. By using
) between
two chromatograms and the corresponding
search window. By using 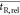 , the algorithm applies the search window
to the chromatogram, and not to the matrix. Consequently, this function
is more robust to variations in peak density in the chromatograms.
Note that the scheme displays a simple hypothetical case for explanatory
purposes.
, the algorithm applies the search window
to the chromatogram, and not to the matrix. Consequently, this function
is more robust to variations in peak density in the chromatograms.
Note that the scheme displays a simple hypothetical case for explanatory
purposes.
To define 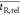 , the
peaks for each chromatogram are ranked
according to intensity and the x most intense peaks
are selected for each, as can be seen in Figure 3. Assuming that these most intense peaks
include likely pairs, the algorithm calculates the relative retention tR,rel for each peak pair. When recording chromatograms
using gradient-scanning techniques, the different gradient slopes
used in the different methods typically result in proportionally different
retention times. As such, tR,rel for retained
peaks is likely to be similar. The algorithm therefore evaluates whether
the element A(i) is greater than
3 times the scaled median absolute derivative (MAD)17 defined as
, the
peaks for each chromatogram are ranked
according to intensity and the x most intense peaks
are selected for each, as can be seen in Figure 3. Assuming that these most intense peaks
include likely pairs, the algorithm calculates the relative retention tR,rel for each peak pair. When recording chromatograms
using gradient-scanning techniques, the different gradient slopes
used in the different methods typically result in proportionally different
retention times. As such, tR,rel for retained
peaks is likely to be similar. The algorithm therefore evaluates whether
the element A(i) is greater than
3 times the scaled median absolute derivative (MAD)17 defined as
| 1 |
where A represents the vector of tR,rel values and s is a scaling factor which equals 1.4826. If the rank order changed due to variation in signal intensity, tR,rel will automatically be recognized as an outlier, unless tR,rel of both pairs is similar (e.g., due to coelution) and tR,rel would be similar and there would be no significant negative effect. Moreover, all pairs are removed that were either unretained or unaffected by the gradient (i.e., system peaks or unretained peaks where tR,rel is close to 1), effectively filtering out everything meeting the criterion of eq 2.
| 2 |
The mean can then be taken of the remaining
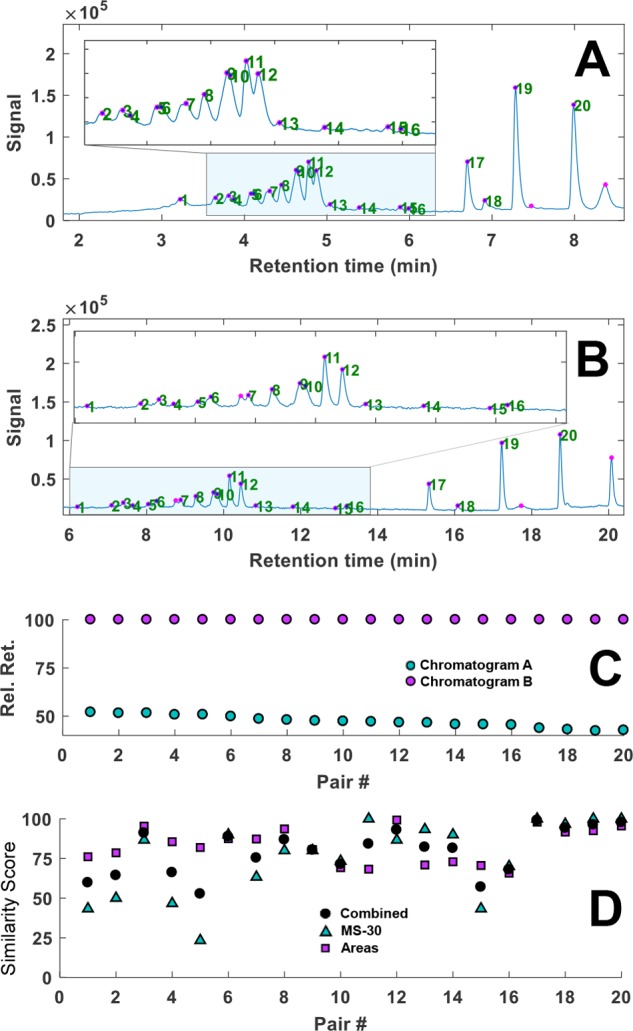
list of relative retention times to obtain 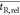 where,
similarly as in the example of Figure 2A, a window of allowed
variation can be set to allow for shifts in retention order. In essence,
the algorithm will only consider a limited number of candidates for
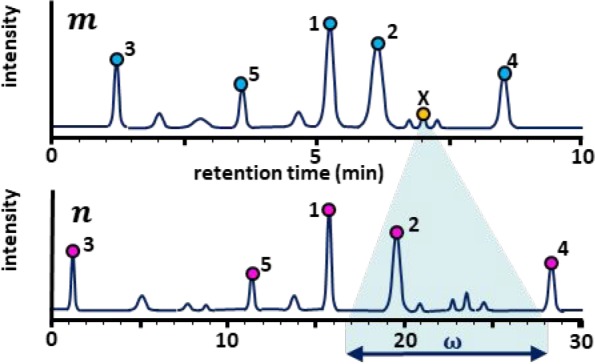
every peak as is reflected in Figure 3 for the peak marked with X. This dynamic approach
is depicted in Figure 2B (see Supporting Information Section S-1 for a real example). In this work, this window was set to 25% (in
both directions). A smaller spread will improve the speed of the algorithm
at the risk of missing pairs.
where,
similarly as in the example of Figure 2A, a window of allowed
variation can be set to allow for shifts in retention order. In essence,
the algorithm will only consider a limited number of candidates for
every peak as is reflected in Figure 3 for the peak marked with X. This dynamic approach
is depicted in Figure 2B (see Supporting Information Section S-1 for a real example). In this work, this window was set to 25% (in
both directions). A smaller spread will improve the speed of the algorithm
at the risk of missing pairs.
Figure 2D displays an example of the effect of this preselection method on the matrix of possible peak-pair combinations in the evaluation block of the algorithm (Figure 1, block 3; to be addressed later). Indeed, for chromatograms recorded using gradient scanning, the likelihood that the correct candidates are paired increases compared to the diagonal approach (Figure 2A).
The ranking step relies on similar peaks appearing in all chromatograms to be paired (i.e., similar or identical analytes) in plausible positions (i.e., by using similar, logically different methods), as is the case for gradient-scanning techniques, where the gradient slope is typically varied and analytes are expected to elute around a proportionally different locations. In case of tracking peaks across chromatograms recorded using different samples, the diagonal method described in Figure 2A can be used. If also the methods used are entirely different [e.g., when searching for orthogonal methods in a comprehensive two-dimensional liquid chromatography (LC × LC) approach], then the entire module of the algorithm described in the Reduction of the Number of Candidate Pairs section must be turned off and the overall speed will be significantly reduced from (less than) 1 min to (several) hours.
Regardless of the route taken, the process detailed in this section will produce a matrix of candidate peak pairs between chromatograms m and n that fall within the search window. This matrix will henceforth be called X.
Comparison
The established array of logical combinations X(m,n) (Figure 1, parts A or B, blue bins) is transferred to the next block of the algorithm, where spectrometric and chromatographic information is compared for each possible pair. In this section, the steps taken to evaluate a possible pair m,n and to determine whether the peaks are likely to represent the same analyte are discussed. This procedure can then be iterated for all pairs in X.
Spectrometric Similarity
Mass spectra offer a wealth of information, which facilitates comparison of two chromatographic peaks m and n. Both m and n contain a mass spectrum, represented by a vector of mass-to-charge ratio (m/z) values i and a vector of intensity values j. To assess the similarity, the algorithm first ranks both m(i,j) and n(i,j) on j, and then extracts the m/z values of the x most intense peaks. In this work, we mainly used x = 30 as it provided a robust performance in combination with our mass spectrometer. Of course, x can be altered to concur with the characteristics of the MS instrument and the ionization method. Next, the ranked vectors mrank and nrank are linearly compared based on the following criteria:
| 3 |
Here, p is the precision of the mass spectrometer (in our case 0.01 Da). If the element m(i) matches element n(i) within the precision limit, the combination is given a score 1. Since xm/z values are compared, the maximum score is x. The relative score is calculated by dividing the score by x and multiplication by 100 to obtain a similarity percentage. We found x = 30 to provide the most robust results and refer to this score as MS-30 (the similarity of the 30 most abundant peaks in mass spectra).
In the event that the relative score exceeds a preset value, in our case 75%, and no additional pair within X(m,:) or X(:,n) exceeds this score [i.e., there are no multiple options for either m(i) or n(i)], then the pair is considered to be likely true.
Chromatographic Peak Similarity
In addition to spectrometric information, there are also chromatographic features which can be considered, such as the statistical moments of a peak. In this study, the zeroth and third moments of peaks m and n were compared (i.e., peak area and vertical asymmetry). The second moment, the variance, was also investigated, but was found to reduce ability of the algorithm to reliably compare two peaks.
While useful, statistical moments rely heavily on the type of mathematical distribution that the peak represents and whether or not the peak is pure. Indeed, an overlapping neighbor can significantly influence the statistical moments. Nevertheless, in case of multiple isomers present in the chromatogram, the mass spectrum will be similar, yet the statistical moments and relative retention time are not necessarily. As a result, it was opted to exclusively assess the statistical moments for logical pairs in the event that the spectroscopic similarity yielded inconclusive results.
In the event that the statistical moments of two peaks are similar, the logical pair is now marked as likely pair and pooled with the likely pairs from the Spectrometric Similarity section. Rejected pairs are pooled with the residual pairs from the Preparation of the Data section.
Evaluation
To evaluate whether a likely pair can be verified and accepted, the algorithm checks a number of scenarios.
Evaluation of Initially Logical Paired Peaks
First, a new but more accurate definition is established of the average relative retention. For all likely pairs from the comparison block, the retention time in chromatogram m, tR,m, is plotted against the ratio of retention times tR,m/tR,n (see Supporting Information Section S-2 for an example). A second-degree polynomial is fitted through the points, which can be used to calculate the likely retention time in chromatogram n, tR,n for any tR,m.
Next, the extracted ion chromatogram (XIC) for the most abundant m/z of the two paired peaks is created. For both chromatograms, the XIC is scanned for local maxima and the retention time of the apex on the total ion-current chromatogram (TIC) is compared with the local maximum found in the XIC. If maxima on the TIC and XIC match, then the algorithm concludes that the most abundant m/z is at its local maximum at the identical location of the likely pair. The algorithm now compares the areas of the XIC peak in chromatograms m and n using a simple trapezoidal numerical integration function. If the similarity of the areas is not satisfactory, the pair is rejected.
One risk associated with the comparison of mass spectra is that a strongly overlapping neighbor peak can significantly influence the mass spectrum of the peak of interest (POI). In the event of partial or complete coelution, a large number of the abundant m/z values will be present in the mass spectrum of the POI and the algorithm may incorrectly conclude that two peaks represent the same analyte when they do not.
The algorithm thus verifies whether the most abundant m/z value of the POI in m matches with that of n. In the event that this is not the case, the XIC is scanned for nearby peaks of the same mass. To avoid incorrect pairing of potentially existing isomers with the POI, the scanning domain is determined by the earlier established relative retention relation with a window of 5% deviation.
Moreover, the XIC for the alternative mass is established for both chromatograms and cross-referenced. If no satisfactory combination is found, the likely pair is rejected. If both m/z values are found in both chromatograms, the clearly coeluting peak is split by the algorithm into two paired peaks. All combinations rejected during the evaluation are now pooled with the residual combinations for further evaluation.
Evaluation of Residual Peaks
Before addressing the further evaluation of residual peaks, it is good to note that all steps taken thus far aimed to significantly reduce the number of combinations for evaluation by the algorithm. More importantly, it should now be evident that, if a combination was incorrectly included within the pool of logical combinations, the evaluation should automatically have corrected this. In any case, the total number of remaining combinations possible should be significantly reduced, as is illustrated in Figure 2D. Here, the gray bins represent combinations that are no longer likely, because one of the two peaks has already been paired with another peak. The white bins represent the remaining possible combinations, all of which will be compared by the algorithm through the procedures explained in the Comparison section and evaluated as explained in the Evaluation of Initially Logical Paired Peaks section.
The residual combinations all go through MS-1 comparison. For each unpaired candidate in chromatogram m, the algorithm scans the XIC for the nearest unpaired peak in chromatogram n, within a range of 10%, or vice versa. If found, the algorithm cross-references its own peak-detection database (Peak Detection section) to see whether the TIC peak was already detected and/or paired. In the event of no conflict, the peaks are paired.
Isomers
In the event that, during the evaluation steps described in the previous section, multiple peaks of the exact identical m/z value are detected/paired, then the algorithm is programmed to treat this as a case of isomers.
In this case, the XIC of the m/z of interest is extracted for both chromatograms, and they are treated as two individual new chromatograms that will be subjected to peak tracking. In essence, this means that all already paired peaks of the same m/z are unpaired and paired again. This is a practical solution in the event that the chromatogram is populated with multiple peaks of the same m/z, in which case the algorithm will struggle to pair partially coeluting isomers.
Evaluation through Retention Curves
One advantage when tracking peaks across chromatograms used for gradient scanning is that the results are immediately used for retention prediction. Typically, the slopes of the two most extreme scanning gradients differ by a factor of 3.10 The retention times of peaks that are manually or algorithmically tracked are combined across chromatograms so that a retention model may be fitted. There are a number of statistical tools to evaluate the ability of the model to describe the data, such as the Akaike information criterion,18 which can be reliably applied if multiple chromatograms are combined simultaneously. Furthermore, logical indicators such as the slope of the obtained retention curve of a compound can also provide evidence as to the likelihood of realistic peak tracking. Supporting Information Section S-6 clarifies how model evaluation can be used to filter wrongly paired peaks.
Experimental Section
Instruments
The LC system used for LC–MS analysis comprised an Agilent 1290 series binary pump (G4220A), an Agilent 1260 Infinity degasser (G1322A), an Agilent Infinity 1290 diode-array detector (DAD, G4212A) equipped with an Agilent Max-Light cartridge cell (G4212-6008, V0 = 1.0 μL), and an Agilent 1100 series autosampler (G1313A). The injection volume was set to 5 μL, and the DAD data (used for manual verification of the automatic pairing results) were recorded at several wavelengths at an acquisition rate of 160 Hz. The system was controlled by OpenLAB CDS Chemstation edition rev. C.01.04 [35] software. For the analysis of the dyes, the flow was split using a stainless-steel tee-connection (P/N U-428, IDEX, Lake Forest, IL, U.S.A.), with a 500 mm × 0.25 mm i.d. tubing to the DAD and 500 mm × 0.12 mm i.d. to the Bruker MicroTOF-Q mass spectrometer (Bruker Daltonik, Bremen, Germany). For the HILIC analyses, 100% of the flow was sent to the MS. The MS was equipped with an electrospray ionization source and configured to run in negative mode at an acquisition rate of 4 Hz. The system was controlled with Compass 1.3 software for MicroTOF-SR1 (MicroTOF control version 3.0, Build 53, Bruker). For the reversed-phase LC studies an Agilent ZORBAX Eclipse Plus C18 Rapid Resolution HT (959941-902, 50 mm × 4.6 mm, 1.8 μm particles, 98 Å pore size) column was used, whereas a Waters Acquity BEH amide (150 mm × 2.1 mm i.d., 1.7 μm particles, 130 Å pore size) column was used for the HILIC study.
Chemicals
Acetonitrile (LC–MS grade) was obtained from Biosolve (Valkenswaard, The Netherlands); deionized water (LiChrosolv, LC–MS grade) was procured from Merck (Darmstadt, Germany). Triethylamine (≥99.5%), dimethyl sulfoxide (DMSO, ≥ 99%), ammonium formate (reagent grade), and formic acid (≥96%) were obtained from Sigma-Aldrich (Darmstadt, Germany). The light-induced, degraded dyestuffs eosine and alizarine were obtained from the reference collection of the Cultural Heritage Agency of The Netherlands (RCE, Amsterdam, The Netherlands).
Analytical Methods
For the dye mixtures, the LC separation was based on our earlier developed fast ion-pair method. A buffer was prepared, containing triethylamine (5 mM) in water with formic acid added to achieve a pH of 3. Mobile phase A consisted of buffer/acetonitrile 95:5 [v/v], and B consisted of buffer/acetonitrile 5:95 [v/v]. The flow rate was 1.85 mL/min. The gradient used was as follows: 0–0.25 min, isocratic at 100% A followed by a min linear gradient to 100% B in 6, 12, or 18 min, maintained at 100% B for 0.5 min, and finally a 0.75 min linear gradient to 100% A. In the above program, the length of the gradient time, tG, was varied to obtain the data needed for gradient scanning. The MS ion source operating conditions were the following: end plate offset −500 V; capillary voltage 3800 V (positive mode −4400 V); nebulizer gas pressure 2.0 bar; drying gas flow 10 L·min–1; source temperature 250 °C. The injection volume was 5 μL.
Data Processing
The entire algorithm was written using MATLAB 2017a (Mathworks, Natick, MA, U.S.A.) for the in-house developed PIOTR program.10 All data were processed using PIOTR. Raw MS data was converted into mzXML format by CompassXport 3.0.13.1 (Bruker Daltonik, Bremen, Germany).
Results and Discussion
Application to Analysis of Alizarin by Ion-Pair Reversed-Phase LC
While the algorithm was tested on a large variety of LC analyses of simple standard mixtures, more challenging samples were required to study the robustness of the algorithm to common practical issues in the separations. The first case presented in this paper is a sample of alizarin in DMSO which was subjected to focused light at 254 nm for 5.5 h. Two chromatograms were recorded using scanning gradients from 100% A to 100% B with a gradient duration (tG) of 6 and 18 min. The TIC chromatograms can be seen in Figure 4, parts A and B, respectively (see Supporting Information Section S-4 for more extensive data). The purple dots reflect the detected peaks that were not excluded due to a lack of peak prominence or being identified as a spurious peak (see Supporting Information Section S-3 for a completely unfiltered chromatogram with all detected peaks). The green numbers depict the coupled peaks.
Figure 4.
(A and B) Gradient-scanning LC–MS TIC chromatograms of light-degraded alizarin using a gradient time of (A) 6 and (B) 18 min. Detected, filtered peaks are depicted with purple markers. The green numbers reflect identified peak pairs. (C) The relative retention times of the matched peak pairs in chromatograms A and B, with the latter set to 100%. (D) Plot of the similarity scores based on statistical moments (■), mass spectra (▲), and the combined score (●) for each peak pair. MS-30 = similarity between the 30 most abundant peaks on the MS spectra (see the Spectrometric Similarity section). The yellow marked peaks are discussed further in the text.
In Figure 4C the relative retention times from the two chromatograms are plotted. The retention times of the first loaded chromatogram are set to 100%, and the retention times of the other chromatogram(s) are plotted relative to this value. In our software we aim to give the end-user the possibility of a complete overview of the data behind the calculations. Thus, significant deviations in Figure 4C can attend the user to a possible (unexpected) shift in elution order, or a wrongly paired set of peaks.
Similarly, Figure 4D displays the different scores that contribute to the overall score per paired set of peaks to allow the end-user to quickly evaluate the pairing performance. The usefulness of the statistical moments becomes apparent for pairs 1 and 2. For these pairs, the constituting chromatographic bands overlap in chromatogram A, which also impacts the MS spectra of these peaks. This is reflected in a poor similarity of the 30 most abundant peaks in both mass spectra (MS-30, see the Spectrometric Similarity section). Computationally, the peaks can still easily be distinguished based on their statistical moments, allowing the algorithm to correctly pair the peaks.
Another issue is illustrated by the missed pair number 16 marked with a yellow dot in Figure 4, parts A and B. These peaks had to be manually paired through the user interface. Their relative retention and similarity scores are marked in yellow in Figure 4, parts C and D. Visually the two peaks are clearly a match; the similarity scores are not optimal, but the MS-30 exceeds the limit of 75%. The algorithm reported that the pair had been accepted initially but rejected as a result of the isomer evaluation (Isomers section).
To detect chromatographic bands of isomers in the XIC, the algorithm applies a simple local-maxima search function. A relatively strict (i.e., high) minimal prominence of the peak is used. This has the advantage that the algorithm will ignore relatively high noise signals at the particular m/z value. However, if the threshold is wrongly chosen, the algorithm may find an unequal number of isomer peaks in the two chromatograms. The latter will result in rejection of the peak. As can be seen in Supporting Information Section S-5, three isomer bands are present in the chromatogram. However, with one of the two gradients these peaks nearly coeluted and the first peak was missed by the local-maxima search. While an adjustment of the minimal prominence would be an obvious solution, the correct threshold for finding the optimal (“true”) number of pairs differs significantly from experiment to experiment.
A third chromatogram was recorded using a gradient time of 12 min, and the retention parameters were obtained for all analytes (see the Evaluation through Retention Curves section). Using the retention parameters, the retention times of the third chromatogram were predicted and compared with the experimental values. As shown in Supporting Information Section S-6, the average prediction error was 0.9%, which is similar to retention-modeling experiments that use manual peak tracking.9,19,20
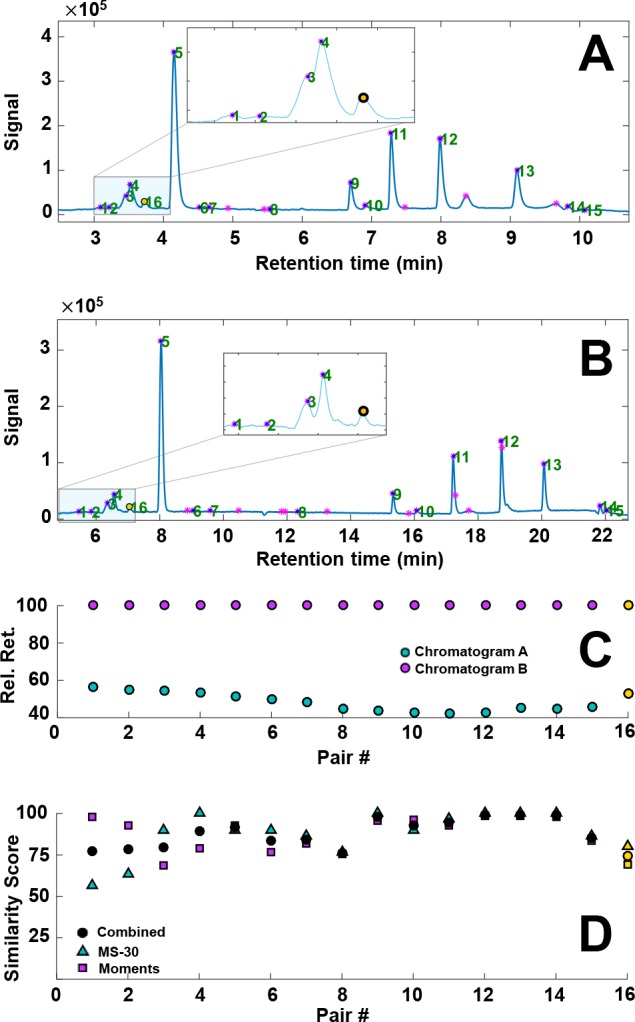
Application to Analysis of Eosin by Ion-Pair Reversed-Phase LC
Similar to alizarin, a sample of eosin dissolved in DMSO was aged by UV light at 254 nm for 5.5 h. The resulting chromatograms, relative retention plot, and similarly scores are shown in Figure 5. The algorithm was generally found to perform well, pairing all visually found peaks. Under the influence of light, eosin can lose up to four bromine atoms (see Supporting Information Section S-9), leading to a number of isomers, which, if coeluting, pose a significant challenge to the algorithm. Supporting Information Section S-7 illustrates a difficult case, which was correctly resolved. However, in some other cases where the chromatographic separation was also poor we observed wrong peak assignments. An example is shown in Supporting Information Section S-8. Similar to alizarin, retention parameters were fitted using the automatically paired peaks and the retention times were predicted for a third chromatogram not used to obtain the retention models. With most (partially coeluting) isomers correctly paired, the overall performance of the algorithm was deemed acceptable with an average prediction error 0.4% (Supporting Information Section S-9).
Figure 5.
(A and B) Gradient-scanning LC–MS TIC chromatograms of light-degraded eosin using gradient times of (A) 6 and (B) 18 min. Detected, filtered peaks are indicated with purple markers; the green numbers reflect identified peak pairs. (C) The relative retention times of the matched peak pairs in chromatograms A and B, with the latter set to 100%. (D) Plot of the similarity scores based on statistical moments (■), mass spectra (▲), and the combined score (●) for each peak pair. MS-30 = similarity between the 30 most abundant peaks on the MS spectra (see the Spectrometric Similarity section).
Conclusions and Outlook
We have developed a peak-tracking algorithm for liquid chromatography coupled with mass spectrometry to track peaks across chromatograms obtained from gradient-scanning techniques and method-optimization tools. The performance of the algorithm was demonstrated using two different samples which included the presence of isomers. The automatically tracked peaks and their consequently fitted retention parameters generally yielded prediction errors of less than 1%. While the algorithm was developed for use with gradient-scanning techniques (i.e., identical sample, different mobile phase composition programs), it can also be applied to chromatograms of different samples, provided that parts of algorithm in the preparation block (Preparation of the Data section), which use the relative retention to limit the number of options so as to enhance the speed, are turned off.
The robustness of the algorithm toward partially coeluting isomers, especially when the separation is not equally good in all of the paired chromatograms, may still be improved. Moreover, we are exploring possibilities or the algorithm to correctly estimate a threshold value, which is representative for the peaks on the chromatogram.
Another expansion is that is currently under investigation involves using the similarity between UV–vis spectra to track peaks. Unlike common reversed-phase behavior, the description of analyte retention in HILIC may necessitate three-parameter retention models, which require more than two scanning chromatograms. A specific goal for the algorithm is thus the ability to be able to track peaks across more than two chromatograms. In its current state, the algorithm supports this, but more testing is required.
Our ultimate goal is for the algorithm to automatically pair peaks across two-dimensional liquid chromatography experiments. Here, the statistical moments of the peak in a second dimension may prove to be of major significance.
Acknowledgments
B.W.J.P. acknowledges the MANIAC project, which is funded by The Netherlands Organisation for Scientific Research (NWO) in the framework of the Programmatic Technology Area PTA-COAST3 of the Fund New Chemical Innovations (project 053.21.113). L.S.R. acknowledges the STAMP project, which is funded under the Horizon 2020—Excellent-Science program of the European Research Council (ERC), project 694151. The sole responsibility of this publication lies with the authors. The European Union is not responsible for any use that may be made of the information contained therein. The authors thank Giacomo Moro for his assistance with obtaining the data on the dye mixtures.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.analchem.8b03929.
Examples of challenging cases for the algorithm with isomers, explanation of the theoretical preselection in more detail, insight in the raw data used for the example cases, and step-by-step explanation of how the peak tracking is used and verified by method-development tools (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Stoll D. R.; Shoykhet K.; Petersson P.; Buckenmaier S. Anal. Chem. 2017, 89 (17), 9260–9267. 10.1021/acs.analchem.7b02046. [DOI] [PubMed] [Google Scholar]
- Pirok B. W. J.; Abdulhussain N.; Aalbers T.; Wouters B.; Peters R. A. H.; Schoenmakers P. J. Anal. Chem. 2017, 89 (17), 9167–9174. 10.1021/acs.analchem.7b01906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gargano A. F. G.; Duffin M.; Navarro P.; Schoenmakers P. J. Anal. Chem. 2016, 88 (3), 1785–1793. 10.1021/acs.analchem.5b04051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pirok B. W. J.; Gargano A. F. G.; Schoenmakers P. J. J. Sep. Sci. 2018, 41 (1), 68–98. 10.1002/jssc.201700863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoll D. R.; Carr P. W. Anal. Chem. 2017, 89 (1), 519–531. 10.1021/acs.analchem.6b03506. [DOI] [PubMed] [Google Scholar]
- Novotná K.; Havliš J.; Havel J. J. Chromatogr. A 2005, 1096 (1–2), 50–57. 10.1016/j.chroma.2005.06.048. [DOI] [PubMed] [Google Scholar]
- Bolanča T.; Cerjan-Stefanović Š.; Regelja M.; Regelja H.; Lončarić S. J. Chromatogr. A 2005, 1085 (1), 74–85. 10.1016/j.chroma.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Dolan J. W.; Lommen D. C.; Snyder L. R. J. Chromatogr. A 1989, 485, 91–112. 10.1016/S0021-9673(01)89134-2. [DOI] [PubMed] [Google Scholar]
- Tyteca E.; Périat A.; Rudaz S.; Desmet G.; Guillarme D. J. Chromatogr. A 2014, 1337, 116–127. 10.1016/j.chroma.2014.02.032. [DOI] [PubMed] [Google Scholar]
- Pirok B. W. J.; Pous-Torres S.; Ortiz-Bolsico C.; Vivó-Truyols G.; Schoenmakers P. J. J. Chromatogr. A 2016, 1450, 29–37. 10.1016/j.chroma.2016.04.061. [DOI] [PubMed] [Google Scholar]
- Barcaru A.; Derks E.; Vivó-Truyols G. Anal. Chim. Acta 2016, 940, 46–55. 10.1016/j.aca.2016.09.001. [DOI] [PubMed] [Google Scholar]
- Molnar I.; Boysen R.; Jekow P. J. Chromatogr. A 1989, 485 (C), 569–579. 10.1016/S0021-9673(01)89163-9. [DOI] [Google Scholar]
- Strasters J. K.; Billiet H. A. H.; de Galan L.; Vandeginste B. G. M. J. Chromatogr. A 1990, 499 (C), 499–522. 10.1016/S0021-9673(00)96996-6. [DOI] [Google Scholar]
- Fredriksson M. J.; Petersson P.; Axelsson B.-O.; Bylund D. J. Chromatogr. A 2010, 1217 (52), 8195–8204. 10.1016/j.chroma.2010.10.083. [DOI] [PubMed] [Google Scholar]
- Fredriksson M. J.; Petersson P.; Axelsson B.-O.; Bylund D. Anal. Chim. Acta 2011, 704 (1–2), 180–188. 10.1016/j.aca.2011.07.047. [DOI] [PubMed] [Google Scholar]
- Peters S.; Vivó-Truyols G.; Marriott P. J.; Schoenmakers P. J. J. Chromatogr. A 2007, 1156 (1-2), 14–24. 10.1016/j.chroma.2006.10.066. [DOI] [PubMed] [Google Scholar]
- Rousseeuw P. J.; Croux C. J. Am. Stat. Assoc. 1993, 88 (424), 1273–1283. 10.1080/01621459.1993.10476408. [DOI] [Google Scholar]
- Akaike H. IEEE Trans. Autom. Control 1974, 19 (6), 716–723. 10.1109/TAC.1974.1100705. [DOI] [Google Scholar]
- Česla P.; Vaňková N.; Křenková J.; Fischer J. J. Chromatogr. A 2016, 1438, 179–188. 10.1016/j.chroma.2016.02.032. [DOI] [PubMed] [Google Scholar]
- Pirok B. W. J.; Molenaar S. R. A.; van Outersterp R. E.; Schoenmakers P. J. J. Chromatogr. A 2017, 1530, 104–111. 10.1016/j.chroma.2017.11.017. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.