Abstract
Background:
Assessing arm and hand function of multiple sclerosis (MS) patients is important as impaired functioning may impact daily activities and reduce quality of life.
Objective:
A short-form of the Arm Function in Multiple Sclerosis Questionnaire (AMSQ), a recently developed patient-reported outcome measure containing 31 items, is developed to allow non-adaptive application.
Methods:
Complete data from 690 patients with MS, recruited via outpatient clinics, a residential center or via a Dutch website aimed at MS patients, were included in the analyses. A graded response model was fit to these data to estimate item response theory (IRT) parameters, which were used to perform post hoc computerized adaptive test (CAT) simulations with a cutoff standard error of measurement (SEM) of 0.32. The optimal test length was determined by the correlation between the static short-form and full-length theta, the mean SEM, and the amount of patients reaching a satisfactory SEM in CAT simulations.
Results and Conclusion:
Based on five selection criteria (i.e. discrimination parameters, total information, times selected in CAT simulations, raw item means, and item content), 10 items were selected for inclusion in the short-form. The score on the final 10-item short-form correlated strongly with the full-length AMSQ and provided reliable ability estimations, indicating its usefulness instrument in research and clinical settings.
Keywords: Arm Function in Multiple Sclerosis Questionnaire, item response model, computerized adaptive testing simulations, multiple sclerosis, psychometrics
Background
Multiple sclerosis (MS) is a progressive disease often resulting in limitations of physical abilities.1,2 One of the most common physical limitations in MS patients relates to arm and hand functioning,3 which may affect daily activities such as washing, dressing, and feeding. Accurate monitoring of arm and hand functioning is important to assess progression of the disease, both in clinical practice and in clinical trials to determine the effectiveness of interventions. Regulatory bodies recommend using patient-reported outcome measures (PROMs),4,5 to include the patient’s perspective. The Arm Function in Multiple Sclerosis Questionnaire (AMSQ) is a 31-item PROM, which has been recently developed and validated to assess limitations in arm and hand functioning in patients with MS.3,6 The AMSQ was developed as a unidimensional MS-specific PROM, by specifically selecting items relevant for patients with MS out of a pool of all available items from existing instruments.
Self-report questionnaires measuring arm/hand function have been developed for other patient groups, such as osteoarthritis,7,8 carpal tunnel syndrome,9 and musculoskeletal conditions.10 However, these instruments are multidimensional, too short to serve as an item bank, include gender-specific items, or do not focus on the specific difficulties faced by MS patients.
The ABILHAND,11 a PRO instrument for measuring manual ability after stroke, has previously demonstrated to perform well in MS,12 although in other studies substantial ceiling effects were observed.13 Reduced measurement precision has been observed for scores further from the center of the scale, which was not improved by adding DASH (disabilities of the arm, shoulder and hand)10 items.14 The ABILHAND items were also not specifically selected for MS and contain items that are not applicable to every patient (i.e. shelling hazelnuts). This supports the further development of the AMSQ as an MS-specific instrument for upper limb function in MS.
The AMSQ was developed using the graded response model (GRM),3 which is a type of item response theory (IRT) model. In IRT models, responses to items in a questionnaire reflect an underlying latent trait. The latent trait levels of respondents are reflected by an ability level theta (θ). In IRT models items can be described by their discrimination (α) and threshold parameters (β). Item discrimination refers to the differentiating ability of an item between low- and high-response categories. The threshold parameters represent the difficulty of a specific response category on an item.
IRT models are used as the basis for computerized adaptive testing (CAT). CAT is a technique that allows a test to limit the items administered to those that are relevant to the patient completing the test. This results in a more efficient theta measurement. CAT simulations of real responses, also known as post hoc CAT simulations, can be used to create short-forms.15–17 In these post hoc CAT simulations, items are continued to be administered to the responses of the patient, until a satisfactory reliable estimate of the theta is reached. This approach allows us to estimate the theta of patients using less items.
The AMSQ was developed as an item bank to be used as a CAT. However, as CAT software will not always be available, a short-form of the AMSQ will facilitate the application of pen and paper or non-adaptive application of the AMSQ. Less items will reduce the burden to patients and completion time of the questionnaire.
This study aims to create a short-form of the AMSQ, using post hoc CAT simulations. The goal is to develop a short-form with fewer items which represents the full-length AMSQ as validly and reliably as possible.
Materials and methods
Data
Anonymous data obtained from 738 Dutch-speaking patients (aged >16 years) with diagnosed definite MS (n = 725) or self-reported MS (n = 13) were used to perform secondary analyses. Patients who completed the 31-item version of the AMSQ3 at the first measurement occasion were included. Information about gender, age, MS duration, and MS type of patients was collected. The majority of patients (n = 590) were recruited via the outpatient clinic at the MS Center of the VU University Medical Center, Amsterdam, the Netherlands, either for regular care or in the context of scientific research. Other patients were recruited via the outpatient clinic at the National MS Center, Melsbroek, Belgium (n = 100); the residential and facility center for physically handicapped, Nieuw Unicum (NU) in Zandvoort, the Netherlands (n = 35); or via a Dutch language website aimed at MS patients (www.msweb.nl) (n = 13). In total, 49 (6.5%) patients had missing responses. As the percentage of patients with missing responses was relatively small, we decided to perform a complete case analysis (n = 690).
Measurements
The AMSQ contains 31 daily activities that require arm and/or hand movement to perform. Patients rate to what extent MS has limited their ability to perform these activities in the past 2 weeks, ranging from 1 (not at all) to 6 (unable to perform this activity). The total sum score ranged from 31 to 186.
Statistical analyses
To create the short-form, we performed a nine-step procedure of real-data post hoc CAT simulations using 10-fold cross-validation18 (see Table 1, adapted from Yu et al.16). These steps can be translated into two main procedures: fitting a GRM model to the data to calibrate the IRT parameters and performing post hoc CAT simulations. These analyses were performed in R.19
Table 1.
Procedure of real-data post hoc CAT simulations in nine steps.
| 1. Check IRT assumptions on the full sample. |
| 2. Randomly divide the data into 10 subsets. |
| 3. Fit a graded response model to the data of all but the current subset and extract the estimated IRT parameters. |
| 4. Use the IRT parameters from step 3 to calculate a full-length estimated theta (θ) of the patients in the current subset using maximum likelihood estimation. |
| 5. Perform CAT simulations based on each patients estimated θ to estimate the θ adaptively, based on the item responses from the patients in the current subset. |
| 6. Compare the adaptively estimated θ with the full-length θ estimates in the current subset. |
| 7. Select optimal test length which results in the greatest similarity and accuracy between the CAT-estimated θ and full-length θ while using a minimum number of items. |
| 8. Repeat steps 2–7 for each subset until all patients have been used in CAT simulations and combine/average the results. |
| 9. Select items based on the selection criteria: discrimination parameters, total information, times selected in CAT simulation, and raw mean. |
CAT: computerized adaptive test; IRT: item response theory.
IRT parameters’ calibration
The underlying assumptions (step 1) for fitting a GRM model are unidimensionality, local independence, and monotonicity.20 A unidimensional questionnaire represents only one latent trait, theta (θ). Unidimensionality was assessed using exploratory principal component analysis (PCA) and confirmatory factor analysis (CFA). A questionnaire is considered unidimensional if the first component explains at least 20% of the variance and if the ratio variability explained between the first and second factor is larger than four.21 In addition, the model fit was assessed by a CFA, using comparative fit index (CFI), the root mean square error of approximation (RMSEA), and the standardized root mean square residual (SRMR). A good fit is indicated by a CFI value >0.95, a SRMR value <0.05 and a RMSEA value <0.05.22 Local independence refers to the assumption that a patient’s responses to the items are not statistically related to each other. Local independence was investigated by inspecting the residual correlations. An item was considered as being local dependent when the residual correlation was >0.20. If an item pair displays local dependence, one could decide to delete one of the items. The monotonicity of items represents the rule that higher answer categories should represent a higher level on the latent trait θ. This can be assessed using Mokken scaling.23 To satisfy monotonicity, all H item values should be >0.30 and the entire scale H should be >0.50.
After the assumptions were satisfied, the data were divided randomly into 10 subsets for cross-validation (step 2). To calibrate the IRT parameters, a GRM model was fit to all data but the current subset, using expectation–maximization algorithm (step 3). This was performed using R’s mirt package.24 The IRT parameters were extracted and the full-length θ of the patients in the current subset was calculated using these IRT parameters and their responses (step 4).
Item reduction using CAT simulations
Post hoc CAT simulations were performed using FirestaR.25 These simulations are done on the remaining subset that was not used in calibrating the IRT parameters (steps 5 and 6). CAT simulations were performed with the maximum posterior weighted information selection criterion and expected a posteriori theta estimator.26 The initial item administered was selected based on the maximum information of the item at the given θ mean of each subset. The optimal length of the short-form was assessed by performing CAT simulations for different lengths of the questionnaire (step 7). The results of these CAT simulations were evaluated using three different methods: the correlation between the CAT-estimated thetas and the full-length thetas, the average standard error of measurement (SEM), and the number of patients that did not reach a satisfactory SEM. In IRT, the SEM represents the reliability of a test for each individual patient. The average SEM indicates the overall reliability of the test. An SEM value of 0.32 can be seen as a reliability of 0.90.27 Once every subset has been used in a simulation, the results of the IRT calibration can be summed and averaged over the 10 subsets (step 8). The advantage of this method is that the results do not depend on one full-sample calibration of the IRT parameters. The patients from the subset that is not used for calibration are considered to be “new patients” to the model, which makes the results of the CAT simulations more reliable. IRT parameters were averaged across subsets. CAT simulation results were either averaged, for item information, average SEM value, and θ correlations, or summed, for times selected in CAT and amount of patients with a SEM >0.32.
Item selection following the CAT simulations (step 9) was based on the following five criteria:17 raw item mean, discrimination parameter, percentage of times selected in CAT, expected item information under a standard normal distribution, and content of the item. Based on these criteria, items were rank-ordered to be able to select the best-performing items. Starting with the discrimination parameter, the best-performing items were selected, taking the broad spectrum of the questionnaire into account by balancing the difficulty (raw mean) of items. Once the best-performing items had been selected, an expert in the field of MS (B.M.J.U.) judged the relevance of the item content of selected items. This resulted in some items being removed or added to the short-form.
Short-form characteristics
To assess the validity of the short-form, the estimated thetas of the full-length AMSQ and the short-form AMSQ were correlated with each other as well as the full-length and short-form sum scores. A strong correlation (>0.70) would indicate a good criterion validity of the short-form. The SEM was calculated and plotted for a sequence of both full-length and short-form theta estimates to compare the range of reliably measured (SEM < 0.32) theta estimates. In addition, the internal consistency of the scale was assessed using Cronbach’s alpha.
Results
Sample characteristics
The sample characteristics can be observed in Table 2. The mean sum score of the AMSQ was 61.4 (standard deviation (SD) = 37.3) and the median was 46.00 (range 31–186). Item means and SDs can be observed in Table 3.
Table 2.
Patient characteristics (n = 690).
| Age (in years) (n = 680) | |
| Mean (SD) | 50.04 (11.96) |
| Min–max | 16–81 |
| MS duration (in years) (n = 652) | |
| Mean (SD) | 14.37 (8.03) |
| Min–max | 0–62 |
| Type of MS (%) (n = 620) | |
| RR | 57.7 |
| SP | 24.4 |
| PP | 12.6 |
| CIS | 0.3 |
| PR | 0.2 |
| Unknown | 4.8 |
| Gender (%) (n = 675) | |
| Male | 36.6 |
| Female | 63.4 |
SD: standard deviation; min: minimum; max: maximum; n: amount of patients; MS: multiple sclerosis; RR: relapsing-remitting; SP: secondary-progressive; PP: primary-progressive; CIS: clinically isolated syndrome; PR: progressive-relapsing.
Table 3.
Means, standard deviations, and estimated item parameters of the AMSQ.
| Item | M | SD | Item parameters |
|||||
|---|---|---|---|---|---|---|---|---|
| α | β1 | β2 | β3 | β4 | β5 | |||
| 1. “Write down a short sentence with a pen” | 2.10 | 1.48 | 2.79 | 0.09 | 0.67 | 0.99 | 1.50 | 2.04 |
| 2. “Grasp small objects, for example, a key or ballpoint pen” | 2.00 | 1.25 | 3.28 | −0.01 | 0.62 | 1.16 | 1.82 | 2.63 |
| 3. “Put on a coat” | 1.83 | 1.35 | 4.22 | 0.34 | 0.82 | 1.23 | 1.57 | 1.82 |
| 4. “Tie shoelaces” | 2.25 | 1.73 | 4.54 | 0.11 | 0.55 | 0.87 | 1.12 | 1.29 |
| 5. “Hold a full plate” | 2.24 | 1.61 | 4.08 | −0.01 | 0.50 | 0.90 | 1.22 | 1.47 |
| 6. “Pour from a bottle into a glass” | 2.11 | 1.49 | 4.40 | 0.05 | 0.58 | 1.01 | 1.35 | 1.68 |
| 7: “Turn the pages of a book” | 1.86 | 1.27 | 3.75 | 0.20 | 0.81 | 1.26 | 1.65 | 2.20 |
| 8. “Use a mouse of a computer” | 1.73 | 1.25 | 3.10 | 0.39 | 1.04 | 1.53 | 1.73 | 2.09 |
| 9. “Use a pen or pencil” | 2.02 | 1.43 | 3.74 | 0.11 | 0.69 | 1.11 | 1.48 | 1.84 |
| 10. “Turn a key in a lock” | 1.87 | 1.31 | 4.03 | 0.22 | 0.83 | 1.23 | 1.67 | 1.89 |
| 11. “Cut off a piece of paper with a pair of scissors” | 1.89 | 1.39 | 5.05 | 0.27 | 0.78 | 1.16 | 1.50 | 1.81 |
| 12. “Fasten a seatbelt in a car” | 1.74 | 1.28 | 4.56 | 0.40 | 0.92 | 1.28 | 1.61 | 1.97 |
| 13. “Fasten buttons” | 2.49 | 1.63 | 4.29 | −0.29 | 0.33 | 0.72 | 1.05 | 1.47 |
| 14. “Open a bottle of soft drink” | 2.23 | 1.54 | 3.01 | −0.10 | 0.57 | 0.97 | 1.35 | 1.70 |
| 15. “Take off a sweater or T-shirt” | 1.74 | 1.23 | 4.14 | 0.35 | 0.91 | 1.40 | 1.70 | 2.01 |
| 16. “Pick up coins from a table” | 2.08 | 1.35 | 3.97 | −0.08 | 0.61 | 1.05 | 1.53 | 2.03 |
| 17. “Use a keyboard” | 1.81 | 1.24 | 3.77 | 0.24 | 0.87 | 1.36 | 1.78 | 2.08 |
| 18. “Zip up a coat” | 1.95 | 1.37 | 5.07 | 0.14 | 0.75 | 1.11 | 1.49 | 1.80 |
| 19. “Carry a shopping bag” | 2.50 | 1.71 | 2.67 | −0.24 | 0.40 | 0.80 | 1.14 | 1.46 |
| 20. “Wash your hands” | 1.48 | 1.08 | 4.52 | 0.76 | 1.18 | 1.53 | 1.86 | 2.20 |
| 21. “Cut something with a knife” | 2.05 | 1.52 | 5.01 | 0.18 | 0.64 | 0.99 | 1.32 | 1.62 |
| 22. “Pierce food with a fork” | 1.70 | 1.16 | 4.38 | 0.38 | 0.97 | 1.40 | 1.81 | 2.20 |
| 23. “Dry off your body” | 1.81 | 1.28 | 3.79 | 0.30 | 0.87 | 1.32 | 1.70 | 2.02 |
| 24. “Open a bottle with a screw cap” | 2.30 | 1.54 | ||||||
| 25. “Unbutton your shirt” | 2.31 | 1.56 | 4.35 | −0.15 | 0.44 | 0.83 | 1.23 | 1.62 |
| 26. “Wash the back of your shoulder” | 2.22 | 1.65 | 3.07 | 0.05 | 0.59 | 0.96 | 1.25 | 1.49 |
| 27. “Wash your hair” | 1.89 | 1.51 | 3.67 | 0.37 | 0.89 | 1.14 | 1.37 | 1.62 |
| 28. “Open a bag of crisps” | 1.96 | 1.44 | 3.97 | 0.21 | 0.74 | 1.15 | 1.46 | 1.78 |
| 29. “Bring a full glass or cup to your mouth” | 1.75 | 1.30 | 3.82 | 0.37 | 1.02 | 1.39 | 1.60 | 1.88 |
| 30. “Put toothpaste on a toothbrush” | 1.69 | 1.27 | 4.64 | 0.47 | 1.01 | 1.35 | 1.62 | 1.80 |
| 31. “Tuck a T-shirt/shirt in the back of your trousers using your hand” | 1.84 | 1.39 | 4.45 | 0.36 | 0.85 | 1.17 | 1.50 | 1.80 |
n = 690; M: mean; SD: standard deviation; AMSQ: Arm Function in Multiple Sclerosis Questionnaire.
Missing values have been listwise deleted; α; discrimination parameter, β1–5; threshold parameters.
IRT calibration
Before fitting a GRM model to the AMSQ data, the IRT assumptions were assessed. Unidimensionality was satisfied, as the first component of the PCA explained 73.1% of the variance and the ratio between the amount of variance explained by the first and second component was 22.4. Results of the fit indices also demonstrated a unidimensional scale (RMSEA = 0.076, standardized root mean square residual (SRMR) = 0.036, CFI = 0.970). Local independence was satisfied as no item pairs showed residual correlations >0.20. Although no item was local dependent, two item pairs were considered as outliers, warranting further investigation of the item content, residual correlations, and item parameters. The first item pair considered for removal was the pair “Open a bottle with a screw cap (24)” and “Open a bottle of soft drink (14).” These items had a residual correlation of 0.13, similar item content, discrimination parameters, and thresholds. For this item pair, the item with the lowest discrimination parameter was chosen to be removed from further analysis. The second pair considered for removal was the item pair “Write down a short sentence with a pen (1)” and “Use a pen or pencil (9).” This pair had a residual correlation of 0.11, similar item content, and threshold parameters. However, these items described different lengths of the same activity, which lead to both items being kept in the analyses. Monotonicity was satisfied as all item H values were >0.30 and the scale H value was 0.76.
After dividing the data into 10 subsets, the GRM model with the remaining 30 items was fit to these subsets to calibrate the IRT parameters. These IRT parameters were averaged across the 10 subsets and can be observed in Table 3.
To determine the optimal test length of the short-form, several test lengths were assessed using CAT simulation.
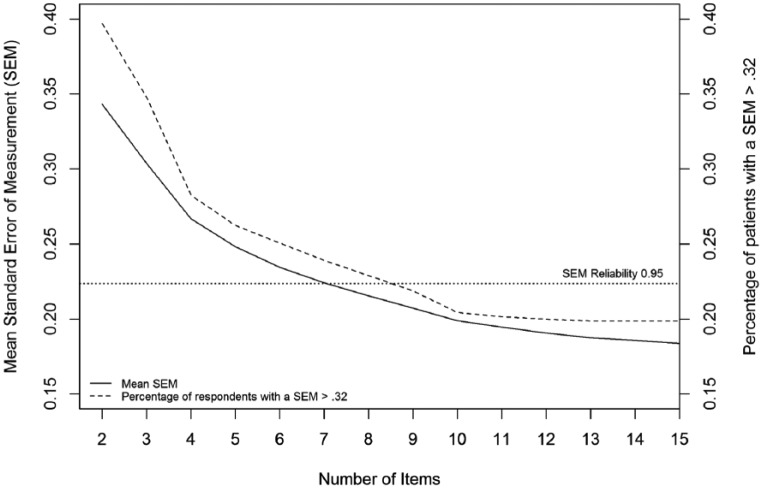
Figure 1 displays the correlation between the short-form and full-length theta of all patients for different test lengths. This correlation has a steep rise until a test length of 10, after which the strength of the correlation levels out. Figure 2 displays the average SEM and shows a steep decline in the average SEM from 1 item to 4 items, which continues decreasing but does decrease less between 4 and 10 items. The proportion of patients who had an SEM value >0.32 are also displayed in Figure 2, showing a large proportion of the patients not reaching a satisfactory SEM value. However, inspecting the full-length SEM values shows that even when using the full-length test, 130 (18.8%) patients did not reach an SEM value <0.32. This is due to the skewness of the data and floor effects of the questionnaire. The amount of patients that did not reach a satisfactory SEM value levels out at around 10 items. Based on the results, 10 items seems to be the optimal choice for test length. Making the test any longer will result in negligible changes in SEM values and theta correlations, while making it shorter will result in less reliable measurements.
Figure 1.
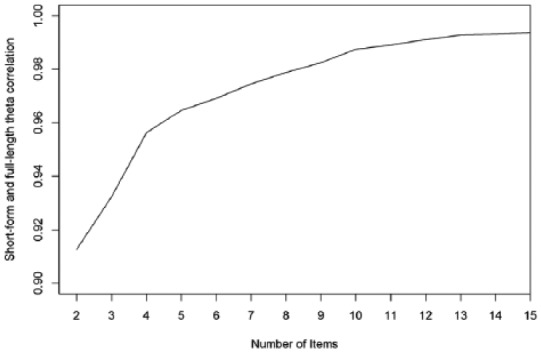
Number of items plotted against the correlation between short-form and full-length theta.
Figure 2.
Number of items plotted against the average SEM value and proportion of patients with an SEM value >0.32 for different number of items used to calculate theta.
Item selection
A total of 10 items were selected for the short-form after applying the five criteria (step 9; see Table 4). The item “Fasten a seatbelt in a car (12)” was not selected in the short-form based on the content of the item. We considered the activity too complex as it can be performed with different hands as well as two-handed, which leaves it open for too much interpretation by the patient. The item “Tuck a T-shirt/shirt in the back of your trousers using your hand (31)” had a high discrimination parameter but was not selected as it was one of the least selected items in the CAT simulations, while other items with similar means were selected more often. The item “Pierce food with a fork (22)” was not selected as the item demonstrated similar characteristics at the same location as items 20 and 30. Due to the similarity of the item content of “Unbutton your shirt (22)” and “Fasten buttons (13),” we decided to keep “Fasten buttons (13),” based on item content. This item may cause less confusion than “Unbutton your shirt (22),” as patients may not use buttoned shirts anymore, for example, due to advanced MS. The final two items included in the short-form were “Hold a full plate (5),” which was added as it requires a patient to carry a heavy object, which was not yet present in the short-form, and “Pick up coins from a table (16),” which is an activity that requires specific precise movement, which was not yet present in the short-form.
Table 4.
Short-form item selection procedure ordered by discrimination parameter.
| Item | α | TI | TS (%) | Raw μ | Rank α | Rank TI | Rank TS | Rank μ |
|---|---|---|---|---|---|---|---|---|
| 18. “Zip up a coat” | 5.07 | 368.41 | 11.97 | 1.95 | 1 | 1 | 1 | 15 |
| 11. “Cut off a piece of paper with a pair of scissors” | 5.05 | 360.02 | 3.55 | 1.89 | 2 | 2 | 6 | 17 |
| 21. “Cut something with a knife” | 5.01 | 349.51 | 2.59 | 2.05 | 3 | 3 | 19 | 11 |
| 30. “Put toothpaste on a toothbrush” | 4.64 | 290.45 | 2.44 | 1.69 | 4 | 12 | 30 | 29 |
| 12. “Fasten a seatbelt in a car” | 4.56 | 316.01 | 2.48 | 1.74 | 5 | 5 | 28 | 25 |
| 4. “Tie shoelaces” | 4.54 | 269.01 | 2.57 | 2.25 | 6 | 15 | 20 | 4 |
| 20. “Wash your hands” | 4.52 | 301.58 | 2.93 | 1.48 | 7 | 8 | 11 | 30 |
| 31. “Tuck a T-shirt/shirt in the back of your trousers using your hand” | 4.45 | 293.10 | 2.48 | 1.84 | 8 | 10 | 29 | 20 |
| 6. “Pour from a bottle into a glass” | 4.40 | 304.59 | 2.61 | 2.11 | 9 | 7 | 15 | 8 |
| 22. “Pierce food with a fork” | 4.38 | 316.46 | 2.61 | 1.70 | 10 | 4 | 17 | 28 |
| 25. “Unbutton your shirt” | 4.35 | 309.79 | 4.75 | 2.31 | 11 | 6 | 3 | 3 |
| 13. “Fasten buttons” | 4.29 | 300.92 | 7.12 | 2.49 | 12 | 9 | 2 | 2 |
| 3. “Put on a coat” | 4.22 | 273.77 | 2.50 | 1.83 | 13 | 14 | 25 | 21 |
| 15. “Take off a sweater or T-shirt” | 4.14 | 278.23 | 2.50 | 1.74 | 14 | 13 | 26 | 26 |
| 5. “Hold a full plate” | 4.08 | 260.20 | 2.99 | 2.24 | 15 | 18 | 10 | 5 |
| 10. “Turn a key in a lock” | 4.03 | 265.37 | 2.57 | 1.87 | 16 | 16 | 21 | 18 |
| 28. “Open a bag of crisps” | 3.97 | 257.50 | 2.57 | 1.96 | 17 | 19 | 22 | 14 |
| 16. “Pick up coins from a table” | 3.97 | 291.61 | 3.36 | 2.08 | 18 | 11 | 8 | 10 |
| 29. “Bring a full glass or cup to your mouth” | 3.82 | 230.89 | 2.52 | 1.75 | 19 | 24 | 24 | 24 |
| 23. “Dry off your body” | 3.79 | 251.39 | 2.52 | 1.81 | 20 | 21 | 23 | 23 |
| 17. “Use a keyboard” | 3.77 | 254.53 | 2.59 | 1.81 | 21 | 20 | 18 | 22 |
| 7. “Turn the pages of a book” | 3.75 | 264.57 | 2.65 | 1.86 | 22 | 17 | 13 | 19 |
| 9. “Use a pen or pencil” | 3.74 | 248.13 | 2.63 | 2.02 | 23 | 22 | 14 | 12 |
| 27. “Wash your hair” | 3.67 | 201.09 | 2.50 | 1.89 | 24 | 25 | 27 | 16 |
| 2. “Grasp small objects, for example a key or ballpoint pen” | 3.28 | 244.27 | 3.42 | 2.00 | 25 | 23 | 7 | 13 |
| 8. “Use a mouse of a computer” | 3.10 | 181.11 | 2.61 | 1.73 | 26 | 26 | 16 | 27 |
| 26. “Wash the back of your shoulder” | 3.07 | 166.54 | 3.03 | 2.22 | 27 | 29 | 9 | 7 |
| 14. “Open a bottle of soft drink” | 3.01 | 181.02 | 3.59 | 2.23 | 28 | 27 | 5 | 6 |
| 1. “Write down a short sentence with a pen” | 2.79 | 169.72 | 2.89 | 2.10 | 29 | 28 | 12 | 9 |
| 19. “Carry a shopping bag” | 2.67 | 146.59 | 4.42 | 2.50 | 30 | 30 | 4 | 1 |
α: discrimination parameter; TI: total information under normal distribution; TS: time selected in CAT simulations; μ: mean. Items in bold were included in the Arm Function in Multiple Sclerosis Questionnaire-Short Form (AMSQ-SF).
Short-form characteristics
The short-form scale displayed strong internal consistency (Cronbach’s α = 0.97). A GRM model was fit on the 10 selected items. The estimated theta values of the Arm Function in Multiple Sclerosis Questionnaire-short form (AMSQ-SF) were correlated with their full-length counterparts, displaying a correlation of 0.97. The sum scores of the short-form were also correlated with the full-length sum scores (r = 0.99). The short-form total information curve can be observed in Figure 3. The short-form offers information among the same broad spectrum as the full-length AMSQ.
Figure 3.
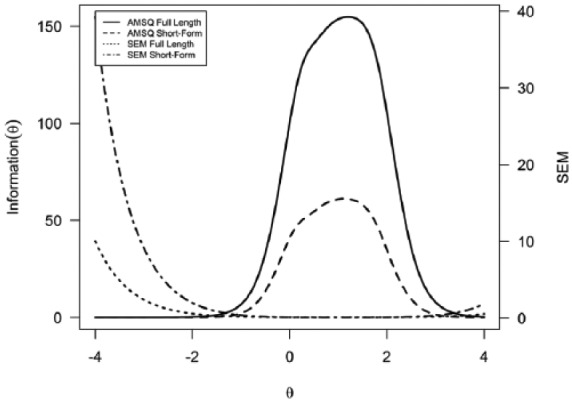
Test information curves and standard error of mea-surement for the AMSQ full item bank and AMSQ short-form.
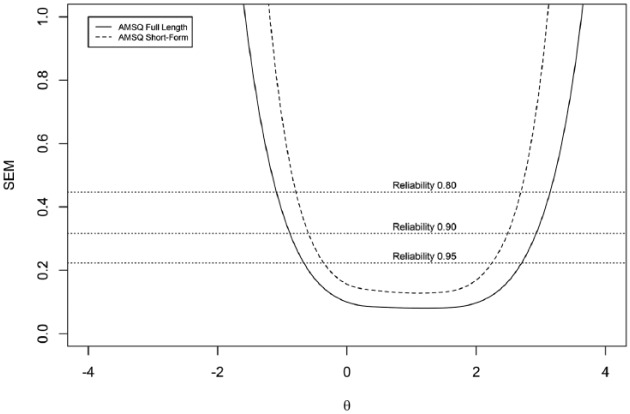
Figure 4 shows the SEM values across a range of theta values for the full-length and short-form AMSQ. It can be observed that the short-form measures the ability of patients reliably across nearly the same range of theta as the full-length item bank.
Figure 4.
SEM values for the full-length and short-form AMSQ.
Discussion
We developed the AMSQ-SF using IRT analyses and CAT simulations. The 10-item AMSQ-SF adequately represents the full-length AMSQ in a clinical MS sample. The AMSQ-SF reliably measured theta values across a similar range as the full-length item bank. In addition, the AMSQ-SF had strong correlations with the full-length AMSQ for both the theta values and the sum scores. These results provide support for the reliability and validity of the created short-form.
In 2014, a systematic review was conducted on upper limb function measurement instruments in MS, including PROMs.28,29 The ABILHAND and the MAM-36 were considered the most suitable PROMs to use.29
The item selection procedure in this study was similar to the development of the ABILHAND/MAM-16, as both these instruments applied IRT models.8,30 The ABILHAND/MAM-16 were developed using a Rasch model, where only difficulty parameters are used. For item selection of the AMSQ-SF, we applied a GRM to take the discriminatory power of items into account. This results in items that provide stronger discrimination between response categories, which means less items are required to provide reliable estimates.17 In addition, we performed post hoc CAT simulations to assess which items would be chosen most often in a CAT if it had the same length as a short-form. The final item selection for the AMSQ-SF was based on the combination of five selection criteria: item means, discrimination parameters, times selected in post hoc CAT simulation, total information, and item content. These additions resulted in an improved item selection procedure.17 It is important to take the skewness of the responses into consideration when looking at the theta estimate correlations as well as the sum score correlations, as people who always answered the lowest response category on all questions will also do this in the short-form and post hoc CAT simulations. If the sample only consisted of MS patients with (severe) arm or hand function problems, the correlations could be lower. This floor effect, however, had little to no impact on the final item selection.
The AMSQ was initially developed to be used as a CAT.3 The post hoc CAT simulations performed in this study indicate that a CAT could outperform a short-form as fewer items would be required to give a reliable estimate of a patient’s theta. Currently, the full-length AMSQ and the 10-item short-form are available for use with sum scores.
In summary, the results indicate that the AMSQ-SF provides an efficient way to measure arm and hand function in MS patients. The short-form provides reliable estimates of arm and hand functioning across a comparable range of ability as the full-length item bank. The AMSQ-SF is a promising assessment tool that could be implemented as outcome measure in research and clinical settings.
Footnotes
Declaration of Conflicting Interests: The author(s) declared the following potential conflicts of interest with respect to the research, authorship, and/or publication of this article: M.D., B.M.J.U., and L.B.M. were the developers of the AMSQ. The AMSQ and AMSQ-SF are available for use by researchers. Please contact bmj.uitdehaag@vumc.nl.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
Contributor Information
Michiel AJ Luijten, Amsterdam UMC, Amsterdam Public Health Research Institute and Department of Epidemiology and Biostatistics, VU University Medical Center, Amsterdam, The Netherlands.
Iris Eekhout, Amsterdam UMC, Amsterdam Public Health Research Institute and Department of Epidemiology and Biostatistics, VU University Medical Center, Amsterdam, The Netherlands/Netherlands Organisation for Applied Scientific Research (TNO), Leiden, The Netherlands.
Marie D’Hooghe, National MS Center Melsbroek, Melsbroek, Belgium/Center for Neurosciences and Faculty of Medicine and Pharmacy, Vrije Universiteit Brussel (VUB), Brussel, Belgium.
Bernard MJ Uitdehaag, Amsterdam UMC, Department of Neurology, VU University Medical Center, Amsterdam, The Netherlands.
Lidwine B Mokkink, Amsterdam UMC, Amsterdam Public Health Research Institute and Department of Epidemiology and Biostatistics, VU University Medical Center, Amsterdam, The Netherlands.
References
- 1. Klevan G, Jacobsen CO, Aarseth JH, et al. Health related quality of life in patients recently diagnosed with multiple sclerosis. Acta Neurol Scand 2014; 129(1): 21–26. [DOI] [PubMed] [Google Scholar]
- 2. Johansson S, Ytterberg C, Claesson IM, et al. High concurrent presence of disability in multiple sclerosis. Associations with perceived health. J Neurol 2007; 254: 767–773. [DOI] [PubMed] [Google Scholar]
- 3. Mokkink LB, Knol DL, van der Linden FH, et al. The Arm Function in Multiple Sclerosis Questionnaire (AMSQ): Development and validation of a new tool using IRT methods. Disabil Rehabil 2015; 37(26): 2445–2451. [DOI] [PubMed] [Google Scholar]
- 4. European Medicines Agency. Reflection paper on the regulatory guidance for the use of health-related quality of life (HRQL) measures in the evaluation of medical products, 2009, http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003637.pdf
- 5. US Department of Health and Human Services, Food and Drug Administration (FDA), Center for Drug Evaluation and Research(CDER), Center for Biologics Evaluation and Research (CBER), and Center for Devices and Radiological Health (CDRH). Guidance for Industry patient-reported outcome measures: Use in medical product development to support labeling claims, 2009, https://www.fda.gov/downloads/drugs/guidances/ucm193282.pdf
- 6. Van Leeuwen LM, Mokkink LB, Kamm CP, et al. Measurement properties of the Arm Function in Multiple Sclerosis Questionnaire (AMSQ): A study based on classical test theory. Disabil Rehabil 2017; 39(20): 2097–2104. [DOI] [PubMed] [Google Scholar]
- 7. Bellamy N, Campbell J, Haraoui B, et al. Clinimetric properties of the AUSCAN Osteoarthritis Hand Index: An evaluation of reliability, validity and responsiveness. Osteoarthritis Cartilage 2002; 10: 863–869. [DOI] [PubMed] [Google Scholar]
- 8. Bellamy N, Campbell J, Haraoui B, et al. Dimensionality and clinical importance of pain and disability in hand osteoarthritis: Development of the Australian/Canadian (AUSCAN) Osteoarthritis Hand Index. Osteoarthritis Cartilage 2002; 10: 855–862. [DOI] [PubMed] [Google Scholar]
- 9. Levine DW, Simmons BP, Koris MJ, et al. A self-administered questionnaire for the assessment of severity of symptoms and functional status in carpal tunnel syndrome. J Bone Joint Surg Am 1993; 75: 1585–1592. [DOI] [PubMed] [Google Scholar]
- 10. Hudak PL, Amadio PC, Bombardier C. Development of an upper extremity outcome measure: The DASH (disabilities of the arm, shoulder and hand) [corrected]. The Upper Extremity Collaborative Group (UECG). Am J Ind Med 1996; 29: 602–608. [DOI] [PubMed] [Google Scholar]
- 11. Penta M, Thonnard JL, Tesio L. ABILHAND: A Rasch-built measure of manual ability. Arch Phys Med Rehabil 1998; 79: 1038–1042. [DOI] [PubMed] [Google Scholar]
- 12. Barrett LE, Cano SJ, Zajicek JP, et al. Can the ABILHAND handle manual ability in MS? Mult Scler 2013; 19(6): 806–815. [DOI] [PubMed] [Google Scholar]
- 13. Marrie RA, Cutter GR, Tyry T, et al. Upper limb impairment is associated with use of assistive devices and unemployment in multiple sclerosis. Mult Scler Relat Disord 2017; 13: 87–92. [DOI] [PubMed] [Google Scholar]
- 14. Barrett LE, Cano SJ, Zajicek JP, et al. Lending a hand: Can DASH items help ABILHAND improve manual ability measurement in multiple sclerosis? Mult Scler 2015; 21(5): 612–621. [DOI] [PubMed] [Google Scholar]
- 15. Roalf DR, Moore TM, Wolk DA, et al. Defining and validating a short-form Montreal Cognitive Assessment (s-MoCA) for use in neurodegenerative disease. J Neurol Neurosurg Psychiatry 2016; 87(12): 1303–1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Yu L, Buysse DJ, Germain A, et al. Development of short-forms from the PROMISTM sleep disturbance and sleep-related impairment item banks. Behav Sleep Med 2011; 10(1): 6–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Choi SW, Reise SP, Pilkonis PA, et al. Efficiency of static and computer adaptive short-forms compared to full-length measures of depressive symptoms. Qual Life Res 2010; 19(1): 125–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. James G, Witten D, Hastie T, et al. An introduction to statistical learning: with applications in R. New York: Springer, 2013. [Google Scholar]
- 19. R Core Team. R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing, 2016. [Google Scholar]
- 20. Yang FM, Kao ST. Item response theory for measurement validity. Shanghai Arch Psychiatry 2014; 26(3): 171–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Reeve BB, Hays RD, Bjorner JB, et al. Psychometric evaluation and calibration of health-related quality of life item banks: Plans for the patient-reported outcomes measurement information system (PROMIS). Med Care 2007; 45(5): S22–S31. [DOI] [PubMed] [Google Scholar]
- 22. Schermelleh-Engel K, Moosbrugger H, Müller H. Evaluating the fit of structural equation models: Tests of significance and descriptive goodness-of-fit measures. Meth Psychol Res 2003; 8(2): 23–74. [Google Scholar]
- 23. Mokken RJ. A theory and procedure of scale analysis. The Hague: Mouton, 1971. [Google Scholar]
- 24. Chalmers RP. mirt: A multidimensional item response theory package for the R environment. J Stat Softw 2012; 48(6): 1–29. [Google Scholar]
- 25. Choi SW. Firestar: Computerized adaptive testing simulation program for polytomous item response theory models. Appl Psychol Meas 2009; 33(8): 644–645. [Google Scholar]
- 26. Choi SW, Swartz RJ. Comparison of CAT item selection criteria for polytomous items. Appl Psychol Meas 2009; 33(6): 171–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Wainer H, Neil JD, Flaugher R, et al. Computerized adaptive testing: A primer. 2nd ed. Mahwah, NJ: Lawrence Erlbaum Associates, 2000. [Google Scholar]
- 28. Lamers I, Feys P. Assessing upper limb function in multiple sclerosis. Mult Scler 2014; 20(7): 775–784. [DOI] [PubMed] [Google Scholar]
- 29. Lamers I, Kelchtermans S, Baert I, et al. Upper limb assessment in multiple sclerosis: A systematic review of outcome measures and their psychometric properties. Arch Phys Med Rehabil 2014; 95(6): 1184–1200. [DOI] [PubMed] [Google Scholar]
- 30. Chen CC, Granger CV, Peimer CA, et al. Manual Ability Measure (MAM-16): A preliminary report on a new patient-centred and task-oriented outcome measure of hand function. J Hand Surg Br 2005; 30(2): 207–216. [DOI] [PubMed] [Google Scholar]