The Structural Basis for Isoform Selective Nitric Oxide Synthase Inhibition by Thiophene-2-Carboximidamides

Abstract

The over production of nitric oxide in the brain by neuronal nitric oxide synthase (nNOS) is associated with a number of neurodegenerative diseases. Although inhibiting nNOS is an important therapeutic goal, it is important not to inhibit endothelial NOS (eNOS) owing to the critical role played by eNOS in maintaining vascular tone. While it has been possible to develop nNOS selective aminopyridine inhibitors, many of the most potent and selective inhibitors exhibit poor bioavailability properties. Our group and others have turned to more biocompatible thiophene-2-carboximidamides (T2C) inhibitors as potential nNOS selective inhibitors. We have used crystallography and computational methods to better understand how and why 2 commercially developed T2C inhibitors exhibit selectivity for human nNOS over human eNOS. As with many of the aminopyridine inhibitors, a critical active site Asp residue in nNOS vs Asn in eNOS is largely responsible for controlling selectivity. We also present thermodynamic integration results to better understand the change in pKa and thus charge of inhibitors once bound to the active site. In addition, relative free energy calculations underscore the importance of enhanced electrostatic stabilization of inhibitors bound to the nNOS active site compared to eNOS.

Graphical Abstract

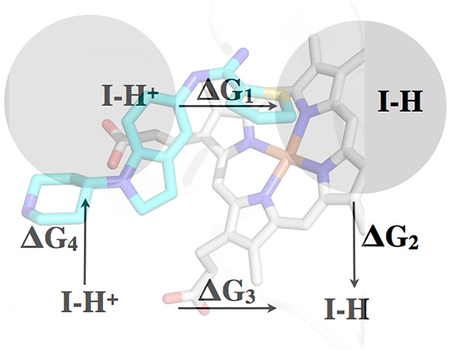
Introduction

Humans and other mammals have three nitric oxide synthase (NOS) isoforms that convert L-arginine to L-citrulline and the potent signaling molecule, NO.¹ Neuronal NOS (nNOS) participates in neural transmission, endothelial NOS (eNOS) regulates blood pressure, and NO generated by inducible NOS (iNOS) is part of macrophage host immune defense system. Given the potency of NO and its ability to cause oxidative damage, the overproduction of NO is associated with various pathological conditions, especially neurodegenerative diseases,² so nNOS is an important therapeutic target. However, a major problem in NOS inhibitor design is selectivity. It is especially important not to block eNOS, owing to its central role in maintaining vascular tone. This is a challenging problem given that the active site of all three human isoforms is so similar. Nevertheless, it has been possible to develop aminopyridine inhibitors that are ~4,000-fold more selective for nNOS over eNOS.³ Some of these aminopyridine inhibitors exhibit remarkable neuroprotective effects in a cerebral palsy rabbit model.⁴ In these studies nNOS-selective inhibitors were found to protect rabbit fetuses from experimentally induced ischemic brain damage, which in saline control animal resulted in death or severe cerebral palsy symptoms.⁴ Despite the excellent selectivity of these aminopyridine inhibitors, the number of high pKa ionizable groups and the large number of rotatable bonds are not optimal for blood-brain barrier penetration and thus limit the potential usefulness of these compounds as neurodegenerative drugs.⁵

Early on in NOS drug development, thiophene-2-carboximidamide (T2C) inhibitors showed better biological properties⁶ and also were found to exhibit in vivo efficacy.^7,8 Unfortunately, early generation T2C inhibitors displayed poor isoform selectivity, ~100-fold for nNOS over eNOS.⁶ Further development of T2C inhibitors by NeurAxon has resulted in inhibitors that are up to 300–400 fold more selective for nNOS over eNOS.^7,8 Moreover, some of these T2C inhibitors show promise in the treatment of migraine headaches⁸ and neuropathic pain.⁷ Another potential target for T2C inhibitors is melanoma. nNOS is upregulated in various melanoma cell lines^9,10, and NO increases cell invasiveness while nNOS inhibitors block melanoma cell growth (e.g., 1, Fig. 1).^9,10. These studies illustrate that there must be a balance between isoform selectivity (up to 4,000-fold with some aminopyridines, e.g., 4, Fig. 1) and better drug-like properties of the T2C inhibitors, although the best selectivity so far is in the range of 500-fold. In this report we have analyzed two of the best NeurAxon inhibitors (2 and 3, Fig. 1) that show promising in vivo properties and compare these with our previous work on T2C inhibitors. These analyses, including crystal structures and computational approaches, also shed light on general principles of NOS inhibition and isoform selectivity.

Figure 1.

Structures of thiophene-2-carboximidamide compounds 1–3 and one of our more selective aminopyridine inhibitors (4). The protonation state and charge when bound to NOS is shown. The K_i (or IC₅₀) values listed were determined with the human enzymes for 1,¹⁰ 2,⁷ 3,⁸ and 4.¹¹

Methods

Computational Approaches

Amber 9 or 14 was used for MM_PBSA and thermodynamic integration (TI) calculations. Inhibitor parameters were assigned using the GAFF force field¹² and AM1-BCC charge scheme,^13,14 as implemented in the Antechamber module in Amber. Heme parameters were taken from Shahrokh et al.¹⁵ No specific bond parameters were used for the tetrahedral Zn²⁺ site located at the dimer interface and coordinated by pairs of symmetry related Cys residues. Instead, the 4 Cys ligands were modeled as Amber CYM residues that have an unprotonated side chain sulfur. The Zn²⁺ remained quite stable with excellent tetrahedral geometry during the simulations. Structures were energy minimized in 3 steps: 1) five hundred cycles of steepest decent followed by 500 cycles of conjugate gradient with only solvent molecules and H atoms allowed to move; 2) the same protocol with all atoms except the inhibitor and heme allowed to move; 3) 1000 cycles of steepest decent followed by 4000 cycles of conjugate gradient with all atoms allowed to move. For molecular dynamics simulations production runs were carried out using a time step of 2 fs and coordinates saved every 20 ps and Langevin dynamics using a collision frequency of 1 ps⁻¹. Periodic boundary conditions were used with a Particle Mesh Ewald implementation of the Ewald sum for the description of long-range electrostatic interactions.¹⁶ In all simulations crystallographically identified ordered water molecules were included.

The relative free energy of binding of various NOS inhibitors was estimated with MM_PBSA¹⁷ as implemented in Amber 9 and 14 using procedures developed in our earlier studies with NOS inhibitors.¹⁸ In this method the total free energy of the NOS-inhibitor complex is taken as the sum of the following energy terms,

$$\text{G}={\text{E}}_{\text{MM}}+{\text{G}}_{\text{solv}}+{\text{G}}_{\text{np}}-{\text{TS}}_{\text{solute}}$$

where E_MM = the total molecular mechanics energy computed with the Sander module in Amber, G_solv is the solvation free energy estimated from the Poisson-Boltzman equation, G_np = the nonpolar solvation energy estimated from the solvent accessible surface area, and TS_solute = the solute entropy. G was computed for the NOS-inhibitor complex (G_complex), NOS alone with the inhibitor removed (G_receptor), and the inhibitor alone (G_inhibitor). The overall free energy of binding was computed from the following equation:

$$\Delta {\text{G}}_{\text{bind}}=\left({\text{G}}_{\text{complex}}-{\text{G}}_{\text{receptor}}-{\text{G}}_{\text{inhibitor}}\right)$$

As others have done¹⁹ the change in solute entropy was ignored. Given that we are comparing exactly the same inhibitor bound to different active sites, ignoring solute entropy introduces little error, although only relative and not absolute free energies can be compared. Similar to what others have found,²⁰ using a single energy minimized structure rather than molecular dynamics averages gives better agreement with experimental data.^11,18 This is especially true for inhibitors where the electron density is well defined.

The change in pKa of the inhibitors bound to the enzyme was estimated using thermodynamic integration (TI) procedures developed by Simonson et al.²¹ In this method the charge of the inhibitor in the protonated state is changed in incremental steps from λ = 0 to λ = 1 to the charge in the unprotonated state. Integration of the potential energy as a function of λ gives the ΔG in moving from one state to the other. The potential energy, U, was assumed to vary linearly with λ

$$\text{U}(\lambda )=(1-\lambda ){\text{U}}_{\text{A}}+\lambda {\text{U}}_{\text{B}}$$

where U_A is starting protonated state and U_B unprotonated. Part of the program output is

$$\partial \text{U}/\partial \lambda ={\text{U}}_{\text{B}}-{\text{U}}_{\text{A}}=\Delta \text{U}$$

The overall ΔG was computed in most cases using 5 λ steps together with the associated weights provided in the Amber manual.

$$\Delta \text{G}=0.11846(\Delta {\text{U}}_{\lambda }{}_{=\mathrm{..04691}})+0.23931(\Delta {\text{U}}_{\lambda }{}_{=0.23076})+0.28444(\Delta {\text{U}}_{\lambda }{}_{=0.5})+0.23931(\Delta {\text{U}}_{\lambda }{}_{=0.95308})+0.11846(\Delta {\text{U}}_{\lambda }{}_{=0.76923})$$

To help speed the calculations by taking larger time steps, hydrogen mass repartitioning using parmed.py²² was used to modify the Amber topology file. Parmed.py also was used to change the charges on inhibitor atoms as needed and set the Lennard Jones terms to 0 for the titrating H atom. The NOS dimer with crystallographic waters with no additional solvent was first energy minimized followed by 1 ns simulation with no periodic boundary. Heavy atoms were restrained with 5 kcal/mol weight. We also carried out periodic boundary simulations with counterions to maintain neutrality. There was no significant difference in the results very likely because both periodic and nonperodic simulations had the same crystallographically identified active site solvent structure. Therefore, the results reported here are for simulations with no additional solvent or periodic boundary which substantially decreases computational time. However, for the inhibitors alone a fully solvated periodic boundary 2 ns simulation were carried out. The pKa when bound to the protein was obtained by the following equation:

$$\text{p}K{\text{a}}_{\text{protein}}=\text{p}K{\text{a}}_{\text{model }}+\left(1/2.303\text{RT}\right)*\Delta \Delta \text{G}$$

The pKa of the inhibitor free in solution was estimated using ChemAxon software (http://www.chemaxon.com)

Inhibitor Complex Crystal Preparation.

The sitting drop vapor diffusion methods were used to grow crystals at 4°C for the heme domains of human nNOS R354A/G357D mutant (10 mg/mL) and human eNOS (7 mg/mL). The mutations used for nNOS are located on the surface far from the active site, either to provent additional trypsin cleavage (R354A) or to improve crystal quality (G357D).²³ The crystal growth conditions are as described previously²⁴ except that the pH for human eNOS was mistakenly reported as 6.5 rather than 7.5 as in the original report.²³ Fresh crystals were first passed stepwise through cryoprotectant solutions and then soaked with 10 mM inhibitor for 3−4 h at 4°C before being flash cooled with liquid nitrogen and stored until data collection. The high concentration of magnesium acetate in the human eNOS growth conditions may also introduce an acetate ion near the active site, as was previously observed in some of the bovine eNOS structures. The presence of this acetate ion can influence the binding mode of inhibitors. To avoid having this acetate ion in the structure, the magnesium acetate (250 mM) in the cryoprotectant solution was replaced with MgCl₂ (100 mM).

X-ray Diffraction Data Collection, Data Processing, and Structural Refinement.

Cryogenic (100 K) X-ray diffraction data were collected remotely at the Stanford Synchrotron Radiation Lightsource (SSRL) through the data collection control software Blu-Ice²⁵ and a crystal-mounting robot. When a CCD detector was used data were typically collected with 0.5° per frame. If a Pilatus pixel array detector was used fine-sliced data were collected with a 0.2° per frame. Raw CCD data frames were indexed, integrated, and scaled using iMOSFLM,²⁶ but the pixel array data were processed with XDS²⁷ and scaled with Aimless.²⁸ The binding of inhibitors was detected by initial difference Fourier maps calculated with REFMAC.²⁹ The inhibitor molecules were then modeled in Coot³⁰ and refined using REFMAC or PHENIX.³¹ The crystal packing of the MgCl₂ soaked heNOS crystals was changed slightly, resulting in a symmetry change from the orthorhombic P2₁2₁2₁ reported previously²³ to monoclinic P2₁, with a β angle only 0.6−0.7° off compared to the original 90°. Therefore, a molecular replacement calculation with PHASER-MR³² was needed to solve the structure. In the P2₁ space group, there are two heNOS dimers in the asymmetric unit. Water molecules were added in PHENIX and checked by Coot. The TLS³³ protocol was implemented in the refinements with each subunit as one TLS group. The Polder map facility in PHENIX was used to calculate the omit density map for the bound inhibitors.³⁴ The refined structures were validated in Coot before deposition in the Protein Data Bank. Data collection and structure refinement statistics are summarize in Table S1 (supporting information).

Synthesis – Compounds 2 and 3 were synthesized according to published procedures.^7,8

Results and Discussion

Crystal Structures

The crystal structures of nNOS complexed to 2 and 3 were solved to a resolution of 1.75Å while the structures of eNOS complexed to 2 and 3 were solved to a resolution of 1.95Å and 2.20Å, respectively (Table S1). The electron density for both 2 and 3, with the exception of the tail end of 2, is very clear, enabling an unambiguous positioning of both inhibitors. As in our previous structures of T2C inhibitors, the T2C group is in position to form ionic interactions with the active site Glu (Fig. 2).

Figure 2.

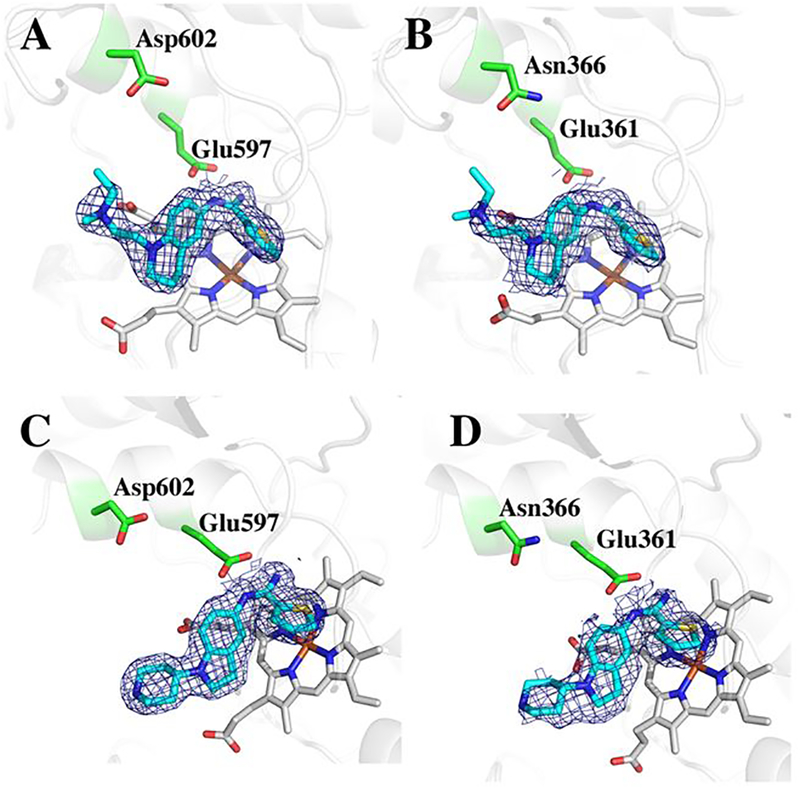
2Fo-Fc electron density maps contoured at 1.0 σ for 2 and 3 bound to human enzymes. A) nNOS-2; B) eNOS-2; C) nNOS-3; D) eNOS-3.

The central tetrahydroquinoline ring of 2 and the indoline ring of 3 occupy nearly identical positions in human nNOS. The tail end tertiary amine of 2 is 3.7Å from heme propionate A, while the N atom of the tail piperidine of 3 is 5.7Å from heme propionate A. Since neither of them form a good H-bonding interaction, this difference appears not to be very significant, as the reported IC₅₀ values for both compounds with nNOS are very similar, 0.097 μM for 2⁷ and 0.11 μM for 3.⁸ Figure 3 shows the previously published structures of 1 bound to rat nNOS. 1 is a potent nNOS inhibitor (K_i ~ 0.005 μM) with an e/n selectivity of ~ 540.¹⁰ In 1 this central bridging amine is situated between both propionates at distances of 3.4 Å and 3.8 Å (Figure 3B).

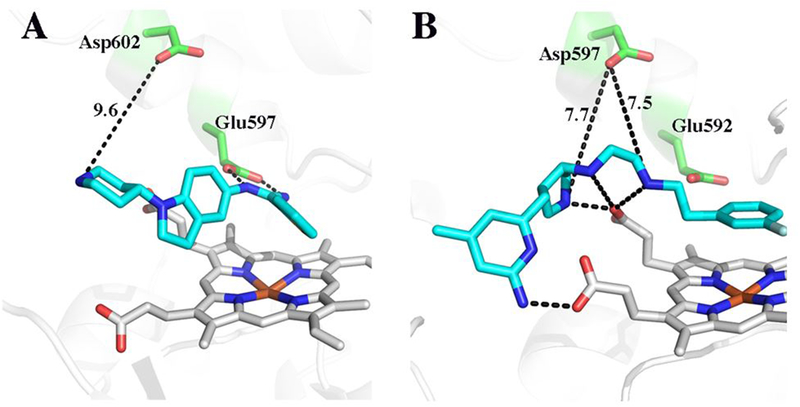
Figure 3.

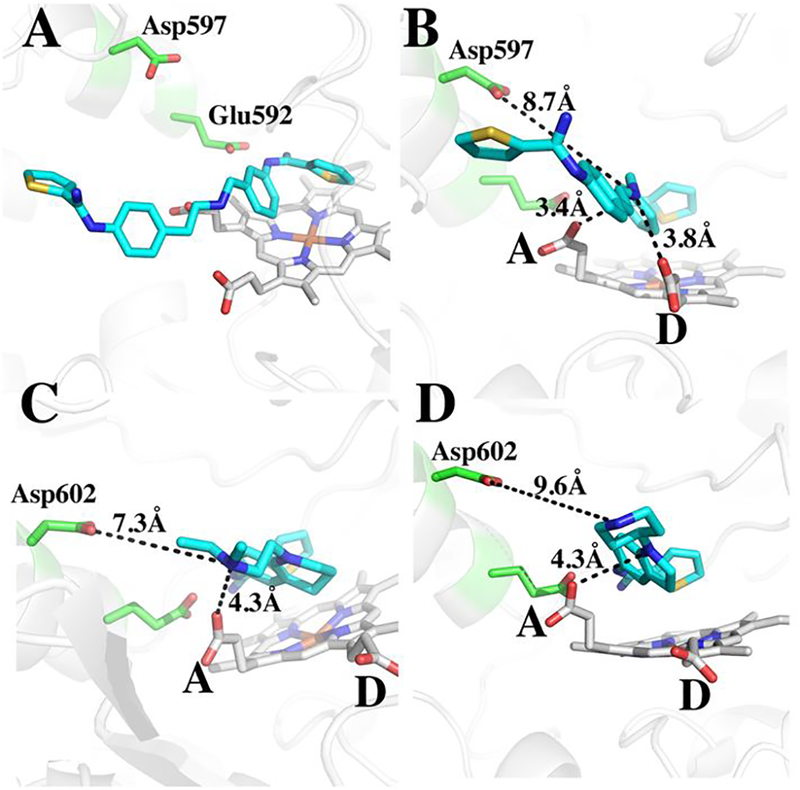
Comparison of binding modes for 1 (A and B in two different views, PDB code 4KCL) bound to rat nNOS, and 2 (C) and 3 (D) bound to human nNOS. In panel C the distance from the tetrahydroquinoline N atom to propionate A is 4.3 Å, from tail amine to propionate A is 3.7Å (not shown), and to Asp602 is 7.3Å; in panel D the distance from the indoline N atom to propionate A is also 4.3 Å, from the piperidine N atom to propionate A is 5.7Å (not shown), to Asp602 is 9.6Å.

With 1, propionate D is able to move “up” toward the inhibitor for better interactions with the inhibitor central amine. This cannot happen with 2 and 3 since the central tetrahydroquinoline or indoline ring would cause steric clashes with propionate D. These differences and the better interactions between the bridging amine could possibly account for why 1 is about 20-fold better as an inhibitor than either 2 or 3.

Estimating Inhibitor pKas Using Thermodynamic Integration

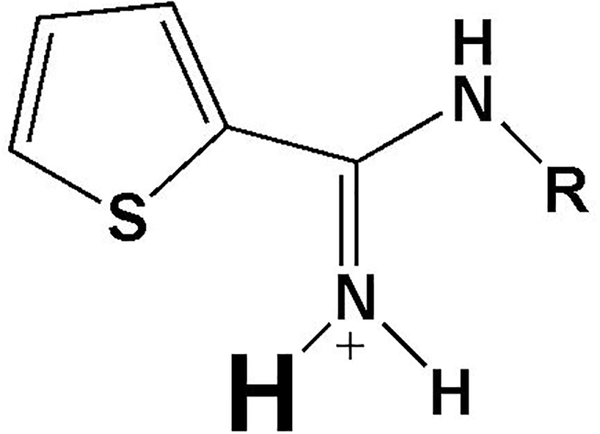
Previous work from our labs has shown that many inhibitors bind more tightly to nNOS than eNOS owing primarily to a single amino acid difference: nNOS has Asp597 where eNOS has Asn368 at that location (Fig. 3).^3,35 A majority of this effort centered on rat nNOS and bovine eNOS, and while we expect the human isoforms to behave similarly, there are far fewer data probing the Asp/Asn difference (Asp602 in human nNOS and Asn366 in human eNOS) in the human isoforms. We therefore probed the influence of this single amino acid difference using the MM_PBSA method that proved quite useful in our previous studies.¹⁸ However, given that NOS inhibitors have at least one and usually more titratable groups, it is important to know if there is a significant change in pKa once bound to the active site so that the correct charge can be assigned to the inhibitor for free energy calculations. Thermodynamic integration methods, where the energy change in moving from the protonated state to the un-protonated state in solution vs. in the protein, most often is used to estimate the change in pKa of amino acid side chains in proteins.²¹ In principle it should be possible to use the same computational methods to estimate the ΔpKa by comparing the ΔG (protonated to un-protonated) free in solution and bound to the protein. Both 2 and 3 have 3 titratable N atoms whose pKa could change once bound to the protein. The ring nitrogens of the tetrahydroquinoline of 2 and indoline of 3 have estimated pKa values of ~1.9 and 3.2, respectively. The tail end tertiary N atom of 2 and the piperidine N atom of 3 give estimated pKa values of 9.2 and 9.8, respectively. Therefore, neither of these groups is expected to change protonation state once bound to NOS. The only pKa in question when bound to the NOS active site is the T2C group with an estimated pKa ~ 6.98 in both 2 and 3. Since the T2C group is buried in the active site near the conserved Glu, the pKa could increase substantially. The results of the thermodynamic integrations are shown in Table 1 and Tables S2 and S3. Two simulations were carried out. One for the nNOS-2 complex using a 3-step integration and the second for the eNOS-3 complex with a 5-step integration. The titrating H atom is the large H atom shown in Table 1 and Tables S2 and S3. In both cases there is a substantial increase in pKa when bound to NOS, indicating that T2C group is fully protonated when bound to the active site. The increase in pKa in nNOS is substantially more than in eNOS. Since this is probably due to the Asn vs Asp difference, we generated the Asn366Asp mutant in silico and reran the TI calculations for eNOS-3 complex. The pKa increases even further, which indicates that the Asp in nNOS vs. Asn in eNOS contributes to additional stability of the T2C group buried in the active site. We also carried out a TI run for the nNOS D602N mutant. As expected, the pKa of 2 drops relative to wild type nNOS again illustrating the important role the Asp vs. Asn difference has on the pKa of the T2C group. Therefore, any functional group with a pKa near neutrality that is buried in the NOS active site and interacts with the conserved Glu will be fully protonated in both nNOS and eNOS.

Table 1.

Results of thermodynamic integration calculations to determine pKa for 2 and 3 free in solution and bound to nNOS or eNOS. The large H atom is the one that titrates.

	ΔG kcal/mol	ΔΔG kcal/mol	pKa
2 free ligand	10.145		6.98
nNOS-2	56.056	45.911	18.86
nNOS-2 D602N	40.688	30.522	14.88
3 free ligand	8.016		6.98
eNOS-3	33.406	25.309	13.55
eNOS-3 N366D	64.200	56.184	21.52

As a basis for comparison, we carried out TI calculation on other N atoms. The tetrahydroquinoline N atom of 2 has an estimated pKa ~ 2, while the indoline ring N atom of 3 has an estimated pKa ~ 3. Both of these atoms are within ~ 4.3 Å of the heme propionate A (Figure 3), so there could potentially be an increase in pKa. However, TI calculations indicate that the tetrahydroquinoline N atom of 2 does experience a significant shift in pKa when bound to nNOS (Table S4). This part of the inhibitor extends out toward solvent and is near two Arg residues at a distance of 5.7 Å and 6.4 Å. It thus appears that the proximity of the tail end of the inhibitors near both a heme propionate and Arg residues results in no net change in pKa.

Relative Binding Free Energy

For the MM_PBSA calculations, we used only 3 since the tail end of 2 is not well ordered in eNOS, while with 3, the electron density is well ordered in both isoforms. When bound to the protein, 3 was modeled as carrying a net +2 charge since the calculations summarized in Table 1 show that the T2C group is fully protonated. However, free in solution the T2C group is about 50% protonated since the estimated pKa is ~ 6.98. Therefore, free in solution 3 was modeled as carrying a net +1.5 charge. The partially protonated state was modeled by averaging the charges of the +1 and +2 models. Results from the MM_PBSA calculations are shown in Table 2.

Table 2.

MM_PBSA calculations for 3 bound to human eNOS and nNOS, and to the in silico generated mutants. ΔG_exp was derived from the published K_i values.⁸ In order to place the calculated values on the same scale as experimental, the ΔG_calc and ΔELEC_calc for wild type nNOS were normalized to ΔG_exp for nNOS. These normalized values are in parentheses.

Enzyme	ΔGcalc kcal/mol	ΔELECcalc kcal/mol	ΔGexp kcal/mol
nNOS wt -3	−63.31	−433.17	−8.96 to −9.20
eNOS N366D -3	−65.03 (−9.70)	−360.49 (−7.87)
eNOS wt -3	−56.46 (−8.43)	−331.27 (−7.23)	−5.46 to −6.48
nNOS D602N -3	−56.89 (−8.49)	−409.10 (−8.92)

In addition to ΔG_calc, also shown in Table 2 is the change in just the electrostatic component ΔELEC_calc. The normalized calculated values are quite close to the range of experimental values derived from K_i measurements, although ΔELEC_calc agrees best. This is probably due to the dominance of electrostatics as the key component in controlling isoform selectivity and shows that the Asp/Asn difference accounts for nearly all of the selectivity for nNOS over eNOS.

The distance between the Asp or Asn from the closest inhibitor N atom is too far, ~ 7 – 9 Å (Figure 3), for direct ionic or H-bonding interactions. Nevertheless, charge-charge interactions depend on the dielectric milieu, and in the confines of the active site, these interactions are expected to be substantially stronger than in solvent.

Conclusions

A comparison between NeurAxon inhibitors 2 and 3 with our inhibitor 1 illustrates the critical role that electrostatic and ionic interactions play in inhibitor potency. The better electrostatic interactions between 1 and the active site account for why 1 is a better inhibitor. These properties of good NOS inhibitors also present a challenge. The NOS active site is charged owing to the conserved buried Glu residue, the heme propionates, and several Arg residues lining the entrance to the active site. As might be expected, the best inhibitors have charged groups that strongly interact primarily with the conserved active site Glu and heme propionates. As we have shown, subtle electrostatic differences between eNOS and nNOS can be exploited for enhanced selectivity. The key here is Asp602 in nNOS vs. Asn366 in eNOS. Although the Asp/Asn does not directly contact any inhibitor atom, the long-range electrostatic effects in the confines of the active site apparently has a large effect. Another new insight from the present study is the change of pKa of the inhibitor when free or bound. An ideal inhibitor should be unprotonated when free in solution for bioavailability but once bound becomes protonated for optimal interactions with active site groups. Our current results coupled with previous studies make it clear that nNOS vs eNOS selectivity is greatest for those inhibitors with multiple charged groups that exploit the Asp/Asn difference. It thus appears that in the design of nNOS selective inhibitors a balance must be achieved between selectivity and bioavailability.

Figure 4.

A comparison of the 3 bound to human nNOS (panel A) and 4 bound to rat nNOS (panel B, PDB code 3JWS). Key distances between the active site Asp and charged groups on the inhibitor are indicated. The unlabeled dashed lines are potential H-bonds ranging from 2.5 – 3.4 Å.