Abstract
DNA quadruplexes have been the subject of investigation because of their biological relevance and because of their potential application in supramolecular chemistry. Similarly, RNA quadruplexes are now gaining increasing attention. Although DNA and RNA quadruplexes are structurally very similar, the latter show higher stability. In this study we report dispersion‐corrected density functional theory (DFT‐D) quantum chemical calculations that were undertaken to understand the difference in stabilities of RNA and DNA quadruplexes. The smallest meaningful model of a stack of quartets, interacting with alkali metal cations, was simulated in an aqueous environment. The energy decomposition analysis allows for in‐depth examination of the interaction energies, emphasising the role of noncovalent interactions and better electrostatics in determining RNA‐GQs higher stabilities, particularly pinpointing the role of the extra 2′‐OH groups. Furthermore, our computations present new insights on why the cation is required for self‐assembly: unexpectedly the cation is not necessary to relieve the repulsion between the oxygen atoms in the central cavity, but it is needed to overcome the entropic penalty.
Keywords: bonding analysis, DNA structures, density functional calculations, noncovalent interactions, quadruplex, RNS structures
Introduction
For more than twenty years, G‐Quadruplex‐DNA (GQ‐DNA) has been a popular investigation topic and a source of lively debate, due to the progressive understanding of its biological roles, its huge therapeutic potential, its flexibility of use in the field of supramolecular chemistry, and its unique chemico‐physical characteristics. GQ‐DNA aggregates have been found in crucial regulatory spots of the human genome, including telomeres, promoters, and immunoglobulin switch regions, as they are involved in cell replication, transcription and immunoglobulin class switch recombination.1
Besides DNA, RNA can also fold up into quadruplex structures. The two main areas of interest concerning the molecular biology of GQ‐RNA regard 5′‐untranslated regions of RNA (5′‐UTR) and the so‐called long telomeric repeat‐containing RNA (TERRA). While the formation of RNA‐GQs in 5′‐UTRs can inhibit2, 3, 4 or induce gene translation,5 TERRA sequences (derived by transcription of telomeric regions) are thought to down‐regulate the activity of the enzyme telomerase and to regulate histone modifications.6, 7, 8, 9
The main building blocks of G‐Quadruplexes (DNA as well as RNA) are constituted of guanine tetrads (G4), held together by Hoogsteen‐type hydrogen bonds (Figure 1). Two or more tetrads can stack on top of each other due to the contribution of electrostatic and dispersion forces.10, 11 Sugar‐phosphate moieties of guanosine monomers constitute the outer backbone of these structures and contribute to their stability (Figure 2). Loops, with various sequences and length, connect the pillars of the backbone, conferring a rich topological diversity.
Figure 1.
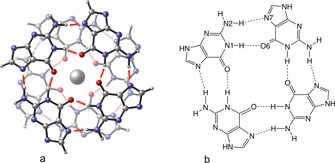
a) A stack of two G‐quartets (arrows present the directionality of the charge‐transfer in the hydrogen bonds) in a parallel configuration. b) Schematic representation of a guanine quartet.
Figure 2.
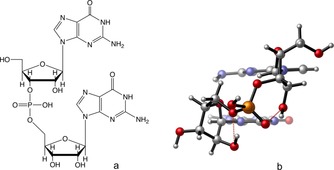
Structure of the guanosine phosphate dimer used in RNA‐GQs with two hydrogen bonds involving ribose and phosphate moieties, a) schematic and b) “balls and sticks” representation.13
In our previous work on the quadruplexes10 we showed that the hydrogen bonds in G4 experience a large synergetic effect. This cooperativity in G4 originates from charge separation occurring with donor–acceptor interactions in the σ‐electron system, and not, as previously assumed, with resonance assistance by the π electrons.
A central cavity, an actual channel, passes through the whole length of GQ structures and is defined by the oxygen atoms of the carbonyl group of guanines. It is well‐known how this central cavity hosts monovalent alkali metal cations according to the generally, but not unanimously, accepted affinity sequence K+>Na+,Rb+≫Li+,Cs+.14 In our previous work, we demonstrated15 how desolvation and the size of the alkali metal cation are both of almost equal importance for the order of affinity.
GQ‐RNA shares the main structural characteristics with GQ‐DNA; however, a consolidated experimental observation is the higher thermodynamic and thermal stability of GQ‐RNA compared with its DNA counterpart,16 which are believed to be due to better stacking of piled tetrads17 and an additional network of hydrogen bonds involving the extra 2′‐OH on the ribose of the RNA,18 with the longest time‐residence being those formed with phosphate oxygen atoms.
The aim of this work is therefore to clarify the chemico‐physical origins of the higher stability of RNA‐GQ compared with DNA‐GQ, confining this investigation to the frame of the smallest meaningful model. Extensive computational analyses of double layer models of RNA‐GQ with sugar‐phosphate backbone based on dispersion‐corrected density functional theory (DFT‐D) in an implicit model of water solvation allow for a fundamental understanding of the energetic components leading to polymerization of guanosine dimers into the scaffold of RNA‐GQ, its interaction with monovalent cations (Li+, Na+, K+, Rb+, and Cs+) and the solvation/desolvation ratio of the resulting RNA‐GQ‐M+ complexes, revealing the main structural and energetic contributions to the superior stability of RNA‐GQ. Further energy decomposition analysis also clarifies the origin of the ability of the scaffold of RNA‐GQ to interact more strongly with monovalent cations compared with its DNA counterpart and its clear electrostatic foundation, providing evidence that the explanation for higher stability of RNA‐GQs already resides in the very core of the quadruplex structure.
Finally, we demystify the role of the cations in the self‐assembly of quadruplex structures, disproving the general postulate that they minimise the repulsive forces between the oxygen atoms in the central channel and corroborating their enthalpic relevance for the thermodynamic stability.
Results and Discussion
Structure and energy of formation
To study the interaction between different monovalent cations and the guanine bases as they are organised in the naturally occurring RNA‐GQ and then to build a solid reference system to be compared with the DNA‐GQ counterpart, we built and computationally analysed the model RNAGQ‐M+, structured as a double layer of guanine quartets, including the sugar‐phosphate backbone (Figure 3). In Table 1 we present geometrical parameters and energies of formation of RNA‐GQs coordinated in turn with no metal, Li+, Na+, K+, Rb+, and Cs+, and report for comparison, data extracted from a previous study15 concerning DNA‐GQs.
Figure 3.
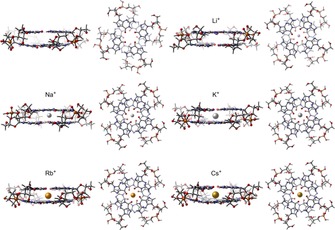
Structures of RNAGQ and RNAGQ‐M+ in which M+ is an alkali metal cation (optimized at the ZORA‐BLYP‐D3(BJ)/TZ2P level of theory in COSMO model of solvation).
Table 1.
Energies of formation and geometrical parameters of the quadruplexes.[a]
| System | M+ | d[O‐M+][b] | N2⋅⋅⋅N7[c] | N1⋅⋅⋅O6[d] |
|
|
|---|---|---|---|---|---|---|
| RNAGQ‐ | no metal | 3.09 | 2.88 | 2.82 | −69.1 | |
| Li+ | 2.12 | 2.90/ 2.80 |
2.80/ 2.83 |
−106.2 | ||
| Na+ | 2.69 | 2.85 | 2.82 | −120.4 | ||
| K+ | 2.83 | 2.88 | 2.83 | −120.8 | ||
| Rb+ | 2.95 | 2.90 | 2.85 | −115.4 | ||
| Cs+ | 3.13 | 2.90 | 2.87 | −107.7 | ||
| DNAGQ‐ | no metal | 3.03 | 2.88 | 2.81 | −62.2 | |
| Li+ | 2.11 | 2.88/2.80 | 2.80/2.81 | −100.2 | ||
| Na+ | 2.69 | 2.84 | 2.81 | −114.5 | ||
| K+ | 2.82 | 2.88 | 2.82 | −115.4 | ||
| Rb+ | 2.95 | 2.90 | 2.84 | −111.1 | ||
| Cs+ | 3.14 | 2.90 | 2.86 | 103.1 |
[a] Energies and geometries computed at ZORA‐BLYP‐D3(BJ)/TZ2P level of theory with COSMO to simulate water. [b] Average distance between the oxygen atoms and the (alkali) metal cation. For the empty scaffold the midpoint of the eight oxygen atoms was taken. For Li+ the value is average for one layer only. [c] Average outer hydrogen bond distance N2(H)⋅⋅⋅N7. For Li+, two values are presented because the quartets are not equal (Li+ lies in the middle of one of the quartets. The first number refers to the noncoordinated quartet). [d] Average inner hydrogen bond distance N1(H)⋅⋅⋅O6.
The energy of formation is formulated in Equation (1):
| (1) |
where E(GQ‐M+)aq is the energy of the metal complex in water in its optimum, GG denotes the guanosine dimer, neutralised at its phosphate moiety with an H+ as counterion, and the term E(M+)aq expresses the computed energy of the alkali metal cations in water (for and , see Figure 4). In our previous work15 we demonstrated how the use of Na+ as counterions do not induce any interesting or noticeable structural change or perturbations in the energy/cation affinity trend. Nevertheless, we report in Table S1 the results of RNAGQ4Na‐K+ and RNAGQ4Na‐Na+ computations to show how also in this case the trend between the two most “sensitive” and energetically close systems clearly remains the same.
Figure 4.
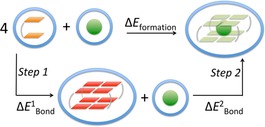
Formation energy of the RNA guanine quadruplexes in solvent, discerned in the two steps of dimers’ association and cationic coordination.
From the geometrical point of view, it is particularly notable how the six reported species differ very little based on their belonging to the RNA or DNA group. These data are also nicely consistent with the few available crystallographic data for geometrical parameters of RNA‐GQ19 where N2(H)⋅⋅⋅N7 is 2.82 and N1(H)⋅⋅⋅O6 is 2.80 and where N2(H)⋅⋅⋅N7 is 2.88, N1(H)⋅⋅⋅O6 is 2.90, d[O‐M+] 2.82, for K+ species.20
The first analysis of [Eq. (1)] immediately reveals two important outcomes of this study: the first concerns the cation affinity sequence for the inner channel of the structures under investigation. Our analysis did not highlight any difference in cation affinity sequence compared with DNAGQ‐M+ species.
Secondly, the respective stabilities of RNA species compared with their DNA counterparts confirm the experimental findings and allow us to justify differences in melting temperatures up to 15 °C.16b
Both findings will be analysed in detail and explained in the following sections by analysing the formation of the quadruplex in two steps: the formation of the empty scaffold ( and the coordination of the metal cation to the scaffold ( (see Figure 4).
Step 1: Analysis of the bond energy of association
To understand individual energetic parameters determining cation affinity sequence and, at the same time, to account for the consequences of the chemico‐physical differences between DNA‐ and RNA‐GQ, we start from the description of the process of formation of the empty scaffold from four individual guanosine dimers and partition the association energy as follows:
The bond energy of association is defined as the difference in energy between the empty scaffold GQ and four times the energy of the dimer, both individually optimised in water [Eq. (2)]:
| (2) |
The “aq” subscript denotes the COSMO computations in aqueous solution and “gas” denotes the computations in the gas phase.
The bond energy can be portioned as given by Equation (3) (see Figure 5):
| (3) |
Figure 5.
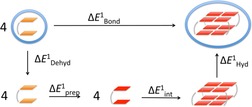
Schematic representation of step 1: partitioning of the bond energy (kcal mol−1) of association of the final empty scaffold from four guanosine dimers.
The mathematical expressions for all the components in the energetic partition are given in the Computational Methods section.
The interaction energy in this model is examined in the framework of the Kohn–Sham molecular orbital model using a quantitative energy decomposition analysis (EDA) that divides the total interaction ( ) into electrostatic interaction, Pauli repulsion, orbital interaction, and dispersion terms [Eq. (4)]:21
| (4) |
The term corresponds to the classical electrostatic interactions between the unperturbed charge distributions of the prepared (i.e., deformed) bases and is usually attractive. The Pauli repulsion comprises the destabilizing interactions between the occupied orbitals and is responsible for any steric repulsion. The orbital interaction accounts for the charge transfer (i.e., donor‐acceptor interactions between occupied orbitals on one moiety and unoccupied orbitals on the other, including the HOMO–LUMO interactions) and polarisation (empty‐occupied orbital mixing on one fragment due to the presence of another fragment). The Δ accounts for the dispersion correction.
The main terms coming from the partition of the association energy, as derived from Eq. (3) and illustrated in Figure 5, are reported in Table 2. The differences between the two groups (RNA‐GQs vs. DNA‐GQs) will be analysed on the basis of individual energetic contribution, leading to a separation in terms of that favours RNA‐GQs of almost 7 kcal mol−1.
Table 2.
Partitioning of the bond energy of association (kcal mol−1) of the final empty scaffold from four guanosine dimers and EDA of relative ΔE int. [a]
| RNAGQ[ ] | DNAGQ[ ] | ||
|---|---|---|---|
|
|
−69.1 | −62.2 | |
|
|
24.3 | 32.8 | |
|
|
115.7 | 103.5 | |
|
|
−209.2 | −198.5 | |
|
|
276.1 | 274.3 | |
|
|
−220.3 | −214.3 | |
|
|
−191.9 | −188.8 | |
|
|
−73.1 | −71.1 |
[a] Energies and geometries computed at ZORA‐BLYP‐D3(BJ)/TZ2P level of theory.
The guanine dimers constituting the scaffold of RNAGQ undergo a smaller deformation in the process of assuming the final conformation compared with the dimers of DNAGQ ( =−8.5 kcal mol−1). The extra hydrogen bonds that form in the backbone of the RNA‐GQ due to the presence of the 2′‐OH of ribose lend the RNA guanine dimers a higher conformational stability, so that the structure of the isolated dimeric components is much closer to the conformation they would assume in the final empty scaffold, as compared with the deoxyribonucleosidic counterpart. The term favors DNA species by more than 12 kcal mol−1. This is due to the extra ‐OH moieties in the backbone of RNA species, the polarity of which leads to a more intense interaction with the watery medium (reproduced by the implicit model of solvation).
The RNA dimers show a much better intermolecular interaction during the association into the tetrameric form ( =−10.7 kcal mol−1 in the gas phase). The more favourable of the RNA group will be examined in the following section by means of Energy Decomposition Analysis7 to deepen our understanding of the physical foundations of the interaction of the four dimers towards the formation of the empty scaffold.
Energy decomposition analysis
In this section we will also compare the two groups (RNA‐GQs vs. DNA‐GQs) to justify and estimate quali‐quantitatively the difference of between them.
Therefore, analysing Table 2, while the dimers of RNA‐GG experience in their interaction a higher repulsion compared with DNA‐GG ( =+1.8 kcal mol−1), all the remaining energetic parameters contributing to the favor the ribonucleosidic species. The contribution of better orbital interaction amounts to −3.6 kcal mol−1 and it is worth noting how RNA‐GG dimers also show a better dispersion interaction, although the most important contribution to the better interaction of dimers of RNA‐GG compared with DNA‐GG comes from a more effective electrostatic attraction of 6 kcal mol−1 (see below).
Step 2: Analysis of the bond energy of metal coordination
In this section we analyse the differences between species inside the same group (RNA‐GQs that coordinate different cations) and the differences between the two groups (RNA‐GQs vs. DNA‐GQs) on the basis of individual energetic contribution leading to separation in terms of [Eq. (5)] (see Table S2):
| (5) |
The bond energy can be portioned as described by Equation (6) (see Figure 6):
| (6) |
Figure 6.
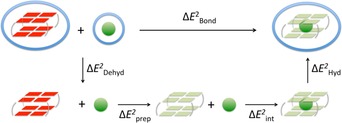
Partitioning of the bonding energy upon formation of the final GQ‐M+ complex from the empty scaffold.
The desolvation and solvation energy can be computed as the energy difference between the solvated and the gas phase. For the definition of all the components that represent this energetic partition, refer to the Computational Methods section.
Concerning the differences between RNA‐GQs that coordinate different cations, the partitioning of the formation energy reveals how the cation affinity sequence obeys the same rules as previously described for DNA‐GQs.15 Focusing on the competition between K+ and Na+, our analysis reveals how the subtle difference (0.4 kcal mol−1) of formation energies in RNA‐GQ derives from a balance between the terms solvation, interaction, and deformation. The interaction energy of the scaffold of RNA‐GQ with Na+ is almost 23 kcal mol−1 better than with K+ and this term is mostly counterbalanced by the solvation/desolvation ratio between the two species (Table S2). This term is directly determined by the of the ions, so that the term favors RNAGQ‐K+ of roughly 19.5 kcal mol−1 (Figure 7). The last term that determines the final difference of bond energy between K+ and Na+ species is : the empty scaffold of RNAGQ‐K+ undergoes a smaller deformation in the process of assuming the final conformation of the complex compared with that of RNAGQ‐Na+ ( −3.8 kcal mol−1).
Figure 7.
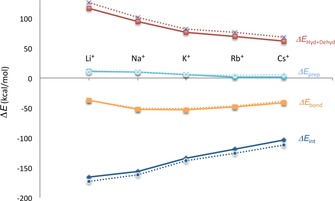
Partitioning of the bonding energy upon formation of the final GQ‐M+ complex from the empty scaffold (RNA‐GQ is represented with dashed lines, DNA‐GQ with continuous lines).
Broadening the analysis to the other species under investigation, we can appreciate how the difference in affinity between K+, Rb+, and Cs+ are less driven by the term so that, in these cases, the plays a major role. On the other hand, the less favourable bond energy of the species RNAGQ‐Li+ is mainly governed by the size of the ion, which determines higher desolvation energy. Furthermore, the size of the Li+ ion determines its positioning on the same plane as one of the quartet, a phenomenon that makes the term less unambiguously comparable with the other species, since the ion deforms the two stacked guanine quartets to different extents.
As noted above, the interaction between the Na+ and the scaffold is ca. 23 kcal mol−1 stronger than for K+. Comparing the species RNAGQ‐K+ and RNAGQ‐Na+ in the frame of the decomposition of interaction energy reveals that this is a result of slightly better electrostatics and orbital interaction for Na+. However, the largest difference comes from the steric repulsion. K+ experiences a much larger Pauli repulsion (of ca. 18 kcal mol−1) than Na+. The sudden increase in only occurs from sodium to potassium (see Figure 8), but not from K+ to Rb+ or Rb+ to Cs+, while the electrostatic contribution decreases linearly from Li+ to Cs+ together with the average distance [O−M+].
Figure 8.
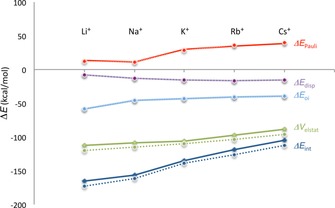
Energy Decomposition Analysis of the interaction between the scaffolds and relative cations, in the geometry they will assume in the final GQ‐M+ complex (gas phase). RNA‐GQ is represented with dashed lines, DNA‐GQ with continuous lines.
Simplified models: The influence of ribosidic ‐OH moieties
Electrostatic attraction acquires bigger relevance in the comparison between RNAGQ‐M+ and DNAGQ‐M+: in the summation of various components contributing to ( ) of the two groups, all the other parameters almost overlap and the only relevant difference is indeed the term , which is at least 3.4 kcal mol−1 more favurable to the ribonucleosidic species (in the case of K+, see Table S3). One of the most interesting findings in this frame is represented in Table 3 and Figure 9 a and b: with the use of a simplified model in which the ribosidic 2′‐OH groups are frozen in the same geometry they assume in the GQ‐RNA‐K+ complex, we suggest that the difference in between RNA and DNA models might be ascribed to the 2′‐OH groups themselves (in this case we refer to eight molecules of water), which can exert a large (−11.3 kcal mol−1 in gas phase) attraction towards the cation even from the distance (average 8.7 Å). Positioning hydrogen atoms at the same coordinates as the oxygens of the 2′‐OH groups, this interaction almost completely vanishes (mimicking the interaction with the ion in DNA‐GQ) (see Table S4).
Table 3.
Energy decomposition analysis for eight formaldehydes.[a]
| Structure |
|
|
|
|
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| empty | 0.6 | 8.4 | 6.8 | −5.3 | −9.3 | |||||
| Li+ | 4.7 | 15.5 | 11.1 | −8.9 | −12.9 | |||||
| Na+ | 4.8 | 16.5 | 12.4 | −10.0 | −14.1 | |||||
| K+ | 3.1 | 11.7 | 10.7 | −7.6 | −11.7 | |||||
| Rb+ | 2.4 | 9.5 | 9.4 | −6.3 | −10.1 | |||||
| Cs+ | 1.9 | 7.7 | 7.7 | −5.1 | −8.4 |
[a] Energies and geometries computed at ZORA‐BLYP‐D3(BJ)/TZ2P level of theory from RNA‐GQ empty structure. All heavy atoms were frozen, except for hydrogen atoms the Z coordinates of which only were constrained to remain on the same plane as the C=O bond.
Figure 9.
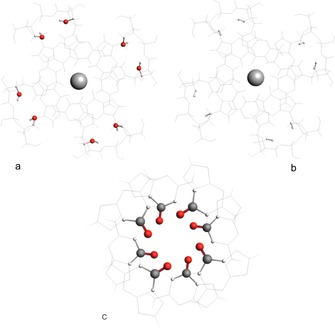
Simplified models of RNAGQ‐K+ complex in which 2′‐OH(s) are substituted by a) H2O and b) H2. The ‐OH moieties are frozen in the same geometry they assume in ribosidic 2′‐OH RNA‐GQ‐K+ complex (a), while the second H is fully relaxed. In the H2 case, the oxygen atoms of the ribosidic 2′‐OH in RNA‐GQ‐K+ complex are replaced at exactly the same position in space by hydrogen atoms (b), and the position of the second hydrogen atom is optimised. c) Top view of the (H2CO)4‐(H2CO)4 stack.
Simplified models: Necessity of the metal cation
The role of metal cation is widely believed to be stabilising the repulsive interactions between the O6 oxygens inside the cavity of the scaffold.22 To analyse this, we have substituted all the guanines in the empty scaffold of RNA‐GQ with formaldehyde, while keeping the C6=O6 at the same position in space, and for the hydrogen atoms only the x and y coordinates are reoptimised (see Figure 9 c and Table 3). The computed interaction energy between these eight formaldehydes in the empty model amounts to 0.6 kcal mol−1. This is for the empty scaffold due to the cancellation of the small Pauli repulsive and electrostatic repulsive energy terms by the attractive orbital interaction and dispersion ( =8.4 kcal mol−1, =6.8 kcal mol−1, =−5.3 kcal mol−1 and =−9.3 kcal mol−1).
The other models (using as initial structures the core of RNA‐GQ‐M+ complexes) show higher repulsive interactions (up to 4.8 kcal mol−1) but we can affirm that the alkali metal cation in the central cavity is only marginally needed to relieve electrostatic repulsion between the oxygen atoms, while it is necessary for the formation of these structures since it causes much more favourable energies of formation (cf. Table 1).
Our thermodynamic properties calculations (based on geometries optimised at ZORA‐BLYP‐D3(BJ)‐DZP and analytical frequencies computed at the same level of theory) indicate how the Gibbs free energy of formation of an empty scaffold in water is actually positive (7.6 kcal mol−1) whereas the value of of RNAGQ‐K+ amounts to −45.3 kcal mol−1. This clearly indicates that the presence of the alkali cation is essential for the assembly of the quadruplex core structure from a thermodynamic point of view, and completely in line with the experimental observation that quadruplexes do not self‐assemble without the assistance of the cation.23
These observations clearly do not offer a complete thermodynamic profile of folding of quadruplex structures, for which other components should be considered (like length and sequence of a wide variety of possible loops and flanking sequences that largely influence the enthalpic balance of the assembly). This analysis sheds light on the thermodynamic impact of cation coordination and helps to elucidate the fundamentals of guanines association into a quadruplex structure, building the basis for further developments of the method towards increasingly encompassing models.
Conclusions
In this study we used dispersion‐corrected density functional theory to examine the differences between RNA‐GQ and DNA‐GQ in terms of stability, and the nature of their interaction with alkali metal cations. An all‐parallel double layer of guanine quartets including phospho‐ribosidic backbone was analysed in implicit model of water solvation.
RNA‐GQ′s cation affinity order has been verified as mostly identical to that calculated for its DNA counterpart. The computation of formation energies complies with the experimental finding of RNA‐GQ being more stable than DNA‐GQ.
Therefore, the partitioning of the association energy linked to the formation of an empty scaffold from four ribonucleosidic dimers highlights how all the energetic parameters concerning this phenomenon favour the formation of the RNA‐GQ scaffold, except for those relative to its solvation/desolvation balance. It is worth noting how the presence of an extra hydrogen bond in the RNA dimer confers higher conformational stability to this constituent, so that the structure of the isolated dimeric components is much closer to the conformation they would assume in the final empty scaffold, as compared with the deoxyribonucleosidic counterpart.
Further decomposition of the interaction energy pinpoints the prevailing role of electrostatic components in determining the more favourable interaction energy of the (four dimers assembling in the) RNA‐GQ scaffold compared to the DNA‐GQ.
Finally, the partitioning of the bond energy resulting from the interaction and deformation of the empty scaffold to accommodate an alkali metal cation in its central channel, reveals how this last passage does not discriminate substantially the formation of the two (RNA‐ and DNA‐GQ) complexes.
The decomposition of the interaction between an empty GQ scaffold and alkali cations ultimately reveals another extremely important detail: also in this frame, electrostatic components exert a primary role in determining the more favourable interaction energy of the RNA‐GQ scaffold compared with the DNA‐GQ towards the cation. With a simplified model constructed to simulate the influence of the 2′‐OH groups (or, in turn, of simple Hs as in deoxyribose) towards the cation we indeed demonstrate that the 2′‐OH groups of the RNA‐GQ backbone can influence the cations directly, playing a role in improving the stability of this species.
The use of another simplified model can facilitate an understanding of the real role of cation coordination as related to the neutralisation of repulsive forces generated by the proximity of O6 rims inside the cage. In all cases, although the interaction of formaldehyde moieties is slightly unfavourable, their mutual repulsion represents a secondary effect and the presence of a cation is mainly required because it consistently enhances the energy of formation of complexes compared with the empty scaffold only. Thermodynamics studies highlight how the formation of an empty scaffold is unfavourable, while the free Gibbs energy of formation of cationic species is notably lower and attractive.
Computational Methods
All the calculations were performed with the Amsterdam Density Functional (ADF) program24, 25 using dispersion‐corrected relativistic density functional theory at the ZORA‐BLYP‐D3(BJ)/TZ2P level for geometry optimizations and energies.26 C 2 symmetry constraints have been imposed on the quadruplexes (we have verified the energy of “NOSYM” RNAGQ‐Na+ and RNAGQ‐K+ optimising them separately and they only differ from the C 2 species by 0.2 kcal mol−1) but no symmetry has been specified for Guanosine dimers (C 1). To make sure a structure of global minimum was reached for both DNA and RNA dimers, they have undergone a conformational search with the ADF module “conformers” (for details Figure S1) prior to geometry optimization.
As opposed to the very rich topological variability of DNA quadruplexes, RNA‐GQ are found to almost invariably adopt an all‐parallel configuration, which implies that all 16 hydrogen bonds of the double layer point in the same direction (Figure 1): this preference is justified with a stronger propensity for ribose moieties (C3′‐endo) to assume an anti glycosidic bond.27 Given this assumption, the models elaborated in this paper all have a parallel arrangement. The starting point for every structure was taken from our previous work on DNA‐GQ,15 with the addition of the necessary ‐OH moiety in 2′ at ribose groups. Solvent effects in water have been estimated by using the conductor‐like screening model (COSMO), as implemented in the ADF program.28 Radii of cations have been computed according to the procedure presented in Ref. 26f and Ref. 15 (see the Supporting Information).
In the following we report details of the partitioning of the bonding energy of association. The preparation energy, , is the energy required to deform the four dimers with the geometry of the solvated state to the geometry they acquire interacting in the solvated final empty scaffold state. The desolvation and solvation energy can be computed as the energy difference between the solvated and the gas phase [Eq. (7), (8)]. The “aq” subscript denotes the COSMO computations in aqueous solution and “gas” the computations in the gas phase.
| (7) |
| (8) |
This partitioning of the association energy, allows us to compute the interaction energy from Equation (9):
| (9) |
where the term accounts for the energy of the final empty scaffold calculated in the gas phase and for the energy of guanosine dimers in the final geometry of the empty scaffold. The passage in gas phase is needed not only for further decomposition, but also justified since structures in water and in the gas phase are almost indistinguishable.12
Equations (10), (11) provide a detailed description of the energy terms of the partitioning of the bonding energy of ionic coordination:
| (10) |
| (11) |
This partitioning of the bond energy of coordination, allows us to compute from Equation (12):
| (12) |
and the interaction energy from Equation (13):
| (13) |
where is the energy of the empty scaffold in the geometry of the complex optimised in water and computed in the gas phase.
Conflict of interest
The authors declare no conflict of interest.
Supporting information
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
Supplementary
Acknowledgements
C.F.G. gratefully acknowledges the financial support from the Netherlands Organization for Scientific Research NWO (ECHO).
F. Zaccaria, C. Fonseca Guerra, Chem. Eur. J. 2018, 24, 16315.
References
- 1. Neidle S., in Ther. Appl. Quadruplex Nucleic Acids, Elsevier, 2012, pp. 1–20. [Google Scholar]
- 2. Kumari S., Bugaut A., Huppert J. L., Balasubramanian S., Nat. Chem. Biol. 2007, 3, 218–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Derecka K., Balkwill G. D., Garner T. P., Hodgman C., Flint A. P. F., Searle M. S., Biochemistry 2010, 49, 7625–7633. [DOI] [PubMed] [Google Scholar]
- 4. Gomez D., Guedin A., Mergny J.-L., Salles B., Riou J.-F., Teulade-Fichou M.-P., Calsou P., Nucleic Acids Res. 2010, 38, 7187–7198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Agarwala P., Pandey S., Mapa K., Maiti S., Biochemistry 2013, 52, 1528–1538. [DOI] [PubMed] [Google Scholar]
- 6. Azzalin C. M., Reichenbach P., Khoriauli L., Giulotto E., Lingner J., Science 2007, 318, 798–801. [DOI] [PubMed] [Google Scholar]
- 7. Xu Y., Suzuki Y., Ito K., Komiyama M., Proc. Natl. Acad. Sci. USA 2010, 107, 14579–14584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Schoeftner S., Blasco M. A., Nat. Cell Biol. 2008, 10, 228–236. [DOI] [PubMed] [Google Scholar]
- 9. Takahama K., Takada A., Tada S., Shimizu M., Sayama K., Kurokawa R., Oyoshi T., Chem. Biol. 2013, 20, 341–350. [DOI] [PubMed] [Google Scholar]
- 10.
- 10a. Fonseca Guerra C., Zijlstra H., Paragi G., Bickelhaupt F. M., Chem. Eur. J. 2011, 17, 12612–12622; [DOI] [PubMed] [Google Scholar]
- 10b. Wolters L. P., Smits N. W. G., Guerra C. F., Phys. Chem. Chem. Phys. 2015, 17, 1585–1592. [DOI] [PubMed] [Google Scholar]
- 11. Yurenko Y. P., Novotný J., Marek R., Chem. Eur. J. 2017, 23, 5573–5584. [DOI] [PubMed] [Google Scholar]
- 12. Rueda M., Luque F. J., Orozco M., J. Am. Chem. Soc. 2006, 128, 3608–3619. [DOI] [PubMed] [Google Scholar]
- 13.CYLview, 1.0b; Legault, C. Y., Université de Sherbrooke, 2009 (http://www.cylview.org).
- 14.
- 14a. Wong A., Wu G., J. Am. Chem. Soc. 2003, 125, 13895–13905; [DOI] [PubMed] [Google Scholar]
- 14b. Detellier C., Laszlo P., J. Am. Chem. Soc. 1980, 102, 1135–1141; [Google Scholar]
- 14c. Pinnavaia T. J., Marshall C. L., Mettler C. M., Fisk C. L., Miles H. T., Becker E. D., J. Am. Chem. Soc. 1978, 100, 3625–3627; [Google Scholar]
- 14d. Ida R., Wu G., J. Am. Chem. Soc. 2008, 130, 3590–3602. [DOI] [PubMed] [Google Scholar]
- 15. Zaccaria F., Paragi G., Fonseca Guerra C., Phys. Chem. Chem. Phys. 2016, 18, 20895–20904. [DOI] [PubMed] [Google Scholar]
- 16.
- 16a. Arora A., Maiti S., J. Phys. Chem. B 2009, 113, 10515–10520; [DOI] [PubMed] [Google Scholar]
- 16b. Joachimi A., Benz A., Hartig J. S., Bioorg. Med. Chem. 2009, 17, 6811–6815. [DOI] [PubMed] [Google Scholar]
- 17. Olsen C. M., Marky L. A., J. Phys. Chem. B 2009, 113, 9–11. [DOI] [PubMed] [Google Scholar]
- 18. Pagano B., Mattia C. A., Cavallo L., Uesugi S., Giancola C., Fraternali F., J. Phys. Chem. B 2008, 112, 12115–12123. [DOI] [PubMed] [Google Scholar]
- 19. Collie G. W., Haider S. M., Neidle S., Parkinson G. N., Nucleic Acids Res. 2010, 38, 5569–5580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Pan B., Xiong Y., Shi K., Sundaralingam M., Structure 2003, 11, 1423–1430. [DOI] [PubMed] [Google Scholar]
- 21. Bickelhaupt F. M., Baerends E. J. in Rev. Comput. Chem. Vol. 15, (Eds.: K. B. Lipkowitz, D. B. Boyd), Wiley, Inc., Hoboken, NJ, USA, 2007, pp. 1–86. [Google Scholar]
- 22. Largy E., Mergny J-L., Gabelica V. in G-Quadruplex Nucleic Acid Structure and Stability, Springer, Cham, 2016, pp. 203–258. [DOI] [PubMed] [Google Scholar]
- 23.
- 23a. Davis J. T., Angew. Chem. Int. Ed. 2004, 43, 668–698; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2004, 116, 684–716; [Google Scholar]
- 23b. Gottarelli G., Masiero S., Mezzina E., Spada G. P., Mariani P., Recanatini M., Helv. Chim. Acta 1998, 81, 2078–2092. [Google Scholar]
- 24. te Velde G., Bickelhaupt F. M., Baerends E. J., Fonseca Guerra C., van Gisbergen S. J. A., Snijders J. G., Ziegler T., J. Comput. Chem. 2001, 22, 931–967. [Google Scholar]
- 25.ADF2016.102, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com; E. J. Baerends, et al.
- 26.
- 26a. Grimme S., Antony J., Ehrlich S., Krieg H., J. Chem. Phys. 2010, 132, 154104; [DOI] [PubMed] [Google Scholar]
- 26b. Grimme S., Ehrlich S., Goerigk L., J. Comput. Chem. 2011, 32, 1456–1465; [DOI] [PubMed] [Google Scholar]
- 26c. Grimme S., J. Comput. Chem. 2004, 25, 1463–1473; [DOI] [PubMed] [Google Scholar]
- 26d. Grimme S., J. Comput. Chem. 2006, 27, 1787–1799; [DOI] [PubMed] [Google Scholar]
- 26e. Fonseca Guerra C., van der Wijst T., Poater J., Swart M., Bickelhaupt F. M., Theor. Chem. Acc. 2010, 125, 245–252; [Google Scholar]
- 26f. van der Wijst T., Fonseca Guerra C., Swart M., Bickelhaupt F. M., Lippert B., Angew. Chem. Int. Ed. 2009, 48, 3285–3287; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2009, 121, 3335–3337. [Google Scholar]
- 27. Halder K., Hartig J. S. in Met. Ions Life Sci., Vol. 9, The Royal Society of Chemistry, 2011, pp. 125–139. [DOI] [PubMed] [Google Scholar]
- 28.
- 28a. Klamt A., Schüürmann G., J. Chem. Soc. Perkin Trans. 2 1993, 799–805; [Google Scholar]
- 28b. Klamt A., J. Phys. Chem. 1995, 99, 2224–2235; [Google Scholar]
- 28c. Pye C., Ziegler T., Theor. Chem. Acc. 1999, 101, 396–408; [Google Scholar]
- 28d. Hamlin T. A., Poater J., Fonseca Guerra C., Bickelhaupt F. M., Phys. Chem. Chem. Phys. 2017, 19, 16969–16978. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
Supplementary


