Structural and functional impact of troponin C-mediated Ca²⁺ sensitization on myofilament lattice spacing and cross-bridge mechanics in mouse cardiac muscle

Abstract

Acto-myosin cross-bridge kinetics are important for beat-to-beat regulation of cardiac contractility; however, physiological and pathophysiological mechanisms for regulation of contractile kinetics are incompletely understood. Here we explored whether thin filament-mediated Ca²⁺ sensitization influences cross-bridge kinetics in permeabilized, osmotically compressed cardiac muscle preparations. We used a murine model of hypertrophic cardiomyopathy (HCM) harboring a cardiac troponin C (cTnC) Ca²⁺-sensitizing mutation, Ala8Val in the regulatory N-domain. We also treated wild-type murine muscle with bepridil, a cTnC-targeting Ca²⁺ sensitizer. Our findings suggest that both methods of increasing myofilament Ca²⁺ sensitivity increase cross-bridge cycling rate measured by the rate of tension redevelopment (k_TR); force per cross-bridge was also enhanced as measured by sinusoidal stiffness and I_1,1/I_1,0 ratio from X-ray diffraction. Computational modeling suggests that Ca²⁺ sensitization through this cTnC mutation or bepridil accelerates k_TR primarily by promoting faster cross-bridge detachment. To elucidate if myofilament structural rearrangements are associated with changes in k_TR, we used small angle X-ray diffraction to simultaneously measure myofilament lattice spacing and isometric force during steady-state Ca²⁺ activations. Within in vivo lattice dimensions, lattice spacing and steady-state isometric force increased significantly at submaximal activation. We conclude that the cTnC N-domain controls force by modulating both the number and rate of cycling cross-bridges, and that the both methods of Ca²⁺ sensitization may act through stabilization of cTnC’s D-helix. Furthermore, we propose that the transient expansion of the myofilament lattice during Ca²⁺ activation may be an additional factor that could increase the rate of cross-bridge cycling in cardiac muscle. These findings may have implications for the pathophysiology of HCM.

1. INTRODUCTION

Contraction of the heart depends on Ca²⁺ binding to the troponin complex. The troponin complex resides in the thin filament of striated myocytes in the heart and skeletal muscle. In cardiac myocytes, the troponin complex is comprised of the Ca²-binding subunit, cardiac troponin C (cTnC), the inhibitory subunit, cardiac troponin I (cTnI), and the tropomyosin-binding subunit, cardiac troponin T (cTnT). A transient rise in intracellular Ca²⁺ levels leads to a series of conformational changes in the thin filament, which ultimately promotes cyclic actin-myosin interactions and relative sliding of the thick (i.e., myosin) and thin (i.e., actin) filaments (1, 2). Considering that the regulatory N-terminal domain of cTnC is the Ca²⁺ sensitive switch, it is not surprising that it plays a central role in regulating force production in striated muscle.

It has been previously suggested that kinetics of cross-bridge cycling are influenced by Ca²⁺dependent activation in striated muscle across multiple vertebrate species (3–13). One of the first studies to demonstrate this relation used detergent skinned (permeabilized) rat ventricular trabeculae and showed that increasing Ca²⁺ concentrations resulted in a concomitant increase in the rate of tension redevelopment (k_TR) (12). This Ca²⁺-dependence of k_TR was subsequently reported in permeabilized rat cardiomyocytes (3) and permeabilized guinea pig trabeculae (13). Noteworthy, even in intact cardiac muscle, it was demonstrated that Ca²⁺ influences tension redevelopment (5). Small molecule cTnC Ca²⁺ sensitizers have also been shown to influence cross-bridge kinetics (9, 14). Although these studies point to a role for Ca²⁺ in regulating crossbridge mechanics beyond steric access to myosin-binding sites on actin, little is known about the direct role of cTnC in modulation of cross-bridge kinetics and the underlying mechanisms.

The sarcomeres of striated muscle cells form a well-ordered lattice comprising a double, hexagonal array of overlapping thin and thick filaments that are responsible for generating contractile force in the heart (1, 15). It has been previously shown that interfilament spacing modulates cross-bridge kinetics in Drosophila flight muscle (16). Mathematical modeling also supports the idea that myofilament lattice spacing may modulate cross-bridge kinetics in striated muscle (17). Furthermore, myofilament lattice spacing (18) and sarcomere length (19) are dynamic during the contraction-relaxation cycles of the heart in vivo. Therefore, lattice spacing may also have a functional role in regulating Ca²⁺-dependent cross-bridge kinetics in cardiac muscle.

In this study, we explored the effects of thin filament Ca²⁺ sensitization on cross-bridge mechanics in permeabilized cardiac ventricular muscle. For all of the experiments in this study, dextran T-500 was included in the solutions to osmotically compress the myofilament lattice to the dimensions found in vivo (18). We found that Ca²⁺-sensitization through the regulatory (N-terminal) domain of cTnC, by either a small molecule Ca²⁺ sensitizer, bepridil (Bep) (14), or a cTnC mouse model of HCM (20), influences both the number and kinetics of acto-myosin cross-bridges. To understand a potential molecular mechanism underlying the Ca²⁺-dependence of acto-myosin kinetics, we used small angle X-ray diffraction to simultaneously measure lattice spacing and steady-state, isometric force. Here we show that lattice spacing increases throughout isometric force development at physiologically-relevant Ca²⁺ concentrations. Expansion of the myofilament lattice may therefore constitute a novel molecular mechanism to mediate contractility in the heart.

2. MATERIALS AND METHODS

2.1. Experimental Animals

All protocols and experimental procedures followed NIH guidelines and were approved by Florida State University’s Animal Care and Use Committee (IACUC). Knock-in mice harboring the cTnC-A8V mutation in both alleles (KI-TnC-A8V^+/+) and wild-type controls (“Ctrl”) were used in this study. These mice have been previously characterized and published by our group (20, 21). KI-TnC-A8V^+/+ mice were shown to develop HCM in the adult stage (20, 22) and are therefore denoted as “HCM.” All animals used in this study ranged from 7–10 months of age.

2.2. Calcium Solutions

Relaxing and activating solutions were calculated using the pCa Calculator (23) and contained: 20 mM 3-[N-morpholino]propanesulfonic acid (MOPS), 7 mM ethylene glycol-bis(2aminoethylether)-N,N,N′,N′-tetraacetic acid (EGTA), 15 mM phosphocreatine, 15 units mL⁻¹ creatine phosphokinase, 2.5 mM MgATP^2-, 1 mM free Mg²⁺, ionic strength maintained constant at 150 mM by adding Kpropionate (KPr), varying [Ca²⁺], pH 7.0. The anion of choice for the pCa solutions was propionate (e.g., CaPr₂, MgPr₂ and KPr). All solutions were made and experiments were performed at room temperature (20–21°C). All solutions contained 3% (w:v) dextran M_r 450,000–650,000 (Sigma-Aldrich, cat. 31392), referred to as “dextran T-500”.

2.3. Cardiac Muscle Preparations

Cardiac permeabilized muscles were prepared as previously described (24). For muscle mechanics studies, excised Ctrl hearts (4 male and 1 female) and HCM hearts (2 males and 2 females) were opened along the septum and pinned onto a Sylgard-coated plate (Sylgard 184 Silicone Elastomer) to expose the left ventricle (LV) to non-ionic detergent 1% Triton X-100 (v:v) in a relaxing pCa 8 solution (10⁻⁸ M, 150 mM ionic strength, 2.5 mM MgATP^2-, pH 7). After 4 hrs incubation in Triton X-100 skinning solution at 4°C, the solution was changed to a relaxing pCa 8 solution containing 51% glycerol (v:v) and stored at -20°C. Isolated papillary muscles were then utilized for mechanical studies within one week. For small angle X-ray diffraction studies, excised Ctrl hearts (2 male, 2 female) and HCM hearts (3 female, 2 male) were cut along the left ventricle parallel to the septum and pinned onto Sylgard-coated plates exposing the left ventricle to non-ionic detergent 1% Triton X-100 and 0.2 mg/ml saponin in relaxing pCa 8 solution for 4 hrs at 4^oC. Papillary muscles and trabeculae were used for lattice spacing measurements within 12 hrs of isolation. Permeabilized Cardiac Muscle Preparations (CMPs) were dissected and their ends attached to aluminum T-clips. For muscle mechanics experiments, end compliance was minimized by chemically fixing the ends using 1% glutaraldehyde (25). Sarcomere length (SL) at pCa 8 was set to 2.1 μm using HeNe laser diffraction. Prior to the start of both mechanical and X-ray diffraction experiments, permeabilized CMPs were incubated for 1 hr in pCa 8 with 3% dextran T-500 solution to compress the myofilament lattice to physiological dimensions.

2.4. Muscle Mechanics

Force was measured using a force transducer (Aurora Scientific Inc. Model 403A) and length was controlled using a high-speed servomotor (Aurora Scientific Inc. Model 322C). Measurements of k_TR were obtained by shortening CMPs (~ 1 mm in length and 0.15 ± 0.01 mm in diameter for WT and 0.16 ± 0.01 mm in diameter for HCM) 20% of L₀ (initial CMP length at pCa 8) for 20 ms at ramp shortening rate ~ V_max, followed by a step 25% rapid re-stretch and release that returned CMP back to L₀. The apparent rate constant was obtained from each tension recovery time course as previously described (8, 26). Briefly, the half-time (t_1/2) of force recovery—an unbiased, model-independent estimate of a kinetic constant—was transformed according to k_TR = τ⁻¹ = -ln(t_1/2)/0.5 and the rate was expressed in units of s⁻¹. Conditions where steady-state, isometric force was below 15% of the maximal force were excluded from the k_TR analysis. Sinusoidal Stiffness (SS) measurements were recorded as previously described (27). Briefly, CMP were oscillated ~ 0.2% L₀ peak-to-peak at 100 Hz with a sampling rate of 1 kHz (i.e., 5-fold above the Nyquist frequency); this frequency was chosen to correspond to the highest frequency used in our previous study and is > 4-fold higher than the highest “dip” frequency at saturating Ca²⁺ in Bode plots of stiffness (21). SS data were analyzed using R Studio Fast Fourier transform and reported in units of MPa. Relative pCa-force and pCa-SS relationships were fit using a 2-parameter, sigmoidal Hill equation, and normalized pCa-force relationships were fit using a 3-parameter, sigmoidal Hill equation as previously described (28).

2.5. Small-Angle X-Ray Diffraction

X-ray diffraction experiments were conducted at the BioCAT undulator-based beamline 18ID at the Advanced Photon Source (Argonne National Labs, Lemont, IL) (29). The CMPs (~ 1 mm in length and 0.35 ± 0.02 mm in diameter for WT and 0.25 ± 0.02 mm in diameter for HCM) were carefully attached to aluminum T-clips between a force transducer (Aurora Scientific model 402A) and a servomotor (Cambridge Technology, model 308B; Aurora Scientific, Aurora, Canada), both mounted on micromanipulators. The CMPs were set to SL 2.1 μm at pCa 8 using HeNe laser diffraction. A custom experimental apparatus allowed simultaneous collection of the X-ray patterns and steady-state force during Ca²⁺ stepwise activation (30). Lattice spacing was measured as described previously (30). The sample-to-detector distance for the small-angle Xray diffraction camera was ~ 3 m and the focal spot size was about 150 × 50 μm in the detector plane. Diffraction images were collected on a CCD-based X-ray detector (Mar 165, Rayonix Inc. Evanston IL). Exposure times were ~ 0.5 s with an incident X-ray flux of ~ 1 × 10¹² photons s⁻¹. To minimize radiation damage to specific regions of each CMP, exposure was distributed along ~ 90% of the length of each CMP by oscillation of the muscle rig using a ZETA microstepping drive and motor (Compumotor Division of Parker Hannifin Corp, Rohnert Park, CA); motion was along the CMP’s longitudinal axis using the default waveform setting of the ZETA drive at a rate of 1 – 2 mm s⁻¹. Lattice spacing (d_1,0) was evaluated from the diffraction pattern using Bragg’s law. Intensities of the 1,0 and 1,1 equatorial reflections (I_1,0 and I_1,1, respectively) were determined from nonlinear least square fits to 1-dimensional projections of the integrated intensity along the equator (31).

2.6. Mathematical Modeling of Tension Redevelopment Kinetics

The relationship between isometric steady-state force and k_TR was modeled using the 3-state model of muscle contraction that was originally described by Landesberg and Sideman (7), and subsequently validated for cardiac muscle (32, 33). The 3-state model for cardiac muscle is a simplified version of a 4-state model that has been used extensively for modeling force-k_TR relations in skeletal muscle (9, 26, 32, 34). The coupled differential equations for the 3-state model were solved for a given set of parameters (f, g, k_OFF and [Ca²⁺]k_ON) using MatLab (release R2016b 9.1.0.441655, The MathWorks, Inc., Natick, MA, USA) as described (33). Parameter estimates (f, g and k_OFF) were iteratively modified from initial starting values to identify best fit values using the Simplex algorithm (35), implemented in MatLab; k_ON was held constant according to values obtained experimentally using WT- or HCM-containing thin filaments in the presence of myosin and MgATP (36) and pCa was varied between 9 and 4 in increments of 0.05 pCa units. Steady-state force and k_TR were calculated for each of the predicted force time courses using algorithms equivalent to those applied to CMP data. Interpolative refinement was then used to estimate k_TR and pCa where the predicted steady-state force matched the experimental force values. Best fit estimates of 3-state model parameters (f, g and k_OFF) were identified according to the least squares criterion where the sum of squared deviations (SSD) to be minimized was modified to include not only the difference between the predicted and measured force-k_TR relations but also the difference between the predicted and measured pCa₅₀ for isometric force; SSD components were weighted to emphasize the maximum k_TR, pCa₅₀, and the maximum force normalized to Ctrl. A maximum relative tolerance of 10⁻⁵ was used to define convergence of the Simplex algorithm for each parameter estimate (f, g and k_OFF) and also the corresponding modified sum of squares for each set of parameter estimates in the simplex.

2.7. Statistical Analysis

Data were reported as mean ± S.E. Statistical significance was tested using one-way ANOVA with post-hoc Student-Newman-Keuls test. When a group failed normality or equal variance, a non-parametric test was used. The specific statistical tests for each parameter can be found in the legends of figures and tables. p<0.05 was considered statistically significant. SigmaPlot version 12 was used for statistical analysis.

3. RESULTS

3.1. Myofilament Ca²⁺ sensitization through the N-domain of cTnC

Although our group has previously reported that KI-cTnC-A8V^+/+ heart muscle exhibits enhanced Ca²⁺ sensitivity of steady-state isometric force production (20, 21), experiments in this present study differed by the presence of dextran T-500. Since it is well known that permeabilizing muscle induces swelling of the myofilament lattice, 3% dextran T-500 was included in all Ca²⁺ solutions to achieve physiological lattice spacing dimensions (18, 37, 38). Steady-state, isometric force was measured as a function of graded Ca²⁺ concentrations in permeabilized cardiac muscle preparations (CMPs) isolated from HCM mouse hearts at SL 2.1 μm in the presence of 3% dextran. Consistent with previous reports, HCM CMPs exhibited a significant leftward shift of the pCa-force relationship, indicating increased myofilament Ca²⁺ sensitivity of isometric force production (HCM vs. Ctrl ΔpCa₅₀ = +0.61 pCa units) (Fig. 1A, 1B, 1D and Table 1).

Figure 1. pCa-force relationship and maximum force at SL 2.1 μm.

A) Normalized steady-state isometric force as a function of pCa. The force values were normalized to the maximum steady-state isometric force in Ctrl CMPs. B) Relative steady-state isometric force as a function of pCa. The force values were normalized to the maximum force of each individual CMPs. C) Maximum steady-state isometric force values for each CMPs. D) pCa₅₀ values for each CMPs. Horizontal bars represent the mean. Data are shown as mean ± S.E. n = 19 Ctrl, 23 HCM and 10 Ctrl+Bep. *p<0.05, statistical tests are described in legend of Table 1.

Table 1.

Contractile Parameters for CMPs at SL 2.1 μm

	Ctrl	HCM	Ctrl+Bep
${\mathbf{F}}_{\mathbf{max}}\left(\frac{\mathbf{m}\mathbf{N}}{\mathbf{m}{\mathbf{m}}^{\mathbf{2}}}\right)$	42.6 ± 3.3	36.7 ± 2.6	39.2 ± 5.0
FpCa50	5.57 ± 0.02	6.18 ± 0.03*,#	5.77 ± 0.04*
nHill	3.0 ± 0.2	2.4 ± 0.4*	1.9 ± 0.2*
ktr max (s−1)	19.3 ± 1.1	24.8 ± 0.9*,#	27.8 ± 1.0*
SSmax (MPa)	2.3 ± 0.3	1.4 ± 0.1*	2.2 ± 0.4
SSpCa50	5.59 ± 0.02	6.28 ± 0.03*,#	5.81 ± 0.04*

F_max = maximum steady-state isometric force; F_pCa50 = pCa needed to reach 50% of the maximum steady-state isometric force; n_Hill = cooperativity of thin filament activation; k_{tr max} = maximum rate of tension redevelopment; SS_max = maximum steady-state sinusoidal stiffness; SS_pCa50 = pCa needed to reach 50% of the maximum steady-state sinusoidal stiffness.

^*p<0.05, HCM or Ctrl+Bep vs. Ctrl

^#p<0.05, HCM vs. Ctrl+Bep

The statistical significance for F_max, F_pCa50, k_{tr max}, SS_pCa50 was determined using one-way ANOVA with post-hoc Student-Newman-Keuls test.

The statistical significance for n_Hill, SS_max was determined using Kruskal-Wallis one-way analysis of variance on ranks.

Number of CMPs = 10–23 per parameter.

As an additional tool to examine the functional effects of Ca²⁺-sensitization through cTnC apart from HCM muscle, we treated Ctrl CMPs with Bep, a small molecule Ca²⁺ sensitizer that is known to bind directly to the regulatory domain of cTnC (14, 39, 40). Upon treatment with 300 μM Bep, Ctrl+Bep CMPs exhibited a significant leftward shift in the pCa-force relationship (Ctrl+Bep vs. Ctrl ΔpCa₅₀ = +0.20 pCa units) (Fig. 1A, 1B, 1D and Table 1), indicating enhanced myofilament Ca²⁺ sensitivity during isometric contraction. These results followed the same myofilament Ca²⁺ sensitivity trend observed for HCM CMPs and are also consistent with previous reports (14). No significant differences in maximum steady-state force among the three preparations were observed (Fig. 1C, Table 1). The cooperativity of thin filament activation (n_Hill) was significantly reduced in both Ca²⁺-sensitized groups compared to Ctrl (HCM = 2.75 ± 0.55, Ctrl+Bep = 1.85 ± 0.16 and Ctrl = 3.34 ± 0.17) (Fig. 1A, 1B and Table 1). In the following experiments, we used HCM and Ctrl+Bep CMPs to probe the effects of cTnC-mediated Ca²⁺sensitization on various mechanical parameters of muscle contraction.

3.2. Two independent methods of increasing Ca²⁺ sensitivity through the N-domain of cTnC also increase k_TR

Several reports have provided evidence showing that Ca²⁺ influences the rate of force production in cardiac muscle (3–7, 12, 41), but little is known about the direct role of cTnC in this process. To this end, we measured k_TR to understand how enhanced myofilament Ca²⁺ sensitivity through cTnC influences contractile kinetics. In most physiologically relevant circumstances, activation-dependence of k_TR provides insight into the actomyosin cross-bridge cycling kinetics at high levels of activation, and the dynamics of individual regulatory units on thin filaments at submaximal levels of activation (8, 9, 26, 32, 34). Representative force and length traces are shown in Figs. 2A-D. HCM CMPs exhibited significantly faster k_TR at all levels of Ca²⁺activation compared to Ctrl CMPs (Fig. 2E, Table 1). Ctrl+Bep CMPs also exhibited significantly faster k_TR at all levels of Ca²⁺-activation compared to Ctrl (Fig. 2E, Table 1). Furthermore, HCM and Ctrl+Bep CMPs display faster k_TR at similar isometric force levels compared to Ctrl (Fig. 2F). These results suggest that the regulatory N-domain of cTnC could play an important role in determining cross-bridge kinetics in cardiac muscle.

Figure 2. The rate of tension redevelopment (k_TR) at SL 2.1 μm.

A and B) Representative tracings of absolute force values as a function of time during the k_TR protocol. C and D) Representative tracings of percentage length variation as a function of time during the k_TR protocol. E) k_TR as a function of increasing Ca²⁺ concentration. Dashed lines were drawn by eye. F) Normalized force vs. k_TR. The force values were normalized to the maximum steady-state isometric force in Ctrl CMPs. Lines represent solutions to the 3-state model in Fig. 5; solid lines represent model solutions using the best fit parameters (f, g, k_OFF) and k_ON listed in Table 2, and dotted lines represent solutions when all four parameters were either increased (upper line) or decreased (lower line) by 2%. Data are shown as mean ± S.E. n = 19 Ctrl, 22 HCM, and 10 Ctrl+Bep.

3.3. Mathematical modeling of k_TR indicates that both methods of increasing Ca²⁺ sensitivity increase cross-bridge kinetics in addition to the expected changes in thin filament regulatory unit dynamics

To understand the source of faster k_TR observed in HCM and Ctrl+Bep CMPs, we used a 3-state model of muscle contraction to explore the effects of HCM and Bep on the cross-bridge attachment (f) and detachment (g) rates (Fig. 2F). The best fit values for g, f and k_OFF are reported in Table 2. Compared to Ctrl, the g values for HCM and Ctrl+Bep CMPs increased by a larger magnitude than f (Table 2). Because maximal k_TR ∝ f + g (42), these analyses suggest that the increased k_TR observed in HCM CMP is due to a faster cross-bridge detachment rate, g, while the increased k_TR in Ctrl+Bep CMP comes from both faster cross-bridge attachment and detachment rates.

Table 2.

Optimized parameter estimates and predictions from the 3-state model depicted in Fig. 5

CMPs	Bepridi l (μΜ)	3-state model fitted parameters				3-state model predictions
		Cross-bridge		Regulatory unit
		f (s−1)	g (s−1)	kON (M−1 s−1) (36)	kOFF (s−1)	pCa50	max force (norm.)	max kTR (s−1)
Ctrl	0	11.8	8.3	1.84×108	1254.4	5.57	1.00	19.3
HCM	0	12.4	12.6	1.34×108	176.6	6.18	0.86	24.8
Ctrl	300	15.6	13.4	1.84×108	702.2	5.77	0.92	27.8

Best fit parameter estimates for three parameters (f, g and k_OFF) were obtained using the Simplex method (see Methods section); values for k_ON were from measurements reported by Pinto et al. (36). These parameter sets were used to illustrate relations between k_TR and steady-state, isometric force in Fig. 2F (solid lines in Fig. 2F); also see the figure for information on the influence of small deviations (+/− 2%) from the best fit parameter estimates on predicted k_TR-force relations (dashed lines in Fig. 2F).

3.4. Ca²⁺ sensitization through the N-domain of cTnC may influence the number of crossbridges

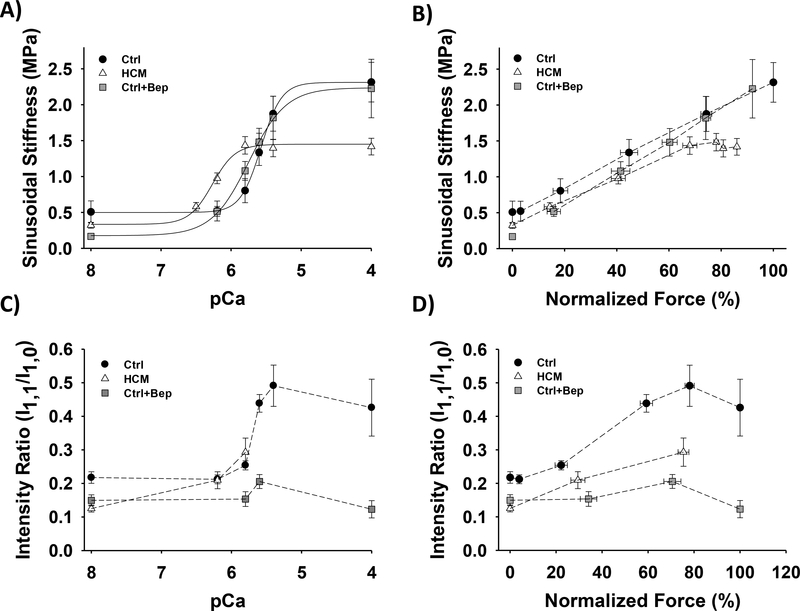
Considering the importance of actin-myosin interactions in the contraction-relaxation cycle of the heart, we sought to examine potential alterations in thin-thick filament interactions as a result of Ca²⁺ sensitization through cTnC. To accomplish this, we measured sinusoidal stiffness (SS) during steady-state, isometric contraction at all levels of Ca²⁺ activation (Fig. 3A and Table 1). Measurements of SS provide insight into the overall number of cross-bridges, although this is modulated by end compliance and compliances within the preparation (43–45) and can be further modulated by cross-bridge kinetics (21) and fundamental properties of the preparation (46). HCM CMPs and Ctrl+Bep CMPs exhibited leftward shifts of pCa-SS relations compared to Ctrl (HCM vs. Ctrl ΔSSpCa₅₀ = +0.69 and Ctrl+Bep vs. Ctrl ΔSSpCa₅₀ = +0.22 pCa units). The exhibited shifts in SSpCa₅₀ were correlated to those observed from the corresponding pCa-force relations (Figs. 2 and 3A, and Table 1). Despite the differences in Ca²⁺ sensitivity, the relationships between SS and normalized force were generally similar for all three preparations across most levels of Ca²⁺-activation (Fig. 3B); the overall linearity of the relationships in Fig. 3B for most levels of Ca²⁺-activation indicates that the primary mechanism by which Ca²⁺ activates force is through recruitment of cross-bridges. At the highest levels of Ca²⁺ activation, however, maximum steady-state SS of HCM CMPs was significantly lower than Ctrl (Fig. 3A, 3B and Table 1), consistent with data at the highest frequency utilized in our prior study (21). In contrast, there was no significant difference in maximum steady-state SS between Ctrl+Bep vs.

Figure 3. Sinusoidal stiffness and small-angle X-ray diffraction analysis in CMPs at SL 2.1 μm.

A) Ca²⁺-dependence of steady-state sinusoidal stiffness. B) Normalized force vs. steady-state sinusoidal stiffness. The force values were normalized to the maximum steady-state isometric force in Ctrl CMPs. Dashed lines were drawn by eye. C) Equatorial diffraction intensity ratios (I_1,1/I_1,0) as a function of pCa. The equatorial diffraction intensities were obtained by small-angle X-ray diffraction. D) Normalized force vs. equatorial intensity ratios. The force values were normalized to the maximum steady-state isometric force in Ctrl CMP. Data are shown as mean ± S.E. n = 19 Ctrl, 23 HCM and 10 Ctrl for sinusoidal stiffness data. The number of CMPs and X-ray shots for the small-angle X-ray diffraction data is presented in supplementary Table 1.

Ctrl (Fig. 3A and Table 1). Assuming that the number of cross-bridges ∝ f/(f + g) (42), the measured differences in maximum SS for the three preparations (Fig. 3A, B) are in the direction predicted from values of f and g obtained from fitting force-k_TR data (Fig. 2F) to the 3-state model (Table 2). The observation that Ctrl and Ca²⁺ sensitized HCM (and Ctrl+Bep) CMPs develop statistically indistinguishable levels of force at saturating Ca²⁺ (Fig. 1C and Table 1) with lower maximum steady-state isometric SS for HCM (Fig. 3A, 3B and Table 1) suggests not only that the number of cross-bridges may be lower in HCM CMPs, but also that the force per cross-bridge could be higher in Ca²⁺-sensitized HCM muscle.

To complement our findings from SS measurements, we also used small-angle X-ray diffraction to collect equatorial intensity ratios (I_1,1/I_1,0) during graded Ca²⁺ activation. Representative diffraction images and intensity profiles are shown in Supplemental Fig. 1. The I_1,1/I_1,0 intensity ratio provides information about mass transfer from thick to thin filaments, which can be used as an index for the number of cross-bridges formed during muscle activation. Consistent with Ctrl SS measurements (Figs. 3A, 3B), I_1,1/I_1,0 generally increased with activation level in Ctrl CMPs (Figs. 3C, 3D). Comparing I_1,1/I_1,0 in both HCM and Ctrl+Bep CMPs with Ctrl at similar levels of Ca²⁺-activated steady-state force, less mass transfer from thick to thin filaments was observed in the Ca²⁺ sensitized CMPs (Fig. 3C, 3D). Taken together, the X-ray and SS measurements both suggest that the number of cross-bridges and force per cross-bridge could be altered in HCM, and possibly Ctrl+Bep, Ca²⁺ sensitized CMPs. These findings therefore demonstrate that a single N-terminal domain point mutation in cTnC perturbs acto-myosin interactions in a Ca²⁺dependent manner. Furthermore, findings from the Ctrl+Bep CMPs support the importance of cTnC-mediated Ca²⁺ sensitization in perturbing thick-thin filament interactions.

3.5. Myofilament lattice spacing increases during Ca²⁺-activated isometric force production

Considering that we observed Ca²⁺-dependent effects on cross-bridge kinetics in both HCM and Bep-treated muscle, we hypothesized that alterations in myofilament lattice spacing may help explain some of these effects. To address this question, we used small angle X-ray diffraction to simultaneously measure isometric force and lattice spacing as a function of Ca²⁺ concentration. Representative diffraction images in various Ca²⁺ solutions are provided in Fig. 4A. It should be noted that there is an inverse relationship between the d_1,0 equatorial distance in the diffraction patterns and myofilament lattice spacing. Starting with the lattice compressed to physiological diastolic dimensions (18, 37, 47) by 3% dextran in relaxing conditions (supplemental Fig. 2), lattice spacing of Ctrl CMPs increased in parallel with increased Ca²⁺-activated, isometric force (Fig. 4B). A similar force-lattice spacing trend was observed at most levels of Ca²⁺ activation for HCM (Fig. 4B) but not Ctrl+Bep CMPs (Fig. 4C), possibly due to a larger lattice spacing for Ctrl+Bep CMPs in relaxing conditions (supplemental Fig. 2). Beginning at equivalent lattice spacing dimensions compared to Ctrl and reaching comparable maximum lattice spacing upon Ca²⁺ activation, Ctrl and HCM CMPs demonstrated similar ranges of lattice spacing (Ctrl Δ = + 2.22 nm and HCM Δ = + 2.35 nm) (Fig. 4D). Bep-sensitized CMPs exhibited an attenuated, activation-associated increase in lattice spacing (Ctrl+Bep Δ = + 0.30 nm) (Fig. 4E and supplemental Fig. 2). Surprisingly, at the highest levels of Ca²⁺ activation, lattice spacing of both HCM and Ctrl+Bep CMPs collapsed while maintaining maximum isometric force (Fig. 4B-E). The physiological significance of this lattice collapse in maximally activated, Ca²⁺ sensitized preparations, is questionable because normal cardiomyocyte contraction occurs at submaximal Ca²⁺ concentrations in the beating heart. Strikingly, significantly larger lattice spacing was observed for both HCM and Ctrl+Bep CMPs compared to Ctrl at submaximal activation (pCa 5.8 and 5.6) due at least in part to increased Ca²⁺ sensitivity (Fig. 4D and 4E).

Figure 4. Simultaneous measurements of myofilament lattice spacing and steady-state isometric force at SL 2.1 μm.

A) Representative images of CMPs small-angle X-ray diffraction in various pCa solutions. The top horizontal line shows a deviation of the d_1,0 as contraction develops and the bottom red line intersects each d_1,0 intensity at the center to demonstrate the decrease in lattice spacing that is being reported. Note the reciprocal relationship between d_1,0 equatorial distances and lattice spacing. B and C) Relative force vs. lattice spacing. The force values were normalized to the maximum force of each individual CMPs. D and E) Ca²⁺-dependence of myofilament lattice spacing. Dashed lines were drawn by eye. *p<0.05 vs. Ctrl, statistical significance was determined by Mann-Whitney U test. A minimum of 20 X-ray shots were obtained at each pCa, for exact number of CMPs and shots and refer to supplementary Table 2 Data are shown as mean ± S.E.

4. DISCUSSION

The major observations from this study using osmotically compressed, permeabilized muscle preparations from mouse heart are as follows. Increased Ca²⁺-sensitivity via the N-domain of cTnC (HCM or Bep) was associated with: (i) increased k_TR at all Ca²⁺-activation levels, which was most readily explained by an increased rate of cross-bridge detachment (g); and (ii) reduced mass transfer from thick to thin filaments (I_1,1/I_1,0 ratio) upon Ca²⁺ activation, and also stiffnessto-force ratio. Myofilament lattice spacing increased with Ca²⁺-activation for both WT and HCM preparations. These results have implications for the pathophysiology associated with some HCM mutations and the physiological interrelationship among thin filament Ca²⁺activation, mechanical kinetics, and myofilament lattice spacing in cardiac muscle.

4.1. Interrelationship between thin filament Ca²⁺-sensitivity and mechanical kinetics

Consistent with our prior studies conducted in the absence of osmotic compression (20, 21, 48), the HCM mutation enhanced myofilament Ca²⁺ sensitivity of steady-state, isometric force in the presence of 3% dextran T-500 (Fig. 1, Table 1). The HCM mutation was also associated with increased Ca²⁺ sensitivity of k_TR (Fig. 2E) and stiffness (Fig. 3A). Interestingly, k_TR was faster at all levels of thin filament Ca²⁺-activation (Fig. 2E), and the increases were markedly beyond what could be attributed to the leftward shift of the force-k_TR relationship (Fig. 2F). At saturating Ca²⁺, this HCM mutation was previously shown to be associated with increased myofibrillar ATPase activity (28, 49) and higher frequencies of oscillatory work during small amplitude, sinusoidal length perturbations (21). Both prior observations at maximal activation, together with the k_TR measurements at maximal and submaximal levels of thin filament Ca²⁺-activation, are indicative of faster cross-bridge cycling. Faster cross-bridge kinetics may be consistent with expectations for an HCM mutant but, at first blush, are surprising for a point mutation on the thin filament. When the force-k_TR and pCa₅₀ data were simultaneously fit (as described in Materials and Methods) to the 3-state model (Fig. 5), we found that not only is k_OFF reduced (7-fold) for HCM compared to WT—as required to explain the leftward shift of the force-pCa relationship— but the cross-bridge detachment rate (g) is increased by ~ 50% with little change in attachment rate (f) (Table 2). This inference from the Ca²⁺ activation-dependence of k_TR is quantitatively consistent with our previous report that the HCM mutation increases cross-bridge detachment rate, as determined from sinusoidal perturbation analysis at maximal Ca²⁺ activation (21).

Figure 5. Schematic of the three-state model of striated muscle contraction.

Faster k_TR at all levels of thin filament Ca²⁺-activation was similarly observed with an independent approach for enhancing myofilament Ca²⁺ sensitivity: treatment of control cardiac muscle with the small molecule Ca²⁺-sensitizer bepridil (Fig. 2). Mechanistically, Bep and HCM-associated A8V mutation augment myofilament Ca²⁺ sensitivity by increasing the Ca²⁺ binding affinity to Ca²⁺-binding regulatory site II in cTnC (14, 36, 50). As with the HCM mutation, fitting the data to the 3-state model (Fig. 5) indicated that not only is k_OFF reduced by almost 2-fold for Bep compared to WT—as required to explain the leftward shift of the forcepCa relationship—but the cross-bridge detachment rate (g) is increased by ~ 60% (Table 2); with Bep, however, cross-bridge attachment rate (f) is increased ~ 30%. Although lower Bep concentrations were shown to have no effect on maximum k_TR in skeletal muscle preparations (51, 52) and human atrial myofibrils (53), it is not clear which of the numerous experimental differences beyond Bep concentration—including species, muscle type, absence of osmotic compression, longer relaxed SL, lower temperature and slower maximal k_TR—might contribute to this difference compared with our finding of a marked increase in both submaximal and maximal k_TR upon Bep treatment of mouse ventricular tissue (Fig 2, Table 1). Intriguingly, a different Ca²⁺ sensitizer, calmidazolium, has also been shown to increase k_TR at submaximal activation in skeletal muscle (9). Like Bep, calmidazolium functions through interactions with the regulatory N-domain of TnC (54).

The above findings suggest that enhanced myofilament Ca²⁺ sensitivity through cTnC may accelerate cross-bridge kinetics, at least under certain circumstances. In support of this possibility, engineered mutations in cTnC (F27W or the double mutant V44Q,F27W) that increase Ca²⁺-binding affinity also increase k_TR at maximal Ca²⁺ activation of cardiac muscle (11); while the double mutant also increases k_TR at submaximal Ca²⁺ activation, the increases at all levels of Ca²⁺ activation were smaller than reported here (Fig. 2). However, in contrast to our findings (Fig. 2), these engineered mutations in cTnC did not alter the force-k_TR relation. Moreover, several mutations in the C-termini of cTnI or cTnT increase both the Ca²⁺ sensitivity of filament sliding in motility assays and also the maximum speed (55, 56), although k_TR has not been measured with these mutations. In addition, although faster k_TR was reported with a Ca²⁺sensitizing mutation in cTnT at submaximal Ca²⁺ activation (57), the increase was less than observed here with a cTnC mutation (Fig. 2) and was restricted to low levels of thin filament Ca²⁺ activation. These observations suggest there may be a mechanistic basis to a relationship between Ca²⁺-sensitization and faster cross-bridge cycling that involves the N-domain of cTnC. Bepridil binds at the N-domain of TnC (14, 39, 40), which is also the location of the HCMassociated A8V mutation used in our present study, the location of engineered mutations by Norman et al. (11), and also the domain to which the C-terminus of cTnI binds in the presence of Ca²⁺ (40, 58). However, a study by Kreutziger et al. (59), using an engineered Ca²⁺-sensitizing mutation in cTnC, L48Q which is also in the regulatory N-domain, showed at most a small but not significant increase in maximal k_TR in mouse ventricular myofibrils, and increases in k_TR only at a low level of Ca²⁺ activation in rat ventricular trabeculae. While the differences in Kreutziger et al.’s (59) study may be attributed to experimental variables—including extraction/reconstitution of cTnC, absence of osmotic compression, longer relaxed SL, lower temperature and slower maximal k_TR—we sought a more specific structural feature that might reconcile our k_TR results (Fig. 2) with those of Kreutziger et al. (59).

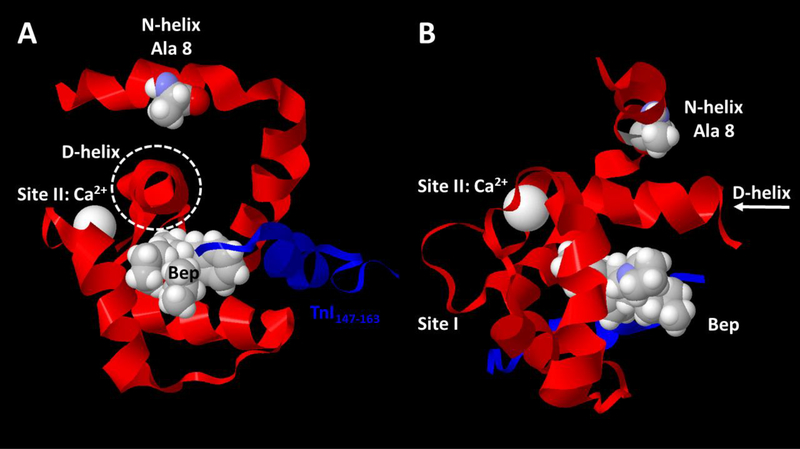
Examination of Wang et al.’s (40) NMR solution structure of cTnC’s N-domain complexed with Ca²⁺, cTnI switch peptide, and Bep (PDB 1LXF) reveals that, unlike Leu 48, Ala 8 and Bep both interact with the D-helix, albeit from opposite sides (Fig. 6). The sidechain of Ala 8 interacts with the sidechain of Val 82, and that interaction would be expected to strengthen with Ala → Val substitution in the HCM mutant, as suggested more generally for stabilization of protein tertiary structure by the branched sidechains in clusters of Ile-Leu-Val residues (60). Bepridil interacts with several residues in the D-helix as well as other parts of cTnC (39, 40). Thus both the HCM mutation and Bep would be expected to stabilize the D-helix relative to the rest of the N-domain. Ca²⁺ affinity at cTnC’s regulatory site could modulated via the D-helix because the D-helix connects directly to the C-terminal side of site II’s EF-hand. In addition, we note that the D-helix also connects to cTnC’s C-domain as part of the DE-helix linker. While the N- and C-domains of TnC are often considered to be independently mobile in the absence of TnI (and TnT) (61, 62), there appears to be some level of structural coordination between the N- and C-domains associated with divalent cation binding any of the functional EF-hands (63) and it is clear that there is functionally significant communication between the N- and C- domains of TnC (64, 65). The current work adds to the likelihood that coupling of the D-helix to site II, and by extension via entire DE-linker to the C-domain, may be important not only for determining Ca²⁺binding affinity of site II but also regulatory unit dynamics and contractile kinetics. Altogether, these findings raise the possibility of portions of the regulatory domain dynamics of cTnC in controlling cross-bridge detachment kinetics in heart muscle.

Figure 6. Structural evaluation suggests a common feature for Ca²⁺-sensitizers bepridil (Bep) and HCM mutation in the N-helix of cTnC, A8V: both interact with the D-helix of cTnC.

NMR structure of the regulatory N-domain of human cTnC complexed with Ca²⁺, Ca²⁺sensitizing molecule Bep, and the switch peptide from human cTnI was adapted from PDB 1LXF model 1 (40) using MatLab molviewer. A) View of cTnC N-domain looking down the Dhelix (within dashed circle) from the direction of cTnC’s C-domain (C-domain not shown). B) Side view of cTnC N-domain; arrow (right) indicates direction of view in panel A. In both panels, peptide backbones are shown as ribbons, with cTnC N-domain ribbon in red and cTnI switch peptide ribbon in blue; cTnC residue Ala 8 is emphasized with space-fill atoms. Ca²⁺ (bound at site II) and Bep are shown as space-fill atoms. Note that cTnC Ala 8 and Bep interact with opposite sides of cTnC’s D-helix which, along with the E-helix (not shown), connects the N- and C- domains.

The 3-state model (Fig. 5) for cardiac muscle and the related 4-state model for skeletal muscle (7, 32), while highly simplified, are capable of capturing the major features of force-k_TR relations under a wide variety of conditions. A major advantage of this model’s simplicity is that the small number of free parameters (three in this study: f, g and k_OFF) allows unambiguous identification of best-fit parameter estimates, as illustrated in Fig. 2F, and summarized in Table 2. We were able to reduce the number of free parameters for the 3-state model from four to three by constraining k_ON to that obtained experimentally (36). The 3-state model incorporates thin filament regulatory unit dynamics that were missing from the 2-state model used by Brenner in an initial investigation of the Ca²⁺-dependence of k_TR (10). The highly simplified nature of the 3-state model, while advantageous in many respects, means that there are many factors that are not included. Experimental measurements and more detailed models suggest that additional parameters—particularly those that may vary with Ca²⁺-activation level such as cooperative interactions among myofilament proteins, activation of the thick filament by force, myofilament compliance, and lattice spacing—could influence the relationship between Ca²⁺, thin filament regulatory unit dynamics, k_TR and force (44, 45, 66–70). We now consider myofilament filament lattice spacing, which we were able to measure during steady-state Ca²⁺-activations of cardiac muscle preparations (Fig. 4).

4.2. Can activation-dependent changes in myofilament lattice spacing influence mechanical kinetics?

Remarkably, the changes in myofilament lattice spacing with graded Ca²⁺ of Ctrl CMPs presented in this current report (Fig. 4D) are quantitatively comparable with those previously observed in living mouse heart (18). Thus, as previously noted, the lattice spacing measurements reported in our study are physiologically relevant, despite the use of permeabilized muscle. In addition to quantitatively similar lattice dimensions, the trend towards an increase in lattice spacing during contraction is supported by several studies (67, 71–73).

Myofilament lattice spacing is determined by the balance of opposing forces that favor lattice expansion against lattice compression. These forces include several components (15); because the preparations were permeabilized with detergent, the compressive force associated with a living cell’s membrane is not considered here.

First to consider is the compressive, osmotic pressure associated with dextran T-500. This high MW polymer is too large to enter the myofilament lattice, and a constant amount (3% w:v) was added to all bathing solutions to compress the filament lattice—which as noted above swells in the absence of the cell membrane and osmotic agents—to physiological dimensions. In the absence of osmotic compression, the lattice spacing of permeabilized muscle preparations— swollen in relaxed conditions—decreases upon Ca²⁺ activation (74). Compression of the filament lattice by osmotic agents, however, allows for activation of permeabilized muscle with no further reduction in lattice spacing (75). It is worth considering that, in addition to increasing osmolarity and thereby creating an osmotic pressure gradient between the bulk solution surrounding the permeabilized muscle preparation and the solution within that surrounds the myofilaments, high MW solutes (and solutes in general) alter properties of the bulk solution such as the activity of water (a_W), viscosity (η), dielectric constant (ε), etc. In addition, macromolecule solutes can act as “crowders” that mimic the crowded intracellular environment (76). While these solution properties affect actomyosin affinity and kinetics when the solutes directly surround the proteins (77, 78), any changes associated with lattice compression by high MW solutes exclusively in the bulk solution are not quantitatively consistent with effects obtained when the solutes are in the solution surrounding actin and myosin. For example, adding dextrans or low MW solutes to the solution surrounding actin and myosin markedly increases solution viscosity and slows actomyosin kinetics in a manner that is inversely proportional to the increase in viscosity (33). Osmotic compression by dextran T-500 in the bulk solution surrounding permeabilized muscle preparations, however, either increases k_TR (68) or causes at most a slight inhibition of k_TR (41). Structural effects within the myofilament lattice of permeabilized muscle when dextran T-500 is added to the bulk solution, such as the closer association of myosin heads with the thick filament (31, 38), are most likely indirect effects, and can be mimicked by lowering the ionic strength and/or lowering the temperature (38, 79), or stretching to longer SL (30).

There are several additional determinants of lattice spacing to consider beyond osmotic compression. The second factor is the radial component of mechanical force due to structural proteins (e.g., titin and z-disc proteins) that are responsible for maintaining the structure of the sarcomere. For example, when the sarcomere is stretched along the long axis of a relaxed myocyte, these proteins impose a compressive, radial force such that the lattice volume remains almost constant (15, 37, 47). If the relationship between diastolic lattice spacing and SL (37, 47) applies during steady-state Ca²⁺-activation, then sarcomere shortening during contraction (due to end compliance) might be quantitatively estimated from changes in lattice spacing. However, additional factors that contribute to radial force may alter this relationship in actively contracting muscle. Third is the electrostatic force associated with surface charge of the myofilaments. This is an expansive force as the thick and thin filaments both have net negative surface charge. Myofilament surface charge can be modified—directly through alteration of net charge, or indirectly by changes in protein structure and the location of acidic and basic sidechains—by the binding of ions (80) and some covalent post-translational modifications (e.g., phosphorylation). Fourth, and finally, is the radial component of cross-bridge force. The main vector of crossbridge force is, of course, along the long axis of the myocyte (17, 75). The radial force of a single, attached cross-bridge varies with lattice spacing such that it can be compressive or expansive, and thus there is an equilibrium value (15, 17, 75, 81). Furthermore, the step size of cycling cross-bridges is predicted to vary in a biphasic manner with lattice spacing (i.e., there is an optimal lattice spacing for cross-bridge function) (17). The total radial force due to all crossbridges in an activated myocyte obviously depends on the number of cross-bridges. Taking into consideration all of these possible factors, it is apparent that the major change in net radial force upon Ca²⁺-activation—leading to the observed lattice expansion—would likely be due to recruited cross-bridges. It is not possible, however, to rule out contributions from components other than the osmotic compressive force due to Dextran T-500, which was constant throughout this study.

Myofilament lattice spacing may modulate cross-bridge kinetics in an invertebrate striated muscle (16), and the same could be true for vertebrate muscles including cardiac muscle. Indeed, measurements of lattice spacing in the heart in situ indicate dynamic changes during the contraction-relaxation cycle and suggest that the myofilament lattice does not maintain a constant volume during force generation (18, 47, 71). Studies in intact skeletal muscle fibers also show changes in lattice volume during contraction and rapid length changes (82). Therefore, it is not surprising that we observed a significant expansion of the myofilament lattice at submaximal Ca²⁺ activation in Ctrl and HCM CMPs, with increased Ca²⁺ sensitivity of HCM compared to Ctrl (Fig. 4D). This increased Ca²⁺ sensitivity of lattice spacing is comparable to that observed for force, k_TR and SS (Figs. 1, 2E and 3A, and Table 1). It is tempting to speculate that lattice expansion (Fig. 4) may play a role in the observed activation-dependent increase of k_TR (Fig. 2). In support of this idea, it was previously shown that osmotic compression of the myofilament lattice in skinned rat cardiac trabeculae by addition of 4% dextran to the bulk solution dampened the k_TR-force relation compared to untreated muscle (41). In the absence of SL control, end compliance allows for sarcomere shortening, the extent to which depends on force and thus the level of Ca²⁺ activation, and thus at least some of the increase in k_TR with Ca²⁺ activation (Fig. 2) could be attributed to sarcomere shortening. As discussed in more detail above, diastolic lattice spacing expands at shorter SL; while this would also be expected during active contraction, it is not clear that the relationship would be quantitatively the same in both systolic and diastolic conditions. Despite this uncertainty, these studies add support to the possibility that lattice spacing may play a role in modulation of contractile kinetics in striated muscle.

How might myofilament lattice spacing influence k_TR if in fact it does so? At high levels of activation, k_TR is primarily determined by cross-bridge cycling rates: k_TR ∝ f + g (42). At low levels of Ca²⁺ activation, k_TR is modulated by the dynamics of thin filament regulatory units, but f and/or g could also vary with activation level in a manner that is not inherent in the 3-state model. Strikingly, the effects of Ctrl+Bep and HCM CMPs on muscle mechanics were generally similar (Figs. 1, 2 and 3), with the exceptions of the force-lattice spacing relation (Fig. 4B, D) and rate of cross-bridge attachment (Table 2). Considering that we observed a larger lattice spacing at low Ca²⁺ levels in Ctrl+Bep CMPs which was not seen in HCM (Fig. 4), we therefore speculate that expansion of the lattice spacing may influence f rather than g. Bep binding to cTnC could have structural effects beyond those associated the N-domain (Fig. 6), as suggested in the structure of Li et al. (39), and it is possible that also Bep binds elsewhere in the sarcomere. However, the overall similarity between the effects of Bep and the HCM mutation on cardiac mechanics suggests that the primary effects of Bep occur through cTnC. The idea of lattice spacing controlling muscle kinetics is not entirely novel. Based on experimental approaches and computational modeling, it has been previously suggested that lattice spacing can influence either rate of cross-bridge attachment and/or detachment in cardiac and skeletal muscle (17, 38).

We cannot fully explain the precipitous collapse of lattice spacing observed at high levels of muscle activation in both Ca²⁺-sensitized CMPs, HCM and Ctrl+Bep (Fig. 4). Because this phenomenon was not observed for Ctrl CMPs (Fig. 4), whatever is responsible appears to be specifically attributable to thin filament Ca²⁺-sensitization. The myofilaments are negatively charged under physiological conditions, i.e. pH ~ 7, ionic strength 150–200 mM (15). At maximal activation (~ pCa 4), the thin filaments of the Ca²⁺-sensitized CMPs would theoretically be saturated with Ca²⁺ ions to a greater extent compared to Ctrl (i.e., non-sensitized) CMPs. In principle, this could reduce the net surface charge of the negatively charged thin filaments, thus reducing the expansive electrostatic force and ultimately leading to collapse of lattice spacing. Regardless of the mechanism, we argue against the physiological relevance of this observation, considering that cardiomyocytes do not operate in such ranges of Ca²⁺ concentrations in vivo (83).

4.3. Thin-to-thick filament force transmission and regulation

An interesting observation in this present study showed that the HCM-associated CMPs were able to achieve the same steady-state isometric force as control preparations with fewer cross-bridges, suggesting that individual myosin heads may generate greater force (Fig. 3B). This was also evident in Bep-treated cardiac muscle (Fig. 3), thus highlighting the contribution of TnCmediated Ca²⁺ sensitization in these effects. X-ray diffraction measurements of the equatorial intensity ratios, which are used as an index of degree of mass shift from thick to thin filaments, presumably due to recruitment of cross-bridges, also showed that HCM and Bep-treated muscle was able to achieve the same given force with a reduced number of cross-bridges (Fig. 3D). Altogether, these results suggest that myofilament Ca²⁺ sensitivity—as determined by stabilization of the D-helix within the regulatory N-domain of cTnC—may be an important determinant of not only cross-bridge kinetics, but also the number of cross-bridges recruited during contraction of the myocardium.

4.4. Implications for HCM pathophysiology

Missense mutations in cardiac thin filament regulatory proteins (e.g. troponin and tropomyosin) are known to cause heritable HCM (84–86). Despite the high prevalence and severe morbidity/mortality associated with HCM, the molecular mechanisms involved in HCM pathogenesis at the level of the sarcomere remain incompletely understood. In this study, we utilized our previously characterized knock-in mouse model of HCM, which harbors a single point mutation (Ala8Val) in cTnC; importantly, this mutation is clinically relevant, as it is associated with inherited forms of cardiomyopathies in human patients (48, 87) and a mouse model (20).

Intracellular Ca²⁺ concentrations in cardiac myocytes range from ~ 100 nM in diastole to ~ 1 μM in systole, which is approximately pCa 7 to pCa 5.8 (83). Remarkably, we found that lattice spacing, force, stiffness, and k_TR were all increased within these physiologically relevant Ca²⁺ concentrations. Most if not all of the increases at a given Ca²⁺ concentration for force and stiffness are due to leftward shift along the pCa axis (increased Ca²⁺ sensitivity), but k_TR is enhanced beyond what can be attributed to the leftward shift alone. Although the peak of the Ca²⁺ transient is reduced in HCM cardiomyocytes (20), this may occur possibly due to an increase in the amount of Ca²⁺ bound to the Ca²⁺ sensitized thin filaments; thus, peak force may still be enhanced in HCM (88). Moreover, we have previously shown that the cTnC-A8V HCM mutation exhibits elevated myofibrillar ATPase activity at physiologically relevant ranges of Ca²⁺ concentrations, with significantly increased activity at pCa 5.8 (49), consistent with the enhanced contractile kinetics observed in this present study. Because increased Ca²⁺ sensitivity is a hallmark of familial hypertrophic cardiomyopathies—not only for the mutation in this study, but in general (84)—any associated increase in cross-bridge cycling through more rapid detachment, and the accompanying increase in ATP utilization, could thus contribute to the hypercontractile phenotype. We conclude that increases in force, stiffness and k_TR, and possibly also lattice spacing, would collectively contribute to the augmented contraction of the heart that is generally associated with HCM.

4.5. Limitations of this study

In the absence of real-time SL control, internal sarcomere shortening can occur (89). Given the inherent difficulties in monitoring SL during cardiac muscle activation, this approach was not utilized in our experiments. Shortening of SL below 2.1 μm (the initial value at pCa 8) due to end compliances could be anticipated to result in: reduced steady-state, Ca²⁺-activated, isometric force and stiffness; reduced Ca²⁺ sensitivity (and pCa₅₀); faster k_TR; and increased lattice spacing. As discussed in greater detail above (Section 4.2), a subset of our results might be explained, in part, by activation-dependent reductions in SL, although it is not possible to quantitatively predict for all of these parameters and at each level of Ca²⁺ activation the extent to which this might possibly be the case. While lattice dimensions are maintained during contraction if SL is held constant in intact cardiac muscle (90), it is important to recall, however, that SL changes dynamically during ventricular filling and ejection phases of the cardiac cycle (19). Therefore, if internal sarcomere shortening occurred in our preparations, our results are nonetheless physiologically relevant. What is more, despite monitoring and maintaining a constant SL using an iterative feedback control system, Moss and colleagues were still able to show a Ca²⁺dependent increase in k_TR (12). Furthermore, we have previously reported that controlling SL has minimal effects on the Ca²⁺ dependence of k_TR in skeletal muscle (8). Interestingly, it has also been reported that activating Ca²⁺, but not SL, influences cross-bridge kinetics (91). It is possible that an experimental approach to analyze cross-bridge kinetics (k_TR vs. sinusoidal length perturbations) may yield conflicting results. In the aforementioned study, sinusoidal length perturbations were used an index of cross-bridge kinetics (91) rather than the k_TR. However, we recently reported that the cTnC A8V HCM mouse model exhibits faster cross-bridge cycling kinetics despite using a different method of analysis (i.e. sinusoidal length perturbation) (21).

Detergent-permeabilized CMPs were used in this study rather than intact muscle, which may not accurately reflect the in vivo environment. However, despite skinning of muscle preparations, our lattice dimensions mirror those observed in vivo (18) owing to the use of 3% dextran in all of our experiments. Another limitation of this study is the use of a murine model to investigate the effects of an HCM-associated mutation, since it is well-known that there are differences in contractile kinetics and Ca²⁺ handling in mice compared to humans (92). However, similar changes in cross-bridge kinetics have been observed using explanted HCM human heart tissue (93, 94).

4.6. Conclusions

In this study, we provide evidence showing that sensitizing the myofilament to Ca²⁺ through stabilizing the D-helix within the regulatory N-domain of cTnC influences both the number and rate of cycling of cross-bridges in cardiac muscle. We also showed that isometric force generation was accompanied by an increase in myofilament lattice spacing. We favor a model in which cross-bridge kinetics and force production are modulated by expansion of the myofilament lattice during cardiac muscle contraction. Taken together, these findings provide novel insights into the molecular mechanisms underlying the contractile regulation of vertebrate myocardium and how these processes can be perturbed in the setting of HCM.