The β-reducing end in α(2–8)-polysialic acid constitutes a unique structural motif

Abstract

Over the years, structural characterizations of α(2–8)-polysialic acid (polySia) in solution have produced inconclusive results. Efforts for obtaining detailed information in this important antigen have focused primarily on the α-linked residues and not on the distinctive characteristics of the terminal ones. The thermodynamically preferred anomeric configuration for the reducing end of sialic acids is β, which has the [I]CO₂^– group equatorial and the OH ([I]OH2) axial, while for all other residues the CO₂^– group is axial. We show that this purportedly minor difference has distinct consequences for the structure of α(2–8)-polySia near the reducing end, as the β configuration places the [I]OH2 in a favorable position for the formation of a hydrogen bond with the carboxylate group of the following residue ([II]CO₂^–). Molecular dynamics (MD) simulations predicted the hydrogen bond, which we subsequently directly detected by NMR. The combination of MD and residual dipolar couplings shows that the net result for the structure of Sia₂-βOH is a stable conformation with well-defined hydration and charge patterns, and consistent with experimental NOE-based hydroxyl and aliphatic inter-proton distances. Moreover, we provide evidence that this distinct conformation is preserved on Sia oligosaccharides, thus constituting a motif that determines the structure and dynamics of α(2–8)-polySia for at least the first two residues of the polymer. We suggest the hypothesis that this structural motif sheds light on a longtime puzzling observation for the requirement of 10 residues of α(2–8)-polySia in order to bind effectively to specific antibodies, about four units more than for analogous cases.

Introduction

Sialic acids (Sias) are glycans constituted by nine carbons and a suite of chemical moieties playing diverse and important roles in cell and molecular interactions (Cohen and Varki 2010). Sias are expressed abundantly in vertebrates and higher invertebrates (Angata and Varki 2002); outside these groups, Sias are found only in a small number of species (Vimr et al. 2004). Among the latter, the majority is constituted by disease-causing gram-negative bacteria to human and animal hosts (Varki 2008). Moreover, microbial Sia metabolism is a virulence determinant in a range of infectious diseases (Vimr et al. 2004). Such is the case for the meningitis-causing bacteria N. meningitidis serogroup B and E. coli K1, whose capsular polysaccharides (CPs) are important virulence factors (Schiffer et al. 1976). The N. meningitidis group B (NMB) CP is a linear homopolymer of (2–8)-α-Neu5Ac (N-acetylneuraminic acid) units, also known as α(2–8)-polysialic acid (polySia), and in bacteria can reach a degree of polymerization of up to 230 Sia units (Pelkonen et al. 1988; Schnaar et al. 2014). Because CPs are less prone to variation among bacterial strains as compared to proteins, they are excellent candidates for vaccine antigens, as has been the case with the development of CP conjugate vaccines against N. meningitidis serogroups A, C, W135, and Y (Cohn et al. 2010). The exception has been the NMB CP that elicits a poor immune response in humans (Wyle et al. 1972). The reason for poor immunogenicity is not known; however, it has been attributed to the fact that humans express α(2–8)-polySia in neural cell-adhesion molecules. Therefore, apprehension that a NMB CP-based vaccine has the potential to induce autoimmune reactions has hampered research and development of a NMB CP-based vaccine (Finne et al. 1983; Saukkonen et al. 1986). However, failure for this concern to materialize among persons carrying anti-CP NMB antibodies has prompted some researchers to call for a NMB CP vaccine development (Robbins et al. 2011). In order to make well-supported decisions in this regard, a detailed understanding of NMB structure and dynamics on varied conditions is among the highest priorities.

Structural characterizations of polySia in solution with varying number of units have been advanced mainly using a combination of NMR experimental techniques and molecular modeling tools; however, no clear consensus has been reached, with proposals ranging from a variety of helical conformations to random coils (Michon et al. 1987; Yamasaki and Bacon 1991; Brisson et al. 1992; Henderson et al. 2003; Battistel et al. 2012). With the goal of obtaining greater detail, studies on short oligomers (two and three residues) with the reducing end capped with a methyl group have been reported as well (Yongye et al. 2008). Similar to the internal residues of α(2–8)-polySia, these oligomers have the anomeric carbon of the end residue locked in the α-configuration, with the $C{O}_{\text{2}}^{\text{−}}$ axial (Figure 1) making it a good model system to study α(2–8)-polySia. However, potential effects arising from the end-cap as compared with the βOH group have not been explored in previous studies. Differences are to be expected, at least in the neighborhood of the reducing end, since the α-configuration represents only about 10% of the population for monomeric Sia in solution. However free α(2–8)-polySia is found mostly (over 99%) with the reducing end in the β configuration (Supplementary data, Figure S1), that is, with the $C{O}_{\text{2}}^{\text{−}}$ equatorial and the OH axial (Figure 1). The biological implication or relevance of the β configuration is unknown since the vast majority of Sias are linked in the α configuration. Nevertheless, most in vitro studies utilize free polySia, hence the findings reported herein are relevant primarily to in vitro studies but may have potential in vivo applications. Hints of the potential importance of the different configuration at the anomeric end were noted as early as 1987 by Jennings and co-workers (Michon et al. 1987). These workers hypothesized that the reducing end structure was one of the reasons why NMB PS (α(2–8)-polySia) needed more Sia units (~10 residues) than the PS from NMC (α(2–9)-polySia, 6 or more residues) to bind optimally to specific antibodies, but provided scarce experimental and theoretical support for their speculative structural model of α(2–8)-polySia at the reducing residue.

Fig. 1.

Chemical structures of Sia_N, corresponding to α(2–8)-linked (Neu5Ac)_N oligomers (with N = 2, 3, 4 or 6), constructed for MD studies. Residue numbers throughout are indicated by roman numerals between square brackets. The adopted torsion angle definitions used for analysis are indicated: ϕ = C1’−C2’−O8−C8; ψ = C2’−O8−C8−C7; ω₈ = O8−C8−C7−O7; ω₇ = O7−C7−C6−O6. The terminal residue was capped with either hydrogen (R = H) or methyl (R = CH₃). Two configurations for the anomeric carbon C2 at residue [I] were considered, resulting in: (A) Sia_N-αOR; (B) Sia_N-βOR.

In the present work we confirm that the reducing end configuration has distinct consequences on the structure of α(2–8)-polySia-βOH in the neighborhood of the reducing end by favoring hydrogen bond (Hbond) formation between the reducing OH and the carboxylate group of the next residue. The existence of this Hbond in a Sia α(2–8)-dimer, indicated as Sia₂-βOH, was first predicted by molecular dynamics (MD) studies and subsequently confirmed by NMR spectroscopy. Direct and indirect support for this Hbond is provided by long range HSQMBC (Williamson et al. 2014) and HSQC-ROESY (Davis 1989) experiments, respectively, and a detailed comparison of NMR residual dipolar couplings (RDCs) with predicted RDCs for Sia₂ conformers from MD trajectories. The image arising from these studies is that of a stable conformation with well-defined hydration and charge patterns. We then explore the persistence of this structural feature by MD on Sia_N oligosaccharides (OS), with N = (2, 3, 4 and 6), and conclude that it remains mostly unaltered for all studied oligomers, forming a motif that is comprised of at least the first two units of the OS. This general conclusion is supported by previously reported OH exchange rates on Sia oligosaccharides (Shinar et al. 2014a).

Results

MD and conformational analysis of Sia₂

To characterize the influence of the reducing end on the structure and dynamics of Sia OS, four Sia₂-OR (R = H or methyl) analogs were generated in-silico with varying configurations at the anomeric end as follows: (1) Sia₂-αOH, (2) Sia₂-βOH, (3) Sia₂-αOMe and (4) Sia₂-βOMe (Figure 1). The βOH form constitutes the major anomeric population in aqueous solutions of PS and OS resulting from chemical or enzymatic hydrolysis of polySia, hence, the isomer is readily observable by NMR experiments. Sia₂-αOH, the minor anomer in aqueous solution, accounts for less than 1% of the population (Supplementary data, Figure S1). Sia₂-αOMe is the molecule previously studied to model the core structure of polySia (Yongye et al. 2008). Sia₂-βOMe is a chimeric form (at least not detected in solution) that allows us to directly gauge the importance of the terminal OH in defining Sia OS shapes by eliminating the partial positive charge associated with the hydroxyl hydrogen while keeping the equatorial orientation of the negatively charged carboxylate group. For analysis, 100,000 snapshots were taken over each of the 1.0 μs MD trajectories.

The first task performed was a statistical analysis of the torsional angles over the MD trajectories of the glycerol linker (ϕ, ψ, ω₈, ω₇) on Sia₂ OS, as defined in Figure 1A. The population analysis, expressed in kcal/mol using a Boltzmann expression, is presented in Figure 2, with two panels per dimer showing the energy maps associated with two dihedral angles each, (ϕ, ψ) on the left and (ω₈, ω₇) on the right. Each horizontal pair of panels corresponds to each of the probed Sia₂ molecules, identified by labels. The torsion energy maps of Sia₂-βOH are placed at the top because it is the predominant form found in solution. They reveal a single deep energy minimum with two higher energy regions, populated at much lower ratios. This is not a typical result for glycans, as numerous reports show that sugar dimers have great freedom of movement about the glycosidic linkages to explore the conformational space, and consequently, are highly flexible (Bush et al. 1999; DeMarco and Woods 2008; Sattelle and Almond 2012; Widmalm 2013). It could be expected that because the presence of four torsional angles, rather than the standard two (ϕ, ψ) glycosidic torsion angles in carbohydrates, the compounded degrees of freedom would further favor flexibility. Indeed, this expectation is fulfilled for the other three Sia₂ models, rows 2–4 in Figure 2, showing the existence of multiple regions with equivalent energy minimums, typical of flexible OS. Furthermore, the overall patterns of the energy maps of Sia₂-αOH and Sia₂-(α/β)OMe are alike, indicative of similar conformers and dynamics being produced by the MD runs.

Fig. 2.

Energy (ϕ, ψ) and (ω₈, ω₇) maps for Sia₂ linkages from MD population ratios (1 μs, 300 K). The color scale in kcal/mol is the same for the four Sia₂ analogs. The plots imply that Sia₂-βOH is largely found in one conformation while the other three analogs are found in multiple conformations. This figure is available in black and white in print and in color at Glycobiology online.

A more detailed examination of the maps reveals that the (ω₈, ω₇) torsions are not affected by the terminal configuration, since for both Sia₂-αOMe and Sia₂-βOMe the energy landscapes are mostly identical. The (ϕ, ψ) energy landscapes show small differences around two local minima [(ϕ, ψ) ~(305, 275) and ~(270, 270)]; however, in these cases, the maps for Sia₂-βOMe are very similar to those of Sia₂-αOH, indicating that the effect is not related to the end group orientation. For Sia₂-αOMe, the energy maps can also be compared with results from Yongye et al. (2008). We observe that our torsional values nearly overlap those reported by Yongye et al. However, regions around ω₈ ~290° and ψ ~280°, shown here as having relatively low energy (bottom panel in Figure 2), were reported as completely unpopulated in research from Yongye et al. We speculate that this difference is due to under-sampling as in the cited work the MD duration was 100 ns, 10 times shorter than in the current report. In conclusion, the results shown in Figure 2 indicate that the orientation of the anomeric OH in Sia₂ is critical for defining the conformation and stabilize the reducing ring's configuration in the β-anomer, while showing little influence over the same characteristics in the α-configuration.

Analysis of Hbond interactions over the MD trajectories of the Sia₂ models revealed geometries consistent with an Hbond (distances and angles) between the anomeric βOH on Sia[I] and the negatively charged carboxylate group on Sia[II] (Figure 3A) for 92.4% of the time, an extraordinarily high fraction of the trajectory time. The average distance between Sia[I](O)H2 and the closest O in Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ for Hbonded conformers was 1.8 ± 0.2 Å. On the other hand, the Sia₂-αOH isomer only formed this Hbond intermittently ~20% of the time. As a donor, αOH also formed Hbonds with Sia[I]O7 (~10%). Despite these interactions, no additional differences were noticed when Sia₂-αOH was compared with the Sia[I]HO2-lacking Sia₂-(α/β)OMe, except for minor differences in depth for the different local minimum on the dihedral maps. These results support the notion of the anomeric αOH having a minor role in determining the molecular conformation.

Fig. 3.

Sia₂-βOH conformation from MD. (A) Sia₂-βOH MD snapshot indicating the predicted Hbond between Sia[I]HO2 and Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ (yellow dashed lines). (B) Average structure of Sia₂-βOH over the entire MD trajectory, highlighting the average solvent density (mesh, level 4.0) surrounding the dimer. This figure is available in black and white in print and in color at Glycobiology online.

An important consequence of the steady structure of Sia₂-βOH is that it provides a meaningful average model derived from the whole MD trajectory (as described in Materials and methods). In general, this procedure leads to virtual structures with seriously distorted geometries due to the variety of conformations adopted by molecules over long MD simulations. Indeed, the average structures obtained from the other three Sia₂ trajectories yielded nonphysical virtual structures. However, the average model of Sia₂-βOH has an almost canonical geometry for the rings and linkage, nearly identical to the single model represented in Figure 3A. Another important consequence of the steady structure of Sia₂-βOH, is the solvation layer established contains a network of Hbonds between the solvent and Sia₂-βOH in the neighborhood of the carboxylate groups, which can be revealed by calculating the density grid for the solvent over the trajectory. This calculation is null for flexible molecules because the water distribution is homogeneous. However, the stabilized Sia₂-βOH structure as result of the Sia[I]OH2–Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ Hbond, provides a matrix of localized partially charged atoms to interact with water and thus leading to a specific solvation pattern. Figure 3B shows the differential density obtained for O (red grid) and H (blue grid) atoms from water molecules in interaction with Sia₂-βOH.

To quantify similarities and differences on overall three-dimensional structure, we performed a total intra/inter-trajectory comparison of the positions for the 12 ring atoms for the four Sia₂ analogs. Since the force field potentials are slightly different for residue I in each analog, they are not adequate as structural reference. Hence, root mean-squared distance (RMSD) fitting minimization of each conformer was performed to the six ring atoms of the Sia[II] residue of a reference conformer. Then the RMSD for the 12 ring atoms in both residues and for all possible pair of conformers was calculated, this time without fitting, to produce results independent of the model selected as reference. The result of this calculation is plotted in Figure 4, where the diagonal and off diagonal quadrants depict intra- and inter-trajectory RMSD comparisons, respectively. The plot clearly shows that, for the whole trajectory, the core structure of Sia₂-βOH (bottom-left quadrant) remains well defined through almost the complete duration of the MD run. As evidenced by the small intra-trajectory RMSD values (lower than 2.0 Å), conformational changes during the MD simulation are minor or fleeting. In contrast, the remaining Sia₂ analogs (second to fourth diagonal quadrants) lack a preferred conformation evidenced by the high RMSD values. Furthermore, the off-diagonal quadrants show that the Sia₂-βOH structure is well differentiated from the other three Sia₂ models, again for the whole trajectories.

Fig. 4.

Intra- and inter-MD trajectories’ RMSD of ring atoms (diagonal and off-diagonal quadrants, respectively) of Sia₂ analogs. To obtain maps independent of the selected reference structure, models were distance minimized to the six ring atoms of the parametrically identical residue Sia[II] in the first frame of the Sia₂-βOH trajectory before calculating the RMSD. Low intra-RMSD values for Sia₂-βOH (<2 Å) indicate a rigid-like molecular frame. The other dimers, in contrast, show high flexibility. The plot is diagonally symmetrical, hence data under the scale in the Sia₂-βOH column can be observed along the Sia₂-βOH row. This figure is available in black and white in print and in color at Glycobiology online.

NMR experiments on Sia₂-βOH

The unexpected prediction for the structure of Sia₂-βOH with the presence of an Hbond over 90% of the time requires experimental support in order to be confirmed. Isomers of monomeric Sia in solution are present in an approximate proportion of 90:10, Sia-βOH to Sia-αOH, as easily determined by integrating the isolated C3 signals of the α/β isomers from 1D ¹³C-NMR experiments (Supplementary data, Figure S1). For dimer and longer OS, this ratio increases up to ~99:1 proportion as obtained by 1D ¹³C-NMR (Supplementary data, Figure S1). Thus, for the purpose of discussing experimental results we consider all Sia OSs to be present in solution solely in the β-configuration, as the other anomer is mostly unobserved.

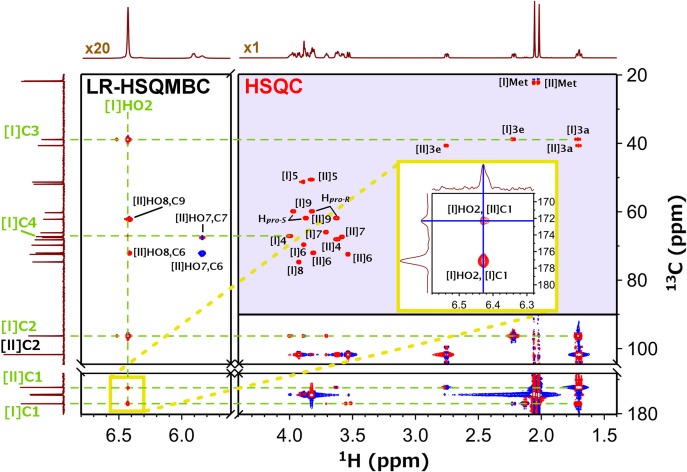
The most direct evidence for Hbonds in solution would be the detection of through-Hbond NMR correlation signals, in this particular case a Sia[I]HO2–Sia[II]C1 correlation. We used optimum conditions for observation of OH signals of anomeric carbons (T = 263 K, pH = 7.0) (Battistel et al. 2017) and ran a modified long-range HSQMBC experiment (Williamson et al. 2014) at 700 MHz to detect the Hbond (Materials and methods; SI). Figure 5 depicts a portion of the spectrum showing the correlation signals of Sia[I]HO2 with its immediate carbon, Sia[I]C2, and both Sia[I]C1 and Sia[II]C1 (assignments obtained from an HSQC-TOCSY experiment, Supplementary data, Figure S2). The inset highlights the region of interest and includes the slices (positions indicated in blue) through Sia[I]HO2 and Sia[II]C1 for clarity. The slice in the ¹H dimension shows an asymmetric peak that indicates an additional overlapping correlation for Sia[II]HO8–Sia[II]C1 (see Supplementary data, Figure S3 for a better comparison). Indeed, this additional Hbond is present in the MD trajectory in a ~2% ratio so it is surprising to observe it at low temperatures. The Sia[I]HO2–Sia[II]C1 correlation unequivocally confirms the existence of an Hbond between Sia[I]HO2 and Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$, albeit the Hbonded population and its persistence at higher temperatures have yet to be established. Moreover, although the conformational space is greatly restricted due to this Hbond, there might be additional conformations compatible with this restraint, which may still differ from the one predicted by MD.

Fig. 5.

LR-HSQMBC spectrum with overlaid HSQC for CH crosspeak identification. The external 1D ¹H (top, with water suppression) and ¹³C spectra (left) were obtained separately. The Sia[I]HO2 chemical shift is 6.429 ppm, which shows Sia[I] intra-residue correlations to C2 (96.3 ppm), C3 (38.9 ppm), C4 (67.2 ppm), and C1 (177.1 ppm). Importantly, Sia[I]HO2 also shows a through-Hbond inter-residue correlation to Sia[II]C1 at 172.4 ppm (inset). The blue lines in the inset locate the traces through the Sia[I]HO2–Sia[II]C1 signal. Sia[II]C1 shows an additional correlation with Sia[II]HO8 at 6.416 ppm, albeit weaker than with Sia[I]HO2. (*: minor conformation, <5%). This figure is available in black and white in print and in color at Glycobiology online.

A highly prevalent conformation as predicted from MD for Sia₂-βOH should result in distinct RDCs (Battistel et al. 2014), readily differentiated from alternative conformations, due to its restrained conformation. We predicted that RDCs would fit well for Sia₂-βOH and yield poor fits to the other structural analogs, due to their flexibility. We used a ¹³C,¹⁵N-enriched sample of Sia₂ weakly oriented in a stretched polyacrylamide gel at 300 K to measure ¹³C-¹H, ¹⁵N-¹H, and ¹³C-¹³C RDC (denoted D_CH, D_NH, and D_CC, respectively), totaling 38 experimental values (Figure 6A, Table I). Then we fit each individual MD model to the measured RDCs using a singular value decomposition (SVD) approach (Losonczi et al. 1999), and assessed the goodness of fits with the quality factor Q (Eq. (1)) (Clore and Garrett 1999). Figure 6B shows the result obtained for the four trajectories of Sia₂ over the length of the simulations. Because of the large variations in Q values from frame to frame (~ ±0.2) due to normal molecular vibrations and internal motion, plus the large number of frames taken into consideration, the curves were smoothed to reveal the individual trajectory trends at predicting the experimental results. The plot clearly shows that the RDC fits to Sia₂-βOH models are significantly and consistently closer to the experimental values over the whole trajectory relative to the other three simulations.

Fig. 6.

Comparison of RDC measurements on Sia₂-βOH with MD results. (A) Measured D on Sia₂-βOH are represented by (nongray) colored bonds in the 3D scheme (values given in Table I). (B) Calculated Q factors for the four Sia₂ MD trajectories (smoothed curves). (C) Experimental vs. calculated RDCs for the average structure of Sia₂-βOH (left, included in Table I) and a snapshot resulting in high Q value (right). The MD major conformation predicts well the experimental RDCs. This figure is available in black and white in print and in color at Glycobiology online.

Table I.

Experimental RDCs (D_meas) and SVD calculated RDCs (D_SVD) for Sia₂-βOH models from the MD trajectory

[residue]bond	Dmeas [Hz]	DSVD Sia2-βOH MD Model Best Q, Q = 0.105	<DSVD> Sia2-βOH MD traj.a <Q> = 0.23 ± 0.06	Back-calculated <DCC/XH> Sia2-βOH MD traj.bQ = 0.34	DSVD for <Sia2-βOH>cQ = 0.19
[I]C3–H3a	6.93 ± 1.0	8.32	4.7 ± 1.46	2.73	5.40
[I]C3–H3e	2.54 ± 0.5	1.37	3.95 ± 2.13	5.92	4.53
[I]C4–H4	8.46 ± 1.2	6.4	4.97 ± 1.43	2.81	7.52
[I]C5–H5	6.47 ± 1.2	4.83	4.49 ± 1.55	2.57	6.10
[I]C6–H6	7.64 ± 0.9	6.5	4.74 ± 1.34	2.89	5.26
[I]C7–H7	3.74 ± 1.4	2.17	5.2 ± 2.1	7.23	5.95
[I]C8–H8	9.41 ± 1.0	5.99	5.3 ± 2.25	7.27	6.87
[I]C9–H9R	3.94 ± 1.1	4.66	4.7 ± 3.28	3.57	NA
[I]C9–H9S	−9.41 ± 1.0	−13.04	−8.87 ± 6.75	−9.88	NA
[II]C3–H3a	8.71 ± 1.2	14.03	9.08 ± 1.33	12.95	11.98
[II]C3–H3e	−3.29 ± 1.0	−9.39	−7.17 ± 2.58	−9.11	−9.80
[II]C4–H4	12.25 ± 2.1	10.85	9.03 ± 1.38	12.73	12.49
[II]C5–H5	13.44 ± 1.1	13.04	9.18 ± 1.6	13.29	11.27
[II]C6–H6	11.35 ± 1.1	9.95	9.06 ± 1.49	12.95	11.77
[II]C7–H7	−13.06 ± 1.3	−9.88	−8.6 ± 2.33	−9.88	−12.45
[II]C8–H8	−4.52 ± 3.6	−4.58	−6.09 ± 5.44	−6.81	NA
[II]C9–H9R	3.45 ± 1.5	3.08	−1.79 ± 7.23	−1.92	NA
[II]C9–H9S	5.25 ± 1.5	5.39	4.93 ± 5.32	6.48	NA
[I]N5–H5N	−3.9 ± 0.4	−3.99	−2.22 ± 1.08	−1.07	−3.48
[II]N5–H5N	−0.4 ± 0.4	−2.54	−3.94 ± 1.19	−5.82	NA
[I]C1–C2	0.38 ± 0.2	0.37	0.42 ± 0.16	0.4	0.41
[I]C2–C3	−1.47 ± 0.1	−1.2	−1.2 ± 0.16	−1.13	−1.38
[I]C3–C4	0.31 ± 0.3	0.39	0.36 ± 0.18	0.37	0.44
[I]C4–C5	−0.03 ± 0.2	0.23	0.34 ± 0.18	0.26	0.28
[I]C5–C6	−1.35 ± 0.3	−1.22	−1.21 ± 0.16	−1.14	−1.35
[I]C6–C7	0.12 ± 0.3	0.05	0.2 ± 0.19	0.16	0.25
[I]C7–C8	−1.46 ± 0.4	−1.16	−1.16 ± 0.16	−1.1	−1.42
[I]C8–C9	0.27 ± 0.2	0.16	0.24 ± 0.21	0.22	0.35
[I]C5N–CMe	0.16 ± 0.5	0.66	0.48 ± 0.24	0.45	NA
[II]C1–C2	1.26 ± 0.1	1.18	0.66 ± 0.14	0.59	0.70
[II]C2–C3	0.3 ± 0.2	0.41	0.46 ± 0.17	0.35	0.68
[II]C3–C4	−1.13 ± 0.3	−0.89	−0.68 ± 0.2	−0.63	−0.87
[II]C4–C5	−0.77 ± 0.2	−0.64	−0.68 ± 0.21	−0.6	−0.88
[II]C5–C6	0.19 ± 0.4	0.39	0.42 ± 0.15	0.31	0.68
[II]C6–C7	−0.79 ± 0.3	−0.56	−0.4 ± 0.2	−0.32	−0.41
[II]C7–C8	0.12 ± 0.3	0.42	0.44 ± 0.17	0.33	NA
[II]C8–C9	−0.82 ± 0.2	−0.14	−0.4 ± 0.3	−0.35	NA
[II]C5N–CMe	−0.76 ± 0.1	−0.8	−0.42 ± 0.29	−0.32	NA

RDCs are grouped by residue ([I], [II]) and bond type (CH, NH, CC).

^aMean values ± standard deviation over the whole MD trajectory. <Q> is the mean of all Q values. Q calculated using Eq. (1) with <D_a^NH> = −21585.2 * <A_a> and <R > . Q = 0.27 using <D_SVD> .

^bColumn contains two complementary sets of data: (i) D_CH and D_NH (indicated as D_XH) back-calculated using measured D_CC for SVD; and (ii) D_CC (indicated as D_XH) back-calculated using measured D_CH and D_NH for SVD.

^cCalculated RDCs for the resulting RMSD minimized average structure from the whole Sia₂-βOH MD trajectory. Shortened bonds in the resulting virtual structure due to motion were not considered (NA).

The above described RDC predictions are derived from single structure models; thus the overall agreement reflected by the sustained low Q values over the trajectory strongly supports that the MD conformations closely represent the state of Sia₂-βOH in solution. An important consequence of the good fittings is that it allowed stereospecific resonance assignments for H9 pro-R’s and H9 pro-S’s, which cannot be performed by traditional NMR methods. Thus, the assignment was achieved by predicting the RDCs for the CH9pro-R/pro-S bonds and comparing with the measured values which was particularly clear in the case of Sia[I]9 (Table I), indicating that H9 ¹H resonances (in ppm) are: δ(Sia[I]H9 pro-R) = 3.813, δ(Sia[I]H9 pro-S) = 3.968, δ(Sia[II]H9 pro-R) = 3.651, and δ(Sia[II]H9 pro-S) = 3.876 (HSQC, Figure 5).

As mentioned earlier, the Sia₂-βOH MD trajectory yielded a well-defined structure for the rings and linker associated with the minimum potential energy represented in Figure 2. However, the glycerol tail of residue Sia[II] was predicted to be much more flexible, which would result in significantly reduced RDC magnitudes. Furthermore, in small molecules like Sia₂, lateral groups’ motions can significantly affect the overall alignment tensor, and thus all RDC values, preventing the separate analysis of molecular regions (Almond and Axelsen 2002; Azurmendi and Bush 2002; Azurmendi et al. 2002; Zweckstetter 2008). Our approach to deal with this problem was to include all measured RDCs and to perform a statistical analysis on the calculated RDCs over the trajectory. Subsequently, mean and standard deviation of the predicted values are compared to the experimental ones to draw inferences from it. Thus, along with (i) experimental and (ii) calculated RDCs for the model with lowest Q from the MD trajectory, Table I lists (iii) the mean and standard deviation for the calculated RDCs over the whole Sia₂-βOH trajectory, (iv) mean back-calculated RDCs (obtained by using either just D_CC or D_CH and D_NH), and (v) calculated for the RMSD minimized averaged structure over the whole trajectory of Sia₂-βOH (Materials and methods).

An initial assessment reveals good overall agreement in all cases, despite the inclusion of RDC values with relatively large experimental error (Sia[II]C8–H8 or Sia[I]C7–C8) or affected by internal motion (Sia[II]C8–H8,C9–H9), that a priori could be problematic. The good fits are further verified by both back-calculating D_CH and D_NH from the best fit alignment tensor parameters derived with just 18 D_CC, as well as predicting the measured D_CC from parameters derived using only the 18 measured D_CH. Given the small number of RDCs used in each case and the relatively high error for some of them, the value of 0.34 for Q is remarkably good. Finally, we back-calculated RDCs for the undistorted bonds of the averaged model shown in Figure 3B, giving an exceptionally good Q value of 0.19 (Figure 6C, left panel; Table I). Clearly, there is a single outlier value (−3.3, −9.8 Hz), corresponding to Sia[II]C3–H3e, most likely due to an underestimate of the RDC averaging from MD. Otherwise, the predicted RDCs lend support to the MD averaged structure. To illustrate the power of Q in discriminating between structural models, we included the right panel in Figure 6C, showing the calculated vs. experimental RDCs for a trajectory model with relatively high Q value. Models with Q ≥ 0.5 are infrequent for the Sia₂-βOH MD trajectory (~1%), but are present on the order of 10% or more for the other three cases. The plot insets are expansions of the D_CC range of values for both models. They show W scaling in Eq. (1) at work (Clore and Garrett 1999), by making Q similarly sensitive to RDC values from bonds containing both low and high γ (magnetogyric ratio) nuclei. In this way all measured RDCs can be analyzed simultaneously. This is particularly relevant in glycans where specific types of RDCs may be insufficient for effective analysis.

Smoothing procedures, as implemented in Figure 6B, yield general trends for trajectories; however, they may obscure important details happening at shorter times than the smoothing range in the system analyzed (100 ns here). This is particularly true for RDCs, because of the ambiguous nature of the technique in relation to the symmetric properties of the alignment tensor solutions may not be unique when utilizing a single orienting medium (Canales et al. 2012). We found that this is the case when trying to correlate the short periods during which the Sia[I]HO2–Sia[II]O1 Hbond breaks with increase in Q values, revealing that there is a second narrow set of open structures compatible with the set of measured RDCs, i.e., with Q values as low as the Hbonded model using the 38 measured RDCs. Figure 7A depicts the Sia[I]HO2–Sia[II]O1 distance over the MD trajectory, which shows the transitions from “closed” Hbonded structures to “open” conformations and back. We expected such transitions to be reflected in Q values obtained by SVD with all the experimental data (panel 7E), however this was not evident for some cases. Interestingly, a correlation between Hbond “breakage” and increase in Q values is obtained when using RDCs from just one of the rings (five D_CH and six D_CC) to determine the overall alignment tensor parameters and then, back-calculating the 38 RDCs and the corresponding Q values (Figure 7, plots F and G). The effect on Q is observed in both cases, but is more pronounced when determining the alignment tensor from Sia[I]-ring RDCs (Figure 7F) over Sia[II]-ring RDCs (Figure 7G), perhaps thanks to the equatorial C1–C2 bond, which is parallel to four out of the five CH RDCs per ring. In summary, RDCs provide essential experimental support at ambient temperature for the existence of the predicted Hbonded structure of Sia₂, but further evidence was desirable.

Fig. 7.

Hbond breakage/formation in Sia₂-βOH correlated to predicted ROEs and RDCs over the MD trajectory. (A) Sia[I]HO2−Sia[II]O1 distance; (B–D) H−H interatomic distances, between structurally diagnostic atoms; (E–G) Q values obtained considering three sets of RDCs (all, nine ring-[I], and nine ring[II], respectively). Both instantaneous (gray) and “smoothed” (colored) values are shown in all panels. Hbonded structures correlate with diagnostic H–H distances <5 Å (predicting specific ROE observations), and yield good RDC predictions. This figure is available in black and white in print and in color at Glycobiology online.

Another strong indication for the presence of an HO2 Hbond in Sia₂-βOH is the recently published OH exchange rate constants in Sia OSs (Shinar et al. 2014a). The reported OH/OD exchange rate constant for HO2 in the dimer was 3.4 s⁻¹, which is two-fold smaller than the next lowest value, and at least an order of magnitude smaller than the rapidly exchanging OHs at pH 7–7.5, 268 K. Based on this rate constant, we measured ROE data (a better alternative than NOE for molecules this size) under varied conditions in order to detect short internuclear distances between Sia[I]HO2 and nearby CHs to compare to structural data from MD simulations. Figure 8A shows the average MD structure of Sia₂-βOH with HO2–H distances that are less than 5 Å, indicated with dashed lines (Supplementary data, Table S1). Predicted inter-residue distances between Sia[I]H6 and Sia[II]H3a,e are distinctive for the MD predicted conformation. For instance, evaluating averaged distances for Sia₂-αOH trajectories, yields 5.07 ± 0.95 Å and 5.21 ± 0.93 Å for Sia[I]H6 and Sia[II]H3a,e, respectively. Furthermore, distance analysis over the trajectory of Sia₂-βOH shows excellent correlation between breakage of the [I]HO2–[II]O1 Hbond (H–O distance > 3 Å; Figure 7A) and departure from the interatomic distance necessary to observe Sia[I]HO2/H6–Sia[II]H3a,e ROE cross peaks (H–H distance limit ~5 Å, Figure 7B–D). Thus, simultaneous observation of ¹H–¹H ROEs between all indicated atoms in Figure 8A is diagnostic support of the averaged MD structure. The HSQC-ROESY spectrum (Figure 8B) shows ¹H correlations to other nearby ¹H's, separated by the chemical shifts of the ¹³C atoms to which the latter are attached. Strips of the HO2 and H3a,e chemical shift regions show (dashed lines) five main ¹³C correlations of HO2 with: Sia[I]C6, Sia[I]C4, Sia[I]C5, Sia[I]C3, and Sia[II]C3. In addition, Sia[I]C6 correlates with both Sia[I]H3 and Sia[II]H3, completing the set of predicted correlations from the structure in Figure 8A. On the other hand Sia[II]C6 correlates only with [II]H3, which serves as control that hydrogen atoms farther than 5 Å do not produce spurious signals. Whole spectra and peak assignments are included in SI. In summary, the discussed HSQC-ROESY results require both, a slow Sia[I]HO2 exchange rate value (i.e., Hbonded) and a restrained conformation with concomitant short distances between Sia[II]H3 and both Sia[I]OH2 and Sia[I]H6, providing strong support for the predicted structure of Sia₂-βOH.

Fig. 8.

Verification of predicted ROEs for Sia₂-βOH. (A) Sia₂-βOH average structure from the MD trajectory. Indicated H–H distances (in parentheses) are given for diagnostic atoms expected to produce NMR through-space correlation signals. (B) HSQC-ROESY spectrum of 270 mM Sia₂ in 10% D₂O/H₂O at 263 K. Dashed lines are used as aids in identifying diagnostic cross peaks from the MD predicted structure of Sia₂-βOH. This figure is available in black and white in print and in color at Glycobiology online.

Observing OH signals requires running experiments at low temperature to slow down OH exchange. In the present case, the highest temperature still compatible with good quality ROE OH signals was 273 K, but evidence of slow exchange at higher temperatures for Sia[I]HO2 comes from temperature coefficients derived from HSQC-TOCSY experiments where the Sia[I]HO2–C2 correlation is observed up to 283 K (Supplementary data, Figure S4). At higher temperatures, slow exchange is still evident from broadening of the ¹³C signal in ¹³C 1D experiments performed in 1:1 solutions of H₂O:D₂O up to 310 K (Supplementary data, Figure S5). All these observations, together with the room temperature RDC experiments, indicate that the averaged MD conformation is a good representation of the actual structure of free Sia₂-βOH in solution, or at least the great majority of the population, directly implying the presence of the stabilizing Sia[I]OH2–Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ Hbond. It is noteworthy that as Sia[I]HO2 exchange rate increases with higher temperatures diagnostic ROE's disappear, consistent with an increased molecular flexibility, yet, none of the experimental data contradicts the MD structure.

MD and conformational analysis of Sia_N

An important question arising from the discussed results is whether the conformation adopted by Sia₂-βOH is conserved in longer OS, namely Sia_N-βOH, with N > 2. To answer this question we performed MD simulations under the same conditions used for Sia₂ on Sia_N oligosaccharides with N = 3, 4 and 6. We then performed intra- and inter-trajectory RMSD analysis similar to the one shown for Sia₂ in Figure 4. As expected, the longer the OS the less the structure is preserved for all residues (higher RMSD, not shown). However, when restricting the analysis to the common 12 ring-atoms in the first two residues of each OS, the intra-trajectory RMSD results for Sia_N-βOH stay below 1.0 Å for almost the whole trajectory in each of the four cases (diagonal quadrants in Figure 9A), indicating that the first two residues are equally restrained in all cases. The inter-trajectory comparisons (off-diagonal quadrants) show no significant difference in the structures adopted by residues [I–II] for Sia_N>2 OS, but there is a detectable difference between those and the conformation adopted by Sia₂, with inter-trajectory RMSD values increasing from ~1.0 to ~2.0 Å. This increase corresponds to a minor change in the average relative orientations between residues Sia[I] and Sia[II], with the Sia[I]OH2–Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ Hbond still effectively stabilizing the anomeric end in the OS. Figure 9B depicts an overlay of the average structures of Sia₂-βOH (in green) and the first two residues of the tetramer ([I–II]Sia₄-βOH, in blue) showing the small difference obtained between the average structures on the common two residues, yielding an RMSD value of 0.006 for the 12 ring atoms. The last two residues in the tetramer model (colored gray) belong to a single model and are included as visual aid, because the spatial average of these residues results in distorted Sia geometries. The nearly perfect overlay of residues [I–II] as well as the presence of Sia[I]OH2 Hbonded to Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ indicates that these residues are a stable structural motif of free Sia OS in solution. Experimental support for this prediction derived from MD comes again from the work by Shinar et al. (2014a), that contains OH exchange values for Sia_N OS with N = [1–6]. The Sia[I]OH2 rates for all OS (i.e., excepting monomer) ranges between ∼3 s⁻¹ and 7 s⁻¹, with the minimum corresponding to the hexamer, suggesting that the Hbond is present on Sia PS as well. By comparison, OH4 rates for all hexamer residues range between 11 s⁻¹ and 17 s⁻¹ (all data obtained at pH 7–7.5, 268 K).

Fig. 9.

The structural motif of the leading two residues of Sia_N-βOH oligomers is conserved. (A) Intra- and inter-MD trajectory RMSD of ring atoms of the two terminal residues for four Sia_N-βOH oligomers (N = 2,3,4 and 6). (B) Overlay of the average structure of Sia₂-βOH and the average structure of the first two residues of Sia₄-βOH (the last two residues belong to a single model and are included only for reference). The plot is diagonally symmetrical, hence data under the scale in the Sia₂-βOH column can be observed along the Sia₂-βOH row. This figure is available in black and white in print and in color at Glycobiology online.

Comparison with crystallographic results

Geometries similar to the ones derived from MD can be found in the X-ray crystallographic database among the few structures reported of Sia_N-βOH. A survey of deposited crystallographic structures on the PDB revealed one entry with oligomers (dimer, trimer, and pentamer) of α(2–8)Neu5Ac bound to the neuroaminidase endoNF (wild-type and two mutants) (Schulz et al. 2010). It might be expected that a small OS bounded to a protein would have its conformation affected by multiple interactions with amino acids, but to our surprise, a 0.211 Å RMSD was obtained between the Sia₂ averaged MD structure and the Sia₂ ligand in endoNF-wt (PDB entry 3GVL), using 15 heavy atoms, six from each ring and three from the linker (Supplementary data, Figure S6). The two mutants reported in the same work (PDB entries 3GVJ and 3GVK) had additional Sia oligomers bound to different sites, but in most cases with the anomeric Sia residue interacting weakly with the protein, and hence poorly defined. The exception was the Sia₃ bound at the active site, with a structure in the anomeric end clearly different from the Hbonded motif predicted in this work. This is not surprising because this Sia₃ is the final product of the catalyzed reaction at the active site, interacting with various amino acids, which may distort the trimer's torsional angles.

Discussion

The availability of better force fields and computational power for implementation of MD techniques open opportunities to investigate aspects of molecular interactions at the atomic level and sometimes to predict unexpected structural features guiding researchers to new experimental challenges that either support or disprove theoretical predictions. A unique feature of MD and related techniques based in theory is that it allows the generation of chimeric compounds or sparsely populated isomers that are experimentally inaccessible to perform comparative studies. In this work we presented examples of both aspects of MD, first predicting an unexpectedly stable conformation for Sia₂-βOH associated with the presence of an Hbond involving the OH on the anomeric Sia[I]C2 and Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$. Second, we generated related compounds in-silico, including an isomer with a very low population in aqueous solution (Sia₂-αOH) and a structural analog, which to our knowledge has not been synthesized (Sia₂-βOMe), to analyze the importance of both the reducing-residue's hydroxyl group and the anomeric configuration, concluding that the two aspects contribute to yield a well-defined conformation for the dimer.

The MD predictions of the Hbond and a stable conformation for Sia₂-βOH led us to seek experimental support by NMR. The presence of the Sia[I]OH2–Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ Hbond was confirmed by a long-range scalar-coupling mediated NMR correlation between Sia[I]HO2–Sia[II]C1. Evidence from RDCs and ROEs strongly support the MD predicted three-dimensional structures. Moreover, diminished OH/OD exchange rate constants obtained by NMR indicate that Sia[I]OH2 exists in an Hbonded state at low temperatures. In addition, the observed H6–H3a,e inter-residue ROEs seem to be possible only for the Hbonded structure. This evidence along with other findings discussed in this report point to the MD predictions as an accurate representation of the dimer in solution. Looking forward, we studied Sia OS of the four forms (Sia_N-[α/β]O[H/Met], N = 2, 3, 4 and 6) to explore if the Hbond and the conformation of the two terminal residues remained stable. Again the MD results indicate that the Hbond and conformation of the two-terminal residues are retained. This result is found to be consistent with slow exchange values previously reported for Sia[I]HO2 in OS from dimer up to hexamer (Shinar et al. 2014b). We conclude that by virtue of the Sia[I]OH2–Sia $\left[\text{II}\right]C{O}_{\text{2}}^{\text{−}}$ Hbond presence, the two terminal residues at the reducing end of α(2–8)-polySia constitute a stable structural motif in free solution, distinct from the extended polymer structure. A longtime puzzling observation is the requirement of 10 residues of α(2–8)-polySia in order to bind effectively to specific antibodies, about four units more than for analogous cases (Michon et al. 1987). The reported findings suggest that the unique structural motif of the β-reducing end on α(2–8)-polySia may be central in understanding this conundrum and has implications for future in vitro studies when purified polySia OS are used.

Materials and methods

Computational methods

MD simulations were performed using the AMBER 14 software package (Case et al. 2015) in a workstation equipped with four GeForce GTX 780 3GB Graphic Processing Units. The Sia_N structures (Figure 1) and parameter files (N = 2, 3, 4 and 6) were created using the XLEaP module included in AMBER with the force-field Glycam-06 h (Kirschner et al. 2008). The initial conformation was produced by energy minimization with the AMBER tool minab using an implicit solvent option. Then, the conformer was charge-neutralized with the appropriate number of Na⁺ counterions (i.e., N Na⁺) and solvated with TIP3P (Jorgensen et al. 1983) explicit water models (or TIP5P (Mahoney and Jorgensen 2000), where indicated), again with the XLEaP module. Cubic periodic boundary conditions were used for dimer (Sia₂), trimer (Sia₃) and tetramer (Sia₄) OS. For hexamer (Sia₆) OS octahedral periodic conditions were used to reduce the number of water molecules required for solvation. The number of water molecules employed was proportional to the spatial extension of the OS and ranged between 682 for Sia₂ to 3759 for Sia₆. Nonbonded van der Waals and electrostatic scaling factors for 1–4 interactions were set to unity (SCEE = SCNB = 1) as required by the Glycam force field. Long range electrostatic interactions were computed with particle-mesh Ewald summation (York et al. 1993), with a nonbonded cutoff distance of 8 Å. The systems were energy minimized and then slowly equilibrated at the target temperature of 300 K finalizing the preparation stage with 800 ps MD run using NPT conditions and an integration time for the equations of motion of 2 fs, with hydrogen-containing covalent bonds constrained to their equilibrium lengths using the SHAKE algorithm (van Gunsteren and Berendsen 1977). The same conditions were used for the 1.0 μs production runs. Independence of initial conditions for the production runs were verified by exchanging the configurations for Sia₂-OH from α to β and vice versa while keeping the respective dihedrals constant and then running a production run after a short energy minimization and equilibration cycle. Likewise, comparisons of trajectories were performed for Sia₂-OH and Sia₆-OH solvated with either TIP3P or TIP5P water models. In none of the cases were meaningful differences uncovered upon analysis.

Processing of trajectories was performed using cpptraj, included in AMBER, and python in-house scripts. For analysis, Hbonds were geometrically defined with cutoff values for donor–acceptor distances (d_DA) of 3.0 Å and angles (θ_D-H-A) of 135°. Average structures of Sia[I–II] from MD trajectories of Sia_N OS were produced by RMSD fitting of 15 atoms comprising the 2×6 ring atoms of the first two Sia_N residues plus the three atoms of the glycerol linker (C7, C8 and O8), and averaging all the atoms positions through the MD trajectory. Figures were created with OriginPro 2015 (www.OriginLab.com; Northampton, MA), PyMol (www.schrodinger.com/pymol), and GIMP (www.gimp.org).

NMR spectroscopy

NMR experiments were performed on natural abundance and uniformly ¹³C,¹⁵N-enriched samples of Sia₂. The natural abundance sample was purchased from Nacalai (Tokyo, Japan) and used without further purification. The isotope enriched polySia sample was produced in-house as described previously, hydrolyzed to dimer and purified by ion-exchange chromatography (Azurmendi et al. 2007; Battistel et al. 2012). NMR samples were prepared at pH 7.0 containing 0.1 (wt %) DSS-d₆ and 0.1 (wt %) NaN₃. The solvent used for measuring RDCs, HSQC-ROESY and LR-HSQMBC was 10% ²H₂O/¹H₂O. Data were collected on a 700 MHz Bruker Avance III equipped with a TCI xyz-gradient CryoProbe. For RDC measurements, 15% acrylamide stretched gels were used as orienting media (Tycko et al. 2000). To circumvent ¹H-¹H strong coupling effects on ¹H-¹³C RDC, the RDCs were measured by the J-modulation method using CTi-HSQC experiments (Yu et al. 2013). ¹H, ¹³C ¹J (¹J_HC) modulation curves were obtained in isotropic and aligned media and RDC values were derived from the curve-fitted ¹J_HC values obtained with the samples in aligned or isotropic media. The spectral windows, carrier frequencies, and digital resolution were 12 and 30 ppm, 4.75 and 65 ppm and 16 and 83 Hz/point in the ¹H and ¹³C dimensions, respectively. For each t₁ point 8 transients were accumulated. ¹H–¹⁵N RDC values were determined from ¹J_HN measured by frequency difference in the ¹H and ¹⁵N dimension of ¹H, ¹⁵N coupled HSQC experiments. The spectral windows, carrier frequencies, and digital resolution in the ¹H and ¹⁵N dimensions were 12 and 5 ppm, 4.75 and 124 ppm and 16 and 3 Hz/point, respectively. For each t₁ point 32 transients were accumulated. From these spectra, ¹H and ¹⁵N 1D traces were extracted and fitted to Gaussian line-shapes in Topspin 3.2. ¹³C–¹³C RDC were obtained using ¹³C-constant time-COSY experiments (Azurmendi and Freedberg 2013), performed using 197 ppm spectral window centered at 100 ppm and 8 and 271 Hz/point resolution for the direct and indirect ¹³C dimensions, respectively.

Individual MD trajectory models were fitted to measured RDCs using a SVD approach (Losonczi et al. 1999), which we implemented as a Python script, to derive alignment tensor parameters that for the given rigid model best reproduce the experimental RDC values. The goodness of fit for each model is assessed with the quality factor Q (Clore and Garrett 1999), as follows (Eq. (1)):

$$\mathit{Q}=\sqrt{\frac{\sum {\left({W\ast D}_{\mathit{calc}}-W\ast D_{\mathit{exp}}\right)}^2}{N{\left(D_a\right)}^2\left(4+3R^2\right)/5}}$$ (1)

where the sum is taken over all N measured RDCs, W is a scaling factor for different atom pairs, and the denominator results from assuming a random uniform distribution of RDC. The values of the scaling factor W in Eq. (1) were 1.0, 0.5 and 5.0 for D_NH, D_CH, and D_CC, respectively (as per the current version of NMRPipe (Delaglio et al. 1995)). The denominator results from assuming a random uniform distribution of RDC (Clore and Garrett 1999), with D_a = D_a^NH = −21585*A_a Hz with the adopted scaling, and R the rhombicity of the alignment tensor. Curve smoothing in Figure 6 was done with a percentile function and a window of 500 points (equivalent to 100 ns) available in OriginPro. NMR data were processed and analyzed using TopSpin 3.2 (www.bruker.com), NMRPipe (http://ibbr.umd.edu/nmrpipe), and MestReNova (www.mestrelab.com).

A 100 mM Sia₂ sample in natural isotopic abundance, pH 7.0, was used for ¹³C-edited ROESY experiments (HSQC-ROESY) (Davis 1989). The spectral windows, carrier frequencies, and digital resolution in the ¹H and ¹³C dimensions were 10 and 58 ppm, 5.1 and 50 ppm, and 3 and 80 Hz/point, respectively. For each t₁ point 128 transients were accumulated. A 100 ms ROESY spinlock was used. For Hbond detection a 200 mM Sia₂ sample, pH 7.0, was used. The spectral windows, carrier frequencies, and digital resolution in the ¹H and ¹³C dimensions were 10 and 180 ppm, 5.1 and 100 ppm, and 3 and 124 Hz/point, respectively. For each t₁ point 320 transients were accumulated. The long-range HSQMBC pulse sequence (Williamson et al. 2014) was adapted to include more efficient water suppression with coherence selection gradients at the first INEPT module and during the refocusing INEPT module at the end of the pulse sequence. Additionally, the water trim pulse was removed from the original pulse sequence to avoid exchangeable proton saturation. Finally, shaped water-selective flip-back pulses were introduced before and after the final simultaneous ¹H and ¹³C 180° pulses in the refocusing INEPT pulse sequence element (Sklenar 1990).

Supplementary data

Supplementary data is available at Glycobiology online.

Conflict of interest statement

None declared.

Abbreviations

CP, capsular polysaccharide; NMB (NMC), N.meningitidis group B (or C); Hbond, hydrogen bond; HON, label of hydrogen attached to oxygen N (natural number); HSQC, heteronuclear single quantum coherence; MD, molecular dynamics; Neu5Ac, N-acetylneuraminic acid; NMR, nuclear magnetic resonance; OH, hydroxyl chemical group; OS, oligosaccharide; PS, polysaccharide; polySia, polysialic acid; RDC, residual dipolar couplings; ROESY, rotating-frame nuclear Overhauser effect correlation spectroscopy; Sia, sialic acid; Sia_N, OS formed with N Sia units; Sia[N], Nth residue of polySia.