RGBM: regularized gradient boosting machines for identification of the transcriptional regulators of discrete glioma subtypes

Abstract

We propose a generic framework for gene regulatory network (GRN) inference approached as a feature selection problem. GRNs obtained using Machine Learning techniques are often dense, whereas real GRNs are rather sparse. We use a Tikonov regularization inspired optimal L-curve criterion that utilizes the edge weight distribution for a given target gene to determine the optimal set of TFs associated with it. Our proposed framework allows to incorporate a mechanistic active biding network based on cis-regulatory motif analysis. We evaluate our regularization framework in conjunction with two non-linear ML techniques, namely gradient boosting machines (GBM) and random-forests (GENIE), resulting in a regularized feature selection based method specifically called RGBM and RGENIE respectively. RGBM has been used to identify the main transcription factors that are causally involved as master regulators of the gene expression signature activated in the FGFR3-TACC3-positive glioblastoma. Here, we illustrate that RGBM identifies the main regulators of the molecular subtypes of brain tumors. Our analysis reveals the identity and corresponding biological activities of the master regulators characterizing the difference between G-CIMP-high and G-CIMP-low subtypes and between PA-like and LGm6-GBM, thus providing a clue to the yet undetermined nature of the transcriptional events among these subtypes.

INTRODUCTION

Changes in environmental and external stimuli lead to variations in gene expression during the proper functioning of living systems. A vital role is played by the transcription factors (TFs), which are proteins that bind to the DNA in the regulatory regions of specific target genes. These TFs can then repress or induce the expression of target genes. Many such transcriptional regulations have been discovered through traditional molecular biology experiments and several of these high-quality mechanistic regulatory interactions have been well documented in TF-target gene databases (1–3).

With the availability of high-throughput experimental techniques for efficiently measuring gene expression, such as DNA micro-arrays and RNA-Seq, our aim now is to design computational models for reverse engineering of gene regulatory networks (GRN) (4) from such data at genomic scale. The accurate reconstruction of GRNs from diverse expression information sources is one of the most important problems in biomedical research (5). Primarily because GRNs can reveal mechanistic hypotheses about differences between phenotypes and sources of diseases (1), which ultimately helps in the identification of therapeutic targets. The problem of inferring GRNs is also one of the most actively pursued problems in computational biology (6) resulted in several DREAM challenges.

This problem is complicated by the noisy and high-dimensional nature of the data (7), which obscures the regulatory network with indirect connections. Another common challenge is to identify and model the non-linear interactions among the TF-target genes in the presence of relatively few samples compared to total number of target genes (i.e. n ≪ p, typical in high dimensional statistics (8)). The majority of methods model the expression of an individual target gene as either a linear or non-linear function of the expression levels of TFs (9–12). They then combine the sub-networks obtained for each target gene to construct the final inferred GRN resulting often in dense networks, whereas in reality, there are only a few transcriptional regulations between the TFs-target genes (6).

There is a plethora of research associated with the problem of inferring GRNs from expression data (10–18). Here, we briefly describe three state-of-the-art methods: ARACNE (19,20), GENIE (21) and ENNET (22) which have been extensively utilized with real data (23,24). ARACNE uses an information theoretic measure, mutual information (25), between the expressions of two genes to generate the corresponding edge weights in the inferred GRN. However, the mutual information values are rarely zero and are plagued by indirect relationships, resulting in many false positives. ARACNE uses a statistical procedure, namely bootstrapping (26), to obtain a minimum threshold for edge weights corresponding to each TF and prunes all those connections associated with a weight is less than the threshold.

GENIE (21), ENNET (22) and SCENIC (27) belong to the category of machine-learning (ML) based on feature selection where the expression vector of each target gene is considered as a dependent variable and the expression matrix corresponding to the list of TFs are the independent variables. GENIE (21), whose novelty is the application of random-forests (RF) (8), is a ML technique that exploits an ensemble of several decision trees to solve the regression task. The advantage of RF is that it can capture non-linear relations between the list of TFs and a given target gene and overcomes the small n, large p problem. Recently, a more accurate non-linear ML technique, the gradient boosting machine (GBM) (28) was employed by ENNET (22) and SCENIC (27) for inferring GRNs. ENNET also solves the regression task using a decision tree. However, it builds the model additively using a boosting procedure where, during each iteration, it adds a new decision tree to the base learner. Each tree is learned by optimizing the least squares loss function between the expression of the dependent variable and the estimated expression vector obtained from the model.

GENIE participated in the DREAM4 and DREAM5 challenges and ENNET was proposed afterwards. Moreover, iRafNet (24) is also a RF based ML technique which was proposed after DREAM challenges took place. All these methods achieved much superior performance w.r.t. AU_pr and AU_roc metrics in comparison to their competitors. A major drawback of these ML methods (21–22,24,29) is that due to lack of regularization a large number of TFs have connections with an individual target gene. Despite the fact that ML-based methods tend to have better performance on simulated data, their success in real applications to uncover important regulators of biological states has not been as wide as the co-expression approached based on mutual information (30) or correlation (31). This is probably due to the difficulties designing of suitable significance thresholds that can be used to select candidate regulatory connections for the purposes of network interrogation through Master Regulator Analysis (32) or Master Regulator Activity (33). Moreover, most current ML-based approaches lack to explicitly model upstream regulators, i.e. network nodes with no incoming connections.

Here, we propose a generic framework for GRN inference using decision tree based ML techniques, like GBM and RF, as core models. The reverse-engineering procedure infers an initial set of transcriptional regulations from expression data using either boosting of regression stumps (GBM) or an ensemble of regression stumps (RF). In order to select suitable thresholds to select the edges in the output network we employ a notion used for identifying the corner of the L-curve criterion (34) in Tikonov regularization (35) on the edge weight distributions (RVI scores). This enable us to select candidate true positive regulations without the need to empirically compute the null distribution of the edge weights function by bootstrapping, such as for example in the case of ARACNE (19). We then re-iterate once through the core GBM or RF model using this optimal list of TFs for each target gene to obtain regularized transcriptional regulations. This pruning step helps to reduce the falsely identified edges while sparsifying the GRN network at the same time.

We also propose a novel heuristic procedure based to identify upstream regulators. The proposed framework allows the user to specify a priori mechanistic active binding network (ABN) of TFs and target genes based on cis-regulatory analysis of active binding sites on the promoters of target genes. This allows to filter-out indirect targets and false positives due to just co-expression. In the presence of an ABN, the reconstructed GRN is a subgraph of it whereas in the absence of such an ABN, the inferred GRN is reconstructed from the expression data. The resulting GRN is sparse, directed and weighted.

The proposed techniques based on our generic framework are hereby referred as Regularized Gradient Boosting Machine (RGBM) and Regularized GENIE (RGENIE) for GBM and RF core models respectively. We evaluated RGBM and RGENIE on DREAM3, DREAM4 and DREAM5 Challenge datasets and simulated RNA-Seq datasets. Both RGBM and RGENIE obtain superior performance relative to ENNET and GENIE in terms of higher values for AU_pr and AU_roc as well as the winner of these competitions by up to 10–15%. RGBM outperforms RGENIE on these datasets, which is expected as the performance of ENNET surpasses that of GENIE.

RGBM has been used to identify the main regulators, of the gene expression signature activated in the FGFR3-TACC3 fusion-positive glioblastoma (36). Here, we evaluate the accuracy of RGBM to identify true targets of one these regulators by validating in vitro the top targets in its regulon. Moreover, we go further and perform a case study by constructing the GRN for glioma tumors using gene expression profiles collected through the cancer genome atlas (TCGA) along with an a priori mechanistic ABN(1) of TFs and their corresponding targets with the goal of identifying the main regulators of the molecular subtypes of glioma using RGBM. Our analysis reveals the identity and corresponding biological activities of the master regulators driving the transformation of G-CIMP-high into the G-CIMP-low subtypes of IDH-mutant glioma and the main differences between PA-like and LGm6-GBM in the IDH-wild-type glioma. This result is a first step to the yet undetermined nature of the transcriptional events driving the evolution among these novel glioma subtypes.

MATERIALS AND METHODS

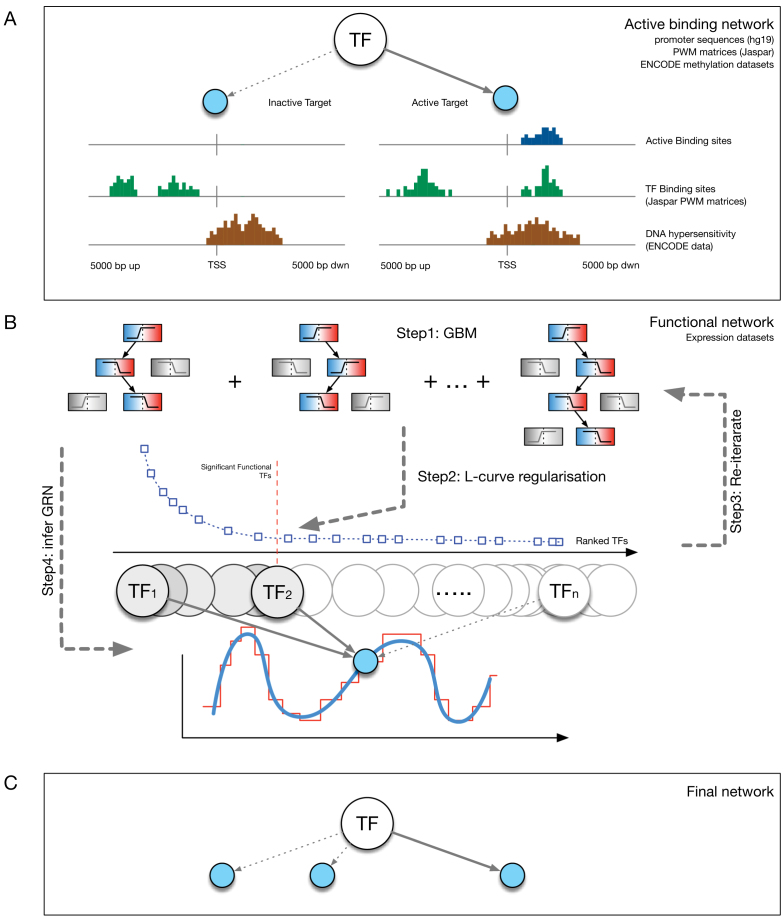
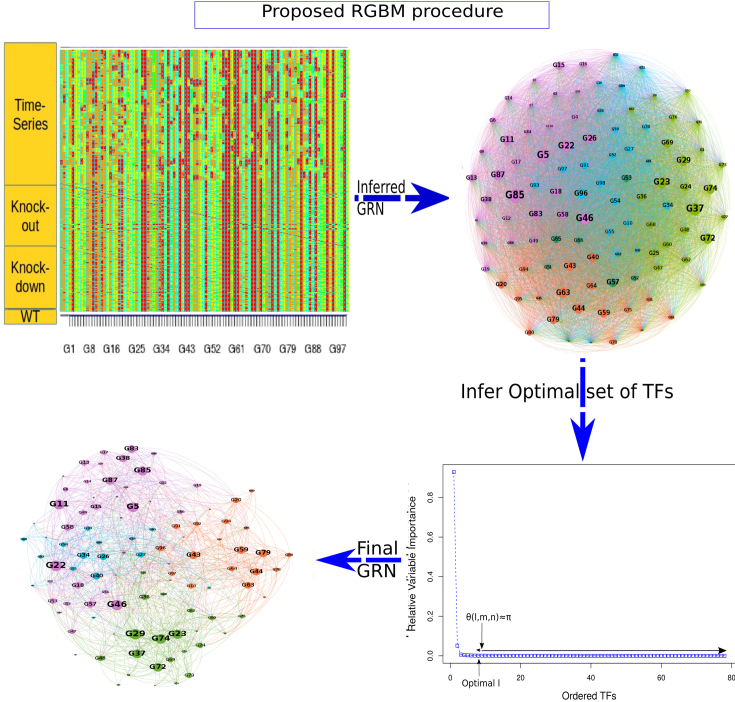
A schematic representation of RGBM approach is illustrated in Figure 1. We first utilize a mechanistic active binding network (ABN) between TFs and their potential targets if such a network is available or can be constructed. The ABN is then fed as prior information to the proposed ML framework. In the absence of an ABN, the GRN is inferred only from the available expression data. A detailed description of the heterogeneous expression datasets that can be handled by our proposed framework is given in Supplementary Section 1.

Figure 1.

Schematic representation of the RGBM approach. (A) First build the active binding network (ABN) and use it as a priori mechanistic network of connections between TFs and target genes, if possible. (B) Illustration of the primary procedure utilized by RGBM. Step1 uses RVI score distribution from a GBM model to rank TFs based on their ability to fit a given target gene. Step2 proposes a regularization step to identify the corner of the discrete L-shaped RVI curve. This results in the optimal set of TFs for a target gene. The proposed regularization step helps to reduce the falsely identified edges associated with a given target gene. It also identifies upstream regulators by using a simple heuristic cut-off on MRVI scores. Step3 is to re-iterate once through the boosting procedure with the optimal set of TFs for each target gene. Step4 is to infer the regulatory sub-graph for each target gene. (C) The final inferred GRN is obtained by combining the regulatory sub-graphs of all target genes and is much sparser than that obtained via ENNET which uses unregularized GBM model to reverse engineer GRN.

The scores obtained from the GBM model are used to rank TFs based on their capability to potentially regulate a target gene. We adopt the the relative variable importance (RVI), it takes value between [0, 1], where a value of RVI(ϕ) = 1 indicates that the TF (ϕ) was the only feature that was required to explain the expression of the target gene among the list of all TFs whereas a value of 0 for a TF indicates that the TF was not regulating the expression of the given target gene. These RVI scores serve as the edge weights between the list of TFs and the given target gene. We utilized a modified version of the triangle method (37) to locate the corner of discrete L-shaped RVI curve as shown in Figure 1B. All the TFs to the left of this position form the optimal set of TFs for that target gene. We also identify the upstream regulators (genes which are not controlled by any regulator and have 0 in-degree in the inferred GRN) using a simple heuristic on the maximum RVI (MRVI) score of all genes. Finally, we re-iterate once through the boosting procedure with the optimal set of TFs for each target gene to assemble the final network. We describe the details of each step of Figure 1 in the following subsections.

Building the ABN

To learn potential regulatory activities between TFs and target genes in the glioma subtypes network, we merge constitutive associations due to active binding sites (ABN) and functional association due to contextual transcriptional activity (Figure 1 A). This allows to filter out indirect associations due to just co-expression and false positives.

The active binding network (ABN) is reconstructed from the collection of TF binding sites that are also active i.e. falling into not methylated regions. Binding sites are predicted with the FIMO (Find Individual Motif Occurrences) tool using 2532 unique motif PWMs (Position Weight Matrices) obtained from Jaspar (38) corresponding to 1203 unique TFs (38–41). The active promoter regions are classified with ChromHMM (v1.10), a Hidden Markov Model that classifies each genome position into 18 different chromatin states (nine states are considered open/active sites: TssA, TssFlnkm, TssFlnkU, TssFlnkD, Tx, EnhG1, EnhG2, EnhA1m, EnhA1) from 98 human epigenomes (42). A binding relationship is considered active if the TF motif signal is significantly (FDR < 0.05) over-represented in the target promoter region (±5 kb TSS, hg19) and, in the same position (at least 1 bp overlapping), the chromatin state is classified as open/active. The ABN consists of 5,850,559 overlapping active sites corresponding to 1,874,570 unique TF associations between 457 TFs and 12,985 target genes.

From the inference problem to a variable selection task

The input of the RGBM is a gene expression matrix E and, optionally, the adjacency matrix of the ABN. In absence of the ABN we assume that every TF can potentially regulate each target gene in the expression matrix. An element of the expression matrix 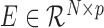i.e. e_ij, i = 1…N and j = 1…p, represents the expression value of jth gene in the ith sample. Let C_j be the list of potential TFs i.e. for each target gene j ∈ {1, …, p}, we sub-divide the problem of inferring the GRN into p independent tasks. For the jth sub-problem, we get the sub-network corresponding to the outgoing edges from the appropriate TFs to the target gene j. To generate this sub-graph, we first create the dependent vector Y_j = E[, j] and a feature expression matrix i.e. matrix of independent variables, X_j = E[, C_j] from the expression matrix E (Supplementary Figure S2) Each of the p sub-problems can mathematically be formulated as:

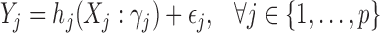(1)

Here, ϵ_j represents random noise and h_j(X_j; γ_j) is the parametric function that maps the TF expression X_j to target (Y_j) while optimizing the parameters γ_j. Our goal is to identify a small number of TFs which drive the expression of the jth gene using the columns of X_j as input features. Essentially, we have to solve a regression problem while inducing sparsity in the feature space, resulting in a subset of the list of TFs, which drive the expression of the jth target gene. This problem, referred as feature or variable selection is usually solved with a linear regression from the feature space to the target space (43–46). Inducing sparsity, have been utilized for GRN inference (15,47–48). These methods can only capture linear relationships and fail to detect non-linear interactions between the TFs and targets, thereby, missing several true positive edges.

In our generic framework, we adopt two tree-based ML methods, namely RF (8,49) and GBM (9) as they solve the aforementioned problem using a non-linear mapping. Additionally, they provide a scheme to generate relative variable importance (RVI) score for each TF which allows to rank the TFs based on their contributions. The RVI scores are further used as edge weights for the sub-network obtained from C_j and the jth target gene. The RVI score measures how useful the each TF is for fitting the expression of jth target gene given the contribution of all the other TFs for that target. The RVI score for a TF ϕ from the core Gradient Boosting Model is computed as (28):

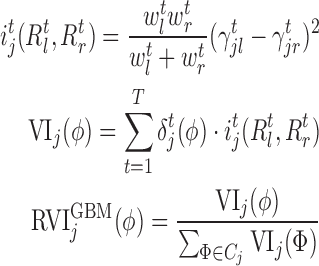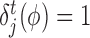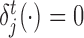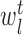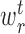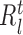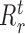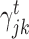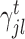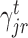Here, , if TF ϕ results in the optimal split for the tth regression tree and the function for all the other TFs at iteration t, and are the number of observations in the left () and right () branches of the tree and the coefficients , k ∈ {l, r}, are the parameters of the decision tree as indicated in Equation 1 for the jth target gene. In case of the least-squares (LS) loss, and are the averages of all the pseudo-residuals (details in Supplementary Section 2) (22,28) falling in regions 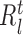and 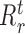respectively. 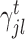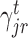Similarly, for least-absolute deviation (LAD) loss, and are the median of all the pseudo-residuals (28) in the disjoint regions 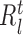and 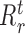respectively.

The TF which results in the optimal split is the one which maximizes the least squares improvement criterion (22,28), i( ·, ·), for regression tree t. For each tree t, we select the TF which can best divide the remaining expressions (pseudo-residuals) of the target gene into two distinct regions.

Similarly, in the case of RF, the RVI score can be represented (21) as:

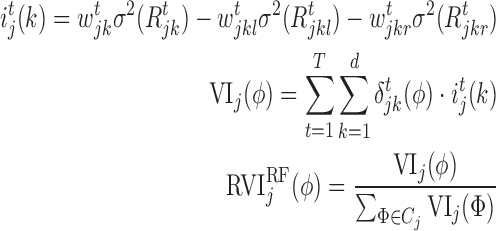where k represents a node in the regression tree, 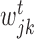, 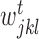and 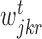correspond to number of samples in node k, the left branch of k and right branch of k respectively, the function σ²( · ) represents the variance of all the expression values in regions 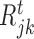, 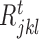and 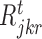and d is total number of nodes in the tth regression tree for target gene j. The overall importance of TF ϕ is then computed by summing the i (· ) values of all tree nodes where this variable is used to split. To determine a split into disjoint regions 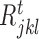and 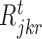, we select the TF (ϕ) which maximizes the function i( · ), thereby indicating that values falling within each region have small variance when compared to the variance obtained from all the expression values at that node. In GENIE3 (21), the authors set 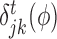as 1 for TF ϕ if it maximizes the 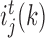criterion and set it to 0 for all other TFs. The TFs that are not selected at all obtain a value of 0 as their importance, and those that are selected close to the root nodes of several trees typically obtain high scores.

The RVI score for a TF is unit-less, as it is the contribution of that TF given the contribution of all other TFs for fitting the expression of a given target gene as observed from the equations above. It takes values between [0, 1]. A large RVI score suggests with high confidence that the corresponding TF is regulating the expression of the given target gene.

The core of the GBM model is explained in detail in the Supplementary Section 2 and we refer the readers to GENIE (21) for a detailed description about the usage of RF for GRN inference. ENNET (22) utilized the LS-Boost (Supplementary Algorithm 1:S1) as GBM model as core function for reverse engineering of gene regulatory network. In our proposed framework, we provide the user with the flexibility of utilizing either LS-Boost (Algorithm S1) or LAD-Boost (Algorithm S2) as the core GBM model for RGBM. This is because it was shown in (28) that LS-Boost performs extremely well for normally distributed expression values whereas LAD-Boost performs better for slash distributed values. Our framework also works well in combination with a core RF model resulting in a regularized version of GENIE(21) namely RGENIE.

We report below the proposed regularization steps in combination with the core GBM model.

Main regularization steps

An important aspect of GRN is sparsity (6), i.e. there are only a few TFs which regulate a target gene and there are a few genes which have no regulations or we can have 0 in-degree (6) nodes in the inferred GRN. Thus, the procedure for reverse engineering GRNs should return sparse networks and should be able to detect such 0 in-degree upstream regulators. The adjacency matrix obtained from core GBM model can be quite dense, as shown in Supplementary Figure S3.

However, when adjacency matrix is converted into an ordered edge-list (ranked in descending order based on edge weights), several of the top ranked connections are indeed true positives, whereas many others small weighted edges are false positives. Hence, there is a possibility to reduce the number of falsely identified transcriptional regulations between the TFs and targets as illustrated below.

The sorted RVI score curve for an individual target gene approximately follows an exponential distribution as demonstrated empirically in Supplementary Figure S4 for GBM and in Supplementary Figure S7 for RF.

In order to identify the optimal set of TFs for each target gene, RGBM uses an idea similar to that used for identifying the corner in discrete L-curve criterion (34,50) in Tikonov regularization (35). The problem in Tikonov L-curve is to identify the corner of a discrete L-curve where the surface of the discrete L-curve is monotonically decreasing. Several algorithms have been proposed for computing the corner of a discrete L-curve, taking into account the need to capture the overall behavior of the curve and avoiding the local corners (34,51–52). RGBM uses a modified variant of the triangle method (37). Specifically, let 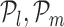and be three points on the RVI curve satisfying l < m < n and let v_{m, l} denote the vector from 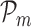to 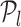. Then, we define the oriented angle θ(l, m, n) ∈ [0, π] associated with the triplet as the angle between the two vectors v_{m, n} and v_{m, l} i.e. θ(l, m, n) = ∠(v_{m, n}, v_{m, l}). With this definition, an angle θ(l, m, n) = π corresponds to the point 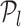, which determines the optimal position (optimal number of TFs) on the RVI curve. The key idea of the triangle method is to consider the following triples of L-curve points: 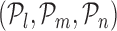, l = 1, …, n − 2, m = l + 1, …, n − 1, where n corresponds to the TF with the least non-zero RVI score (RVI_j( · )) for the j^th target gene. By using this idea, we identify as the corner the first triple where the oriented angle θ(l, m, n) is either equal to π or is maximum. If the angle θ(l, m, n) = π, then that part of the RVI curve is already “flat” w.r.t. the least contributing TF and the position l represents the optimal number of TFs for the jth target gene. All the TFs to the left of position l (including l) form the optimal set of TFs that regulate the target gene j as shown in Figure 3. The worst-case complexity of the triangle method is O(p²). However, for a 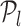, if 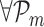, the oriented angles 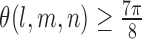then optimal corner corresponds to this l as the L-curve is almost flat from l and hence considered flat from 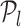(34). Thus, all TFs to left of 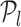and including 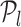constitute the list of regulators for that target gene. This acts as an early stopping criterion and helps to reduce the complexity of the triangle method. The majority of the RVI curves have an approximately exponential distribution, so we can quickly reach the position where the oriented angle first becomes π and avoid unnecessary computations as indicated in Algorithm 1. From our experiments, we empirically found that the proposed technique requires much lower number steps on average to infer the optimal set of TFs for each target gene because of the exponential nature of the RVI score distribution. Moreover, the computation of the optimal set of TFs for each target gene can be performed in parallel.

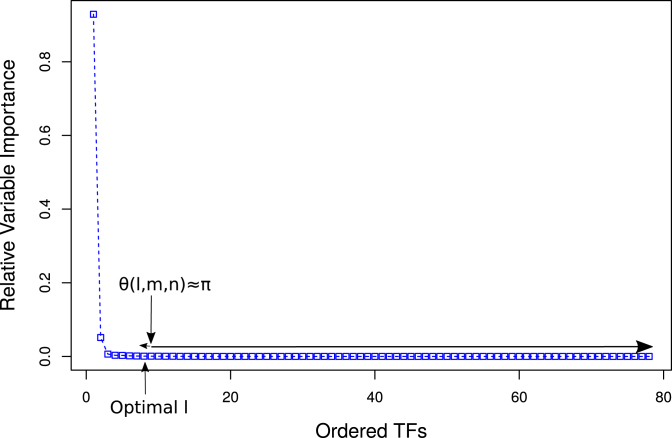
Figure 3.

Optimal set of TFs obtained from the RVI curve of gene ‘G1’ for Network 1 from DREAM4 challenge using a triangle method (37) based technique which is commonly employed for identifying the corner in the Tikonov L-curve. We can see that the right most non-negative RVI score is at an x-axis position close to 80. This indicates that there are at least 20 TFs which had RVI(ϕ) = 0 for gene ‘G1’.

Another key feature of RGBM is the detection of upstream regulators, i.e. nodes which have no incoming edges in the inferred GRN, for which we devised a simple heuristic. From Figure 4A, we observe that for several target genes the maximum RVI (MRVI) score is >0.5. But there are a few outlier genes for which the MRVI score is much smaller (O(10⁻¹) or O(10⁻²)) indicating that the given set of TFs cannot drive the expression of these target genes. In order to detect these outliers, we transform the MRVI score into the inverse maximum relative variable importance (IMRVI) score using the inverse cumulative density function (Ψ( · )) on the MRVI score distribution as illustrated below:

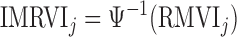(2)

By using this function it becomes easy to identify the heuristic cut-off ρ = μ_IMRVI − 1.64 × σ_IMRVI corresponding to ≈5th percentile of the IMRVI score distribution that is allocated to the outliers. All the genes whose IMRVI score is to the left of the ‘red’ line in Figure 4 are considered as candidate outliers. For these candidate outliers, if the cardinality (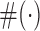) of the optimal set of TFs satisfies: 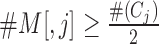, then it is an indication that its difficult for this set of TFs to fit the expression of the given target gene as more than half the set of TFs are getting low RVI scores, close to the MRVI score for that target gene.

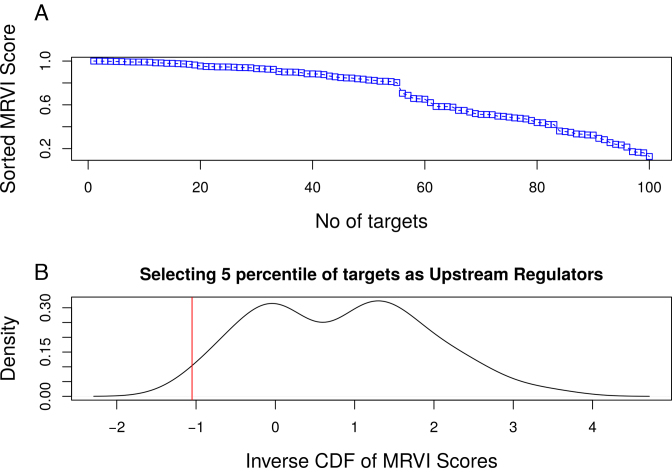
Figure 4.

Subfigure A represents the MRVI score distribution for all the 100 targets of Network 1 from DREAM4 challenge. Subfigure B corresponds to inverse cumulative density function of the MRVI scores (IMRVI). Here the ‘red’ vertical line represents the heuristic cut-off ρ s.t. all targets whose MRVI score is less than ρ are selected as 0 in-degree genes and correspond to 5 percentile of the distribution.

We select and prune out such genes as 0 in-degree targets, or upstream regulators, in the final inferred GRN. For example, for the 5th target gene, the MRVI score is ≈0.2, which is very close to the smallest MRVI score in MRVI score distribution as depicted in Figure 4 A. Moreover, there are 51 TFs with relatively small non-zero RVI scores for the 5th target gene, as shown in Figure 2. Hence, the 5th gene is considered an upstream regulator in the inferred GRN.

Figure 2.

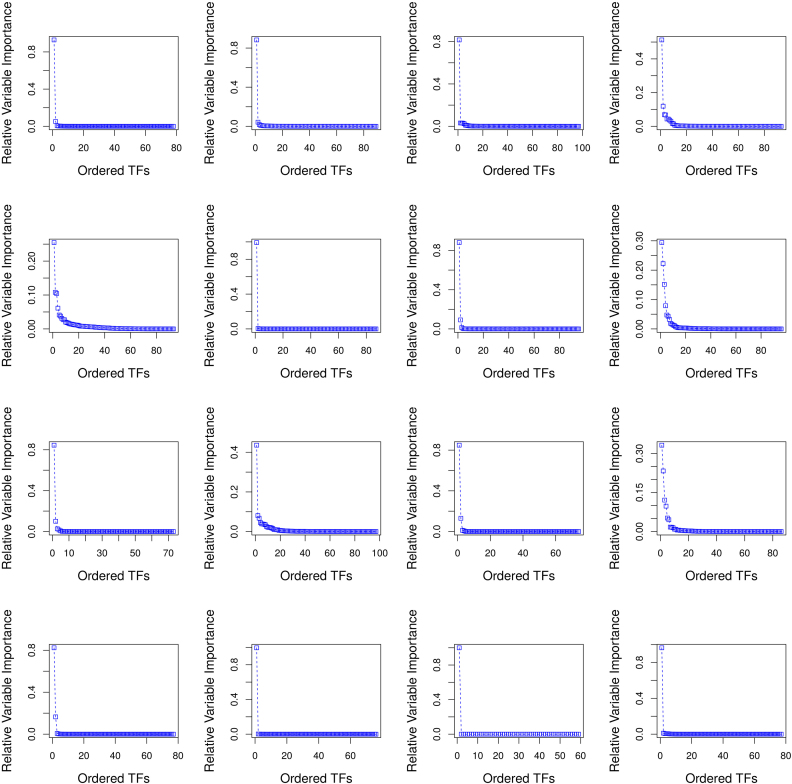
Sorted RVI score curves for the first 16 targets of Network 1 from DREAM4 challenge. The target genes are ordered in row-format from left to right (i.e. 1–4 target genes in row 1, 5–8 target genes in row 2, etc.) We can empirically observe that the sorted RVI curves ≈ follows an exponential distribution w.r.t. the number of TFs for each target gene. This is further verified by a near linear fit to the log (RVI) scores w.r.t. the set of TFs as showcased in Supplementary Figure S4. Thus, there are only a few TFs which are strongly regulating the expression of a target gene.

Once we have obtained the optimal set of TFs for an individual target gene, we re-iterate through the core GBM model. All these steps together form the RGBM technique for re-constructing GRNs as showcased in Algorithm 2 and illustrated via Figure 5.

Figure 5.

Final inferred GRN (A_final) obtained as a result of RGBM Algorithm (Algorithm 2) on Network 1 for DREAM4 challenge. The final inferred GRN has 1144 edges between 100 nodes whose edge weights are >3.3 × 10⁻¹⁵ (machine precision). A_final is much more sparse in comparison to A₁ which is obtained after initial GBM modeling. In network A_final, we have greatly reduced the number of falsely identified transcriptional regulations in A₁. We also identified 4 dense communities or clusters in inferred network A₁ using kernel spectral clustering (71). Nodes belonging to a cluster and edges originating from the nodes in these clusters have the same color. The size of each node is proportional to its out-degree. We observe that the communities present in A_final have fewer edges and thus have much lower density than the clusters in A₁.

Post-transcriptional TF activity

TF activity is determined using an algorithm that allows computationally inferring protein activity from gene expression profile data on an individual sample basis. The activity of a TF, defined as a metric that quantifies the activation of the transcriptional program of a specific regulator in each sample S_i, is calculated as follows:

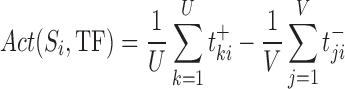(3)

where 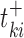is the expression level of the kth positive target of the MR in the ith sample, 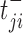is the expression level of the jth negative target of the MR in the ith sample, U (V) the number of positive (negative) targets present in the regulon of the considered MR. If Act(S_i, TF) > 0, the TF is active in that particular sample. f Act(S_i, TF) < 0, the TF is inversely activated and if Act(S_i, TF) ≈ 0 it is non-active. To identify the main Master Regulators of glioma subtypes reported in Section 4, we use supervised analysis of the activity function defined in equation (3) using the Wilcoxon test (53).

Cell culture, lentiviral infection and quantitative RT-PCR

Human astrocytes (HA) (54) were cultured in DMEM supplemented with 10% fetal bovine serum (FBS, Sigma). Cells were routinely tested for mycoplasma contamination using the Mycoplasma Plus PCR Primer Set (Agilent Technologies) and were found to be negative. Cell authentication was performed using short tandem repeats (STR) at the ATCC facility. Human astrocytes were infected either with the lentiviral vector pLOC–vector or pLOC–PPARGC1A.

Total RNA was prepared using the Trizol reagent (Invitrogen) and cDNA was synthesized using SuperScript II Reverse Transcriptase (Invitrogen) as described in (32). Quantitative RT–PCR (qRT–PCR) was performed with a Roche 480 thermal cycler, using SYBR Green PCR Master Mix (Applied Biosystems). Primers used in qRT–PCR are listed in Supplementary Table S4. qRT–PCR results were analyzed by DDCt method using 18S as housekeeping gene.

RESULTS AND DISCUSSION

For GBM based RGBM, we use the same parameters corresponding to the optimal parameter settings for ENNET (22). Similarly, for the RF based RGENIE, we use the parameters which correspond to the optimal parameter setting for GENIE (21). Additional details about the parameter setting for proposed RGBM and RGENIE models can be found in Supplementary Section 4.

RGBM outperforms state-of-the-art on DREAM Challenge Data

We assessed the performance of the proposed RGBM models using LS-Boost and LAD-Boost as core models and RGENIE using RF as core model on universally accepted benchmark networks of 100 or more genes from the DREAM3, DREAM4 and DREAM5 challenges (55–57) and compared them with several state-of-the-art GRN inference methods. For the purpose of comparison, we selected several methods including ENNET (22), GENIE (21), iRafNet (24), ARACNE (19) and the winner of each DREAM challenge. Among all the DREAM challenge networks, we performed experiments on in-silico networks of size 100 from DREAM3 and DREAM4, and on three benchmark (out of which two are real) networks from the DREAM5 challenge.

The DREAM3 and DREAM4 challenges comprise five in-silico networks whose expression matrices E are simulated using GeneNetWeaver (58) software. Benchmark networks were constructed as sub-networks of systems of transcriptional regulations from known model organisms namely Escherichia coli and Saccharomyces cerevisiae. In our experiments, we focus on networks of size 100, which are the largest in the DREAM3 suite. There are several additional sources of information available for these networks, such as knockout, knockdown, and wildtype expressions apart from the time-series information. However, most of the state-of-the-art techniques do not necessarily utilize all these heterogeneous information sources. We showcase the best results generated for the DREAM3 and DREAM4 challenge networks using the optimal combination of information sources for different GRN inference methods in Table 1.

Table 1. Comparison of RGBM and RGENIE with a other of inference methods on DREAM3 and DREAM4 networks of size 100.

Methods	Data used	DREAM3 experiments
		Network 1		Network 2		Network 3		Network 4		Network 5
		AU pr	AU roc	AU pr	AU roc	AU pr	AU roc	AU pr	AU roc	AU pr	AU roc
RGBM (LS-Boost)	KO,KD,WT	0.699	0.903	0.888	0.965	0.597	0.900	0.571	0.861	0.460	0.787
RGBM (LAD-Boost)	KO,KD,WT	0.683	0.903	0.870*	0.963*	0.562*	0.900	0.535*	0.853*	0.400	0.770
ENNET	KO,KD,WT,MTS	0.627	0.901	0.865+	0.963+	0.552+	0.892	0.522+	0.842	0.384	0.765
RGENIE	KO,KD,WT	0.521	0.870	0.821−	0.899	0.456	0.812	0.478−	0.778	0.356	0.718
GENIE	KO,KD,WT	0.430	0.850	0.782	0.883	0.372	0.729	0.423	0.724	0.314	0.656
iRafNet	KO,KD,WT	0.528	0.878	0.812	0.901	0.484	0.864	0.482	0.772	0.364	0.736
ARACNE	KO,KD,WT	0.348	0.781	0.656	0.813	0.285	0.669	0.396	0.662	0.274	0.583
Winner (72)	KO, WT	0.694	0.948	0.806	0.960	0.493	0.915	0.469	0.853	0.433	0.783
Methods	Data Used	DREAM4 Experiments
		Network 1		Network 2		Network 3		Network 4		Network 5
		AUpr	AUroc	AUpr	AUroc	AUpr	AUroc	AUpr	AUroc	AUpr	AUroc
RGBM (LS-Boost)	KO,KD,WT,MTS	0.709	0.936	0.561	0.878*	0.525	0.911	0.616	0.903	0.450	0.893
RGBM (LAD-Boost)	KO,KD,WT,MTS	0.682*	0.924*	0.525*	0.895	0.490*	0.907*	0.566*	0.903	0.413*	0.885*
ENNET	KO,KD,WT	0.604+	0.893	0.456+	0.856+	0.421+	0.865+	0.506+	0.878+	0.264+	0.828+
RGENIE	KO,WT	0.448	0.902	0.330	0.792	0.374	0.834−	0.362−	0.840	0.218−	0.773−
GENIE	KO,WT	0.338	0.864	0.309	0.748	0.277	0.782	0.267	0.808	0.114	0.720
iRafNet	KO,TS	0.552	0.901	0.337	0.799	0.414	0.835	0.421	0.847	0.298	0.792
ARACNE	KO,KD,WT	0.279	0.781	0.256	0.691	0.205	0.669	0.196	0.699	0.074	0.583
Winner (73)	KO	0.536	0.914	0.377	0.801	0.390	0.833	0.349	0.842	0.213	0.759

Here, we provide the mean AU_pr and AU_roc values for 10 random runs of different inference methods. Here, KO, knockout; KD, knockdown; WT, wildtype; MTS, modified smoothed version of the time-series data. The best results are highlighted in bold. *, +, − represent the quality metric values where RGBM (LAD-Boost), ENNET and RGENIE techniques, respectively outperform the winner of DREAM3 and DREAM4 challenges.

We observe from Table 1 that the best source of information for almost all the GRN inference methods are the knockout, knockdown, and wildtype expressions for DREAM3 challenge. But in case of the DREAM4 challenge, all available heterogeneous information sources are useful for RGBM models, whereas knockout, knockdown, and wildtype expressions are useful for ENNET and ARACNE, while the knockout and wildtype expression are optimal for RGENIE and GENIE. From Table 1, we showcase that ARACNE performs the worst on all DREAM3 and DREAM4 challenge datasets. RF based methods GENIE, iRafNet and RGENIE are inferior to GBM based methods ENNET and RGBM, for both the DREAM3 and DREAM4 challenge. But, RGENIE significantly outperforms GENIE w.r.t quality metrics AU_pr and AU_roc on all DREAM3 and DREAM4 challenge datasets. Similarly, RGBM using LS-Boost as the core model significantly outperforms ENNET as well as the winner on several networks for both of these challenges.

Both RGBM and RGENIE gain maximum benefit from the proposed regularization steps by removing falsely identified edges and can efficiently detect 0 in-degree genes. As a result these methods gain a lot in terms of precision and recall. However, RGBM (LS-Boost) clearly performs the best on the majority of the datasets from the DREAM3 and DREAM4 challenge.

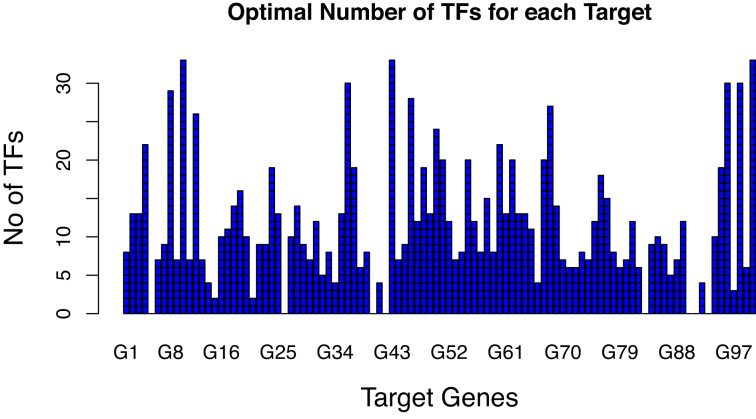
Figure 6 illustrates the optimal number of TFs identified by proposed Algorithm 1 for each target gene and passed as network M either to Algorithm S1 or Algorithm S2 to infer the final GRN for Network 1 of DREAM4 challenge. We observe that several genes (including ‘G5’, ‘G26’, ‘G40’, ‘G42’ etc.) have 0 TFs connected to them and inferred as the 0 in-degree upstream regulators.

Figure 6.

Optimal number of TFs for each target gene obtained from proposed Algorithm 1 for Network 1 of DREAM4 challenge.

Two benchmark networks in the DREAM5 (6) challenge of different sizes and structure were generated using a Prokaryotic model organism (E. coli) and a Eukaryotic model organism (S. cerevisiae) corresponding to Network 3 and Network 4 respectively. The time-series data of only Network 1 was simulated in-silico, the two other sets of expression data were measured in real experiments. DREAM5 was the first challenge where participants were asked to infer GRNs for large-scale real datasets, i.e. for O(10³) target genes and O(10²) known TFs. Gold standard networks were obtained from two sources: the RegulonDB database (59), and the Gene Ontology (GO) annotations (60). The E. coli network of the DREAM5 challenge consisted of 4297 target genes, 296 TFs and the corresponding gold standard has 2066 interactions. Similarly, the S. cerevisiae network comprises 5667 targets, 183 TFs and the corresponding gold standard has 2528 regulatory interactions (6). The results of all the inference methods for DREAM5 expression data using the optimal combination of information sources are summarized in Table 2. Network 2 from DREAM5 was ignored as the gold standard network was not well constructed (6,22).

Table 2. Comparison of RGBM and RGENIE with inference methods on DREAM5 networks of varying sizes.

Methods	Data used	DREAM5 experiments
		Network 1		Network 3		Network 4
		AU pr	AU roc	AU pr	AU roc	AU pr	AU roc
RGBM (LS-Boost)	KO,Exp	0.537	0.846*	0.086	0.633*	0.048	0.546
RGBM (LAD-Boost)	KO,Exp	0.513*	0.842*	0.084	0.628*	0.047*	0.544*
ENNET	KO,Exp	0.432+	0.857	0.069	0.632+	0.021	0.532+
iRafNet	KO,MTS,Exp	0.364	0.813	0.112	0.641	0.021	0.523
RGENIE	Exp	0.343−	0.821−	0.104−	0.623−	0.022−	0.524−
GENIE (Winner)	Exp	0.291	0.814	0.094	0.619	0.021	0.517
TIGRESS (15)	KO,Exp	0.301	0.782	0.069	0.595	0.020	0.517
CLR (18)	Exp	0.217	0.666	0.050	0.538	0.018	0.505
ARACNE	Exp	0.099	0.545	0.029	0.512	0.017	0.500

Here, we provide the mean AU_pr and AU_roc values for 10 random runs of different inference methods. Here, KO, knockout; KD, knockdown; WT, wildtype; MTS, modified smoothed version of the time-series data; Exp, steady-state gene expression. The best results are highlighted in bold. *, + and − represent the quality metric values where RGBM, ENNET and RGENIE techniques respectively defeat the winner of DREAM5 challenge, i.e. GENIE.

RGBM using LS-Boost core model gives better results than other methods w.r.t evaluation metrics AU_pr and AU_roc on Network 4 as illustrated in Table 2. It easily defeats the winner (GENIE) of the DREAM5 challenge and outperforms recent state-of-the-art GRN inference methods iRafNet and ENNET. Similarly, the performance of RGENIE surpasses that of GENIE. However, RGBM performs much better than RGENIE on Network 4 whereas it is defeated by RGENIE w.r.t. AU_pr for Network 3. We observe from Table 1 and Table 2 that RGBM based on the LS-Boost model usually has a better performance than RGBM based on the LAD-Boost model for both in-silico and real datasets. Hence, for all further experimental comparisons, we will use RGBM based on the core LS-Boost model.

Interestingly, the predictions for real expression profiles (DREAM5 challenge—Networks 3 and 4) result in extremely low precision-recall values as depicted in Table 2. One of the reasons for the poor performance of all the inference methods for such expression data is the fact that experimentally derived pathways, and consequently gold standards obtained from them, are not necessarily complete, regardless of how well the model organism is known. Additionally, there are regulators of gene expression other than TFs, such as miRNA and siRNA, which also drive the expression of these genes.

RGBM outperforms state-of-the-art on synthetic RNA-Seq data

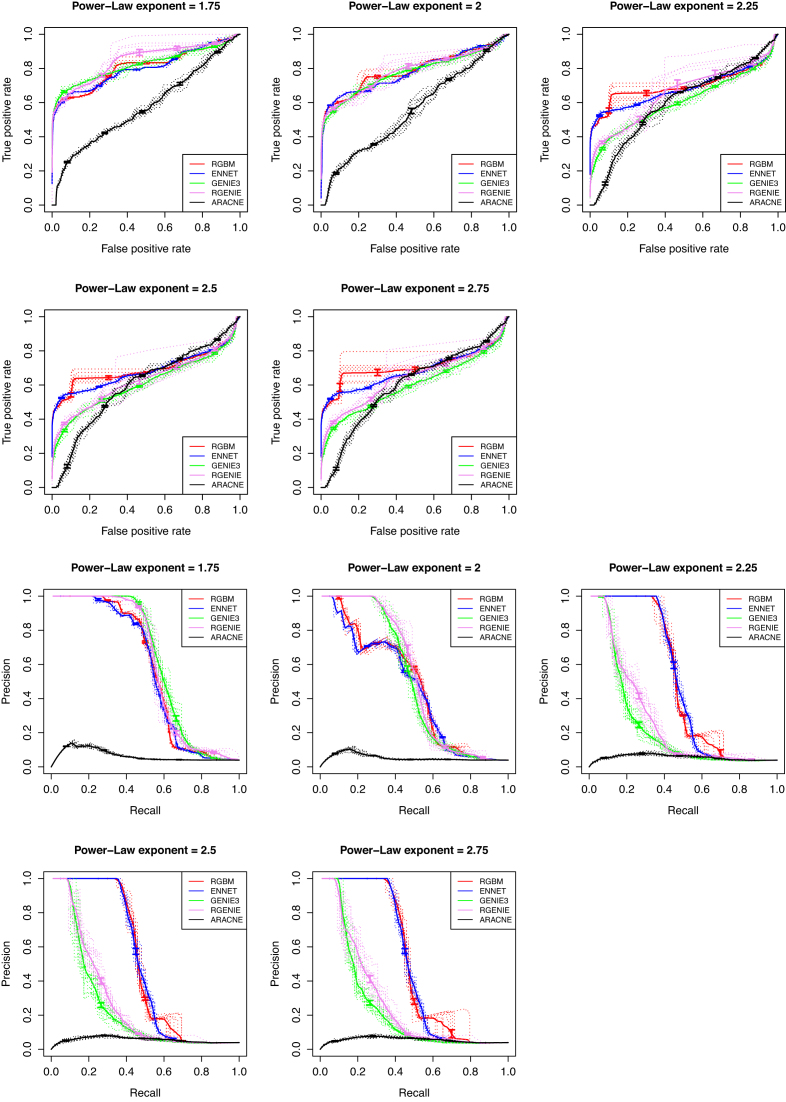
We conducted additional experiments on simulated RNA-Seq data. We used our R package synRNASeqNet (https://cran.r-project.org/web/packages/synRNASeqNet) to generate RNA-Seq expression matrices. It uses a stochastic Barabási-Albert (BA) model (61) to build random scale-free networks using a preferential attachment mechanism with power exponent α and simulated RNA-Seq counts from a Poisson multivariate distribution (62). For our experiments, we generated 5 RNA-Seq expression (E) matrices comprised of 500 RNA-Seq counts for 50 target genes using power exponent values α ∈ {1.75, 2, 2.25, 2.5, 2.75} respectively and repeated this procedure 10 times. In this experiment, we are not provided with any additional information, such as knockout or knockdown, and the active binding network (ABN) is not present. We use evaluation metrics like AU_pr and AU_roc to compare the proposed RGBM (using LS-Boost) and RGENIE with state-of-the-art GRN inference methods, including ENNET, GENIE and ARACNE. Figure 7 illustrates the performance of various GRN inference methods w.r.t. ROC and PR curves.The performance of RGBM and RGENIE is compared with ENNET, GENIE and ARACNE for five different experimental settings as shown in Table 3.

Figure 7.

Comparison of RGBM and RGENIE with ENNET, GENIE3 and ARACNE w.r.t. AU_roc and AU_pr curves for five different RNA-Seq experiments.

Table 3. Comparison of proposed RGBM and RGENIE techniques with ENNET, GENIE and ARACNE GRN inference methods w.r.t. evaluation metrics AU_roc and AU_pr for reverse-engineering GRNs from RNA-Seq counts where the underlying ground-truth network follows a BA preferential attachment model with exponent α. Here no additional information (ABN or knockout or knockdown) is available.

Methods	RNA-Seq experiments
	Exponent α = 1.75		Exponent α = 2		Exponent α = 2.25		Exponent 2.5		Exponent 2.75
	AU pr	AU roc	AU pr	AU roc	AU pr	AU roc	AU pr	AU roc	AU pr	AU roc
RGBM	0.575	0.808	0.470	0.789	0.498	0.700	0.500	0.695	0.506	0.709
ENNET	0.566	0.802	0.454	0.780	0.495	0.685	0.494	0.684	0.494	0.684
RGENIE	0.605	0.846	0.528	0.785	0.270	0.652	0.272	0.626	0.274	0.641
GENIE	0.622	0.822	0.507	0.777	0.235	0.607	0.245	0.610	0.241	0.601
ARACNE	0.065	0.575	0.053	0.556	0.056	0.600	0.055	0.600	0.055	0.600

Here, the evaluation metrics AU_roc and AU_pr represent the mean value of these evaluation metrics for 10 random runs of each setting. We can observe from Figure 7 and Table 3 that RGBM performs the best as preferential attachment increases and the degree distribution becomes more skewed for the synthetic RNA-Seq networks. However, for smaller values of α, the RF based inference methods GENIE and RGENIE are better than RGBM. But their performance decreases drastically w.r.t. the evaluation metric AU_pr for increasing values of preferential attachment exponent α, suggesting that RF based GRNs are obscured by false identified edges and are inferior to GBM based methods when trying to reverse engineer GRNs where very few TFs (hubs) are regulating a majority of the target genes.

In both DREAM challenge and synthetic RNA-Seq experiments, GBM based RGBM outperforms almost always the RF based RGENIE method. Hence, we only used the proposed RGBM method for additional experiments as depicted in Supplementary Section 5 and in our real case-study to identify the master regulators of different glioma cancer subtypes.

RGBM identifies the master regulators of glioma cancer subtypes

The results in the previous paragraphs have shown that RGBM is a promising technique to efficiently recover the regulatory structure of small and large gene networks. Here, we apply RGBM for the identification of Master Regulators of tumor subtypes in human glioma, the most frequent primary brain tumor in adults (63). In the cancer field, master regulators (MR) have been defined as gene products (mostly TFs) necessary and sufficient for the expression of particular tumor-specific signatures typically associated with specific tumor phenotypes (e.g. pro-neural vs. mesenchymal). In the case of malignant gliomas, reverse engineering has been used to successfully predict the experimentally validated transcriptional regulatory network responsible for activation of the highly aggressive mesenchymal gene expression signature of malignant glioma (32). A master regulator gene can be defined as a network hub whose regulon exhibits a statistically significant enrichment of the given phenotype signature, which expresses a cellular phenotype of interest, such as tumor subtype. MARINa (MAster Regulator INference algorithm) is an algorithm to identify MRs starting from a GRN and a list of differentially expressed genes (64). This specific algorithm was successfully applied previously (32) to identify Stat3 and C/EBPβ as the two TFs hierarchically placed at the top of the transcriptional network of mesenchymal high-grade glioma. We use MARINa in conjunction with the GRN inferred using RGBM on a Pan-glioma dataset.

Recently, the Pan-Glioma Analysis Working Group of the The Cancer Genome Atlas (TCGA) project analyzed the largest collection of human glioma ever reported (23). It has been shown that, using a combination of DNA copy number and mutation information, together with DNA methylation and mRNA gene expression, human gliomas can be robustly divided into seven major subtypes defined as G-CIMP-low, G-CIMP-high, Codel, Mesenchymal-Like, Classic-Like, LGm6-GBM and PA-like (23). The first key division of human glioma is driven by the status of the IDH1 gene, whereby IDH1 mutations are typically characterized by a relatively more favorable clinical course of the disease. IDH1 mutations are associated with a hypermethylation phenotype of glioma (G-CIMP, (65)). However, our Pan-glioma study reported that IDH-mutant tumors lacking co-deletion of Chromosome 1p and 19q are a heterogeneous subgroup characterized predominantly by the G-CIMP-high subtype and less frequently by the G-CIMP-low subgroup. This last is characterized by relative loss of the DNA hypermethylation profile, worse clinical outcomes and likely represents the progressive evolution of G-CIMP-high gliomas toward a more aggressive tumor phenotype (23). However, the transcriptional network and the set of MRs responsible for the transformation of G-CIMP-high into G-CIMP-low gliomas remained elusive.

Among the large group of IDH-wildtype tumors (typically characterized by a worse prognosis when compared to IDH-mutant glioma), we discovered that, within a particular methylation-driven cluster (LGm6) and at variance with the other methylation-driven clusters of IDH-wildtype tumors, the lower grade gliomas (LGG) display significantly better clinical outcome than GBM tumors (GBM-LGm6). We defined these LGG tumors as PA-like based on their expression and genomic similarity with the pediatric tumor Pylocitic Astrocytoma. However, for the transition from G-CIMP-high into G-CIMP-low gliomas, the determinants of the malignant progression of PA-like LGG into GBM-LGm6 remained unknown. Here, we applied our novel computational RGBM approach to infer the MRs responsible for the progression of G-CIMP-high into G-CIMP-low IDH-mutant glioma and those driving progression of PA-like LGG into LGm6-GBM IDH-wildtype tumors respectively.

Toward this aim, we first built the Pan-glioma network between 457 TFs and 12 985 target genes. An ABN network was to used as prior for the RGBM algorithm and for the expression matrix we used the TCGA Pan-glioma dataset (23) including 1250 samples (463 IDH-mutant and 653 IDH-wild-type), 583 of which were profiled with Agilent and 667 with RNA-Seq Illumina HiSeq downloaded from the TCGA portal. The batch effects between the two platforms were corrected as reported in (66) using the COMBAT algorithm (67) having tumor type and profiling platform as covariates. Subsequently, quantile normalization is applied to the whole matrix. The inferred Pan-glioma RGBM network is shown in Supplementary Figure 8 (F8) and contains 39 192 connections with an average regulon size of 85.8 genes. To identify the MRs displaying the highest differential activity for each group, we ranked MR activity for each TF among for all the seven glioma subtypes.

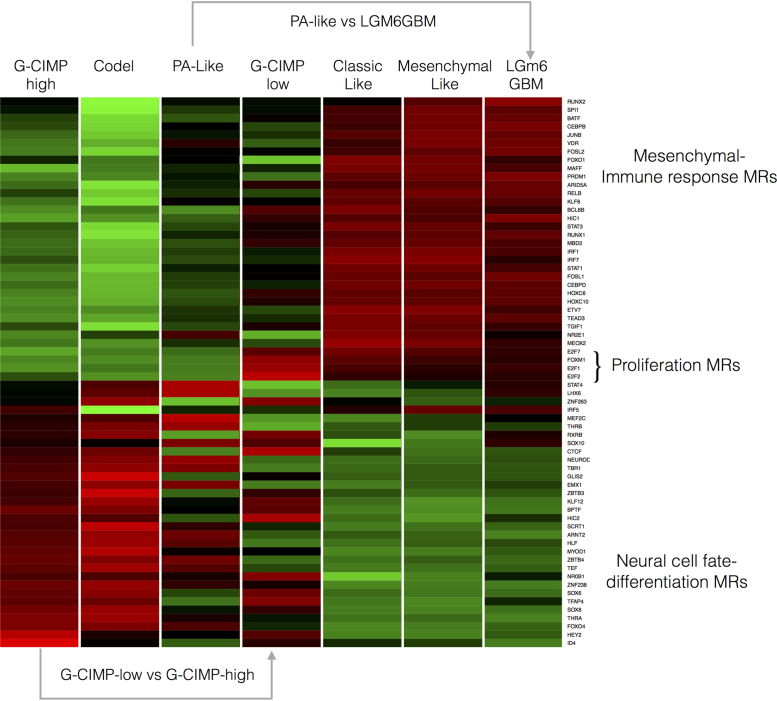
The top MRs exhibiting differential activity among the glioma groups are shown in Supplementary Figure S9 and their average activity in Figure 8. We found that RGBM-based MR analysis efficiently separates an IDH-mutant dominated cluster of gliomas including each of the three IDH-mutant subtypes (G-CIMP-high, G-GIMP-low and Codel) from an IDH-wildtype group including Mesenchymal-Like, Classic-Like and LGm6-GBM. This finding indicates that RGBM correctly identifies biologically-defined subgroups in terms of the activity of MRs. The MRs characterizing IDH-mutant glioma include known regulators of cell fate and differentiation of the nervous system, therefore, indicating that these tumors are driven by a more differentiated set of TFs that are retained from the neural tissue of origin (e.g. NEUROD2, MEF2C, EMX1, etc.). Conversely, the MRs whose activity is enriched in IDH-wildtype glioma are well-known TFs driving the mesenchymal transformation, immune response and the higher aggressiveness that characterizes the IDH-wildtype glioma (STAT3, CEBPB, FOSL2, BATF and RUNX2, etc). Remarkably, while the G-CIMP-low subtype showed a general pattern of activation of MRs that includes this subtype within the IDH-mutant group of gliomas, when compared to the G-CIMP-high subtype, G-CIMP-low glioma displays a distinct loss of activation of neural cell fate/differentiation-specific MRs (see for example the activity of the crucial neural TFs NEUROD2, MEF2C and EMX1) with corresponding activation of a small but distinct set of TFs that drive cell cycle progression and proliferation (E2F1, E2F2, E2F7 and FOXM1). This finding indicates that the evolution of the G-CIMP-high into the G-CIMP-low subtype of glioma is driven by (i) loss of the activity of neural-specific TFs and (ii) gain of a proliferative capacity driven by activation of cell cycle/proliferation-specific MRs.

Figure 8.

Average MR activity in the seven glioma subtypes.

Concerning the PA-like into LGm6-GBM, we note that, despite being sustained by an IDH-wildtype status, PA-like LGG cluster within the IDH-mutant subgroup of glioma, with higher activity of Neural cell fate/differentiation-specific MRs and inactive Mesenchymal-immune response MRs. Therefore, the evolution of PA-like LGG into LGm6-GBM is marked by gain of the hallmark aggressive MR activity of high grade glioma with corresponding loss of the MRs defining the neural cell of origin of these tumors.

Taken together, the application of the RGBM approach to the recently reported Pan-Glioma dataset revealed the identity and corresponding biological activities of the MRs driving transformation of the G-CIMP-high into the G-CIMP-low subtype of glioma and PA-like into LGm6-GBM, thus, providing a clue to the yet undetermined nature of the transcriptional events driving the evolution among these novel glioma subtypes.

RGBM identifies the master regulators of the mechanism of action of FGFR3-TACC3 fusion in glioblastoma

FGFR3-TACC3 fusions are recurrent chromosomal rearrangement that generate in-frame oncogenic gene fusions first discovered in glioblastoma (GBM) (68) and subsequently found in many other tumors. Currently, FGFR3-TACC3 gene fusions are considered one the most recurrent chromosomal translocations across multiple types of human cancer (69). Recently, we used RGBM to identify PGC1α and ERRγ as the key MRs that are necessary for the activation of mitochondrial metabolism and oncogenesis of tumors harboring FGFR3-TACC3 (36).

In this study, we have extensively validated the computational approach using a large set of experimental systems spanning from mouse and human cell cultures in vitro to tumor models of Drosophila, mice and humans in vivo (36). Here, we selected the set of 627 IDH-wildtype glioma from the expression dataset described above to build the RGBM network. To have a more comprehensive set of regulators, even without the availability of the PWMs, we used a predefined list of 2137 gene regulators/transcription factors (TRs) and an all-ones matrix as ABN, i.e. no prior mechanistic information. The final network contains 300 969 edges (median regulon size: 141) between the 2137 regulators and the 12 985 target genes. The key regulators of this oncogenic alteration were identified as those with the most significant differential activity between eleven TACC3-FGFR3 fusion-positive samples and 616 fusion-negative samples (Supplementary Figure S10).

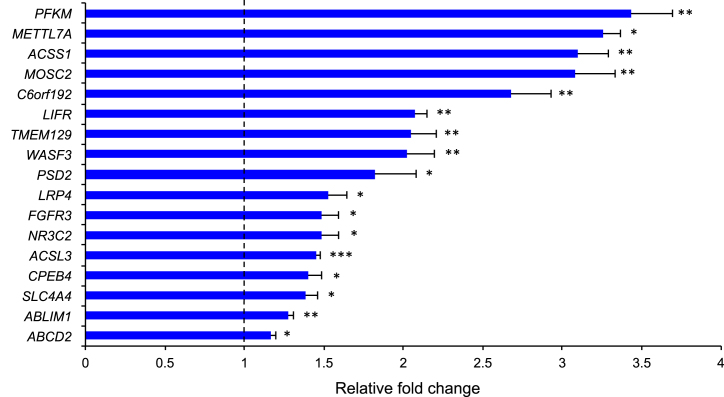
We then sought to identify and experimentally validate the gene targets of the PGC1α transcriptional co-activator inferred by RGBM in glioma harboring FGFR3-TACC3 gene fusions, which is a context of maximal activity for this MR. Under this scenario, RGBM identified a regulon of positively regulated targets of PGC1α comprising 243 genes. To validate the predictions made by RGBM for PGC1α target genes, we ectopically expressed PPARGC1A (the gene encoding for PGC1α) in immortalized human astrocytes and evaluated the changes of expression of the top 30 targets in the regulon predicted by RGBM by quantitative RT–PCR (qRT–PCR). We validated primers for efficient PCR from the cDNA of 22 of the top 30 targets and found that the expression of 17 of the 22 genes (77%) was up-regulated by PGC1α, thus confirming that they are bona-fide PGC1α target genes (Figure 9, Supplementary Table S5). This fraction of experimentally validated targets is notably high when compared to similar validation studies of gene network inference algorithms. For example in (70), the authors performed RNAi–mediated gene knockdown experiments in two colorectal cancer cell lines targeting eight key genes in the RAS pathway and evaluate the percentages of correctly identified targets from several gene network inference algorithms. They report an accuracy of 46% for the gene HRAS.

Figure 9.

qRT-PCR from HA–vector or HA–PPARGC1A. Data are fold changes relative to vector (dotted line) of one representative experiment (data are mean±standard deviation, n = 3 technical replicates). P-values were calculated using a two-tailed t-test with unequal variance. P-value: * < 0.05; ** < 0.01; *** < 0.001.

DISCUSSION AND CONCLUSIONS

In this paper, we proposed a novel GRN inference framework, whose core model for deducing transcriptional regulations for each target gene can either be boosting of regression stumps (GBM) or ensemble of decision trees (RF). We showcased that the proposed GBM based RGBM method provides efficient results with both the LS-Boost and the LAD-Boost loss functions. Similarly, the proposed RF based RGENIE method easily outperforms GENIE on several in-silico and two real (E. coli and S. cerevisiae) datasets. Our key contributions are:

• Sparsifying the GRN network inferred from tree-based ML techniques (GBM/RF) using a Tikonov regularization inspired optimal L-curve criterion on the edge-weight distribution obtained from the RVI scores of a target gene to determine the optimal set of TFs associated with it.

• Propose a simple heuristic based on the maximum variable importance score for all the genes to detect nodes with 0 in-degree or genes which are not regulated by other genes i.e. are upstream regulators.

• Incorporation of prior knowledge in the form of a mechanistic active binding network.

• Show that RGBM beats several state-of-the-art GRN inference methods like ARACNE, ENNET, GENIE w.r.t. evaluation metrics AU_pr and AU_roc by 10–15% for various DREAM challenge datasets.

• Show through synthetic RNA-Seq experiments that random-forest based methods are inferior to gradient boosting machines for inferring GRNs where very few TFs (hubs) are regulating a majority of the target genes.

• Identification of the main regulators of the different molecular subtypes of brain tumors i.e. master regulators driving transformation of the G-CIMP-high into G-CIMP-low and PA-like into LGm6-GBM subtypes of glioma.

• Identification and validation of the main regulators of the mechanism of action of FGFR3-TACC3 fusion in glioblastomas.

AVAILABILITY

RGBM is available for download on CRAN at https://cran.rproject.org/web/packages/RGBM.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.

FUNDING

MiUR (Ministero dellUniversite della Ricerca) [FIRB2012-RBFR12QW4I]; Fondazione Biogem. Funding for open access charge: Qatar Computing Research Institute.

Conflict of interest statement. None declared.