The future of quantum biology

Abstract

Biological systems are dynamical, constantly exchanging energy and matter with the environment in order to maintain the non-equilibrium state synonymous with living. Developments in observational techniques have allowed us to study biological dynamics on increasingly small scales. Such studies have revealed evidence of quantum mechanical effects, which cannot be accounted for by classical physics, in a range of biological processes. Quantum biology is the study of such processes, and here we provide an outline of the current state of the field, as well as insights into future directions.

1. Introduction

Quantum mechanics is the fundamental theory that describes the properties of subatomic particles, atoms, molecules, molecular assemblies and possibly beyond. Quantum mechanics operates on the nanometre and sub-nanometre scales and is at the basis of fundamental life processes such as photosynthesis, respiration and vision. In quantum mechanics, all objects have wave-like properties, and when they interact, quantum coherence describes the correlations between the physical quantities describing such objects due to this wave-like nature.

In photosynthesis, respiration and vision, the models that have been developed in the past are fundamentally quantum mechanical. They describe energy transfer and electron transfer in a framework based on surface hopping. The dynamics described by these models are often ‘exponential’ and follow from the application of Fermi’s Golden Rule [1,2]. As a consequence of averaging the rate of transfer over a large and quasi-continuous distribution of final states the calculated dynamics no longer display coherences and interference phenomena. In photosynthetic reaction centres and light-harvesting complexes, oscillatory phenomena were observed in numerous studies performed in the 1990s and were typically ascribed to the formation of vibrational or mixed electronic–vibrational wavepackets. The reported detection of the remarkably long-lived (660 fs and longer) electronic quantum coherence during excitation energy transfer in a photosynthetic system revived interest in the role of ‘non-trivial’ quantum mechanics to explain the fundamental life processes of living organisms [3]. However, the idea that quantum phenomena—like coherence—may play a functional role in macroscopic living systems is not new. In 1932, 10 years after quantum physicist Niels Bohr was awarded the Nobel Prize for his work on the atomic structure, he delivered a lecture entitled ‘Light and Life’ at the International Congress on Light Therapy in Copenhagen [4]. This raised the question of whether quantum theory could contribute to a scientific understanding of living systems. In attendance was an intrigued Max Delbrück, a young physicist who later helped to establish the field of molecular biology and won a Nobel Prize in 1969 for his discoveries in genetics [5].

All living systems are made up of molecules, and fundamentally all molecules are described by quantum mechanics. Traditionally, however, the vast separation of scales between systems described by quantum mechanics and those studied in biology, as well as the seemingly different properties of inanimate and animate matter, has maintained some separation between the two bodies of knowledge. Recently, developments in experimental techniques such as ultrafast spectroscopy [6], single molecule spectroscopy [7–11], time-resolved microscopy [12–14] and single particle imaging [15–18] have enabled us to study biological dynamics on increasingly small length and time scales, revealing a variety of processes necessary for the function of the living system that depend on a delicate interplay between quantum and classical physical effects.

Quantum biology is the application of quantum theory to aspects of biology for which classical physics fails to give an accurate description. In spite of this simple definition, there remains debate over the aims and role of the field in the scientific community. This article offers a perspective on where quantum biology stands today, and identifies potential avenues for further progress in the field.

2. What is quantum biology?

Biology, in its current paradigm, has had wide success in applying classical models to living systems. In most cases, subtle quantum effects on (inter)molecular scales do not play a determining role in overall biological function. Here, ‘function’ is a broad concept. For example: How do vision and photosynthesis work on a molecular level and on an ultrafast time scale? How does DNA, with stacked nucleotides separated by about 0.3 nm, deal with UV photons? How does an enzyme catalyse an essential biochemical reaction? How does our brain with neurons organized on a sub-nanometre scale deal with such an amazing amount of information? How do DNA replication and expression work? All these biological functions should, of course, be considered in the context of evolutionary fitness. The differences between a classical approximation and a quantum-mechanical model are generally thought to be negligible in these cases, even though at the basis every process is entirely governed by the laws of quantum mechanics. What happens at the ill-defined border between the quantum and classical regimes? More importantly, are there essential biological functions that ‘appear’ classical but in reality are not? The role of quantum biology is precisely to expose and unravel this connection.

Fundamentally, all matter—animate or inanimate—is quantum mechanical, being constituted of ions, atoms and/or molecules whose equilibrium properties are accurately determined by quantum theory. As a result, it could be claimed that all of biology is quantum mechanical. However, this definition does not address the dynamical nature of biological processes, or the fact that a classical description of intermolecular dynamics seems often sufficient. Quantum biology should, therefore, be defined in terms of the physical ‘correctness’ of the models used and the consistency in the explanatory capabilities of classical versus quantum mechanical models of a particular biological process.

As we investigate biological systems on nanoscales and larger, we find that there exist processes in biological organisms, detailed in this article, for which it is currently thought that a quantum mechanical description is necessary to fully characterize the behaviour of the relevant subsystem. While quantum effects are difficult to observe on macroscopic time and length scales, processes necessary for the overall function and therefore survival of the organism seem to rely on dynamical quantum-mechanical effects at the intermolecular scale. It is precisely the interplay between these time and length scales that quantum biology investigates with the aim to build a consistent physical picture.

Grand hopes for quantum biology may include a contribution to a definition and understanding of life, or to an understanding of the brain and consciousness. However, these problems are as old as science itself, and a better approach is to ask whether quantum biology can contribute to a framework in which we can repose these questions in such a way as to get new answers. The study of biological processes operating efficiently at the boundary between the realms of quantum and classical physics is already contributing to improved physical descriptions of this quantum-to-classical transition.

More immediately, quantum biology promises to give rise to design principles for biologically inspired quantum nanotechnologies, with the ability to perform efficiently at a fundamental level in noisy environments at room temperature and even make use of these ‘noisy environments’ to preserve or even enhance the quantum properties [19,20]. Through engineering such systems, it may be possible to test and quantify the extent to which quantum effects can enhance processes and functions found in biology, and ultimately answer whether these quantum effects may have been purposefully selected in the design of the systems. Importantly, however, quantum bioinspired technologies can also be intrinsically useful independently from the organisms that inspired them.

3. Quantum mechanics: an introduction for biologists

At the beginning of the twentieth century, the success of classical physics in describing all observable phenomena had begun to be challenged in certain respects. In 1900, as a means to explain the spectral energy distribution of blackbody radiation, Planck introduced the idea that interactions between matter and electromagnetic radiation of frequency ν are quantized, occurring only in integer multiples of hν, where h is the fundamental Planck constant. Five years later, Einstein further developed the notion of energy quantization by extending it to include the photon, a quantum of light. This concept is illustrated by the photoelectric effect where light incident on a material leads to the emission of electrons. It is, however, not the intensity of the light that determines this emission but rather its frequency. Even low-intensity light of a suitable frequency will lead to electrons being emitted whereas high-intensity light below this threshold frequency will have no effect. Einstein explained this by proposing that in this instance light behaves as a particle rather than a wave, with discrete energies hν that can be transferred to the electrons in a material. Bohr’s 1913 model of the hydrogen atom, with its discrete energy states, and Compton’s 1923 work with X-rays all contributed to the beginning of a new era in modern physics. These ways of explaining blackbody radiation and the photoelectric effect, as well as atomic stability and spectroscopy, led to the development of quantum mechanics, a theory that has proved extremely successful in predicting and describing microphysical systems [21,22].

Whereas Planck and Einstein began the quantum revolution by postulating that radiation also demonstrates particle-like behaviour, de Broglie, in 1923, made the complementary suggestion that matter itself has wave-like properties, with a wavelength related to its momentum through Planck’s constant. This hypothesis suggested that matter waves should undergo diffraction, which was subsequently proved by experiments that demonstrated that particles such as electrons showed interference patterns. Schrödinger built on this observation in his formulation of quantum mechanics, which describes the dynamics of microscopic systems through the use of wave mechanics. The formulation of quantum mechanics allows for the investigation of a number of important facets of a quantum state: its mathematical description at any time t, how to calculate different physical quantities associated with this state and how to describe the evolution of the state in time [21,22].

Quantum mechanics is a mathematical framework that identifies an isolated physical system with a quantum state that completely characterizes the system and is denoted by |ψ〉, and a Hilbert space 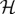that contains all states available to the system. The time evolution of a system described by a state vector |ψ 〉 obeys the Schrödinger equation,

3.1

where 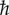is the reduced Planck constant and H(t) is the Hamiltonian, which represents the energy levels of the system and the interaction between parts of the system.

One of the more fascinating aspects of quantum theory is that for two quantum states |ψ₁〉 and |ψ₂〉 describing a system, a linear combination of these two states, α₁|ψ₁〉 + α₂|ψ₂〉, also describes the system. This combination or superposition of states constituting the Hilbert space is written more generally as

3.2

where each normalized orthogonal state |ψ_i〉 in the superposition is weighted by complex number α_i, where 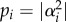is the probability of finding the system in that state. It is here that quantum mechanics parts company with the classical world. The existence of superposition states in the quantum regime results in uniquely quantum-mechanical properties, which are often counterintuitive. For example, quantum coherence describes the well-defined relationship between the individual states constituting a superposition, and quantum entanglement is a special form of correlation between quantum states. An excellent example is the delocalization of electronic states in photosynthesis that is crucial to explain the speed and efficiency of electronic energy transfer and charge separation at the basis of photosynthesis [23]. The probabilistic approach of quantum mechanics also allows for the concept of tunnelling, which predicts the possibility of a quantum particle to pass through a potential barrier that would otherwise be forbidden by classical mechanics [21,22]. A very good example of the latter is the efficient transfer of electrons between a donor and an acceptor, as in photosynthetic reaction centres and respiratory complexes, where the electron has to pass the high energy protein barrier [24].

It is these specifically quantum properties such as superposition, coherence, entanglement and tunnelling that are described, in this review, as integral to a new understanding of biological phenomena as diverse as photosynthesis, magnetoreception, olfaction, enzyme catalysis, respiration and neurotransmission [25–27].

4. Transport processes

At a fundamental level, the dynamics in biological systems are associated with the transfer of energy and charge, the latter of which involves electrons, protons and ions. Excitation energy transfer and charge transfer in photosynthesis are the most well-established areas of quantum biology, and a more recent area of investigation is the study of enzyme catalysis, which often relies on the coupling of electrons and protons to control the transport of multiple charges.

4.1. Photosynthesis

A prolific class of organisms has been living on sunlight energy for over 3 billion years, using a process called photosynthesis to convert sunlight energy into forms useful for their survival. The overall efficiency with which photosynthetic organisms convert sunlight energy to biomass under typical conditions is fairly low (at best a few per cent [28,29]), since neither is all incoming sunlight absorbed, nor is all absorbed energy converted into biomass. However, the primary light-harvesting stage of photosynthesis proceeds with near-perfect quantum efficiency. This means that under optimal conditions (low light intensities and no stress) for almost every photon absorbed and transferred by the light-harvesting antennae, an electron is transferred within the photosynthetic reaction centre.

Light-harvesting antennae range from quasi-disordered self-assembled aggregates [30] to highly symmetric configurations of pigments bound to protein scaffolds [31,32]. The light-harvesting complexes that constitute the total antenna system are connected to a reaction centre, which is the single unit of the photosynthetic apparatus capable of carrying out a transmembrane charge separation [33].

Experiments performed by isolating both light-harvesting complexes and reaction centres from natural photosynthetic systems, whilst mimicking physiological environmental conditions, have shed much light on the in vivo functioning of the photosynthetic light-collecting system. It is well-established that the primary photosynthetic processes of energy and charge transfer exhibit essential quantum mechanical properties, such as delocalization, wavepackets, coherence and superradiance, and that classical models do not accurately describe the ensuing dynamics.

4.1.1. Excitation energy transfer

As early as 1938, Franck & Teller [34] proposed a quantum coherent mechanism for excitation energy transfer in photosynthesis. They considered the diffusion of a Frenkel exciton, which is a coherent superposition of the electronic excitations of the individual photosynthetic pigments (figure 1). With the advent of femtosecond transient absorption spectroscopy in the early 1990s, long-lived vibrational coherences, lasting on the order of a picosecond, were detected for bacterial and plant light-harvesting complexes [35–40]. During the past 14 years, advanced ultrafast techniques, known as two-dimensional electronic spectroscopy (2D-ES), have been used to monitor the decay of coherent superpositions of vibrational states and vibronic (mixed excitonic–vibrational) states in light-harvesting complexes. The two-dimensional spectra revealed the presence of cross peaks [41] that oscillated in time [42]. A large number of studies associated the cross peaks with couplings between exciton states, while their oscillations were assigned to electronic quantum coherence, i.e. coherent superpositions between exciton states [42]. The first such study, which was conducted on the Fenna–Matthews–Olson (FMO) complex of green sulfur bacteria and published in 2007 by the Fleming group, revealed that particular coherences lasted surprisingly long (660 fs) [3]. In 2009, similar oscillatory signals were revealed for the main light-harvesting complex of higher plants (LHCII) and were interpreted as quantum-coherent energy transfer [43]. These initial results were obtained at cryogenic temperatures. An important development was the detection in 2010, independently by the Engel [44] and Scholes [45] groups, of similar coherent oscillations at physiological temperatures in FMO and light-harvesting complexes of two species of marine cryptophyte algae, respectively.

Figure 1.

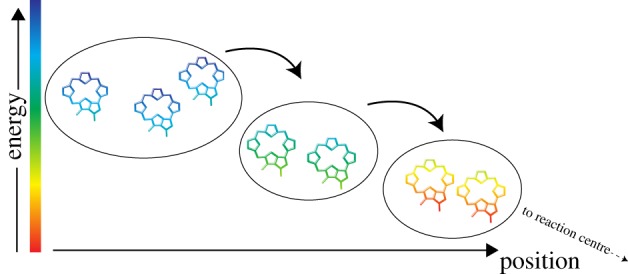
A schematic illustrating the concept of excitation energy transfer in photosynthetic light-harvesting complexes. The ovals depict pigment clusters in which strong excitonic coupling occurs while the arrows represent incoherent transfer of the energy amongst the clusters. Within each cluster, the energy is delocalized over all pigments and is transferred coherently.

Generally, quantum coherence at physiological temperatures is observed to be fragile compared to that at cryogenic temperatures, since the environmental noise increases with increasing temperature, leading to shorter decoherence times. These results are therefore interesting, both from the perspective of quantum information processing, where a major challenge is to maintain quantum coherence in systems that unavoidably interact with an environment, and from the perspective of quantum biology, which investigates whether fundamental aspects of the functioning of living systems can only be explained quantum mechanically.

Inspired by the surprising phenomenon interpreted as long-living quantum coherence in warm, noisy, complex and yet remarkably efficient energy transfer systems, many models of environment-assisted quantum transport have been proposed. The aim has been to relate the phenomenon of quantum coherence across multiple chromophoric sites in photosynthetic pigment–proteins to the extreme efficiency of the excitation energy transfer process, typically within approximate spin-boson models of the system. Contrary to the intuition that noise will reduce the performance of a system, it has been found that interaction with an environment can result in increased transport efficiency [19,20]. Light-harvesting complexes consist of a number of pigments with generally differing site energies. If this energy difference is larger than the pigment–pigment coupling, then transitions will be suppressed. Dephasing noise can shift the site energies, thereby helping to overcome these energy gaps, and improving transport between sites without the loss of excitations from the system [46].

After much theoretical evidence both for and against long-lived (up to a few picoseconds) electronic coherence, very recent 2D-ES studies on the FMO complex have shown unambiguously that these long-lived coherences originate mainly from ground state vibrations and not from exciton–exciton superpositions [47,48]. It was found that quantum beatings related to electronic coherences have a small amplitude and decay within only 60–240 fs. However, experimental confirmation of excited-state vibronic coherence was also found [48] and its role in excitation energy transfer in photosynthesis remains to be determined.

One may then ask whether the role of quantum coherence—excitons as well as vibronic coherences—in light harvesting is optimized, or is simply a consequence of the proximity of pigments in pigment–protein complexes. The robustness of environmentally assisted transport with respect to variations in the system or environmental characteristics has also been investigated and results show that this robustness can be exploited in the design of highly efficient quantum transport systems [49,50]. The convergence of time scales in photosynthesis has been proposed as an example of the ‘quantum Goldilocks effect’: that natural selection tends to drive quantum systems to a parameter set where the resulting degree of quantum coherence is ‘just right’ for attaining maximum efficiency and optimal control [51].

In general, the observation of oscillatory dynamics is not sufficient to rule out classical descriptions of the same behaviour, and the quantum modelling of environment-assisted transport in photosynthesis has not been without controversy. However, more recent work [52] has shown unambiguously that the non-classical properties of environmental vibrational motions may assist excitation energy transfer in photosynthetic LHCs on the sub-picosecond time scale and at room temperature. These ideas should be verified experimentally by examining whether mutational variants of photosynthetic LHCs alter the degree of quantum coherence, the coherence lifetime, and consequently also the energy-transfer efficiency.

4.1.2. Charge transfer

Charge separation in photosynthesis is one of the most efficient phenomena in nature, with a quantum efficiency that approaches unity. The contributing processes happen on different time scales, from subpicoseconds to milliseconds, and involve the interplay between disorder and coherence, mediated by vibronic states (mixtures of vibrational and excitonic states). Charge separation represents a very good candidate for understanding the role of quantum physics in biology. Since charge separation happens on the microsecond time scale, quantum effects are generally not directly visible at such a macroscopic level. However, the charge separation mechanism can be represented by a chain of different processes, with the early steps on ultrafast time scales and involving only a few molecules, and the overall efficiency depending on each one of the steps.

In 1966, DeVault and Chance observed a temperature dependence of the electron transfer in purple bacterial reaction centres that could not be accounted for by classical physics [53]. They proposed the behaviour to show evidence of quantum mechanical tunnelling [54], and laid the foundation for the concept of electron and nuclear tunnelling in biology [42]. While Marcus’ theory of electron transfer neglects nuclear tunnelling [2], and can therefore underestimate the electron transfer rate at low temperatures, semi-classical Marcus theory can be extended to a fully quantum-mechanical treatment based on the theory of non-radiative transitions that includes nuclear tunnelling, and which gives a good prediction for the increasing rate of charge separation with decreasing temperature. If it is assumed that charge separation is strongly coupled to some harmonic vibrational mode, then the rate is given by the Jortner rate. However, this is based on the assumption that vibrational relaxation occurs on much shorter time scales than electron transfer, which is not the case for very fast transfer events. Ultrafast photoinduced electron transfer reactions are so quick that during the electron transfer from the donor to the acceptor complete vibrational relaxation does not occur. Vibrational relaxation usually occurs on a picosecond or sub-picosecond time scale, and ultrafast electron transfer reactions proceed on the same scale [55].

2D-ES experiments on the reaction centre of Photosystem II of higher plants have revealed long-lived oscillations of specific cross peaks, similarly as for light-harvesting complexes, and were interpreted as electronic coherences between excitons as well as between exciton and charge-transfer states (figure 2) [56]. Strong correlation was observed between the degree of coherence and efficient and ultrafast charge separation [56]. The experimental results were reproduced quantitatively by a quantum coherent model featuring new energy transfer pathways that do not appear classically between a plethora of vibronic states [56–58]. Specifically, the simulations showed that the observed cross-peak oscillations can be maintained by specific vibrational modes, where the modes assisting the resonant transfer are primarily intrinsic to the pigment, while the pigment excitonic transitions are tuned mainly by the protein scaffold to match the energy of these modes. Therefore, while non-trivial quantum effects may appear hidden on a macroscopic level, they seem to contribute fundamentally to the biological machinery of charge separation. Charge transfer, therefore, represents a very good process for understanding the role of quantum physics in biology.

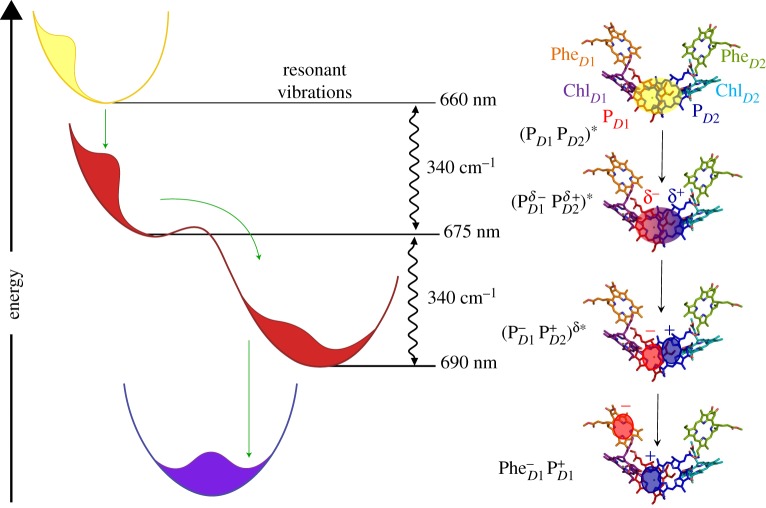
Figure 2.

Schematic of quantum-coherent charge separation in the Photosystem II reaction centre of higher plants along one of at least two existing pathways, according to the model in [23]. On the left are four wavepackets on harmonic potentials, each corresponding to a different state along the charge separation pathway. For each state, the key pigments and approximate location and sign of the charge clouds are shown on the right. Horizontal lines depict absorption peaks at the specified wavelength of the corresponding state shown on the right, while the wavy arrows depict resonance interaction with the indicated vibrational mode. The symbols δ and * represent charge-transfer character and exciton character, respectively. The nature of the four states are 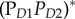—a high exciton state, 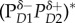—an exciton state with some charge-transfer character, 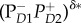—a charge-transfer state mixed with an exciton state, and 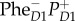—the final charge-separated state. Note that an intermediate between the last two states, involving Chl_D1, is omitted. The first three steps involve coherent relaxation due to coupling with a vibrational mode, while the last step involves incoherent transfer. Symbols: D1 and D2, two branches of the symmetric reaction centre structure; Chl, chlorophyll; P, primary electron donor/special-pair Chl; Phe, pheophytin. Adapted from Romero et al. [23].

Hence, experimental and theoretical evidence shows that single vibrational modes in a statically disordered landscape very likely assist transport in both light harvesting and charge separation in photosynthetic organisms, with the pigment excitonic transitions tuned by the protein scaffold to match the energy of the vibrational mode assisting the resonant transfer [52,56]. Nuclear–electronic (vibronic) coupling is an important mechanism in the light-induced function of molecular systems, in general, and in a specific designed system. The outcome of light-induced electron transfer has also been shown to be radically altered by mode-specific infrared excitation of vibrations that are coupled to the electron transfer pathway [59].

4.1.3. Single molecule spectroscopy

Single molecule experiments present an interesting and promising approach to investigate quantum features of photosynthetic complexes. Results of 2D-ES suggest an intimate role of the environment in the form of molecular vibrations on quantum coherent energy and electron transfer processes. This environment changes from complex to complex as well as on relatively slow time scales (milliseconds to minutes), as suggested by the distinct, time-varying energy transfer pathways reported in studies on single light-harvesting complexes [11,60–62]. Owing to this heterogeneity, generally termed ‘static disorder’, which originates from relatively slow protein conformational dynamic fluctuations, the decay of oscillations of spectral features is strongly affected by ensemble averaging. By avoiding ensemble averaging in single molecule experiments, quantum coherences could be scaled to the microscopic domain, which might shed more light on the physiological significance of this quantum phenomenon.

Static disorder also strongly affects the fate of an excitation in a light-harvesting complex by changing the probability of the excitation to be trapped in an energy sink [63,64] or by pigment clusters that are not neighbouring other complexes in the photosystem [65]. A detailed understanding of the fine control of the photodynamics by external influences on the light-harvesting complex, such as which occur during non-photochemical quenching, an important regulatory mechanism to dissipate excess energy in photosynthesis, is still missing. The role of vibration-assisted energy transfer and sampling of energy-transfer pathways may be clarified by single molecule coherent control experiments.

Recently, based on a series of experimental observations of magnetic field effects in the photosynthetic reaction centre, the direct role of the quantum-mechanical property of spin has been proposed in a quantum protective mechanism in photosynthesis [66]. Understanding regulatory and protective mechanisms in photosynthesis, as well as the resolution and control of these processes on time scales down to femtoseconds, has strong application in the investigation of crop failure under drought stress or conditions of high solar irradiation, as well as in the development of next-generation bioinspired solar cells.

A complementary way of accessing information about purely quantum-mechanical features in single molecules is to look for distinct quantum mechanical fingerprints, such as non-classical sub-Poissonian statistics in higher-order correlation functions or the statistics of some observable violating the Bell or Cauchy–Schwartz inequality. The non-classicality of initially thermalized vibrations has been shown to be induced via coherent exciton–vibration interactions and unambiguously indicated by negativities in the phase-space quasi-probability distribution of the effective collective mode coupled to the electronic dynamics, even with incoherent input of excitation. These results suggest that investigation of the non-classical properties of vibrational motions assisting excitation and charge transport, photoreception and chemical sensing processes could be a touchstone for revealing a role for non-trivial quantum phenomena in biology [52,67]. However, performing such investigations on the single molecule level is highly challenging due to the requirements for both ultrafast (femtosecond to nanosecond) time resolution and high photon counting rates.

4.1.4. Artificial photosynthesis

A claim from the field of quantum biology has been that developing a detailed understanding of photosynthesis on a microscopic scale, especially the primary stages thereof, will enable us to engineer biologically inspired artificial photosynthetic systems harnessing sunlight energy efficiently using Earth-abundant elements such as carbon, oxygen, nitrogen, etc. There have already been significant developments surrounding the design of such systems (e.g. [68–73]). A molecular approach to artificial photosynthesis is one among many contenders to convert solar energy into biofuel. Here, natural photosynthesis is investigated in order to extract design principles and then try to develop better photosystems based on these principles. A primary limitation of current systems is storage as well as the instability of their catalysts caused by an over-accumulation of charge. Counterbalancing of charge separation is essential, e.g. through coupled proton motion [74].

An important principle in quantum biologically inspired design is the presence of excitons: they are responsible for more efficient light absorption, faster energy funnelling (i.e. faster decay along the energy gradient), faster energy transfer and more efficient (irreversible) trapping of excitations by the reaction centre [75]. Moreover, their quantum behaviour is evident through their wave-like interference of different pathways and the way in which vibrational modes of the protein environment interact with the pigments (adding to the delocalization and extracting or absorbing vibrational energy) to facilitate the energy transfer in the complex.

Investigations of primary charge transfer in a prototypical artificial reaction centre have revealed correlated wave-like motion of electrons and nuclei on a time scale of a few tens of femtoseconds as a driving mechanism of the photoinduced current generation cycle [76]. It is important to include turnover in assessing such systems and not only efficiency. Resilient, stable systems are required for good turnover, which could perhaps be achieved via some kind of protective polymer wrapping around pigments [77]. For example, strategies for making artificial membrane-embedded proteins involving transmembranal BChl-binding protein maquettes have been investigated [78].

The challenges for the study of exciton transport in photosynthesis, including the disordered nature of the pigment networks, fluctuating exciton energy levels on similar time scales and coupled to exciton dynamics, also arise in other, non-biological settings. A specific example where insights and ideas that initially arose in quantum biology prove useful is in recent research into organic photovoltaics (PV). These are solar cells, made from a combination of two different man-made molecular semiconductors. The electron donor semiconductor is typically a polymer, while the acceptor is typically the fullerene derivative [6,6]-phenyl-C61-butyric acid methyl ester. Strongly bound Frenkel excitons are generated inside the device, which then diffuse until they reach an interface between donor and acceptor regions. The donor and acceptor have different chemical potentials, and this provides a driving force to dissociate excitons at the interface into free charges, which can then diffuse to opposite electrodes. However, since the Coulomb interaction is long-ranged, and organic materials have low dielectric constants, the electron and hole experience a binding energy 10 times deeper than k_BT at room temperature, even after they have dissociated onto different molecules on either side of the interface. The overwhelming majority of devices consequently extract far fewer charges from the electrodes than are generated by the incoming light, leading to low power conversion efficiencies.

Yet in recent years, a small number of highly efficient devices have emerged, and near 100% charge extraction efficiencies have been reported [79,80]. A great amount of work has been done to identify the origin of efficient long-ranged charge separation in this subset. Experimental work has demonstrated that organic photovoltaics and photosynthesis share some striking coincidences. It was initially thought that charge separation at donor–acceptor interfaces would occur on picosecond to nanosecond time scales, which could be described by classical charge hops driven by thermal fluctuations. A number of experiments have observed that a substantial fraction of free charges are generated within just 100 femtoseconds of the exciton reaching an interface, just as femtosecond coherences and dynamics have been observed during photosynthetic exciton transport. Transport on such time scales is impossible to explain within classical Marcus ‘hopping’ models and the coherent transfer must explicitly be included [81,82].

Understanding these observations requires detailed modelling of charge transport near the donor–acceptor interface. Crucially, charges moving in organic semiconductors experience all three key properties of pigment–protein complexes listed above: high disorder, molecular fluctuations and reorganization. It is, therefore, perhaps not surprising that similar phenomena emerge. Theories of exciton transport in photosynthesis typically involve the interplay of partially delocalized states and noise-assisted transport, describing how transport through a network can be enhanced if the exciton or charge is coupled moderately strongly to molecular vibrational modes. It is increasingly the consensus view that partially delocalized states also arise in efficient organic photovoltaic systems, and it has also been argued that the charge separation process is enabled by noise within aggregated regions of the acceptor semiconductor. A number of theoretical groups working on organic photovoltaics now apply an open-quantum systems approach, using methods strongly influenced by early studies of photosynthetic light-harvesting complexes [83–86].

The potential for quantum biology to contribute to developing sustainable energy technologies is often claimed as a motivation for the field, and in particular for understanding quantum-coherent excitation energy transfer in photosynthetic systems. Progressing from this general claim to practical energy systems, however, requires more specific proposals for engineering quantum energy transfer into environmentally sustainable and economically scalable systems. Just as a foundational question in quantum biology itself asks how nanoscale phenomena can substantially affect macroscopic behaviour in an organism, the potential to exploit quantum-biological phenomena in engineered macroscopic energy systems depends on whether such phenomena can significantly influence system-scale operation under environmental and economic constraints. The development of existing renewable energy technologies such as silicon-based PV has taught that purely physical performance criteria such as energy-conversion efficiency are often less important than techno-economic performance measures such as life cycle analysis. Existing extremely efficient photovoltaic cells are too expensive for most practical applications and in some cases require elements with such low abundances that they would not be globally scalable even if affordable. Addressing these limitations has been a central concern in recent PV research, for example, through the development of organic PV materials.

Other global-scale considerations are important in assessing the potential of quantum biology in sustainable energy development. Globally, less than 20% of energy is consumed as electricity; almost all of the remaining 80% is consumed as fuel at final consumption. Although the share of energy consumed as electricity is steadily growing, fuel is likely to remain dominant within the time frame of tipping points in anthropogenic climate change and fossil-fuel depletion. There is, therefore, an urgent demand for renewable-fuel technologies such as engineered and/or artificial photosynthetic systems, rather than simply more efficient PV cells for electricity generation. Developing photosynthetic energy systems requires an integrated systems approach, with light-harvesting components being just one part of a complex (bio)physico-chemical system that should ideally be optimized for system-scale performance. The importance of quantum-dynamical effects in light harvesting within such a system can be fairly assessed only by balancing reductionistic analyses of subsystems against a holistic analysis of the overall system. Such considerations can help to focus the efforts of quantum-biology researchers whose main motivation is sustainable energy development. The key lesson is that an integrated systems approach is essential in order to relate global system-scale objectives to engineerable parameters across the spectrum of scales in the energy system, including at the nanoscale, where quantum-dynamical phenomena play an important role.

4.2. Enzyme catalysis

Enzymes are essential for cellular function through their catalysis of biochemical reactions that may have very low reaction rates otherwise. Understanding of the physical mechanism of the rate acceleration is a difficult topic of investigation. Transition-state theory has been used as the basis of explanations of enzyme catalysis, but recent theoretical and experimental developments have highlighted potential roles for quantum-mechanical tunnelling in enzyme-catalysed multiple-hydrogen transfer, and there has been a focus on depicting hydrogen transfer within a quantum-mechanical formalism [87]. Standard models for describing quantum tunnelling have been shown to explain experimental enzyme data, so long as one accounts for the fact that enzymes have many possible different structures [88]. Interesting and topical questions include whether local vibrational motions of the protein could provide the enzyme with catalytic advantage by coupling to the reaction coordinate and whether particular dynamical motions of the protein could have been selected to assist in the catalysis.

Enzymes often rely on the coupling of electrons and protons to control charge transport and catalysis [87]. In biological energy storage, the importance of proton translocation driven by electron transfer was first noted in 1961 [89], and since then, proton-coupled electron transfer mechanisms [90] have been shown to underlie amino acid radical generation and transport [91] along with the activation of most substrate bonds at enzyme-active sites [92].

5. Sensing

Living systems are constantly updating internal processes based on information obtained from their sensing of the environment. Small changes in the environment can necessitate macroscopic changes in the functioning of the organism. There are proposals that several biological sensing mechanisms are so sensitive as to detect changes in the environment on a quantum level. These proposals are outlined in the subsections below.

5.1. Magnetoreception

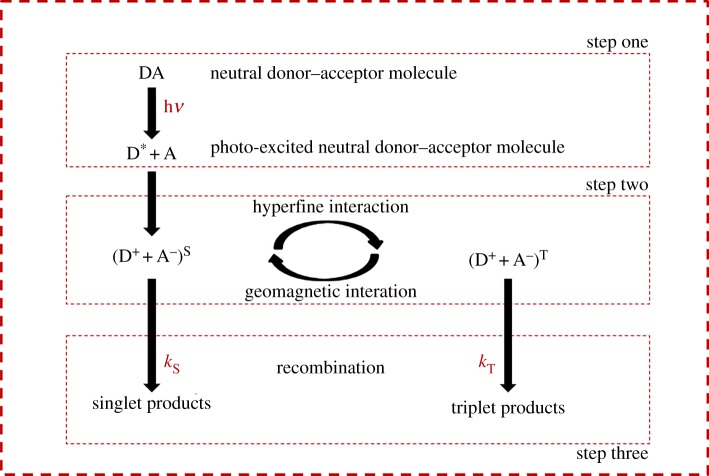
The quantum theory of bird migration is not a new one. In its fourth decade since Schulten first proposed it [93], the radical pair mechanism is well established in both experimental and theoretical investigations of avian magnetoreception and is one of the main alternative (to photosynthesis) examples used as evidence for the field of quantum biology. The mechanism can be described in three steps (figure 3). After an initial step where photoexcitation causes electron transfer and pair formation, the radical pair oscillates between singlet and triplet spin states before a final step of recombination and neural interpretation. It is the singlet–triplet mixing that experiences the influence of the Earth’s magnetic field and that has offered some way of explaining behavioural observations such as the light-dependence [94], inclination aspect [95] and resonance effects of the avian compass [96,97].

Figure 3.

The three steps of the radical pair mechanism. In the first step, a photon incident on the donor molecule causes one of the electrons of the pair to be donated to the acceptor to create the spatially separated but spin-correlated radical pair. In the second step, the radical pair oscillates between singlet and triplet states under the influence of the Zeeman and hyperfine effects. The third step is comprised of spin-dependent recombination into the chemical product.

The radical pair theory has given rise to numerous papers on compass coherence and entanglement and offers a convincing argument for compass behaviour (see [98] and references therein for a review of the subject). However, there remains some doubt as to whether the compass mechanism is truly a quantum phenomenon or can be described using a semi-classical framework. In response to this it has been suggested that the incredible accuracy of the compass is the result of avoided crossings of the spin energy levels of radicals formed in cryptochromes, a process that is genuinely quantum mechanical [99].

Progress has also been made in resolving the structure of the mechanism. Cryptochrome, the biological molecule proposed as the site of magnetoreception, is viable for various reasons. There is evidence that in plants, weak magnetic fields enhance cryptochrome responses [100]. That cryptochromes might mediate magnetic responses in animals has also been documented for the case of fruit flies [101,102]. It seems a logical next step to more complex living creatures, especially since four different types of cryptochrome have been confirmed in the eyes of migratory birds [103] and cryptochromes from the migratory garden warbler form radicals with millisecond lifetimes under the influence of the blue spectral range [104]. More recently, two studies have offered strong evidence for one of these four cryptochromes, Cry4, playing a role in the avian compass. Cry4 is expressed at a constant level rather than a cyclical pattern; this constancy is necessary for efficient navigation [105]. The double-cone localization of Cry4 as well as the fact that it is upregulated during the migration periods of migratory birds but not in chickens, is further confirmation that the molecule is viable as a magnetoreceptor [106].

The future of avian migration as a topic for quantum biology will then rely on a more detailed grasp of the spin dynamics of cryptochrome in an Earth-strength magnetic field and how this might explain some behavioural questions that have been posed, one of which is how to reconcile different observations of the disorienting effects of applied oscillating radiofrequency fields. Cryptochrome, among other things, is responsible for regulating circadian rhythms and closely resembles the DNA repair enzyme photolyase [107,108]. A better understanding of the interaction of cryptochrome with the Earth’s magnetic field could lead to further insight into other biological processes in more complex organisms which might display quantum effects.

5.2. Olfaction

Olfaction is the system by which living organisms ‘smell’ thousands of different molecules. How just several hundred different types of receptors that bind to odourants in humans, and several tens in fruit flies, result in such an amazingly sensitive molecular recognition system has remained a mystery. An intriguing theory, first proposed in 1928 [109], is that our sense of smell relies on the quantum-mechanical vibrational mode of the odourant molecule. In 1996, the theory was revived through the proposal that protein-coupled receptors are measuring molecular vibrations using inelastic electron tunnelling rather than responding to molecular keys fitting molecular locks, working by shape alone [110]. According to this theory, an electron will tunnel from a donor to acceptor site only when the energy difference between these sites is matched by the vibrational energy of the odourant. This vibrational theory of olfaction is reminiscent of phonon-assisted transport of excitons in photosynthesis, illustrating the fundamental role of quantized vibrations in quantum biology.

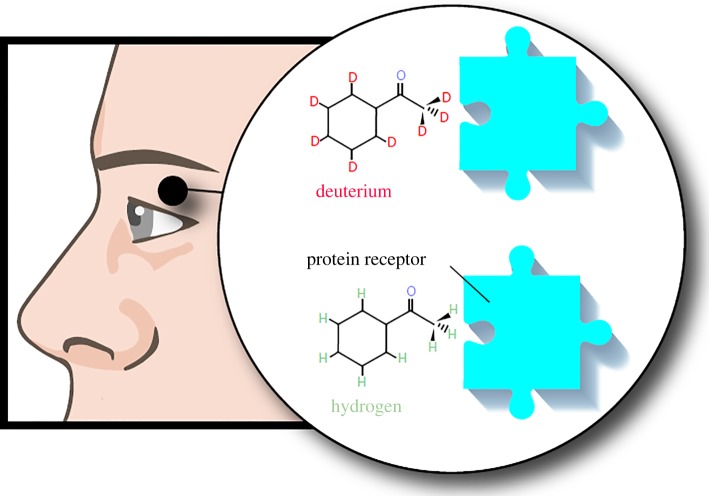
In support of the theory, experiments with fruit flies have indicated that shape and size of odourants are insufficient for detection. For example, the substitution with deuterium of hydrogen results in an odour change despite the fact that the two molecules have the same shape (figure 4) [111]. Furthermore, molecules with similar vibrational frequencies have been observed to elicit similar reactions from fruit flies in spite of being unrelated chemically [111]. The physical viability and efficiency of the proposed mechanism using a simple but general theoretical model was shown in 2007 [112]. The next step is to engineer biologically inspired room-temperature molecular sensing devices.

Figure 4.

A schematic illustrating the possible role of quantum effects in olfaction. Where previously olfaction has been proposed to depend on the shape and size of odourants fitting a specific receptor, experiments with fruit flies have indicated that the substitution of hydrogen with deuterium results in an odour change in spite of their having the same shape. This suggests that vibrational frequency might play a role in the detection of odourants [111].

5.3. Cognition

The question of whether quantum physics could play a role in solving the yet unresolved body–mind problem of how the physiognomy of the brain accounts for conscious thinking is by no means new. Michael Lockwood’s Mind, body and the quantum from 1989 [113] or Henry Stapp’s 2009 Mindful universe [114] are examples of a number of monographs with a philosophical or popular science angle on the problem. A large amount of attention as well as criticism have also been levelled at the ideas of Roger Penrose and Stuart Hameroff, who proposed that parts of the cytoskeleton in neural cells, namely the microtubules, perform quantum computation based on what they call ‘orchestrated objective reduction’, a mechanism drawn from Penrose’s theory of ‘quantum gravity’ [115]. Another branch of science touches the question of the ‘quantum brain’ from a more pragmatic angle: quantum neural network research attempts to exploit quantum computation in order to improve artificial neural network models widely used in machine learning. These artificial neural network models are historically derived from the dynamics of biological neural nets [116,117], and are thus close to the question of the compatibility of quantum dynamics and neural computation. However, a crucial point has been made by Max Tegmark [118] who estimates decoherence time scales for ions involved in the propagation of action potentials to be 10 to 20 orders of magnitude smaller than relevant time scales of neural dynamics. In other words, quantum coherence of the ions involved in neural dynamics would be destroyed long before macroscopic dynamics could be influenced. A potential theory of quantum effects in biological neural networks would thus have to show how the macroscopic dynamics of biological neural nets can emerge from coherent dynamics on a much smaller scale. Promising research in this direction has been done by Matthew Fisher who has proposed that phosphorus can act as a neural qubit allowing quantum processing to occur in the brain, and that this quantumness is protected by so-called Posner molecules, which bind phosphate ions with calcium ions. Entangled Posner molecules then trigger non-local quantum correlations of neuron firing rates [119].

The study of anaesthetics leads to experimental roads to studying consciousness. So far, all we can say about consciousness is that it is ‘soluble in chloroform’ [120] and also in an array of molecules very different from one another. In a recent article on the study of consciousness [121] Turin and his co-workers discovered that a number of general anaesthetics reversibly increase the electron spin content in Drosophila, an effect absent from anaesthetic-resistant mutant flies. They propose that general anaesthetics change the structure of the highest occupied molecular orbital of certain molecules, facilitating electron transport between a donor and acceptor that puts the brain in an unconscious state. If this proves true, the changes in the structure of a molecule calculated by density functional theory, a tool from quantum theory, would have an impact on a macroscopic scale. Electron spin measurements have furthermore been crucial to observe the effects. Especially in a broader definition of quantum biology such findings are very encouraging and show the potential contribution the discipline could make.

6. Origins of life

The identification of quantum effects in primitive organisms such as bacteria has resulted in the successful application of open quantum systems models to energy and charge transfer processes in photosynthetic systems, as well as suggesting that quantum effects may have played an important role in the emergence of the very first living systems from the inanimate matter of which they are constituted.

The detection of the molecular precursors of life in interstellar ices suggests that the building blocks of life could possibly have emerged in space and been delivered to Earth by objects such as comets or meteorites. However, standard computational quantum chemistry cannot account for the variety and richness of chemistry occurring in the interstellar medium. For example, hydrogen cyanide (HCN) oligomers may have played a significant role in the synthesis of a wide range of prebiotic molecules [122–126], and recently, dimeric forms of HCN (cyanomethanimine) [127] have been detected in the interstellar medium. However, it has been found that interstellar gas-phase production routes are incapable of producing significant amounts of HCN [128,129], in spite of its detection.

The theoretical study of the spontaneous generation of prebiotic molecules in the interstellar medium is performed most fundamentally in the framework of open quantum systems. A low temperature interstellar icy environment strongly coupled to a simple molecular system such as HCN, and excited by incident UV radiation, can be investigated using appropriate well-known approximations from the field of quantum biology.

A much more difficult question is how the first living systems may have emerged from these prebiotic molecules, if at all. Despite remarkable work in viable DNA design [130], we have not yet been able to synthesize even a small functional peptide from basic components, and are still a long way from understanding exactly what distinguishes a collection of molecules from the collection of molecules that make up a living system, and what role quantum effects may have played in the origins of life.

7. Quantum biology and complexity

Complexity may be defined as the non-compressibility of the description of a system. If there is no basis set that simplifies the problem, the system is complex. Quantum features visible in macroscopic biosystems have to survive transition to high spectral densities. Chaotic fluctuations in the spectrum contain information about universal features of the dynamics of the system. The emerging field of quantum biology is concerned with interactions between dynamical phenomena at well-separated length and time scales, from femtosecond energy transfer processes in molecular assemblies at the nanoscale to survival and reproduction within ecosystems at the scales of overall organisms.

It is important to note that nature cannot select against the quantum-mechanical nature of chemistry. For example, it is not possible to design a plant with a light-harvesting complex that consists of compounds that defy quantum mechanical description. Biology describes systems that are evolutionarily selected for at the scales of entire organisms. The results of selection are mediated through genetic processes that can affect biological subsystems only down to a certain scale, and the physical details of what happens below that scale are immune to biological selection. Quantum biology then concerns whether or not quantum-dynamical processes that can be selected for—at the scales of proteins, for example—can affect macroscopic organismal dynamics. That is, if quantum behaviour at the nanoscale is to convey a selective advantage, it must be selectable and this selection takes place at the scale of the overall organism. We might claim, therefore, that only subsystems that can exist in quantum and classical variants are of interest, since one or the other can be selected by evolution. This trivializes the claim that all biology is quantum biology because it depends on chemistry and all chemistry is quantum at atomic and molecular scales; thus it is impossible for evolution to select anything other than quantum subsystems here. Precisely what range of length and time scales can be inhabited by subsystems of interest to quantum biology (because they could conceivably exist in quantum and classical variants) is an open question. The issue of scaling will prove important to the further progress of quantum biology [131].

8. Discussion and conclusion

The first book on quantum biology is entitled Physics of the mystery of organic molecules by Pascual Jordan [132]. Since its publication in 1932, however, many mysteries about the nature of life remain. It is clear that coarse-grained classical models fail to give an accurate picture of a range of processes taking place in living systems. The matter of ongoing debate then, is the extent to which quantum effects play a non-trivial role in such biological processes.

A useful path towards answering this question is through the engineering of biologically inspired quantum technologies that can outperform classical devices designed for the same purpose, for example, for energy harnessing or environmental sensing. If quantum effects on a macroscopic scale play a role in getting the job done better in certain processes perfected over billions of years at physiological temperatures and in immensely complex systems, then there exists a wealth of information in the biological world from which to draw inspiration for our own technologies.

In this direction, a prototype quantum heat engine, which clearly illustrates a quantum design principle whereby a coherent exchange of single energy quanta between electronic and vibrational degrees of freedom can enhance a light-harvesting system’s power above what is possible by thermal mechanisms alone, has been proposed. Its quantum advantage using thermodynamic measures of performance has been quantified, and the principle’s applicability for realistic biological structures demonstrated [133].

Quantum biology investigates biological function and regulation of this function, which is connected to static disorder. Single molecule spectroscopy gives us a unique, powerful lens on the role of static disorder, which connects biological function (i.e. projected onto the macroscopic/organismal scale) with quantum-mechanical phenomena. Quantum biology is also concerned with interactions between dynamical phenomena at well-separated length and time scales, from femtosecond energy transfer processes in molecular assemblies at the nanoscale to survival and reproduction within ecosystems at the scales of overall organisms.

While quantum biology is set to demonstrate in the next few decades the extent to which bioinspired quantum devices can outperform classical analogues, a deeper question is how quantum-dynamical phenomena at the nanoscale can provide a selective advantage to an overall organism. Addressing this question rigorously demands an account of how macroscale physical observables significant to organismal fitness can depend predictably on nanoscale quantum dynamical variables. Reciprocally, we must also account for how quantum subsystems at the nanoscale can depend on macroscale dynamics of organisms through evolution. Progress on this question may be assisted by a theoretical framework that allows organism-scale models to be parametrized by nanoscale models. This may be provided by the tools of multiscale analysis within the field of complex systems theory. We might also conceive of experiments in which wild-type organisms known to exhibit long-lived quantum-coherent processes at the nanoscale compete with genetically modified organisms in which such processes are known to be absent. Such an experiment—akin to those done regularly by biologists—may offer clear insight into whether quantum-biological phenomena can provide a selective advantage to organisms, as well add credibility to quantum biology as a field of biology.

Data accessibility

This article has no additional data.

Authors' contributions

F.P. and R.v.G. conceived the study. All authors discussed the results and wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

A.M., B.A., I.S. and F.P. were supported by the South African Research Chair Initiative of the Department of Science and Technology and the National Research Foundation. M.F., J.M.G., R.H. and R.v.G were supported by the VU University Amsterdam, TOP grant no. 700.58.305 from the Foundation of Chemical Sciences part of NWO, and the advanced investigator grant no. 267333, PHOTPROT from the European Research Council. R.v.G. was additionally supported by the Royal Dutch Academy of Sciences (KNAW). S.L.S. acknowledges funding from the Winton Programme for the Physics of Sustainability. A.K.R. was funded by the ARC Centre of Excellence for Engineered Quantum Systems. T.P.J.K. was supported by the University of Pretoria’s Research Development Programme.