Metabolic cost underlies task-dependent variations in motor unit recruitment

Abstract

Mammalian skeletal muscles are comprised of many motor units, each containing a group of muscle fibres that have common contractile properties: these can be broadly categorized as slow and fast twitch muscle fibres. Motor units are typically recruited in an orderly fashion following the ‘size principle’, in which slower motor units would be recruited for low intensity contraction; a metabolically cheap and fatigue-resistant strategy. However, this recruitment strategy poses a mechanical paradox for fast, low intensity contractions, in which the recruitment of slower fibres, as predicted by the size principle, would be metabolically more costly than the recruitment of faster fibres that are more efficient at higher contraction speeds. Hence, it would be mechanically and metabolically more effective for recruitment strategies to vary in response to contraction speed so that the intrinsic efficiencies and contraction speeds of the recruited muscle fibres are matched to the mechanical demands of the task. In this study, we evaluated the effectiveness of a novel, mixed cost function within a musculoskeletal simulation, which includes the metabolic cost of contraction, to predict the recruitment of different muscle fibre types across a range of loads and speeds. Our results show that a metabolically informed cost function predicts favoured recruitment of slower muscle fibres for slower and isometric tasks versus recruitment that favours faster muscles fibres for higher velocity contractions. This cost function predicts a change in recruitment patterns consistent with experimental observations, and also predicts a less expensive metabolic cost for these muscle contractions regardless of speed of the movement. Hence, our findings support the premise that varying motor recruitment strategies to match the mechanical demands of a movement task results in a mechanically and metabolically sensible way to deploy the different types of motor unit.

1. Introduction

Mammalian muscles contain many motor units; each comprising of a bundle of muscle fibres with generally similar contractile properties. However, the contractile properties of muscle fibres among different motor units within a muscle typically vary [1,2] and can be broadly categorized into slow twitch and fast twitch motor units. When the muscle is activated, the activation level of each motor unit can also vary, as well as the population of motor units that are recruited. An ‘orderly’ recruitment plan of motor units based on motor unit size was introduced by Henneman and colleagues [3,4], in which motor units innervated by the smallest motorneurons are most excitable and recruited first, and motor units innervated by the largest motorneurons are least excitable and recruited last. During orderly recruitment, motor units recruited first have slower muscle contractile properties than motor units with higher thresholds and faster contractile properties that are recruited later [5,6]. Given this pattern of neural recruitment, the fastest motor units would only be recruited at the highest level of motor activity. Because the contractile properties of different types of muscle fibres vary, the population of motor units that is recruited affects the mechanics of a muscle when it contracts [7–10].

This ‘size principle’ of orderly recruitment has advantages in the relative simplicity of its control pattern, leading to efficient and fatigue-resistant contractions when motor activity is low or contractions are slow [11]. However, orderly recruitment based on size can pose a mechanical paradox at fast velocities. Fast muscle fibres generate greater power and are mechanically more efficient during fast contractions than slow fibres [12,13]. Thus, for mechanical and energetic reasons, it makes sense to favour the recruitment of faster motor units for high-velocity contractions, even if the force and required activity is low; which is when the size principle would predict that slower motor units are recruited [14,15].

Studies have shown that the size principle of recruitment can be altered depending on the context of the movement task (for review see [16]). Varied coordination patterns between muscles of different fibre-type composition have been observed in both animal and human studies depending on the movement velocity [17–21]. Although it is experimentally more challenging to detect, evidence indicates that recruitment patterns among motor units within muscles can also be altered depending on the mechanics of the task, with slower motor units being suppressed for both high velocity and high frequency contractions [14,15,21–24].

The direct experimental measures of muscle force and length that are required to evaluate the biomechanical function of a muscle's contraction, however, have only been made for a limited number of muscles, in a limited number of studies. Because of this, computer simulations are commonly used to predict muscle activity during dynamic movements for the many muscles for which measurements have not been made (e.g. [25,26]). Nevertheless, the majority of muscle models do not consider the heterogeneity of fibre-type properties [27], orderly recruitment plan [28] or recruitment patterns of muscle fibres that may depend on the mechanics of the task [8,9,29,30]. Hence, muscle models that do not include these fibre-type and recruitment properties may not be able to adequately predict the recruitment patterns and the subsequent force and function of muscles contracting under dynamic conditions of movement. Muscle activations are typically predicted by specifying a cost function believed to mimic the strategy chosen by the central nervous system to solve the muscle redundancy problem while satisfying a set of constraints that represent the musculoskeletal system. A commonly used cost function is to minimize the muscle activation required to perform a movement [31,32]. However, faster motor units that generate higher forces than slower motor units when they shorten would produce similar force at lower activations and thus would always be favoured by such a cost function [30]; this would contravene the generally accepted size-principle pattern of recruitment.

The purpose of this study was to evaluate the effectiveness of a novel, mixed cost function that includes the metabolic cost of contraction, over the typical activation-based cost function. We hypothesized that a metabolically informed cost function would favour the activation of slow motor units at isometric and slow contraction speeds, consistent with the size principle that is known to be effective in these conditions. However, we additionally hypothesized that the same mixed cost function would favour the recruitment of faster motor units for faster movements and contraction speeds, in a manner consistent with experimental studies [21,22] but not predicted by the orderly recruitment size principle.

2. Methodology

2.1. Approach to the problem

To test our hypotheses for an appropriate cost function, muscle fibre heterogeneity and motor recruitment patterns during different contraction speeds, we generated simulations using experimental data, an adapted musculoskeletal model and dynamic optimization techniques.

The musculoskeletal model was based on an existing generic musculoskeletal model of the lower limb [33] adapted to suit the aims of this study. To simulate muscle fibre heterogeneity, we used an alternative approach to our previous implementation in Lai et al. [30]. Previously, the fast and slow muscle fibres within a muscle were represented as two parallel muscle–tendon units (MTU) connected to a MTU that represented a shared tendon. In contrast, for practical and computational reasons, in this study we used two parallel MTUs that had identical muscle attachment points and force generating capacities. The series elastic element of both MTUs was set to be rigid, and thus, the absolute muscle fibre length and velocity in the MTUs were identical. Hence, the configuration was analogous to two distinct fast and slow motor unit populations within a single muscle. To test the two different cost functions implemented in our model, we solved an optimal control problem using direct collocation methods and predicted time-varying muscle activations. To predict muscle fibre recruitment patterns during different contraction speeds, the musculoskeletal model was driven to track the simulated dynamics of a typical ramped isometric contraction experiment and experimental data collected across a range of pedalling conditions [29].

2.2. Musculoskeletal model

The adapted musculoskeletal model used in this study included thigh, shank, foot and pedal segments of the right leg. The model had eight degrees of freedom (d.f.); the hip was modelled as a six d.f. joint that positioned and orientated of the right leg in the global space to match the experimental data, the knee and ankle joints were modelled as one d.f. hinge joints and the pedal was welded to the foot segment. The model was driven by three MTUs. As stated previously, two MTUs were used to represent two muscle fibre types within a single bi-articular plantarflexor. The remaining MTU represented a uni-articular ankle dorsiflexor. The muscle–tendon properties of the plantarflexor and dorsiflexor MTUs were taken from medial gastrocnemius and tibialis anterior muscles, respectively, reported by Rajagopal et al. [34] with updated optimal fibre lengths and tendon slack lengths reported in Lai et al. [33]. Each MTU actuator consisted of a massless Hill-type actuator with contractile and series elastic elements. The contractile element represented the muscle fibre with normalized active force–length (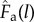) and force–velocity (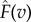) relationships and a passive force–length relationship (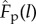) [35]. These relationships were scaled for each MTU to their maximum isometric force (F₀), optimal fibre length (l₀) and pennation angle at optimal fibre length. The series elastic element that represented the free tendon and other connective tissues was assumed to be rigid in this study. This assumption neglects the influence of tendon compliance on muscle fibre behaviour (see Discussion). However, because it was unchanged for all simulations, this assumption does not influence the variation in predicted activations across contraction speeds. Ideal linear and torque actuators were applied at the hip and knee joints to drive these joints without muscle actuation and to account for the bi-articular configuration of the ankle plantarflexor (i.e. the medial gastrocnemius spans the knee and ankle joints).

2.3. Metabolic energy model

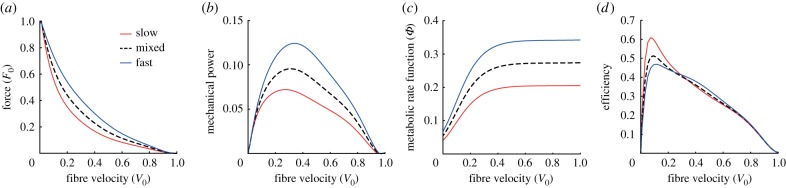
To predict metabolic rate, we used the metabolic model defined by Minetti & Alexander [36] (figure 1). The metabolic model was defined by a nonlinear metabolic rate function that was proportional to the fibre velocity and scaled linearly with activation (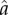), F₀ and maximum contraction velocity (V₀) (figure 1). The metabolic rate function was calibrated to experimental data from frog sartorius muscle under various contraction conditions [37]. This metabolic model has been shown to predict metabolic rates during running that were consistent with complex metabolic models derived from the First Law of Thermodynamics and the free energy liberated by ATP hydrolysis during cross-bridge cycling [38]. Furthermore, this metabolic model was chosen because it was smooth and continuous to the second derivative, and hence was well-suited for dynamic optimization; the method used in this study to predict muscle recruitment patterns [39]. We modified the metabolic rate function to account for muscle fibre type by including a scaling factor so that the mechanical efficiency of purely slow and fast muscle fibre types were consistent with experimentally reported isokinetic concentric contractions in mice [40] as well as another metabolic model that accounted for fibre types in humans [28]. Similar mechanical efficiencies were reported in other mammalian skeletal muscles [41,42]. We also assumed that the scaling factor of the rate function varied linearly with the V₀ of each fibre type. For example, the scaling factor for a mixed muscle fibre type predicted a metabolic rate that was the average of the purely slow and fast muscle fibre types. Mechanical efficiency was defined as mechanical power output divided by metabolic rate.

Figure 1.

(a) Normalized muscle force, (b) mechanical power, (c) metabolic rate and (d) efficiency properties of the three muscle fibre types used in this study plotted against normalized fibre velocity. Fibre velocity was normalized by the maximum contraction velocity (V₀). Muscle force was normalized by the maximum isometric force (F₀). Mechanical power was calculated as the product of muscle force and muscle fibre velocity. Metabolic rate function was adapted from Minetti & Alexander [36]. Mechanical efficiency was the calculated as mechanical power over metabolic rate. (Online version in colour.)

2.4. Muscle fibre type properties

To represent slow, mixed and fast muscle fibre types, the muscle properties of two muscle fibre types of the plantarflexor were varied via three properties: V₀, the curvature of the concentric portion of the force–velocity relationship and the activation and deactivation time constants for the first-order excitation–activation dynamics [26]. V₀ of the slow, mixed and fast fibres was set at 5, 7.5 and 10 l₀ s⁻¹, respectively, consistent with previous modelling studies of muscle fibre types [8,23] and within the range reported for human muscle [43]. The curvature of the force–velocity curve of the slow, mixed and fast fibres were fitted to the curvature value, k, defined in Otten's formulation of 0.18, 0.235 and 0.25, respectively [44]. Specifically, the curvature of the faster muscle fibre was significantly flatter than that of the slow muscle fibre (figure 1). The activation time constants for the first-order excitation–activation dynamics of the slow, mixed and fast fibres were 45, 35 and 25 ms, respectively, derived from reported values from tetanic contractions in cats [30,45]. The deactivation time constants were set such that the ratio of activation to deactivation time constants was 0.6 for all muscle fibre types [26]. Two muscle fibre combinations were used in the plantarflexor in this study; (i) one muscle fibre was assigned purely fast contractile properties and the other was assigned purely slow contractile properties, or (ii) both muscle fibres were assigned identical mixed contractile properties. Note that the F₀ of the two muscle fibres were identical and unchanged for all simulations. The dorsiflexor muscle fibres were assigned mixed fibre properties connected to a rigid tendon and remained unchanged for all simulations. In all simulations, the predicted activation patterns of the dorsiflexor muscle were similar in timing and magnitude irrespective of alterations to the properties of the muscle fibres of the plantarflexor and the cost function described below.

2.5. Experimental and simulated data during different contraction speeds

To generate simulations of different contraction speeds, we drove the musculoskeletal model to track the dynamics of experimental data collected from a range of pedalling conditions. Experimental data were taken from three female cyclists (mean ± s.d., age: 28.3 ± 5.9 years; height: 169.2 ± 4.2 cm, mass: 66.3 ± 2.0 kg) pedalling on a stationary bicycle (Indoor Trainer, SRM, Julich, Germany) as part of a larger study [29,46]. Informed consent was obtained from the cyclists and the protocol was approved by the Institutional Review Boards at Simon Fraser University and Harvard University. For this study, we extracted and analysed six pedalling conditions; one condition at a cadence of 60 RPM at an average crank torque of 44 N m and five conditions at five cadences (60, 80, 100, 120 and 140 RPM) at an average crank torque of 13–14 N m. The average powers for these pedalling conditions were 275, 80, 115, 135, 165 and 200 W, respectively. 3D marker trajectories of 15 active markers attached on the thigh, shank, foot and pedal of the right leg were collected at 100 Hz using a motion capture system (Certus Optotrak, NDI, Waterloo, Canada). Pedal force normal and radial to the crank were collected at 2000 Hz using instrumented pedals (Powerforce, Radlabor, Freiburg, Germany). One crank cycle was taken from each trial and used as the tracking data for the simulations.

To generate simulations during an isometric contraction, we drove the musculoskeletal model to track a simulated experiment that recreated the dynamics of a typical isometric ramped plantarflexion experiment. In the simulated experiment, all the joint angles and angular velocities including the ankle and knee joints were held constant at the anatomical neutral standing position (i.e. knee and ankle angles were set at 180° and 90°, respectively). A simulated ramped increase and decrease in external force was then applied to the foot segment of the model over 1.5 s, which provided sufficient time for all the muscle fibres to fully activate and deactivate. Peak external force was equivalent to 80% of the combined F₀ of both muscle fibres.

2.6. Problem formulation

To solve the optimal control problem, we interfaced the application programming interface (API) of an open-source musculoskeletal modelling software, OpenSim (v. 3.3) [25,47], an open-source interior point optimizer (IPOPT) (v. 3.11.0) [48] and MATLAB (The MathWorks Inc., USA). Similar approaches have been used in previous studies to generate predictive simulations of a leg extension [49], jumping [50] and locomotion [51]. OpenSim was used to harness its robust multibody dynamics engine and other numerical operations, IPOPT, a software package of interior-point optimization methods to solve large-scale, gradient-based nonlinear optimization problems, was used to solve the parameter optimization problem using a direct collocation approach, and MATLAB was used to interface the two software packages.

Firstly, the adapted generic musculoskeletal model was scaled to the anthropometric measurements of each cyclist. The subject-specific models were used to compute hip, knee and ankle angles and net joint torques using the inverse kinematics and dynamic tools in OpenSim, respectively. In addition, time-varying moment arms of the muscles were obtained as a function of the joint angles. The time-varying hip translations and rotations for each trial were then prescribed to the subject-specific model thus constraining the forces and torques at each of the degrees of freedom. The experimental, time-varying pedal reaction forces were also applied to the pedal segment for each trial.

An optimal control problem was formulated to solve for a set of controls (excitations) and state variables that minimized a cost function (J) while satisfying a set of equality path constraints that represented the system dynamic equations of motion:

2.1

where u are the controls including the neural excitations and ideal torque actuators and x are the state variables including the generalized coordinates, generalized angular velocities and muscle activations. In addition, bound inequality constraints were applied on the states and controls where the controls and muscle activations were bounded between 0 (no excitation/activation) and 1 (maximally excited/activated).

Two weighted cost functions were used in this study. Both cost functions consisted of a physiological term (J_phy) and a data-tracking term (J_track),

2.2

where s_phy and s_track are the scaling factors for the physiological and tracking terms, respectively. These scaling factors were determined such that physiological term contributed the majority of the total cost (greater than 90% for all simulations).

Two separate weighted physiological terms were used in this study. The first criterion, termed min-activation, was the commonly used physiological criterion to minimize the sum of the muscle activations squared [31,32],

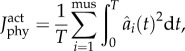2.3

where T is the cycle duration, mus is the number of muscles and 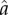is muscle activation.

The second physiological criterion, termed min-metabolic-activation function, was a novel, mixed function to minimize the weighted sum of the total metabolic cost of transport and the sum of the muscle activations squared,

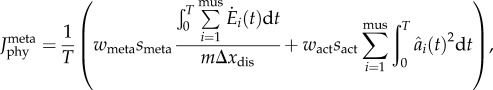2.4

where s_meta and s_act are scaling factors of the metabolic and activation terms, respectively, w_meta and w_act are weighting factors of the metabolic and activation terms, respectively, 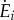is the metabolic rate, m is the total mass of the subject-specific musculoskeletal model and Δx_dis is the rotational distance travelled by the pedal around the crank centre over one crank cycle The scaling factors were adjusted such that the two cost functions had the same order of magnitude and weighting factors were weighted such that their sum was equal to one. The scaling and weighting factors were kept constant for all simulations. The rotational distance represented the distance travelled by the lower limb rather than the distance travelled by the wheel during cycling or the distance travelled by centre of mass of the body during walking; both are typically used to normalize the cost of transport. However, because the pedalling experiments were performed on an ergometer and the gear ratio between the crank and the wheel was unknown, we were unable to obtain the distance travelled by the wheel during a crank cycle. Nevertheless, this difference only influences the scaling factors for the two cost functions and, thus, will have a negligible influence on the optimal solution and the predicted muscle activation patterns. Minimizing the sum of muscle activations squared was included to avoid excessively activating any one single MTU actuator [52], which occurred in our preliminary simulations and generated unphysiological co-activation between synergistic muscles. However, it was weighted such that the metabolic term contributed the majority of the total physiological cost (greater than 70% for all simulations).

The data-tracking term was included to minimize the sum of the errors squared between the experimental and simulated state variables,

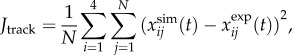2.5

where 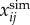and 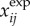are the simulated and experimental state variable i at time interval j over the total number of intervals N. The four tracked state variables were the ankle and knee angles and angular velocities. Similar approaches have been employed in optimal control problems of pedalling [53] and running [38].

2.7. Data-driven dynamic optimization simulations

To solve the dynamic optimization simulations, the optimal control problem was converted to a parameter optimization problem using direct collocation methods. The state and controls were discretised in time into 50 evenly spaced nodes and the system dynamics were converted into algebraic equality constraints via forward finite difference approximation [54,55].

The simulations began from a random initial guess for the controls and state variables. Each problem had a total of 550 unknowns and 847 equality and inequality constraints. The constraint tolerance was set at 10⁻⁶. All optimizations were run on a desktop computer with a 3.50 GHz, Intel i5-4690 K processor and 16 GB of RAM. On average, it took about 15 min for each optimization to converge to the optimal solution and satisfy the constraint tolerance.

2.8. Data analysis

Net ankle torques from the simulations were calculated as the summation of the product of the predicted muscle force and time-varying moment arms of the muscles spanning the ankle. Simulation ankle angles and net ankle torques were compared with equivalent experimental values. For the simulations that tracked the experimental data of pedalling, all predicted muscle activations of the muscle fibre types per pedalling condition per cyclist were time-normalized and group mean ± s.d. values were calculated. Mean activation of two muscle fibre types of the plantarflexor for the crank cycle and for the duration of the simulated ramped plantarflexion were calculated. Total metabolic cost due to the muscle fibres of the plantarflexor was also calculated.

A total of 64 simulations were performed; 60 that tracked the experimental pedalling data (three cyclists, five pedalling conditions, two muscle fibre combinations, two cost functions) and four that tracked the simulated ramped isometric plantarflexion experiment (one cyclist, one condition, two fibre combinations, two cost functions).

For statistical analysis, we calculated the ratio of the slow and fast fibre mean activations in simulations of pedalling where the muscle fibre combination in the plantarflexor was assigned purely slow and fast contractile properties. A two-way repeated-measures ANOVA was performed using R (v. 3.5) [56] to test whether the cost criteria (two levels: min-activation and min-metabolic-activation) and pedalling conditions (six levels) had a significant effect on the ratio. If a significant main effect was obtained, post hoc paired t-tests were conducted to determine whether significant differences existed between each comparison. The p-value for level of significance was set at 0.05.

3. Results

The predicted ankle angles and net ankle torques compared well with the experimental data of pedalling (figure 2). Average r² and root mean square errors (RMSE) between the predicted and experimental ankle angles across pedalling conditions were 0.99 ± 0.01 and 0.79 ± 0.22°, respectively. Average r² and RMSE between net ankle torques across pedalling conditions were 0.97 ± 0.01 and 2.22 ± 0.68 N m, respectively.

Figure 2.

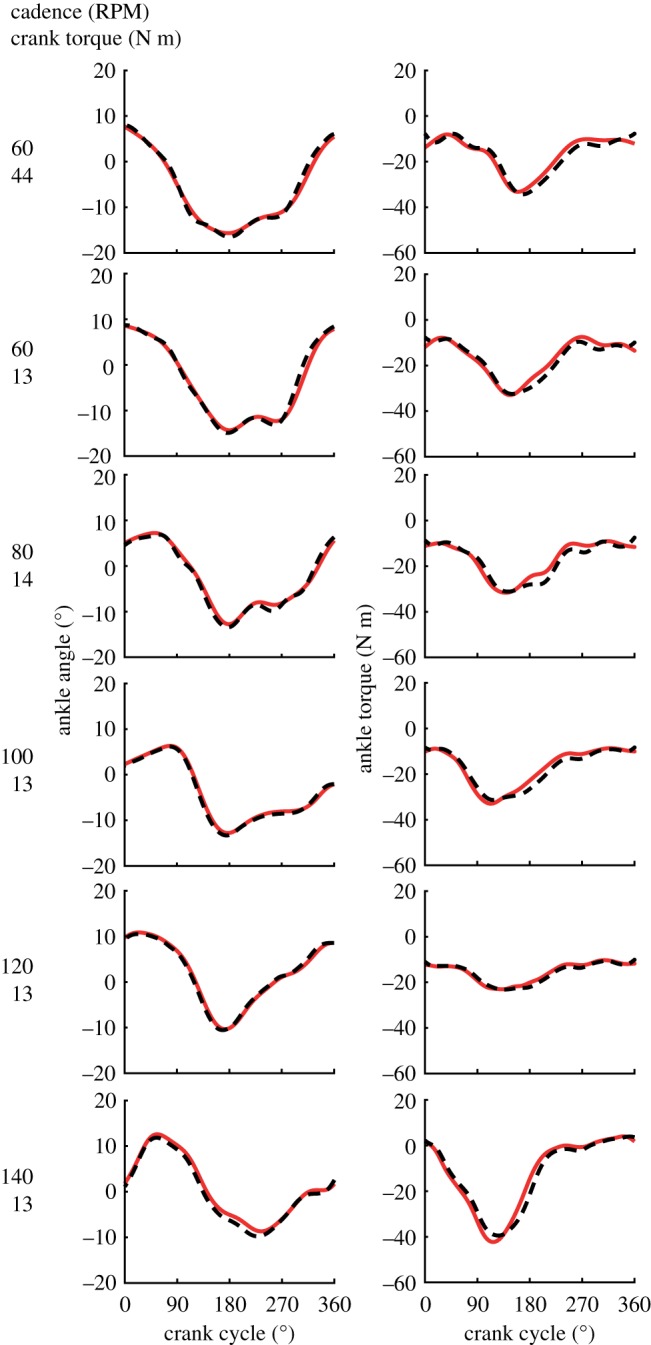
Mean experimental and simulation ankle angles (top) and net joint torques (bottom) for three cyclists across the six pedalling conditions. (Online version in colour.)

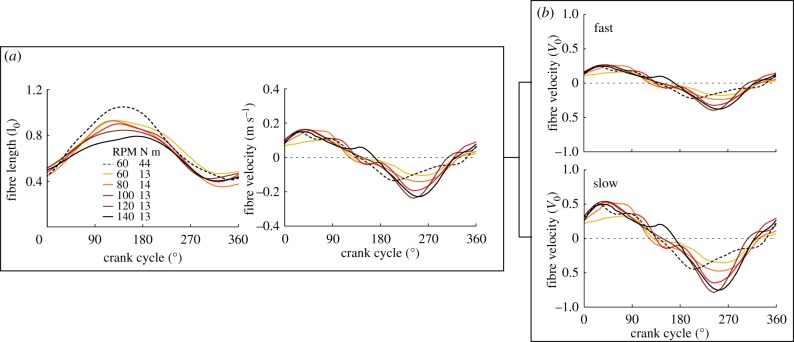
Muscle fibre velocity in the plantarflexor increased with faster pedalling cadences (figure 3). Specifically, at an average crank torque of 13–14 N m, peak absolute fibre contraction velocity in the muscle fibres of the plantarflexor increased from −0.11 m s⁻¹ at 60 RPM to −0.23 m s⁻¹ at 140 RPM (figure 3a). This increase in contraction velocity was equivalent to an increase in normalized fibre velocity in the fast fibres from −0.17 l₀ s⁻¹ to −0.38 l₀ s⁻¹ and in the slow fibres from −0.35 l₀ s⁻¹ to −0.77 l₀ s⁻¹ (figure 3b). Time-varying normalized muscle fibre lengths underwent similar trajectories across the six pedalling conditions.

Figure 3.

(a) Muscle normalized fibre lengths and absolute fibre velocities of the ankle plantarflexors for three cyclists across the six pedalling conditions. (b) Mean normalized muscle fibre velocities of the fast (top) and slow (bottom) fibres of the plantarflexors. Fibre lengths and velocities were normalized to optimal fibre length (l₀) and maximum contraction velocity (V₀), respectively. Positive and negative fibre velocities represent lengthening and shortening, respectively. (Online version in colour.)

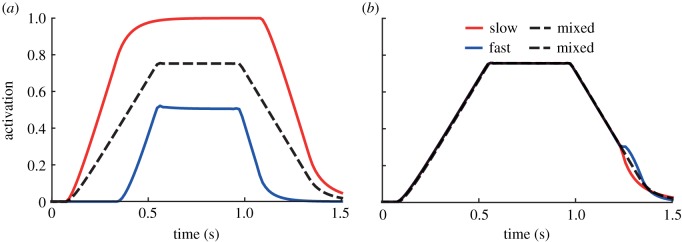
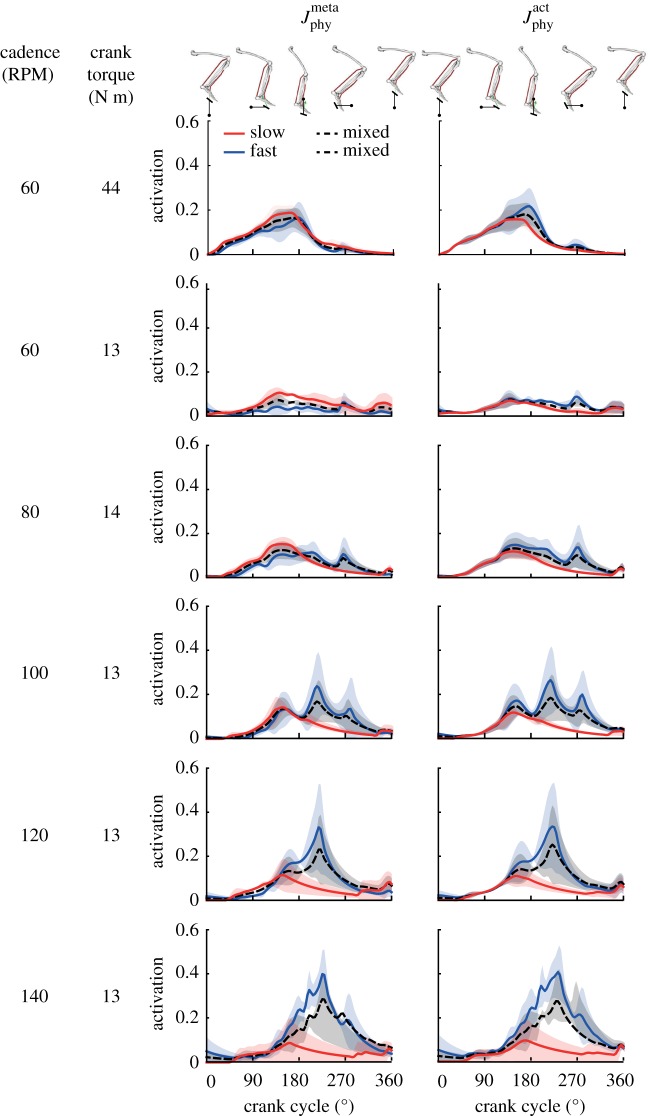
Predicted muscle activation patterns of the slow and fast muscle fibres in the plantarflexor during the simulated isometric plantarflexion were consistent with orderly recruitment only when the min-metabolic-activation criterion was used (figure 4a). Specifically, using the min-metabolic-activation criterion, the slower fibres were activated first when the external force was ramped up and the faster muscle fibres were activated only when the slower fibres were not capable of activating to generate sufficient force to resist the external load. The opposite occurred when the external force was ramped down, the faster fibres were deactivated first and the slower fibres were deactivated only when the faster fibres were fully deactivated. In contrast, using the min-activation criterion, the predicted muscle activation patterns were consistent with the profile of the ramped up and down external force and were unchanged irrespective of the combination of muscle fibres chosen (figure 4b). As expected, the activation patterns in the simulations with two mixed fibres (dotted lines) were consistent irrespective of cost criterion. The time-varying activation patterns using the min-metabolic-activation criterion resulted in a higher mean activation in the slower fibres compared with the faster fibres during the isometric contraction (figure 6a). This discrepancy in mean activation during the isometric contraction was not present when using the min-activation criterion (figure 6b).

Figure 4.

Predicted time-varying muscle activations of the muscle fibre types of the plantarflexor during a simulated ramped isometric plantarflexion. Simulations were performed using the two muscle fibre combinations assigned to the plantarflexor fibres: (1) one purely slow fibre and one purely fast fibre (slow–fast), and (2) two mixed fibres (mixed–mixed) and using the two weighted cost functions: (a) min-metabolic-activation (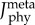) and (b) min-activation (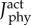). (Online version in colour.)

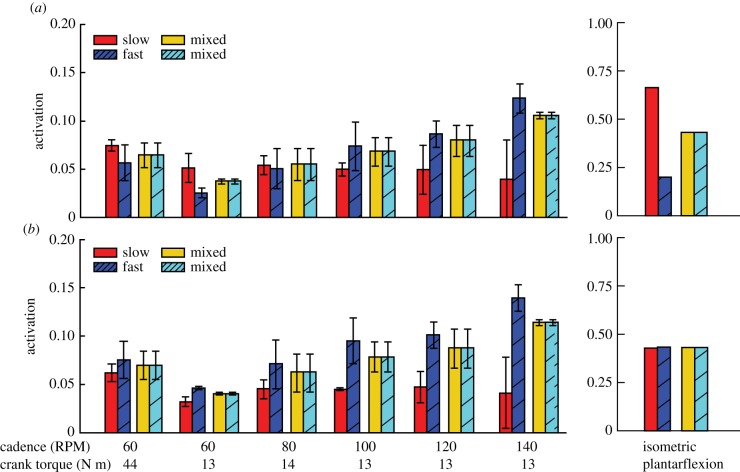
Figure 6.

Mean activations of the muscle fibre types of the plantarflexor across six pedalling conditions and one simulated ramped isometric plantarflexion. Two muscle fibre combinations (slow–fast and mixed–mixed) and two weighted cost functions ((a) min-metabolic-activation function (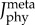) and (b) min-activations (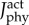)) were used. Note that the mixed–mixed plantarflexor fibre combination (yellow and cyan bars) was predicted in separate simulations to the slow and fast (red and blue bars) plantarflexor fibre combination. (Online version in colour.)

Predicted activation patterns of slow and fast fibres of the plantarflexor were consistent with orderly recruitment during pedalling at slower cadences and only when the min-metabolic-activation criterion was used; yet, simulations using both cost criteria led to a shift that favoured activating the faster fibres at faster cadences (figures 5 and 6). At the slower cadences of 60–80 RPM, when the min-metabolic-activation criterion was used, predicted activation patterns and mean activations of the slower fibres were consistently greater than the faster fibres even with an increase in crank torque from 13 N m to 44 N m (figures 5 and 6a). This preference of activating the slow fibres compared with the fast fibres was further shown in the ratio of slow-to-fast fibre mean activations (table 1). Yet, as cadence increased to faster cadences of 100–140 RPM, simulations using the min-metabolic-activation criterion predicted increasingly greater mean activation in the faster fibres compared with increasingly lower mean activation in the slower fibres (figure 6a; table 1; p = 0.011). In contrast, when the min-activation criterion was used, the time-varying activation patterns and mean activation of the faster fibres were consistently greater than the slower fibres irrespective of crank torque or cadence across pedalling conditions (figure 6b; table 1). Similar to the simulations using the min-metabolic-activation criterion, at faster cadences, mean activation in the faster fibres increased while it decreased in the slower fibres (p = 0.011); though, the ratio of slow-to-fast fibre mean activations using the min-activation criterion was always significantly lower than the ratio using the min-metabolic-activation criterion (p = 0.022). The predicted mean activation of the mixed muscle fibres increased with both greater crank torque and crank cadence irrespective of the physiological criterion used.

Figure 5.

Predicted time-varying muscle activations (mean ± 1 s.d.) of the plantarflexor muscle fibre types for three cyclists across six pedalling conditions. Muscle activation was bounded between 0 (no activation) to 1 (fully activated). The model images above the plots depict the orientation of the lower limb and the crank. Two muscle fibre combinations (slow–fast and mixed–mixed) and two weighted cost functions (min-metabolic-activation function (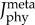) (left) and min-activations (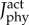) (right)) were used. (Online version in colour.)

Table 1.

The ratio of slow and fast fibre mean activations in simulations of pedalling for which the muscle fibre combination in the plantarflexor was assigned purely slow and fast contractile properties and the two weighted cost functions were used. A ratio greater than one represented a preference of activating the slow fibres over the fast fibres.

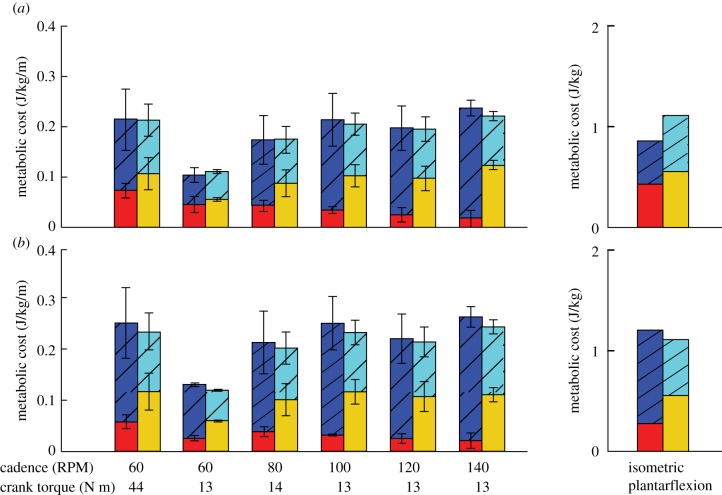
Total normalized metabolic cost in the muscle fibres of the plantarflexor were on average 0.04 J kg⁻¹ m⁻¹ lower in simulations using the min-metabolic-activation criterion compared with the min-activation criterion (figure 7). In addition, in simulations using the min-metabolic-activation criterion and when slow and fast muscle fibres were assigned to the plantarflexor compared with having mixed fibres, total metabolic cost of the plantarflexor was decreased by 0.25 J kg⁻¹ during the isometric plantarflexion. Last, as cadence increased during pedalling, a higher total metabolic cost occurred when the plantarflexor fibres were assigned slow and fast properties compared with mixed fibres, predominantly driven by an increased contribution of fast fibres to the total metabolic cost irrespective of the physiological criterion used.

Figure 7.

Total metabolic cost of the muscle fibre in the plantarflexor across six pedalling conditions and one simulated ramped isometric plantarflexion. Two muscle fibre combinations (slow–fast and mixed–mixed) and two weighted cost functions ((a) min-metabolic-activation function (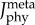) and (b) min-activations (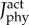)) were used. Metabolic cost was normalized by the mass of the musculoskeletal model and the rotational distance travelled by the pedal around the crank centre over one crank cycle. (Online version in colour.)

4. Discussion

Orderly motor recruitment based on the size principle is generally well accepted and has been determined experimentally during isometric and slow contractions (e.g. [4,57]). During slow contractions, the relatively simple control pattern and preferred recruitment of smaller motor units consisting of slower, more fatigue-resistant muscle fibres makes mechanical and energetic sense because at these contraction speeds, slow motor units have higher normalized power output and mechanical efficiency compared with larger motor units consisting of faster muscle fibres [11]. Our musculoskeletal simulations that used a metabolically informed cost function were consistent with the size principle during isometric and slow contractions, for which it predicted preferred recruitment of the slower muscle fibres compared with faster muscle fibres. Hence, minimizing the metabolic cost of a muscle contraction may be a strategy used for the recruitment of slower muscle fibres at slower contraction speeds with the goal of satisfying the mechanical demands of the task in the most efficient or economic way possible [16].

However, the size principle poses a mechanical paradox at faster contraction speeds and high cycle frequencies. At low muscle activity, the size principle would predict that the slower fibres are recruited, however the faster fibres produce greater power and are more mechanically efficient at fast speeds and can activate and deactivate more rapidly, and thus would be mechanically more effective at the faster speeds. Altered recruitment strategies that favour the faster fibres have been shown to occur for high speed and high frequency contractions [22]. Previous cycling studies have suggested that the recruitment of faster fibres is favoured over the slower fibres at higher cadence cycling [21,22]. This premise has been evaluated through the relative changes in the EMG frequency spectra and activation levels when cycling against a range of powers and cadences. Similar shifts to faster fibre recruitment have been found using EMG-based analyses in rats [15] and goats [23] running on treadmills where faster fibres were favoured for fast running on the flat as opposed to slow walking up an incline. Shifts to faster fibre recruitment have been observed in glycogen depletion studies in bushbabies [58] when comparing steady running with explosive jumping. Thus, it is not surprising that our mechanically and energetically consistent musculoskeletal simulations predicted preferred recruitment of the faster muscle fibres when pedalling at the faster cadences of 100–140 RPM (figures 5 and 6). For example, when pedalling at 100 RPM where recruitment strategies first shifted to preferential activation of faster muscle fibres using the min-metabolic-activation cost function, the faster fibres operated at normalized fibre velocities that were approximately 10% more efficient compared with the slower muscle fibres at the time of peak activation (approx. 220° crank cycle; figure 1). This discrepancy in mechanical efficiency increased to approximately 20% at 140 RPM. Interestingly, the mechanical efficiency at the time of peak activation could be used to distinguish the recruitment between the faster and slower muscle fibres when assessed across the whole range of mechanical conditions tested here; this further indicates that recruitment strategies may be driven by the mechanical demands of the task.

We recently speculated that the commonly used cost function for musculoskeletal simulations, of minimizing the sum of muscle activations, was inadequate for investigating motor unit recruitment between muscle fibre types with varying mechanical demands and that alternative cost functions may be necessary [30]. Minimizing the sum of muscle activations was initially proposed as a cost function that incorporated a physiological basis to solving the muscle redundancy problem similar to previous criteria such as minimizing muscle fatigue [32,59]. It has since been shown to predict muscle activation patterns that were temporally consistent with EMG activity during walking [60] and running [61]. However, our current study provides evidence that a cost function that only minimizes muscle activation cannot predict known recruitment strategies, such as the size principle, during isometric and slow contraction because it consistently favours the recruitment of faster fibres over the slower fibres due to differences in their F–V relationship. In contrast, the mixed, weighted cost function (min-metabolic-activation, equation (2.4)) that minimizes the metabolic cost of muscle force generation and muscle activations that we have tested here was capable of predicting muscle activation patterns that were consistent with known and observed recruitment strategies, based on the size principle, during isometric and slow contractions as well as preferential recruitment of faster muscle fibres at faster contraction speeds (figures 4–6).

The recruitment strategy among motor units within a muscle is analogous to the coordination strategies between synergistic muscles with different fibre type proportions. It has also been shown that the coordination patterns between muscles of different fibre-type composition vary in response to the mechanical demands of the task at this higher architectural level. In particular, there are examples of muscles with higher proportions of faster fibres being favoured for faster contraction speeds (in man: [21,62,63]; in animals: [19,20]) and higher contraction frequencies [17]. Hence, we suggest that the coordination patterns between muscles could be better predicted in musculoskeletal simulations (when assessed across a range of mechanical demands) if the mechanical and energetic consequences of the different fibre-type proportions are considered, and the simulations include the minimization of metabolic cost. Hence, we argue that a metabolically informed cost function should be used in conjunction with physiological muscle fibre type properties to investigate motor recruitment both within a muscle and coordination between synergistic muscles with different fibre type proportions.

When evaluating the results from this study, it is important to consider the methodological approaches used. First, we changed multiple muscle fibre properties to simulate different muscle fibre types; each is likely to have an influence on the predicted recruitment patterns of the muscle fibres and thus each is needed to test the sensitivity of the choices of parameter used in the simulations. The modifications that represented the properties of different muscle fibre types: maximum contraction velocity (V₀), the curvature of the concentric portion of the F–V relationship and the activation–deactivation time constants, were implemented in the model separately. Then both cost functions were simulated for one cyclist at a crank cadence of 60 RPM and a constant torque of 13 N m, and predicted muscle activation patterns and mean activation levels were compared. Twelve additional simulations were performed. We found that all properties positively correlated with greater muscle activation levels across the crank cycle and higher mean activations in the slower muscle fibres compared with faster fibres only when the min-metabolic-activation criterion was used; consistent with our main findings. Second, unlike our previous implementation of different muscle fibre types, we did not include a tendon element in series with the muscle fibres [30], potentially influencing the length, velocities and the power output of the muscle fibres in the ankle plantarflexor muscle. Tendon compliance, particularly in the ankle plantarflexors, has been shown to decouple muscle fibre behaviour from the measured joint dynamics during movement, allowing the muscle fibres to operate at reduced contraction speeds; more favourable for force generation on their F–V relationship (e.g. [64–66]). Hence, the high contraction speeds of the plantarflexor fibres found in our simulations, in particular at faster cadences, may not be representative of the physiological contraction speed of the plantarflexors during these pedalling conditions. Furthermore, the possible metabolic savings due to a shared compliant tendon were not included and hence, may influence the metabolic cost predicted by the model. Akin to our previous study [30] we used the standard components available in OpenSim to avoid altering the source code and impairing computational performance. In addition, the force production in the ankle plantarflexors during the simulated movement tasks was relatively low compared with other movements such as running [67], thus the absence of a compliant tendon will likely to have minimal influence on the overall metabolic cost, particularly between different cost functions and muscle fibre type combinations. Despite this, our representation of different muscle fibre types as two parallel MTUs with rigid tendons to represent slower and faster muscle fibres within a single muscle was sufficient to test our hypothesis and investigate how recruitment strategies vary with changes in the mechanical demands of a movement task.

Third, unlike previous motor unit pool models used to simulate motor recruitment (e.g. [68,69]), we did not include any predefined excitatory drive or relative excitability of pool of motor units that would have prescribed recruitment patterns on the model. Specifically, in previous models, motor recruitment patterns were based on predefined recruitment threshold excitations and firing rate linearly increased with excitatory drive irrespective of the muscle fibre length, muscle fibre velocity and the mechanical demands of the movement task. In contrast, we represented different motor units as distinct muscle fibre types in a mechanically and energetically consistent musculoskeletal environment and allowed the simulation to predict recruitment patterns that optimized a given cost function. This difference allowed us to test whether different recruitment patterns emerged for different mechanical tasks in response to the different cost functions. Indeed, our results show that if the minimization of metabolic cost is included in the cost function and used to control motor unit recruitment, the recruitment patterns change according to mechanical task in a mechanically sensible fashion. Last, model-predicted muscle activation patterns are often compared with EMG activity of the muscles to evaluate the model outputs. Akin to our previous study [30], the abstract nature of the musculoskeletal model used in this study and the lack of other synergistic and antagonistic muscles at the ankle and knee joints restricted direct comparisons with EMG signals. In spite of this, the properties, attachment points and moment arms assigned to the ankle plantarflexor used in this study were taken from the medial gastrocnemius, which has been shown in previous experimental studies to exhibit the greatest shift in recruitment strategies of all the major lower limb muscles with varying mechanical demands [21], and indeed shows recruitment patterns that vary from isometric [70] to high speed shortening [22]. Thus, the findings that predicted recruitment patterns in slower and faster muscle fibres with respect to variation in pedalling cadence (and thus, muscle contraction speed) are consistent with these experimental measurements.

In summary, our study shows that a mechanically and energetically sensible musculoskeletal modelling environment, in conjunction with an appropriate cost function, is capable of predicting muscle activation patterns that are consistent with known motor recruitment strategies when the mechanical demands of the task are varied. This simulation framework provides a means in which to further investigate motor recruitment across different architectural levels, such as a wider continuum of motor units within a muscle and coordination patterns between synergistic muscles with different fibre type proportions, in relation to varying movement tasks.

Ethics

The institutional human research ethics committee approved the study.

Data accessibility

The supporting data used in this manuscript are available in our SimTK project repository at https://simtk.org/projects/nmlmuscle.

Authors' contributions

A.K.M.L. designed the study, carried out all the simulations, analysed and interpreted the results, and drafted and revised the manuscript; A.A.B. designed the study, and helped draft and revise the manuscript; J.M.W. designed the study, helped in the acquisition of data, interpreted the results and helped draft and revise the manuscript. All authors gave their final approval for publication.

Competing interests

We declare we have no competing interests

Funding

This study was financially supported by a National Center for Simulation in Rehabilitation Research Pilot Project Award and Visiting Scholar Fellowship and a National Institutes of Health grant no. 2R01AR055648.