Aerodynamics of manoeuvring flight in brown long-eared bats (Plecotus auritus)

Abstract

In this study, we explicitly examine the aerodynamics of manoeuvring flight in animals. We studied brown long-eared bats flying in a wind tunnel while performing basic sideways manoeuvres. We used particle image velocimetry in combination with high-speed filming to link aerodynamics and kinematics to understand the mechanistic basis of manoeuvres. We predicted that the bats would primarily use the downstroke to generate the asymmetries for the manoeuvre since it has been shown previously that the majority of forces are generated during this phase of the wingbeat. We found instead that the bats more often used the upstroke than they used the downstroke for this. We also found that the bats used both drag/thrust-based and lift-based asymmetries to perform the manoeuvre and that they even frequently switch between these within the course of a manoeuvre. We conclude that the bats used three main modes: lift asymmetries during downstroke, thrust/drag asymmetries during downstroke and thrust/drag asymmetries during upstroke. For future studies, we hypothesize that lift asymmetries are used for fast turns and thrust/drag for slow turns and that the choice between up- and downstroke depends on the timing of when the bat needs to generate asymmetries.

1. Introduction

Flight has evolved independently in four animal groups, three of which are extant: insects, birds and bats, and the ability to fly probably accounts for much of the evolutionary success of all three groups. Recent years have advanced our understanding of animal flight considerably, primarily through kinematic and aerodynamic studies of steady flight. However, manoeuvring flight is likely to be much more crucial for an animal's survival as this is the principal component of, for example, prey pursuit, predator avoidance or negotiating an obstacle. Several studies have investigated manoeuvring flight but then focused on kinematics with subsequent modelling of the aerodynamics based on kinematics (e.g. [1–7]). Thus, our understanding of the aerodynamics of manoeuvring flight is primarily based on inferred measurements, while direct measurements are lacking.

To execute a manoeuvre in flight, e.g. a sideways turn, an animal needs to generate bilateral asymmetries with the wings and/or tail, either through differences in magnitude of force or in the timing of forces within the wingbeat. These asymmetries then result in a change in the attitude of the body and the flight trajectory. The change in trajectory needs to be achieved through a reorientation of the net aerodynamic force; for example, by banking the body, as has been shown in several animals (e.g. [5–9]). Changes of body attitude, on the other hand, can be achieved through asymmetries either in aerodynamic forces or in inertial force, as described for pigeons (Columba livia) based on aerodynamics inferred from kinematics [6,7]. In this study, we have focused on the aerodynamic part of sideways turns in animals using bats as models.

We studied the aerodynamics and kinematics of two brown long-eared bats (Plecotus auritus) flying at a moderate flight speed in a wind tunnel while performing controlled sideways manoeuvres. The brown long-eared bat has been the subject for studies on flight for a long time, including horizontal flapping flight [10], hovering flight [11], turning flight [12] and the aerodynamics of their large ears [13,14]. The aim of our study was to investigate a simple and non-challenging manoeuvre that represents a routine behaviour of the animals. We designed a simple stimulus in the form of a food item (mealworm) on a sting attached to a movable slider that, when translated laterally, made it possible to induce the bats to pursue the target and thereby execute a controlled, voluntary and repeatable sideways manoeuvre.

Based on prior knowledge of the aerodynamics of bats and other animals we made the following predictions.

• (i)Since it has been shown previously that the majority of the forces are generated during the downstroke at medium flight speeds in bats, e.g. [15–17], we expected that the bats will use the downstroke mainly to perform the manoeuvre.
• (ii)Since several previous studies on manoeuvring flight in animals have shown that they commonly roll to make a banking turn, e.g. [5–9], we expected to find that the most common way for the bats to perform the manoeuvre is to produce a difference in lift to create a roll moment that would result in a banking turn.
• (iii)We expected to see that the bats used both asymmetries in timing of forces as well as magnitude of forces, since both of these approaches would be a potential way to perform the manoeuvre.

We used high-speed stereo particle image velocimetry (PIV) to obtain quantitative measurements, with high spatial and temporal resolution, of the air flows behind the bats and combined these data with simultaneous stereo high-speed video, recording kinematics. The time-resolved aerodynamic data allowed for detailed analysis of the forces created dynamically through the wingbeat. We used the aerodynamic and kinematic data to link them together in order to understand the mechanistic basis for the execution of the manoeuvre. Our aim was to identify the fundamental and general ways in which bats perform basic manoeuvres and through these achieve a conceptual understanding of manoeuvring flight in animals in general.

2. Material and methods

2.1. The brown long-eared bat

The brown long-eared bat (P. auritus) is a common European species. It is insectivorous and primarily uses a ‘gleaning’ hunting strategy, i.e. it picks its prey off leaves and tree trunks in flight. We chose this species because it can easily be trained to fly in a wind tunnel and, owing to the gleaning behaviour, encouraged to follow and pick a moving prey. See Experimental set-up for how we used this behaviour.

We used two individuals, both males, for our experiments that were trained in the wind tunnel for two months prior to the study. Both bats were flown at V_∞ = 2.5 m s⁻¹ for all measurements. This flight speed was chosen firstly because we wanted to investigate a slow flight speed at which the bats commonly forage in the wild and secondly because the bats appeared to fly comfortably in the wind tunnel at this speed.

Morphological details of the two bats are shown in table 1.

Table 1.

Morphological details of the two bats used in the experiments. AR, aspect ratio.

	mass (g)	span (m)	wing area (m2)	mean chord (m)	AR	wing loading N (m−2)
Bat 1	9.3	0.251	0.0097	0.039	6.4	9.41
Bat 2	9.6	0.242	0.0095	0.039	6.2	9.91

2.2. Experimental set-up

2.2.1. The lateral movement stimuli

To induce a controlled and repeatable lateral manoeuvre by the bats we constructed a device that would let them follow a moving prey. The device consisted of a thin (2 mm) carbon fibre sting (320 mm long) put on a slider (width/spanwise: 265 mm, depth/streamwise: 40 mm, height/vertical: 10 mm) that was controlled by means of a metal push rod (2 mm thick) extending outside the test section. This allowed the operator to control the movement of the sting and the timing of the onset and end of the movement. At the tip of the sting, we attached a mealworm with a rubber band. When the bat approached the prey we manually translated the prey sideways (randomly alternating between left and right between trials) by means of the push rod and the bat followed the mealworm, performing a gentle and controlled sideways manoeuvre. This simple set-up worked very well and served the purpose both of positioning the bats in the required location for measurements within the test section and making the bats perform the type of basic manoeuvre that we intended to study.

2.2.2. High-speed filming: set-up and processing

For kinematic measurements, we filmed the bats with two synchronized HighSpeedStar3 cameras (resolution 1024 × 1024 pixels; LaVision, Göttingen, Germany), one looking straight from above the animal and one obliquely from above and in front of the animal. The cameras operated at 640 Hz and were controlled with DaVis7 (LaVision, Göttingen, Germany); each recording was 1066 frames long, or 1.66 s. Cameras were manually triggered by the operator when the bat approached the sting holding the mealworm. The same trigger signal also triggered the PIV system (see below). We calibrated the cameras using a Matlab software developed by Dr Simon Walker (University of Leeds, UK), which uses a calibration plate with dots on a grid photographed multiple times, approximately 30 frames, at different locations and orientations within the measurement volume and then uses direct linear transform to calculate camera coefficients.

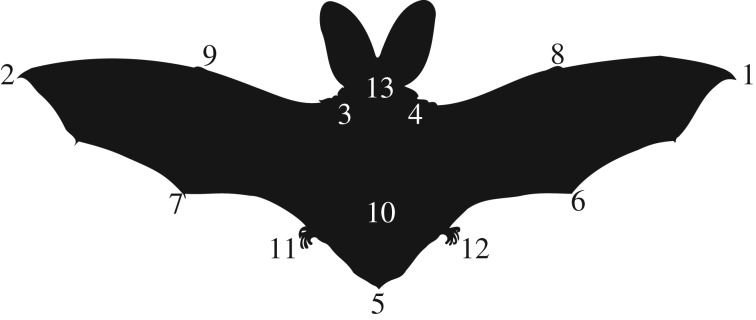
From the recorded sequences, we made a selection based on the following criteria: (i) the bat should be in the correct location for both kinematic camera views and for the PIV cameras to capture the complete wake throughout the manoeuvre, (ii) the bat followed the prey but did not touch it, and (iii) the bat was performing a smooth manoeuvre without interruptions or unsteadiness throughout the complete motion. We then manually digitized 13 points on the body, tail and wings in both camera views based on natural landmarks (figure 1). Using the calibration described above, we converted the points from two dimensions to three dimensions and calculated kinematic parameters (see below).

Figure 1.

Illustration of the digitized points for kinematic analysis. 1: right wingtip, 2: left wingtip, 3: left shoulder, 4: right shoulder, 5: tail tip, 6: tip of right hand fifth digit, 7: tip of left hand fifth digit, 8: base of right side thumb, 9: base of left side thumb, 10: base of tail, 11: centre of left foot, 12: centre of right foot, 13: centre of head.

2.2.3. Particle image velocimetry: set-up and processing

For the PIV measurements, we used a two-camera stereo set-up with transverse laser sheet (approx. 2.5–3 mm thick) positioned approximately 200 mm downstream of the animals (which corresponds to about one wavelength of the wingbeat cycle). We used two Imager pro HS 4 M cameras (resolution: 2016 × 2016 pixels; LaVision, Göttingen, Germany) fitted with Nikkor 50 mm 1.4D lenses and looking obliquely from above and behind the measurement area. The difference in viewing angles of the two cameras towards the measurement area was 33° laterally to create the stereo view. A transverse light sheet was generated with a LDY304PIV double pulsed laser (Litron Lasers Ltd, Rugby, UK) operating at f = 640 Hz and at dt = 150 µm (time between the image pairs used for vector calculations). This dt was set at a relatively short duration for this speed in order to facilitate the use of a thin sheet that distinctly defines the PIV plane. Pixel displacement measured on the wake at mid-downstroke was approximately: x: 1.7 pixels, y: 1.7 pixels, z: 2.3 pixels (x: spanwise, y: vertical and z: streamwise). Cameras were triggered manually by the operator with the same trigger signal that triggered the kinematics cameras. Each recording was 917 frames long or 1.43 s and our measurement area (the overlapping field of view of the two cameras) was approximately 450 × 450 mm to allow for the lateral movement of the bat. The air was seeded with di-ethyl-hexyl-sebacat particles (approx. 1 µm) dispensed with a compressed air aerosol generator (LaVision). Cameras were calibrated by following the calibration routine in DaVis 8 (LaVison) and using a 200 × 200 mm dual-plane calibration plate (LaVision, type 22). The calibration was finalized by running the self-calibration routine in DaVis 8.

We pre-processed raw images by ‘subtract sliding minimum’ over 3 pixels. The images were then stereo processed using the stereo cross-correlation graphics processing unit routine with decreasing correlation box size from 64 × 64 pixels with 50% overlap for the first pass to 24 × 24 pixels and 50% overlap for the final (fifth) pass resulting in a vector spacing of 0.0033 m. Between passes, we used a median filter to remove erroneous vectors that were more than two times the RMS of neighbouring vectors and applied smoothing (3 × 3 pixels). This did not smooth the final vectors but only improved the refining of the vectors for the next pass in the correlation algorithm. For the final pass, we used the high-accuracy mode. The calculated vector fields then required no post-processing apart from a 3 × 3 smoothing.

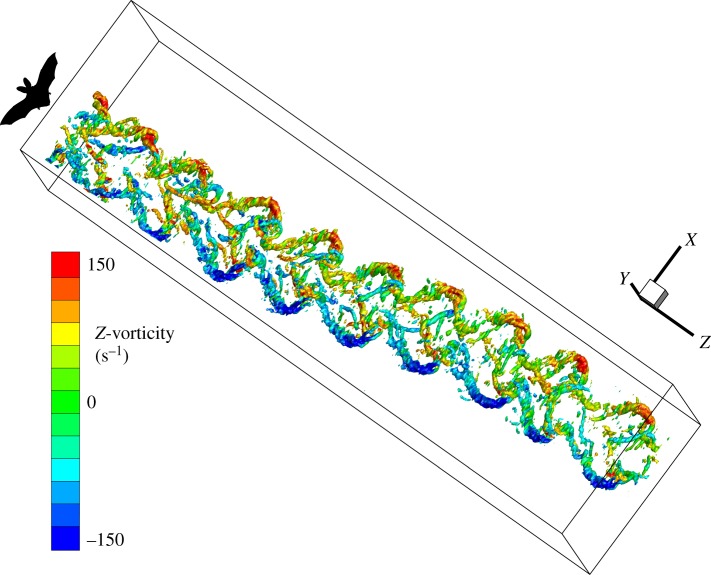
For wake visualizations, we constructed three-dimensional matrices of stacked vector fields displaced by a distance corresponding to the flight speed. This resulted in a total vector spacing of 0.0033 m in-plane (or spacing of unique vectors of 0.0066 m because of the 50% overlap) and 0.0039 m out-of-plane (V_∞/f = 2.5/640). The matrices were imported into Tecplot 360 (Tecplot, Inc.), which we used to calculate the Q-criterion (e.g. [18]) for vortex identification and to plot three-dimensional iso-surfaces (figure 2).

Figure 2.

Example sequence of a manoeuvre. The wake is illustrated as the iso-surface of the Q-criterion at Q = 0.002 coloured by Z-vorticity. In this example sequence, the bat makes a leftward turn of about 160 mm lateral displacement over a forward flight distance of approximately 1.8 m.

2.3. Kinematic analysis

2.3.1. Wing kinematics

We analysed the following kinematic parameters for the two separate wings that we considered most likely to be involved in generating the asymmetrical forces for the manoeuvre. (i) Amplitude (distance from top to bottom of the vertical excursion of the wingtip trajectory), (ii) angle of attack (the angle the wing makes towards the horizon at mid-wing, points 8–6 and 9–7), and (iii) wing length (the distance between the shoulder joint and the wing tip). The effective angle of attack, including the flapping motion of the wing, is presented in the electronic supplementary material, S2. See figure 1 for illustration of the geometry and the digitized points that were used.

2.3.2. Tail kinematics

The brown long-eared bat has a relatively large tail membrane connecting the feet and tail and is able to control the shape of the tail to a large degree. The tail has been shown previously to significantly influence flight control, in particular through ventral movement of the feet [19]. Therefore, we predicted that the tail plays a role in executing the manoeuvres with the biggest effect from deflection of the tail by up and down movement of the legs and feet. We calculated the angle between the horizontal and the line between the tail base and feet as a measure of angle of attack of the tail on the left and right side separately (points 10–11 and 10–12; figure 1).

2.3.3. Body kinematics: roll, yaw and pitch

We calculated the body rotation in all three axes: (i) roll (rotation around the longitudinal body axis), calculated from the line between the two shoulder joints (points 3 and 4), (ii) yaw (rotation around the vertical axis), calculated from the line between the head and the tail base (points 10 and 13), and (iii) pitch (rotation around the spanwise axis), calculated from the line between the head and the halfway point between the shoulders (point 10 and points 3–4).

2.4. Aerodynamic analysis

2.4.1. Lift

The instantaneous lift (for each frame) was calculated as

2.1

where ρ is air density (standard 1.225 kg m⁻³ was used), V_∞ is the flight speed, ω_z is the out-of-plane (z-direction) vorticity at each vector location, x is spanwise, y is vertical and is the spanwise distance from the centre of the body to the corresponding vector location. The centre of the wake system was manually pinpointed for each frame based on wake features, primarily wingtip and wing root vortices. The centre point was then used as the divider between left and right and equation (2.1) was used to calculate lift for the left and right wing separately.

2.4.2. Thrust and drag

Thrust and drag were calculated from the accelerations and decelerations in the wake behind the right and left wing separately. For this, we manually digitized the position of the wingtip vortex in each frame and used the velocities within a box around this position from the body centreline to outboard of the complete wingtip vortex and above and below the wing to include the full wake of each wing. From the velocities, we calculated thrust and drag as

2.2

where V_z is the local velocities in the wake. To clarify, this is the mass flow rate, multiplied by the difference in the velocities in the wake and the freestream flow, ΔV = V_z − V_∞, over the complete area of interest (A) behind each wing. If V_z is slower than V_∞, i.e. V_z − V_∞ < 0, this represents drag, and if V_z − V_∞ > 0 it represents thrust.

2.4.3. Quantifying asymmetries

To facilitate analysis and presentation of the results we divided the manoeuvre into three different phases. (i) Initiation of the manoeuvre: the bat has registered that the prey has started to move and responds by altering the kinematics to follow it. (ii) Lateral displacement: the bat is moving sideways to track the prey. (iii) Termination of the manoeuvre: the bat has registered that the prey has stopped moving and is now terminating the lateral displacement, resuming a stable position in front of the prey again.

For each of the wingbeats involved in a particular phase, we extracted the thrust/drag or lift (depending on the mechanism used; see below) over 10 frames around the peak in force generation. Using half the wing length as proxy for the mean moment arm we used the thrust/drag or lift measurements to make an estimate of the mean moment around either the yaw (if thrust/drag) or roll axis (if lift) during the force peak for both wings. From the moments of both wings, we calculated the net moment, giving us a measure of the ‘strength’ of the manoeuvre. We used mN as the unit for force and m as the unit for length, so the unit for our moment is mN·m (millinewton metre).

3. Results

In total, we analysed 10 sequences (approx. 6800 PIV frames and 13600 high-speed video frames) with manoeuvring behaviour from two individuals, seven for individual 1 and three for individual 2.

The lateral translation of the prey was on average 107 ± 9.7 mm and the duration of the motion was 0.61 ± 0.14 s, resulting in an average lateral velocity of 0.18 ± 0.04 m s⁻¹. With a flight speed of 2.5 m s⁻¹, this corresponded to only 4° change in heading direction, resulting in a shallow turn as intended. The bats were steady in the streamwise direction throughout the manoeuvre, as can be seen in the supplementary example video. A two-dimensional top-down plot of the trajectories of the bats and prey is presented in the electronic supplementary material, figure S1. The bats typically approached the prey in level flight and maintained altitude throughout the manoeuvre with a small variation of approximately ±10 mm. The average lift calculated from the wake accounted for on average 83 ± 8.6% of the weight of the animals.

The bat's reaction time, i.e. the time from the initial prey movement to bat response—when the bat starts moving laterally with the prey—was on average 0.136 ± 0.034 s. The bats typically ‘caught up’ with the prey towards the final third of prey movement, on average 0.43 ± 0.13 s into the translation.

Over the complete manoeuvre, from stable forward flight over initiation, displacement and termination of the manoeuvre back to stable forward flight, we found general wake elements: wingtip vortices, root vortices and reversed vortex loops typical for bat flight as shown in previous studies (e.g. [14,20–25]). The overall structure and shape of the wake throughout a complete sideways manoeuvre is illustrated in figure 2. Here, the bat makes a leftward turn of about 160 mm lateral displacement over a forward flight distance of approximately 1.8 m. The first two wingbeats are symmetrical before the bat starts turning, followed by a single distinctly asymmetrical wingbeat, which represents the start of the manoeuvre. The bat then moves laterally over three wingbeats and then stabilizes within a single wingbeat after which it resumes symmetrical wingbeats.

Below follows a characterizing account of the kinematics and aerodynamics of the three manoeuvring phases: initiation, displacement and termination. To illustrate the results, we refer to figures that show example sequences of the different manoeuvring approaches used by the bats. We found no apparent difference between the two individuals, so the data were pooled and treated equally.

3.1. Initiation of the manoeuvre

The bats initiate the manoeuvre during either the downstroke or the upstroke.

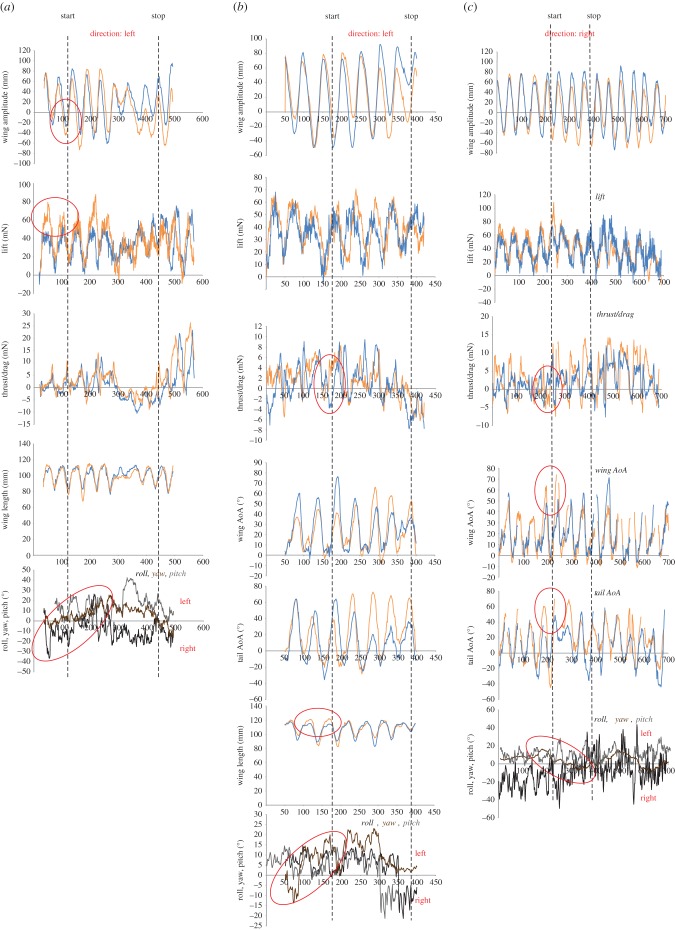
In a downstroke-initiated manoeuvre the bat performs two main alternations to the kinematics of the downstroke. (i) Larger amplitude and/or longer wing length on the opposite wing to the direction of the following manoeuvre (hereafter called ‘outward’) to generate extra lift, yielding a primarily rolling turn (figure 3a). The average roll moment (n = 3) during the force peak was 1.31 ± 1.23 mN·m (mean ± s.d.). (ii) Longer wing length and higher angle of attack on the outward wing to generate extra thrust in combination with increased angle of attack during the following upstroke on the inward wing and inward part of the tail to generate extra drag, yielding a yaw-dominated turn (figure 3b). The average yaw moment (n = 2) during the force peak was 0.28 ± 0.030 mN·m.

Figure 3.

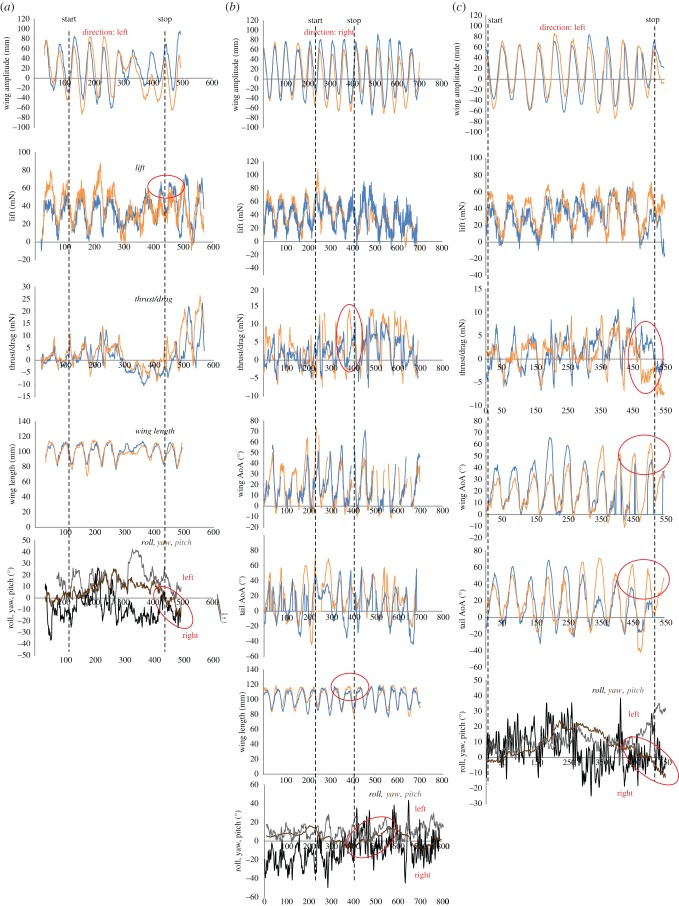
Examples of initiation phase of the manoeuvre. Orange lines show right side and blue lines show left side. (a) Downstroke with asymmetries in lift, causing a rolling motion. Differences in how deep the wings are beaten, the difference in lift and the change in roll are encircled. Direction: Left. Bat 2. Net roll moment during peak force: 1.23 mN·m. (b) Downstroke with asymmetries in thrust and drag, causing a yawing motion. Differences in thrust/drag, wing length and the change in yaw are encircled. Direction: Left. Bat 1. Net yaw moment during peak force: 0.31 mN·m. (c) Upstroke with asymmetries in thrust and drag, causing a yawing motion. Differences in thrust/drag, wing and tail angle of attack (AoA) and the change in yaw are encircled. Direction: Right. Bat 1. Net yaw moment during peak force: 0.25 mN·m.

In an upstroke-initiated manoeuvre the bats had a higher angle of attack on the wing on the same side as the direction of the following manoeuvre (hereafter referred to as ‘inward’) and/or inward part of the tail by supressing the inward foot to generate drag on one side while thrust is generated on the other, yielding a yaw-dominated turn (figure 3c). The average yaw moment (n = 4) during the force peak was 0.26 ± 0.091 mN·m.

3.2. The lateral displacement

Similar to the initiation of the manoeuvre, the displacement is performed either through upstroke or downstroke asymmetries.

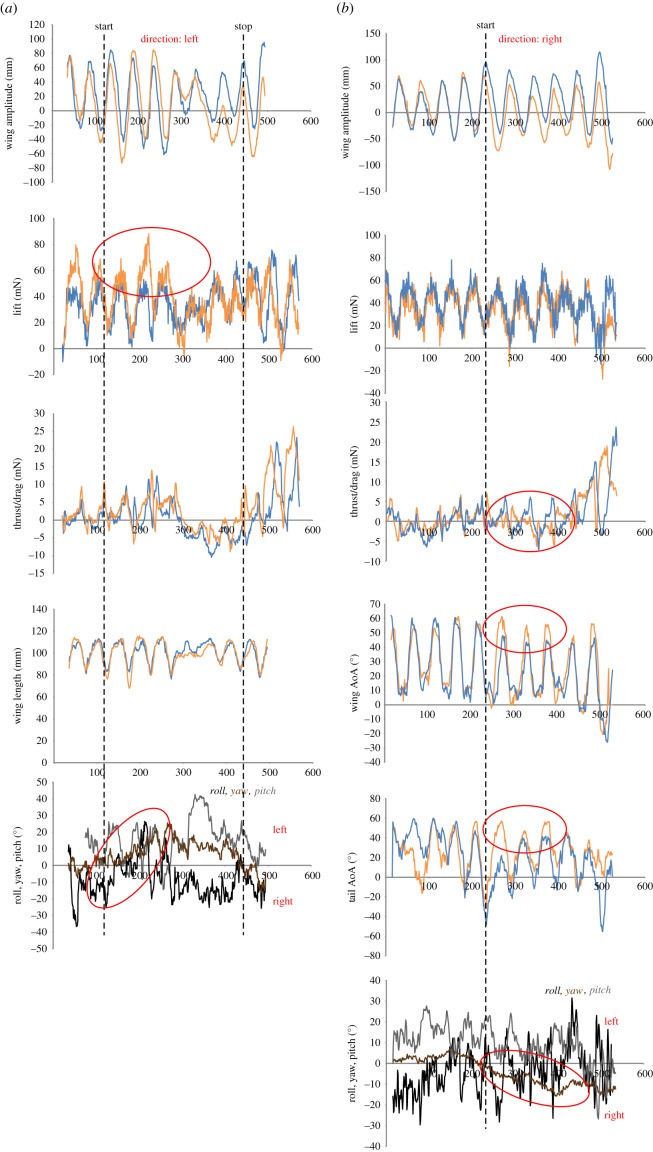
When the downstroke is the active agent for the lateral movement it is maintained through asymmetric amplitude and/or wing length to generate extra lift on the outward wing resulting in a rolling turn (figure 4a), similar to type i in the initiation phase. The average roll moment (n = 2) during the force peak was 1.44 ± 0.53 mN·m.

Figure 4.

Examples of the displacement phase of the manoeuvre. Orange lines show right side and blue lines show left side. (a) Downstroke with asymmetries in lift, causing a rolling motion. Differences in lift and the change in roll are encircled. Direction: Left. Bat 2. Net roll moment during peak force: 1.06 mN·m. (b) Upstroke with asymmetries in thrust and drag, causing a yawing motion. Differences in thrust/drag, wing and tail angle of attack (AoA) and the change in yaw are encircled. Direction: Right. Bat 2. Net yaw moment during peak force: 0.29 mN·m.

When the upstroke is the active agent, this is likewise similar to the initiation phase, with a high angle of attack on the inward wing and inward part of the tail to generate drag, while thrust is generated on the outward side, resulting in a yawing turn (figure 4b). The average yaw moment (n = 8) was 0.18 ± 0.056 mN·m. Eight of the 10 sequences are ‘upstroke sequences’ and only two are ‘downstroke sequences’. Out of these, bat 1 did six upstroke sequences and one downstroke sequence and bat 2 did two upstroke sequences and one downstroke sequence.

3.3. Termination of the manoeuvre

In total, eight sequences contained a stabilization phase, whereas in the two remaining sequences the bats did the initiation of the manoeuvre, followed the feeder through the displacement, but instead of stabilizing in front of the feeder at the end of the translation the bats continued the sideways motion laterally passing and moving away from the feeder. In the sequences containing stabilization, the bats used the downstroke in three instances and the upstroke in five instances. In the downstroke-based stabilization, the bats either used asymmetrical lift, providing a roll motion (figure 5a), or thrust/drag, resulting in a yaw motion (figure 5b). The roll moment (n = 1) during the force peak in the lift-based stabilization was 0.82 mN·m and the average yaw moment (n = 2) during the force peak in the thrust/drag-based stabilization was 0.54 ± 0.22 mN·m.

Figure 5.

Examples of the termination phase of the manoeuvre. Orange lines show right side and blue lines show left side. (a) Downstroke with asymmetries in lift, causing a rolling motion. Differences in lift and the change in roll are encircled. Direction: Left. Bat 2. Net roll moment during peak force: 0.82 mN·m. (b) Downstroke with asymmetries in thrust and drag, causing a yawing motion. Differences in thrust/drag, wing length and the change in yaw are encircled. Direction: Right. Bat 1. Net yaw moment during peak force: 0.69 mN·m. (c) Upstroke with asymmetries in thrust and drag, causing a yawing motion. Differences in thrust/drag, wing and tail angle of attack (AoA) and the change in yaw are encircled. Direction: Left. Bat 1. Net yaw moment during peak force: 0.30 mN·m.

The upstroke-based stabilizations were all performed using asymmetrical thrust/drag, resulting in yaw (figure 5c). The average yaw moment (n = 5) during the force peak was 0.36 ± 0.20 mN·m.

4. Discussion

We made three predictions prior to our study of how the bats would most probably perform the manoeuvre:

• (i) using primarily downstroke as the active agent—the bats did use the downstroke, but the most common way was in fact to use the upstroke;

• (ii) using asymmetries in lift rather than drag and thrust—the bats did perform rolling turns using lift asymmetries, but the most common way was to perform a yawing turn using thrust and drag asymmetries;

• (iii) using both asymmetries in timing and magnitude of forces—the bats did, in fact, primarily use differences in magnitude of forces.

4.1. Three main modes of creating asymmetries

To generalize the different ways in which the bats executed the manoeuvre, three main modes can be discerned: (i) lift asymmetries during the downstroke, (ii) thrust/drag asymmetries during upstroke, and (iii) thrust/drag asymmetries during downstroke. Each of these will be discussed below. Somewhat surprisingly, the most commonly used method was thrust/drag asymmetries during upstroke, which appeared at some phase of the manoeuvre in seven out of 10 sequences. Lift asymmetries during downstroke and thrust/drag asymmetries during downstroke were used in three sequences each.

Contrary to our predictions, the bats did not use asymmetries in timing of forces to any large degree, but rather asymmetries in magnitude of forces. Adjusting the timing of forces, rather than the magnitude of them, may appear as a relatively ‘simple’ way to generate lateral asymmetries in flight, since it would not involve any difference in the magnitude of the force generated. However, it may well be that it is, from a mechanistic point of view, easier to generate extra forces rather than changing the timing. In this way the main flight muscles can continue to beat in synchrony and only small changes in the wingbeat kinematics are required, e.g. wing and tail angle of attack, wing length and amplitude as observed in this study.

4.1.1. Lift during downstroke

Generating extra lift on the outward wing during the downstroke to make a rolling turn was the type of manoeuvre that we predicted to be the most common. However, it turns out that, of the 10 sequences analysed and through the three different phases (i.e. 30 instances in total), the bats only used this method in six cases. To achieve extra lift the bats beat the outward wing deeper during the downstroke and/or extended the outward wing more during the downstroke compared with the inward wing. Both of these actions are rather subtle, which is to be expected for such a small manoeuvre.

Performing a rolling turn is an effective way of turning quickly, because the large lift vector counteracting gravity is suddenly tilted laterally and used to create the sideways force. This type of turn is therefore expected for fast manoeuvres. A yawing turn is slower, since the forces driving the manoeuvre need to be created and not just reoriented, but a yaw turn conversely implies a more precise and easier to control manoeuvre. It can be compared to a pilot flying an aircraft and making small yaw adjustments to the flight path by using the rudder rather than rolling using the ailerons [26]. The yaw turn is thus expected for smaller manoeuvres like those performed by our bats and may explain the dominance of yawing turns in our dataset. Consequently, we would expect to see an increase in lift-based rolling turns with increasing turning speed.

4.1.2. Drag and thrust during upstroke

The most commonly used method to create asymmetries across all sequences and phases was to generate extra drag on the inward wing and side of the tail and thrust on the outward side to create a yawing turn (20 of 30 cases). This is a somewhat surprising finding since the upstroke at this flight speed is relatively inactive compared with the downstroke. However, other bat species are known to generate a moderate amount of thrust during the upstroke (e.g. [10,17]), but then only at higher speeds (above 5 m s⁻¹). In light of this finding, it appears to be a reasonable way to generate the required asymmetries. Using a part of the wingstroke which is otherwise largely ‘unused’ to generate the subtle lateral asymmetries in forces required to perform the manoeuvre may be an efficient strategy. Iriarte-Díaz & Swartz [9] found that fruit bats also use the upstroke to initiate a turn. However, in those bats, it resulted in a banked turn, which suggests that they do not use the same mechanism to generate the asymmetries, but that using the upstroke is not restricted to brown long-eared bats.

The drag created during the manoeuvre is most probably an effect of the increased angle of attack of the wings and tail on the inward side—effectively braking—but the origin of the thrust is less obvious. It may be that the bats produce thrust at the end of the upstroke, resulting in a reversed vortex loop, as has been shown in previous studies (e.g. [15,24,25]). Reversed vortex loops are found at the end of the upstroke also in the wake of our bats. However, it is difficult to determine if this is the source of thrust since the reversed vortex loops appear so briefly and require a very precise account for the timing in the force trace in relation to the wingbeat cycle, which was not possible to achieve with the current data.

4.1.3. Thrust during downstroke

Generating thrust on the outward wing to perform a yawing turn was observed in only four instances across all sequences and phases and only during the initiation and termination phases. The increased thrust appears to be achieved by extending the outward wing to a small degree more than the inward wing during the downstroke, which still results in a rather large difference in thrust and drag.

4.2. Choice of mode

Bats appear to be highly flexible when it comes to choosing the different ways in which to generate the required force asymmetries to perform a sideways manoeuvre. They appear to choose the mode based on the phase within the wingbeat at the time when they detect the motion of the stimulus. However, whether this is true or there is another reason for the choice of the mode is impossible to determine with the current data. We searched for a correlation between the onset of the translational motion of the prey and which wingbeat phase was used for initiation by the bat but did not find such a correlation. To address this properly, a more directed study with less comprehensive aerodynamic and kinematic analysis should be performed in order to make it possible to increase the number of trails and obtain a larger dataset for analysis of the timing.

Bats are not only very flexible at the initiation of a manoeuvre, but also change between the different modes within a manoeuvre. It was in fact only in two sequences that the bat chose the same mode through initiation, displacement and termination. In all other sequences, the bats changed modes throughout the manoeuvre. This indicates a high level of behavioural flexibility, which may represent a robust strategy that results in an ability to cope with a wide range of situations. It is also inherently logical that bats have this flexibility since otherwise reaction speed would be constrained by the wingbeat cycle, which is relatively slow compared with the potential neuro-muscular reaction time. However, based on this limited dataset with a rather focused aim to investigate fundamental properties of manoeuvring behaviours it is not possible to draw any firm conclusions regarding this flexibility.

During the training period leading up to the flight sessions when the measurements were made, the bats improved their technique for flying in the tunnel and for following the prey. It was our impression, however, that the bats had arrived at a preferred way of executing the manoeuvre well before the measurement period started, and thus we do not believe that the bats changed their behaviour during the measurement period due to learning.

4.3. Reaction times

The time that elapsed between the start of the prey movement and when the bats started to move in the direction of the prey was on average 136 ms. This can be compared with the average of 82–178 ms (open air and close to the surface of water, respectively) measured as the behavioural reaction time for Daubenton's bat (Myotis daubentonii) during prey pursuit [27]. The average reaction times for our bats are longer than the minimum open air reaction times of the Daubenton's bat, but the two reaction times determined for the Daubenton's bat brackets that of our bats, so they are roughly similar. It is also important to note that we do not know the motivational level of the bats in our study and cannot assume that they are trying to react to the movement by the prey as fast as their reaction time allows them to. The fastest reaction time (94 ms) was half of the slowest (188 ms) in our data, which suggests that the bats did not always attempt to follow the prey as fast as they could. The aim of this study was not to study the maximum performance of the bats, but rather a routine behaviour where the moving prey was only used as a stimulus in order to elicit the desired manoeuvre.

4.4. Force estimates

We find that in cases where the bats performed a yawing turn by means of asymmetries in trust and drag the average peak yaw moment was fairly similar throughout the different stages in the manoeuvre and different modes, roughly around 0.3 mN·m. In lift-based rolling turns the moment was generally stronger, roughly around 1.2 mN·m. This is in line with the reasoning previously stated in §4.1.1 and in [20] that tilting the lift vector typically generates a faster turn, while creating asymmetries in thrust and drag typically results in a slower turn.

The approach we have taken in the analysis is to quantify the total forces on the left and right side of the animal—lift, drag and thrust. In this approach, we quantify the forces by integrating over the complete area behind the left and right side of the animal, thereby circumventing the need to identify individual wake elements and instead deriving the net sum of the forces generated by the entire wake. These estimates of the complete forces on the two sides of the animal can then be directly related to the change in attitude of the flying animal (roll, yaw and pitch). This approach results in a robust estimate since it does not rely on successfully identifying individual wake structures. As the level of detail in the reconstructed wakes has increased, an increasing number of small structures have been revealed that make the main wake structures, wingtip, root and tail vortices, less obvious. Therefore, accounting for the complete vorticity in the wake is potentially a better approach for accurate force estimates. In this study, we measured the forces downstream from the animals and it is important to realize that the wake will have deformed and developed between the time of the creation of forces on the wing and the time we capture it in the measurement plane (e.g. [28]). We also rely on the assumption that the type of quasi-steady analysis that we do when calculating forces is a sufficient approximation of the true forces generated. As such, the forces we measure and calculate are not a perfect representation of the forces that acted on the animal. The average weight support for the 10 sequences was 83%, suggesting that the method fails to capture the complete lift force, but it may also be that the bats typically did a slight descent towards the prey, even if it is not apparent in the trajectories. In this study, where the focus was on the asymmetries between forces, rather than the absolute values, the forces measured in the wake most probably are a sufficient approximation of the true forces.

5. Concluding remarks

The technological development of flow visualizations during the last few years is evident from the tremendous increase in the level of detail of the representations of wakes in recent literature (e.g. [29–32]). Owing to the increase in temporal and spatial resolution of modern PIV systems it is now possible to capture the dynamics of wakes to a level where the subtle asymmetries generated during manoeuvres can also be detected.

Despite the superficially simple nature of the shallow sideways turn, we find a variety of different ways that the bats perform the manoeuvre. We also find that none of our predictions was entirely correct. We can conclude that manoeuvring, even in its simplest form, is complex and, owing to the subtleness of the asymmetries in forces created, challenging to analyse. We were, however, able to identify patterns in the kinematics and aerodynamics and to explain the connection between them, which gives us a good basis for more in-depth studies of manoeuvring flight. Given the great flexibility of the bat wing it is perhaps not surprising that we find such a large pallet of possible solutions to manoeuvring. Whether birds and insects show similar behaviours when executing manoeuvres remains to be seen as we move on to studying these taxa under similar experimental conditions. Future directions will include both other taxa and exploration of other scenarios, e.g. by changing the flight speed, the lateral speed of the prey (and hence the speed and sharpness of the turning manoeuvre) and the direction of the prey movement to also include vertical movements, to investigate how execution of manoeuvres changes. Furthermore, future investigations will also include a directed study with more trials and less comprehensive aerodynamic analysis to investigate what affects the bats' decision when choosing which one of the different ways of executing the manoeuvre to use. This could include, for example, the distance between bat and prey, centre-of-mass movement (speed/acceleration), wingbeat phase, head orientation and body pitch.

Ethics

The study was performed in accordance with approved experimental guidelines. Procedures were approved by the Malmö-Lund animal ethics committee, Sweden (M 33–13).

Data accessibility

Raw data in the form of data files containing the three-dimensional velocity vectors from the PIV measurements and Excel files containing three-dimensional coordinates from the kinematics are deposited in the Dryad Digital Repository [33].

Authors' contributions

P.H. was the principal investigator and planned the study. L.J. trained the bats. P.H. and L.J performed the experiments. P.H. did the PIV processing and analysis. P.H. conducted the digitization of the kinematic data with help from two students (credited under acknowledgements) and did the kinematic analysis. P.H. discussed the results with L.J and A.H. P.H. drafted the manuscript. L.J and A.H. gave comments and made revisions to the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by an infrastructure grant from Lund University (PIV equipment) to A.H., and the Swedish Research Council (www.vr.se) to P.H. (621-2013-4838) and A.H. (621-2012-3585, 621-2016-03625), by the Crafoord Foundation (www.crafoord.se) to P.H. (20140698), the Danish Council for independent research (www.ufm.dk) and Centre for Biorobotics to L.J.