Pillar versus dimple patterned surfaces for wettability and adhesion with varying scales

Abstract

Inspired by biological topographical surfaces, micropatterned elastomeric surfaces with square pillars and dimples of different geometry scales were fabricated. Their wettability and adhesion properties with various liquids were systematically investigated and compared with flat surfaces. Interesting results were obtained in the case of silicone oil (the toe-pad-like wetting case) in that the scale-dependent wettability and adhesion performed inversely for pillars and dimples. Micropillars significantly enhanced the surface wettability with a geometry scale dependence, whereas the dimples suppressed the wettability independent of the geometry scale. The adhesion force of the micropillars increased with an increase of the geometry scale. However, in the case of the micro-dimples, the adhesion force obviously decreased with an increase of the geometry scale. This behaviour was attributed to the fact that pillars are ‘open’ to oil but dimples are ‘close’ to oil, presenting different orientations to the solid–liquid interface.

1. Introduction

Recent studies on natural organisms have revealed that many of the remarkable adhesive properties of the surface epithelium can be achieved by evolved micro- and nanostructures. The most widely studied and well-understood property is that of the adhesive structure on the toe pads of geckos [1–3], which comprise hundreds of thousands of micro keratinous hairs (called setae), which then branches into hundreds of even finer hairs (called spatula) [4–7]. With these hierarchically organized structures, the toe pads of geckos can achieve intimate contact with the different substrate and achieve a high adhesive strength via the interaction of van der Waals forces.

Apart from the dry adhesion of geckos, there are many fascinating additional examples of biological models that demonstrate strong adhesion with a variety of surfaces under wet conditions. Amphibians such as tree frogs, torrent frogs, and newts can attach to and climb along wet substrates without slipping or falling off [8–12]. An examination of their toe pads reveals that their epidermises are usually decorated with a polygonal micro-structure of epidermal cells separated by mucus-filled channels [13–15]. The results of numerous experimental investigations suggest that these specialized polygonal patterns allow the toe pads to expel redundant fluid out of the contact area and into the space between the pad epidermis and the substrate to achieve a ‘close contact’ situation (called draining effect). Subsequently, a boundary friction occurs when a shear load is applied [9,16–18]. Apart from the polygonal channels of wet toe pads, there is another functional structure for wet adhesion that is observed in nature. A cup-shaped sucker is used by octopuses to move across and adhere to the sea floor. This sucker is muscular-hydrostat which can be controlled by the octopus' muscles to flex, expand and contract to achieve attachment and detachment events [19,20]. In general, the aforementioned two different biological models can both achieve a reliable attachment under wet condition.

Inspired by these findings, much effort has been direct to the study of synthetic micropatterned surfaces to mimic the extraordinary cases of adhesion observed in certain biological organisms. Varenberg and Gorb performed a pioneering study on tree-frog like micropatterned polymer surfaces [21]. They found that hexagonal pillars function as friction-oriented structures during wet sliding and play a positive role during attachment. Considering their secretion wetted biological pads, Drotlef et al. noted that the higher friction forces of polygonal pillar patterns favour climbing rather than a flat surface under wet conditions [22]. Huang et al. also demonstrated the superior frictional ability of polygonal pillars compared to other investigated patterns [13]. For suction microstructures, a study by Nanni et al. showed that micro-dimples allow the adhesion performance on flat surfaces and the suction strength to be tuned by their depth [23]. Recently, the sucker of an octopus which adds a bulge to the dimple was mimicked by Baik et al. The experiments showed that this configuration allows for a significant enhancement of adhesion under wet conditions [24]. By investigating these biomimetic features, although both the draining effect and the suction are demonstrated to achieve highly efficient wet attachment, the configurations of their microstructures orientate differently in a solid–liquid interface. The polygonal pillars separated by through channels are ‘open’ to liquids, whereas the discrete dimples are ‘close’ to liquids. Such an inverse orientation of structures is interesting if they are evaluated and compared in terms of their wetting ability and adhesion under the same conditions. Moreover, as indicated by Arzt et al., the scale behaves as a strong influence on the performance of the attachment of biological structures [25]. Thus, the scale effect should be considered for the performances of microstructured surfaces. However, little research has been conducted so on these important aspects in bioinspired wet adhesion systems.

In this report, quadrate pillars and dimples with varying scales were fabricated by lithography and demoulding. The wettability of micropillars and dimples were investigated with water and silicone oil and compared to the results for a flat surface. Meanwhile, the adhesive performances of pillars, dimples, and a flat surface were also studied and compared under dry, water and silicone oil conditions.

2. Material and methods

2.1. Mould preparation

The moulds for casting patterns were fabricated using conventional photolithography processing on silica glasses. The photoresist used was AZ P4620 and the covering film was 8.5 µm. An optical lithography writer (Durham, UK) was used for exposure with fields of 10 × 10 mm² and all films were subsequently developed in AZ 400 K of 1 : 4 for moulds.

2.2. Sample preparation

Polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) was mixed with a prepolymer to the cross-linker ratio of 10 : 1. For a softer surface, 10 cs dimethyl silicone oil (PMX-200, Dow Corning) was also added to the mixture (0.5 : 1 silicone oil : prepolymer). The mixture was degassed and poured onto the moulds and cured at 70°C for 12 h in a vacuum oven. After careful demolding, the elasticity modulus of the samples was determined to be 0.635 MPa and the shore hardness was 33.45 HA [26]. The surface patterns were characterized using white-light interferometry (Bruker, USA) and scanning electron microscopy (SEM; Hitachi, Japan). The SEM images of the dimples and pillars with varying scales are presented in figure 1, and the pattern geometrical parameters of length (L), space (S), height (H) and depth (D) are also listed. The scale magnification of the patterns is presented as ×1–10 and the area density for all patterns is 80%.

Figure 1.

SEM micrographs showing (a–e) pillars and (f–j) dimples with varying scales.

The values for L, S, H and D represent the length, space, height and depth of the pillars or dimples.

2.3. Wettability measurements

In this work, two liquids, deionized water, and silicone oil were employed to characterize the wettability of the patterned surfaces. For water, static contact angle (CA) measurements were performed on substrates using the sessile drop method with a volume of 3 µl. For the dimethyl silicone oil (PMX-200, 10cs, Dow Corning), because of the low surface energy (20.1 mN m⁻¹) it spreads widely on PDMS and it was, therefore, difficult to perform the static CA measurement. Hence, the wettability of the oil on the samples was investigated by the wetting/spreading area. More specifically, a 0.3 µl droplet was placed onto sample surfaces, then a digital microscope (Keyence, Japan) was used to evaluate the liquid spreading area. Each test was performed a minimum of five times.

2.4. Adhesion measurements

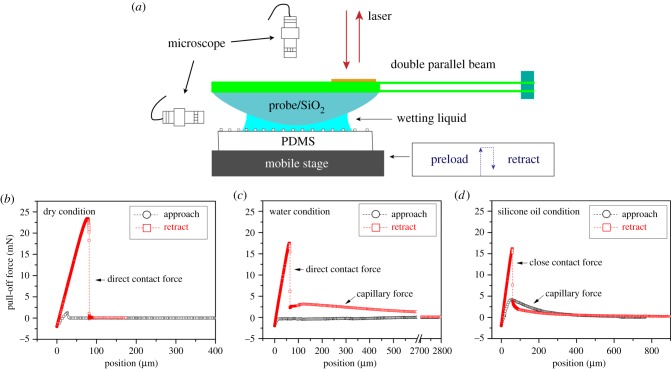
Adhesion measurements were performed using a custom-made set-up, as previously described in [27]. The PDMS samples were placed on an integrated mobile stage, while the glass probe (18.5 mm in curve radius) was mounted at the end of a cantilever with a thin film force sensor (figure 2a). The wet adhesion test process is briefly described as follows: firstly, a 3 µl liquid drop was placed on the sample using a micropipette, then the sample was positioned at the centre of the glass probe under the control of a microscope system. The samples were then brought into contact with the probe at a load of 2 mN. After a holding time of 5 s, the piezo first retracted at a speed of 1 µm s⁻¹ to perform the short-range detachment event dominated by van der Waals forces. When the mobile stage was beyond the piezo range (100 µm), a step motor was launched at a speed of 10 µm s⁻¹ to break the long-range capillary interaction. The entire adhesion measurement process was monitored using an in situ optical system. Each test was performed at least five times. Figure 2b–d shows representative force–distance row curves measured on a flat surface under dry, water and silicone oil conditions. Two distinct components, short-range direct/close contact force and long-range capillary force contribute to the wet adhesion. This is discussed in detail in our previous work [26].

Figure 2.

(a) Schematic illustration of the measurement set-up, and force–distance curves of the flat surface obtained under (b) dry conditions, (c) water conditions and (d) silicone oil conditions.

3. Results

3.1. The wettability on dimples and pillars at different scales

Figure 3 shows the static CAs of water measured on flat and patterned surfaces at five different scales (some representative droplets are shown in the electronic supplementary material, figure S1). The drop on the flat surface clearly exhibits a hydrophobic behaviour with a static CA of about 100°. The introduction of pillars and dimples both significantly enhanced the hydrophobicity of the PDMS surface, and this increased the CAs behaviour with geometry scale dependence. The highest CA was achieved at the scale of ×1 for pillars and the scale of ×3 for dimples. However, the lowest CAs for both patterns were achieved at the largest scale of ×10. Generally, the apparent CAs of patterns increased with the shrinkage of the geometry scale. Comparing the two patterns for wetting at the same scales, the dimples exhibited a higher repellence to water than the pillars.

Figure 3.

Static contact angles of water on dimples, pillars and flat surface with varying scales.

Because the silicone oil spreads easily over the PDMS presenting a nearly total wetting case (toe-pad-like wetting case [22,26]), the wettability of the samples was estimated from the liquid wetting area. Figure 4a shows a quantitative comparison of the wetting areas of the silicone oil droplet measured as a function of time on the flat and patterned surface (the scale of ×3). When the same volume of silicone oil was deposited on the sample, the wetting area of liquid was nearly the same at approximately 0.95 mm². As time elapsed, the droplet spread out over the surface and the wetting area increased. After 26 s, for the flat control, the wetting area increased nearly 404% as compared to initial area. The patterned surfaces exhibited interesting behaviours in terms of wetting: different configurations of patterns induced different effects on the spreading of the droplet (figure 4c; electronic supplementary material, video S1). Compared with the flat control, the pillars exhibited a faster increase in oil drop spreading and after 26 s the wetting area had increased by nearly 1396%. In the case of the dimples, the rate of spreading was lower. After 26 s, the wetting area only increased by approximately 71%. Figure 4b shows how the geometry scale of patterns influences the silicone oil wetting area. It is observed that the scale of the pillars had a significant influence on their wetting area. Moreover, the trend with varying scale presented a convex curve, and the highest value is obtained at ×7 scale. However, for the dimples, the wetting area was nearly constant with changes to the geometry scale. It therefore seems that the liquid spreading area is independent of the pattern scale in this case.

Figure 4.

Wettability of silicone oil on dimples, pillars and flat. (a) Wetting area of flat and patterned surfaces (the scale of ×3) versus elapsed time. (b) Wetting area of patterned surfaces with varying scales at 20 s. (c) Representative micrographs of wetting areas for flat and patterned surfaces (×3).

3.2. The adhesion on dimples and pillars at different scales

Figure 5 shows the measured adhesion forces as a function of geometry scale for the patterns under different wetting conditions. For comparison, the values obtained for a flat sample are also included. It can be determined that in the dry case (figure 5a), the adhesion force for the flat sample was about 22.9 mN, but this value was significantly reduced for the patterned samples. The patterned surfaces with dimples recorded the lowest adhesion force. A comparison of the patterns based on the geometry scale revealed that the adhesion force of the pillars increases slightly with the increase of scale, but for dimples, the scale seems to have little effect on the adhesion.

Figure 5.

Adhesion force versus geometry scale of patterns for different wetting conditions: (a) dry, (b) water and (c) silicone oil.

The adhesion behaviours of patterned surfaces with different scales in water are shown in figure 5b. In the case of the patterns with large scales (pillars at the scale of ×5, ×6, ×7 and dimples at the scale of ×6, ×7) the adhesion performances dependence on the patterns and their geometry scale are similar to the dry case. The pillars show a lower adhesion, which increases slightly with geometry scales, and the dimples show the lowest adhesion, which does not appear to change with the geometry scale. In the case of the small geometry scale, both the pillars and dimples present a very small adhesion force value of approximately 2.5 mN, and no significant difference can be observed between them. The adhesion decreased by 76% for pillars and 56% for dimples when compared with the mean value at a large geometry scale. It appears that the geometry scale effect produced a critical boundary which divides the water adhesion behaviour of patterned surfaces.

Figure 5c shows the adhesion force of patterns as a function of the geometry scale in the presence of silicone oil (toe-pad-like wetting case [22,26]). The pillar patterned surface with increasing geometry scale showed a higher adhesion force. The maximum value of 15.8 mN was found at the largest scale of ×10. By contrast, for dimples, the adhesion force strongly decreased with increasing geometry scale. The smallest scale ×1 achieved the maximum adhesion force of 15 mN. In comparison to the flat control, both the pillars and the dimples exhibited slightly superior adhesion at their optimal geometry scale. In summary, for the open configuration of pillars, a large scale favours adhesion, but for the closed configuration of dimples, the small-scale exhibited a higher adhesion under the oil condition. Interestingly, this principle coincides with the evolved structures (a combination of micro-scaled pillars and nano-scaled concave fibre-tips) of tree-frog toe pads for wet attachments [28].

4. Discussion

4.1. Pillars, dimples for scale-dependent wettability

As usual, the Cassie–Baxter mode [29,30] is employed here in an attempt to understand the large increase of the hydrophobicity on patterned surfaces with pillars and dimples (figure 3). From a previous study [18], the wettability of a surface decorated with large, simple micropatterns was commonly configured in the transition from the Wenzel to Cassie–Baxter mode. For the concave parts of the patterned surfaces, the gravitational effect of liquid is counteracted by capillarity forces (figure 6a). Some air was captured and retained in the solid–liquid interface, which can greatly improve apparent CAs. Based on this observation, it is reasonable to attribute the variation in the CAs with geometry scale to the manner in which the patterned surfaces capture air. In the case of large geometry scales, the channels (pillar patterned surface) or dimples that are located in the contact of liquid and solid are few and large, which increases the gravitational effect and lowers the capillary interaction. Hence, it is not well-suited for capturing air. However, for patterns with small geometry scales, although they possess an invariable area density, the greater the abundance and the smaller the size of the concave parts (channels, dimples) on solid–liquid interfaces, the lower the gravitational effect and the capillary interaction is enhanced. As such, a large amount of air is captured to increase the CAs, presenting the Cassie–Baxter mode. A comparison of the two patterns reveals that the dimples are associated with higher CAs than the dimples at the same scale. This is because the closed configuration of the dimples is more favourable to the capture of air than the open channels of the pillars.

Figure 6.

The influence of pillars and dimples on wettability for (a) water, (b) silicone oil.

Unlike the case of water, owing to the lower polarizability of silicone oil compared to PDMS, the oil drop spreads widely on a solid surface, exhibiting a nearly total wetting regime [31]. In comparison to the flat sample, the patterned surfaces behaved differently during spreading: the open configuration of pillars increased the wetting area, whereas the closed configuration of dimples decreased the wetting area (figure 4a,c). Microscopic observations of the advancing boundary of the oil drop were performed to gain additional insight into pattern effect. As shown in figure 6b, the advancing boundary on the flat sample is a straight line and moves together across the surface. However, considering the pillars (×3 scale), the advancing boundary line was greatly deformed and accelerated through the existing open channels. Clearly, the increased wettability associated with the pillars is a result of the capillary effect caused by the narrow, cross-linked channels. When an oil drop is deposited on the dimples (×3 scale), its expanded flow was obstructed by close dimples, and the advancing boundary line was also deformed by the shape of the dimple. These behaviours are probably attributable to the higher resisted pressure that is easily induced by the edge from the flat surface to the dimple bluffs in the onward oil following the Laplace rule, and thereby obstructs the spreading process for close dimples [32].

Moreover, as determined in figure 4b, the geometry scale can significantly influence the wetting areas of the pillars, while there is little impact observed for the dimples. In the case of the former, the wetting area with scales is a result of comprehensive effect. This is because the capillary effect is more pronounced as the cross-linked channels become narrower. However, the narrowing of channels can also restrict the volume and velocity of oil through them. Consequently, the wetting area of the pillars initially increased then decreased with the decreased geometry scale, achieving a maximum at ×7. For the dimples, the expanded wetting area is obstructed by their close bluffs. In this case, the total length of the dimple bluffs is constant, which leads to an invariable obstruction because the area density is the same for all scales. As expected, the geometry scale for the dimples is almost negligible.

4.2. Pillars, dimples for scale-dependent adhesion

Compared with flat control, the decorated patterns show a reduced tendency for adhesion in the dry case (figure 5a). The surface that is patterned with pillars exhibit a lower adhesion force, and the lowest adhesion is observed for the pattern with the dimples. In the former, this observation may be owing to the loss of actual direct contact area (figure 7a), which does not seem to be outweighed by the adhesion enhancement owing to contact splitting for flat punch tips [23,33,34]. Although concave shapes are often characterized by a suction effect for adhesion, it is not easy for the dimples to demonstrate strong adhesion to the spherical probe at a low preload in the dry case. The suggestion of losing direct contact can provide some insight into the adhesion case for the dimples (figure 7a). In addition, the results of scale effect on patterns for adhesion shows a slight increase for pillars, but little effect for dimples. It is possible that the pull-off response of the spherical probe can be influenced by the size of the pillars on the split surface but is insensitive to that of the dimples ensconced on a continuous surface under the same area density.

Figure 7.

The influence of pillars and dimples on adhesion in (a) dry, (b) water and (c) silicone oil case.

In contrast to the dry contact, the supply of water complicates the adhesion behaviour with the influence of the capillary interaction (figure 2c) and a probable thin liquid film between the probe and samples. From a global perspective on pattern adhesion (figure 5b), it can be determined that the large-scale results in a large adhesion force, while the small-scale correspondingly leads to small adhesion. To understand the origin of this behaviour, the scale effect on the wettability of the patterns should be taken into account. In the case of the large-scale, the relatively low apparent CAs of the patterned surfaces suggest a low repulsion to water drops. If the probe indents a drop for an adhesion test, the low repulsion of the surface is not able to produce sufficient resistance to facilitate water spreading. As a result, the water drop is impaled and squeezed out, and a dewetting event occurs [35,36]. In this case, the adhesion depends heavily on the direct contact force, but not on the capillary interaction between the probe and the substrate [22]. Thus, the adhesion has relatively large values and varies with the patterns and geometry scales in a similar manner to the dry condition. However, for patterns with a small geometry scale, a significant amount of air is captured which increases the repulsion to water drops. This leads to more resistance for water spreading when the drop is indented by the probe. With a comparatively small preload, the probe, cannot impale the sandwiched film to directly contact the substrate (figure 7b; electronic supplementary material, video S2). Therefore, only the capillary interaction during the detachment event contributes to the adhesion, which results in a low pull-force and insensitivity to patterns and scale effect.

The results for adhesion under silicone oil suggest that the geometry of the scale dependence of the pull-off forces behave differently for pillars and dimples. As described in the preceding section, the silicone oil spreads out onto the PDMS, approaching a total wetting case (toe-pad-like wetting case), which allows a stable sandwiched film to exist between the contact pair of probe and substrate (figure 7c) [37]. It should be noted that this sandwiched film is very thin; probably several nanometres thickness and achieves a close contact [38]. The force–displacement curve measured on the flat sample also demonstrates that not only the capillary effect but also the close contact forces contribute to wet adhesion (figure 2d). Compared to the dry and water case, such contact cases behave similarly to the case of the attachment of hydrophilic biological epidermis to a wet substrate. Referring to previous studies, the open configuration of the polygonal pillar-shaped cells (amphibian toe pads) characterize a draining effect (figure 7c), which can strengthen the close contact by expelling liquid out of the contact area via squeezing and deformation [21,22]. Under the same area density, the large deformation of pillars and a large flow of channels can produce a correspondingly large pump power for draining, which reduces the thickness of the film to achieve closer contact. Therefore, the adhesion forces associated with the pillars increase with the increase of the geometry scale and the largest value is achieved with the largest scale.

According to a previous study [24], the suction effect of closed configuration for sucker-like dimples mainly contributes to adhesion under silicone oil because oil easily enters and seals the holes (figure 7c). Regarding the measured results, it is clear that the suction effect is adversely influenced by an increase in scale. The possible reason is that as a result of the soft matrix that is used, the smaller the dimples, the more fitted contact that occurs with the rough probe surface, and the stronger the adhesive suction. This is similar to the contact splitting principle of animal seta [39]. Finally, compared to a flat control, both optimized configurations of the pillars and dimples for different scales, provide valuable insight into the requirements for reliable adhesion under oil conditions.

5. Conclusion

A series of experiments were performed to investigate the effects of different-scaled micropillars and micro-dimples on the wettability and adhesion of a PDMS surface with various liquids. From the results and discussions, the main findings can be summarized as follows.

• (i)In the case of water, the introductions of pillars and dimples both effectively increased the apparent CAs owing to the air capturing effect, and a high hydrophobicity is exhibited at the small scale.
• (ii)In the case of silicone oil, different configurations of patterns lead to different surface wetting behaviours. The opened pillars increased surface wettability by creating channels with a scale dependence, whereas the closed dimples decreased surface wettability owing to edge obstruction, independent of the geometry scale.
• (iii)For dry contact, the surface patterns of pillars and dimples decreased the adhesion force owing to the loss of the actual contact area. The geometry scale seems to have no significant influence on adhesion behaviour.
• (iv)The degree of adhesion of pillars and dimples in water exhibited a scale dependence. The small-scale patterns produced a water film separating the probe from the surface, and the adhesion was dominated by capillary force and exhibited low values. At large scales, the adhesion depends heavily on the direct contact force induced by the dewetting effect and presented a similar behaviour to the dry case.
• (v)In the case of the silicone oil, the configuration of the patterns had a strong influence on the scale-dependent adhesion. The adhesion of opened pillars increased with an enlargement of the scale, whereas for dimples, the adhesion force increased with a shrinkage of the scale. This effect was attributed to the different adhesion modes of the patterns (the draining effect for pillars and the suction effect for dimples).

Data accessibility

Data supporting this study are provided in the paper and electronic supplementary material.

Authors' contributions

M.L., Q.D., W.H. and X.W. designed the research; M.L. performed the research and wrote the paper.

Competing interest

We declare we have no competing interests.

Funding

This research was supported by the National Nature Science Foundation of China (NSFC) (grant no. 51675268) and the Fundamental Research Funds for the Central Universities (grant no. NZ2016106).