Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Nov 2;10(48):41738–41746. doi: 10.1021/acsami.8b10033

Influence of Humidity on Contact Resistance in Graphene Devices

Arne Quellmalz †, Anderson D Smith ‡,§, Karim Elgammal ∥,⊥, Xuge Fan †, Anna Delin ∥,⊥,#, Mikael Östling ‡, Max Lemme ¶,∇, Kristinn B Gylfason †,*, Frank Niklaus †,*
PMCID: PMC6284205  PMID: 30387599

Abstract

graphic file with name am-2018-100332_0006.jpg

The electrical contact resistance at metal–graphene interfaces can significantly degrade the properties of graphene devices and is currently hindering the full exploitation of graphene’s potential. Therefore, the influence of environmental factors, such as humidity, on the metal–graphene contact resistance is of interest for all graphene devices that operate without hermetic packaging. We experimentally studied the influence of humidity on bottom-contacted chemical-vapor-deposited (CVD) graphene–gold contacts, by extracting the contact resistance from transmission line model (TLM) test structures. Our results indicate that the contact resistance is not significantly affected by changes in relative humidity (RH). This behavior is in contrast to the measured humidity sensitivity 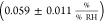Inline graphic of graphene’s sheet resistance. In addition, we employ density functional theory (DFT) simulations to support our experimental observations. Our DFT simulation results demonstrate that the electronic structure of the graphene sheet on top of silica is much more sensitive to adsorbed water molecules than the charge density at the interface between gold and graphene. Thus, we predict no degradation of device performance by alterations in contact resistance when such contacts are exposed to humidity. This knowledge underlines that bottom-contacting of graphene is a viable approach for a variety of graphene devices and the back end of the line integration on top of conventional integrated circuits.

Keywords: graphene, contact resistance, sheet resistance, humidity sensitivity, bottom-contact, integration

Introduction

Since its discovery,1 graphene has attracted much attention because of its fascinating electronic properties. π-Bonds of neighboring carbon atoms provide delocalized electrons, which account for its high conductivity and charge carrier mobility.2 These properties lead to a wide range of potential applications in electronics.3 Graphene’s electronic properties are eminently sensitive to changes in its environment. Consequently, graphene has been employed in sensors with outstanding sensitivity.4−7 Gas and humidity sensing based on graphene have been studied intensively, whereby graphene has demonstrated fast response and recovery times.8−13 The humidity sensitivity of graphene is caused by direct adsorption of water molecules onto its surface and can therefore be inhibited by a covering passivation layer. This enables simultaneous integration of graphene-based humidity sensors with other graphene components.14 Similar effects and preventative strategies were identified for other atomically thin materials such as molybdenum disulfide (MoS2).15

Electrical contacts to graphene are formed either by metal deposition on top of graphene (top-contacting) or by transferring graphene on top of existing metallization (bottom-contacting). Top-contacting is the predominant approach for experimental graphene devices. However, bottom-contacting has potential advantages because it reduces the number of process steps after the graphene transfer, which reduces the risk of defect formation and potential sources of residues on top of the graphene sheet. For the same reason, bottom-contacts are advantageous for the realization of devices with suspended graphene and enable the integration of graphene at the back end of the line of conventional semiconductor process flows on top of integrated circuits with metal interconnects.5,16,17 One limiting factor in developing high-performance graphene devices is the contact resistance at the metal–graphene interface—a high contact resistance can significantly degrade device properties.18−20 Therefore, a number of studies have investigated how to characterize and reduce the resistance of metal–graphene contacts.21−26 Cadore et al. found that the naturally created heterojunction at metal–graphene contacts is modulated in an asymmetric and reversible manner by hydrogen molecules at the metal–graphene interface.27 However, to our knowledge, no experimental investigation of the influence of humidity on contact resistance has been reported. For top-contacts, the covering metallization impedes direct adsorption of water molecules onto the graphene surface, although it is plausible that molecules diffuse between the layers to the metal–graphene interface.11,27 In contrast, bottom-contacted graphene is exposed to the ambient gas atmosphere and water molecules certainly adsorb on its surface. The potential influence of humidity on the metal–graphene contact resistance is of interest for all graphene devices that operate without hermetic packaging in a potentially humid environment because their performance might be subject to variations. Examples of such applications include electronic and spintronic devices, photodetectors and modulators in optical systems, nanoelectromechanical sensors, flexible and transparent electronics, as well as graphene-based components for energy storage.5,13,17,28−30 In general, experimental work on graphene devices in laboratory environments is likely to be influenced by variations in humidity because prototype devices are typically neither packaged nor hermetically sealed.

In this work, we study the influence of humidity on contact resistance in bottom-contacted chemical-vapor-deposited (CVD) graphene devices, by experimentally extracting the contact resistance from transmission line model (TLM) test structures at various humidity levels. To this end, we compare the sensitivity of graphene’s sheet resistance and contact resistance to variations in humidity. In addition, we employ density functional theory (DFT) simulations to investigate the effect of adsorbate water molecules on the electronic structure at the gold–graphene interface.

Results and Discussion

A TLM device consists of a graphene patch placed on an electrically insulating substrate with multiple metal electrodes of various spacings (Figure 1c). The measured resistances between neighboring electrode pairs are used for a TLM evaluation which determines the contact resistance between the graphene sheet and the metal electrodes. Furthermore, the TLM evaluation yields the sheet resistance of the graphene patch.

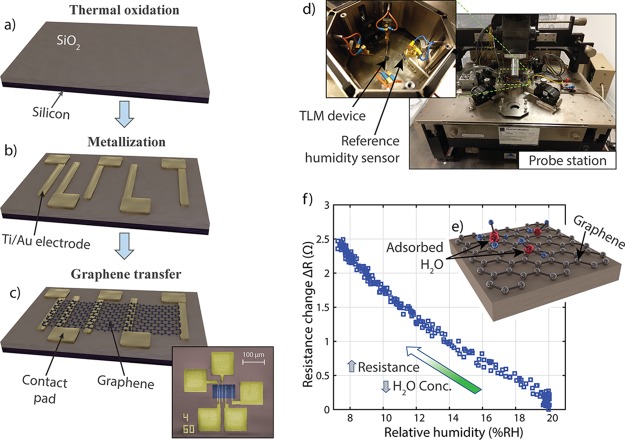
Figure 1.

Figure 1

Open in a new tab

(a–c) Schematic process flow of TLM device fabrication: (a) Thermal oxide (300 nm thick) was grown on a silicon substrate. (b) Metal electrodes were deposited by evaporation and structured using a lift-off process. (c) Graphene was transferred to the substrate and etched into a rectangular patch using O2 plasma. Bottom right: Colorized scanning electron microscopy (SEM) picture of a TLM device with gold contacts (yellow) and a 60 μm wide graphene area (blue). (d) Manual probe station for device characterization. The inset shows a device contacted by probe needles and the reference humidity sensor at the bottom-right. (e) Schematic illustration of water molecules adsorbing on the graphene surface. (f) Measured resistance change of a graphene device (60 μm by 24 μm) as the relative humidity (RH) is decreased.

Schematics of the device fabrication and a colorized SEM picture are shown in Figure 1a–c, while additional details are provided in the Methods section. A layer of 300 nm SiO2 (silica) was formed by thermal oxidation of a p-type doped silicon wafer. After a standard photolithographic process, layers of 20 nm Ti and 80 nm gold were deposited by electron beam evaporation. The metal electrodes and probe pads on the substrate were structured through lift-off of the underlying photoresist layer. CVD graphene was transferred from copper foil using a wet transfer technique.5 Finally, the graphene sheet was patterned into a rectangular patch by a second lithography and an etching step in O2 plasma. It connects the underlying metal electrodes, which are oriented perpendicularly at the point of contact. Beyond the graphene patch, the electrodes expand and form contact pads for electrical probing of the device.

Upon completion of the fabrication, the device was placed inside the shielded chamber of a manual probe station for electrical characterization (Figure 1d). A detailed description of the setup and the procedure is given in the Methods section. During characterization, dehumidified air was introduced into the chamber, which allowed the gradual reduction of humidity from 20% RH down to approximately 7% RH. Probe needles placed on the contact pads connected the device to a parameter analyzer, allowing real-time measurements of the device resistance between two electrodes. The device resistance is composed of the gold–graphene contact resistance in series with the resistance of the intermediate graphene sheet.

Figure 1e illustrates schematically the adsorption of water molecules on the graphene surface in a humid environment. The influence on the resistance of a graphene device with 60 μm width and 24 μm spacing between the electrodes was measured as dry air was introduced into the chamber. This procedure gradually decreased the RH from 20% RH to about 7% RH, whereby the device resistance increased by about 2.5 Ω (Figure 1f). This behavior is consistent with the previously described resistive graphene humidity sensing, which reports increasing resistance with decreasing humidity.13,31,32 The variation in resistance originates from changes of graphene’s electronic structure by the adsorbed water molecules on the graphene surface. Both a shift of the Dirac point and a bending of the energy bands around the Dirac point are plausible reasons for this change of the electronic structure. However, the individual contribution of these effects is an interesting research question, which is outside the scope of this work.

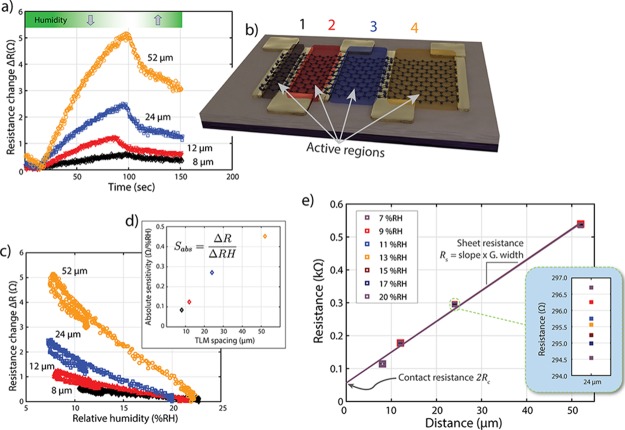
The acquired data in Figure 2a depict the change in resistance of a TLM device under variation of the humidity. Here, each dataset corresponds to one graphene sheet length, with labeling and coloration matching the schematic illustration in Figure 2b. Starting from environmental conditions, the inlet of dehumidified air was opened for a period of about 100 s, which gradually reduced the RH inside the chamber to its minimum value of around 7% RH. Consequently, the recorded resistance of the graphene device increased. After closing the valve, ambient humid air diffused into the setup and successively increased the humidity, thereby causing the device resistance to decrease. Figure 2c plots the same data as in Figure 2a against the recorded RH. The change in resistance shows a linear dependency on the RH.

Figure 2.

Figure 2

Open in a new tab

(a) Change of the device resistance during a measurement cycle. Starting from environmental conditions, dehumidified air was pumped into the chamber for about 100 s. After closing the inlet, ambient humid air diffused into the chamber. The four datasets show the response of graphene patches of different lengths. (b) Schematic illustration of a TLM device. Colorized regions represent graphene areas of varying length contacted by neighboring electrodes. (c) Change in the device resistance as a function of the RH [same datasets as in (a)]. Note the linear dependence. (d) Absolute sensitivity (Sabs) of the measured graphene device at corresponding TLM spacings. (e) TLM plots for evaluation of the contact resistance Rc and the sheet resistance Rs of a single device at various humidity levels. The interception of the linear fit (black line) with the Y-axis yields the contact resistance 2Rc of the two gold–graphene contacts used for probing. The slope of the linear fit and the width of the graphene sheet determine the sheet resistance Rs. Note that the data points and linear fits are nearly indistinguishable. 20% RH: Rc = 28.2 Ω (contact area: 4 × 60 μm2), Rs = 559.9 Ω/square, coefficient of determination R2 = 0.994.

The absolute sensitivity Sabs of the TLM structure to variation in humidity is shown in Figure 2d. Here, Sabs is defined as the ratio of the change in resistance ΔR and the change in relative humidity ΔRH (eq 1).

graphic file with name am-2018-100332_m002.jpg 1

The absolute sensitivity of the graphene devices increases with the spacing of the electrodes, that is, with the length of the intermediate graphene sheet (Figure 2d). This behavior is significant as it suggests that the sensitivity of graphene patches to humidity may be varied by geometrical design parameters.

The obtained resistance values at various humidity levels in the measurement chamber are plotted against the respective electrode spacing of the TLM device (Figure 2e). The solid lines represent a linear fit to the resistance versus distance data. Note that the data points and the linear fits are nearly indistinguishable for the selected scaling. The extrapolated residual resistance at zero contact spacing provides the contact resistance 2Rc of the two gold–graphene contacts connecting the intermediate graphene sheet. The sheet resistance Rs of the graphene patch is calculated by multiplication of the slope of the linear fit with the width of the graphene patch. For this measurement, the contact resistance at ambient humidity level (20% RH) amounts to 56.4 Ω, that is, 28.2 Ω per gold–graphene contact (contact area: 4 × 60 μm2), while the sheet resistance is 559.9 Ω/square (coefficient of determination R2 = 0.994).

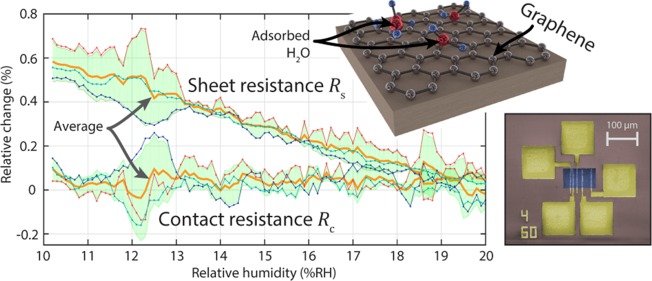
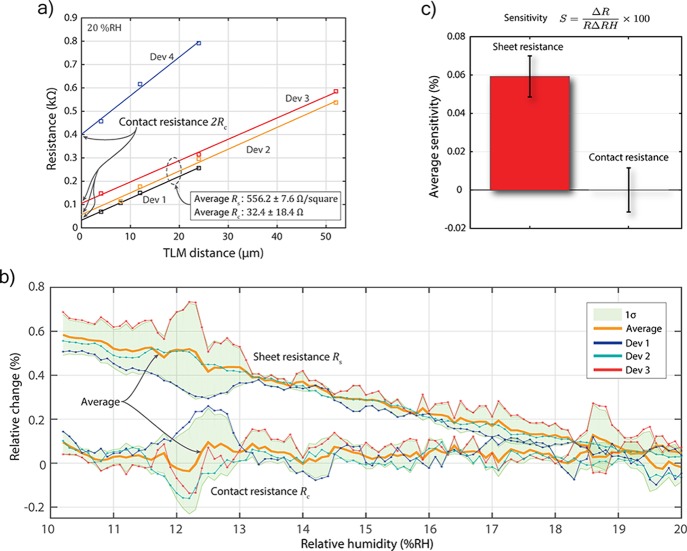
Figure 3 summarizes the resistance measurements. Only TLM devices with defect-free contacts were included in the evaluation. Assuming similar contact resistance and a constant sheet resistance within each TLM device, a linear relationship between contact spacing and measured resistance is expected. Therefore, devices with a linear correlation coefficient R2 below 0.996 were neglected. The evaluation of three TLM devices at initial conditions yields an average contact resistance of Rc = 32 ± 18 Ω (1920 ± 1080 Ω μm) and an average sheet resistance of 556.2 ± 7.6 Ω/square (Figure 3a). Our values of the sheet resistance are in line with previous literature studying graphene on SiO2.26,33 Our measured contact resistances are 1.6 to 2.4 times higher than previously reported values by Passi et al. and Russo et al. for devices without additional treatment to reduce their contact resistance (1518 and 800 Ω μm, respectively).23,25 This discrepancy might be due to a difference in contact design because we place the graphene on top of the metallization rather than below, as in those cases. Also, Zhang et al. hint at the long-term degradation of contact resistance after exposure to air which can be reversed by hydrogen annealing in case of nickel graphene contacts.34 The steep slope, that is, the abnormal sheet resistance, of device 4 indicates possible defects or contamination of the graphene sheet. Therefore, this device was not considered in the averaging. The relative change in contact resistance Rc and sheet resistance Rs with change in RH is compared for three devices (Figure 3b). Solid bold lines (orange) are the average of the respective data sets. The shaded areas represent one standard deviation (1σ).

Figure 3.

Figure 3

Open in a new tab

(a) Extraction of gold–graphene contact resistance on four TLM devices. Solid lines represent a linear fit of the square data points. (b) Relative change in gold–graphene contact resistance Rc and sheet resistance Rs with relative humidity. Solid bold lines (orange) are the average of the respective data sets. The shaded areas represent one standard deviation (1σ). (c) Comparison of the averaged sensitivity (S) of sheet and contact resistance (1σ error bars).

To quantify the influence of the relative humidity on Rc and Rs, the averaged sensitivity S is calculated for both resistances (Figure 3c). The sensitivity is derived by using eq 2 and defined as the ratio of percent change in resistance and the change in relative humidity in percent.

graphic file with name am-2018-100332_m003.jpg 2

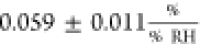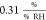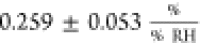In this work, the mean sensitivity of the sheet resistance amounts to Inline graphic. In a previous study on similar devices, we obtained Inline graphic.13 Chen et al. also studied the humidity sensitivity of the sheet resistance but defined the response to changes in RH as the relative change in device current at constant bias voltage and obtained values up to 18.1% when increasing the RH from 44 to 98%.35 To directly compare these results with our measurements, we calculated the sensitivity according to eq 2, which yields Inline graphic. We believe that our selection of devices with strictly ohmic behavior is the reason for the lower humidity sensitivity we observed here. The graphene in these devices is likely to have the least material imperfections, such as grain boundaries, wrinkles, and cracks. CVD graphene, as employed here, has intrinsic grain boundaries between adjacent regions of single-crystalline graphene.36,37 Also, strain of the graphene layer resulting from the transfer process might contribute to the formation of wrinkles and cracks.38 Both effects are likely to influence graphene’s sensitivity to humidity.39

Another possible explanation for variation in humidity sensitivity is polymer residues on the graphene originating from the transfer and lithography processes. They affect the number of surface sites available for molecule adsorption, and hence varying amounts of residuals might result. Thermal annealing has been employed to remove polymer residues from graphene;40 however, our devices were not annealed.

In this work, the sensitivity of the contact resistance averages to 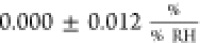Inline graphic—implying that Rc is not significantly affected by changes in humidity. This behavior is in clear contrast to the humidity sensitivity of graphene’s sheet resistance obtained in the very same measurement.

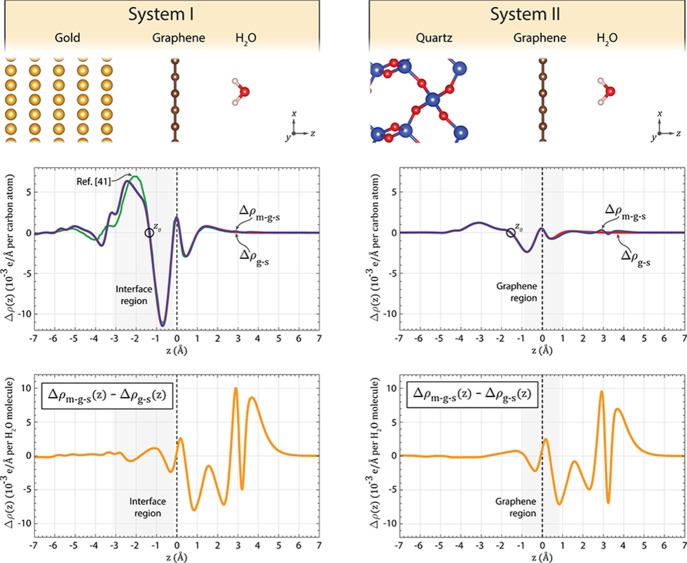
The electronic structure of graphene sheets is sensitive to both the choice of substrate material and the presence of adsorbates.13,31,42,43 For a qualitative comparison of graphene’s electronic structure in the contact regions and in the intermediate regions of the TLM devices, density functional theory (DFT) calculations were performed on two systems: system I, with gold as substrate (representing the contact regions), and system II, with α-quartz as substrate (representing the silica in intermediate regions). The top row of Figure 4 illustrates the configuration of the two systems.

Figure 4.

Figure 4

Open in a new tab

Plane-averaged charge density differences (PACDDs) computed with DFT (see Supporting Information). Left column: Data for the gold/graphene/H2O system. Right column: Data for the quartz/graphene/H2O system. Top row: Illustrations of the geometrical configurations of the analyzed systems. Middle row: Δρg-s(z) (blue) and Δρm-g-s(z) (red). The open black circle shows the position of the central node. Data from ref (41) are shown in green. Bottom row: The difference between Δρm-g-s(z) and Δρg–s(z) per adsorbed water molecule. The shaded areas indicate the part of the systems, which is relevant for the contact resistance (interface region) and sheet resistance (graphene region), respectively.

In the second row of the left column of Figure 4, we show the plane-averaged charge density difference (PACDD) (see Supporting Information) associated with the formation of the gold–graphene interface of system I (Δρg-s(z), red line). Additionally, we compare it to the PACDD describing the charge displacement in the gold/graphene/H2O molecule system referring to the situation when all three parts are isolated from each other (Δρm-g-s(z), blue line). The right column shows the corresponding data for system II. Our results suggest that the addition of a water molecule has a negligible effect on the charge displacement in the interface region between the graphene and the gold substrate, that is, the part of the system relevant for the contact resistance—the blue and red curves are overlying. This implies that the potential barrier which the electrons must overcome on their way between the graphene and the gold contacts is unaltered by the water molecule. Therefore, it is reasonable to expect that the contact resistance also remains unaltered, at least for the rather low surface concentration of water molecules assumed in our computation. On the other hand, earlier work by us and others13,31,42,43 clearly demonstrates that water adsorption on graphene on top of silica significantly changes the electronic structure of the graphene sheet, that is, the part of the system relevant for the sheet resistance. Therefore, it is expected that water adsorption also impacts the sheet resistance significantly, which agrees with the experimental data shown in Figure 3b.

For the gold/graphene system, we also included PACDD data computed with DFT by Khomyakov et al. (Figure 4, second row, left column).41 To be able to directly compare the data in ref (41) with our data, we recalculated the charge q per graphene carbon atom responsible for the dipole associated with the bonding between the graphene and the substrate (data for gold/graphene in Figure 5 in ref (41)) by numerically integrating the plotted data (see Supporting Information). We then rescaled their data to obtain the value q = 0.008 e per carbon atom which is stated in the same paper, thus making the data in Figure 5 in ref (41) internally consistent. Integrating our own data in the same way (i.e., from the central node z0 to plus or minus infinity, see Supporting Information), we find q = 0.0084 e per carbon atom, in excellent agreement with the result in ref (41). As evident from Figure 4 (second row, left column), our curve and the rescaled curve from ref (41) are, overall, very similar. Some differences can be seen in the region −5 to −2 Å below the graphene sheet. Because the setups of the two calculations differ in several respects (e.g., different exchange–correlation functional and size of the supercell), some discrepancies are expected.

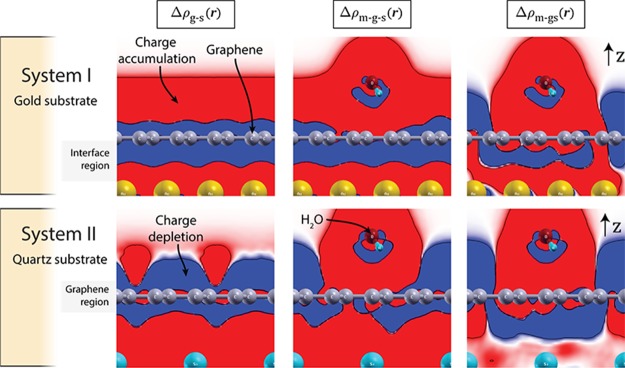
It is instructive to compare the gold/graphene system with the quartz/graphene system. According to our calculations, the electron transfer from the substrate/graphene system to the adsorbed water molecule is similar for both systems (0.05 and 0.04 e per H2O molecule for the gold/graphene and quartz/graphene system, respectively). The main difference between the two systems is the extent of the charge displacement associated with the formation of the substrate-graphene interface. A comparison of the two graphs in the middle row in Figure 4 reveals that the charge displacement in the quartz/graphene systems is several times smaller than in the gold/graphene system. For neither system, the adsorbed water molecule causes any visible change of the charge displacement in the interface region between the substrate and the graphene, that is, in the part of the system that affects the contact resistance. However, as we have already shown in refs13,31,42,44 the electronic structure of the part of the system relevant for the sheet resistance, that is, the region in immediate vicinity of the graphene sheet, is clearly affected by adsorbed molecules. Because quartz is an electrical insulator, the electrons are forced to flow in the graphene sheet only. Therefore, the transport of electrons, or in other words the sheet resistance, is indeed affected by the addition of water molecules on top of the graphene. The different effect on the electronic structure in the graphene region and in the interface region is visible in the two-dimensional contour plots of the charge density difference (CDD) (see Supporting Information) of the two systems, cutting through the plane of the water molecule (Figure 5). The regions of charge accumulation (red) and depletion (blue) are clearly different, and hence we qualitatively expect a different effect of adsorbed water molecules on the contact and sheet resistance, respectively.

Figure 5.

Figure 5

Open in a new tab

Two-dimensional contour plots of the CDD in a plane cutting through the water molecule (computed with DFT, see Supporting Information). Top row: Gold/graphene/H2O system. Bottom row: quartz/graphene/H2O system. Red and blue regions represent charge accumulation and depletion, respectively. The isovalue is set to 0.00001 e Å–3. The CDD plots were generated by using XCrySDen visualization program.45 The shaded areas indicate the part of the systems, which is relevant for the contact resistance (interface region) and sheet resistance (graphene region), respectively.

To further clarify the effect of adsorbed water molecules on the graphene surface, we plot the difference between Δρm-g-s(z) and Δρg-s(z) for both systems (third row of Figure 4). Note that in this row, the normalization is done per water molecule instead of per carbon atom. These plots reveal that the net effect of the adsorbed water molecule on the charge displacement is very similar for both gold and quartz substrates and that there is in fact a small but clearly visible change of the charge displacement in the interface region (−3 Å ≤ z ≤ 0). At very high concentrations of water molecules on the graphene surface, it is therefore conceivable that a measurable effect on the contact resistance emerges. We note, however, that the relevant comparison is not the effect of water adsorption on the two interface regions of system I and II, but rather the effect on the contact resistance in system I in relation to the effect on the sheet resistance in system II, and that these two resistances emerge from the two different regions of the systems, as already mentioned. In summary, our simulations demonstrate that, overall, the electronic structure of the graphene sheet on top of quartz is much more sensitive to adsorbed water molecules, compared to the charge density in the interface region between gold and graphene. This in turn suggests that the sheet resistance is expected to change much more than the contact resistance for varying concentration of water molecules on the graphene surface. This conclusion agrees with the experimentally measured data in Figure 3b, where the sheet resistance changes significantly with RH, whereas the contact resistance remains virtually unaffected.

Conclusions

We experimentally show that the gold–graphene contact resistance of bottom-contacts is not significantly affected by changes in humidity. This invariance of the contact resistance to adsorbed molecules on the graphene surface is in accordance with the observation of invariable contact resistance irrespective of the number of graphene layers and unaffected properties of graphene below the contact metal of top-contacted devices by electrostatics.18,46 Also, this behavior is in clear contrast to the humidity sensitivity of graphene’s sheet resistance (in this work: 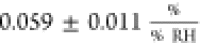Inline graphic) which has been reported in a multitude of publications.13,32,47 Our experimental results agree well with simulations based on DFT. Because of the similarity of electronic properties between different metallic substrates, we expect our results to be indicative for metal–graphene bottom-contacts in general. This includes materials such as aluminum, titanium, and nickel which are utilized in metal interconnect layers of conventional complementary metal–oxide–semiconductor (CMOS) integrated circuits. However, it should be noted that many of these metals form insulating oxides at their surfaces, which degrade the contact resistance and hence makes the usage of these metals more challenging.34 It is feasible to deposit inert gold as metallization on the top metal interconnect layer of CMOS circuits.48,49 This approach emphasizes the suitability of integrating bottom-contacted graphene at the back end of the line. With regards to graphene-based devices, we thus predict no degradation of performance by alterations in contact resistance when exposed to humidity. Taken together, our findings reinforce that bottom-contacts are suitable for reliable integration of graphene. However, our quantification of the humidity sensitivity of graphene’s sheet resistance indicates the importance of a controlled environment in experimental work on graphene devices in general and the necessity of reporting minute details of the measurement conditions.

Methods

Fabrication of TLM Devices

First, a 300 nm thick layer of SiO2 (silica) was formed by thermal oxidation of a p-type doped silicon wafer with 100 mm diameter and 525 μm thickness (Figure 1a). An adhesion layer of 20 nm Ti and a contact layer of 80 nm gold were deposited by electron beam evaporation. Metal electrodes and probe pads were formed using a lift-off process (Figure 1b). CVD graphene50 (Graphenea Inc., Spain) was transferred from copper foil using a wet transfer technique.5 Next, the covering graphene sheet was patterned into a rectangular patch by a photolithographic process and etching in O2 plasma. Finally, the resist mask was removed in acetone/isopropanol and the samples were dried in air (Figure 1c) (see Supporting Information for details).

Characterization and Setup

The TLM device was placed inside the shielded chamber of a manual probe station (Cascade Microtech Inc.) for electrical characterization (Figure 1d). During characterization, a valve-controlled inlet introduced dehumidified air into the chamber for about 100 s, gradually reducing the RH from environmental conditions (approx. 23% RH) down to about 7% RH. After closing the inlet, ambient humid air diffused into the chamber which successively increased the humidity. The RH inside the chamber was monitored by a commercial HJH-4000 humidity sensor (Honeywell International Inc.; settling time: <70 ms, response time: 5 s). Probe needles placed on the contact pads connected the device to a Keithley SCS4200 parameter analyzer (Figure 1d) which allowed real-time measurement of the device resistance between two electrodes at a dc bias voltage of 100–200 mV.

DFT Simulations

DFT simulations were performed using the plane-wave basis set Quantum Espresso (QE) code.51 The two systems addressed differ by the substrate type. System I features a gold (111) surface slab as the substrate and system II features an undercoordinated silicon-terminated (0001) α-quartz substrate. A graphene supercell is relaxed on top of the substrates, and then a water molecule is relaxed on top of the substrate/graphene system in the two-leg down configuration, which has been demonstrated to be the most stable configuration for water on top of graphene.52 The output from the converged DFT simulations was used to compute the charge displacement upon formation of the substrate/graphene system and also the effect of adding a water molecule on top of the graphene (see Supporting Information for details).

Acknowledgments

This work was partially supported by the European Research Council through the Starting Grant M&M’s (no. 277879) and InteGraDe (307311), by VINNOVA through grants 2016-01655 and 2017-05108, by VR through the GEMS grant (2015-05112), and by the China Scholarship Council (CSC) through a scholarship grant. A.D. acknowledges financial support from Vetenskapsrådet (grant numbers VR 2015-04608 and VR 2016-05980) and Swedish Energy Agency (grant number STEM P40147-1). The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center (NSC), Linköping University, the PDC Centre for High Performance Computing (PDC-HPC), KTH, and the High Performance Computing Center North (HPC2N), Umeå University.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.8b10033.

  • Supplementary methods for the fabrication of TLM devices and DFT simulations (PDF)

Author Contributions

○ A.Q. and A.D.S. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

am8b10033_si_001.pdf (92.3KB, pdf)

References

  1. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  2. Bolotin K. I.; Sikes K. J.; Jiang Z.; Klima M.; Fudenberg G.; Hone J.; Kim P.; Stormer H. L. Ultrahigh Electron Mobility in Suspended Graphene. Solid State Commun. 2008, 146, 351–355. 10.1016/j.ssc.2008.02.024. [DOI] [Google Scholar]
  3. Choi W.; Lahiri I.; Seelaboyina R.; Kang Y. S. Synthesis of Graphene and Its Applications: A Review. Crit. Rev. Solid State Mater. Sci. 2010, 35, 52–71. 10.1080/10408430903505036. [DOI] [Google Scholar]
  4. Schedin F.; Geim A. K.; Morozov S. V.; Hill E. W.; Blake P.; Katsnelson M. I.; Novoselov K. S. Detection of Individual Gas Molecules Adsorbed on Graphene. Nat. Mater. 2007, 6, 652–655. 10.1038/nmat1967. [DOI] [PubMed] [Google Scholar]
  5. Smith A. D.; Niklaus F.; Paussa A.; Vaziri S.; Fischer A. C.; Sterner M.; Forsberg F.; Delin A.; Esseni D.; Palestri P.; Östling M.; Lemme M. C. Electromechanical Piezoresistive Sensing in Suspended Graphene Membranes. Nano Lett. 2013, 13, 3237–3242. 10.1021/nl401352k. [DOI] [PubMed] [Google Scholar]
  6. Fong K. C.; Schwab K. C. Ultrasensitive and Wide-Bandwidth Thermal Measurements of Graphene at Low Temperatures. Phys. Rev. X 2012, 2, 031006. 10.1103/physrevx.2.031006. [DOI] [Google Scholar]
  7. Xia F.; Mueller T.; Lin Y.-m.; Valdes-Garcia A.; Avouris P. Ultrafast Graphene Photodetector. Nat. Nanotechnol. 2009, 4, 839–843. 10.1038/nnano.2009.292. [DOI] [PubMed] [Google Scholar]
  8. Massera E.; La Ferrara V.; Miglietta M.; Polichetti T.; Nasti I.; Di Francia G. Gas Sensors Based on Graphene—Comparison of Two Different Fabrication Approaches. Chim. Oggi 2012, 30 (2), 29–31. [Google Scholar]
  9. Fowler J. D.; Allen M. J.; Tung V. C.; Yang Y.; Kaner R. B.; Weiller B. H. Practical Chemical Sensors from Chemically Derived Graphene. ACS Nano 2009, 3, 301–306. 10.1021/nn800593m. [DOI] [PubMed] [Google Scholar]
  10. Gautam M.; Jayatissa A. H. Graphene Based Field Effect Transistor for the Detection of Ammonia. J. Appl. Phys. 2012, 112, 064304. 10.1063/1.4752272. [DOI] [Google Scholar]
  11. He Q.; Wu S.; Yin Z.; Zhang H. Graphene-Based Electronic Sensors. Chem. Sci. 2012, 3, 1764–1772. 10.1039/c2sc20205k. [DOI] [Google Scholar]
  12. Wehling T. O.; Novoselov K. S.; Morozov S. V.; Vdovin E. E.; Katsnelson M. I.; Geim A. K.; Lichtenstein A. I. Molecular Doping of Graphene. Nano Lett. 2008, 8, 173–177. 10.1021/nl072364w. [DOI] [PubMed] [Google Scholar]
  13. Smith A. D.; Elgammal K.; Niklaus F.; Delin A.; Fischer A. C.; Vaziri S.; Forsberg F.; Råsander M.; Hugosson H.; Bergqvist L.; et al. Resistive Graphene Humidity Sensors with Rapid and Direct Electrical Readout. Nanoscale 2015, 7, 19099–19109. 10.1039/c5nr06038a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Smith A. D.; Elgammal K.; Fan X.; Lemme M.; Delin A.; Niklaus F.; Östling M.. Toward Effective Passivation of Graphene to Humidity Sensing Effects. 46th European Solid-State Device Research Conference (ESSDERC), 2016; pp 299–302. [Google Scholar]
  15. Late D. J.; Liu B.; Matte H. S. S. R.; Dravid V. P.; Rao C. N. R. Hysteresis in Single-Layer MoS2 Field Effect Transistors. ACS Nano 2012, 6, 5635–5641. 10.1021/nn301572c. [DOI] [PubMed] [Google Scholar]
  16. Bunch J. S.; van der Zande A. M.; Verbridge S. S.; Frank I. W.; Tanenbaum D. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Electromechanical Resonators from Graphene Sheets. Science 2007, 315, 490–493. 10.1126/science.1136836. [DOI] [PubMed] [Google Scholar]
  17. Smith A. D.; Vaziri S.; Rodriguez S.; Östling M.; Lemme M. C. Large Scale Integration of Graphene Transistors for Potential Applications in the Back End of the Line. Solid-State Electron. 2015, 108, 61–66. 10.1016/j.sse.2014.12.014. [DOI] [Google Scholar]
  18. Venugopal A.; Colombo L.; Vogel E. M. Contact Resistance in Few and Multilayer Graphene Devices. Appl. Phys. Lett. 2010, 96, 013512. 10.1063/1.3290248. [DOI] [Google Scholar]
  19. Schwierz F. Graphene Transistors: Status, Prospects, and Problems. Proc. IEEE 2013, 101, 1567–1584. 10.1109/jproc.2013.2257633. [DOI] [Google Scholar]
  20. Nagashio K.; Nishimura T.; Kita K.; Toriumi A.. Metal/Graphene Contact as a Performance Killer of Ultra-High Mobility Graphene Analysis of Intrinsic Mobility and Contact Resistance. IEEE International Electron Devices Meeting (IEDM), 2009; pp 1–4.
  21. Han S.-J.; Chen Z.; Bol A. A.; Sun Y. Channel-Length-Dependent Transport Behaviors of Graphene Field-Effect Transistors. IEEE Electron Device Lett. 2011, 32, 812–814. 10.1109/led.2011.2131113. [DOI] [Google Scholar]
  22. Robinson J. A.; LaBella M.; Zhu M.; Hollander M.; Kasarda R.; Hughes Z.; Trumbull K.; Cavalero R.; Snyder D. Contacting Graphene. Appl. Phys. Lett. 2011, 98, 053103. 10.1063/1.3549183. [DOI] [Google Scholar]
  23. Russo S.; Craciun M. F.; Yamamoto M.; Morpurgo A. F.; Tarucha S. Contact Resistance in Graphene-Based Devices. Phys. E 2010, 42, 677–679. 10.1016/j.physe.2009.11.080. [DOI] [Google Scholar]
  24. Xia F.; Perebeinos V.; Lin Y.-m.; Wu Y.; Avouris P. The Origins and Limits of Metal-Graphene Junction Resistance. Nat. Nanotechnol. 2011, 6, 179–184. 10.1038/nnano.2011.6. [DOI] [PubMed] [Google Scholar]
  25. Passi V.; Gahoi A.; Ruhkopf J.; Kataria S.; Vaurette F.; Pallecchi E.; Happy H.; Lemme M. C.. Contact Resistance Study of “Edge-Contacted” Metal-Graphene Interfaces. 46th European Solid-State Device Research Conference (ESSDERC), 2016; pp 236–239.
  26. Venica S.; Driussi F.; Gahoi A.; Passi V.; Palestri P.; Lemme M. C.; Selmi L.. Detailed Characterization and Critical Discussion of Series Resistance in Graphene-Metal Contacts. International Conference of Microelectronic Test Structures (ICMTS), 2017; pp 1–5.
  27. Cadore A. R.; Mania E.; de Morais E. A.; Watanabe T.; Taniguchi T.; Lacerda R. G.; Campos L. C. Metal-Graphene Heterojunction Modulation via H2 Interaction. Appl. Phys. Lett. 2016, 109, 033109. 10.1063/1.4959560. [DOI] [Google Scholar]
  28. Hurst A. M.; Lee S.; Cha W.; Hone J.. A Graphene Accelerometer. 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), 2015; pp 865–868.
  29. Liu M.; Yin X.; Ulin-Avila E.; Geng B.; Zentgraf T.; Ju L.; Wang F.; Zhang X. A Graphene-Based Broadband Optical Modulator. Nature 2011, 474, 64–67. 10.1038/nature10067. [DOI] [PubMed] [Google Scholar]
  30. Gan X.; Shiue R.-J.; Gao Y.; Meric I.; Heinz T. F.; Shepard K.; Hone J.; Assefa S.; Englund D. Chip-Integrated Ultrafast Graphene Photodetector with High Responsivity. Nat. Photonics 2013, 7, 883–887. 10.1038/nphoton.2013.253. [DOI] [Google Scholar]
  31. Elgammal K.; Hugosson H. W.; Smith A. D.; Råsander M.; Bergqvist L.; Delin A. Density Functional Calculations of Graphene-Based Humidity and Carbon Dioxide Sensors: Effect of Silica and Sapphire Substrates. Surf. Sci. 2017, 663, 23–30. 10.1016/j.susc.2017.04.009. [DOI] [Google Scholar]
  32. Melios C.; Centeno A.; Zurutuza A.; Panchal V.; Giusca C. E.; Spencer S.; Silva S. R. P.; Kazakova O. Effects of Humidity on the Electronic Properties of Graphene Prepared by Chemical Vapour Deposition. Carbon 2016, 103, 273–280. 10.1016/j.carbon.2016.03.018. [DOI] [Google Scholar]
  33. Kidambi P. R.; Ducati C.; Dlubak B.; Gardiner D.; Weatherup R. S.; Martin M.-B.; Seneor P.; Coles H.; Hofmann S. The Parameter Space of Graphene Chemical Vapor Deposition on Polycrystalline Cu. J. Phys. Chem. C 2012, 116, 22492–22501. 10.1021/jp303597m. [DOI] [Google Scholar]
  34. Zhang Z.; Yang F.; Agnihotri P.; Lee J. U.; Lloyd J. R. Reverse Degradation of Nickel Graphene Junction by Hydrogen Annealing. AIP Adv. 2016, 6, 025301. 10.1063/1.4941572. [DOI] [Google Scholar]
  35. Chen M.-C.; Hsu C.-L.; Hsueh T.-J. Fabrication of Humidity Sensor Based on Bilayer Graphene. IEEE Electron Device Lett. 2014, 35, 590–592. 10.1109/led.2014.2310741. [DOI] [Google Scholar]
  36. Yu Q.; Jauregui L. A.; Wu W.; Colby R.; Tian J.; Su Z.; Cao H.; Liu Z.; Pandey D.; Wei D.; Chung T. F.; Peng P.; Guisinger N. P.; Stach E. A.; Bao J.; Pei S.-S.; Chen Y. P. Control and Characterization of Individual Grains and Grain Boundaries in Graphene Grown by Chemical Vapour Deposition. Nat. Mater. 2011, 10, 443–449. 10.1038/nmat3010. [DOI] [PubMed] [Google Scholar]
  37. Xu G.; Zhang Y.; Duan X.; Balandin A. A.; Wang K. L. Variability Effects in Graphene: Challenges and Opportunities for Device Engineering and Applications. Proc. IEEE 2013, 101, 1670–1688. 10.1109/jproc.2013.2247971. [DOI] [Google Scholar]
  38. Smith A. D.; Wagner S.; Kataria S.; Malm B. G.; Lemme M. C.; Östling M. Wafer-Scale Statistical Analysis of Graphene Field-Effect Transistors-Part II: Analysis of Device Properties. IEEE Trans. Electron Devices 2017, 64, 3927–3933. 10.1109/ted.2017.2727823. [DOI] [Google Scholar]
  39. Yasaei P.; Kumar B.; Hantehzadeh R.; Kayyalha M.; Baskin A.; Repnin N.; Wang C.; Klie R. F.; Chen Y. P.; Král P.; Salehi-Khojin A. Chemical Sensing with Switchable Transport Channels in Graphene Grain Boundaries. Nat. Commun. 2014, 5, 4911. 10.1038/ncomms5911. [DOI] [PubMed] [Google Scholar]
  40. Raja S. N.; Osenberg D.; Choi K.; Gyu Park H.; Poulikakos D. Annealing and Polycrystallinity Effects on the Thermal Conductivity of Supported CVD Graphene Monolayers. Nanoscale 2017, 9, 15515–15524. 10.1039/c7nr05346k. [DOI] [PubMed] [Google Scholar]
  41. Khomyakov P. A.; Giovannetti G.; Rusu P. C.; Brocks G.; van den Brink J.; Kelly P. J. First-Principles Study of the Interaction and Charge Transfer between Graphene and Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 195425. 10.1103/physrevb.79.195425. [DOI] [Google Scholar]
  42. Smith A. D.; Elgammal K.; Fan X.; Lemme M. C.; Delin A.; Råsander M.; Bergqvist L.; Schröder S.; Fischer A. C.; Niklaus F.; Östling M. Graphene-Based CO2 Sensing and Its Cross-Sensitivity with Humidity. RSC Adv. 2017, 7, 22329–22339. 10.1039/c7ra02821k. [DOI] [Google Scholar]
  43. Wehling T. O.; Lichtenstein A. I.; Katsnelson M. I. First-Principles Studies of Water Adsorption on Graphene: The Role of the Substrate. Appl. Phys. Lett. 2008, 93, 202110. 10.1063/1.3033202. [DOI] [Google Scholar]
  44. Fan X.; Elgammal K.; Smith A. D.; Östling M.; Delin A.; Lemme M. C.; Niklaus F. Humidity and CO2 Gas Sensing Properties of Double-Layer Graphene. Carbon 2018, 127, 576–587. 10.1016/j.carbon.2017.11.038. [DOI] [Google Scholar]
  45. Kokalj A. XCrySDen-a new program for displaying crystalline structures and electron densities. J. Mol. Graphics Modell. 1999, 17, 176–179. 10.1016/s1093-3263(99)00028-5. [DOI] [PubMed] [Google Scholar]
  46. Venica S.; Driussi F.; Gahoi A.; Palestri P.; Lemme M. C.; Selmi L. On the Adequacy of the Transmission Line Model to Describe the Graphene-Metal Contact Resistance. IEEE Trans. Electron Devices 2018, 65, 1589–1596. 10.1109/ted.2018.2802946. [DOI] [Google Scholar]
  47. Ghosh A.; Late D. J.; Panchakarla L. S.; Govindaraj A.; Rao C. N. R. NO2 and Humidity Sensing Characteristics of Few-Layer Graphenes. J. Exp. Nanosci. 2009, 4, 313–322. 10.1080/17458080903115379. [DOI] [Google Scholar]
  48. Wycisk M.; Tönnesen T.; Binder J.; Michaelis S.; Timme H.-J. Low-Cost Post-CMOS Integration of Electroplated Microstructures for Inertial Sensing. Sens. Actuators, A 2000, 83, 93–100. 10.1016/s0924-4247(00)00295-8. [DOI] [Google Scholar]
  49. Forsberg F.; Roxhed N.; Ericsson P.; Wissmar S.; Niklaus F.; Stemme G.. High-Performance Quantum-Well Silicon-Germanium Bolometers Using IC-Compatible Integration for Low-Cost Infrared Imagers. TRANSDUCERS 2009-2009 International Solid-State Sensors, Actuators and Microsystems Conference, 2009; pp 2214–2217.
  50. Kataria S.; Wagner S.; Ruhkopf J.; Gahoi A.; Pandey H.; Bornemann R.; Vaziri S.; Smith A. D.; Ostling M.; Lemme M. C. Chemical Vapor Deposited Graphene: From Synthesis to Applications. Phys. Status Solidi A 2014, 211, 2439–2449. 10.1002/pssa.201400049. [DOI] [Google Scholar]
  51. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; Dal Corso A.; de Gironcoli S.; Fabris S.; Fratesi G.; Gebauer R.; Gerstmann U.; Gougoussis C.; Kokalj A.; Lazzeri M.; Martin-Samos L.; Marzari N.; Mauri F.; Mazzarello R.; Paolini S.; Pasquarello A.; Paulatto L.; Sbraccia C.; Scandolo S.; Sclauzero G.; Seitsonen A. P.; Smogunov A.; Umari P.; Wentzcovitch R. M. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21, 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  52. Hong G.; Han Y.; Schutzius T. M.; Wang Y.; Pan Y.; Hu M.; Jie J.; Sharma C. S.; Müller U.; Poulikakos D. On the Mechanism of Hydrophilicity of Graphene. Nano Lett. 2016, 16, 4447–4453. 10.1021/acs.nanolett.6b01594. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am8b10033_si_001.pdf (92.3KB, pdf)

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES