Polarizable Force Field for RNA Based on the Classical Drude Oscillator

Abstract

RNA molecules are highly dynamic and capable of adopting a wide range of complex, folded structures. The factors driving the folding and dynamics of these structures are dependent upon a balance of base pairing, hydration, base stacking, ion interactions, and the conformational sampling of the 2’-hydroxyl group in the ribose sugar. The representation of these features is a challenge for empirical force fields used in molecular dynamics simulations. Towards meeting this challenge, the inclusion of explicit electronic polarization is important in accurately modeling RNA structure. In this work, we present a polarizable force field for RNA based on the classical Drude oscillator model, which represents electronic degrees of freedom via negatively charged particles attached to their parent atoms by harmonic springs. Beginning with parametrization against quantum mechanical base stacking interaction energy and conformational energy data, we have extended the Drude-2017 nucleic acid force field to include RNA. The conformational sampling of a range of RNA sequences were used to validate the force field, including canonical A-form RNA duplexes, stem-loops, and complex tertiary folds that bind multiple Mg²⁺ ions. Overall, the Drude-2017 RNA force field reproduces important properties of these structures, including the conformational sampling of the 2’-hydroxyl and key interactions with Mg²⁺ ions.

INTRODUCTION

RNA serves many roles in the cell, from information transfer in transcription (mRNA), structural and catalytic roles in protein translation (tRNA and rRNA), gene silencing via RNA interference, catalysis (ribozymes), and controlling gene expression through metabolite-sensing riboswitches. The diversity of RNA function is reflected in the diversity of secondary and tertiary structures that it can adopt, many of which have unusually high stability.^[1-7] In contrast to DNA, which is typically found as a duplex formed from two separate strands, RNA is primarily single-stranded. RNA folding is governed by a variety of factors, including noncanonical base-pairing, interactions with monovalent and divalent ions, and conformational sampling of the 2’-hydroxyl group that increases the number and types of hydrogen bonds that can be formed within the oligonucleotide chain, as discussed below. Many folded RNA structures, such as those found in riboswitch aptamer sequences, have sufficient structural plasticity as to interconvert between several states in response to metabolites or other environmental signals. Interactions with ions, particularly Mg²⁺, govern RNA folding and also function to stabilize the folded state,^[8,9] which may include tight bends in the polynucleotide backbone. The small size and subsequent charge density of the Mg²⁺ ion can effectively shield the negative charge on the RNA phosphodiester backbone and stabilize tight turns to give rise to complex tertiary structures.^[10]

The stability of DNA and RNA depends on a balance of electrostatic and van der Waals forces, among which base stacking and hydrogen bonding are particularly important. The ability of an atomistic force field to capture these forces is essential for carrying out accurate molecular dynamics (MD) simulations. To this end, numerous fixed-charge (additive) all-atom force fields have been developed to simulate DNA and RNA,^[11-20] and RNA structural dynamics have been extensively studied using MD simulations, as reviewed elsewhere.^[21-23] Previous work has indicated that the conformational sampling of the 2’-hydroxyl group in RNA has important implications for the flexibility of the backbone.^[24] Specifically, canonical helices are associated with the “base” configuration of the 2’-hydroxyl that facilitates a water-mediated hydrogen bond to a nitrogen atom in the base, whereas noncanonical structures are associated with 2’-hydroxyl groups oriented towards the O3’ or O4’ atoms of the ribose sugar, behavior that confers greater flexibility on the structure.^[24-27] Additionally, the 2’-hydroxyl group can stabilize loop regions in secondary RNA folds by forming hydrogen bonds to bases and phosphodiester backbone moieties.^[28] Thus, describing 2’-hydroxyl conformational sampling and nonbonded interactions accurately is a critical factor in evaluating the reliability of MD simulations. As such, assessing these interactions has been important in improving the additive CHARMM36 force field for nucleic acids.^[14,15,24]

Towards a more accurate representation of biomolecules, several groups have developed empirical force fields that explicitly account for electronic polarization, including fluctuating charge models,^[29-33] and induced dipole models such as AMOEBA.^[34-37] We have introduced a polarizable force field based on the classical Drude oscillator model for proteins,^[38] DNA,^[39-42] carbohydrates,^[43-45] and lipids.^[46,47] The Drude oscillator model^[48-50] explicitly represents electronic polarization response by attaching negatively charged particles (Drude oscillators) to the non-hydrogen atoms of the system via harmonic springs. The charges on the Drude oscillator (q_D) and core atom (q_A) are assigned according to the atomic polarizability (α) of the atom:

$$\alpha =\frac{q_D^2}{k_D}$$ (1)

where k_D is the force constant on the spring representing the harmonic bond between the Drude oscillator and its parent atom. This model offers an improved representation of the electrostatics in complex biomolecular systems relative to traditional, additive force fields. In additive models, gas-phase dipole moments of molecules are typically overestimated by 20% or more to approximate the mean-field response in the condensed phase.^[51,52] The polarizable model, on the other hand, allows for explicit electronic response as a function of changes in local electric fields. In addition, the Drude model allows for the application of van der Waals parameters to the oscillators themselves, thereby representing steric electronic effects.^[53] This capability has been exploited by our laboratory in the development of Mg^2+[54] and halogen parameters.^[55] Recent studies using the Drude polarizable model for DNA have shown that inclusion of electronic polarization is important for capturing ion-induced structural changes in DNA,^[56] ion competition around DNA,^[57] and in the energetics of base flipping.^[58] In those studies, additive models failed to reproduce sensitive dynamics, indicating that the Drude electrostatic model is a better representation of physical reality.

The present work extends the existing Drude-2017 DNA force field^[41,42] to include RNA to create a comprehensive Drude polarizable force field for nucleic acids. Specific emphasis is placed on proper sampling of the 2’-hydroxyl group of the ribose sugar, base stacking interactions, and interactions of the 2’-hydroxyl group with water. Starting from quantum mechanical (QM) calculations using model compounds to develop parameters that accurately capture conformational energetics and conformation-specific dipole response, we have constructed the full force field for RNA. Microsecond validation simulations performed on both canonical A-form helices and noncanonical, secondary and tertiary RNA structures are used to assess the quality of the force field.

METHODS

General Approach for Quantum and Molecular Mechanical Calculations.

Parametrization of the force field began with QM calculations on a variety of model compounds detailed below. The first step in this process was to perform a geometry optimization, in some cases with specific degrees of freedom constrained to ideal values to enforce a canonical geometry, while allowing other degrees of freedom to relax freely. Details for any constraints applied to specific model compound calculations are given below. All QM geometry optimizations were performed using the Gaussian03 program,^[59] using MP2/6-31G* or MP2/6-31+G* model chemistries for uncharged or charged systems, respectively. Single-point energy evaluations of optimized geometries were performed in Q-Chem^[60] using larger basis sets, described below for each type of calculation. All interaction energy calculations (base stacking and water interactions) included counterpoise correction^[61] for basis-set superposition error (BSSE).^[62] For potential energy surfaces, target dihedrals were scanned over 360° in intervals of 15°. Non-target degrees of freedom were allowed to relax unless otherwise noted, as in some instances preserving ideal geometries was preferred.

Corresponding molecular mechanical (MM) calculations were performed using the Drude-2017 force field in the CHARMM program.^[63] All MM calculations were performed analogously to the corresponding QM calculations; that is, any fixed degrees of freedom during QM optimizations were similarly restrained in CHARMM to ensure a direct comparison between the results. For single-point energy evaluations or dipole moment calculations, the atomic coordinates were restrained using a force constant of 10⁷ kcal mol⁻¹ Å⁻² and the Drude oscillators were allowed to relax via energy minimization.

Base Stacking Calculations.

Following the method of McDonald et al.,^[64] which was also applied in our recent refinement of DNA base parameters,^[41,42] interaction energies between bases in uracil-containing stacked monomers were calculated by fixing intermolecular degrees of freedom (rise, slide, shift, twist, roll, and tilt) while allowing intramolecular degrees of freedom to relax. Structures were initially built in canonical, A-form RNA configurations according to fiber diffraction data of Arnott et al.^[65] and subsequently optimized using the MP2/aug-cc-pVDZ model chemistry. Single-point interaction energies of the optimized structures were carried out using the DF-SCS-MP2/aug-cc-pVTZ model chemistry.

All of the atom types used to describe uracil in the Drude force field are shared by cytosine and thymine, which were refined in our previous work on DNA.^[41,42] The electrostatic parameters derived by Baker et al.^[66] for uracil were applied in conjunction with the refined LJ parameters of the Drude-2017 atom types and evaluated in CHARMM^[63] by enforcing the intermolecular restraints described above via the LONEPAIR facility. Intramolecular degrees of freedom of each base were allowed to relax freely, after which the interaction energy was calculated as the difference between the energy of the energy-minimized stacked monomer system and the sum of the individually energy-minimized bases. As will be shown below, the agreement of the Drude force field with the QM base stacking interaction energies was satisfactory and no additional refinement was required.

Uracil-Water Interactions.

The balance of interactions between bases (base pairing and stacking) and between bases and water will dictate, in part, the stability of nucleic acid structure. To that end, a central feature of the Drude polarizable force field is an accurate description of the interactions of bases with water. The specific target data are QM interaction energies between a single water molecule and each of the non-hydrogen atoms in the base (Figure 1). The target data were generated in a previous study by Baker et al.^[67] Briefly, after QM geometry optimization of uracil, water molecules, held rigid in the same geometry as the SWM4-NDP polarizable model,^[68] were placed at an initial distance of 2.5 Å away from each non-hydrogen atom in the base, either out of the plane of the base (Figure 1A) or in the plane of the base (Figure 1B). With fixed internal geometries, the distance between the water molecule and the base was optimized, after which single-point energy evaluations were performed using the RIMP2/cc-pVQZ model chemistry.

Figure 1.

Interaction orientations for (A) out-of-plane and (B) in-plane water molecules with 1-methyluracil. Note that only one water molecule was present in each optimization and interaction energy calculation; the composite image illustrates all poses considered during parametrization.

Heats of Sublimation and Crystal Simulations.

To further evaluate the quality of nonbonded interactions between the bases in the condensed phase, crystal simulations of uracil and 1-methyluracil were performed to determine the heats of sublimation (ΔH_sub) and molecular volumes (V_m). The methods and results for these simulations were described previously for the four DNA bases.^[41] Briefly, the coordinates for both crystals^[69,70] were obtained from the Cambridge Structural Database^[71] and replicated using the CRYSTAL facility in CHARMM such that there were 32 molecules in the uracil crystal and 64 molecules in the 1-methyluracil crystal. The crystal configurations were energy-minimized and ten independent simulations were initiated using different random seeds for velocity generation. These simulations were carried out for 500 ps, with the first 100 ps discarded as equilibration. Simulations were performed under an NPT ensemble, allowing for full anisotropic flexibility of the unit cell. For determination of ΔH_sub, simulations of uracil were performed at both 298 K (standard state) and 439 K (experimentally determined sublimation temperature), and 398 K for 1-methyluracil, the experimentally determined sublimation temperature. For gas-phase sampling, ten independent simulations of one molecule were performed for 2.5 ns, discarding the first 100 ps as equilibration. All crystal simulations to determine V_m were conducted at the same experimental temperature at which the structure was obtained (298 K for uracil and 15 K for 1-methyluracil). All simulations were performed in CHARMM, using the extended Lagrangian velocity Verlet integration method.^[72] Temperature was regulated using a dual Langevin thermostat, coupling the Drude oscillators to a low-temperature relative thermostat at 1 K with a friction coefficient of 10.0 ps⁻¹, and coupling the remaining real atoms to a thermostat set to the temperatures listed above with a friction coefficient of 5.0 ps⁻¹. In all simulations, the Lennard-Jones potential was switched smoothly to zero from 10 – 12 Å, and neighbor lists were updated heuristically within 16 Å. Electrostatic interactions were computed with the particle mesh Ewald method^[73] using a real-space cutoff of 12 Å with κ = 0.34 and sixth-order spline interpolation. The Drude “hard wall constraint”^[46] was imposed at 0.2 Å to prevent polarization catastrophe.

Values of ΔH_sub were calculated according to the following equation:

$$\Delta H_{\mathit{sub}}=\langle U_{\mathit{gas}}\rangle -\frac{\langle U_{\mathit{crystal}}\rangle }{N_{\mathit{mol}}}+\mathit{RT}$$ (2)

where T is the absolute temperature (K) and R is the gas constant. N_mol is the number of molecules in the crystal unit cell. The time-averaged potential energies in the gas and crystal states are <U_gas> and <U_crystal>, respectively.

χ Dihedral Parameter Fitting.

The coordinates of the four RNA nucleosides (adenosine, cytidine, guanosine, and uridine) were constructed in CHARMM. Backbone torsions β, γ, and ε were fixed in their canonical A-RNA values (174°, 57°, and 211°, respectively) and North (C3’-endo) pucker in the ribose ring was enforced by fixing ν₀ (O4’-C4’-C1’-C2’) at 0°.^[74] The glycosidic linkage (χ, O4’-C1’-N1-C2 for pyrimidines and O4’-C1’-N9-C4 for purines) was scanned as described above. Following QM optimization of each conformation, single-point energies were evaluated using the RIMP2/cc-pVTZ model chemistry. Corresponding molecular mechanical calculations were carried out in CHARMM, and parameter fitting was carried out using a Monte Carlo/simulated annealing (MC/SA) protocol^[75] utilized in our previous work in refining the Drude-2017 DNA force field.^[41] Briefly, the target function was the root-mean-square difference (RMSD) between the computed force field energy and QM energy. MC moves were performed in parameter space, adjusting only the dihedral force constants; a move was accepted if the RMSD decreased or if the Metropolis criterion was accepted. Temperature was scaled periodically and convergence was defined as two consecutive steps producing a difference in RMSD of 0.001 or smaller.

Parametrization of the 2’-Hydroxyl Group.

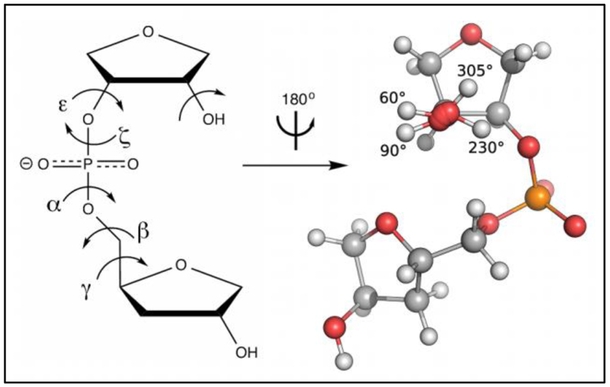
As in the development of the additive CHARMM36 force field,^{[14,15,76,77]} the principal model compound used in the parametrization of the Drude RNA force field was R3PS (Figure 2), which encompasses all the relevant degrees of freedom of the phosphodiester backbone of RNA as well as the 2’-hydroxyl. A previous QM study showed that the interplay between the backbone and 2’-hydroxyl group is important in determining the local flexibility and hydration properties of RNA.^[24] As such, backbone dihedrals, 2’-hydroxyl dihedrals, electrostatic properties, and water interactions are all intimately linked and must be carefully considered in the parametrization of the polarizable force field.

Figure 2.

Left, the structure of R3PS with backbone torsions labeled and the 2’-hydroxyl group used for parametrization indicated with a curved arrow. Right, the conformations of the 2’-hydroxyl (based on the C1’-C2’-O2’-H2’ dihedral angle) used for validating water interactions: 60° and 90° (base), 230° (O3’), and 305° (O4’).

Bonded and nonbonded parameters for R3PS were initially taken from the Drude-2017 DNA force field,^[41,42] and the 2’-hydroxyl group was assigned the nonbonded parameters of the Drude model of 2-propanol developed as part of the primary and secondary alcohol series.^[78] The initial configuration of R3PS was generated using the CHARMM program.^[63]

The first step in the parametrization was to refine the electrostatic terms (atomic charges, atomic polarizabilities, and Thole screening factors) of the 2’-hydroxyl group. The study of R3PS conformational energetics by Denning and MacKerell^[24] yielded a set of configurations based on the rotation of each backbone torsion and the 2’-hydroxyl. In these two-dimensional (2D) scans, each backbone torsion was restrained to values over 360° in increments of 15°. For each of these configurations, the 2’-hydroxyl torsion (defined as C1’-C2’-O2’-H2’) was also scanned in 15° increments over 360°. All other backbone torsions were restrained to their canonical A-RNA values. The dipole moments of these configurations served as the target data for the electrostatic refinement of the 2’-hydroxyl. The dipole moment of R3PS using the Drude force field was evaluated on the optimized geometry using fixed atomic coordinates while allowing the Drude oscillators to relax. The 2’-hydroxyl electrostatic terms were empirically adjusted by targeting the QM dipole moments computed using the MP2/6–31+G* model chemistry.

Parametrization of the dihedral terms for the 2’-hydroxyl group began with one-dimensional (1D) scans of the 2’-hydroxyl on the 5’-sugar of R3PS; the 2’-hydroxyl group on the 3’-sugar was kept fixed at 180° to simplify the fitting protocol. R3PS was constructed in an canonical A-RNA configuration during the scans, with all backbone torsions fixed at their canonical values and each sugar fixed in North pucker by restraining ν₀ to 0°. After QM optimization, the energy of each configuration was evaluated using the RIMP2/cc-pVTZ model chemistry.

Two dihedrals governing the conformation of the 2’-hydroxyl were included in the parametrization, C3’-C2’-O2’-H2’ and C1’-C2’-O2’-H2’. Initial parameters were taken from the existing Drude alcohol parameter set^[78] and were subsequently refined using the in-house Monte Carlo/simulated annealing protocol. Briefly, the target error function was the root-mean-square difference (RMSD) between the QM and Drude force field conformational energies. The force constants for each of the dihedral terms were allowed to vary, and new parameter sets were accepted if the RMSD decreased or if an increase in RMSD was acceptable according to the Metropolis criterion with an initial temperature of 500 K. The temperature was periodically scaled down by a factor of 0.75 until the difference in RMSD between parameter sets produced in consecutive Monte Carlo steps was less than 0.001 kcal mol^-1.

Interactions of the 2’-Hydroxyl Group with Water.

Interactions of water with the 2’-hydroxyl group were calculated at several representative values of the 2’-hydroxyl dihedral that included base (60° and 90°), O3’ (230°), and O4’ (305°) orientations (Figure 2). Backbone dihedrals (α, β, γ, ε, ζ, Figure 2) were fixed at their canonical A-RNA values, and North pucker was enforced by setting ν₀ = 0° during QM and MM calculations. Water molecules were kept rigid in the same internal geometry as the SWM4-NDP water model^[68] during QM optimizations.

Backbone Dihedral Parameter Fitting.

Given the interdependence of the RNA backbone and 2’-hydroxyl conformations on the resulting conformational sampling and energetics of RNA,^[24] these parameters had to be considered simultaneously in the fitting of force field parameters. Use of the Drude-2017 DNA parameters^[41,42] yielded poor behavior and reproduction of QM target data (not shown), thus requiring further optimization for use in RNA. To avoid a complete reparametrization of the Drude nucleic acid force field, a new, RNA-specific atom type was introduced to represent the O3’ atom in each nucleotide. The Lennard-Jones and electrostatic parameters of this atom are identical to those of the O3’ atom in DNA, but by its introduction, the α, ε, and ζ dihedral parameters could be fit freely. This approach is justifiable due to the fact that the local electronic environment near the O3’ is different between DNA and RNA due to the presence of the 2’-hydroxyl group. Additionally, doing so avoids completely reparametrizing the atoms of the sugar-phosphate backbone while allowing for compatibility among the DNA and RNA parameters, yielding a full nucleic acid parameter set. In the course of parameter optimization, it was also discovered that the γ torsion required additional tuning, and there was no way to avoid tuning without affecting the DNA force field. The γ parameters were subsequently optimized, and as will be shown below, the modifications made have no substantive effect on the properties of DNA in the system studied.

Dihedral refinement of the α, γ, ε, and ζ torsions in RNA was approached as follows. The conformational energy of R3PS was determined as a function of target dihedral rotation for chosen configurations of the 2’-hydroxyl group (90°, 180°, and 300°). These 1D surfaces were taken from 2D MP2/6–31+G*//RIMP2/cc-pVTZ QM potential energy surfaces calculated by Denning and MacKerell.^[24] The MC/SA protocol described above was used to refine the dihedral parameters for each of the backbone torsions. Following the 1D fitting of both the 2’-hydroxyl and all backbone dihedral terms, the conformational energetics of R3PS were evaluated against the full 2D QM potential energy surfaces.^[24]

RNA Validation Simulations.

To assess the quality of the newly derived parameters in full-length RNA, several systems were studied, covering both canonical and noncanonical structures (Table 1). Initial coordinates for all systems were obtained from the Protein Databank (PDB),^[79] to which any missing hydrogen atoms were added in CHARMM. All systems were initially prepared and equilibrated using the additive CHARMM36 force field.^[14,15] Each RNA was then centered within a cubic simulation cell with a minimum distance between the solute and the box edge of 10 Å filled with CHARMM-modified TIP3P water.^[80–82] Ions were added according to experimental conditions. Experimental buffers that contained <100 mM salt were modeled using neutralizing Na⁺ or K⁺ counterions, as appropriate. Any ions bound to the RNA structures in the crystal structure were retained, and in the case of the VS ribozyme (PDB 1YN2), Mn²⁺ ions, which were experimental surrogates for Mg²⁺, were replaced by Mg²⁺ ions for the simulations. Solvated systems were subjected to energy minimization in CHARMM^[63] by performing 1000 steps of steepest descent minimization followed by 2000 steps of adopted-basis set Newton-Raphson minimization. Solvent equilibration was performed using NAMD,^[83] for 1 ns under an NPT ensemble with restraints (k = 5.0 kcal mol⁻¹ Å⁻²) on all non-hydrogen RNA atoms, including any bound ions. Mobile ions in solution were not restrained during equilibration. Temperature was maintained at 298 K using Langevin dynamics with a friction coefficient of 5.0 ps⁻¹ and pressure was maintained at 1 atm with the Langevin piston method^[84] with a 200-fs oscillation period and 100-fs decay time. Bonds involving hydrogen atoms were constrained using SHAKE.^[85] Short-range van der Waals forces were switched to zero from 10 – 12 Å. Electrostatic interactions were calculated with PME,^[73,86] with a real-space cutoff of 12 Å. Neighbor lists were updated within 16 Å.

Table 1.

List of RNA systems used for force field training and validation.

	Method	PDB ID	Size (nt)	Notes
dsRNA, A-form helix	X-ray	1RNA[87]	28	400 mM MgCl2
dsRNA, A-form helixa	X-ray	1SDR[88]	24	100 mM NaCl
dsRNA, A-form helix	NMR	1YFV[89]	16	G·A mismatch, neutralizing Na+
Stem-loopa	NMR	1UUU[90]	19	100 mM NaCl
Stem-loop	NMR	2KOC[91]	14	UUCG loop, 100 mM KCl
Stem-loop	NMR	1YN1[92]	17	Neutralizing Na+
Stem-loop	NMR	1YN2[92]	17	Bound Mg2+, neutralizing Na+
Ribosomal RNA	X-ray	1HC8[93]	58	Bound Mg2+, K+, 150 mM KCl
Adenine riboswitch	X-ray	1Y26[94]	71	Apo and holo, bound Mg2+, neutralizing K+

^aThe dsRNA 1SDR and stem-loop 1UUU structures served as a training set for optimization of force field parameters. All other structures are considered an unbiased evaluation of the force field.

The equilibrated systems were converted to the Drude polarizable model, adding Drude oscillators to all non-hydrogen atoms and constructing lone pairs using CHARMM. This process also converted TIP3P water to polarizable SWM4-NDP water^[68] and ions to their polarizable forms, with monovalent ion parameters taken from Yu et al^[95] and Mg²⁺ parameters taken from our recent work.^[54] The polarizable systems were again subjected to energy minimization in CHARMM to relax the Drude oscillators, after which an additional 1-ns of restrained equilibration was carried out in NAMD, using the extended Lagrangian method for integrating Drude particle positions, implemented in NAMD as Langevin dynamics.^[72,96] The same protocol described above was applied, with the exception that the Drude force field applies a potential switch to the Lennard-Jones interactions rather than a force switch. Additionally, temperature was regulated in the polarizable systems using a dual thermostat approach,^[72] coupling the Drude oscillators to a low-temperature relative thermostat at 1 K, and all real atoms to a thermostat at ambient temperature.

Following equilibration, restraints were removed and simulations were carried out in OpenMM^[97,98] for 1.0 μs using the same integration scheme as described above for NAMD, except that in the OpenMM simulations, pressure was maintained at 1 atm using a Monte Carlo barostat, attempting box scaling every 25 fs.

To verify that the new force field parameters for the γ torsion did not adversely affect DNA, an additional 1-μs simulation of the Dickerson-Drew dodecamer (EcoRI recognition sequence) was performed in the same manner as the RNA simulations. The initial coordinates were taken from PDB accession code 1BNA^[99] and was used in our previous validation of the Drude-2017 DNA force field.^[42]

RESULTS AND DISCUSSION

Base Stacking Interaction Energies.

LJ parameters for the atom types comprising uracil were taken from our recent reparametrization of DNA bases^[41] without modification. The electrostatic parameters for uracil were taken from previous work by Baker et al.^[66] All other base parameters were taken from the Drude-2017 DNA force field.^[41,42] Using this force field model, we compared with QM base stacking energies for canonical, stacked A-RNA base dimers containing uracil. The Drude-2013 interaction energies were generally too weak (Table 2), consistent with the same observation with the DNA bases.^[41] The new parameters yielded interaction energies that were found to be in excellent agreement with the QM base stacking energies (Table 2) and were used without further modification. In principle, it is possible to perform additional tuning of the electrostatic parameters as was done for the DNA bases, but given the excellent level of agreement with the QM base stacking energies, and the pre-existing quality of agreement with QM dipole moments and gas-phase molecular polarizabilities with the electrostatic parameters from Baker et al.,^[66] such additional refinement was deemed unnecessary.

Table 2.

Total interaction energies (kcal mol⁻¹) for uracil-containing base stacked dimers.

Sequence	A-RNA
	QM*	C36	Drude-2013	Drude-2017
AU	−5.79	−6.01	−5.16	−5.66
CU	−6.86	−6.13	−5.27	−6.29
GU	−4.34	−6.14	−2.71	−3.53
UA	−5.97	−6.19	−4.58	−5.32
UC	−4.26	−5.10	−4.89	−6.09
UG	−2.93	−3.48	−2.33	−3.16
UU	−1.90	−2.93	−1.73	−1.96
Avg. Diff.		−0.56	0.77	0.01
Unsigned Avg. Diff.		0.77	0.95	0.61
RMSD		0.85	1.19	0.69
Spearman ρ		0.82	0.82	0.75
Pearson ρ		0.90	0.88	0.87

^*QM energies calculated using the MP2/aug-cc-pVDZ//DF-SCS-MP2/aug-cc-pVTZ model chemistry. “C36” denotes the additive CHARMM36 force field.^[14,15] “Drude-2013” denotes base parameters from Baker et al.^[66] “Drude-2017” denotes the parameters developed in the present work.

Uracil-Water Interactions.

The balance of base-base and base-water interactions is important for the stability of nucleic acid structures. To that end, we assessed the agreement of interactions of water with 1-methyluracil using the Drude-2017 force field to those obtained by QM calculations. The results of those calculations are shown in Table 3. In general, the Drude-2017 force field does not differ substantially from the previous base parameters,^[67] though there are some modest improvements using the new force field, particularly in out-of-plane interactions. This outcome is unsurprising given that the electrostatic parameters of the bases will dominate interactions with water, and the present force field uses the previous electrostatic parameters in conjunction with the refined LJ terms.

Table 3.

Water interaction energies (IE, kcal mol⁻¹) and minimum-energy distances (r, Å) for 1-methyluracil.

Interaction	QM		Drude-2013*		Drude-2017
	IE	r	IE	r	ΔIE	Δr
N1 oop	−0.10	2.34	−1.26	2.24	−1.26	2.24
C2 oop	−1.14	2.48	−1.29	2.44	−1.29	2.44
O2 oop	−3.82	2.06	−2.69	2.16	−2.69	2.16
O2 180	−4.30	2.02	−3.33	2.10	−3.33	2.10
O2 (N1)	−5.07	1.98	−3.65	2.00	−3.65	2.00
O2 (N3)	−5.40	1.92	−3.92	1.96	−3.92	1.96
N3 oop	−0.99	2.36	−1.24	2.28	−1.24	2.28
H3 180	−4.32	1.91	−4.82	1.86	−4.82	1.86
C4 oop	−1.70	2.52	−2.63	2.32	−2.63	2.32
O4 oop	−3.81	2.11	−4.35	2.10	−4.35	2.10
O4 180	−4.42	2.02	−4.73	2.05	−4.73	2.05
O4 (N3)	−5.90	1.90	−5.84	1.91	−5.84	1.91
O4 (C5)	−5.70	1.97	−4.90	2.09	−4.90	2.09
C5 oop	−1.49	2.45	−1.17	2.43	−1.17	2.43
H5 180	−1.95	2.26	−1.07	2.58	−1.07	2.58
C6 oop	−0.35	2.58	0.37	2.76	0.37	2.76
H6 180	−3.77	2.20	−6.82	2.12	−6.82	2.12
Avg. Diff. (all)			−0.14	−0.05	0.05	0.02
Abs. Avg. Diff. (all)			0.89	0.10	0.86	0.09
RMS Diff. (all)			1.15	0.14	1.14	0.12
Avg. Diff. (out-of-plane)			−0.13	−0.11	−0.11	−0.02
Abs. Avg. Diff. (out-of-plane)			0.66	0.13	0.65	0.09
RMS Diff. (out-of-plane)			0.77	0.15	0.75	0.11
Avg. Diff. (in-plane)			−0.14	0.00	0.19	0.05
Abs. Avg. Diff. (in-plane)			1.09	0.08	1.05	0.08
RMS Diff. (in-plane)			1.35	0.11	1.34	0.12

^*Some values obtained using the Drude-2013 differ from those reported by Baker et al.^[66] due to refinement, especially of internal terms, during the course of the development of the Drude-2013 DNA force field.^[39,40]

Heats of Sublimation and Crystal Volumes.

A useful metric in assessing the quality of small-molecule nonbonded parameters is to perform simulations of those species in a crystal form. These systems are highly ordered, allowing for a simple quantification of crystal volumes (V_m) as well as calculating heats of sublimation (ΔH_sub), which reflect the quality of the interaction energies between the species. The calculated ΔH_sub for both uracil and 1-methyluracil are listed in Table 4, and V_m are listed in Table 5. The ΔH_sub values are systematically too favorable using the new Drude-2017 parameter set, similar to our previous findings regarding the DNA bases.^[41] We attribute this behavior to hydrogen-bonding interactions involving the O2 and O4 atoms of uracil, which use the OD2C1B atom type. The R_min/2 parameter for this atom type was reduced during parameter fitting when targeting base stacking interaction energies in the DNA bases.^[41] This shortened radius leads to more favorable interactions in crystal systems. In the context of V_m, these favorable interactions make a small improvement in the agreement of the Drude-2017 force field with experimental data (Table 5), particularly in the case of 1-methyluracil.

Table 4.

Heats of sublimation (ΔH_sub, kcal mol⁻¹). Results are the average of ten independent simulations. Experimental reference values are taken from Chickos and Acree.^[100]

Base	Experiment	Temp (K)	Drude-2013*	% Diff	Drude-2017	% Diff
Ura	30.35	439	29.02	−1.3	30.31	−0.1
	31.30	298	30.01	−4.1	31.46	0.5
Me-Ura	26.89	398	27.94	3.9	29.55	9.9
Avg. Diff.			−0.52	−0.5%	0.93	3.4%
AUE			1.22		0.95
RMSD			1.23		1.54

^*Some values obtained using the Drude-2013 differ from those reported by Baker et al.^[66] due to refinement, especially of internal terms, during the course of the development of the Drude-2013 DNA force field.^[39,40]

Table 5.

Molecular volumes (V_m, ų). Results are the average of ten independent simulations.

Base	Experiment	Temp (K)	Drude-2013*	% Diff	Drude-2017	% Diff
Ura	115.8[70]	298	114.4	−1.4	116.7	0.8
Me-Ura	134.1[69]	15	136.3	1.7	135.4	1.0
Avg. Diff.			0.40	0.2%	1.10	0.9%
AUE			1.80		1.10
RMSD			1.84		1.12

^*Some values obtained using the Drude-2013 differ from those reported by Baker et al.^[66] due to refinement, especially of internal terms, during the course of the development of the Drude-2013 DNA force field.^[39,40]

Optimized Electrostatic Parameters for the 2’-Hydroxyl Group.

The first step in optimizing the parameters for the 2’-hydroxyl group was to tune the electrostatic parameters (charges, atomic polarizabilities, and Thole screening factors). By targeting QM dipole moments as a function of the conformations of the backbone and 2’-hydroxyl torsions, the approach serves as an indicator of the quality of the electronic behavior in the context of the R3PS model compound across a wide range of canonical and noncanonical geometries. The initial electrostatic parameters for the 2’-hydroxyl group were taken from 2-propanol, developed as part of the primary and secondary alcohol series in the Drude force field.^[78] Direct application of those parameters led to empirical dipole moments that were systematically too high by 1–2 D relative to the QM values. To improve the quality of these surfaces, we reduced the magnitude of the charges on the lone pairs on the oxygen atom, and subsequently compensated for this adjustment in charge by reducing the magnitude of the charge on the hydroxyl hydrogen atom (H2’). The shielding of the O2’ atom was enhanced by lowering its atomic Thole screening factor. The final, optimized parameters for the 2’-hydroxyl group (Table 6) led to excellent agreement with dipole moments calculated with the MP2/6–31+G* model chemistry (Figure 3) as well as the interactions with water, as described in the following section.

Table 6.

Optimized electrostatic parameters for the 2’-hydroxyl group.

Parameter	C2’	H2’’	O2’	H2’	LP a
qA (e) b	1.934	0.100	1.375	0.260	−0.180
qD (e)c	−1.934		−1.375
α (Å3)	1.242		0.628
Thole factor	1.103		0.181

^aThere are two lone pairs (LP) attached to each O2’ atom that carry the O2’ partial atomic charge.

^bCharge on the indicated atom and

^cthe Drude oscillator attached to that atom.

Figure 3.

The 2D QM (top row) and Drude-2017 force field (bottom row) dipole moment surfaces for the 2’-hydroxyl group as a function of each of the backbone phosphodiester torsions (α, β, γ, ε, and ζ). The dipole moment scale is in Debye. The R3PS model compound with each of the torsions labeled is shown at the top left. The calculated QM dipole moments were obtained with the MP2/6–31+G* model chemistry and are taken from work by Denning and MacKerell.^[24]

Water Interactions of the RNA 2’-Hydroxyl Group.

Conformational sampling of the 2’-hydroxyl group in RNA is influenced, in part, by hydration.^[14,24] Therefore, an accurate representation of water interactions with this group is essential for modeling RNA. Having adjusted the electrostatic parameters of this group by targeting the R3PS molecular dipole moment, the quality of these parameters was additionally examined in the context of interactions with individual water molecules. Four poses of water around the 2’-hydroxyl group were examined in the present study. In the first, the water molecule acts as a hydrogen-bond acceptor, with the H2’ atom of the 2’-hydroxyl as the donor (H2’ donor). In the remaining three poses, the water molecule serves as a hydrogen-bond donor, with the O2’ atom serving as the acceptor with the water aligned along the bisector of the C2’-O2’-H2’ angle (O2’ bis), and interacting with each of the two oxygen lone pairs (lp 0 and lp 180). Additional possible poses of water were excluded from use as target data due to either steric clashes with other atoms in R3PS that made geometry optimization impossible, or those in which water interacted extensively with other R3PS atoms, such that these poses were dominated by interactions aside from the 2’-hydroxyl. The final list of poses used as target data and their corresponding interaction energies and distances are shown in Table 7.

Table 7.

Water interactions with the 2’-hydroxyl group of R3PS. Interaction energies (IE, kcal mol⁻¹) are calculated at the RIMP2/cc-pVQZ level of theory following geometry optimization with the MP2/6–31+G* model chemistry. Distances (Å) were calculated from the MP2/6-31+G* optimized geometries. Base, O3’, and O4’ geometries are as defined by Denning and MacKerell,^[24] and the exact value of the C1’-C2’-O2’-H2’ dihedral for each selected geometry is shown in parenthesis.

	QM		Drude-2017
Base (60°)	IE	r	IE	r
H2’ donor	−2.49	2.04	−1.19	2.04
O2’ bis	−6.41	2.27	−6.51	2.04
O2’ lp 180	−2.24	3.60	−3.30	3.34
	Avg. Diff.		0.05	−0.11
	Abs. Avg. Diff.		0.82	0.16
Base (90°)	IE	r	IE	r
O2’ bis	−5.65	2.08	−6.00	1.96
O2’ lp 0	−2.47	5.87	−2.77	6.18
O2’ lp 180	−6.61	2.08	−7.23	1.93
	Avg. Diff.		−0.42	0.01
	Abs. Avg. Diff.		0.42	0.20
O3’ (230°)	IE	r	IE	r
O2’ bis	−8.68	1.95	−8.14	1.86
O2’ lp 0	−6.32	2.09	−6.29	1.99
O2’ lp 180	−2.47	3.84	−3.24	4.05
	Avg. Diff.		−0.07	0.01
	Abs. Avg. Diff.		0.45	0.13
O4’ (305°)	IE	r	IE	r
O2’ bis	−3.16	3.25	−3.29	4.01
O2’ lp 0	−8.94	1.97	−8.67	1.84
	Avg. Diff.		0.07	0.32
	Abs. Avg. Diff.		0.20	0.44
	Avg. Diff. (all)		−0.11	0.03
	Abs. Avg. Diff. (all)		0.50	0.21
	RMSD (all)		0.59	0.28

2’-Hydroxyl Dihedral Parameter Fitting.

Following the adjustment of electrostatic parameters, torsional parameters for the 2’-hydroxyl were parametrized by targeting a 1D potential energy surface for the rotation of the 2’-hydroxyl of the 5’-sugar in R3PS. The ability of the Drude force field to reproduce QM conformational energetics, especially for noncanonical geometries, has been cited as a primary reason behind the quality of the previous Drude-2013 DNA force field,^[39] and RNA structure is sensitive to 2’-hydroxyl sampling.^[14,24] Therefore, obtaining good conformational energetics is critical to producing an accurate force field. The results of the potential energy scan for the 2’-hydroxyl group using the final, optimized force field parameters are shown in Figure 4. The Drude potential energy surface matches the QM data well, producing the same positions and magnitudes of the minima and the barrier between them.

Figure 4.

One-dimensional potential energy scan of the 2’-hydroxyl group on the 5’-sugar in R3PS. QM energies were evaluated using the RIMP2/cc-pVTZ model chemistry after MP2/6–31+G* optimization.

Backbone Dihedral Parameter Fitting.

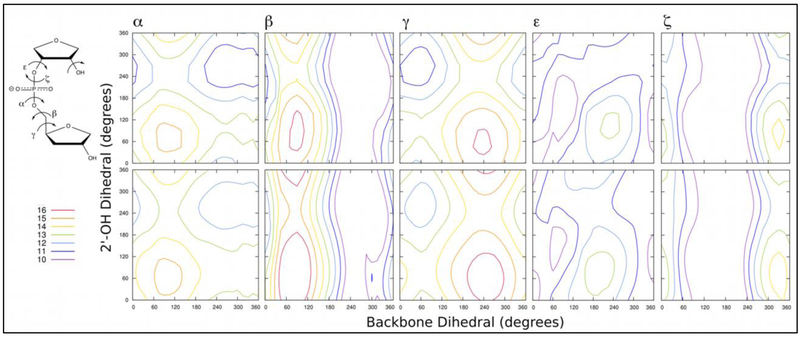
Given the interrelationship between the position of the 2’-hydroxyl and RNA backbone flexibility,^[24] it is necessary to consider them simultaneously. Having determined a suitable parameter set for the dihedral rotation of the 2’-hydroxyl group, we proceeded to refining backbone terms. Target data for backbone refinement were two-dimensional potential energy surfaces of the R3PS model compound as a function of both the 2’-hydroxyl configuration and the target backbone dihedral. Backbone dihedral parameters were determined by taking one-dimensional slices of the surfaces at fixed values of the 2’-hydroxyl (90°, 180°, and 300°). Attempts at fitting to the full potential energy surfaces did not yield usable parameters, as there are several features in all surfaces that arise due to the fact that the QM calculations were carried out in vacuo, leading to overly strong hydrogen bonding interactions in some regions of the surfaces that are not relevant to RNA and led to distortions in dsRNA simulations (data not shown). While it is possible to obtain close agreement between the QM target surfaces and those produced by the empirical force field, this level of agreement was undesirable.

Having fit the one-dimensional surfaces, the obtained parameters were validated in the full two-dimensional surfaces. Results are shown in Figure 5. In general, the Drude-2017 force field produces good agreement with the overall shapes of the target QM potential energy surfaces, capturing all of the positions of minima associated with canonical values of each of the backbone dihedrals in RNA. The Drude-2017 surfaces are, in general, somewhat more sharply defined than the QM surfaces, which tend to have broad minima, but as stated above, many of the configurations in those minima were a result of overly favorable intramolecular interactions that are not significantly sampled in solvated, full-length RNA.

Figure 5.

The 2D QM (top row) and Drude-2017 force field (bottom row) energy surfaces for the 2’-hydroxyl group as a function of each of the backbone phosphodiester torsions (α, β, γ, ε, and ζ). The energy scale is in kcal mol^-1. QM energy surfaces were obtained at the MP2/6–31+G*//RIMP2/cc-pVTZ level of theory and are taken from work by Denning and MacKerell.^[24]

The initial refinement strategy for these dihedrals relied on a unique O3’ atom type to be used in RNA (see Methods) to allow free tuning of α, ε, and ζ dihedral parameters without impacting DNA, which already produced good dihedral distributions.^[42] However, during the course of initial parameter evaluation, it became clear that refinement of the γ torsion would be necessary, thus potentially impacting the behavior of DNA. The α, ε, and ζ dihedral parameters remain unique to RNA, but the new γ parameters are applied to both RNA and DNA. As will be shown below, the new γ parameters led to acceptable behavior in the EcoRI DNA duplex. All newly added and refined dihedrals for RNA and DNA are shown in Table 8.

Table 8.

Optimized dihedral parameters for the 2’-hydroxyl and backbone torsions.

Torsion	k (kcal mol−1 rad−2)	Multiplicity	Phase Angle (°)
C1’-C2’-O2’-H2’	2.360	1	0.0
	0.830	2	0.0
	0.340	3	0.0
C3’-C2’-O2’-H2’	2.360	1	0.0
O3’-P-O5’-C5’ (α)	2.500	1	180.0
O1P/O2P-P-O5’-C5’ (α2)	0.300	3	0.0
O5’-C5’-C4’-C3’ (γ)	1.708	1	180.0
	0.305	2	0.0
	0.344	3	0.0
O5’-C5’-C4’-O4’ (γ2)	1.631	1	180.0
C4’-C3’-O3’-P (ε)	2.653	1	180.0
C3’-O3’-P-O5’ (ζ)	2.250	1	180.0
C3’-O3’-P-O1P/O2P (ζ2)	0.500	1	0.0
	1.500	2	180.0
	0.750	3	0.0

χ Dihedral Refinement.

As RNA structures can adopt many complex folds requiring noncanonical orientations of the nucleobases, an accurate description of the glycosidic (χ) torsion is important for the performance of the force field. To this end, we targeted one-dimensional dihedral scans of RNA nucleosides. Anticipating the need for consistency between DNA and RNA systems, this refinement was carried out as part of the development of the Drude-2017 DNA force field, and therefore no new parameters are introduced here. Results of the χ dihedral refinement are shown in Figure 6. The minima at χ ~ 200° that are characteristic of canonical A-RNA are well reproduced in all four RNA nucleosides. Each nucleoside features a prominent local minimum in the syn region of the χ surface. The Drude-2017 force field models this minimum well for guanosine, and to a lesser extent, adenosine, but the energy of these states for both pyrimidines are overestimated by the force field. We observed a similar outcome in the deoxypyrimidines in our previous work on the Drude-2017 DNA force field.^[41] It is possible that the electronegative base atoms, such as O2 in both cytosine and uracil, are interacting unfavorably with the ribofuranose ring, requiring additional optimization in the future. As the syn state of these nucleosides is rarely observed,^[101] the current agreement was deemed adequate for the present version of the force field.

Figure 6.

One-dimensional χ potential energy surfaces in each of the four RNA nucleosides. QM energies were evaluated using the RIMP2/cc-pVTZ model chemistry after MP2/6–31G* optimization.

Simulations of Canonical Duplex RNA Structures.

The first validation of the Drude-2017 RNA force field was an examination of the stability of canonical dsRNA structures. Two dsRNA were chosen for this assessment, one (PDB 1RNA)^[87] composed entirely of adenine and uracil and the other (PDB 1SDR)^[88] containing 40% guanine and cytosine. The 1RNA sequence was previously identified as challenging to model due to its low melting temperature and sensitivity to 2’-hydroxyl sampling;^[14] it is stabilized in solution either at low temperature or in the presence of large amounts of Mg²⁺.^[87] In this work, we have chosen to use a high MgCl₂ concentration of 400 mM to both stabilize the 1RNA sequence according to previously used experimental conditions.^[87] The 1SDR sequence was simulated in 100 mM NaCl, reflecting typical simulation conditions. We reiterate that multiple simulations of the 1RNA and 1SDR sequences were performed during the parameter optimization process with results from those simulations used to drive additional optimization (not shown). The results below are for the final parameters; the remaining RNA systems in Table 1, excluding the non-canonical 1UUU structure, were only simulated using the final parameter set and, thus, may be considered true validation cases.

Both the 1RNA and 1SDR sequences were stable over the course of 1-μs MD simulations. The average RMSD of non-terminal heavy atoms in 1RNA was 1.8 ± 0.3 Å, and for 1SDR it was 1.9 ± 0.5 Å. Despite some transient fluctuations (Figure 7), the overall structures were well preserved relative to their crystal reference structures, indicating no systematic unfolding or distortion of these canonical A-form helices. Some fraying of the terminal base pairs was observed in both the 1RNA and 1SDR simulations, but no structural distortions occurred beyond the end base pair in each duplex. The backbone and glycosidic dihedral sampling in each of these structures also agreed well with crystal survey data (Figure 8), confirming that the conformational ensembles of 1RNA and 1SDR were compatible with expected behavior of canonical dsRNA. Additional analysis of the helicoidal parameters of each base pair similarly revealed that the dsRNA ensembles are compatible with crystal survey data (Supporting Figure S1), including the systematically elevated roll value in the 1RNA structure. In this system, the average roll value was 11.2 ± 11.1°, in agreement with the experimentally determined value of 9.4 ± 5.2°.

Figure 7.

Left, RMSD time series for non-terminal heavy atoms of both of the canonical dsRNA sequences with respect to the experimentally determined crystal structures (black). Running averages over 5-ns windows (red) are shown to smooth fluctuations. Right, structural snapshots of 1RNA (top, red) and 1SDR (bottom, blue) from the end of 1-μs simulations overlaid on the corresponding crystal structures (gray).

Figure 8.

Backbone and glycosidic linkage dihedral distributions for 1RNA and 1SDR, overlaid with RNA crystal survey data.

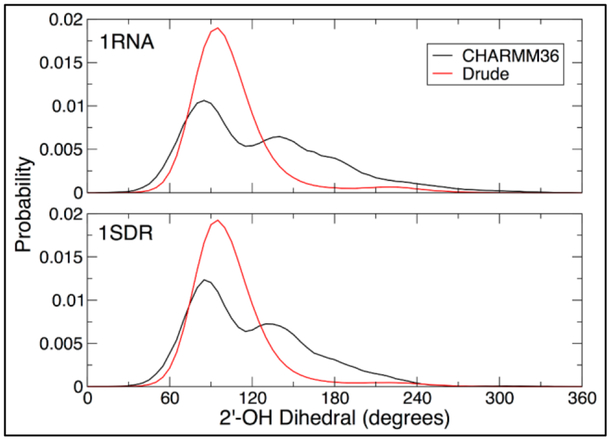
Another important aspect of dsRNA structural stability is the sampling of the 2’-hydroxyl groups. For canonical, A-form RNA structures, the 2’-hydroxyl group is expected to sample primarily “base” configurations, with C1’-C2’-O2’-H2’ dihedral values ranging from 60°−120°.^[24] In the refinement of the additive CHARMM36 force field, the reparametrization of dihedral parameters related to the 2’-hydroxyl was crucial in stabilizing RNA structures, confirming its importance in the production of an accurate RNA force field.^[14] As there is limited structural information about 2’-hydroxyl orientations from crystal and NMR structures, a comparison of the 2’-hydroxyl dihedral sampling in 1RNA and 1SDR with the Drude-2017 force field and CHARMM36 is shown in Figure 9. The CHARMM36 simulations confirm the previously observed dihedral sampling,^[14] with a major peak in the base region and a shoulder above 120°, towards the O3’ orientation at 180°. The Drude-2017 results show a more prominent peak in the base region and only small amounts of O3’ sampling, indicating that the base orientation dominates over all other 2’-hydroxyl configurations in dsRNA, as expected. In conjunction with the fact that the Drude-2017 force field produced stable simulations of these structures, it can be concluded that the 2’-hydroxyl sampling in the force field is appropriate in simulations of canonical, A-form RNA.

Figure 9.

Distributions of 2’-hydroxyl dihedrals in additive (CHARMM36) and polarizable (Drude) 1RNA and 1SDR systems, taken from 1-μs simulations.

Simulations of a G·A Mismatched dsRNA.

Base-pair mismatches are common in RNA structures. To assess the ability of the Drude-2017 RNA force field to model such structures, we performed a 1-μs simulation of the 1YFV RNA duplex, which contains G·A mismatches at its central two base pairs. Structural determination by solution NMR^[89] provides a wealth of data to which the simulation results can be compared to test the quality of the force field. An important note regarding these comparisons is that experimental data were collected at 308 K,^[89] whereas the MD simulations were performed at 298 K, so some level of discrepancy may be introduced as a result. The 1YFV structure remained stable over the 1-μs simulation, maintaining an average non-terminal heavy atom RMSD of 0.8 ± 0.2 Å. The quality of the dihedral sampling of the force field was compared to experimentally determined ³J-coupling values. Dihedral values from each snapshot were converted to ³J-coupling via the following Karplus equations for the β torsion:

$${}^{3}J_{H{5}^{\prime }-P}=\frac{1}{N}\sum \begin{array}{c}N\hfill \\ i=1\hfill \end{array}15.3{\mathit{cos}}^2\left({\beta }_i-120°\right)-6.1\mathit{cos}\left({\beta }_i-120°\right)+1.6$$ (3)

$${}^{3}J_{H{5}^{″}-P}=\frac{1}{N}\sum \begin{array}{c}N\hfill \\ i=1\hfill \end{array}15.3{\mathit{cos}}^2\left({\beta }_i+120°\right)-6.1\mathit{cos}\left({\beta }_i+120°\right)+1.6$$ (4)

For the γ torsion:

$${}^{3}J_{H{4}^{\prime }-H{5}^{\prime }}=\frac{1}{N}\sum \begin{array}{c}N\hfill \\ i=1\hfill \end{array}9.7{\mathit{cos}}^2\left({\gamma }_i-120°\right)+1.8\mathit{cos}\left({\gamma }_i-120°\right)$$ (5)

$${}^{3}J_{H{4}^{\prime }-H{5}^{″}}=\frac{1}{N}\sum \begin{array}{c}N\hfill \\ i=1\hfill \end{array}9.7{\mathit{cos}}^2\left({\gamma }_i\right)+1.8\mathit{cos}\left({\gamma }_i\right)$$ (6)

For the ε torsion:

$${}^{3}J_{H{3}^{\prime }-P}=\frac{1}{N}\sum \begin{array}{c}N\hfill \\ i=1\hfill \end{array}15.3{\mathit{cos}}^2({\epsilon }_i+120°)-6.1\mathit{cos}({\epsilon }_i+120°)+1.6$$ (7)

For the sugar torsions ν₁, ν₂, and ν₃:

$${}^{3}J\left({\nu }_n\right)=\frac{1}{N}\sum \begin{array}{c}N\hfill \\ i=1\hfill \end{array}9.67{\mathit{cos}}^2\left({\nu }_{n_i}\right)-2.03\mathit{cos}\left({\nu }_{n_i}\right)$$ (8)

Calculated ³J-coupling values were averaged over equivalent positions in the palindromic nucleotides. Results are listed in Tables 9–11. Overall, there is good agreement between the results produced by MD simulations with the Drude-2017 force field and those obtained experimentally. There are some deviations, particularly in the sugar torsions, suggesting that the Drude force field, while primarily sampling the expected North pucker form, does not capture the correct amplitude of these pseudodihedrals. Towards the 5’-terminal of each nucleotide chain, the North amplitude is overestimated, whereas at the 3’-terminal Cyt8, the North amplitude is underestimated. Sugar pucker conformations of the central residues (Gua2-Cyt7) were modeled accurately. A comparison of the individual sugar dihedrals reveals these tendencies (Supporting Information Table S1). When comparing the sugar dihedral values for non-terminal nucleotides from the MD trajectory against the deposited 1YFV PDB structure, it is clear that ν₁ is generally overestimated by 3–5°, ν₂ underestimated by 2°, and ν₃ is generally modeled very accurately. Taking into account the standard fluctuations of these values and the fact that only a single NMR conformation is deposited in the PDB, the agreement for these central nucleotides is very strong. Additional verification against dsRNA structures determined by NMR is warranted in the future.

Table 9.

Sugar torsion ¹H-¹H ³J-coupling constants (Hz) for the 1YFV system. Experimental values are taken from Santa Lucia et al.^[89] MD values are the time averages of the 1-μs simulation. Error bars for the MD data are the root-mean-square (RMS) fluctuations over the entire time series.

Nucleotide	v1 (H1’-H2’)		ν2 (H2’-H3’)		ν3 (H3’-H4’)
	Expt.	MD	Expt.	MD	Expt.	MD
G1	2 ± 1	0.5 ± 0.7			8 ± 2	11.2 ± 0.5
G2	< 2	0.5 ± 0.6	5 ± 1	3.1 ± 0.8	9 ± 1	11.1 ± 0.5
C3	< 2	0.6 ± 0.6
G4	2 ± 1	0.4 ± 0.5	5 ± 1	3.5 ± 0.9	10 ± 2	10.8 ± 0.7
A5	< 2	0.5 ± 0.7	5 ± 1	3.2 ± 0.9	10 ± 1	11.1 ± 0.6
G6			5 ± 1	3.1 ± 0.9
C7	< 2	0.5 ± 0.6	5 ± 1	3.3 ± 0.9	9 ± 2	11.1 ± 0.5
C8	3 ± 1	0.9 ± 0.4	5 ± 1	4.4 ± 1.1	9 ± 2	3.5 ± 4.5

Table 11.

Backbone ε and β torsion ¹H-³¹P ³J-coupling constants (Hz) for the 1YFV system. Experimental values are taken from Santa Lucia et al.^[89] MD values are the time averages of the 1-μs simulation. Error bars for the MD data are the RMS fluctuations over the entire time series.

Nucleotide	ε (H3’-P)		β1 (H5’-P)		β2 (H5’’-P)
	Expt.	MD	Expt.	MD	Expt.	MD
G1	9 ± 1	6.8 ± 1.9
G2	7 ± 3	7.2 ± 1.7			7 ± 1	1.4 ± 0.5
C3	11 ± 1	9.2 ± 1.3
G4	7 ± 1	2.6 ± 1.4	4 ± 1	4.2 ± 1.6	< 3	1.6 ± 0.8
A5	10 ± 1	9.9 ± 1.0	5 ± 1	3.1 ± 1.6	5 ± 3	2.4 ± 1.8
G6	10 ± 3	6.4 ± 1.7			5 ± 1	1.6 ± 0.8
C7	10 ± 1	7.7 ± 1.6	5 ± 1	4.7 ± 1.7	< 3	1.5 ± 0.7
C8			< 3	3.9 ± 1.7	4 ± 1	1.9 ± 1.2

Canonical, A-form RNA helices typically sample γ conformations in the gauche⁺ region (Figure 8). In the simulation of the 1YFV structure, we obtained good agreement between the NMR ³J-coupling constants related to this torsion. For example, the trend upon going from G1 to G2 and G4 to G5 or the γ₁-associated constant is reproduced, which is important for the latter given that the G·A mismatches are located at positions 4 and 5 in the oligonucleotide. In addition, the γ values were in close agreement with those of the deposited PDB structure (Supporting Information Table S2), aside from the 5’-terminal guanine nucleotide, which fluctuated over a large range. Despite such flexibility, the computed ³J-coupling constants for the γ₁ and γ₂ torsions agreed well with experimental data (Table 10).

Table 10.

Backbone γ torsion ¹H-¹H ³J-coupling constants (Hz) for the 1YFV system. Experimental values are taken from Santa Lucia et al.^[89] MD values are the time averages of the 1-μs simulation. Error bars for the MD data are the RMS fluctuations over the entire time series.

Nucleotide	γ1 (H4’-H5’)		γ2 (H4’-H5’’)
	Expt.	MD	Expt.	MD
G1	6 ± 1	6.5 ± 2.0	< 3	3.7 ± 1.9
G2	4 ± 1	3.2 ± 1.5	< 3	3.7 ± 1.6
C3	< 3	4.2 ± 1.5	< 3	2.7 ± 1.3
G4	< 3	2.9 ± 1.3	< 3	4.0 ± 1.4
A5	4 ± 1	3.4 ± 1.5	< 3	3.5 ± 1.5
G6
C7	< 3	4.1 ± 1.5	< 3	2.8 ± 1.3
C8	< 3	4.6 ± 1.8	< 3	2.4 ± 1.5

Backbone ε and β torsions are reported experimentally via H-P ³J-coupling constants. Results of these calculations are shown in Table 11 and corresponding dihedral values from the MD simulations and NMR structure are reported in Supporting Information Table S3. The trends in the ³J-coupling constants for the ε torsion are largely reproduced by the force field, with the decrease going from C3 to G4 followed by the increase upon going to A5 reproduced, though the calculated coupling constant for G4 is underestimated. Based on the modeled NMR structure the agreement for the ε torsion is strong, and in near-quantitative agreement at the G·A mismatch at positions 4 and 5 (Table S3), despite the apparent mismatch in the ³J-coupling constants in Table 11. In contrast to the canonical ε value of 211° in A-form RNA (Figure 8), Gua4 and Ade5 in 1YFV are modeled in the NMR ensemble with ε ~180° and ~220°, respectively. Drude-2017 reproduces these values well (Supporting Information Table S3), indicating that the ε dihedral parameters are sufficiently accurate, which is difficult given the “soft” nature of this torsion, manifesting itself in broad minima in the intrinsic potential energy surface (Figure 5). The apparent discrepancy between the ³J-coupling constants and the dihedral values in the NMR ensemble reflects the underdetermined nature of RNA structural modeling, leading to a challenge in assessing force field quality and emphasizing the need to examine both the primary NMR data (here, the ³J-coupling constants) as well as the modeled ensemble. Further analysis of NMR-derived RNA structures would be beneficial in the future to more completely characterize the behavior of this backbone torsion and the agreement of the Drude-2017 force field in this regard.

Intra- and inter-residue distances can be quantified experimentally from nuclear Overhauser effects (NOE). The comparison between these distances and those obtained during the MD simulation are shown in Tables 12–13. All distances are in quantitative agreement with the experimental distances, with the exception of Cyt8, the terminal nucleotide in each chain. The results for Cyt8 reflect a slightly greater flexibility than is experimentally observed, which is related to the overestimated flexibility of the sugar in this nucleotide (Table 9, Supporting Information Table S1). The wider range of sugar conformational sampling produced using the Drude-2017 force field gives rise to greater inter-nucleotide distances than experimentally characterized, requiring further refinement in the future.

Table 12.

Intra-nucleotide distances (Å) in the 1YFV system. Experimental values are taken from Santa Lucia et al.^[89] MD values are the time averages of the 1-μs simulation. Error bars for the MD data are the RMS fluctuations over the entire time series.

Nucleotide	H8/H6-H1’		H8/H6-H2’		H8/H6-H3’
	Expt.	MD	Expt.	MD	Expt.	MD
G1	3.9 ± 0.8	3.7 ± 0.1	4.0 ± 0.8	4.3 ± 0.2	3.5 ± 0.6	3.1 ± 0.3
G2	4.4 ± 0.8	3.8 ± 0.1	3.6 ± 0.8	4.0 ± 0.2	> 2.4	2.8 ± 0.2
C3	3.5 ± 0.8	3.5 ± 0.1	3.3 ± 0.6	3.8 ± 0.1	3.1 ± 0.6	2.6 ± 0.2
G4	3.7 ± 0.8	3.8 ± 0.1	3.5 ± 0.7	4.0 ± 0.2	2.8 ± 0.6	2.7 ± 0.2
A5	3.7 ± 0.8	3.7 ± 0.1	4.0 ± 0.8	4.2 ± 0.2	3.0 ± 0.6	3.1 ± 0.3
G6			> 3.5	4.0 ± 0.2	2.9 ± 0.6	2.8 ± 0.2
C7	3.6 ± 0.8	3.5 ± 0.1			2.7 ± 0.5	2.5 ± 0.2
C8	3.7 ± 0.8	3.6 ± 0.1	3.2 ± 0.6	2.7 ± 0.6	2.5 ± 0.5	3.8 ± 0.7

Table 13.

Inter-nucleotide distances (Å) in the 1YFV system. Experimental values are taken from Santa Lucia et al.^[89] Values in parenthesis reflect the distances most essential to the structural refinement. Error bars for the MD data are the RMS fluctuations over the entire time series.

Nucleotides	H1’-H8/H6		H2’-H8/H6		H3’-H8/H6
	Expt.	MD	Expt.	MD	Expt.	MD
G1-G2	4.7 ± 0.8	4.9 ± 0.2	2.6 ± 0.5	2.3 ± 0.2	> 2.4	3.2 ± 0.3
G2-C3	4.2 ± 0.8	4.8 ± 0.2	2.7 ± 0.5	2.1 ± 0.2	3.8 ± 0.8	3.3 ± 0.3
C3-G4	4.2 ± 0.8	5.2 ± 0.4	2.7 ± 0.5 (2.2)	2.8 ± 0.5	3.0 ± 0.6 (2.6)	2.6 ± 0.3
G4-A5	4.4 ± 0.8	4.5 ± 0.3	3.2 ± 0.6 (2.7)	2.5 ± 0.3	> 4.0 (4.5)	4.6 ± 0.3
A5-G6	4.5 ± 0.8	5.3 ± 0.4	3.1 ± 0.6 (3.3)	3.2 ± 0.6	2.7 ± 0.5 (2.2)	2.4 ± 0.2
G6-C7			2.3 ± 0.5	2.1 ± 0.2	3.1 ± 0.6	3.5 ± 0.3
C7-C8	3.8 ± 1.0	5.2 ± 0.3	2.3 ± 0.5	2.5 ± 0.4	3.5 ± 0.6	3.3 ± 0.3

Simulations of RNA Stem-Loops.

As RNA tetraloop structures are important to stabilizing RNA secondary structure, they serve as an important indicator of force field quality.^{[28,102–104]} Four RNA stem-loop structures were simulated in this work: 1UUU, 2KOC, 1YN2, and 1YN1. All experimental structures were determined by solution NMR. The 1UUU stem-loop served as part of the training set for the force field, while the remaining three stem-loops comprised an unbiased test set.

To characterize the agreement of the 1UUU simulation data with experiments, we compared the computed scalar ³J-coupling constants with those reported by Sich et al.^[90] The best-resolved ³J-coupling constants from the experiment are reported in Table 14. Additional values were reported by Sich et al., but due to degeneracy, weak crosspeaks, and some peak overlap, not all of those data were used in structural refinement for 1UUU.^[90] Full comparisons to these data are given in Supporting Information Tables S4-S6. The agreement of the Drude-2017 simulation results with the best-resolved ³J-coupling constants from experiments (Table 14) and other ³J-coupling constants (Supporting Information Tables S4-S6) is strong, indicating that the simulation produced experimentally compatible results across nucleotides in both the canonical stem and noncanonical loop regions (Figure 10). There are several signals, particularly for the ε torsion, that are not well reproduced by the force field, but as observed above in the case of the 1YFV dsRNA, even small dihedral discrepancies may produce large deviations in ³J-coupling constants. An examination of the backbone dihedral angle distributions in the loop region from the NMR ensemble and the Drude-2017 simulation reveals that there are some deviations in the sampled values of ε relative to those present in the NMR ensemble (Supporting Figure S2). Other backbone torsions are well modeled, including gauche⁺ states for both α and ζ, which are not observed in canonical dsRNA. The ε potential energy surface (Figure 5) is characterized by multiple minima separated by low barriers, indicating that this torsion is amenable to conformational change and as such, could be a source of error in the force field. Further work will be necessary to identify the root cause of the structural deviations, though minor, in the 1UUU sequence.

Table 14.

Scalar ³J-coupling constants (Hz) for the 1UUU stem-loop structure. Experimental values are taken from Sich et al.^[90] MD values are the time averages of the 1-μs simulation. Error bars for the MD data are the RMS fluctuations over the entire time series.

Nucleotide	Signal	Torsion	Expt. 3J (Hz)	MD 3J (Hz)
Ura5	H1’-H2’	ν1	0.7 ± 1	0.6 ± 0.7
Ura5	H2’-H3’	ν2	4.2 ± 1	3.4 ± 0.9
Ura5	H3’-H4’	ν3	11.0 ± 1	11.1 ± 0.5
Ura11	H5’-P	β1	4.5 ± 3	5.0 ± 2.1
Ura11	H5’’-P	β2	4.5 ± 3	1.7 ± 1.1
Cyt12	H4’-H5’	γ1	1.4 ± 2	2.7 ± 1.5
Cyt12	H4’-H5’’	γ2	3.7 ± 2	4.4 ± 1.8
Cyt18	H3’-P	ε	9.0 ± 2	9.3 ± 1.6

Figure 10.

Experimentally determined structure of the 1UUU stem-loop ssRNA. Nucleotides with well resolved scalar ³J-coupling constants are labeled.

Having verified the conformational ensemble of the 1UUU stem-loop in terms of NMR scalar ³J-coupling constants, we proceeded to analyze the performance of the Drude-2017 force field in other ssRNA stem-loop structures. The first of these was taken from PDB 2KOC, which features a UUCG tetraloop motif.^[91] Over the course of the 1-μs MD simulation, the 2KOC stem-loop remained stable, with a non-terminal heavy atom RMSD of 1.3 ± 0.2 Å. To assess the stability of the UUCG motif, we computed the hydrogen bonding distances of specific interactions that are critical for UUCG loop stability: Ura6(O2)-Gua9(N1), Ura6(O2’)-Gua9(O6), and Ura7(O2’)-Gua9(N7), and Cyt8(N4)-Ura7(O2P), as shown in Figure 11. None of these interactions were specifically targeted during parameter optimization, thus providing an unbiased assessment of the force field.

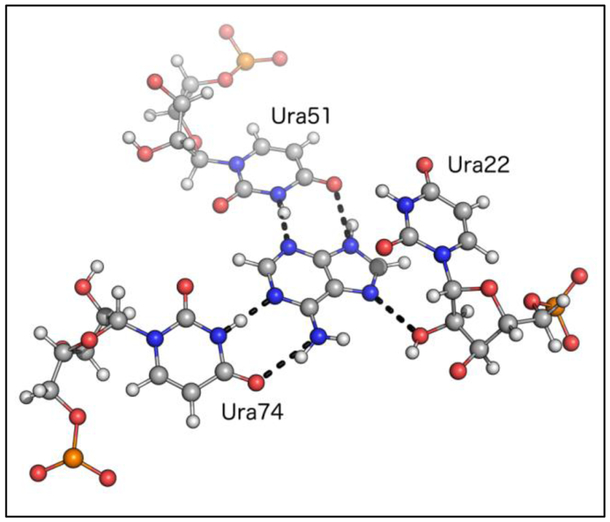
Figure 11.

Preservation of noncanonical hydrogen bonds in the UUCG motif of the 2KOC stem-loop structure. (A) Time series of the individual distances indicated (black dots). The red, dashed lines represent the calculated distances from the starting NMR structure. (B) A rendering of the interactions that stabilize the UUCG motif, corresponding to the distances plotted in panel (A).

Each of the four critical hydrogen bonds was generally preserved throughout the majority of the simulation, though the interaction distances for the heavy atoms involved are slightly longer than the assigned positions in the NMR structure (Figure 11A). Over the majority of the trajectory, the donor-acceptor distance values were below 3.5 Å, the standard threshold for determining the presence of a hydrogen bond. The experimentally assigned positions yield interatomic distances below 2.8 Å, which would correspond to very strong hydrogen bonds at unusually short distances. While such geometries are possible, there may also be some error associated with these assignments. Overall, the persistence of hydrogen bonding between atoms not typically engaged in such interactions demonstrates that the Drude-2017 force field can satisfactorily model stabilizing forces in noncanonical secondary structure elements in RNA, a critical test for the viability of the force field. Banáš et al. carried out an extensive comparison of the performance of AMBER parameter sets using this structure, finding the stability of these hydrogen-bonding interactions critically depended on a proper representation of the Gua9 χ torsion.^[28] Using the Drude-2017 force field derived here, each of these same hydrogen bonds was equally stable, if not more so, than with the best AMBER variants explored in that study.

In addition, the backbone dihedral angles in the noncanonical loop region are well modeled with the Drude-2017 force field. Despite some under-sampling of the gauche⁺ region for the α torsion, all other backbone dihedral angles were in good agreement with the values calculated from the NMR ensemble (Supporting Figure S2). This observation suggests that despite some deviations in ε noted above for the 1UUU sequence, the source of error in that system likely has multiple contributions, as the ε torsion is modeled accurately in 2KOC and therefore is not likely the root cause of the deviations in 1UUU.

The 1YN1 and 1YN2 stem-loop structures^[92] are the same sequence, the Varkud satellite ribozyme stem-loop V (SL5). In 1YN2, the positions of Mg²⁺ ions that bind to this stem-loop were assigned based on NMR experiments in the presence of hydrated Mn²⁺. We performed simulations of both structures solvated in an aqueous solution with neutralizing Na⁺ ions to approximate the solution conditions used in the NMR experiments (buffered 50 mM NaCl).^[92] The 1YN2 simulation included four Mg²⁺ ions that were substituted for the four experimentally assigned Mn²⁺ ions while no Mg²⁺ was included in the 1YN1 simulation. This allowed for an understanding of the impact of Mg²⁺ on the loop conformational sampling in the simulations. Despite the fact that both the 1YN1 and 1YN2 experimental structures were determined in the presence of Mg²⁺, the structures are not equivalent. The RMSD of non-hydrogen atoms between these two structures is 0.7 Å, and for the loop region it is 0.3 Å, indicating that while similar, there are some differences in the assigned atomic positions that may reflect changes induced upon exposure of SL5 to Mn²⁺. As such, the SL5 simulation without Mg²⁺ was initiated from the coordinates of PDB entry 1YN1 and the simulation with Mg²⁺ from PDB entry 1YN2. In principle, a simulation of SL5 without Mg²⁺ could have been initiated from 1YN2 by stripping the Mg²⁺ ions from the initial coordinates, however we chose to start from 1YN1 due to the fact that small differences in the starting coordinates would remove any bias towards the Mg²⁺-bound conformation.

The loop structures of 1YN1 and 1YN2 are stabilized by stacking of Gua697, Ade698, and Cyt699 in both the presence and absence of Mg²⁺. The presence of Mg²⁺ helps stabilize two hydrogen bonds: Ura696 (N3)-Cyt696 (O2P) and Ura696 (O2’)-Ade698 (N7), and promotes the formation of a tight turn in the Gua697 backbone, with α = 116° in the absence of Mg²⁺ shifting to α = 167° in the presence of Mg²⁺. Several other interactions in the SL5 loop region are known to be sensitive to the presence of Mg²⁺.^[92] The first is a hydrogen bond between Ura696 (N3) and the backbone non-bridging oxygens in the phosphate group of Cyt699. In the NMR ensemble of the Mg²⁺-containing system, this distance is between 4.06 – 5.25 Å. In the 1YN2 simulation, this distance averaged 5.7 ± 0.9 Å, slightly longer than in the experimental ensemble. In contrast, this hydrogen bond broke in the 1YN1 simulation, averaging a distance of 8.3 ± 3.5 Å, indicating that the presence of Mg²⁺ is required to maintain this interaction. Another important hydrogen bond is formed between Ura696 (O2’) and Ade698 (N7); it is present at a distance of 2.43 Å in the starting NMR structures. This hydrogen bond was not stable in either 1YN1 or 1YN2 simulations. It quickly broke and sampled distances of 9.7 ± 1.9 Å in 1YN2 and 12.2 ± 1.9 Å in 1YN1.

In addition to hydrogen bonds in the loop region, an anion-π interaction exists between the Ura696 base and the phosphate group of Ade698. This interaction persisted in the 1YN2 simulation at an average center-of-mass (COM) distance of 5.5 ± 0.6 Å, but it broke in the 1YN1 simulation, with an average COM distance of 9.8 ± 1.1 Å.

The architecture of the SL5 loop depends on the tight backbone turn at Gua697 mentioned above. In the absence of Mg²⁺, the α dihedral of Gua697 is 116° and shifts to 167° in the presence of Mg²⁺.^[92] These dihedrals were not well maintained in either of our simulations. In the 1YN1 simulation, the Gua697 α dihedral was, on average 302 ± 48° and in 1YN2 it was 283 ± 95°. Both of these values are similar to the canonical α value in A-form RNA (291°). The 2’-hydroxyl of Gua697 in both the 1YN1 and 1YN2 simulations primarily sampled base configurations, with average 2’-hydroxyl dihedral values of 106 ± 31° and 103 ± 26°, respectively. The balance of sampling in α and 2’-hydroxyl dihedrals at this position in SL5 was likely incorrect and the loop distorted to adopt a more canonical conformation. The 2D potential energy surface of R3PS shows a broad α minimum extending from ~120˚ to 300˚ (Figure 5), with the latter corresponding to canonical A-form RNA. Attempts to obtain better agreement between the Drude-2017 and QM surfaces, in which the Drude conformational energies of α in the vicinity of 120 to 240˚ were lower, led to badly distorted canonical dsRNA (data not shown), and those parameter sets were not pursued. While the inability to sample the non-canonical conformation of α for this nucleotide may be associated with the dihedral parameters, the conformation in the region is impacted by the Ura696 (N3) to Cyt699 phosphate and anion-π interactions mentioned above as well as other non-typical nonbonded interactions, such as U696(O1P) to G697(O2P), at 4.01 Å in 1YN1. It is clear from the results of the 1YN1 and 1YN2 stem-loop simulations that additional careful refinement is needed to stabilize tight turns at noncanonical values of α.

Finally, since the 1YN2 structure has experimentally assigned divalent ion binding sites, an examination of ion dynamics is relevant. We computed grid free energy (GFE) maps of Mg²⁺ ions during the simulation (Supporting Figure S3), which reflect how favorable a given region on the RNA surface is relative to the occupancy of a given volume in bulk solution. These results indicate that in the Drude-2017 simulations, the Mg²⁺ ions sample a large volume around the noncanonical loop of the 1YN2 structure. This outcome is not unexpected, as each of the Mg²⁺ ions is coordinated indirectly, that is, via water-mediated interactions to the RNA. The extent to which the ions move may be related to the distortions in the α torsion described above, therefore further interpretation of these maps is beyond the scope of this work.

Conformational Sampling of the 2’-Hydroxyl in Stem-Loop RNA.

A shift in the 2’-hydroxyl group from base configurations to O3’ and O4’ orientations is associated with greater flexibility in RNA structure.^[24] To examine this phenomenon in the four stem-loop structures simulated here, we analyzed the 2’-hydroxyl dihedral time series and produced the distributions shown in Figure 12. Each stem region is structurally similar to canonical A-form RNA, and as a result, the base orientation dominates. The loop regions, which adopt noncanonical geometries, are expected to be more flexible. In our simulations, there was a slight shift towards O3’ and O4’ orientations in the 1UUU and 2KOC systems, and more pronounced shifts in the 1YN1 and 1YN2 systems (Figure 12), despite the deficiency regarding the α sampling noted above in the 1YN1 and 1YN2 systems. In the 2KOC stem-loop structure, the Ura6 and Ura7 2’-hydroxyl groups participated in loop-stabilizing hydrogen bonding interactions that were well preserved during the trajectory (Figure 11), restricting their conformational sampling. Thus, it is unsurprising that the residues in the UUCG loop of 2KOC did not exhibit a pronounced shift towards O3’ and O4’ orientations of the 2’-hydroxyl as their comparative rigidity is required for stabilizing secondary structure. Thus, the 2’-hydroxyl parameters allow for conformational variability in different environments that is likely important for the sampling of non-canonical structures in RNA.

Figure 12.

2’-hydroxyl dihedral distributions for the four stem-loop RNA systems.

Properties of Base Dipole Moments in Stem-Loop RNA.

An important property of any polarizable force field is the ability to alter electronic structure in response to changes in local electric fields. In DNA and RNA systems, bases can be stacked and thus mostly desolvated or extruded from duplex states and exposed to water. Their dipole moments are expected to respond accordingly, as we have previously shown this to be an important feature in capturing an accurate representation of DNA base flipping thermodynamics.^[58] The four RNA stem-loop structures allow for a similar investigation into the properties of base dipole moments as a function of their secondary structure. Bases in the stem regions, which resemble canonical, A-form RNA, are stacked and engage in Watson-Crick hydrogen bonding. Bases in the loops, however, engage in noncanonical hydrogen bonding interactions and are generally more solvent-exposed.

Distributions of base dipole moments in stem and loop regions for each of the four RNA stem-loop systems are shown in Figure 13. In general, cytosine and guanine bases, which have intrinsically large dipole moments, did not respond strongly to changes in their solvent exposure, which has been observed previously.^[58] On the other hand, adenine and uracil responded strongly to being exposed to water, with dipole moment increases on the order of 0.5 – 1 D. This observation suggests that variations in the base dipole moments in different environments likely contribute to stabilization of non-canonical conformations. Additional studies will be required to more closely investigate the implications of base polarization on RNA conformational ensembles and thermodynamic driving forces, and it is clear that the Drude-2017 force field will be useful in providing insights into these phenomena.

Figure 13.

Base dipole moment distributions for the four stem-loop RNA systems.

Simulations of Large RNA with Complex Tertiary Structures.

Having established that the Drude-2017 force field serves as a reasonable model of RNA secondary structures, we tested its ability to model large RNA molecules with tertiary structures. The first of these was the 23S rRNA from Bacillus stearothermophilus, which has 12 Mg²⁺ ions bound to it, as well as a buried K⁺ ion that stabilizes a tight turn in the structure.^[93] The buried K⁺ is coordinated by non-bridging oxygen atoms of Ade20 and Ade23. In the MD simulation with the Drude-2017 force field, the rRNA structure underwent progressive structural changes, primarily due to flexibility of the loop regions linked by the K⁺-stabilized turn, reflected in a heavy-atom RMSD that stabilized around 3 Å after 600 ns of simulation (Figure 14A). The increased flexibility of the loops was due, in part, to diffusion of the bound K⁺ into bulk solution. Over time, K⁺ ions from the bulk solution re-entered this binding site, interacting with Ade20 and Ade23, re-establishing native-like coordination by the end of the 1-μs simulation (Figure 14B,C). The dissociation of the buried K⁺ ion resulted in only local distortions to nucleotides 32–39 (1082–1089 in the full-length structure) and 42–47 (1092–1097 in the full-length structure, Figure 14D). Both of these regions correspond to noncanonical loops that interact with the helical core of the rRNA via tertiary interactions. Thus, despite reversible binding of K⁺ in the occluded binding site, distortions were confined to only loop residues and the overall structure of the rRNA remained well preserved. We note that there are comparatively large RMSD values for Ade7 (1057) and Gua9 (1059), which shifted in response to the shift observed in nucleotides 32–39.

Figure 14.

Structure and ion sampling in the 1HC8 rRNA system. (A) RMSD of all non-hydrogen atoms in the rRNA structure. (B) Minimum distance between the non-bridging O2P atom of Ade20 and any K⁺ ion. (C) Minimum distance between the non-bridging O1P atom of Ade23 and any K⁺ ion. (D) RMSD of all non-hydrogen atoms in each nucleotide over the final 400 ns. (E) Grid free energy maps of K⁺ and Mg²⁺ ions around the rRNA structure. The RNA is shown in lines with a backbone cartoon trace and crystallographically identified ions are shown as spheres (K⁺ in magenta and Mg²⁺ in green). Grid free energy maps are shown as mesh surfaces (K⁺ in magenta and Mg²⁺ in green) at a threshold of −3.5 kcal mol^-1.

Despite the dissociation of the crystallographic K⁺ after ~300 ns of simulation time, the process proved to be reversible on the microsecond time scale, and K⁺ ions sampled several sites near the buried loop region (Figure 14E). Additionally, the 12 bound Mg²⁺ ions remained near their original locations (Figure 14E), with some variability in the positions of those that interacted with the 23S rRNA indirectly via water-mediated interactions. Regions of high affinity for ions were identified by computing GFE maps of the ion positions. While such analysis is limited by the long lifetimes of Mg²⁺ ions bound to RNA,^[105,106] the resulting maps (Figure 14E) suggest that there are several favorable sites for K⁺ and Mg²⁺ ions on the 23S rRNA surface beyond those identified crystallographically. These results are consistent with our findings using a Grand Canonical Monte Carlo (GCMC) approach to sample the Mg²⁺ distribution of this RNA structure with the additive CHARMM36 force field.^[107]

While the reversible binding of K⁺ and desolvation of bulk K⁺ to participate in direct coordination with phosphate groups is plausible on the examined time scale, it will be important to investigate cooperative polarization effects on the binding of K⁺ and other monovalent ions to RNA structures in future work. The buried K⁺ is ligated by several phosphate groups in the 23S rRNA structure and is therefore positioned in an environment with considerable negative charge density. In the Drude force field, ion interactions were parametrized and validated in terms of their interactions with a single base or dimethylphosphate.^[40] Multibody effects may be considerably different when there are multiple ligands for these ions, as has been shown recently in the case of protein functional groups.^[108] Encouragingly, the Mg²⁺ coordination was stable on the microsecond time scale, consistent with experimentally determined timescales,^[105,106] with directly coordinated ions remaining bound and water-mediated Mg²⁺ sampling nearby sites on the RNA surface (Figure 14E). These outcomes suggest that the recent parametrization of the interactions between this divalent ion and nucleic acid moieties^[54] is satisfactory.

The last structure with complex tertiary interactions that we analyzed using the Drude-2017 force field was the Vibrio vulnificus adenine riboswitch.^[94] The structure binds one adenine molecule and five Mg²⁺ ions. We performed simulations of the adenine riboswitch in both the holo and apo states; the latter was generated by removing the free adenine base from the structure. These two simulations test the ability of the Drude-2017 force field to maintain the noncanonical hydrogen bonding between the riboswitch and adenine, probe structural changes as a result of the removal of adenine, and further explore Mg²⁺ sampling. Concerning the overall structural integrity of the systems, the apo form of the riboswitch underwent a structural change involving the opening of the P2-P3 kissing loop interface, with an average RMSD of all non-hydrogen atoms of 3.9 ± 0.6 Å. The holo form of the riboswitch better preserved its overall architecture, with a stable P2-P3 interface and an average RMSD of 3.2 ± 0.6 Å (Figure 15).

Figure 15.

Dynamics of the 1Y26 adenine riboswitch. (A) RMSD of all heavy atoms in the apo and holo forms of the riboswitch. (B) GFE maps of Mg²⁺ in the apo system, with important structural regions of the riboswitch labeled. (C) GFE maps of Mg²⁺ in the holo system. The RNA is shown in lines with a backbone cartoon trace and crystallographically identified Mg²⁺ are shown as green spheres. Grid free energy maps are shown as green mesh surfaces at a threshold of −3.5 kcal mol^-1.

The Mg²⁺ ions bound to the adenine riboswitch sampled the areas around their crystallographically identified sites, primarily around the P2 and P3 helices (Figure 15B,C). One fully hydrated ion, indirectly coordinated to the P2 helix, did not remain in the assigned site, instead sampling other sites on the riboswitch surface. The position of this ion may be a consequence of crystal packing interactions, such that its sampling of other sites in solution is not unexpected. Differential ion sampling was observed between the apo and holo states; the opening of the P2-P3 kissing loop interactions in the apo state allowed for Mg²⁺ ion sampling in the greater accessible volume at this interface (Figure 15B), whereas the tighter interface in the holo simulation did not allow for such extensive sampling (Figure 15C).

In the holo riboswitch simulation, the binding of the free adenine base remained stable throughout the 1-μs simulation. Key hydrogen bonding interactions between the base and surrounding nucleotides (Figure 16) in the riboswitch were preserved at or near the distances observed in the crystal structure (Table 16).

Figure 16.

Hydrogen bonds stabilizing the binding of adenine to the adenine riboswitch. Putative hydrogen bonds are shown as dashed lines.

Table 16.

Hydrogen bonding distances in the holo adenine riboswitch simulation. Error bars for the MD data are the RMS fluctuations over the entire time series.

Hydrogen Bond	Reference Distance (Å)a	Drude-2017 Distance (Å)b
Ade (N7) – Ura22 (O2’)	2.78	3.6 ± 0.8
Ade (N3) – Ura51 (N3)	2.77	2.8 ± 0.1
Ade (N9) – Ura51 (O4)	2.93	3.1 ± 0.2
Ade (N1) – Ura74 (N3)	2.65	2.8 ± 0.2
Ade (N6) – Ura74 (O4)	2.87	2.8 ± 0.3

^aThe distance of each interaction measured in the 1Y26 crystal structure.

^bThe average and RMS fluctuation from the 1-μs MD simulation.

The interactions between adenine and Ura74 are canonical Watson-Crick hydrogen bonding, so it is unsurprising that they were well maintained during the simulation. This outcome is important as Ura74 is the determinant for adenine specificity for the riboswitch.^[94] Ura51 interacts with the sugar face of adenine (N1 and N9), and Ura22 forms a hydrogen bond with the adenine N7 atom via its 2’-hydroxyl group. Adenine hydrogen bonds with Ura51 were slightly longer than crystallographic reference distances during the Drude-2017 simulation but were within error of the experimental values (Table 15). The hydrogen bond between the adenine N7 atom and the 2’-hydroxyl group of Ura22 was the least well preserved, with an average distance of 3.6 ± 0.8 Å, longer than the typical hydrogen bonding limit of 3.5 Å. It is notable, however, that this hydrogen bond was present for 55% of the trajectory using this distance criterion, indicating that it was generally preserved despite being somewhat flexible. In the starting crystal structure, the sugar pucker of Ura22 is South/C2’-endo, and to form a hydrogen bond to the adenine N7 atom requires the 2’-hydroxyl group to be in the base orientation. In the apo simulation, these features are preserved but the structure is more flexible in the holo simulation (Supporting Figure S4). These observations indicate that parameters related to sugar pucker and the 2’-hydroxyl orientation may require some refinement to better capture these effects, which are known to be coupled.^[109]

Table 15.

Hydrogen bonding distances in the 2KOC stem-loop simulation. Error bars for the MD data are the RMS fluctuations over the entire time series.

Hydrogen Bond	Reference Distance (Å)a	Drude-2017 Distance (Å)b	% H-Bond Formationc
Ura6(O2) – Gua9(N1)	2.77	2.9 ± 0.1	99.7
Ura6(O2’) – Gua9(O6)	2.66	3.0 ± 0.3	94.5
Ura7(O2’) – Gua9(N7)	2.76	3.2 ± 0.3	87.2
Cyt8(N4) – Ura7(O2P)	2.76	3.7 ± 1.1	60.5

^aThe distance measured in the first model of the 2KOC NMR ensemble.

^bThe average and RMS fluctuation from the 1-μs MD simulation.

^cThe percentage of time frames in which the donor-acceptor distance was ≤ 3.5 Å.

Stability of dsDNA Using the Updated Drude-2017 Force Field.

Since the refinement of RNA backbone dihedral parameters required an adjustment of the γ dihedral, which overlaps with DNA, it was important to verify that the new parameters did not deleteriously affect DNA structure, which was well described by the Drude-2017 DNA force field.^[42] To test the new force field, we performed a 1-μs MD simulation of the Dickerson-Drew dodecamer (EcoRI, PDB 1BNA),^[99] which contains a central AATT sequence and is therefore a good system to investigate DNA stability due to the weaker stacking of AT relative to GC,^[64] which was previously identified as a deficiency in the Drude-2013 DNA force field^[39] and was corrected in Drude-2017.^[41,42] The EcoRI structure remained stable over the course of the simulation, with a non-terminal heavy atom RMSD of 1.5 ± 0.3 Å (Figure 17A), identical to the previous simulation of EcoRI with the Drude-2017 DNA force field.^[42] The new γ parameters did lead to a shift in the distribution of γ dihedrals in the structure, resulting in a slightly larger discrepancy with respect to crystal survey data (Figure 17B). Recent analysis of water distributions around O5’ and O3’ atoms in duplex DNA and RNA suggests that water molecules make close contact with these atoms due to a small Lennard-Jones radius on this atom type, which may influence backbone dihedral conformational ensembles. Thus, the deviations from ideal structures may be due, in part, to interactions with water rather than exclusively due to the changes to internal parameters in DNA and RNA. We verified that the conformational energetics of the updated Drude-2017 force field agree well with QM target data, with energy minima at 45° in T3PS, the DNA model compound (Supporting Information Figure S5). Sampling at ~60° observed in the EcoRI simulation (Figure 17B), implying a role for solvation effects. Refinement of backbone-water interactions is underway to correct this deficiency. Despite these minor differences, the application of the new γ parameters to duplex DNA does not yield any distortions and the Drude-2017 force field is therefore appropriate for simulations of both DNA and RNA.

Figure 17.

Properties of EcoRI with the new γ dihedral parameters. (A) RMSD of non-terminal, non-hydrogen atoms. The red, dashed line represents the average value, 1.5 Å. (B) Distributions of γ dihedral values from MD simulations compared to a crystal survey described previously.^[42] “Drude-2017 (DNA)” refers to the results of the published Drude-2017 DNA force field and “Drude-2017 (DNA+RNA)” refers to the simulation performed here after refinement of γ and other RNA-related terms.

CONCLUSIONS

This study has presented an empirical force field for RNA based on the classical Drude oscillator model, an extension of the existing Drude-2017 nucleic acid force field, which previously only covered DNA.^[39,40] The application of our recently refined LJ parameters for atom types in DNA bases^[41] led to base stacking interaction energies for uracil-containing stacked monomers that compared well with high-level QM interaction energies and are a better representation of base stacking than both the previous Drude-2013^[66] and additive CHARMM36 force fields.^[14,15] By targeting QM conformational energetics, dipole moments, and water interactions, the Drude-2017 nucleic acid force field was further extended to include parameters for the 2’-hydroxyl moiety of the ribose sugar and refined backbone dihedral parameters for the α, γ, ε, and ζ torsions. In conjunction with our work to balance the interactions of Mg²⁺ with nucleic acid moieties,^[54] the present force field is a comprehensive model of RNA-ion interactions that are important for folding and tertiary structure stability.

The Drude-2017 force field is an accurate model of RNA secondary structures, as demonstrated by good agreement with crystal surveys of canonical, A-form duplex RNA and NMR data on stem-loop structures, including NOE distances and scalar ³J-coupling constants for systems with both canonical and noncanonical base-pairing and other hydrogen bonding interactions. Deviations in the structure of the SL5 structure are due to a suboptimal representation of the α torsion, and are potentially related to nonbonded interactions including interactions with ions. Further work will be necessary to determine which parameters require adjustment and to further characterize the cooperativity of the nonbonded interactions and torsions, and their role in RNA structure.

Large RNA with complex tertiary structures were generally modeled well with the Drude-2017 force field, though the observed reversible binding of K⁺ in the 23S rRNA structure requires additional validation and examination of cooperative polarization effects in regions of high negative charge density, a parametrization challenge that is unique to polarizable force fields. In the adenine riboswitch, the binding pose of the adenine base, preserved by a combination of Watson-Crick and noncanonical hydrogen bonding, was well maintained. Mg²⁺ ions sampled the P2 and P3 helices in the riboswitch near their crystallographically assigned sites, with additional sampling observed in the apo simulation at the P2-P3 kissing loop interface, which opened up in the simulation as a result of removing the bound adenine.

In summary, the presented force field was able to model a range of structural properties of RNA in aqueous solution. While limitations in the model are noted, it offers a novel tool for studies of the structure and dynamics of RNA at the atomistic level. Moreover, its compatibility with the remainder of the Drude polarizable force field, including proteins, lipids, and carbohydrates, will allow for studies of heterogeneous biomolecular systems using a fully polarizable model. The force field, to be called Drude-2017, will be made available publicly on the MacKerell group website (http://mackerell.umaryland.edu/) and will be incorporated into the Drude Prepper module of CHARMM-GUI^[110] (http://www.charmm-gui.org) as well as included with future releases of the CHARMM program. Future revisions will address the Lennard-Jones parameters for O3’ and O5’ atoms to improve hydration properties, minor refinement of nucleobase electrostatic parameters to avoid over-polarization, which may contribute to the deviations in V_m and ΔH_sub discussed above and in previous work on the Drude-2017 DNA force field,^[41] as well as other issues discussed above.