Measuring the Effects of Employment Protection Policies: Theory and Evidence from the Americans with Disabilities Act

Abstract

Title I of the Americans with Disabilities Act (ADA) is an employment protection policy for disabled workers. By exploiting cross-state variation in pre-ADA legislation, we measure the effects of the law on transition rates of disabled workers. We find a decline in employment-to-non-employment transitions after the ADA, with an insignificant change in flow into employment. We use a model to disentangle the costs of firing and hiring imposed by the ADA. Our findings suggest that the ADA induces firms to fire less frequently but become more selective with new hires, impacting the aggregate productivity of the workforce and output of the economy.

1. Introduction

The Americans with Disabilities Act (ADA) of 1990 is a civil rights law intended to protect people with disabilities from discrimination. Title I of the ADA covers employment protection, allowing employees who feel they have been discriminated against to file charges against their employers. Thus, while the ADA protects workers with disabilities, it simultaneously places constraints on (potential) employers with regard to disabled employees. In 2017, the total number of charges filed under the ADA accounted for 32% of all filings under the Equal Employment Opportunity Commission (EEOC),¹ and $135 million in monetary benefits was issued. With the passage of the ADA Amendments in 2008² and the aging of the American population, increasingly more individuals are expected to benefit from the law, imposing higher costs on firms with (and those planning on hiring) disabled employees.

While there are studies focusing on the ADA’s impact on employment rates (e.g., Acemoglu and Angrist, 2001; and DeLeire, 2000), analysis on worker flows is limited. However, understanding the changes in worker flows caused by the ADA is important. As is well-known in macro-labor literature (e.g., Blanchard and Portugal, 2001), employment protections make labor markets sclerotic: firms face higher costs in firing and hiring, and workers’ duration of both employment and unemployment increase. These equilibrium consequences may have aggregate efficiency effects. This paper complements the literature by (i) empirically measuring the effects of the ADA on worker flows into and out of employment; (ii) analyzing the equilibrium effects on transition flows of both disabled and non-disabled workers; and (iii) disentangling the regulatory costs of the hiring and firing clauses of the ADA and measuring the aggregate impacts of those clauses to the economy.

Our first goal is to estimate the impact of the ADA on workers’ labor market transition flows between employment and non-employment. We identify the effect of employment protection using a difference-indifferences estimation based on the cross-state variation in pre-ADA labor laws. We generate a comprehensive measure for employment protection by extending the similarity measure of Jolls (2004) and Jolls and Prescott (2004), using the scope of coverage documented in Percy (1989).³ According to our classification, we find that before the enactment of the ADA, 34 states had already implemented labor protection laws for the disabled that were similar to the ADA; these serve as our control group. We compare the labor market performance of disabled and non-disabled workers in these control states with those in 11 other states with weaker labor protection prior to the ADA.⁴

Our estimation results show that the introduction of the ADA decreased the annual employment-tonon-employment transition rate of the disabled by 3.5 to 4.3 percentage points (21.8 to 26.8%), without improving their non-employment-to-employment transition rate. Although not statistically significant, we also find a decline in transition flows into employment. Overall, we find no significant improvement (or deterioration) in employment rates caused by the ADA. Our findings are robust to controlling for time trends, clustering of standard errors, and choice of sample periods.

To better understand the relationship between the policy and labor market outcomes, and to build a framework for a quantitative analysis, we extend the model presented in Mortensen and Pissarides (1994) by incorporating the costs imposed on firms in their hiring and firing practices. We find that when faced with firing costs under the ADA, firms terminate employment less frequently but become more selective in hiring new workers. Simultaneously, the rise in job termination costs reduces the profitability of creating a new job. As a consequence, even though the policy targets disabled workers, it affects all workers in the labor market (general equilibrium effect).

Lastly, using the changes in worker flows from the empirical part as our targets, we conduct a quantitative analysis to measure the hiring and firing cost parameters of the model and the aggregate consequences of the ADA. We find that due to the ADA, firms face expected firing and hiring costs of 9.2% and 0.9%, respectively, of average monthly wages in the calibrated economy. The asymmetric costs associated with firing and hiring of disabled workers induce firms to retain more existing workers by firing less frequently while being more selective in hiring new workers. Overall, the latter effect dominates, increasing the average productivity of the employed disabled workers. However, due to lower employment, aggregate output declines in the post-ADA economy. Furthermore, higher costs decrease job creation, leading to a 12% decline in the equilibrium job-finding rate of workers. This decline in the equilibrium job-finding rates underscores the importance of evaluating policies in a general equilibrium model incorporating endogenous responses of firms to government policies.

The ADA is an employment protection policy targeting a specific group of workers. This paper is thus broadly related to the literature studying the effects of employment protection policies. There are many studies that focus on the theoretical and empirical implications of firing and hiring restrictions. While some focus on the aggregate employment rate effects of these policies (e.g., Bentolila and Bertola, 1990), others use search and matching frameworks to analyze the effects on worker flows both theoretically and empirically (e.g., Lazear, 1990; Hopenhayn and Rogerson, 1993; Blanchard and Portugal, 2001; Pissarides, 2001; Ljungqvist, 2002). Most of these papers use the differences in cross-country labor market regulations (e.g., U.S. vs. European countries, or between different European countries) to identify the impacts of strong employment protection policies. Recently, Kugler and Pica (2008) uses an Italian reform that increased dismissal costs for small firms and empirically show that the reform lowered the accessions and separations of workers, but did not impact the employment rate. While the labor market policies they study are applicable to all workers in the labor market, the ADA is applicable only for disabled workers. Our paper thus models this targeted employment protection policy and shows its potential effects on all workers in the market through general equilibrium, within the model and empirically.

The paper is also directly related to the previous literature assessing the impact of the ADA.⁵ These papers have adopted frictionless labor market models and have measured labor market outcomes using stock variables such as the employment rate and the labor force participation rate (see, for example, Acemoglu and Angrist, 2001 and DeLeire, 2000). However, as emphasized in the studies of general employment protection policies, underlying the effects of the ADA on employment might be important changes in worker flows into and out of employment. We complement the literature by providing a comprehensive evaluation of the law, jointly exploring its effects on worker flows and employment rates for all workers in the labor market.

The paper also fits into a broader labor economics literature addressing general equilibrium effects of policy changes. The indirect effect of employment protection is an example of general equilibrium effects from implicit taxes in labor market policies discussed in Hagedorn and Manovskii (2008), Hagedorn, Karahan, Manovskii and Mitman (2013), and Chodorow-Reich and Karabarbounis (2016), among others.

The remainder of the paper is organized as follows. Section 2 contains descriptions of our dataset and the definition of key variables used in the empirical analyses. In Section 3, we explain our empirical approach and document its results. To conduct quantitative analysis, we introduce our model and characterize the effects of employment protection policies in Section 4. Section 5 presents the quantitative analysis results of our ADA evaluation, and Section 6 concludes.

2. Data

In this section, we give a brief overview of the two key variables of interest we use in our empirical analysis in Section 3: the measure of the degree of employment protection and worker flows.

2.1. State-Level Employment Protection Variables

According to Sales, Powell and Duizend (1982), most states established their own legislation against discrimination based on disability in the 1970s in various sectors, including education and housing. As no federal guidelines for these regulations existed at the time, Sales et al. (1982) note that there were variations across states in the strength of the laws’ protection. In this section, we explain how we define the degree of employment protection for each state prior to the enactment of the ADA in July 1990.

We construct the measure of state-level employment protection based on two criteria: similarity to the ADA and the scope (coverage) of the legislation. For the first criterion, we follow the classification of Jolls (2004) and Jolls and Prescott (2004). According to the analysis in those papers, the four key elements of the ADA compared to the previous employment protections are the prohibition of discrimination based on disability in hiring, firing, and compensation for workers, and the provision of reasonable accommodations. Based on these criteria, 18 states had already implemented state-level labor protection laws for the disabled that were similar to the ADA (full protection). Of the remaining states, 29 had enacted limited labor protection prior to the ADA that included anti-discrimination laws but did not provide more than one major clause of the ADA (weak protection), while the remaining 3 states did not have any state-level protection laws in place (no protection).

The second criterion that we incorporate is the scope of the protection provided by each state’s legislation. The ADA is enforced for both public and private employers and covers physical and mental disabilities. In contrast to the wide range of coverage under the ADA, however, some states provided employment protection only to public sector employees or only for individuals with a specific subset of physical disabilities. For instance, the employment protection laws of the state of Idaho strictly prohibited discrimination prior to the ADA and is classified as a full-protection state for the similarity criterion. However, the law excluded the private sector; only public employers were covered under the law. Since less than 15% of the state’s workers were public employees, it is difficult to reasonably conclude that disabled residents in Idaho could easily claim these legal protections.

To reflect the range of employment protection laws, we adopt the definition of the scope of protection from Percy (1989). We classify a state as having broad coverage in employment protection if it included both public and private sectors and covered individuals with physical and mental disabilities. Thirty-seven states satisfied these criteria. In eight additional states, employment laws did not include either the private sector or mental disabilities and thus only had partial coverage. The remaining five states excluded both the private sector and mental disabilities, providing only restricted coverage by only enforcing the laws for public sector employers and covering workers with physical disabilities (if at all).

For our empirical analysis, we define a group of strong protection states and a group of no protection states by combining these two criteria. We classify a state as providing strong protection if its legislation included both (i) at least two out of the four major nondiscrimination clauses in Title I of the ADA and (ii) covered private sector employees with a broad set of disabilities. Table 1 documents our classification results by criterion, and Table 2 reports the list of states for each group.

Table 1:

Classification of State Legislation

			Similarity
			Full 18	Weak 29	No 3
	Broad	37	14	23	0
Scope/Coverage	Partial	8	2	6	0
	Restricted	5	2	0	3

Note: In Table 1, we report the classification results of the two criteria, the similarity of their pre-ADA employment protection laws to the ADA (Full, Weak, or No), and their scope (Broad, Partial, or Restricted) based on the state’s legislation in 1989. The number of states included in the strong protection is written in bold, and the rest, are classified as the no-protection states.

Table 2:

List of States by the Degree of Employment Protection

Classification	List of States
No Protection	Alabama, Alaska, Arkansas, Delaware, Florida, Hawaii, Idaho, Kansas, Kentucky, Mississippi, Nevada
Strong Protection	Arizona, California, Colorado, Connecticut, Georgia, Illinois, Indiana, Iowa, Louisiana, Maine, Maryland, Massachusetts, Michigan, Minnesota, Missouri, Montana, Nebraska, New Hampshire, New Jersey, New Mexico, New York, North Carolina, North Dakota, Ohio, Oklahoma, Oregon, Pennsylvania, Rhode Island, South Carolina, South Dakota, Tennessee, Texas, Utah, Vermont, Virginia, Washington, West Virginia, Wisconsin, Wyoming

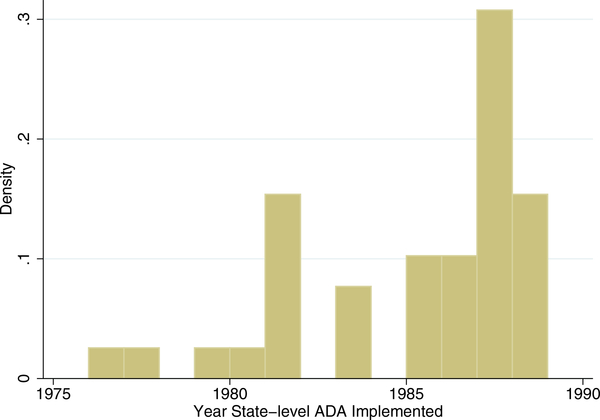
According to our definition, some states had implemented strong employment protection policies for disabled individuals as early as 1976. By comparing the evolution of the legislation, we find that a significant number of states passed their state-level amendments in labor laws and implemented strong protection in the 1980s. By the time the ADA was introduced in 1990, there were 39 states providing strong protection against discrimination based on disability. After excluding five states for which we were unable to identify an exact year in which strong protection was enacted,⁶ we use the remaining 34 states with strong protection as our control group and the other 11 states as the treatment group in our empirical analysis.⁷ We summarize the evolution of state-level employment protection laws in Figures 1 and 2. While our benchmark analysis does not utilize data on the specific year in which employment protection was implemented at the state level, as a robustness analysis, we exploit this variation to study the impact of employment protection and report the results in Section 3.3.

Figure 1: Distribution of Legislation Years.

Note: Figure 1 plots the distribution of years in which states had adopted strong employment protection laws either by passing a new legislation or amending an existing one.

Figure 2: Geographical Distributions in 1981, 1985, and 1989.

Note: Figure 2 illustrates the geographical variation of the legal changes in the 1980s (1981, 1985, and 1989 from left to right). The states with strong employment protection laws are shaded in black, and those with weak protection are in white. There were five states for which we could not identify the exact years the legislation was enacted; these are marked in gray in the maps. The discussion of our classification criteria is described in more detail in the main text.

2.2. Matched March CPS

The main data source for our analysis is the matched Annual Social and Economic Supplement from the Current Population Survey (March CPS). Although the CPS is a cross-sectional dataset, its sampling rotation allows researchers to link the same housing units in two consecutive years. Initially, respondents participate in the survey for four consecutive months. These respondents re-enter the survey after an eight-monthlong gap. Therefore, in principle, we can match respondents who have survey histories with less than four months in year t once they return in year t + 1. Using this feature, we construct a (pseudo-)panel dataset after matching these housing units by testing the consistency of demographic information of the residents—gender, race, age, and educational attainment, following Madrian and Lefgren (2000).⁸

While the matching process has its limitations, the matched CPS provides unique opportunities to address our research question.⁹ Originally designed for measuring unemployment rates, the CPS provides information on labor market status at an individual level. We categorize a respondent’s labor market status into two possible outcomes, employment and non-employment, and define the transition variables as the changes in labor market statuses between year t and t +1.¹⁰

Another advantage of CPS is that it provides an individual’s work disability status along with their labor market performance. Starting in 1981, the March CPS began collecting information on whether individuals have any form of health problems causing work limitations. The relevant question reads “Does the respondent have a health problem or a disability which prevents work or which limits the kind or amount of work [the respondent can do]?” We use the respondents’ self-reported answers on their disability status to classify individuals with disabilities.¹¹

Table 3 summarizes the sample mean of our key variables of interest by disability status. We construct the labor market outcomes—employment rates and annual transition rates between employment and nonemployment—by disability status, using the male working-age population (from ages 23 to 65).¹² All aggregate variables are computed using the March supplement weight.

Table 3:

Transition Rates between Employment and Non-Employment

Labor Market Transition			Disability Status
t	t + 1		Disabled (%)	Non-disabled (%)
Employed	Employed	(E-to-E)	83	94
	Non-employed	(E-to-N)	17	6
Non-employed	Employed	(N-to-E)	10	34
	Non-employed	(N-to-N)	90	66

Note: Table 3 reports the annual transition rates between employment and non-employment using the matched March CPS from 1981 to 2000. Non-employment includes unemployment and non-participants in the labor force.

3. Empirical Analysis

In the previous section, we presented the rich heterogeneity in state-level labor market policies protecting disabled workers against discrimination in the 1980s. By exploiting this spatial variation in labor laws, we conduct a difference-in-differences (DD) estimation to evaluate the effects of the ADA on labor market outcomes of disabled and non-disabled workers.¹³

3.1. Empirical Estimation Strategy

For disabled individuals living in 11 states that had either no or weak protection against discrimination (the treatment group), the implementation of the ADA would have been a relatively significant change compared to the change that the 34 states with pre-existing strong protection (the control group) would have perceived. Therefore, we can identify the effects of the ADA by comparing data from individuals in those two groups before and after the enactment of the ADA as follows:

$$y_{i,s,t}={\beta }_0+X_{i,s,t}{\beta }_1+{\beta }_2{\mathbb{I}}_{\{t\ge ADA\}}+{\beta }_3{\mathbb{I}}_{\{s=\text{No}\text{Protection}\}}+{\beta }_4{\mathbb{I}}_{\{t\ge ADA\}}\times {\mathbb{I}}_{\{s=\text{No}\text{Protection}\}}+{\epsilon }_{i,s,t},$$ (1)

where 𝜀_i,s,t represents a classical error term. Our dependent variables are the labor market outcomes of an individual i living in a state s between time t — 1 and t. In particular, we are interested in the change in probabilities of job separation (from employment to non-employment) and finding (from unemployment or non-employment to employment). Individual characteristics are contained in X_i,s,t, which includes age and dummies for education. The dummy variable 𝕀_{{s=No Protection}}, which takes the value 1 if the individual lived in a no-protection state, is constructed based on his state of residence from the CPS and uses the classification of states by the degree of protection defined in Table 2. While our benchmark analysis uses linear trends, we also present results with time dummies and quadratic trends. As summarized in Table 4, the coefficient of interest that reflects the effect of the law is β₄, and we are particularly interested in the sign of the estimator.

Table 4:

Summary of the Estimation

	Pre-ADA	Post-ADA	Δt	ΔΔ
No Protection	β3	β2 + β3 + β4	β2 + β4
Protection	-	β2	β2
Δs	β3	β3 + β4		β4

Choice of Sample Periods

In our baseline analysis, we use sample periods from 1981 to 1999 and compare the labor market outcomes for 1981–1991 and 1992–1999 between strong- and no-protection groups. While a DD analysis assumes that the policy change occurred in a given period, the implementation of the new regulation was in fact a continuous process. The first draft of the ADA was introduced in 1988 during the 100th Congress, and the final version was signed by President George H.W. Bush on July 26, 1990, after a series of debates, hearings, and testimonies. The regulations were issued in 1991 and finally came into effect in July 1992. We assume the post-ADA period started in 1992 in our estimation.

Even though we have access to a dataset for the 2000s, we restrict our timeframe for the post-ADA periods to 1999 because major changes influencing the interpretation of the ADA came into being in 2000. The ADA of 1990 defined disability as “a physical or mental impairment that substantially limits one or more major life activities” (42 U.S.C. § 12102(2)(A)). After the enactment of the law, the question of whether the evaluation of an individual’s disability status should be in his medicated state or not became an issue. Eventually, on June 22, 1999, the Supreme Court heard two cases challenging the definition of disabilities covered under the ADA. The court ruled that an individual is disabled under the definition of the ADA if his physical or mental conditions cannot be offset by either medical devices or medicines. As a result, the eligibility of the ADA was restricted after these rulings, and we therefore focus on periods before the clarification in the definition of disabilities were made. In sum, we include 15 sample years in our benchmark analysis: 10 observations from 1981 to 1991 before the ADA and five observations from 1992 to 1999 after the ADA.¹⁴

3.2. Estimation Results

We report the estimation results of Equation (1) on disabled and non-disabled workers and also report the results from allowing age-specific ADA effects.

Disabled Workers: Flows out of Employment

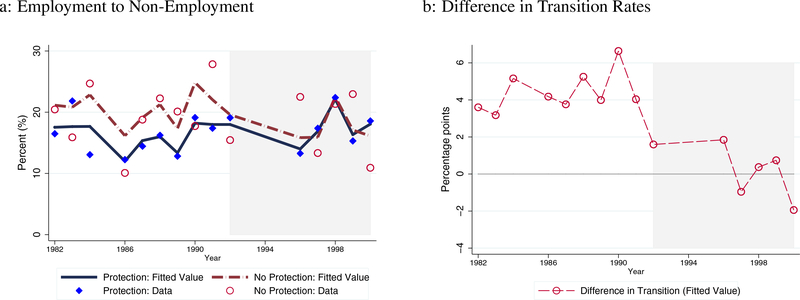
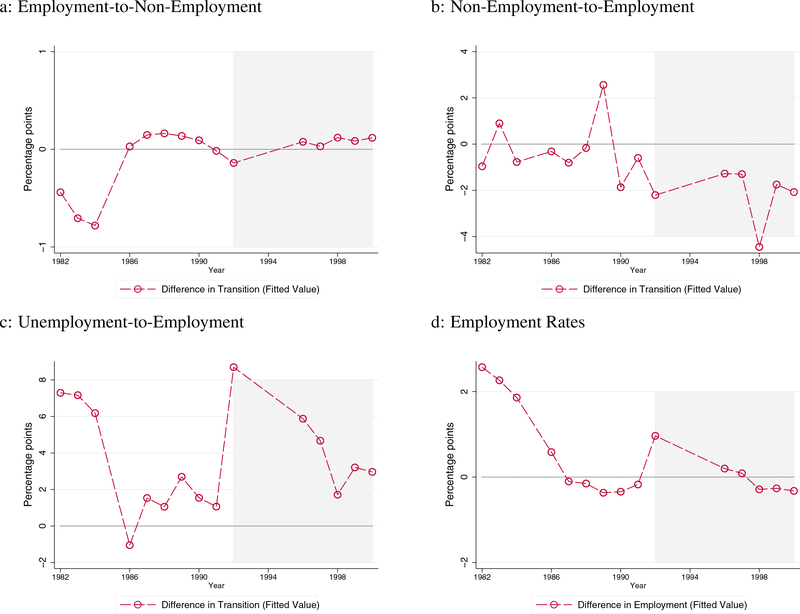
Table 5 reports the estimation results of Equation (1). The estimated coefficients in the No-Protection × Post-ADA dummy suggest that workers with disabilities residing in states without protection experienced an approximately 3.5 to 4.3 percentage point (pp) decline in employment-to-non-employment transition rates after the implementation of the ADA. In Figure 3, we illustrate the time-series employment-to-non-employment transition rates along with the fitted values based on our estimation with aggregate linear trends in the left panel. On the right panel is the difference in transition rates, calculated from the left panel. As is clear from the fitted lines, the decrease in exit flows from employment is sizable enough to shrink the gap in transition rates (approximately 3.6 to 4.1 pp as shown in the coefficient estimates for the No-Protection dummy) between the two groups after the ADA.

Table 5:

Effects of the ADA on Disabled Workers’ Transition from Employment to Non-Employment

Coefficient	Linear	Quadratic	Time Dummy
No Protection	0.036***	0.041**	0.037***
	(0.013)	(0.019)	(0.013)
After ADA	−0.062**	−0.052**	−0.061
	(0.028)	(0.031)	(0.079)
No Protection	−0.037*	−0.043**	−0.035*
× After ADA	(0.021)	(0.019)	(0.020)
R2	0.027	0.028	0.033
# of obs.		3,885

Note: Table 5 reports regression coefficients of the benchmark analysis. The regression also controls for education and age as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

Figure 3: Disabled Workers’ Transition from Employment to Non-Employment Before and After the ADA.

Note: Figures 3a and 3b illustrate the estimation results of employment-to-non-employment rates. Circle (red) and diamond (blue) markers in Figure 3a represent the average transition rates of the treatment and control groups, respectively. The lines indicate the average estimated transition rates based on the estimation. Figure 3b shows the difference in these transition rates.

Disabled Workers: Flows into Employment

We turn our attention to transition flows into employment. First, we restrict our samples to unemployed workers and estimate the DD coefficients for the unemployment-to-employment transition rates. The results are summarized in the first three columns of Table 6. Similar to the opposite transition flows from employment to non-employment, we find that the flows declined after the ADA.

Table 6:

Effects of the ADA on Disabled Workers’ Transition into Employment

Coefficient	Unemployment to Employment			Non-Employment to Employment
	Linear	Quadratic	Time Dummy	Linear	Quadratic	Time Dummy
No Protection	0.162*	0.152*	0.206*	−6.23	−5.04	−0.06***
	(0.091)	(0.088)	(0.015)	(8.34)	(7.05)	(0.01)
After ADA	−0.063	−0.154**	−0.343*	0.03	0.03	−0.042
	(0.124)	(0.036)	(0.192)	(0.04)	(0.04)	(0.028)
No Protection	−0.176*	−0.132	−0.138	−0.05	−0.04	0.010
× After ADA	(0.103)	(0.103)	(0.098)	(0.05)	(0.05)	(0.017)
R2	0.152	0.155	0.196	0.037	0.037	0.036
# of obs.		488			8,561

Note: Table 6 reports regression coefficients of the benchmark analysis. Regression also controls for education and age as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

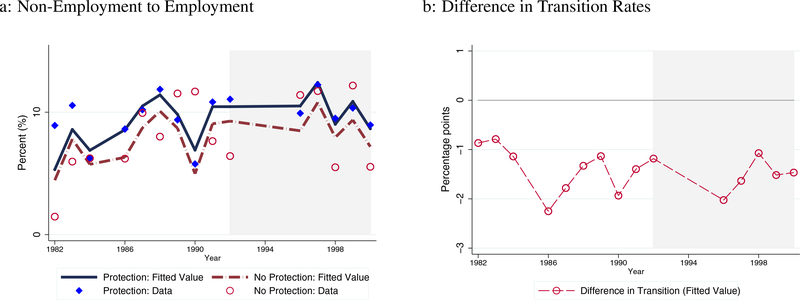
As there are only a few hundred observations of unemployed disabled workers, we expand the sample to individuals who are not employed in year t.¹⁵ We run the same DD estimation on non-employment- to-employment rates and summarize the results in the fourth to sixth columns of Table 6. We find that the negative coefficients in non-employment-to-employment transition are only about 25% of those in unemployment-to-employment transitions. This finding may indicate that individuals who are currently out of the labor force may exert different job search efforts compared to the unemployed. The results for the transition from non-employment to employment are also graphically represented in Figure 4, where the left panel represents the estimated transition rates, and the right, the differences of the estimated flows across the two groups.

Figure 4: Disabled Workers’ Transition from Non-Employment to Employment Before and After the ADA.

Note: Figures 4a and 4b illustrate the estimation results of non-employment-to-employment rates. Circle (red) and diamond (blue) markers in Figure 4a represent the average transition rates of the treatment and control groups, respectively. The lines indicate the average estimated transition rates based on the estimation. Figure 4b shows the difference in these transition rates.

Disabled Workers: Employment Rates

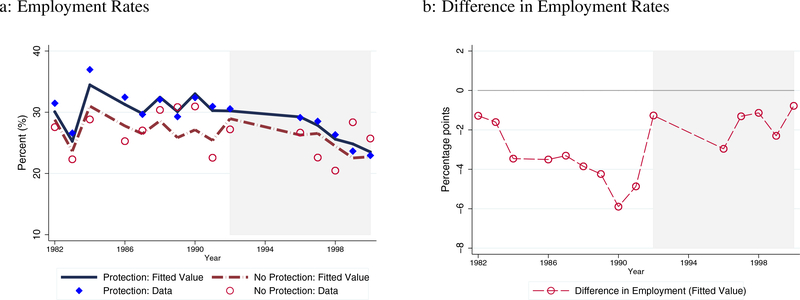
Lastly, we investigate how these changes in transition rates translated into the change in employment rates. To answer this question, we run the DD regression on the employment rates of the disabled. Table 7 and Figure 5 document the regression results. We find that the change in employment was negative but not significant.

Table 7:

Effects of the ADA on Disabled Workers’ Employment Rates

Coefficient	Linear	Quadratic	Time Dummy
No Protection	−16.21**	−14.75*	−0.21***
	(7.39)	(8.09)	(0.01)
After ADA	0.08***	0.08***	−0.03
	(0.03)	(0.03)	(0.03)
No Protection	−0.03	−0.01	0.03
× After ADA	(0.04)	(0.01)	(0.02)
R2	0.07	0.07	0.07
# of obs.		12,142

Note: Table 7 reports regression coefficients of the benchmark analysis. Regression also controls for education and age as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

Figure 5: Disabled Workers’ Employment Rates Before and After the ADA.

Note: Figures 5a and 5b illustrate the estimation results of employment rates. Circle (red) and diamond (blue) markers in Figure 5a represent the average employment rates of the treatment and control groups, respectively. The lines indicate the average estimated employment rates based on the estimation. Figure 5b shows the difference in these employment rates.

To examine the consistency of our findings, we compare this direct estimation result in Table 7 to the predicted employment rate change based on the estimated flow rates. The law of motion, e_t+1 = (1 — EU_t) e_t + UE_t (1 — e_t), indicates that the future employment will change by —ΔEUe_t + ΔUE (1 — e_t). For states without employment protection, the average employment rate was 27.1%. Before and after the ADA, the employment-to-non-employment and non-employment-to-employment rates reduced by 3.5 to and 4.0 to 5.0 pp, respectively. These estimates imply the reduction of employment ranges between 1.7 and 2.7 pp, which lies within the range of our estimated effects on employment.

Outcomes of Non-Disabled Workers

Non-disabled workers in no-protection states might have experienced spillover effects through regulatory changes in the labor market. We use the benchmark estimation structure to study the effects on non-disabled workers and summarize the results in Table 8.¹⁶ We find that states without protection experienced higher churning rates before and after the ADA. Further, while we do not observe significant changes in transition rates associated with the ADA, the magnitude of coefficients vary across flows into and out of employment.

Table 8:

Effects of the ADA on Non-Disabled Workers’ Labor Market Outcomes

Coefficient	Emp. to Non-Emp.	Unemp. to Emp.	Non-Emp. to Emp.	Employment
No Protection	0.022***	0.146***	0.005	−13.26***
	(0.002)	(0.018)	(0.008)	(1.94)
After ADA	0.033***	−0.011*	−.055**	0.05***
	(0.005)	(0.050)	(0.027)	(0.006)
No Protection	−0.001	0.040	−0.030	−0.04***
× After ADA	(0.003)	(0.046)	(0.019)	(0.01)
R2	0.009	0.029	0.112	0.073
# of obs.	117,280	5,403	14,335	131,615

Note: Table 8 reports regression coefficients of the benchmark analysis. Regression also controls for education and age as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

It is worth noting that the ADA was a policy targeted towards disabled workers. Thus, the direct effects on hiring and firing decisions for non-disabled workers might have been small. However, there could have been spillover effects that manifest through changes in the equilibrium market tightness. As flows into employment are affected by the latter, we might expect to see a higher coefficient in non-employment-toemployment transition relative to employment-to-non-employment transition. Overall, we observe lower employment rate of non-disabled workers after the ADA.

Age-Specific DD Analysis

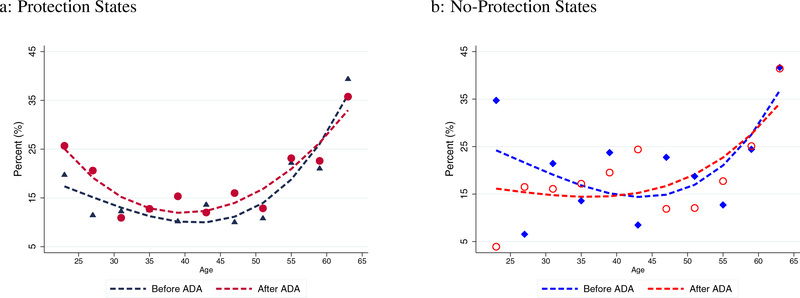
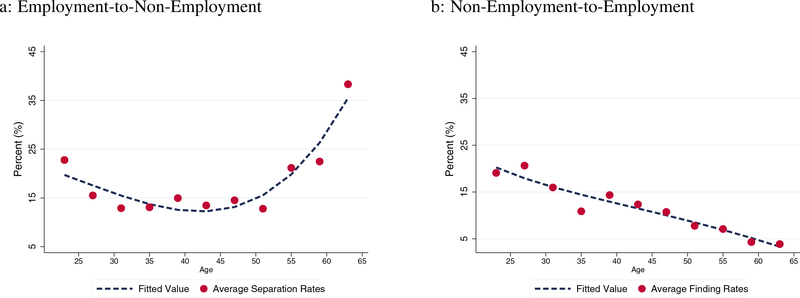
It is well-known that an individual’s labor market transition rates change over his life-cycle.¹⁷ While the benchmark analysis includes age as one of the control variables, it does not allow for possible differential effects of the ADA by age group. To explore the possible age-specific effects of the ADA, we first plot the average transition rates from employment to non-employment for disabled workers over the life-cycle in protection (left panel) and no-protection states (right panel) in Figure 6.¹⁸ We observe that the individuals in pre-existing protection states exhibit a U-shaped transition rate before and after the ADA, and a higher transition rate over all ages (except the very last) after the ADA. On the other hand, the younger workers in no-protection states experienced a decline in transition rates from employment to non-employment after the ADA.¹⁹

Figure 6: Life-Cycle Profile of Employment-to-Non-Employment Transition by Age Group.

Note: Figures 6a and 6b illustrate the weighted average of employment-to-non-employment transition rates for states with and without pre-existing employment protection, respectively. Triangle (diamond) and circle markers represent the data before and after the ADA, respectively. Dashed lines are fitted values of these data points in quadratic age.

To statistically test the heterogeneity of the ADA effects by age group, we divide the sample into two age groups, young (from ages 23 to 48) and old (from ages 49 to 64), and conduct two separate DD estimations. As summarized in Table 9, we find that the decrease in the job-separation rate was more pronounced among the younger cohorts. A possible explanation for this finding is that marginal workers, who could be most affected by firing and hiring restrictions (as we also show in the model and quantitative analysis that follows), tend to be younger workers.

Table 9:

Effects of the ADA on Disabled Workers’ Transitions by Age Group

Coefficient	Employment to Non-Employment		Non-Employment to Employment
	Young	Old	Young	Old
No Protection	0.130***	0.006	−0.166***	0.011
	(0.014)	(0.026)	(0.025)	(0.007)
After ADA	−0.082	−0.055	−0.091*	0.004
	(0.095)	(0.089)	(0.050)	(0.019)
No Protection	−0.041*	−0.027	0.031	−0.006
× After ADA	(0.023)	(0.041)	(0.033)	(0.012)
R2	0.032	0.086	0.031	0.021
# of obs.	2,203	1,682	3,353	5,208

Note: Table 9 reports regression coefficients of age-specific DD analysis. An individual is classified as young if he is between the age of 23 and 48, and old otherwise. Regression also controls for education and age as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

3.3. Robustness Analyses

In this section, we present the results from robustness analyses. First, we conduct DD analysis using grouplevel data. Second, we conduct a difference-in-difference-in-differences (DDD) analysis in which nondisabled workers serve as a control group. Lastly, we exploit the state-specific adoption year of employment protection policies. The estimation results for disabled workers from these analyses are summarized in Table 10, and we relegate the full results to Appendix B.2.

Table 10:

Summary of Robustness Analyses Results

Model Specification	Coefficient	Emp. to Non-Emp.	Unemp. to Emp.	Non-Emp. to Emp.
a. Group-Level Analysis	No Protection	−0.040**	0.011	0.006
	× After ADA	(0.021)	(0.106)	(0.016)
	R2	0.43	0.08	0.22
	# of obs.	30	30	30
b. DDD	Disabled	−0.031*	−0.192**	0.013
	× No Protection	(0.018)	(0.099)	(0.019)
	× After ADA
	R2	0.017	0.032	0.155
	# of obs.	120,861	5,891	22,896
c. Staggering Policy	State-level Protection	−0.03***	−0.02	0.02
		(0.01)	(0.10)	(0.01)
	R2	0.028	0.185	0.037
	# of obs.	4,760	651	10,909

Note: Table 10 reports regression coefficients fromrobustness analyses. Numbers in parentheses are standard errors clusteredby state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

Group-level Analysis

In our benchmark analysis, we studied the effects of the ADA by applying a standard DD model on individual-level labor market outcomes. Such regression analyses may underestimate the size of standard errors when there exist common group errors. We addressed this issue by clustering standard errors at the state level.

As a robustness analysis, we use an alternative two-step approach to adjust for group-level errors, as suggested by Donald and Lang (2007). In the first stage, we compute the mean of dependent variables for each cell (group and year, e.g., flow into employment of disabled workers residing in no-protection states). In the subsequent stage, we compare the difference between groups to estimate the effects of the ADA. As we use 15 periods of observation for the treatment and control groups, there are total of 30 observations available for this analysis. Panel A of Table 11 summarizes the results. We find that, similar to the individuallevel analysis, flow from employment to non-employment declined by 4 pp due to the ADA, while effects on other flows are insignificant.

Table 11:

Calibrated Parameters

Parameter	Value	Description
A. Outside the Model
β	0.996	Discount factor
bD	0.9μD	Value of home production, disabled (90% of average productivity)
bND	0.75μND	Value of home production, non-disabled (75% of average productivity)
𝜂	0.5	Nash-bargaining parameter of worker
B. Within the Model
κ	8.257	Vacancy-posting cost
γ	0.981	Elasticity of p (𝜃) w.r.t. market tightness θ
δ	0.006	Exogenous job destruction rate
𝜙D	0.013	Probability of redrawing productivity, disabled
𝜙ND	0.078	Probability of redrawing productivity, non-disabled
μD	1.000	Average productivity, disabled (normalization)
μND	1.923	Average productivity, non-disabled
${\sigma }_z^2$	0.231	Variance of productivity distribution
CF,D	12.963	Firing cost of the disabled under the ADA
CH,D	0.828	Hiring cost of the disabled under the ADA

Note: Table 11 reports the values of the calibrated parameters. Part A reports parameters calibrated a priori, and part B reports the parameters calibrated within the model jointly to match the benchmark economy (without policy) and the changes in the equilibrium transition rates between the benchmark economy and the economy under the ADA.

Difference-in-Difference-in-Differences Analysis (DDD)

In our benchmark analysis, we conduct a DD regression to measure the treatment effect of the ADA by comparing the change in transition of disabled workers before and after the employment protection. One might worry, however, that pre-existing state-laws differ from the ADA, and disabled workers with pre-existing protection may not be an appropriate control group for quantifying the effects of the ADA on the disabled.

To address this issue, we conduct a difference-in-difference-in-differences (DDD) analysis that includes non-disabled workers as an alternative comparison group. We estimate Equation (2) for working-age male workers with and without disabilities during the same time frame.

$$\begin{gathered} y_{i,s,t}={\beta }_0+{\beta }_1{X}_{i,s,t}+{\beta }_2{\mathbb{I}}_{\{t\ge ADA\}}+{\beta }_3{\mathbb{I}}_{\{i=\text{Disabled}\}}+{\beta }_4{\mathbb{I}}_{\{s=\text{No}\text{Protection}\}} \\ +{\beta }_5{\mathbb{I}}_{\{t\ge ADA\}}\times {\mathbb{I}}_{\{i=\text{Disabled}\}}+{\beta }_6{\mathbb{I}}_{\{t\ge ADA\}}\times {\mathbb{I}}_{\{s=\text{No}\text{Protection}\}} \\ +{\beta }_7{\mathbb{I}}_{\{i=\text{Disabled}\}}\times {\mathbb{I}}_{\{s=\text{No}\text{Protection}\}}+{\beta }_8{\mathbb{I}}_{\{t\ge ADA\}}{\mathbb{I}}_{\{i=\text{Disabled}\}}\times {\mathbb{I}}_{\{s=\text{No}\text{Protection}\}}+{\epsilon }_{i,s,t}. \end{gathered}$$ (2)

Panel B in Table 10 summarizes the coefficients from this estimation. We find that both employment-to-non-employment and unemployment-to-employment flows exhibit significant and sizable declines similar to our benchmark specification.

Staggering Policy

In our benchmark analysis, we categorize states into treatment and control groups and collapse each group’s observations into pre- and post- time dummies, i.e., pre- and post-time dummies were group-specific. While this aggregation method allows us to reduce potential bias in standard errors related to serial correlation, we disregarded state-level variation in enactment timing during the 1980s.

In this robustness analysis, we utilize this variation (shown in Figures 1 and 2) and run a DD analysis with a state-level dummy variable for the enactment of state-level ADA, as specified by the following equation:

$$y_{i,s,t}={\alpha }_0+X_{i,s,t}{\alpha }_1+{\alpha }_2{\mathbb{I}}_{\{s,t=\text{Protection}\}}+{\alpha }_{3,t}{\text{year}}_t+{\alpha }_{4,s}{\text{state}}_s+{\epsilon }_{i,s,t}.$$ (3)

The dummy variable 𝕀_{s,_{t=Protection}} which is now state- and year-dependent, equals 1 if the state adopted ADA-like employment protection for the disabled and zero otherwise. For states without pre-existing employment protection, this variable is identical to the previous post-year dummy. For states with pre-existing ADA, however, this variable is state-specific, and the coefficient α₂ estimates the effect of employment protection. Panel C of Table 10 reports a significant decline in the disabled’s transition from employment to non-employment. We conclude that whether it was protection at the federal or state level, the effect of employment protection on employment-to-non-employment transition was negative and significant.

These robustness analyses further strengthen our findings on the impact of the ADA: disabled workers experienced a decline in their transition flow from employment to non-employment, but the effect on their transition into employment was insignificant.

4. A Model of Employment Protection

In this section, we build an equilibrium model of the labor market with search friction to analyze the effects of employment protection policies. Using this model, we illustrate two distinctive effects of employment protection. As intended, the policy induces firms to retain workers during employment (direct effects). However, it also creates general equilibrium effects as firms face higher costs when creating a new job. As a consequence, firms additionally respond to employment protection by (i) substituting current employees for new hires and (ii) reducing the number of jobs created. Therefore, the net effect on employment rates of the disabled workers under employment protection is ambiguous.

4.1. Model Environments

Time is discrete and continues forever. The economy is populated by individuals of type i ∈ {D,ND}, where D denotes workers who are disabled, and ND denotes workers who are non-disabled. Individual type is observable and fixed over time. Denote the share of each type in the economy by 𝜋_i, with 𝜋_D + 𝜋_ND = 1. When employed, workers are subject to idiosyncratic productivity $z\in [\underset{\_}{z},\overline{z}]$, which is observable and follows a known, type-dependent distribution F_i (z). Assume F_ND (z) first-order stochastically dominates F_D (z) so that F_nd (z) < F_d (z) for ∀z, implying that the expected productivity of a non-disabled worker is higher than that of a disabled worker.20 The productivity is redrawn each period with probability 𝜙_i; while employed.

The economy is also populated by a positive measure of a continuum of firms. Firms have access to a production technology that translates a worker with productivity z into z units of final goods. Both workers and firms have linear utility and discount the future at rate β ∈ (0,1).

We assume that the search process is random and governed by a constant returns-to-scale matching function m (u, v), where v represents the total number of vacancies posted by firms, and u represents the total number of unemployed workers. Using the definition of market tightness (or the vacancy-to-unemployment ratio) θ = v/u, we can write the probability of filling a vacancy as q (𝜃) ≡ m (u, v) /v = m (𝜃⁻¹,1) and the job-finding rate of a worker as p (𝜃) = 𝜃q (𝜃).21

The timing of the model goes as follows. In the beginning of a period, a δ ∈ (0,1) fraction of matches dissolves exogenously. Firms create a vacancy by paying a cost κ. Then, workers and firms meet through a search process at which time firms observe the type of the worker i and draw their idiosyncratic productivity z from F_i (z). If the firm decides to hire the worker, they bargain over the next-stage production plan according to the Nash-bargaining rules, with bargaining power η and 1 — η, respectively. If the firm decides not to hire the worker, it pays C_H,i, a cost for terminating the hiring process.22 Endogenous job destruction may occur among existing matches at the bargaining stage. Employers separating from their workers are subject to termination costs C_F,i. Lastly, firms and workers who survive the process produce output and consume their surpluses.

4.2. A Competitive Equilibrium

Our model extends that of Mortensen and Pissarides (1994) by incorporating employment protection policies.23As the workers’ problems are standard, we specify the firms’ value functions and the free-entry condition to understand the role of policies. The value of hiring a type-i’ worker with productivity z at wage w is specified as

$$\begin{gathered} J_i(w,z) \\ =z-w+\beta (1-\delta )\left[\left(1-{\varphi }_i\right)J_i(w(z),z)+{\varphi }_i{\int }_{\underset{\_}{z}}^{\overline{z}}\left\{r_i(\widehat{z})J_i(w(\widehat{z}),\widehat{z})-\left(1-r_i(\widehat{z})\right)C_{F,i}\right\}d{F}_i(\widehat{z})\right], \end{gathered}$$ (4)

where r_i (z) represents the optimal retention policy of the firm. The firing cost C_F,i is incurred when the firm is separated with the worker, lowering the value. The expected value of hiring a worker type-i is then

$$V_i=q(\theta )\left[{\int }_{\underset{\_}{z}}^{\overline{z}}\left\{h_i(\widehat{z})J_i(w(\widehat{z}),\widehat{z})-\left(1-h_i(\widehat{z})\right)C_{H,i}\right\}d{F}_i(\widehat{z})\right],$$ (5)

where hi (z) is the optimal hiring policy of the firm. Similar to the firing cost, C_H,i enters the firm’s value function and affects its hiring decision.

First, as is standard in this environment, firms use reservation productivities for retention and firing, that is, there exist cutoff reservation productivities z_F,i (θ) and z_H,i (θ), such that all workers above such productivity are retained and hired, respectively. In the absence of government intervention (i.e., C_H,i = C_F,i = 0 for ∀i), conditional on a worker type-i, the reservation productivities for hiring and firing are equalized. This result is driven by the fact that the firms’ surpluses from an incumbent and a newly hired worker are identical (therefore, firms impose the same standard in firing and hiring). Second, when firms face the same firing and hiring costs across types (i.e., C_H,i = C_F,i for ∀i), the expected value of hiring a non-disabled worker is higher than that of a disabled worker because of the differences in their underlying productivity processes. As a consequence, hiring and retention standards are less stringent for non-disabled workers and the non-disabled workers’ equilibrium employment rate is higher.²⁴

Due to the reservation-productivity property, the competitive equilibrium of the model is fully characterized by the cutoff productivities and equilibrium market tightness. The last condition for equilibrium is the free-entry condition of firms, which is expressed as $-\kappa +{\sum }_i{\tilde{\pi }}_i{V}_i=0$, where ${\tilde{\pi }}_i$ represents the share of type-i workers among the total unemployed workforce. With some algebra, we can express this condition as

$$\frac{1}{1-\eta }\left\{\frac{\kappa }{q(\theta )}+\sum _i{\tilde{\pi }}_i{C}_{H,i}\right\}=\sum _i{\tilde{\pi }}_i\left[{\int }_{z_{H,i}}^{\overline{z}}\left\{\frac{\widehat{z}-z_{H,i}}{1-\beta (1-\delta )\left(1-{\varphi }_i\right)}\right\}d{F}_i(\widehat{z})\right].$$ (6)

As is evident from equations (4), (5), and (6), C_F,i and C_H,i affect the firms’ value functions and the equilibrium free-entry condition. First of all, because both workers are in the same labor market, when hiring cost C_H,_i increases even for one type, all other types are adversely affected through changes in the market tightness (θ). The size of this general equilibrium effect depends on the relative share of worker types among the unemployed $\left({\tilde{\pi }}_i\right)$ and the elasticity of the matching function with respect to the market tightness, i.e., the responsiveness of the job-finding rate with respect to the changes in market tightness.

We can further show that an increase in firing cost of a type-i worker lowers the reservation productivity for firing (more likely to be retained, conditional on θ), increases the reservation productivity for hiring (less likely to be hired, conditional on θ), and lowers the equilibrium market tightness as the overall expected return per post declines. Unlike the firing costs, hiring costs affect reservation productivities as well as the zero-profit condition directly, and their impact on equilibrium outcomes cannot be directly shown.²⁵

4.3. Worker Flows and Employment Rates

Can we interpret a small change in employment as evidence that firms viewed the penalties upon violating the ADA as insignificant? In this section, we show that there can be an alternative explanation for this observation. When the costs of firing are significant, firms do indeed reduce the rate of job termination (due to the direct impact of the policy). However, subsequent indirect effects generate a decline in inflow toward employment, dampening the law’s overall impact on employment.

In our model, the transition rate from employment to non-employment is given by EU_i = δ + (1 — δ) 𝜙_iF (z_F,_i), while the inflow to employment from non-employment is UE_i = p (θ)[1 — F_i (z_h,i)] ²⁶ From the observations in the previous section, we can show that an increase in firing costs impact cutoff productivities and equilibrium market tightness to force both the EU_i and UE_i transition rates to fall.²⁷ Thus, the net effect of the policy on employment can be small even though the underlying costs of firing (C_F;i) are sizable enough to change firms’ hiring and firing practices. In the next, we combine the empirical results and the model to disentangle the size of these costs and measure the aggregate effect of the law.

5. Quantitative Analysis

In Section 3 of our empirical analysis, we found significant declines in transition rates to non-employment, suggesting a rise in the costs of employment termination. In this section, we use the presented model in Section 4 as a laboratory to quantitatively evaluate the size of the hiring and firing costs imposed under the ADA using the empirical findings. We then illustrate the effects of the policy on aggregate productivity and output.

To do so, we calibrate the parameters of the model by mapping the model to the U.S. labor markets before the ADA (in which hiring and firing costs are normalized to zero for all workers, i.e., C_H,_i = C_F,i = 0) with two types of workers, disabled (i = D) and non-disabled (i = ND). Moreover, we jointly estimate policy parameters C_H,_D and C_F,_D to match the empirical findings (changes in transition flows caused by the ADA) from Section 3.²⁸ We assume that the policy parameters for the non-disabled workers did not change as a result of the ADA. In the following, we document the calibration procedure and results of our quantitative analysis.

5.1. Choice of Functional Forms

Following Shimer (2005), we assume that the search process is determined by a matching function p (θ) = min{θ^γ, 1} with γ ∈ (0,1). Utility and production functions are both linear. Firms pay a vacancy creation cost κ. Individuals who are not working enjoy flow utility b_i, which reflects both monetary benefits and utility from leisure activities. While employed, the value of employment depends on productivity z and its distribution F_i (z), the on-the-job probability of redrawing idiosyncratic productivity ϕ_i, and the exogenous job-destruction rate δ. We assume that the productivity z follows a log-Normal distribution with variance ${\sigma }_z^2$ and type-specific mean ${\mu }_i=m_i-{\sigma }_z^2/2$ so that the mean of the average productivity is exp (m_i) regardless of the value of ${\sigma }_z^2$.²⁹ In order to preserve the first-order stochastic dominance, we use a common variance on productivity distribution across types.

5.2. Calibration

Our model period is one month. As discussed in Shimer (2012), researchers only observe workers’ transitions if switches occur during the sampling periods but miss potential transitions before or after these periods. This time aggregation issue could be severe if we use a wider window for constructing transition rates. In order to address potential concerns from using annual transition flows in our estimation, we let our simulation exercise be subject to the same aggregation bias as in the matched March CPS. In subsequent simulation periods, we compute annual transition rates over 12 months. The monthly discount factor β is set to be consistent with a 5% annual interest rate so that β⁻¹ = (1.05)^1/12.

The share of disabled workers is π_D = 0.083, and the share of non-disabled workers is π_ND = 0.917. We set m_D = 1, which normalizes the mean productivity of disabled workers to μ_D = exp (1). The value of the outside option for the disabled is b_D = 0.9μ_D (90% of the average productivity) to reflect the combined value from leisure and monetary compensation from disability insurance. The outside option of the nondisabled is 75% of the average productivity, so b_ND = 0.75μ_ΝD, consistent with the values in the literature (Menzio and Shi, 2011). The ratio of home production to average productivity for the disabled is higher than that of the non-disabled, reflecting the findings from empirical literature on disabled workers. Finkelstein, Luttmer and Notowidigdo (2009) document that individuals with poor health value their leisure more than their healthier counterparts. Furthermore, the replacement ratio of the Social Security Disability Program (DI) is 40% to 60% (Autor and Duggan, 2006; French and Song, 2014) at the 50th and 10th percentile of the earnings distribution, which is more generous than the unemployment insurance program.³⁰ The Nash bargaining parameter of worker η is 0.5.

The remaining parameters calibrated within the model are κ, the vacancy-posting cost; γ, the elasticity of p (θ) with respect to θ; δ, the exogenous job destruction rate (common across types); 𝜙_i;, the type- dependent probability of redrawing productivity; μ_ΝΟ, the average productivity of non-disabled workers; ${\sigma }_z^2$, the variance of idiosyncratic productivity distribution; and two policy parameters, C_h,_d and C_F,_D. We calibrate these 9 parameters jointly to match worker transition rates before the ADA (4), the change in transition rates pre- and post-ADA (4), and the wage ratio between the two types (1). As our model does not distinguish between unemployed workers and non-participants, we use transition rates between employment and non-employment as our targets. The labor market parameters κ, 𝜙_i, and δ and the productivity distribution parameters μ_ΝD and ${\sigma }_z^2$ jointly affect the transition rates and the differences in transition rates across types. Further, the changes in transition rates of disabled workers are driven by the direct effects from changes in the cost parameters (C_h,_d and C_F,_D) and the indirect effect from equilibrium market tightness. As the cost parameters have heterogeneous impacts on transition rates, we can infer the size of these costs by matching the changes in employment-to-non-employment and non-employment-to-employment transitions. Moreover, for non-disabled workers, whose policy parameters did not change in response to the ADA, any changes in their transition rates are due to general equilibrium effects, which is controlled by the elasticity parameter in the matching function (γ).³¹ We summarize the parameter values in Table 12 and report the calibration targets and the model performance in Table 13.

Table 12:

Calibration Targets (Data vs. Model)

Moment	Data	Model
Annual Transition Flows Pre-ADA
Disabled: Employment to Non-employment	16.5%	16.9%
Disabled: Non-employment to Employment	6.3%	5.9%
Non-Disabled: Employment to Non-employment	8.6%	9.0%
Non-Disabled: Non-employment to Employment	33.7%	33.7%
Wage Ratio (Non-Disabled to Disabled)	1.54	1.54
Difference between Post-ADA and Pre-ADA Outcomes
Disabled: Employment to Non-employment	—3.7pp (2.1)	— 3.4pp
Disabled: Non-employment to Employment	—5.0pp (5.0)	— 4.3pp
Non-Disabled: Employment to Non-employment	0.1pp (0.3)	0.1pp
Non-Disabled: Non-employment to Employment	—3.0pp (1.9)	—3.2pp

Note: Table 12 reports calibration targets and their values from the model. See the discussion in the text for detailed information on the targets.

The calibrated model is able to match the transition flows of workers before the enactment of the ADA and the wage ratio between the non-disabled and the disabled, as shown in the top section of Table 13.³² Also reported are the point estimates and standard errors (in parentheses) of our estimation results in percentage points, from Tables 5, 6, and 8 (linear trend specification) in Section 3, which are used as targets. We found a large and significant drop in the employment-to-non-employment transition rate of disabled workers, which were similar to our empirical moments. While the transition rate of the disabled from non-employment to employment decreased, the impact was not significant (as shown by the large standard errors) in the empirical analysis, and the model prediction lies within the confidence interval. Through the general equilibrium effect, the model predicts that the increased costs on the disabled also affect non-disabled workers. Furthermore, for non-disabled workers, the effect on flow from non-employment to employment is larger than the opposite flow, as the former is directly influenced by the equilibrium job finding rate.

5.3. The Costs of Firing and Hiring Discrimination and the Impact of the ADA

The estimated cost, imposed by the ADA (C_F,_D), that firms pay upon firing a disabled worker is 12.96. Moreover, the estimated cost of hiring discrimination (Ch,d), that is the cost a firm pays if it decides not to hire a disabled worker after drawing a productivity shock, is 0.83. These costs are approximately 61% and 4% of the average annual wage in the calibrated economy.³³ The high level of firing cost is necessary to match the drop in the flow from employment to non-employment. While the size of the estimated firing cost seems large, it is important to note that the cost is incurred only when a disabled worker is separated, which happens with probability δ + (1 — δ) <𝜙_DF_D (z_F,D) (sum of the probability that a job is exogenously destructed, and conditional on continuation, the probability of redrawing a productivity that is below the cutoff) each month. When we convert the estimated firing cost into monthly expenses, it translates into 9.2% of the average monthly wage.³⁴ An analogous procedure yields the expected cost of not hiring a disabled worker equivalent to 0.9% the average monthly wage. ³⁵

When these costs are imposed on firms, the reservation productivities and market tightness are adjusted in equilibrium. As we discuss in Section 4.2, in an economy without government intervention (no firing or hiring costs), the reservation productivities for retention and hiring are equalized. With the implementation of the ADA, however, it is no longer the case. As predicted by the model, the increased costs of firing induces firms to fire disabled workers less frequently (cutoff decreases by 15% in the calibrated model). Moreover, because the hiring cost is lower than the firing cost, the reservation productivity for hiring a new disabled worker increases (by 9%).³⁶ Even though non-disabled workers do not face direct government regulation, their reservation productivities (for both retention and hiring) are lowered as non-disabled workers are relatively more attractive than the disabled. However, all workers now face the equilibrium market tightness that is 12% lower due to the decline in the expected profit from creating a vacancy.

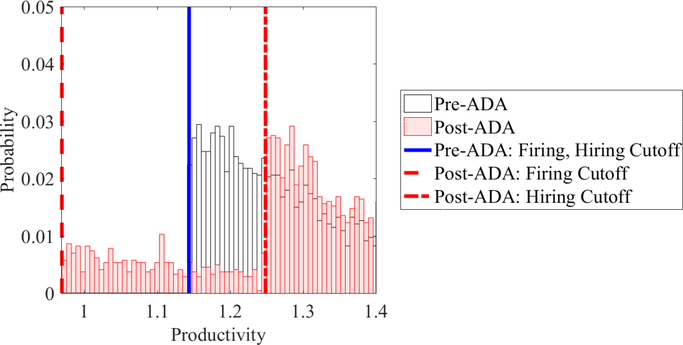
These endogenous responses of firms in their hiring and firing decisions have aggregate consequences. Due to the decrease in the reservation productivity of retention, continuing disabled workers have relatively lower productivity. On the other hand, the new entrants have higher productivity compared to the benchmark economy. Figure 7, where we plot the productivity distributions of disabled workers (those who are employed) and reservation productivities for firing and hiring from the simulated model pre- and post-ADA, graphically shows these results. First, note that compared to the benchmark economy, marginal workers have lower productivity (the mass of workers between the post-ADA firing cutoff and pre-ADA firing cutoff). These represent workers kept by firms due to high firing costs who would otherwise have been fired if the ADA were not in place. At the same time, due to higher hiring standards, in the post-ADA economy, there are relatively less workers who are below the new hiring cutoff (less workers between pre-ADA hiring and post-ADA hiring cutoffs compared to pre-ADA), but more workers above the post-ADA hiring cutoff. Overall, we find that these distortions in the productivity distribution lead to a 1.6% increase in the average productivity of the disabled workforce, as the effect from selective hiring (which increases the average productivity) dominates.³⁷ While the average productivity of disabled workers is higher, their employment rate falls. If we assume the empirically estimated employment rate changes (3 pp drop), we find that the aggregate output drops by 0.02%.

Figure 7: Productivity Distribution Pre- and Post-ADA.

Note: Figure 7 shows the simulated productivity distribution of disabled workers (truncated to the right to focus on marginal workers) pre- and post-ADA. The reservation productivities for firing and hiring are the same in the benchmark economy, but due to heterogenous costs, they diverge post-ADA: firing standards are relaxed, while hiring standards become more strict.

The quantitative analysis of this section highlights the benefits of conducting a policy analysis with worker flows. First, by studying the changes in worker transitions, we are able to disentangle the relative strengths of the hiring and firing clauses of the ADA. Second, we analyze the average productivity and output consequences on the workforce, driven by the endogenous changes in the hiring and firing standards imposed by firms, in response to the regulation. Focusing on only the employment rate changes driven by the ADA is not able to capture the consequences that we discussed.

6. Conclusion

This paper analyzed the effects of Title I of the Americans with Disabilities Act, an employment protection policy for disabled workers in the United States. We exploit the cross-state variations in employment protection laws prior to the ADA and empirically estimate the effects of the ADA on transition flows of all workers. Then, we use a frictional labor market model to show the impact of firing and hiring costs on firms’ retention and hiring decisions, and the general equilibrium effects of those costs. Lastly, we combine the empirical results and the model to estimate the costs of firing and hiring clauses of the ADA. Our findings suggest that the large firing cost imposed by the ADA led to a decrease in the disabled’s flow from employment to non-employment. Further, due to the distortions in firms’ hiring and firing decisions, the equilibrium market tightness decreased, and the aggregate productivity and output were impacted.

Our empirical results suggest that the ADA reduced firing of disabled workers, but at the same time, had a negative impact on their job-finding rates. While we focused on understanding and evaluating the impact of the current employment protection policy in the United States, an important follow-up line of inquiry is to investigate how we can provide better future labor market policies for the disabled. With the aging of population, we expect a further increase in the number of people with disabilities in coming years. Thus, it is important to not only understand the effects of labor market and social insurance policies against disability risks, but also to address the optimal design of them. Our findings highlight that it is crucial to factor firms’ endogenous responses into this discussion for a comprehensive analysis.

A Extended Description of the Model in Section 4

A.1 Problems of the Worker

We denote h_i (z) as the optimal policy function for the hiring decision based on the realization of idiosyncratic productivity z. Taking the expectation over possible realization of productivity, the value function of the unemployed worker is

$$U_i=b_i+\beta {\int }_{\underset{\_}{z}}^{\overline{z}}\left\{p(\theta )h_i(\widehat{z})W_i(w(\widehat{z}),\widehat{z})+\left(1-p(\theta )h_i(\widehat{z})\right)U_i\right\}d{F}_i(\widehat{z}).$$ (7)

The unemployed worker is employed if he is matched with an employer (probability p(θ)) and the employer decides to hire him after observing his productivity (h_i(z)).

Similarly, denoting the optimal policy function for the existing match as r_i (z), equation (8) presents the value of an employed type-i worker of productivity z with wage w:

$$W_i(w,z)=w+\beta \left[\delta U_i+(1-\delta )\{\left(1-{\varphi }_i\right)W_i(w(z),z)+{\varphi }_i{\int }_{\underset{\_}{z}}^{\overline{z}}{r}_i(\widehat{z})W_i(w(\widehat{z}),\widehat{z})+\left(1-r_i(\widehat{z})\right)U_{i}d{F}_i(\widehat{z})\}\right].$$ (8)

The employed worker with productivity z receives w today. In the following period, the worker becomes unemployed with an exogenous probability δ; or if a new productivity is drawn (with probability 𝜙_ί) and the employer decides not to hire him (probability 1 - r_i(z)).

A.2 Competitive Equilibrium

Surplus Function We define the surplus of an existing match, S_i (w, z) = W_i (w,z) + J_i (w,z) - U_i + C_F,_i. Using the standard technique, we can show that the match surplus is independent of the wage and only depends on the worker type, i, and his idiosyncratic productivity level, z.

$$\begin{gathered} S_i(z)=z-b_i+\beta (1-\delta )\left(1-{\varphi }_i\right)S_i(z)+\beta (1-\delta ){\varphi }_i{\int }_{\underset{\_}{z}}^{\overline{z}}{r}_i(\widehat{z})S_i(\widehat{z})d{F}_i(\widehat{z}) \\ -\beta \eta p(\theta ){\int }_{\underset{\_}{z}}^{\overline{z}}{h}_i(\widehat{z})S_i(\widehat{z})d{F}_i(\widehat{z})+\{1-\beta (1-\delta )\}{C}_{F,i} \end{gathered}$$

The surplus of a newly formed match is ${\tilde{S}}_i(z)=S_i(z)-C_{F,i}+C_{H,i}$.

Lemma 1. S_i(z) and ${\tilde{S}}_i(z)$ are linear and strictly increasing in z.

Proof. From equation above,

$$\begin{gathered} S_i(z)=\frac{1}{1-\beta (1-\delta )\left(1-{\varphi }_i\right)}[z-b_i+\beta (1-\delta ){\varphi }_i{\int }_{\underset{\_}{z}}^{\overline{z}}{r}_i(\widehat{z})S_i(\widehat{z})d{F}_i(\widehat{z}) \\ -\beta \eta p(\theta ){\int }_{\underset{\_}{z}}^{\overline{z}}{h}_i(\widehat{z})S_i(\widehat{z})d{F}_i(\widehat{z})+\{1-\beta (1-\delta )\}{C}_{F,i}], \end{gathered}$$

and $S_i^{\prime }\left(z\right)$ = {1–β (1 – δ)(1 – ϕ_i)}⁻¹ > 0. The fact that ${\tilde{S}}_i(z)$ is linear and strictly increasing in z follows from ${\tilde{S}}_i(z)=S_i(z)-C_{F,i}+C_{H,i}$. □

Reservation Productivity in Hiring and Retention Given the surplus function above, it is straightforward from the equilibrium condition for the worker’s participation and the firm’s job creation, to show the following lemma. Reservation Productivity in Hiring and Retention

Given the surplus function above, it is straightforward from the equilibrium condition for the worker’s participation and the firm’s job creation, to show the following lemma.

Lemma 2. During the Nash bargaining stage of an existing match,

$$\{\begin{array}{l}{r}_i(z)=1if{S}_i(z)>0\\ r_i(z)=0otherwise.\end{array}$$

Lemmas 1 and 2 guarantee the existence and uniqueness of reservation productivity such that a firm is indifferent between being idle and active. For a given market tightness θ, we can thus define the reservation productivities z_f,i (θ) and z_h,i (θ) such that S_i (z_f,I; θ) = 0 and S_i (z_h,_i; θ) – C_F,_i + C_H,_i = 0. Using the fact that the share of Nash bargaining outcome is proportional to its bargaining power, the optimal reservation productivity in retention is determined by

$$z_{f,i}+\beta (1-\delta ){\varphi }_i{\int }_{z_{f,i}}^{\overline{z}}\frac{1-F_i(\widehat{z})}{1-\beta (1-\delta )\left(1-{\varphi }_i\right)}d\widehat{z}=b_i+\frac{\beta \eta }{1-\eta }\theta \kappa +\frac{\beta \eta p(\theta )}{1-\eta }{C}_{H,i}-\{1-\beta (1-\delta )\}{C}_{F,i};$$ (9)

and hiring decision, by

$$\begin{gathered} z_{h,i}+\beta (1-\delta ){\varphi }_i{\int }_{z_{f,i}}^{\overline{z}}\frac{1-F_i(\widehat{z})}{1-\beta (1-\delta )(1-\varphi )}d\widehat{z} \\ =b_i+\frac{\beta \eta }{1-\eta }\theta \kappa +\beta (1-\delta ){\varphi }_i{C}_{F,i}+\left[\frac{\beta \eta p(\theta )}{1-\eta }-\{1-\beta (1-\delta )\left(1-{\varphi }_i\right)\}\right]C_{H,i}. \end{gathered}$$ (10)

Lemma 3. Define z_h,i, and Z_f,i, as reservation productivities for hiring and firing respectively, satisfying equations (9) and (10).

1. For ∀θ > 0, z_h,i (θ) > z_f,i (θ) if and only if C_f,i > C_h,i.

2. If market tightness is higher, firing and hiring criteria becomes more stringent: z_f,i, (θ) and z_h,_i, (θ) are increasing in θ.

3. If policies and productivity redrawing probabilities (𝜙_i,) are symmetric across types, for a given market tightness θ, high types face less stringent criteria in hiring and firing: If C_H,_i, = C_H and C_F,_i, = C_F, z_f,i+1 (θ) < z_f,ί (θ) and z_h,i+1 (θ) < z_h,i (θ).

Proof. Taking difference between equations (9) and (10), we can show

$$z_{h,i}=z_{f,i}+\left\{1-\beta (1-\delta )\left(1-{\varphi }_i\right)\right\}\left(C_{F,i}-C_{H,i}\right).$$ (11)

Since 1 – β (1 - δ )(1 - 𝜙_ί) > 0, z_f,ί > z_h,i if and only if C_f,i < C_h,i.

Given θ, define an implicit function that satisfies the optimal condition for job continuation/worker retention problem (9) such that

$$\begin{gathered} G_{f,i}\left(z_{f,i},\theta \right)=z_{f,i}+\beta (1-\delta ){\varphi }_i{\int }_{z_{f,i}}^{\overline{z}}\frac{1-F_i(\widehat{z})}{1-\beta (1-\delta )\left(1-{\varphi }_i\right)}d\widehat{z} \\ -\left[b_i+\frac{\beta \eta }{1-\eta }\left\{\theta \kappa +p(\theta )C_{H,i}\right\}-\{1-\beta (1-\delta )\}{C}_{F,i}\right]=0. \end{gathered}$$ (12)

Applying the implicit function theorem,

$$\frac{d{z}_{f,i}}{d\theta }=\frac{\beta \eta \left(\kappa +p^{\prime }(\theta )C_{H,i}\right)}{1-\eta }\times {\left[1-\frac{\beta (1-\delta ){\varphi }_i\left(1-F_i\left(z_{f,i}\right)\right)}{1-\beta (1-\delta )\left(1-{\varphi }_i\right)}\right]}^{-1}>0,$$ (13)

as the job-finding rate p (θ) is an increasing function of θ. It is straightforward from (11) and (13) that $z_{h,i}^{\prime }(\theta )>0$.

The last lemma follows directly from first-order-stochastic-dominance of i + 1-type worker’s productivity distribution to i-type worker’s productivity distribution. □

Zero-Profit Condition The free-entry condition is written as

$$\frac{1}{1-\eta }\left\{\frac{\kappa }{q(\theta )}+\sum _i{\tilde{\pi }}_i{C}_{H,i}\right\}=\sum _i{\tilde{\pi }}_i\left[{\int }_{z_{H,i}}^{\overline{z}}\left\{\frac{\widehat{z}-z_{H,i}}{1-\beta (1-\delta )(1-{\varphi }_i)}\right\}d{F}_i(\widehat{z})\right].$$ (14)

$$\sum _i{\tilde{\pi }}_i\left[\frac{1}{1-\eta }\left\{\frac{\kappa }{q(\theta )}+C_{H,i}\right\}\right]=\sum _i{\tilde{\pi }}_i\left[{\int }_{z_h}^{\overline{z}}\left\{\frac{\widehat{z}-z_{f,i}}{1-\beta (1-\delta )\left(1-{\varphi }_i\right)}+C_{H,i}-C_{F,i}\right\}d{F}_i(\widehat{z})\right].$$

Lemma 4. Define ${\tilde{z}}_{f,i}$ and ${\tilde{z}}_{h,i}$ as reservation productivities satisfying equation (14).

1. ${\tilde{z}}_{f,i}(\theta )$ is decreasing in θ.

2. ${\tilde{z}}_{h,i}(\theta )$ is decreasing in θ.

Proof. Using the zero-profit condition under free-entry of firms in equation (14), we can derive another type-specific optimal condition for the cutoff and equilibrium market tightness. Let

$$\begin{gathered} G_{z,i}\left(z_{f,i},\theta \right) \\ ={\int }_{z_h(z_{f,i})}^{\overline{z}}\left\{\frac{\widehat{z}-z_{f,i}}{1-\beta (1-\delta )(1-\varphi )}+C_{H,i}-C_{F,i}\right\}dF(\widehat{z})-\frac{1}{1-\eta }\left\{\frac{\kappa }{q(\theta )}+C_{H,i}\right\} \\ =0, \end{gathered}$$ (15)

with

$$\begin{gathered} \frac{d{\tilde{z}}_{f,i}}{d\theta }=\left\{\frac{\kappa }{1-\eta }\times \frac{q^{\prime }(\theta )}{q^2(\theta )}\right\} \\ \times {\left[\frac{1-F\left(z_{h,i}\left(z_{f,i}\right)\right)}{1-\beta (1-\delta )(1-\varphi )}+\left\{\frac{z_{h,i}\left(z_{f,i}\right)-z_{f,i}}{1-\beta (1-\delta )(1-\varphi )}+C_{H,i}-C_{F,i}\right\}f\left(z_{h,i}\left(z_{f,i}\right)\right)\right]}^{-1}. \end{gathered}$$

By substituting the linear relationship between z_h,i and z_f,i in equation (11), we find

$$\frac{d{\tilde{z}}_{f,i}}{d\theta }=\left\{\frac{\kappa }{1-\eta }\times \frac{q^{\prime }(\theta )}{q^2(\theta )}\right\}\times {\left\{\frac{1-F\left(z_{h,i}\left(z_{f,i}\right)\right)}{1-\beta (1-\delta )(1-\varphi )}\right\}}^{-1}<0$$

as q′ (θ) < 0. The derivative of $d{\tilde{z}}_h/d\theta <0$ as z_h is a linear transformation of z_f. □

Lemmas (3) and (4) allow us to prove the following existence and additional characteristics of equilibrium.

Proposition 5. The equilibrium θ* and the cut-offs ${\left\{z_{f,i}^{*}\left({\theta }^{*}\right),z_{h,i}^{*}\left({\theta }^{*}\right)\right\}}_{i\in I}$ exist.

Proof. By the definition of equilibrium, $\left(z_{f,i}^{*}\left({\theta }^{*}\right),{\theta }^{*}\right)$ satisfies both (12) and (15) simultaneously. From the boundary conditions of the matching functions, lim_θ→∞ z_f,i(θ)=∞ and ${\lim }_{\theta \to \infty }{\tilde{z}}_{f,i}(\theta )=-\infty$. From Lemmas (3) and (4), both functions are continuous and monotonic; $z_{f,i}^{\prime }(\theta )>0$ and ${\tilde{z}}_{f,i}^{\prime }(\theta )<0$. Therefore, there exists a unique θ* that satisfies $z_{f,i}\left({\theta }^{*}\right)={\tilde{z}}_{f,i}\left({\theta }^{*}\right)$ as long as $z_{f,i}(0)<{\tilde{z}}_{f,i}(0)$. □

A.3 Comparative Statics: The Role of Employment Protection

We now explore how the equilibrium outcome evolves along with the change in policy parameters C_f,_i. Equations (9) and (10) and Lemma 3 already imply that given the market tightness, the increase in the degree of protection lowers the threshold for production reservation. We first formally establish these relationships in Lemma 6.

Lemma 6. Suppose firing cost increases, i.e., ${\check{C}}_{F,i}>C_{F,i}$.

1. Reservation productivity for retention decreases, i.e., $z_{f,i}\left(\theta ;{\check{C}}_{F,i}\right)<z_{f,i}\left(\theta ;C_{F,i}\right)$ for ∀θ > 0.

2. Reservation productivity for hiring increases, i.e., $z_{h,i}\left(\theta ;{\check{C}}_{F,i}\right)<z_{h,i}\left(\theta ;C_{F,i}\right)$ for ∀θ > 0.

Proof. From equation (12), we get

$$\frac{\partial z_{f,i}}{\partial C_{F,i}}=-(1-\beta (1-\delta ))\times {\left[1-\frac{\beta (1-\delta ){\varphi }_i\left(1-F_i\left(z_{f,i}\right)\right)}{1-\beta (1-\delta )\left(1-{\varphi }_i\right)}\right]}^{-1}<0,$$

and using the fact that z_h,i = z_f,i + {1 - β (1 - δ) (1 - 𝜙_i)} (C_f,i - C_H,i),

$$\begin{gathered} \frac{\partial z_{h,i}}{\partial C_{F,i}}=\frac{\partial z_{f,i}}{\partial C_{F,i}}+\left\{1-\beta (1-\delta )(1-{\varphi }_i)\right\} \\ =\left\{1-\beta (1-\delta )(1-{\varphi }_i)\right\}\left[1-\frac{1-\beta (1-\delta )}{1-\beta (1-\delta )(1-{\varphi }_i{F}_i(z_{f,i}))}\right]>0. \end{gathered}$$

□

As the zero-profit condition for ${\tilde{z}}_{h,i}(\theta )$ does not involve C_f,i, we can characterize the equilibrium of the economy with higher C_f,_i as follows:

Proposition 7. Suppose firing cost increases, i.e., ${\check{C}}_{F,i}>C_{F,i}$. The equilibrium market tightness is lower (${\theta }^{*}({\check{C}}_F)<{\theta }^{*}(C_F)$); reservation productivity for retention is lower ($z_f({\theta }^{*}({\check{C}}_F))<z_f({\theta }^{*}(C_F))$) and reservation productivity for hiring is higher ($z_h({\theta }^{*}({\check{C}}_F))<z_h({\theta }^{*}(C_F))$).

Proof. This is straightforward from Lemma 6. □

B Additional Tables and Figures

B.1 Data Appendix

Table 13:

Summary Statistics by Group

Variable	No Protection		Protection
	Pre-ADA	Post-ADA	Pre-ADA	Post-ADA
age (years)	42.9	42.9	42.4	42.4
college or more (%)	22.4	34.1	26.1	38.5
disabled (%)	10.0	10.5	8.6	8.0
# of obs.	17,297	13,990	44,719	69,013

Note: Table 13 documents the average statistics before and after the ADA by group using the matched March CPS. Pre- and Post-ADA period is defined as years in 1981–1990 and 1991–2000, respectively.

Figure 8: The Share of Disabled by Group.

Note: Figure 8 illustrates the trends of disability by group. We compute the share of disabled among the working-age male individuals based on the work disability variable in matched March CPS.

Table 14:

ADA Charges by Issue Category

Issue Category	2011	2012	2013	2014	2015
Hiring	1,552	1,509	1,512	1,541	1,513
	(3.1%)	(2.9%)	(2.9%)	(2.9%)	(2.7%)
Promotion, Benefits, and Wages	1,777	1,822	1,873	1,879	1,976
	(3.6%)	(3.5%)	(3.6%)	(3.5%)	(3.5%)
Discharge and Layoff	15,462	15,942	15,598	15,098	16,159
	(31.0%)	(30.7%)	(29.6%)	(28.4%)	(28.6%)
Reasonable Accommodations	8,566	9,041	9,496	9,765	10,781
	(17.2%)	(17.4%)	(18.0%)	(18.3%)	(19.1%)

Note: Table 14 reports the number of cases the EEOC received from 2011 to 2015. The charge statistics are available from the EEOC website: www.eeoc.gov/eeoc/statistics/enforcement/charges.cfm and www.eeoc.gov/eeoc/statistics/enforcement/ada-charges.cfm. The number of receipts include all charges filed under the ADA and those filed concurrently under Title VII of the Civil Rights Act, Equal Pay Act (EPA), and Age Discrimination in Employment Act (ADEA). The number in parentheses reports the percentage share out of total cases under the ADA. Data in earlier years or charges under the ADA only are not publicly available.

B.2 Additional DD Analysis Results

We report the detailed results of the difference-in-differences (DD) estimation in Section 3. Explanations on estimation strategies as well as data sources are available in the main text.

DD for the Non-Disabled

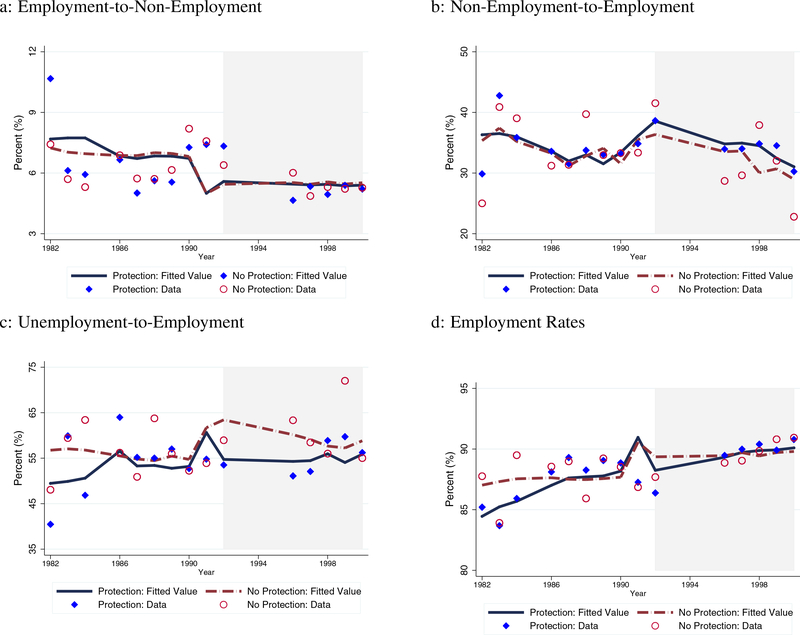
Table 15 reports the DD estimation results for non-disabled workers. We report three alternative specifications: year dummies, linear time trends, and quadratic trends. Figures 9 and 10 illustrate the time-trends of labor market transition as well as employment rates. Markers in Figure 9 indicate the observations from the data, and the fitted lines indicate the predicted values based on the estimation results.

Figure 9: Non-Disabled: Estimated Transition Rates.

Note: Figures 9a, 9b, 9c, and 9d illustrate the estimation results of labor market outcomes of the non-disabled. Red and blue markers in Figure 3a represent the average of treatment and control groups, respectively. The lines indicate the average estimated transition and employment rates based on estimation.

Figure 10: Non-Disabled: Difference in Estimated Transition Rates.

Note: Figures report the difference in estimated labor market outcomes of the non-disabled between treatment and control groups. The specification for the estimation includes age, education, year and state dummies, and linear time-trend.

Table 15:

Non-Disabled: Labor Market Transitions

a. Non-employment-to-Employment
Coefficient	Linear	Quadratic	Time Dummy
	(1)	(2)	(3)
No Protection	0.022***	0.022***	0.018***
	(0.002)	(0.003)	(0.002)
After ADA	−0.033***	−0.033***	−0.009
	(0.005)	(0.005)	(0.013)
No Protection	−0.001	−0.001	−0.003
× After ADA	(0.003)	(0.004)	(0.003)
R2	0.009	0.009	0.010
# of obs.		117,280
b. Unemployment-to-Employment
Coefficient	Linear	Quadratic	Time Dummy
	(1)	(2)	(3)
No Protection	0.152***	0.145***	0.146***
	(0.018)	(0.022)	(0.018)
After ADA	0.025	−0.008	−0.011*
	(0.038)	(0.055)	(0.050)
No Protection	0.020	0.037	0.040
× After ADA	(0.050)	(0.056)	(0.046)
R2	0.022	0.022	0.029
# of obs.		5,403
c. Non-employment-to-Employment
Coefficient	Linear	Quadratic	Time Dummy
	(1)	(2)	(3)
No Protection	23.07***	26.14***	0.005
	(6.005)	(5.768)	(0.008)
After ADA	−0.0005	0.008	−.055**
	(0.024)	(0.030)	(0.027)
No Protection	0.009	0.011	−0.030*
× After ADA	(0.035)	(0.035)	(0.019)
R2	0.136	0.136	0.112
# of obs.		14,335

Note: Table 15 reports regression coefficients of difference-in-differences analysis of non-disabled workers. Regression also controls for education and age, as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

Age-Specific DD Analysis

This section documents changes in disabled workers’ labor market transition rates by age. Figures in 11 illustrate the overall life-cycle pattern of labor market transition rates based on matched March CPS from 1981 to 2000. The red markers indicate the weighted average for each age bin, and the dashed lines are fitted values of data in quadratic. Figures in 12 decompose the same life-cycle profiles of job-finding rates by time and group.

Figure 11: Disabled Workers’ Transition Rates over the Life-Cycle.

Note: Figures 11a and 11b illustrate the weighted average of labor transition rates of the disabled by age group for years from 1981 to 2000. Red markers in the figures represent the actual data, and the dashed lines indicate the estimated transition rates in quadratic age.

Figure 12: Life-Cycle Profile of Non-Employment-to-Employment by Group.

Note: Figures 12a and 12b illustrate the weighted average of employment-to-non-employment transition rates for states with and without preexisting employment protection, respectively. Blue and red markers in Figures 12a and 12b represent the data before and after the ADA. Dashed lines are fitted values of these data points in quadratic age.

DD on Quit Rates An alternative explanation for the decrease of flows into non-employment is that employees with disabilities receive better accommodations (as employers are required to provide reasonable accommodations under the ADA). In this case, we would find fewer disabled workers quit. Using our matched dataset, we can directly test the labor supply-side margin. The dataset contains a variable which asks recent dropouts from the labor force whether the main reason that caused them to quit or retire from their job was their poor health status.³⁸ Thus, this variable provides information on whether workers with disabilities changed their labor supply and retirement decisions after the ADA.

Table 16:

DD Analysis: Left the Labor Force Due to Poor Health

Coefficient	Left the Labor Force Due to Poor Health
	Linear	Quadratic	Time Dummy
	(1)	(2)	(3)
No Protection	−0.045***	−0.045***	−0.045***
	(0.017)	(0.017)	(0.016)
After ADA	−0.004	−0.004	−0.009
	(0.044)	(0.044)	(0.045)
No Protection	−0.024	−0.024	−0.021
× After ADA	(0.030)	(0.030)	(0.028)
R2	0.069	0.069	0.065
# of obs.		8,384

Note: Table 16 reports regression coefficients of difference-in-differences analysis onhealth-related quitrates. Regression also controls for education and age, as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

Table 16 summarizes the results of our analysis. Regardless of specification, the effects of the ADA on the share of the exiting workforce turns out to be insignificant. Most of the difference between the two groups remained constant during the sample periods. Indeed, according to Hill, Maestas and Mullen (2015), once disabled, 75% of disabled individuals (who are thus eligible to request accommodations) did not receive accommodations from their employers even after the ADA. Therefore, even if the accommodation provision might reduce the involuntary exit of disabled workers from employment, the quantitative magnitude of the impact of this provision could be small.

B.3 DDD Analysis

Table 17:

Summary of DDD estimation

		Before ADA	After ADA	Δt	ΔΔ
Disabled	No Protection	β3 + β4 + β7	β2 + β3 + β4 + β5 + β6 + β7 + β8	β2 + β5 + β6 + β8
	Protection	β3	β2 + β3 + β5	β2 + β5
	Δs	β4+ β7	β4+ β6 + β7 + β8		β6 + β8
Non-Disabled	No Protection	β4	β2 +β4 + β6	β2 + β6
	Protection	-	β2	β2
	Δs	β4	β4+ β6		β6
ΔΔΔ					β8

Table 18:

Coefficient Estimation Results: DDD

Coefficient	Employment to Non-Employment	Unemployment to Employment	Non-employment to Employment	Employment
	(1)	(2)	(3)	(4)
Disabled	−0.091***	−0.108***	−0.205***	−0.53***
	(0.009)	(0.030)	(0.008)	(0.01)
No Protection	−0.018***	0.152***	−0.008	−0.04***
	(0.002)	(0.019)	(0.008)	(0.005)
After ADA	0.011	−0.037	0.008	0.01
	(0.014)	(0.044)	(0.018)	(0.01)
Disabled	−0.021	0.002	0.008	−0.07***
× After ADA	(0.013)	(0.074)	(0.014)	(0.02)
No Protection	0.003	0.048	−0.018	0.003
× After ADA	(0.003)	(0.048)	(0.018)	(0.01)
Disabled	−0.034	0.009	−0.019	−0.03
× No Protection	(0.021)	(0.084)	(0.014)	(0.02)
Disabled	−0.030*	−0.192**	0.013	0.03
× No Protection	(0.018)	(0.099)	(0.019)	(0.03)
× After ADA
R2	0.017	0.032	0.155	0.234
# of obs.	120,861	5,891	22,896	143,757

Note: Table 18 reports regression coefficients of difference-in-difference-in-differences analysis. Regression also controls for education and age, as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

B.4 Staggering Policy

Table 19:

Staggering Policy Estimation: Labor Market Transition Rates

a. Employment-to-Non-Employment
Coefficient	Linear	Quadratic	Time Dummy
	(1)	(2)	(3)
State-level Protection	−0.03***	−0.02*	−0.03
	(0.01)	(0.01)	(0.02)
R2	0.028	0.028	0.056
# of obs.		4,760
b. Unemployment-to-Employment
Coefficient	Linear	Quadratic	Time Dummy
	(1)	(2)	(3)
State-level Protection	−0.02	0.01	−0.03
	(0.10)	(0.08)	(0.08)
R2	0.185	0.134	0.164
# of obs.		651
c. Non-Employment-to-Employment
Coefficient	Linear	Quadratic	Time Dummy
	(1)	(2)	(3)
State-level Protection	0.02	0.01	0.004
	(0.01)	(0.01)	(0.02)
R2	0.037	0.037	0.039
# of obs.		10,909

Note: Table 19 reports regression coefficients of state-level difference-in-differences analysis. Regression also controls for education and age, as well as state and year dummies. Numbers in parentheses are standard errors clustered by state.

^***p < 1%,

^**p < 5%, and

^*p < 10%.

B.5 Robustness Analysis: Recalibration with Outside Options of Different Values

We conduct robustness analyses by considering the effects of the values of outside options on quantitative results. In the benchmark analysis, we use empirical measures of outside options for disabled workers (b_D = 0.9μ_D) and non-disabled workers (b_ND = 0.75μ_D). As both workers participate in the same labor market, the heterogeneity in the outside values can lead to different parameter values and impacts of the policies. We thus recalibrate the model under lower (b_ND = 0.65μ_ND) and higher (b_ND = 0.80μ_ND) outside options for the non-disabled; we discuss the parameters and quantitative results in the following.

Table 20 presents the selected parameters from the recalibrated models. While parameters are jointly determined to match the key labor market outcomes (and therefore it is difficult to pin down a one-to-one relationship between a parameter and a data moment), we observe broad patterns in the estimated parameters. In particular, as we increase the value of the outside option for non-disabled workers, labor market parameters are adjusted—lower vacancy posting costs (κ), average productivity of non-disabled workers (μ_ND), and standard deviation of the productivity distribution (σ_z)—to match the employment and wage ratio moments. Consequently, the estimated policy cost parameters increase with larger outside options.

Importantly, we find that the quantitative properties of the policy costs under these specifications are similar to those in the benchmark model; the estimated firing cost (C_F,_D) ranges between 9 and 9.5% and hiring cost (C_H,_D) between 0.3 and 2% of the equilibrium wages in the model. Consistent with the benchmark model, firing costs are estimated to be higher than hiring costs, and larger costs are necessary under higher outside options to match the changes in labor market outcomes for both types of workers after the ADA.

Table 20:

Selected Parameter Estimates in Robustness Analysis

	Value of Outside Option for the Non-disabled (bND)
	0.65μND	0.75μND (benchmark)	0.80μND
κ	9.26	8.26	6.04
μND	2.00	1.92	1.73
σz	0.27	0.23	0.12
CF,D (% wage)	9.0	9.2	9.5
CH,D (% wage)	0.3	0.9	2.0

Note: In all cases, the value of the outside option for the disabled is fixed at 90% of that worker’s productivity, i.e., b_D = 0.9μ_D The model performance is similar to that in the benchmark case across all three specifications.

In Figure 13, we report the resulting productivity effects before and after the ADA. Similar to the benchmark economy, firms are less likely to fire (the firing cutoff decreases) and more likely to hire (the hiring cutoff increases) after the ADA. When the value of the outside option of the non-disabled increases (Figure 13c), we observe a larger shift in the post-ADA distribution of workforce relative to the case with lower option value (Figure 13a). We find that in the former case, the increase in productivity of the disabled is larger, at 1.8% (relative to 1.6% in the benchmark case). In contrast, with lower outside option for the disabled, we find a negligible impact on average productivity as the effects from relaxed firing and more selective hiring offset each other.

Figure 13: Productivity Distribution Pre- and Post-ADA in Robustness Analysis.

Note: The figures plot the productivity distribution of disabled workers before and after the ADA in the re-calibrated model with (a) low and (c) high outside option values for non-disabled workers. We also include (b), the benchmark case for comparison. As in Figure 7, white bars represent pre-ADA productivity distribution; red (shaded) bars, post-ADA productivity distribution; solid (blue) line, pre-ADA hiring and firing cutoffs; dashed (red) line, post-ADA firing cutoffs; and dash-dot (red) line, post-ADA hiring cutoffs.