Neural mechanisms of sustained attention are rhythmic

Summary

Classic models of attention suggest that sustained neural firing constitutes a neural correlate of sustained attention. However, recent evidence indicates that behavioral performance fluctuates over time, exhibiting temporal dynamics that closely resemble the spectral features of ongoing, oscillatory brain activity. Therefore, it has been proposed that periodic neuronal excitability fluctuations might shape attentional allocation and overt behavior. However, empirical evidence to support this notion is sparse. Here, we address this issue by examining data from large-scale subdural recordings, using two different attention tasks that track perceptual ability at high temporal resolution. Our results reveal that perceptual outcome varies as a function of the theta phase even in states of sustained spatial attention. These effects were robust at the single-subject level, suggesting that rhythmic perceptual sampling is an inherent property of the frontoparietal attention network. Collectively, these findings support the notion that the functional architecture of top-down attention is intrinsically rhythmic.

eTOC

Helfrich et al. demonstrate that the neural basis of sustained attention is rhythmic. Using human intracranial recordings, they show that attentional allocation and overt behavior are modulated by a ~4 Hz theta rhythm that predicts endogenous excitability fluctuations.

Introduction

A long-standing question in models of sensory perception is whether perception is discrete or continuous (VanRullen, 2016a; VanRullen and Koch, 2003). Likewise, it has been debated whether the allocation of ‘sustained’ attention to one cued location is actually sustained or instead waxes and wanes over time (Buschman and Kastner, 2015). These considerations raise the possibility that our seemingly continuous experience of the world is actually constructed from a rapid, sequential sampling of the environment. Given that neuronal oscillations are ubiquitous in neural recordings (Buzsáki and Draguhn, 2004), it has been suggested that rhythmic brain activity might support the periodic sampling of the environment (Bishop, 1932; Valera et al., 1981; VanRullen and Koch, 2003). Hence, endogenous oscillatory brain activity might shape our perception of the world on a rapid timescale (Helfrich and Knight, 2016; Siegel et al., 2012). In the past, the functional role of neuronal oscillations has often only been inferred by assessing binary task contrasts, e.g. attend vs. non-attend, which integrated activity over longer time windows (Buschman and Kastner, 2015; Siegel et al., 2008). However, in order to establish a direct link between ongoing brain activity and behavior (Thut et al., 2012), it is desirable to sample behavioral outcome on a fine-grained temporal scale matching the timescale of endogenous brain activity (VanRullen, 2016a).

Previous behavioral and scalp EEG studies reported evidence for periodicities in bottom-up perception and top-down guided behavior (Fiebelkorn et al., 2013; Fontolan et al., 2014; Helfrich et al., 2017; Henry et al., 2014; Landau and Fries, 2012; Neuling et al., 2012; Spaak et al., 2014; Wöstmann et al., 2016; Zion Golumbic et al., 2013). For example, EEG studies have shown that the detection of a close-to-sensory-threshold target can be linked to neuronal oscillations in the range from 7-10 Hz (Busch and VanRullen, 2010, 2010; Busch et al., 2009; Mathewson et al., 2009). Behavioral studies have reported evidence of an ‘attentional spotlight’ mechanism, whereby attention alternately samples two spatial locations at anti-phasic ~4 Hz rhythms (Busch and VanRullen, 2010; Fiebelkorn et al., 2013; Landau et al., 2015; VanRullen et al., 2007). It remains unclear, however, whether these theta rhythms originate in early visual cortex or elsewhere (Busch and VanRullen, 2010; Dugué et al., 2015), and behavioral and M/EEG data lack sufficient spatiotemporal resolution to resolve the origins of rhythmic sampling during attention (VanRullen, 2016a).

In particular, it is unclear (I) which anatomical correlates constitute the structural basis for rhythmic sampling in the human brain. Furthermore, (II) it is unresolved how rhythmic sampling is functionally organized and distributed across cortical networks. (III) The limited spatiotemporal resolution of methods employed in previous studies could not resolve whether behavioral periodicities are a direct result of spontaneous, ongoing, oscillatory brain activity, which is generated at the neuronal population level. (IV) Finally, it remains unknown if rhythmic sampling results from the inherent functional architecture of cortical networks or if rhythmic sampling is instead task and context dependent.

In the present study, we address these unanswered questions by combining subdural recordings in humans with two different attention tasks (Egly et al., 1994; Szczepanski et al., 2014) that probed behavioral outcome on a rapid timescale. Electrocorticography (ECoG) provides the spatiotemporal resolution necessary to precisely track the ongoing brain dynamics that influence instantaneous human behavior. We specifically tested the hypothesis that low frequency oscillations - previously observed in behavioral time courses - are a direct result of periodic excitability fluctuations in the same time range. We predicted that cortical high frequency band (HFB) activity, a proxy for cortical excitability and population spiking in humans (Rich and Wallis, 2017; Watson et al., 2017), is modulated by low frequency activity. We focused on HFB activity and not evoked narrow-band gamma oscillations (Landau et al., 2015), since narrow-band gamma oscillations do not predict local spiking activity or cortical excitability (Ray and Maunsell, 2011; Watson et al., 2017). We hypothesized that the phase of these low frequency oscillations would predict behavioral outcomes on a trial-by-trial basis not only in V1 (Dugué et al., 2016; Landau et al., 2015), but in widespread regions of the fronto-parietal attention network, facilitating interregional information transfer (Buschman and Kastner, 2015; Helfrich and Knight, 2016; Sellers et al., 2016).

Results

We recorded intracranial EEG from a total of 15 pharmacoresistant epilepsy patients (32.80 years ± 12.63, mean ± SD; 8 female) who underwent pre-surgical monitoring with extensive electrode coverage of frontal and parieto-occipital areas in left and right hemispheres. The participants performed one of two spatial attention tasks, where they were asked to covertly monitor a cued location and indicate the appearance of a target after a variable cue-target delay. This experimental design allowed us to probe whether behavioral performance varied as a function of the cue-target interval. We utilized two different behavioral metrics. In experiment 1, participants (N = 7) performed a target detection task where the target luminance was titrated to perceptual threshold and detection accuracy was measured, while participants in experiment 2 (N = 8) performed a reaction time task where the target was presented above sensory threshold in the cued visual field.

Covert visual attention samples the environment at a theta rhythm

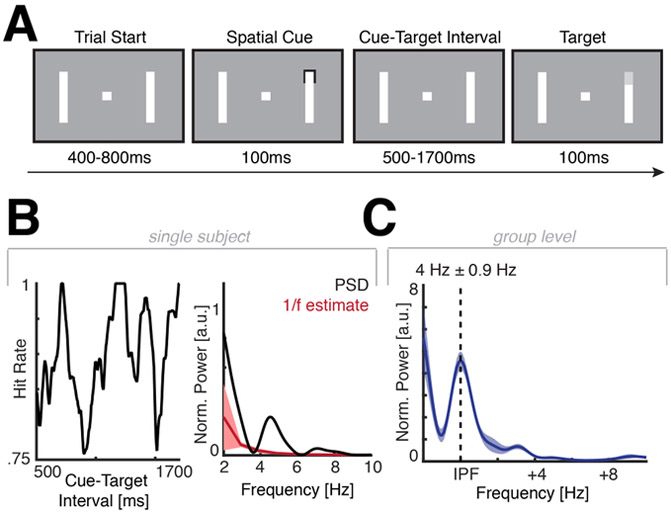
In the first experiment, participants performed a variant of an object-based attention task (Fiebelkorn et al., 2013). We cued participants to one of four possible locations (Figure 1A) and asked them to indicate the appearance of a close-to-sensory-threshold target after a variable cue-target-interval (500 – 1700ms). We continuously adjusted the luminance of the target to ensure that participants performed at approximately 80% accuracy (75.91% ± 11.80%, mean ± SD; t₆ = −0.92, p = 0.3945). We then assessed whether the hit rate varied as a function of the cue-target-interval. We observed strong fluctuations of detection accuracy in the behavioral time course in every participant (Figure 1B, left panel and Figure S1). In order to test whether these fluctuations exhibited an intrinsic temporal profile, we utilized irregular resampling (Wen and Liu, 2016) to separate non-oscillatory 1/f activity from the oscillatory component (Figure 1B, right panel). Across participants, we found that the behavioral time courses exhibited periodic fluctuations in the theta-band (3.99 Hz ± 0.88 Hz, mean ± SD; Figure 1C), where the observed spectrum exceeded the 1/f estimate (mean + 3SD; p < 0.001; see Figure 1B and Figure S1). We also utilized a more conventional permutation approach, which confirmed that the time courses exhibit a significant oscillation in the theta-band (z = 2.20 ± 0.55 (mean ± SEM); combined p < 0.0001; Figure S2A/B). Furthermore, we observed the same effect when a different method for the 1/f correction was utilized (Figure S2C) or the averaging window was decreased to 50ms. These findings suggest that attention does not sample the cued location continuously, but periodically at approximately 4 Hz.

Figure 1. Task design and behavioral results of experiment 1.

(A) Schematic task design. Participants initiated the trial start by pressing a button. After a variable delay, a brief spatial cue indicated the most likely position of the upcoming target (72% validity). Then, a variable cue-target-interval followed (500 – 1700ms), before a close-to-sensory-threshold target appeared at either the cued location, an uncued location or was omitted. Participants released the button when they detected the target. (B) Left: Time-resolved behavioral time course from subject S7 (see also Figure S1). Note the waxing and waning pattern over time. Right: FFT of the behavioral time course (black). In order to disentangle fractal 1/f and oscillatory components, we estimated the background 1/f spectrum (red; mean ± 3 SD) and only considered distinct peaks that exceeded this distribution. (c) Group level results after peak alignment to the individual peak frequency (IPF). We detected a peak in the theta-band with a mean of ~4 Hz in every participant (Figure S1).

Cortical high frequency activity is nested in theta-band oscillations

We hypothesized that the 4 Hz rhythmic sampling that we observed in individual behavioral time courses might be the result of periodic fluctuations in cortical excitability. To test this idea, we analyzed intracranial EEG data from a total of 614 artifact- and epilepsy-free electrodes (Figure 2A and Figure S1) and extracted the high-frequency band (HFB; 70-150 Hz) activity, which has been shown to be a reliable proxy of population spiking activity (Rich and Wallis, 2017). Based on an electrode’s response to the cue (0 – 0.5s), we classified electrodes into cue-responsive (cue+) or cue-unresponsive (cue-; Figure 2B). We found enhanced HFB activity at cue+ sites during the target interval (0.5 – 1.7s; grand-average across subjects; cluster-based permutation test: p = 0.0010, d = 1.55), as well as after target presentation (cluster from 0 – 0.59s; p = 0.0010, d = 2.55). Next, we assessed the modulation of HFB during the selection process at cue+ electrodes by contrasting activity at cued and uncued locations. Averaging across trials revealed spatially specific enhanced delay activity prior to the target onset at the cued location (Figure S3A). However, this apparent enhanced delay activity did not reflect what we observed on single trials, where the HFB activity waxed and waned during the cue-target-interval (Figure 2C). In order to test whether the fluctuations in HFB amplitude exhibited rhythmic modulations, we extracted all HFB peaks from the cue-target interval, excluding peaks that reflected cue− or target-evoked activity (i.e., peaks within 0.3s after cue presentation and before target presentation). Then we performed peak-triggered averaging of the raw, unfiltered time series. Figure 2D depicts a single electrode example indicating that HFB activity was nested in an ongoing 4 Hz oscillation. In order to quantify this effect, we spectrally decomposed the peak-triggered averages by means of an FFT analysis (± 0.5s) and again compared cue+ and cue− electrodes (see Figure 2E for a single subject example). We found that a theta-band oscillation was present in the peak-triggered averages of cue+, but not of cue− electrodes (Figure 2F; permutation test: p = 0.0110, d = 0.26). In addition, we also tested if this process was spatially selective (Figure S3B). Our results indicate that the modulation of HFB activity by ongoing theta was stronger at the cued than the uncued locations in all subjects. Furthermore, we utilized irregular resampling to confirm the presence of oscillatory theta-band activity (Figure S3C), which was distinct from cortical sources of alpha-band (8-12 Hz) activity (Figure S3D). We also utilized conventional cross-frequency coupling metrics to confirm that this approach reliably detected theta-gamma cross-frequency coupling (Figure S4). Taken together, these findings provide evidence that cortical excitability is rhythmically modulated by theta-band oscillations (Canolty et al., 2006).

Figure 2. High frequency band activity is nested in cortical theta oscillations.

(A) Overlap of all implanted electrodes in experiment 1 across all subjects (N = 7) overlaid on a standardized brain in MNI space. See Figure S1 for individual electrode placement. (B) Grand-average HFB time courses (mean ± SEM across subjects) of either cue-locked (left) or target-locked HFB activity (right). Note the apparent sustained activity at cue-responsive (cue+; cue-unresponsive electrodes: cue-) electrodes in cue-target-interval (grey shaded), which was also spatially selective (Figure S3A). (C) Three single trial examples from a cue+ parietal electrode. Upper: Note the response to the cue (black line). However, after the offset of the cue+ (grey line), the HFB activity waxes and wanes and is not as static as Figure 2B and Figure S3A suggested. Target onset is depicted by black dashed line and the response is depicted in green. Note that trial 3 (lower panel) was a miss. Next, we detected all the HFB peaks (red asterisks) after cue offset (grey) and before target onset (black dashed line). (D) Peak-triggered average (± 0.5s; HFB peak at 0s) of the same parietal electrode. Note that the HFB peak is nested in an ongoing 4 Hz oscillation (black depicts the average, grey line a sine fit to the average). (E) Subject-level results. Left: FFT spectra (mean ± SEM) across all cue+ and cue− channels. Note the peak at 4 Hz for cue-responsive electrodes, which was again also spatially selective (Figure S3B) Center: Grand-average peak-triggered average across all cue+ electrodes (mean ± SEM) can easily be approximated by a 4 Hz sine fit (grey line) and reflects the peak in the power spectrum (Left). Right: Note that no similar peak was detected at the cue− electrodes (red). (F) Mean-normalized group-level results (error bars indicate bootstrapped 95% confidence intervals (CI) around the mean in red; black dots/grey lines depict individual participants). All subjects exhibited enhanced theta-band power in the peak-triggered spectra at cue+ electrodes. The arrow indicates the example subject (Figure 2E).

Theta phase predicts target detection performance

In order to establish a direct link between behavioral fluctuations and ongoing cortical theta-band dynamics, we computed low-frequency phase-resolved behavioral time courses (Figure 3A). We divided the underlying phases of 17 logarithmically spaced frequencies (2-32 Hz) into 50 equally distributed bins and computed the average hit rate for all trials within a 90° window centered on every phase bin. We then calculated the normalized Kullback-Leibler divergence of the observed distribution against a uniform distribution (Figure 3A, left panel) to quantify how strongly the observed distribution was modulated by the phase of the low frequency activity. We obtained a surrogate distribution by randomly shuffling the condition labels (correct/incorrect; Figure 3A, center and right panel). This approach allowed us to investigate which phase of a low frequency oscillation predicted subsequent behavior (Figure 3B) and if such phase modulation occurred differentially at cue+ and cue− electrodes (Figure 3C). We found evidence for enhanced rhythmic sampling at cue+ electrodes in every participant (Figure 3D; permutation test: p = 0.0091, d = 0.62). These findings demonstrate that the phase of ongoing theta-band activity during the cue-target-interval predicted subsequent perception. Notably, this effect was not confounded by differences in low frequency oscillatory power (Figure S3E) or event-related potentials (Figure S3F). Figure 4A depicts the spatial extent of the observed effects for a single subject (see Figure S5 for data from all participants), highlighting comparable effects between left and right hemispheres. Across subjects, we observed theta-band phase-dependent rhythmic sampling in inferior parietal regions, in the intraparietal sulcus and adjacent superior parietal areas as well as in frontal eye fields (FEF) and adjacent regions in the frontal lobe. These findings indicate that theta-mediated fluctuations in cortical excitability in widespread cortical regions are behaviorally relevant and predict visual detection performance.

Figure 3. Theta-phase dependent hit rate modulation.

(A) Analytical approach exemplified for a single parietal electrode. Left: Phase-resolved hit rates in the range from 3-5 Hz. Note the non-uniform distribution across 50 bins (± 45°). We calculated the normalize d Kullback-Leibler divergence against a uniform distribution. Center: We then randomly shuffled condition labels (correct/incorrect) and repeated the analysis. The histogram shows the distribution of KL values after 1000 iterations. The observed value is indicated in red and was then z-scored relative to the mean and SD of the surrogate distribution. Right: This analysis was performed for 17 logarithmically spaced frequencies ranging from 2-32 Hz. The grey shaded area depicts the mean of the surrogate distribution ± 2 SD. The red line indicates observed values. Note that only the 4 Hz phase significantly predicted the hit rate, while no significant modulation was detected at any other frequency bin. (B) Same data as in panel A, but now the hit rate is color-coded and displayed as a function of phase and frequency. Again, note the modulation around 4 Hz. (C) Grand-average (mean ± SEM) across all electrodes for this subject. Note that rhythmic sampling is enhanced in lower frequencies at cue+ electrodes. (D) Mean-normalized group-level results (in red: error bars indicate bootstrapped 95% CI around the mean; black dots/grey lines depict individual participants). All subjects exhibited enhanced rhythmic theta-band (~ 4 Hz) sampling at cue+ electrodes. The arrow indicates the example subject (Figure 3C).

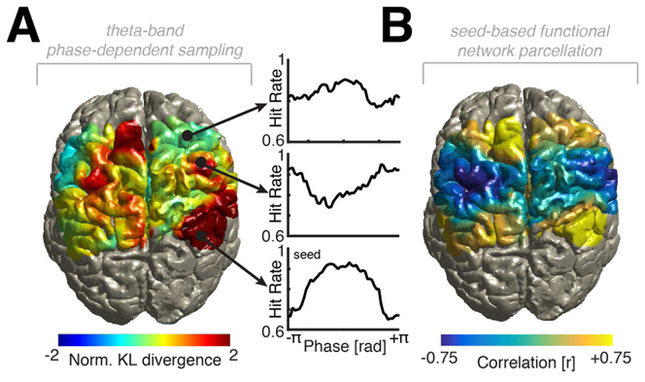
Figure 4. Large-scale network dynamics underlying rhythmic perceptual sampling.

(A) Left: Topographical depiction of rhythmic sampling in one example participant who was implanted with bilateral grids. Note that multiple regions contributed to the rhythmic sampling including frontal regions (upper right), sensorimotor regions (center right) and parietal regions (lower right). See Figure S5 for data from all participants. We seeded the electrode with the strongest phase-dependent behavioral modulation (lower right, located in IPS5). (B) Then we calculated seed-based correlations based on the phase-resolved behavioral data, which indicated that parietal and frontal areas exhibit the same preferred phase for optimal behavior.

Theta phase-resolved behavior delineates frontoparietal network interactions

Next, we aimed to assess how different nodes of the frontoparietal network contributed to the functional organization of rhythmic attentional sampling in the human brain. To address this, we employed a seed-based functional connectivity approach, where we defined the electrode with the highest normalized Kullback-Leibler divergence as a seed (Figure 4A, right lower panel) and computed correlations to all other electrodes (Figure 4B). This approach indicated that distant regions in the fronto-parietal network exhibit similar phase-behavior-relationships (see Figure S4C and Figure S5 for data from all subjects).

Rhythmic behavioral sampling is independent of task structure

In a second experiment, we investigated whether the observed theta-mediated rhythmic sampling in experiment 1 is a fundamental feature of attention allocation implementation in the frontoparietal network, or if the observed results were task-specific. To accomplish this, we utilized a reaction time task, where subjects only had to monitor two and not three spatial locations (Szczepanski et al., 2014). In addition, we presented the informative visual field cue at fixation and not in the periphery. Participants (N = 8) were instructed to maintain fixation and were cued to allocate their attention to either the left or right visual field (Figure 5A). After a variable cue-target-interval (1000 – 2000ms), the participants had to respond to a target that was embedded among flickering visual distractors. Participants performed this task with high accuracy (hit rate 97.21% ± 1.13%; mean ± SEM; Szczepanski et al., 2014). This approach allowed us to assess the reaction time as a function of the cue-target-interval (Figure 5B). We again separated oscillatory components and 1/f background contributions by means of irregular resampling, as employed in Experiment 1, and found that the behavioral time courses in every subject exhibited periodic fluctuations in the theta band that exceeded the 1/f estimate by more than 3 SD (p < 0.001; 4.14 ± 1.34 Hz, mean ± SD; Figure 5C and Figure S6). These findings from two different attention tasks provide strong evidence that human attentional allocation is not evenly distributed across time, but fluctuates as a function of endogenous oscillatory brain activity. Thus, rhythmic sampling appears to be a general property of spatial attention regardless of specific task structure. Furthermore, we conducted a control experiment in healthy participants who performed both tasks (Figure S2D-F) and found that theta-band dynamics across tasks were significantly correlated, explaining ~35% of the behavioral variance.

Figure 5. Task design and behavioral results of experiment 2.

(A) Schematic task design. Participants fixated a cross on a dynamic background with a number of visual distractors (red), which were randomly switched on or off. After a variable delay a centrally presented spatial cue indicated the hemifield that participants should covertly monitor. After variable cue-target-interval (1000 – 2000ms) a blue square was presented at the target and subject responded if the target was presented in the cued hemifield. (B) Left: Time-resolved behavioral time course from one example subject (see also Figure S6). Note the waxing and waning pattern over time. Right: FFT of the behavioral time course (black) and the fractal 1/f component (red). Note the strong peak around 4-5 Hz.(c) Group level results after peak alignment to the individual peak frequency (IPF). We detected a peak in the theta-band with a mean of ~4.1 Hz in every participant (Figure S6).

Neural correlates of rhythmic attentional sampling in the frontoparietal network

To investigate the neural correlates of this behavioral effect, we analyzed intracranial EEG from 758 electrodes (Figure 6A). We extracted the HFB activity and observed enhanced delay activity during the cue-target-interval (1 – 2s; p = 0.0010, d = 1.05) and after target presentation (cluster from 0 – 0.77s; p = 0.0010, d = 1.88), which as in experiment 1 did not reflect single trial dynamics (Figure 6B), but showed strong spatial selectivity for cued than uncued locations (cluster test: p = 0.0010). Peak-triggered averaging and spectral decomposition revealed multiple spectral peaks in the low frequency range in which the HFB activity was nested (Figure 6C). However, we only found a modulation at group level by a theta rhythm around 4 Hz (Figure 6D; permutation test: p = 0.0230, d = 0.21) and not in the alpha-band (8-12 Hz; p = 0.8137). After irregular resampling and discounting the 1/f background activity, we also observed distinct sources of theta and alpha-band activity (Figure S3D), which were comparable to the results obtained in the first experiment.

Figure 6. Neural correlates of rhythmic attentional sampling in experiment 2.

Overlap of all implanted electrodes in experiment 2 across all subjects (N = 8) overlaid on a standardized brain in MNI space. See Figure S6 for individual electrode placement. (B) Grand-average HFB time courses (mean ± SEM) of either cue-locked (left) or target-locked HFB activity (right). (C) Upper: Peak-triggered average (± 0.5s; HFB peak at 0s; mean ± SEM) of all cue+ electrodes (blue) and an unconstrained sine fit (grey, ~7 Hz). Lower: FFT spectra of peak-triggered averages for cue+ (blue) and cue− electrodes (red). Note a peak around 3-4 Hz and around 7-8 Hz. (D) Mean-normalized group-level results (error bars indicate bootstrapped 95% CI around the mean (in red); black dots/grey lines depict individual participants). All subjects exhibited enhanced ~4 Hz power in the peak-triggered spectra at cue+ electrodes. This effect was not significant in the alpha-band. The arrow indicates the example subject (Figure 6C). (E) Left: Observed (red) and surrogate (grey shaded; mean ± 2SD) phase-dependent reaction time modulation for one parietal electrode. Right: Color-coded reaction time as a function of phase and frequency from the same electrode. (F) Grand-average (mean ± SEM) across all electrodes for this subject. Note that rhythmic sampling is enhanced in lower frequencies at cue+ electrodes. (G) Mean-normalized group-level results (error bars indicate bootstrapped 95% CI around the mean (in red); black dots/grey lines depict individual participants) reflecting enhanced rhythmic theta-band sampling at cue+ electrodes. The arrow indicates the example subject (Figure 6F).

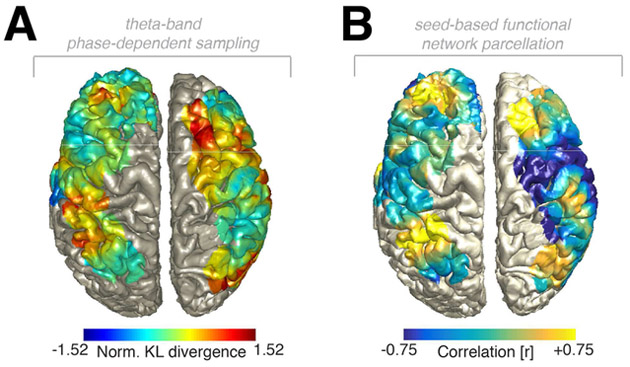
Then we tested the behavioral relevance of the theta-band phase by calculating low-frequency phase-resolved behavioral time courses and quantified the degree of non-uniformity by calculating the normalized Kullback-Leibler divergence (Figure 6E) against a surrogate distribution where reaction times were shuffled. We observed evidence for a systematic relationship between theta-band phase and subsequent reaction times on the single-trial (Figure 6E), single-subject (Figure 6F and Figure S7) and group levels (Figure 6G; permutation test: p = 0.0069, d = 0.46). Figure 7A highlights the spatial extent of the theta-band phase-dependent sampling, which is in accordance with the results from experiment 1. Functional network parcellation again highlighted that the functional relationship between ongoing theta phase and perception was similar across distant areas in the fronto-parietal network (Figure 7B, Figure S4D and Figure S7).

Figure 7. Large-scale dynamics of rhythmic perceptual sampling in experiment 2.

(A) Topographical depiction of rhythmic sampling. Note that the left and right hemispheres depict two different subjects, but show a consistent pattern with strong rhythmic sampling in parietal and frontal areas. See also Figure S7. (B) Seed-based functional network parcellation highlights similar functional relationships between the ongoing theta phase and behavior in parietal and frontal regions.

Taken together, the results from experiment 2 confirm the findings of experiment 1. The collective results suggest that oscillatory brain activity, generated at the population level in widespread cortical networks, shapes human perception and behavior on a rapid time scale.

Discussion

Our results demonstrate that rhythmic behavioral fluctuations in humans during sustained attention at a cued location are the direct result of endogenous oscillatory fluctuations in excitability, as indexed by HFB activity. These fluctuations in excitability shape both perception and behavioral performance on a sub-second time scale. Our findings reveal that (I) intrinsic theta-band activity in the frontoparietal attention network samples the environment rhythmically, even in states of ‘sustained’ attention at the cued location. (II) We demonstrate that cortical excitability, as indexed by HFB activity, is nested within ongoing theta-band activity, (III) which is being generated at the population level of cortical networks. (IV) Crucially, our results from two independent studies highlight that the observed effects are an inherent characteristic of the functional organization of the fronto-parietal attention network, where theta oscillations support attentional rhythmic sampling irrespective of task structure and context.

Visual attention samples space rhythmically and not continuously

There is a longstanding debate whether perception is discrete or continuous (VanRullen, 2016a). We perceive the world as continuous, but several lines of research have provided indirect evidence that perception and attention are not uniformly distributed across time and space, but exhibit intrinsic temporal profiles that match the timescale of endogenous oscillatory brain activity (Buschman and Kastner, 2015; Helfrich and Knight, 2016; VanRullen, 2016a). This raised the intriguing hypothesis that intrinsic brain activity shapes how we perceive the world around us. For example, several groups reported that tracking of different spatial locations or different object varies as a function of a ~4 Hz rhythm (Dugué et al., 2015, 2016; Fiebelkorn et al., 2013; Holcombe and Chen, 2013; Landau and Fries, 2012).

Why would the cortex operate in a rhythmic mode? It has been argued that a rhythmic process might have functional advantages and that endogenous phase-alignment, to external, behaviorally relevant cues facilitates subsequent performance (Calderone et al., 2014). Likewise, it has been proposed that rhythmic sampling might be more energy efficient and that the brain switches from a ‘continuous’ to a ‘rhythmic’ processing mode in states when prior information is available (Schroeder and Lakatos, 2009).

Another intriguing observation is that the rhythms observed during covert attention exhibit theta-range temporal profiles similar to overt behaviors, such as sniffing, whisking or saccadic eye movements (VanRullen, 2016a). Furthermore, there seems to be a tight interplay between theta oscillations and micro-saccadic eye movements, with these fixational eye movements preferentially occurring at certain theta phase angles (Bosman et al., 2009; Lowet et al., 2016). Importantly, several studies have shown that rhythmic attentional sampling is not a micro-saccade artifact (Fiebelkorn et al., 2018; Landau et al., 2015; Spyropoulos et al., 2018). This leads to the hypothesis that covert sampling of the environment informs subsequent overt behavior, with the most salient event covertly selected from the visual environment for the next saccade (Bellet et al., 2017; Helfrich, 2017) by e.g. the motor system as previously observed in auditory attention studies (Morillon et al., 2014).

Currently, there is no consensus on how to implement spectral analysis on sparse behavioral time course data (Helfrich, 2017; Zoefel and Sokoliuk, 2014). Previous studies utilized surrogate distributions to infer if a certain frequency-band has more power than expected by chance (Fiebelkorn et al., 2013). However, this approach does not explicitly test for the presence of oscillations (Haller et al., 2018). Here, we used a novel approach to disentangle oscillatory from aperiodic 1/f components (Wen and Liu, 2016), which has not previously been applied to behavioral data. This method yielded highly comparable results to the more conventional permutation approach and indicated that low frequency oscillations were present in the behavioral time course, despite inter-individual differences in the exact peak frequency, which span multiple canonical frequency bands, such as the delta (1 – 4 Hz), theta (4 – 8 Hz) and alpha band (8 – 12 Hz). While there was variability in individual peak frequencies, all analyses linking behavior to electrophysiology (for individual spectra see Figure S5 and Figure S7) indicated a tight link between theta oscillations and behavior.

Rhythmic synchronization in the frontoparietal network constitutes the functional architecture of visual attention

Functional imaging results in humans as well as a multitude of findings from invasive recordings in rodents and non-human primates have linked attentional processing to the frontoparietal network (Buschman and Kastner, 2015). While long-range theta-band synchronization (Bastos et al., 2015; Sellers et al., 2016) or theta-gamma cross-frequency coupling (Canolty et al., 2006; Szczepanski et al., 2014) was commonly observed in the fronto-parietal network, the behavioral relevance was only indirectly inferred by e.g. comparing trials with correct/incorrect or fast/slow responses. Furthermore, the limited spatial resolution of scalp EEG pointed towards frontal or parietal sources of rhythmic sampling (Busch et al., 2009; Busch and VanRullen, 2010; Mathewson et al., 2009), without assessing the functional interactions and mutual dependencies. In addition, in several studies the spectral content of the sensory input matched the endogenous frequency (de Graaf et al., 2013; Spaak et al., 2014). This hampers the interpretability of observed effects since sensory-evoked effects masked intrinsically generated dynamics (Breska and Deouell, 2017).

Our present findings clarify previous results by demonstrating that multiple cortical sources in the frontal and parietal cortex engage in rhythmic sampling of the environment. We sampled behavior at a fine-grained temporal scale to highlight, on a trial-by-trial basis, how the phase of ongoing theta oscillations controls cortical excitability and shapes human perception and behavioral outcome. Furthermore, our findings are in line with the idea that low frequency oscillations preferentially support long-range cortico-cortical coupling (Helfrich and Knight, 2016; Siegel et al., 2012), where theta organizes mainly feedforward information flow from sensory to association areas (Bastos et al., 2015; Spyropoulos et al., 2018), possibly through travelling waves (Zhang et al., 2018). One testable question, which could be addressed in future studies involving patients with focal frontal or parietal lesion is how the disruption of the frontoparietal network modulates rhythmic sampling processes. Given that behavioral time courses exhibit multiple spectral peaks, which might reflect distinct contributions (e.g. theta could primarily signal top-down components, while alpha may signal bottom-up components; Bellet et al., 2017; Helfrich et al., 2017; Jia et al., 2017; VanRullen, 2016a), we speculate that frontal and parietal lesions will exhibit differential spectral signatures that may be observable in behavioral time courses.

It is unclear how nodes of the fronto-parietal network are synchronized to precisely time information transfer. One testable hypothesis in animal models emerging from our findings is that the pulvinar, a set of nuclei in the visual thalamus connected to frontal and parietal areas, might orchestrate and coordinate network activity (Halassa and Kastner, 2017; Saalmann et al., 2012). Likewise, animal models are ideally suited to collect a sufficiently high number of trials to study attention effects at uncued locations, which cannot be achieved in patient populations given the limited time available for recordings in epilepsy monitoring units.

Population activity might determine the time scale of cognition

Classic models of attention, decision-making or working memory are often characterized by persistent and not time-varying neuronal activity (Stokes and Spaak, 2016). For instance, in the case of working memory, persistent delay activity was though to constitute a hallmark of how information is maintained online (Christophel et al., 2017). However, recent advances revealed that data averaged across hundreds of trials does not appropriately reflect single trial dynamics (Lundqvist et al., 2016). While background activity has often been considered to reflect noise, novel high-resolution recordings indicate that single trial dynamics carry information in a time-varying population code (Stokes et al., 2013; Wolff et al., 2017).

In the present study, we show that sustained activity at the cued location during ‘sustained’ attention did not reflect single trial dynamics (Stokes and Spaak, 2016). Importantly, our present results only reflect intrinsic, ongoing dynamics and are not confounded by continuous sensory input during the rhythmic sampling process, which might elicit narrow-banded gamma oscillations (Landau et al., 2015). In contrast, we observed (I) that HFB was nested in ongoing theta-band activity and exhibited a waxing and waning pattern, not apparent in grand averages. (II) That this theta-band activity was generated at the population level in the fronto-parietal network and predicted behavioral outcome on a rapid timescale. These findings collectively suggest that the resulting behavior is shaped by ongoing oscillatory brain activity. We speculate that this rhythmic sampling at the cued location is the result of monitoring several spatial locations simultaneously (three in experiment 1 and two in experiment 2) and that attention is rhythmically re-weighted between the different possible locations. Hence, this implies that the underlying sampling rhythm could be 2-3 times faster, in line with previous findings that reported evidence for attentional rhythmic sampling in the low alpha range around 7-10 Hz, which samples different spatial locations sequentially (Busch and VanRullen, 2010; Busch et al., 2009; Dugué et al., 2015; Fiebelkorn et al., 2013; Helfrich et al., 2017; Landau and Fries, 2012; VanRullen, 2016a).

Comparative electrophysiology to bridge different experiments

The present study was conducted with human epilepsy patients who underwent pre-surgical evaluation and all experiments were performed on the epilepsy-monitoring unit. While direct brain recordings in humans provide rare and valuable data, the experiments have to be tailored to clinical circumstances and individual patients needs. In the present experiment, this resulted in significantly lower trial numbers that can typically be gathered from healthy participants, e.g. in case of experiment 1 we collected an average of 190 trials per patient, which constitutes a fraction of the trials (~11%) as compared to recent behavioral studies (Fiebelkorn et al., 2013) who gathered 1764 trials per subject. Hence, we focused our analyses on the validly cue trials (72%) and averaged trials over 100ms time windows to have a sufficient number of samples per time bin. Thus, we cannot report on the time-resolved performance for invalidly cued trials in experiment 1. Regardless, we observed strong evidence for rhythmic sampling in the behavioral time courses in line with recent findings (Fiebelkorn et al., 2013, 2018; Landau and Fries, 2012; Landau et al., 2015). Likewise, in experiment 2, subjects were instructed to withhold their response when the target appeared in the un-cued hemi field, which impedes time-resolved behavioral analyses (Szczepanski et al., 2014). Studies in healthy subjects (Fiebelkorn et al., 2013; Landau and Fries, 2012) and primates (Fiebelkorn et al., 2018) are ideally suited to assess performance over time for invalidly cued trials. Thus, our present results need to be interpreted in the context of studies in healthy human participants (Dugué et al., 2015; Fiebelkorn et al., 2013; Helfrich et al., 2017; Henry et al., 2014; Jia et al., 2017; Landau and Fries, 2012) as well as primates (Bellet et al., 2017; Fiebelkorn et al., 2018), which jointly suggest that multiple rhythms modulate behavior on a rapid time scale and that different neuronal populations exhibit anti-phasic relationships (Lakatos et al., 2013; Landau et al., 2015).

In direct comparison to Fiebelkorn et al. (2018), it may appear striking that we observed similar effects in the theta-band, but not e.g. in the beta-band (15 – 30 Hz). However, in the present study we used subdural grid electrodes, which span large portions of the neocortex, but which primarily record from superficial cortical layers (Parvizi and Kastner, 2018). In contrast, recordings spanning all cortical layers in primates indicate that the beta-band rhythm emerges from deeper layers, which we might not capture using ECoG grids (Bastos et al., 2018) outside of motor cortex. Hence, we conclude that a multimodal approach involving experiments in several species and spanning several spatiotemporal scales can jointly elucidate the neural mechanisms underlying rhythmic attentional sampling.

Conclusions

Our findings reveal a fundamental neurophysiologic mechanism involving the spatiotemporal organization of attention in the human brain. We demonstrate that population activity in the theta-band predicts behavior on a sub-second time scale by rhythmically adjusting cortical excitability in states of sustained attention at the cued location. These findings have important implications for how attention, a central construct in cognitive neuroscience, is conceptualized and implemented in large-scale neuronal circuits (Buschman and Kastner, 2015; Stokes and Spaak, 2016). We propose that neural oscillations dynamically allocate limited resources based on sensory information content and endogenous priors.

The present results also add to the emerging notion that human behavior is supported by rhythmic neuronal populations (Eichenbaum, 2017; Fusi et al., 2016). This consideration is in line with evidence that HFB activity indexes cognitive processing with a high spatiotemporal resolution in both human and non-human primates and is modulated by rhythmic low frequency activity (Rich and Wallis, 2017; Watson et al., 2017). Given similar effects were observed in two independent experiments utilizing different task structures, we suggest that this rhythmic sampling is an inherent feature of the fronto-parietal network that shapes the individual experience of the world.

Our results have potential clinical relevance for neuropsychiatric disorders with increasing evidence of disordered network activity (Calderone et al., 2014; Voytek and Knight, 2015). Attention is a distributed rhythmic process, which cannot simply be modulated by changing the balance between excitatory and inhibitory drive, but might benefit from interventions targeting the underlying rhythmic architecture (Fröhlich, 2014). This suggests that population activity might provide a novel target for tailored interventions that engage neuronal oscillations, e.g. by means of rhythmic non-invasive brain stimulation.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Randolph Helfrich (rhelfrich@berkeley.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Participants

We obtained intracranial recordings from a total of 15 epilepsy patients who underwent pre-surgical monitoring with implanted grid electrodes. Seven patients participated in study 1 (35.29 ± 12.42 years; mean ± SD; 5 female) and were recruited from the University of California, Irvine Medical Center, USA (N = 6) and the California Pacific Medical Center (CPMC), San Francisco, USA (N = 1). In study 2, we recruited 8 patients (30.63 ± 13.22 years; mean ± SD; 3 female) from Children’s Hospital in Oakland, CA, USA (N = 1), Johns Hopkins Hospital in Baltimore, MD, USA (N = 1) and Stanford Hospital, CA, USA (N = 6). Electrode placement was exclusively guided by clinical considerations and all patients provided written informed consent to participate in the study. All procedures were approved by the Institutional Review Board at every site as well as by the Committee for Protection of Human Subjects at the University of California, Berkeley (Protocol number: 2010-02-783) and conducted in accordance with the Declaration of Helsinki. Patients were implanted with either grid or strip electrodes with 1 cm spacing. In one participant (S4), we included an additional 8 contact depth probe that was inserted into occipital cortex. For the control experiment (Figure S2D-F), we recruited an additional group of healthy volunteers who were paid for their participation (N = 14, 24.86 ± 5.55 years; mean ± SD; 6 female) from the University of California, Berkeley.

METHOD DETAILS

Experimental design and procedure

Behavioral tasks

All participants performed a spatial attention task. In experiment 1, participants performed a variant of the Egly-Driver task (Egly et al., 1994; Fiebelkorn et al., 2013). Stimulus presentation was controlled with Presentation Software (Neurobehavioral Systems Inc.). Subject sat ~60 cm away from the laptop screen. Subjects initiated the trial start by pressing down the left mouse button. Then two bar objects appeared and were either vertically or horizontally oriented. After a variable delay (400 – 800ms), a brief spatial cue (100 ms) in the periphery around one bar indicated the location where the target was most likely to occur (72% cue validity). This cue was equally likely to appear at any of the four quadrants. After the cue, we introduced a variable cue-target-interval (500 – 1700ms) with a low number of catch trials (10%) where no subsequent target was presented. Targets could randomly appear at any time point during the cue-target-interval. Targets could also appear at uncued locations, which could either be part of the same object or not (18%). If the target appeared at the different object, it was shown at a location equidistant from the cued location to avoid distance confounds. Participants indicated that they detected the target by releasing the mouse button and received auditory feedback on whether they performed the trial correctly or not. We continuously tracked behavioral performance and adjusted the target luminance in steps of one RGB value every 15 trials to achieve an overall accuracy of ~80% correct. The experimenter monitored continuous fixation, and the results from the patient cohort are similar to a previous study that probed the same task and used a cohort of healthy adult participants whose eye movements were closely monitored (Fiebelkorn et al., 2013). All subjects responded with the hand contralateral to the implanted grid. Participant S6 (bilateral grids) responded with the left hand. All participants were asked to perform up to 5 blocks of 60 trials each (190 trials ± 67; mean ± SD). Note, we adjusted several parameters in comparison to a previous study (Fiebelkorn et al., 2013) to accommodate the unique clinical setting in which were the present data set was collected. In particular, performance was titrated to 80% instead of 65% to keep the subjects engaged. To increase the yield of correct responses, we adjusted the cue-target interval to 500-1700 ms instead of 300-1100 ms to minimize the ramp-up effect that Fiebelkorn et al. observed in the time range from 300-500 ms.

In experiment 2 (Figure 5A), the participants performed a reaction time task and were either cued to the left or the right hemifield by a central cue. Stimulus presentation was controlled with EPrime software (Psychology Software Tools Inc.). Subjects sat ~60 cm away from the laptop screen. Note, that in this experiment the cue was on the screen until the trial ended. Subjects were instructed to maintain fixation and covertly shift their attention to the cued hemifield. After a variable cue-target-interval (1000 – 2000ms), a blue square target appeared, which remained on the screen until the subject responded or the trial timed out after another 2000ms. Targets appeared randomly during the cue-target-interval. Subjects responded to targets in the cued hemifield, but were instructed to withhold a response to targets that were presented in the opposite hemifield. Six out of eight subject responded with the hand ipsilateral to the grid. In addition, a number of the red distractors located anywhere on the screen was randomly turned on or off to increase attentional competition. Participants performed 6 blocks of 42 trials each. Eye movements were visually monitored and the experimenter ensured that subjects maintained central fixation throughout the trials. A previous study demonstrated that eye movements in this task were negligible and did not contribute to the observed theta-gamma interactions (Szczepanski et al., 2014).

ECoG data acquisition

Intracranial EEG data and peripheral data (photodiode) were acquired using a Nihon Kohden recording system (UC Irvine, CPMC and Children’s Hospital, 128/256 channel, 1000/5000 Hz digitization rate), a Natus Medical Inc. Stellate Harmonie recording system (Johns Hopkins, 128 channel, 1000 Hz digitization rate) or a Tucker Davis Technologies recording system (Stanford, 128 channel, 3052 Hz digitization rate).

CT and MRI data acquisition

We obtained anonymized postoperative CT scans and presurgical MRI scans, which were routinely acquired during clinical care.

QUANTIFICATION AND STATISTICAL ANALYSIS

Behavioral data analysis

In experiment 1, we analyzed the hit rate at the cued location as a function of the cue-target-interval. We utilized a variant of the original Egly-Driver task (Egly et al., 1994; Fiebelkorn et al., 2013). This task design was tailored to assess hit rates over time, which were titrated to ~80% correct in an adaptive procedure. We focused on the hit rates given that reaction time courses exhibited prominent Hazard functions, since the probability for the target occurrence increased over the cue-target-interval.

To extract the behavioral time course, we shifted a 100ms window in steps of 1ms from 500 – 1700 ms and re-calculated the hit rate across all validly cued trials in the respective time window. We used relatively long windows of 100ms, because some bins did not contain behavioral estimates in some subjects with lower trial numbers if a window of e.g. 50 ms had been used due to the random target presentation. The traces were smoothed and missing data points interpolated by using a 25-point boxcar moving average. This approach yielded a time course per participant at a sampling rate of 1000 Hz. We obtained spectral estimates from a Fast Fourier Transform (FFT) after applying a Hanning window and zero padding the data to 10 seconds to increase the frequency resolution to 0.1 Hz. In order to estimate the 1/f background activity and disentangle oscillatory from fractal components, we utilized irregular resampling (IRASA, see below; (Wen and Liu, 2016)), based on a time window that had 75% length of the total signal and a step size of 0.05 s. Oscillatory peaks were defined as the strongest distinct peak that exceeded the 1/f distribution in the range from 2-10 Hz. In order to obtain a better estimate of the individual peak frequency, the subsequent alignment was performed on the zero padded data.

We utilized the same approach in experiment 2, but calculated the reaction time as a function of the cue-target-interval. Trials exceeding 2 SD above the median reaction time were excluded and only correct responses at the cued location were considered. Given the shorter cue-target-interval (1s duration), we also adjusted the sliding window for the irregular resampling procedure to 75% total length. Again, we performed peak detection and alignment on the zero padded data to increase the frequency resolution and improve peak frequency estimates.

EEG data

Preprocessing:

A neurologist manually inspected all intracranial EEG channels to identify channels with epileptiform activity and artifacts. Contaminated channels and epochs were removed prior to all analyses. Then the data were linearly detrended, demeaned and notch filtered at 60 Hz and all harmonics as well as re-referenced to a local common average (per grid or per strip/probe) in experiment 1 using Fieldtrip. Data from experiment 2 was already filtered and common average referenced as described previously (Szczepanski et al., 2014).

Trial definition:

We extracted 8 second long, partially overlapping trials to facilitate subsequent filtering, spectral analyses and re-epoching to target onset given the long cue-target and response intervals. In experiment 1, trials were extracted from −3 to +5 seconds around cue onset. In experiment 2, individual trials were extracted from −2 to +6 seconds around cue onset.

HFB analysis:

We extracted the high frequency band (HFB) activity by band-pass filtering the raw time courses in eight non-overlapping 10 Hz wide bins ranging from 70-150 Hz and applying a Hilbert transform to extract the instantaneous amplitude using band-pass filtering with the default settings as implemented in Fieldtrip (ft_preprocessing). Then every trace was separately baseline corrected by means of a z-score relative to a bootstrapped baseline distribution prior to cue onset (−0.2s to 0s, 1000 iterations; (Flinker et al., 2015)). Note that this approach accounts for the 1/f signal drop off in the high frequency band with increasing frequencies. Finally, we discarded the edges to avoid filter artifacts and extracted individual non-overlapping trials either relative to cue onset (−0.5 to 3.5s) or relative to target onset (−1.5 to 1.5s).

Cue-responsive electrode classification:

We classified an electrode as cue-responsive at a given location when the average HFB response to the cue exceeded a z-score of 1.96 (corresponding to a two-tailed p-value of 0.05) for at least 10% of consecutive samples in the cue period (0 – 0.5s). Note that this approach separated the electrode selection time window from the test time window (cue target interval experiment 1: 0.5 – 1.7s, experiment 2: 1 – 2s).

Peak-triggered averaging and spectral analysis:

In order to test whether HFB activity was nested in ongoing oscillatory activity, we utilized an approach that is similar to spike-triggered averaging used in single unit electrophysiology (Brown et al., 2004). This approach allowed us to exclude multiple evoked transients that were present in the signal (e.g. cue onset, variable target onset, response), which are known to give rise to spurious CFC (Aru et al., 2015; Cole and Voytek, 2017; Gerber et al., 2016), when additional filtering is applied. Similar to spike-triggered averaging (Brown et al., 2004), we first detected all the HFB peaks in a given trial and at a given channel after the evoked response (> 0.3s) and prior to the target onset, which varied on a trial-by-trial basis. Then we aligned the raw unfiltered signal relative to the HFB peaks and epoched it in the range from −0.5 to 0.5s around the HFB peaks. To assess the spectral content of these 1 second long epochs, we transformed the data by means of a FFT after applying a Hanning window. We also fit an unconstrained sine wave (using the fit function in Matlab, with no specified parameters but the argument ‘sin1’: [curve] = fit(x,y,‘sin1’)) to the peak-locked average to highlight the presence of an ongoing oscillation in the raw, averaged traces. Note that this approach is comparable with more traditional CFC analyses. In case of dataset 2, it had previously been reported that only the 2-5 Hz phase significantly modulated HFB activity during attentional allocation (Szczepanski et al., 2014). We replicate and extend this finding using the peak-triggered method. To demonstrate that our results are independent of the exact CFC metric, four well-established CFC metrics were calculated on a one second time epoch prior to target onset between the theta-phase and the high-frequency band amplitude. We tested the Modulation Index by Tort et al. (Tort et al., 2008), as well as the Canolty Modulation Index (Canolty et al., 2006), the phase-locking technique (Helfrich et al., 2017; Szczepanski et al., 2014) as well as circular-linear correlations (Berens, 2009) as an intuitive metric of what CFC should capture. We utilized the Tort MI as a the reference metric (Figure S4) given that it has been demonstrated that the Tort MI robustly detects CFC when data epochs are noisy and short (Huelsemann et al., 2018).

Irregular resampling (IRASA):

In order to disentangle true oscillatory components the prominent 1/f background activity, we utilized irregular-resampling auto-spectral analysis (IRASA; (Wen and Liu, 2016)). IRASA takes advantage of the fact that irregularly resampling of the neuronal signals by pairwise non-integer values (resampling factor rf and corresponding factor rf*: e.g. 1.2 and 0.8) slightly shifts the peak frequency of oscillatory signals by compressing or stretching the underlying signal. However, the 1/f component remains comparable. This procedure was then repeated in small, overlapping windows (3 seconds, 0.5s step size) and resampling was always done in a pairwise fashion for factor h and the corresponding resampling factor rf* = 2 – r (resampling factors rf: 1.1-1.9 in 0.05 steps). For each window, we calculated the auto-power spectrum by means of a FFT after applying a Hanning window. Then all auto-spectra were median-averaged to obtain the power spectrum of the 1/f component, where resampled oscillatory components were averaged out. Finally, the resampled 1/f PSD is subtracted from the original PSD to obtain the oscillatory residuals.

Spectral analysis:

For time-frequency decomposition of cue− and target-locked responses in the range from 2 – 32 Hz (33 logarithmically spaced bins), we utilized a 500ms sliding Hanning window, which we advanced in 50ms steps from −0.5 to 3.5s (cue-locked) or from −2.5 to 1.5s (target-locked). Spectral estimates in the range from 32 – 256 Hz we computed using the multitaper method based on discrete prolate spheroidal sequences in 24 logarithmically spaced bins (Mitra and Pesaran, 1999). We adjusted the temporal and spectral smoothing to approximately match a 250ms time window and ½ octave frequency smoothing. We baseline-corrected the spectral estimates per frequency band by a z-score relative to a bootstrapped baseline distribution (−0.2 to 0s before cue onset).

Event-related potentials:

We extracted the ERPs from the epoched data after 30 Hz low pass filtering and applying an absolute baseline-correction (−0.2 to 0s before cue onset).

Phase-dependent modulation of behavior:

In order to test if the phase of the ongoing oscillatory activity significantly predicted either the hit rate (experiment 1) or reaction times (experiment 2), we band-pass filtered the signal in 17 logarithmically spaced bins from 2 – 32 Hz (± center-frequency / 4) using the function eegfilt.m with default settings as implemented in eeglab. Note we filtered the aggregated trials to avoid edge artifacts and filtered the data front- and backwards to minimize phase distortions (Delorme and Makeig, 2004). For experiment 1, we only utilized trials where the target appeared at the correctly cued location. In experiment 2, only utilized trials where the target appeared at the cued location and was successfully detected were included. After filtering, we applied a Hilbert transform and extracted the instantaneous phase angles. Then we binned the phase angles at target onset into 50 equally distributed bins and computed the average phase-resolved behavior per channel and frequency bin (experiment 1: hit rate; experiment 2: reaction time) across all trials within a 90° window centered on every phase bin. Then we calculated the normalized Kullback-Leibler divergence of the observed distribution P (formula 1; phase-dependent behavior per channel and frequency pair was normalized by its sum) against a uniform mean distribution Q to quantify how strongly the observed distribution was non-uniformly distributed (formula 2).

$$P=\frac{{\mathit{behavior}}_{\mathit{CH},f}(\varphi )}{\Sigma {\mathit{behavior}}_{\mathit{CH},f}(\varphi )}$$ (1)

$$D_{\mathit{KL}}(P,Q)=\sum P\ast \text{log}(\frac{P}{Q})$$ (2)

Then we obtained a surrogate distribution D_surr by randomly shuffling the condition labels 1000 times (experiment 1: correct/incorrect; experiment 2: reaction times). This approach allowed to us to investigate which low frequency phase predicted subsequent behavior. We normalized the Kullback-Leibler divergence by subtracting the mean and dividing by the standard deviation of surrogate distribution (formula 3).

$$D_{\mathit{KL}\mathit{norm}.}(P,Q)=\frac{D_{\mathit{KL}}(P,Q)-\mathit{mean}(D_{\mathit{surr}}(P,Q))}{\mathit{std}(D_{\mathit{surr}}(P,Q))}$$ (3)

Functional network parcellation and circular statistics:

In order to delineate functional networks, we utilized a seed-based functional connectivity approach. First, in every subject we defined the electrode as seed electrode that exhibited the highest normalized Kullback-Leibler divergence in the theta-band (3-5 Hz). Then we calculated the Pearson correlation coefficient between the phase-resolved behavior at the seed electrode and all other electrodes, which yielded a correlation map that was bounded at ±1. In three cases, the seed was in the sensorimotor network, while in all other subjects, the seed was in the frontoparietal network. In order to have comparable color scales across all functional networks, we inverted the color scale in these subjects.

Electrode localization

First, we transformed both the pre-implant MRI and the post-implant CT into Talairach space. Then we segmented the MRI using Freesurfer 5.3.0 (Dale et al., 1999) and then co-registered the T1 to the CT. 3D electrode coordinates were determined using the Fieldtrip toolbox (Oostenveld et al., 2011; Stolk et al., 2017) on the co-registered CT scan. We corrected for the brain shift that is often observed after large craniotomies (Dykstra et al., 2012). Finally, we warped the aligned electrodes onto a template brain in MNI space. Electrode position was defined using the VTPM atlas (Wang et al., 2015). For all electrodes, where no label was assigned, we repeated the process and assigned a label from the AFNI atlas (Lancaster et al., 1997). We manually verified and corrected the assigned atlas position after inspection of the electrode reconstruction in native Talairach space. In addition, we used a functional criterion to confirm the location of FEF. Therefore, only electrodes in the Precentral Gyrus or Middle Frontal Cortex were considered and we required that electrodes were cue-responsive and showed a stronger response to contralateral than ipsilateral presented cues. Electrodes in the vicinity of the TPJ were manually assigned, because TPJ definitions were not included in the VTPM or the AFNI atlas.

Statistical analysis

Throughout, we report single subject data and highlight effects that generalize across the population and were observed in every participant. Unless stated otherwise, we used cluster-based permutation tests for the electrophysiological data to correct for multiple comparisons as implemented in Fieldtrip (MonteCarlo method; 1000 iterations; maxsum criterion; (Maris and Oostenveld, 2007)) based on either paired or unpaired two-tailed t-tests. Clusters were either formed in time (e.g. Figure 2B, 6B, S3A) or in the time-frequency domain (Figure S3E). Furthermore, we used two-tailed paired t-tests (e.g. Figure 1C, 2F, 3D, 5C, 6D, 6G) to infer significance at group level. However, given that parametric tests are not designed for small N, we utilized a permutation approach to infer significance by randomly shuffling subject labels and repeating the t-test 10000 times. P-values were then computed from the observed t-value relative to the surrogate distribution. To reduce between subject variance in order to facilitate visualization, we mean normalized the value pairs for every subject to a mean of 1. We included bootstrapped 95% confidence interval, which were computed using a double-iterative procedure (ibootci by Andrew Penn; see key resource table). In order to infer significant rhythmic sampling we created a null distribution by randomly shuffling condition labels (experiment 1: correct/incorrect; experiment 2: reaction times; Figure 3A/6E), which were then submitted to the same spectral analysis (Figure S2A/B). We then z-scored the observed distribution relative to the surrogate distribution. We obtained p-values by either transforming z-values into p-values using the normal cumulative distribution function ϕ or using the method by the method by Stouffer et al. (Stouffer et al., 1951; VanRullen, 2016b), which was also used to combine p-values across different Spearman correlation values comparing the different CFC estimates (Figure S4). Here, every p-value is turned into an equivalent z-score using the inverse normal cumulative distribution function ϕ⁻¹. Subsequently, we combined z-scores across observers and then turned the averaged z-scores into a probability using the cumulative distribution function ϕ according to the following formula:

$${\mathrm{p}}_{\text{combined}}=1-\mathrm{\varphi }({\sum }_{\mathrm{i}=1:\mathrm{N}}{\mathrm{\varphi }}^{-1}\frac{1-{\mathrm{p}}_{\mathrm{i}}}{\sqrt{\mathrm{N}}})$$

KEY RESOURCE TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
Presentation	Neurobehavioral Systems Inc.	https://www.neurobs.com
EPrime	Psychology Software Tools Inc.	https://pstnet.com/
MATLAB 2015a	MathWorks Inc.	RRID: SCR_001622
EEGLAB 13_4_4b	(Delorme and Makeig, 2004)	https://sccn.ucsd.edu/eeglab/index.php
FieldTrip 20170912	(Oostenveld et al., 2011)	http://www.fieldtriptoolbox.org/
CircStat 2012	(Berens, 2009)	https://philippberens.wordpress.com/code/circstats/
IRASA	(Wen and Liu, 2016)	https://purr.purdue.edu/publications/1987/1
SPM8	(Penny et al., 2011)	http://www.fil.ion.ucl.ac.uk/spm/
Freesurfer 5.3.0	(Dale et al., 1999)	https://surfer.nmr.mgh.harvard.edu/
ibootci	Andrew Penn; MATLAB central	https://mathworks.com/matlabcentral/fileexchange/52741-ibootci

We furthermore used Pearson’s correlation coefficient to delineate functional networks (Figure 4B/7B). Effect sizes were calculated using Cohen’s d, the correlation coefficient rho or the resultant vector length. Circular statistics as the Rayleigh test (Figure S4C/D), which tests for circular non-uniformity were carried out using the CircStat toolbox (Berens, 2009).

DATA AND SOFTWARE AVAILABILITY

Freely available software and algorithms used for analysis are listed in the resource table. All custom scripts and data contained in this manuscript are available upon request from the Lead Contact.

Highlights.

• The functional architecture of attention is rhythmic

• Frontoparietal theta activity predicts behavior on a rapid time scale

• Theta activity controls cortical excitability and information flow

• Rhythmic sampling is independent of task structure and context