Best Practices for Quantification of Uncertainty and Sampling Quality in Molecular Simulations [Article v1.0]

Abstract

The quantitative assessment of uncertainty and sampling quality is essential in molecular simulation. Many systems of interest are highly complex, often at the edge of current computational capabilities. Modelers must therefore analyze and communicate statistical uncertainties so that “consumers” of simulated data understand its significance and limitations. This article covers key analyses appropriate for trajectory data generated by conventional simulation methods such as molecular dynamics and (single Markov chain) Monte Carlo. It also provides guidance for analyzing some ‘enhanced’ sampling approaches. We do not discuss systematic errors arising, e.g., from inaccuracy in the chosen model or force field.

1. Introduction: Scope and definitions

1.1. Scope

Simulating molecular systems that are interesting by today’s standards, whether for biomolecular research, materials science, or a related field, is a challenging task. However, computational scientists are often dazzled by the system-specific issues that emerge from such problems and fail to recognize that even “simple” simulations (e.g., alkanes) require significant care [1]. In particular, questions often arise regarding the best way to adequately sample the desired phase-space or estimate uncertainties. And while such questions are not unique to molecular modeling, their importance cannot be overstated: the usefulness of a simulated result ultimately hinges on being able to confidently and accurately report uncertainties along with any given prediction [2]. In the context of techniques such as molecular dynamics (MD) and Monte Carlo (MC), these considerations are especially important, given that even large-scale modern computing resources do not guarantee adequate sampling.

This article therefore aims to provide best-practices for reporting simulated observables, assessing confidence in simulations, and deriving uncertainty estimates (more colloquially, “error bars”) based on a variety of statistical techniques applicable to physics-based sampling methods and their associated “enhanced” counterparts. As a general rule, we advocate a tiered approach to computational modeling. In particular, workflows should begin with back-of-the-envelope calculations to determine the feasibility of a given computation, followed by the actual simulation(s). Semi-quantitative checks can then be used to check for adequate sampling and assess the quality of data. Only once these steps have been performed should one actually construct estimates of observables and uncertainties. In this way, modelers avoid unnecessary waste by continuously gauging the likelihood that subsequent steps will be successful. Moreover, this approach can help to identify seemingly reasonable data that may have little value for prediction and/or be the result of a poorly run simulation.

It is worth emphasizing that in the last few years, many works have developed and advocated for uncertainty quantification (UQ) methods not traditionally used in the MD and MC communities. In some cases, these methods buck trends that have become longstanding conventions, e.g., the practice of only using uncorrelated data to construct statistical estimates. One goal of this manuscript is therefore to advocate newer UQ methods when these are demonstrably better. Along these lines, we wish to remind the reader that better results are not only obtained from faster computers, but also by using data more thoughtfully. It is also important to appreciate that debate continues even among professional statisticians on what analyses to perform and report [3].

The reader should be aware that there is not a “one-size-fits-all” approach to UQ. Ultimately, we take the perspective that uncertainty quantification in its broadest sense aims to provide actionable information for making decisions, e.g., in an industrial research and development setting or in planning future academic studies. A simulation protocol and subsequent analysis of its results should therefore take into account the intended audience and/or decisions to be made on the basis of the computation. In some cases, quick-and-dirty workflows can indeed be useful if the goal is to only provide order-of-magnitude estimates of some quantity. We also note that uncertainties can often be estimated through a variety of techniques, and there may not be consensus as to which, if any, are best. Thus, a critical component of any UQ analysis is communication, e.g., of the assumptions being made, the UQ tools used, and the way that results are interpreted. Educated decisions can only be made through an understanding of both the process of estimating uncertainty and its numerical results.

While UQ is a central topic of this manuscript, our scope is limited to issues associated with sampling and related uncertainty estimates. We do not address systematic errors arising from inaccuracy of force-fields, the underlying model, or parametric choices such as the choice of a thermostat time-constant. See, for example, Refs. [4–7] for msethods that address such problems. Similarly, we did not address bugs and other implementation errors, which will generally introduce systematic errors. Finally, we do not consider model-form error and related issues that arise when comparing simulated predictions with experiment. Rather, we take the raw trajectory data at face value, assuming that it is a valid description of the system of interest.¹

1.2. Key Definitions

In order to make the discussion that follows more precise, we first define key terms used in subsequent sections. We caution that while many of these concepts are familiar, our terminology follows the International Vocabulary of Metrology (VIM) [8], a standard that sometimes differs from the conventional or common language of engineering statistics. For additional information about or clarification of the statistical meaning of terms in the VIM, we suggest that readers consult the Guide to the expression of uncertainty in measurement (GUM) [9].

For clarity, we highlight a few differences between conventional terms and the VIM usage employed throughout this article. Readers should study the term “standard uncertainty” which is sometimes estimated by (in common parlance) the “standard error of the mean”; however, the VIM term for the latter is the “experimental standard deviation of the mean.” In cases of lexical ambiguity, the reader should assume that we hold to the definition of terms as given in the VIM.

Note also that the glossary is presented in a logical, rather than alphabetical order. We strongly encourage reading it through in its entirety because of the structure and potentially unfamiliar terminology. Importantly, we also recommend reading the discussion that immediately follows, since this (i) explains the rationale for adopting the chosen language, (ii) discusses the limited relationship between statistics and uncertainty quantification, and (iii) thereby clarifies our perspective on best-practices.

1.2.1. Glossary of Statistical Terms

• Random quantity: A quantity whose numerical value is inherently unknowable or unpredictable. Observations or measurements taken from a molecular simulation are treated as random quantities².

• True value: The value of a quantity that is consistent with its definition and is the objective of an idealized measurement or simulation. The adjective “true” is often dropped when reference to the definition is clear by context [8, 9].

• Expectation value: If P(x) is the probability density of a continuous random quantity x, then the expectation value is given by the formula

  $$\langle x\rangle =\int dxP(x)x.$$ (1)
  In the case that x adopts discrete values x₁, x₂, … with corresponding fractional (absolute) probabilities P(x_j), we instead write

  $$\langle x\rangle =\sum _j{x}_{j}P\left(x_j\right).$$ (2)

  Note that P(x) is dimensionless when x is discrete as shown agove. When x is continuous, as in Eq. 1, P(x) must have units reciprocal to x, e.g., if x has units of kg, then P(x) has units of 1/kg. Furthermore, whether x is discrete or continuous, P(x) should always be normalized to ensure a total probability of unity.

• Variance:³ Taking P(x) as defined previously, the variance of a random quantity is a measure of how much it can fluctuate, given by the formula

  $${\sigma }_x^2=\int dxP(x){(x-\langle x\rangle )}^2.$$ (3)
  If x assume discrete values, the corresponding definition becomes

  $${\sigma }_x^2=\sum _{j}P\left(x_j\right){\left(x_j-\langle x\rangle \right)}^2.$$ (4)

• Standard Deviation: The positive square root of the variance, denoted σ_x. This is a measure of the width of the distribution of x, and is, in itself, not a measure of the statistical uncertainty; see below.

• Arithmetic mean: An estimate of the (true) expectation value of a random quantity, given by the formula

  $$\overline{x}=\frac{1}{n}\sum _{j=1}^n{x}_j$$ (5)

  where x_j is an experimental or simulated realization of the random variable and n is the number of samples.

  Remark: This quantity is often called the “sample mean.” Note that a proper realization of a random variable (with no systematic bias) will yield values distributed according to P(x), so $\overline{x}\to \langle x\rangle$ as n → ∞.

• Standard Uncertainty: Uncertainty in a result (e.g., estimation of a true value) as expressed in terms of a standard deviation.⁴

• Experimental standard deviation:⁵ An estimate of the (true) standard deviation of a random variable, given by the formula⁶

  $$s(x)=\sqrt{\frac{{\sum }_{j=1}^n{\left(x_j-\overline{x}\right)}^2}{n-1}}$$ (6)

  The square of the experimental standard deviation, denoted s² (x), is the experimental variance.

  Remark: This quantity is often called the “sample standard deviation.” Additionally, s (x) is a statistical property of the specific set of observations {x₁, x₂, …, x_n}, not of the random quantity x in general. Thus, s (x) is sometimes written as s (x_j) for emphasis of this property.

• Linearly uncorrelated observables: If quantities x and y have mean values 〈x〉 and 〈y〉, then x and y are linearly uncorrelated if

  $$\langle (x-\langle x\rangle )(y-\langle y\rangle )\rangle =0$$ (7)

  Remark: The concepts of linear uncorrelation and independence of random variables are often conflated. Two variables can be correlated even if Eq. 7 is 0, e.g. when a scatter plot of the two variables forms a circle. Truly independent variables have zero linear and higher-order correlations, such that the joint density of two random variables x and y can be decomposed as P(x, y) = P(x)P(y), which is a stronger condition than linear uncorrelation. Empirically testing for independence, however, is not practical, nor is it necessary for any of the estimates discussed in this work.

• Experimental standard deviation of the mean: An estimate of the standard deviation of the distribution of the arithmetic mean, given by the formula

  $$s(\overline{x})=\frac{s(x)}{\sqrt{n}},$$ (8)

  where the realizations of x_j are assumed to be linearly uncorrelated.⁷

  Remark: This quantity is often called the “standard error.”

• Raw data: The numbers that the computer program directly generates as it proceeds through a sequence of states. For example, a MC simulation generates a sequence of configurations, for which there are associated properties such as the instantaneous pressure, temperature, volume, etc.

• Derived observables: Quantities derived from “nontrivial” analyses of raw data, e.g., properties that may not be computed for a single configuration such as free energies.

• Correlation time: In time-series data of a random quantity x(t) (e.g., a physical property from a MC or MD trajectory; the sequence of trials moves is treated as a “time series” in MC), the correlation time (denoted here as τ) is the longest separation time Δt over which x(t) and x(t+Δt) remain (linearly) correlated.⁸ (See Eq. 10 for mathematical definition and Sec. 7.3.1 for discussion.) Thus, the correlation time can be interpreted as the time over which the system retains memory of its previous states. Such correlations are often stationary, meaning that τ is independent of t. Roughly speaking, the total simulation time divided by the longest correlation time yields an order-of-magnitude estimate of the number of (linearly) uncorrelated samples generated by a simulation. See Sec. 7.3.1. Note that the correlation time can be infinite.

• Two-sided confidence interval: An interval, typically stated as $\langle x\rangle =\overline{x}\pm U$, which is expected to contain the possible values attributed to 〈x〉 given the experimental measurements of x_j and a certain level of confidence, denoted p. The size of the confidence interval, known as the expanded uncertainty, is defined by $U=ks(\overline{x})$ where k is the coverage factor [8].⁹ The level of confidence p is typically given as a percentage, e.g., 95 %. Hence, the confidence interval is typically described as “the p % confidence interval” for a given value of p.

• Coverage Factor: The factor k which is multiplied by the experimental standard deviation of the mean $s(\overline{x})$ to obtain the expanded uncertainty, typically in the range of 2 to 3. In general, k is selected based on the chosen level of confidence p and probability distribution that characterizes the measurement result x_j. For Gaussian-distributed data, k is determined from the t-distribution, based on the level of confidence p and the number of measurements in the experimental sample.¹⁰ See Sec. 7.5 for further discussion on the selection of k and the resultant computation of confidence intervals.

1.2.2. Terminology and its relation to our broader perspective on uncertainty

As surveyed by Refs. [8, 9], the discussion that originally motivated many of theses definitions appears rather philosophical. However, there are practical issues at stake related to both the content of the definitions as well as the need to adopt their usage. We review such issues now.

At the heart of the matter is the observation that any uncertainty analysis, no matter how thorough, is inherently subjective. This can can be understood, for example, by noting that the arithmetic mean is itself actually a random quantity that only approximates the true expectation value.¹¹ Because its variation relative to the true value depends on the number of samples (notwithstanding a little bad luck), one could therefore argue that a better mean is always obtained by collecting more data. We cannot collect data indefinitely, however, so the quality of an estimate necessarily depends on a choice of when to stop. Ultimately, this discussion forces us to acknowledge that the role of any uncertainty estimate is to facilitate decision making, and, as such, the thoroughness of any analysis should be tailored to the decision at hand.

Practically speaking, the definitions as put forth by the VIM attempt to reflect this perspective while also capturing ideas that the statistics community have long found useful. For example, the concept of an “experimental standard deviation of the mean” is nothing more than the “standard error of the mean.” However, the adjective “experimental” explicitly acknowledges that the estimate is in fact obtained from observation (and not analytical results), while the use of “deviation” in place of “error” emphasizes that the latter is unknowable. Similar considerations apply to the term “experimental standard deviation,” which is more commonly referred to as the “sample standard deviation.”

It is important to note that subjectivity as identified in this discussion does not arise just from questions of sampling. In particular, methods such as parametric bootstrap and correlation analyses (discussed below) invoke modeling assumptions that can never be objectively tested. Moreover, experts may not even agree on how to compute a derived quantity, which leads to ambiguity in what we mean by a “true value” [11]. That we should consider these issues carefully and assess their impacts on any prediction is reflected in the definition of the “standard uncertainty,” which does not actually tell us how to compute uncertainties. Rather it is the task of the modeler to consider the impacts of their assumptions and choices when formulating a final uncertainty estimate. To this end, the language we use plays a large role in how well these considerations are communicated.

As a final thought, we reiterate that the goal of an uncertainty analysis is not necessarily to perform the most thorough computations possible, but rather to communicate clearly and openly what has been assumed and done. We cannot predict every use-case for data that we generate, nor can we anticipate the decisions that will be made on the basis of our predictions. The importance of clearly communicating therefore rests on the fact that in doing so, we allow others to decide for themselves whether our analysis is sufficient or requires revisiting. To this end, consistent and precise use of language plays an important, if understated role.

2. Best Practices Checklist

Our overall recommendations are summarized in the checklist presented on the following page, which should facilitate avoiding common errors and adhering to good practices.

QUANTIFYING UNCERTAINTY AND SAMPLING QUALITY IN MOLECULAR SIMULATION.

• Plan your study carefully by starting with pre-simulation sanity checks. There is no guarantee that any method, enhanced or otherwise, can sample the system of interest. See Sec. 3

  • Consult best-practices papers on simulation background and planning/setup. See: https://github.com/MobleyLab/basic_simulation_training
  • Estimate whether system timescales are known experimentally and feasible computationally based on published literature. If timescales are too long for straight-ahead MD, investigate enhanced-sampling methods for systems of similar complexity. The same concept applies to MC, based on the number of MC trial moves instead of actual time.
  • Read up on sampling assessment and uncertainty estimation, from this article or another source (e.g., Ref. [12]). Understanding uncertainty will help in the planning of a simulation (e.g., ensure collection of sufficient data).
  • Consider multiple runs instead of a single simulation. Diverse starting structures enable a check on sampling for equilibrium ensembles, which should not depend on the starting structure. Multiple runs may be especially useful in assessing uncertainty for enhanced sampling methods.
  • Check and validate your code/method via a simple benchmark system. See: https://github.com/shirtsgroup/software-physical-validation

• Do not “cherry-pick” data that provides hoped-for outcomes. This practice is ethically questionable and, at a minimum, can significantly bias your conclusions. Use all of the available data unless there is an objective and compelling reason not to, e.g., the simulation setup was incorrect or a sampling metric indicated that the simulation was not equilibrated. When used, sampling metrics should be applied uniformly to all simulations to further avoid bias.

• Perform simple, semiquantitative checks which can rule out (but not ensure) sufficient sampling. It is easier to diagnose insufficient sampling than to demonstrate good sampling. See Sec. 4.

  • Critically examine the time series of a number of observables, both those of interest and others. Is each time series fluctuating about an average value or drifting overall? What states are expected and what are seen? Are there a significant number of transitions between states?
  • If multiple runs have been performed, compare results (e.g., time series, distributions, etc.) from different simulations.
  • An individual trajectory can be divided into two parts and analyzed as if two simulations had been run.

• Remove an “equilibration” (a.k.a. “burn-in”, or transient) portion of a single MD or MC trajectory and perform analyses only on the remaining “production” portion of trajectory. An initial configuration is unlikely to be representative of the desired ensemble and the system must be allowed to relax so that low probability states are not overrepresented in collected data. See Sec. 5.

• Consider computing a quantitative measure of global sampling, i.e., attempt to estimate the number of statistically independent samples in a trajectory. Sequential configurations are highly correlated because one configuration is generated from the preceding one, and estimating the degree of correlation is essential to understanding overall simulation quality. See Secs. 6 and 7.3.1.

• Quantify uncertainty in specific observables of interest using confidence intervals. The statistical uncertainty in, e.g., the arithmetic mean of an observable decreases as more independent samples are obtained and can be much smaller than the experimental standard deviation of that observable. See Sec. 7.

• Use special care when designing uncertainty analyses for simulations with enhanced sampling methods. The use of multiple, potentially correlated trajectories within a single enhanced-sampling simulation can invalidate the assumptions underpinning traditional analyses of uncertainty. See Sec. 8.

• Report a complete description of your uncertainty quantification procedure, detailed enough to permit reproduction of reported findings. Describe the meaning and basis of uncertainties given in figures or tables in the captions for those items, e.g., “Error bars represent 95% confidence intervals based on bootstrapping results from the independent simulations.” Provide expanded discussion of or references for the uncertainty analysis if the method is non-trivial. We strongly urge publication of unprocessed simulation data (measurements/observations) and postprocessing scripts, perhaps using public data or software repositories, so that readers can exactly reproduce the processed results and uncertainty estimates. The non-uniformity of uncertainty quantification procedures in the modern literature underscores the value of clarity and transparency going forward.

3. Pre-simulation “sanity checks” and planning tips

Sampling a molecular system that is complex enough to be “interesting” in modern science is often extremely challenging, and similar difficulties apply to studies of “simple” systems [1]. Therefore, a small amount of effort spent planning a study can pay off many times over. In the worst case, a poorly planned study can lead to weeks or months of simulations and analyses that yield questionable results.

With this in mind, one of the objectives of this document is to provide a set of benchmark practices against which reviewers and other scientists can judge the quality of a given work. If you read this guide in its entirety before performing a simulation, you will have a much better sense of what constitutes (in our minds) a thoughtful simulation study. Thus, we strongly advise that readers review and understand the concepts presented here, as well as in related reviews [9, 12, 13]

In a generic sense, the overall goal of a computational study is to be able to draw statistically significant conclusions regarding a particular phenomenon. To this end, “good statistics” usually follow from repeated observations of a quantity-of-interest. While such information can be obtained in a number of ways, time-series data are a natural output of many simulations and is therefore a commonly used to achieve the desired sampling.¹² It is important to recognize that time-series data usually displays a certain amount of autocorrelation in the sense that the numerical values of nearby points in the series tend to cluster close to one another. Intuition dictates that correlated data does not reveal fully “new” information about the quantity-of-interest, and so we require uncorrelated samples to achieve meaningful sampling [14].¹³

Thus, it is critical to ask: what are the pertinent timescales of the system? Unfortunately, this question must be answered individually for each system. You will want to study the experimental and computational literature for your particular system, although we warn that a published prior simulation of a given length does not in itself validate a new simulation of a similar or slightly increased length. In the end, your data should be examined using statistical tools, such as the autocorrelation analysis described in Secs. 4.1 and 7.3.1. Be warned that a system may possess states (regions of configuration space) that, although important, are never visited in a given simulation set because of insufficient computational time [12] and, furthermore, this type of error will not be discovered through the analyses presented below. Finally, note that “system” here does not necessarily refer to a complete simulation (e.g., a biological system with protein, solvent, ions, etc); it can also refer to some subset of the simulation for which data are desired. For example, if one is only interested in the dynamics of a binding site in a protein, it probably is not necessary to observe the unfolding and refolding of that protein as well.

One general strategy that will allow you to understand the relevant timescales in a system is to perform several repeats of the same simulation protocol. As described below, repeats can be used to assess variance in any observable within the time you have run your simulation. When performing repeat simulations, it is generally advised to use different starting states which are as diverse as possible; then, differences among the runs can be an indicator of inadequate sampling of the equilibrium distribution. Alternatively, performing multiple runs from the same starting state will yield behavior particular to that starting state; information about (potential) equilibrium is obtained only if the runs are long enough.

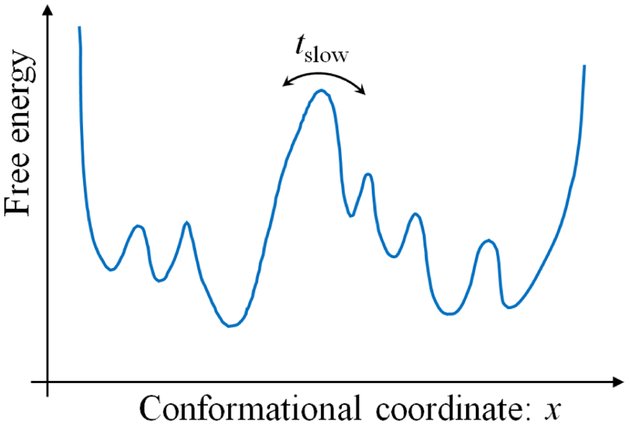
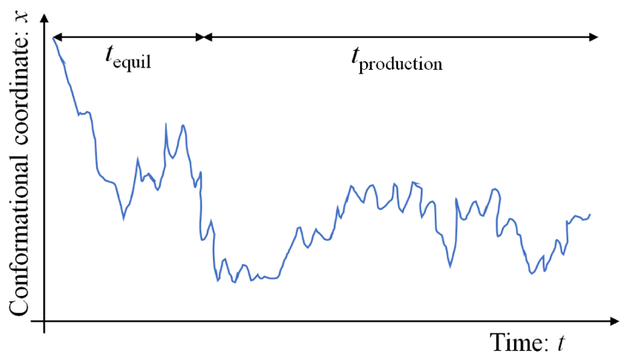
A toy model illustrates some of these timescale issues and their effects on sampling. Consider the “double well” free energy landscape shown in Fig. 1, and note that the slowest timescale is associated with crossing the largest barrier. Generally, you should expect that the value of any observable (e.g., x itself or another coordinate not shown or a function of those coordinates) will depend on which of the two dominant basins the system occupies. In turn, the equilibrium average of an observable will require sampling the two basins according to their equilibrium populations. In order to directly sample these basins, however, the length of a trajectory will have to be orders of magnitude greater than the slowest timescale, i.e., the largest barrier should be crossed multiple times. Only in this way can the relative populations of states be inferred from time spent in each state. Stated differently, the equilibrium populations follow from the transition rates [15–17] which can be estimated from multiple events. For completeness, we note that there is no guarantee that sampling of a given system will be limited by a dominant barrier. Instead, a system could exhibit a generally rough landscape with many pathways between states of interest. Nevertheless, the same cautions apply.

Figure 1.

Schematic illustration of a free energy landscape dominated by a slow process. The timescales associated with a system will often reflect “activated” (energy-climbing) processes, although they could also indicate diffusion times for traversing a rough landscape with many small barriers. In the figure, the largest barrier is associated with the slowest timescale t_slow, and the danger for conventional MD simulations is that the total length of the simulation may be inadequate to generate the barrier crossing.

What should be done if a determination is made that a system’s timescales are too long for direct simulation? The two main options would be to consider a more simplified (“coarse-grained”) model [18, 19] or an enhanced sampling technique (see Sec. 8). Modelers should keep in mind that enhanced sampling methods are not foolproof but have their own limitations which should be considered carefully.

Lastly, whatever simulation protocol you pursue, be sure to use a well-validated piece of software [https://github.com/shirtsgroup/software-physical-validation]. If you are using your own code, check it against independent simulations on other software for a system that can be readily sampled, e.g., Ref. [20].

4. Qualitative and semiquantitative checks that can rule out good sampling

It is difficult to establish with certainty that good sampling has been achieved, but it is not difficult to rule out high-quality sampling. Here we elaborate on some relatively simple tests that can quickly bring out inadequacies in sampling.

Generally speaking, analysis routines that extract information from raw simulated data are often formulated on the basis of physical intuition about how that data should behave. Before proceeding to quantitative data analysis and uncertainty quantification, it is therefore useful to assess the extent to which data conforms to these expectations and the requirements imposed by either the modeler or the analysis routines. Such tasks help reduce subjectivity of predictions and offer insight into when a simulation protocol should be revisited to better understand its meaningfulness [11]. Unfortunately, general recipes for assessing data quality are impossible to formulate, owing to the range of physical quantities of interest to modelers. Nonetheless, several example procedures will help clarify the matter.

4.1. Zeroth-order system-wide tests

The simplest test for poor sampling is lack of equilibration: if the system is still noticeably relaxing from its starting conformation, statistical sampling has not even begun, and thus by definition is poor. As a result, the very first test should be to verify that the basic equilibration has occurred. To check for this, one should inspect the time series for a number of simple scalar values, such as potential energy, system size (and area, if you are simulating a membrane or other system where one dimension is distinct from the others), temperature (if you are simulating in the NVE ensemble), and/or density (if simulating in the isothermal-isobaric ensemble).

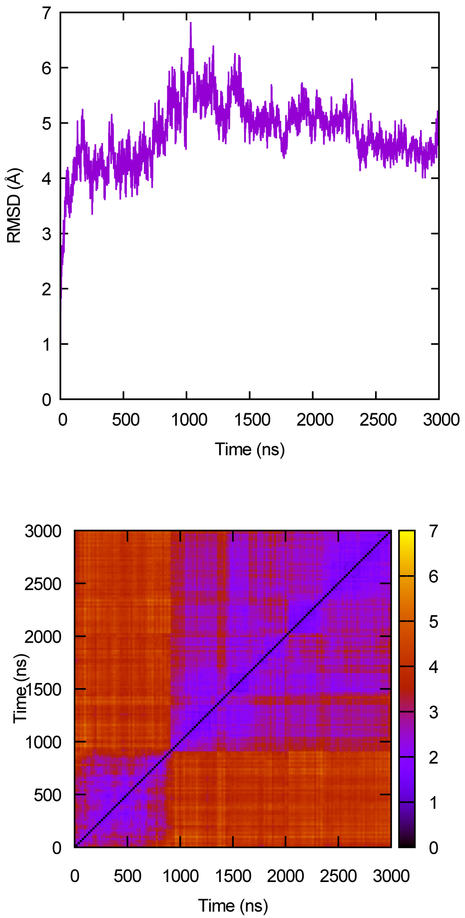
Simple visual inspection is often sufficient to determine that the simulation is systematically changing, although more sophisticated methods have been proposed (see Sec. 5). If any value appears to be systematically changing, then the system may not be equilibrated and further investigation is warranted. See, for example, the time trace in Fig. 2. After the rapid rise, the value shows slower changes; however, it does not fluctuate repeatedly about an average value, implying it has not been well-sampled.

Figure 2.

RMSD as a measure of convergence. The upper panel shows the α-carbon RMSD of the protein rhodopsin from its starting structure as a function of time. The lower panel shows the all-to-all RMSD map computed from the same trajectory. Color scale is the RMSD, in Å. Data from Ref. [21].

4.2. Tests based on configurational distance measures (e.g., RMSD)

Because a system with N particles has a 3N dimensional configuration-space (the full set of x, y, z coordinates), it is generally difficult to assess the extent to which the simulation has adequately explored these degrees-of-freedom. Thus, modelers often project out all but a few degrees of freedom, e.g., monitoring a “distance” in configuration space as described below or keeping track of only certain dihedral angles. In this lower dimensional subspace, it can be easier to track transitions between states and monitor similarity between configurations. However, the interpretation of such analyses requires care.

By employing a configuration-space “distance”, several useful qualitative checks can be performed. Such a distance is commonly employed in biomolecular simulations (e.g., RMSD, defined below) but analogous measures could be employed for other types of systems. A configuration-space distance is a simple scalar function quantifying the similarity between two molecular configurations and can be used in a variety of ways to probe sampling.

To understand the basic idea behind using a distance to assess sampling, consider first a one-dimensional system, as sketched in Fig. 1. If we perform a simulation and monitor the x coordinate alone, without knowing anything about the landscape, we can get an idea of the sampling performed simply by monitoring x as a function of time. If we see numerous transitions among apparent metastable regions (where the x values fluctuates rapidly about a local mean), we can conclude that sampling likely was adequate for the configuration space seen in the simulation. An important caveat is that we know nothing about states that were never visited. On the other hand, if the time trace of x changes primarily in just one direction or exhibits few transitions among apparent metastable regions, we can conclude that sampling was poor – again without knowledge of the energy landscape.

The same basic procedures (and more) can be followed once we precisely define a configurational distance between two configurations. A typical example is the root-mean-square deviation,

$$\text{RMSD}(r,s)=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left|r_i-s_i\right|}^2},$$ (9)

where r_i and s_i are the Cartesian coordinates of atom i in two distinct configurations r and s which have been optimally aligned [22], so that the RMSD is the minimum “distance” between the configurations. It is not uncommon to use only a subset of the atoms (e.g., protein backbone, only secondary structure elements) when computing the RMSD, in order to filter out the higher-frequency fluctuations. Another configuration-space metric is the dihedral angle distance which sums over all distances for pairs of selected angles. Note that configurational distances generally suffer from the degeneracy problem: the fact that many different configurations can be the same distance from any given reference. This is analogous to the increasing number of points in three-dimensional space with increasing radial distance from a reference point, except much worse because of the dimensionality. For an exploration of expected RMSD distributions for biomolecular systems see the work of Pitera [23].

Some qualitative tools for assessing global sampling based on RMSD were reviewed in prior work [12]. The classic time-series plot of RMSD with respect to a crystal or other single reference structure (Fig. 2) can immediately indicate whether the structure is still systematically changing. Although this kind of plot was historically used as a sampling test, it should really be considered as another equilibration test like those discussed above. Moreover, it is not even a particularly good test of equilibration, because the degeneracy of RMSD means you cannot tell if the simulation is exploring new states that are equidistant from the chosen reference. The upper panel of Fig. 2 shows a typical curve of this sort, taken from a simulation of the G protein-coupled receptor rhodopsin [21]; the curve increases rapidly over the few nanoseconds and then roughly plateaus. It is difficult to assign meaning to the other features on the curve.

A better RMSD-based convergence measure is the all-to-all RMSD plot; taking the RMSD of each snapshot in the trajectory with respect to all others allows you to use RMSD for what it does best, identifying very similar structures. The lower panel of Fig. 2 shows an example of this kind of plot, applied to the same rhodopsin trajectory. By definition, all such plots have values of zero along the diagonal, and occupation of a given state shows up as a block of similar RMSD along the diagonal; in this case, there are 2 main states, with one transition occurring roughly 800 ns into the trajectory. Off diagonal “peaks” (regions of low RMSD between structures sampled far apart in time) indicate that the system is revisiting previously sampled states, a necessary condition for good statistics. In this case, the initial state is never sampled after the first transition as seen from the lack of low RMSD values following ~800 ns with respect to configurations prior to that point; however, there are a number of small transitions within the second state based on low RMSD values occurring among configurations following ~800 ns.

4.3. Analyzing the qualitative behavior of data

In many cases, analysis of simulated outputs relies on determining or extracting information from a regime in which data are expected to behave a certain way. For example, we might anticipate that a given dataset should have linear regimes or more generically look like a convex function. However, typical sources of fluctuations in simulations often introduce noise that can distort the character of data and thereby render such analyses difficult or even impossible to approach objectively. It is therefore often useful to systematically assess the extent to which raw data conforms to our expectations and requirements.

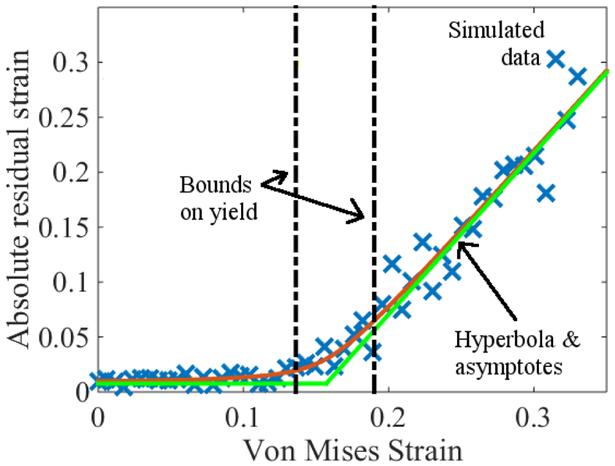
In the context of materials science, simulations of yield-strain ϵ_y (loosely speaking, the deformation at which a material fails) provide one such example. In particular, intuition and experiments tells us that upon deforming a material by a fraction 1 + ϵ, it should recover its original dimensions if ϵ ≤ ϵ_y and have a residual strain ϵ_r = ϵ − ϵ_y if ϵ ≥ ϵ_y [24]. Thus, residual-strain data should exhibit bilinear behavior, with slopes indicating whether the material is in the pre- or post-yield regime.

In experimental data, these regimes are generally distinct and connected by a sharp transition. In simulated data, however, the transition in ϵ_r around yield is generally smooth and not piece-wise linear, owing to the timescale limitations of MD. Thus, it is useful to perform analyses that can objectively identify the asymptotic regimes without need for input from a modeler. One way to achieve this is by fitting residual strain to a hyperbola. In doing so, the proximity of data to the asymptotes illustrates the extent to which simulated ϵ_r conforms to the expectation that ϵ_r = 0 when ϵ < ϵ_y. See Fig. 3 and Refs. [11, 24] for more examples and discussion.

Figure 3.

Residual strain ϵ_r as a function of applied strain ϵ. Blue × denote simulated data, whereas the smooth curve is a hyperbola fit to the data. The green lines are asymptotes; their intersection can be taken as an estimate of ϵ_y. Bounds on yield are computed by the synthetic data method discussed in Sec. 7.6. From, “Estimation and uncertainty quantification of yield via strain recovery simulations,” P. Patrone, CAMX 2016 Conference Proceedings. Reprinted courtesy of the National Institute of Standards and Technology, U.S. Department of Commerce. Not copyrightable in the United States.

While extending this approach to other types of simulations invariably depends on the problem at hand, we recognize a few generic principles. In particular, it is sometimes possible to test the quality of data by fitting it to global (not piece-wise or local!) functions that exhibit characteristics we desire of the former. By testing the goodness of this fit, we can assess the extent to which the data captures the entire structure of the fit-function and therefore conforms to expectations. We note that this task can even be done in the absence of a known fit function, given only more generic properties such as convexity. See, for example, the discussion in Ref. [14].

4.4. Tests based on independent simulations and related ideas

When estimating any statistical property, multiple measurements are required to characterize the underlying model with high confidence. Consider, for example, the probability that an unbiased coin will land heads-up as estimated in terms of the relative fraction coin-flips that give this result. This fraction approximated in terms of a single flip (measurement) will always yield a grossly incorrect probability, since only one outcome (heads or tails) can ever be represented by this procedure. However, as more flips (measurements) are made, the relative fraction of outcomes will converge to the correct probability, i.e., the former represents and increasingly good estimate of the latter.

In an analogous way, we often use “convergence” in the context of simulations to describe the extent to which an estimator (e.g., an arithmetic mean) approaches some true value (i.e., the corresponding expectation of an observable) with increasing amounts of data. In many cases, however, the true value is not known a priori, so that we cannot be sure what value a given estimator should be approaching. In such cases, it is common to use the overlap of independent estimates and confidence intervals as a proxy for convergence because the associated clustering suggests a shared if unknown mean. Conversely, lack of such “convergence” is a strong indication that sampling is poor.

There are two approaches to obtaining independent measurements. Arguably the best is to have multiple independent simulations, each with different initial conditions. Ideally these conditions should be chosen so as to span the space to be sampled, which provides confidence that simulations are not being trapped in a local minimum. Consider, for example, the task of sampling the ϕ and ψ torsions of alanine dipeptide. To accomplish this, one could initialize these angles in the alpha-helical conformation and then run a second simulation initialized in the polyproline II conformation. It is important to note, however, that the starting conditions only need to be varied enough so that the desired space is sampled. For example, if the goal is to sample protein folding and unfolding, there should be some simulations started from the folded conformation and some from the unfolded, but if it is not important to consider protein folding, initial unfolded conformations may not be needed.

However, the “many short trajectories” strategy has a number of limitations that must be also be considered. First, as a rule one does not know the underlying ensemble in advance (else, we might not need to do the simulation!), which complicates the generation of a diverse set of initial states. When simulating large biomolecules (e.g. proteins or nucleic acids), “diverse” initial structures are often constructed using the crystal or NMR structure coupled with randomized placement of surrounding water molecules, ions, etc. If the true ensemble contains protein states with significant structural variations, it is possible that no number of short simulations would actually capture transitions, particularly if the transitions themselves are slow. In that case, each individual trajectory must be of significant duration in order to have any meaning relevant to the underlying ensemble. The minimum duration needed to achieve significance is highly system dependent, and estimating it in advance requires an understanding of the relevant timescales in the system and what properties are to be calculated. Second, one must equilibrate each new trajectory, which can appreciably increase the computational cost of running many short trajectories, depending on the quality of the initial states.

One can also try to estimate statistical uncertainties directly from a single simulation by dividing it into two or more subsets (“blocks”). However this can at times be problematic because it can be more difficult to tell if the system is biased by shared initial conditions (e.g., trapped in a local energy minimum). Those employing this approach should take extra care to assess their results (see Sec. 7.3.2).

Autocorrelation analyses applied to trajectory blocks can be used to better understand the extent to which a time series represents an equilibrated system. In particular, systems at steady state (which includes equilibrium) by definition have statistical properties that are time-invariant. Thus, correlations between a single observable at different times depend only on the relative spacing (or “lag”) between the time steps. That is, the autocorrelation function of observable x, denoted C, has the stationarity property

$$C\left(x_k,x_{k+j}\right)\equiv \frac{\overline{\left(x_k-\overline{x}\right)\left(x_{k+j}-\overline{x}\right)}}{s{(x)}^2}\Rightarrow C_j$$ (10)

where C_j is independent of the time step k. With this in mind, one can partition a given time series into continuous blocks, compute the autocorrelation for a collection of lags j, and compare between blocks. Estimates of C_j that are independent of the block suggest an equilibrated (or at least a steady-state) system, whereas significant changes in the autocorrelation may indicate an unequilibrated system. Importantly, this technique can help to distinguish long-timescale trends in apparently equilibrated data.

Combined Clustering

Cluster analysis is a means by which data points are grouped together based on a similarity (or distance) metric. For example, cluster analysis can be used to identify the major conformational substates of a biomolecule from molecular dynamics trajectory data using coordinate RMSD as a distance metric. For an in-depth discussion of cluster analysis as applied to biomolecular simulations data, see Ref. [26].

One useful technique for evaluating convergence of structure populations is so-called “combined clustering”. Briefly, in this method two or more independent trajectories are combined into a single trajectory (or a single trajectory is divided into two or more parts), on which cluster analysis is performed. Clusters represents groupings of configurations for which intra-group similarity is higher than inter-group similarity [27].

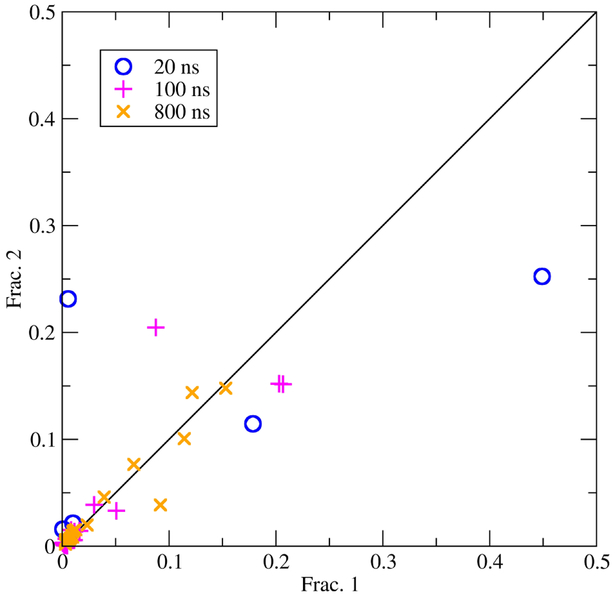
The resulting clusters are then split according to the trajectory (or part of the trajectory) they originally came from. If simulations are converged then each part will have similar populations for any given cluster. Indications of poor convergence are large deviations in cluster populations, or clusters that show up in one part but not others. Figure 4 shows results from combined clustering of two independent trajectories as a plot of cluster population fraction from the first trajectory compared to the second. If the two independent trajectories are perfectly converged then all points should fall on the X=Y line. As simulation time increases the cluster populations from the independent trajectories are in better agreement, which indicates the simulations are converging. For another example of performing combined cluster analysis see Ref. [28].

Figure 4.

Combined clustering between two independent trajectories as a measure of convergence. The X axis is the population of a cluster from trajectory 1, while the Y axis is the population of that cluster from trajectory 2. Cluster populations are show after 20, 100, and 800 ns of sampling. The simulations used to generate the data used in this plot are described in Ref. [25].

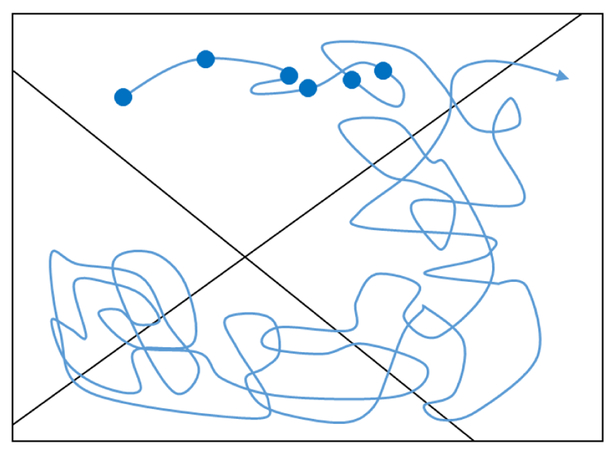
5. Determining and removing an equilibration or ‘burn-in’ portion of a trajectory

The “equilibration” or “burn-in” time t_equil represents the initial part of a single continuous trajectory (whether from MD or MC) that is discarded for purposes of data analysis of equilibrium or steady-state properties; the remaining trajectory data are often called “production” data. See Fig. 5. Discarding data may seem counterproductive, but there is no reason to expect that the initial configurations of a trajectory will be important in the ensemble ultimately obtained. Including early-time data, therefore, can systematically bias results.

Figure 5.

The equilibration and production segments of a trajectory. “Equilibration” over the time t_equil represents transient behavior while the initial configuration relaxes toward configurations more representative of the equilibrium ensemble. Readers are encouraged to select t_equil in a systematic way based on published literature. If you find strong sensitivity of “production” data to the choice of t_equil, this suggests additional sampling is required.

To illustrate these points, consider the process of relaxing an initial, crystalline configuration of a protein to its amorphous counterpart in an aqueous environment. While the initial structure might seem to be intrinsically valuable, remember that configurations representative of the crystal structure may never appear in an aqueous system. As a result, the initial structure may be subject to unphysical forces and/or transitions that provide useless, if not misleading information about the system behavior.¹⁴ Note that relaxation/equilibration should be viewed as a means to an end: for equilibrium sampling, we only care that the relaxed state is representative of any local energy minimum that the system might sample, not how we arrived at that state, which is ultimately why data generated during equilibration can be discarded.

The RMSD trace in Fig. 2 illustrates typical behavior of a system undergoing relaxation. Note the very rapid RMSD increase in the first ≈200 ns. Part of this increase is simply entropic: the volume of phase space within 1 Å of a protein structure is extremely small, so that the process of thermalizing rapidly increases the RMSD from the starting structure, regardless of how favorable or representative that structure is. Thus, examining that initial rapid increase is not helpful in determining an equilibration time. However, in this case, the RMSD continues to increase past 3 Å, which is larger than the amplitude of simple thermal fluctuations (shown by Fig. 2B), indicating an initial drift to a new structure, followed by sampling.

Accepting that some data should be discarded, it is not hard to see that we want to avoid discarding too much data, given that many systems of interest are extremely expensive to simulate. In statistical terms, we want to remove bias but also minimize uncertainty (variance) through adequate sampling. Before addressing this problem, however, we emphasize that the very notion of separating a trajectory into equilibration and production segments only makes sense if the system has indeed reached configurations important in the equilibrium ensemble. While it is generally impossible to guarantee this has occurred, some easy checks for determining that this has not occurred are described in Sec. 4. It is essential to perform those basic checks before analyzing data with a more sophisticated approach that may assume a trajectory has a substantial amount of true equilibrium sampling.

A robust approach to determining the equilibration time is discussed in [29], which generalizes the notion of reverse cumulative averaging [30] to observables that do not necessarily have Gaussian distributions. The key idea is to analyze time-series data considering the effect of discarding various trial values of the initial equilibration interval, t_equil (Fig. 5), and selecting the value that maximizes the effective number of uncorrelated samples of the remaining production region. This effective sample size is estimated from the number of samples in the production region divided by the number of temporally correlated samples required to produce one effectively uncorrelated sample, based on an auto-correlation analysis. At sufficiently large t_equil, the majority of the initial relaxation transient is excluded, and the method selects the largest production region for which correlation times remain short to maximize the number of uncorrelated samples. Care must be taken in the case that the simulation is insufficiently long to sample many transitions among kinetically metastable states, however, or else this approach can simply result in restricting the production region to the last sampled metastable basin. A simpler qualitative analysis based on comparing forward and reverse estimates of observables [31] may also be helpful. Readers may want to compare auto-correlation times for individual observables to the global “decorrelation time” [32] described in Sec. 6. As another general check, if values of observables estimated from the production phase depend sensitively on the choice of t_equil, it is likely that further sampling is required.

6. Quantification of Global Sampling

With ideal trajectory data, one would hope to be able to compute arbitrary observables with reasonably small error bars. During a simulation, it is not uncommon to monitor specific observables of interest, but after the data are obtained, it may prove necessary to compute observables not previously considered. These points motivate the task of estimating global sampling quality, which can be framed most simply in the context of single-trajectory data: “Among the very large number of simulation frames (snapshots), how many are statistically independent?” This number is called the effective sample size. From a dynamical perspective evoking auto-correlation ideas, which also apply to Monte Carlo data, how long must one wait before the system completely loses memory of its prior con-figuration? The methods noted in this section build on ideas already presented in Sec. 4 on qualitative sampling analysis, but attempt to go a step further to quantify sampling quality.

We emphasize that no single method described here has emerged as a clear best practice. However, because the global assessment methods provide a powerful window into overall sampling quality, which could easily be masked in the analysis of single observables (Sec. 7), we strongly encourage their use. The reader is encouraged to try one or more of the approaches in order to understand the limitations of their data.

A key caveat is needed before proceeding. Analysis of trajectory data generally cannot make inferences about parts of configuration space not visited [12]. It is generally impossible to know whether configurational states absent from a trajectory are appropriately absent because they are highly improbable (extremely high energy) or because the simulation simply failed to visit them because of a high barrier or random chance.

6.1. Global sampling assessment for a single trajectory

Two methods applicable for a single trajectory were previously introduced by some of the present authors, exploiting the fact that trajectories typically are correlated in time. That is, each configuration evolves from and is most similar to the immediately preceding configuration; this picture holds for standard MD and Markov-chain MC. Both analysis methods are implemented as part of the software package LOOS [33, 34].

Lyman and Zuckerman proposed a global “decorrelation” analysis by mapping a trajectory to a discretization of con-figuration space (set of all x, y, z coordinates) and analyzing the resulting statistics [32]. See Fig. 6. Configuration space is discretized into bins based on Voronoi cells¹⁵ of structurally similar configurations, e.g., using RMSD defined in Eq. 9 or another configurational similarity measure; reference con-figurations for the Voronoi binning are chosen at random or more systematically as described in [32]. Once configuration space is discretized, the trajectory frames can be classified accordingly, leading to a discrete (i.e., ‘multinomial’) distribution (Fig. 6). The analysis method is based on the observation that the variance for any bin of a multinomial distribution is known, given the bin populations (from trajectory counts) and a specified number of independent samples drawn from the distribution [32]. The knowledge of the expected variance allows testing of increasing waiting times between configurations drawn from the trajectory to determine when and if the variance approaches that expected for independent samples. The minimum waiting time yielding agreement with ideal (i.e., uncorrelated) statistics yields an estimate for the decorrelation/memory time, which in turns implies an overall effective sample size.

Figure 6.

The basis for “decorrelation analysis” [32]. From a continuous trajectory (blue curve), configurations can be extracted at equally spaced time points (filled circles) with each such configuration categorized as belonging to one of a set of arbitrary states (delineated by straight black lines). If the configurations are statistically independent – if they are sufficiently decorrelated – then their statistical behavior will match that predicted by a multinomial distribution consistent with the trajectory’s fractional populations in each state. A range of time-spacings can be analyzed to determined if and when such independence occurs.

A second method, employing block covariance analysis (BCOM), was presented by Romo and Grossfield [35] building on ideas by Hess [36]. In essence, the method combines two standard error analysis techniques — block averaging [37] and bootstrapping [38] — with covariance overlap, which quantitatively measures the similarity of modes determined from principal component analysis (PCA) [36]. PCA in essence generates a new coordinate system for representing the fluctuation in the system while tracking the importance of each vector; the central idea of the method is to exploit the fact that as sampling improves, the modes generated by PCA should become more similar, and the covariance overlap will approach unity in the limit of infinite sampling.

When applying BCOM, the principal components are computed from subsets of the trajectory, and the similarity of the modes evaluated as a function of subset size; as the subsets get larger, the resulting modes become more similar. This is done both for contiguous blocks of trajectory data (block averaging), and again for randomly chosen subsets of trajectory frames (bootstrapping); taking the ratio of the two values as a function of block size yields the degree of correlation in the data. Fitting that ratio to a sum of exponentials allows one to extract the relaxation times in the sampling. The key advantage of this method over others is that it implicitly takes into account the number of substates; the longest correlation time is the time required not to make a transition, but to sample a scattering of the relevant states.

6.2. Global sampling assessment for multiple independent trajectories

When sampling is performed using multiple independent trajectories (whether MD or MC), additional care is required. Analyses based solely on the assumption of sequential correlations may break down because of the unknown relationship between separate trajectories.

Zhang et al. extended the decorrelation/variance analysis noted above, while still retaining the basic strategy of inferring sample size based on variance [39]. To enable assessment of multiple trajectories, the new approach focused on conformational state populations, arguing that the states fundamentally underlie equilibrium observables. Here, a state is defined as a finite region of configuration space, which ideally consists of configurations among which transitions are faster than transitions among states; in practice, such states can be approximated based on kinetic-clustering Voronoi cells according to the inter-state transition times [39]. Once states are defined, the approach then uses the variances in state populations among trajectories to estimate the effective sample size, motivated by the decorrelation approach [32] described above.

Nemec and Hoffmann proposed related sampling measures geared specifically for analyzing and comparing multiple trajectories [40]. These measures again do not require user input of specific observables but only a measure of the difference between conformations, which was taken to the be the RMSD. Nemec and Hoffmann provide formulas for quantifying the conformational overlap among trajectories (addressing whether the same configurational states were sampled) and the density agreement (addressing whether conformational regions were sampled with equal probabilities).

7. Computing error in specific observables

7.1. Basics

Here we address the simple but critical question, “What error bar should I report?” In general, there is no one-best practice for choosing error bars [2]. However, in the context of simulations, we can nonetheless identify common goals when reporting such estimates: 1) to help authors and readers better understand uncertainty in data; and 2) to provide readers with realistic information about the reproducibility of a given result.

With this in mind, we recommend the following: (a) in fields where there is a definitive standard for reporting uncertainty, the authors should follow existing conventions; (b) otherwise, such as for biomolecular simulations, authors should report (and graph) their best estimates of 95 % confidence intervals. (c) when feasible and especially for a small number of independent measurements (n < 10), authors should consider plotting all of the points instead of an average with error bars.

We emphasize that as opposed to standard uncertainties $\left[s(\overline{x})\right]$, confidence intervals have several practical benefits that justify their usage. In particular, they directly quantify the range in which the average value of an observed quantity is expected to fall, which is more relatable to everyday experience than, say, the moments of a probability distribution. As such, confidence intervals can help authors and readers better understand the implications of an uncertainty analysis. Moreover, downstream consumers of a given paper may include less statistically oriented readers for whom confidence intervals are a more meaningful measure of variation.

In a related vein, error bars expressed in integer multiples of $s(\overline{x})$ can be misinterpreted as unrealistically under or overestimating uncertainty if taken at face value. For example, reporting $3s(\overline{x})$ uncertainties for a normal random variable amounts to a 99.7 % level of confidence, which is likely to be a significant overestimate for many applications. On the other hand, $1s(\overline{x})$ uncertainties only correspond to a 68 % level of confidence, which may be too low. Given that many readers may not take the time to make such conversions in their heads, we feel that it is safest for modelers to explicitly state the confidence level of their error bar or reported confidence interval.

In recommending 95 % confidence intervals, we are admittedly attempting to address a social issue that nevertheless has important implications for science as a whole. In particular, the authors of a study and the reputation of their field do not benefit in the long run by under-representing uncertainty, since this may lead to incorrect conclusions. Just as importantly, many of the same problems can arise if uncertainties are reported in a technically correct but obscure and difficult-to-interpret manner. For example, $1s(\overline{x})$ error bars may not overlap and thereby mask the inability to statistically distinguish two quantities, since the corresponding confidence intervals are only 68 %. With this in mind, we therefore wish to emphasize that visual impressions conveyed by figures in a paper are of primary importance. Regardless of what a research paper may explain carefully in text, error bars on graphs create a lasting impression and must be as informative and accurate as possible. If 95 % confidence intervals are reported, the expert reader can easily estimate the smaller standard uncertainty (especially if it is noted in the text), but showing a graph with overly small error bars is bound to mislead most readers, even experts who do not search out the fine print.

As a final note, we remind readers that only significant figures should be reported. Additional digits beyond the precision implicit in the uncertainty are unhelpful at best, and potentially misleading to readers who may not be aware of the limitations of simulations or statistical analyses generally. For example, if the mean of a quantity is calculated to be1.23456 with uncertainty ±0.1 based on a 95 % confidence interval, then only two significant figures should be reported for the mean (1.2).

7.2. Overview of procedures for computing a confidence interval

We remind readers that they should perform the semiquantitative sampling checks (Sec. 4) before attempting to quantify uncertainty. If the observable of interest is not fluctuating about a mean value but largely increasing or decreasing during the course of a simulation, a reliable quantitative estimate for the observable or its associated uncertainty cannot be obtained.

For observables passing the qualitative tests noted above in Sec. 4, we advocate obtaining confidence intervals in one of two ways:

• For observables that are Gaussian-distributed (or assumed to be, as an approximation or due to lack of information), an appropriately chosen coverage factor k (typically in the range of 2 to 3; see Sec. 7.5 for further details) is multiplied by the standard uncertainty $s(\overline{x})$ to yield the expanded uncertainty, which estimates the 95 % confidence interval.

• For non-Gaussian observables, a bootstrapping approach (Sec. 7.6) should be used. An example of a potentially non-Gaussian observable is a rate-constant, which must be positive but could exhibit significant variance. As such, a confidence interval estimated with a coverage factor may lead to an unphysical negative lower limit. In contrast, bootstrapping does not assume an underlying distribution but instead constructs a confidence interval based on the recorded data values, and the limits cannot fall outside the extreme data values; nevertheless, bootstrapped confidence intervals can have shortcomings [41, 42]. Bootstrapping is also sometimes useful for estimating uncertainties associated with derived observables.

Below we describe approaches for estimating the standard uncertainty $s(\overline{x})$ from a single trajectory with a coverage factor k as well as the bootstrapping approach for direct confidence-interval estimation. Whether using a coverage factor and standard uncertainty or bootstrapping, one requires an estimate for the independent number of observations in a given simulation. This requires care, but may be accomplished based on the effective sample size described in Sec. 6, via block averaging, or by analysis of a time-correlation function. However, these methods have their limitations and must be used with caution. In particular, both block averaging and autocorrelation analyses will produce effective sample sizes that depend on the quantity of interest. To produce reliable answers, one must therefore identify and track the slowest relevant degree of freedom in the system, which can be a non-trivial task. Even apparently fast-varying properties may have significant statistical error if they are coupled to slower varying ones, and this error in uncertainty estimation may not be readily identifiable by solely examining the fast-varying time series.

In the absence of a reliable estimate for the number of independent observations, one can perform n independent simulations and calculate the standard deviation s (x) for quantity x (which could be the ensemble average of a raw data output or a derived observable) among the n simulations, yielding a standard uncertainty of $s(\overline{x})=s(x)/\sqrt{n}$ When computing the uncertainty with this approach, it is important to ensure that each starting configuration is also independent or else to recognize and report that the uncertainty refers to simulations started from a particular configuration. The means to obtain independent starting configurations is system-dependent, but might involve repeating the protocol used to construct a configuration (solvating a protein, inserting liquid molecules in a box, etc.), and/or using different seeds to generate random configurations, velocities, etc. However, readers are cautioned that for complex systems, it may be effectively impossible to generate truly independent starting configurations pertinent to the ensemble of interest. For example, a simulation of a protein in water will nearly always start from the experimental structure, which introduces some correlation in the resulting simulations even when the remaining simulation components (water, salt, etc.) are regenerated de novo.

7.3. Dealing with correlated time-series data

When samples of a simulated observable are independent, the experimental standard deviation of the mean (i.e., Eq. 8) can be used as an estimate of the corresponding standard uncertainty. Due to correlations, however, the number of independent samples in a simulation is neither equal to the number of observations nor known a priori; thus Eq. 8 is not directly useful. To overcome this problem, a variety of techniques have been developed to estimate the effective number of independent samples in a dataset. Two methods in particular have gained considerable traction in recent years: (i) autocorrelation analyses, which directly estimate the number of independent samples in a time series; and (ii) block averaging, which projects a time series onto a smaller dataset of (approximately) independent samples. We now discuss these methods in more detail.

7.3.1. Autocorrelation method for estimating the standard uncertainty

Conceptually, autocorrelation analyses directly compute the effective number of independent samples N_ind in a time series, taking into account “redundant” (or even possibly new) information arising from correlations.¹⁶ In particular, this approach invokes the fact that the statistical properties of steady-state simulations (e.g., those in equilibrium or non-equilibrium steady state) are, by definition, time-invariant. As such, correlations between an observable computed at two different times depends only on the lag (i.e., difference) between those times, not their absolute values.

This observation motivates one to compute an autocorrelation function. Specifically, one computes the stationary autocorrelation function C_j as given in Eq. 10 for a set of lags j. Then, the number of independent samples is estimated by¹⁷

$$N_{\text{ ind }}=\frac{N}{1+2{\sum }_{j=1}^{N_{\max }}{C}_j}$$ (11)

where N_max is an appropriately chosen maximum number of lags (see below). Note that N_ind need not be an integer. Finally, the standard uncertainty is estimated via

$$s(\overline{x})=\frac{s(x)}{\sqrt{N_{\text{ind}}}}$$ (12)

We note that the experimental standard deviation of the observable x is used in Eq. 12 to estimate the uncertainty. Strictly speaking, the standard uncertainty should be estimated using the true standard deviation of x (e.g., σ_x); given that the true standard deviation is unknown, the experimental standard deviation is used in its place as an estimate of σ_x [14].

In evaluating Eq. (11), the value of N_max must be chosen with some care. Roughly speaking, N_max should be large enough so that the sum is converged and insensitive to the choice of upper bound. Although a very large value of N_max might seem necessary for slowly decaying autocorrelation functions, appropriate truncations of the sum will introduce negligible error, even if the correlation time is infinite. We refer readers to discussions elsewhere on this topic, for example, Refs. [12, 43–45]. In typical situations, N_max can be set to any value greater than τ, since in principle C_j = 0 for all j > τ. However, care must be exercised to avoid integrating pure noise over too large of an interval, since this can generate Brownian motion; see, for example, Ref. [46] and references contained therein.

7.3.2. Block averaging method for estimating the standard uncertainty

The main idea behind block averaging is to permit the direct usage of Eq. 6 by projecting the original dataset onto one comprised of only independent samples, so that there is no need to compute N_ind. Acknowledging that typical MD time series have a finite-correlation time τ, we recognize that a continuous block of M data-points will only be correlated with its adjacent blocks through its first and last τ points, provided τ is small compared to the block size M. That is, correlations will be on the order of τ/M, which goes to zero in the limit of large blocks.

This observation motivates a technique known as block averaging [12, 37, 47, 48]. Briefly, the set of N observations {x₁, …, x_N} are converted to a set of M “block averages” $\left\{x_1^b,\dots ,x_M^b\right\}$, where a block average $x_j^b$ is the arithmetic mean of n (the block size) sequential measurements of x:

$$x_j^b=\frac{\sum _{k=1+\left(j-1\right)n}^{jn}{x}_k}{n}$$ (13)

From this set of block averages, one may then compute the arithmetic mean of the block averages, ${\overline{x}}^b$, which is an estimator for 〈x〉.¹⁸ Following, one computes the experimental standard deviation of the block averages, $s\left({\overline{x}}^b\right)$, using Eq. 6. Lastly, the standard uncertainty of ${\overline{x}}^b$ is just the experimental standard deviation of the mean given the set of M block averages:

$$s\left({\overline{x}}^b\right)=\frac{s\left(x^b\right)}{\sqrt{M}}$$ (14)

This standard uncertainty may then be used to calculate a confidence interval on ${\overline{x}}^b$.

It is important to note that for statistical purposes, the blocks must all be of the same size in order to be identically distributed, and thereby satisfy the requirements of Eq. 8. It is also important to systematically assess the impact of block size on the corresponding estimates. In particular, as the blocks get longer, the block averages should decorrelate and $s\left({\overline{x}}^b\right)$ should plateau [12, 37]. Another approach is to measure the block correlation and to use it to improve the selection of the block size and, hence, uncertainty estimate [49]. We stress that this final step of adjusting the block size and recomputing the block standard uncertainty is absolutely necessary. Otherwise, the blocks may be correlated, yielding an uncertainty that is not meaningful.

7.4. Propagation of uncertainty

Oftentimes we run simulations for the purposes of computing derived quantities, i.e., those that arise from some analysis applied to raw data. In such cases, it is necessary to propagate uncertainties in the raw data through the corresponding analysis to arrive at the uncertainties associated with the derived quantity. Frequently, this can be accomplished through a linear propagation analysis using Taylor series, which yields simple and useful formulas.

The foundation for this approach lies in rigorous results for the propagation of error through linear functions of random variables. For a derived observable that is a linear function of M uncorrelated raw data measurements, e.g.,

$$F\left(\left\{x_i\right\}\right)=c+\sum _{i=1}^M{a}_i{x}_i,$$ (15)

where c is a constant, the experimental variance of F may be rigorously expressed as [50]

$$s^2(F)=\sum _{i=1}^M{a}_i^2{s}^2\left(x_i\right)$$ (16)

A key assumption in Eq. 16 is that the raw data, {x_i}, are linearly uncorrelated (see Eq. 7). If any observed quantities are correlated, the uncertainty in F must include “covariance” terms. The reader may consult Sec. 2.5.5, “Propagation of error considerations” in Ref. [50] for further discussion. For reasons of tractability, we restrict the discussion here to linearly uncorrelated observables or the assumption thereof.

The situation for a nonlinear derived quantity is much more complicated and, as a result, rigorous expressions for the uncertainty of such functions are rarely used in practice. As a simplification, however, one approximates the nonlinear derived quantity as a Taylor-series expansion about a reference point, i.e.,

$$F\left(\left\{x_i\right\}\right)\approx F\left(\left\{{\overline{x}}_i\right\}\right)+\sum _{j=1}^M{\left(\frac{\partial F}{\partial x_j}\right)|}_{\left\{{\overline{x}}_i\right\}}\left(x_j-{\overline{x}}_j\right)+\dots$$ (17)

The deviation of a particular measurement from its mean, ${ϵ}_i=x_i-{\overline{x}}_i$, is itself a random quantity, and the uncertainty in those measurements is propagated into uncertainty in F. Note that the ratio ${ϵ}_i/{\overline{x}}_i$ is the so-called “noise-to-signal” ratio, which vanishes in the limit of a precise measurement. With this linear approximation of F, which is analogous to Eq. 15 with a_i = (∂F/∂x_i), and the assumption that the raw data are uncorrelated, the variance in F may be approximated by

$$s^2(F)\approx {\sum _{j=1}^M{\left(\frac{\partial F}{\partial x_j}\right)}^2|}_{\left\{{\overline{x}}_i\right\}}{s}^2\left(x_j\right)$$ (18)

A simple example illustrates this procedure. Consider, in particular, the task of estimating the uncertainty in a measurement of density, ρ = m/V, from a time series of volumes output by a constant pressure simulation, where m is the (constant) system mass and V is the (fluctuating) system volume. Application of Eq. 18 to the definition of ρ yields

$$s^2(\rho )\approx {\left(\frac{N}{{\overline{V}}^2}\right)}^2{s}^2(V)$$ (19)

$$s(\rho )\approx \overline{\rho }\frac{s(V)}{\overline{V}}$$ (20)

with $\overline{\rho }=N/\overline{V}$. This approximation of the experimental standard deviation may be used to estimate a confidence interval on $\overline{\rho }$ or for other purposes.

In general, approximations in the spirit of Eq. 20 are useful and easy to generalize to higher-dimensional settings in which the derived observable is a nonlinear combination of many data-points or sets. However, the method does have limits. In particular, it rests on the assumption of a small noise-to-signal ratio, which may not be valid for all simulated data. If there is doubt as to the quality of an estimate, the uncertainty should therefore be estimated with alternative approaches such as bootstrapping in order to validate the linear approximation. See also the pooling analysis of Ref. [11] for a method of assessing the validity of linear approximations.

7.5. From standard uncertainty to confidence interval for Gaussian variables

Once a standard uncertainty value is obtained for a Gaussian-distributed random variable with mean 〈x〉, and the number of independent samples n has been estimated, the 95 %-confidence interval $[\overline{x}-ks(\overline{x}),\overline{x}+ks(\overline{x})]$ can be constructed on the basis of an established look-up table (or a statistics software model) for the coverage factor k based on n. The theoretical basis for the table is the “Student” or “t” distribution, which is not Gaussian, but governs the behavior of an average derived from n independent Gaussian variables [9]. Table 1 lists k for two-sided 95 % confidence intervals for select values of n.

Table 1.

Coverage factors k required for a two-sided 95 % confidence interval for a Gaussian variable [9]. Note that k increases with decreasing sample size. This in turn implies that smaller samples yield higher uncertainty for a given estimation of the experimental standard deviation.

n (independent samples)	k (coverage factor)
6	2.57
11	2.23
16	2.13
21	2.09
26	2.06
51	2.01
101	1.98

As a reminder, multi-modally distributed variables with multiple peaks in their distributions cannot be considered Gaussian random variables. Variables with a strict upper or lower limit (such as a non-negative quantity) and long-tailed distributions are also not Gaussian. These cases should be treated with bootstrapping.

7.6. Bootstrapping

Bootstrapping is an approach to uncertainty estimation that does not assume a particular distribution for the observable of interest or a particular kind of relationship between the observable and variables directly obtained from simulation [38]. A full discussion of bootstrapping and resampling methods is outside the scope of this article; we will cover the broad strokes here, and suggest interested readers consult excellent discussions elsewhere for more details (e.g. Refs. [41], [42], and, particularly, [38]).

In nonparametric bootstrapping, new, “synthetic” data sets (corresponding to hypothetical simulation runs) are created by drawing n samples (configurations) from the original collection that was generated during the actual run. The same sample may be selected twice, while others may not be selected at all in a process called “sampling with replacement.” In doing so, these synthetic sets will be different even though they all have the same number of samples and draw from the same pool of data. Having created a new set, the data are analyzed to determine the derived quantity of interest, and this process is repeated to produce multiple estimates of the quantity. The distribution of “synthetic” observables can be directly used to construct a 95 % confidence interval from the 2.5 percentile to the 97.5 percentile value. Readers are cautioned that bootstrapping confidence intervals are not quantitatively reliable in certain cases such as with small-sample sizes or distributions that are skewed or heavy-tailed [41, 42].

The process described above assumes that the original simulation data are uncorrelated. If this is not the case, then the resampling method can be reformulated in one of two ways. The first option is to estimate the number of independent samples in the original set (e.g., using an autocorrelation method [29, 32]) and to pull only that many samples to create the new data sets. The second option is to group the samples into blocks that are uncorrelated based on analyzing varying block sizes (see Sec. 7.3.2) and to then use the block averages as the samples for bootstrapping.

Alternatively, one could use the difference between errors estimated via block averaging and bootstrapping as a measure of the correlation; if one tracks the bootstrapped and block-averaged estimates of a quantity’s uncertainty as a function of block size, the only difference between the two modes of calculation is whether the data are correlated. The decay in the ratio of the two quantities as a function of time is a measure of the correlation time in the sample [35].

7.6.1. Bootstrapping variants

An alternate approach that can directly account for correlations is called parametric bootstrapping. The main idea behind this method is to model the original data as a deterministic function (which can be zero, constant, or have free parameters) plus additive noise. The parameters of this model, including the structure of the noise (i.e., its covariance), can be determined through a statistical inference procedure. Having calibrated the model, random number generators can be used to sample the noise, which is then added back to the trial function to generate a synthetic data set. As with the nonparametric bootstrap, the generated data can be used to compute the derived quantity of interest, and the uncertainty can be obtained from the statistics of the values compute with different generated sets.

To further clarify the procedure of parametric bootstrapping, consider the simplest case in which the data are a collection of uncorrelated random variables fluctuating about a constant mean. In this situation, one could estimate (I) the deterministic part of a parametric model using the sample mean $\overline{x}$ of the data, and (II) the stochastic part as a Gaussian random variable whose variance equals the sample variance. If instead the data are correlated (e.g., as in a time series of simulated observables), one can postulate a covariance function to describe the structure of this randomness. Often these covariance functions are formulated with free parameters (often called “hyperparameters”) that characterize properties such as the noise-scale and characteristic length of correlations [51]. In such cases, determining the hyperparameters may require more sophisticated techniques such as maximum likelihood analyses or Bayesian approaches; see, for example, Ref. [51]. See also Refs. [11, 24, 52] for examples and practical implementations applied to cases in which the deterministic component of the data is not constant.

It is important to note that various bootstrapping approaches can and often are used as uncertainty propagation tools. Nonetheless, care should be exercised when using such methods with either nonlinear functions or naturally constrained functions. For example, consider application of the parametric bootstrap technique to a free energy calculation,

$$\beta \text{Δ}A=-\ln \left[\overline{\exp (-\beta \text{Δ}U)}\right]$$ (21)

If synthetic samples are drawn for exp(–βΔU) from, say, a Gaussian centered at 1 with a standard deviation of 0.5, new estimates will eventually output negative numbers. This is, of course, mathematically nonsensical for the exponential function. Thus, one should be aware of any distributional assumptions imposed either by the physics of the problem or the mathematical analyses of synthetic data.

Lastly, an alternative to bootstrapping is the “jackknife” method [53–55] (also outlined in Ref. [38]). It operates similar to the bootstrap as a resampling technique, but it uses synthetic data sets created by subtraction of some number of samples rather than replacement; as such it is often categorized as a variant of the bootstrap (even though it predates the bootstrap). Since it operates by sample deletion, it may be better suited to smaller data sets for which a few samples may be overrepresented in the synthetic data set created by the bootstrap replacement technique. Ultimately, though, the results are similar in that the jackknife technique creates a distribution of derived observables that can be used to compute an arithmetic mean, an estimate of the standard uncertainty, and confidence intervals.

7.7. Dark uncertainty analyses

In some cases, multiple simulations of the same physical observable τ may yield predictions whose error bars do not overlap. This situation can arise, for example, in simulations of the glass transition temperature when undersampling the crosslinked network structure of certain polymers. In such cases, it is reasonable to postulate an unaccounted for source of uncertainty, which we colorfully refer to as “dark uncertainty” [11]. In the context of a statistical model, we postulate that the probability of a simulation output depends on the unobserved or “true” mean value $\overline{\tau }$, an uncertainty ${\sigma }_i^2$ whose value is specific to the simulation (estimated, e.g., according to uncertainty propagation), and the unaccounted-for dark uncertainty y². (For simplicity, the ${\sigma }_i^2$ and y² should be treated as variances.)

While details are beyond this scope of this document, such a model motivates an estimate of $\overline{\tau }$ of the form

$$\overline{\tau }\approx \mathcal{T}\propto \sum _i\frac{T_i}{{\sigma }_i^2+y^2},$$ (22)

where Τ is a “consensus” or weighted-mean estimate of the true mean $\overline{\tau }$, T_i is the prediction from the ith simulation, ${\sigma }_i^2$ is its associated “within-simulation” uncertainty, and y² is the “dark” or “between-simulation” uncertainty; note that the latter does not depend on i. The variable y² can be estimated from a maximum-likelihood analysis of the data and amounts to numerically solving a relatively simple nonlinear equation (see Ref. [11]). Equation 22 is useful insofar as it weights simulated results according to their certainty while reducing the impact of overconfident predictions (e.g., having small ${\sigma }_i^2$). Additional details on this method are provided in Ref. [11] and the references contained therein.

7.8. Propagation across multiple steps

In some instances, it is useful and/or necessary to propagate uncertainty across different simulation steps. This occurs, for example, when the property of a constant pressure system can only be computed using constant volume simulations (e.g., for certain viscosity calculations). In such cases, uncertainty in the system volume must be accounted for in the final property prediction, which carries its own uncertainties associated with the simulation protocol, input parameters, etc. Related issues arise when attempting to account for uncertainty in force-field parameters [5–7].

Addressing these uncertainty propagation tasks may be as simple as performing a linear or bootstrap analysis as previously described, but at each step of the simulation protocol. In other cases, especially when propagation must be performed between different simulations, such approaches are computationally expensive and, thus, infeasible. A variety of methods (surrogate modeling, polynomial chaos, Gaussian-process regression, etc.) are being actively explored by the community, but in many instances few, if any approaches, have emerged as widely accepted strategies. We encourage the reader to stay informed of current literature, some of which is referenced herein [56].

8. Assessing Uncertainty in Enhanced Sampling Simulations

While recent advances in computational hardware have allowed MD simulations of systems with biological relevance to routinely reach timescales ranging from hundreds of ns to μs, in many cases this is still not long enough to obtain equilibrated (i.e., Boltzmann-weighted) structural populations. Intrinsic timescales of the systems may be much longer. Enhanced sampling methods can be used to obtain well-converged ensembles faster than conventional MD. In general, enhanced sampling methods work through a combination of modifying the underlying energy landscape and/or thermodynamic parameters to increase the rate at which energy barriers are crossed along with some form of reweighting to recover the unbiased ensemble [15]. However, such methods do not guarantee a converged ensemble, and care must be taken when using and evaluating enhanced sampling methods.

Generally speaking, uncertainty analysis is more challenging for data generated by an enhanced sampling method. The family of enhanced equilibrium sampling methods, examples of which include replica exchange and variants [57–59], local elevation [60], conformational flooding [61], metadynamics [62, 63], and adaptive biasing force [64–66] to name a few, are complex and the resulting data may have a highly non-trivial correlation structure. In replica exchange, for example, the ensemble at a temperature of interest will be based on multiple return visits of different sequentially correlated trajectories.

Before performing an enhanced-sampling simulation, consider carefully whether the technique is needed, and consult the literature for best practices in setting up a simulation. Even a straightforward MD simulation requires considerable planning, and the complexity is much greater for enhanced techniques.

Given the subtleties of these sampling approaches, when possible, consider taking a “bottom line” approach, and assessing sampling based on multiple independent runs. The variance among these runs, if the approach is not biased, will help to quantify the overall sampling. Note that methods applicable to global assessment of multiple trajectories (Sec.6.2) should be valid for analyzing multiple runs of an arbitrary method. However, a caveat for the approach of Zhang et al. [39] is that some dynamics trajectory segments would be required to perform state construction by kinetic clustering.

8.1. Replica Exchange Molecular Dynamics

One of the most popular enhanced sampling methods is replica exchange MD (REMD) [58]; see also [57]. Broadly speaking, REMD consists of running parallel MD simulations on a number of non-interacting replicas of a system, each with a different Hamiltonian and/or thermodynamic parameters (e.g., temperature), and periodically exchanging system coordinates between replicas according to a Metropolis criterion which maintains Boltzmann-factor sampling for all replicas.

In order to assess the results of a REMD simulation, it is important to consider not just the overall convergence of the simulation to the correct Boltzmann-weighted ensemble of structures (via e.g., combined clustering, see Sec. 4), but how efficiently the REMD simulation is doing so. These concepts are termed “thermodynamic efficiency” and “mixing efficiency” by Abraham and Gready [67], and it is quite possible to achieve one without the other; both must be assessed. In order for sampling to be efficient, coordinates must be able to move freely in replica space.

In practical settings, several metrics are often used to assess these two efficiencies, a few of which we list below. In these definitions, note that we refer to both “coordinate trajectories” and “replica trajectories”. A “coordinate trajectory” follows an individual system’s continuous trajectory as it traverses replica space (e.g., a system experiencing multiple temperatures as it is exchanged during a temperature REMD simulation). A “replica trajectory” is the sequence of configurations corresponding to a single replica under fixed Hamiltonian and thermodynamic conditions, (e.g., all structures at a temperature of 300 K in a temperature REMD simulation). Thus, a replica trajectory consists of concatenated coordinate-trajectory segments and vice versa.

Below are several checks that should be applied to REMD simulation data.

• Exchange acceptance. The exchange acceptance rate (i.e., the number of exchanges divided by the number of exchange attempts) between neighboring replicas should be roughly equivalent to each other and to the target acceptance rate. A low exchange acceptance between neighboring replicas relative to the average exchange acceptance rate creates a bottleneck in replica space which in turn can lead to poor sampling of the overall configuration space. In such cases, the replica spacing may need to be decreased or additional replicas used. Conversely, a high exchange acceptance rate between neighboring replicas relative to the average exchange acceptance rate may indicate that more resources than necessary are being used to simulate replicates, and that good sampling can be achieved with fewer replicas or larger replica spacing.

• Replica round trips. The time taken for a coordinate trajectory to travel from the lowest replica to the highest and back is called the replica “round trip” time. Over the course of a REMD simulation, any given coordinate trajectory should make multiple round trips. The rationale behind this is that every replica should contribute to enhancing the sampling of every set of starting coordinates. One can look at the average, minimum, and maximum round trip times among the coordinate trajectories: these should be similar for any given set of coordinates. See e.g., Fig. 6 in [25]. If they are not, it is likely due to one or more bottlenecks in replica space which can be identified by a relatively low exchange acceptance rate (see the previous bullet point).

• Replica residence time. The time a coordinate trajectory spends at a replica is called the “replica residence time”. For replica sampling to be efficient, the replica residence time for each set of starting coordinates at each replica should be roughly equivalent. If it is not (i.e., if a set of starting coordinates is spending a much larger amount of time at certain replicas compared to the overall average) this can also indicate one or more bottlenecks in replica space. An example of this is shown in Fig. 7 in Ref. [25].

• Distributions of quantities calculated from coordinate trajectories. If all coordinates are moving freely in replica space, they should eventually converge to the same ensemble of structures. Comparing distributions of various quantities from coordinate trajectories can provide a measure of how converged the simulation is. For example, one can compare the distribution of RMSD values of coordinate trajectories to a common reference structure; see e.g., Fig. 8 in Ref. [68]. Poor overlap can be an indication that replica efficiency is poor or the simulation is not yet converged.

All of the above quantities (replica residence time, round trip time, lifetimes etc) can be calculated with CPPTRAJ [69], which is freely available from https://github.com/Amber-MD/cpptraj or as part of AmberTools (http://ambermd.org).

It may also be useful to perform multiple REMD runs. Using the standard uncertainty among runs can quantify uncertainty and provide the basis for a confidence interval with an appropriate coverage factor - see definitions in Sec. 1. If the ensembles produced depend significantly on the set of starting configurations, that is a sign of incomplete sampling.

8.2. Weighted Ensemble simulations

The weighted ensemble (WE) method orchestrates an ensemble of trajectories that are intermittently pruned or replicated in order to enhance sampling of difficult-to-access regions of configuration space [70]. The final set of trajectories can be visualized as a tree structure based on the occasional replication and pruning events. WE is an unbiased method that can be used to sample rare transient behavior [71] as well as steady states [72] including equilibrium [73].

Like other enhanced sampling methods, WE’s tree of trajectories has a complex correlation structure requiring care for uncertainty analysis. It is important to understand the basic theory and limitations of the WE method, as is discussed in a WE overview document.

From a practical standpoint, the safest way to assess uncertainty in WE simulations is to run multiple instances (which can be seeded from identical or different starting structures depending on the desired calculation) from which a variance and standard uncertainty in any observable can be calculated. Note particularly that WE tracks the time evolution of observables as the system relaxes (perhaps quite slowly) to equilibrium or another steady state [71]; hence, the variance computed in an observable from multiple runs should be based on values at the same time point.

When it is necessary to estimate uncertainty based on a single WE run, the user should treat the (ensemble-weighted) value of an observable measured over time much like an observable in a standard single MD simulation; this is because the correlations in ensemble averages are sequential in time. First, as discussed in Sec. 4, the time trace of the observable should be inspected for relaxation to a nearly constant value about which fluctuations occur. A transient/equilibration period should be removed in analogy to MD - see Sec. 5 - and then best practices for single observable uncertainties should be followed as described in Sec. 7. Despite this rather neat analogy to conventional MD, experience has shown that run to-run variance in WE simulations of challenging systems can be large, so multiple runs are advised. In the future, variance-reduction techniques may alleviate the need for multiple runs.

9. Concluding Discussion

As computational scientists, we often spend vast resources modeling complex systems. With the thought and care involved in setting up these simulations, it is therefore surprising that significantly less time may be spent thinking about how to analyze and understand the validity of the generated data. Do our simulations not deserve better?

We have spent some twenty odd pages telling you, reader, how and why you should run more simulations and do more analyses to vet the reliability of any given result. Given that any one of these tasks could take as long as running a production simulation, we face the invariable reality that uncertainty quantification (UQ) can substantially increase the time required to complete a project. Thus, we wish to adjust our readers’ expectations: the time needed to perform a simulation study is not the time spent simulating. Rather, it is the time needed to: (i) generate data; (ii) thoughtfully analyze it (whether by means of a posteriori UQ methods or additional simulations); and (iii) clearly communicate the means to and interpretations of the resulting uncertainties.

Ultimately we take the perspective that this extra effort gives us more confidence in our computational results. While this benefit may seem soft, note that industrial stakeholders actively use simulations and simulated results to make costly economic decisions. Thus, it could be argued that by not doing UQ, we invariably diminish the usefulness of simulations, and thus contribute to debate concerning their reliability and financial value.

UQ goes hand-in-hand with the quest for reproducibility. We should always keep in mind the fundamental principle that scientific results are reproducible. If we cannot state the certainty with which we believe a result, we cannot assess its reproducibility. If our results cannot be reproduced, what value do they have?

UQ is an evolving field, but the underlying principles are not expected to change. We intend that this article will be updated to include best practices across an ever-broadening array of techniques, but even so, individual studies may require some adaptation and creativity. It is fair to say that UQ is a practitioners’ field. You know your data best and should be able to assess its quality based on fundamental statistical principles and (variations of) the approaches described here.

As a final note, we encourage readers to comment or add to this guide using the issue tracker of its GitHub repository [https://github.com/dmzuckerman/Sampling-Uncertainty].