The Outcome-Representation Learning model: a novel reinforcement learning model of the Iowa Gambling Task

Abstract

The Iowa Gambling Task (IGT) is widely used to study decision making within healthy and psychiatric populations. However, the complexity of the IGT makes it difficult to attribute variation in performance to specific cognitive processes. Several cognitive models have been proposed for the IGT in an effort to address this problem, but currently no single model shows optimal performance for both short- and long-term prediction accuracy and parameter recovery. Here, we propose the Outcome-Representation Learning (ORL) model, a novel model that provides the best compromise between competing models. We test the performance of the ORL model on 393 subjects’ data collected across multiple research sites, and we show that the ORL reveals distinct patterns of decision making in substance using populations. Our work highlights the importance of using multiple model comparison metrics to make valid inference with cognitive models and sheds light on learning mechanisms that play a role in underweighting of rare events.

1. Introduction

There is a growing interest among researchers to develop and apply computational (i.e. cognitive) models to classical assessment tools to help guide clinical decision making (e.g., Ahn & Busemeyer, 2016; Batchelder, 1998; McFall & Townsend, 1998; Neufeld, Vollick, Carter, Boksman, & Jetté, 2002; Ratcliff, Spieler, & Mckoon, 2000; Treat, McFall, Viken, & Kruschke, 2001; Wallsten, Pleskac, & Lejuez, 2005). Despite this interest, clinical assessment has yet to be influenced by the many computational assays available today (see, Ahn & Busemeyer, 2016). There are many potential reasons for this, but two important factors are the lack of both: (1) precise characterizations of neurocognitive processes, and (2) optimal, externally valid paradigms for assessing psychiatric conditions.

The Iowa Gambling Task (IGT) is an example, which was successfully used to classify various clinical populations from healthy populations (e.g., Bechara, Damasio, Damasio, & Anderson, 1994; Bechara et al., 2001). Originally developed to detect damage in ventromedial prefrontal brain regions, the IGT has since been used to identify a variety of decision making deficits across a wide range of clinical populations (e.g., Grant, Contoreggi, & London, 2000; Shurman, Horan, & Nuechterlein, 2005; Stout, Rodawalt, & Siemers, 2001; Whitlow et al., 2004). While the IGT is highly sensitive to decision making deficits, the specific underlying neurocognitive processes that are responsible for these observed deficits are difficult to identify using only behavioral performance data.

To address the lack of specificity provided by the IGT, multiple computational models have been proposed which aim to break down the decision making process into its component parts (Ahn, Busemeyer, Wagenmakers, & Stout, 2008; Busemeyer & Stout, 2002; d'Acremont, Lu, Li, Van der Linden, & Bechara, 2009; Worthy, Pang, & Byrne, 2013b), and the modeling approach has been applied to several clinical populations (for a review, see Ahn, Dai, Vassileva, Busemeyer, & Stout, 2016). In particular, the first cognitive model proposed for the IGT—termed the Expectancy-Valence Learning (EVL) model (Busemeyer & Stout, 2002)—was used to identify differences in cognitive mechanisms between healthy controls and multiple clinical populations ranging from those with substance use to neuropsychiatric disorders (Yechiam, Busemeyer, Stout, & Bechara, 2005). The EVL led to several new competing models, which capture participants’ decision making behavior more accurately. Specifically, two models show excellent performance: (1) the Prospect Valence Learning model with Delta rule (PVL-Delta) shows excellent long-term prediction accuracy and parameter recovery (Ahn et al., 2008; 2014; Steingroever, Wetzels, & Wagenmakers, 2013; 2014), and (2) the Value-Plus-Perseverance model (VPP) shows excellent short-term prediction accuracy (Ahn et al., 2014; Worthy et al., 2013b). Long-term prediction accuracy (a.k.a., absolute performance; Steingroever, Wetzels, & Wagenmakers, 2014) is defined as how well a model can generate the whole choice patterns when only the fitted parameters are used, and short-term prediction accuracy is defined as a measure of model prediction accuracy on one-step-ahead trials using fitted parameters and a history of choices while penalizing model complexity. Parameter recovery performance indicates how well “true” model parameters can be estimated (i.e. recovered) after they are used to simulate behavior, which is essential for making valid inference with model parameters (Donkin, Brown, Heathcote, & Wagenmakers, 2011; Wagenmakers, van der Maas, & Grasman, 2007). Because all three of these metrics are important in understanding how well model parameters capture the true cognitive processes underlying decision making (see Heathcote, Brown, & Wagenmakers, 2015) and there is no single model that shows good performance in all three metrics, it is unclear which model should be used to make inference on the IGT.

Additionally, no studies to our knowledge have explicitly assessed different models’ performance across the multiple versions of the IGT. While many studies to date have employed the original version of the task developed in 1994 (Bechara et al., 1994), the modified version has a non-stationary payoff structure (see section 2.2) and is widely used in practical applications involving populations with severe decision making impairments (e.g., Ahn et al., 2014; Bechara & Damasio, 2002). Importantly, a model that performs well across both versions of the task would be more generalizable to other experience-based cognitive tasks which are used extensively in the decision making and cognitive science literature.

To develop a new and improved computational model for the IGT, it is necessary to first identify the cognitive strategies that decision makers may engage in during IGT administration. In the sections that follow, we describe four separable cognitive strategies/effects that are consistently observed in IGT behavioral data including: (1) maximizing long-term expected value, (2) maximizing win frequency, (3) choice perseveration, and (4) reversal learning. As mentioned previously, the IGT falls under the umbrella of more general experience-based cognitive tasks, so a model that accurately captures these multiple strategies has broad implications for models of decisions from experience.

1.1. Expected value

In experience-based cognitive tasks, people typically learn the long-term expected value of choice alternatives across trials and make choices appropriately. The IGT is a specific instantiation of an experienced-based task in which people make decisions based on expected value (e.g., Bechara, Damasio, Damasio, & Anderson, 1994; Beitz, Salthouse, & Davis, 2014). In fact, the most common metric used to summarize IGT behavioral performance is the difference between the number of “good” versus “bad” decks selected, where good and bad decks are those with positive and negative expected values, respectively. For example, in Bechara et al.’s (1994) original work, the net good minus bad deck selections was used to successfully differentiate healthy controls from individuals with ventromedial prefrontal cortex damage. However, it has since become clear that healthy subjects do not always learn to make optimal selections (see Steingroever, Wetzels, Horstmann, Neumann, & Wagenmakers, 2013b), which is consistent with extant literature on experience-based tasks (e.g., Erev & Barron, 2005). In extreme cases, healthy controls make decisions similar to that of severely impaired decision makers when evaluated using expected value criterion alone (e.g., Caroselli, Hiscock, Scheibel, & Ingram, 2006).

The PVL-Delta and VPP models both assume that decision makers first value the outcomes according to the Prospect Theory utility function (Kahneman & Tversky, 1979), and the resulting subjective utilities are then used to update decision makers’ trial-by-trial expectations using the delta rule (i.e. the simplified Rescorla-Wagner updating rule; see Rescorla & Wagner, 1972). Together, the Prospect Theory utility shape and loss aversion parameters determine which decks decision makers learn to prefer—holding other parameters constant, low loss aversion can lead to a preference for disadvantageous decks (i.e. decks A and B) because large losses become discounted, while a shape parameter closer to 0 (and below 1) makes decks with frequent gains more valuable than those with infrequent gains despite having the same objective expected value (see section 2.3; Ahn et al., 2008). Notably, reduced loss aversion on the IGT, but not a difference in utility shape, has been linked to decision making deficits in multiple clinical populations (Ahn et al., 2014; Vassileva et al., 2013), suggesting that differential valuation of gains versus losses is an individual difference with potential real-world implications. Therefore, a new IGT model should capture differential valuation of gains versus losses.

1.2. Win frequency

In experience-based paradigms like the IGT, it is well known that a majority of individuals have strong preferences for choices (i.e. decks) that win frequently, irrespective to long-term expected value (e.g., Barron & Erev, 2003; Chiu & Lin, 2007; Chiu et al., 2008; Yechiam, Stout, Busemeyer, Rock, & Finn, 2005). For example, across studies using the IGT, deck B (win frequency=90%) is often more preferred than deck A (win frequency=50%) despite the long-term value of the two decks being equivalent (Lin, Chiu, Lee, & Hsieh, 2007; Steingroever et al., 2013b). In fact, this preference is so strong that most healthy subjects fail to make optimal decisions when the IGT task structure is altered so that good and bad decks have low and high win frequency, respectively (Chiu et al. 2008).

In principle, decision makers may prefer deck B over more advantageous options because they do not accurately account for rare events (i.e. 1 large loss per 10 trials; see Fig. 1). Barron & Erev (2003) describe this general tendency as an underweighting of rare events that may be attributable to multiple cognitive mechanisms including recency effects, estimation error, and/or reliance on cognitive heuristics (see Hertwig & Erev, 2009). However, it is clear from the IGT literature that recency effects alone cannot account for the observed preferences for decks with high win frequency. For example, Steingroever et al. (2013a) showed that the Expectancy Valence Learning model (EVL; Busemeyer & Stout, 2002)—despite capturing recency effects using the delta learning rule—cannot account for the win frequency effect in the IGT. Conversely, the concave downwards Prospect Theory utility function utilized by the PVL-Delta and VPP allows for both models to implicitly account for win frequency (see section 2.3; Ahn et al., 2008). Further, the structure of the IGT is such that the high win frequency decks (i.e. B and D) each have a single loss, so the loss aversion parameter in both the PVL-Delta and VPP models may directly underweight the rare, negative outcomes in these decks. Therefore, the PVL-Delta and VPP implicitly capture win frequency effects and underweighting of rare events through the Prospect Theory utility function, but their parameters do not dissociate the effects of loss aversion or valuation (i.e. the utility shape) from that of win frequency. Relatedly, the individual posterior distributions of the utility shape parameter are sometimes not well estimated (e.g., confined around a boundary value), which is problematic from a modeling perspective. This is a potentially important oversight given the centrality of win frequency to healthy participants’ IGT performance, which may differentiate healthy from clinical samples (see Steingroever, et al., 2013b). Moreover, a model that explicitly accounts for win frequency may offer insight into experience-based underweighting of rare events.

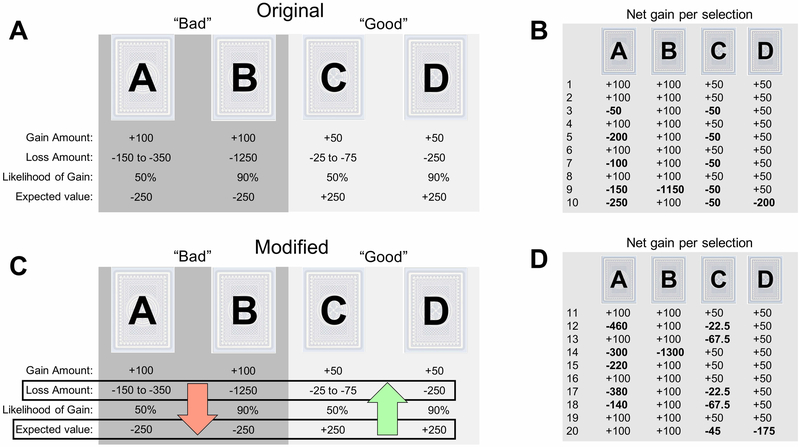
Figure 1: Structure of the original and modified versions of the IGT.

Notes. (a) The original version of the Iowa Gambling Task (IGT) maintains a stationary payoff distribution for all 100 trials. Decks A and B are both “bad” decks, each with an expected value of −250 points. In contrast, decks C and D are both “good” decks, each with an expected value of +250 points. Additionally, decks B and D both have a 90% chance of gaining points when chosen, whereas decks A and C have only a 50% chance. We present net outcomes here, but during the actual task, participants will see a gain and loss after each selection. Actual gains presented are +100 and +50 for the bad and good decks, respectively. Actual losses range in value depending on the deck. (b) Net gains (i.e. sum of actual gain and loss) for the first ten draws from each deck. (c) The modified version of the IGT is equivalent to the original version in all respects but one: the losses in the modified version become more and less severe in the bad and good decks, respectively, resulting in a drifting payoff distribution that makes the good decks easier to identify over time. The loss values change in a stepwise manner, where they are incremented after every ten draws from a given deck. (d) Net gains for the second set of ten draws (i.e. draws 11-20) from the modified IGT. Note that the first ten draws are identical to the original version, and that the bad decks have decreased in expected value while the good decks have increased.

1.3. Perseveration

A series of studies shows that IGT choice preferences can be explained well by heuristic models of choice perseveration—the tendency to continue selecting an option regardless of the choice value. In particular, Worthy et al. (2013a) showed that win-stay/lose-switch choice strategies exhibit good short-term prediction accuracy relative to typical reinforcement learning models, indicating that many decision makers may engage in simple stay/switch strategies that obfuscate inferences made on their learning processes. Furthermore, decay learning rules (Erev & Roth, 1998) provide better short-term prediction accuracy than typical updating rules (i.e. the delta rule), which may be because they can mimic choice perseveration heuristics by increasing the probability that recently selected decks are chosen again (Ahn et al., 2008). Finally, despite the IGT being designed to capture the exploration-exploitation trade-off (Bechara et al., 1994), recent studies show that healthy participants fail to show evidence of progressing from a state of exploration to exploitation across trials (Steingroever et al., 2013b). Instead, participants’ individual tendencies to perseverate on or frequently switch choices remain relatively stable over time. Therefore, a new IGT model should capture decision makers’ tendencies to stay versus switch decks. Otherwise, other model parameters of theoretical interest (e.g., learning rates, loss aversion, etc.) may become conflated with perseverative tendencies.

1.4. Reversal learning

Due to the structure of both the original (Bechara et al., 1994) and modified (Bechara et al., 2001) versions of the IGT (see section 2.2 for the details of the task structure), reversal learning plays a critical role in some people’s decision making process. For example, deck B appears optimal after its first 8 selections (+100 point rewards on each selection), but the expected value becomes negative after a large loss (−1,150 points) on the ninth selection. Because many decision makers begin the IGT with a pronounced preference for deck B, which rapidly declines over the first 20-30 trials (see, Steingroever et al., 2014), it is crucial that models can quickly reverse the preference for deck B after a large loss is encountered. In fact, participants who show performance deficits on the original version of the IGT become indistinguishable from healthy controls when the deck structure is altered to make the bad decks less appealing during the first few draws, and this increase in performance is strongly predictive of reversal learning abilities (Fellows & Farah, 2005).

Neither the PVL-Delta nor the VPP models were developed to account for reversal learning. However, the perseverance heuristic in the VPP can potentially mimic short-term effects of reversal learning by increasing the probability of selecting the same choice after a gain while increasing the probability of switching choices after a loss (see section 2.3; Worthy et al., 2013b). Both reversal learning and counter-factual (i.e. fictive) updating models can exhibit this behavior by updating the unchosen option utilities in reference to the chosen option outcome (e.g., Gläscher, Hampton, & O'Doherty, 2009; Lohrenz, McCabe, Camerer, & Montague, 2007). Unlike the VPP’s perseverance heuristic, counter-factual updating can speed the learning process itself, which can lead to more rapid, long-term preference reversals. Importantly, reversal learning/counter-factual reasoning is a well-replicated behavioral phenomenon (see Roese & Summerville, 2005) and has strong support in the model-based cognitive neuroscience literature in application to reinforcement learning tasks (i.e. experience-based tasks; Gläscher, Hampton, & O'Doherty, 2009; Hampton, Bossaerts, & O’Doherty, 2006).

1.5. The current study

In summary, current state-of-the-art computational models of the IGT do not (1) explicitly account for the various effects observed in behavioral data, or (2) provide a compromise between the multiple different model comparison metrics used for model selection (i.e. short- and long-term prediction accuracy and parameter recovery). Here, we present the Outcome-Representation Learning model (ORL), a novel reinforcement learning model which explicitly accounts for the effects of expected value, gain-loss frequency, choice perseveration, and reversal-learning with only 5 free parameters. By fitting 393 subjects’ IGT choice data, we show that the ORL model provides good short- and long-term prediction accuracy and parameter recovery in comparison to the PVL-Delta and VPP models. Furthermore, the ORL performs consistently well for both the original and modified version of the IGT and on data collected across multiple different research sites. Finally, we apply the ORL to IGT data collected from amphetamine, heroin, and cannabis users (Ahn et al., 2014; Fridberg et al., 2010), and we show that the ORL identifies theoretically meaningful differences in decision making between substance using groups which are supported by prior studies.

2. Methods

2.1. Participants

We used IGT data collected from multiple studies to validate the ORL model including: (1) an openly-accessible, “many labs” collaboration dataset containing IGT data from 247 healthy participants across 8 independent studies (Steingroever et al., 2015)¹; (2) data from Ahn et al. (2014) where 48 healthy controls, and 43 pure heroin and 38 pure amphetamine users in protracted abstinence completed a modified version of the IGT; and (3) data from Fridberg et al. (2010), where 17 chronic cannabis users completed the original version of the IGT². Table 1 summarizes the multiple datasets used in the current study. In total, our study includes data from 393 participants. See the cited studies for specific details on the participants included in each dataset.

Table 1.

Breakdown of datasets used in the current study

Dataset	N	Population	IGT Version	Study Citation
Kjome	19	Healthy	Modified	Kjome et al. (2010)
Premkumar	25	Healthy	Modified	Premkumar et al. (2008)
Wood	153	Healthy	Modified	Wood et al. (2005)
Worthy	35	Healthy	Original	Worthy et al. (2013b)
Ahn	48	Healthy	Modified	Ahn et al. (2014)
Ahn	38	Amphetamine	Modified	Ahn et al. (2014)
Ahn	43	Heroin	Modified	Ahn et al. (2014)
Fridberg	15	Healthy	Original	Fridberg et al. (2010)
Fridberg	17	Cannabis	Original	Fridberg et al. (2010)

2.2. Tasks

In both versions of the IGT, decks A and B are considered “bad” decks because they have a negative expected value, and decks C and D are “good” decks because they have a positive expected value (Fig. 1a and 1c). The order of cards within each deck (for both versions) is predetermined so that each subject will experience the same sequence of outcomes when drawing from a given deck (e.g., Fig. 1b and 1d). The original version of the IGT maintains a stationary payoff distribution throughout the task (Bechara et al., 1994), whereas the payoff distribution of the modified version changes over trials (Bechara et al., 2001)—the net losses in good and bad decks become less and more extreme, respectively, after every 10 selections made from a given deck (c.f. Fig. 1b to 1d).

2.3. Reinforcement learning models

Prospect Valence Learning model with delta rule (PVL-Delta).

The PVL-Delta model (Ahn et al., 2008) uses a prospect theory utility function (Kahneman & Tversky, 1979) to transform realized, objective monetary outcomes into subjective utilities:

$$u(t)=\{\begin{array}{cc}x{(t)}^{\alpha },\hfill & \text{if}x(t)\ge 0\hfill \\ -\lambda {\mid x(t)\mid }^{\alpha },\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (1)

Above, t denotes the trial number, u(t) is the subjective utility of the experienced outcome, x(t) is the experienced net outcome (i.e. the amount won minus amount lost on trial t), and α(0 < α < 2) and λ (0 < λ < 10) are free parameters which govern the shape of the utility function and sensitivity to losses relative to gains, respectively. The α parameter in the Prospect Theory utility function can account for the win frequency effect (e.g., Chiu et al., 2008). For example, when α < 1, the summed subjective utility of receiving $1 five times is greater than receiving $5 once (i.e. the utility curve is concave for positive outcomes and convex for negative ones), so decision makers with an α below 1 would be expected to prefer decks with high win frequency over objectively equivalent decks which win less often (Ahn et al., 2008). Likewise, if λ > 1, the subjective experience of a given loss is greater in magnitude than an equivalent gain, which captures the idea that “losses loom larger than equivalent gains” (Kahneman & Tversky, 1979) when being subjectively evaluated. Note that when making decisions from experience—as in the IGT—the modal participant does not typically show loss aversion (Erev, Ert & Yechiam, 008); instead, participants tend to underweight rare events (e.g., Barron & Erev, 2003; Hertwig, Barron, Weber, & Erev, 2004). Previous modeling analyses with the IGT have exhibited a similar pattern, where group-level loss aversion parameters are mostly below 1 (e.g., Ahn et al., 2014).

The PVL-Delta model assumes that decision makers update their expected values for each deck using a simplified variant of the Rescorla-Wagner rule (i.e. the delta rule; Rescorla & Wagner, 1972):

$$E_j(t+1)=E_j(t)+A\cdot (u(t)-E_j(t))$$ (2)

Here, E_j(t) is the expected value of chosen deck j on trial t, and A(0 < A < 1) is a learning rate controlling how quickly decision makers integrate recent outcomes into their expected value for a given deck. Expected values are entered into a softmax function to generate choice probabilities:

$$\mathit{Pr}[D(t+1)=j]=\frac{e^{\theta \cdot E_j(t+1)}}{\sum _{k=1}^4{e}^{\theta \cdot E_k(t+1)}}$$ (3)

where D(t) is the chosen deck on trail t, and θ is determined by:

$$\theta =3^c-1$$ (4)

Here, c(0 < c < 5) is a free parameter which represents trial-independent choice consistency (Yechiam & Ert, 2007). If c is close to 0 or 5, it indicates that decision makers are responding randomly or (near)deterministically, respectively, with respect to their expected values for each deck. Altogether, the PVL-Delta model contains 4 free parameters (A, α, c, λ).

Value-Plus-Perseverance model (VPP).

The VPP model expands upon the PVL-Delta model by adding an additional term for choice perseverance (Worthy et al., 2013b):

$$P_j(t+1)=\{\begin{array}{cc}K\cdot P_j(t)+{ϵ}_P,\hfill & \text{if}x(t)\ge 0\hfill \\ K\cdot P_j(t)+{ϵ}_N,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (5)

P_j(t) indicates the perseveration value for chosen deck j on trial t, which decays by K (0 < K < 1) on each trial. When chosen, the perseveration value for deck j is updated by ϵ_P(− ∞ < ϵ_p < ∞) or ϵ_N(−∞ < ϵ_N < ∞) based on the sign of outcome. Positive values for ϵ_P and ϵ_N indicate tendencies for decision makers to “perseverate” the deck chosen on the previous trial, whereas negative values indicate a switching tendency.

The VPP assumes that the expected value (from the PVL-Delta model) and perseveration terms are integrated into a single value signal:

$$V_j(t+1)=\omega \cdot E_j(t+1)+(1-\omega )\cdot P_j(t+1)$$ (6)

where ω (0 < ω < 1) is a parameter that controls the weight given to the expected value and perseveration signals. As ω approaches 0 or 1, the VPP reduces to the perseveration model or the PVL-Delta model alone, respectively. The VPP uses the same softmax function as the PVL-Delta to generate choice probabilities, except that E_j(t + 1) is replaced with V_j(t + 1). Altogether, the VPP contains 8 free parameters (A, α, c, λ, ϵ_P, ϵ_N, K, ω).

Outcome-Representation Learning model (ORL).

Here, we propose the ORL as a novel learning model for the IGT. Unlike the PVL-Delta and VPP models, the ORL assumes that the expected value and win frequency for each deck are tracked separately as opposed to implicitly within the Prospect Theory utility function (Pang, Blanco, Maddox, & Worthy, 2016).³ Note that separate tracking of expected value and win frequency makes the ORL similar to the class of risk-sensitive reinforcement learning models which forgo maximizing expected value to minimize potential risks (e.g., Mihatsch & Neuneier, 2002). The expected value of a deck is updated with separate learning rates for positive and negative outcomes:

$${\mathit{EV}}_j(t+1)=\{\begin{array}{cc}{\mathit{EV}}_j(t)+A_{\mathit{rew}}\cdot (x(t)-{\mathit{EV}}_j(t)),\hfill & \text{if}x(t)\ge 0\hfill \\ {\mathit{EV}}_j(t)+A_{\mathit{pun}}\cdot (x(t)-{\mathit{EV}}_j(t)),\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (7)

where EV_j(t) denotes the expected value of chosen deck j on trial t, and A_rew (0 < A_rew < 1) and A_pun (0 < A_pun < 1) are learning rates which are used to update expectations after reward (i.e. positive) and punishment (i.e. negative) outcomes, respectively. Unlike the PVL-Delta and VPP models, the ORL is updating expected values using the objective outcome x(t), not the subjective utility u(t).

The use of separate learning rates for positive versus negative outcomes allows for the ORL model to account for over- and under-sensitivity to losses and gains, similar to the loss aversion parameter shared by the PVL-Delta and VPP. Specifically, the larger the difference is between the positive and negative learning rates, the more learning is dominated by either positive or negative outcomes. We used separate learning rates, as opposed to a loss-aversion parameterization, because there is strong neurobiological and behavioral evidence for learning models with separate learning rates for positive versus negative outcomes (e.g., Doll, Jacobs, Sanfey, & Frank, 2009; Gershman, 2015). For example, Parkinson’s patients learn more quickly from negative compared to positive outcomes, and dopamine medication reverses this bias (Frank, Seeberger, & O’Reilly, 2004). Additionally, positive and negative learning rates are modulated by genes that are partially responsible for striatal dopamine functioning (Frank, Moustafa, Haughey, Curran, & Hutchison, 2007), and more recent evidence implicates striatal D1 and D2 receptor stimulation in learning from positive and negative outcomes, respectively (Cox et al., 2015).

To account for the win frequency effect, the ORL separately tracks win frequency as follows:

$${\mathit{EF}}_j(t+1)=\{\begin{array}{cc}{\mathit{EF}}_j(t)+A_{\mathit{rew}}\cdot (\mathit{sgn}(x(t))-{\mathit{EF}}_j(t)),\hfill & \text{if}x(t)\ge 0\hfill \\ {\mathit{EF}}_j(t)+A_{\mathit{pun}}\cdot (\mathit{sgn}(x(t))-{\mathit{EF}}_j(t)),\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (8)

where EF_j(t) denotes the “expected outcome frequency”, A_rew (0 < A_rew < 1) and A_pun (0 < A_pun < 1) are learning rates shared with the expected value learning rule, and sgn(x(t)) returns 1, 0, or −1 for positive, 0, or negative outcome values on trial t, respectively. The ORL model also includes a reversal-learning component for EF_j (t). EF_j′ (t) refers to the expected outcome frequency of all unchosen decks j′ on trial t:

$${\mathit{EF}}_{j^{\prime }}(t+1)=\{\begin{array}{cc}{\mathit{EF}}_{j^{\prime }}(t)+A_{\mathit{pun}}\cdot (\frac{-\mathrm{sgn}(x(t))}{C}-{\mathit{EF}}_{j^{\prime }}(t)),\hfill & \text{if}x(t)\ge 0\hfill \\ {\mathit{EF}}_{j^{\prime }}(t)+A_{\mathit{rew}}\cdot (\frac{-\mathrm{sgn}(x(t))}{C}-{\mathit{EF}}_{j^{\prime }}(t)),\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (9)

Here, the learning rates are shared from the expected value learning rule, and C is the number of possible alternative choices to chosen deck j. Note that when updating unchosen decks j′, the reward learning rate is used if the chosen outcome was negative and the punishment learning rate is used if the chosen outcome was positive. Because there are 4 possible choices in both versions of the IGT, there are always 3 possible alternative choices. Therefore, C is set to 3 in the current study. Note that if there were only a single alternative choice (e.g. simple two-choice tasks), C would be set to 1 and the frequency heuristic would reduce to a “double-updating” rule often used to model choice behavior in probabilistic reversal learning tasks (e.g., Gläscher, Hampton, & O'Doherty, 2009).⁴

The ORL model also employs a simple choice perseverance model to capture decision makers’ tendencies to stay or switch decks, irrespective to the outcome:

$${\mathit{PS}}_j(t+1)=\{\begin{array}{cc}\frac{1}{1+K},\hfill & \text{if}D(t)=j\hfill \\ \frac{{\mathit{PS}}_j(t)}{1+K},\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (10)

where K is determined by:

$$K=3^{K^{\prime }}-1$$ (11)

Here, PS_j (t) is the perseverance weight of deck j on trial t, and K is a decay parameter controlling how quickly decision makers forget their past deck choices. K′ is estimated ∈ [0,5], therefore K ∈ [0,242] (see equation 11). The above model implies that the perseverance weight of the chosen deck is set to 1 on each trial, and subsequently all perseverance weights decay exponentially before a choice is made on the next trial. We used this parameterization because it showed the best performance for estimating K compared to other parameterizations (e.g., PS_j (t + 1) = PS_j(t) × K). Low or high values for K suggest that decision makers remember long or short histories of their own deck selections, respectively.

The ORL model assumes that value, frequency, and perseverance signals are integrated in a linear fashion to generate a single value signal for each deck:

$$V_j(t+1)={\mathit{EV}}_j(t+1)+{\mathit{EF}}_j(t+1)\cdot {\beta }_F+{\mathit{PS}}_j(t+1)\cdot {\beta }_P$$ (12)

Here, β_F(− ∞ < β_F < ∞) and β_P (−∞ < β_P < ∞) are weights which reflect the effect of outcome frequency and perseverance on total value with respect to the expected value of each deck. Therefore, values for β_F less than or greater than 0 indicate that decision makers prefer decks with low or high win frequency, respectively. Additionally, values for β_P less than or greater than 0 indicate that decision makers prefer to switch or stay with recently chosen decks, respectively. Note that the expected value (EV) is a reference point which frequency and perseverance effects are evaluated against, so the ORL assumes that the “weight” of EV is equal to 1.

The ORL uses the same softmax function as the VPP to generate choice probabilities, except that the choice consistency/inverse temperature parameter (θ) is set to 1. We do not estimate choice consistency for the ORL due to parameter identifiability problems between θ, β_F, and β_P. Altogether, the ORL contains 5 free parameters (A_rew, A_pun, K, β_F, β_P).⁵

The ORL model will be added to hBayesDM, an easy-to-use R toolbox for computational modeling of a variety of different reinforcement learning and decision making models using hierarchical Bayesian analysis (Ahn, Haines, & Zhang, 2017). Additionally, all R codes used to preprocess, fit, simulate, and plot our results will be uploaded to our GitHub repository upon publication of this manuscript (https://github.com/CCS-Lab).

2.4. Hierarchical Bayesian analysis

We used hierarchical Bayesian analysis (HBA) to estimate free parameters for each model (Kruschke, 2015; M. D. Lee, 2011; M. D. Lee & Wagenmakers, 2011; Rouder & Lu, 2005; Shiffrin, Lee, Kim, & Wagenmakers, 2008). HBA offers many benefits over more conventional approaches (i.e. maximum likelihood estimation) including: (1) modeling of individual differences with shrinkage (i.e. pooling) across subjects, (2) computation of posterior distributions as opposed to point estimates. Previous studies show that HBA leads to more accurate individual-level parameter recovery than the individual MLE approach (e.g., Ahn, Krawitz, Kim, Busemeyer, & Brown, 2011).

HBA was conducted using Stan (version 2.15.1), a probabilistic programming language which uses Hamiltonian Monte Carlo (HMC), a variant of Markov Chain Monte Carlo (MCMC), to efficiently sample from high-dimensional probabilistic models as specified by the user (Carpenter, Gelman, Hoffman, & Lee, 2016). For each dataset used in the current study, we assumed that individual-level parameters were drawn from group-level distributions. Group-level distributions were assumed to be normally distributed, where the priors for locations (i.e. means) and scales (i.e. standard deviations) were assigned normal distributions. Additionally, we used non-centered parameterizations to minimize the dependence between group-level location and scale parameters (Betancourt & Girolami, 2013). Bounded parameters (e.g. learning rates ∈ (0,1)) were estimated in an unconstrained space and then probit-transformed to the constrained space–and scaled if necessary–to maximize MCMC efficiency within the parameter space (Ahn et al., 2014; 2017; Wetzels et al., 2010). Using the reward learning rate A_rew from the ORL model as an example, formal specification of the bounded parameters followed the form:

$$\begin{array}{cc}\hfill {\mu }_{A_{\mathit{rew}}}& \sim \text{Normal}(0,1)\hfill \\ \hfill {\sigma }_{A_{\mathit{rew}}}& \sim \text{Normal}(0,0.2)\hfill \\ \hfill {{\mathbf{A}}_{\mathbf{rew}}}^{\prime }& \sim \text{Normal}(0,1)\hfill \\ \hfill {\mathbf{A}}_{\mathbf{rew}}& =\text{Probit}({\mu }_{A_{\mathit{rew}}}+{\sigma }_{A_{\mathit{rew}}}\cdot {{\mathbf{A}}_{\mathbf{rew}}}^{\prime })\hfill \end{array}$$ (13)

where μ_Arew and σ_Arew are the location and scale parameters for the group-level distribution, A_rew′ is a vector of individual-level parameters on the unconstrained space, A_rew is a vector of individual-level parameters after they have been probit-transformed back to the constrained space, and probit(x) is the inverse cumulative distribution function of the standard normal distribution. This parameterization ensures that after being probit-transformed, the hyper-prior distribution over the subject-level parameters is (near)uniform between the parameter bounds. For parameters bounded ∈ (0, upper) (e.g. K), we used the same parameterization as above but scaled to the upper bound accordingly:

$$\mathbf{K}=\text{Probit}({\mu }_K+{\sigma }_K\cdot {\mathbf{K}}^{\prime })\cdot 5$$ (14)

For unbounded parameters (e.g., β_F), we used the same parameterization outline in equation 13 except we set the hyper-standard deviation to a half-Cacuhy(0, 1). All models were sampled for 4,000 iterations, with the first 1,500 as warmup (i.e. burn-in), across 4 sampling chains for a total of 10,000 posterior samples for each parameter. Convergence to target distributions was checked visually by observing trace-plots and numerically by computing Gelman-Rubin—also known as $\widehat{R}$—statistics for each parameter (Gelman & Rubin, 1992). $\widehat{R}$ values for all models were below 1.1, suggesting that the variance between chains did not outweigh variance within chains.

2.5. Model comparison: Leave-one-out information criterion

We used the leave-one-out information criterion (LOOIC) to compare one-step-ahead prediction accuracy across models. LOOIC is an approximation to full leave-one-out prediction accuracy that can be computed using the log pointwise posterior predictive density (lpd) of observed data (Vehtari, Gelman, & Gabry, 2017). Here, we computed the lpd by taking the log likelihood of each subject’s actual choice on trial t + 1 conditional on their parameter estimates and choices from trials ∈{1,2, … , t}. This procedure is iterated for all trials and for each posterior sample. Log likelihoods are then summed across trials within subjects. This summation results in an N × S lpd matrix, where N is the number of subjects and S is the number of posterior samples. We used the loo R package (Vehtari et al., 2017) to estimate the LOOIC from the lpd matrix. LOOIC is on the deviance scale, where lower values indicate better model fits.

2.6. Model comparison: Choice simulation

We used the simulation method to compare long-term prediction accuracy across models (Ahn et al., 2008; Steingroever et al., 2014). The simulation method involves two steps: (1) models are fit to each group’s data, and (2) fitted model parameters from step 1 are used to simulate subjects’ choice behavior given the task payoff structure. Simulated and true choice patterns are then compared to determine how well the model parameters capture subjects’ choice behavior. In the current study, we employ a fully Bayesian simulation method, which takes random draws from each subject’s joint posterior distribution across fitted model parameters to simulate choice data (Steingroever et al., 2014; Steingroever, Wetzels, & Wagenmakers, 2013a). We iterated this procedure 1,000 times for each subject (i.e. 1,000 draws from individual-level, joint posteriors), and choice probabilities for each deck were stored for each iteration. We then averaged the choice probabilities for each deck across iterations and then subjects. Finally, we computed the mean squared deviation (MSD) between the experimental and simulated choice probabilities as follows:

$$\text{MSD}=\frac{1}{4.n}\sum _{t=1}^n\sum _{j=1}^4{({\stackrel{‒}{D}}_{{\mathit{exp}}_j}(t)-{\stackrel{‒}{D}}_{{\mathit{sim}}_j}(t))}^2,$$ (15)

where n is the number of trials, t is the trial number, j is the deck number, ${\overline{D}}_{\mathit{exp}}(t)$ is the average across-subject probability of choosing deck j on trial t, and ${\overline{D}}_{\mathit{sim}}(t)$ is the average across-subject simulated probability (across 1,000 iterations as described above) of selecting deck j on trial t. Before computing MSD scores, we smoothed the experimental data (i.e. ${\overline{D}}_{\mathit{exp}}(t)$) with a moving average of window size 7 (Ahn et al., 2008). Additionally, this method is different from a posterior predictive check because it does not condition on observed response data (Gelman, Hwang, & Vehtari, 2013).

2.7. Model comparison: Parameter recovery

Parameter recovery is a method used to determine how well a model can estimate (i.e. recover) known parameter values, and it typically follows two steps: (1) choice data are simulated using a set of true parameters for a given model and task structure, and (2) the model is fit to the simulated choice data and the recovered parameter estimates are compared to the true parameters (e.g., Ahn et al., 2011; Donkin, Brown, Heathcote, & Wagenmakers, 2011; Wagenmakers, van der Maas, & Grasman, 2007). We used the same set of parameters to simulate choices from the modified and original IGT task structure. We generated the parameter set by taking the means of the individual-level posterior distributions of each model fit to the 48 control subjects’ data from Ahn et al. (2014) to ensure that the true parameter values were reasonably distributed and representative of human decision makers for each model.

We used two different parameter recovery methods. First, we compared the means of the posterior distributions for each individual-level parameter, and for each model, to the true parameters by plotting all the parameter values in a standardized space. We transformed parameters by z-scoring the recovered posterior means of each parameter by the mean and standard deviation of true parameters (i.e. the parameter set used to simulate choices) across individual-level parameters, which allowed us to determine how well the location of true parameters was recovered for each parameter and model. Second, we compared each of the true parameters to the entire posterior distribution of the respective recovered parameter by computing rank-ordered (i.e. Spearman’s) correlations between the true and recovered parameter values across individual-level parameters. We iterated this procedure over each sample from the joint posterior distribution to estimate how well the rank-order between true parameters could be recovered for each parameter and model. The rank-order is particularly important for making inferences on relative parameter differences between subjects. Together, the parameter recovery methods we used here allowed us to infer how well each model could recover parameters in an absolute and relative sense.

3. Results

3.1. Model comparison: Leave-one-out information criterion

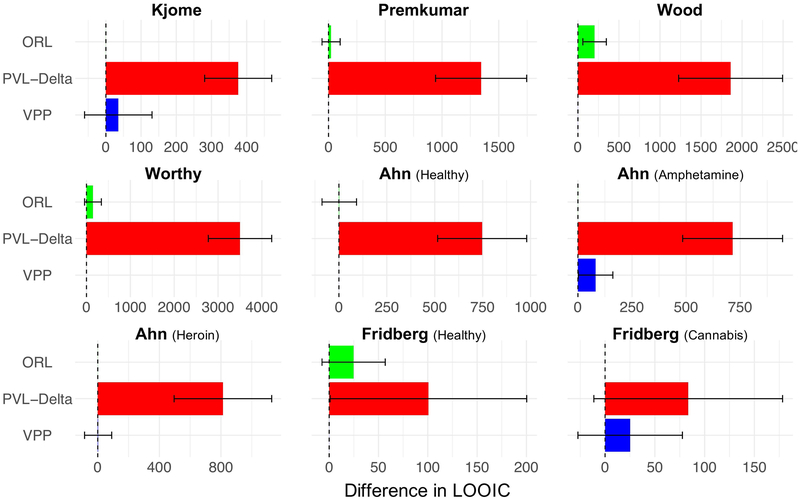
Fig. 2 shows the one-step-ahead leave-one-out information criterion (LOOIC) performance for each model and datasets used in the current study. As seen in the graphs, while the ORL and VPP outperform the PVL-Delta, they show similar performance to one another. Notably, the ORL outperformed the VPP in all three substance using groups, albeit by only a negligible amount in heroin users. Altogether, the LOOIC comparisons suggest that the ORL shows similar short-term prediction performance to the VPP (i.e. better than the PVL-Delta) across both versions of the IGT and across multiple populations with different decision making strategies despite the fact that the ORL has three fewer parameters than the VPP (5 vs. 8).

Figure 2: Post-hoc model fits across models and datasets.

Note. Results of the leave-one-out information criterion (LOOIC) model comparison on one-step-ahead (i.e. short-term) prediction accuracy for each of the datasets analyzed in the current study. Lower LOOIC values indicate better model performance. LOOIC values were baselined by the best model in each comparison. The dashed line represents the zero point (i.e. best model LOOIC = 0), and any deviations from the zero point represent competing model LOOIC values. Error bars represent 2 standard errors on the difference between the best model and the respective competing model.

3.2. Model comparison: Choice simulation

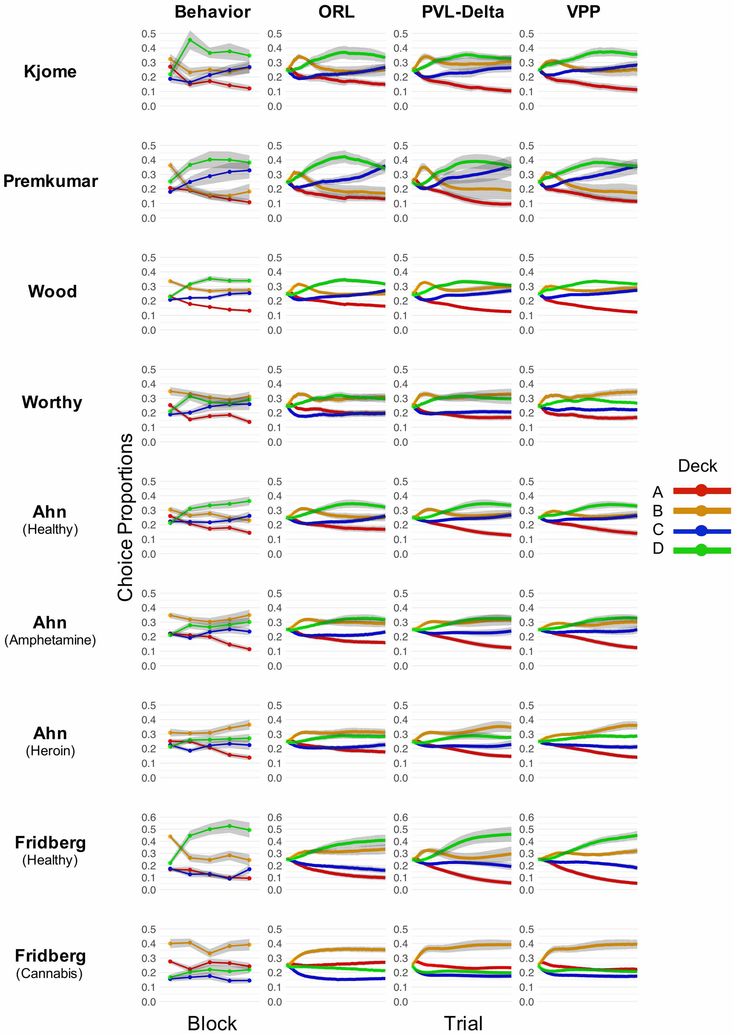
The raw choice data and choice simulations for each dataset are depicted in Fig. 3, and the mean squared deviations (MSDs) are shown in Table 2. Similarly to previous analyses (Ahn et al., 2014; Steingroever et al., 2013a), the PVL-Delta showed good simulation performance for both modified and original IGT versions in both healthy control and substance using groups. Unlike previous analyses (Ahn et al., 2014; but see Worthy et al., 2013b), the VPP showed similar performance to the PVL-Delta across datasets.⁶ Altogether, the simulation results are less clear on which of the models performs best for long-term prediction accuracy. In fact, the variation in performance between datasets is much greater than the variation in performance between models within each dataset (see Table 2).

Figure 3: True versus simulated choice proportions across time.

Note. Behavioral and simulation performance for the healthy control data for each of the datasets in the current study. Choice behavior is summarized per block, where blocks were constructed by calculating the proportion of choices made from each deck, across subjects, in 20-trial increments (i.e. block 1 = trials 1-20, block 2 = trials 21-40, etc.). Choice proportions across subjects are represented by points, and grey ribbons indicate 1 standard error. In general, subjects begin with a preference for deck B, but learn to prefer deck D as they progress through the task. Additionally, subjects show a clear preference for decks with high win frequency (B and D) over alternatives. Simulation performance is summarized per trial, across subjects within each dataset. The grey ribbons represent 1 standard error across subjects’ averaged simulated choice probabilities.

Table 2.

Mean squared deviations of true from simulated choice probabilities

	Dataset
Model	1	2	3	4	5	6	7	8	9
ORL	41.6	20.3	6.9	23.4	7.4	15.4	9.7	81.5	25.1
PVL-Delta	44.9	20.6	4.4	17.3	8.5	12.9	7.7	72.8	18.8
VPP	44.7	20.9	6.0	16.9	8.8	15.0	9.0	85.5	20.6

Note. 1 = Kjome; 2 = Premkumar; 3 = Wood; 4 = Worthy; 5 = Ahn (Healthy); 6 = Ahn (Amphetamine); 7 = Ahn (Heroin); 8 = Fridberg (Healthy); 9 = Fridberg (Cannabis). The lowest mean squared deviation (MSD) is bolded within each dataset.

3.3. Model comparison: Parameter recovery

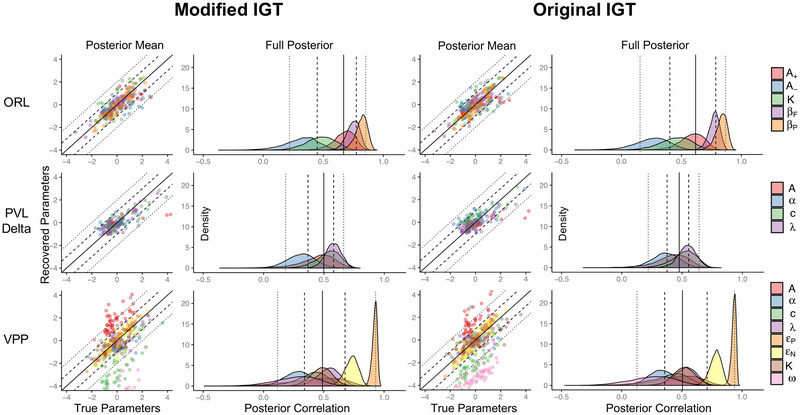
Parameter recovery results for both versions of the IGT are shown in Fig. 4. For the modified IGT, the PVL-Delta and ORL both show good parameter recovery across model parameters while the VPP performs poorly. For the VPP, the recovered posterior means were systematically higher than the true parameters for the learning rate (A), and systematically lower for the choice consistency (c) and reinforcement weight (ω). For the PVL-Delta and ORL, recovered posterior means were well-distributed around the true parameter means. Additionally, the full posterior recovery results for the VPP showed much more variable correlations between true parameters and the recovered posteriors compared to the PVL-Delta and ORL, suggesting that the PVL-Delta and ORL provide more precise posterior estimates and better capture the variance between individual-level parameter estimates (i.e. “subjects”) compared to the VPP. For the original IGT, parameter recovery results were similar. While the VPP showed slightly better performance in the original IGT, still the posterior means for ω and c were systematically lower and posterior means for A were systematically higher than their true values. Together, the parameter recovery results suggest that both the PVL-Delta and ORL provide more accurate and precise parameter estimates than the VPP for both versions of the IGT.

Figure 4: Parameter recovery results across models and versions of the IGT.

Note. Parameter recovery results for the modified and original IGT tasks. Each task structure was simulated for each model using the same set of 48 individual-level parameter sets across modified and original task structures. Posterior mean results show comparisons of the true parameters with the means of the posterior distributions of the recovered parameters after being standardized. We standardized parameters by z-scoring the true and recovered posterior means by the mean and standard deviation of each of the 48 true parameter sets. This method allowed us to visualize the bias in recovered posterior means, where any values falling above or below the solid diagonal line indicate higher or lower recovered means in reference to the true parameters, respectively. Dashed and dotted lines reflect 1 and 2 standard deviations in the standardized space, respectively. Note that some parameter values fell outside of the graphs (particularly for the VPP), but zooming out further obfuscates the results. Full posterior recovery results were generated by computing a Spearman’s rank-order correlation between each set of individual-level true parameters and the respective set of individual-level recovered parameters for each sample in the recovered posterior distribution. Full posterior recovery results therefore represent the uncertainty in recovering the relative positions of the true parameters across all individual-level parameters (i.e. across all “subjects”). Distributions with mass closer to 1 indicate that the order between true parameters is recovered well for a given parameter and model. Dotted lines represent 2.5% and 97.5% quantiles, dashed lines represent 25% and 75% quantiles, and the solid line represents the median. Quantiles were calculated across all parameters.

3.4. Applications to substance users

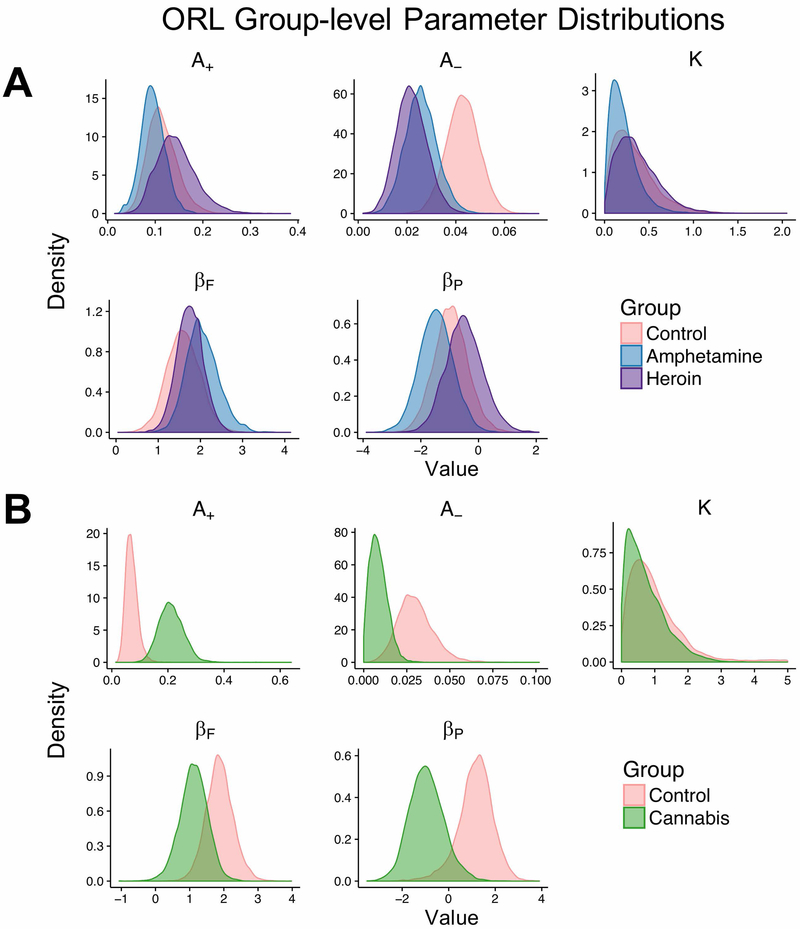
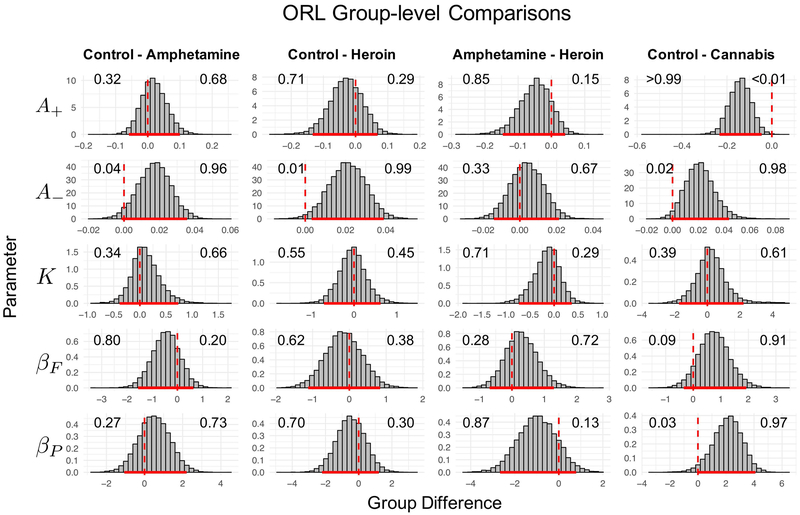
Because the ORL consistently performed as well or better than competing models across all groups in the current study, we used the ORL to examine group differences in model parameters. Note that we only compared substance using groups to the healthy control groups within the same studies to minimize any potential between-study effects. Fig. 5 and Fig. 6 show the posterior estimates and differences in posterior estimates for each group, respectively. Below, we use the term “strong evidence” to refer to group differences where the 95% highest density interval (HDI) excludes 0 (Kruschke, 2015). We do not endorse binary interpretations of significant differences using this threshold, and we refer readers to the graphical comparisons (Fig. 6) to judge parameters for meaningful differences. Within the dataset from Ahn et al. (2014), the heroin using group showed strong evidence of lower punishment learning rates than healthy controls (95% HDI = [0.003, 0.04]). A low punishment learning rate indicates less updating of expectations after experiencing a loss, a finding which is consistent with prior studies showing that heroin users have lower loss-aversion than controls (Ahn et al., 2014). We did not find strong evidence of differences between amphetamine and heroin users. However, there was some evidence (see Fig. 6) that amphetamine users had more negative perseverance weights than heroin users (95% HDI = [−2.67, 0.79]). Within the dataset from Fridberg et al. (2010), chronic cannabis users showed strong evidence of greater reward learning rates (95% HDI = [−0.23, −0.05]) and some evidence of lower punishment learning rates (95% HDI = [−0.001, 0.04]) compared to healthy controls, which is consistent with a previous analysis of this dataset using the PVL-Delta model showing that cannabis users were more sensitive to rewards and less sensitive to losses compared to healthy controls (Fridberg et al., 2010). Lastly, cannabis users showed strong evidence for more negative perseverance weights than healthy controls (95% HDI = [0.004, 4.09]), indicating a strong preference toward switching, as opposed to perseverating on, choices irrespective to the expected value of each deck.

Figure 5: Group-level ORL parameters across healthy and substance using groups.

Notes. (a) Group-level parameter distributions for the healthy controls, amphetamine users, and heroin users who underwent the modified IGT. (b) Group-level parameter distributions for the healthy controls and chronic cannabis users who underwent the original IGT.

Figure 6: Differences in group-level ORL parameters between healthy and substance using groups.

Note. Differences in group-level parameter distributions (for the ORL) between healthy controls and substance using groups. Solid red lines highlight the 95% highest posterior density interval (HDI), and dashed red lines reflect the 0 point. Values on the left and right sides of each graph represent the proportion of each distribution falling below and above the 0 point, respectively. Note that groups were compared within studies to minimize any confounding effects of task implementation, study design, and other site-specific experimental details.

4. Discussion

We present a novel cognitive model (the ORL) for the IGT which shows excellent short- and long-term prediction accuracy across both versions of the task and across an array of different clinical populations. The ORL explicitly models the four most consistent trends found in IGT behavioral data including long-term expected value, gain-loss frequency, perseverance, and reversal-learning. Overall, we showed that the ORL outperformed or showed comparable performance to competing models in all three model comparison indices including: post-hoc test (LOOIC), simulation performance, and parameter recovery. The results suggest that future research using the IGT should consider the ORL a top choice for cognitive modeling analyses.

Consistent with prior studies, our model comparison results suggest that any single measure used to compare models might not be sufficient (Ahn et al., 2008; 2014; Steingroever et al., 2014; Yechiam & Ert, 2007). For example, we found that the ORL consistently outperformed the VPP using parameter recovery metrics yet performed similarly to the VPP in short- and long-term prediction accuracy. Our results underscore the importance of using many model comparison metrics in deciding between competing cognitive models (Heathcote, Brown, & Wagenmakers, 2015; Palminteri, Wyart, & Koechlin, 2017). Many studies use only information criteria such as LOOIC (e.g. Akaike or Bayesian information criteria) when choosing one among many cognitive models, and our results suggest that this may lead to imprecise inferences. Indeed, despite the VPP performing excellently when assessed using information criteria alone (i.e. LOOIC), the parameter recovery results indicate that multiple VPP model parameters might be imprecise at the subject-level and biased at the group-level (see Fig. 4). For cognitive models to be useful in identifying individual differences (e.g., for clinical decision making), it is crucial that future studies conduct parameter recovery tests to ensure that parameter interpretations are valid.

When applied to IGT performance of pure substance users, the ORL revealed that heroin users in protracted abstinence were less sensitive to punishments (i.e. lower punishment learning rates) compared to healthy controls. The finding of lower punishment sensitivity in the heroin-using group is consistent with Ahn et al. (2014), where heroin users showed lower loss aversion (i.e. λ from the VPP) than healthy controls. We also found some evidence that amphetamine users engaged in more switching behavior than heroin users (see β_P in Fig.’s 5 and 6). Although weak in comparison to other reported differences, this finding is consistent with a previous study showing that high levels of experience seeking traits are positively and negatively predictive of amphetamine and heroin users, respectively (Ahn & Vassileva, 2016). Notably, behavioral summaries of the amphetamine and heroin user’s choice preferences were indistinguishable (see Ahn et al., 2014). Additionally, the ORL revealed that chronic cannabis users were more sensitive to rewards (i.e. higher reward learning rates) and more likely to engage in exploratory behavior (i.e. more negative perseveration weight) than healthy controls. These findings converge with previous modeling results using the PVL-Delta (Fridberg et al., 2010) and with pharmacological studies showing that cannabis administration can increase sensitivity to rewards (and not punishments) which in turn may lead to more risk-taking behaviors (Lane, 2002; Lane, Cherek, Tcheremissine, Lieving, & Pietras, 2005). Importantly, our finding that chronic cannabis users tend to engage in exploratory behavior—irrespective to the value of each deck—suggests that the high levels of risk-taking induced by acute cannabis consumption may have long-lasting effects that influence not only sensitivity to rewards, but also the tendency to seek out novel stimuli. Future studies may further clarify the temporal relationship between reward sensitivity and sensation seeking in cannabis users by applying the ORL to cross-sectional or longitudinal samples. Finally, research by our own and other groups consistently reveals that computational model parameters are more sensitive to dissociating substance-specific and disorder-specific neurocognitive profiles than standard neurobehavioral performance indices (see Ahn et al., 2016 for a review). Such parameters show significant potential as novel computational markers for addiction and other forms of psychopathology, which could help refine neurocognitive phenotypes and develop more rigorous mechanistic models of psychiatric disorders (Ahn & Busemeyer, 2016).

Our results have implications for a wide range of cognitive tasks that involve learning from experience. In particular, our finding that differential learning rates for positive and negative outcomes can capture the same behavioral patterns that have previously been attributed to a loss aversion parameter (cf. controls versus heroin users in Fig. 5 to findings published in Ahn et al. [2014]) suggests that the underweighting of rare events that is observed in experience-based tasks may arise from learning, rather than valuation mechanisms (e.g., Barron & Erev, 2003; Hertwig, Barron, Weber, & Erev, 2004). While the ORL limits this underweighting to tasks including outcomes in both gain and loss domains, future studies may extend the model to capture decisions in purely gain or loss domains by modifying the function that codes outcomes as gains versus losses (see equations 7–9). One potential solution could be to code outcomes as gains versus losses based on the sign of the prediction error rather than the objective outcome; in fact, cognitive models utilizing separate learning rates for positive versus negative prediction errors are gaining popularity in the decision sciences due to their theoretical and empirical support (e.g., Gershman, 2015).