Modeling Mechano-driven and Immuno-mediated Aortic Maladaptation in Hypertension

Abstract

Uncontrolled hypertension is a primary risk factor for diverse cardiovascular diseases and thus remains responsible for significant morbidity and mortality. Hypertension leads to marked changes in the composition, structure, properties, and function of central arteries, hence there has long been interest in quantifying the associated wall mechanics. Indeed, over the past twenty years there has been increasing interest in formulating mathematical models of the evolving geometry and biomechanical behavior of central arteries that occur during hypertension. In this paper, we introduce a new mathematical model of growth (changes in mass) and remodeling (changes in microstructure) of the aortic wall for an animal model of induced hypertension that exhibits both mechano-driven and immunomediated matrix turnover. In particular, we present a bilayered model of the aortic wall to account for differences in medial versus adventitial growth and remodeling and we include mechanical stress and inflammatory cell density as determinants of matrix turnover. Using this approach, we can capture results from a recent report of adventitial fibrosis that resulted in marked aortic maladaptation in hypertension. We submit that this model can also be used to identify novel hypotheses to guide future experimentation.

1 Introduction

Cells of the normal aortic wall – namely, endothelial cells of the intima, smooth muscle cells of the media, and fibroblasts of the adventitia – are exquisitely sensitive to alterations in their mechanical environment (Davies 2009; Haga et al 2007; Chiquet et al 2003). Modest alterations in mechanical loading typically elicit changes in gene expression that tend to return the biomechanical state towards normal via a process referred to as mechanical homeostasis (Humphrey 2008b). It is well known, for example, that the aortic wall thickens in response to sustained elevations in blood pressure due to smooth muscle hyperplasia/hypertrophy and extracellular matrix deposition, which together tend to restore the mean circumferential wall stress towards its normal value. Many studies have sought to quantify the mechanical state of the aorta in terms of transmural distributions of wall stress prior to hypertension as well as at different times during its development (see, Humphrey 2002; Hayashi and Naiki 2009). Additionally, over the past 20 years many other studies have sought to formulate mathematical models that enable one to capture the time-course of the growth (change in mass) and remodeling (change in microstructure) processes that underlie aortic changes in hypertension (e.g., Rachev et al 1996; Taber and Eggers 1996; Gleason and Humphrey 2004; Tsamis et al 2009; Rachev and Gleason 2011).

Mathematical models of vascular growth and remodeling (G&R) have advanced significantly since the first papers of the mid-1990s. These advances have been driven by increasingly sophisticated theoretical concepts and detailed experimental findings. Regarding the latter, recent data reveal a dramatic influence of inflammation-mediated adventitial fibrosis in multiple murine models of induced hypertension (Wu et al 2014, 2016), which has been shown to be maladaptive from a mechanobiological perspective (Bersi et al 2016). In particular, mechano-adaptation of an artery can often be defined in terms of changes in luminal radius a and wall thickness h that restore toward normal both the mean flow-induced wall shear stress (τ_w = 4μQ/(πa³), where Q is the blood flowrate and μ is the blood viscosity) and the mean pressure-induced circumferential wall stress (σ_θθ = Pa/h, where P is transmural blood pressure). The associated morphological consequences are, a → ε^1/3a_o and h → γε^1/3h_o, where ε is the fold-change in blood flow and γ is the fold-change in blood pressure, with a subscript o denoting an original homeostatic value (Humphrey 2008a). Assuming preserved cardiac output (ε ≃ 1), findings in Bersi et al (2016) reveal that γ≃ 1.36 over two-to-four weeks of angiotensin-II induced hypertension in normal adult male mice C57BL/6J, but h/h_o > 2.5 in the descending thoracic aorta over this same period. That is, thickening was grossly excessive relative to the mechanical stimulus. Moreover, most of the maladaptive thickening of the wall occurred in the adventitia where there was excessive accumulation of fibrillar collagens and evidence of infiltrating inflammatory (CD45+) cells.

In this paper, we present a new bilayered model of G&R of the descending thoracic aorta for adult, male wild-type mice subjected to sustained angiotensin-II induced hypertension, with systolic pressures reaching 167 – 172mmHg over two-to-four weeks of exposure. This G&R model employs a constrained mixture approach (Humphrey and Rajagopal 2002), with a new approach to address roles of inflammation in matrix turnover. Not only does the proposed model capture the experimental findings, it allows one to generate hypotheses that can guide future experiments.

2 Methods

2.1 Wall Mechanics

Arterial mechanics can typically be described quasistatically (Humphrey and Na 2002). Moreover, due to the existence of residual stress, one can often represent well the wall stress in terms of mean values, even for a bilayered wall (Bellini et al 2014). Hence, consider mean, layer-specific (M-media, A-adventitia) equilibrium equations, in terms of Cauchy stress (θ-circumferential, z-axial), that must hold at any G&R time:

$${\sigma }_{M\theta \theta }{h}_M+{\sigma }_{A\theta \theta }{h}_A=Pa,$$ (1)

$${\sigma }_{\mathit{Mzz}}{h}_M(2a+h_M)+{\sigma }_{\mathit{Azz}}{h}_A(2a+2h_M+h_A)=f_z,$$ (2)

where P is the distending pressure and f_z is the axial force. Moreover, a is the luminal radius whereas h_M and h_A are medial and adventitial thicknesses. To these equations we add constitutive equations for stress. Noting that the arterial wall contains multiple structurally-significant constituents (α = 1, 2, …,N), we use a constrained mixture approach for each layer (Bellini et al 2014; Latorre and Humphrey 2018) and let

$${\mathit{\sigma }}_{\mathit{\Gamma }}(s)=\sum _{\alpha =1}^N{\mathit{\sigma }}_{\mathit{\Gamma }}^{\alpha }(s)=p_{\mathit{\Gamma }}(s)\mathbf{I},\mathit{\Gamma }=M,A$$ (3)

wherein we have assumed that both layers (Γ = M,A) are (transiently) incompressible, which is enforced via layer-specific Lagrange multipliers p_Γ. Importantly, the values of stress can evolve due to G&R processes.

2.2 Constrained Mixture framework

Prior studies have demonstrated that many types of arterial G&R can be captured well with a constrained mixture model (Baek et al 2007; Valentín and Humphrey 2009; Wilson et al 2012). It can be shown that, for any G&R time s, the layer-specific extra part of the Cauchy stresses can be computed via

$${\mathit{\sigma }}_{\mathit{\Gamma }}^{\alpha }(s)=\frac{1}{\rho }{\int }_{-\infty }^s{m}_{\mathit{\Gamma }}^{\alpha }(\tau )q_{\mathit{\Gamma }}^{\alpha }(s,\tau ){\widehat{\mathit{\sigma }}}_{\mathit{\Gamma }}^{\alpha }(s,\tau )d\tau$$ (4)

where (Latorre and Humphrey 2018)

$${\widehat{\mathit{\sigma }}}_{\mathit{\Gamma }}^{\alpha }(s,\tau )=\frac{1}{J_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)}{\mathbf{F}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s){\widehat{\mathbf{S}}}_{\mathit{\Gamma }}^{\alpha }(s,\tau ){\mathbf{F}}_{\mathit{\Gamma }n(\tau )}^{\alpha T}(s)$$ (5)

with n (τ) denoting potentially evolving constituent-specific natural (stress-free) configurations, $J_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)=det{\mathbf{F}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)$, and

$${\widehat{\mathbf{S}}}_{\mathit{\Gamma }}^{\alpha }(s,\tau )\equiv {\widehat{\mathbf{S}}}_{\mathit{\Gamma }}^{\alpha }({\mathbf{C}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s))=2\frac{\partial {\widehat{W}}^{\alpha }({\mathbf{C}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s))}{\partial {\mathbf{C}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)}.$$ (6)

Note the three primary layer-specific (Γ = M,A) and constituent-specific (α = 1, 2, …,N) constitutive functions in this constrained mixture formulation: the stored energy function ${\widehat{W}}^{\alpha }({\mathbf{C}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s))$, which depends on layer-and constituent-specific deformations ${\mathbf{C}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)$, the rate of production of mass per unit current volume $m_{\mathit{\Gamma }}^{\alpha }(\tau )>0$, and the survival function $q_{\mathit{\Gamma }}^{\alpha }(s,\tau )\in [0,1]$, which quantifies the part of constituent α that was produced at time τ and survives to time s. Finally, ${\mathbf{C}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)={\mathbf{F}}_{\mathit{\Gamma }n(\tau )}^{\alpha T}(s){\mathbf{F}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)$ where ${\mathbf{F}}_{\mathit{\Gamma }n(\tau )}^{\alpha }(s)={\mathbf{F}}_{\mathit{\Gamma }}(s){\mathbf{F}}_{\mathit{\Gamma }}^{-1}(\tau ){\mathbf{G}}_{\mathit{\Gamma }}^{\alpha }$, with F_Γ (s) and F_Γ (τ) capturing mixture-level deformations relative to a common reference configuration and ${\mathbf{G}}_{\mathit{\Gamma }}^{\alpha }$ denoting the “deposition stretch” at which the constituent is incorporated within extant tissue.

Following prior studies, we let the stored energy function for elastin have a neoHookean form (Latorre and Humphrey 2018)

$${\widehat{W}}^e({\mathbf{C}}_{\mathit{\Gamma }}^e(s))=\frac{c^e}{2}({\mathbf{C}}_{\mathit{\Gamma }}^e(s):\mathbf{I}-3)$$ (7)

with ${\mathbf{C}}_{\mathit{\Gamma }}^e(s)\equiv {\mathbf{C}}_{\mathit{\Gamma }n(0)}^e(s)$, while that for collagen and smooth muscle has a Fung-type exponential form (Latorre and Humphrey 2018)

$${\widehat{W}}^{\alpha }({\lambda }_{n(\tau )}^{\alpha }(s))=\frac{c_1^{\alpha }}{4c_2^{\alpha }}\left[e^{c_2^{\alpha }{({\lambda }_{n(\tau )}^{\alpha 2}(s)-1)}^2}-1\right],$$ (8)

with ${\lambda }_{n(\tau )}^{\alpha }(s)$, α = m, c, the corresponding stretch. Importantly, motivated by the aforementioned studies on induced hypertension in the mouse (Wu et al 2014; Bersi et al 2016), we let the rate of production of mass per unit reference volume $m_{\mathit{\Gamma }R}^{\alpha }=(det{\mathbf{F}}_{\mathit{\Gamma }})m_{\mathit{\Gamma }}^{\alpha }$ be

$$m_{\mathit{\Gamma }R}^{\alpha }(\tau )=k_{\mathit{\Gamma }}^{\alpha }(\tau ){\rho }_{\mathit{\Gamma }R}^{\alpha }(\tau ){\mathit{\Upsilon }}_{\mathit{\Gamma }}^{\alpha }(\tau )$$ (9)

and, consistent with a first-order kinetic decay,

$$q_{\mathit{\Gamma }}^{\alpha }(s,\tau )=exp\left(-{\int }_{\tau }^s{k}_{\mathit{\Gamma }}^{\alpha }(t)dt\right),$$ (10)

where $k_{\mathit{\Gamma }}^{\alpha }$ is a rate parameter quantifying constituent removal, ${\rho }_{\mathit{\Gamma }R}^{\alpha }$ is a referential (apparent) mass density, and ${\mathit{\Upsilon }}_{\mathit{\Gamma }}^{\alpha }$ is a mechano- and immuno-biological stimulus function. In particular ${\mathit{\Upsilon }}_{\mathit{\Gamma }}^{\alpha }=1$ recovers a balanced turnover, with production offset precisely by removal (Latorre and Humphrey 2018; Valentín et al 2009). Following consideration of multiple possible constitutive assumptions, we let

$$k_{\mathit{\Gamma }}^{\alpha }(t)=k_{\mathit{\Gamma }o}^{\alpha }\left(1+{(\mathit{\Delta }\sigma (t))}^2\right)$$ (11)

and

$${\mathit{\Upsilon }}_{\mathit{\Gamma }}^{\alpha }(\tau )=1+K_{\mathit{\Gamma }\sigma }^{\alpha }\mathit{\Delta }\sigma (\tau )-K_{\mathit{\Gamma }\tau }^{\alpha }\mathit{\Delta }{\tau }_w(\tau )+K_{\mathit{\Gamma }\phi }^{\alpha }\mathit{\Delta }{\varrho }_{\phi }(\tau )$$ (12)

where

$$\mathit{\Delta }\sigma =\frac{{\sigma }_{\theta \theta }+{\sigma }_{zz}}{{\sigma }_{\theta \theta o}+{\sigma }_{\mathit{zzo}}}-1,\mathit{\Delta }{\tau }_w=\frac{{\tau }_w}{{\tau }_{wo}}-1,$$ (13)

and subscript o denotes original homeostatic. Importantly, Δϱ_φ = ϱ_φ/(ϱ_φ)_max represents an inflammatory cell fraction (from 0 to 1) relative to its maximum possible density; it can be prescribed based on experimental findings (e.g., CD45+ staining) or determined via a constitutive relation. Finally, $k_{\mathit{\Gamma }o}^{\alpha }$ is an original (homeostatic) rate parameter while $K_{\mathit{\Gamma }\sigma }^{\alpha },K_{\mathit{\Gamma }\tau }^{\alpha }$, and $K_{\mathit{\Gamma }\phi }^{\alpha }$ are non-dimensional gain-type parameters that modulate changes in cell/matrix production rate as a function of differences in normal wall stress and wall shear stress from homeostatic targets as well as a normalized activated inflammatory cell density, respectively. Clearly, increases in wall stress above normal can both increase matrix production (often in a new state) and increase removal (typically of prior overstressed constituents) while increases in flow/wall shear stress slow collagen production (e.g., nitric oxide is increased in cases of increased flow and it slows collagen production by smooth muscle cells and fibroblasts). Increased inflammatory cells not only can stimulate matrix production (e.g., via interleukin-17a production by T-cells), they can also drive matrix removal. Notwithstanding the associated complex, coupled mechanisms, we currently drive increased removal based on Δσ ≠ 0 since wall stress also drives inflammation (Bersi et al 2017).

Whereas remodeling results largely from replacement of prior overstressed constituents with new ones having preferred deposition stretches, growth (in this case largely wall thickening) results primarily from mass production exceeding removal. Hence, consistent with Eq. (4), layer- and constituent-specific referential mass densities evolve as follows (Latorre and Humphrey 2018)

$${\rho }_{\mathit{\Gamma }R}^{\alpha }(s)={\int }_{-\infty }^s{m}_{\mathit{\Gamma }R}^{\alpha }(\tau )q_{\mathit{\Gamma }}^{\alpha }(s,\tau )d\tau ,$$ (14)

where we assume that the total tissue (mixture) spatial mass density $\rho \equiv {\rho }_{\mathit{\Gamma }}=\sum {\rho }_{\mathit{\Gamma }}^{\alpha }$ remains constant for all G&R times s, with ${\rho }_{\mathit{\Gamma }}^{\alpha }={\rho }_{\mathit{\Gamma }R}^{\alpha }/det{\mathbf{F}}_{\mathit{\Gamma }}$. It proves useful, too, to delineate associated spatial ${\varphi }_{\mathit{\Gamma }}^{\alpha }=p_{\mathit{\Gamma }}^{\alpha }/\rho$ and referential ${\varphi }_{\mathit{\Gamma }R}^{\alpha }={\rho }_{\mathit{\Gamma }R}^{\alpha }/\rho$ mass fractions, with ${\varphi }_M^e+{\varphi }_M^m+{\varphi }_M^c=1$ in the media and ${\varphi }_A^e+{\varphi }_A^c=1$ in the adventitia, which is dominated by collagen.

2.3 Parameter values

Whereas the constrained mixture framework is general, the constitutive assumptions are problem specific. Our choice of constitutive relations seeks to yield appropriate emergent solutions for evolving geometry and material properties with the simplest relations possible while building on previous successes (cf. Valentín et al 2009). Here, we briefly describe our method for parameter estimation based largely on experimental findings in Wu et al (2014) and Bersi et al (2016) for a particular mouse model of hypertension for which information is available on the time course of changes in blood pressure, wall composition, and material properties with known roles of inflammatory cells.

Bersi et al (2014) confirmed that biaxial stress-stretch data can be accurately reproduced from knowledge of the geometry, constitutive relation with best-fit parameters, and loading conditions. Hence, using information from Tables S1 and S2 in Bersi et al (2016), we recreated the biaxial data and determined best-fit values for the original (labeled Sham in Bersi et al (2016)) and evolved (4wk Ang II ) biaxial stress-stretch data. Because of the observed maladaptive evolution in Bersi et al (2016), we let the elastic material parameters for collagen and smooth muscle (which turnover continuously) potentially evolve, whereby we determined: material parameters in the neoHookean (constant) and Fung-type (original/evolved) relations for elastin, collagen, and circumferential smooth muscle as well as appropriate deposition streches for elastin (constant) as well as collagen and smooth muscle (original/evolved). Because the previous constrained mixture model yields a mass-based rule-of-mixture expression for stresses for transient elastic (biaxial) responses, we also recreated (original and evolved) histological fractions from Figure 3 in Bersi et al (2016) consistent, again, with predicted relations for our constrained mixture model for G&R (cf. Latorre and Humphrey 2018). Finally, because collagen fibers can be oriented in circumferential (θ), axial (z), and symmetric diagonal (d, with angle α₀) directions, the fit to biaxial data incorporated layer- and orientation-specific fractions of collagen within each layer (cf. Bellini et al 2014): ${\beta }_M^z={\beta }_A^z$, and ${\beta }_A^{\theta }$, with ${\beta }_M^d=1-{\beta }_M^z$ and ${\beta }_A^d=1-{\beta }_A^{\theta }-{\beta }_A^z$, and where ${\beta }_M^{\theta }=0$ because medial circumferential collagen and smooth muscle are combined into a single contribution, collectivelly referred to as medial circumferential smooth muscle m. Due to the many model parameters to be determined from experimental data, each having its own significance, a progressive determination procedure was designed. See Appendix 1 for additional details regarding parameter estimation.

Finally, we recently showed that given appropriate timescales s_G&R/s_ext ≪ 1, where s_G&R is a characteristic time of the G&R process and s_ext is a characteristic time of the external loading stimulus, one can derive rate-independent relations that approximate predictions of a full (hereditary integral based) constrained mixture formulation (Latorre and Humphrey 2018). Based on the data in Bersi et al (2016), s_ext ~7 – 14 days (for both pressure elevation and inflammatory cell infiltration) whereas we estimated s_G&R ~7 – 14 days in induced hypertension (cf. Nissen et al 1978). Hence, s_G&R/s_ext ~ 1 and we used the full constrained mixture model. Yet, prior simulations suggested that this rate-independent approximation is better in cases of sustained changes in pressure over long periods than for cases of sustained changes in flow or especially changes in axial stretch. For evaluative purposes, therefore, we also performed some simulations using the conceptually simpler, and computationally more efficient, rate-independent formulation. Briefly, a quasi-equilibrium formulation of this type presumes that the arterial wall adapts almost instantaneously to the given external perturbations at each G&R time s, hence making possible a pre-integration of Eq. (14) at each s, which yields

$${\mathit{\Upsilon }}_{\mathit{\Gamma }}^{\alpha }(s)\approx 1,\forall s$$ (15)

Similarly, an approximate integration of Eq. (4) for smooth muscle and collagen, which yet turn over continuously during the actual evolution, yields

$${\mathit{\sigma }}_{\mathit{\Gamma }}^0(s)\approx {\varphi }_{\mathit{\Gamma }}^{\alpha }(s){\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{\Gamma }}^{\alpha },\forall s$$ (16)

with ${\stackrel{\sim }{\mathit{\sigma }}}_{\mathit{\Gamma }}^{\alpha }={\mathbf{G}}_{\mathit{\Gamma }}^{\alpha }{\widehat{\mathbf{S}}}_{\mathit{\Gamma }}^{\alpha }({\mathbf{G}}_{\mathit{\Gamma }}^{\alpha 2}){\mathbf{G}}_{\mathit{\Gamma }}^{\alpha }$, so all of the integral equations are simplified to algebraic equations and one need not store the past history of each cohort of the structurally-significant constituents within the arterial wall. Indeed, consideration of Eqs. (15) and (16), instead of the hereditary integral-type Eqs. (14) and (4), along with additional equilibrium relations evaluated at the current G&R time s, lead to an equivalent nonlinear system of algebraic equations that can be solved easily and efficiently at each time s (Latorre and Humphrey 2018), which we will use as explained below.

3 Results

Table 1 provides a list of model parameters, both those prescribed based on experimental findings (e.g., mass fractions based on histology, geometry based on videomicroscopy, and axial stretches based on mechanical tests) and those estimated based on either nonlinear regressions of data (e.g., deposition stretches and parameters for elastin, smooth muscle, and collagen) or G&R calculations (e.g., gain-type parameters). Note, for example, the much larger values of deposition stretch $G_i^{\alpha }$ for elastic fibers than collagen fibers as expected since elastin is produced in the perinatal period and stretched further during somatic growth; the deposition stretch includes both contributions to elastin since the G&R time s = 0 corresponds to the age of mice (~ 13 weeks) at the time angiotensin II infusion was initiated to induce hypertension. Note, too, that although a neoHookean relation is used to describe the mechanical behavior of the elastin-dominated matrix (with constant parameter c^e = 89.71 kPa for all G&R times), the unequal circumferential ( $G_{\theta }^e=1.90$) and axial ( $G_z^e=1.62$) deposition stretches implies modest anisotropy (cf. Rezakhaniha et al 2011) when the in vivo (original homeostatic) configuration is taken as a reference, as we do. It can also be shown that the computed strain energy parameters for smooth muscle and collagen, along with their respective deposition stretches, are such that their contribution to the in vivo wall stress is less at the evolved maladaptive state (h) than in the original one (o). For example, for adventitial collagen, which we predict to dominate in diagonal directions (with ${\beta }_A^d=1-{\beta }_A^{\theta }-{\beta }_A^z=0.877$), the Cauchy stress at the constituent level σ̂ is (Latorre and Humphrey 2018, cf. also Eq. (16))

Table 1.

G&R model parameters for both an original/normal (subscript o) and an evolved-to new homeostatic (subscript h), descending thoracic aorta due to angiotensin-induced hypertension in the mouse. Note that “Elastin”, “Muscle”, and “Collagen” parameters represent elastin-dominated isotropic and smooth muscle/collagen-dominated anisotropic contributions, with glycosaminoglycans and other constituents not specified explicitly. Superscript + or − refer to behaviors in tension or compression; subscripts M and A refer to medial and adventitial respectively. See Appendix 1 for additional definitions and further details regarding material characterization.

Prescribed data from Bersi et al (2016)
Artery Mass Density	ρ	1050 kg/m3
Inner Radius, Thicknesses (o)	ao, hMo, hAo	[0.6468, 0.0284, 0.0118]mm
Inner Radius, Thicknesses (h)	ah, hMh, hAh	[0.6034, 0.0503, 0.0613]mm
Medial Mass Fractions (o)	${\varphi }_{Mo}^e,{\varphi }_{Mo}^m,{\varphi }_{Mo}^c$	[0.4714, 0.4714, 0.0572]
Adventitial Mass Fractions (o)	${\varphi }_{Ao}^e,{\varphi }_{Ao}^c$	[0.0333, 0.9667]
Medial Mass Fractions (h)	${\varphi }_{Mh}^e,{\varphi }_{Mh}^m,{\varphi }_{Mh}^c$	[0.2799, 0.6271, 0.0930]
Adventitial Mass Fractions (h)	${\varphi }_{Ah}^e,{\varphi }_{Ah}^c$	[0.0063, 0.9937]
In vivo Axial Stretch (o, h)	${\lambda }_{zo}^{iv},{\lambda }_{zh}^{iv}$	[1.62, 1.34]
Progressive best-fit to data in Bersi et al (2016)
Diagonal Collagen Orientation	α0	29.91o
Layer-specific Collagen Fractions	${\beta }_A^{\theta },{\beta }_M^z={\beta }_A^z$	[0.056, 0.067]
Elastin Material Parameter	ce	89.71 kPa
Elastin Deposition Stretches	$G_r^e,G_{\theta }^e,G_z^e$	[1/(1.90 · 1.62), 1.90, 1.62]
Muscle Parameters Tens. (o)	$c_{1o}^{m+},c_{2o}^{m+}$	[261.4 kPa, 0.24]
Muscle Parameters Comp. (o)	$c_{1o}^{m-},c_{2o}^{m-}$	[249.5 kPa, 0.15]
Collagen Parameters Tens. (o)	$c_{1o}^{c+},c_{2o}^{c+}$	[234.9 kPa, 4.08]
Collagen Parameters Comp. (o)	$c_{1o}^{c-},c_{2o}^{c-}$	[29.14 kPa, 4.08]
Deposition Stretches (o)	$G_o^m,G_o^c$	[1.20, 1.25]
Muscle Parameters Tens. (h)	$c_{1h}^{m+},c_{2h}^{m+}$	[155.7 kPa, 1.20]
Muscle Parameters Comp. (h)	$c_{1h}^{m-},c_{2h}^{m-}$	[54.35 kPa, 1.20]
Collagen Parameters Tens. (h)	$c_{1h}^{c+},c_{2h}^{c+}$	[27.68 kPa, 9.98]
Collagen Parameters Comp. (h)	$c_{1h}^{c-},c_{2h}^{c-}$	[0.523 kPa, 3.11]
Deposition Stretches (h)	$G_h^m,G_h^c$	[1.23, 1.21]
Estimated/calculated from Bersi et al (2016)
Medial Collagen Gains	$K_{M\sigma }^c,K_{M\tau }^c,K_{M\phi }^c$	[2.00, 2.50, 1.74]
Medial Smooth Muscle Gains	$K_{M\sigma }^m,K_{M\tau }^m,K_{M\phi }^m$	[1.60, 2.00, 1.39]
Adventitial Collagen Gains	$K_{A\sigma }^c,K_{A\tau }^c,K_{A\phi }^c$	[3.33, 4.17, 2.90]
Mass Removal Rates	$k_o^m,k_o^c$	[1/7, 1/7] day−1

$${\widehat{\sigma }}_{Ao}^c=c_{1o}^{c+}{G}_o^{c2}(G_o^{c2}-1)e^{c_{2o}^{c+}{(G_o^{c2}-1)}^2}\approx 750\text{kPa}$$ (17)

at state o (in tension), and

$${\widehat{\sigma }}_{Ah}^c=c_{1h}^{c+}{G}_h^{c2}(G_h^{c2}-1)e^{c_{2h}^{c+}{(G_h^{c2}-1)}^2}\approx 160\text{kPa}$$ (18)

at state h (in tension), which contributes, in part, to the reduction in both circumferential and axial wall stresses reported in Figure 2 in Bersi et al (2016). We also computed greater values of gain-type parameters for adventitial collagen than for medial smooth muscle/collagen, which, for common estimated rate parameters $k_o^m=k_o^c~1/s_{G\&R}$, are consistent with the higher (exuberant) production of adventitial fibrillar collagen observed in Bersi et al (2016), see Appendix 1 herein. Finally, even though the hyperelastic bilayered model of Bellini et al (2014) was used in Bersi et al (2016) (Table S3, Figure 4) to provide insight into the differential roles and adaptations of both layers, a direct comparison between our computed parameters and those reported in Table S3 in Bersi et al (2016) is not possible due, mainly, to the different constitutive modeling characteristics and hypotheses (e.g., constant versus different elastin parameters, computed versus prescribed deposition stretches, thin-walled versus thick-walled model). The outcomes in terms of mean stress and stiffness provided by both (G&R and hyperelastic) constrained mixture models at fixed G&R times were yet consistent.

Fig. 4.

Evolution of biaxial elastic (transient) responses between the initial state, P = P_o and Δϱ_φ = 0 (at day 0), and the final hypertensive state, P = 1.36P_o and Δϱ_φ = 1 (at day 28). Whereas results at P_o and 1.36P_o were computed after an actual adaptation using the full G&R model, and matched the experimental findings (Figure 1), intermediate results were predicted after virtual adaptations to partial increases in pressure and inflammatory burden using the rate-independent G&R model. Pressure-diameter tests (a,c) at respective in vivo axial stretches, and force-length tests (b,d) at respective in vivo inner pressures, as well as additional predictions for stretch λ^iv (e), material stiffness c_ijkl (f), and stored energy density (g) at respective in vivo states. Note the predicted nonlinear progression in evolved results, particularly evident in the pressure-diameter and axial stiffness predictions.

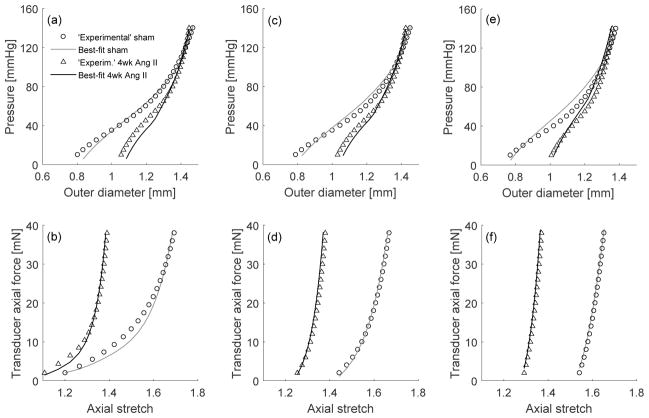
Figure 1 shows model fits to mechanical testing data from Bersi et al (2016) before (Sham) and 28 days after initiating the angiotensin II infusion that raised blood pressure. For model determination completeness, we fitted results for six testing protocols —namely pressure-diameter tests at 0.95, 1.00, and 1.05 fold the respective in vivo axial stretch, as well as force-length tests at fixed pressures of 60, 100, and 140mmHg— each performed at two different G&R times, that is, twelve tests in total. Importantly, our single G&R model captured well both normal and hypertensive behaviors, with the elastin parameter c^e and deposition stretches G^e remaining the same (with associated elastic deformations between original and evolved in vivo states given by Eqs. (25) and (27) in Appendix 1), since elastin does not turnover appreciably in maturity.

Fig. 1.

Material characterization at s = 0 (normotensive; open circles) and s = 28 (hypertensive; open triangles) days using a single constitutive model that evolves through G&R. In particular, elastin deforms elastically between in vivo states at day 0 and day 28, with constant mass, stored energy function parameters, and original (at day 0) deposition streches. In contrast, referential mass densities, stored energy function parameters, and deposition stretches of smooth muscle and collagen, which turnover continuously, are allowed to evolve between in vivo states at days 0 and 28. Pressure-diameter tests (a,c,e) at axial stretches ( $0.95\times {\lambda }_z^{iv},{\lambda }_z^{iv},1.05\times {\lambda }_z^{iv}$), respectively (with ${\lambda }_z^{iv}={\lambda }_{zo}^{iv}$ or ${\lambda }_z^{iv}={\lambda }_{zh}^{iv}$, see Table 1), as well as force-length tests (b,d,f) at (60, 100, 140)mmHg, respectively (cf. Bersi et al 2016). Note, thus, that the nonlinear least-squares regression yielded best-fit parameters by fitting 12 different experimental protocols collectively, see Appendix 1.

Figure 2 compares two simulations — one with a mechano-stimulus consisting of a rapid rise (within 7 days) to a new mean arterial pressure (P_h = 1.36P_o) that persists until 28 days (the period of study in Bersi et al (2016)) and one with both a mechano- and an immuno-stimulus. As it can be seen, the stimulus function ϒ_Γ was stronger in the adventitia than in the media as expected since the adventitia serves in part as a protective sheath in cases of acute rapid increases in pressure and thus bears proportionally greater increases in stress (cf. Bellini et al 2014). Of course, the overall stimulus is greater with inflammation (Eq. (12)). Consistent with the constituent- and layer-specific stimulus for G&R, there was increased mass accumulation and wall thickening in both layers in both cases, though greater in the adventitia and in the case of the inflammatory burden. Albeit not shown, the evolved total wall thickness h = h_M+h_A was 1.45-fold greater than baseline for the mechano-stimulus alone, which revealed a mechanoadaptation only 7% greater than perfect (which would be h_h/h_o → P_h/P_o = 1.36; Humphrey 2008a). As easily seen in the nonlinear algebraic equations for an associated mechanobiologically equilibrated model (Latorre and Humphrey 2018, but also Gleason et al 2004), this difference between computed and ideal adaptations is due mainly to the high content of (unchanging) elastin in this particular case (33% overall). In stark contrast, the predicted evolved wall thickness h_h was 2.80-fold greater than baseline for the immuno-mechano-stimulus, similar to the 2.78-fold increase reported by Bersi et al (2016) (cf. Table S1 therein). Note that, in this case, both model predictions and experimental results include the adverse effect of elastin. Indeed, full model predictions with inflammation also matched very well the experimental finding of a 1.77-fold increase in medial thickness (model prediction 1.78-fold) and 5.20-fold increase in adventitial thickness (model prediction 5.25-fold). We estimated these experimental values from Bersi et al (2016) upon calculation of the (original) medial-adventitial interface radius r_MAo = 675 μm using mass-related data (Table 1). Both experiments and model revealed that increased collagen, especially in the adventitia, was largely responsible for these increases. Interestingly, the fit-to-data (Table 1) necessitated that the new/remodeled collagen in the presence of inflammation behave differently: $c_1^c$ evolved, for fibers experiencing tension, from $c_{1o}^{c+}=234.9\text{kPa}$ to $c_{1h}^{c+}=27.68\text{kPa}$, while $c_2^c$ evolved from $c_{2o}^{c+}=4.08$ to $c_{2h}^{c+}=9.98$. Deposition stretches were found to be different as well; recall, e.g., Eqs. (17) and (18). These changes, along with the novel consideration of the inflammation term in the G&R-stimulus function of Eq. (12), were ultimately responsible for the maladaptive G&R response predicted by the mathematical model. Indeed, for the adaptive case including only a mechano-stimulus (see Figure 2), we assumed constant values $c_1^{m,c}(s)=c_{1o}^{m,c}$ and $c_2^{m,c}(s)=c_{2o}^{m,c}$ and the same (original) deposition stretches for all G&R times s, as usual in normal adaptation analyses (cf. Valentín et al 2009).

Fig. 2.

Full G&R model predicted evolution of geometric and mass properties following a fast 1.36-fold increase in mean arterial pressure that persists up to s = 28 days. Cases predicted with (solid) and without (dashed) inflammatory effects. Shown, too, are experimental values (open symbols) extracted from Bersi et al (2016).

Although s_G&R/s_ext ~ 1, we nevertheless evaluated the ability of a rate-independent (pseudoelastic) formulation to model G&R including the additional inflammatory effects. Surprisingly, the rate-independent simulation matched reasonably well the full solution (Figure 3), especially after ~ 10 days. Given this finding, Figure 4.a, b shows simulated pressure-diameter and axial force-stretch results (solid lines) at day 0 and day 28 based on the full immuno-mechano-stimulated G&R model as well as predicted intermediate states based on the associated rate-independent model. The results at days 0 and 28 match well the experimental findings in Figure 1 of Bersi et al (2016), where we note that, for further comparison with an ideal mechanoadaptive case, we simulated force-length tests at respective in vivo pressures rather than at a common pressure as used in in vitro testing comparisons (indeed, simulations at 100mmHg at day 0 and 28 matched well the biaxial data in Bersi et al (2016), recall Figure 1). The estimated results (dashed), based on virtual full adaptations computed with the rate-independent model for pressure elevations and inflammatory burdens 25%, 50%, or 75% of that experienced in the actual experiment (recall that actual values were P_h → 1.36P_o and Δϱ_φh → 1 within 14 days that remained constant up to 28 days), predicted a smooth, progressive evolution of changes. To be clear, in these virtual experiments we first computed immuno-mechano-biologically equilibrated responses for partial increments in pressure and inflammation and, once virtually relaxed, we superimposed transient elastic deformations during numerically simulated biaxial tests. In this way, one can easily compute the potential evolution of the structural behavior (recall Figure 3). Similarly, Figure 4.c, d shows predictions for fully evolved Cauchy stress-stretch behaviors at days 0 and 28 (solid, using the full G&R model) as well as virtual results for different values of sustained pressures and inflammatory cell infiltration (dashed, using the rate-independent model). The former matches well the results in Bersi et al (2016) while the latter appears reasonable despite the lack of data to which to compare. Finally, Figure 4.e–g shows predicted values of evolving circumferential and axial stretch, circumferential and axial stiffness, and elastic stored energy (relative to a potential stress-free configuration). The results again match well the limited experimental findings, with circumferential stiffness nearly maintained while circumferential and axial stretch, axial stiffness, and stored energy (per unit current volume) decreased.

Fig. 3.

Predicted evolution of geometric and mass properties following a fast 1.36-fold increase in mean arterial pressure that persists up to s = 28 days, including inflammatory effects. Evolutions computed with the full (hereditary integral, solid line) formulation and its associated rate-independent (dashed) model. Shown, too, are experimental values (open symbols) extracted from Bersi et al (2016). Note the surprisingly reasonable agreement between the two models beyond ~ 10 days despite an estimated s_G&R/s_ext ~ 1.

Figure 5 shows simulations for cases of sustained hypertension not studied experimentally: persistent inflammation versus partial or total elimination of inflammation after the 28 days at which a standard angiotensin II delivery pump ceases to dispense this peptide. The model predicts that idealized vessels should approach a mechano-adapted state (a → a_o, h → 1.36h_o) within the subsequent 28 days (i.e., s = 56 days total) if all inflammatory stimuli are eliminated (on and after day 28) and if the smooth muscle and collagen continue to turn over at an accelerated rate (half-lives on the order of 7 days rather than a normal 70 days; Nissen et al (1978)); indeed, these predictions also suggest recovery of the original values of elastic parameters and deposition stretches. In contrast, Figure 6 shows a pure mechano-adaptation to a pressure increase (P_h = 1.36P_o) without any inflammation at any time. Note that the structural properties evolved as expected due to wall thickening while stress-stretch properties remained similar. Although circumferential stiffness remains nearly unchanged in the perfect mechano-adaptation, axial stiffness tends to increase probably to offset the progressive decrease in axial stretch due to collagen deposition without changes in elastin. Stored energy (per current volume) also decreases likely due to the increase in constraining collagen needed to thicken the wall and restore wall stresses towards normal. Finally, Figure 7 illustrates, for purposes of comparison, consequences of a theoretically ideal mechano-adaptation, in the absence of any inflammation but with elastin allowed to turnover (as would occur in development alone). Particularly interesting is that all material properties essentially remain unchanged, except, of course, for the stored energy per unit reference volume, which increases in accordance with a wall thickening with constant energy storage per unit current volume.

Fig. 5.

Full G&R model predicted evolution of geometric and mass properties following a sustained 1.36-fold increase in pressure up to 12 weeks. Cases predicted with persistent, partially reduced, or totally reduced inflammatory effects after 4 weeks of angiotensin infusion suggest only partial recovery towards previously predicted (×, Figure 2) or ideal (*, Humphrey 2008a) mechano-adapted states by 12 weeks.

Fig. 6.

Predicted evolution of biaxial elastic (transient) responses between the initial state, P = P_o, and a final hypertensive state, P = 1.36P_o, without inflammatory effects (Δϱ_φ = 0 for all cases). A complete (virtual) mechano-adaptation is assumed for each case prior to calculation of respective transient responses. Pressure-diameter tests (a,c) at respective in vivo axial stretches, and force-length tests (b,d) at respective in vivo inner pressures, as well as additional predictions for stretch λ^iv (e), material stiffness c_ijkl (f), and stored energy density (g) at respective in vivo states.

Fig. 7.

Predicted evolution of biaxial elastic (transient) responses between the initial state, P = P_o, and a final hypertensive state, P = 1.36P_o, without inflammatory effects (Δϱ_φ = 0 for all cases), but with an assumed full turnover of all constituents (including elastin). A complete (virtual) mechano-adaptation is assumed for each case prior to calculation of respective transient responses. Pressure-diameter tests (a,c) at respective in vivo axial stretches, and force-length tests (b,d) at respective in vivo inner pressures, as well as additional predictions for stretch λ^iv (e), material stiffness c_ijkl (f), and stored energy density (g) at respective in vivo states. Results are consistent with Gleason et al (2004), suggesting that turnover of all constituents is needed for perfect adaptation, as perhaps in development.

4 Discussion

Many prior mathematical models of hypertension-induced G&R in central arteries have assumed a radially homogenized wall (i.e., single layer), both for mathematical convenience and due to the lack of data at the time on layer-specific changes in composition or properties. See, for example, Rachev et al (1996), Fridez et al (2001), Gleason and Humphrey (2004), and Tsamis et al (2009). Although Rachev and Gleason (2011) also considered a single-layered model of the wall, they allowed spatial inhomogeneities to evolve in response to a sustained elevation in pressure, which can capture some effects of a layered wall. Others, including Taber and Eggers (1996), Alford et al (2008), and Rachev et al (2013), explicitly considered bilayered models of the wall to delineate the different compositions and properties of the media and adventitia. As we noted previously, bilayeredmodels are particularly important when focusing on mechanobiological responses (Bellini et al 2014) since medial smooth muscle cells and adventitial fibroblasts may have different homeostatic targets; uni-layered models, in contrast, are particularly useful for specifying material properties for simulations of solid-fluid interactions (Figueroa et al 2009).

Most prior G&R simulations have also focused on mechano-adaptive remodeling. A notable counter-example, Rachev et al (2013) delineated adaptive and maladaptive G&R (of the coronary artery) in hypertension, noting that adventitial remodeling is particularly important in maladaptive remodeling in response to elevated pressure-loading. Their work focused on the long-term response, however, not the time-course of the evolving changes. Moreover, like all prior G&R simulations, Rachev and colleagues did not address directly the potential role in inflammation in driving the maladaptation. We previously introduced an explicit model of mechano- and immuno-mediated vascular G&R in the context of tissue engineered vascular grafts wherein a polymeric scaffold is implanted and allowed to degrade in vivo while host cells produce neotissue to form the evolving graft (Miller et al 2014). In this case, inflammation results from the expected foreign body response and its time-course appears to track that of polymer presence. Hence, the inflammatory burden was prescribed phenomenologically (using a gamma distribution function) and assumed to influence both the turnover (production and removal) and stiffness of the deposited collagen. The model represented well the observed evolving behaviors of the venous grafts.

The development of inflammation in angiotensin II induced hypertension in the mouse is very different, however, and thus demanded a new approach. Histopathological findings suggest that the elastic laminae of the media remain intact over the two-to-four weeks of induced hypertension (Bersi et al 2016), which may contribute to the continued immuno-privilege of the media (Tellides and Pober 2015). Hence, we assumed that there were lower inflammatory effects in the media (through lower gain-type parameters, see Table 1) and that medial elastin retained its original elastic properties and did not turnover. In contrast, the adventitia showed tremendous increases in fibrillar collagen and inflammatory cells (Bersi et al 2016). We thus postulated that inflammation-driven collagen turnover was proportional to an evolving fraction of inflammatory cells. Indeed, elegant experiments by Wu et al (2014) demonstrated that T-cells (and their production of IL-17a) are critical in stimulating adventitial fibrosis in angiotensin II and DOCA salt induced hypertension. In order to fit the biomechanical data, we also found that we needed to modify the stiffness of the newly produced adventitial collagen. We let

$$c_{1,2}^{m,c}(\mathit{\Delta }{\varrho }_{\phi })={c_{1,2}^{m,c}|}_o+f(\mathit{\Delta }{\varrho }_{\phi })\left({c_{1,2}^{m,c}|}_h-{c_{1,2}^{m,c}|}_o\right)$$ (19)

where subscript o denotes an original homeostatic value (from day 0 data) and h denotes an evolved homeostatic value (from day 28 data, Figure 1), with the function f (Δϱ_φ) (satisfying f (0) = 0 and f (1) = 1) driving the generally nonlinear evolution of parameters. This prescribed change in stiffness appears consistent with our prior report, using a different murine model of hypertension, that the percentage of thinner:thicker collagen fibers increased in the adventitia (Eberth et al 2010).

As noted by Bersi et al (2016), immuno-mediated G&R responses appear to be responsible for the maladaptive changes in wall composition and properties. Our model and associated simulations captured these findings (Figures 1, 2, 4). Of particular interest, the experimental data suggested that biomechanical consequences of the G&R remained the same from day 14 to 28 (cf. Figure 2 in Bersi et al 2016), suggesting that a “new homeostatic” target had been reached. In our model, this equates to the immuno-mechano-stimulus function ${\mathit{\Upsilon }}_{\mathit{\Gamma }}^{\alpha }(\tau )\to 1$ for all τ ≥ 14 days (Figure 2). That is,

$$K_{\mathit{\Gamma }\sigma }^{\alpha }\mathit{\Delta }{\sigma }_h-K_{\mathit{\Gamma }\tau }^{\alpha }\mathit{\Delta }{\tau }_{wh}+K_{\mathit{\Gamma }\phi }^{\alpha }\mathit{\Delta }{\varrho }_{\phi h}\to 0$$ (20a)

Because of the persistence of the T-cells observed experimentally over this period, Δϱ_φh > 0, hence $K_{\mathit{\Gamma }\sigma }^{\alpha }\mathit{\Delta }{\sigma }_h-K_{\mathit{\Gamma }\tau }^{\alpha }\mathit{\Delta }{\tau }_{wh}\to -K_{\mathit{\Gamma }\phi }^{\alpha }\mathit{\Delta }{\varrho }_{\phi h}$ with all gain-type parameters strictly positive. Albeit not measured, it appears that the volumetric flow rate Q likely did not change much since inner radius changed only slightly (a changed from 667 μm to 617 μm; Table S1 in Bersi et al (2016) and Figure 2 herein), not significantly. Hence, mean wall shear stress (τ_w = 4μQ/(πa³) with μ viscosity) likely did not change much. The persistent response observed in vivo from 14 to 28 days thus suggests that (with Δτ_wh ~ 0 for simplicity)

$$\mathit{\Delta }{\sigma }_h\equiv \left(\frac{{\sigma }_{\theta \theta h}+{\sigma }_{\mathit{zzh}}}{{\sigma }_{\theta \theta o}+{\sigma }_{\mathit{zzo}}}-1\right)\to -\frac{K_{\mathit{\Gamma }\phi }^{\alpha }}{K_{\mathit{\Gamma }\sigma }^{\alpha }}\mathit{\Delta }{\varrho }_{\phi h}$$ (20b)

or that “new homeostatic” values of in-plane wall stress must necessarily be lower than the original homeostatic values, consistent with Figures 1 and 2 in Bersi et al (2016). This possibility (Figure 4 herein) merits focused attention, particularly from the perspective of possible evolving mechano-sensing targets or mechano-regulated capabilities (cf. Humphrey et al 2014). Perhaps this phenomena could be similar to baroreceptor resetting in hypertension.

Another consequence of Eq. (20b), of course, is that mechano-adaptation as modeled herein requires that the inflammatory stimulus vanishes. Simulations in Figure 2 confirm that the vessel could mechano-adapt in the absence of inflammation, consistent with angiotensin II studies in immunocompromised mice (Rag1^−/−) in Wu et al (2014). Such has been the assumption in prior G&R simulations of hypertensive adaptations (Rachev et al 1996, Fridez et al 2001, Gleason and Humphrey 2004, Tsamis et al 2009, Rachev and Gleason 2011, Taber and Eggers 1996, Alford et al 2008, and Rachev et al 2013). Clearly, however, both the recent data and the present results reveal the need to include and understand potential complications due to inflammation. The virtual simulations in Figures 5 and 6 suggest that partial or full blocking of inflammation following its onset could be beneficial, consistent with some studies on aging-induced structural stiffening in mice and its partial reversal when inflammation/oxidative stress is reduced (Durrant et al 2009; Lesniewski et al 2011).Much research is needed, however, particularly regarding the potential to reverse prior effects of inflammation even after its subsequent elimination.

In conclusion, arteries tend to adapt to changes in mechanical loading and G&R simulations can both describe and predict reasonably well the related evolving changes in geometry and properties. Based on recent data on the direct roles of inflammation in affecting such responses in both tissue engineered vascular grafts and mouse models of hypertension, however, there is strong motivation to develop immuno-mechanobiological models. Whereas we have either prescribed or modeled the inflammatory effects, based on measured endpoints, there is also a pressing need for true immunobiological models that can be coupled with mechanobiological models. The potential remains great.

Appendix 1: Material model determination

Progressive nonlinear regression

• 1Recreate biaxial data (P –d, f –P; f –λ, P –λ) using the given geometry (Table S1) and mean (bulk) mechanical properties (Table S2) from Bersi et al (2016) for Sham (day 0) and 4wk-Ang-II (day 28).
• 2
  Use an extended (bilayered, rule-of-mixture-based) elastic arterial model with original (layer-specific) mass fractions [ ${\varphi }_{\mathit{\Gamma }o}^e,{\varphi }_{\mathit{\Gamma }o}^m,{\varphi }_{\mathit{\Gamma }o}^c$] from Bersi et al (2016) and a calculated medial-adventitial interface radius in the traction-free configuration r_MAtf (using relative area fractions) to determine geometry- and mass-related material parameters α₀, ${\beta }_M^z={\beta }_A^z$, and ${\beta }_A^{\theta }$ (with ${\beta }_M^d=1-{\beta }_M^z$ and ${\beta }_A^d=1-{\beta }_A^{\theta }-{\beta }_A^z$) by fitting the biaxial data (at day 0) generated in Step 1, whereupon we obtain (layer- and orientation-specific) original mass fractions

  $$\begin{gathered} {\varphi }_{Mo}=[{\varphi }_{Mo}^e,{\varphi }_{Mo}^{m,\theta },{\varphi }_{Mo}^{c,z},{\varphi }_{Mo}^{c,d}] \\ =[{\varphi }_{Mo}^e,{\varphi }_{Mo}^m,{\varphi }_{Mo}^c{\beta }_M^z,{\varphi }_{Mo}^c{\beta }_M^d] \end{gathered}$$ (21)
  and

  $$\begin{gathered} {\varphi }_{Ao}=[{\varphi }_{Ao}^e,{\varphi }_{Ao}^{c,\theta },{\varphi }_{Ao}^{c,z},{\varphi }_{Ao}^{c,d}] \\ =[{\varphi }_{Ao}^e,{\varphi }_{Ao}^c{\beta }_A^{\theta },{\varphi }_{Ao}^c{\beta }_A^z,{\varphi }_{Ao}^c{\beta }_A^d]. \end{gathered}$$ (22)

  Assume a fixed value α₀ for s ∈ [0, 28] days (Table 1). Because different cohorts of collagen within each layer share the same turnover characteristics (Table 1), ${\beta }_M^z={\beta }_A^z$ and ${\beta }_A^{\theta }$ remain constant for s ∈ [0, 28] days as well (cf. Latorre and Humphrey 2018).

• 3
  From estimated mass fractions [ ${\varphi }_{\mathit{\Gamma }h}^e,{\varphi }_{\mathit{\Gamma }h}^m,{\varphi }_{\mathit{\Gamma }h}^c$] at s = 28 days from Figure 3.b in Bersi et al (2016), obtain (layer- and orientation-specific) evolved homeostatic mass fractions

  $$\begin{gathered} {\varphi }_{Mh}=[{\varphi }_{Mh}^e,{\varphi }_{Mh}^{m,\theta },{\varphi }_{Mh}^{c,z},{\varphi }_{Mh}^{c,d}] \\ =[{\varphi }_{Mh}^e,{\varphi }_{Mh}^m,{\varphi }_{Mh}^c{\beta }_M^z,{\varphi }_{Mh}^c{\beta }_M^d] \end{gathered}$$ (23)
  and

  $$\begin{gathered} {\varphi }_{Ah}=[{\varphi }_{Ah}^e,{\varphi }_{Ah}^{c,\theta },{\varphi }_{Ah}^{c,z},{\varphi }_{Ah}^{c,d}] \\ =[{\varphi }_{Ah}^e,{\varphi }_{Ah}^c{\beta }_A^{\theta },{\varphi }_{Ah}^c{\beta }_A^z,{\varphi }_{Ah}^c{\beta }_A^d]. \end{gathered}$$ (24)
• 4Given deposition stretches for elastin $G_{\theta }^e$ and $G_z^e$, with $G_r^e=1/(G_{\theta }^e{G}_z^e)$:
  1. Use the extended (bilayered, rule-of-mixture) arterial model, now including deposition stretches (cf. Latorre and Humphrey 2018), with original homeostatic mass fractions from Step 2, elastin deformed at the original in vivo state as

     $${\mathbf{F}}_{\mathit{\Gamma }o}^e={\mathbf{G}}^e$$ (25)
     and smooth muscle and collagen with original in vivo equilibrium stresses

     $${\widehat{\mathit{\sigma }}}_{\mathit{\Gamma }o}^{\alpha }={\mathbf{G}}_o^{\alpha }{\widehat{\mathbf{S}}}_{\mathit{\Gamma }o}^{\alpha }{\mathbf{G}}_o^{\alpha },$$ (26)

     to determine original material parameters (at s = 0 days) $c_o^e,c_{1o}^{m+},c_{2o}^{m+},c_{1o}^{c+},c_{2o}^{c+},G_o^m$, and $G_o^c$, by fitting respective biaxial data generated in Step 1, including only measurements wherein smooth muscle and all collagen fiber families experience tension (Bellini et al 2014). Fix these values for substep 4.b.

  2. Determine original material parameters for compressed smooth muscle and collagen fibers/glycosaminoglycans, $c_{1o}^{m-},c_{2o}^{m-},c_{1o}^{c-}$, and $c_{2o}^{c-}$, by fitting all biaxial (original) measurements generated in Step 1 (Bellini et al 2014; Latorre et al 2017).

  3. Use a G&R-evolved elastic arterial model (cf. Latorre and Humphrey 2018), with evolved homeostatic mass fractions from Step 3, elastin deformed elastically at the new in vivo state as

     $${\mathbf{F}}_{\mathit{\Gamma }h}^e={\mathbf{F}}_{\mathit{\Gamma }h}{\mathbf{G}}^e$$ (27)
     and smooth muscle and collagen with evolved in vivo equilibrium stresses

     $${\widehat{\mathit{\sigma }}}_{\mathit{\Gamma }h}^{\alpha }={\mathbf{G}}_h^{\alpha }{\widehat{\mathbf{S}}}_{\mathit{\Gamma }h}^{\alpha }{\mathbf{G}}_h^{\alpha },$$ (28)

     to determine evolved material parameters (at s = 28 days) $c_{1h}^{m+},c_{2h}^{m+},c_{1h}^{c+},c_{2h}^{c+},G_h^m$, and $G_h^c$, with $c_h^e=c_o^e\equiv c^e$, by fitting respective biaxial data generated in Step 1, including only measurements wherein smooth muscle and all collagen fiber families experience tension. Fix these values for substep 4.d.

  4. Determine evolved material parameters for compressed smooth muscle and collagen fibers/glycosaminoglycans, $c_{1h}^{m-},c_{2h}^{m-},c_{1h}^{c-}$, and $c_{2h}^{c-}$, by fitting all biaxial (evolved) measurements generated in Step 1.

  5. Compute the associated error between measured and predicted in vivo axial stretches at days 0 and 28.

• 5Perform an iterative procedure to determine optimal elastin deposition stretches $G_{\theta }^e$ and $G_z^e$ in Step 4 such that a global fitting error in Steps 4.b,d,e is minimized according to a predefined objective function. This yields the overall best-fit values in Table 1.

Additional estimations

• 6
  Observing that evolved variables at 2 and 4 weeks after Ang II infusion (Figure 2 in Bersi et al 2016) are almost the same, we can assume that the G&R response is, in practice, immunomechanobiologically adapted at 2 weeks. Knowing that adaptations following increases in pressure are “forgiving” (when compared to adaptations following increases in flow rate or axial stretch, see Latorre and Humphrey 2018), we can estimate a characteristic time for collagen and smooth muscle turnover of the order s_G&R ≲ 2 weeks. Thus, because of the lack of additional experimental data (i.e., measured between s = 0 and s = 14 days, when the G&R evolution takes place), we estimate $k_o^m=k_o^c=7{\text{day}}^{-1}$. Recall from Latorre and Humphrey (2018) that the gain parameters $K_{\mathit{\Gamma }\sigma }^{\alpha }$ and $K_{\mathit{\Gamma }\tau }^{\alpha }$ also affect the adaptation process. Again, due to the lack of experimental data describing the evolution process, we estimate values $K_{M\sigma }^c=2$ and $K_{M\tau }^c=2.5$ for medial collagen. Comparing geometries and mass fractions in Steps 2 and 3, while considering model-consistent relations for the evolution of smooth muscle and collagen mass densities (Latorre and Humphrey 2018), we can estimate ${\eta }_{\mathit{\Upsilon }}^m=0.8$ and ${\eta }_{\mathit{\Upsilon }}^c=1.667$, hence we obtain $K_{M\sigma }^m={\eta }_{\mathit{\Upsilon }}^m{K}_{M\sigma }^c=1.6$ and $K_{M\tau }^m={\eta }_{\mathit{\Upsilon }}^m{K}_{M\tau }^c=2$, as well as $K_{A\sigma }^c={\eta }_{\mathit{\Upsilon }}^c{K}_{M\sigma }^c=3.33$ and $K_{A\tau }^c={\eta }_{\mathit{\Upsilon }}^c{K}_{M\tau }^c=4.17$. Finally, from the immunomechanobiological equilibrium condition ${\mathit{\Upsilon }}_{Mh}^c=1$ (cf. Eq. (20a)), we obtain

  $$K_{M\sigma }^c\mathit{\Delta }{\sigma }_h-K_{M\tau }^c\mathit{\Delta }{\tau }_{wh}+K_{M\phi }^c\mathit{\Delta }{\varrho }_{\phi h}=0$$ (29)
  whereupon, with Δϱ_φh = 1, Δσ_h < 0, and Δτ_wh > 0 also known (cf. Eq. (20b)),

  $$K_{M\phi }^c=K_{M\tau }^c\mathit{\Delta }{\tau }_{wh}-K_{M\sigma }^c\mathit{\Delta }{\sigma }_h=1.74>0$$ (30)

  so $K_{M\phi }^m={\eta }_{\mathit{\Upsilon }}^m{K}_{M\phi }^c=1.39$ and $K_{A\phi }^c={\eta }_{\mathit{\Upsilon }}^c{K}_{M\phi }^c=2.90$.

• 7
  Due to the lack of additional experimental data during the actual G&R evolution, we assume an evolution of material parameters $c_1^m,c_2^m,c_1^c,c_2^c$, G^m, and G^c in terms of inflammatory cell level, say ςⁱ (Δϱ_φ), common for all parameters (recall, e.g., Eq. (19))

  $$\varsigma (\mathit{\Delta }{\varrho }_{\phi })={\varsigma }_o+f(\mathit{\Delta }{\varrho }_{\phi })({\varsigma }_h-{\varsigma }_o)$$ (31)

  where f(Δϱ_φ) = (Δϱ_φ)^1/3 proved useful to illustrate some qualitative results including inflammatory effects in the evolution (Figures 2–5). This nonlinear evolution, common for all evolving parameters, is a hypothesis that should be tested against (or determined from) additional experimental data obtained during actual G&R evolutions. Indeed, note that each parameter ςⁱ could evolve between its corresponding values ${\varsigma }_o^i$ and ${\varsigma }_h^i$ independent of other parameters.