Abstract.
The purpose of this investigation is to test whether a poroelastic model with enhanced structure can capture in vivo interstitial pressure dynamics in a brain undergoing mock surgical loads. Using interstitial pressure data from a porcine study, we use an inverse model to reconstruct material properties in an effort to capture these in vivo brain tissue dynamics. Four distinct models for the reconstruction of parameters are investigated (full anatomical condition description, condition without dural septa description, condition without ventricle boundary description, and the conventional fully saturated model). These models are systematic in their development to isolate the influence of three model characteristics: the dural septa, the treatment of the ventricles, and the treatment of the brain as a saturated media. This study demonstrates that to capture appropriate pressure compartmentalization, interstitial pressure gradients, pressure transient effects, and deformations within the brain, the proposed boundary conditions and structural enhancement coupled with a heterogeneous description invoking partial saturation are needed in a biphasic poroelastic model. These findings suggest that with enhanced anatomical modeling and appropriate model assumptions, poroelastic models can be used to capture quite complex brain deformations and interstitial pressure dynamics.
Keywords: computational modeling, biomechanics, finite element modeling, poroelastic, brain, pressure gradient
1. Introduction
Elevated intracranial pressure (ICP) can result from a variety of factors including cerebral edema, tumors, intracranial hemorrhages, accumulation of cerebrospinal fluid (CSF), and venous obstructions.1 As a part of patient care in these disorders, ICP is sometimes monitored. Further, accurately monitoring elevated ICP is of real clinical relevance. In several studies of traumatic brain injury, it was indicated that patients who had their ICP monitored had a decrease in mortality.2 There are multiple methods to monitor ICP including intraparenchymal and intraventricular techniques, which provide statistically similar measurements.3 Experimental evidence suggests that ICP can vary spatially within the brain. This was suggested in a porcine study where an extradural temporal mass lesion was simulated with an epidural balloon.4 A similar porcine experiment with an expanding frontal mass reported similar pressure gradient findings.5 In a clinical study, four patients with unilateral mass lesions (temporal tip contusion, internal capsule hemorrhage, subdural hematoma, and temporal tip hematoma) had bilateral subarachnoid pressure bolts inserted to measure ICP.6 In all four cases, differential ICPs were found. The current standard of care is to measure ICP at one point in the brain and as a result of these findings, the authors suggested modifying how ICP is monitored in this patient population.6 Interhemispheric ICP gradients were also observed in a nonhuman primate study of reperfused hemispheric strokes.7 It also was suggested that multiple ICP monitoring sites should be used in patients with midline shift and/or mass lesions to account for interhemispheric supratentorial ICP gradients.8 With these pressure gradients in mind, the placement of ICP monitoring devices is important. However, multiple monitors can increase the risk of infection in patients. A noninvasive means of estimating pressure gradients could improve accurate measurement of ICP across the brain without increasing risk to the patient.
One method to noninvasively estimate pressure gradients would be through the development of patient-specific computational models. There is an extensive history of using computational models in a patient-specific manner.9–11 Appropriate modeling of brain biomechanics for interventional applications has significant clinical implications, with the potential to provide noninvasive prediction of therapy delivery,12 reduce intraprocedural imaging requirements,13 and reduce unnecessary procedures.14,15 The brain’s anatomy and mechanical behavior is complex, and this paper suggests that without careful modeling consideration, predictions can be confounded. Brain tissue exhibits mechanical heterogeneity and anisotropy. The Monro–Kellie doctrine has been a central working description of brain biomechanics, which states that the cranial cavity is a fixed volume that is the sum of the volumes of brain tissue, intracranial blood, and CSF.16 Treating the brain as only a solid tissue (often the case in models) negates the brain’s biphasic nature. With respect to the exchange with interstitial fluid spaces within brain tissue, gray matter is not easily distorted and typically changes fluid content by , whereas white matter has a more compliant structure and can increase as much as 10%.17 Another important feature of the brain is that it is encapsulated by the dura.1 The dura extends into folds of the brain forming the dural septa, consisting of the falx cerebri and the tentorium cerebelli. The dural septa serve the purpose of reducing displacements during motion.1 The sulci are the grooves in the brain, and the gyri are the plateaus formed by boundary ridges of sulci pairs.1 Also, the ventricular cavities are filled with CSF and are connected to the central canal within the spinal cord and the space around the brain.1 The brain tissue also consists of gray and white matters.1
To accurately model brain biomechanics, quantifying the material properties of gray and white matters is necessary. There have been attempts to quantify the brain’s material properties,18,19 yet no consensus has been reached. One approach is to quantify these properties using magnetic resonance (MR) elastography.18 Other approaches have been performed that correlated properties of gray and white matters in rectangular tissue samples undergoing shear testing under conditions of large strain.19 These types of studies, which range from in vitro to in vivo testing, vary in protocols and results.20 The inconsistent property values obtained in these studies have led to variability within existing biomechanical modeling applications.
Moreover, despite extensive research done on biomechanical modeling of the brain, there is no consensus on what representation should be used.21,14 Model types include viscoelastic,22 poroelastic,23 elastic,24 hyperelastic,25 and microchannel flow26 models. From a physiological perspective, we suggest that the poroelastic description of the brain is most appropriate due to its ability to account for both solid and fluid components within the cranial cavity. This work investigates a poroelastic model, which treats the brain as a material consisting of both an elastic solid matrix and a fluid component. We further suggest this biphasic representation is in better intuitive agreement with the Monro–Kellie Doctrine as well.
With respect to enhanced anatomical modeling of the brain, some work has already been accomplished.27 One group used an inhomogeneous patient-specific model of the brain.27 In another investigation, improved deformation behavior was found in seven clinical cases by accounting for the dural septa.13 These investigations, among others, point toward the significance of accounting for brain geometry in modeling approaches. Ultimately, the predominant reason for variations in representation, both constitutive and geometric, arises from common investigational approaches that attempt to study soft-tissue in isolation rather than generating systems for in vivo observation. Unfortunately, this is a product of the extremely challenging nature of in vivo work and the deployment of instrumentation within that domain. This study tests whether a poroelastic biphasic model with enhanced anatomical features could can capture in vivo interstitial pressures under mock surgical loading.
Three important contributions in this investigation are reported. First, the ability to accurately model in vivo interstitial pressures in a porcine experiment using a poroelastic model, including measured pressure gradients, is demonstrated. While this does not validate the use of the poroelastic model for the brain under all loading conditions, it does provide meaningful evidence for its appropriateness in the biomechanical modeling of the brain under quasistatic surgical conditions. The second contribution is a systematic investigation of boundary conditions and anatomically based mesh specifications, necessary to recapitulate the compartmentalization of ICP often seen with intracranial space-occupying deformations. Finally, a set of approximate values describing brain tissue material properties in poroelastic biomechanical models is provided as an initial approach toward the generation of more accurate brain biomechanical models. As a whole, this work demonstrates the use of computational models as a means to investigate the complex interplay of boundary conditions, anatomical constraints, and material properties needed to capture ICP gradients and compartmentalization in the brain in response to acute space-occupying deformations.
2. Materials and Methods
2.1. In Vivo Porcine Data
The in vivo data used for this investigation were collected in a previous study.28 The data reflects a porcine study, approved by the Institutional Animal Care and Use Committee, on a series of Yorkshire pigs (Parson’s Farm, Hadley, Massachusetts).28 Once anesthetized, the porcine subject had pressure transducers (Johnson & Johnson Codman Microsensor ICP Transducer ∼ Raynham, Massachusetts, Part No. 82-6631) implanted in the midbrain/frontal region of both hemispheres.28 One transducer was placed in the hemisphere ipsilateral to the mock surgical load, explained below, while the other transducer was placed in the contralateral hemisphere. These sensors measured interstitial pressures throughout the experiment. Before any procedure was performed, a -weighted MR image of the neuroanatomy was acquired.28 After MR imaging, stainless steel beads (1-mm diameter) were surgically implanted to monitor tissue movement.28 A temporal craniotomy was performed, and a lateral compression was applied to create a mock surgical load against the intact dura using a piston-like source. This piston was attached to a stereotactic frame and translated in increments of 2 and 4 mm.28 A baseline computed tomography (CT) scan of the head was obtained. A CT scan was performed after each piston translation, enabling the measurement of the bead displacements at the conclusion of each translation. The interstitial pressure was measured continuously in both hemispheres. A complete description of the protocols is in the original study.28 For this investigation, the pressure and displacement data from three piston translations (8, 10, and 12 mm) were used.
2.2. Biphasic Poroelastic Model
With respect to our representation of brain biomechanics, a poroelastic model derived from Biot’s description of consolidation theory29 and adapted for use in surgical loading is used.30 The governing equations are
| (1) |
| (2) |
The variables in Eqs. (1) and (2) are identified in Table 1. Equation (1) relates mechanical equilibirum to the interstitial pressure gradient. Equation (2) relates volumetric strain to the conservation of fluid in a porous media.
Table 1.
Equation variables.
| Symbol | Meaning | Units |
|---|---|---|
| Interstitial pressure | Pa | |
| Displacement vector | m | |
| Tissue shear modulus | Pa | |
| Young’s modulus | Pa | |
| Poisson’s ratio | (unitless quantity) | |
| Ratio of fluid volume extracted to volume change of tissue under compression | (unitless quantity) | |
| Void compressibility constant (amount of fluid capable of being forced into a tissue constant in volume) | ||
| Hydraulic conductivity |
The governing equations are solved using the Galerkin finite element method in three-dimensions.31 The finite element representation of Eqs. (1) and (2) has been previously described.32,33 A fully-implicit time stepping routine is used with a time step of 90 s. The total time varies based on the length of the experimental piston push, which was chosen to be of a timescale representative of typical intraprocedural surgical manipulations (3 to 15 min over a 2- to 3-h procedure). The first calculated pressure value from the solution occurs 90 s after the designated start time, which represents the peak pressure that occurs at each piston translation. It should be noted that Eqs. (1) and (2) from Biot’s model represent a temporally slow-evolving system whereby inertial effects at the early transient are neglected in the physical description. This quasistatic dynamic system coupled to the numerical characteristics of a previous stability analysis of the system resulted in the selection of this time step.33
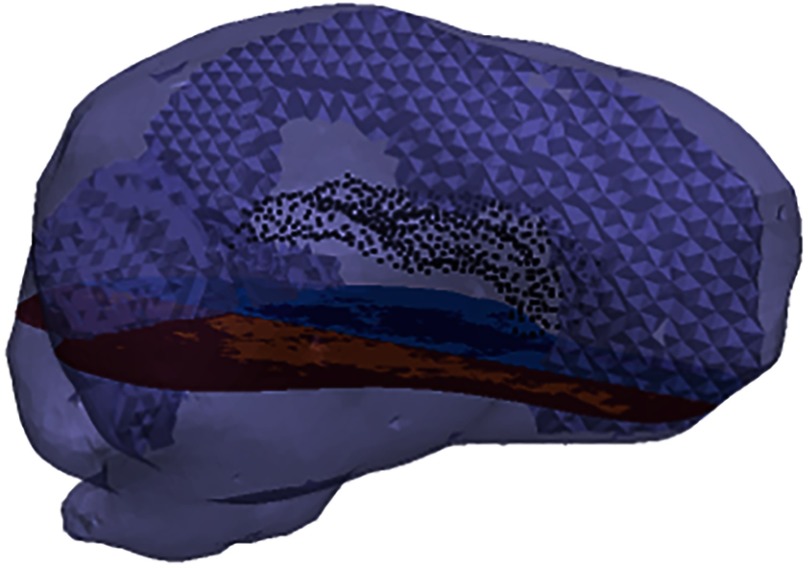
Two finite element meshes, representing the same porcine subject, are generated. The linear tetrahedral element meshes, visualized by the outer boundary of Fig. 1, are generated from manual segmentation of the MR volume.34 The CT and MR spaces are coregistered using ANALYZE Version 7.5—Biomedical Imaging Resource (Mayo Foundation, Rochester, Minnesota), ensuring that the transducer and bead positions determined in measurement space (CT) are all located in the computational model space (MR).28 To represent heterogeneity, the tetrahedral elements are classified according to the corresponding white and gray matters within an element from MR intensity.28,35 This is visualized in Fig. 1 in the axial slice. Ventricles were treated as a separate structure and serve as an internal boundary. The ventricular boundary surface is shown by the black points in Fig. 1.
Fig. 1.
Finite element mesh representation of the porcine brain. The dural septa splits are discernible within the mesh. The black points within the mesh visualize the nodes of the boundary between the brain parenchyma and the ventricles. The slice through the mesh visualizes the distinction between gray and white matters within the parenchyma. There is an additional distinction, which is not enforced in this study, between the tissues in either hemisphere.
Of the two meshes generated, one captures gray matter, white matter, and ventricles, but not the dural septa. The dural septa, visualized in Fig. 1, are incorporated using manual segmentation and a custom mesh splitting code that splits the mesh at specified planes. The second mesh generated contains this dural septa operation to study the dural septa’s anatomical influence.
The values for both gray and white matters are designated with Young’s modulus of 2100 Pa and Poisson’s ratio of 0.45. In previous work, these homogeneous values were optimally determined to match a wide swath of loading conditions.36 We chose to enforce these in the model to reduce the degrees of freedom toward matching the transient interstitial pressure gradient data. In the previous work, from which the values were obtained, the same governing equations were employed in the context of a different porcine brain experiment.36 Material properties of hydraulic conductivity () and the saturation constants (, ) are the subjects of material property determination for both matters. These six material properties (, , and for both gray and white matters) are fit using an inverse problem approach.
The geometric description of the mesh does not account for gyri and sulci. We hypothesize that the lack of resolution of these fine anatomical features leads to an effective source of bulk compliance, so variability in the saturation constants is allowed to accommodate for this. These parameters have been historically prescribed as and indicating a fully saturated media.13,28 Similar to what others have observed experimentally,4,5 the propagation of pressure spatial distributions for this experiment, in response to a space-occupying deformation at the macroscopic tissue scale level, seems to contradict this saturation assumption at the more coarse scale (meaning , ). This led to our approach suggesting that some of the finer fissure systems are acting as a source of compliance, much like the ventricular system does for space-occupying lesions.37,38
2.3. Model Sensitivity to Boundary Conditions
The boundary conditions, meshes, and the material properties being estimated were systematically varied to isolate the influence of three features (dural septa, ventricle boundary condition, and saturation parameters), which reflect the creation of three model conditions that allowed for variations in the anatomical and saturation assumptions: (1) the full anatomical model description, (2) the full anatomical description without dural septa, and (3) the full anatomical description without the ventricle boundary description. For completeness, a more conventional model: (4) the full anatomical description with full saturation (, ) was also included. The boundary conditions of each model are explained in detail below, and a summary of these boundary conditions is shown in Table 2.
Table 2.
Summary of model conditions.
| Dural septa present | Ventricle treated as reference pressure | Unsaturated effects allowed (, ) | Number of fit material properties | |
|---|---|---|---|---|
| FACD | a | a | a | 6 |
| CwoDSD | a | a | 6 | |
| CwoVBD | a | a | 6 | |
| CFSM | a | a | 2 |
Indicates that the boundary is active.
2.3.1. Full anatomical condition description (FACD)
The full anatomical condition description (FACD) represents the model containing the full realization of the dural septa, ventricles, saturation constants, and heterogeneity. In FACD, the inverse model identifies the six model parameters associated with the material properties that best fit the measured interstitial pressure dynamics. These six properties are (), (), (), (), (), and (). Hydraulic conductivity and saturation parameters are represented by and , , respectively. Variable saturation parameters allow for compliance in the fluid component. The far-field cortical surfaces are fixed in displacement and experience no fluid drainage.28 This decision is supported by the intact dura. The brain stem was modeled as stress-free and does not permit fluid drainage.39 Locations at the piston application are designated displacements associated with 8, 10, and 12 mm,28 and no drainage. The displacements of consecutive piston pushes do not rely on the previous loading as an initial condition. The region surrounding the piston area is stress-free and does not allow fluid drainage.28 Consistent with the dural septa’s role, the associated nodes are fixed in displacement and do not permit fluid drainage. Clinically, the ICP reference point is defined at the level of the foramen of Monro.40 Additionally, the ventricular system is continuous with the central spinal canal.1 We hypothesize that this permits the ventricles, when the dura is not compromised, to act as a reference pressure for the brain. As the ventricles represent a compliant internal boundary that can drain upon loading, they are allowed to deform, and the boundary pressure is zero, serving as a reference pressure. The solution of FACD incorporates the influence of the dural septa, ventricles, and sulci and gyri. To isolate the influence of these individual features, they are systematically removed within the three model conditions below.
2.3.2. Condition without dural septa description (CwoDSD)
To study dural septa influence, a model condition is created that eliminated the dural septa and its associated boundary condition from the FACD. Similar to FACD, this model fits the same six material properties.
2.3.3. Condition without ventricle boundary description (CwoVBD)
This model condition defines the influence of the ventricle boundary condition. The mesh includes the dural septa split and boundary conditions. However, the ventricles are considered nondraining surfaces. It is necessary to designate a reference pressure to be able to solve the system of equations. Using a previously used representation,28 the brain stem surface is a constant reference pressure of zero. Similar to FACD and condition without dural septa description (CwoDSD), the same six material properties are fit.
2.3.4. Conventional fully saturated model (CFSM)
The last model formulation is the traditional use of Biot’s consolidation theory to represent the brain. More specifically, in this case, the brain is treated as a fully saturated media ( and for gray and white-matters).13,28 This reduces the parameterization to and . In the former conditions, unsaturated effects are allowed to accommodate missing structural compliance associated with sulci and gyri. In conventional fully saturated model (CFSM), this is terminated in favor of the more common assumptions.
2.4. Inverse Model
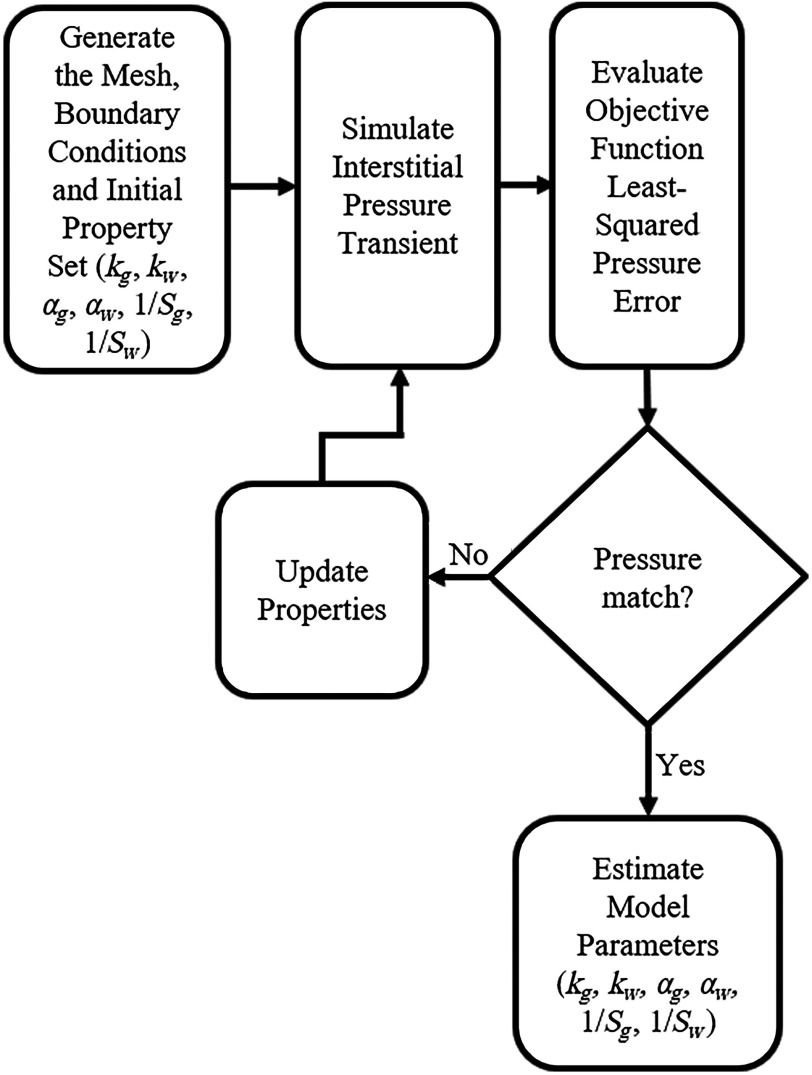
The inverse model analysis in this work estimates the material properties to best fit measured interstitial pressure values from the transducers, given varying structural and material representations described above. This procedure is shown in Fig. 2. For all, except for the CFSM traditional framework, the parameters , , , , , and are estimated with this approach. With respect to the CFSM, only the two hydraulic conductivity parameters are estimated. The material properties for each condition are independently estimated for each translation. To ensure repeatability, 20 randomized initial starting property guesses are performed for each piston translation for each inverse reconstruction. Therefore, there are 240 distinct executions of the inverse model (4 model conditions, 3 piston translations, and 20 initial guesses each). The 20 initial guesses are generated by randomly perturbing each property value by . We should note, similar to many self-starting optimizations within the context of real experimental noise, this problem does require a good initial guess to avoid local minima and regularization to improve optimization behavior. To review, each inverse problem is driven by the objective function based on the acquired bilateral interstitial pressure data and to establish some sense of repeatability, 20 initial guesses were used and allowed to converge to a minimum. Also note, prior to the 20 randomized initial guesses, the baseline initial guesses were determined empirically to ensure that the values were reasonable for use in the inverse model; the noise was added subsequent to these guess determinations to ensure a more robust determination of properties.
Fig. 2.
Schematic illustrating the inverse model used to fit the model calculated ICP to the experimentally measured ICP while estimating the material properties.
These randomized initial guesses are input into the poroelastic, finite element model, with the appropriate boundary conditions, time step, and mesh. The interstitial pressure transient is simulated with the model based on a current guess at the material property distribution and an inverse problem approach is used to fit the material properties such that the difference between measured interstitial pressure at the two transducers and its simulated counterpart is minimized using a nonlinear least-squares constrained optimization in MATLAB (MathWorks Inc., Natick, Massachusetts). The objective function is a relative sum-squared error (SSE) metric between experimentally measured pressure transients and its model-calculated counterpart and is calculated as
| (3) |
where and are the experimentally measured and model-determined pressures, respectively. represents pressure value at the ’th time point in the transient.
With respect to Eq. (3), the experimental data consist of 200 data points (100 per transducer) evenly sampled along in time. Since the number of model calculated points is substantially less, due to the 90-s time step, the intratime point values are linearly interpolated to fully utilize the experimental data. Using a customized trust region reflective optimization in MATLAB (MathWorks Inc., Natick, Massachusetts), property values are iteratively estimated to minimize the SSE. The selection of the trust region method was based on its ability to combine the benefits of steepest descent and Newton-like methods. When tested, the trust region method was able to converge without stagnation, despite estimating parameters of very different orders of magnitude. This is important given the nature of the data and property values being fit. A custom convergence criteria is used based on the convergence of the SSE calculated at every iteration tested in work not shown. The SSE in Eq. (3) is used to measure quality of model fit.
Following parameter estimation of the 240 runs, forward solves of the poroelastic model using the estimated parameters are performed, generating pressure and displacement solutions. We designate two result types: (1) the “best fit” is the parameter set that achieves the smallest SSE for a specific piston translation in a given model condition; (2) we denote the “average pressure result” as an average given initial guess variability, as 20 parameter estimations for each piston translation and model condition are performed.
The inverse model is fit to the measured interstitial pressure, so the bead displacements serve as a source of validation. The percent shift correction is calculated using Eq. (4):
| (4) |
where and are the experimentally measured and model-determined displacement vectors, respectively.
3. Results
3.1. Optimization Performance
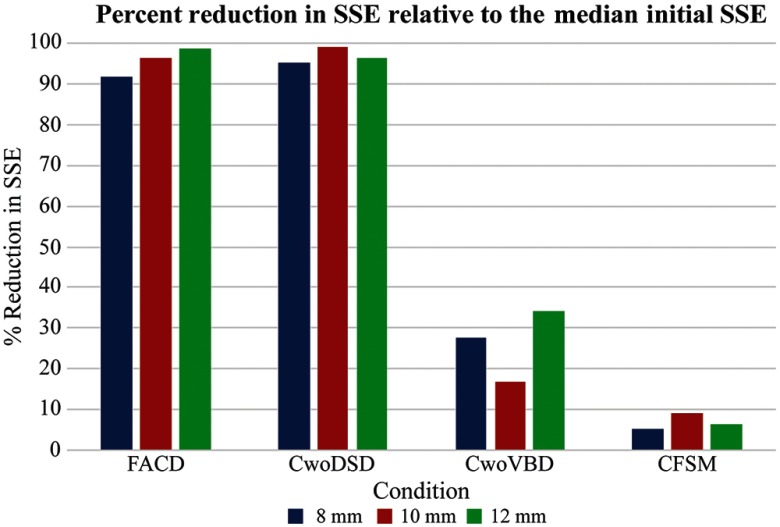
The convergence performance associated with this inverse problem model-fitting can be seen in Fig. 3, which reflects the percent SSE change relative to the median initial SSE in each set of 20 runs. A marked similarity with a substantive change in the objective function error with FACD and CwoDSD is seen. With descriptions condition without ventricle boundary description (CwoVBD) and CFSM, there is overall poor fit performance with very little reduction of the objective function.
Fig. 3.
Percent change in the median SSE at convergence relative to the median initial SSE over the set of 20 runs for each model representation of the brain. It shows a greater reduction in SSE and thus a better model fit for FACD and CwoDSD relative to CwoVBD and CFSM.
3.2. Interstitial Pressure
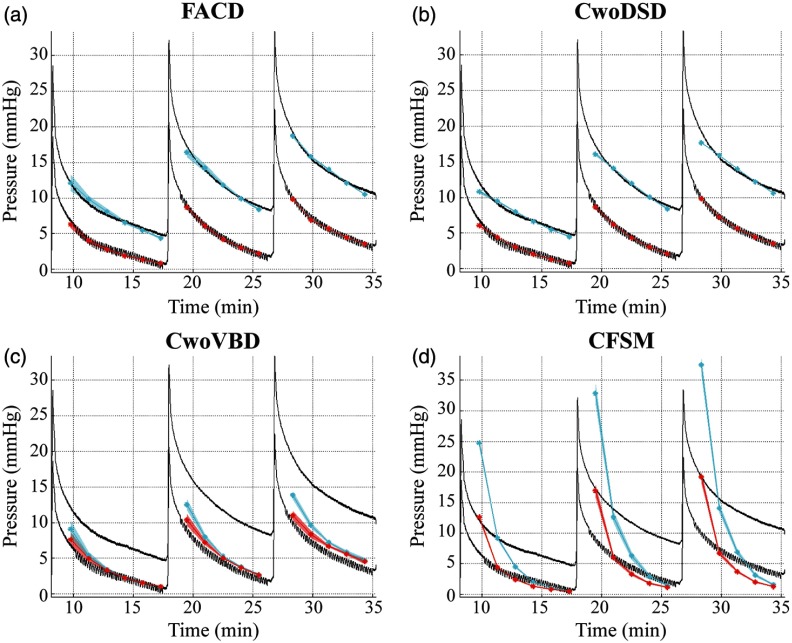
Qualitatively and quantitatively the calculated interstitial pressures are assessed. In Fig. 4, observing the measured in vivo interstitial pressure, there is a sustained interhemispheric gradient and distinct transient behavior. The shaded regions represent the average model reconstructed pressure +/− two standard deviations with respect to the variable initial guesses. In all Fig. 4 panels, it is evident the methods provide repeatable fits within the initial guess range. The pressure fits shown in Fig. 4 are obtained from forward runs of the biphasic model using the optimized parameter values obtained during the 240 runs. Figure 4(a) representing FACD, shows that the enforced anatomical specificity captures the interhemispheric pressure amplitude and gradient, and transient. Figure 4(b) represents CwoDSD and shows the quality of the estimated trend of pressure obtained by the solution of the inverse problem is comparable to FACD’s fits, which is illustrated in statistical testing below. Figure 4(c) represents CwoVBD, and not only does it result in inaccurate pressure magnitudes, but it also does not maintain the sustained interhemispheric pressure gradient. Figure 4(d) represents CFSM, and while initially there is a pressure gradient, it is not sustained over time. Additionally, the pressure is poorly estimated throughout the duration for CFSM.
Fig. 4.
Experimental and model-estimated pressure for each boundary condition. The solid black lines represent experimental pressure data measured with the transducers. The solid cyan and red lines are the average pressure results in the near hemisphere transducer and far hemisphere transducer, respectively. The translucent red and cyan areas are +/− two standard deviations of the average pressure result calculated at each time point. The pressure fits are the model estimated pressure obtained by the solution of the inverse problem for (a) the full anatomical condition (FACD), (b) the dural septa not included (CwoDSD), (c) the ventricle boundary condition not included (CwoVBD), and (d) the brain tissue treated as fully saturated (CFSM).
Using the Kruskal–Wallis test, the SSE’s of the final solution per model type to one another are compared. The result of this indicated that the solutions, shown in Fig. 4, came from statistically different distributions. Based on test statistics from this group comparison, a pairwise comparison is performed between the groups, which indicated that the solutions of FACD and CwoDSD are not significantly different from each other, but are both significantly different than the other two conditions. Additionally, using the Wilcoxon rank sum test, the SSE’s of the final solution for each model type are compared to one another to determine if statistically significant differences exist between model conditions. This shows that the pressure solutions of FACD, CwoDSD, CwoVBD, and CFSM are all statistically significantly different looking over all of the piston pushes. Based on the difference between measured and model estimated pressures, the best pressure fit is associated with CwoDSD; however, FACD is statistically comparable in the 12-mm piston translation using the Wilcoxon rank sum test. CwoVBD produces a dramatic decrease in the quality of fit, and CFSM results in the worst fit, with respect to average SSE.
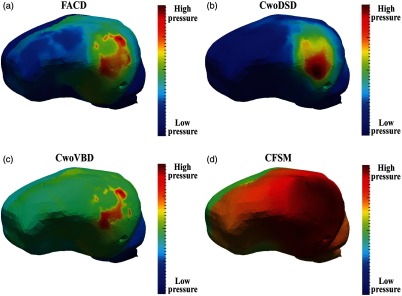
Qualitatively, the compartmentalization of the interstitial pressure can be visualized in Fig. 5. The images were individually scaled to capture the relative pressure distribution in each model condition. In Fig. 5(a), which represents FACD, there are higher pressures in the hemisphere ipsilateral to the piston. There is also a distinction between the pressure within the ipsilateral hemisphere relative to the contralateral hemisphere and cerebellum. In CwoDSD, there was no interhemispheric compartmentalization as shown in Fig. 5(b). In CwoVBD, compartmentalization between the hemispheres and the cerebrum and cerebellum is evident, shown Fig. 5(c); however the extent of the interhemispheric difference is less distinct than in FACD. In Fig. 5(d), which represents CFSM, there is a compartmentalization effect between the ipsilateral and contralateral hemispheres with the area of elevated pressure more pervasive. Additionally, there are higher pressures present in the cerebellum and brain stem regions.
Fig. 5.
Differences in pressure compartmentalization are seen based on the model conditions. For representation, the pressure values are scaled to the minimum and maximum of the specific solutions shown above. The solutions shown represent the best fits from each model condition from the first time step of the 10-mm piston translation for (a) all anatomical conditions (FACD) enforced, (b) the dural septa not included (CwoDSD), (c) the ventricle boundary condition not enforced (CwoVBD), and (d) the brain tissue treated as fully saturated (CFSM).
3.3. Shift Correction
Since the inverse model is fit to the experimental interstitial pressure, the bead displacements provide an internal source of validation. They also quantify the quality of the fits for the solid tissue component. To compare displacements, the percent shift correction is calculated using Eq. (4) at the conclusion of the piston translations per model condition performed (Table 3). The runs evaluated were the best fits for each of the piston translations and conditions, respectively. Table 3 shows the best shift correction is consistently accomplished in CwoDSD.
Table 3.
Percent shift correction.
| Condition | Piston translation | ||
|---|---|---|---|
| 8 mm | 10 mm | 12 mm | |
| FACD | 60.0 | 57.6 | 53.7 |
| CwoDSD | 64.5 | 70.3 | 73.8 |
| CwoVBD | 58.1 | 60.2 | 64.8 |
| CFSM | 60.0 | 65.0 | 67.4 |
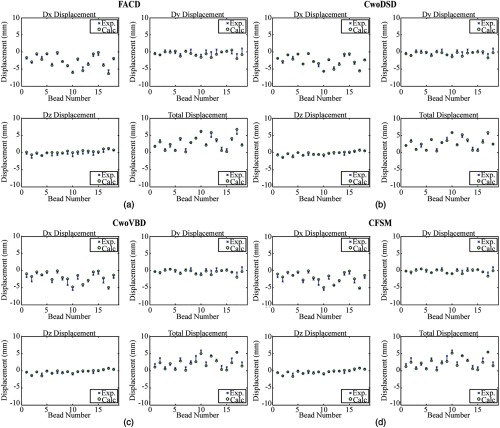
Looking at individual bead displacements at the 10-mm piston translation, which reflects the general behavior, the same trend was observed (Fig. 6). Comparing all panels, it is evident that all model conditions were able to calculate shift corrections comparably.
Fig. 6.
Displacement calculations from the best fits runs from the 10-mm piston translation quantify the model calculated (Calc.) bead displacements at the conclusion of the simulated piston translation and compare them to the experimentally (Exp.) measured displacements. In each panel, the top left, top right, and bottom left subfigures represent the displacement calculations in the , , and axes respectively, while the subfigure on the bottom right represents the total displacement.
Evaluating the same set of piston translations shown in Table 3, the Wilcoxon rank sum test is used to determine if the quality of displacement fits is statistically different between conditions. For each model condition type and piston translation, for the 18 beads is calculated for the run with the smallest SSE. Then, the conditions are compared with respect to these sets of measurements (18 beads at every piston translation). Although some piston-specific comparisons revealed statistical significance, these differences were not present in every comparison. Therefore, shift corrections between conditions were considered not statistically significantly different.
3.4. Property Reconstruction
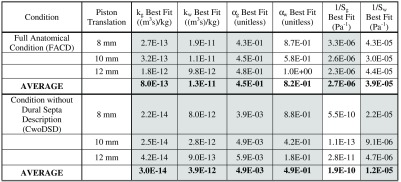
With respect to Fig. 3, it seems clear that the ventricular boundary and the fully compliant material parameter description are necessary for pressure distribution matching. This is more readily apparent in Fig. 4, which demonstrates that gradients are not captured by these descriptions. As a result, Fig. 7 shows the properties found in the best fits for FACD and CwoDSD. The property values estimated for gray and white matters are consistently different in all best fit properties across all piston translations and model conditions. This suggests heterogeneous material property descriptions are appropriate. Observing the changes in the best fits of and , there is a change in magnitude with translation changes with consistently greater than which is consistent with the literature. Although not always true, trends closer to the historical value of 1 in contrast to , which trends lower. The reconstructions of and were all nonzero, indicating a need for compliance for appropriate matching.
Fig. 7.
Estimated properties summary (gray shaded columns represent monotonic behavior with piston translation).
4. Discussion
The error reduction results in Fig. 3 and pressure results shown in Figs. 4(a) and 4(b) reflect that interstitial pressure can be appropriately modeled using both FACD and CwoDSD conditions. The mismatch between the experimental pressure data and the model estimated pressure obtained by the solution of the inverse problem for CwoVBD and CFSM [Fig. 4(c) and 4(d)] is likely due to the necessary contributions of anatomic structure (i.e., inclusion of ventricular boundary) and compliance in material property description (i.e., relaxation of the saturation assumption). Despite the same optimization algorithm being used, in the CwoVBD and CFSM conditions, the parameters found with the solution of the inverse problem could not match the experimental pressure (Fig. 4). This is also indicated by the illustration of the inverse problem’s convergence shown with SSE in Fig. 3. Incorrectly describing the anatomy of the brain in these model conditions likely caused these discrepancies. This is further evidence for FACD being most appropriate for accurate estimation of ICP.
Comparing the pressure distributions of Fig. 5(b), it is evident that the dural septa boundary defines the compartmentalization of pressure between hemispheres and between the cerebrum and cerebellum; however, further investigation with multiple pressure transducers is needed to more fully capture the compartmentalization effect. The percent shift correction in CwoDSD is consistently better than other conditions (Table 3 and Fig. 6). To some degree, this was expected as all other material properties (namely, the Young’s modulus and Poisson’s ratio) were optimized under conditions that used a homogenous mesh without dural septa in previous work (quite similar to CwoDSD conditions that likely explain the monotonic increase in accuracy).36 With respect to FACD, with progressively larger deformations, the displacement predicting fidelity behaves monotonically with displacement prediction performance decreasing with increased deformation. This performance difference is likely due to FACD being over constrained due to the enforcement of the dural septa boundary conditions. However, note that the model calculated shift corrections were not statistically significantly different from one another at every piston translation among these two models. Additionally, in future works treating the dural septa as a stiff coupled, or uncoupled membrane,41 versus a rigid planar separation, may be advisable. To more appropriately address, a combined objective function (pressure and displacement) would be a viable direction to investigate more accurately capturing both displacement and pressure dynamics; however, in such an endeavor, more interstitial pressure measurements are likely needed as well as temporally coupled measurements of bead displacements, a challenging experiment.
Excluding the ventricle boundary condition resulted in a substantially worse result, reflected by inaccurate interstitial pressures. The results of Figs. 4(c) and 5(c) indicate that the pressures in both hemispheres were similar in magnitude. This indicates that the appropriate treatment of the ventricle boundary has significant impact on brain models. The decision to treat the boundary as a reference was motivated from clinical practice, which treats the level of the foramen of Monro as the ICP zero point.40
Treating the brain as a fully saturated tissue [Fig. 4(d)] is the current convention in the literature when biphasic models are used.13,28 The results of this paper indicate this may not be appropriate at the macroscopic surgical scale. The magnitudes of the experimental data were not matched, and the interhemispheric gradient was not sustained. The differences between Figs. 4(a) and 4(d) reflect that enabling the tissue to be unsaturated yields a substantial improvement in the quality of fit. The results of the percent shift correction are also comparable to FACD (Table 3 and Fig. 6). In a previous study of volume regulation, the results led to a hypothesis that brain interstitial space could experience volume variations based on stresses present.17 It is not definite what phenomena the saturation terms are capturing, but we hypothesize that the evacuation of fluid from fissures and sulci spaces into subarachnoid spaces during compression is the phenomenon that is introducing a net compliance in the macroscopic tissue descriptions.
The necessary goal of this work was to match the pressure gradients in the tissue and given the level of fit from Fig. 3, only FACD and CwoDSD are appropriate and, as such, reported in Fig. 7. The properties estimated in the two models are discernibly different, which speaks to the variability depending on model sophistication. One interesting observation is that in many of the material parameters of Fig. 7, monotonicity is seen with the degree of piston translation (all gray columns of Fig. 7). This would indicate a need for a material nonlinearity to better capture the entire performance of the system over varying surgical loading. Additionally, it is important to note that the values reported in Fig. 7 are in reasonable agreement with other studies in the literature that also investigated the modeling of interstitial pressure in brain tissue.42–44 For example, in a study by Kalyanasundaram et al.44 that focused on predicting the distribution of drugs delivered to the brain, they reported values of and as and , respectively. It should also be noted that there is some ambiguity in the literature on the value of these properties relative to heterogeneity.43,44 For example, in the work reported by Basser, values of and were and , respectively.43 While some disagreement exists, it is important to realize that there is reasonable agreement in the scale of these data. In addition, none of these studies attempted to fit parameters as in the inverse model approach reported here, which provides added novelty to this work.43
We should note, however, one shortcoming of this work is in regard to instrumentation. The inverse model is driven by two transducers’ pressure transients in only two locations within the brain taken over a finite length of time. Although the reason for this was the natural experimental constraints of brain volume, this certainly limits fidelity of the property reconstructions.
However, the full anatomical condition in conjunction with the poroelastic model under modified saturation assumptions demonstrates an ability to capture in vivo interstitial pressures and tissue deformation. It also reflects the compartmentalization of interstitial pressure, agreeing with clinical observations.6,45 With respect to anatomical constraints, the presence of the dural septa is less critical than the ventricular structure with respect to cross-hemisphere pressure gradient development; however, there are modest differences in distribution amplitude with the septa. Based on the results of FACD, we infer that the incorporation of heterogeneity with gray and white matters is appropriate. Lastly, in Fig. 4 the relaxation of the saturation assumption leads to considerably better matching and sustaining of pressure gradients over the transient [i.e., Fig. 4(d) with CFSM shows early gradient but nonsustained, a noted limitation in the original study28].
5. Conclusions
The purposes of this investigation are to accurately model in vivo interstitial pressures, determine the anatomical specificity necessary to capture interstitial pressures and their cross-parenchymal gradients accurately, and to estimate brain material property values. The results provide strong evidence for the utility of a poroelastic representation and the pivotal role that certain anatomical features play in accurately modeling pressure and deformation. To the best of our knowledge, the model reconstructions in the full anatomical condition description have not been accomplished in other studies of in vivo modeling. This work highlights the importance of incorporating features, such as tissue heterogeneity, the ventricles, and the dural septa in future biomechanical models. It also challenges conventional assumptions regarding poroelastic theory applied to brain biomechanics at the macroscopic level and postulates that sulci and gyri may be an apparent source of compliance in measurements. While we cannot conclusively say that adding fluid-compliance is explained by the evacuation of intrasulci/intrafissure fluid into subarachnoid spaces without further model development, it is evident that its incorporation results in better capturing of interstitial pressure magnitudes, transient behavior, and importantly the spatial gradient—effects that were very challenging and elusive to capture in past modeling efforts. While preliminary in nature, the work presented could have applications in modeling elevated ICP to predict potential in vivo pressure gradients that could be used to inform patient care or influence deployment of convection-enhanced delivery of therapeutics.
Acknowledgments
This work was supported by the NIH—National Institute of Neurological Disorders and Stroke R01NS049251, and the NIH Training Grant No. T32 EB021937. The authors would like to thank Professor of Surgery, P. Jack Hoopes, DVM, PhD from Geisel School of Medicine, Dartmouth College for his assistance in generating the original data from Ref. 28.
Biographies
Saramati Narasimhan received her BS degree in biomedical engineering from the University of Miami in December 2013 and received her MS degree in biomedical engineering from Vanderbilt University in December 2017. Currently, she is a PhD candidate in the Department of Biomedical Engineering at Vanderbilt University. She is pursuing her PhD in the Biomedical Modeling Laboratory (BML). Her research interests include biomechanics, translational research with surgical applications, computational modeling, inverse problems, and tumor growth modeling.
Jared A. Weis received his MS and PhD degrees in biomedical engineering from Vanderbilt University and his BS degree in biomedical engineering from Washington University in St. Louis. He is an assistant professor of biomedical engineering at Wake Forest School of Medicine. His research interests are concentrated in developing and deploying computational modeling and noninvasive imaging methodologies to explore tumor growth and response to therapy with an emphasis on driving therapeutic interventions and developing decision-support technologies.
Hernán F. J. González received his MS degree in biomedical engineering from the University of Miami in 2013. He joined the Vanderbilt University Medical Scientist Training program in the summer of 2014 and is in the fifth year of the MD/PhD program. Currently, he is pursuing his PhD in biomedical engineering in the Brain Imaging and Electrophysiology Network (BIEN) Lab. His research interests are in the use of multimodal techniques to study connectivity in neurological disease.
Reid C. Thompson is currently William F. Meacham professor and chairman of Neurological Surgery at Vanderbilt Medical Center, Nashville, TN. He has served as the director of neurosurgical oncology and director of the Vanderbilt Brain Tumor Center for 16 years. His previous clinical appointments have been at Cedars–Sinai Medical Center. He had carried out a fellowship in cerebrovascular neurosurgery at Stanford University, and completed his residency in neurosurgery at Johns Hopkins University.
Michael I. Miga received his PhD in biomedical engineering from Dartmouth College in 1998. He joined Vanderbilt University in spring of 2001 and is the Harvie Branscomb professor at Vanderbilt. He is a professor of biomedical engineering, radiology, and neurological surgery. He is the Biomedical Modeling Laboratory director and cofounder of the Vanderbilt Institute for Surgery and Engineering. His research interests are in computational modeling and inverse problems for therapeutic applications and imaging.
Disclosures
The authors of this paper have no conflicts of interest or disclosures.
References
- 1.Siegel A., Sapru H. N., Essential Neuroscience, 3rd ed, Lippincott Williams & Wilkins, Baltimore, Maryland: (2015). [Google Scholar]
- 2.Yuan Q., et al. , “Impact of intracranial pressure monitoring on mortality in patients with traumatic brain injury: a systematic review and meta-analysis,” J. Neurosurg. 122(3), 574–587 (2015). 10.3171/2014.10.JNS1460 [DOI] [PubMed] [Google Scholar]
- 3.Vender J., et al. , “An evaluation and comparison of intraventricular, intraparenchymal, and fluid-coupled techniques for intracranial pressure monitoring in patients with severe traumatic brain injury,” J. Clin. Monit. Comput. 25(4), 231–236 (2011). 10.1007/s10877-011-9300-6 [DOI] [PubMed] [Google Scholar]
- 4.Wolfla C. E., Luerssen T. G., Bowman R. M., “Regional brain tissue pressure gradients created by expanding extradural temporal mass lesion,” J. Neurosurg. 86(3), 505–510 (1997). 10.3171/jns.1997.86.3.0505 [DOI] [PubMed] [Google Scholar]
- 5.Wolfla C. E., et al. , “Brain tissue pressure gradients created by expanding frontal epidural mass lesion,” J. Neurosurg. 84(4), 642–647 (1996). 10.3171/jns.1996.84.4.0642 [DOI] [PubMed] [Google Scholar]
- 6.Weaver D. D., Winn H. R., Jane J. A., “Differential intracranial pressure in patients with unilateral mass lesions,” J. Neurosurg. 56(5), 660–665 (1982). 10.3171/jns.1982.56.5.0660 [DOI] [PubMed] [Google Scholar]
- 7.D’Ambrosio A. L., et al. , “Interhemispheric intracranial pressure gradients in nonhuman primate stroke,” Surg. Neurol. 58(5), 295–301 (2002). 10.1016/S0090-3019(02)00817-0 [DOI] [PubMed] [Google Scholar]
- 8.Sahuquillo J., et al. , “Interhemispheric supratentorial intracranial pressure gradients in head-injured patients: are they clinically important?,” J. Neurosurg. 90(1), 16–26 (1999). 10.3171/jns.1999.90.1.0016 [DOI] [PubMed] [Google Scholar]
- 9.Miller K., Chinzei K., “Constitutive modelling of brain tissue: experiment and theory,” J. Biomech. 30(11–12), 1115–1121 (1997). 10.1016/S0021-9290(97)00092-4 [DOI] [PubMed] [Google Scholar]
- 10.Mostayed A., et al. , “Biomechanical model as a registration tool for image-guided neurosurgery: evaluation against BSpline registration,” Ann. Biomed. Eng. 41(11), 2409–2425 (2013). 10.1007/s10439-013-0838-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sun K., et al. , “Near real-time computer assisted surgery for brain shift correction using biomechanical models,” IEEE J. Transl. Eng. Health Med. 2, 2500113 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dai W., et al. , “Voxelized model of brain infusion that accounts for small feature fissures: comparison with magnetic resonance tracer studies,” J. Biomech. Eng. 138(5), 051007 (2016). 10.1115/1.4032626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen I., et al. , “Intraoperative brain shift compensation: accounting for dural septa,” IEEE Trans. Biomed. Eng. 58(3), 499–508 (2011). 10.1109/TBME.2010.2093896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Miga M. I., “Computational modeling for enhancing soft tissue image guided surgery: an application in neurosurgery,” Ann. Biomed. Eng. 44(1), 128–138 (2016). 10.1007/s10439-015-1433-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Narasimhan S., et al. , “Differentiating tumor recurrence from radiation-induced necrosis: an image-based mathematical modeling framework,” in IEEE Int. Symp. on Biomedical Imaging (ISBI), IEEE, Washington D.C., pp. 839–842 (2018). 10.1109/ISBI.2018.8363702 [DOI] [Google Scholar]
- 16.Monro A., Observations on the Structure and Functions of the Nervous System (1783). [Google Scholar]
- 17.Doczi T., “Volume regulation of the brain tissue-a survey,” Acta Neurochir (Wien), 121(1–2), 1–8 (1993). 10.1007/BF01405174 [DOI] [PubMed] [Google Scholar]
- 18.Green M. A., Bilston L. E., Sinkus R., “In vivo brain viscoelastic properties measured by magnetic resonance elastography,” NMR Biomed. 21(7), 755–764 (2008). 10.1002/nbm.1254 [DOI] [PubMed] [Google Scholar]
- 19.Prange M. T., Margulies S. S., “Regional, directional, and age-dependent properties of the brain undergoing large deformation,” J. Biomech. Eng. 124(2), 244–252 (2002). 10.1115/1.1449907 [DOI] [PubMed] [Google Scholar]
- 20.Chatelin S., Constantinesco A., Willinger R., “Fifty years of brain tissue mechanical testing: from in vitro to in vivo investigations,” Biorheology 47(5–6), 255–276 (2010). [DOI] [PubMed] [Google Scholar]
- 21.Gerard I. J., et al. , “Brain shift in neuronavigation of brain tumors: a review,” Med. Image Anal. 35, 403–420 (2017). 10.1016/j.media.2016.08.007 [DOI] [PubMed] [Google Scholar]
- 22.Hagemann A., Rohr K., Stiehl H. S., “Coupling of fluid and elastic models for biomechanical simulations of brain deformations using FEM,” Med. Image Anal. 6(4), 375–388 (2002). 10.1016/S1361-8415(02)00059-2 [DOI] [PubMed] [Google Scholar]
- 23.Miga M. I., et al. , “Modeling of retraction and resection for intraoperative updating of images,” Neurosurgery 49(1), 75–85 (2001). 10.1097/00006123-200107000-00012 [DOI] [PubMed] [Google Scholar]
- 24.DeLorenzo C., et al. , “Volumetric intraoperative brain deformation compensation: model development and phantom validation,” IEEE Trans. Med. Imaging 31(8), 1607–1619 (2012). 10.1109/TMI.2012.2197407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Karami G., et al. , “A micromechanical hyperelastic modeling of brain white matter under large deformation,” J. Mech. Behav. Biomed. Mater. 2(3), 243–254 (2009). 10.1016/j.jmbbm.2008.08.003 [DOI] [PubMed] [Google Scholar]
- 26.Parker K. J., “Are rapid changes in brain elasticity possible?,” Phys. Med. Biol. 62(18), 7425–7439 (2017). 10.1088/1361-6560/aa8380 [DOI] [PubMed] [Google Scholar]
- 27.Hu J., et al. , “Intraoperative brain shift prediction using a 3D inhomogeneous patient-specific finite element model,” J. Neurosurg. 106(1), 164–169 (2007). 10.3171/jns.2007.106.1.164 [DOI] [PubMed] [Google Scholar]
- 28.Miga M. I., et al. , “In vivo modeling of interstitial pressure in the brain under surgical load using finite elements,” J. Biomech. Eng. 122(4), 354–363 (2000). 10.1115/1.1288207 [DOI] [PubMed] [Google Scholar]
- 29.Biot M. A., “General theory of three-dimensional consolidation,” J. Appl. Phys. 12(2), 155–164 (1941). 10.1063/1.1712886 [DOI] [Google Scholar]
- 30.Miga M. I., Development and Quantification of a 3D Brain Deformation Model for Model-Updated Image-Guided Stereotactic Neurosurgery, Dartmouth College, Hanover: (1998). [Google Scholar]
- 31.Lynch D. R., Numerical Partial Differential Equations for Environmental Scientists and Engineers: A First Practical Course, Springer Science & Business Media, New York, NY: (2005). [Google Scholar]
- 32.Paulsen K. D., et al. , “A computational model for tracking subsurface tissue deformation during stereotactic neurosurgery,” IEEE Trans. Biomed. Eng. 46(2), 213–225 (1999). 10.1109/10.740884 [DOI] [PubMed] [Google Scholar]
- 33.Miga M. I., Paulsen K. D., Kennedy F. E., “Von Neumann stability analysis of Biot’s general two-dimensional theory of consolidation,” Int. J. Numer. Methods Eng. 43, 955–974 (1998). [DOI] [Google Scholar]
- 34.Sullivan J. M. J., Charron G., Paulsen K. D., “A three-dimensional mesh generator for arbitrary multiple material domains,” Finite Elem. Anal. Design 25(3–4), 219–241 (1997). 10.1016/S0168-874X(96)00027-3 [DOI] [Google Scholar]
- 35.Miga M. I., et al. , “In vivo analysis of heterogeneous brain deformation computations for model-updated image guidance,” Comput. Methods Biomech. Biomed. Eng. 3(2), 129–146 (2000). 10.1080/10255840008915260 [DOI] [PubMed] [Google Scholar]
- 36.Miga M. I., et al. , “Modeling surgical loads to account for subsurface tissue deformation during stereotactic neurosurgery,” Proc. SPIE 3254, 501–511 (1998). 10.1117/12.308202 [DOI] [Google Scholar]
- 37.Dawant B. M., et al. , “Brain atlas deformation in the presence of small and large space-occupying tumors,” Comput. Aided Surg. 7(1), 1–10 (2002). 10.3109/10929080209146012 [DOI] [PubMed] [Google Scholar]
- 38.Maier S. E., Sun Y., Mulkern R. V., “Diffusion imaging of brain tumors,” NMR Biomed. 23(7), 849–864 (2010). 10.1002/nbm.1544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Osgood M., et al. , “Rapid unexpected brain herniation in association with renal replacement therapy in acute brain injury: caution in the neurocritical care unit,” Neurocrit. Care 22(2), 176–183 (2015). 10.1007/s12028-014-0064-y [DOI] [PubMed] [Google Scholar]
- 40.Freeman W. D., “Management of Intracranial Pressure,” Continuum (Minneap Minn) 21(5 Neurocritical Care), 1299–1323 (2015). [DOI] [PubMed] [Google Scholar]
- 41.Miga M. I., et al. , “Model-updated image-guided neurosurgery using the finite element method: incorporation of the falx cerebri,” Lect. Not. Comput. Sci. 900–909 (1999). 10.1007/10704282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nagashima T., Shirakuni T., Rapoport S. I., “A two-dimensional, finite element analysis of vasogenic brain edema,” Neurol. Med. Chir. 30(1), 1–9 (1990). 10.2176/nmc.30.1 [DOI] [PubMed] [Google Scholar]
- 43.Basser P. J., “Interstitial pressure, volume, and flow during infusion into brain tissue,” Microvasc. Res. 44(2), 143–165 (1992). 10.1016/0026-2862(92)90077-3 [DOI] [PubMed] [Google Scholar]
- 44.Kalyanasundaram S., Calhoun V. D., Leong K. W., “A finite element model for predicting the distribution of drugs delivered intracranially to the brain,” Am. J. Physiol. 273(5 Pt 2), R1810–R1821 (1997). [DOI] [PubMed] [Google Scholar]
- 45.Carhuapoma J. R., et al. , “Interhemispheric intracranial pressure gradients in massive cerebral infarction,” J. Neurosurg. Anesthesiol. 14(4), 299–303 (2002). 10.1097/00008506-200210000-00005 [DOI] [PubMed] [Google Scholar]