Prediction of Chemotherapy Response in Ovarian Cancer Patients Using a New Clustered Quantitative Image Marker

Abstract

This study aimed to investigate the feasibility of integrating image features computed from both spatial and frequency domain to better describe the tumor heterogeneity for precise prediction of tumor response to postsurgical chemotherapy in patients with advanced-stage ovarian cancer. A computer-aided scheme was applied to first compute 133 features from five categories namely, shape & density, Fast Fourier Transform (FFT), Discrete Cosine Transform (DCT), Wavelet, and Gray Level Difference Method (GLDM). An optimal feature cluster was then determined by the scheme using the particle swarm optimization (PSO) algorithm aiming to achieve an enhanced discrimination power that was unattainable with the single features. The scheme was tested using a balanced dataset (responders and non-responders defined using 6- month PFS) retrospectively collected from 120 ovarian cancer patients. By evaluating the performance of the individual features among the five categories, the DCT features achieved the highest predicting accuracy than the features in other groups. By comparison, a quantitative image marker generated from the optimal feature cluster yielded the area under ROC curve (AUC) of 0.86, while the top performing single feature only had an AUC of 0.74. Furthermore, it was observed that the features computed from the frequency domain were as important as those computed from the spatial domain. In conclusion, this study demonstrates the potential of our proposed new quantitative image marker fused with the features computed from both spatial and frequency domain for a reliable prediction of tumor response to postsurgical chemotherapy.

1. Introduction

Ovarian cancer is characterized by the highest mortality rate among the gynecologic malignancies [1]. In clinical practice, there is no effective screening method for early detection of ovarian cancer. As a result, the majority of ovarian cancers are diagnosed in the advanced stages of cancer progression when the tumors have already disseminated. After diagnosis, the primary cytoreduction and chemotherapy are necessary to obliterate the primary tumor and suppress the metastatic tumors [2]. Since there is a large variation among patients’ response to chemotherapy in clinical trials and/or routine treatment due to individual variability and tumor heterogeneity [3], the prediction of the potential clinical benefit of chemotherapy at early stage is useful to distinguish patients who will benefit from the specific chemotherapy from those merely exposed to the toxicity of the chemotherapy. However, this is still a challenging problem in the pursuit of personalized medicine for tailoring medical treatment to individual characteristics of patients. To address this clinical challenge, extensive studies have been conducted to identify biomarkers that may be intimately associated with patient response to chemotherapies, such as CA 125 level [4] or human epididymis protein 4 [5]. However, effectiveness of such biomarkers varies with a variety of epidemic and clinical factors of patients; and is compromised when distinguishing between localized and diffuse tumor recurrence [6, 7].

Alternatively, many imaging modalities have been developed for monitoring tumor response to chemotherapies [8, 9], including computed tomography (CT), positron emission tomography (PET) /CT, diffusion-weighted or dynamic contrast enhanced magnetic resonance imaging (MRI) and magnetic resonance spectroscopy. CT offers fast scanning speed, high spatial resolution and good reproducibility [10, 11], but suffers from the low soft contrast [12] and is limited in its assessment of small (~ 1 cm) tumor nodules for detection of recurrent ovarian cancer [13]. Ultrasound also has poor sensitivity in detecting military peritoneal seeding, and disease on the peritoneum and in the omentum with lesions less than 1 to 2cm [14]. In comparison to CT, MRI demonstrates superior soft tissue contrast and allows for precise tissue characterization with advanced techniques such as diffusion, spectroscopy and perfusion, but MRI scans are much more expensive than CT scans and take longer time to acquire the data. Due to the broad availability and low cost, CT is still used as the routine imaging method for most ovarian cancer patients. When monitoring tumor response to chemotherapy, sequential CT images are acquired prior to and after the therapy. The post-therapy CT scans are usually performed every 6–9 weeks, covering 2–3 treatment cycles.

For evaluation of tumor response to chemotherapy, a few of target lesions are usually selected to be representative of all involved organs and analyzed as a whole to assign the result, as with the Response Evaluation Criteria in Solid Tumors (RECIST 1.1) criteria [15]. Using the RECIST, the change in tumor diameter is assessed to stratify the patients into four different categories (i.e., complete response, partial response, stable disease, and progressive disease); however, since the tumor diameter in the RECIST is evaluated only in one dimension, the result usually has poor correlation with the patient’s outcome [16, 17]. Thus, identifying effective image features and developing optimal machine learning based prediction methods have attracted great research and development interest in medical imaging field.

In the last twenty years, a variety of imaging features have been exploited to handle medical classification and detection tasks, including intensity (e.g., contrast, skewness, kurtosis) and shape features (e.g., area, circularity and convexity) for classifications of masses in mammograms [18–21], wavelet and Fourier features used for lung nodule identification [22–24], gray-level co-occurrence matrix established for liver tumor detection [25]. The shape and density features are particularly useful to characterize the geometric properties of tumors, while FFT, DCT and Wavelet features are mostly used to describe energy distributions at different frequencies, making them advantageous to quantify the tumor heterogeneity that has been recognized as an important factor for the determination of the tumor resistance to the drug [26]. Furthermore, wavelet features are especially sensitive to energy convergence at the boundaries. By comparison, GLDM features are important to identify and compute the textures for assessment of the heterogeneity in tumor textual details [27–29]. A wide range of methods have been developed to compute Fourier and wavelet features. One example of establishing FFT features was provided in [30] where the 2D boundary was converted into 1D wave signal (via polar-rectangular coordinate transformation) for using FFT to extract clinically meaningful features for identifying the malignant lung nodules. Another example for wavelet feature extraction was presented by Abubacker et al. [31], describing the shape, density and texture features in the form of multi-level wavelet decompositions of the masses depicted on digital mammograms. Most of the previously reported studies utilized the features falling into one or two of the above mentioned groups. The assembly of features from more diversified groups, however, could lead to an improved discrimination power by integrating specific discrimination power of the features in each group.

For this purpose, this study aimed to compute and fuse more diversified quantitative image features to generate a new quantitative image marker for early prediction of ovarian cancer prognosis. The computer-aided scheme was first developed to extract the tumor heterogeneity features in both the spatial and frequency domains. Next, the feature pool was optimized using a particle swarm optimization (PSO) approach that iteratively drove the particle to generate a candidate feature cluster toward the best known prediction performance based on a leave-one- case-out cross-validation method. Then, to assess the performance of the single features and the new quantitative image marker resulting from the optimal feature cluster, the area under the ROC curve (AUC value) was computed to assess the discrimination or prediction power of the features and new quantitative image marker. Meanwhile, we also compared the effectiveness of the spatial domain features with that of the frequency domain features.

2. Materials and Methods

2.1. Database

With the institutional review board (IRB) approval, a CT image dataset was retrospectively collected, which consists of 120 ovarian cancer patients (Table 1). These patients were enrolled in clinical trials for new chemotherapy development at our collaborated medical center. The inclusion criteria of subjects for this study were: 1) the patients were diagnosed with recurrent ovarian/peritoneal/tubal carcinoma of high grade histology (e.g., serous, endometrioid and undifferentiated); 2) they were treated with systemic chemotherapy after the primary cytoreduction; and 3) the pre- and post-therapy CT examinations are available, with the first post-therapy examination taken 6–8 weeks after starting the therapy. Following the imaging procedures suggested by RECIST 1.1 [15], a routine protocol was implemented in this study, as with the reported ovarian cancer research such as [32–34] using the similar imaging intervals and [35] utilizing the comparable scanner settings. Specifically, either GE Light Speed VCT 64-row detector or GE Discovery 600 16-row detector machines was used to acquire the CT images based on a standard CT scanning image acquisition protocol. In accordance with the protocol, the image acquisition was conducted with a tube voltage of 120 kVp and a current ranging from 100 to 600mA, which varied based on body size of the patients. Helical axial images were obtained on patients’ chest, abdomen, pelvis 60 seconds after injecting 100 cc contrast agent of iopamidol with a rate of 2–3cc/sec (Isovue 370, Bracco Diagnostics, Inc.). During the image acquisition, the pitch was 1.25 mm, and the slice thickness was 5 mm. The clinical data including the RECIST assessment results and 6-month PFS was also collected for comparing the performance with the new quantitative image marker developed in this study. The clinical data collected during the trials revealed that 68 patients are responders with 6-month PFS “Yes”, while 52 patients are non-responders who hardly show response to the therapies with apparent cancer progression.

Table 1.

Patient demographic and clinical characteristics

Characteristic		6-Month PFS
		Yes	No
Number of patients		68 (57%)	52 (43%)
Age		66±10	69±9
Number of tumors		119 (52%)	110 (48%)
Average tumor diameter (before therapy)		28 mm	24 mm
Agent	Platinum (+/− taxanes)	26	15
	Microtubule toxins +/− other agents	28	24
	Gemcitabine	3	1
	Topoisomerase inhibitors	0	1
	Anthracyclines	5	6
	Targeted agents	1	0
	Bevacizmab and similar	5	2
	Immune agents	0	0
	PARPi	0	3

2.2. Three-dimensional Tumor segmentation

A computer-assisted segmentation module was previously developed to segment metastatic tumors that had been tracked and marked by radiologists. This module started the segmentation from a slice containing a tumor identified by a radiologist. Using the slice as a reference, the module sequentially segmented the same tumor on the adjacent slices until the tumor eventually disappeared. Given each slice, we utilized a hybrid algorithm described in our previous work [36] to perform a semi-automatic extraction of tumors of interest. The segmentation was initiated with the central slice of tumor marked by a radiologist to segment the tumors of interest only. Since many metastatic tumors in different abdominal sections were captured with faint boundaries that led to spurious edges by the algorithm, all the automatically generated boundary contours were further visually examined, and corrected if necessary to ensure the segmentation accuracy.

2.3. Quantitative imaging features

In this study, we first applied a computer-aided scheme to compute a total of 133 features in both the spatial and frequency domain and classified them into five groups, namely, shape & density and Gray Level Difference Method (GLDM) in the spatial domain, and Fast Fourier Transform (FFT), Discrete Cosine Transform (DCT), and Wavelet in the frequency domain. Among them, 28 features were included in the Shape & Density group (Table 2), consisting of tumor shape features (i.e., compactness, surface to tumor volume ratio and spherical disproportion of the 3D tumors), and tumor density features as derived from quantities such as Iso-intensity, energy and entropy to describe tumor heterogeneity. For the FFT, DCT, Wavelet groups, each group includes 15 features computed using the same statistical measures, which are correlation, energy, entropy, kurtosis, maximum, minimum, range, mean, median, root-mean-square (RMS), skewness, standard deviation, sum deviation, mean deviation, uniformity. The GLDM group included 60 features, i.e., the 15 features associated with the same 15 statistical measures evaluated in each of four directions [37].

Table 2.

A list of features from the Shape & Density group

Feature Class	Feature description
Shape	Volume, surface area, convexity, compactness, surface to tumor volume ratio, sphericity, spherical disproportion, max radius
Density	Std, mean, median, iso-intensity, mean fluctuation, std fluctuation, energy, entropy, mean deviation, sum deviation, contrast, correlation, homogeneity, kurtosis, RMS, mean gradiant, Std gradiant, skewness, Std ratio of tumor to boundary, uniformity

By comparison, the Shape & density features described entire tumor-containing images, but the FFT, DCT, Wavelet, and GLDM features were block-based localized features. To create the localized features, each target image was first divided into 8×8- or 9×9-pixel blocks and then fed into the FFT, DCT, Wavelet or GLDM algorithms to construct a feature vector, as illustrated in Figures 1 and 2. Those feature vectors for different blocks were combined into a feature matrix to derive quantitative imaging features from the statistical measures. The details about computation of the FFT, DCT, Wavelet, and GLDM features are provided as follows.

Figure 1:

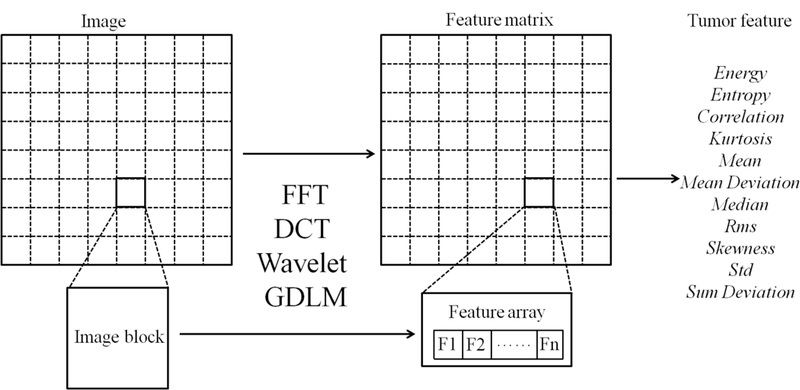
A schematic diagram of the block-based imaging feature extraction

Figure 2:

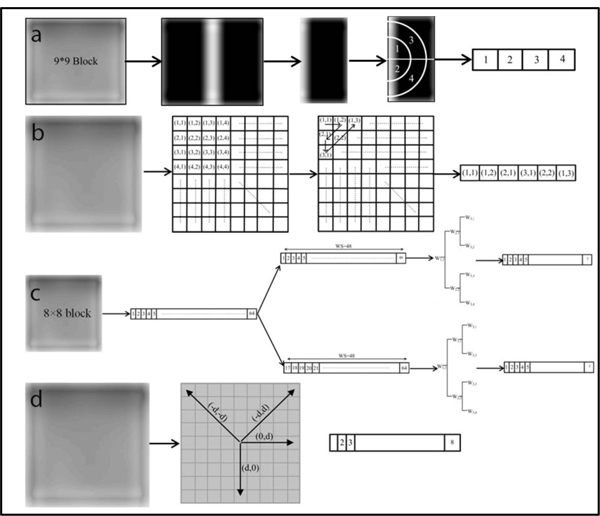
The feature array constructed for each block using the (a) FFT, (b) DCT, (c) Wavelet, and (d) GTDM. The process of establishing the four types of features can be summarized as follows. To start, each target slice was divided into either 8×8 or 9×9-pixel blocks (Figure 1), followed by image denoising. Each block was then processed with these four methods to generate the respective coefficient matrix. The representative part of the coefficient matrix for each block was determined accordingly (a-d) and arranged into a feature array. The feature arrays for all blocks were assembled to build a feature matrix that was directly used to compute the four types of features. For (a), we calculated the standard deviation of the FFT coefficients for the quarter annular regions to generate the feature array. In (b), six of upper left corner elements of the generated coefficient matrix were collected for each block and rearranged as a feature vector. As for (c), the pixel values of each 8 × 8-pixel block were rearranged as a 1-D vector that was further separated into two sequences, each of which contained 48 elements with 32 element overlap. The log root mean square (LRMS) value 9 was then calculated for the six sub-bands and the original sequence (i.e. W₁₁) to establish 7 features elements for each sequence. For each 8 × 8-pixel block in (d), we evaluated the P function for eight gray levels in four different directions, leading to a total of 32 elements.

Prior to calculation of the FFT features [38], each target slice was divided into 9 × 9-pixel blocks and then denoised with a median filter for removing salt and pepper noise, and a low-pass filter to suppress high-frequency noises. Due to the symmetry of frequency spectrum with respect to its center, the half of the 9× 9 FFT coefficient matrix was preserved for each block and further divided into quarter annular regions (marked with regions 1–4 in Figure 2). The standard deviation of the FFT coefficients was then calculated for each of the four regions to generate a four-element feature array. The assembly of the feature arrays for all blocks yielded a feature matrix that was directly used for establishing the FFT features with the statistical measures. Similarly, when establishing the DCT features [39], we divided an image slice into 8 × 8-pixel blocks and analyzed these blocks individually with the DCT algorithm. Six of upper left corner elements of the generated coefficient matrix were collected for each block and rearranged as a feature vector Figure 2b). The assembly of the 6-element feature vectors was performed to build a large feature matrix to derive the DCT features.

To extract wavelet features [40], the pixel values of each 8×8-pixel block were rearranged as a 1-D vector that was further separated into two sequences, each of which contained 48 elements with 32 element overlap (one containing the first 48 elements of the vector and the other having the last 48 elements). Given each sequence, six sub-bands including W₂,₁, W₂,₂, W₃,₁, W₃,₂, W₃,₃, W₃,₄ (Figure 2c) were generated using the discrete wavelet transform (DWT) algorithm. The log root mean square (LRMS) value φ was then calculated for the six sub-bands and the original sequence (i.e. W₁,₁) to establish 7 elements for each sequence, leading to a total of 14 elements for each block.

$$\phi =\mathit{log}(\sqrt{mean(W_{i,j}{}^2)}$$ 1)

As for the GLDM features, they were derived from the P function [37], which can be expressed as the probability density function of gray level i for any given displacement vector $d=(dx,dy)$,

$$P(i|d)=\mathit{Prob}(diff(n,m)=i)$$ 2)

where $diff(n,m)=|I(n,m)-I(n+d,m+d)|$. For each divided 8×8-pixel block, we calculated the P function for eight gray levels in four different directions: (0, d), (−d, d), (d, 0), and (−d, −d). The increment d was set to be 4 for all calculation (Figure 2d).

The above-described procedures for extraction of the five groups of features were applied on both the pre- (ℱ) and post-therapy ($\widehat{\mathcal{F}}$) CT images to identify any feature changes due to the treatment. Such feature changes that were formulated as $\Delta {\mathcal{F}}_i=\frac{{\widehat{\mathcal{F}}}_i-{\mathcal{F}}_i}{{\mathcal{F}}_i},i=1,\dots m$. were finally used in the prediction of response to the therapy. In accordance with the RECIST criteria that usually consider up to five tumors per patient, we averaged the feature values of the same number of tumors for each patient.

To assess the prediction performance of individual features, we first computed the area under the ROC curve (AUC) using a ROC curve fitting program (ROCKIT http://www-radiology.uchicago.edu/krl/, University of Chicago), which is based on an adapted bi-normal model with maximum likelihood estimation method. Using the AUC value as an indicator of feature discrimination power, all the features were sorted to determine the best performers. We further analyzed the performance difference among different feature groups (i.e. the DCT, FFT, Wavelet, etc) and different statistic groups (e.g. energy, RMS, mean, etc).

2.4. Feature optimization

Given the initial feature pool including 133 features, all the features with an AUC above 0.65 will be used to generate the optimal feature cluster using particle swarm optimization (PSO) algorithm [41, 42]. As indicated by the flow chart in Figure 3, the PSO algorithm works by assigning a set of particles (as variables to be optimized) that diffuse in the search space, each of which could be a potential solution for the optimization problem. At each iteration, two best values are recorded for each particle: (i) the best local solution it has achieved so far (p_ld); and (ii) the best global value that has been obtained so far by any particle in the population (p_gd). All the particles are gradually guided toward the best known position in the search space. In our implementation, each particle represented a weight vector that would be applied to the individual features). There existed 200 particles as candidate solutions in the search space at each iteration step. The particles’ positions were initialized with a uniformly distributed random vector, and their best positions were initialized to its initial positions. At each iteration, the particles’ positions (or the weight vectors) would have incremental changes that were determined only by the discrepancies between the current positions and the best known local and global positions. The update is computed by the following formula,

Figure 3:

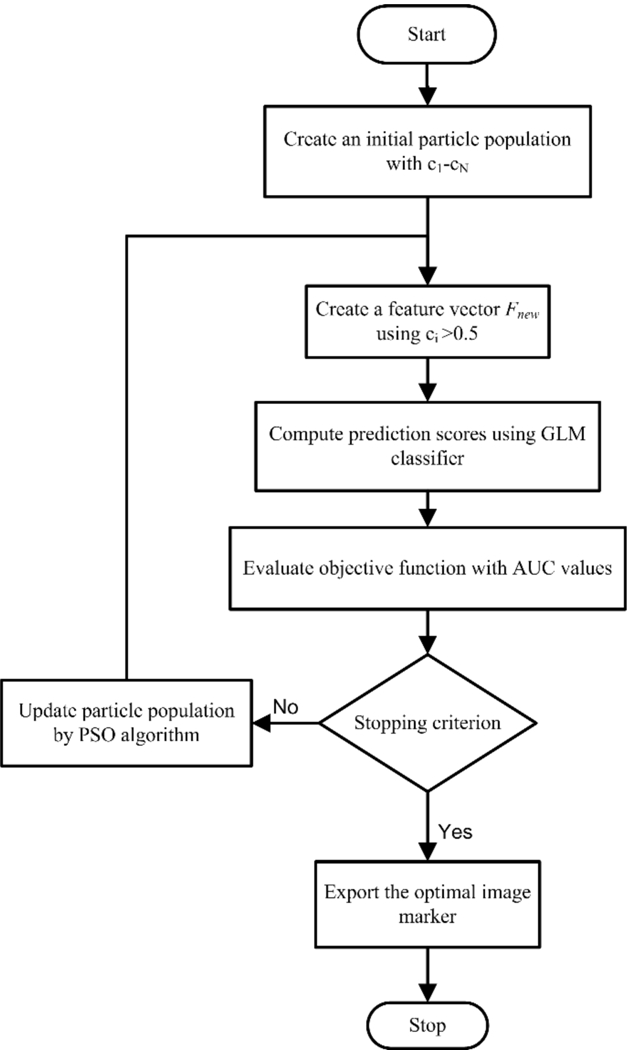
The flowchart of feature optimization using the PSO approach

$$z_{id}(n+1)=z_{id}(n)+v_{id}(n+1)$$ 3)

where z_id and v_id denote the position and moving speed of the particle i at the n_th iteration, and the moving speed v_id was given by,

$$v_{id}(n+1)=w{v}_{id}(n)+{\alpha }_1\gamma (p_{ld}-z_{id}(n))+{\alpha }_2\gamma (p_{gd}-z_{id}(n))$$ 4)

As explained earlier, p_ld and p_gd were the local and global optimal positions over the n_th iterations; w, α1 and α2 were predefined coefficients; γ was a random number with a value falling into [0, 1].

As a new feature vector $\overrightarrow{\mathcal{F}}$ was formed at each iteration, the features with coefficient c that were smaller than 0.5 were considered non-significant features and removed. With a stopping criterion of 40 iterations, an optimal feature cluster was iteratively searched by minimizing an objective function ψ, which is designed to indicate the prediction error,

$$\psi =\mathrm{argmin}\left(\mathbf{|}1-\overline{{\mu }_A}\mathbf{|}+\mathbf{\left|}{\sigma }_{\overline{{\mu }_A}}\mathbf{\right|}\right)$$ 5)

To calculate the mean ($\overline{{\mu }_A}$) and standard deviation (${\sigma }_{\overline{{\mu }_A}}$) of the AUC value in Equation 5, we adopted the Generalized linear model (GLM) [43, 44] to obtain the classification scores for all the samples. GLMs extends a linear regress model, involving three components: (i) a random component Y_i, specifying the conditional distribution of the response variable; (ii) a linear predictor (i.e., a linear function of regressors X_ij that is pre-specified functions of the explanatory (predictor) variables); and (iii) an invertible linearizing link function ${\text{Ψ}}^{-1}$, which transforms the expectation of the response variable μ_i, to the linear predictor,${\text{μ}}_{\text{i}}=\text{Ψ}\left({\text{β}}_0+{\text{β}}_1{\text{X}}_{\text{i}1}+{\text{β}}_2{\text{X}}_{\text{i}2}\dots \right)$. To fit a GLM into our problem, we selected Binomial as family type to encompass binary data, 0 (No) or 1 (Yes) for Y_i. Consequently, we use Logit link specific to Binomial distribution to map the interval of μ_i that is confined to the unit interval [0,1] to the entire real line, from −∞ to +∞. To evaluate the predictive performance of the developed model, we implemented internal validation (with cross-validation technique) in the current study, which is considered as the most appropriate method for limited data by the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) Statement [45]. Specifically, the model performance was assessed by leave-one-out cross validation, where the data set was split into N folds, N is the number of data points in the set; and in each fold, the GLM classifier was trained on all the data except for one point and a prediction is made for that point. The result was counted as the prediction score for that test point; and the process was repeated as many times as the number of points in the set. This ensures that the model is trained on sufficient samples given a limited dataset without a case selection bias as widely used in previous studies [29, 46].

3. Results

3.1. 3D tumor segmentation

As illustrated in Figure 4, the same tumor appearing on a series of z-stack CT image slices was segmented by a slice-by-slice strategy. Usually the central slice contained the largest tumor area, which had been visually marked by the radiologist. The tumor area decreased gradually in the 1st, 2nd, and 3rd adjacent slices, and it eventually disappreared in the 4th adjacent slice (Figure 4a). Accordingly, the segmention scheme started with the identification of the tumor boundary on the central slice, leading to a centeral point of the tumor that is used to guide the segmentation on the remaining slices (Figure 4b). The segmented tumors are shown in Figure 4c.

Figure 4:

An illustration of tumor segmentation by outlining its boundary contours.

3.2. Evaluation of the spatial andfrequency domain features

Figure 5 compares the AUC values among different statistical measures (e.g., energy, entropy and skewness) and different groups (e.g., FFT, DCT and Wavelet). Among all the 133 features (involving 15 statistical measures and 5 different methods), 48 features (i.e. 36% of the total features) achieved an AUC value higher than 0.65 (Figure 5a), among which skewnessGLDM4, RmsGLDM4 and meanGLDM4 were the top three performers with an AUC value of 0.740±0.092, 0.731±0.094, 0.720±0.092, respectively. Figure 5b compares the performance of the five different groups. Our statistical analysis indicated that the DCT- and FFT- related features yield the highest and lowest average AUC, that is, 0.634±0.098 and 0.565±0.094, respectively. Moreover, the difference between the performances of these two groups was statistically significant (with P < 0.01). We averaged the AUC values of each of 15 statistical measures in all the five groups, as shown in Figure 5c. Our result shows that these statistical measures led to AUC values ranging from ~0.5 to ~0.7. The energy and sumDeviation exhibits a significant difference in their performance, while most of the remaining measures generated indistinguishable AUC values, that is, approximately 0.6. Taken together, the data indicates the superiority of the DCT method over the other four methods, and the effectiveness of almost all the chosen statistical measures in our study.

Figure 5:

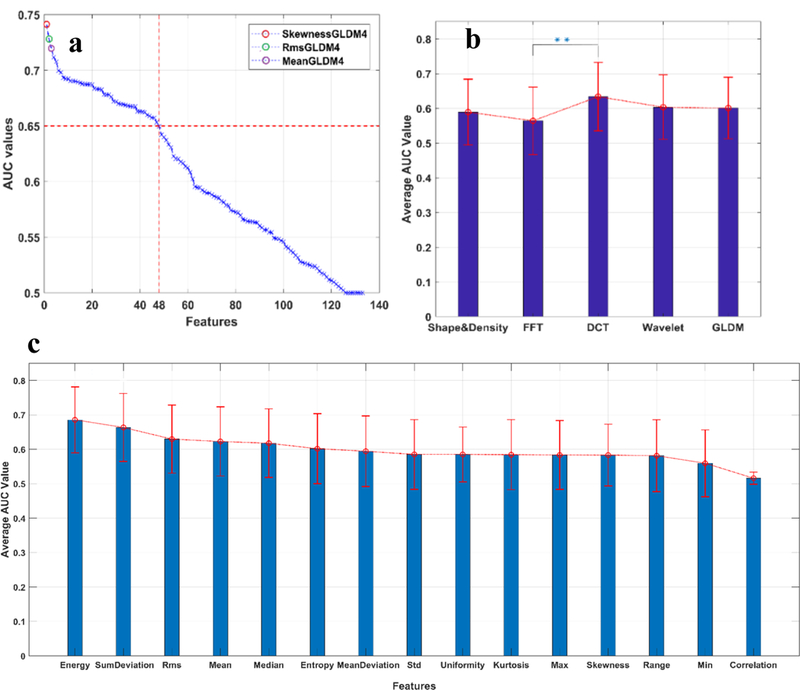
The performance of the spatial and frequency domain features. All the features were sorted using the AUC value as an indicator of feature discrimination power. The top performing features are indicated with color circles in (a).From (a), it can also be observed that 48 of total 133 features (i.e. 36%) achieve an AUC value higher than 0.65. (b) shows comparison of the average performance of the five group features. The result showed that the DCT group was significantly more effective than the FFT group, and slightly advantageous over the other three groups. (c) displays the average performance of each of the 15 statistical measures. Although the performance of the energy and sumDeviation were found to be significantly distinct, most of the remaining measures generated compatible AUC values, i.e., around 0.6, suggesting the effectiveness of almost all the chosen statistical measures in our study.

3.3. Correlation analysis of features

We computed the Pearson correlation coefficients for a total of 133 features, with 120 observations for each feature. The resultant correlation matrix of the 133 features is the matrix of correlation coefficients for each pairwise feature combination. The heat map in Figure 6a reveals that the shape & density group has features with less dependence compared to FFT, DCT, Wavelet and GLDM. One possible reason for the existence of higher correlation coefficients for these four groups is that after the image transformation, the same set of statistical measures were applied onto the images to generate the corresponding features. We further counted the number of correlation coefficients falling into the six categories (Figure 6b), with the mean value of each category indicated on the x-axis. The chart shows more than 70% of the absolute correlation coefficients were less than 0.3, indicating that the feature pool designed in our study provides a comprehensive view of the tumors, but containing little redundant information.

Figure 6.

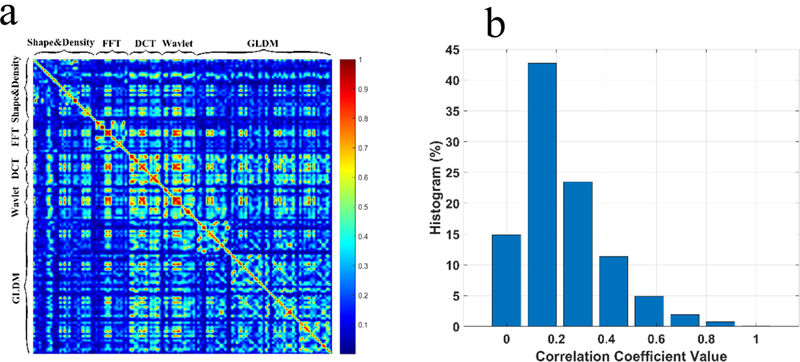
Correlation analysis of features, (a) The heat map of the Pearson correlation coefficients, (b) Histogram of correlation coefficients for the features.

3.4. Assessment of the performance of image marker optimized with the PSO approach

Figure 7a provides the convergence curve of the feature optimization using the PSO algorithm, showing a remarkably decrease in the value of the objective function within the first 10 iterations, followed by a slow convergence during the next 20 iterations. The value decreased to 0.19 after the 10th iteration, and reduced to slightly below 0.18 after the next 20 iterations. Meanwhile, the AUC increased by 21% to 0.855±0.037 over 30 iterations, as illustrated in Figure 7a. Accordingly, we examined and displayed the classification performances the synthetic features generated at the end of 10, 20, and 30 iterations in Figure 7b. As discussed earlier in the Methods section, the PSO assigned each feature a weight during each iteration and generated a new synthetic feature by combining those features with significant weights. By the end of the 40 iterations, the feature pool was narrowed down to a total of 11 features (with the weights coded by color) belonging to four groups, namely, Shape&density (4), DCT (3), GLDM (3) and Wavelet (1),as shown in Table 3. Moreover, the features in the Shape&density group generally had larger weights than some in the DCT and GLDM groups, indicating the importance of those features in establishing the optimal synthetic feature. As can be seen from Figure 7c, the synthetic optimal feature achieved a considerable better result than the best single feature, indicating the effectiveness of the optimization process with the PSO algorithm. We further assessed the significance of those components associated with the 6-month PFS result (Table 3), together with 95% confidence intervals (CIs) for the AUC value of each individual feature. The result shows the P values range from 0.002 to 0.017, including 8 components less than 0.01, indicating the strong association of those features with the patient outcome. Moreover, most of those features came from the frequency domain analysis, suggesting their importance in providing complementary information to spatial domain features that were conventionally used in cancer prognosis.

Figure 7:

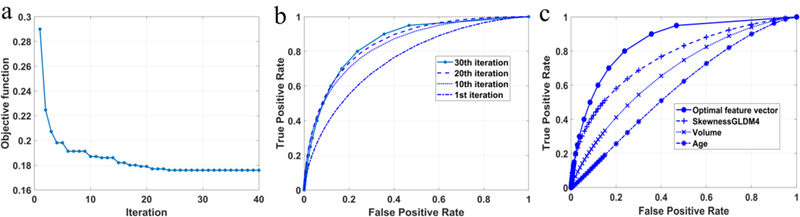
The performance of optimization with the PSO algorithm. (a) The convergence curve of the objective function that minimizes the negative mean of the AUC value for the synthetic feature. (b) The ROC curves generated every 10 iterations. A significant change of the area size was observed between the first and 10^th iterations. (c) The comparison between the optimal synthetic feature, the best-performing single feature, tumor volume analysis, and patient age.

Table 3.

The statistics of the optimal feature cluster

	Type	Coef	Lower 95% (AUC)	Upper 95% (AUC)	P
SkewnessGLDM4	GLDM	1	0.62	0.83	0.017
EnergyGLDM4	GLDM	l	0.62	0.81	0.008
CorrelationWAV	Wavelet	1	0.61	0.79	0.022
EnergyDCT	DCT	1	0.61	0.79	0.003
Energy	S&D	1	0.61	0.79	0.005
SkewnessGLDMl	GLDM	0.63	0.58	0.77	0.002
SurfaceArea	S&D	0.97	0.60	0.78	0.004
SphericalDisproportion	S&D	1	0.59	0.77	0.011
SumDeviation	S&D	1	0.58	0.76	0.002
RangeDCT	DCT	0.58	0.56	0.76	0.004
MeanDCT	DCT	0.65	0.58	0.76	0.004

Table 4 shows a confusion matrix to compare the performance of the imaging marker (optimized with the PSO approach) and radiologists’ assessment results based on the RECIST criteria. By further examining the result, the overall prediction accuracy levels of 78.3%, and 70.8% were achieved by the imaging marker and radiologists’ assessment, respectively. It is noted that the radiologists’ rating was slightly accurate to identify true positives, but more inclined to produce larger false positive errors.

Table 4.

The confusion matrix for imaging marker and pre-recorded radiologist’s assessment

Prediction\6-month PFS	Imaging marker		Radiologists’ Assessment
	Yes	No	Yes	No
Yes	59	17	61	28
No	9	35	7	24

4. Discussion

According to the Radiomics concept [26], developing new quantitative image markers to predict responses of ovarian cancer patients is a promising and cost-effective approach to assess efficacy of the post-surgical chemotherapy. It provides a new quantitative decision-making supporting tool to help establish the precision medicine that takes the individual variability of different patients into account [47]. In this study, we proposed and evaluated a new quantitative image marker to predict response of ovarian cancer patients to the chemotherapy. For this purpose, a comprehensive list of image features was explored and computed from both spatial and frequency domain aiming to more effectively extract the heterogeneity information of the metastatic tumors in patients with advanced-stage ovarian cancer, which can provide higher discriminatory power for the early-stage prediction of the chemotherapy responses.

In order to help effectively predict prognosis of ovarian cancer patients and/or their response to the chemotherapy, a number of previous studies have been reported to identify and test variety of genomics based biomarkers [48–50] and imaging markers that captured tumor heterogeneity in the spatial domain, especially the volumetric changes of the tumors [36, 51, 52]. By comparison, this study is different from the previous studies in the following two unique aspects:

First, we built the extensive feature pool that included 133 features composed of classical statistical measures to characterize tumor formation not only in the spatial domain, but also in the frequency domain. To extract such frequency domain information, we computed FFT, DCT, Wavelet features on the CT images, which contained abstract, but copious pattern information on tumor heterogeneity as those in the spatial domain. By evaluating the prediction performance of every single feature, the top three features were skewness, RMS, and Average GLDM values. Considering the nature of these three features created in spatial domain, we may conclude that the change of the variance in tumor density arising after the treatment may effectively manifest the therapy efficacy. However, if we averaged the performance of the features in each of five different categories, the DCT features was observed to be more effective than the other groups, showing the significance of acquiring such frequency domain features. Furthermore, a close examination of the features in the frequency domain revealed that almost all of them were associated with an AUC values greater than or equal to 0.6, which may imply that those features were positively relevant to the prediction of early chemo-response in ovarian cancer.

Second, we further generated a new quantitative image marker by combining the weighted features selected by the PSO algorithm. The PSO algorithm eventually selected 11 features to generate the image marker. By grouping these features into different feature categories, we observed that there are 7 and 4 features computed from the spatial and frequency domain, respectively, which indicates that the frequency domain features are at least as important as the spatial domain features in the establishment of this new image marker. Compared to an AUC value of 0.743±0.085 attained by the best single feature, the resultant image marker effectively increased AUC value to 0.855±0.037. Moreover, we found that the PSO algorithm converged very efficiently, evidenced by a 21% increase in the AUC value after 30 iterations.

Despite the encouraging results, we recognize that this study has the following limitations. First, the database we used was only from one institution with a limited number of cases; therefore, a more diversified dataset including the cases from more than one institutions would be desirable to further test the reliability and robustness of our proposed scheme. Interpretation and reproducibility are recognized as key factors in the field of radiomics. Large quantities of high- level (or synthetic) features from radiomics studies significantly impede clinical interpretation. In this regard, the establishment of a knowledge database has been suggested to define high-level tumor imaging characteristic for enriching interpretation in medical centers [53]. Another concern that arises from radiomics is the reproducibility of results that depend on a number of factors, including technical complexity, study design, imaging parameters, and standardization for validation study. Therefore, a well-designed radiomics study should be validated against an entirely independent data set from a distinct institution [54]. Second, we did not associate features with patients taking different chemotherapy drugs or possessing different demographic characteristics (e.g., geographic region, age, tumor stage and grade). The cancer patients in each category may have their unique underlying biological responses to the therapies, which should be better described by a feature cluster specifically optimized for this subcategory. Third, we only extracted the prognostic information from radiographic images. The recent studies demonstrated a rich collection of quantitative features from histology images are strongly associated with cancer prognosis. Thus, it would be meaningful in the future study to integrate the quantitative histopathologic image features to further improve the prediction accuracy.