Treatment plan complexity does not predict IROC Houston anthropomorphic head and neck phantom performance

Abstract

Previous works indicate that intensity-modulated radiotherapy (IMRT) and volumetric modulated arc therapy (VMAT) plans that are highly complex may produce more errors in dose calculation and treatment delivery. Multiple complexity metrics have been proposed and associated with IMRT QA results, but their relationships with plan performance using in situ dose measurements have not been thoroughly investigated. This study aimed to evaluate the relationships between IMRT treatment plan complexity and anthropomorphic phantom performance in order to assess the extent to which plan complexity is related to dosimetric performance in the IROC phantom credentialing program. Sixteen complexity metrics, including the modulation complexity score (MCS), several modulation indices, and total monitor units (MU) delivered, were evaluated for 343 head and neck phantom irradiations, comprising both IMRT (step-and-shoot and sliding window techniques) and VMAT. Spearman’s correlations were used to explore the relationship between complexity and plan performance, as measured by the dosimetric differences between the treatment planning system (TPS) and thermoluminescent dosimeter (TLD) measurement, as well as film gamma analysis. Relationships were likewise determined for several combinations of subpopulations, based on the linear accelerator model, TPS used, and delivery modality. Evaluation of the complexity metrics presented here yielded no significant relationships (p > 0.01, Bonferroni-corrected) and all correlations were weak (less than ±0.30). These results indicate that complexity metrics have limited predictive utility in assessing plan performance in multi-institutional comparisons of IMRT plans. Other factors affecting plan accuracy, such as dosimetric modeling or multileaf collimator (MLC) performance, should be investigated to determine a more probable cause for dose delivery errors.

1. INTRODUCTION

Intensity modulated radiation therapy (IMRT), including volumetric modulated arc therapy (VMAT), is currently a standard of care technique for many disease sites. This delivery technique allows for better dose conformity than traditional three-dimensional conformal radiation therapy while simultaneously sparing normal tissues from extraneous radiation dose. However, this technique also requires variations in multileaf collimator (MLC) motion, as well as gantry rotation speed and dose rate in some cases. Such sources of variability increase the plan “complexity,” a term describing the frequency and amplitude of fluctuations in IMRT dose distributions (Mohan et al., 2000). Thus, a simple IMRT treatment consists of large beam apertures of regular shapes, and complex IMRT beams tend to have small, narrow, or irregularly shaped apertures.

Many have previously reported that the degree of complexity (i.e. beam modulation) may be associated with greater uncertainties in radiation treatments (McNiven, Sharpe and Purdie, 2010; Younge et al., 2012; Masi et al., 2013; Crowe et al., 2014; Du et al., 2014; Park et al., 2014; Götstedt, Hauer and Bäck, 2015). This is a logical supposition as high-complexity treatment plans include more challenging dose calculations and increased sensitivity to mechanical delivery performance, especially when using very small fields. The potential for delivery errors associated with highly complex plans has ushered the need to characterize and mitigate complexity in IMRT. To do so, researchers have developed several metrics as indicators of plan complexity, consisting of both fluence map-based and aperture-based metrics (McNiven, Sharpe and Purdie, 2010; Younge et al., 2012; Masi et al., 2013; Crowe et al., 2014; Du et al., 2014; Park et al., 2014; Götstedt, Hauer and Bäck, 2015). Fluence map-based metrics, such as the modulation index proposed by Webb, et al., measure the variations in photon fluence between adjacent pixels in a fluence map (Webb, 2003). Aperture-based approaches measure complexity by directly measuring the irregularity of the treatment field, as defined by the MLC, although some metrics also evaluate other plan parameters, such as leaf speed and variations of the dose rate and gantry speed.

Complexity metrics have also been suggested to be a time-efficient complement to current IMRT quality assurance (QA) methods, as they further inform the extent of beam modulation in the treatment and therefore may flag cases where the plan modulation is higher than would normally be expected. This application is of particular interest to the Imaging and Radiation Oncology Core Houston (IROC) Quality Assurance Center. IROC seeks to confirm that institutions participating in National Cancer Institute sponsored clinical trials, including those utilizing IMRT, can calculate and deliver radiation doses consistently and accurately. For IMRT, this is done through the use of end-to-end anthropomorphic phantom irradiations whereby institutions irradiate an IROC phantom containing thermoluminescent dosimeters (TLD) and radiochromic film (Molineu et al., 2005). The measured dose distribution is then compared to the institution’s calculated dose distribution. Yet, even with improvements in IMRT planning and delivery over time, and relatively lax dosimetric agreement criteria for the phantom (7%), a sizeable percentage of institutions continue to fail the phantom test; only 85–90% of institutions have passed in recent years (Molineu et al., 2013). Of concern, dose calculation inaccuracies have been shown to be a leading cause of treatment delivery error (Carson et al., 2016; Kerns et al., 2017). If complexity could be used to predict treatment accuracy, such analysis would aid in identifying the cause of phantom failures.

Therefore, the purpose of this study was to investigate the relationship between treatment plan complexity and treatment accuracy, with the aim of identifying which complexity metrics best predict planning and/or delivery errors and how much complexity contributes to dosimetric errors in IMRT delivery. To date, a comprehensive evaluation of a broad range of complexity metrics, has not been done, particularly using a single, controlled patient geometry. This evaluation, as performed using IROC phantoms, has the potential to identify metrics related to the agreement between dose calculations and measurements. In addition, the information produced in this work may be used to better inform the treatment planning process or guide QA testing in order to mitigate potential errors.

2. METHODS

2.1. Phantom plans

A total of 343 IMRT and VMAT irradiations of IROC’s head and neck (H&N) phantom (including 11 repeat irradiations) were performed by 312 different institutions between September 2011 and December 2016 as part of IROC’s phantom credentialing program. The H&N phantom was chosen for evaluation because it is the most frequently irradiated phantom and is the default credentialing phantom for IMRT. The phantom contains two PTV targets and an organ at risk, and the dose was assessed with 6 double-loaded TLD and two sheets of film. Phantom performance was evaluated by comparing the dose calculated by the TPS with the dose actually delivered. Additional details on the phantom and analysis program are available in the literature (Molineu et al, 2005).

Despite the uniform geometry and planning objectives, the phantom irradiations were done with a broad cohort of delivery methods, and thereby a variety of different complexities. The demographics of these are detailed in Table 1. This cohort was limited to 6 MV photon treatments administered by Varian and Elekta linear accelerators, which account for the vast majority of H&N phantom irradiations. For all of these irradiations, institutions irradiated identical phantoms and were instructed to follow the same IROC protocol for phantom irradiation, thus achieving very similar dose distributions (Molineu et al., 2005).

Table 1.

Demographics of IMRT technique, treatment planning system (TPS), linear accelerator manufacturer, and linac-TPS combination for the sample of this study.

	N	%
IMRT technique
Dynamic MLC	93	27.1
Static MLC	43	12.5
VMAT	207	60.3
Linear accelerator manufacturer
Elekta	39	11.4
Varian	304	88.6
Treatment planning system
Eclipse	249	72.6
Pinnacle	69	20.1
RayStation	9	2.6
Other*	16	4.7
Linac-TPS combination
Elekta-Eclipse	1	0.3
Elekta-Pinnacle	24	7.0
Elekta-RayStation	4	1.2
Varian-Eclipse	248	72.3
Varian-Pinnacle	45	13.1
Varian-RayStation	5	1.5

^*Other TPS include XiO, iPlan, Monaco, and Oncentra

2.2. Complexity metrics

In this study, sixteen identified measures of complexity were computed for each of the 343 phantom plans in order to provide a comprehensive view of complexity definitions, including both aperture-based and fluence map-based metrics. Here we considered both established measures of IMRT complexity from the literature, as well as several additional metrics describing variations within the MLC position, gantry position, and dose rate, thus allowing for a more well-rounded assessment of IMRT treatment delivery. For each of the metrics described herein, complexity was calculated for each beam or arc in a treatment plan, and subsequently averaged for all beams or arcs to yield the plan’s average complexity. The following indices were evaluated:

• a)Total monitor units (MU) delivered. In general, a high degree of complexity is typically associated with a large number of MU; this has been used as a surrogate for treatment plan complexity previously, though correlations have not been definitive (Masi et al., 2013; Agnew, Irvine and McGarry, 2014; Kry et al., 2014; Crowe et al., 2015).
• b)Modulation complexity score (MCS) (McNiven, Sharpe and Purdie, 2010). The MCS aims to characterize beam complexity in terms of the aperture shapes and area present throughout treatment. This metric was originally conceptualized for step-and-shoot delivery but was later adapted for sliding window and VMAT techniques (Masi et al., 2013). A smaller MCS indicates more complex apertures.
• c)Edge metric (EM) (Younge et al., 2012). This metric defines complexity as a ratio of MLC side length edge to aperture area. In this study the original recommendations for the input parameters (C1 = 0 and C2 = 1) were used. A larger EM index signifies larger positional differences between adjacent leaves.
• d)Plan irregularity (PI) and plan modulation (PM) (Du et al., 2014). PI describes the noncircularity of the MLC apertures, whereas PM indicates to what extent the beam delivery is delivered into smaller apertures.
• e)Modulation indices (MI_speed, MI_accel, MI_total) (Park et al., 2014). MI_speed and MI_accel evaluate the extent of variation within the speed and acceleration of the MLC, respectively. In addition to these variations, MI_total also considers variations in gantry speed and dose rate to quantify the total delivery complexity.
• f)Leaf travel (LT) (Masi et al., 2013). LT indicates the average distance traveled by the MLC leaves. Because LT was originally designed for single full arc treatments, this metric is divided by the treatment’s corresponding arc length to allow for comparisons with treatments with multiple arcs or partial arcs. Here the metric is denoted “LT/AL” to establish this modification.
• g)Mean dose rate variation. This metric is defined as the sum of dose rate variations from all control points, divided by arc length (to allow comparisons of plans with different numbers of control points).
• h)Mean gantry speed variation. Like mean dose rate variation, this index is the sum of variations in gantry speed, divided by arc length.
• i)Percentage of MLC gaps >10 mm. This metric describes the cumulative window width for MLC leaves. Plans with a small cumulative metric indicate the use of many small MLC gaps. Here we choose 10 mm as an appropriate threshold in order to delineate the difference between large and small leaf gaps.
• j)Mean tongue and groove index. This index is calculated for each pair of leaves and for each control point as a fraction of the MLC gap adjacent to a consecutive leave. The mean index is then obtained by averaging all the pairs of leaves inside the beam and all the control points.
• k)MLC interdigitation. This index characterizes the overlap between consecutive leaves from opposing banks with respect to the maximum interdigitation, taking into account the complete irradiated area outline of the MLC.
• l)Mean MLC speed variation. The mean variation in MLC speed is computed as the sum of MLC speed variations (i.e. MLC accelerations), divided by the total leaf travel.
• m)Mean Gap speed variation. The mean variation of gap sizes is computed as the sum of gap size variations, divided by the total leaf travel.

2.3. Data analysis

To quantify the previously described complexity indices, a MATLAB-based software called PlanAnalyzer was used to read the DICOM plans submitted by the institutions undergoing phantom credentialing (Hernandez et al., 2018). These measures of plan complexity were compared against the dosimetric error found for each delivered plan. The average TLD error was defined as the average magnitude percentage difference between the TPS-calculated doses and the corresponding measured doses for the TLD in the H&N phantom (6 TLD per phantom). Because point dosimetry may not fully characterize the irradiation conditions, plan error was also measured by the percentage pixels passing from radiochromic film gamma analysis, following IROC’s protocol for analysis with the criteria of 7% dose agreement and 4 mm distance to agreement (Molineu et al., 2013).

Correlations between complexity metrics and phantom plan error were determined using Spearman’s rank-order correlation coefficients (with Bonferroni corrections applied for multiple comparisons). For the purposes of this work, the strength of the association in absolute value was defined as follows: 0–0.19 was regarded as “no correlation,” 0.20–0.39 as “weak,” 0.40–0.59 as “moderate,” and 0.60–1 as “strong.” Correlations were evaluated for the entire sample, as well as according to TPS (Pinnacle and Eclipse), machine type, and delivery technique, as delineated in Table 1. Similarly, poor phantom results, those with at least one TLD measuring >5% error, were segregated, and the same analyses were applied to visualize whether such clinically underperforming plans had distinguishing features.

3. RESULTS

3.1. The relationship between TLD-based plan error and complexity metrics

Despite the uniformity of the phantom and dose objectives, the plans in this study had a comprehensive assortment of treatment complexities; for example, monitor units (MU) used in delivery ranged from 458 to 3358 with a mean of 1883. Figure 1 shows the distributions of the MCS and corresponding plan error for the total sample and multiple subsamples examined in this work. Visually, these distributions represent poor ability of complexity metrics to be utilized as a means of distinguishing irradiations prone to error, at least under the circumstances examined herein. Other complexity metrics appeared similarly and yielded indistinguishable relationships.

Figure 1.

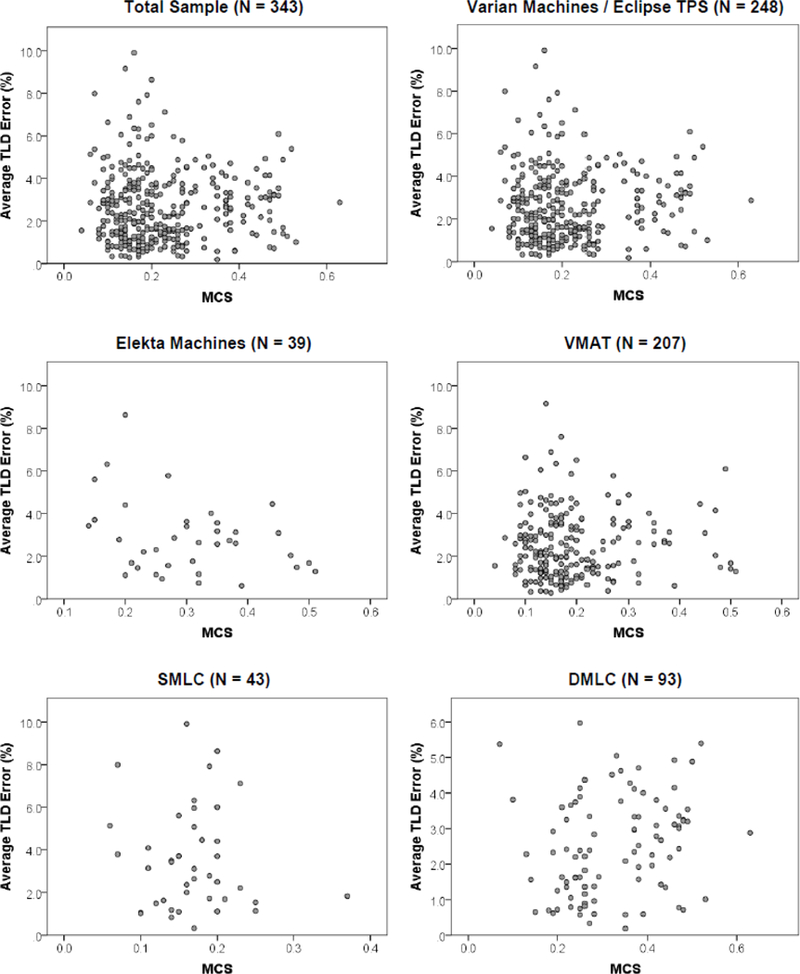
Scatter plots of average absolute TLD error versus complexity metrics for the whole sample and several subsamples in this work. The distributions showed no correlation between the measured TLD error and the assessed complexity metric, here shown as the MCS (smaller values of MCS correspond to more complex plans). SMLC = static MLC, DMLC = dynamic MLC.

Relationships between complexity metrics and plan error are shown in Table 2. The only index to achieve significance was MLC interdigitation (p < 0.003); no other complexity metric significantly predicted dosimetric inaccuracies in the calculation or delivery of the radiation dose. However, even this single significant relationship, found for the total sample and also only Varian machines, had a very low correlation strength (|rs| < 0.18), which indicated no clinically meaningful relationship by our criteria. The highest correlation was found between LT/AL and Elekta machines supported by Pinnacle (r_s = −0.395, p = 0.116), but this correlation coefficient was still classified as “weak” and was not found to be a significant relationship, partly due to the small subsample size. From this data, it is evident that complexity metrics are not related to the TLD error observed in IROC’s H&N phantom practice, regardless of delivery technique, TPS, or machine manufacturer.

Table 2.

Summary of Spearman correlations (r_s) comparing average absolute TLD error and complexity metric value for the subsamples described in this study (i.e. machine manufacturer, TPS, or delivery method).

	MU	MCS	EM	PI	PM	MI speed	MI accel.	MI total	LT/AL	Mean DR Var.	Mean GS Var.	Gap >10mm	Mean TG	MLC Inter- digitation	Mean MLC Speed Var.	Mean Gap Speed Var.
All Machines  rs N = 343 p	−0.025 0.645	0.031 0.570	−0.119 0.027	−0.082 0.130	−0.018 0.742	−0.024 0.655	−0.028 0.599	−0.007 0.899	−0.006 0.931	0.025 0.650	−0.006 0.917	−0.018 0.740	−0.080 0.141	−0.176 0.001*	−0.132 0.015	−0.134 0.013
Varian Machines  rs N = 304 p	−0.022 0.699	0.040 0.484	−0.107 0.063	−0.065 0.256	−0.011 0.853	−0.010 0.864	−0.011 0.853	0.008 0.896	0.002 0.976	0.039 0.500	0.008 0.890	0.015 0.798	−0.065 0.256	−0.174 0.002*	−0.120 0.036	−0.124 0.030
Elekta Machines  rs N = 39 p	−0.016 0.924	−0.303 0.061	−0.150 0.363	−0.071 0.668	0.016 0.922	−0.241 0.140	−0.223 0.173	−0.283 0.081	−0.095 0.636	−0.237 0.147	−0.227 0.165	−0.044 0.791	−0.075 0.649	0.002 0.991	−0.130 0.429	−0.174 0.289
Pinnacle TPS  rs N = 69 p	0.208 0.087	−0.103 0.397	0.233 0.054	0.188 0.122	0.158 0.196	0.018 0.883	0.022 0.855	0.020 0.872	−0.173 0.274	0.002 0.986	0.049 0.688	0.200 0.100	0.171 0.159	0.089 0.466	0.140 0.253	0.159 0.193
Eclipse TPS  rs N = 249 p	0.025 0.697	0.017 0.785	−0.093 0.142	−0.058 0.364	0.055 0.390	−0.080 0.208	−0.066 0.298	−0.070 0.269	−0.059 0.467	−0.063 0.322	−0.075 0.236	0.029 0.646	−0.022 0.730	−0.110 0.082	−0.131 0.039	−0.104 0.102
Varian + Eclipse  rs N = 248 p	0.024 0.708	0.019 0.768	−0.094 0.141	−0.058 0.362	0.056 0.382	−0.078 0.221	−0.065 0.306	−0.070 0.274	−0.054 0.509	−0.065 0.309	−0.076 0.236	0.028 0.659	−0.022 0.725	−0.114 0.073	−0.131 0.039	−0.106 0.096
Varian + Pinnacle  rs N = 45 p	0.143 0.349	0.116 0.447	0.235 0.121	0.200 0.187	0.080 0.603	0.149 0.327	0.124 0.417	0.127 0.405	0.327 0.110	0.103 0.499	0.192 0.207	0.144 0.344	0.124 0.417	−0.042 0.782	0.231 0.127	0.242 0.109
Elekta + Pinnacle  rs N = 24 p	0.296 0.160	−0.446 0.029	0.131 0.541	0.120 0.576	0.225 0.291	−0.295 0.161	−0.282 0.182	−0.314 0.135	−0.395 0.116	−0.311 0.139	−0.187 0.381	0.244 0.250	0.195 0.361	0.203 0.341	−0.144 0.502	−0.111 0.607
VMAT  rs N = 207 p	0.005 0.945	0.021 0.765	−0.077 0.272	−0.008 0.903	0.040 0.571	0.100 0.151	0.089 0.200	0.148 0.033	−0.006 0.931	0.122 0.079	0.119 0.086	0.176 0.011	−0.008 0.904	−0.140 0.044	−0.159 0.022	−0.177 0.011
DMLC  rs N = 93 p	−0.218 0.036	0.240 0.021	−0.188 0.071	−0.079 0.450	−0.088 0.402							−0.052 0.623	−0.179 0.086	−0.220 0.034	0.065 0.534	0.160 0.127
SMLC  rs N = 43 p	0.212 0.172	0.057 0.719	−0.003 0.987	0.119 0.446	0.097 0.535							0.067 0.670	0.111 0.480	−0.031 0.846

^*Correlation is significant at the 0.3% level (required for Bonferroni correction)

Note: DMLC = dynamic MLC, SMLC = static MLC, MU = monitor units, MCS = Modulation Complexity Score, EM = Edge Metric, PI = Plan Irregularity, PM = Plan Modulation, MI = Modulation Index, LT/AL = leaf travel per arc length, DR = dose rate, GS = gantry speed, TG = tongue and groove.

3.2. The relationship between gamma-based plan error and complexity metrics

Figure 2 shows the distributions of treatment complexity and corresponding average film gamma percentage pixels passing for two prominent metrics, MCS and MU. Much like the results of Section 3.1, no significant relationships were evident, regardless of how the sample was broken down (r_s < 0.206, p > 0.05). Upon further inspection, this result is expected because the average absolute TLD error is correlated with the average gamma pass rate (r_s = −0.464, p < 0.001), meaning similar information is provided by both methods of plan error measurement.

Figure 2.

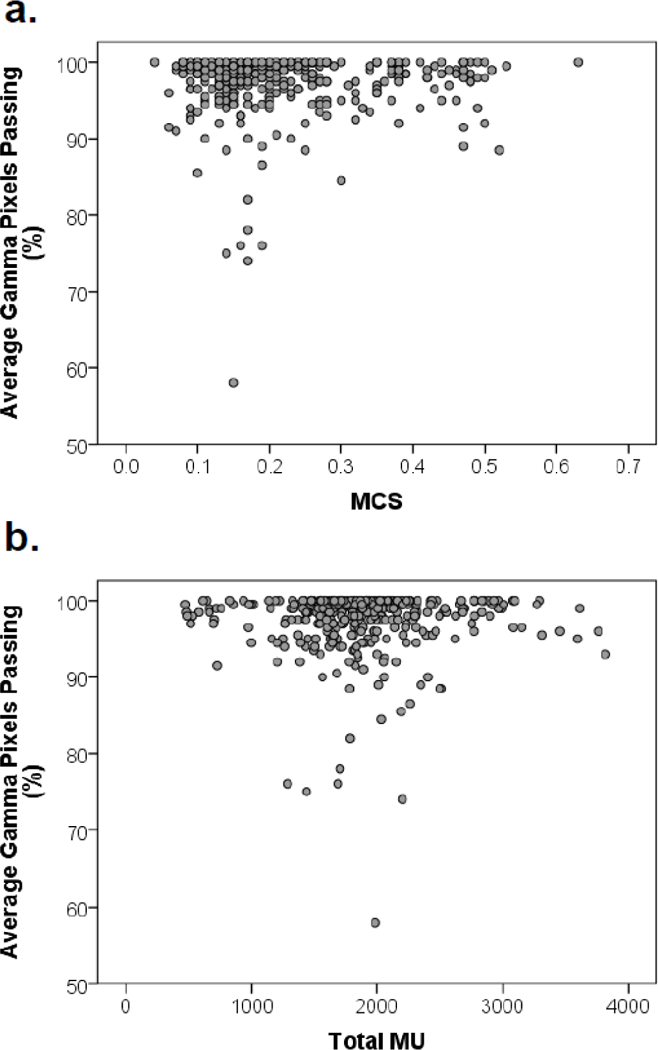
Scatter plots of average gamma pass rate versus complexity metrics for all irradiations examined in this work: (a) modulation complexity score (MCS), (b) total monitor units (MU).

3.3. The relationship between poor performing phantom irradiations and complexity metrics

Of the 343 phantom irradiations initially analyzed, 96 cases were identified as “poor performers” based on a threshold of 5% TLD dose error for any given TLD within the phantom. Figure 3 depicts two distributions of treatment complexity and corresponding plan error. Like previous cases, no relationships were found to be significant, meaning that trends could not be distinguished in even the most concerning of irradiations.

Figure 3.

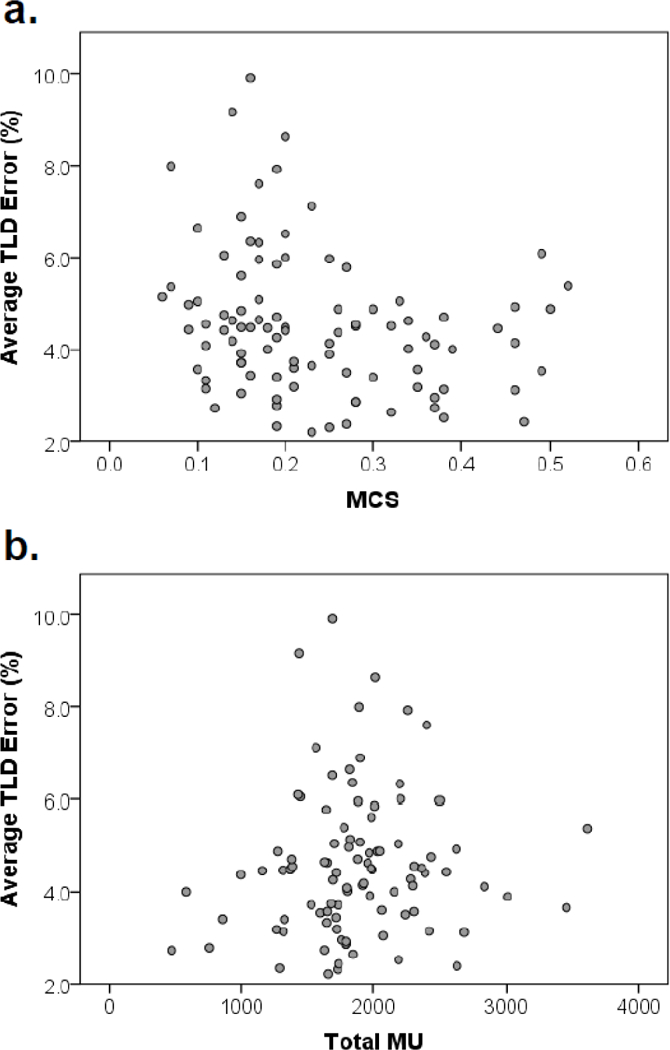
Scatter plots of average TLD error versus complexity metrics for poor performing phantom irradiations: (a) modulation complexity score (MCS), (b) total monitor units (MU).

4. DISCUSSION

In this study, we examined several known measures of complexity, as well as additional plan metrics. These metrics generally have clear physical meanings that describe the beam aperture or fluence. The rationale for examining sixteen metrics was because others have suggested that a single measure may not be able to reveal all the details of the complexity in IMRT plans, nor may an individual metric be suitable for all TPSs (Du et al., 2014; Hernandez et al., 2018). By evaluating several metrics, we quantify different aspects of complexity and generate a much clearer, more comprehensive picture of a treatment plan and its potential challenges. Here the use of complexity metrics allowed for the potential identification of specific relationships that can influence plan performance in IROC’s uniform phantom program.

Unfortunately, the results of this work show that there are no observable correlations between complexity metrics and the observed plan error in recent IROC H&N phantom performance. These results are interesting because they corroborate well with preliminary work that evaluated the utility of the MCS with a small cohort of H&N phantom plans on a single machine (Tonigan, 2011). It was expected that certain metrics would not produce strong correlations based on typical clinical practices: for example, variations of the dose rate are generally well-controlled, and many IMRT plans do not have any dose rate variation. Other studies have also described how some metrics, such as the MCS, do not have a large effect on IMRT QA performance, which may then translate to a lack of relationship in our work (McNiven, Sharpe and Purdie, 2010; Rajasekaran et al., 2015). Additionally, certain metrics provide similar information, as was determined by Hernandez et al. in their comparisons of MCS, PI, and EM, meaning these indices should consequently produce similar results (Hernandez et al., 2018). However, what is somewhat surprising from this work is that none of the sixteen complexity metrics even remotely produced viable relationships with the IROC H&N phantom results under the range of conditions evaluated. Our analyses show that complexity metrics were poor tools for predicting phantom performance and may have limited utility in determining the accuracy of treatment delivery.

Previous works examining IMRT complexity have shown mixed success in determining relationships with plan performance. Götstedt, et al. observed strong correlations between several metrics and gamma pass rates for both EBT3 film and portal imaging using a variety of MLC aperture shapes (Götstedt, Hauer and Bäck, 2015). Likewise, both Masi et al. and Agnew et al. determined that the MCS correlates with gamma analyses for patient-specific QA (Masi et al., 2013; Agnew, Irvine and McGarry, 2014). Building on these ideas, Crowe, et al. suggested that there exist threshold complexity values that can defined to identify plans that are likely to fail QA (Crowe et al., 2014). However, others, such as Du, et al. and McNiven, et al., conceded that their proposed complexity indices did not yield correlations with plan quality metrics (including IMRT QA) but could still have utility in limiting the uncertainty in IMRT performance (McNiven, Sharpe and Purdie, 2010; Du et al., 2014). Of particular interest, the work of McGarry et al., which observed QA phantom irradiations from multiple institutions, discovered weak but significant relationships between MU and plan quality, as well as MCS and plan quality, for all linear accelerators or Varian accelerators considered in their work (McGarry et al., 2016). The work presented here clearly shows no indication of significant relationships between complexity and plan performance based on a relatively large sample of irradiations performed using multiple TPS, linear accelerator models, and delivery techniques.

In previous works relating complexity and plan quality, patient-specific IMRT QA was typically used as a measure for plan performance accuracy. More recently, IMRT QA has come under scrutiny because of it is inability to discriminate unacceptable plans (Kruse, 2010; Nelms, Zhen and Tomé, 2011; Kry et al., 2014; Stojadinovic et al., 2015). Between different institutions, IMRT QA is completed using a plethora of devices, delivery techniques, and criteria for acceptability, which also limit the reproducibility and applicability of results derived from IMRT QA analysis. This work differs from previous studies of IMRT plan complexity in that it is among the first to examine complexity on a single patient geometry, the H&N phantom, using in situ dose measurement to characterize plan error for a multitude of institutions. Although both IMRT QA and IROC phantoms are designed to verify the accurate delivery of IMRT, this distinction is important because the phantom provides a direct comparison between the dose that was planned and that which was delivered, whereas IMRT QA measurements serve as a proxy for treatment accuracy. The H&N phantom is advantageous because all the plans observed had similar treatment objectives, thus eliminating the variability found between patient plans. This phantom also has a conceptual advantage over IMRT QA because its analysis was designed with consistent dose delivery in mind: all its irradiations are processed, analyzed, and evaluated in a consistent manner, and the uncertainties of this process are documented and well controlled (Molineu et al., 2005). Such standardized treatment limits variability and allows for better understanding of overall performance trends in the radiotherapy community.

However, this approach is not without its own limitations. While the phantom test can control for many factors that other studies could not, such as patient geometry, this process also introduces other forms of variance, which can arise from the multitude of beam models used to calculate the dose distributions. Additionally, because the phantom is an end-to-end assessment of the treatment delivery process, it is possible that some of the plan errors observed here do not have a causal link with treatment delivery, but rather other external factors, such as phantom setup. Fortunately, based on IROC experience, incorrect setup does not contribute near as much to phantom errors as do systematic dosimetric inaccuracies (Carson et al., 2016). There may also exist cases for which our methods are not sufficiently sensitive to characterize dose errors caused by excessively complexity plans, yet these would not be of clinical concern, as the measurement uncertainty for each double-loaded TLD is approximately 1.6% (Kirby, Hanson and Johnston, 1992). Lastly, another factor that was not examined, but would pose a valid concern for patient treatment, is the potential effect of motion. Longer treatment times, as is common with high complexity treatments, may increase the sensitivity of dose accuracy to patient/target motion, but this could not be tested with a static phantom.

Though limiting the complexity of a plan may be good practice to limit some planning and delivery uncertainties, other factors may contribute to the degradation of plan accuracy. First and foremost of possibilities is the TPS calculation, which includes the beam modeling and inputs for beam characterization. The use of MLC-shaped beam segments, as is standard in IMRT, requires accurate modeling of several factors, including the leaf end, leaf transmission, and inter-leaf leakage (Ezzell et al., 2009). If modeled improperly, the dose distributions delivered through MLC-defined apertures will have introduced error; systematic dosimetric errors have been documented for small fields (Followill et al., 2012). Second, errors could be related to phantom or QA device positioning, which is user-dependent. Third, errors could be caused by inaccurate machine delivery characteristics, especially concerning the MLC positioning and dose rate accuracies. Because complexity measurement cannot encompass all potential failure modes, it is essential that these and other treatment delivery factors also be considered when assessing the potential for poor plan performance.

5. CONCLUSIONS

This study evaluated IMRT treatment plan complexity metrics with the purpose of identifying those which best predicted irradiation errors. Surprisingly, existing complexity metrics were universally not predictive of dosimetric errors in the IROC H&N phantom irradiations. That is, all metrics evaluated in this study failed to show a statistically significant relationship between phantom performance and the degree of complexity of the treatment plan, regardless of delivery technique, machine model, or treatment planning system. This is interesting, because unlike previous experiments evaluating complexity metrics, the irradiated geometry is constant and without the heterogeneities or uncertainties found in real patient cases. These findings indicate that variations in beam complexity could not explain the disparities in phantom plan performance and that other factors affecting treatment delivery, such as beam modeling inaccuracies, dictate the accuracy of phantom treatment plans.