Jacobian-Based Task-Space Motion Planning for MRI-Actuated Continuum Robots

Abstract

Robot-assisted medical interventions, such as robotic catheter ablation, often require the robot to perform tasks on a tissue surface. This paper presents a task-space motion planning method that generates actuation trajectories which steer the end- effector of the MRI-actuated robot along desired trajectories on the surface. The continuum robot is modeled using the pseudo-rigid-body model, where the continuum body of the robot is approximated by rigid links joined by flexible joints. The quasistatic motion model of the robot is formulated as a potential energy minimization problem. The Jacobian of the quasistatic motion model is used in calculating the actuations that steer the tip in the desired directions. The proposed method is validated experimentally in a clinical 3-T MRI scanner.

I. INTRODUCTION

THIS work focuses on the class of continuum robotic manipulators that are made of thin elastic rods. This particular type of continuum robots has several characteristics that make it especially appealing to medical applications. First, continuum robots are compliant, i.e., their elasticity allows them to conform to their surroundings, which makes it easier to navigate continuum robots in confined spaces. Their compliance makes it less likely that the robots will damage the surrounding tissue; therefore, continuum robots are potentially safer for the patient. The elasticity of the robots also provides intrinsic force sensing, where contact forces can be estimated from the shape of the robot and the applied actuation. Another appealing characteristic of continuum robots is that they are generally easier to miniaturize than their traditional counter-parts that rely on pin joints.

The MRI-actuated continuum robot, otherwise known as MRI-actuated robotic catheter, is a robotic catheter designed to operate while the patient is inside the bore of an MRI scanner. This setup has two main advantages. First, the MRI scanner poses no radiation-exposure threat to the patient, while also providing images with superior soft-tissue visualization. The images from the scanner can also be used to estimate the configuration of the robot without the use of additional sensing equipment. Moreover, the MRI scanner provides the robotic catheter with a strong magnetic field, which is used for remote-steering of the robot. Remote steering is enabled by electromagnetic coils attached to the body of the robot. When electrical currents are applied, the coils produce magnetic moments that bend the robot under the scanner’s magnetic field [1]. This magnetic actuation scheme has no friction or backlash problems, and the actuation bandwidth is much higher than that of the mechanical bandwidth of the robot. A prototype of the MRI-actuated catheter is shown in Figure 1.

Fig. 1:

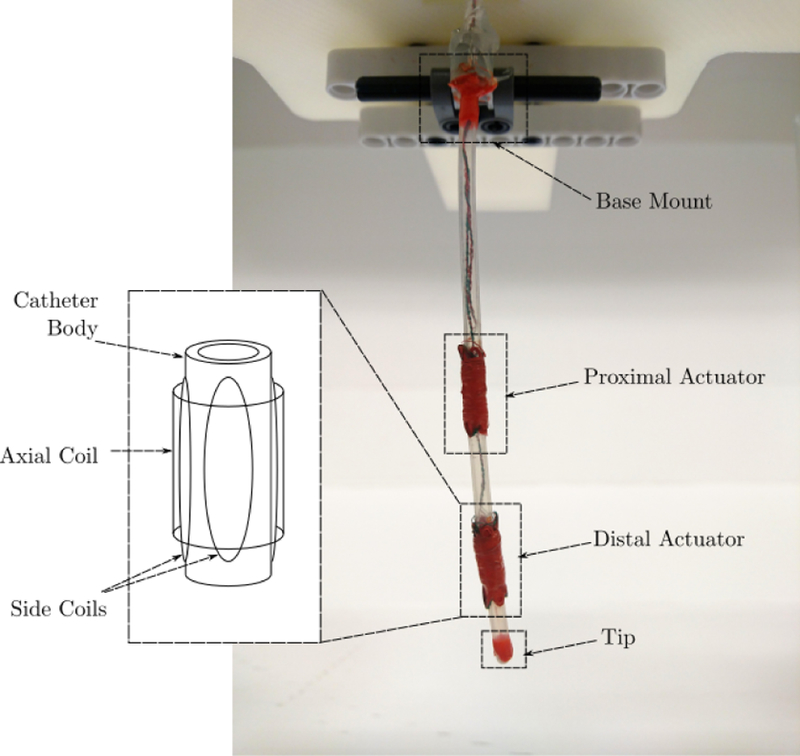
MRI-actuated catheter with two actuators. Each actuator has three mutually orthogonal coils that can generate magnetic moments in any direction. The cross products between the magnetic moments and the MRI scanner’s magnetic field are the torques that remotely steer the robot.

Catheter interventions, such as catheter ablation, require the continuum robot to perform tasks on a tissue surface. In order to perform a given task, the robot must maintain contact with the surface while moving its end-effector on the surface. This is also known as task-space control in robotics, where the goal is to calculate an actuation trajectory that results in the desired end-effector trajectory in the task space. For serial manipulators with motorized joints, the joint-space trajectory for a given task can be calculated either by discretizing tip trajectory and solving inverse kinematics along the discrete trajectory, or by using the Jacobian of the robot’s forward kinematics to calculate joint velocities from workspace velocities. The latter method is often more practical, because solving inverse kinematics involves solving a set of nonlinear equations, which can be very computationally expensive. The Jacobian approach also lends itself well to feedback control in the task space, where task-space errors are used to regulate the robot along the desired trajectory [2].

Since a continuum robot usually moves slowly during a medical procedure, the robot is often assumed to be moving quasistatically, i.e., the robot has enough time to reach its equilibrium configuration for a given actuation [3]. The quasistatic configuration of the robot for a given actuation can be formulated as a potential energy optimization problem. This paper presents a task-space motion planning method for MRI-actuated continuum robots based on the Jacobian approach. The first Jacobian is similar to the Jacobian of serial manipulators, and it depends only on how the shape of the robot is parameterized. The shape of the robot is represented by the pseudo-rigid-body (PRB) model, where the continuum body of the robot is approximated by n + 1 rigid links joined by n flexible joints, and the Jacobian of the forward kinematics of the PRB model can be calculated analytically. The Jacobian of a continuum robot with quasistatic motion can be separated into two parts, where the first Jacobian is the Jacobian of the robot’s forward kinematics, and the second Jacobian is the Jacobian of the mapping between the actuation and the quasistatic shape of the robot. The potential energy minimization problem then becomes an implicit mapping between the actuation and the quasistatic configuration, and its Jacobian can be obtained through the implicit function theorem. The proposed method is experimentally validated in a 3-T clinical MRI scanner, where the robot performs three different trajectories on a rigid surface.

The rest of the paper is organized as follows. Related work is presented in Section II. The PRB model of the continuum robot is presented in Section III. The Jacobian-based motion planning method is presented in Section IV. Experimental validation of the proposed method is presented in Section V. Conclusions are presented in Section VI.

II. RELATED WORK

Continuum robots can be categorized by their actuation methods. Pull-wire mechanisms have been used for actuating continuum robots [4]–[7], similar to cable-driven manipulators. Some robots have pneumatic actuation [6], [8]. Another type of continuum robots have pre-curved concentric tubes, and the desired shape of the robot is achieved by sliding and rotating the tubes [9], [10]. Alternatively, continuum robots can be actuated magnetically. Stereotaxis Niobe Magnetic Navigation System uses two permanent magnets mounted on pivoting arms to steer the tip of a continuum robot equipped with permanent magnets. The pivoting arms change the configurations of the external magnets to remotely steer the robot [11]. Spatial manipulation of a continuum robot with a magnetic actuation system similar to the Niobe system is presented in [12]. Continuum robots equipped with permanent magnets can also be controlled by an external magnetic field that is manipulated electrically [13], [14].

Trajectory generation based on the Jacobian, which is common approach for serial manipulators, is applicable to continuum robots. There are multiple ways of calculating the Jacobian for continuum robots. The Jacobian can be calculated from finite differences of forward kinematics [4], [12], [15], or symbolic differentiation [6]. Alternatively, when the motion of the robot is assumed to be quasistatic, the Jacobian can be calculated from the implicit function defined by the equilibrium condition [16], [17]. Bajo and Simaan perform hybrid position/force control of a multi-backbone tendon-driven continuum robot using the Jacobian [18]. Yip and Camarillo present model-less hybrid position/force control of a multi-backbone tendon-driven continuum robot, where the Jacobian is estimated from sensor data [19]. The model- less control method demonstrates its ability to perform cardiac ablation tasks in [20]. Besides the Jacobian-based methods, sampling-based motion planners have also been adapted for continuum robots, e.g., [21]–[23]. Planning problems can also be formulated as optimization problems, e.g., [24], [25].

This work presents the PRB model of magnetically-actuated MRI-guided continuum robots. The PRB model is generalized to the spatial case, where both planar and torsional rotations are included. This work also presents the first task-space control method that combines the potential energy minimization framework with explicit task-space constraints. The model of the catheter in this work extends the free-space model presented in [26] by incorporating a surface constraint to the potential energy formulation. The motion planning method in this work improves upon the method presented in [27] by extending the quasistatic formulation presented in [16], [17] to the case where the continuum robot has to perform tasks on a two-dimensional surface. The present work is different from [18] because it does not rely on the geometric relationship between the actuation parameters and the shape of the robot in calculating the Jacobian, instead the Jacobian is calculated from the implicit function defined by the potential energy minimization problem, which can be easily extended to different continuum robots and kinematic models. The planning method presented in this work is also different from [19] and [20] because it is a model-based method. While model-based methods generally require higher computational effort, they provide a platform in which the knowledge of the underlying physics of the robot can be seamlessly integrated with sensor measurements, either in a classical feedback control framework [2], or in a probabilistic framework [28].

III. MATHEMATICAL MODEL

A PRB model with n spherical joints, shown in Figure 2, has 3n degrees of freedom, where each joint has three degrees of freedom, two bending and one twisting. The PRB model approximates the compliance of a continuum robot with a torsional spring attached to each degree of freedom. The continuously changing curvature of the centerline of the catheter is approximated by the rotations of the spherical joints and the translations along the rigid links. The PRB model can be interpreted as a Dirac delta function approximation of the curvature of a continuum robot as a function of the arc length.

Fig. 2:

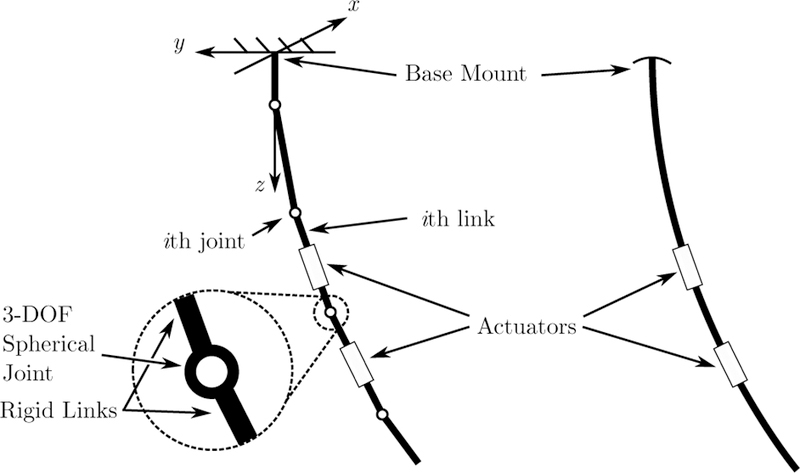
The MRI-actuated catheter with two actuators (right) and the corresponding PRB model (left).

Forward kinematics of the PRB model with spherical joints is presented in Section III-A. The potential energy minimization formulation of the quasistatic motion model is presented in Section III-B. Mathematical notations used in this paper generally follow those of [2].

A. Forward Kinematics

For industrial serial manipulators, a spherical wrist is modeled as three sequential revolute joints, where the axes of rotation intersect at a common point. In such cases, the sequential joints accurately model a spherical wrist where each rotation is actuated by a motor. However, this model is not applicable to the PRB model of a continuum robot, because the model assumes an order of rotation exists amongst the degrees of freedom. In order to accurately model the spherical joints in the PRB model without assuming an order of rotation, the rotation of the ith joint is parameterized by three rotation angles as follows, θ_i = [θ_i,1 θ_i,2 θ_i,3]^T $\in {ℝ}^3$. The orientation of the link above the ith joint with respect to the (i − 1)th joint is given by $e^{\widehat{\theta }}$ , where the wedge symbol (˄) maps the ${ℝ}^3$ vector representation to the ${ℝ}^{3\times 3}$ matrix representation of an element of so(3), with the inverse mapping denoted by the vee symbol (˅), and the exponential function maps an element of so(3) to an element of SO(3).

Once the spherical joint is parameterized, rigid body motion of the robot can be defined as follows. A twist, denoted by ξ ϵ se(3), is an infinitesimal generator of SE(3). Let q_i denote the initial position of the ith joint with respect to the spatial frame. The twist of the ith joint can be written as an ${ℝ}^{\text{6}}$ vector or an ${ℝ}^{4\times 4}$ matrix as follows,

$${\text{ξ}}_i\left({\theta }_i\right)=\left[\begin{array}{c}-\theta \times q_i\\ {\theta }_i\end{array}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}or\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\stackrel{\wedge }{\text{ξ}}}_i\left({\theta }_i\right)=\left[\begin{array}{cc}{\widehat{\theta }}_i& -{\theta }_i\times q_i\\ 0& 0\end{array}\right]$$ (1)

Similarly to rigid body rotation, for the rigid body motion case, ˄ maps the ${ℝ}^{\text{6}}$ vector representation to the ${ℝ}^{4\times 4}$ matrix representation of an element of se(3), with the inverse mapping denoted by ˅. The shape of the PRB model of the catheter with n spherical joints is completely described by the joint angle vector $\theta ={\left[{\theta }_1^T{\theta }_2^T\cdot \cdot \cdot \hspace{0.17em}\hspace{0.17em}{\theta }_n^T\right]}^T\hspace{0.17em}\in \mathcal{C}\subset {ℝ}^{3n}\hspace{0.17em},$ where C denotes the set of all possible joint angles, also known as the configuration space.

The configuration of a coordinate frame A attached to the jth link given joint angles θ, denoted by gsa(θ) ϵ SE(3), is calculated from the product of exponentials formula as follows,

$$g_{sa}\left(\theta \right)=e^{{\stackrel{\wedge }{\text{ξ}}}_1\left({\theta }_1\right)}{e}^{{\stackrel{\wedge }{\text{ξ}}}_{\text{2}}\left({\theta }_2\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}·\hspace{0.17em}\hspace{0.17em}·\hspace{0.17em}\hspace{0.17em}·}{e}^{{\stackrel{\wedge }{\text{ξ}}}_j\left({\theta }_j\right)}{g}_{sa}\left(0\right)\hspace{0.17em},$$ (2)

where g_sa(0) is the configuration of the frame A when θ = 0, i.e., when the catheter is perfectly straight.

B. Potential Energy Minimization

Continuum robots are inherently underactuated because their continuum bodies have infinite degrees of freedom, while there are finite actuation degrees of freedom. The quasistatic assumption resolves the underactuation problem by assuming that the robots move slowly enough that they can be considered as being in perpetual equilibrium. This is a reasonable assumption in medical applications, because surgical continuum robots usually move slowly compare to their mechanical bandwidth [3]. The quasistatic configuration of a continuum robot can be calculated either by solving the constitutive equations, or by minimizing the potential energy. This work extends the potential energy minimization formulation in [26] to include a surface constraint. The quasistatic configuration of the catheter given external forces and actuation currents is calculated by minimizing the potential energy of the catheter subjected to the surface constraint as follows,

$$\begin{array}{c}\min \\ \theta \in c\end{array}\frac{1}{2}{\theta }^{T}K\theta -\sum _i{F}_i^T{p}_i\left(\theta \right)-\sum _j{B}_j{\left(\theta \right)}^T{\mu }_j\left(u_j\right)\hspace{0.17em},$$ (3a)

$$\text{s.t..}h\left(\theta \right)\le 0.$$ (3b)

The first term in the objective function (3a) is the potential energy due to the internal stiffness of the catheter, where K is a constant, positive definite spring stiffness matrix. The next term is the work done by external forces, where F_i is a conservative force acting on the catheter at p_i(θ). The effect of gravity can also be expressed as conservative forces acting on the center of masses of the links. The last term is the summation of the work from the magnetic moments from the actuators [29], where B_j(θ) is the MRI’s magnetic field vector written in the jth actuator body frame, µ_j is the magnetic moment of the jth actuator expressed in its body frame, and u_j are the currents sent to the jth actuator.

The surface is represented by the inequality constraint (3b). The constraint is defined such that when the catheter is in contact with the surface, h(θ) = 0, and when the catheter is not in contact, h(θ) < 0. This inequality constraint makes it possible to use the optimization problem (3) to calculate the equilibrium configuration of the catheter both when it is in contact as well as in free space.

IV. MOTION PLANNING

Let the position of the catheter’s tip in the workspace be denoted by $x\in {ℝ}^3$.The Jacobian of the mapping from actuations to tip positions can be written as a production the Jacobian of forward kinematics and the Jacobian of the quasistatic motion model using the chain rule as follows,

$$dx=\underset{J_k}{\underbrace{\frac{\partial x}{\partial \theta }}}\underset{J_q}{\underbrace{\frac{\partial \theta }{\partial u}}}du,$$ (4)

where J_k is the forward kinematics Jacobian, and J_q is the quasistatic Jacobian. The derivation of the forward kinematics and the quasistatic Jacobians are presented in Section IV-A and IV-B, respectively. Task-space motion planning of the catheter is presented in Section IV-C, where the aforementioned Jacobians, combined with the Jacobian of the surface, yield a linear relationship between the differential of the end-effector position of the surface and the differential of the actuation.

A. Forward Kinematics Jacobian

Recall that the configuration of a frame attached to the catheter can be written as a product of exponentials, as described in (2).

$$\left[\begin{array}{c}x\\ 1\end{array}\right]=e^{{\stackrel{\wedge }{\text{ξ}}}_1}{e}^{{\stackrel{\wedge }{\text{ξ}}}_2}{e}^{{\stackrel{\wedge }{\text{ξ}}}_3}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_n}\left[\begin{array}{c}{x}_0\\ 1\end{array}\right]\hspace{0.17em},$$ (5)

Where $x\in {ℝ}^3$ is the position of the end-effector given all the joint angles, and $x_0\in {ℝ}^3$ is the initial tip position when all the joint angles are zeros. Since the mapping from the joint angles to the end-effector position only depends on the kinematic model, its partial derivative can be calculated algebraically. To simplify the calculation, J_k is partitioned into columns as follows,

$$J_k=\left[\frac{\partial x}{\partial {\theta }_{1,1}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\cdot \cdot \cdot \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial x}{\partial {\theta }_{i,j}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\cdot \cdot \cdot \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial x}{\partial {\theta }_{n,3}}\right]\hspace{0.17em}\hspace{0.17em},$$ (6)

where i ϵ { 1, 2, . . ., n} is the joint number, and j ϵ { 1, 2, 3} is the jth degree of freedom of the joint. Each column of the right-hand side of (6) is obtained by differentiating (5) with respect to the corresponding joint angle as follows,

$$\left[\begin{array}{c}\frac{\partial x}{\partial {\theta }_{i,j}}\\ 0\end{array}\right]=e^{{\stackrel{\wedge }{\text{ξ}}}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_{i-1}}\frac{\partial e^{{\stackrel{\wedge }{\text{ξ}}}_i}}{\partial {\theta }_{i,j}}{e}^{{\stackrel{\wedge }{\text{ξ}}}_i{+}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_n}\left[\begin{array}{c}{x}_0\\ 1\end{array}\right]\hspace{0.17em}\hspace{0.17em},$$ (7a)

$$=e^{{\stackrel{\wedge }{\text{ξ}}}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_{i-1}}\underset{{\stackrel{\wedge }{\text{ξ}}}_{i,j}}{\underbrace{\left(\frac{\partial e^{{\stackrel{\wedge }{\text{ξ}}}_i}}{\partial {\theta }_{i,j}}{e}^{-}{}^{{\stackrel{\wedge }{\text{ξ}}}_i}\right)}}{\text{e}}^{{\stackrel{\wedge }{\text{ξ}}}_i}{e}^{{\stackrel{\wedge }{\text{ξ}}}_i{+}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_n}\left[\begin{array}{c}{x}_0\\ 1\end{array}\right]\hspace{0.17em}\hspace{0.17em},$$ (7b)

$$=e^{{\stackrel{\wedge }{\text{ξ}}}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_{i-1}}{\stackrel{\wedge }{\text{ξ}}}_{i,j}{\text{e}}^{{\stackrel{\wedge }{\text{ξ}}}_i}{e}^{{\stackrel{\wedge }{\text{ξ}}}_i{+}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_n}\left[\begin{array}{c}{x}_0\\ 1\end{array}\right]\hspace{0.17em}\hspace{0.17em},$$ (7c)

$$e^{{\stackrel{\wedge }{\text{ξ}}}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_{i-1}}{\stackrel{\wedge }{\text{ξ}}}_{i,j}{e}^{-}{}^{{\stackrel{\wedge }{\text{ξ}}}_i{-}_1}\cdot \cdot \cdot e^{-}{}^{{\stackrel{\wedge }{\text{ξ}}}_1}\left[\begin{array}{c}x\\ 1\end{array}\right]\hspace{0.17em}\hspace{0.17em},$$ (7d)

$$={\left({\text{Ad}}_{\left(e^{{\stackrel{\wedge }{\text{ξ}}}_1}\cdot \cdot \cdot e^{{\stackrel{\wedge }{\text{ξ}}}_{i-1}}\right)}{\text{ξ}}_{i,j}\right)}^{\wedge }\left[\begin{array}{c}x\\ 1\end{array}\right]\hspace{0.17em}\hspace{0.17em}\cdot$$ (7e)

B. Quasistatic Jacobian

The quasistatic Jacobian can be obtained from the Jacobian of the implicit function defined by (3). Let $\mathcal{L}:\mathcal{C}\to ℝ$ denote the Lagrangian of the optimization problem (3). Suppose θ is a (local) minimizer, then it satisfies the first-order optimality condition

$$\nabla \mathcal{L}\left(\theta \right)=K\theta +N\left(\theta \right)+\nabla h\left(\theta \right)\lambda \hspace{0.17em}-\tau \left(\theta ,u\right)=0,$$ (8)

Where

$$N\left(\theta \right)=-\sum _i{F}_i^T\partial p_i/\partial \theta \hspace{0.17em},$$

$$\tau \left(\theta ,u\right)=\sum _j{\mu }_j^T\left(u_j\right)\partial B_j/\partial \theta .$$

Define a vector-valued function $f:\mathcal{C}\times \mathcal{U}\to {ℝ}^{3n}$ as

$$f\left(\theta ,u\right):=\nabla \mathcal{L}\left(\theta \right)=K\theta +N\left(\theta \right)+\nabla h\left(\theta \right)\lambda -\tau \left(\theta ,u\right).$$ (9)

Then (8) is simply f (θ, u) = 0, which defines the implicit function between θ and u. If ∂f /∂θ is nonsingular, then J_q can be calculated as follows,

$$J_q=\frac{\partial \theta }{\partial u}=-{\left(\frac{\partial f}{\partial \theta }\right)}^{-1}\left(\frac{\partial f}{\partial u}\right).$$ (10)

Note that ∂f /∂θ is simply the Hessian of the Lagrangian. The Hessian can be calculated using automatic differentiation, the finite difference method, or symbolic differentiation. In this work, the Jacobian of the Lagrangian is calculated analytically, and the Hessian is obtained by differentiating the Jacobian using the finite difference method. The other term on the right- hand-side of (10) is ∂f /∂u. Since the only term in f that is a function of u is $\tau$, which is linear with respect to u (see Appendix A), hence ∂f /∂u is a matrix function of θ but not is independent of u.

C. Actuation Calculation

Let h(θ, y) = 0 denote the surface constraint with explicit dependency on the surface coordinates, denoted by $y\in {ℝ}^2$. The tangent space of the constraint is defined by

$$\frac{\partial h}{\partial \theta }d\theta +\frac{\partial h}{\partial y}dy=0.$$

The constraint can be written as h(θ, y) = p(θ) - q(y) where p maps joint angles to tip positions in the workspace, and q maps surface coordinates to workspace position, i.e., x = p(θ) and x = q(y). Therefore, the forward kinematics Jacobian can be written as J_k = ∂p/∂θ = ∂h/∂θ. Let the Jacobian of q be denoted by $G^T=\partial q/\partial y=-\partial h/\partial y$, then the differential constraint above becomes

$$J_{k}d\theta =G^{T}dy.$$ (11)

Substituting (10) into (11) yields the desired linear relationship

$$J_k{J}_{q}du=G^{T}dy.$$

In the case that the actuators have more degrees of freedom than the task, it is possible to have an actuation that moves the catheter in such a way that the end-effector remains at the same position of the surface. This type of motion is known as internal motion. Let H_e be the matrix whose rows are in the null space of J_k and are mutually orthogonal amongst themselves, then the internal motion, denoted by dv, can be obtained from the following linear relationship,

$$\left[\begin{array}{c}{J}_k\\ H_e\end{array}\right]J_{q}du=\left[\begin{array}{cc}{G}^T& 0\\ 0& I\end{array}\right]\left[\begin{array}{c}dy\\ dv\end{array}\right]$$

The redundancy of the actuation with respect to the task can be resolved by the following optimization problem,

$$\begin{array}{c}\min \\ du,dv\end{array}\frac{1}{2}\left({‖du‖}^2+\text{γ}{‖dv‖}^2\right),$$ (12a)

$$\text{s.t.}\left[\begin{array}{c}{J}_k\\ H_e\end{array}\right]J_{q}du=\left[\begin{array}{cc}{G}^T& 0\\ 0& I\end{array}\right]\left[\begin{array}{c}dy\\ du\end{array}\right],$$ (12b)

where the desired tip motion on the surface is expressed as the constraint, and γ is the weight of the internal motion. Note that (12) is a quadratic programing, and consequently has a closed-form solution [30].

The task-space motion planning algorithm is summarized in Algorithm 1. The algorithm takes as inputs the initial joint angles (θ₀), a sequence of via points on the desired end-effector trajectory $\left({\overline{y}}_1:n\right)$ , and a step size (σ). The algorithm iteratively drives the tip of the catheter towards the next via point in the sequence. Once the via point is reached, the algorithm moves on to the next via point. The algorithm works as follows. In Line 3, the

forward_kinematics

function calculates the end-effector position from the initial joint angles using the forward kinematics equation described in (2). The end-effector position is projected onto the surface coordinates in Line 4. The algorithm loops over all the via points between Lines 5 and 19. For each via point, the algorithm tries to bring the end- effector to the via point through a sequence of actuations. First, the end-effector motion, denoted by dy, is calculated in Line 6. The end-effector motion is compared to the step size in Line 7. If the end-effector motion is larger than a fraction of the step size, i.e., dy > ασ, 0 < α < 1, the algorithm continues to move the end-effector toward the via point, otherwise it continues to the next via point. Between Lines 8 to 10, the end- effector motion is normalized if it is larger than the step size. In Line 11, the

inverse_kinematics

function calculates an actuation update, denoted by du, from dy by solving the optimization problem (12). A new actuation is calculated from the previous actuation and the actuation update in Lines 13. The

simulate

function in Line 14 integrates the equations of motion described in [27] with the new actuation to obtain a new joint angle vector. A new end-effector position in the spatial frame calculated from the new joint angle vector in Line 15 is projected onto the surface coordinates in Line 16, and a new end-effector motion is calculated from the new end- effector position in Line 17. Once all the via points are visited, the algorithm returns the resulting actuation sequence.

V. EXPERIMENTAL VALIDATION

A. Setup

The experimental setup is similar to the one reported in [26], with two notable changes. First, the catheter prototype in this work has two actuators, where each actuator has three mutually orthogonal coils. The body of the catheter is made of a silicone rubber tube with the outer diameter of 3.2 mm and the length of 104.0 mm (Part number: T2011, QOSINA). The coils are made of heavy insulated 38-gauge solid core enameled copper wire (Adapt Industries, LLC, Salisbury, MD, USA). The catheter is mounted on top of an aquarium that is placed on a foam pad. The other notable addition to the setup is a rectangular piece of acrylic mounted on the bottom of the aquarium that serves as the task space. Experiments are conducted with the catheter setup placed at the isocenter of a 3- T MRI scanner (Skyra, Siemens Medical Solutions, Erlangen, Germany). A 60 fps high definition camera with a resolution of 1080 1920 pixels (Flea3 FL3-U3–32S2C by Point Grey, Richmond, BC, Canada) is used to capture the images of the catheter during the experiments. For safety reasons, the camera is placed at the far end of the MRI suite, approximately 6 m away from the isocenter of the scanner. A mirror is placed on the foam pad next to the catheter at approximately 45 degree angle measured from the side of the aquarium. By placing the mirror at an approximately 45 degree angle, the mirror serves and a virtual camera that view the catheter from the side. The catheter setup is shown in Figure 3.

$$\underset{¯}{\begin{array}{l}\overline{\underset{¯}{\begin{array}{l}\text{Algorithm}\hspace{0.17em}1\hspace{0.17em}\text{Task-Space Motion Planning Algorithm for the }\\ \text{RoboticCatheter}\end{array}}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{procedure}\hspace{0.33em}\text{taskspace\_plannining}\left({\theta }_0,{\overline{y}}_{\text{1:}n},\sigma \right)\\ \hspace{0.33em}\hspace{0.33em}2:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}t=0\\ \hspace{0.33em}\hspace{0.33em}3:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{x}_t=\text{forward\_kinematics}\left({\theta }_0\right)\\ \hspace{0.33em}\hspace{0.33em}4:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{y}_t=\text{project}\left({\text{X}}_{\text{t}}\right)\\ \hspace{0.33em}\hspace{0.33em}5:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{for}\hspace{0.17em}\text{all}\hspace{0.17em}i=1,2,\mathrm{...},n\hspace{0.17em}\text{do}\\ \hspace{0.33em}\hspace{0.33em}6:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}dy={\overline{y}}_i-y_t\\ \hspace{0.33em}\hspace{0.33em}7:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{while}\hspace{0.33em}‖dy‖>\alpha \sigma \hspace{0.33em}\text{do}\\ \hspace{0.33em}\hspace{0.33em}8:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{if}‖dy‖>\sigma \hspace{0.33em}\text{then}\\ \hspace{0.33em}\hspace{0.33em}9:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}dy=\sigma \hspace{0.33em}dy/‖dy‖\hspace{0.33em}\\ \hspace{0.33em}10:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{end}\hspace{0.33em}\text{if}\\ \hspace{0.33em}11:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}du=\text{inverse\_kinematics}\left({\theta }_t,dy\right)\\ \hspace{0.33em}12:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}t=t+1\\ \hspace{0.33em}13:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{u}_t=u_{t-1}+du\\ \hspace{0.33em}14:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\theta }_t=\text{simulate}\left({\theta }_{t-1},u_t\right)\\ \hspace{0.33em}15:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{x}_t=\text{forward\_kinematics}\left({\theta }_t\right)\\ \hspace{0.33em}16:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{y}_t=\text{project}\left(x_t\right)\\ \hspace{0.33em}17:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}dy={\overline{y}}_i-y_t\\ \hspace{0.33em}18:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{end}\hspace{0.33em}\text{while}\\ \hspace{0.33em}19:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{end}\hspace{0.33em}\text{for}\\ \hspace{0.33em}20:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{return}\hspace{0.33em}{u}_t,\forall t\\ \hspace{0.33em}21:\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\text{end}\hspace{0.33em}\text{procedure}\end{array}}$$

Three trajectories, namely rectangular, rhomboid (diamond- shaped), and circular trajectories, are considered in the experiment. The rectangular and the rhomboid trajectories demonstrate the capability of the catheter to move in straight lines in different directions, while the circular trajectory represents a common trajectory found in applications such as catheter ablation. The trajectories are discretized into via points. The catheter is assumed to be perfectly straight initially, i.e., ${\theta }_i=0,\forall i$. Then the catheter moves toward the surface and make contact. Once the catheter is in contact with the surface, the catheter moves its tip toward the center of its workspace on the surface, then the catheter’s tip is driven along the desired trajectories with actuation trajectories generated using Algorithm 1. The PRB model used in the experiment has nine joints, where the two actuation coils are on individual links, and the rest of the catheter is divided equally into the remaining seven links. The step size in Algorithm 1 is set to 2 mm, which is slightly smaller than the outer diameter of the catheter. Nine links are chosen for its balanced trade-off between computation time and accuracy based on the previous work [31]. Algorithm 1 is implement in MATLAB on a computer running macOS 10.13.6 with 2.8 GHz Intel Core i7 CPU and 8 GB of memory. The position of the end-effector of the catheter on the surface is read from a piece graph paper with 2-mm grid affixed to the surface, as observed from the camera images.

Fig. 3:

Experimental setup.

B. Results

The initial deflection of the catheter with zero actuation is often not perfectly straight, and it is difficult to accurately predict the initial deflection prior to the experiment. Consequently, the initial shape recorded during the experiment is estimated and included in the simulations as the shape that minimizes the potential energy with zero actuation. The results are shown in Figure 4, which compares the simulated trajectories of the catheter’s end-effector on the surface without initial deflection, the simulated trajectories where initial deflection is taken into account, and the actual trajectories obtained from the experiment. The root-mean-square errors between the observed trajectories and the simulated trajectories with initial deflection are 6.03 mm, 7.86 mm, and 7.68 mm for the rectangular, the rhomboid, and the circular trajectories, respectively. The trajectories take 13.8 s, 9.2 s, and 14.2 s to complete. While the errors are high compared to the human anatomy, it is to be expected since the trajectories are executed as open-loop trajectories, which are susceptible to offset and drift types of errors. Note that the errors are lower than the errors of the free-space trajectories of the previous prototype presented in [26]. The two main computational intensive tasks in Algorithm 1 are inverse kinematics in Line 11 and the simulation in Line 14. It takes 0.1330 second on average to calculate the Jacobians and solve (12) for a new actuation in Line 11, and 1.045 second on average to simulate the catheter using MATLAB’s ode45.

Fig. 4:

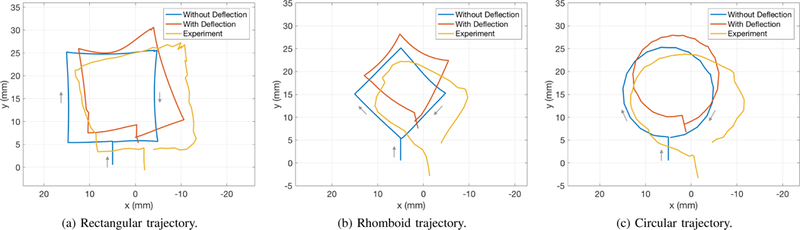
Comparisons between the simulated trajectories without initial deflection (blue), with initial deflection (red), and the experimental (yellow) trajectories. The trajectories are expressed in the surface coordinates.

A possible source of the offset error is the mismatch in the initial conditions of the catheter, such as the initial deflection of the catheter at rest, the pose of the surface etc., between the current experiments and the experiment in which the model parameters are obtained. The effect of the mismatch in the initial shape can be seen when comparing the trajectories computed prior to the experiment without the initial deflection and the trajectories computed with the initial deflection obtained from the experiment. Note that when the initial deflection is taken into account, the model predicts similar shifts along the x-axis in Figure 4. The error along the y-axis is likely due to the errors in the distance and the slope of the surface, which is mounted at the bottom of the aquarium independently of the catheter. A calibration routine executed at the beginning of each experiment will be useful in reducing such error and is a part of future work.

The model of the catheter is another possible source of both offset and drift errors. Since the PRB model approximates the continuum body of the catheter with discrete links, some offset between the model and the observed results is likely. The problem is further complicated with the surface, whose nonuniform friction coefficient can cause further drift when the trajectories are perform open-loop. However, the three trajectories in Figure 4 demonstrate that the Jacobian derived in Section IV can be used to drive the tip of the catheter on the surface in all directions. This means the Jacobian can be used in conjunction with a catheter localization algorithm as a closed-loop control system that regulates the tip of the catheter along the desired trajectory. Closed-loop control has been demonstrated to be effective in reducing the errors between desired and actual trajectories [14], [27]. Nevertheless, closed- loop control of the catheter requires real-time localization using MRI images, which is beyond the scope of this work.

VI. CONCLUSIONS

This paper presents a motion planning method for the MRI- actuated continuum robot. The kinematics of the robot is modeled using the PRB model. The quasistatic motion model of the robot is formulated as a constrained potential energy minimization problem, where the task space is represented by an inequality constraint. The actuation trajectories that yield the desired surface trajectories are calculated using the differential surface constraint, the forward kinematics Jacobian, and the quasistatic Jacobian. Experimental results show that the motion planning method is capable of generating desired end- effector trajectories in the task space. While the experimental trajectories exhibit drift and offset errors, it is expected since the trajectories are executed as open-loop trajectories. The present work focuses on how to calculate the Jacobian for task-space motion and how to use the Jacobian to drive the catheter’s end-effector in desired directions. As a part of future work, a C++ implementation of the presented method will be integrated with real-time MRI localization for closed-loop control of the catheter. Once closed-loop control is achieved, a comprehensive validation with quantitative analysis will be performed.

APPENDIX A

ACTUATION JOINT TORQUES

Consider the kth actuator. Let $C_k\in {ℝ}^{3\times 3}$ denote the orientations of the actuator’s coils, $S_k\in {ℝ}^{3\times 3}$ denote a diagonal matrix whose diagonal elements represent the total surface areas of the coils, and $u_k\in {ℝ}^3$ denote the currents applied to the coils. Then the magnetic moments from the actuator is µ_k = C_kS_ku_k.

Next, we will show that the gradient of the work of the actuator’s magnetic moment in the MRI scanner’s magnetic field is precisely the joint torques due to the Lorentz force of the magnetic moment. In order to simplify the notations in this part of the derivation, only one actuator is considered and the index k is dropped. Let W (θ, u) denote the work due to the magnetic moment µ_b the magnetic field B_b, where the subscript b denotes the body frame (and the subscript s denotes the spatial frame). Let the orientation of the actuator with respect to the base frame be denoted by g_sa(θ) ϵ SE(3), and the rotational part of g_sa(θ) and g_sa(0) are denoted by R and R₀, respectively. The work of the magnetic moment is $W=B_b^T{\mu }_b$ The element of the gradient of W due to θ_i,j is given by,

$$\begin{gathered} \frac{\partial W}{\partial {\theta }_{i,j}}=\frac{\partial B_b^T}{\partial {\theta }_{i,j}}{\mu }_b=\frac{\partial B_s^{T}R\left(\theta \right)}{\partial {\theta }_{i,j}}{\mu }_b=B_s^T\frac{\partial R\left(\theta \right)}{\partial {\theta }_{i,j}}{\mu }_b \\ =B_s^T\left(e^{{\theta }_1}\cdot \cdot \cdot e^{{\theta }_{i-1}}\frac{\partial e^{{\theta }_i}}{\partial {\theta }_{i,j}}{e}^{{\theta }_i{+}_1}\cdot \cdot \cdot e^{{\theta }_n}{R}_{\text{0}}\right){\mu }_b \\ =B_s^T\left(e^{{\theta }_1}\cdot \cdot \cdot e^{{\theta }_{i-1}}\underset{{\stackrel{\wedge }{\text{ω}}}_{j,j}}{\underbrace{\frac{\partial e^{{\theta }_i}}{\partial {\theta }_{i,j}}{e}^{-{\theta }_i}}}{e}^{{\theta }_i}{e}^{{\theta }_i{+}_1}\cdot \cdot \cdot e^{{\theta }_n}{R}_{\text{0}}\right){\mu }_b \\ =B_s^{T}R{R}^{-1}\left(e^{{\theta }_1}\cdot \cdot \cdot e^{{\theta }_{i-1}}{\stackrel{\wedge }{\text{ω}}}_{i,j}{e}^{{\theta }_i}\cdot \cdot \cdot e^{{\theta }_n}{R}_0\right){\mu }_b \\ =B_s^{T}R\underset{{\stackrel{\wedge }{\text{ω}}}_{i,j}^{†}\hspace{0.17em}}{\underbrace{\left(R_0^{-1}\cdot \cdot \cdot e^{-{\theta }_i}{\stackrel{\wedge }{\text{ω}}}_{i,j}{e}^{{\theta }_i}\cdot \cdot \cdot e^{{\theta }_n}{R}_0\right)}}{\mu }_b \\ =B_b^T{\stackrel{\wedge }{\text{ω}}}_{i,j}^{†}{\mu }_b=B_b^T\left({\omega }_{i,j}^{†}\times {\mu }_b\right)={\omega }_{i,j}^{†}\left({\mu }_b\times B_b\right). \end{gathered}$$

Note that ${\omega }_{i,j}^{†}$ is the rotational part of the body manipulator Jacobian [2]. So, the equation above can be written together with the translational part as

$$\frac{\partial W}{\partial {\theta }_{i,j}}={\text{ξ}}_{i,j}^{†T}\left[\begin{array}{c}0\\ {\mu }_b\times B_b\end{array}\right].$$

Therefore, the gradient of W can be written as a wrench due to the Lorentz of the magnetic moment acting on the actuator as follows,

$$\frac{\partial W^T}{\partial \theta }=\left[\begin{array}{c}{\text{ξ}}_{1,1}^{†T}\\ ⋮\\ {\text{ξ}}_{i,j}^{†T}\\ ⋮\\ {\text{ξ}}_{n.3}^{†T}\end{array}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{c}0\\ {\mu }_b\times B_b\end{array}\right]\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}{J}_{sa}^{bT}\hspace{0.17em}\left[\begin{array}{c}0\\ {\mu }_b\times B_b\end{array}\right]\hspace{0.17em}\hspace{0.17em},$$

Where $J_{sa}^b$ is the body manipulator Jacobian at the actuator [2], [26], [32]. Now let W_k(θ, u_k) denote the work from the kth actuator, then the joint torques from the kth actuator is ${\tau }_k\left(\theta ,u_k\right)=\partial W_k/\partial \theta$, and the total joint torques due to actuation is $\tau \left(\theta ,u\right)={\sum }_k{\tau }_k\left(\theta ,u_k\right).$ Since all of the operations is linear with respect to $u,\tau$ is also linear in u.