Heritability and genetic architecture of reproduction-related traits in a temperate oak species

Abstract

Reproduction, one of the main components of plant fitness, is highly variable in response to environmental cues, but little is known about the genetic determinism underlying reproduction-related traits in forest tree species. There is therefore an urgent need to characterize the genetic architecture of those traits if we are to predict the evolutionary trajectories of forest populations facing rapidly changing environment and mitigate their impacts. Using a full-sib family of pedunculate oak (Quercus robur), we investigated the within population variability of seed production and mean seed mass during four consecutive years. Reproductive traits were highly variable between trees and between years. The high narrow sense heritability and evolvability estimated underline the important genetic effect on the variability in seed production and mean seed mass. Despite a large variability over years, reproductive traits show significant genetic correlation between years. Furthermore, for the first time in forest tree species, quantitative trait loci (QTLs) associated with seed production and mean mass of a seed have been identified. While it is commonly assumed and observed that fitness-traits have low narrow sense heritabilities, our findings show that reproduction-related traits may undergo evolutionary changes under selective pressure and may be determinant for tree adaptation.

1. Introduction

Tree fitness defines the ability of an individual to survive, grow and reproduce in an environment. Numerous studies have investigated to which extent the phenotypic variation of growth and survival in response to environmental changes was genetically or environmentally driven in forest tree species but there is a lack of studies investigating reproduction (Kang et al., 2003; Santos del Blanco et al., 2010; Santos-del-Blanco et al., 2012). Yet, understanding the variability in tree reproduction is essential in order to assess the process of adaptation of forest tree species in response to environmental changes (Aitken et al., 2008; Anderson, 2016). Increased reproduction enhances fitness of trees through different processes. For example, higher seed production increases the probability of dispersion by animals (Howe and Smallwood, 1982; Schupp et al., 2010; Traveset et al., 2014) and thus enhances population growth and dynamics. Long-distance dispersion generally due to scatter-hoarding, i.e. the way animals buried their seeds for latter consumption, favors regeneration because (1) seed dispersed escape density-dependent competition under the mother tree and (2) because during years of abundant seed production, buried seeds will not all be consumed by predators (Vander Wall, 2010). Furthermore, the variability in seed size within a same species also plays a role as it is correlated with the germination rate (Gómez, 2004; Walters and Reich, 2000). Thus, because of the larger amount of reserves, bigger seed are more likely to survive to infestation from insects and seedlings’ early development is favored (Bonal et al., 2007; Sousa et al., 2003).

Tree reproduction is highly variable in response to environmental changes. Previous studies have shown large variations in seed production, seed size or seed germination along environmental gradients and across years (in oaks Caignard et al., 2017; Koenig et al., 2009; in pine Lopez-Toledo et al., 2017; in black spruce Sirois, 2000). Part of this variation is driven by environmental changes such as temperature and precipitation. For example, seed production in European oak species increases with a rise in temperature during the period of pollination (Caignard et al., 2017; Schermer et al. submitted) and decreases with increasing drought occurring during late summer (Bogdziewicz et al., 2017; Pérez-Ramos et al., 2010; Sanchez-Humanes and Espelta, 2011). While numerous studies have investigated the phenotypic variability of reproduction traits in response to environmental changes little is known about the genetic source of this variation.

Common garden experiments have been useful in documenting genetically based differentiation among and within populations but few have focused on the genetic variations of reproductive traits, most likely because their assessments can only be made on reproductively mature trees while other fitness related traits can be measured on juvenile traits. In comparison, the genetics of reproductive traits have been already explored for annual plants (Alonso-Blanco et al., 1999; Mitchell-Olds, 1996), plant crops (Doligez et al., 2002; Houel et al., 2015; Kadri et al., 2017) and fruit trees (Guitton et al., 2011; Sadok et al., 2013; Wu et al., 2014). For example, quantitative traits loci (QTLs) associated with seed size, seed number or size at first reproduction were detected for Arabidopsis thaliana (Alonso-Blanco et al., 1999) and Vitis vinifera (Doligez et al., 2002). In fruit trees, genetic investigations were oriented towards flowering and fruiting phenology (Dirlewanger et al., 2012; Romeu et al., 2014) and biennial fruit bearing, i.e. the yearly alternation of flowering and fruiting (Guitton et al., 2011; Sadok et al., 2013; Shalom et al., 2012). In forest trees, the phenological variation of the apical buds has been extensively investigated in recent years (Derory et al., 2010; Jermstad et al., 2001; Pelgas et al., 2011; Scotti-Saintagne et al., 2004) but very few studies have targeted the genetic variation of reproduction within population (Bilir et al., 2006; Sıvacıoglu et al., 2009; Tsubomura et al., 2012) and even fewer have attempted to detect QTLs underlying reproductive traits (see Ujino-Ihara et al., 2012 for male strobilus abundance). Finally, Pearse et al. (2016) strongly advocated for assessing heritability of masting related traits, while recalling that relevant data may already exist (El Kassaby and Barclay, 1992). As the selective response to environmental changes, and so the capacity of adaptation of tree population largely depend on the genetic variations and the genetic architecture underlying fitness related traits, it is necessary to investigate more reproduction.

In this study we assessed the phenotypic and genetic variation of reproductive traits and searched for their underlying quantitative trait loci (QTL) in a full-sib family of a broadly distributed temperate oak species (Quercus robur L.). Our main objectives were to (i) subdivide the total phenotypic variation of reproductive traits into environmental and genetic components (ii) to dissect the genetic architecture of reproductive traits by detecting their underlying QTLs (iii) to examine the stability of QTLs expression over successive years.

2. Material and Methods

2.1. Experimental design

A full-sib family originating from a controlled cross of pedunculate oak (Quercus robur) was used. The male parent (A4) was selected in a park close to Arcachon in the South West of France (44°40’N, 1°11’W) and the female parent (3P) originated from the INRA forest research station of Pierroton (44°44’N, 0°46’W). The controlled cross was carried out in 1992 and provided 278 seedlings, which subsequently were vegetatively propagated. Rooted cuttings from 207 genotypes (with approximately ten clonal replicates per genotype) were planted in the field in 2000 at the INRA’s experimental unit of Bourran (44°20’N, 0°24’W), located in the south west of France (Saintagne et al., 2004). Spacing of trees was 4m x 1.5m at the plantation. In 2012 a systematic thinning was carried out in the parcel, reducing the overall density by one half on average with a total amount of 1130 individuals. On average, the annual precipitation was 650.1 mm and the average temperature was 13.9°C from 2014 to 2017, i.e. during the four years of monitoring (Table 1).

Table 1.

Description of the experimental design for reproductive and growth traits

	Reproduction				Growth
	2014	2015	2016	2017	2014
Total number of genotypes	117	170	170	170	206
Total number of individuals (clonal replicates)	173	331	339	337	1130
Mean number of clonal replicates per genotype	1.48	1.95	1.99	1.98	5.46
Maximum amount of clonal replicates per genotype	4	6	6	6	10
Yearly averaged temperature (°C)	14.2	14.0	13.6	13.7	14.2
Yearly sum of precipitation (mm)	792.5	511.5	707.5	589.0	792.5

Genetic linkage maps were established for both parents (3P and A4) using gene-based SNP (Bodénès et al., 2016). Using the JoinMap procedure, a subset of SNP markers evenly distributed along the 12 linkage groups (LG) was selected to reconstruct two new parental linkage maps for QTL analysis. In total, the male and female linkage maps used for QTL detection contain 341 and 345 markers, respectively.

Monitoring reproduction

During spring 2014, when the trees were 16 years old since they were vegetatively propagated from the ortet (and 23 since seed production), we set up nets to collect acorns at 1 m above the ground under the whole canopy of each tree (Figure S1). The nets were stretched at the individual scale every two rows within the design and the trees which were very close to one another within a given row (i.e with no trees cut between them after thinning) were not sampled for recording reproduction, as their canopies were intermingled (Figure S1). In total seed crop was assessed on 173, 331, 339 and 337 individuals (clonal replicates) in 2014, 2015, 2016 and 2017 corresponding from 117 to 170 different genotypes over the four years (Table 1). In what follows the full sib genotypes will be called clones. Trees were planted within a randomized incomplete block design comprising 8 blocks with 47 ± 6 individuals per block. The number of clonal replicates per clone per block was one and the overall mean number of replicates used for this study varied between 1.48 and 1.99 (Table 1). To minimize predation and facilitate the acorns sorting, trees were harvested twice during mid-October and mid-November by collecting all the material (litter and acorns) deposited in the nets. Acorns were sorted from the rest of the litter in the laboratory and dried at room temperature.

Then, the total amount of seed produced N_tot, the total mass of seeds produced M_tot in g and the mean mass of one seed M_a in g were assessed. Along the last three years of measurement (2015, 2016 and 2017) we also estimated the coefficient of variation of each individual CV_i and the mean coefficient of synchrony r_i (Buonaccorsi et al., 2003). To estimate r_i, we assessed a correlation matrix between individuals using Pearson coefficient, and estimate the average coefficient for each of them. As the number of trees assessed in 2014 was much lower due to technical constraints related to the stretching of the nets, data of 2014 were not used in this analysis. In addition, diameter at breast height (D in mm) and height (H in m) of each tree were measured in 2014 and the ratio between reproduction and growth (N_tot/D) were calculated for each year in order to normalize the total seed production relative to the size of the tree.

2.2. Statistical analysis

We used a univariate linear mixed effect model to assess the genetic parameter of reproductive and growth traits for the four years of measurement:

$$Y_{\text{ijk}}=\text{μ}+{\text{b}}_{\text{i}}+C_j+{\epsilon }_{ijk}$$ [1]

where Y_ijk denotes the observed phenotypic value of clone replicates k of clone j in block i, µ the overall mean, b_i the fixed effect associated with block i, C_j the random effect associated with clone j (genetic effect) and ε_ijk the residuals. In addition to assess the multi-annual variability we used an additional univariate linear mixed model for each trait:

$$Y_{\text{ijkl}}=\mathrm{\text{μ}}+{\text{b}}_{\text{ij}}+{\text{t}}_{\text{l}}+C_j+{\epsilon }_{ijkl}$$ [2]

where Y_ijkl is the observed phenotypic value of clone j in block i and year l and t_l the fixed effect associated to year l. For both models, the reproductive traits M_tot, N_tot and the ratio N_tot/D were log transformed. Best linear unbiased predictions (BLUPs) of random effects were estimated for each trait and within each year from the two linear mixed effect models. Year-Year correlations were estimated for phenotypic and BLUP values of log (N_tot + 1), log (M_tot +1), log (N_tot/D + 1) and M_a using Pearson coefficient, thus leading to values close to phenotypic and genotypic correlations. In addition, the differences between years for the same traits were tested using an analysis of variance (ANOVA). Finally, genetic correlations were also estimated between reproductive and growth traits, using the BLUPs estimated from the multi-annual model for reproductive traits and the BLUPs estimated in 2014 for growth traits.

Variances of random clone effects were used to estimate the genetic parameters of each trait. Following Scotti-Saintagne et al. (2004) we assume that the environmental effect was absorbed by the variance among replicates (cuttings) of a same genotype (clone). Considering that the cuttings were full sibs, the clonal variance estimated $({\sigma }_c^2)$ was equal to the within full-sib family $({\sigma }_w^2)$, where:

$${\sigma }_c^2=\frac{1}{2}{V}_A+\frac{3}{4}{V}_D$$ [3]

Here, V_A is the additive genetic variance and V_D is the dominance variance. To estimate the narrow sense heritability (h²) of each trait, which represents the proportion of phenotypic variance that can be attributed to V_A, we considered two cases encompassing the likely range of the dominance variance (V_D = 0 and $V_D=\frac{1}{2}{V}_A$), as V_D is generally lower than V_A in forest trees (Cornelius 1994). Thus, we estimated h² using:

$$(i)h_0^2=\frac{2{\sigma }_C^2}{2{\sigma }_C^2+{\sigma }_{\epsilon }^2}\text{and}(ii)h_{1/2}^2=\frac{\frac{8}{7}{\sigma }_C^2}{\frac{12}{7}{\sigma }_C^2+{\sigma }_{\epsilon }^2}$$ [4]

Confidence intervals of narrow sense heritability values were estimated using the method of Visscher and Godard (2014) applied to a single full sib family, assuming that the true values of heritability and phenotypic variance corresponded to the estimated values.

In addition, we also estimated the repeatability, expressing the proportion of the phenotypic variance of clonal means due to the clone effect, using:

$$R=\frac{{\sigma }_C^2}{{\sigma }_C^2+\frac{{\sigma }_{\epsilon }^2}{n_0}}$$ [4]

where $({\sigma }_{\epsilon }^2)$ is the environmental here residual variance and n₀ is the number of cuttings per clone.

Finally, we also estimated the evolvability (Hansen et al., 2011) for the two cases previously described for the estimation of h², using:

$$(i)e_0=\frac{2{\sigma }_C^2}{m^2}\text{and}(ii)e_{1/2}=\frac{\frac{8}{7}{\sigma }_C^2}{m^2}$$ [6]

were m is the mean of the trait. For N_tot, M_tot and N_tot/D, we estimated the evolvabilities of the non-transformed data since as reported by Hansen et al. (2011), the additive variance of the log-transformed data is approximately equal to the evolvability of the non-transformed scale. Evolvability is a mean standardized measure of the additive variation, in comparison to heritability which is a variance standardized measure of additive variation. It was shown earlier (Hansen et la., 2011) that the latter might respond more to the environmental variance (which is on the denominator of heritability) than to the additive variance (which is on the numerator). To reduce the noise created by the environmental variance on heritability, Hansen et al. (2011) recommended to estimate evolvability as well.

The analyses were performed in R Studio version 1.0.153 (R core team 2014). All the linear mixed effect models were fitted by the restricted maximum likelihood (REML) method in the lme4 R package (Bates et al., 2014; Bolker et al., 2009).

2.3. QTL detection

Quantitative trait locus (QTL) mapping was performed using Haley-Knott regression (Haley and Knott, 1992) in R/qtl package (Broman et al., 2003) with 1cM step using the BLUP values. QTLs were selected using a stepwise model selection approach (Manichaikul et al., 2009) based on a significant threshold at 5% error rate made from 1000 permutations. The 95 % confidence interval was calculated for each selected QTL using Bayesian methods (Manichaikul et al., 2006). The effect of each QTL and the percentage of phenotypic variance explained (PEV) were also estimated. In addition, we also used a two QTL model when the results of one QTL model suggested the likely presence of a second QTL on the same linkage group, LG₃ (Figure S3). The scantwo function on R/QTL was used in this case (Figure S4).

3. Results

3.1. Phenotypic and genetic variation of reproductive traits

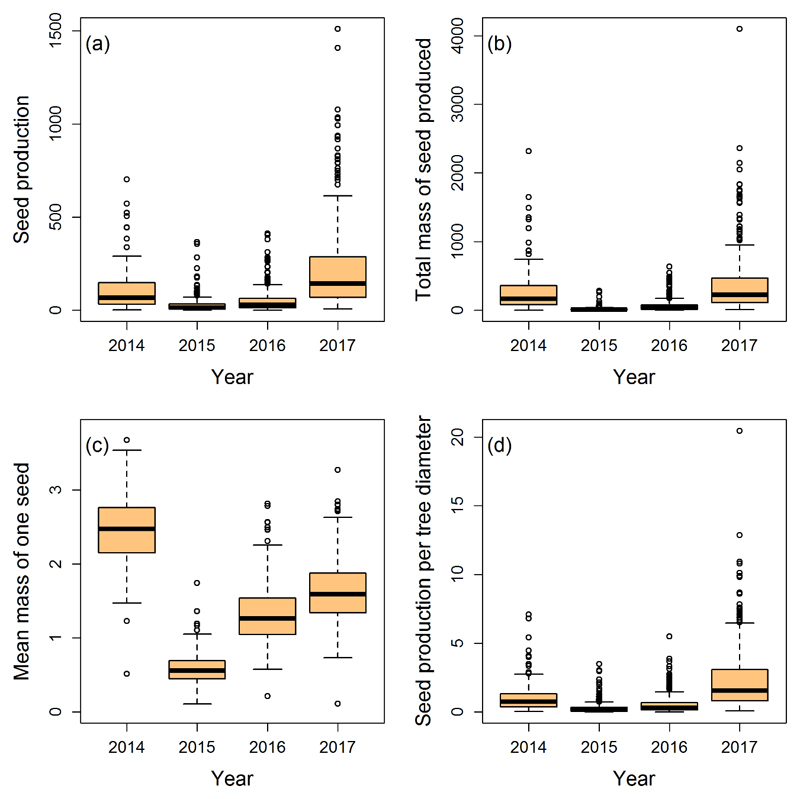
Large phenotypic variation was observed for seed production and size over the four years (Figure 1). Mean annual number of acorns per tree (N_tot) varied between 27.8 and 226.6 seeds while N_tot/D varied between 0.54 and 2.34 seeds per mm and M_tot between 16.1 and 385.9 gramme. Similar results can be observed when comparing seed production of a given tree over years (Inter-annual coefficient of variation for N_tot amounts to 1.05 ± 0.29, for the four years and 1.07 ± 0.35 for the last three years). On average the production of seeds was higher in 2014 and 2017 (Figure 1a, b and d) and the mean mass of one seed was higher in 2014 (Figure 1c) with an average mass of 2.5 g. Furthermore, within a given year we observed a large inter-individual variability for all reproductive traits (Figure 1). The large differences between marginal and conditional coefficient of determination (R²_m and R²_c) observed for most of the annual and multi-annual traits (trait over the four years of monitoring, see model [2]), show that the clone random effect of the linear mixed effect model explains most of the variability predicted by model 1 for one-year traits and by model 2 for multi-annual traits (Table 2). Clonal repeatability varied between 0.22 for M_a to 0.70 for N_tot and N_tot/D, suggesting that the between clonal variance was almost as large as the within clonal variance. One can notice that the difference between R²_m and R²_c, estimated from the multi-annual model of the mean mass of one acorn (M_a), is lower than for the other traits (R²_m = 0.05 and R²_c = 0.1). This discrepancy is most likely due to the large differences of mean acorn mass between years already pointed out. The narrow sense heritabilities (h²₀ and h²_1/2) estimated for each year were moderate and similar over time for every reproductive trait monitored (Table 2). For each year, the highest heritabilities were observed for N_tot and N_tot/D and the lowest heritabilities were estimated for M_a, in most cases the heritabilities estimated for growth traits (D and H) were lower than for reproductive traits. In comparison, very high evolvabilities were observed for N_tot and M_tot, ranging from 0.37 to 1.24 but there were more moderate for N_tot/D. The evolvabilities estimated were much lower for Ma (ranging from 0.0008 and 0.04), H, D nevertheless there are still relatively high compared to the other estimated valued in the literature except for H (Hansen et al., 2011). Heritability values of the masting related traits (coefficient of variation CV_i and coefficient of synchrony r_i) were of the same magnitude than values of the reproduction related traits (Table 2).

Figure 1.

Boxplots of the 4 phenotypic traits represented for each year. Seed production, total mass of seed produced (g) and seed production per tree diameter (seed.mm^-1) were log transformed. The mean mass of one seed was assessed in grammes.

Table 2.

Estimation of the marginal and conditional coefficient of determination (R²m and R²c), the mean clone repeatability (R), the narrow sense heritabilities (h²₀ and h²_1/2) and the evolvabilities (e₀ and e_1/2) for each trait and each year monitored (from 2014 to 2017)). The interval of confidence of the narrow sense heritabilities were estimated at 95% using the method from Visscher and Goddard (2014).

Trait	Year	n0	R2m	R2c	R	h20	h21/2	e0	e1/2
Ntot	2014	1.48	0.02	0.43	0.52	0.59 [0.23, 0.95]	0.37 [-0.03, 0.77]	1.02	0.58
Ntot	2015	1.95	0.07	0.48	0.61	0.62 [0.32, 0.92]	0.39 [0.05, 0.72]	1.24	0.71
Ntot	2016	2.00	0.04	0.33	0.46	0.46 [0.13, 0.78]	0.28 [-0.06, 0.62]	0.76	0.43
Ntot	2017	1.98	0.02	0.54	0.69	0.69 [0.41, 0.97]	0.44 [0.11, 0.77]	1.03	0.58
Ntot	Multi-Annual	2.00	0.13	0.35	0.70	0.40 [0.07, 0.73]	0.38 [0.04, 0.71]	0.89	0.51
Mtot	2014	1.48	0.01	0.41	0.50	0.58 [0.21, 0.95]	0.36 [-0.04, 0.76]	1.16	0.66
Mtot	2015	1.94	0.07	0.47	0.60	0.60 [0.30, 0.90]	0.38 [0.04, 0.71]	1.09	0.62
Mtot	2016	2.00	0.07	0.32	0.43	0.43 [0.10, 0.76]	0.26 [-0.08, 0.60]	0.78	0.44
Mtot	2017	1.98	0.04	0.54	0.69	0.69 [0.41, 0.97]	0.44 [0.11, 0.77]	1.16	0.67
Mtot	Multi-Annual	2.00	0.13	0.23	0.49	0.22 [-0.11, 0.55]	0.13 [-0.15, 0.41]	0.65	0.37
Ma	2014	1.48	0.01	0.31	0.39	0.46 [0.07, 0.85]	0.28 [-0.12, 0.68]	0.0211	0.0121
Ma	2015	1.88	0.05	0.21	0.27	0.28 [-0.06, 0.62]	0.17 [-0.14, 0.48]	0.0402	0.0230
Ma	2016	1.93	0.07	0.19	0.22	0.22 [-0.11, 0.55]	0.13 [-0.15, 0.41]	0.0210	0.0120
Ma	2017	1.98	0.21	0.42	0.42	0.42 [0.09, 0.75]	0.26 [-0.08, 0.60]	0.0278	0.0159
Ma	Multi-Annual	1.93	0.05	0.1	0.28	0.10 [-0.15, 0.35]	0.06 [-0.12, 0.24]	0.0014	0.0008
Ntot/D	2014	1.48	0.02	0.43	0.52	0.59 [0.22, 0.96]	0.37 [-0.03, 0.78]	0.15	0.08
Ntot/D	2015	1.95	0.04	0.5	0.64	0.65 [0.36, 0.94]	0.41 [0.07, 0.74]	0.05	0.03
Ntot/D	2016	2.00	0.08	0.46	0.58	0.58 [0.28, 0.88]	0.36 [0.02, 0.70]	0.08	0.04
Ntot/D	2017	1.98	0.02	0.54	0.70	0.70 [0.42, 0.98]	0.44 [0.11, 0.77]	0.34	0.19
Ntot/D	Multi-Annual	2.00	0.16	0.36	0.68	0.38 [0.04, 0.71]	0.23 [-0.10, 0.56]	0.11	0.06
CVi	Multi-Annual	1.93	0.14	0.42	0.48	0.49 [0.17, 0.81]	0.30 [-0.04, 0.64]	0.0593	0.0339
ri	Multi-Annual	1.98	0.07	0.3	0.4	0.40 [0.07, 0.73]	0.24 [-0.10, 0.58]	0.0332	0.0190
D	2014	5.46	0	0.15	0.48	0.25 [-0.06, 0.56]	0.15 [-0.13, 0.43]	0.017	0.0098
H	2014	5.46	0	0.23	0.62	0.37 [0.06, 0.68]	0.22 [-0.09, 0.53]	7.76e-5	4.44e-5

no: mean number of clonal replicates per genotype; Multi-annual: trait value over the for years; h²₀ and h²_1/2 :narrow sense heritabilities assuming dominance variance = 0 and dominance variance = ½ of the additive variance; e₀ and e_1/2: evolvabilities assuming dominance variance =0 and dominance variance = ½ additive variance

3.2. Phenotypic and genetic correlations between traits over time

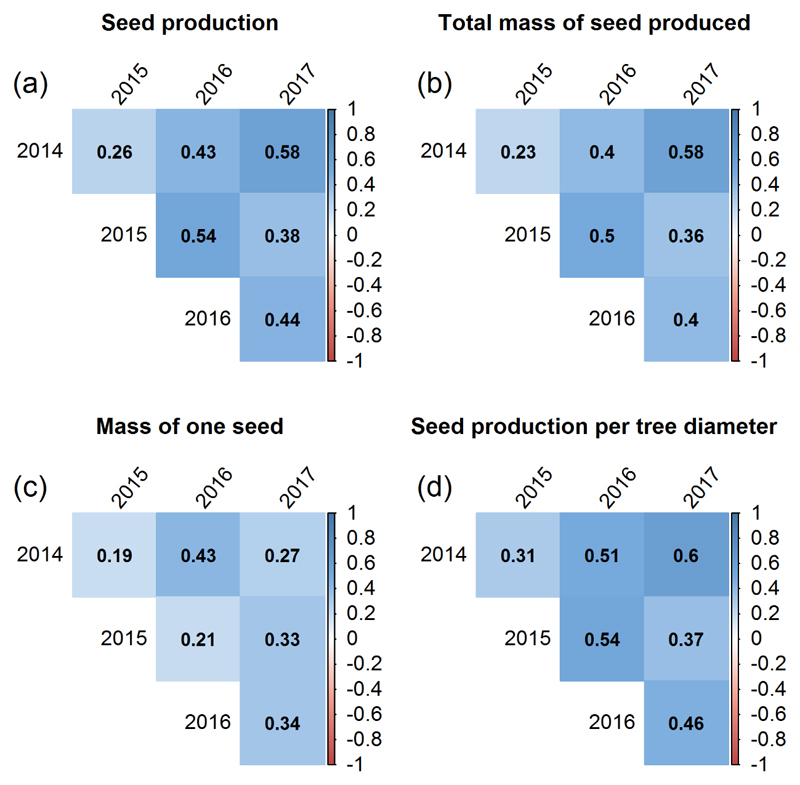
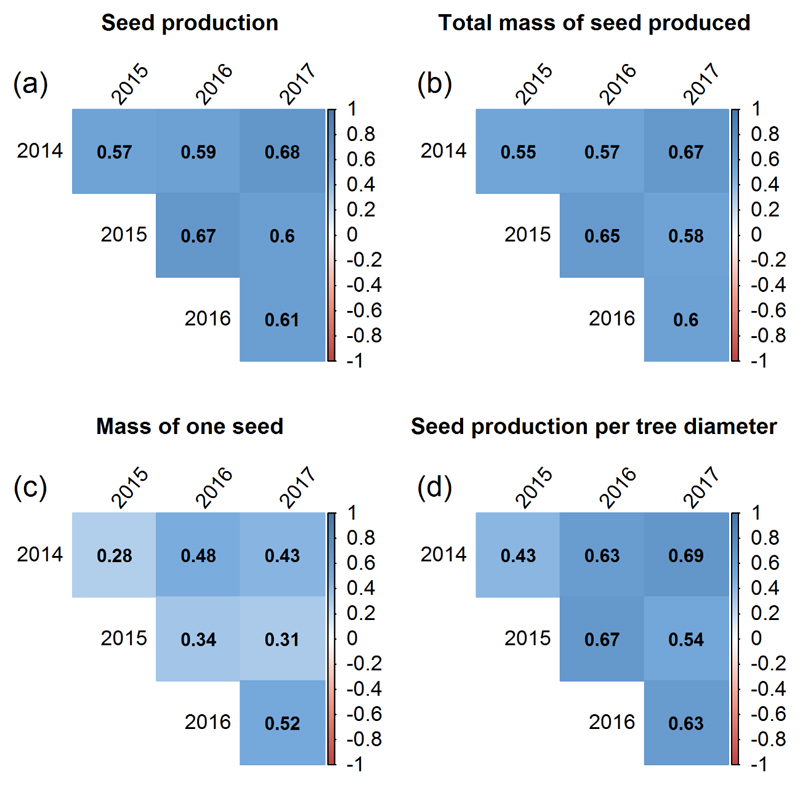
Phenotypic and genotypic correlations between traits over years were positive. For all six pairwise year-year combinations the phenotypic and genotypic correlations were significant for each trait. The coefficients of Pearson (Figure 2 and 3) were, in most cases, higher for the estimated BLUP values than for the phenotypic values with one exception for M_a (2015-2017), for which the phenotypic correlation (r = 0.33) was higher than the estimated genotypic value (r = 0.31). In average, the year-year genotypic and phenotypic correlations were much lower for M_a than for the three other traits. In addition, the highest r values for the genotypic and phenotypic correlations were observed between 2014 and 2017 for log(N_tot+1), log(M_tot+1) and log(N_tot/D + 1), while for M_a, the highest phenotypic correlation was observed between 2014 and 2016 and the highest genotypic correlation between 2016 and 2017. The genotypic correlations of reproductive traits with growth traits (H and D) were positive for M_tot, N_tot and nearer 0 for M_a and N_tot/D (Figure S2).

Figure 2.

Correlation between years, estimated for the phenotypic values of each trait using the coefficient of Pearson. Phenotypic values were log transformed for seed production (a), total mass of seed produced (b) and seed production per tree diameter (d).

Figure 3.

Correlation between years, estimated for the genetic values (BLUPs) of each trait using the coefficient of Pearson. Genetic values of seed production (a), total mass of seed produced (b) and seed production per tree diameter (d) were estimated on the log-transformed phenotypic values.

3.3. QTL detection (Table 2)

Annual and multi-annual models were used to detect the QTLs of reproductive traits. We detected significant QTLs for all traits related to reproduction and growth but not for CV_i neither for r_i. For M_a we detected significant QTLs on both maps (Male and Female), 1 QTL on the female linkage group 1 (LG₁F) for 2016, 2017 and for the multi-annual model, and 2 QTLs on LG₇M (male linkage group 7) for 2016 on LG₁₁M for the multi-annual model (Table 3, Figure S5). The QTLs detected on LG₁F were, for the three cases, located at 26 cM and the percentage of phenotypic explained variance (PEV) was of the same amount over the years: 9.80 % in 2016, 8.08 % in 2017 and 12.81 % over the four years, but the confidence intervals in 2016 and 2017 were much larger. For traits related to seed production (M_tot, N_tot and N_tot/D) we detected significant QTLs at the same location on LG₃F in 2015, 2016, and 2017 and across the three years with the multi-annual model. The positions were very similar through time and between traits. The highest PEVs on this linkage group were observed for N_tot, with 10.94% in 2015, 15.01% in 2016, 17.51 % in 2017 and 16.47 % for across the four years. In addition, on LG₁₁M, we also detected highly significant QTLs for the same traits than previously in 2014, 2016, and 2017 and across all years. The highest PEVs observed were for N_tot/D with respectively 15.38%, 17.54%, 12.32% and 14.11% in 2014, 2016, and 2017 and across all years. Another QTL was detected on the male map for traits related to seed production: for N_tot in 2014 and N_tot/D in 2014 on LG₅M. For both cases the position estimated on the linkage group was 65.03 cM and the PEV amounted to 10.11 % and 13.84 % respectively. Finally we also detected a significant QTL for N_tot/D in 2015 on LG₁₂F but the PEV estimated was relatively low (7.69 %) compared to the other QTLs.

Table 3.

Significant QTLs detected for each trait and their related statistics.

Trait	Year	Parent	n	LG	Position	LOD	BCI	PEV	p.value
Ma	2016	Female	168	1	25	3.76	8.85 – 38.00	9.8	<0.001
	2016	Male	168	7	50.08	2.99	36.00 – 58.87	7.86	<0.001
	2017	Female	169	1	26.47	3.11	12.00 – 48.00	8.07	<0.001
	Multi-Annual	Female	170	1	26.00	5.06	20.81– 38.00	12.81	<0.001
	Multi-Annual	Male	170	11	34.29	3.24	25.49– 52.00	8.39	<0.001
Mtot	2014	Male	117	11	54.01	2.97	15.00 – 58.73	11.03	<0.001
	2015	Female	169	3	32.56	3.29	7 – 37.24	8.53	<0.001
	2016	Female	169	3	33.8	5.86	13.24 – 36.00	14.75	<0.001
	2016	Male	169	11	23.6	6.34	10.72 – 34.29	15.87	<0.001
	2017	Female	170	3	28.00	6.78	24.00 – 33.00	16.77	<0.001
	2017	Male	170	11	23.6	5.12	14.00 – 54.01	12.96	<0.001
	Multi-Annual	Female	170	3	31.00	5.85	12.93 – 34.44	14.65	<0.001
	Multi-Annual	Male	170	11	23.6	6.16	14.00 – 34.00	15.36	<0.001
Ntot	2014	Male	117	5	65.03	2.7	45.00 – 72.24	10.11	<0.001
	2014	Male	117	11	54.01	3.02	13 – 58.73	11.24	<0.001
	2015	Female	170	3	32.56	4.28	8.86 – 36.62	10.94	<0.001
	2016	Female	170	3	31	6	13.24 – 35.05	15.01	<0.001
	2016	Male	170	11	23	5.81	10.00 – 33.00	14.56	<0.001
	2017	Female	170	3	29.00	7.76	25.00 – 32.00	17.51	<0.001
	2017	Male	170	11	23.6	4.21	10.00 – 54.01	10.78	<0.001
	Multi-Annual	Female	170	3	31.63	6.64	13.24– 34.75	16.47	<0.001
	Multi-Annual	Male	170	11	23.00	4.73	10.00 – 52.00	12.04	<0.001
Ntot/D	2014	Male	117	5	65.03	3.78	56.78 – 72.24	13.84	<0.001
	2014	Male	117	11	22	4.24	13.00 – 56.00	15.38	<0.001
	2015	Female	170	3	32.6	3.24	4.00 – 39.13	8.41	<0.001
	2015	Female	170	12	19	2.95	10.00 – 30.69	7.69	<0.001
	2016	Female	170	3	31	5.51	16.00 – 36.62	13.86	<0.001
	2016	Male	170	11	10.72	7.12	10.00 – 32.00	17.54	<0.001
	2017	Female	170	3	30.00	7.50	25.19 – 33.00	18.40	<0.001
	2017	Male	170	11	23.6	4.85	10.00 – 54.01	12.32	<0.001
	Multi-Annual	Female	170	2	30.98	3.23	16.58 – 41.00	8.10	<0.001
	Multi-Annual	Female	170	3	32.00	3.28	17.00 – 40.00	8.21	<0.001
	Multi-Annual	Male	170	11	22.00	5.56	10.72 – 33.00	13.54	<0.001

Year: year of monitoring; Multi-annual: trait value over the four years; Parent: Female or male genetic map; n: number of clonal replicates per genotype; LG: Linkage group; Position: Position of the QTL on LG in cM; BCI: Confidence interval of the position at 95% indicated in cM; PEV: Percentage of phenotypic explained variance by a QTL; p.value: significance level.

4. Discussion

Reproduction in forest tree species is highly variable between and within populations (Haymes and Fox, 2012; Kang et al., 2003; Pérez-Ramos et al., 2014). Although few studies have shown and quantified the genetic contribution to the between population variation of reproductive traits (Santos-del-Blanco et al., 2012), our study is one of the first to investigate the genetic variation within a single population. Using a full-sib family of Quercus robur, this study highlights a large variability of reproductive traits at the within population level, and underlines the important contribution of genetic effects. Furthermore, we detected for the first time in forest tree species quantitative trait loci (QTLs) associated with seed production and the mean mass of a seed. Despite a large phenotypic variability over years, the genetic contribution to reproduction was highly correlated between years.

4.1. Large genetic variation of reproductive traits

The repeated assessment of reproduction related traits over four years resulted in estimates of large phenotypic variability for N_tot, M_tot and N_tot/D and to a lesser extent seed size (M_a), as well as for masting related traits (CV_i and r_i) In addition, the estimated heritability and evolvability values suggested significant and substantial genetic contributions to the phenotypic variability. It is tempting to compare our values of heritability and evolvability to other reported values in trees; however, the scarce published tree studies reported broad sense heritabilities (H²), which are larger than narrow sense heritabilities. Nevertheless, our results suggest slightly larger genetic (additive) variance of reproductive traits in oaks than in other species. For example Sıvacıoglu et al. (2009) reported H² values ranging from 0.18 to 0.38 for cone production in Pinus sylvestris while H² was found lower, around 0.15 in Pinus pinea (Mutke et al., 2005). These values are similar to the H² estimated for female and male inflorescences in pines and spruces (Bilir et al., 2006; Nikkanen and Ruotsalainen, 2000; Sıvacıoglu et al., 2009). For example H² values estimated for female and male flowering were around 0.38, in Picea abies (Nikkanen and Ruotsalainen, 2000) and 0.12 in Pinus sylvestris (Bilir et al., 2006). Compared to other traits commonly assessed in forest trees and especially in oak, narrow sense heritability values (h²) assessed here on reproduction traits are slightly lower than for phenological traits (Baliuckas and Pliura, 2004; Alberto et al., 2011; Firmat et al., 2017), about the same magnitude than wood density and wood anatomical related traits (Nepveu, 1982, 1984; Mather et al., 1993; Savill et al., 1993), and higher than growth traits (see our results, Jensen et al., 1997; Bogdan, et al. 2004,2017; Barzdajn, 2008). Therefore, our results suggest that reproduction traits in trees may undergo evolutionary changes if they are targets of selection under ongoing environmental changes.

Over the four years of monitoring, seed production was highly variable and synchronized between trees. This phenomenon, also known as masting or mast-seeding, is characteristic of several forest tree species including oak species (Koenig et al., 1996, 1994). The coefficient of variation (CVi) and the coefficient of synchrony (r_i) estimated for each individual are common measures of the ability to express multi-annual variability of seed production and synchrony among trees, respectively (Buonaccorsi et al., 2003). The moderate heritability estimated for both CV_i (h²₀ = 0.49 and h²_1/2 = 0.30) and r_i (h²₀ = 0.40 and h²_1/2 = 0.24) suggests that the variation of both measures, estimated from 2015 to 2017, were partly due to genetic effects. While the period of monitoring was relatively short in our study, these results suggest that masting-related traits might be heritable. To our knowledge, no study has attempted so far to study the genetic determinism of masting while it is commonly assumed that it is an adaptive response to the selection pressure by predators (Kelly and Sork, 2002). Our results should however be considered as very preliminary, as long-term longitudinal monitoring would be necessary to estimate the genetic contribution of masting related traits.

Despite the large multi-annual variability and the significant sensitivity of reproduction to environmental changes, the genetic contribution was highly correlated over time. Thus, our results showed that most prolific trees were the same during the four years of monitoring, regardless of the overall level of seed crop within each year. For every trait assessed, heritabilities estimated using the multi-annual model was lower than the heritabilities estimated within single year. These differences may be explained by the increase of the residual variation over years due to the changes of biotic and abiotic conditions over time. Evidence for the inter-annual variation of the residual variance is also suggested by the changes of single year heritabilities over years. Similar trends were also observed in other species; for example broad sense heritability (H²) of female and male inflorescence production in Picea abies (Nikkanen and Ruotsalainen, 2000) and cone production in Pinus sylvestris (Kroon et al., 2009) changed substantially over years. Despite variation of the overall mean and variance of reproductive traits over years, phenotypic and genetic correlations between years were quite high suggesting that monitoring of reproduction for genetic evaluation of clones can be limited to a very few numbers of years, if masting is not foreseen as an objective of the study.

While it is commonly assumed and observed that fitness-traits have low narrow sense heritabilities (Hoffmann et al., 2016; Price and Schluter, 1991), we obtained relatively high values for reproductive traits which are known to be main components of tree fitness. Merilä and Sheldon, (1999) have shown that contrary to what was admitted before, the low heritability of fitness traits was mostly explained by high residual variances including the environmental and dominance variance. Admittedly we assumed in our estimation of narrow sense heritability that dominance (on a broader scale non-additive) variance was lower than additive variance in trees based on earlier reported values (White et al., 2007). Our assumption of low V_D may account for the discrepancy between observed values and predicted values based on evolutionary theory of fitness related traits. However, the underestimation of the residual variance would have a lesser impact on evolvability which is a standardization of the additive variance on the mean of the trait. And evolvability values still suggest that there is large additive variation existing in this oak clonal trial. Indeed, with a few exceptions our reported values of evolvability are in the upper half of all reported values of various species in the meta-analysis of Hansen et al. (2011). An alternative interpretation of the moderate values of genetic variation we found for reproductive traits is that four years assessments of reproduction at a still young stage of oak trees might not provide a relevant proxy of fitness. Hence the traits we measured might not have undergo so far sufficient selection pressures to the point to erode the genetic variation of the trait. Finally, the evolutionary implications of our results are still questionable, as estimates of heritability in our study were done in an experimental design where micro-environmental variation is minimized. These estimates should be compared in the future with in situ estimates, which can now be obtained by retrieving realized genetic relatedness among trees using large numbers of genetic markers (Lesur et al., 2018; Vinkhuysen et al., 2013).

4.2. Genetic architecture

Our QTL detection was implemented in a trial prone to sampling biases known as the Beavis effect (Beavis 1998). Typically, when the sample size (number of clones in our experiment) is less than 100, then the statistical power to detect QTLs of small effects are low, and their effects are inflated. Because of our limited sample size, our results should be interpreted with caution. We have likely only detected QTLs with major effects, and their effects may also have been overestimated. Thus, the refined genetic architecture (number of QTLs and distribution of their effects) needs still further investigations based on the distribution of allelic effects as was done by Hall et al. 2016

Despite statistical limitations for exploring the genetic architecture, our results have important biological implications regarding potential genomic regions containing genes that contribute to the variation of reproduction traits. Indeed, for seed production, significant QTLs on LG₃F and LG₁₁M were repeatedly detected over years, explaining from 8.21 to 18.40 and 10.70 to 17.54 percent of the phenotypic variance, respectively. The inferred position on the linkage groups were almost identical between years. Although we found a significant QTL on LG₁₁M for M_a with the multi-annual model, the other QTLs identified were not co-localized with the QTLs identified for the seed production related traits, even with the QTLs detected for M_tot. These genomic regions will be targets for association studies in natural populations to reduce their range within the genome and narrow down the search of candidate genes within the genome of Quercus robur that was recently sequenced (Plomion et al., 2016, 2018). As very few studies have attempted to dissect the genetic architecture of tree reproduction, it is difficult to compare our results with earlier reported studies. While Ujino-Ihara et al. (2012) undertook detection of QTLs associated with the production of male strobili in Cryptomeria japonica, to our knowledge, seed production and seed size have never been investigated in forest tree species. In fruit trees, numerous studies investigated the genetic determinism of biennial fruit bearing i.e. the irregular fruit production of a tree over consecutive years. Guitton et al. (2011) found that the QTLs associated with biennial bearing co-localized with genomic regions containing genes involved in floral development (floral integration gene, meristem identity gene and gibberellin oxidase gene). These results illustrate how our results could further lead to the identification of candidate genes by refining genomic regions containing the 3 major QTLs that we detected.

Finally, it is worthwhile checking whether the QTLs of reproduction related traits may colocalize with QTLs of other important traits particularly growth and phenology that were investigated earlier on the same QTL mapping pedigree (Scotti-Saintagne, 2004; Derory et al. 2010). While, the likely positive correlation between tree size and non-normalized seed production (N_tot) may lead to detect similar QTLs for N_tot and growth traits, the cross comparison of our results with QTLs of growth resulted in only one notable co-localization. LG₅M for the total tree height in 2001 and for N_tot and N_tot/D in 2014. Due to the low sample size in 2014 and the absence of repetition for the QTL on LG₅M, the co-localization of QTLs of seed production and growth on this region is weak. Apart from this region, no co-localization was observed between growth and reproduction. Potential co-localization may witness negative pleiotropic effects that may support the negative mechanistic trade-off between growth and reproduction that has often been reported in the literature (Camarero et al., 2010; Drobyshev et al., 2010; Han et al., 2008; Ishihara and Kikuzawa, 2009; Koenig and Knops, 1998; Monks and Kelly, 2006; Silvertown and Dodd, 1999). The lack of co-localization of QTLs in our study may thus be in line with the more recent hypothesis by Knops et al. (2007) that the negative correlation observed might not be causal, or that the trade-off may only be driven by environmental effects. Furthermore, the positive or non-genetic correlation observed between growth and reproductive traits (Figure S2), confirmed the likely absence of a trade-off between both. Furthermore, the positive or non-genetic correlation observed between growth and reproductive traits (Figure S2), confirmed the likely absence of a trade-off between both. The cross comparison of our results with QTLs of phenology (bud burst) resulted in only one notable co-localization on one linkage group (LG₁₁M), which would support genetic correlation with leaf phenology, seed production and seed size if the gene effects at the co-localized QTLs are strong.