Quasiharmonic Analysis of the Energy Landscapes of Dihydrofolate Reductase from Piezophiles and Mesophiles

Abstract

A quasiharmonic analysis (QHA) method is used to compare the potential energy landscapes of dihydrofolate reductase (DHFR) from a piezophile (pressure-loving organism), Moritella profunda (Mp), and a mesophile, Escherichia coli (Ec). The QHA method considers atomic fluctuations of the protein as motions of an atom in a local effective potential created by neighboring atoms and quantitates it in terms of effective force constants, isothermal compressibilities, and thermal expansivities. The analysis indicates that the underlying potential energy surface of MpDHFR is inherently softer than that of EcDHFR. In addition, on picosecond timescales, the energy surfaces become more similar at the growth conditions of Mp and Ec. On these timescales, DHFR behaves as expected; namely, increasing temperature makes the effective energy minimum less steep because thermal fluctuations increase the available volume whereas increasing pressure steepens it because compression reduces the available volume. Our longer simulations show that on nanosecond timescales, increasing temperature has a similar effect as on picosecond timescales because thermal fluctuations increase the volume even more on a longer timescale. However, these simulations also indicate that on nanosecond timescales, pressure makes the local potential less steep, contrary to picosecond timescales. Further examination of the QHA indicates the nanosecond pressure response may originate at picosecond timescales at the exterior of the protein, which suggests that protein-water interactions may be involved. The results may lead to understanding adaptations in enzymes made by piezophiles that enable them to function at higher pressures.

TOC Graphic

INTRODUCTION

The characterization of the effects of pressure and temperature on enzymes, and the adaptations Nature utilizes to protect against these effects, has implications for understanding how extremophiles adapt to live and grow under extreme conditions as well as how pathogenic microbes might develop resistance to preservation by temperature (i.e., pasteurization) or by pressure (i.e., pascalization).^1–2 Comparisons of homologous proteins from extremophiles and mesophiles have long been used to identify adaptations for extremes, particularly of temperature. Since proteins need to function at the growth conditions (i.e., growth temperature T_G, growth pressure P_G, etc.) of the parent organisms, the growth conditions can be considered to be the “corresponding states” where proteins from extremophiles and mesophiles should have similar behavior.^3–4 Thus, both the stability and flexibility of homologous enzymes tend to be similar near their corresponding states so that good activity is maintained at their growth conditions.^3–4 Moreover, resistance to a particular extreme is not necessarily greater for an enzyme from an extremophile that lives under that extreme than from a mesophile, as long as the enzyme maintains sufficient stability and flexibility for activity, as exemplified enzymes from psychrophiles (cold-loving) often having higher cold-unfolding temperatures that those from mesophiles.^5–6 However, while stability can be quantified by the free energy of unfolding or the unfolding temperature, no real consensus exists on what are good measures of flexibility.

Our interest is mainly on the effects of pressure of enzymes. One of the best characterized pair of piezophile (pressure-loving) and mesophile enzymes is dihydrofolate reductase (DHFR) from Moritella profunda (Mp), with a P_G, or optimal growth pressure, of 220 atm at 6 °C (the T_G, or optimal growth temperature, is 2 °C at 1 atm),⁷ and E. coli, with a presumed T_G of 37 °C at 1 atm. Thorough experimental comparisons have been made of the pressure dependence of the activity and stability of MpDHFR with EcDHFR.⁸ At 25 °C, MpDHFR has maximum enzyme activity at 500 atm while EcDHFR shows monotonic inactivation by pressure above 1 atm, which suggests pressure adaptations of MpDHFR, although structural differences are not apparent between the three crystal structures of MpDHFR and those of EcDHFR. The initial increase in activity of MpDHFR appears to be due to the presence of glutamate at residue 27 rather than the aspartate found in EcDHFR.⁹ However, the initial increase in enzyme activity with pressure for DHFR from deep-sea bacteria.¹⁰ Another interesting observation is that the unfolding pressure at 25 °C is 2700 atm for EcDHFR but only 700 atm for MpDHFR (both measurements were for the apo-enzyme, which is less stable than the folate bound form), indicating MpDHFR is actually more sensitive to pressure denaturation.⁸ The marginal stability of enzymes from piezophiles has been noted for DHFR from other piezophiles as well as other enzymes, and is actually more general than the initial increase in enzyme activity with pressure.¹⁰ This suggests that flexibility is more important for these deep-sea enzymes, although this may be an adaptation for the cold temperatures of the deep sea rather than for the high pressures.⁴

Our group has been examining the mean square fluctuations (MSF) of atomic coordinates as a measure of flexibility for corresponding states activity. Since our interest is in variations of temperature and pressure, GTP is used to refer collectively to T_G and P_G. Our molecular dynamics (MD) simulations of MpDHFR and EcDHFR indicate that MSF on a longer timescale (i.e., greater than 1 ns) might be a good marker of corresponding states flexibility because they become similar at the GTP of the organism from which the DHFR was isolated.¹¹ The MSF increase with temperature due to thermal fluctuations, consistent with numerous studies including X-ray¹² and MD simulations.¹³ Intriguingly, while the MSF decrease slightly with pressure on a short timescale (i.e., less than 1 ns) where local harmonic motions predominate, they increase with pressure on a longer timescale (i.e., greater than 1 ns) where more collective modes appear. The latter suggests that pressure may actually enhance flexibility by making collective modes more accessible, which is also consistent with experimental observations of pressure induced unfolding¹⁴ and pressure induced conformational shifts.¹⁵ Thus, an enzyme might be adapted to function under higher pressure by changes in its “material” properties and/or its barriers to collective motions.

Recently, our group has developed a method for analyzing pressure and temperature effects on the energy landscape of proteins or other globular macromolecules in solution.¹⁶ The quasiharmonic analysis (QHA) method assumes that the fluctuations for a given protein atom can be described as motion in an effective potential energy well created by its neighboring atoms. This energy well is described using a quasiharmonic approximation as a harmonic well with an effective force “constant” that is volume dependent, and any temperature and pressure dependence of the effective force constant k(P,T) is only through this volume dependence. In addition, the pressure and temperature dependences of the fluctuations are assumed to differ above and below a protein dynamical transition temperature T_g. The transition has been ascribed to be the onset of collective motions.^12,17–18 Above T_g, k(P,T) where the pressure dependence is given by an intrinsic isothermal compressibility κ_T, which measures the protein response to pressure, and the temperature dependence is given by an intrinsic isobaric thermal expansivity α_P, which measures the protein response to temperature. Below T_g, the fluctuations are assumed to be no longer temperature dependent and so the temperature dependence is frozen as its T_g value; i.e., for all T ≤ T_g, k(P,T_g) = k_g(P) where the pressure dependence is described by the same κ_T as above T_g. The energy landscape of a protein is explored by calculating the average atomic MSF (or mean-square displacements) from a “P-T” grid of short simulations at different probe pressures and temperatures (henceforth, P and T will refer to these probe pressures and temperatures). The simulations at each P-T condition must be short enough so the protein (and thus energy surface) does not relax away from the initial structure but long enough to explore the energy surface. Previously, the method was demonstrated using picosecond mean-square displacements calculated from a P-T grid of 1-ns simulations for hen egg white lysozyme by Smith, Zewail, and co-workers.¹⁹ A simulation length of 1 ns appears to be a good compromise since it is shorter than the 4 ns used to equilibrate to new P-T conditions in our previous equilibrium studies¹¹ but long enough to adequately sample collective motions, which occur on the picosecond or larger timescale.

Here, the goal is to understand how pressure and temperature affect proteins such that the MSF appear to show corresponding states behavior in the 50-ns simulations of EcDHFR and MpDHFR; in other words, why their MSF are similar at the GTP of their parent organisms. In particular, the apparent difference in effects of pressure on sub-nanosecond versus supra-nanosecond timescales is explored. The energy landscapes of these two proteins at different temperatures and pressures are explored using QHA of average 10 ps MSF from a P-T grid of 1-ns simulations beginning from simulations of EcDHFR and MpDHFR that are completely equilibrated at pressure P_eq and temperature T_eq. The equilibration conditions included GTP of the parent organism and a common temperature of 279 K and common pressure of 1 atm, which are collectively referred to as the CTP. The common temperature was chosen as 279 K since the simulations of MpDHFR at 298 K show continuing deviation from the crystal structure during over 50 ns and experimentally MpDHFR shows signs of unfolding at 298 K.²⁰ First, the effects of T_eq on the MSF of EcDHFR and the effects of P_eq on the MSF of MpDHFR are examined. Next, transition from CTP to GTP was compared for EcDHFR and MpDHFR, including differences between MSF from the interior and the exterior of the protein. Finally, the effects of pressure on the MSF of MpDHFR from the interior and the exterior of the protein were examined in light of the 50 ns MSF of MpDHFR.

THEORY

The theory follows previously reported work,¹⁶ which is described briefly here; additional details can be found in that work. A quasiharmonic approximation assumes that force constant varies due to changes in volume, so that P, T effects are only on volume of the system. Thus, the potential energy minimum is assumed to have a pressure and temperature dependent effective spring constant k(P,T)

$$dk(P,T)={\left(\frac{\partial k}{\partial V}\right)}_T{\left(\frac{\partial V}{\partial P}\right)}_{T}dP+{\left(\frac{\partial k}{\partial V}\right)}_T{\left(\frac{\partial V}{\partial T}\right)}_{P}dT$$ (1)

The quantities in Eq. 1 can be identified with various thermodynamic parameters. For instance, the isothermal compressibility is

$${\kappa }_T=-\frac{1}{V}{\left(\frac{\partial V}{\partial P}\right)}_T={\kappa }_{T,0}{\left(\frac{V(P)}{V(P_0)}\right)}^{\mu }$$ (2)

where the second equality describes the dependence of κ_T on V in which κ_T,0 = κ_T(P₀) and μ is a non-linearity index, and the isobaric thermal expansivity is

$${\alpha }_P=\frac{1}{V}{\left(\frac{\partial V}{\partial T}\right)}_P={\alpha }_{P,0}{\left(\frac{V(T)}{V(T_0)}\right)}^{\nu }$$ (3)

where the second equality describes the dependence of κ_T on V in which α_P,0 = α_P(T₀) and ν is another non-linearity index. The volume dependence of these quantities can be determined with respect to a reference pressure P₀ and a reference temperature T₀, and Δ denotes differences with respect to reference quantities. Our previous work¹⁶ indicates μ = 1 and ν = 0 for the temperatures and pressures used here. In addition, if the oscillators are independent (i.e. classical Einstein oscillators)

$$\frac{V}{k}{\left(\frac{\partial k}{\partial V}\right)}_T=-\frac{2}{3}$$ (4)

Thus, one can obtain

$$k(P,T)=k_0{\left[exp(-{\alpha }_{P,0}\Delta T)(1+{\kappa }_{T,0}\Delta P)\right]}^{2/3}$$ (5)

for μ = 1 and ν = 0 where k₀ = k(P₀, T₀). Furthermore, if κ_T is assumed to be independent of T, κ_T,0 = κ_T(P₀, T₀) and if α_P is assumed independent of P, α_P,0 = α_P(P₀, T₀).

At high temperatures, the local atomic fluctuations of the protein are assumed to include transitions to other substates that lead to volume changes. Thus, their potential energy wells are described as quasiharmonic with volume dependent force constants k(P,T) that exhibit pressure and temperature dependence via a temperature-independent κ_T and a pressure-independent α_P, respectively (Eq. 7). The mean-square fluctuations σ²(P, T) = 3k_BT/k(P,T) are thus given by

$${\sigma }^2(P,T)={\sigma }^2{}_0\frac{T}{T_0}{\left[exp(-{\alpha }_{P,0}\Delta T)(1+{\kappa }_{T,0}\Delta P)\right]}^{-2/3}$$ (6)

for μ = 1 and ν = 0 where σ ₀² = σ ²(P₀, T₀). Because of the assumption of independent oscillators, κ_T and α_P will overestimate values for the entire protein if there are collective modes present.

Below T_g, the local atomic fluctuations are assumed to no longer include transitions to other substates while pressure can still cause volume changes by compressing the protein. This implies the underlying potential energy surface at a given pressure is being explored.¹⁹ Thus, the magnitude of k at a given P becomes frozen at T_g while the dependence on P is assumed to be the same as above T_g. The mean-square fluctuations for the glass region (T < T_g) can then be related to values at T_g by

$${\sigma }_g{}^2(P)={\sigma }^2{}_0\frac{T_g(P)}{T_0}{\left[exp(-{\alpha }_{P,0}(T_g(P)-T_0))(1+{\kappa }_{T,0}\Delta P)\right]}^{-2/3}$$ (7)

for μ = 1 and ν = 0. The values of σ₀², α_P,0, and κ_T,0 take on the values from the high temperature region. The pressure-dependence of T_g is assumed to be given by

$$T_g(P)=T_{g,0}-c\Delta P$$ (8)

where T_g,0 is T_g at the reference pressure and c is a constant, which are the only unknowns.

METHODS

A quasiharmonic analysis (QHA) entails analyzing fluctuations from a P-T grid of short simulations from an equilibrated structure. The short simulations here were initiated from previously reported equilibrated simulations¹¹ using same protocols, so the methods are described briefly here and additional details can be found in the previous work. The starting coordinates for the proteins in the previous work were obtained from the Protein Data Bank (PDB)²¹ for EcDHFR (PDB ID: 1RX2)²² and MpDHFR (PDB ID: 2ZZA) with tetrahydrofolate (THF) built in. MD simulations and other coordinate manipulations were performed using the molecular mechanics package CHARMM version 37b2, except for MpDHFR at 279 K, 1 atm, which was run on LoBoS using version 40b2.²³ The set-up was performed in CHARMMing²⁴ using default protocols except as noted. The CHARMM36 all-atom nonpolarizable potential energy parameter set^25–26 was used for the proteins. However, water was modeled by TIP4P-Ew²⁷ because of the importance of the properties of water under pressure. Additionally, a force field for THF was generated using the CHARMM Generalized Force Field server (cgenff.paramchem.org). The simulations utilized the leapfrog Verlet algorithm with a time step of 0.001 ps and were maintained in the NPT ensemble with the Nosé-Hoover algorithm^28–29 for the thermostat and barostat. Periodic boundary conditions and the particle mesh Ewald (PME) summation algorithm with a k-space grid spacing of about 0.34 ų⁰ were used. The rhombic dodecahedral simulation box has a distance between faces of ~71 Å and each protein was in 0.15 M KCl, so that there were 7420 water molecules, 27 K⁺ and 14 Cl⁻ for EcDHFR and 7414 water molecules, 26 K⁺, and 15 Cl⁻ for MpDHFR. After heating for 100 ps and pressurizing the 220 atm simulations for 22 ps, the simulations were allowed to equilibrate unperturbed for 4 ns after which the 50-ns production run was collected. In addition, a 10-ns simulation at T = 279 K, P = 300 atm for MpDHFR was performed for this work, which was heated for 100 ps and pressurized for 30 ps, then allowed to equilibrate unperturbed for 4 ns after which the 10-ns production run was collected.

The previously reported MSF from the 50 ns equilibrium simulations of DHFR in aqueous solution¹¹ were calculated by averaging fluctuations with respect to the average position over 10 ns intervals and then performing a second average over the 5 10 ns-intervals in the 50 ns simulation. The latter was used to generate error bars. For 10 ns simulation of MpDHFR at 279 K, 300 atm, there was only one 10 ns interval so no error bars are given.

A P-T grid of short simulations at all combinations of P = 1, 3000, 5000, 7000, and 10,000 atm and T = 40, 80, 120, 160, 200, 240, 279, 310 K were initiated from the final coordinates after 50 ns at T_eq = T_G = 310 K and P_eq = P_G = 1 atm for EcDHFR, and T_eq = T_G = 279 K and P_eq = P_G = 220 atm for MpDHFR, and from the final coordinates after 10 ns at T_eq = 298 K, P_eq = 1 atm and T_eq = 279 K, P_eq = 1 atm for EcDHFR T_eq = 279 K, P_eq = 1 atm and T_eq = 279 K, P_eq = 300 atm for MpDHFR. The P-T grid simulations do not represent the protein at the new P-T conditions; instead, they are used to probe the protein energy landscape of the equilibrated structures. Thus, the object is to allow as little relaxation of the equilibrated structure to the new P-T conditions as possible. The initial velocities of the atoms were obtained by scaling the final velocities of the simulations mentioned above by a factor of √(T/T_eq) and the system was run at T and P_eq with velocities scaled every 0.2 ps if the temperature was outside the window of T ± 10 K, for a total of 60 ps. After that, the system was run at T and P with velocities scaled every 0.2 ps if the temperature was outside the window of T ± 10 K, for another 60 ps, in which time the root mean-squared deviation (RMSD) from the starting structure stabilized. Finally, the system was simulated using identical methods for 1 ns each with coordinates saved every 0.1 ps. While there are large pressure fluctuations (~200 atm) even in NPT MD simulations, the period of the fluctuations about the mean value is ~2 ps so that the average pressure felt by the protein during the 1 ns simulations is distinguishable between 1 and 220 atm.

The MSF averaged over the heavy atoms, σ²(P, T), were calculated for each of the P-T grid simulations. The MSF were calculated by averaging fluctuations with respect to the average position over 10 ps intervals and then performing a second average over the 100 10 ps-intervals in the 1 ns simulation. The fits to the quasiharmonic equations were performed using gnuplot. The reference state is P₀ = 1 atm and T₀ = 279 K, the CTP. First, σ²(P, T) from the MD simulation data for P = 1, 3000, 5000, 7000, and 10,000 atm and T = 200, 240, 279, 310 K were fit using Eq. 6 for T > T_g to find values and error bars for σ₀², α_P, and κ_T,0. Next, σ²(P, T) from the MD simulation data for P = 1, 3000, 5000, 7000, and 10,000 atm and T = 40, 80, 120, 160 K were fit using Eq. 7-9 for T < T_g to find values for T_g,0 and c. Here, the pressure dependence of T_g was opposite of what was found in the previous QHA of lysozyme,¹¹ which we attribute to relaxation of the structure at higher pressures due to the pressurization procedure used in generating the P-T grid simulations.¹⁹ Since the values of T_g and c affect k_g(P₀), they were fixed at the values of the structures equilibrated at CTP for all the QHA of the DHFR from a given species.

RESULTS AND DISCUSSION

A QHA of the energy landscapes of MpDHFR and EcDHFR at different P_eq and T_eq are used to examine MSF on a picosecond (specifically, 10 ps) timescale, which are compared to MSF on a nanosecond (specifically, 10 ns) timescale from the 50 ns simulations. Fitted values of the parameters are in Table S1 of the Supporting Information. Effective force constants are examined rather than average MSF (calculated via k = 3k_BT/σ²) because the explicit temperature dependence is removed and the only temperature dependence is via changes in the structure due to T_eq. The picosecond timescale is examined using the force constants from the QHA at several states: k_g(P₀), the force constant below T_g at P₀, as a measure of the underlying potential energy surface;¹⁹ k₀ = k(P_0,T₀), the force constant at the reference state, for comparisons at the CTP of P₀ = 1 atm and T₀ = 279 K; and k_eq = k(P_eq,T_eq), the force constant at the state where the protein was equilibrated, for direct comparisons to the nanosecond timescale results, namely, k_eq(MD), the effective force constant from the 50-ns simulations. In addition, κ_T,0 and α_P,₀ from the QHA are used to separate the effects of changes in volume due to pressure and temperature. For the QHA, T_g,0 = 189 K and c = −1.0 K/katm for MpDHFR at all T_eq and P_eq and T_g,0 = 187, c = −0.8 K/katm for EcDHFR at all T_eq and P_eq.

Effects of T_eq on the energy landscape.

First, the energy landscape of EcDHFR as a function of T_eq at P_eq = 1 atm was examined (Fig. 1). Since k_g(P₀) decreases slightly with T_eq (~3% over 30 K), temperature is widening the underlying potential energy well. Above T_g, κ_T,0 increases slightly with T_eq (~5% over 30 K) while α_P,₀ > 0 is almost independent of T_eq (within > ~0.3% over 30 K); the latter implies that the expansion of wells over this range of T_eq is predicted well by α_P,₀. At constant pressure, since α_P,₀ is essentially constant, k₀ at CTP also decreases slightly with T_eq (~3% over 30 K). However, k_eq accounts for the change in volume that occurs between T₀ = 279 K and T_eq so it drops considerably with temperature (~20% over 30 K). In the 50 ns simulations, k_eq(MD) are much lower relative to QHA k_eq indicating larger fluctuations, but the relative decrease in k_eq(MD) with increasing T_eq (~20% over 30 K) is the same as in k_eq, so the decrease appears to be the consequence of the same effects at longer timescales, which allow more collective motions. In other words, proteins equilibrated at higher temperatures tend to have softer wells because the atoms are further apart due to thermal expansion.

Figure 1.

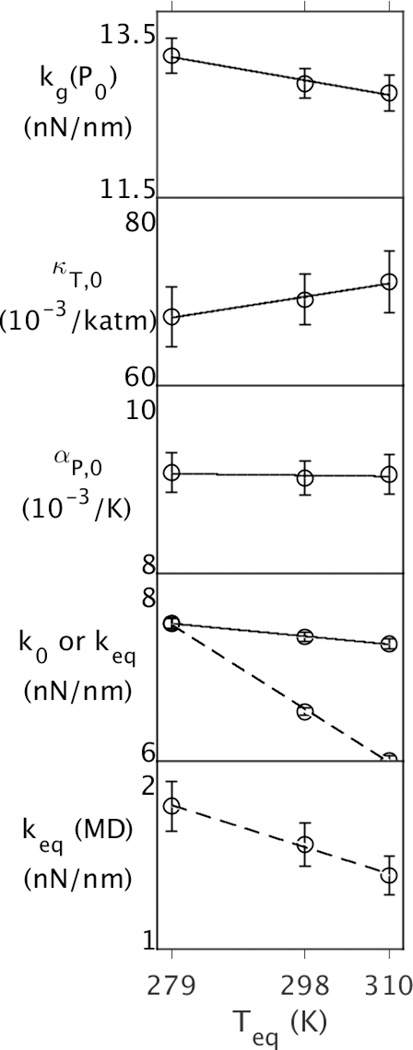
Properties of EcDHFR as function of T_eq at P_eq = P_G = 1 atm, where T_eq and P_eq are temperatures and pressures of 50 ns simulations. The top four panels contain properties from the QHA, and the bottom contains properties from the 50 ns simulation. Effective force constants at (P_eq,T_eq) are denoted by dashed lines in the bottom two panels.

Effects of P_eq on the energy landscape.

Next, the energy landscape of MpDHFR as a function of P_eq at T_eq = 279 K was examined (Fig. 2). Since k_g(P₀) increases slightly with P_eq (~3% over 300 atm), pressure is compressing the underlying potential well, making it narrower. Above T_g, κ_T,0 is almost independent of P_eq (within ~1.5% over 300 atm); the latter implies that the compression of the protein structure over this range of P_eq is predicted well by κ_T,0. In addition, α_P,₀ very slightly increases with P_eq (~3% over 300 atm) so that k₀ decreases with respect k_g(P₀) to at higher pressure and becomes almost constant with pressure (within ~0.7% over 300 atm). However, while k_eq accounts for the change in volume that occurs between P₀ = 1 atm and P_eq, the change in pressure is small so it only increases slightly with pressure (~2% over 300 atm). Interestingly, k_eq(MD) actually decreases as MpDHFR is equilibrated at higher pressure (27% over 300 atm). This will be addressed below.

Figure 2.

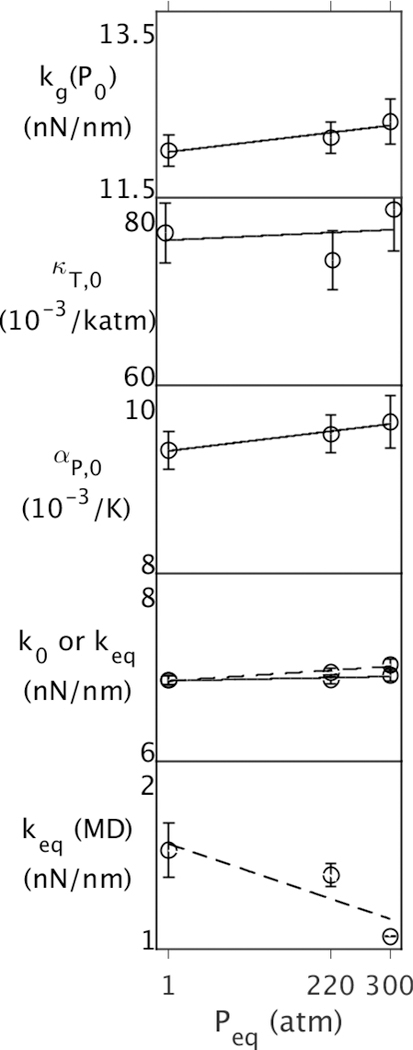
Properties of MpDHFR as function of P_eq at T_eq = T_G = 279 K, where T_eq and P_eq are temperatures and pressures of 50 ns simulations. The top four panels contain properties from the QHA, and the bottom contains properties from the 50 ns simulation. Effective force constants at (P_eq,T_eq) are denoted by dashed lines in the bottom two panels.

Adaptation to Extremes.

The differences between EcDHFR and MpDHFR are examined here for the entire protein and as well as being localized by dividing the protein into an interior region containing the active site and an exterior region (Fig. 3). The energy landscapes of EcDHFR and MpDHFR were compared for the entire protein and the interior vs. exterior (Fig. 4). In general, the k_g(P₀) of the underlying potential is larger for EcDHFR regardless of T_eq, which is consistent with more hydrogen bonds and ions pairs in the crystal structures of EcDHFR than MpDHFR.¹¹ In addition, since k_g(P₀) is lower at increasing T_eq while k_g(P₀) is higher at increasing P_eq, EcDHFR GTP is closer to MpDHFR at their respective GTP than at CTP. Above T_g, κ_T,0 is larger for MpDHFR, which also appears to be a consequence of the lower packing density in MpDHFR. In addition, since κ_T,0 is lower at increasing P_eq, MpDHFR is closer to EcDHFR at their respective GTP. However, while α_P,₀ is larger for MpDHFR, there is less dependence on T_eq or P_eq where the protein was equilibrated.

Figure 3.

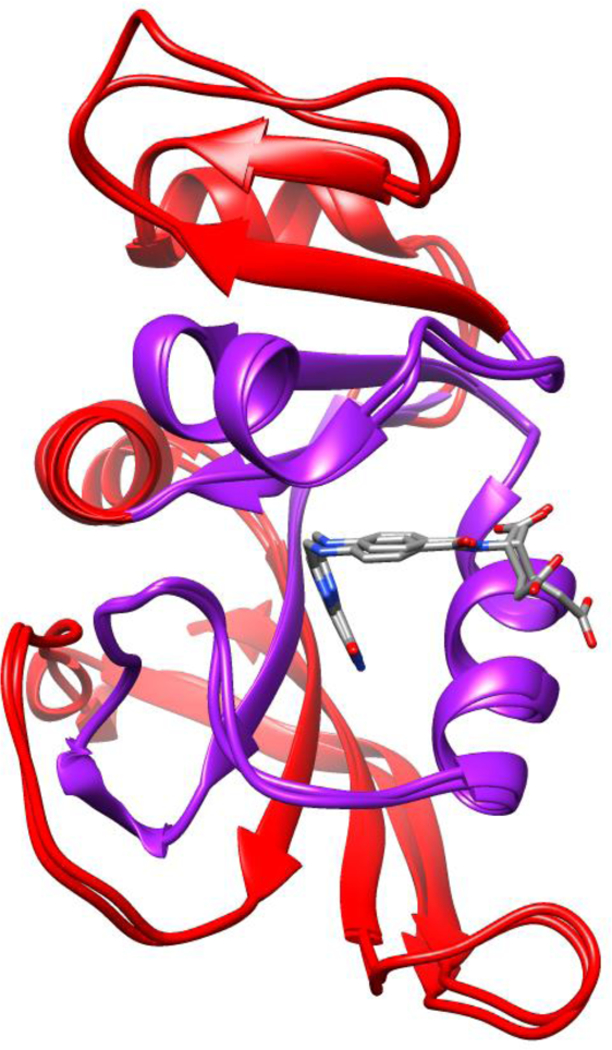
Superposed crystal structures of EcDHFR (PDB ID: 1RX2) and MpDHFR (PDB ID: 2ZZA) with division into the interior (purple) vs. exterior (red) indicated.

Figure 4.

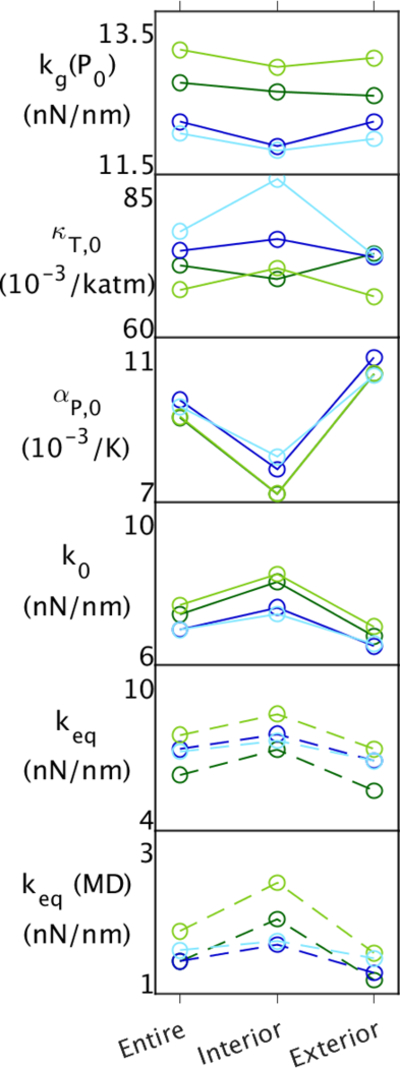
Properties of EcDHFR and MpDHFR for the entire protein, the interior, and the exterior at the CTP of 279 K, 1 atm (light green or blue, respectively), and at the corresponding GTP either 310 K, 1 atm (dark green) or 279 K, 220 atm (dark blue). The top five panels contain properties from the QHA, and the bottom contains properties from the 50 ns simulation. Effective force constants at (P_eq,T_eq) are denoted by dashed lines in the bottom two panels.

The k_g is relatively constant for the interior and exterior regardless of protein, so that the underlying well appears independent of location in the protein. In addition, α_P,₀ is significantly larger on the exterior than the interior regardless of protein. Thus, temperature increases the fluctuations at the exterior, as expected, because the thermal motion increases for all atoms, both protein and solvent, and the protein is less restricted at the surface. However, κ_T,0 is larger on the interior for MpDHFR at the CTP, but decreases in the interior as the pressure is increased to its GTP. This indicates that the interior is compressed by pressure, presumably by decreasing the size of internal cavities in the protein, while the exterior does not because water packs closer to the polypeptide with fewer cavities. κ_T,0 is also larger on the interior for EcDHFR at the CTP, but interestingly the exterior increases more as the temperature is increased to its GTP, presumably because temperature increases the fluctuations at the exterior. κ_T,0 is fairly uniform between the interior and the exterior for both EcDHFR and MpDHFR at their GTP. Thus, k₀ shifts uniformly lower as EcDHFR goes from its CTP to its GTP because α_P,₀ is the same uniform throughout.

The more pronounced decrease in k_eq(MD) with increasing T_eq for EcDHFR is also uniform between the interior and exterior, which further supports that they are consequence of the same effects at longer timescales, which allow more collective motions. However, while the pressure difference between CTP and GTP for MpDHFR is minimal so that variations in κ_T,0 do not affect k₀, there is a slight difference between α_P,₀ for the interior and exterior, which is consequently mirrored in k₀ so that it actually becomes lower with pressure on the exterior. A decrease in k_eq(MD) with increasing pressure is also seen for the exterior, which further supports that pressure is making the exterior more flexible.

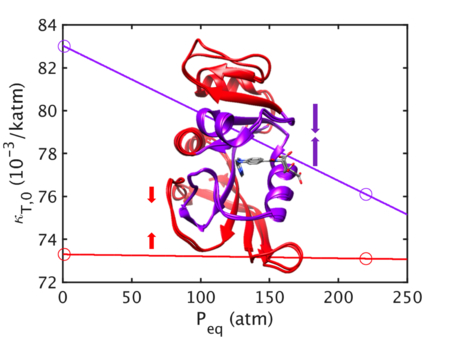
Implications for the nanosecond timescale.

As mentioned above, the temperature effects on the picosecond timescale are mirrored on the nanosecond timescale while pressure effects appear to differ between these timescales. In particular, k_eq from the QHA and k_eq(MD) from the 50 ns simulations both show a 20% decrease over 30°, while k_eq shows a 2% increase and k_eq(MD) shows a 27% decrease over 300 atm. Clues as to where the changes in behavior with pressure can be in the QHA by examining the behavior of the interior versus exterior as a function of P_eq (Fig. 5). While k_g indicates that pressure is making the wells of the underlying potential steeper, which would correlate with lowering α_P,₀, it appears that α_P,₀ is lowered only in the interior but actually increases on the exterior. Increased α_P,₀ causes the force constants above T_g to be lowered according to Eqn. 5. This indicates that pressure may have another effect on exterior atoms other than compression. For instance, protein-water interactions may be affected. Moreover, given that the k_eq from the QHA and k_eq(MD) from the 50 ns simulations show an overall increase in the MSF with timescale (Fig. 1, bottom two panels), the k_eq(MD) decrease in with pressure may be due to further increases in α_P,₀ with timescale.

Figure 5.

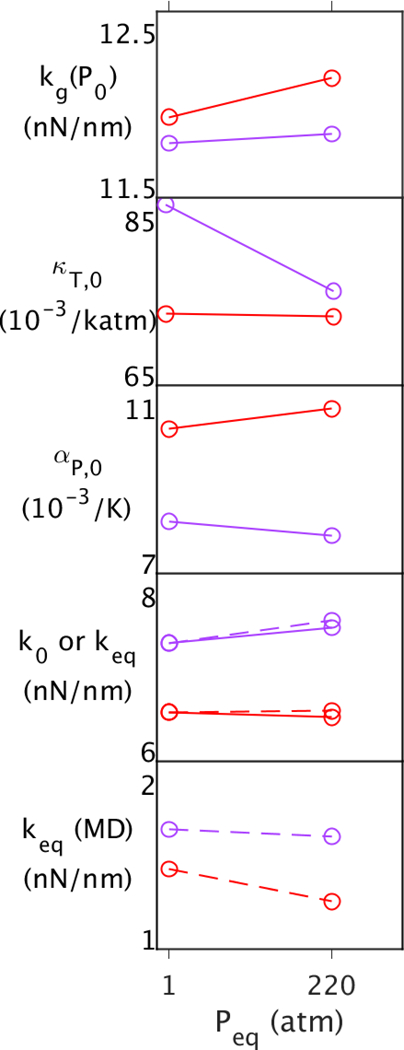
Properties of the interior (purple) and exterior (red) of MpDHFR as function of P_eq at T_eq = T_G = 279 K, where T_eq and P_eq are temperatures and pressures of 50 ns simulations. The top four panels contain properties from the QHA, and the bottom contains properties from the 50 ns simulation. Effective force constants at (P_eq,T_eq) are denoted by dashed lines in the bottom two panels.

CONCLUSIONS

A quasiharmonic analysis of ps fluctuations has been used to compare energy landscapes of a piezophile and mesophile enzyme. Overall, the QHA indicates that the underlying potential energy surface of MpDHFR has shallower wells and thus weaker interactions than EcDHFR because k_g(P₀) is smaller for MpDHFR. In addition, by all measures, MpDHFR and EcDHFR tend to move toward more similar values when the structures are equilibrated at GTP than at CTP, supporting that the GTP is “corresponding state” for enzymes. The isothermal compressibility κ_T,0 at low temperatures tends to be greater on the interior than exterior, but pressure appears to decrease it more in the interior so becomes more homogeneous throughout. On the other hand, the thermal expansivity α_P,₀ is greater on the exterior than interior, and pressure appears to decrease it on the interior but increase it on the exterior. This is contrary to what might be expected from compressive effects alone. Altogether, this indicates that temperature affects the structure in the same manner on the ps timescale as on the ns timescale, while pressure does not. Moreover, since the exterior seems to have more of a reduction in steepness than the interior with pressure, it may involve protein-water interactions