Constructing treatment decision rules based on scalar and functional predictors when moderators of treatment effect are unknown

Summary

Treatment response heterogeneity poses serious challenges for selecting treatment for many diseases. To better understand this heterogeneity and to help in determining the best patient-specific treatments for a given disease, many clinical trials are collecting large amounts of patient-level data prior to administering treatment in the hope that some of these data can be used to identify moderators of treatment effect. These data can range from simple scalar values to complex functional data such as curves or images. Combining these various types of baseline data to discover “biosignatures” of treatment response is crucial for advancing precision medicine. Motivated by the problem of selecting optimal treatment for subjects with depression based on clinical and neuroimaging data, we present an approach that both (1) identifies covariates associated with differential treatment effect and (2) estimates a treatment decision rule based on these covariates. We focus on settings where there is a potentially large collection of candidate biomarkers consisting of both scalar and functional data. The validity of the proposed approach is justified via extensive simulation experiments and illustrated using data from a placebo-controlled clinical trial investigating antidepressant treatment response in subjects with depression.

1. Introduction and Motivation

In both clinical trials and clinical practice, it is common to observe considerable heterogeneity in response to a treatment for subjects with the same disease. Examples of diseases for which there is substantial heterogeneity in treatment response include various types of cancers (Verma, 2012), psychiatric disorders like autism (Masi et al., 2017), and diabetes (Hardin et al., 2013), to name only a few. In fact, a specific treatment that is beneficial for one type of patient can be ineffective or even harmful for another. This makes the task of selecting treatment for many diseases difficult since few treatments are versatile enough to work for all patients. This is a major problem that precision medicine attempts to solve: finding the optimal treatment for the individual at the right time. Unfortunately, information on how or even which patient characteristics can be used to tailor treatment selection is unavailable in many instances.

One disease for which this is a particularly crucial problem is major depressive disorder (MDD). Recent studies have suggested that less than 40% of MDD patients achieve remission after completing a lengthy course of first-line treatment (McGrath et al., 2013). Such a low remission rate may be greatly improved if clinicians are better able to identify patient characteristics that define subgroups of patients who will benefit most from a given treatment. Furthermore, placebo response rates can be high in MDD treatment trials and analyses of results from previous trials that have compared placebo to active medications, including a class of commonly used antidepressants know as selective serotonin reuptake inhibitors (SSRIs), have found that some subjects worsen with an antidepressant, i.e., would fare better on placebo (Gueorguieva et al., 2011). Accordingly, psychiatric investigators are interested in finding “biosignatures” of antidepressant treatment response. These biosignatures involve a set of biomarkers that, in some possibly complex combination, can be used to help clinicians determine who will fare better or worse on a given treatment. The set of candidate biomarkers can be large and/or complex: large in the sense that there may be numerous biomarkers to consider (many of which might be irrelevant to the treatment decision) and/or complex in the sense that the biomarkers may consist of both scalar values and functional data (Ramsay and Silverman, 2005) such as curves or images.

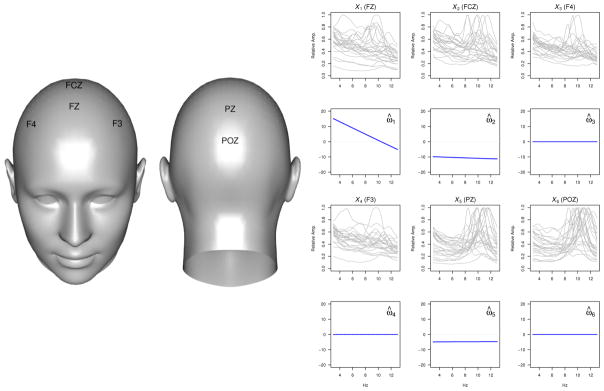
Interest in this problem is motivated by our involvement in an ongoing study investigating heterogeneous treatment response among those with MDD. This study is a randomized controlled trial (RCT) in which subjects with MDD are assigned to either placebo or to an SSRI, sertraline. At baseline many patient characteristics are collected including typical scalar measures (e.g., age, gender, 17-item Hamilton Depression Rating Scale (HAM-D) score, and education level) as well as functional data providing information about brain structure and function. The functional baseline data considered in this application are derived from electroencephalography (EEG) measurements under resting condition. We focus on measures from 6 electrodes of a 72-electrode montage, namely those at the FZ, FCZ, F4, F3, PZ, and POZ locations illustrated in the left panel of Figure 4 since measures from regions corresponding to the locations of these electrodes have been suggested to be related to antidepressant treatment response in previous studies. The functional data of interest correspond to the curves giving the scaled current source density (CSD) amplitude spectrum values over a frequency range of 3 to 13 Hz when the participants’ eyes are closed. Sets of CSD curves corresponding to the 6 electrodes are available for all subjects. Curves for a sample of 25 subjects are shown in the first and third rows of the right panel in Figure 4. The response of interest is HAM-D score after 8 weeks on treatment. Our goal is to use these baseline data, both the scalar and functional measures, along with treatment assignment, to (1) identify moderators of antidepressant treatment effect and (2) develop a rule for selecting the optimal treatment, either placebo or sertraline, for an individual such that HAM-D score is as low as possible at week 8.

Fig. 4.

Left: EEG scalp electrodes used in the analysis. Right: Relative CSD amplitude curves for test set subjects (rows 1 and 3) and the corresponding estimated contrast coefficients (rows 2 and 4).

One simple and commonly used approach for dealing with functional data collected in clinical trials is to reduce these data to “expert-derived” scalar quantities which are then used in subsequent analyses. For example, the EEG amplitude spectra might be reduced to the average amplitude over the frequency domain of interest. These averages may then be investigated as potential scalar modifiers of treatment effect and used to construct treatment decision rules. There are a host of recently developed methods, incorporating variable selection procedures, that can be used to construct decision rules based on scalar covariates including those proposed by Qian and Murphy (2011), Zhang et al. (2012a), Zhao et al. (2012), Tian et al. (2014), and Zhou et al. (2015). We argue that this approach has the potential to mask important relationships between the functional data and the effect of treatment on the outcome of interest. Consequently, this may lead to inferior treatment decision rule estimators.

Methodological developments that allow for functional data to be incorporated into treatment decision rules is extremely limited. To our knowledge McKeague and Qian (2014), Ciarleglio et al. (2015), Ciarleglio et al. (2016), and Laber and Staicu (2017) are the only ones to investigate treatment regime estimation when the baseline covariates include functional data. Though the approaches presented in these papers bring us closer to being able to address the motivating problem, each assumes that the covariates that moderate the effect of treatment on outcome are identified a priori. There is currently no published research on variable selection for treatment regimes when functional data are among the set of candidate biomarkers, yet the demand for such procedures is clear in the present application and will increase as modern clinical trials continue to collect huge amounts of data like those described above.

In what follows, we present an approach that extends and enhances the tools that are currently available for estimating treatment decision rules in settings where baseline covariates consist of scalar and functional data and where the treatment effect moderators are not known a priori. Specifically, we present an approach that (1) allows for scalar and functional covariates to be used to model treatment response without reducing those functions to scalar summaries, (2) selects important baseline biomarkers (including functional variables) that inform treatment selection in a data-driven manner and uses those variables to construct a treatment decision rule, and (3) helps to reduce bias associated with model misspecification by obviating the need to directly model the “main effect” of the predictors. The approach presented here is general enough to be used for any disease type and for a wide array of functional predictors.

The rest of the article is organized as follows. Section 2 gives a brief discussion on the framework of potential outcomes and describes the approach for developing a treatment regime. This is followed in Section 3 by an explanation of the penalized fitting procedure that we employ to estimate a decision rule. We demonstrate the performance of the approach on simulated data in a variety of realistic settings in Section 4. In Section 5 we apply the approach to data from the study described above. We conclude in Section 6 with a review and discussion of future directions of research.

2. Framework and Methodology

Consider data from an RCT in which there are n subjects sampled from a patient population of interest and each subject is randomly assigned one of two possible treatments. Let A = ±1, be the binary treatment assignment indicator. Assume that P(A = 1) = P(A = −1) = 1/2. For each subject we observe a collection of baseline covariates consisting of scalar values and functions, independent of treatment assignment. Denote the set of baseline scalar covariates by a (p + 1)-dimensional vector Z = (1, Z₁, …, Z_p)^⊤ and denote the set of baseline functional covariates by the q-element set of functions X = {X₁, …, X_q}. Here we assume that X₁, …, X_q are square-integrable one-dimensional functional random variables over their respective domains (X_ℓ : D_ℓ ⊂ ℝ → ℝ, ℓ = 1, …, q). Although we present only one-dimensional (1-D) functional predictors here, it is possible to extend our approach to higher dimensional functional random variables such as images.

Let Y be the response of interest and assume without loss of generality that larger values of Y are desirable. The observed data are given by (Y_i, A_i, Z_i, X_i), i = 1, …, n, which are independent and identically distributed with Z_i = (1, Z_1i, …, Z_pi), X_i = {X_1i, …, X_qi}, and X_ℓi(s) is the value of ith subject’s ℓth functional covariate at s. We wish to use these data to construct a rule for assigning treatment, often referred to as a “treatment regime” (Murphy, 2003), to future subjects in such a way that the selected treatment yields better outcome values (on average) than the alternative treatment for these subjects. As in Zhang et al. (2012b), we formalize the notion of an optimal treatment regime by defining the potential outcomes Y^*(−1) and Y^*(1) to be the values of the outcome that would be observed if a subject was assigned treatment −1 or 1 respectively. We assume that subjects are independent and we make several assumptions that are standard in causal inference (Rubin, 1978): (A1) Consistency: Y = Y^*(1) · (1 + A)/2 + Y^*(−1) · (1 − A)/2; (A2) No unmeasured confounders: A is independent of Y^*(−1) and Y^*(1) conditional on Z and X; and (A3) Positivity: for every covariate profile, there is a non-zero probability of receiving either treatment. Both (A2) and (A3) are automatically satisfied in an RCT setting.

A treatment regime is a function, g, that maps the baseline covariates (Z, X) to {−1, 1} such that a patient with baseline covariates (Z = z, X = x) will receive treatment 1 if g(z, x) = 1 and will receive treatment −1 if g(z, x) = −1. The “optimal treatment regime,” $g_{\mathcal{G}}^{\mathit{opt}}$, is the function that maximizes the expected value of the response among some class of functions 𝒢 , so that $g_{\mathcal{G}}^{\mathit{opt}}(\mathit{Z},\mathit{X})={\text{argmax}}_{g\in \mathcal{G}}E[Y^{\ast }\{g(\mathit{Z},\mathit{X})\}]$. In practice, the functions comprising the class 𝒢 are directly related to the choice of models used in modeling the response (or some relevant function of the response). The class 𝒢 that we consider consists of functional linear models that incorporate both scalar and functional covariates. Keeping this in mind, in what follows, we drop the subscript 𝒢.

With the framework and assumptions discussed above, we have that E[Y^*{g(Z, X)}] = E_{(Z, X)}[E(Y |Z, X, A = 1){1+g(Z, X)}/2+E(Y |Z, X, A = −1){1−g(Z, X)}/2] where E_(Z,X)(·) denotes expectation with respect to the joint distribution of (Z, X) and it is easy to see that the optimal treatment regime is given by

$$g^{\mathit{opt}}(\mathit{Z},\mathit{X})=\mathit{sign}\{E(Y\mid \mathit{Z},\mathit{X},A=1)-E(Y\mid \mathit{Z},\mathit{X},A=-1)\},$$ (1)

where sign(x) = −1 if x < 0, 0 if x = 0, and 1 if x > 0. In the case where E(Y |Z, X, A = 1) = E(Y |Z, X, A = −1), one might employ a randomization procedure to select treatment or use whichever treatment is currently the standard of care.

2.1. The Decision Rule

Suppose that Y is a continuous response. We begin by considering the following general working model for relating baseline covariates and treatment to the response:

$$Y=h_{\mathit{\alpha },\mathit{\beta }}(\mathit{Z},\mathit{X})+f_{\mathit{\gamma },\mathit{\omega }}(\mathit{Z},\mathit{X})·\frac{A}{2}+\epsilon ,$$ (2)

where h_α,β(Z, X) and f_γ,ω(Z, X) are some potentially complicated functions of the baseline scalar and functional covariates and ε has mean 0 and variance ${\sigma }_{\epsilon }^2$. The “main effect” component, h_α,β(Z, X), depends on parameter vector, α, corresponding to the scalar covariates and a set of parameter functions, β, corresponding to the functional covariates. Similarly, the “interaction effect” component, $f_{\mathit{\gamma },\mathit{\omega }}(\mathit{Z},\mathit{X})·\frac{A}{2}$, depends on parameter vector, γ, and a set of parameter functions, ω. For example, if h and f are linear functions of the baseline covariates then we have $h_{\mathit{\alpha },\mathit{\beta }}(\mathit{Z},\mathit{X})={\mathit{\alpha }}^{\top }\mathit{Z}+{\sum }_{\ell =1}^q\int {\beta }_{\ell }(s)X_{\ell }(s)ds$ and $f_{\mathit{\gamma },\mathit{\omega }}(\mathit{Z},\mathit{X})={\mathit{\gamma }}^{\top }\mathit{Z}+{\sum }_{\ell =1}^q\int {\omega }_{\ell }(s)X_{\ell }(s)ds$ so that β = {β₁, …, β_q} and ω = {ω₁, …, ω_q}. The function f is typically referred to as the “contrast” and so we will refer to γ and ω as the scalar and functional contrast coefficients respectively. In what follows we require that f be a function that is linear in its scalar and functional parameters. We will refer to this class of functions by ℱ.

Including an interaction term in this way allows for the effect of treatment to depend on the baseline covariates, reflecting heterogenous response to treatment. Consequently, the value of f_γ,ω(z, x) can be used to decide which of two treatments will yield the best outcome for a subject with baseline covariate profile (Z = z, X = x). Under model (2) we have that the treatment effect is

$$E\{Y^{\ast }(1)-Y^{\ast }(-1)\mid \mathit{Z}=\mathit{z},\mathit{X}=\mathit{x}\}=f_{\mathit{\gamma },\mathit{\omega }}(\mathit{z},\mathit{x}),$$ (3)

and by (1) we can use g^opt(Z, X) = sign {f_γ,ω(z, x)} for a treatment decision rule.

Since primary interest lies in estimating the parameters γ and ω in order to obtain a treatment decision rule, we employ an approach that parallels that of Tian et al. (2014). First, note that E(2Y A|Z = z, X = x) = f_γ,ω(z, x). Therefore we can estimate γ and ω by minimizing

$$\frac{1}{n}\sum _{i=1}^n{\{2Y_i{A}_i-f_{\mathit{\gamma },\mathit{\omega }}({\mathit{Z}}_i,{\mathit{X}}_i)\}}^2,$$ (4)

with respect to γ and ω to obtain the estimates γ̂ and ω̂ respectively. Tian et al. (2014) refer to this as the “modified outcome method.” We note that f is a working model and in practice will not likely be identical to the true model. Hence minimizing (4) provides estimates for γ^* and ω^*, the limiting values of γ̂ and ω̂ respectively. Although the model may be misspecified, it is still reasonable to use the estimator of f_γ^*,ω^* as an interaction effect since the estimation of f_γ^*,ω^* seeks the best function of the baseline covariates in the space ℱ to approximate the causal treatment effect.

Although not considered in this paper, it may be of interest to develop a decision rule in which the response is not continuous. In this setting, it may not make sense to employ the modified outcome method. However, noticing that the minimizer of (4) can be expressed by

$$\underset{\mathit{\gamma },\mathit{\omega }}{\text{argmin}}\frac{1}{n}\sum _{i=1}^n{\left\{Y_i-\frac{f_{\mathit{\gamma },\mathit{\omega }}({\mathit{Z}}_i,{\mathit{X}}_i)A_i}{2}\right\}}^2,$$ (5)

it follows that one can regress the original response on the interaction terms in the working model

$$E(Y\mid \mathit{Z},\mathit{X},A)=f_{\mathit{\gamma },\mathit{\omega }}(\mathit{Z},\mathit{X})·\frac{A}{2},$$ (6)

to obtain estimates for the contrast coefficients. This approach can be used for generalized outcomes including continuous, binary, and survival responses, conditional on selecting an appropriate link function to relate the expected value of the outcome to the interaction effect component and minimizing an appropriately chosen loss function. Tian et al. (2014) refer to this as the “modified covariates approach.” Assuming that f is linear in the parameters, we simply need to multiply each scalar and functional covariate by half the corresponding treatment indicator and treat these modified covariates as the predictors in a partial functional linear model. We propose to use model (6) to obtain f_{γ̂, ω̂}(Z, X). Then the treatment decision rule for a new subject with baseline covariate profile (Z = z, X = x) will be given by ĝ(z, x) = sign {f_{γ̂, ω̂}(Z, X)}.

This approach is appealing since it (1) obviates the need to directly model the main effects thus side-stepping issues with misspecification of that component of the model; (2) allows for a causal interpretation of f regardless of the adequacy of (6) (Tian et al., 2014); (3) can be generalized to non-continuous outcomes; and (4) allows for flexible penalized model fitting.

3. Model Fitting with Variable Selection

3.1. Representation and Penalty

First, we consider representing each ω_ℓ, ℓ = 1, …, q, with a pre-defined set of basis functions (e.g., B-splines, wavelets, or polynomials). Such a basis is given by b_ℓ(s) = {b_ℓ1(s), …, b_ℓKℓ(s)} and we have

$${\omega }_{\ell }(s)=\sum _{k=1}^{K_{\ell }}{\eta }_{\ell k}{b}_{\ell k}(s),$$ (7)

where the representation is better as K_ℓ gets larger. We assume that K_ℓ can be taken large enough to allow for the coefficient functions to be well represented by the basis expansions given in (7). If the functional predictors, X_ℓi, are observed without error and are densely sampled on an equally spaced grid of points, {s_ℓ1, …, s_ℓNℓ}, then the integral terms comprising f_γ,ω can be approximated by Riemann sums (e.g., Wood (2011)):

$$\int {\omega }_{\ell }(s)X_{\ell i}(s)ds\approx \sum _{k=1}^{K_{\ell }}\left({\mathrm{\Delta }}_{\ell }\sum _{m=1}^{N_k}{b}_{\ell k}(s_{\ell m})X_{\ell i}(s_{\ell m})\right){\eta }_{\ell k}={\mathit{\eta }}_{\ell }^{\top }{\mathit{X}}_{\ell i},\ell =1,\dots ,q,$$ (8)

where Δ_ℓ = s_ℓm − s_ℓ,m−1 is the distance between adjacent points at which X_ℓi is measured, $X_{\ell ik}={\mathrm{\Delta }}_{\ell }{\sum }_{m=1}^{N_k}{X}_{\ell i}(s_{\ell m})b_{\ell k}(s_{\ell m})$, X_ℓi = (X_ℓi1, …, X_ℓiKℓ)^⊤ are the predictors in the basis space, and η_ℓ = (η_ℓ1, …, η_ℓKℓ)^⊤.

We have noted that the optimal treatment regime depends only on the contrast which depends on γ and ω. Since it is likely to be the case that we collect many baseline covariates but expect only a few to influence the treatment effect, we might expect that many elements of γ and many groups of elements of $\mathit{\eta }={({\mathit{\eta }}_1^{\top },\dots ,{\mathit{\eta }}_q^{\top })}^{\top }$ are equal to zero where the “groups” are indexed by ℓ = 1, …, q, corresponding to η_ℓ. Motivated by these considerations, we choose to capitalize on existing shrinkage penalties for scalar and functional variable selection. There are many penalties available for fitting regression models with scalar predictors. Some commonly used ones are the lasso (Tibshirani, 1996), adaptive lasso (Zou, 2006), elastic net (Zou and Hastie, 2005), and SCAD (Fan and Li, 2001). However, there are fewer penalties available for models with functional predictors. Two recently developed approaches are FuSSO (Oliva et al., 2014) and the sparsity-smoothness penalty of Meier et al. (2009) utilized in Gertheiss et al. (2013). We adopt a strategy similar to that taken in Gertheiss et al. (2013). To select important variables and estimate their effects, we ideally solve

$$\underset{\mathit{\gamma },\mathit{\omega }}{min}{L}_n(\mathit{\gamma },\mathit{\omega })+\lambda \left\{\sum _{j=2}^{p+1}J({\gamma }_j)+\sum _{\ell =1}^q{P}_{{\rho }_{\ell }}({\omega }_{\ell })\right\},$$ (9)

where L_n(γ,ω) is the argument of (5), J(γ_j) = |γ_j|, $P_{{\rho }_{\ell }}({\omega }_{\ell })={\left({\Vert {\omega }_{\ell }\Vert }^2+{\rho }_{\ell }{\Vert {\omega }_{\ell }^{″}\Vert }^2\right)}^{1/2},{\Vert {\omega }_{\ell }\Vert }^2=\int {\omega }_{\ell }^2(s)ds$, and ${\omega }_{\ell }^{″}(s)={\partial }^2{\omega }_{\ell }(s)/\partial s^2$. The tuning parameters, λ and ρ_ℓ, ℓ = 1, …, q, are non-negative values that control the sparsity of the model and the smoothness of the estimates. λ directly controls the sparsity of the estimated model. Large values of λ result in sparser models in which many/most scalar and functional contrast coefficients are set to zero. The tuning parameters ρ₁, …, ρ_q control the smoothness of the estimated effects corresponding to the selected functional covariates. Large ρ_ℓ values result in coefficient estimates that are close to linear while small values can result in complicated estimates that may be difficult to interpret. We refer to ρ₁, …, ρ_q as the functional tuning parameters. Note that we do not penalize the main effect of treatment (scalar covariate with j = 1).

Using the basis representation discussed above, we can re-express (9) as

$$\underset{\mathit{\gamma },\mathit{\eta }}{min}{L}_n^a(\mathit{\gamma },\mathit{\eta })+\lambda \left[\sum _{j=2}^{p+1}\mid {\gamma }_j\mid +\sum _{\ell =1}^q{\{{\mathit{\eta }}_{\ell }^{\top }({\mathbf{\Psi }}_{\ell }+{\rho }_{\ell }{\mathbf{\Omega }}_{\ell }){\mathit{\eta }}_{\ell }\}}^{1/2}\right],$$ (10)

where $L_n^a$ is the approximate loss after representation, Ψ_ℓ is a K_ℓ × K_ℓ matrix whose (u, v) element is given by ∫ b_ℓu(s)b_ℓv(s)ds, and Ω_ℓ is also a K_ℓ ×K_ℓ matrix whose (u, v) element is given by $\int b_{\ell u}^{″}(s)b_{\ell v}^{″}(s)ds$, u, v = 1, …, K_ℓ.

Next, we show that the solution to (10) can be viewed as a solution to the general group lasso problem (Gertheiss et al., 2013). Let K_ρℓ,ℓ = Ψ_ℓ + ρ_ℓΩ_ℓ and let ${\mathit{K}}_{{\rho }_{\ell },\ell }={\mathit{R}}_{{\rho }_{\ell },\ell }{\mathit{R}}_{{\rho }_{\ell },\ell }^{\top }$ be the Cholesky decomposition of K_ρℓ,ℓ. Define ${\stackrel{⌣}{\mathit{\eta }}}_{\ell }={\mathit{R}}_{{\rho }_{\ell },\ell }^{\top }{\mathit{\eta }}_{\ell }$ and ${\stackrel{⌣}{\mathit{X}}}_{\ell }={\mathit{R}}_{{\rho }_{\ell },\ell }^{-1}{\mathit{X}}_{\ell }$. Furthermore, let $\mathit{\xi }={({\gamma }_1,\dots ,{\gamma }_{p+1},{\stackrel{⌣}{\mathit{\eta }}}_1^{\top },\dots ,{\stackrel{⌣}{\mathit{\eta }}}_q^{\top })}^{\top }={({\mathit{\xi }}_1^{\top },\dots ,{\mathit{\xi }}_{p+1}^{\top },{\mathit{\xi }}_{p+2}^{\top },\dots ,{\mathit{\xi }}_{p+q+1}^{\top })}^{\top }$ and ${\stackrel{\sim }{\mathit{Z}}}_i={\left(Z_{1i},\dots ,Z_{p+1,i},{\stackrel{⌣}{\mathit{X}}}_{1i}^{\top },\dots ,{\stackrel{⌣}{\mathit{X}}}_{qi}^{\top }\right)}^{\top }={({\stackrel{\sim }{\mathit{Z}}}_{1i}^{\top },\dots ,{\stackrel{\sim }{\mathit{Z}}}_{p+1,i}^{\top },{\stackrel{\sim }{\mathit{Z}}}_{p+2,i}^{\top },\dots ,{\stackrel{\sim }{\mathit{Z}}}_{p+q+1,i}^{\top })}^{\top }$ so that, in the case of a continuous outcome, the approximate loss function can be written as

$$L_n^a(\mathit{\xi })=\frac{1}{n}\sum _{i=1}^n{\left(Y_i-\sum _{G=1}^{p+q+1}{\stackrel{\sim }{\mathit{Z}}}_{Gi}·\frac{A_i}{2}{\mathit{\xi }}_G\right)}^2.$$ (11)

We can now re-express (10) as

$$\underset{\mathit{\xi }}{min}{L}_n^a(\mathit{\xi })+\lambda \sum _{G=2}^{p+q+1}\Vert {\mathit{\xi }}_G\Vert ,$$ (12)

where ||ξ_G|| is the Euclidean norm of ξ_G, the Gth vector-component of the vector ξ. Hence, for a fixed set of functional tuning parameter values, we have a group lasso penalty where the first p + 1 groups correspond to singleton sets of the baseline scalar covariates including the treatment indicator and the remaining q groups, indexed by G = p + 2, …, p + q + 1, correspond to the q baseline functional covariates. Note that the group variable selection in (12) directly corresponds to scalar (group size = 1) and functional (group size = number of basis coefficients used in the representation) variable selection in (9). For fixed values of λ and ρ₁, …, ρ_q, (12) can be fit using any existing software that provides estimates for group lasso models. We employ the R package grplasso (Meier, 2015) to fit the model.

We have found it to be beneficial to allow for differential shrinkage and selection of the contrast coefficients in a similar fashion to that proposed by Zou (2006) with the adaptive lasso. The weights that we employ are denoted by $w_j^s$ and $w_{\ell }^f$ corresponding to the scalar and functional contrast coefficients respectively. These weights are incorporated into the penalty such that $J({\gamma }_j)=w_j^s\mid {\gamma }_j\mid$ and $P_{{\rho }_{\ell }}({\omega }_{\ell })={\left(w_{\ell }^f{\Vert {\omega }_{\ell }\Vert }^2+{\rho }_{\ell }{\Vert {\omega }_{\ell }^{″}\Vert }^2\right)}^{1/2}$. Gertheiss et al. (2013) consider a similar scheme and provide evidence via simulations that the weighted penalty outperforms the un-weighted penalty with respect to both estimation and prediction. As their paper only considers functional covariates, the specific weights that they employ are given by $w_{\ell }^f=1/\Vert {\stackrel{\sim }{\omega }}_{\ell }\Vert$ where ω̃_ℓ is an “initial” estimate of ω_ℓ from a fitting procedure that does not perform variable selection. Large values of $w_{\ell }^f$ result in greater penalization whereas small values result in less penalization.

We propose using a similar strategy to compute weights for both the scalar and functional terms in the model. To obtain the weights $w_j^s=1/\mid {\stackrel{\sim }{\gamma }}_j\mid$ and $w_{\ell }^f=1/\Vert {\stackrel{\sim }{\omega }}_{\ell }\Vert$ we compute $\underset{\mathit{\xi }}{min}{L}_n^a(\mathit{\xi })+\kappa {\sum }_{G=2}^{p+q+1}{\Vert {\mathit{\xi }}_G\Vert }^2$, with non-negative tuning parameter κ. This corresponds to performing a ridge regression fit to obtain an initial estimate, ξ̃, for ξ. We then compute the weights using ${\stackrel{\sim }{\gamma }}_m={\stackrel{\sim }{\mathit{\xi }}}_m^{\top }$ (scalar) for m = 1, …, p + 1 and since ${({\mathit{R}}_{{\rho }_m,m}^{\top })}^{-1}{\stackrel{\sim }{\mathit{\xi }}}_m^{\top }={\stackrel{\sim }{\mathit{\eta }}}_{m-p-1}$ (vector) for m = p+2, …, p+q+1 we take ${\stackrel{\sim }{\omega }}_{\ell }={\sum }_{k=1}^{K_{\ell }}{\stackrel{\sim }{\eta }}_{\ell k}{b}_{\ell k}(s)$ for ℓ = 1, …, q. In our experience, we have found that employing appropriately selected weights using our proposed scheme can lead to superior variable and treatment selection performance.

3.2. Sparse, Irregularly Sampled, and Error-Contaminated Functional Covariates

In practice, it is possible that the functional covariates collected at baseline are either sparsely observed, sampled at different times or locations across subjects, observed with error, or any combination of the three. If any of these hold, then the approach proposed above is not directly applicable to the observed functional covariates and an initial step for reconstructing the underlying functions is required.

In the simulations and application below, we perform this initial step of de-noising and reconstructing the functional curves from the raw data. Because our functional covariates are observed on a dense grid of points, we adopt the approach of Gertheiss et al. (2013) and employ local polynomial smoothing. We refer the reader to Gertheiss et al. (2013) for a brief discussion of several other approaches available for curve reconstruction.

Once an appropriate reconstruction technique has been chosen and applied, the underlying functions are estimated and evaluated on a dense grid of argument values. These estimates are treated as though they are the true functional covariates and we can apply the method laid out in Sections 2 and 3.

3.3. Tuning Parameter Selection

The values of the tuning parameters, λ, ρ₁, …, and ρ_q, are unknown and need to be selected prior to fitting the treatment regime model. K-fold cross-validation (CV) (Stone, 1974) is a commonly used method for selecting the tuning parameters and we employ it here. The number of folds is often taken to be either 5 or 10 and the goal is to select the set of tuning parameters that optimize some criterion. Tuning parameters selected via K-fold CV are often chosen to minimize prediction error. However, since our goal is to construct a treatment regime that maximizes the expected value of the outcome in the population, we choose to maximize the CV value of the estimated treatment regime as done in Qian and Murphy (2011). The same K-fold CV procedure can also be employed to select the tuning parameter κ needed for obtaining weights for the adaptive penalty.

The number of tuning parameters associated with estimating the contrast is q+1 and therefore grows with the number of functional covariates. Even a moderate number of functional covariates can require substantial computing time when using K-fold CV to select the tuning parameters. However, in some instances, it may be possible to greatly reduce the number of tuning parameters, thus making K-fold CV a viable approach. If we are willing to assume that the functional contrast coefficients are similarly smooth then we can set ρ₁ = … = ρ_q = ρ for computational convenience. We are then left with only two tuning parameters, λ and ρ, to select. This may be appropriate when the baseline functional covariates are all of the same type (e.g., all amplitude spectra curves derived from EEG) or in circumstances when there are different types of functional covariates, but there is reason to believe that the corresponding contrast coefficients are similarly smooth. One approach for determining the suitability of this assumption is to investigate the initial contrast coefficient estimates derived from the ridge regression model that is used to construct the weights for the adaptive penalty. If the ridge contrast coefficient function estimates are all similarly smooth or sets of function estimates are similarly smooth, then the number of tuning parameters can be reduced. Otherwise, we recommend allowing for a possibly different smoothing parameter for each contrast coefficient function.

Another alternative that can be used to reduce the number of tuning parameters, suggested by a reviewer, is to use adaptive weights. Using this approach, one has a single smoothing tuning parameter, ρ, and adaptive covariate-specific smoothing tuning parameter values given by ρ_ℓ = ρϕ_ℓ (ℓ = 1, …, q) where ${\varphi }_{\ell }=1/\Vert {\widehat{\stackrel{\sim }{\omega }}}_{\ell }^{″}\Vert$ and ${\widehat{\stackrel{\sim }{\omega }}}_{\ell }^{″}$ is the estimate for the second derivative of the ℓth initial ridge contrast coefficient function estimate.

3.4. Augmentation to Improve Efficiency

As pointed out in Tian et al. (2014), if model (6) is misspecified, it may be possible to find a more efficient estimate of the contrast coefficients by augmenting the objective function in (11). Consider a function a(z̃) : ℝ^ν → ℝ^ν where $\nu =p+1+{\sum }_{\ell =1}^q{K}_{\ell }$. Since we assume that treatment is randomly assigned, it follows that E{A_ia(Z̃_i)} = 0 and so the minimizer of the augmented objective function given by

$$\frac{1}{n}\sum _{i=1}^n\left\{\frac{1}{2}{\left(Y_i-{\mathit{\xi }}^{\top }{\stackrel{\sim }{\mathit{Z}}}_i·\frac{A_i}{2}\right)}^2-{\mathit{\xi }}^{\top }a({\stackrel{\sim }{\mathit{Z}}}_i)·A_i\right\},$$ (13)

converges to the same limit as the minimizer of (11). The function a(·) should be selected such that the minimizer of (13) will have smaller variance than the minimizer of (11). We refer to a(·) as the “augmentation function.” Tian et al. (2014) show that the optimal augmentation function (i.e., the one that will minimize the variance of the estimator of the contrast coefficients (in our setting)) is given by $a_0(\stackrel{\sim }{\mathit{Z}})=-\frac{1}{2}\stackrel{\sim }{\mathit{Z}}E(Y\mid \stackrel{\sim }{\mathit{Z}}=\stackrel{\sim }{\mathit{z}})$. In order to obtain the estimator from the augmented objective function, we first need to compute a₀(z̃). To do this we fit a model E(Y | Z̃) = θ^⊤B(Z̃) where B(Z̃) is an appropriately chosen function of Z̃. In practice the identity function might be used as a working model so that the mean value of Y is essentially a linear function of the baseline covariates. Once an estimate of a₀(z̃) say $\widehat{a}(\stackrel{\sim }{\mathit{Z}})=-\frac{1}{2}\stackrel{\sim }{\mathit{z}}{\widehat{\mathit{\theta }}}^{\top }B(\stackrel{\sim }{\mathit{Z}})$ is computed we have that the augmented estimator minimizes

$$\sum _{i=1}^n\left\{\frac{1}{2}{\left(Y_i-{\mathit{\xi }}^{\top }{\stackrel{\sim }{\mathit{Z}}}_i·\frac{A_i}{2}\right)}^2-{\mathit{\xi }}^{\top }\widehat{a}({\stackrel{\sim }{\mathit{Z}}}_i)·A_i\right\}=\sum _{i=1}^n\frac{1}{2}{\left\{Y_i-{\widehat{\mathit{\theta }}}^{\top }B({\stackrel{\sim }{\mathit{Z}}}_i)-{\mathit{\xi }}^{\top }{\stackrel{\sim }{\mathit{Z}}}_i·\frac{A_i}{2}\right\}}^2+C,$$

where C is a constant.

Here we briefly outline the procedure for obtaining the contrast coefficients using the augmented objective function:

1. Choose the form of E(Y | Z̃) = θ^⊤B(Z̃) and obtain an estimate θ̂. The procedure for obtaining θ̂ may parallel the procedure used to obtain ξ̂ that is discussed in Section 3.1 (i.e., perform an initial ridge regression fit to obtain weights then perform a penalized fitting procedure like that corresponding to (9) with weights incorporated into the penalty).

   • Note: If K-fold CV is used to select tuning parameters involved in the estimation of θ̂, we suggest that they should be selected so that the CV prediction error is minimized (instead of maximizing value) because the purpose of augmentation is to improve the signal to noise ratio. We use this approach in the simulations and application.

2. Form adjusted responses for each observation: Ỹ_i = Y_i − θ̂^⊤B(Z̃_i).

3. Use the modified covariates method described in Section 3.1 with Ỹ_i as the response to obtain the estimated treatment regime.

4. Numerical Investigations

We demonstrate the performance of our proposed method in a series of simulation experiments. For each experiment, the simulated data is generated to be similar to that encountered in the motivating application described in Section 1. The data for each observation consist of scalar covariates, 1-D functional covariates, a treatment indicator, and a response that is generated from a known function of some combination of the scalar and functional covariates and the treatment indicator. Different functional relationships are considered under a variety of settings. We are primarily interested in assessing performance with respect to selection of baseline covariates that influence treatment effect and selection of the optimal treatment.

4.1. Generating Scalar and Functional Baseline Covariates and Treatment Indicators

The treatment assignment indicator, A, is generated independently of the other covariates such that P(A = 1) = P(A = −1) = 1/2. The vector of baseline scalar covariates, (Z₁, …, Z_p)^⊤, is generated from a multivariate normal distribution with each component having mean 0 and variance 1. Correlation between the components is corr(Z_j, Z_k) = 0.5^|j−k|. We let Z = (1, Z₁, …, Z_p)^⊤. In each setting, p = 5 or 100.

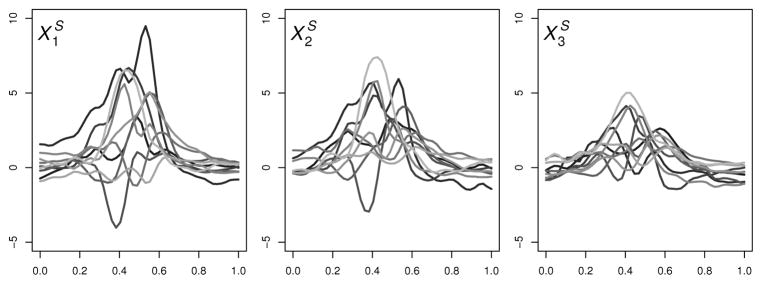
A detailed outline of how we generate the 1-D functional covariates is provided in Web Appendix A. We refer to the ℓ-th simulated 1-D functional covariate as $X_{\ell }^S$, ℓ = 1, …, q. Figure 1 shows 10 sets of three functional covariates, { $X_1^S,X_2^S,X_3^S$}, from those used in our simulations. The domain for each function is [0, 1]. In each simulation setting, q = 3 or 10.

Fig. 1.

Simulated 1-D covariates.

4.2. Generating Responses

We consider two sets of four models (scenarios) for generating responses which we refer to as Simulation Set A and Simulation Set B. Table 1 shows all of the parameter values including plots of the coefficient functions for both Simulation Sets A and B that are described below. For each scenario we generate a test set with N = 100,000 independent observations. These are used to evaluate treatment selection performance.

Table 1.

Parameters for response models in Simulation Sets A and B for Scenarios 1–4 and average treatment responses based on 10⁶ observations. (A “−” indicates that the parameter is not applicable in the scenario. 0_d is a zero-vector of length d. In settings with p = 5 we have a = 3 and b = ø. In settings with p = 100 we have a = 98 and b = 95.) In Set A, the vertical axes for β₁ and β₂ range from −0.30 to 0.30 in Scenarios 1 and 2 and from −0.04 to 0.04 in Scenarios 3 and 4. The vertical axes for ω₁, ω₃, and ω₂₂ range from −0.10 to 0.10 in all Scenarios. In Set B, the vertical axes for β₁ and β₂ range from −0.20 to 0.20 in Scenarios 1 and 2 and from −0.10 to 0.10 in Scenarios 3 and 4. The vertical axes for ω₁, ω₃, and ω₂₂ range from −0.20 to 0.20 in all Scenarios.

Simulation Set A
Parameter	Scenario 1 Comparable Main & Interaction Effects	Scenario 2 Large Main & Small Interaction Effects	Scenario 3 Comparable Main & Interaction Effects	Scenario 4 Large Main & Small Interaction Effects
α⊤	(5, 1, −1, 0a)	(5, 2, −2, 0a)	(5, 0.71, 0, −0.71, 0, 0.71, 0b)	(5, 1, 0, −1, 0, 1, 0b)
β1, β2
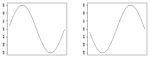
γ⊤	(−0.50, 1, 03, −1, 0b)	(−0.50, 1, 03, −1, 0b)	(−0.50, 1, 03, −1, 0b)	(−0.50, 1, 03, −1, 0b)
ω;1, ω3
ω22	–	–
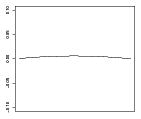
E{Y*(−1)}	4.40	3.82	6.14	7.29
E{Y*(1)}	4.43	3.85	6.18	7.32
E{Y*(gopt)}	5.65	5.06	7.45	8.59
Simulation Set B
Parameter	Scenario 1 Comparable Main & Interaction Effects	Scenario 2 Large Main & Small Interaction Effects	Scenario 3 Comparable Main & Interaction Effects	Scenario 4 Large Main & Small Interaction Effects
α⊤	(5, 0.5, −0.5, 0a)	(5, 1, −1, 0a)	(5, 0.38, 0, −0.38, 0, 0.38, 0b)	(5, 0.5, 0, −0.5, 0, 0.5, 0b)
β1, β2
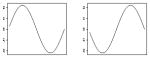
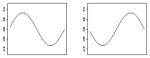
γ⊤	(−0.25, 0.5, 03, −0.5, 0b)	(−0.25, 0.5, 03, −0.5, 0b)	(−0.25, 0.5, 03, −0.5, 0b)	(−0.25, 0.5, 03, −0.5, 0b)
ω;1, ω3
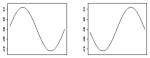
ω22	–	–
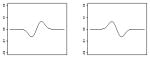
E{Y*(−1)}	4.69	4.26	5.89	6.50
E{Y*(1)}	4.46	4.03	5.67	6.27
E{Y*(gopt)}	5.37	4.94	6.64	7.24

4.2.1. Simulation Set A Responses

We consider four scenarios for generating the responses. In Scenarios 1 and 2 the responses are generated from models that are linear in the parameters of interest. Specifically, the response model is given by

$$Y={\mathit{\alpha }}^{\top }\mathit{Z}+\int {\beta }_1(s)X_1(s)ds+\int {\beta }_2(s)X_2(s)ds+\left\{{\mathit{\gamma }}^{\top }\mathit{Z}+\int {\omega }_1(s)X_1(s)ds+\int {\omega }_3(s)X_3(s)ds\right\}·A+\epsilon ,$$ (14)

where for Scenario 1, α and γ are given in Table 1 and β₁(s) = 0.15sin(2πs), β₂(s) = −0.15sin(2πs), ${\omega }_1(s)=\frac{25}{3}{s}^2{e}^{-10s}$, and ${\omega }_3(s)=-\frac{25}{3}{s}^2{c}^{-10s}$. In Scenario 2, α and γ are given in Table 1, β₁(s) = 0.30sin(2πs), β₂(s) = −0.30sin(2πs), and ω₁ and ω₃ are the same as in Scenario 1.

In Scenarios 3 and 4 the response models are given by

$$Y={\left\{{\mathit{\alpha }}^{\top }\mathit{Z}+\int {\beta }_1(s)X_1(s)ds+\int {\beta }_2(s)X_2(s)ds\right\}}^2+\left\{{\mathit{\gamma }}^{\top }\mathit{Z}+\int {\omega }_1(s)X_1(s)ds+\int {\omega }_3(s)X_3(s)ds+\int {\omega }_{22}(s)Z_2{X}_2(s)\right\}·A+\epsilon ,$$ (15)

where for Scenario 3, α and γ are given in Table 1 and β₁(s) = 0.0355sin(2πs), β₂(s) = −0.0355sin(2πs), ${\omega }_1(s)=\frac{25}{3}{s}^2{e}^{-10s},{\omega }_3(s)=-\frac{25}{3}{s}^2{e}^{-10s}$, and ω₂₂(s) = −0.02304s(s−1). In Scenario 4, α and γ are given in Table 1 and β₁(s) = 0.05sin(2πs), β₂(s) = −0.05sin(2πs), and ω₁, ω₃ and ω₂₂ are the same as in Scenario 3. We note that neither the main effect nor the contrast component of the model are linear in parameters corresponding to the baseline covariates.

Throughout, we have ε ~ N(0, σ²) and independent of the other terms. The scalar and functional coefficients as well as σ² are selected such that in Scenarios 1 and 3 there are relatively moderate main effects where the variation in the response attributable to the main effect, interaction, and random error are about 37.5%, 37.5%, and 25% respectively while Scenarios 2 and 4 correspond to relatively large main effects where the variation in the response attributable to the main effect, interaction, and random error are about 70%, 20%, and 10% respectively. In our experience, it is more common to encounter settings like Scenarios 2 and 4, in which the moderator effect is small relative to the main effect. This is especially true in many psychiatric applications like the one that we present in Section 5.

4.2.2. Simulation Set B Responses

In the second set of simulations, the forms of the response models are the same as those used in Simulation Set A but the parameter values in the various scenarios differ. Here Scenario 1 uses response model (14) where α and γ are given in Table 1 and β₁(s) = 0.11sin(2πs), β₂(s) = −0.11sin(2πs), ${\omega }_1(s)=\frac{1}{6\sqrt{2\pi }}\left\{-e^{-\frac{8}{9}{(12s-5)}^2}+e^{-\frac{8}{9}{(12s-7)}^2}\right\}$, and ${\omega }_3(s)=\frac{1}{6\sqrt{2\pi }}\left\{e^{-\frac{8}{9}{(12s-5)}^2}+e^{-\frac{8}{9}{(12s-7)}^2}\right\}$. Scenario 2 also uses response model (14) where α and γ are given in Table 1, β₁(s) = 0.22sin(2πs), β₂(s) = −0.22sin(2πs), and γ, ω₁, and ω₃ are the same as in Scenario 1.

Scenario 3 uses response model (15) where α and γ are given in Table 1, β₁(s) = 0.0825sin(2πs), β₂(s) = −0.0825sin(2πs), ω₁ and ω₃ are the same as in Scenario 1, and ω₂₂(s) = −0.02304s(s − 1). Scenario 4 also uses response model (15) where α and γ are given in Table 1, β₁(s) = 0.055sin(2πs), β₂(s) = −0.055sin(2πs), and ω₁, ω₃, and ω₂₂(s) are the same as in Scenario 3.

As in Simulation Set A, we have ε ~ N(0, σ²) and the scalar and functional coefficients as well as σ² are selected so that the main effect, interaction, and random error contribute to the same proportion of variation in the response specified in Scenarios 1–4 of Simulation Set A.

4.3. Settings

We consider two settings for the number of baseline covariates available: (I.) p = 5 and q = 3 or (II.) p = 100 and q = 10. Since we employ a working model for the contrast that is linear in the baseline covariates it follows that in Setting I we have 3 informative scalars (including treatment) with 3 spurious scalars and 2 informative functions with 1 spurious function and in Setting II we have 3 informative scalars (including treatment) with 98 spurious scalars and 2 informative functions with 8 spurious functions.

In addition to settings where the simulated 1-D functions are assumed to be the true covariates, we also consider settings in which random error is added to the 1-D functions after the responses have been generated and these contaminated covariates are used to fit the treatment regime models. In these contaminated settings, we add N(0, 1) noise to each value of each 1-D function.

Lastly, we consider three sample sizes n = 100, 200, or 400. We perform 100 simulation experiments for each combination of settings.

4.4. Methods Compared

We compare five methods for estimating treatment regimes in the various settings. The first two are the methods described above which allow for both scalar and functional covariates: (1) our modified covariates method, which we refer to as “MC” and (2) our modified covariates method with augmentation, which we refer to as “MC-A.” The three remaining methods are recently-developed treatment regime estimation approaches that perform variable selection but only allow for scalar covariates. They are: (3) the approach proposed by Tian et al. (2014), a modified covariates method with augmentation using a lasso penalty, which we refer to as “MC-AL,” (4) an augmented outcome weighted learning approach proposed by Liu et al. (2017), which we refer to as “OWL,” and (5) a two-stage classification procedure proposed by Zhang et al. (2012a) in which the contrast is first estimated using method (3) and then a weight and label are constructed from the contrast estimate followed by the use of classification and regression trees (CART) to construct the treatment decision rule. We refer to this last method as “MC-CART.” Since the MC-AL, OWL, and MC-CART methods can only handle scalar covariates, we first take the averages of each of the 1-D functional covariates then use those averages as scalar covariates in each method. This mirrors the common practice of reducing functional data to scalar summaries prior to model fitting.

For both the MC and MC-A methods, we modeled the contrast as a linear function of all of the baseline covariates available in the setting. For the MC-A method we also modeled B(Z̃) as a linear function of the baseline covariates. For all functional covariates, we used a B-spline basis of order 4 with K_ℓ = 25 basis functions. We found this number of basis functions to be more than large enough to capture the complexity of all of the coefficient functions across all experimental settings. All tuning parameters were selected via 10-fold CV. For selecting tuning parameters to compute the augmentation component in the MC-A method, we sought to minimize the CV prediction error. For selecting the tuning parameters to estimate the contrast coefficients (either with or without augmentation), we sought to minimize the CV value of the decision rule as was done in Qian and Murphy (2011). We used one smoothing parameter, ρ, to govern the smoothness of the estimated contrast coefficients. In all experiments, ρ is selected from the set {10⁻⁶, 10⁻⁵, …, 10⁵, 10⁶} and the tuning parameter λ is selected from a grid of 100 possible values that depend on the value of ρ being simultaneously considered. We describe how these grids are constructed in Web Appendix B. For those settings in which the 1-D functional predictors are contaminated by noise, the predictors are first smoothed via local polynomial smoothing using the glkerns function from the lokern package (Herrmann, 2014) in R, then these smooth estimates are treated as the true predictors and the MC and MC-A methods are carried out as usual.

For the MC-AL method, we model both the contrast and the augmentation functions as linear functions of the baseline covariates (where the 1-D predictors have been converted to scalars via averaging). As with the MC-A method, the tuning parameter for the augmentation term is found by minimizing the 10-fold CV prediction error and the tuning parameter for the contrast is found by maximizing the 10-fold CV value of the decision rule. We use the glmnet and cv.glmnet (modified to allow for maximizing the value) functions from the glmnet package (Friedman et al., 2010) in R to implement the MC-AL method. For the OWL method (carried out using our own R code), the augmentation term is computed using the same approach as in the MC-AL method and a support vector machine (SVM) (Cortes and Vapnik, 1995) with hinge loss is used to construct the treatment decision rule based on a linear combination of the available baseline covariates. The regularization parameter for the SVM is selected from the set {0.1, 0.25, 0.50, 0.75} using 10-fold CV. For the MC-CART method, we used the estimate of the contrast derived from the MC-AL method to compute a weight and class for each observation. These were used to construct a classification tree using the rpart function from the rpart package (Therneau et al., 2015) in R. All baseline covariates were considered for growing the tree. The tree was then pruned using the prune function with default settings to obtain the estimated decision rule. For further information on specifics related to the MC-AL, OWL, or MC-CART methods, we refer the reader to Tian et al. (2014), Liu et al. (2017), and Zhang et al. (2012a) respectively.

For those settings in which the 1-D functional predictors are contaminated by noise, the predictors are smoothed as described above. Then averages of the smoothed curves are computed and used as predictors in the MC-AL, OWL, or MC-CART methods.

4.5. Evaluation Metrics

To evaluate the performance of our methods with respect to selecting covariates that inform treatment selection, we compute the average number of correctly and incorrectly identified non-zero contrast coefficient estimates over the 100 simulation experiments in each setting. Recall that in all settings, there are only 3 informative scalars, including treatment, and 2 informative functions.

We evaluate treatment assignment accuracy for each estimated regime on independent testing data. The model estimates are used to compute the treatment assignment ĝ(z_i, x_i) = sign {f_{γ̂, ω̂}(z_i, x_i)} for the ith test observation. We then evaluate the treatment selection performance by computing the expected value of the response under the selected treatment, E{Y ^*(ĝ)}, in the independent test sets. For comparison, we computed approximations to the average treatment response under treatment −1 (E{Y^*(−1)}), under treatment 1 (E{Y^*(1)}), and under the optimal treatment (E{Y^*(g^opt)}) in the population based on 10⁶ observations (independent of both the training and test sets) generated under each true model. These values are provided in Table 1 for each scenario.

For each estimated treatment regime, we also compute the percent correct decisions (PCD) given by $1-\frac{1}{2N}{\sum }_{i=1}^N\mid \mathit{sign}\left\{f_{\widehat{\mathit{\gamma }},\widehat{\mathit{\omega }}}({\mathit{z}}_i,{\mathit{x}}_i)\right\}-\mathit{sign}\{\delta ({\mathit{z}}_i,{\mathit{x}}_i)\}\mid$, where δ(z_i, x_i) is the contrast value for the ith test observation under the true model, and take the average of these accuracies over the 100 replications in each setting.

4.6. Numerical Investigation Results

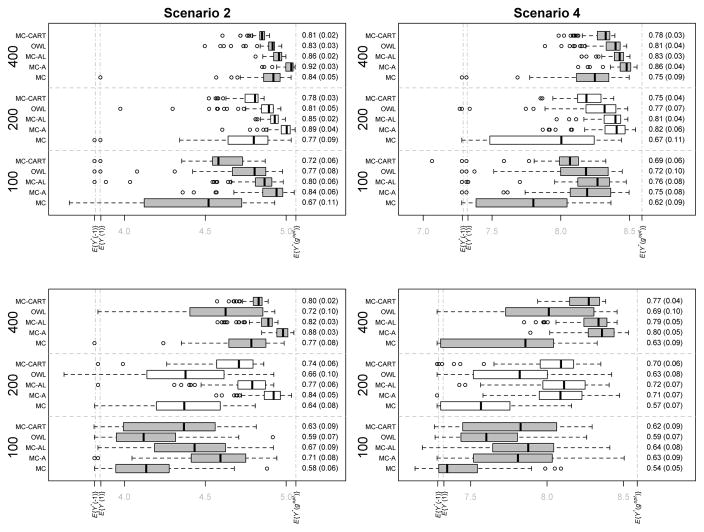
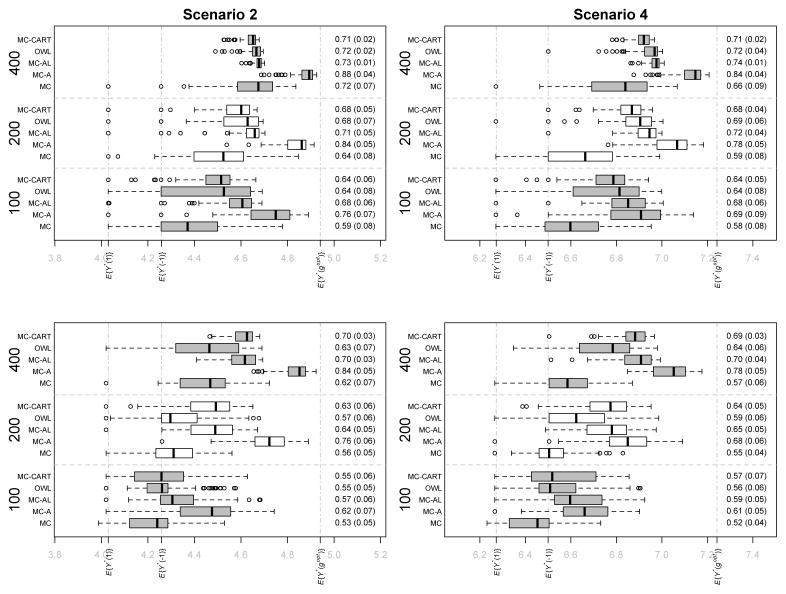
We focus on the results derived from Scenarios 2 and 4 (small moderator effects) in Simulation Settings A and B in which the functional covariates are observed with error. These are representative of our findings based on the other settings. Full results for all settings are provided in Web Appendix C.

Tables 2 and 3 provide information on performance of the five methods with respect to moderator selection in Simulation Settings A and B respectively. The top halves of Tables 2 and 3 show that the MC-A and MC-AL methods perform similarly and better than the other three methods with respect to the selection of true scalar moderators (first mean under each method). The OWL and MC-CART methods also tend to perform well in identifying the true scalar moderators, especially for larger sample sizes. The MC method typically performs worst in this regard. With respect to selecting true functional moderators (second mean under each method), the MC-A method dominates all other methods. This is especially clear in the settings with p = 100, q = 10. Performance of the OWL and MC-CART methods is particularly poor in identifying the functional moderators.

Table 2.

Simulation Set A (with error in functional predictors) Scenarios 2 and 4. Each set of values corresponds to the mean_(sd) scalar covariates selected, mean_(sd) functional covariates selected for each setting and method. Top: Mean_(sd) number of correctly identified moderators. The best case is 3 true scalar and 2 true functional moderators selected. Bottom: Mean_(sd) number of covariates that are incorrectly identified as moderators. The best case is 0 spurious scalar and 0 spurious functional covariates selected.

	n	MC	MC-A	MC-AL	OWL	MC-CART
Mean number of correctly identified moderators.
p = 5, q = 3: Best Case = 3 scalars, 2 functions; Worst Case = 0 scalars, 0 functions
Sc. 2	100	2.32(0.78), 1.40(0.85)	2.95(0.26), 1.68(0.63)	2.95(0.22), 1.05(0.83)	2.75(0.54), 0.41(0.57)	2.52(0.56), 0.04(0.20)
	200	2.83(0.49), 1.69(0.61)	2.99(0.10), 1.63(0.58)	3.00(0.00), 1.32(0.76)	2.92(0.31), 0.58(0.67)	2.96(0.20), 0.11(0.31)
	400	2.96(0.24), 1.72(0.51)	3.00(0.00), 1.77(0.49)	3.00(0.00), 1.40(0.79)	2.96(0.20), 0.47(0.61)	3.00(0.00), 0.10(0.30)
Sc. 4	100	2.07(0.73), 1.26(0.85)	2.63(0.56), 1.49(0.70)	2.78(0.48), 1.00(0.85)	2.54(0.64), 0.60(0.70)	2.19(0.54), 0.08(0.27)
	200	2.33(0.74), 1.31(0.86)	2.89(0.31), 1.73(0.55)	2.98(0.14), 1.25(0.82)	2.86(0.38), 0.57(0.66)	2.71(0.46), 0.12(0.33)
	400	2.74(0.50), 1.61(0.67)	2.99(0.10), 1.72(0.55)	3.00(0.00), 1.17(0.87)	2.93(0.26), 0.47(0.59)	2.92(0.27), 0.15(0.39)
p = 100, q= 10: Best Case = 3 scalars, 2 functions; Worst Case = 0 scalars, 0 functions
Sc. 2	100	2.00(0.80), 0.96(0.78)	2.89(0.35), 1.09(0.79)	2.84(0.42), 0.44(0.64)	2.27(0.79), 0.27(0.57)	1.93(0.67), 0.01(0.10)
	200	2.54(0.74), 0.98(0.80)	3.00(0.00), 1.45(0.70)	2.98(0.20), 0.52(0.69)	2.64(0.64), 0.28(0.51)	2.75(0.48), 0.02(0.14)
	400	2.90(0.36), 0.95(0.80)	3.00(0.00), 1.75(0.50)	3.00(0.00), 0.77(0.80)	2.72(0.53), 0.26(0.52)	2.99(0.10), 0.02(0.14)
Sc. 4	100	1.55(0.69), 0.66(0.82)	2.39(0.71), 0.98(0.80)	2.55(0.58), 0.37(0.61)	2.28(0.67), 0.28(0.53)	1.75(0.56), 0.03(0.17)
	200	2.00(0.77), 0.92(0.90)	2.81(0.46), 1.44(0.72)	2.83(0.38), 0.50(0.70)	2.54(0.61), 0.37(0.60)	2.34(0.57), 0.02(0.14)
	400	2.14(0.75), 0.88(0.86)	2.98(0.14), 1.53(0.70)	2.99(0.10), 0.37(0.63)	2.68(0.57), 0.27(0.51)	2.83(0.38), 0.01(0.10)
Mean number of covariates that are incorrectly identified as moderators.
p = 5, q = 3: Best Case = 0 scalars, 0 functions; Worst Case = 3 scalars, 1 function
Sc. 2	100	1.06(1.03), 0.65(0.48)	0.96(1.02), 0.72(0.45)	1.51(1.18), 0.33(0.47)	0.64(0.76), 0.15(0.36)	0.08(0.27), 0.03(0.17)
	200	1.45(1.09), 0.73(0.45)	0.73(0.90), 0.55(0.50)	1.45(1.18), 0.31(0.46)	0.45(0.67), 0.08(0.27)	0.06(0.24), 0.03(0.17)
	400	1.21(0.97), 0.76(0.43)	0.63(0.82), 0.62(0.49)	1.13(1.06), 0.31(0.46)	0.23(0.45), 0.07(0.26)	0.02(0.14), 0.01(0.10)
Sc. 4	100	1.07(1.06), 0.62(0.49)	1.23(1.03), 0.72(0.45)	1.84(1.12), 0.37(0.49)	1.09(1.07), 0.22(0.42)	0.12(0.41), 0.04(0.20)
	200	1.11(0.99), 0.59(0.49)	1.16(1.04), 0.66(0.48)	1.78(1.12), 0.36(0.48)	0.92(0.88), 0.20(0.40)	0.32(0.51), 0.02(0.14)
	400	1.38(1.00), 0.73(0.45)	1.25(1.04), 0.67(0.47)	1.71(1.14), 0.32(0.47)	0.61(0.72), 0.09(0.29)	0.29(0.52), 0.05(0.22)
p = 100, q = 10: Best Case = 0 scalars, 0 functions; Worst Case = 98 scalars, 8 functions
Sc. 2	100	17.67(17.44), 3.42(2.59)	19.51(15.83), 2.83(2.24)	29.75(27.22), 0.81(1.19)	25.86(21.34), 1.44(1.67)	0.76(1.04), 0.06(0.24)
	200	16.64(16.15), 2.84(2.31)	15.73(15.51), 3.12(2.23)	19.43(21.97), 0.76(1.35)	21.61(20.19), 1.07(1.38)	0.40(0.71), 0.05(0.26)
	400	9.61(9.48), 2.55(1.65)	19.26(17.53), 3.23(2.26)	17.62(24.77), 0.79(1.63)	15.09(16.43), 0.97(1.27)	0.13(0.39), 0.03(0.17)
Sc. 4	100	14.64(20.33), 2.37(2.58)	21.06(18.23), 3.21(2.71)	27.43(26.40), 0.94(1.43)	26.40(24.59), 1.25(1.87)	1.01(1.34), 0.03(0.17)
	200	20.80(22.97), 3.26(2.96)	24.04(17.47), 4.07(2.34)	27.53(27.58), 1.02(1.93)	26.79(21.84), 1.33(1.61)	0.73(1.14), 0.05(0.22)
	400	13.22(17.07), 2.50(2.47)	18.60(16.42), 3.44(2.18)	16.70(23.30), 0.58(1.37)	23.44(22.54), 1.26(1.58)	0.57(1.07), 0.01(0.10)

Table 3.

Simulation Set B (with error in functional predictors) Scenarios 2 and 4. Each set of values corresponds to the mean_(sd) scalar covariates selected, mean_(sd) functional covariates selected for each setting and method. Top: Mean_(sd) number of correctly identified moderators. The best case is 3 true scalar and 2 true functional moderators selected. Bottom: Mean_(sd) number of covariates that are incorrectly identified as moderators. The best case is 0 spurious scalar and 0 spurious functional covariates selected.

	n	MC	MC-A	MC-AL	OWL	MC-CART
Mean number of correctly identified moderators.
p = 5, q = 3: Best Case = 3 scalars, 2 functions; Worst Case = 0 scalars, 0 functions
Sc. 2	100	2.00(0.85), 1.40(0.84)	2.83(0.43), 1.79(0.54)	2.87(0.39), 0.97(0.81)	2.24(0.83), 0.16(0.37)	2.22(0.70), 0.08(0.27)
	200	2.31(0.77), 1.45(0.85)	2.98(0.14), 1.95(0.22)	2.93(0.36), 0.95(0.78)	2.61(0.69), 0.12(0.38)	2.74(0.54), 0.03(0.17)
	400	2.74(0.52), 1.78(0.56)	3.00(0.00), 1.98(0.14)	3.00(0.00), 1.05(0.87)	2.96(0.20), 0.10(0.30)	2.98(0.14), 0.06(0.24)
Sc. 4	100	1.90(0.75), 1.22(0.89)	2.59(0.65), 1.65(0.67)	2.72(0.53), 0.89(0.87)	2.33(0.71), 0.28(0.47)	2.11(0.62), 0.10(0.30)
	200	2.04(0.83), 1.23(0.92)	2.90(0.33), 1.80(0.47)	2.92(0.31), 0.86(0.78)	2.68(0.62), 0.21(0.46)	2.60(0.53), 0.06(0.24)
	400	2.35(0.77), 1.56(0.78)	2.98(0.14), 1.92(0.31)	3.00(0.00), 1.17(0.88)	2.86(0.40), 0.12(0.33)	2.90(0.30), 0.08(0.31)
p = 100, q = 10: Best Case = 3 scalars, 2 functions; Worst Case = 0 scalars, 0 functions
Sc. 2	100	1.54(0.72), 0.83(0.85)	2.43(0.73), 1.07(0.86)	2.52(0.76), 0.41(0.70)	1.61(0.71), 0.08(0.31)	1.44(0.64), 0.02(0.14)
	200	1.85(0.82), 0.97(0.85)	2.98(0.20), 1.58(0.64)	2.86(0.43), 0.45(0.76)	2.02(0.82), 0.11(0.31)	2.32(0.62), 0.00(0.00)
	400	2.13(0.85), 0.98(0.84)	3.00(0.00), 1.94(0.28)	3.00(0.00), 0.31(0.63)	2.49(0.67), 0.07(0.26)	2.93(0.26), 0.01(0.10)
Sc. 4	100	1.35(0.61), 0.60(0.80)	2.29(0.66), 0.97(0.87)	2.42(0.64), 0.34(0.58)	1.98(0.80), 0.20(0.49)	1.46(0.52), 0.01(0.10)
	200	1.69(0.77), 0.86(0.86)	2.72(0.53), 1.44(0.69)	2.74(0.52), 0.27(0.60)	2.12(0.78), 0.11(0.40)	2.11(0.63), 0.00(0.00)
	400	1.85(0.81), 0.84(0.86)	2.98(0.14), 1.75(0.52)	2.98(0.14), 0.38(0.65)	2.58(0.62), 0.18(0.44)	2.72(0.47), 0.00(0.00)
Mean number of covariates that are incorrectly identi_ed as moderators.
p = 5, q = 3: Best Case = 0 scalars, 0 functions; Worst Case = 3 scalars, 1 function
Sc. 2	100	1.04(1.02), 0.63(0.49)	1.24(1.11), 0.73(0.45)	1.83(1.11), 0.31(0.46)	0.40(0.64), 0.05(0.22)	0.18(0.44), 0.01(0.10)
	200	1.20(1.07), 0.73(0.45)	0.87(1.00), 0.68(0.47)	1.61(1.13), 0.30(0.46)	0.44(0.62), 0.11(0.31)	0.16(0.39), 0.01(0.10)
	400	1.38(1.05), 0.83(0.38)	0.65(0.90), 0.63(0.49)	1.70(1.22), 0.33(0.47)	0.26(0.46), 0.03(0.17)	0.10(0.30), 0.03(0.17)
Sc. 4	100	1.10(1.11), 0.58(0.50)	1.30(1.04), 0.70(0.46)	1.68(1.04), 0.37(0.49)	0.88(0.92), 0.13(0.34)	0.33(0.55), 0.05(0.22)
	200	1.04(1.12), 0.56(0.50)	1.31(0.94), 0.74(0.44)	1.74(1.05), 0.33(0.47)	0.70(0.69), 0.10(0.30)	0.30(0.48), 0.02(0.14)
	400	1.42(1.08), 0.72(0.45)	1.34(1.00), 0.67(0.47)	2.08(1.03), 0.44(0.50)	0.66(0.68), 0.07(0.26)	0.51(0.63), 0.01(0.10)
p = 100, q = 10: Best Case = 0 scalars, 0 functions; Worst Case = 98 scalars, 8 functions
Sc. 2	100	18.48(20.12), 2.93(2.79)	20.42(15.62), 3.24(2.46)	33.73(28.17), 1.06(1.38)	11.62(14.93), 0.59(1.14)	1.24(1.28), 0.06(0.24)
	200	22.07(24.35), 3.29(2.86)	17.36(16.71), 4.08(2.37)	32.66(31.87), 1.53(2.48)	12.05(13.27), 0.56(0.92)	1.21(1.69), 0.07(0.26)
	400	15.48(20.56), 3.11(2.60)	19.59(16.76), 4.62(2.51)	23.32(26.50), 0.96(1.74)	11.37(12.84), 0.69(1.15)	0.73(1.20), 0.06(0.28)
Sc. 4	100	15.34(19.75), 2.13(2.57)	21.89(17.78), 3.26(2.57)	29.03(26.56), 0.91(1.37)	19.01(21.68), 0.96(1.62)	1.02(1.29), 0.04(0.20)
	200	23.14(25.35), 2.97(2.98)	23.82(17.16), 4.26(2.42)	28.49(28.27), 1.10(2.00)	15.32(16.45), 0.49(0.85)	1.08(1.40), 0.03(0.17)
	400	17.89(23.22), 3.12(3.02)	17.51(16.09), 4.40(2.34)	25.30(26.51), 1.01(1.80)	15.53(17.28), 0.81(1.07)	0.97(1.36), 0.05(0.26)

The bottom halves of Tables 2 and 3 show the mean number of spurious scalars (first mean under each method) and mean number of spurious functions (second mean under each method) that were incorrectly identified by each method as moderators. The best performing method in this regard is MC-CART since it tends to avoid identifying spurious covariates as moderators. However, this appears to be at the cost of failing to identifying the true moderators. Though the MC and MC-A methods tend to over-select spurious functional covariates, the tables show that, on average, performance measures are well under the “worst case” possible values.

Figures 2 and 3 show box plots of the E{Y^*(ĝ)} values for the estimated regimes as well as the mean (sd) PCDs for each method in each setting. The MC-A method dominates the MC, OWL, and MC-CART method across all settings with typically higher values in the test set and larger average PCDs. Figures 2 and 3 show that the MC-A method performs considerably better than the MC method, indicating that augmentation can improve efficiency by factoring out variation that is unrelated to differential treatment effect and minimizes the effect of model misspecification. The MC-A method dominates the MC-AL method in the majority of settings. In Simulation Set A, the true functional contrast coefficients are such that, reducing the 1-D predictors to scalars via averaging and using the MC-AL method tends to result in contrast coefficient estimates with the same sign as those estimated from the MC-A method, thus resulting in similar treatment selection results for the two methods. These “near linear” contrast functions are similar to those that we estimated based on the clinical trial data analyzed in Section 5. This is why, although the MC-A method appears better than MC-AL with respect to optimal treatment selection in Simulation Set A, it is only marginally so. In contrast, the true functional contrast coefficients in Simulation Set B are such that reducing the 1-D functions to scalars results in the loss of salient features that are needed to correctly estimate the contrast and so the MC-A method performs substantially better with respect to PCD and value of the estimated decision rule when compared with all other methods. These simulations show that there can be considerable benefits to accounting for the functional nature of the covariates using the MC-A approach.

Fig. 2.

Simulation Set A (with error in functional predictors) Scenarios 2 and 4. Boxplots of expected values of response in test sets under estimated optimal regime for the 100 experiments in each setting. First Row Settings with p = 5, q = 3. Second Row Settings with p = 100, q = 10. Sample sizes and treatment regime estimation methods are on the vertical axis. Expected values of the decision rule is on the horizontal axis with E{Y^*(−1)},E{Y^*(1)}, and E{Y^*(g^opt)} marked. Mean (sd) PCD for each method and sample size combination shown on the right of each plot.

Fig. 3.

Simulation Set B (with error in functional predictors) Scenarios 2 and 4. Boxplots of expected values of response in test sets under estimated optimal regime for the 100 experiments in each setting. First Row Settings with p = 5, q = 3. Second Row Settings with p = 100, q = 10. Sample sizes and treatment regime estimation methods are on the vertical axis. Expected values of the decision rule is on the horizontal axis with E{Y^*(−1)},E{Y ^*(1)}, and E{Y^*(g^opt)} marked. Mean (sd) PCD for each method and sample size combination shown on the right of each plot.

5. Application to MDD Clinical Trial Data

We now apply our MC-A method as well as competing scalar methods to data from our study comparing placebo and sertraline in the treatment of MDD. Data from 132 subjects are available. Prior to treatment assignment, baseline scalar and functional imaging data, including EEG amplitude spectra curves, were collected. Subjects were monitored via depression assessments at 1, 2, 3, 4 ,6, and 8 weeks after initiation of their randomly assigned treatment. The primary endpoint of interest is the HAM-D score at week 8. Lower values of HAM-D score are desirable.

Although there are many baseline scalar and functional covariates available, we restrict attention to a relatively small subset. The baseline scalar values under consideration are HAM-D score (Z₁), sex (Z₂; 0 = male, 1 = female), age (Z₃), and years of education (Z₄). The baseline functional covariates under consideration are the six scaled CSD amplitude spectra curves discussed in Section 1. The amplitude values are scaled by dividing by the largest amplitude value across the frequency domain. The right panel of Figure 4, shows a sample of the relative amplitude spectra for the FZ (X₁), FCZ (X₂), F4 (X₃), F3 (X₄), PZ (X₅), and POZ (X₆) electrodes.

In this data set, 48% of the subjects were randomized to the sertraline, the mean baseline HAM-D score is 18.94, 64% are female, the mean age is 37.95, and the mean number of years of education is 15.06. We split the data into a randomly selected training set of 107 subjects and validation set of 25. Using the training set, we employed our MC-A method. We first smoothed the functional covariates using the same procedure employed in the simulations discussed above. For the six functional covariates, we used a B-spline basis of order 4 with K_ℓ = 25 basis functions and used 5-fold CV to select the tuning parameters, λ and ρ₁ = … = ρ₆ = ρ. The estimated treatment regime is given by

$$\widehat{g}(\mathit{Z},\mathit{X})=-\mathit{sign}\{2.957-0.676Z_1-0.415Z_2-1.021Z_3+1.111Z_4+\int {\widehat{\omega }}_1(s)X_1(s)ds+\int {\widehat{\omega }}_2(s)X_2(s)ds+\int {\widehat{\omega }}_5(s)X_5(s)ds\},$$

where ω̂₁, ω̂₂, and ω̂₅ are shown in Figure 4. (Note: we take the opposite of the estimated sign of the contrast since lower values of HAM-D are preferred.) All four scalar baseline covariates are included. Of the six functional covariates, only the relative amplitude curves corresponding to the FZ, FCZ, and PZ electrodes are selected to remain in the model. The contrast coefficient functions for the selected functional covariates are approximately linear and nearly constant in the case of ω̂₂ and ω̂₅. This indicates that it may make sense to simply use the scalar average values of the relative CSD curves from the FCZ and PZ electrodes in estimating the decision rule. We note that the CV procedure selected the largest smoothing parameter value from our grid of possible values for ρ.

For comparison, we also applied the MC-AL, OWL, and MC-CART methods to the training set of 107 subjects using the same procedures described in Section 4.4 with 5-fold CV to select all tuning parameters. The mean values for each of the six relative amplitude curves were computed for each subject and these scalar values were used as potential treatment effect moderators in the MC-AL, OWL, and MC-CART methods. The treatment regimes estimated via the MC-AL and MC-CART methods selected no moderators and recommend sertraline for all subjects. The OWL method selected sex as the only variable to remain in the SVM that determined the estimated treatment regime. The corresponding rule assigns sertraline to all females and placebo to all males.

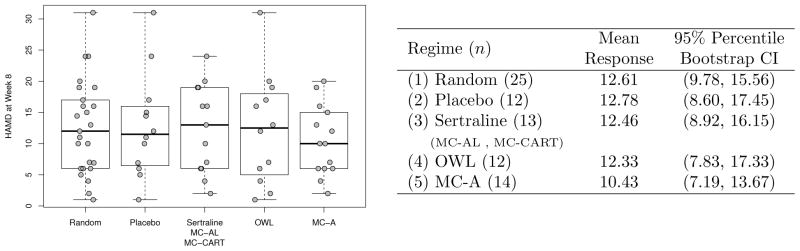
For each subject in the validation set we use the estimated treatment regimes to predict the optimal treatment based on the selected covariates. We compared the average value of the response among the following groups based on the different treatment regimes: (1) all validation subjects under random treatment assignment, (2) all validation subjects who received placebo, (3) all validation subjects who received sertraline (corresponds to optimal treatment based on MC-AL and MC-CART methods), (4) all validation subjects who received optimal treatment based on the treatment rule estimated via the OWL method, and (5) all validation subjects who received the optimal treatment according to ĝ, based on the MC-A method. Figure 5 shows box plots of the response values in the validation set under these five treatment assignment rules as well as a table with the average values of the responses and 95% percentile bootstrap confidence intervals based on 5000 bootstrap replications. From the table we see that the estimated regime based on our MC-A method yields the lowest mean HAM-D score at week 8 when compared to all other regimes, suggesting its superiority. The estimated regime based on our MC-A method assigned the active treatment to about 70% of subjects in the test set and assigned placebo to around 30%. Among those 14 subjects in the test set who actually received the treatment that was assigned based on the MC-A method, 10 (of the 13 subjects receiving sertraline) were assigned to sertraline and 4 (of the 12 subjects receiving placebo) were assigned to placebo. We note that the bootstrap confidence intervals are rather wide, making it difficult to conclusively recommend a treatment rule based on any method. This is not surprising considering the small size of the validation set and the variability of both the outcome and predictors. Access to additional potential moderators such as genetic or other imaging measures may lead to an even better performing treatment decision rule based on the MC-A method.

Fig. 5.

Left: Boxplots of week 8 HAMD scores for test set subjects under different regimes. Right: Mean response (lower values are better) and 95% bootstrap confidence intervals under different regimes in the test set.

6. Discussion

We have presented an approach for simultaneously selecting important baseline scalar and functional predictors in order to construct treatment decision rules. The approach presented here builds on the previous work in McKeague and Qian (2014), Tian et al. (2014), and Ciarleglio et al. (2015) but is tailored specifically for settings like those encountered in the application presented in Section 5 where many potential scalar and functional baseline covariates are available for estimating a treatment decision rule. Specifically, our approach extends the single functional covariate decision rule described in McKeague and Qian (2014) to multiple functional and scalar covariates. Additionally, the proposed approach incorporates variable selection of both scalar and functional covariates. This was not considered in either McKeague and Qian (2014) or Ciarleglio et al. (2015). We view this as a major advantage especially in cases where there is little or no clinical guidance on which variables (either scalar or functional) can inform treatment selection. As in Tian et al. (2014), our method is based on the approach of modified covariates, but extended to both scalar and functional covariates.

Our simulation studies suggest that, provided that we select a reasonable form for the augmentation function, the augmented modified covariates approach is preferable to the modified covariates method with respect to selection of the optimal treatment. The augmented approach can perform fairly well even in settings in which the working model for the contrast is mis-specified. The results also suggest that overfitting and false-discovery are still concerns with the augmented method. Accordingly, we view the proposed method as a tool for exploring the relationship between potentially informative baseline covariates and the response and that these relationships need to be validated using independent data.

The approach presented here offers an appealing alternative to the common practice of reducing functional data to scalar summaries and using those scalar summary values to develop a treatment response model or decision rule. We have demonstrated via simulation that the use of these scalar summaries can result in either incomplete or incorrect estimates of the relationship between the baseline covariates and the response of interest. The proposed modified covariates approach that allows for scalar and functional covariates can give superior treatment selection when this is the case. Before reducing functional covariates to scalar summaries, we recommend using the proposed augmented approach first, inspecting the contrast coefficient functions, and then deciding whether these estimates support the reduction of the functional covariates to scalar summaries. If they do, then we suggest using other treatment regime estimation procedures that perform variable selection but do not handle functional predictors such as those described in Qian and Murphy (2011), Zhang et al. (2012a), Lu et al. (2013), Tian et al. (2014) (which is the MC-AL method we present above), or Liu et al. (2017).

Finally, we mention some possible extensions of our work. Although we are concerned here with continuous responses, these methods can be extended to include binary or time-to-event responses. We have also limited our treatment here to data arising from an RCT in which random treatment allocation is 1:1. When the allocation is not 1:1, it is possible to weight the observations according to the probability of receiving the treatment corresponding to that observation. Tian et al. (2014) provide theoretical justification for this weighting. When data arise from an observational study, the causal interpretation of the contrast may no longer be valid since the covariates and the treatment assignment may no longer be independent. In this case, one may still employ the modified covariates methods, provided that a good propensity score model can be estimated so that observations can be appropriately matched or weighted. One final extension that is particularly important in developing treatment rules for MDD is the incorporation of functional responses (e.g., trajectory of HAM-D over time) into the treatment regime framework in addition to selecting important scalar and functional baseline biomarkers that can inform treatment selection.