Ultrasound-based formation of nano-Pickering emulsions investigated via in-situ SAXS

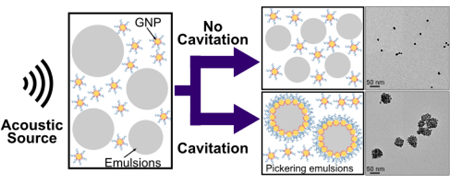
Graphical Abstract:

Introduction:ⁱ

Emulsions are metastable dispersions of two immisciblwere synthesized using methods adapted by Lae liquids that form an apparently homogeneous material (i.e. macroscopically). Without stabilizers, emulsions are intrinsically unstable and ultimately will separate into two different phases.¹ Although surfactants commonly stabilize emulsions, solid particles have also been demonstrated to be effective stabilizers producing systems called Pickering emulsions.^2–4 Based on the wettability of the particles, either oil-in-water or water-in-oil Pickering emulsions are formed.³ Other advantages of Pickering emulsions include a significant increase in the emulsion’s resistance to coalescence, increased energy barriers to eject particles from the emulsion interface (i.e. nearly irreversible adsorption), and decreased toxicity to living cells.^5–7 Consequently, Pickering emulsions can be used effectively in fields such as food science & engineering, oil recovery, cosmetics, and biomedical technologies.^6,8–12

Despite the wide range of potential applications, Pickering emulsions have not always been used extensively because of the challenges in controlling their synthesis. The formation of Pickering emulsions is known to be sensitive to particle shape, size, surface properties, and concentrations.⁶ Further, even if particles have adequate properties to stabilize an emulsion interface, factors such as energy barriers can prevent spontaneous adsorption.^13,14

Electrostatic repulsion is one such known energy barrier that can effectively prevent spontaneous particle adsorption. Still, it can be overcome by altering the charge on the particle surface using surface chemical functionalization or by altering the solvent’s environment (e.g. pH or ionic strength).^15–17 Another possible barrier is steric repulsion, which is common for polymer-functionalized particles acting as stabilizing agents. In this case, polymer layers form a physical barrier preventing particle adsorption.^18,19 Steric repulsion can be overcome by applying mechanical forces such as high shear mixing, high-pressure homogenization, or sonication.^20–22 In this work we carefully analyze the role of acoustic cavitation in overcoming such energy barriers using controlled sonication.

Of all methods for applying mechanical forces to synthesize Pickering emulsions, sonication is the most frequently used. Bath or probe-type sonicators are common tools in most colloid laboratories. These emit strong acoustic waves in the ultrasound frequency range (>20 kHz) for mechanical agitation, redispersion, emulsification, and/or glassware cleaning. Sonication is also effective in Pickering emulsion synthesis because it can simultaneously emulsify and force particle adsorption onto droplet interfaces. However, laboratory sonicators are rarely calibrated and acoustic settings and sonication times are usually selected by personal experience and/or trial and error resulting in widely variable results. Moreover, most of these instruments produce poorly defined acoustic fields and do not provide information on important acoustic parameters (e.g. local acoustic pressure). Furthermore, differences in experimental parameters including probe/bath geometry, sample positioning, sample volume and vessel material, affect acoustic conditions and produce drastic variations in sonication results from system to system and sample to sample. For most studies reported in the literature, sonication is often treated as a ‘black box’ with little attention given to the underlying physics controlling these processes.

In controlled ultrasound experiments, the acoustic frequency, pressure (intensity), duration, and pulse repetition frequency (or duty cycle) are carefully controlled. Acoustic radiation force, which scales proportionally with the square of acoustic pressure, could provide nanoparticles with the momentum necessary to both move in the dispersion and overcome energy barriers between the nanoparticle and the emulsion interface. Alternatively, cavitation could form and violently collapse vapor cavities in the liquid, producing locally high pressures, stresses, and temperatures that would induce the formation of Pickering emulsions.^23,24

This work uses in-situ scattering methods to understand the process of Pickering emulsion synthesis under controlled acoustic fields. The model system examined here consists of oil-in-water emulsions insonated in the presence of polymer-coated amphiphilic gold nanoparticles (GNP). In previous studies, our lab has shown that these types of GNPs are effective in stabilizing both hydrocarbon and perfluorocarbon emulsions.^22,25 This work mainly focuses on the use of perfluorinated oils for Pickering emulsion formation due to the increased interest in utilizing Pickering emulsion contrast agents for medical imaging. Previously, we have shown that Pickering emulsions with perfluorinated cores can be a potential theranostic agents for sono-photoacoustic imaging.^25–30 These Pickering emulsions can be activated using a combination of ultrasound and laser pulses to provide significant contrast for sono-photoacoustic imaging and can simultaneously break blood clots.²⁶ Nevertheless, hydrogenated alkane oils such as hexadecane, are also included in this study in order to compare observations with Pickering emulsions that are of general interest for other applications.^31–34

Structural changes occurring within the samples are characterized using ultra-small angle X-ray scattering (USAXS) during sonication within a custom build focused ultrasound sample environment.^35,36 Compared to other techniques which can only characterize the samples before and after the formation of Pickering emulsions, USAXS is a unique technique because it provides us with the ability to quantitatively examine structural changes during the application of acoustic forces. Moreover, the custom build sample environment enables user defined control over the transmitted acoustic settings (e.g. acoustic pressure, pulse duration, and pulse repetition frequency) while simultaneously monitoring for cavitation events. By varying the acoustic pressures, sonication times and the types of oils, we systematically explore the role of sonication parameters and emulsion composition in the formation of Pickering emulsions.

Materials and Methods:

Sample Preparation:

Gold (III) chloride trihydrate, sodium citrate dihydrate (>99.9%, CAS: 16961–25-4), hexadecane 99 %, CAS:544–76-3), butanethiol (99%, CAS: 109–79-5), and sulfuric acid (98%, CAS: 7664–93-9) were purchased from Sigma-Aldrich (St. Louis, MO, USA). 10 kDa thiolterminated poly (ethylene glycol) methyl ether (95%, PEG-thiol) was purchased from Polymer Source (Dorval, Quebec, Canada). Perfluoroalkanes including perfluorononane (99%, CAS:37596–2), perfluorooctane (90%, CAS:307–34-6), and perfluorohexane (98%, CAS:355–42-0) were obtained from Synquest Laboratories (Alachua, FL, USA). Colloidal gold nanoparticles of ~12 nm average diameter were synthesized using methods described by Frens.³⁷ All alkane and perfluoroalkane oils were fully linear with no branching. All glassware used in synthesizing gold nanoparticles was cleaned with a critical cleaning detergent Liquinox® (Alconox, Inc., NY, USA), sonicated in a sonication bath for 30 minutes, and set in an acid bath with Nochromix solution (Nochromix® powder, Godax Labs Inc., MD, USA, dissolved in pure sulfuric acid) for an hour to remove any potential residual organic material. GNPs with a dosing of 8 PEG-thiol chains/nm² and 20 butanethiol chains/nm² were synthesized using methods adapted by Larson-Smith et al.^26,38

Coarse oil-in-water emulsions were prepared in a separate container by sonicating 1 vol% of oil (i.e. perfluorinated oils or hexadecane) in deionized water using a Branson Digital Sonifier S-450 with a 3 mm tapered microtip (Branson Ultrasonics, CT, USA) at 30% amplitude 50% duty cycle (i.e. 0.1 seconds on and 0.1 seconds off) for a total of 20 seconds of sonication time. The coarse surfactant-free emulsions were then added to GNP dispersions to form a 50:1 oil to gold volume ratio. The final volume fraction of oil in the sample was 3.4×10^-3. Each emulsion sample was freshly prepared before conducting experiments to avoid coarsening due to coalescence. The dispersions of oil droplets and nanoparticles were then sonicated using a focused ultrasound sample environment at various acoustic conditions. GNPs without emulsions and emulsions without nanoparticles were also sonicated as controls. An overall schematic diagram of the process for functionalizing GNP and synthesizing Pickering emulsion using ultrasound is shown in Figure 1.

Figure 1.

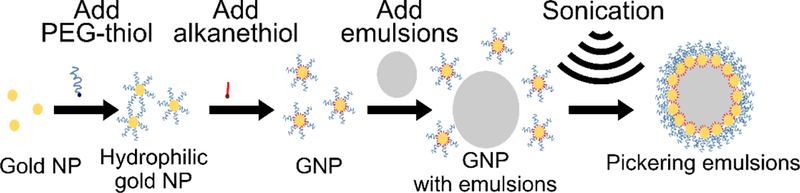
Overall schematic diagram of functionalizing GNP and Pickering emulsion formation.

USAXS Measurements and Data Analysis

USAXS experiments were performed using a custom designed acoustic sample environment.³⁵ For each acoustic experiment, 2 coaxially aligned 1.24 MHz focused ultrasound transducers (Sonic Concepts H-102, f-number 0.98, 64 mm diameter, Sonic Concepts Inc., Bothell, WA, USA) were pulsed at acoustic pressures ranging from 0 to 7.2 MPa, at a repetition frequency (PRF) of 6.2 kHz and a 20% duty cycle. Samples were insonated for a total of 3 minutes at each USAXS time-point measurement unless otherwise specified. The two face-toface transducers were alternated at a rate of 1 Hz to prevent material buildup at one side of the sample holder due to acoustic radiation forces. All USAXS experiments were performed in a standard Bonse-Hart instrument configuration at beamline 9-ID-C in Advanced Photon SourceArgonne National Lab.³⁹ The energy of the X-ray beam was 21 keV.

The recorded USAXS scattering data was reduced to an absolute scale and desmeared using Indra module of SAS software.^40,41 The desmeared scattering data was then modeled with two different models to describe these complex system, which may contain multiple coexisting components e.g. ‘free’ particles, undecorated oil droplets, and droplets with adsorbed particles). In the first model, a sum of two polydisperse sphere populations, was used for samples containing GNPs and emulsions when no particle adsorption occurred (i.e. Pickering emulsions were not being formed). For these samples, it was assumed that GNPs and emulsion droplets were not interacting with each other, which is a good assumption in the dilute conditions used in this study. Therefore, this was considered as a system containing two independent populations of spheres. The modeling of this 2-sphere system was performed using Irena to obtain size distributions (log-normal) and volume fractions for each component.

For samples and conditions that would form Pickering emulsions, a generalized scattering model developed by Debye was used to fit the scattering profiles. The Debye model can be used to model any arbitrary shape as long as it is composed of spherical subunits with known relative position.⁴² For Pickering emulsion systems, this was constructed as a large sphere (i.e. droplet) evenly decorated by smaller spheres (i.e. gold nanoparticles) corresponding to a certain area coverage. Model details are included in the supplemental information section. This model is similar to a raspberry model that has been previously described but it is better suited to describe the correlations between particles at the emulsion-water interface (i.e. curved spherical interface) at the expense of more expensive computations.⁴³ Specific modeling parameters were found using a least squares routine coded into MATLAB. Size, surface coverage, volume fraction of the Pickering emulsion, and the amount of remaining non-adsorbed gold nanoparticles could be obtained using the Debye model.

Cavitation Analysis

Ultrasound signal analysis was performed using MATLAB to implement methods adapted from Fabiilli, et al.⁴⁴ In short, a Hamming window was applied centered on the acoustic time of flight from the focused transducer to the sample. Fast Fourier transforms (FFTs) of windowed signals were calculated and an average power for the signal at high frequencies (background signal) was subtracted. Cavitation power was then obtained by summing power values between 0.1 to 0.5 MHz to highlight non-linear signals that emerge due to the effects of cavitation when this is present.

The mean acoustic power was also obtained for a water sample at low acoustic pressures without cavitation. A cavitation threshold was defined to correspond to signals larger than 4 times the mean acoustic power of the water sample within this frequency window. The cavitation probability was then calculated by summing the number of signals whose cavitation power was greater than the cavitation threshold and dividing this by the total number of incident acoustic pulses. The cavitation threshold for each sample was found by fitting a sigmoid curve to a plot of the acoustic pressure versus cavitation probability and calculating the 50% crossing point.

UV-Vis Characterization:

Optical extinction spectra were measured over the range of 300–1100 nm using ultraviolet-visible (UV-Vis) spectroscopy (Thermo Scientific Evolution 300, Thermo Fisher Scientific, MA, USA). All samples were diluted 20 times in deionized water to avoid surpassing an extinction value greater than 2.

TEM Analysis:

Samples before and after sonication were also dried and imaged using a FEI Tecnai G2 F20 Transmission Electron Microscope (TEM) operating at 200 kV. TEM samples were prepared by diluting gold nanoparticle or Pickering emulsion dispersions 50 times in deionized water to prevent particle clustering during drying. The diluted dispersion was then deposited on a carbon TEM grid and allowed to dry in a desiccator for at least 24 hours before performing measurements.

Results:

GNPs, such as those used in this study, have been previously shown to form Pickering emulsions when sonicated in the presence of oil.^22,38 Yet, we also found that these GNPs would not spontaneously form Pickering emulsions by direct adsorption (e.g. simply mixing particles and oil emulsions) or by applying moderate shear (e.g. magnetic stirring). Under these conditions, optical extinction spectra showed no significant changes compared to those obtained from GNPs alone, which had a narrow peak at 520 nm characteristic of gold nanoparticle plasmonic resonance (Figure 2). The formation of Pickering emulsions usually red shifts the optical extinction spectrum as nanoparticles are packed in close proximity and interparticle plasmonic resonance begins to dominate.^22,45 Of all methods tested, sonication was the only one that reliably produced Pickering emulsions.

Figure 2.

UV-Vis extinction spectra of GNP with perfluorooctane emulsions (a) allowed to rest, (b) magnetically stirred, and (c) sonicated. Insert: Photographs of the corresponding samples.

To further explore the role of sonication in Pickering emulsion synthesis, a sample containing GNPs and perfluorooctane was sonicated in the acoustic sample environment at various acoustic pressures. Scattered acoustic signals were also recorded for cavitation detection. An example of the frequency spectrum for a sample with and without cavitation events is shown in Figure 3(a). When there is no cavitation, the only peak is found at the transducer fundamental frequency. At higher acoustic pressures, peak intensities at the carrier frequency (and its harmonics) increase proportionally. In addition, inertial cavitation from bubble collapse produced additional broadband noise, which is especially evident at lower frequencies. The cavitation probability curve was plotted for each sample using the calculated cavitation probability at each pressure (Figure 3 (b)). The cavitation threshold was estimated to be 6.4 MPa for this sample. Cavitation analysis of pure water shows that the emulsions reduced the cavitation threshold from 7.3 to 6.4 MPa.

Figure 3.

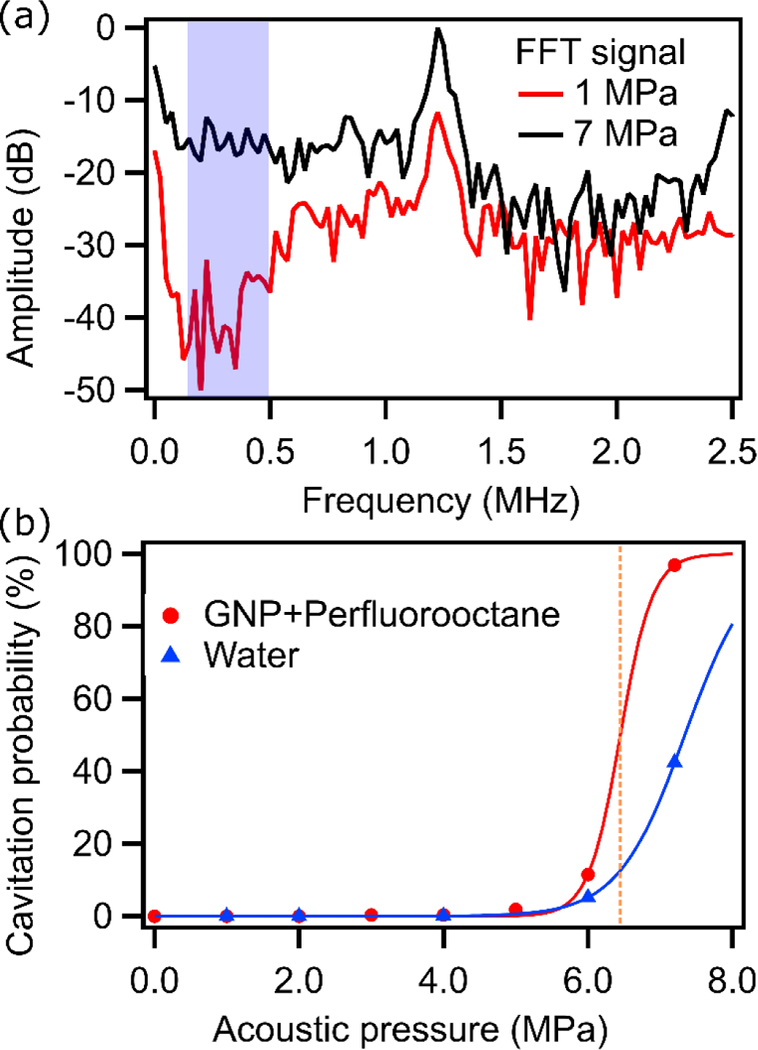
(a) An example frequency spectrum of GNP with perfluorooctane sonicated above (7.2 MPa) and below (1.0 MPa) the cavitation threshold. Cavitation detection was performed using amplitudes in the highlighted area. (b) Cavitation probability curves for GNP with perfluorooctane and pure water as obtained from acoustic analysis.

TEM images of samples sonicated at various acoustic pressures further showed that Pickering emulsions would only form by sonicating GNPs and emulsions at cavitation pressures of 7.2 MPa (Figure 4). Regardless of aging time, GNP particles did not spontaneously adsorb onto the perfluorooctane droplet interface to form Pickering emulsions. Moreover, Pickering emulsion formation did not appear to scale proportionally with acoustic pressure, indicating a cavitation-based mechanism was essential for this sample.

Figure 4.

TEM images of GNP (i.e. no oil present) (a) before sonication, (b) sonicated at 1 MPa (no cavitation), (c) sonicated at 7.2 MPa (cavitation). Images of GNP in the presence of perfluorooctane emulsions (d) before sonication, (e) sonicated at 1 MPa, and (f) sonicated at 7.2 MPa.

Structural changes were also quantified using USAXS during sonication. USAXS can probe material structures over multiple length scales (1–10,000 nm) and in their native dispersed state during ultrasound manipulation. This removes potential structural changes due to aging or drying that may occur when preparing TEM samples, which requires high vacuum. Two main changes in scattering profiles were observed with increasing acoustic pressure; one in the low-q (q < 0.01 Å⁻¹) and the other in the mid-q regions (0.01 < q < 0.07 Å⁻¹) shown in Figure 5 (a). Low-q changes are typically associated with a change in the droplet size distribution while changes in the mid-q region are characteristic features for Pickering emulsion formation.²² Based on the collected scattering data, only samples sonicated at 7.2 MPa showed this characteristic inflection.

Figure 5.

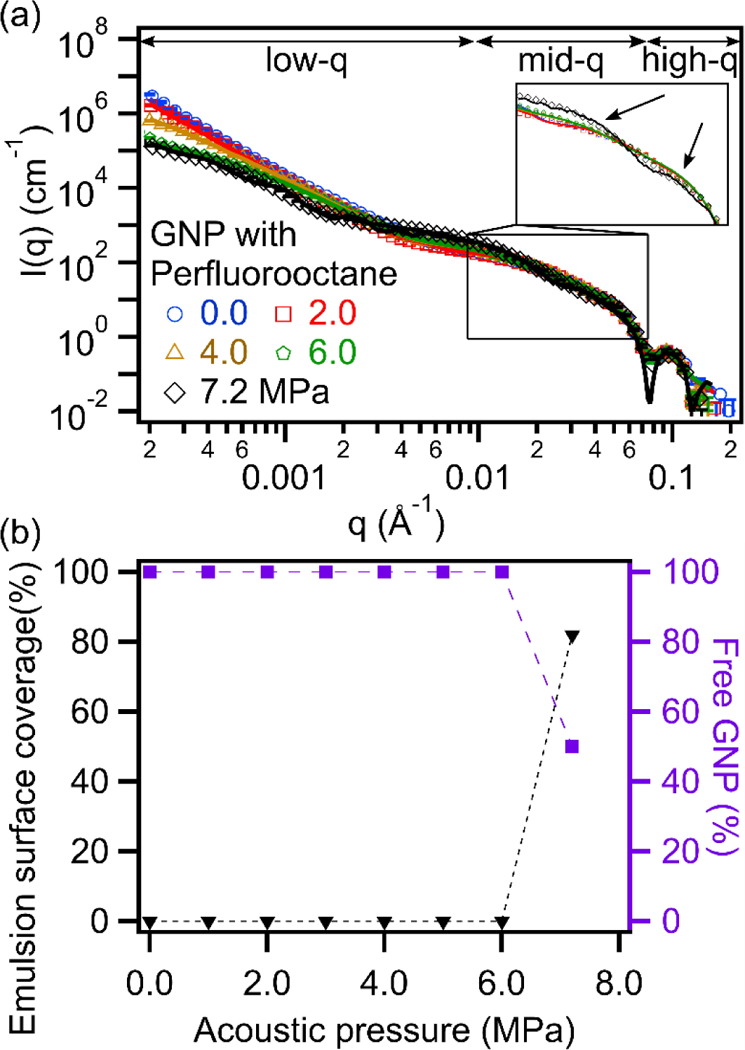
(a) Desmeared USAXS profiles of GNP with perfluorooctane sonicated at various acoustic pressures. A model containing 2 spheres was used to fit the sample sonicated at acoustic pressures lower than the cavitation threshold (<6.4 MPa), and a Debye model was used to fit the sample sonicated at 7.2 MPa. Scattering length densities were fixed for water (9.47×10⁻⁶ Å⁻²), gold (124.69×10⁻⁶ Å⁻²) and perfluorooctane (14.47×10⁻⁶ Å⁻²). (b) Quantification of the emulsion surface coverage and amount of excess ‘free’ GNPs.

The sizes and volume fractions of GNPs in the sample were obtained by modeling the scattering curves before sonication. Based on modeling results, GNPs consisted mostly of particles of 6.0 nm radii with a polydispersity (PDI, non-uniformity of the particles) of 0.12 (78.5 vol% of the total GNPs). PDI provides information on the non-uniformity of the particles and in our model was defined as the square of the standard deviation divided by the mean radius. However, a smaller fraction (21.5 vol%) of larger particles (13.3 nm radii with a PDI of 0.19) were also present. The total GNP volume fraction was estimated based on the scattering to be 5.8×10⁻⁵.

For samples sonicated below 7.2 MPa, TEM images and USAXS scattering curves suggest that no Pickering emulsions would be formed. Therefore, the system was modelled as a non-interacting combination of individual GNPs and emulsions. Results from modeling the samples confirm, as expected, that the size and volume fraction of GNPs did not change when varying the applied acoustic pressure. On the other hand, perfluorooctane emulsion sizes, distributions, and volume fractions changed, as demonstrated in Figure 6.

Figure 6.

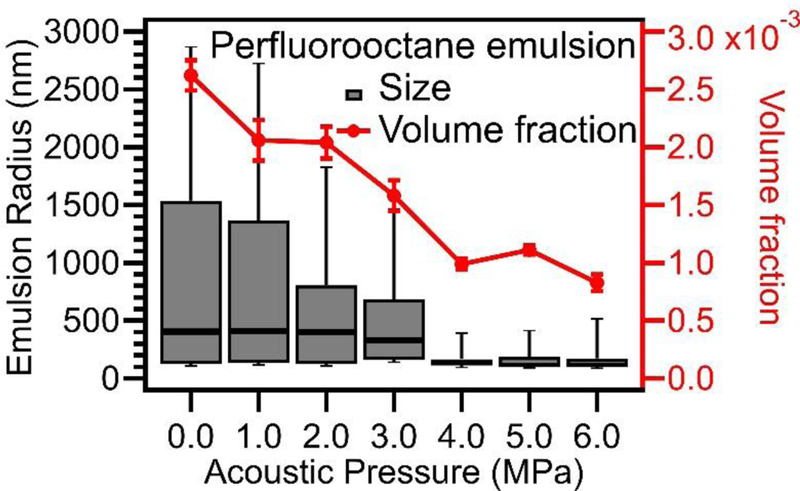
Perfluorooctane emulsion size distribution (box plot) obtained from USAXS modeling showing emulsion size and emulsion volume fraction both decreased with increasing applied acoustic pressures. For the box and whisker plot, the box portion, from bottom to top, represents the 25^th percentile, median, and 75^th percentile of the distribution. The whisker portion represents the 10% percentile and 90% percentile.

Based on these modeling results, it was determined that the sizes of polydisperse emulsions significantly decreased with increasing applied acoustic pressures. The estimated emulsion volume fraction also decreased, suggesting that there was a significant loss of oil through vaporization during sonication. Additional details and modeling of GNP with perfluorooctane emulsions are provided in the supplemental information (Figure S3).

A Debye model was used to fit 1-D scattering curves to reproduce impotrant scattering features of Pickering emulsions. Based on the modeled results, it was determined that two populations of Pickering emulsions of different sizes were present in the sample sonicated at 7.2 MPa (Figure 5a). For this sample, 60.9 vol% of the Pickering emulsions had a mean radius of 19.7 nm and 39.1 vol% had a mean radius of 213.2 nm. A single emulsion size distribution would not fit the data. The remaining volume fraction of emulsion droplets in the system at these conditions was 5.0 × 10⁻⁴ (i.e. equivalent to 79.9% volume loss). All droplets were densely packed with GNPs with a surface coverage of ~82%, close to maximum packing and consistent with results observed in TEM images. However, not all GNPs were bound to an emulsion interface. Despite a GNP volume fraction of 5.8×10⁻⁵, approximately 59% of the particles were still un-bound and diffusing freely in the continuous phase. The surface coverage and excess of ‘free’ GNPs as a function of acoustic pressure is plotted Figure 5(b). All major changes coincided with crossing the cavitation threshold for this sample. In contrast, the size of the perfluorooctane droplets changes well before reaching the cavitation threshold. This suggests that cavitation was not necessary to alter the original droplet size distribution but it is indeed essential to induce the adsorption of the GNPs to the emulsion interface. One disadvantage of our explicit Debye model was that the PDI of GNPs was not considered since it greatly increased computation times and required assumptions to be made on the relative adsorption of large and small particles at the oil-water interface.

Sonication time was also investigated to determine whether total time or the presence of cavitation was more important in Pickering emulsion formation. Two different samples of GNPs containing perfluorooctane emulsions were sonicated at different acoustic pressures, one above and one below the cavitation threshold. The sub-threshold sample did not show any characteristic features of Pickering emulsion regardless of sonication time (Figure 7). The only observed changes in the scattering profile were due to changes in the perfluorooctane emulsion size distribution. On the other hand, the sample sonicated at 7.2 MPa showed an immediate change in the scattering profile.

Figure 7.

Scattering profiles of GNP with perfluorooctane sonicated at (a) 4 MPa (no cavitation) and (b) 7.2 MPa (cavitation) with increasing sonication time.

All data obtained with perfluorooctane as the emulsion core suggests that cavitation events were crucial for Pickering emulsion formation. To further test this, we also analyzed oils with different boiling points including perfluorohexane (b.p,= 56°C), perfluorononane (b.p.=124°C), and hexadecane (b.p.= 287°C). The cavitation probability curves for these emulsions (Figure 8) showed that despite using oils of different boiling point, all of the samples had similar cavitation thresholds.

Figure 8.

Cavitation probability curves for GNPs with perfluorohexane (T_boiling = 56°C), perfluorononane (T_boiling = 125°C), and hexadecane (T_boiling = 286.8°C) emulsions versus pure water.

The corresponding USAXS profiles for samples sonicated at acoustic pressures above (7.2 MPa) or below (6 MPa) the cavitation threshold are shown in Figure 9. Results for all of the samples showed that Pickering emulsions were only formed when sonicated above the cavitation threshold. The fine details observed in the calculated models were due to the assumption that all GNPs are monodisperse and evenly distributed at the emulsion interface. This created large intensity fluctuations in the model that were ‘smeared’ out in the experimental USAXS data. However, the most important parameters (i.e. emulsion size, emulsion packing density, and amount of free GNP) in Pickering emulsion system were adequately captured and were unaffected by these intensity fluctuations. The estimated values of the important Pickering emulsion parameters, boiling point of the emulsions, and estimated cavitation thresholds are summarized in table 1. All samples were prepared using the same batch of GNPs. Therefore, when modeling the scattering profiles, GNP particle size distributions were kept constant. The GNP volume fraction on the other hand was not constant due to possible small variations when pipetting.

Figure 9.

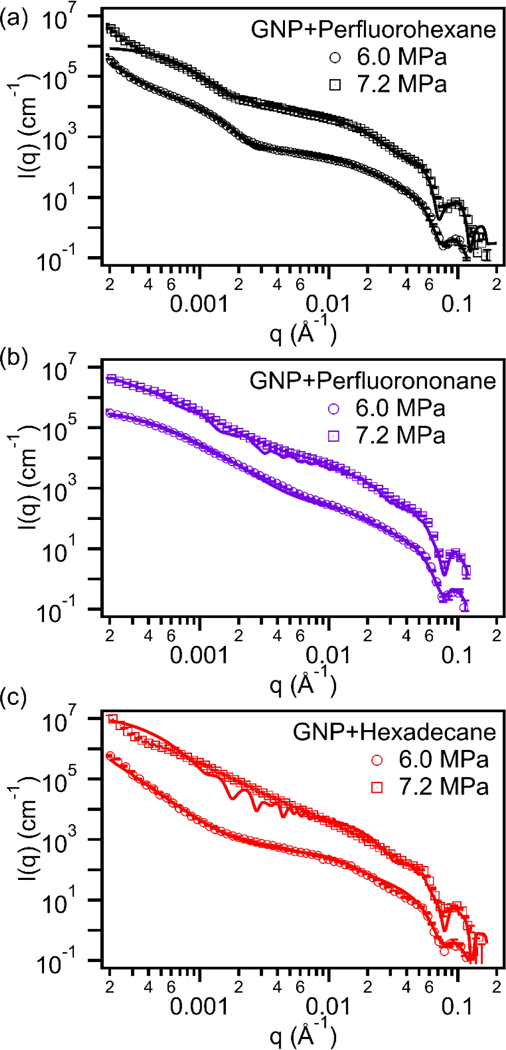
USAXS data for GNP with (a) perfluorohexane, (b) perfluorononane, and (c) hexadecane emulsions sonicated at acoustic pressures below (6 MPa) and above (7.2 MPa) the cavitation threshold (Scattering data was shifted in the vertical direction by 1.5×10⁶ cm⁻¹ to show the changes in the scattering curve). The scattering length densities of perfluorohexane (13.76×10⁻⁶ Å⁻²), perfluorononane (14.74×10⁻⁶ Å⁻²), and hexadecane (7.55×10⁻⁶ Å⁻²), were kept constant during the modeling process.

Table 1.

Boiling point, cavitation threshold, and Debye parameters obtained for different Pickering emulsions.

Emulsion core	Boiling point (°C)	Cavitation threshold (MPa)	GNP volume fraction	Pickering emulsion radius: R+2rsmall (nm)	PDI	Emulsion volume fraction	Excess ‘Free’ GNP (%)
Perfluoro- hexane	56	6.4	6.4 ×10−5	17.1 (76.5 vol%)	0.5	6.0×10−4 (73.5% loss)	59.7
				217.2 (23.5 vol%)	0.3
Perfluoro- octane	104	6.4	5.8 ×10−5	19.7 (60.9 vol%)	0.1	5.0×10−4 (79.9% loss)	59.0
				213.2 (39.1 vol%)	0.4
Perfluoro- nonane	124	6.6	7.2 ×10−5	29.2 (36.0 vol%)	0.4	3.1×10−3 (12.2% loss)	45.9
				223.2 (64.0 vol%)	0.5
Hexadecane	287	6.4	6.9 ×10−5	362.2	0.3	3.5×10−3 (12.5% loss)	56.0

Based on USAXS modeling results, most samples produced two polydisperse size distributions of Pickering emulsions. Using lower boiling point oils resulted in forming smaller Pickering emulsions and in more emulsion volume loss due to vaporization. Only the scattering fits for the hexadecane sample, which has the highest boiling point, suggested that there was only one size distribution of droplets with a high PDI. Nevertheless, regardless of the emulsion boiling point there is always a large amount of ‘free’ GNPs remaining within the system. Additional details on the Debye model and the explanation on how the different parameters (i.e. free GNP%) were estimated are discussed in the supplemental information section.

Discussion:

Based on the results it was clear that cavitation was required to produce Pickering emulsions in these systems. Although TEM is useful for directly visualizing the nanostructure, it could only be performed ex-situ and under high vacuum leading to the evaporation of the solvents. Moreover, TEM could only provide a limited field of view and the nanostructures can be affected by the drying process (e.g. GNP aggregation or deflated Pickering emulsion due to oil evaporation). For example, emulsion droplets decorated by particles are deflated and appear as dense aggregates of particles (Figure 4f). On the other hand, when oil is not present, very small levels of aggregation is observed. The formation of small aggregates in samples that do not have oil (Figure 4c) is likely triggered by cavitation events that may also provide enough mechanical energy to overcome the steric stabilization that is provided by the surface-bound PEG chains. Still, the extend of aggregation is clearly limited and much smaller than what is observed in the presence of oil.

In contrast to TEM, USAXS is better suited to provide a direct structural analysis of the ensemble-averaged nanostructures directly from the dispersion state and while the sample is being manipulated with acoustic fields. Scattering profile for the same GNP control samples were acquired (supplemental information Figure S7) and results demonstrated that large aggregates were formed during sonication when oil was not present. Thus, USAXS was chosen as our main characterization technique to examine the formation of Pickering emulsions. Other techniques including UV-vis, TEM and Fourier-transform infrared spectroscopy (supplemental information Figure S8) were performed to support observations made from the scattering measurements and to guide in the selection of a suitable scattering model for quantitative analysis.

Although bubbles are known to have large contrast due to their low density, cavitation bubbles are not detected using USAXS due to the long measurement times. This was further explained by Li et al. by evaluating the cavitation of pure water and pure ethanol during similar USAXS measurements.⁴⁶ Since cavitation bubble nucleation and collapse occurs over microsecond time scales, the short bubble lifetimes, relative to the total USAXS scan time (3 minutes), means that the total contribution of cavitation bubbles to the scattering is negligible.

USAXS results also showed that applying acoustic fields without cavitation resulted in a decrease in emulsion size and, for some samples, a significant loss of oil. The observed emulsion size change suggests that shear forces provided by just the acoustic fields, without cavitation, are sufficient to destabilize the interface to break emulsions into smaller droplets. This phenomenon was also observed by Kaci et al. where they synthesized sunflower oil emulsions in water using a high-frequency acoustic source.⁴⁷ The oil loss detected during sonication of perfluorocarbon samples is likely due to the volatility of these oils, which are of significant interest for ultrasound and photoacoustic contrast agents.⁴⁸ Lower boiling point perfluorocarbons (e.g. perfluorohexane, vapor pressure: 27 kPa at 25°C) are incredibly volatile and can evaporate at room temperature even in emulsified form. Thermal heating in samples due to acoustic forces can further facilitate emulsion vaporization. Thus, sonicating samples to induce droplet vaporization without achieving re-condensation results in irreversible vaporization. The applied acoustic pressure and time-scales may not be sufficient to achieve re-condensation of some bubbles back into droplets for the more volatile oils. This results in the irrecoverable loss of oil. In this study, we used a family of oils of variable susceptibility to vaporization in order to evaluate the influence of this effect on the way Pickering emulsions are typically synthesized.

Fortunately, in-situ analysis of these processes via USAXS enables quantification of droplet size distributions and volume fractions directly with only one technique. This observation is also similar to results from Fabiilli et al., who examined the process of sonicating perfluorocarbons with focused acoustic waves.⁴⁴ They showed that the emulsion vaporization threshold and the inertial cavitation threshold could be different. For lower boiling point perfluorocarbon emulsions (i.e. perfluorohexane and perfluoropentane), the irreversible oil vaporization threshold could be significantly lower than the reversible cavitation threshold. Schad et al. later did a similar study using two receiving transducers to record reflected acoustic signals.⁴⁹ They revealed that the difference between the two thresholds is a function of both emulsion size and the applied acoustic frequency. Smaller droplets and lower acoustic frequencies prevented irreversible vaporization of emulsion droplets.

After analyzing the acoustic data for all samples, it was also found that all samples had similar cavitation thresholds regardless of the oil that was used. This finding is similar to results obtained by Giesecke and Hynynen, who compared cavitation thresholds for various fluorinated emulsions.⁵⁰ Several studies have also showed that the Laplace pressure, from interfacial tension, plays a significant role in stabilizing micro/nano-droplets and in increasing the boiling point of the droplets.^51,52 Because of this enhanced droplet stability, it is difficult to conclusively determine if cavitation nucleated exclusively from the droplet core, from the bulk fluid or in both phases. Moreover, the ~3 minute acquisition rate of the USAXS prevented us from resolving the transient nature of cavitation bubble growth and collapse.

It is logical that cavitation of the oil core is more likely to occur with low boiling point oil droplets (e.g. perfluorohexane), while cavitation of the solvent phase would be more likely with high boiling point oils (e.g. hexadecane). However, when also taking into account the low volume fraction of the emulsions that were used here, it would be expected that there will be a higher probability of cavitation events initiating in the solvent phase than within droplets.

Given two potential sources of cavitation, we hypothesize two possible ultrasound assisted Pickering emulsion formation mechanisms (Figure 10). The first assumes that cavitation events occur in the bulk fluid (i.e. water). Momentum transfer from the fluid to the particles and droplets due to surrounding random cavitation events could overcome the stabilizing energy barriers that otherwise prevent spontaneous adsorption of the nanoparticles to the oil-water interface. The second potential mechanism would be due to droplet or oil cavitation. During the rapid expansion (i.e. vaporization) and subsequent collapse (i.e. re-condensation) of oil micro/nano-droplets reversibly converting to gas bubbles, droplets expand up to an order of magnitude in diameter (three orders of magnitude in volume). The high interfacial velocities and large displacements during abrupt bubble expansion steps could entrap and induce GNPs in the surrounding medium to adsorb onto the droplet interface. Unfortunately, we are currently unable to differentiate between cavitation of the solvent versus the droplet phase due to the different time scales. However, this may be possible to study in the future with faster X-ray scattering techniques such as time resolved SAXS, which can provide scattering profiles on a sub microsecond time scale, using synchronization to acoustic pulses. The sample composition could also be altered to further favor where the cavitation events will occur. An example of a future experiment may include using a more volatile solvent (i.e. ethanol/water mixture) and smaller sized high boiling point emulsions (i.e. perfluorodecalin). Using the proposed samples could potentially prevent emulsions from cavitating and examine a system where cavitation events only occur in the continuous phase.

Figure 10.

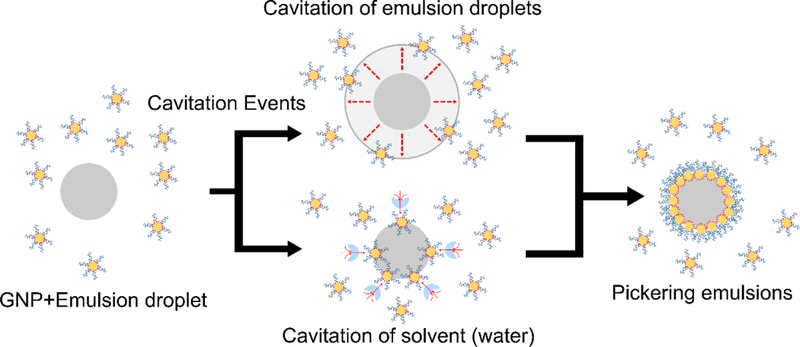
Schematic depiction of possible mechanisms for Pickering emulsion synthesis. Cavitation events in either the oil phase (top route) or the solvent phase (bottom route) could provide sufficient energy to overcome energy barriers for particle adsorption.

Finally, we find that all synthesized Pickering emulsions had the same estimated surface coverage regardless of the type of oil used. The estimated value was similar to the theoretical maximum achievable surface coverage (~82%) when accounting for the butanethiol film thickness on gold surfaces.⁵³ Having a surface coverage close to the theoretical maximum was reasonable given the strong adsorption energy. GNPs can also pack onto any ‘open’ emulsion surface until maximum surface coverage is reached during sonication. Interestingly, the results also show that 45–60% of the GNPs would remain ‘free’ in dispersion without adsorption to the oil-water interface. This value seemed to be somewhat insensitive to the oil type or to the sonication process. One explanation for the presence of excess free particles was due to the statistical nature of droplet breakup and interfacial stabilization. In order to achieve 100% particle adsorption, it would be necessary for ultrasound to produce new interfaces (i.e. breaking droplets) that were rapidly decorated with ‘free’ nanoparticles before any coalescence could take place. However, in reality particle adsorption and interface formation processes may have widely variable time scales. In addition, ultrasound may also act to expel particles from interfaces in the same way that it may also act to mechanically push ‘free’ particles to induce adsorption. Another potential explanation for this observation is from the emulsion stability stand point. According to Binks et al., droplet surfaces that are not fully decorated by particles and that lacking an excess of ‘free’ particles would coalesce until reaching maximum surface coverage or would otherwise result in the formation of macroscopic oil films covering the walls of the sample holder.⁵⁴ Our results suggest a potential steady state between adsorbed and excess ‘free’ particles in the system. This would need to be further investigated with other emulsion systems.

Based on these results, a few strategies can be suggested to improve the cavitation conditions for Pickering emulsion synthesis, which is crucial when designing Pickering emulsions for use as medical contrast agents or for other applications.^25–28,55 The frequency used in this experiment (i.e. 1.24 MHz) was higher than that commonly used in traditional laboratory sonication (i.e. 20–75 kHz). Although a higher frequency allowed us to sonicate the samples at a relatively high pressure without cavitation, it also resulted in significant oil evaporation, up to 80 volume percent of the dosed low boiling point emulsions, throughout the 30-minute sonication time. A lower frequency source (e.g. sonication bath or probe sonicator) could achieve a lower cavitation thresholds and insonate a larger volume.

Another method to minimize emulsion loss is to use smaller initial droplets for Pickering emulsion synthesis. Nano-sized emulsions prepared using techniques such as high-pressure homogenization or spontaneous emulsification will produce higher Laplace pressures that can stabilize emulsions and prevent them from vaporizing during sonication. One example of spontaneous emulsification is the ouzo method where oil is first dissolved in a solvent (e.g. ethanol) and water is then added to induce the formation of small emulsion droplets. This spontaneous emulsification method is a reliable way to produce monodisperse nanoemulsions from volatile oils.⁵⁶ In general, direct analysis of emulsification via in-situ scattering presents a unique opportunity to understand the complex physics at play in these processes.

Conclusion:

In this study, we provide a direct analysis of Pickering emulsion synthesis using amphiphilic gold nanoparticles and several different perfluorinated and hydrogenated alkanes. A specially designed acoustic system, producing fields of well-defined shape and controllable intensity, was used along with ultra-small angle X-ray scattering (USAXS) to provide direct structural information on emulsion systems during simultaneous sonication. All previous works have only been able to characterize Pickering emulsions before and after synthesis but not during synthesis.^4,8,22,31,33 Significantly, this work demonstrates, for the first time, that the formation of Pickering emulsions using sterically stabilized particles requires cavitation to occur due to the application of acoustic fields. No particle adsorption could be detected under weak acoustic fields that resulted in no cavitation. Moreover, we also demonstrate that there is significant loss of oil occurring during the sonication process when the volatility of the oil is high. In contrast, the loss becomes minimal when using high boiling point oils. Additionally, results show that there is also an excess of ‘free’ un-adsorbed particles (45–60%) present in all cases and conditions explored in this work. This suggests that processes leading to interface generation (i.e. drop breakup), interface destruction (i.e. drop coalescence), particle adsorption and particle desorption are all likely occurring simultaneously during ultrasound application and an excess of particles seems to always remain. USAXS results also show that Pickering emulsions were densely coated with gold nanoparticles achieving surface coverage that is near the close-packing limit. Interestingly, the boiling point of the core oil did not correlate with changes to the cavitation threshold or with surface coverage of the synthesized Pickering emulsion. However, this parameter did affect the final droplet size distribution and the volume fraction of Pickering emulsion droplets remaining in the system.

The main finding of this report is that structural changes could be correlated to cavitation events and that spontaneous particle adsorption did not occur in any case. This finding is extremely pertinent when designing Pickering emulsion systems for use in applications such as medical contrast agents, cosmetics and/or consumer products. Interestingly, cavitation events were detected at similar pressures regardless of the emulsion boiling point. Two potential mechanisms were also proposed to describe how different cavitation sources could induce adsorption of amphiphilic gold nanoparticles onto emulsion surfaces. Future experiments include the use of time resolved SAXS to differentiate between cavitation of the solvent versus the droplet phase.

Glossary

GNP

Polymer-coated amphiphilic gold nanoparticles

PEG-thiol

Thiol-terminated poly (ethylene glycol) methyl ether

FFT

Fast Fourier transforms

SAXS

Small-angle X-ray scattering

USAXS

Ultra-small-angle X-ray scattering

UV-Vis

Ultraviolet-visible spectroscopy

TEM

Transmission electron microscope