SUMMARY
Optical recordings of neural activity in behaving animals can reveal the neural correlates of decision making, but brain motion, which often accompanies behavior, compromises these measurements. Two-photon point-scanning microscopy is especially sensitive to motion artifacts, and two-photon recording of activity has required rigid coupling between the brain and microscope. We developed a two-photon tracking microscope with extremely low-latency (360 μs) feedback implemented in hardware. This microscope can maintain continuous focus on neurons moving with velocities of 3 mm/s and accelerations of 1 m/s2 both in-plane and axially. We recorded calcium dynamics of motor neurons and inter-neurons in unrestrained freely behaving fruit fly larvae, correlating neural activity with stimulus presentations and behavioral outputs, and we measured light-induced depolarization of a visual interneuron in a moving animal using a genetically encoded voltage indicator. Our technique can be extended to stabilize recordings in a variety of moving substrates.
In Brief
Optically measuring neural activity in behaving animals is complicated by motion artifacts. Rigidly fixing the microscope to the animal perturbs behavior and does not work for small model organisms. Karagyozov et al. demonstrate a two-photon tracking microscope with real-time feedback to record from neurons moving rapidly in three dimensions.
Graphical Abstract
INTRODUCTION
To understand how the brain selects and enacts behaviors, it is desirable to record activity in behaving animals. Optical recording of neural activity is a standard technique in systems neuroscience, but optical measurements in freely behaving animals pose challenges (Hamel et al., 2015; Kerr and Nimmerjahn, 2012). Behavior is expressed as motion, and motion of the brain limits the accuracy of optical imaging techniques. Optical measurement of neural activity requires precisely quantifying light emitted by a fluorescent indicator. Movement of a labeled neuron relative to the microscope objective will alter the efficiency with which the indicator is excited and emissions collected, as will changes in the position or properties of scattering elements between the objective and neuron, resulting in a fluorescence signal that varies due to motion, but not neural activity.
One solution to the problem of brain motion is to rigidly couple the brain to the objective. For example, mice (Dombeck et al., 2010) and adult flies (Seelig et al., 2010) can be head-fixed to the objective while exploring virtual environments controlled by motion of the animal’s legs or wings, or the microscope itself can be mounted on a behaving rodent (Hamel et al., 2015; Sawinski et al., 2009; Zong et al., 2017). Larval zebrafish have been paralyzed and embedded in agar with fictive motion readout through electrical recording of the motor neurons (Ahrens et al., 2012).
Small transparent genetic model organisms are particularly suited to optical interrogation, because indicators may be genetically targeted to neurons of interest and the nervous system is optically accessible without surgery or implantation. These organisms offer the possibility of recording from intact, unrestrained, and freely behaving animals, using feedback to keep the brain centered in a larger imaging volume and ratiometric techniques to correct for motion artifacts, an approach applied most successfully in C. elegans (Faumont et al., 2011; Nguyen et al., 2016; Venkatachalam et al., 2016).
In other transparent organisms, a modified light-sheet technique has been used to locate the positions (but not yet the activities) of neurons in moving Drosophila larvae (Bouchard et al., 2015). Spinning disk confocal microscopy was used to measure population-level activity in newly hatched crawling Drosophila larvae (Heckscher et al., 2015). Extended depth-of-field microscopy (Cong et al., 2017) and structured illumination microscopy (Kim et al., 2017) were used to record from neurons in moving zebrafish, and neural activity has been measured using wide-field fluorescence microscopy in Hydra confined to a plane (Dupre and Yuste, 2017). All these measurements used single-photon fluorescence excitation. This can be problematic; scattering limits imaging in thicker and less transparent models, and the excitation light complicates the simultaneous use of optogenetic reagents while providing an unwanted visual stimulus.
Here, we report a two-photon microscope capable of recording neural activity in freely and three-dimensionally moving intact translucent animals. We apply this microscope to the study of larval Drosophila, an attractive model in which to study circuits that mediate decision making (Larderet et al., 2017; Ohyama et al., 2015; Tastekin et al., 2015). The larva has an optically accessible brain, simple behaviors, a wiring diagram (Berck et al., 2016; Eichler et al., 2017; Larderet et al., 2017), and powerful genetic reagents to label neurons throughout the brain (Jenett et al., 2012; Li et al., 2014). Scattering in the cuticle and viscera and peristaltic contractions that jerk the brain internally in three dimensions (Sun and Heckscher, 2016) have made it difficult to record activity from behaving larvae. We overcome these challenges, recording from targeted motor neurons and interneurons in freely behaving second-instar larvae, demonstrating two-photon cellular recordings of calcium and voltage dynamics in intact and behaving animals without rigid coupling to the microscope objective.
RESULTS
Construction and Testing of the Tracking Microscope
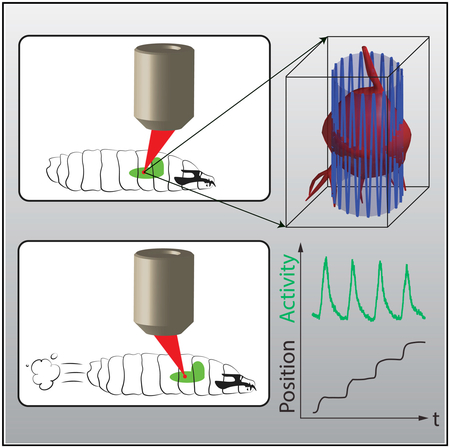
Recording from three-dimensionally moving neurons requires rapidly sampling an extended volume. We first constructed a point-scanning volumetric two-photon microscope (Figure 1A) using an ultrasonic acousto-optic lens (TAG lens) as a resonant axial (z) scanner (Kong et al., 2015). Our ultimate goal was not to form an image of the neurons but to reveal their activities, so instead of imaging a moving brain volume, we decided to track and record only the cell bodies of selected neurons.
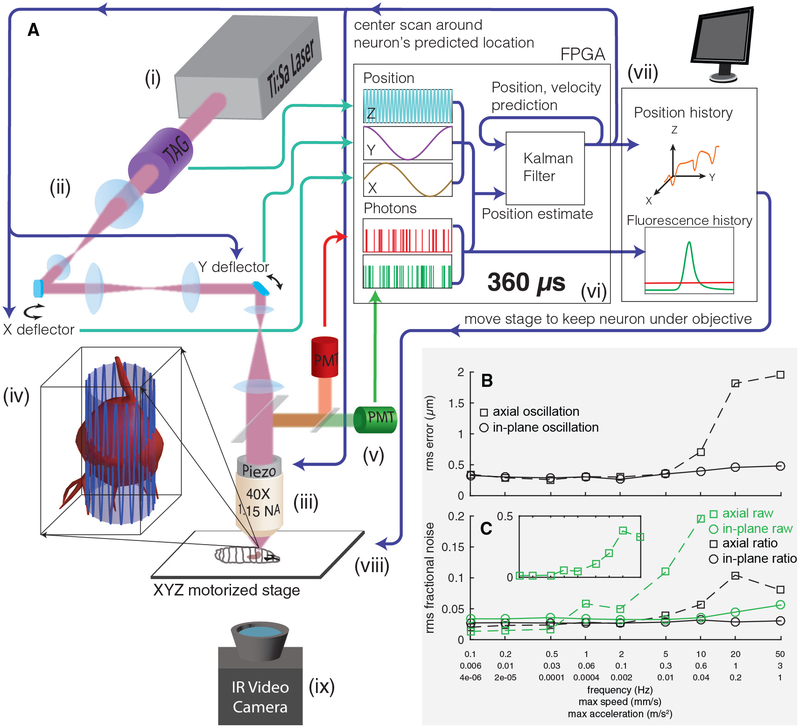
Figure 1. Tracking a Moving Neuron.
(A) Schematic of apparatus. Pulsed infrared excitation light is provided by a Ti:Sa laser (i). Scan optics consisting of two galvanometric mirrors and a resonant ultrasonic lens (ii) shape a wavefront that is relayed on to the back aperture of a piezo-mounted 40× objective (iii), scanning the two-photon excitation focal spot in a cylindrical pattern about a targeted neuron (iv). The scan pattern, schematized by the lightly shaded cylinder and oscillating blue line, has a diameter (7–8 μm) ~75% of that of the targeted neuron. The height of the cylinder (37 μm) has been shortened and the number of z oscillations reduced for clarity. Red and green fluorescence emission is captured by separate photomultiplier tubes (v). A field-programmable gate array (FPGA) (vi) correlates photon emission with focal spot position to create an estimate of the neuron’s location. A Kalman filter integrates all previous estimates to produce a prediction of the neuron’s position and velocity. The predicted center location is updated every 360 μs, and each cylindrical scan is centered on the neuron’s newly predicted location. The predicted position of the neuron and the number of red and green photons counted are sent to a computer (vii), which records data to disk for later analysis and controls a 3-axis stage (viii) to return the neuron to the natural center of the imaging system. A low-magnification infrared (IR) video camera placed below the stage (ix) records the posture of the larva for behavioral analysis.
(B and C) Tracking error (B) and noise in fluorescence (C) versus speed and acceleration. A single neuron was tracked while being oscillated in a 20 μm peak-to-peak sinusoidal wave at varying frequencies, either in the focal plane or axially. Note the logarithmic x axis, which is labeled with the frequency of oscillation (f) as well as the maximum speed (=A ∗ 2πf) and maximum acceleration (=A ∗ (2πf)2). A = 10 μm for all oscillations. See also Figure S1.
We began by tracking and recording from the cell body of a single neuron (Faumont et al., 2011), with plans to extend the tracking scheme to multineuronal and volumetric recording. In larval Drosophila, activity in a single neuron can have profound behavioral consequences (Gepner et al., 2015; Louis et al., 2008; Ohyama et al., 2015; Tastekin et al., 2015), and no method currently exists to reveal such activity in behaving larvae.
We adopted the “tracking fluorescence correlation spectroscopy (FCS)” technique from single-molecule biophysics (Berglund and Mabuchi, 2005; Enderlein, 2000). To track a biomolecule in two dimensions, tracking FCS scans the excitation focus in a circle around the putative location of a labeled target. The fluorescence emission at each point is used to calculate an estimate of the target’s location as well as an uncertainty in that estimate. This estimate is combined with the previous ones to form a new best estimate of the target’s location, and the next circle is executed about this updated location. Several approaches can be used to extend this method to three dimensions (Levi et al., 2005; McHale et al., 2007). We used the TAG lens resonant axial scanner in combination with galvanometric mirrors to create a cylindrical scan pattern (Figure 1A), an approach independently developed for molecular tracking (Hou et al., 2017).
Figure 1A shows a schematic of our tracking scheme. We moved the focus of our pulsed excitation laser in a cylinder 7–8 μm in diameter and 37 μm in height through the soma of the cell. The pulsed laser wavelength of 990 nm excited both GCaMP6f (Chen et al., 2013), a green indicator of neural activity, and hexameric mCherry (Shearin et al., 2014), which provided a stable red baseline for tracking and ratiometric correction. We collected emission from the two proteins on separate PMTs and correlated the photon count rate with the position of the focal spot to calculate both an estimate of the neuron’s position and an uncertainty in that estimate. A Kalman filter (Fields and Cohen, 2011; Kalman, 1960) formed the best estimate of the neuron’s position and velocity given all previous measurements and their errors, and we centered the next scan on the neuron’s newly predicted center location. Each cycle took 360 μs, and the entire process was implemented in hardware using a field programmable gate array (FPGA). We used a piezo objective scanner to maintain the neuron’s axial position near the natural focal plane of the objective, while a slower feedback loop used a 3-axis stage to return the neuron to the center of the field of view. An infrared camera beneath the stage recorded the larva’s motion for behavioral analysis.
To test the tracking device, we created a larva expressing hexameric mCherry and hexameric GFP (Shearin et al., 2014) in anterior corner cell (aCC) and RP2 motor neurons (Pulver et al., 2015) in the larva’s ventral nerve cord (VNC). We immobilized the larva and used a 3-axis piezo stage to oscillate it in a sinusoidal motion with 10 μm amplitude and varying frequencies while tracking a single neuron. Our goal was to test the efficiency of the tracking algorithm for rapid movements, so we disengaged the slower-stage feedback loop.
We measured the spatial accuracy of the tracker versus frequency of oscillation for x (in-plane) and z (axial) sinusoids (Figure 1B). For in-plane motion, the root mean square (RMS) error ranged between 300 and 500 nm up to an oscillation frequency of 50 Hz, the highest we could achieve with our piezo stage. The neuron’s peak speed was over 3 mm/s and the peak acceleration was 1 m/s2, but the tracker was able to follow the neuron’s motion within <10% of the cell-body diameter. For out-of-plane motion, the tracking performance began to degrade at speeds exceeding 0.3 mm/s, but even at the highest speeds, the tracker never lost the neuron and remained within the soma.
We asked how much noise tracking would add to a measurement of neural activity. We calculated the RMS noise in GFP emission in a 0.1–100 Hz bandwidth, divided by the mean emission (Figure 1C). For in-plane motion, the fractional RMS noise ranged from 3% to 7%. For axial motion, the fractional RMS noise increased rapidly for oscillations above 5 Hz, correlating with the increasing positional tracking error. Would ratiometric measurement correct these artifacts? We found the fractional RMS noise in the green/red ratio remained below 5% for in-plane motion and 12% for axial motion.
Tracking multiple neurons (discussed later) requires the ability to rapidly move the focal spot from one neuron to the next. A limit of our galvanometric microscope is that these transitions cannot be achieved quickly, especially for distant neurons. Using acousto-optic deflectors, any two spots within the focal volume of the objective would be equally accessible, and our ability to track multiple neurons would be limited by how frequently an individual neuron must be sampled to maintain a lock. To determine this limit, we disabled photon counting and feedback for a progressively larger fraction of the time (Figure S1). We found that using only 10% of the available time, we were able to maintain a lock on a neuron moving up to 0.6 mm/s.
Recording from a Motor Neuron in a Crawling Larva without Motion Artifacts
To record activity in behaving larvae, we needed to temporarily immobilize each larva to locate the neurons we wished to track. We created a microfluidic device to reversibly hold the larva (Ghannad-Rezaie et al., 2012). When the device was engaged, the larva was immobilized against the coverslip. When the larva was released to allow motion, residual compression held the larva’s dorsal surface against the coverslip to improve optical access; this modestly slowed the larva but allowed normal movements like forward and backward crawling and body bending.
We first recorded from motor neurons in the larva’s VNC. In dissected (Fushiki et al., 2016; Lemon et al., 2015; Pulver et al., 2015) or immobilized (Video S1) animals, these neurons show patterned waves of activity that could represent fictive crawling but at a much lower frequency than actual peristaltic crawling, presumably because needed proprioceptive feedback is missing (Itakura et al., 2015). We reasoned that if we recorded from these neurons in moving animals, then we should see activity that was timed with peristaltic crawling. Indeed, when we recorded from a motor neuron (Figure S2) labeled with GCaMP6f (Chen et al., 2013) in a crawling larva (Figure 2A; Video S2), we found clear peaks of activity coincide with each burst of forward motion.
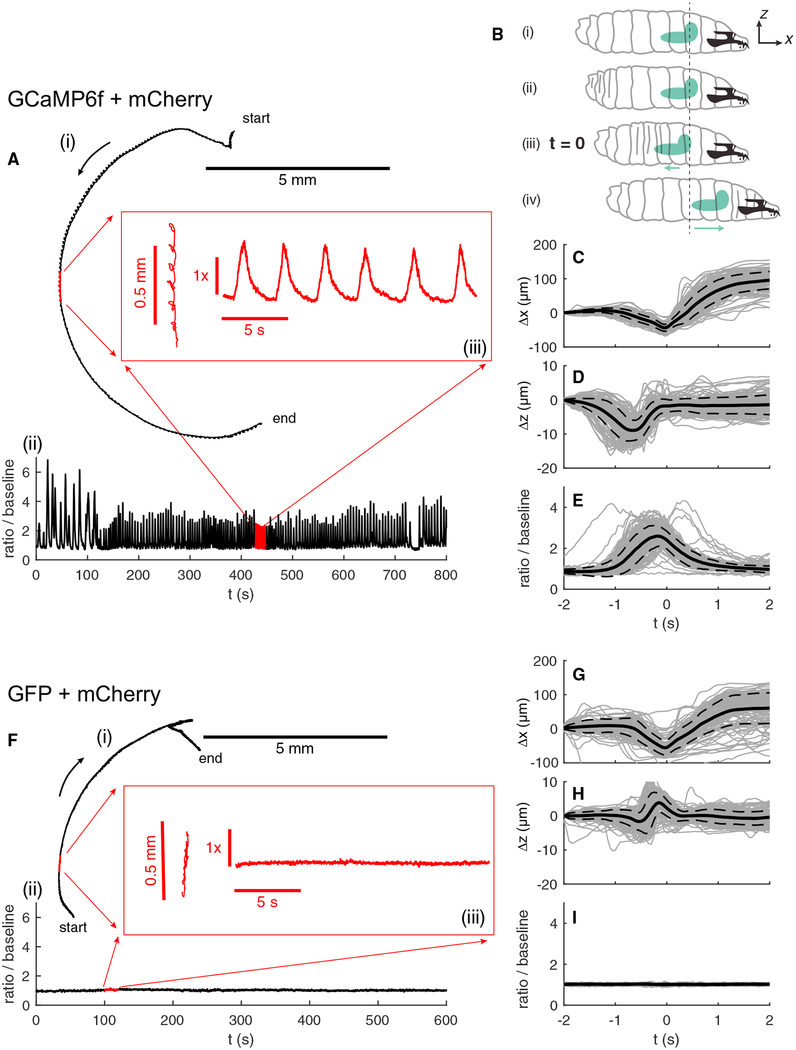
Figure 2. Single Motor Neuron Activity in a Crawling Larva.
(A) Path (i) and activity (ii) of a motor neuron labeled with GCaMP6f and hexameric mCherry. For the first 110 s, the larva was crawling backward. Red inset (iii) shows an expanded view of the path and activity during indicated 20-s time interval.
(B) Sketch of larva’s peristaltic cycle (Sun and Heckscher, 2016). (i) Initial position of the larva and reference coordinate system. (ii) The larva initiates a peristaltic wave with a posterior contraction. (iii) As the wave passes forward, the brain first moves backward toward the posterior.
(C–E)Displacement along the direction of motion (C), axial displacement (D), and ratiometric activity measure (E) of the neuron versus time in peristaltic cycle. t = 0 represents the point in each cycle at which the brain is furthest back. Individual traces are shown in light gray; the mean trace is in solid black, and the dashed lines represent one SD from the mean. Δx and Δz represent displacement in the direction of motion and axially from the position at t = −2 s. n = 135 peristaltic cycles.
(F–I) The same measurements as shown in (A) and (C)–(E), but for a motor neuron labeled with hexameric GFP and hexameric mCherry. (F) corresponds to (A), (G) to (C), (H) to (D), and (I) to (E). n = 130 peristaltic cycles.
In (C)–(E) and (G)–(I), the time at which the brain is furthest back is set to the reference time t = 0. (iv) The brain and anterior of the larva move forward together as the larva completes the peristaltic cycle.
If the motor neuron’s activity is responsible for coordinating peristalsis, we expected the activity to be phase-locked to the motion. With each peristaltic cycle, the brain first moves backward (and down slightly) before accelerating forward (Sun and Heckscher, 2016). We chose the point at which the brain is furthest back as a marker of a particular point in the peristaltic cycle (Figure 2B) and aligned both the motion of the neuron and the ratiometric activity measure to this time point (Figures 2C–2E). The activity is coherent and phase-locked to the forward motion.
Peristaltic crawling moves and deforms the brain as well as the cuticle and intermediate viscera. Could the observed changes in fluorescence ratio be due to an artifact associated with this motion? As a control, we made similar measurements in larvae whose motor neurons were labeled with hexameric GFP and hexameric mCherry. GFP fluorescence is not sensitive to calcium concentration, so if the oscillations we observed in GCaMP6f-expressing neurons reflected calcium dynamics, then we expected them to be absent in GFP-expressing neurons. Indeed, we found the ratio of GFP to mCherry emission to be stable throughout the movement (Figures 2F–2I; Video S3).
Sequential Recordings from Motor Neurons in the Same Crawling Larva Reveal Activity Timed to Behavior
Next, we explored how the timing of activity in VNC motor neurons varied with position. We immobilized the larva, selected a single neuron to track, released the larva to record both behavior and activity (Figures 3A and S2), and then repeated the cycle with a new neuron (4 total in the same animal).
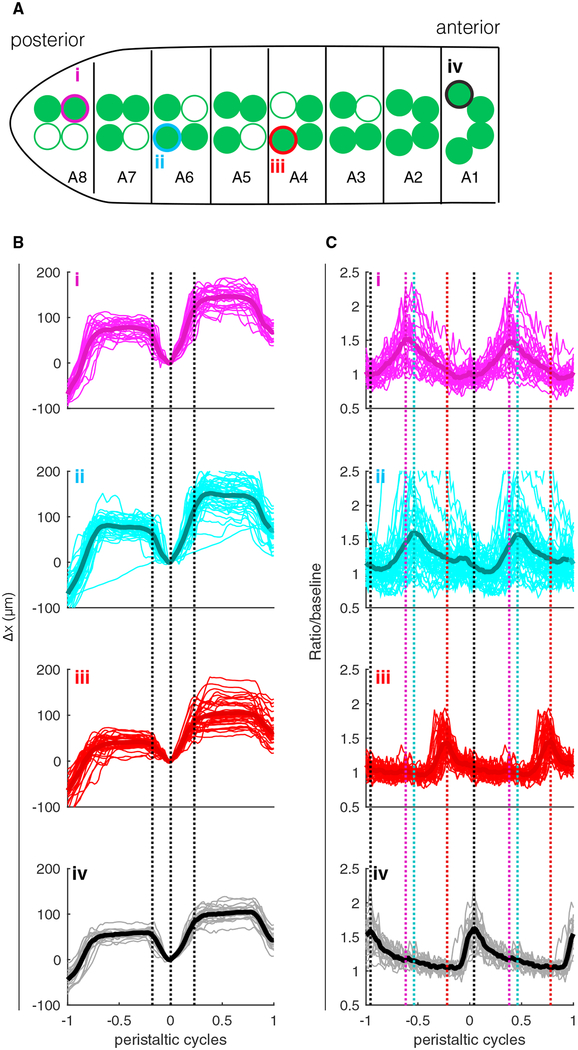
Figure 3. Serial Measurements of Motor Neuron Activity throughout the VNC of Single Larva.
(A) Sketch showing the locations in the VNC of motor neurons chosen for tracking; color and roman numerals match the labels in (B) and (C). A8–A1 label segments based on observed positions of cell bodies. Open circles indicate cell bodies were not visible in epifluorescence image.
(B and C) Position of the neuron along the direction of travel (B) and ratiometric activity measure (C) aligned to peristaltic cycle. On the horizontal axis, 0 represents the time at which the brain was furthest back in a given cycle, and −1 and +1 represent the times at which the brain was furthest back in the previous cycle and next cycle, respectively. The typical peristaltic period was 6–10 s. Light lines represent individual traces, and thick lines represent the mean. In (B), black dashed lines show the points of maximal average acceleration for all traces together and are meant to highlight the stereotypy of the aligned motion pattern between traces. In (C), the colored dashed lines show the points of maximum activity for the corresponding traces and are meant to aid comparison of the peak locations between traces. From top to bottom, n = 26, 43, 35, and 20 peristaltic cycles.
See also Figures S2 and S3.
We sought to determine whether the neurons fired at different points in the peristaltic cycle. As for the single-neuron experiment shown in Figure 2, we aligned the temporal axis with t = 0 at the point in the peristaltic cycle where the brain was furthest back. We expected both the motion and the activity to be more naturally tied to the local peristaltic period than to a global clock, so to allow comparison between neurons as this period varied, we further aligned the temporal axis so each peristaltic cycle took 1 unit of time.
When we performed this alignment, we found each of the 4 neurons moved in the same stereotyped pattern (Figure 3B) but that each neuron was most active at a different point in the peristaltic cycle, with more posterior neurons active earlier (Figure 3C).
In these and some later experiments, we used higher excitation power to selectively bleach the red fluorescence of neurons near the tracked ones. This eased identification of the tracked neuron in epifluorescence images and eliminated a rare failure mode of the tracker—the tracker “jumping” from the targeted neuron to a neighbor. Selective bleaching is only a convenience and was not used in several of the experiments presented here (Figures 2, 5C, 6A–6C, and 6H). Nevertheless, bleaching off-target neurons is useful, especially when confronted with “dirty” lines or clusters of neurons of the same lineage that are difficult to distinguish genetically. We therefore sought to determine whether acute photobleaching of a small population of neurons had detectable adverse effects.
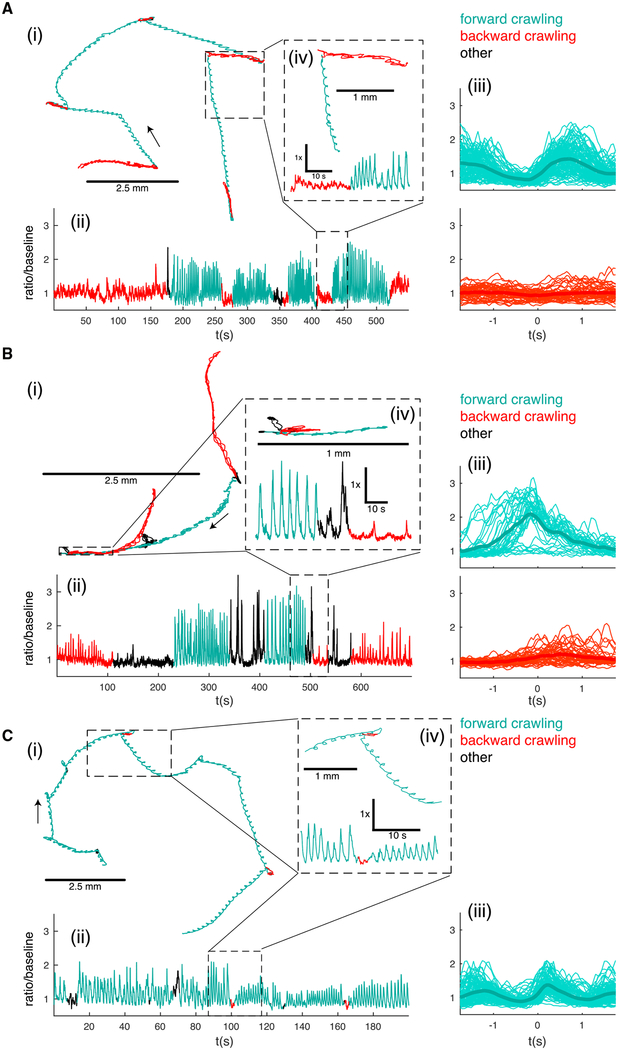
Figure 5. A27h Premotor Interneurons Recorded in Larvae Crawling Forward and Backward.
(A) Path (i), activity (ii), and activity aligned to forward and reverse peristaltic cycles (iii) of an A27h premotor interneuron located at the posterior of the VNC (A8 segment). The inset (iv) shows an expanded view of the path and activity for a backward to forward crawling transition (inset time = 48 s, 24 s each backward and forward crawling). n = 114 forward cycles and 51 reverse cycles.
(B) Path (i), activity (ii), and activity aligned to forward and reverse peristaltic cycles (iii) of a more anterior A27h premotor interneuron (A1 segment). The inset (iv) shows an expanded view of the path and activity for a forward to backward crawling transition (inset total time = 75 s, 30 s forward, 15 s body bend and hunch, 30 s backward). n = 38 forward cycles, 46 reverse cycles.
(C) Path (i), activity (ii), and activity aligned to forward peristaltic cycles only (iii) of a more anterior A27h premotor interneuron (A1 segment) in a larva crawling on an agar coated coverslip without contact to the dorsal surface. The inset (iv) shows an expanded view of the path and activity for a selected 30-s period. n = 108 forward cycles.
The behavioral state of the animal is indicated by color (red for backward crawling, teal for forward crawling, and black for other behaviors, like pausing and bending the body without either forward or backward movement). (iii) t = 0 is the time when the brain is closest to the tail. Light lines represent individual traces; thick lines represent mean. See also Figure S2 and Videos S5, S6, S7, and S8.
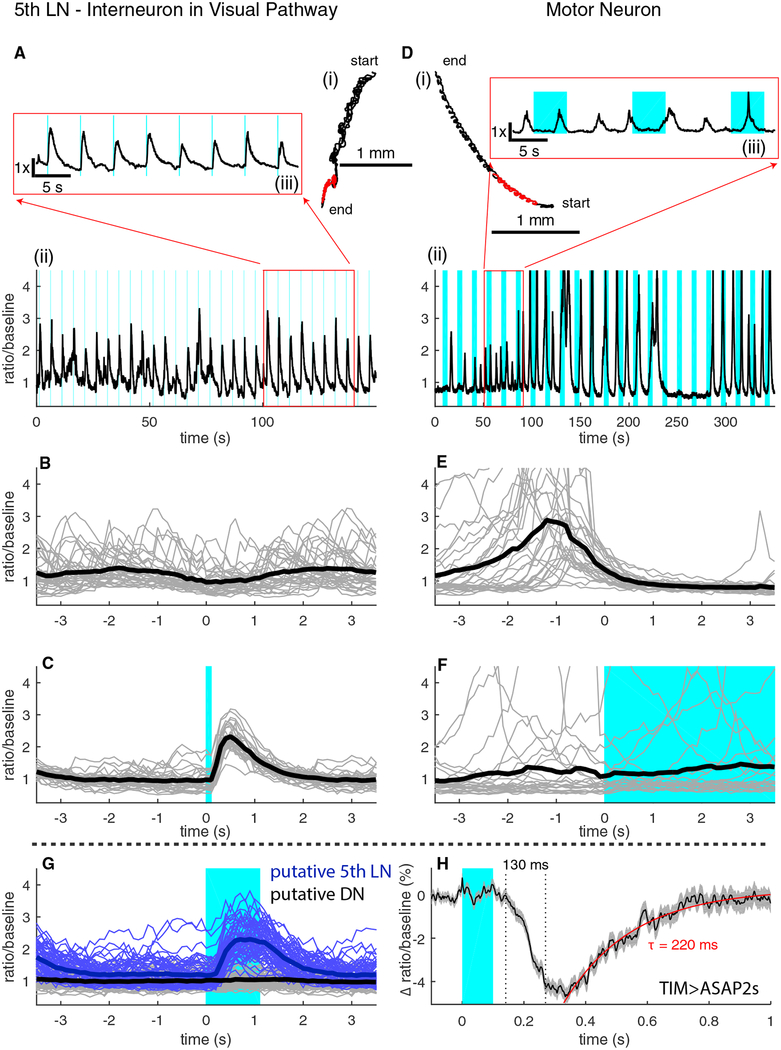
Figure 6. Recording Activity from an Interneuron in the Visual System.
(A) Trajectory (i) and ratiometric activity measure (ii) of the 5th LaN. The inset (iii) shows the activity for the highlighted portion of the track.
(B) Activity of the 5th LaN temporally aligned to the peristaltic cycle.
(C) Activity of the 5th LaN aligned to the onset of blue light stimulus (n = 30 light presentations).
(D) Trajectory (i) and ratiometric activity measure (ii) of an aCC/RP2 motor neuron. The inset (iii) shows the activity for the highlighted portion of the track.
(E) Activity of the motor neuron temporally aligned to the peristaltic cycle (n = 30 peristaltic cycles).
(F) Activity of the motor neuron aligned to the onset of the blue light stimulus (n = 23 light presentations).
(G) Simultaneous recording in a moving larva from two TIM-expressing neurons, aligned to the onset of the light stimulus (n = 61 light presentations).
(H) Voltage measurement in a moving larva. Graph shows mean and SEM in the change in the ratio of ASAP2s to hexameric mCherry fluorescence. ASAP2s decreases in brightness with increasing internal voltage (n = 400 light presentations).
In (B), (C), and (E)–(G), light lines represent individual traces, and thick lines represent mean. In all panels, shaded blue regions indicate visual stimulus presentation. See also Figure S5.
We reasoned that as the motor neurons form part of a rhythmic motor circuit, defects in motor neuron function would be most apparent as disruptions in the frequency of peristaltic crawling. We measured the frequency of peristaltic crawling using machine vision software (Gershow et al., 2012) before and after photobleaching a section of the VNC (Figure S3). The peak frequency of forward peristalsis was unchanged, indicating that any changes in the function of the motor circuit due to the bleaching were too subtle for us to detect.
Simultaneous Recording from Two Motor Neurons Reveals Exact Timing Differences and Confirms the Tracker’s Spatial Accuracy
It would be preferable to record from neurons simultaneously rather than rely on synchronization via a behavioral clock. To follow two neurons at a time, we programmed the microscope to execute four cylindrical tracking cycles around a neuron to update its position and sample its activity, then move to a nearby neuron and follow it for four cycles before jumping back. We allowed two cycles (720 μs) for travel time between the two neurons, so the tracker was active two-thirds of the time, one-third on each neuron.
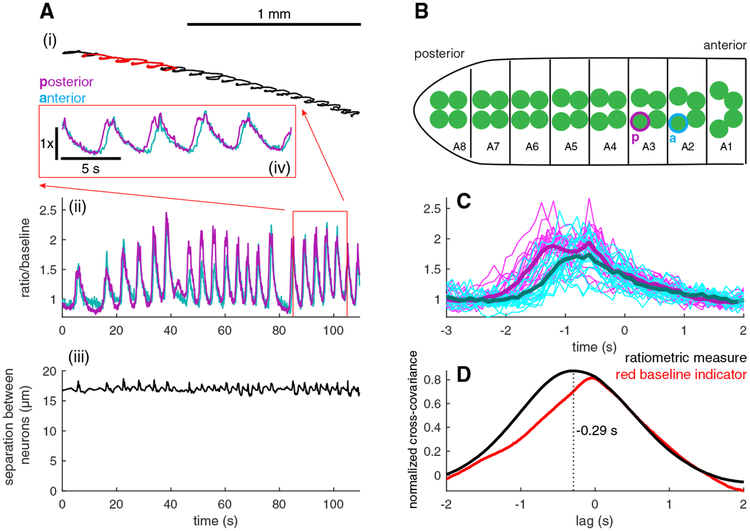
Figure 4A and Video S4 show recordings of position and activity made from two VNC motor neurons (Figures 4B and S2) in a larva crawling forward. To confirm the quality of the tracking, we measured the distance between the two neurons. If the tracker imprecisely found the positions of the two neurons, then the distance between would vary by an amount corresponding to the error in location. We found the distance between the two neurons remained nearly constant (mean, 17.0 μm; SD,0.4 μm), indicating the same two neurons were tracked continuously and precisely (Figure 4A).
Figure 4. Simultaneous Tracking and Measurement of Activity from Motor Neurons in Adjacent Segments.
(A) Trajectory of the midpoint between two tracked neurons (i), ratiometric activity measure (ii) for each neuron, and measured distance between neuron centers (iii) versus time. The inset (iv) shows the activity measures for the two neurons for the highlighted portion of the track.
(B) The neuron whose activity is represented by the magenta traces in (A) is posterior to the neuron represented by cyan traces as shown. Sketch indicates the positions in the VNC of the two tracked neurons.
(C) Activities of the two neurons temporally aligned to the peristaltic cycle (light lines represent individual traces, and thick lines represent the mean) (n = 20 peristaltic cycles).
(D) Normalized cross-covariance between the activities (black line) and mCherry emissions (red line) of the posterior and anterior neurons. The ratiometric calcium measure of the posterior neuron leads the anterior by 290 ms, while there is no lag between the mCherry signals.
We aligned both neurons’ activities to the peristaltic cycle and found the more posterior neuron to be active earlier (Figure 4C) in the cycle. To confirm that the posterior neuron led the anterior neuron, we calculated the cross-covariance between the two neurons’ activities (Figure 4D). The location of the maximum of the cross-covariance tells the delay between the two signals.
We found a maximum at τ = −0.29 s, indicating activity in the posterior neuron led the anterior by 290 ms. As a control, we calculated the cross-covariance between the red fluorescent signals of each neuron and found the peak correlation to be at zero lag. Thus, the ratiometric measure of activity in the posterior neuron leads the anterior neuron because the calcium transients in the posterior neuron lead those in the anterior and not due to motion artifacts.
Activity in a Premotor Interneuron Correlates with Behavioral State
We sought to further explore the utility of combined measurements of activity and behavior in the larva. Recent work (Fushiki et al., 2016) has identified A27h, an excitatory premotor inter-neuron, as an important component of the circuit coordinating peristaltic motion. Imaging in a dissected preparation showed that activity in the A27h neuron coordinates with waves of motor neuron activity propagating from posterior to anterior but that the neuron is silent when waves propagate in the reverse direction. A27h receives direct input from 3 peripheral neurons, including the proprioceptor abdominal posterior ventral multidendritic neuron (vpda); these peripheral neurons also make axo-axonic contact with the larval GABAergic dorsolateral (GDL) neuron, a strong inhibitory input to A27h (Fushiki et al., 2016). In the isolated CNS preparation, all of these peripheral inputs are removed, and we wondered if A27h might function differently in an intact crawling larva receiving proprioceptive feedback.
We recorded from A27h interneurons in larvae exploring our microfluidic device. We used sudden changes in the compression applied by the device as a stimulus to encourage transitions between forward and backward crawling and were able to observe multiple transitions while recording from a posterior (A8) A27h interneuron (Figures 5A and S2; Video S5). The neuron was active in sync with the peristaltic cycle during forward, but not backward, crawling, in agreement with the isolated CNS recordings (Fushiki et al., 2016) We recorded from an A27h inter-neuron in a more anterior segment (A1) and found it too was active selectively during forward peristalsis (Figures 5B and S2; Video S6). We aligned the activities of the neurons to brain motion during peristalsis (Figures 5A and 5B) and found during forward motion that the posterior neuron was active earlier in the cycle than the anterior one. As in the dissected prep, A27h neurons in moving animals encode crawling direction and phase of the peristaltic cycle, supporting the identification of waves of VNC activity in dissected animals as fictive crawling.
Recording from a Completely Uncompressed Larva
Most behavioral assays study larvae crawling on agar with no mechanical contact to their dorsal surfaces. We sought to demonstrate that our microscope could record from similarly situated animals. We created a modified microfluidic device with a 300 μm deep central well and capped this device with a glass slide coated with a thin (~150 μm) layer of agarose gel on to which we placed a larva. We applied compression to the larva to identify neurons, but upon release, the larva was free to crawl on the gel with its ventral surface toward the microscope objective and no contact to its dorsal surface. To show that neither dorsal compression nor bleaching of off-target neurons is necessary for the function of our microscope, we performed this experiment without photobleaching prior to tracking.
We recorded from an A27h interneuron in A1 (Figure S2) while the larva explored the agar-coated coverslip (Figure 5C; Videos S7 and S8). To make sure that the dorsal surface remained completely unperturbed, we did not attempt to induce reversal by manipulating the microfluidic device, and the larva initiated only two individual reverse waves, during which the interneuron appeared to be silent. The frequency and speed of forward peristalsis were similar to those of larvae crawling on agar gels used in behavioral assays. The peak velocity of the tracked neuron routinely exceeded 1 mm/s, demonstrating that rapid tracking can be achieved in behaving subjects.
Compared to recording from a lightly compressed larva, we observed a greater motion-correlated coincident fluctuation in the red and green fluorescence channels (Figure S4); this fluctuation was corrected by ratiometric measurement. With dorsal compression (Figure 5B), the A1 interneuron showed greater activity peaks and the forward motion of the brain occurred later relative to the neuron’s activity peak, likely because dorsal contact increased the effort required to contract a segment and delayed the translation of muscle activation to motion.
Light-Evoked Calcium and Voltage Responses of an Interneuron in the Visual Pathway
Behavioral responses to stimuli are often variable, even when the stimulus itself is precisely repeated. Understanding the neural basis of this variability requires simultaneous measurement of the activity and behavior. Larval Drosophila’s variable response to visual stimuli has been studied in the context of uni- and multi-sensory decision making (Kane et al., 2013; Gepner et al., 2015; Keene et al., 2011; Scantlebury et al., 2007). Because the larva is clear and the visual organ is located in close proximity to the brain (Keene et al., 2011; Sprecher et al., 2011), optically probing visual circuits in behaving larvae requires multiphoton tracking microscopy.
The “5th LaN,” an interneuron innervating the larval optical neuropil (Larderet et al., 2017) and required for light avoidance, responds to blue light presentation to the larval visual organ (Kane et al., 2013; Keene et al., 2011). To demonstrate our microscope’s ability to record activity encoding visual cues in behaving animals, we recorded from the 5th LaN while presenting short pulses of blue light to a freely moving larva (Figure 6A and S5). We expect that because the 5th LaN is early in the visual pathway, its activity should encode the light stimulus and not motor output. We aligned the activity of the neuron to its motion (as in Figure 2) and found little variation in the mean activity versus the time within the peristaltic cycle (Figure 6B), showing that the measured activity of the neuron does not reflect the larva’s peristaltic motion. Aligning the activity of the neuron to the onset of the blue light stimulus, on the other hand (Figure 6C), shows a consistent response to light presentation.
The measured response of the 5th LaN to blue light is temporally displaced from the light presentation and of longer duration (Figure 6C), so it is unlikely that this measurement reflects crosstalk from the stimulus presentation. As a further control, we recorded from a motor neuron while presenting long light pulses (Figure 6D). In contrast to the visual interneuron, the motor neuron’s activity was correlated with motion (Figure 6E) but did not reflect the stimulus presentation (Figure 6F).
Our ability to simultaneously record from neighboring neurons allowed an additional control. We recorded simultaneously from the nearby cell bodies of two neurons labeled by tim-Gal4;crygal80 (one light responsive and one not). Based on the positions of these two neurons’ cell bodies (Figure S5), we believed them to be the 5th LaN and one of the DN2 neurons, which are known not to respond to light. One of the neurons responded reliably to blue light presentation, while the other showed no response to light stimulation (Figure 6G). That the ratiometric measure revealed a light-evoked calcium transient in only one of the neurons cannot be explained by motion artifact or stimulus crosstalk.
Voltage Recording in a Freely Moving Animal
The high sampling rate of our tracking microscope makes it particularly suitable for use with optical indicators of transmembrane voltage. We asked whether we would be able to measure voltage transients in freely behaving larvae. We co-expressed the voltage indicator ASAP2s (Chamberland et al., 2017) with hexameric mCherry in neurons labeled by tim-gal4;cry-gal80. We then presented a repeating blue light stimulus (100 ms on, 925 ms off) to an unrestrained larva crawling on an agar-coated coverslip while we tracked and recorded the fluorescence of an LaN cell body. As with other examples of in vivo voltage measurements in Drosophila (Chamberland et al., 2017), we aggregated the responses to repeated stimulus presentation to increase the signal-to-noise ratio.
We found an average change in fluorescence ratio (ASAP2s decreases in brightness in response to depolarization) of 4.5% beginning 140 ms after stimulus onset (Figure 6H). Full depolarization took ~130 ms, and the ratio decayed exponentially with a time constant of 220 ms. In trial-averaged measurements of the axon terminals of adult L2 visual neurons, a change of 5% was observed with a time to peak of 70 ms and an exponential decay constant of 110 ms (Chamberland et al., 2017). The difference in time constants may be due to measurement in axon terminals versus the cell body or in faster temporal processing in the adult visual system.
DISCUSSION
Comparison to Previous Work in the Larva
Several attempts have been made to adapt technology developed for recording neural activity in other organisms to the larva. A tracking microscope operating according to similar principles to the Berg bacterial tracker (Berg and Brown, 1972) was used to record neural activity in freely behaving C. elegans but only demonstrated to follow the positions (without activity readout) of neurons in behaving Drosophila larvae (Faumont et al., 2011). Swept confocally-aligned planar excitation (SCAPE) microscopy was used to record neural activity in head-fixed mice but in larvae was only demonstrated to follow the positions of peripheral neurons (Bouchard et al., 2015). A spinning disk confocal microscope with three dimensional motion tracking was used to record from a significant fraction of the neurons of a movingC. elegans but in larvae was only able to record the responses of peripheral thermosensory neurons to temperature changes “during a bout of spontaneous quiescence” (i.e., when the larva was not moving; Venkatachalam et al., 2016).
In a larger work exploring the role of Eve+ interneurons in generating body bends, spinning disk confocal microscopy was used to visualize thermogenetically (TRPA1) induced activity of a population of ~80–100 interneurons in a newly hatched crawling larva (Heckscher et al., 2015). Brief epochs were chosen when the measured fluorescence intensity of the left half of the VNC decreased while the fluorescence intensity of the right half increased. During these epochs, the larva’s tail moved to the left. Activity was not measured during forward crawling. Left-right switches in fluorescence intensity were never observed in an isolated CNS preparation, and as no controls against motion artifacts were presented, it is impossible to assess what fraction of the observed fluorescence change in the free larva was due to motion. Discounting possible motion artifacts, what was presented in that work—short and intermittent measurement of the combined activities of ~100 TRPA1-driven neurons in a newly hatched larva—is very different from what we show in this work: continuous monitoring of innate activity with cellular resolution and high signal-to-noise ratio in freely behaving second-instar larvae over durations of minutes and distances of centimeters.
Advantages of Two-Photon Tracking Microscopy
Optical recordings in transparent model organisms offer the potential to understand how neural dynamics encode and process information. Away from the sensory periphery, as neurons’ roles shift from processing sensory input to controlling behavioral responses, activity recorded in an immobilized animal becomes progressively harder to interpret. Here, we show that it is possible to make two-photon recordings of neural activity at cellular resolution in an intact freely behaving transparent model organism. Our two-photon tracking microscope will allow measurement in a wide range of behaving visually responsive semi-transparent animals, including larval Drosophila, larval Platynereis (Randel et al., 2014), and Hydra (Dupre and Yuste, 2017).
As they develop, translucent animals become larger and less transparent, rendering two-photon excitation a necessity for imaging throughout the interior. Most of the reagents for sparsely labeling neurons in the larval CNS have been characterized in later developmental stages (Li et al., 2014), so it is desirable to conduct experiments in more developed larvae. Two-photon excitation helps avoid cross-talk with optogenetic reagents and potential effects of phototoxicity and eliminates a confounding visual stimulus from visible excitation light (Dupre and Yuste, 2017).
The ability to precisely locate fiducial markers in moving tissue has applications beyond measurement of neural activity, for instance in targeting optogenetic stimulation to specific neurons. In both calibration experiments (Figure 1B) and behaving animals (Figure 4A), we tracked moving neurons with a measured spatial precision of better than half a micron. Despite continuously focusing on a single neuron for extended periods, we did not find photobleaching to interfere with tracking or measuring activity.
Tracking Many Neurons and Volumetric Imaging in Moving Animals
Our ability to simultaneously track more than two neurons was limited by the need to physically move the mirrors to move the focal spot from one neuron to the next. However, we could maintain focus on a single neuron using only one-tenth of the microscope’s tracking time (Figure S1), indicating that with non-inertial scanners, we could track 10 separated neurons simultaneously. Combining non-inertial scanning with a tracking algorithm that used correlations in the neurons’ motions would allow us to follow an arbitrarily large number of labeled neurons as long as they were all contained within the same focal volume and well separated from each other.
To record from densely labeled tissue or from amorphous neuropil, we would track fiducial markers to establish a stable coordinate system and carry out volumetric imaging with respect to this coordinate system. Our tracking algorithm can be adapted to provide real-time three-dimensional motion correction in random access microscopy. True three dimensional random access microscopy (Duemani Reddy et al., 2008; Nadella et al., 2016; Szalay et al., 2016) is technically involved, but a hybrid solution using acousto-optic x-y scanning and a TAG lens for resonant z scanning would be more straightforward to implement.
STAR★METHODS
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental Models: Organisms/Strains | ||
| w[1118];20XUAS-IVS-GCaMP6f | Bloomington Stock Center | 42747; RRID: BDSC_42747 |
| y[1]w[*];Sp/CyO;20XUAS-6XmCherry-HA | Bloomington Stock Center | 52268; RRID: BDSC_52268 |
| y[1] w[*]; 20XUAS-6XGFP/CyO | Bloomington Stock Center | 52261; RRID: BDSC_52261 |
| w;+;RRAF-Gal4, UAS-GCaMP6f | Stefan Pulver, University of St Andrews | N/A |
| y[1] w[*];;eve-GAL4.RRK/TM3, Sb | Bloomington Stock Center | 42739; RRID: BDSC_42739 |
| Cry-Gal80;A3(tim-Gal4) | Simon Sprecher, University of Fribourg | N/A |
| GMR36G02-GAL4 | Bloomington Stock Center | 49939; RRID: BDSC_49939 |
| w[1118]/Dp(1;Y)y[+]; CyO/Bl; TM2/TM6B, Tb | Bloomington Stock Center | 3704; RRID: BDSC_3704 |
| w[*]; P{y[+t7.7] w[+mC] = 20XUAS-ASAP2s}attP40 | Bloomington Stock Center | 76246; RRID: BDSC_76246 |
| yy[1] w[*]; wg[Sp-1]/CyO, P{Wee-P.ph0}Bacc[Wee-P20]; P{y[+t7.7] w[+mC] = 20XUAS-6XmCherry-HA}attP2 | Bloomington Stock Center | 52268; RRID: BDSC_52268 |
| Software and Algorithms | ||
| HelioScan | Langer et al., 2013 | https://github.com/HelioScan/HelioScan |
| Modified HelioScan | this paper | https://github.com/GershowLab/HelioScan |
| MAGAT Analyzer | Gershow et al., 2012 | https://github.com/samuellab/MAGATAnalyzer |
| MATLAB | Mathworks | |
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Marc Gershow (marc.gershow@nyu.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Fly strains
The following fly strains were used:
w[1118];20XUAS-IVS-GCaMP6f (Bloomington Stock #42747)
y[1]w[*];Sp/CyO;20XUAS-6XmCherry-HA (Bloomington stock #52268)
y[1] w[*]; 20XUAS-6XGFP/CyO (Bloomington stock #52261)
w;+;RRAF-Gal4, UAS-GCaMP6f (gift from Stefan Pulver, University of St Andrews)
y[1] w[*];;eve-GAL4.RRK/TM3, Sb (Bloomington stock #42739)
Cry-Gal80;A3(tim-Gal4) (gift from Simon Sprecher, University of Fribourg)
GMR36G02-GAL4 (Bloomington stock #49939)
w[1118]/Dp(1;Y)y[+]; CyO/Bl; TM2/TM6B, Tb (Bloomington stock #3704)
w[*]; Py[+t7.7] w[+mC] = 20XUAS-ASAP2sattP40 (Blooming stock #76246)
yy[1] w[*]; wg[Sp-1]/CyO, PWee-P.ph0Bacc[Wee-P20]; Py[+t7.7] w[+mC] = 20XUAS-6XmCherry-HAattP2 (Bloomington stock#52268)
Crosses
Figures 1 and 2F–2I: w; 20XUAS-6XGFP; 20XUAS-6XmCherry-HA (created from Bloomington stock #52261 and #52268 using#3704 balancer) crossed to eve-GAL4.RRK
Figures 2A–2E and 6D–6F: w;+;RRAF-Gal4,UAS-GCaMP6f crossed to UAS-6XmCherry-HA
Figures 3 and 4 and Video S1: w;+;RRAF-Gal4,UAS-GCaMP6f crossed to w; 20XUAS-GCaMP6f; 20XUAS-6XmCherry-HA(created from Bloomington stock #42747 and #52268 using #3704 balancer)
Figure 5: w; 20XUAS-GCaMP6f; 20XUAS-6XmCherry-HA crossed to GMR36G02-GAL4 (Bloomington stock #49939)
Figures 6A–6C and 6G: w; 20XUAS-GCaMP6f; 20XUAS-6XmCherry-HA crossed to Cry-Gal80;tim-Gal4*
Figure 6H: w; ASAP2s/CyO; 20XUAS-6XmCherry-HA/Dr (derived from stocks 52268 and 76246) crossed to Cry-Gal80;tim-Gal4* - larvae were hand selected for expression of both fluorescent proteins.
*in our lab conditions, we observed gal4 driven expression of transgenes in the Pdf expressing LaNs as well as the 5th LaN due to incomplete suppression by Cry-Gal80.
F1 progeny of both sexes were used for experiments.
Larvae
Flies were placed in vials and allowed to lay eggs for 24 hours at 25°C on standard cornmeal-based food. Second instar larvae, 48–72 hr AEL, were separated from the food with 30% sucrose solution and washed in water. Larvae were hand selected for size and proper expression of fluorescent proteins prior to use in experiments.
Identification of motor neurons
The lines we used, RRAF-Gal4 and RRK-Gal4 are reported to label aCC and RP2 motor neurons in some conditions and only aCC motor neurons in others (Fushiki et al., 2016; Pulver et al., 2015; Ghannad-Rezaie et al., 2012). We observed labeling of both aCC and RP2 neurons, with some stochasticity in expression. We imaged immobilized RRAF > GCaMP6f,mCherry larvae (same genotype as used in Figures 3 and 4) under a fluorescence dissecting scope (Nikon SMZ18, 1.6x objective) and found that all of these neurons were active during fictive crawling and during constrained movement (Video S1). We did not attempt to differentiate between aCC and RP2 neurons. We identified the segmental locations of motor neurons based on the position of their cell bodies, assuming the most posterior labeled neurons were in A8 (Figure S2).
METHOD DETAILS
Microfluidic device
In order to allow rapid prototyping and more complex device profiles, we used SLA three-dimensional printing to create microfluidic masters for casting (Chan et al., 2015; Comina et al., 2014). Masters were designed in Autodesk Inventor and printed on an Ember three-dimensional printer (Autodesk, USA) using black prototyping resin (Colorado Photopolymer Solutions). After printing, masters were washed in isopropyl alcohol, air-dried, and baked at 65C for 45 minutes to remove volatile additives and non-crosslinked resin. Baked masters were oxygen plasma cleaned for 10 minutes followed by silanization in a vacuum dessicator with 20 μL of trichloro (1H,1H,2H,2H-perfluoro-octyl) silane (Sigma Aldrich) for at least 4 hours. PDMS (Sylgard 184 dow corning, 10:1 base:cure agent) was poured over the master and baked at 75C for 2 hours. This process resulted in reliable curing and release of PDMS from the master.
The microfluidic device uses vacuum compression to achieve reversible immobilization (Ghannad-Rezaie et al., 2012). The device was designed with three sections: a circular section (diameter 9 mm, depth 200 μm), surrounded by an inner ring (inner diameter 9mm, outer diameter 11.5 mm, depth 100 μm) and an outer ring (inner diameter 11.5 mm, outer diameter 13.5 mm, depth 200 μm). The outer ring has a small rectangular channel which is connected via tubing to a vacuum pump. These dimensions were chosen to allow second instar larvae to freely move in the center chamber. The bottom of the PDMS device was bonded to a glass slide for support; a hole was drilled in the slide to allow access for the vacuum connection. A larva was placed into the device along with water for lubrication, then a coverslip was placed on top and held in place using elastic bands (Scunci Girl No Damage Polyband Elastics, Conair Corporation, Stamford, CT). When vacuum is applied to the outer ring, the central chamber is pressed up against the coverslip until the inner ring contacts the coverslip, controlling the compression. When the vacuum is released the larva is free to move, with residual compression serving to keep the dorsal surface in contact with the coverslip (the compression can be fine-tuned by partial release of the vacuum). This process can be repeated without harm to the larva.
For the experiment of Figure 5C: to allow the larva to move completely unrestrained, we extended the depth of our circular chamber to 300 μm and we let the larva crawl ventral side up on an agarose coated coverslip. In this case we fully released the vacuum so that the larva did not touch the chamber on its dorsal side and therefore experienced no pressure on its dorsal side.
To make thin agarose coating we poured hot 4% agarose (Apex, bioresearch products) in water on a coverslip laying flat on the bench. We then pressed a glass slide on top of the coverslip using 100 μm shims as a separation between the coverslip and slide. We allowed for agarose to cool down and then peeled off the coverslip from the glass slide. We measured the resulting agarose films to be between 120 and 180 μm thick. The coated coverslips were stored in a humidified environment until use to prevent agarose from drying out.
Volumetric Two-Photon Microscope
Our volumetric microscope was a custom-built upright microscope with galvanometric mirror-based in plane scanning and resonant axial scanning (Kong et al., 2015). Excitation was provided by a tunable Ti:Sa laser with an 80 MHz repetition rate (Chameleon Ultra II, Coherent, Santa Clara, CA); for all experiments described, the excitation wavelength was 990 nm. Beam power was controlled with a Pockels cell (Model 350, Conoptics, Danbury, CT) between crossed polarizers. The power was adjusted for each sample, but the typical power, as measured at the back of the objective was 16 mW. For the ASAP2s experiment (Figure 6H), the excitation wavelength was 920 nm and the power at the back of the objective was 36.3 mW. The scan optics consisted of a pair of galvanometric mirrors (8310K, Cambridge Technology, Bedford, MA) separated by a 4f relay (2 lenses: f = 100mm, AC508–100-B-ML, Thorlabs, Newton, NJ) followed by scan (f = 40 mm, AC254–040-B-ML, Thorlabs) and tube (f = 200 mm, AC508–200-ML, Thorlabs) lenses. For all experiments described, a 40X, 1.15 NA water immersion objective was used (N40XLWD, Nikon), mounted on a 100 micron piezo scanner (Nano-F 100S, Mad City Labs, Madison, WI).
To add a resonant z scan, we placed a TAG resonant ultrasonic lens (TL25β.B.NIR controlled by TAG Drv Kit 3.2, TAG Optics, Princeton, NJ) before the microscope in a conjugate plane to the scan mirrors. To determine the exact phase of the lens (Kong et al., 2015), we sent a 660 nm laser beam (LP660-SF60, Thorlabs) separated from the excitation laser by dicroic beamsplitters (ZT543rdc, Chroma Technology) in the reverse direction through the TAG lens then through an iris onto a photodiode (DET10A, Thor-labs). The power measured by the photodiode varied with the phase of the lens. We fed the photodiode output into a PLL based on the 74HCT9046A (NXP Semiconductors), the output of which we used to determine the phase of the lens and hence the position of the focal spot in z. The phase shift was fine-tuned by matching the images produced on the “fly-forward” and “fly-backward” portions of the resonant cycle. The lens was operated at a frequency of 70 kHz. For the experiments of Figures 5C, 6H, and S3, the peak-peak amplitude of the axial oscillation was 18.5 μm, and for all other experiments, it was 37 μm, which resulted in quasi-linear axial scan ranges (see discussion in volumetric two-photon microscope software below) of approximately 15 μm and 30 μm respectively.
Emitted photons were separated spectrally from the excitation beam by a dichroic beamsplitter, then separated into a red and a green channel by a filter cube containing a dichroic beam splitter and bandpass filters (ZT543rdc, ET510/80 m, Chroma Technology and FF02–650, Semrock) and then detected by separate PMTs (R9880U-210 and R9880U-20, Hamamatsu) operating in photon counting mode. These elements were all mounted in the Scientifica Multiphoton Detection Unit (MDU, Scientifica, Sussex, UK). PMT pulses were shaped and converted to digital logic levels by the Hamamatsu Photon Counting Unit C9744. Samples were mounted on a 3-axis motor driven stage (FTP-2000 ASI instruments). The microscope was controlled by a Windows PC and a National Instruments PCIe-7842R multifunction DAQ with on-board FPGA running custom software based on HelioScan (see Volu-metric Two-Photon Microscope Software below).
Epifluorescence imaging
To initially locate and identify neurons prior to tracking, we used wide-field epifluorescence imaging through the same objective as used for two-photon imaging. We removed the long-pass dichroic filter in the MDU from the beam path and inserted a mirror between the scan and tube lens to redirect the light path to travel through a filter cube (either MDF-GFP or MDF-TOM, Thorlabs) and on to a CMOS camera (acA2040–90um, Basler). Depending the fluorophore being imaged, excitation was provided via the filter cube by the collimated output of either a blue (M470L3, Thorlabs) or green (M565L3, Thorlabs) led.
Bleach mode
To allow unambiguous identification of tracked neurons in epifluorescence images and to avoid the tracker jumping between adjacent neurons in densely labeled tissue, we found it helpful to photobleach the fluorescent proteins in cells near the one(s) being tracked. To do this easily, we added a “bleach mode” to the microscope in volumetric imaging mode. We first selected the neuron(s) to be tracked and then engaged “bleach mode,” which modulated the Pockels cell voltage to image the surrounding volume using a high excitation power (180 mW, as measured at the back aperture of the objective, versus 16 mW in normal imaging mode) while turning the excitation off completely over the target neurons. Bleach mode was used in advance of tracking for the experiments described in Figures 3, 4, 5A, 5B, and 6G.
Control against circuit defects due to bleaching of motor neurons
In order to determine whether bleaching off-target neurons affects the motor system, we performed a control experiment, measuring the peristaltic frequency in RRAF > GCaMP6f, mCherry larvae before and after bleaching. Second instar larvae were separated from food using 30% w/v sucrose solution. Larvae were stored until use in sucrose solution for at least 15 minutes and up to 4 hours. For each larva: The larva was removed from sucrose, washed in DI water, and transfered to a black agar gel (2.5% w/v agar, 0.75% w/v activated charcoal). The larva was recorded for 10 mins under infrared illumination using a 4 MP global shutter CMOS camera (Basler acA2040–90umNIR, Graftek Imaging) operating at 20 fps and a 35 mm focal length lens (Fujinon CF35HA-1, B&H Photo, New York, NY). We analyzed peristaltic motion via the detected movement of the tail position using the MAGAT Analyzer software (Gershow et al., 2012). We next moved the larva under the two-photon microscope, immobilizing it using the same device we used for tracking experiments and following the usual protocol for pre-tracking bleaching. After locating the VNC using epifluorescence microscopy, we exposed a field of view of 25 μm × 25 μm × 15 μm (3 to 6 aCC/RP2 neurons) to 180 mW (measured at the back of the objective) of 990nm laser light, until the brightness of mCherry was reduced to 1/3 of the initial brightness (~2min). The total immobilization time for each larva was between 6 and 11 minutes. Following treatment, the larva was returned to sucrose solution for 15 minutes, washed, and then transfered to a black agar gel for recording and analysis.
In a second “mock” group, we proceeded as above, expect that during the 2 min “bleach” period, we maintained the excitation power at the level normally used for 2P imaging (22.5 mW measured at the back of the objective). No bleaching was observed during this imaging. For the bleach group, 10 larvae were initially tracked and bleached, and two larvae were lost during handling (n = 8 larvae fully analyzed). In the mock group, 4 larvae were initially tracked and mock bleached, and one larva failed to move after being placed on the agar gel following mock bleaching (n = 3 larvae fully analyzed).
Volumetric Two-Photon Microscope Software
We based our microscope software on the open source Helioscan package written in LabView (Langer et al., 2013). As the TAG lens acts as a resonant axial scanner, we rewrote the FPGA-based resonant scanning package to use the z axis as the fast axis (140 kHz line rate), with the x axis as an intermediate speed (~ 1 kHz line rate), and the y axis as the slowest axis. In order to achieve high volumetric imaging rate, we used all three axes bidirectionally (recording during both the trace and re-trace portion). To overcome the effects of hysteresis, we used the analog outputs of the galvanometer control boards to determine the true position of the focal spot while scanning.
The focus of the system of objective and TAG lens oscillated sinusoidally in time with a frequency of 70 kHz. We divided each oscillation into two scans, one with the focal spot moving away from the objective and one moving toward it. As is standard in resonance scanning, each axial scan was divided into a discrete number of voxels of equal temporal duration, resulting in some distortion due to the nonlinearity of the z position versus time. We used the central 60% of the sinusoidal z scan, meaning that voxels at the extreme of the scan had an axial extent 59% of the voxels in the scan center. For each axial line, the FPGA recorded the x and y position of the galvo (ignoring movement of the galvos during the ~4.2 μs z line duration) and streamed this position along with the photon counts per voxel to the computer. This data was used to assemble image volumes for display or recording. Separate volumes could be formed for the two axial scan directions, allowing us to precisely calibrate a phase delay relative to the TAG lens cycle to bring the two scan directions into alignment.
Tracking Microscope
The tracking algorithm was based on the tracking FCS method (Berglund and Mabuchi, 2006, 2005). The FPGA directed the x and y galvos to move in a circle of defined radius, centered about the predicted location of the center of the neuron being tracked (taking into account the estimated velocity of motion). The galvos followed this circle faithfully, with a phase-lag that dependedon the driving frequency. To correct for the phase-lag, the actual position of the focal spot, as reported by the galvo control boards, was used for all calculations. With each circular scan the FPGA calculated the estimated displacement of the true center of the neuron from the center of the scan (see feedback relations below). To avoid including other cells or autofluorescent background material in the estimate of the neuron’s location or its intensity, only the portion of the resonant scan within ± ~8 μm of the estimated center was used for fluorescence measurement.
The FPGA based tracking algorithm reported the location of the neuron within the focal volume and its velocity and used the mirrors and objective piezo to center the cylindrical scan on the neuron. Feedback to the mirrors was updated with every scan, creating a latency of 360 μs. Fast axial re-centering was accomplished by selecting a portion of the TAG axial scan centered on the neuron’s predicted location, again with a latency of 360 μs. Signals to the objective piezo were lowpassed on the FPGA to 70Hz to fit within the bandwidth of the scanner. A separate PID feedback loop running on the computer moved the stage to return the neuron to the natural focus of the objective. Re-centering commands were sent to the stage every 25 ms.
Feedback Relations
In this discussion and following, x and y represent displacements in the focal plane of the objective and z represents axial displacement. Our cylindrical scan pattern (radius = rscan) was contained radially within the soma and extended axially well beyond the bounds of the neuron. With each cycle, we calculated the sum of all locations where photons were detected and also kept track of the total number of photons.
| (1) |
| (2) |
where tk represents times when photons were detected. We used these sums to estimate (Δx, Δy, Δz), how much the neuron was displaced from the center of the scan, as well as the uncertainty, expressed as a variance, (RΔx, RΔy, RΔz) in this estimate. Derivation of these results, following Berglund and Mabuchi (Berglund and Mabuchi, 2006), is found later in the methods and assumes that the intensity distribution of the neuron is cylindrically symmetric.
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Where I(r) represents the fluorescent labeling intensity averaged along z at a distance r from the center of the neuron, and Izz = ∫z2I(rscan,z)dz/∫I(rscan,z)dz is the second moment of the intensity distribution along the z axis at the scan radius. rscan can be chosen to minimize the x and y measurement error. Noting that Nphoton∝I(r),
| (9) |
| (10) |
| (11) |
at the minimum error location. For a Gaussian intensity distribution, , this minimum is found at and g = 1, recapitulating the result in (Berglund and Mabuchi, 2006). If we consider the neuron to be a uniformly labeled sphere of radius R, , remembering that I(r) represents the z projection of the intensity distribution. In this case, the minimum tracking error is actually found at r = R, an impractical choice. As a compromise between maximizing photon collection and minimizing tracking error, we chose rscan = 3/4R.
Of course, the neuron is not actually a uniformly labeled perfect sphere; the choice of intensity distribution alters only prefactors in the gain applied to the measured center of mass location of each scan and the estimate of the measurement error. In the Kalman filter (algorithm below), these prefactors always appear in combination with quantities dependent on other parameter choices. In practice, we frequently chose g = 1 and adjusted other parameters to assure smooth tracking.
Kalman Filter
With each cycle, we obtained an estimate of the offset of the neuron from the scan location and an uncertainty in this estimate. To combine this series of uncertain measurements, we used a Kalman filter whose model parameters were the position and velocity of the neuron. We treated movement in each axis independently and used a separate filter for each. Along each axis, the state variable was represented as a two dimensional vector, x, the coordinate of the neuron center and v, the velocity along that axis. The uncertainty in the estimate was represented by a covariance matrix, P.
| (12) |
| (13) |
The Kalman filter consists of an update step, which propagates the model forward in time and a measurement step, which updates the model given new measurement data.
Update step
We ran the update step with each FPGA cycle, at 40 MHz. Thus, in deriving the update rules below, we ignore terms of order Δt2 or higher.
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Dx and Dv represent expected diffusion in the position and velocity of the neuron; the smaller these values, the smoother the expected path and the more past measurements are factored in to the current location estimate. Dx and Dv were chosen by a combination of simulation and trial-and-error.
Measurement step
With each complete cycle, we form an estimate of the offset of the neuron from the scan center and the variance in this estimate (see Feedback Relations above). We incorporate the new measurements independently on each axis as follows, with the superscript (−)indicating the pre-measurement-step values.
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
g and are calculated on the computer prior to tracking and passed as fixed parameters to the FPGA. Computation of d−1 requires multiple FPGA cycles; the entire measurement step takes about 1 μs.
The tracker can also be run with a purely spatially diffusive prior. In this case v,Dv,pxv,and pvv are all held fixed to 0. We often chose this mode for the z tracker, as the small range of movement imposed by the spacing between the PDMS and coverslip in the micro-fluidic device limited achievable axial velocities.
Multiple Neuron Tracking
To track two neurons, we tracked the first neuron an integral number of cycles, Ntrack, then switched the target of the scan to the next neuron, waited Ndelay cycles without feedback for the mirrors to reach the new position, and then tracked the second neuron for Ntrack cycles, before switching back and repeating the cycle. For the experiments described in Figures 4 and 6G, Ntrack = 4 and Ndelay = 2, which means each neuron was tracked for 1.43 ms out of every 4.29 ms. While a neuron was not being tracked, we updated its position using the last estimated velocity, but because of limited FPGA resources, we did not update the uncertainty (P). The midpoint between the neurons was used as the input to the stage and objective piezo feedback loops.
Calibration
To carry out the calibration experiments of Figure 1, we immobilized a larva expressing hexameric GFP and mCherry in its motor neurons between a coverslip and a slide mounted on a 3-axis piezo driven stage (MDT630B, Thorlabs). We drove the open-loop controller with a sinusoidal wave from a function generator to generate oscillations with amplitudes of 10 μm, the largest supported by the 20 μm travel of the piezo stage. Because the controller was open-loop, we did not have an independent record of the position of the stage versus time. The amplitude and frequency of the oscillation were determined by our input to the function generator; we fit the phase to the measured path for each oscillation to determine the true location of the neuron versus time. The tracking error (Figure 1B) represents the RMS difference between the measured path and this fit.
In the axial (z) oscillation experiments, the objective piezo scanner lagged behind the tracked position of the neuron by 8 to 13 ms. For oscillations above 10 Hz, this delay comprised a significant fraction of the oscillatory cycle; at 20 Hz, the piezo was 90 degrees out of phase and at 50 Hz, the piezo feedback was 180 degrees out of phase. In these cases, the tracking performance would have been improved by disabling the piezo feedback, but we chose to leave the feedback enabled to match experimental conditions.
Video Recording Behavior
Larvae were recorded from below using a Basler aca640–90um CMOS camera and a 50 mm focal length c-mount lens (MVL50TM23, Thorlabs) used at a greater distance from the sensor for increased magnification. Darkfield infrared illumination was provided by the collimated output of an 850nm fiber coupled infrared led (M850F2, Thorlabs) aimed at an oblique angle from above the larva to penetrate beneath the objective. An 850 nm bandpass filter (FBH850–40, Thorlabs) was placed in front of the lens to attenuate the incoming light from the Ti:Sa laser.
Integrating Blue Light Stimulus
Blue light stimulus was provided by the collimated output of a 450 nm laser (LP450-SF15 Thorlabs) directed from the side above the larva. We inserted a 473 nm longpass filter (LP02–473RU, Semrock) behind the objective to block transmission of this light to the photomultiplier tubes. However, we found that even with filters in place, turning on the blue light increased the green PMT count rate by an amount comparable to the recovered GCaMP6f fluorescence. This signal was likely due to autofluorescence or phosphorescence in the larval tissue, as it required the presence of a larva beneath the objective. We therefore modulated the laser to only turn on when the TAG lens was at the extremes of its focus cycle – a time when we were not using the PMT signals for either measurement or feedback. The combination of filtering and out-of-phase light presentation was sufficient to eliminate cross-talk between the blue light presentation and measurements of neural activity. Timing the stimulus light to the phase of the TAG lens meant that when the stimulus was on, the blue light flickered on and off at 140 kHz, far too fast for the larva to detect.
The approximately 5mm diameter stimulus laser beam had a power density of 0.05 W/m2 measured transverse to the beam. Because the light entered at an oblique angle between the objective and the larva and was subject to scattering and reflection, it is difficult to precisely estimate the power density of the light at the larva’s photoreceptors.
Relation between locations of photon detections and displacement of the neuron
We derive an estimate of the neuron’s position and the uncertainty in this estimate for a cylindrical scan and arbitrary radial intensity distributions, extending the derivation in Berglund and Mabuchi (Berglund and Mabuchi, 2006). We describe the neuron as a distribution of fluorescent label. Given fixed laser power and properties of the microscope optical train, the expected rate at which photons will be captured by the PMTs is a function of the position of the focal spot within the neuron, .
We scan the laser beam in a cylindrical path, , with ω2 ≫ ω1, r0 <rneuron, and ZA ≫ rneuron. The first two coordinates (X,Y) are in the focal plane of the objective and the third z is aligned along the axis. For convenience ω2 is large integer multiple of ω1 (ω2 = 25 ω1 in this work). As the laser beam moves through the sample, we record a sequence of photon arrivals. represents the rate of photon arrivals, where tk is the time of arrival of the kth photon. T(t) obeys Poisson statistics, so
| (28) |
| (29) |
The basis for our estimation of the neuron’s displacement is a calculation at the end of each cycle of the sum of the position of the focal spot at the times when photons were emitted;
| (30) |
The expected value of this sum is given by
| (31) |
| (32) |
We will now calculate how this expected value depends on the displacement of the neuron from the origin of the scan. We will assume that the intensity distribution has cylindrical symmetry, that is . We will first consider a displacement in x (or equivalently y), then a displacement in z. We will consider a scan centered about the origin, with the intensity distribution of the neuron centered a distance Δx away along the x axis.
| (33) |
Because the axial (z) oscillations are much faster than the in-plane rotation of the focal spot, in the above integral, we will replace the intensity I(r,z) with the average intensity over a z-scan at a given radial position
| (34) |
Using this approximation, and assuming a small displacement, Δx ≪ r0, we find
| (35) |
| (36) |
The expected number of photons collected during the scan is . Using this relation, we can define an estimator for the x displacement.
| (37) |
| (38) |
| (39) |
We can now calculate the variance in this estimate, . To do this, we will need to calculate the related quantity
| (40) |
| (41) |
| (42) |
| (43) |
| (44) |
| (45) |
| (46) |
| (47) |
The calculation for z displacement proceeds along similar lines. We again use the fact that the z oscillation is much faster than the rotation to write
| (48) |
We assume that the z scan extends well beyond the neuron; hence the z displacement in time is linear over the portion of the scan with appreciable fluorescence, z≈Zaω2t, and we extend the limits of the integration to infinity.
| (50) |
| (51) |
| (52) |
| (53) |
| (54) |
| (55) |
Following the same methods as for the x computation, we find that
| (56) |
QUANTIFICATION AND STATISTICAL ANALYSIS
Videos of behavior were saved as avi files, and tracking microscope output containing position of the tracker, position of the stage, and photon counts, was written to a text file. At the beginning and end of tracking, the tracker flashed off the infrared illumination used by the video camera, allowing synchronization of the video and the tracker to within the frame rate of the camera. The MATLAB function adapthisteq was used to enhance the contrast of the video images. Data were further analyzed in MATLAB.
The tracker recorded the number of red and green photons collected with each revolution of the spot through a neuron. These counts had significant variation due to Poisson statistics. To estimate the underlying rates, we used a Stochastic Point Process Smoother (Eden et al., 2004) with the following model
| (57) |
| (58) |
| (59) |
where W is the covariance matrix (uncertainty) for the estimates of θ1 and θ2, and Q1 and Q2 represent a prior belief in how rapidly the parameters θ1 and θ2 will change. The ratiometric measure of activity is given by exp (θ2). We chose and , reflecting a belief that the variation in recorded intensity due to factors other than calcium dynamics should be faster than the variation due to calcium dynamics. The choice of Q1 and Q2 sets the bandwidth of the filter, but otherwise has limited impact on the results in this work. Other methods for estimating the ratio, like low-pass filtering the green and red signals then dividing, also produce similar results.
Cross-covariance
The normalized cross-covariance shown in Figure 4D is calculated as
| (60) |
where Δrp(t) and Δra(t) represent the deviation from the mean ratio for the posterior and anterior neurons respectively.
Ratiometric baseline correction
The red and green indicators bleached at different rates, causing a long duration shift in the ratiometric intensity baseline. In a typical recording, after 15 minutes of tracking a single neuron, mCherry fluorescence was 40% of its initial value, and GCaMP6f was not measurably bleached. To correct for this, we found the ratiometric baseline by fitting the ratiometric measure to an exponential function (rbase = a exp (bt)) using a truncated cost function that discards large upward deviations. The baseline corrected ratiometric measure shown in all figures (ratio/baseline) is the instantaneous estimate of the ratio divided by this baseline.
DATA AND SOFTWARE AVAILABILITY
Our modifications to HelioScan (Langer et al., 2013) implementing the tracking algorithm are available on GitHub at https://github.com/GershowLab/HelioScan.
Supplementary Material
Highlights.
Two-photon microscope tracks neurons with submicron and submillisecond precision
Cellular recording of neural activity in intact freely behaving larval flies
Ratiometric calcium and voltage recordings in brain and ventral nerve cord
Correlation of activity with sensory input and behavior
ACKNOWLEDGMENTS
We thank Shy Shoham, Meng Cui, Margarita Kaplow, Marco Tedaldi, and Justin Blau for discussions and Stefan Pulver and Simon Sprecher for strains. M.M.S. participated in the CSHL Neurobiology of Drosophila course with support from a Helmsley Fellowship. This work was supported by NSF award 1455015, NIH award 1DP2EB022359, and a Sloan Research Fellowship to M.G. The following ORCIDs apply to the authors: 0000-0003-2349-5002 (M.M.S), 0000-0001-6611-5941 (A.L), and 0000-0001-7528-6101 (M.G.).
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information includes five figures and eight videos and can be found with this article online at https://doi.org/10.1016/j.celrep.2018.10.013.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Ahrens MB, Li JM, Orger MB, Robson DN, Schier AF, Engert F, and Portugues R (2012). Brain-wide neuronal dynamics during motor adaptation in zebrafish. Nature 485, 471–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berck ME, Khandelwal A, Claus L, Hernandez-Nunez L, Si G, Tabone CJ, Li F, Truman JW, Fetter RD, Louis M, et al. (2016). The wiring diagram of a glomerular olfactory system. eLife 5, e14859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg HC, and Brown DA (1972). Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 239, 500–504. [DOI] [PubMed] [Google Scholar]
- Berglund A, and Mabuchi H (2005). Tracking-FCS: fluorescence correlation spectroscopy of individual particles. Opt. Express 13, 8069–8082. [DOI] [PubMed] [Google Scholar]
- Berglund AJ, and Mabuchi H (2006). Performance bounds on single-particle tracking by fluorescence modulation. Appl. Phys. B 83, 127–133. [Google Scholar]
- Bouchard MB, Voleti V, Mendes CS, Lacefield C, Grueber WB, Mann RS, Bruno RM, and Hillman EMC (2015). Swept confocally-aligned planar excitation (SCAPE) microscopy for high speed volumetric imaging of behaving organisms. Nat. Photonics 9, 113–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chamberland S, Yang HH, Pan MM, Evans SW, Guan S, Chavarha M, Yang Y, Salesse C, Wu H, Wu JC, et al. (2017). Fast two-photon imaging of subcellular voltage dynamics in neuronal tissue with genetically encoded indicators. eLife 6, e25690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan HN, Chen Y, Shu Y, Chen Y, Tian Q, and Wu H (2015). Direct, one-step molding of 3d-printed structures for convenient fabrication of truly 3d pdms microfluidic chips. Microfluid. Nanofluidics 19, 1–10. [Google Scholar]
- Chen T-W, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comina G, Suska A, and Filippini D (2014). PDMS lab-on-a-chip fabrication using 3D printed templates. Lab Chip 14, 424–430. [DOI] [PubMed] [Google Scholar]
- Cong L, Wang Z, Chai Y, Hang W, Shang C, Yang W, Bai L, Du J, Wang K, and Wen Q (2017). Rapid whole brain imaging of neural activity in freely behaving larval zebrafish (Danio rerio). eLife 6, e28158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dombeck DA, Harvey CD, Tian L, Looger LL, and Tank DW (2010). Functional imaging of hippocampal place cells at cellular resolution during virtual navigation. Nat. Neurosci 13, 1433–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duemani Reddy G, Kelleher K, Fink R, and Saggau P (2008). Three-dimensional random access multiphoton microscopy for functional imaging of neuronal activity. Nat. Neurosci 11, 713–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupre C, and Yuste R (2017). Non-overlapping Neural Networks in Hydra vulgaris. Curr. Biol 27, 1085–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eden UT, Frank LM, Barbieri R, Solo V, and Brown EN (2004). Dynamic analysis of neural encoding by point process adaptive filtering. Neural Comput 16, 971–998. [DOI] [PubMed] [Google Scholar]
- Eichler K, Li F, Litwin-Kumar A, Park Y, Andrade I, Schneider-Mizell CM, Saumweber T, Huser A, Eschbach C, Gerber B, et al. (2017). The complete connectome of a learning and memory centre in an insect brain. Nature 548, 175–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enderlein J (2000). Tracking of fluorescent molecules diffusing within membranes. Appl. Phys. B 71, 773–777. [Google Scholar]
- Faumont S, Rondeau G, Thiele TR, Lawton KJ, McCormick KE, Sottile M, Griesbeck O, Heckscher ES, Roberts WM, Doe CQ, and Lockery SR (2011). An image-free opto-mechanical system for creating virtual environments and imaging neuronal activity in freely moving Caenorhabditis elegans. PLoS ONE 6, e24666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fields AP, and Cohen AE (2011). Electrokinetic trapping at the one nano-meter limit. Proc. Natl. Acad. Sci. USA 108, 8937–8942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fushiki A, Zwart MF, Kohsaka H, Fetter RD, Cardona A, and Nose A (2016). A circuit mechanism for the propagation of waves of muscle contraction in Drosophila. eLife 5, e13253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gepner R, Mihovilovic Skanata M, Bernat NM, Kaplow M, and Gershow M (2015). Computations underlying Drosophila photo-taxis, odor-taxis, and multi-sensory integration. eLife 4, e06229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershow M, Berck M, Mathew D, Luo L, Kane EA, Carlson JR, and Samuel ADT (2012). Controlling airborne cues to study small animal navigation. Nat. Methods 9, 290–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghannad-Rezaie M, Wang X, Mishra B, Collins C, and Chronis N (2012). Microfluidic chips for in vivo imaging of cellular responses to neural injury in Drosophila larvae. PLoS ONE 7, e29869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamel EJO, Grewe BF, Parker JG, and Schnitzer MJ (2015). Cellular level brain imaging in behaving mammals: an engineering approach. Neuron 86, 140–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckscher ES, Zarin AA, Faumont S, Clark MQ, Manning L, Fushiki A, Schneider-Mizell CM, Fetter RD, Truman JW, Zwart MF, et al. (2015). Even-Skipped(+) Interneurons Are Core Components of a Sensori-motor Circuit that Maintains Left-Right Symmetric Muscle Contraction Amplitude. Neuron 88, 314–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou S, Lang X, and Welsher K (2017). Robust real-time 3D single-particle tracking using a dynamically moving laser spot. Opt. Lett 42, 2390–2393. [DOI] [PubMed] [Google Scholar]
- Itakura Y, Kohsaka H, Ohyama T, Zlatic M, Pulver SR, and Nose A (2015). Identification of Inhibitory Premotor Interneurons Activated at a Late Phase in a Motor Cycle during Drosophila Larval Locomotion. PLoS ONE 10, e0136660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenett A, Rubin GM, Ngo T-TB, Shepherd D, Murphy C, Dionne H, Pfeiffer BD, Cavallaro A, Hall D, Jeter J, et al. (2012). A GAL4-driver line resource for Drosophila neurobiology. Cell Rep 2, 991–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalman RE (1960). A new approach to linear filtering and prediction problems. J. Basic Eng 82, 35–45. [Google Scholar]
- Kane EA, Gershow M, Afonso B, Larderet I, Klein M, Carter AR, de Bivort BL, Sprecher SG, and Samuel AD (2013). Sensorimotor structure of Drosophila larva phototaxis. Proc. Natl. Acad. Sci. USA 110, E3868–E3877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keene AC, Mazzoni EO, Zhen J, Younger MA, Yamaguchi S, Blau J, Desplan C, and Sprecher SG (2011). Distinct visual pathways mediate Drosophila larval light avoidance and circadian clock entrainment.J. Neurosci 31, 6527–6534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr JND, and Nimmerjahn A (2012). Functional imaging in freely moving animals. Curr. Opin. Neurobiol 22, 45–53. [DOI] [PubMed] [Google Scholar]
- Kim DH, Kim J, Marques JC, Grama A, Hildebrand DGC, Gu W, Li JM, and Robson DN (2017). Pan-neuronal calcium imaging with cellular resolution in freely swimming zebrafish. Nat. Methods 14, 1107–1114. [DOI] [PubMed] [Google Scholar]
- Kong L, Tang J, Little JP, Yu Y, Lämmermann T, Lin CP, Germain RN, and Cui M (2015). Continuous volumetric imaging via an optical phase-locked ultrasound lens. Nat. Methods 12, 759–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langer D, van ‘t Hoff M, Keller AJ, Nagaraja C, Pfäffli OA, Göldi M, Kasper H, and Helmchen F (2013). HelioScan: a software framework for controlling in vivo microscopy setups with high hardware flexibility, functional diversity and extendibility. J. Neurosci. Methods 215, 38–52. [DOI] [PubMed] [Google Scholar]
- Larderet I, Fritsch PMJ, Gendre N, Neagu-Maier GL, Fetter RD, Schneider-Mizell CM, Truman JW, Zlatic M, Cardona A, and Sprecher SG (2017). Organization of the Drosophila larval visual circuit. eLife 6, e28387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemon WC, Pulver SR, Höckendorf B, McDole K, Branson K, Freeman J, and Keller PJ (2015). Whole-central nervous system functional imaging in larval Drosophila. Nat. Commun 6, 7924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levi V, Ruan Q, and Gratton E (2005). 3-D particle tracking in a two-photon microscope: application to the study of molecular dynamics in cells. Biophys.J 88, 2919–2928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H-H, Kroll JR, Lennox SM, Ogundeyi O, Jeter J, Depasquale G, and Truman JW (2014). A GAL4 driver resource for developmental and behavioral studies on the larval CNS of Drosophila. Cell Rep 8, 897–908. [DOI] [PubMed] [Google Scholar]
- Louis M, Huber T, Benton R, Sakmar TP, and Vosshall LB (2008). Bilateral olfactory sensory input enhances chemotaxis behavior. Nat. Neurosci 11, 187–199. [DOI] [PubMed] [Google Scholar]
- McHale K, Berglund AJ, and Mabuchi H (2007). Quantum dot photon statistics measured by three-dimensional particle tracking. Nano Lett 7, 3535–3539. [DOI] [PubMed] [Google Scholar]
- Nadella KMNS, Ro s H, Baragli C, Griffiths VA, Konstantinou G, Koimtzis T, Evans GJ, Kirkby PA, and Silver RA (2016). Random-access scanning microscopy for 3D imaging in awake behaving animals. Nat. Methods 13, 1001–1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen JP, Shipley FB, Linder AN, Plummer GS, Liu M, Setru SU, Shaevitz JW, and Leifer AM (2016). Whole-brain calcium imaging with cellular resolution in freely behaving Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA 113, E1074–E1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohyama T, Schneider-Mizell CM, Fetter RD, Aleman JV, Franconville R, Rivera-Alba M, Mensh BD, Branson KM, Simpson JH, Truman JW, et al. (2015). A multilevel multimodal circuit enhances action selection in Drosophila. Nature 520, 633–639. [DOI] [PubMed] [Google Scholar]
- Pulver SR, Bayley TG, Taylor AL, Berni J, Bate M, and Hedwig B (2015). Imaging fictive locomotor patterns in larval Drosophila.J. Neurophysiol 114, 2564–2577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randel N, Asadulina A, Bezares-Calderón LA, Verasztó C, Williams EA, Conzelmann M, Shahidi R, and Jékely G (2014). Neuronal connectome of a sensory-motor circuit for visual navigation. eLife 3, e02730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawinski J, Wallace DJ, Greenberg DS, Grossmann S, Denk W, and Kerr JND (2009). Visually evoked activity in cortical cells imaged in freely moving animals. Proc. Natl. Acad. Sci. USA 106, 19557–19562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scantlebury N, Sajic R, and Campos AR (2007). Kinematic analysis of Drosophila larval locomotion in response to intermittent light pulses. Behav. Genet 37, 513–524. [DOI] [PubMed] [Google Scholar]
- Seelig JD, Chiappe ME, Lott GK, Dutta A, Osborne JE, Reiser MB, and Jayaraman V (2010). Two-photon calcium imaging from head-fixed Drosophila during optomotor walking behavior. Nat. Methods 7, 535–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shearin HK, Macdonald IS, Spector LP, and Stowers RS (2014). Hexameric GFP and mCherry reporters for the Drosophila GAL4, Q, and LexA transcription systems. Genetics 196, 951–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprecher SG, Cardona A, and Hartenstein V (2011). The Drosophila larval visual system: high-resolution analysis of a simple visual neuropil. Dev. Biol 358, 33–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun X, and Heckscher ES (2016). Using linear agarose channels to study Drosophila larval crawling behavior. J. Vis. Exp 117, e54892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szalay G, Judák L, Katona G,Ócsai K, Juhász G, Veress M, Szadai Z, Fehér A, Tompa T, Chiovini B, et al. (2016). Fast 3d imaging of spine, dendritic, and neuronal assemblies in behaving animals. Neuron 92, 723–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tastekin I, Riedl J, Schilling-Kurz V, Gomez-Marin A, Truman JW, and Louis M (2015). Role of the subesophageal zone in sensorimotor control of orientation in Drosophila larva. Curr. Biol 25, 1448–1460. [DOI] [PubMed] [Google Scholar]
- Venkatachalam V, Ji N, Wang X, Clark C, Mitchell JK, Klein M, Tabone CJ, Florman J, Ji H, Greenwood J, et al. (2016). Pan-neuronal imaging in roaming Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA 113, E1082–E1088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zong W, Wu R, Li M, Hu Y, Li Y, Li J, Rong H, Wu H, Xu Y, Lu Y, et al. (2017). Fast high-resolution miniature two-photon microscopy for brain imaging in freely behaving mice. Nat. Methods 14, 713–719. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.