Abstract
In the present study, we study formation flight with two flying wing configurations. A low speed wind tunnel test is conducted to validate the accuracy of the Computational Fluid Dynamics (CFD). Two optimization procedures are implemented at a high subsonic speed. The free stream Mach number is kept at 0.85, the lead aircraft's angle of attack is 2°, and the following aircraft's angle of attack is 2° as well. The maximum lift-to-drag ratio of the following aircraft is achieved as the lateral spacing is 0.853 b, and the vertical offset is 0.022 b (b is the wingspan). As much as 24.7% induced drag reduction is achieved at the optimized state. A pair of counter-rotating vortices interact and weaken each other. By analyzing the Kriging model constructed in the optimization procedure, it seems that the following aircraft's aerodynamic performance is sensitive to lateral spacing and vertical spacing, but insensitive to longitudinal spacing in close-formation flight. The best drag reduction position places in the following aircraft's wing tip is positioned at the core of the leading aircraft's wing tip vortex.
Keywords: Aerospace engineering, Mechanics
1. Introduction
Birds are usually viewed in formation flight either in an echelon mode or in a lambda mode when they migrate (Wieselsberger, 1914). It is believed that the energy saved when birds are in formation flight at proper positions. Formation flight has also received more and more attention in aviation industry and national defense because it plays a key role in aircraft stealth, especially in fighter groups. Generally, the close-formation flight is always employed for stealth fighter groups, which is able to reduce the Radar-Cross Section (RCS) (Lissaman and Schollenberger, 1970; Weimerskirch et al., 2001). However, there are few reports on near-field close formation flight. Moreover, the reported works are focused on low-speed aircraft such as straight-wing aircraft and the T38 training plane. Recently, the low aspect ratio blended flying wing configuration with a high speed is a promising candidate for the next generation fighter. Compared with a traditional configuration, the Blended-wing-body (BWB) configuration has advantageous lift to drag ratios (Maskew, 1977; Blake and Multhopp, 1998). The BWB configuration has also stealth properties, but the reduction of induced drag performance in the near-field close-formation flight is not explored to date.
Most of the research about the formation flight has concentrated on analytical modeling using potential flow techniques. For instance, Atilla and Sriram put forward a complex model to predict the movement of the following aircraft based on an improved horse-shoe vortex model (Atilla et al., 2005). When comparing wind tunnel test results with predictions from a vortex lattice method, William and David found that the maximum induced drag reduction was over-predicted, which was 25%–40% (William and Gingras, 2004). As an alternative method to the horse-shoe vortex model, the Computational Fluid Dynamic (CFD) becomes a powerful tool for aerodynamics analysis. Since the amount of mesh grids for a close-formation flight case is about 10 million which is possible to be dealt with a common study computer, and it is appropriate to study close-formation flight by solving Navier-Stokes equations. More accurate results than a vortex lattice method could be acquired because the viscosity effect will be considered adequately.
Herein, we utilize the CFD method to optimize the positional parameters of the near-field close-formation flight. A dynamic mesh technique is employed to obtain different formations. The maximum lift-to-drag ratio (K, K=CL/CD, where CL and CD are lift and drag force, respectively.)
Of the following aircraft is identified by using a Kriging surrogate model, which is also can be used to analyze the influence of positional parameters. Moreover, a low speed wind tunnel test is conducted to validate the accuracy of the CFD method.
2. Experimental
2.1. Mesh transformation
To study how the positional parameters impact aerodynamic performance of the following aircraft, the RBF_TFI (Radial Basis Function and Transfinite Interpolation) (Rendall and Allen, 2009) technique, a structured mesh transformation skill for CFD, was used at first to alter the formation parameters, such as longitudinal spacing, lateral spacing and vertical spacing. Two steps are needed in mesh transformation. The first step is radial basis function interpolation, which is dealt with motion of edges of grid blocks. Generally, the control function has the following expression as Eq. (1).
| (1) |
where is grid point's displacement, x is the grid point's coordinates, is coordinates of the grid node which is chosen as basis point of radial basis function, is the distance, N is the number of basis points, is radial basis function, and is interpolation coefficients which can be obtained by a matrix reverse calculation. The radial basis function used in present work is the same as Wendland's C2 (Rendall and Allen, 2009). The second step is to calculate new coordinates of grids that are in the grid blocks. Soni (1985) has introduced a good TFI method based on arc length. This method is used here.
2.2. Optimization method
An efficient global optimization (EGO) method was chosen to conduct optimization procedure. This method is based on a Kriging surrogate model. An expected improvement (EI) function is calculated using the Kriging surrogate model to find the least value and then to get the parameters which most need to be validated. The aerodynamic coefficients are obtained by calculating flow under new formation. This process is repeated until optimization procedure completes. Kriging model has a general expression as Eq. (2).
| (2) |
Where x is designed vector or an independent variable, is regression model, and is fluctuation which simulates deviations to real value. In present work, x is positional-parameter vector, and, the objective function is the following aircraft's lift-to-drag ratio. The EI function points out the searching direction in optimization procedure. Parameters where the EI function has the least value either are the candidates or have the most prediction error. So it is expected that the final positional-parameter vector is not locally optimized but globally optimized. EI function has the following expression as Eq. (3).
| (3) |
where is a predicted lift-to-drag ratio by Kriging model, is the predicted standard deviation of , and is the minimum lift-to-drag ratio which has been validated in that iterative. is cumulative distribution function for Gaussian mixture distribution, and is probability density function for Gaussian mixture distribution. The Mach number (0.9), pitch angle (2°), and Reynolds number (19 millions) are employed as the calculation conditions.
For classic EGO method, one vector or sampling point is obtained in an iterative mentioned above. Generally, the new points that will be validated in iteration may assemble around the optimization point. It brings a problem that the constructed Kriging model has low fidelity in prediction of aerodynamic performance. To overcome this disadvantage, we do 10 points (the original plus 9 additional) to make the statistical model in Eq. (2) more accurate. The Latin hypercube design is used to obtain the 9 added points. The principle is that distances between new points and all pre-existing points are as large as possible. An iterative calculation is needed here. Finally, sampling points are even in the whole parameters spaces.
At the beginning of optimization procedure, there are 20 sampling points which are also obtained by Latin hypercube design for constructing the initial Kriging model. 10 new sampling points are validated in each iterative. Genetic algorithm is used to find the least value of EI function and to get the corresponding parameters.
2.3. Wind tunnel test
The aerodynamic forces and moments of the following aircraft are obtained by solving a set of 3D compressible Navier-Stokes equations, and Spalart-Allmaras turbulence model is used to deal with pulsing. The finite volume method is used to discretize these equations in the calculation zone. A low speed wind tunnel test was conducted in 1 Meter Unsteady Wind-Tunnel belonging to Nanjing University of Aeronautics and Astronautics to validate the accuracy of the calculation results. The lead aircraft was supported by a tail sting which was jointed to a vertical vane rod mounted on a frame of axes to achieve different relative positions accurately (lateral spacing and vertical spacing). The following aircraft was supported by primary support system of the wind tunnel to change its angle of attack. The aerodynamic forces and moments of the following aircraft were measured by an inner six-component strain-gage balance.
3. Results and discussion
3.1. Formation flight model
The model of the two-aircraft formation flight is studied as shown in Fig. 1. One aircraft is in the front and the other aircraft follows in the back. Both aircraft have the same flying wing configuration. Fig. 1 (a) shows the appearance of the aircraft. It consists of a 65-deg delta wing and a saw-tooth trailing edge with sweep angles of 47-deg. The formation and coordinates system are shown in Fig. 1 (b), x is longitudinal spacing, y is lateral spacing and z is vertical spacing within the formation, and the left following aircraft is not shown.
Fig. 1.
(a) Appearance of flying wing aircraft. (b) Schematic of formation and coordinates system.
Fig. 2 shows the original mesh and the altered mesh which exhibits a changed formation stance. In present work, only three positional parameters are changed, and the angles of attack of the two aircrafts are fixed. The lead aircraft's angle of attack is 2°, and the following aircraft's angle of attack is 2° as well.
Fig. 2.
Grids of close-formation flight: a) original grids, b) altered grids.
A symmetric boundary condition is used in the symmetry plane of the lead aircraft. So the left following aircraft is not shown for a better observation. The initial formation state is, and . Three positional parameters are changed in S which is the design space. is the displacement of the following aircraft from the original position, and the three parameters are dimensionless by wingspan as shown in Eq. (4).
| (4) |
Five iterations are implemented, which means 70 times flow calculation have been down. The optimization results have been obtained after two iterations. The maximum lift-to-drag ratio is achieved at with about 24.7% induced drag reduction. In other words, when the following aircraft's wing overlaps with the lead aircraft's wing by 14.7% wingspan, the following aircraft's aerodynamic performance improved most significantly. In the vertical direction, the following aircraft is a little lower than the lead aircraft. Wake vortexes generated by the lead aircraft would descend due to induced velocity. When the vortexes pass by the following aircraft's longitudinal position, their vertical position would be lower than .
3.2. Experimental demonstration of the accuracy for computational fluid dynamics
An optical image of experimental models mounted in test section is shown in Fig. 3 (a). The velocity of the free stream is 25 m/s. The interference of the lead aircraft model's supports has been corrected. The results at the state of αL = 4°, αF = 4° derived from test and calculation are presented in Fig. 5. Since the model used in William and David's wind tunnel test are similar to the flying wing model (William and Gingras, 2004), and Reynolds number is close to this test, their results are presented in Fig. 3 (b) as well. It should be noted that αL = 8°, αF = 8° in William and David's test. Fig. 3 (b) shows that predicted results are in well agreement with the experimental results.
Fig. 3.
(a) Flying wing models mounted in test section. (b) Incremental lift coefficients with different lateral spacing (, ).
Fig. 5.
Distribution of predicted aerodynamic coefficients: a) lift-to-drag ratio, b) lift coefficient, c) drag coefficient.
In order to compare CFD and experiment results on the simulation ability of the transonic aerodynamic features of the low aspect ratio flying wing configuration, the SST turbulent modeling is applied. Based on the results of simulation and experimental data (William and Gingras, 2004), the lift increases linearly when the angle of attack is less than 4° (Fig. 4a and b). The CFD results are in good agreement with the experiment, even while the evident vortex lift appears as the angle of attack is higher than 4°.
Fig. 4.
Comparison of (a) lift force and (b) drag force coefficients obtained by CFD calculation and experimental measurement at a high subsonic state (Mach number = 0.9).
3.3. Distribution of the following aircraft's aerodynamic coefficients
As mentioned above, the Kriging model constructed in optimization procedure has a high fidelity in the prediction of the following aircraft's aerodynamic performance. It is easy to study the influence of three positional parameters on aerodynamic performance by using the Kriging model. Fig. 5 shows the distribution of the following aircraft's aerodynamic coefficients which are predicted by the Kriging model. The maximum lift-to-drag ratio is only correlated to a large lift coefficient and a small drag coefficient. The position corresponding to the minimum drag coefficient is more inboard than the maximum lift coefficient position. The sensitivity of the following aircraft's lift-to-drag ratio to three positional parameters is very distinct. Obviously, it is sensitive to lateral spacing and vertical spacing, but insensitive to longitudinal spacing in this study's parameter range (1–10).
It's well known that prediction accuracy become bad when the independent parameters are on boundaries. The optimization done in three-dimension design space shows that the best point is almost on the boundary of the plane. To avoid the optimized point that is not the global best point and consider the longitudinal spacing which is little significant, a second optimization was implemented in plane. Two positional parameters are changed in as Eq. (5).
| (5) |
Eight iterations and 100 times calculation of flow have been down. After six iterations, the results converged as shown in Fig. 6. Maximum lift-to-drag ratio (K = , Where CL and CD are lift and drag force, respectively.) is achieved at, which is 6.8% larger than the first optimization as listed in Table 1. The lateral position is a little further out than the first optimization. The distribution of aerodynamic coefficients predicted by the new Kriging model that is constructed in the second optimization procedure is shown in Fig. 7. It has the same tendencies as Fig. 5. Considering mesh transformation error and calculation error, the two optimizations are well consistent with each other.
Fig. 6.
The convergence process of the optimization iteration.
Table 1.
Comparison of two optimization methods.
| Methods | CL | CD | K |
|---|---|---|---|
| Optimization results 1 | 0.151 | 0.0086 | 17.4787 |
| Optimization results 2 | 0.1564 | 0.0084 | 18.6617 |
Fig. 7.
Distribution of new predicted aerodynamic coefficients: a) lift-to-drag ratio, b) lift coefficient, c) drag coefficient.
3.4. Interaction of the vortexes shed off the lead and the following aircrafts
The interaction between vortexes from the lead aircraft and the following aircraft is observed respectively at the optimized formation state and original state. A positive Q is used to indicate vortexes in flow field. As Q > 0 means that the distribution of pressure is high at around, while it is low at the center. The iso-surfaces of Q can depict vortex circumference, where Q is the second invariable of velocity gradient tensor. It has following expression as Eq. (6).
| (6) |
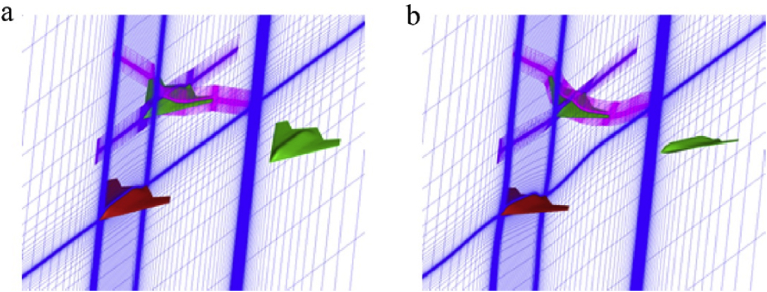
Where is the derivative of velocity in i direction by parameter j. Fig. 8 shows Q = 0.0002 iso-surfaces in flow field. At the optimized formation state, the right wing tip vortex generated by the lead aircraft collides on the left wing tip of the following aircraft, and then the vortex splits into two parts. The small one flows over the following aircraft's wing tip, and the big one is deflected downwards. It seems that this right wing tip vortex is weakened after it passes the following aircraft's wing tip. At the meantime, the left wing tip vortex generated by the following aircraft rolls up and moves inboard. Obviously, the left wing tip vortex is weaker than that of the isolated aircraft. There is a fourth vortex at the left wing tip of the following aircraft. It is a little lower than the small part of the lead aircraft's right wing tip vortex, and the left wing tip vortex generated by the following aircraft, but it is higher than the big part of the lead aircraft's right wing tip vortex.
Fig. 8.
Q = 0.0002 iso-surfaces in flow field: a) original formation state, b) optimized formation state.
Compared with the right wing tip vortex of the following plane, the fourth vortex shedding from the left sawtooth is somewhat enhanced. The reason may be that the front aircraft has a small vortex (counterclockwise) due to the mirror effect produced by the wing surface (clockwise), which makes the wing surface strong near the clockwise rotation, leading to a strong vortex strength. Because of the presence of the interaction between the wake vortex of the front aircraft and the following aircraft, the wake vortex of the following aircraft is generally weakened. Therefore, the induced resistance of the following aircraft decreases. Under the optimized formation, the wingtip vortex of the front aircraft exactly collides with the roll position of the left wing tip vortex. At this time, the strongest counter-rotating vortex interactions occur, producing a maximum of the lift-to-drag ratio. Fig. 8 shows the state that the front vortex has no impact on the following aircraft. However, the vortex from the left side of the following aircraft still becomes weak thanks to the mutual inducement of the two vortices which results in a slight increase in the vortex core positions.
4. Conclusion
In conclusion, an optimization method of close-formation flight consisting of two aircraft has been presented. The following aircraft's lift-to-drag ratio is the cost function, and three positional parameters are variables. The optimized results showed that the following aircraft's lift-to-drag ratio achieves a maximum value when the wing tips overlap by 14.7% span, and the following aircraft goes down by 2.2% span with about 24.7% induced drag reduction. The following aircraft's aerodynamic performance is sensitive to lateral spacing and vertical spacing, but insensitive to longitudinal spacing in close-formation flight. The structure of vortexes is analyzed at the optimized state by Q criterion. The following aircraft's wake vortexes which are close to the lead aircraft are weakened, leading to a reduction of induced drag. A low speed wind tunnel test has been conducted to validate accuracy of calculation results. The good agreement is found between predicted and experimental lift coefficients. Besides, a second optimization has been implemented in two-dimension design space to validate the optimization conducted in three-dimension design space. It shows that the optimization method has a good convergence in the whole variable space.
Declarations
Author contribution statement
Tao Yang: Conceived and designed the experiments; Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Liu Zhiyong, Lin Jun: Analyzed and interpreted the data; Wrote the paper.
Xiong Neng: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Sun Yan: Performed the experiments; Contributed reagents, materials, analysis tools or data.
Funding statement
This work was supported by National Natural Science Foundation of China (11372337).
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Atilla Dogan, Sriram Venkataramanan, William Blake. Modeling of aerodynamic coupling between aircraft in close proximity. J. Aircraft. 2005;42(4):941–955. [Google Scholar]
- Blake W.B., Multhopp D. Design, performance and modeling considerations for close formation flight. AIAA. 1998:98–4343. [Google Scholar]
- Lissaman P.B.S., Schollenberger C.A. Formation flight of birds. Science. 1970;168(3934):1003–1100. doi: 10.1126/science.168.3934.1003. May. [DOI] [PubMed] [Google Scholar]
- Maskew B. 1977. Formation Flying Benefits Based on Vortex Lattice Calculations. NASA CR-151974. [Google Scholar]
- Rendall T., Allen C. Efficient mesh motion using radial basis functions with data reduction algorithms. J. Comput. Phys. 2009;228(17):6231–6249. [Google Scholar]
- Soni B.K. 7th Computational Physics Conference, Cincinnati, Ohio, 12–15. October. 1985. Two- and three-dimensional grid generation for internal flow applications of computational Fluid dynamics. [Google Scholar]
- Weimerskirch H., Martin J., Clerquin Y. Energy saving in flight formation. Nature. 2001;413:697–698. doi: 10.1038/35099670. October. [DOI] [PubMed] [Google Scholar]
- Wieselsberger C. 1914. Zeitschrift. Flugtechnik. Motorluftschiffahrt. 5; pp. 225–229. [Google Scholar]
- William B., Gingras David R. Comparison of predicted and measured formation flight interference effects. J. Aircraft. 2004;41(2):201–207. [Google Scholar]