Inferring Transmission Histories of Rare Alleles in Population-Scale Genealogies

Abstract

Learning the transmission history of alleles through a family or population plays an important role in evolutionary, demographic, and medical genetic studies. Most classical models of population genetics have attempted to do so under the assumption that the genealogy of a population is unavailable and that its idiosyncrasies can be described by a small number of parameters describing population size and mate choice dynamics. Large genetic samples have increased sensitivity to such modeling assumptions, and large-scale genealogical datasets become a useful tool to investigate realistic genealogies. However, analyses in such large datasets are often intractable using conventional methods. We present an efficient method to infer transmission paths of rare alleles through population-scale genealogies. Based on backward-time Monte Carlo simulations of genetic inheritance, we use an importance sampling scheme to dramatically speed up convergence. The approach can take advantage of available genotypes of subsets of individuals in the genealogy including haplotype structure as well as information about the mode of inheritance and general prevalence of a mutation or disease in the population. Using a high-quality genealogical dataset of more than three million married individuals in the Quebec founder population, we apply the method to reconstruct the transmission history of chronic atrial and intestinal dysrhythmia (CAID), a rare recessive disease. We identify the most likely early carriers of the mutation and geographically map the expected carrier rate in the present-day French-Canadian population of Quebec.

Introduction

A large number of Mendelian disorders derive from well-characterized rare genetic variants (see OMIM in Web Resources). Characterizing the population frequency and geographic distribution of such variants plays a central role in apportioning financial resources toward individual diagnostics, population screening, and genetic counseling services.^{1, 2} However, assessing regional population frequencies requires thorough clinical or genetic testing which can be costly, especially when disease mutations are rare.

Genealogical data, where available, can provide information about disease risk in untyped individuals: immediate family history is a key factor in deciding screening regimes for a range of diseases³ such as breast cancer^{4, 5, 6} and colorectal cancer.⁷ Broader relatedness patterns are used to determine screening regimes for population-specific traits, especially in founder populations.^{3, 8, 9}

Extended family history bridges the gap between immediate family history and population-scale risk, but it is often unavailable and incomplete. Even when available, it demands careful statistical analysis. Here we are interested in using large-scale genealogies to investigate individual risk factors at the population scale, by inferring the transmission path of disease alleles within a genealogy.

We will focus on genealogical records provided by the BALSAC database (see Web Resources), which contains 2.9 million vital event records, such as those relating to birth, death, and marriage, and consider a single connected genealogy of more than 3.4 million individuals stretching from the arrival of European settlers in the Canadian province of Quebec in the 17th century up until the present day, and spanning multiple regional founder effects.¹⁰

Performing statistical analyses in such large genealogies is challenging. Both forward and backward simulations can be performed efficiently in very large genealogies.^{11, 12} However, neither can be easily conditioned on observed data: forward simulations (allele dropping) are unlikely to produce the observed distribution of carriers, while unbiased backward simulations (allele climbing) are unlikely to produce plausible coalescence histories for rare variants, as we show in the Material and Methods section below.

While many robust statistical tools exist for performing inference within genealogies, primarily for the purpose of performing linkage analysis,^{13, 14, 15, 16, 17, 18, 19} few are able to handle thousands of samples, let alone millions. Geyer and Thompson used a simulated tempering MCMC scheme to impute ancestral carrier status in a Hutterite genealogy with 2,024 members.²⁰ Generalizing MCMC approaches to much larger genealogies presents formidable challenges for memory usage and convergence (E. Thompson, personal communication).

Previous work estimating prevalence using population-scale genealogies used heuristics to estimate regional prevalences across regions. For example, Chong et al.¹² used forward simulations to estimate the distribution of allele frequencies of mutations derived from a single founder, but without taking into account specific carrier status of present individuals. Similarly, Vézina et al.⁵ estimated regional prevalences of a mutation in BRCA1 in Quebec using an earlier version of the BALSAC database. They first identified a likely founder carrier of the mutation, using a heuristic based on differential genetic contribution to case and control subjects, and then mapped the genetic contribution of this ancestor to each of 23 geographic regions in Quebec. Another feasible heuristic, for rare variants, is to estimate the mean kinship of individuals in a given region to known case subjects. Neither heuristic models correlations in genotypes among case subjects, which can bias estimates.

The work presented here aims to provide a more accurate and rigorous statistical framework for generating regional estimates, and more generally performing inference in very large genealogies that are being generated on academic, private, and participatory platforms (see BALSAC in Web Resources).^{21, 22, 23, 24} We present a general and scalable method and software package, ISGen, which uses importance sampling and careful software implementation to perform carrier risk analysis in such databases. ISGen takes as input available genotypes of specific individuals within the genealogy, including known case subjects, carriers, and genotyped relatives. It can use information about population-level estimates of the carrier rate in the general population as well as haplotype sharing information. ISGen uses importance-weighted allele climbing to efficiently explore transmission history space for neutral or recessive lethal alleles. Simulations show that it can be used to estimate regional prevalences more accurately than approaches based on kinship alone.

Because ISGen computes the likelihoods of a large number of possible inheritance paths consistent with an observed set of known case subjects and carriers, it can also be used to compute the posterior probability that a given ancestor introduced the mutation in the population through mutation or immigration. We use this method to infer the most likely ancestral origin of a rare allele causing chronic atrial and intestinal dysrhythmia (CAID [MIM: 616201]), a recessive disorder within the present-day population of Quebec, Canada, from among the first Europeans to settle in the area in the early 17th century. We then map the expected frequency of the allele in 23 regions of Quebec. The Material and Methods section presents the technical details of the algorithm and implementation, as well as validation results, while the Applications section presents the analysis of the CAID allele.

Material and Methods

Data and Initialization

ISGen explores, through Monte Carlo simulation, the set of possible genotype assignments within a genealogy that are consistent with observed genotypes and with other assumptions about the inheritance mode and ancestral frequency. At the beginning of a simulation, most genotypes are unknown (i.e., unassigned), and only the genotypes of known case subjects, carriers, and their relatives are set to their observed values. The genealogical relationships themselves are recorded as a table of parent-offspring triplets, as shown in Figure S1.

Monte Carlo Simulations

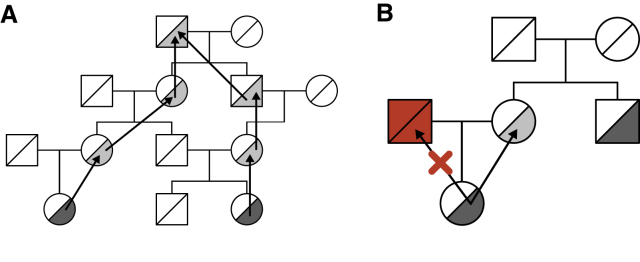
After initialization, the process of allele climbing begins. We simulate the inheritance of each minor allele through either the maternal or paternal side, setting unobserved parental alleles to match those of the climbing allele. This simulated inheritance continues upward through grandparents and more distant ancestors until reaching the “founders” of the genealogy, i.e., individuals with one or two missing parents in the genealogy (Figure 1A). In practice, because the BALSAC dataset relies on marriage records, there are no “half-founders” with a single known parent in the genealogy, and in the following we use founders to refer to individuals with no parents in the genealogy. When multiple minor allele copies are inherited from the same individual, we say that they coalesce if they are inherited from (i.e., climb to) the same allele copy, otherwise the individual is inferred to be a homozygote.

Figure 1.

Importance Sampling in Genealogies

(A) Alleles are assigned to probands and then climb up the genealogy by choosing to follow either maternal or paternal inheritance.

(B) In the simplest importance sampling scheme, ISGen ensures that the red individual is never assigned an allele, since then full coalescence within the genealogy would be impossible. It adjusts the likelihood by a factor of 1/2 to avoid biasing maximum likelihood estimate.

Major and minor alleles can be treated in a symmetric manner during allele climbing. However, because the number of major allele copies in the population is usually much greater than that of minor alleles, we find it more numerically efficient to first perform allele climbing on minor alleles as outlined in this section, and then use a different procedure for estimating likelihood based on major allele carriers, which is outlined later in this section. Similarly, haplotype information is included at a later stage and is also outlined below.

By tracing lineages of each minor allele copy through the genealogy, we define a possible allele transmission history consistent with the observed carriers. This history defines an inheritance path, the set of individuals either known or inferred to carry a minor allele. It is possible (indeed overwhelmingly likely) for a randomly sampled inheritance path not to have fully coalesced within the genealogy.

We focus on alleles that are rare among the founders. Specifically, we assume that the allele frequency in the ancestral population from which the founders originate is $\omega \ll 1/N_{founders}$, where N_founders is the number of founders, implying that the allele most likely came from a single founder. The assumption of a single origin is not central to the approach, but it simplifies the description and speeds up the inference. It is a reasonable assumption for rare diseases in small founder populations,¹² but a relaxation of this assumption is outlined in the Discussion.

To compute the likelihood that ancestor a contributed the set of haplotypes c that were observed to carry the minor allele, we simply compute the proportion of simulations that coalesce from c into ancestor a. Let S be the observed event that all haplotypes in c carry the minor allele. Let $\text{Γ}$ denote a simulated inheritance path ascending from c, and let A be a random variable representing the founder who carried the minor allele. If ${\mathrm{1}}_a\left(\text{Γ}\right)$ is the indicator function for whether $\text{Γ}$ coalesces to founder a, and M the number of Monte Carlo iterations, we estimate the likelihood as

$$P\left(S|A=a\right)=P\left(\text{Γ}\text{coalesces}\text{to}a\right)=E\left[{\mathrm{1}}_a\left(\text{Γ}\right)\right]\simeq \frac{1}{M}\sum _{j=1}^M{\mathrm{1}}_a\left({\text{Γ}}_j\right),$$ (Equation 1)

where the last step is a Monte Carlo integration, and ${\text{Γ}}_j$ is the inheritance path constructed in simulation j, drawn from distribution $p\left({\text{Γ}}_j\right)$ defined by the allele climbing process.

Assuming a flat prior for all ancestors a in the set $\mathcal{A}$ of all founding ancestors, Bayes theorem provides the normalized posterior probability that a is the founding carrier:

$$P\left(A=a|S\right)=\frac{P\left(S|A=a\right)P\left(A=a\right)}{{\sum }_{a^{\text{'}}\in \mathcal{A}}P\left(S|A=a^{\text{'}}\right)P\left(A=a^{\text{'}}\right)}=\frac{P\left(S|A=a\right)}{{\sum }_{a^{\text{'}}\in \mathcal{A}}P\left(S|A=a^{\text{'}}\right)}.$$ (Equation 2)

In practice, we perform a single Monte Carlo simulation to estimate simultaneously $P\left(S|A=a\right)$ for all ancestors a. Even then, because coalescence to a single ancestor is a very rare occurrence in a large genealogy, the majority of simulations yield ${\mathrm{1}}_a\left({\text{Γ}}_j\right)=0$ for all a and do not inform our likelihood estimate.

Importance Sampling

The Monte Carlo distribution $p\left(\text{Γ}\right)$ generates mostly inheritance paths with zero likelihood. To improve convergence, importance sampling uses a heuristic proposal distribution $q\left(\text{Γ}\right)$ to favor higher-likelihood paths. As long as we account for the over-representation of these paths, the resulting estimates are unbiased.

A Simple Importance Sampling Scheme

In the course of a simulation, it is simple to assess whether individuals in an incomplete inheritance path share a common ancestor. When simulating an allele inheritance, a simple importance sampling scheme would be to verify whether each of the maternal and paternal paths is consistent with eventual coalescence and forbid inconsistent choices (Figure 1B). Being “consistent with coalescence” means sharing a common ancestor with the other lineages in the sample and, in the case of a homozygote, sharing such a common ancestor through both paternal and maternal lineages.

This defines a simple proposal distribution $q\left(\text{Γ}\right)$ under which all paths coalesce to a single ancestor a and contribute to the likelihood. To obtain unbiased likelihood estimates, we need to identify the likelihood ratio $p\left(\text{Γ}\right)/q\left(\text{Γ}\right)$ for each sample path $\text{Γ}$. The Monte Carlo sampling probability for $\text{Γ}$ is

$$p\left(\text{Γ}\right)=2^{-\alpha }$$

where $\alpha =\alpha \left(\text{Γ}\right)$ is the number of allele transmissions in $\text{Γ}$. If $\text{Γ}$ coalesces to a single ancestor $a,$ it has a higher probability under q:

$$q\left(\text{Γ}\right)=2^{-\left(\alpha -\beta -\gamma \right)}$$

where β is the number of transmissions with only one valid maternal/paternal path consistent with coalescence and γ is the number of times a homozygote inconsistent with coalescence could have been created during the climbing process (homozygotes need a path to coalescence through both parents). Thus the likelihood ratio is

$$\frac{p\left(\text{Γ}\right)}{q\left(\text{Γ}\right)}=2^{-\beta -\gamma }.$$ (Equation 3)

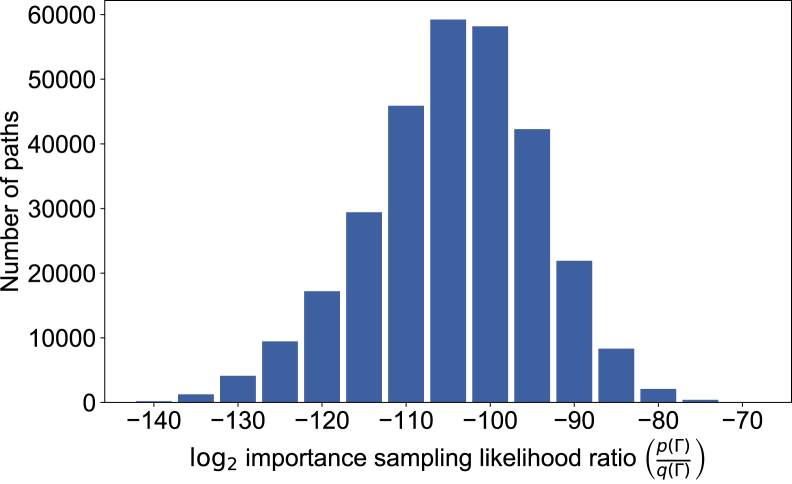
For patient panels of tens of individuals in the BALSAC genealogy, a representative histogram of values for this ratio are shown in Figure 2. The importance sampling estimate of $P\left(S|A=a\right)$ is then

$$\begin{array}{c}P\left(S|A=a\right)\simeq \frac{1}{M}\sum _{j=1}^M{\mathrm{1}}_a\left({\text{Γ}}_j\right)\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}\\ =\frac{1}{M}\sum _{j=1}^M{\mathrm{1}}_a\left({\text{Γ}}_j\right)2^{-{\beta }_j-{\gamma }_j}\end{array}$$ (Equation 4)

where ${\text{Γ}}_j$ denotes the inheritance path drawn from q in simulation j.

Figure 2.

Importance Sampling Likelihood Ratio Distribution

300K inheritance paths, simulated from a single patient panel within the BALSAC genealogy.

This framework is flexible enough to include rather general conditions on the inheritance paths. For example, if we climb an allele known to cause a lethal recessive disease, we can ensure there are no homozygous individuals in our simulated lineages by using importance sampling to avoid simulating homozygotes altogether: we do this when applying ISGen to a lethal recessive disease in the Applications section.

We present a more elaborate importance sampling scheme below, but for clarity of exposition we use the simple scheme presented above to introduce model extensions.

Incorporating Major Alleles and the Observed Allele Frequency

Through allele climbing, Equation 4 computes the probability that a given ancestor gave rise to specific minor alleles. However, a complete model must also take into account the distribution of major alleles. We use two approaches to model this distribution, depending on the type of information that is available.

If we have information about the genotype of close relatives to carriers, we simply simulate the transmission of these known major alleles, forbidding coalescence between lineages carrying different alleles. Because we do not assume a common origin within the genealogy for major alleles, their inheritance can be simulated without importance sampling to ensure coalescence.

Carriers of major alleles who are not closely related to case subjects have a weak individual impact on trajectory likelihoods, but collectively can contribute substantially. Rather than simulating allele climbing for millions of major alleles (which would be feasible but slow), we treat unrelated homozygotes for the major allele in an average manner. In addition to being numerically convenient, this approach is the best we can do when population-wide allele prevalence was estimated from a sample without genealogical information, as is the case for the CAID allele examined in the Applications section.

We use a “climb-then-drop” approach, climbing from the minor carriers to generate inheritance paths, then dropping alleles from individuals within simulated inheritance paths back down to the present-day population to estimate major and minor allele prevalence in the general population. This climb-then-drop approach is possible because of the fixed genealogy: a full simulation of the transmission of alleles through a genealogy requires choosing a paternal or maternal transmission at each node, but the order in which these choices are made does not affect the likelihood. We can therefore first simulate the transmissions among ancestors to the known carriers, by climbing alleles and ensuring that they find a common ancestor, and only then proceed to assign the downstream transmissions by dropping these simulated alleles through the rest of the genealogy.

Let F be the random variable representing the minor allele frequency in the present-day population and f its observed value in a population sample collected independently of the genealogy. Dropping alleles from transmission history $\text{Γ}$ allows us to estimate $P\left(F=f|\text{Γ},S,A=a\right)$, the distribution of the allele frequency conditional on $\text{Γ}$ and the observed event S (see Appendix C for mathematical details). Appendix B shows that we can estimate the joint probability of the observed carriers and global allele frequencies as

$$P\left(S,F=f|A=a\right)\simeq \frac{1}{M}\sum _{j=1}^M{\mathrm{1}}_a\left({\text{Γ}}_j\right)\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}P\left(F=f|{\text{Γ}}_j,S,A=a\right).$$ (Equation 5)

We can then refine the posterior probability that ancestor a was the origin of the allele within the genealogy by conditioning on F as well as S:

$$P\left(A=a|S,F=f\right)=\frac{P\left(S,F=f|A=a\right)}{{\sum }_{a^{\text{'}}\in \mathcal{A}}P\left(S,F=f|A=a^{\text{'}}\right)}.$$ (Equation 6)

Directly estimating $P\left(F=f|{\text{Γ}}_j,S,A=a\right)$ by dropping alleles from ${\text{Γ}}_j$ is possible but computationally costly: to get a distribution of f, we need many dropping simulations for each ${\text{Γ}}_j$. To avoid this computational cost, we propose an approximation that reuses a single set of dropping simulations across all individuals. A naive approach would estimate the present-day frequency of the minor allele as a sum over dropping contributions from all individuals in ${\text{Γ}}_j$. Unfortunately, since individuals in ${\text{Γ}}_j$ are parentally related, the contributions of individuals in ${\text{Γ}}_j$ to the present-day allele frequency are necessarily overlapping.

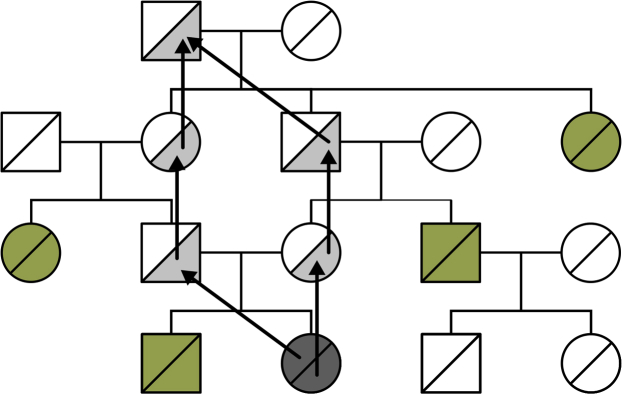
To avoid double-counting, we define the boundary $\partial {\text{Γ}}_j$ of the inheritance path ${\text{Γ}}_j$ as the offspring of all individuals in the path, excluding those in the path itself (see Figure 3). We then compute the global allele frequency as a sum over individuals in $\partial {\text{Γ}}_j$, assumed to contribute approximately independently to the present-day allele frequency. We validated such estimates of $P\left(F=f|\text{Γ}\right)$ by comparing the results to simulated allele drops from the whole inheritance path, and we see excellent agreement (see Figure S3 and Appendix C for mathematical details).

Figure 3.

Boundary of an Inheritance Path

The boundary of an inheritance path is the set of first-generation descendants (shown in green) of any individuals within the path.

Haplotype Sharing

Carriers of the minor allele also share a finite haplotype, and the length of the shared haplotype contains information about its origin and transmission history. As a first step toward incorporating this information, we explicitly model the likelihood of the maximum shared haplotype length—the longest haplotype shared among all carriers of the minor allele. A similar derivation can be found in Boehnke et al.²⁴

Since we simulate every transmission event in the genealogy, we can also explicitly model the breakdown of a shared haplotype by recombination. The length of this shared haplotype will be the distance between the first recombination in the 3′ direction and the first recombination in the 5′ direction.

If we assume that recombination follows a Poisson process with a rate of one recombination per Morgan per generation, the waiting distance until the first recombination in either direction from the locus of interest is exponentially distributed with rate corresponding to the number of transmission events below the most recent common ancestor (MRCA) of the carriers. The distribution of shared haplotype lengths will therefore be a sum of two exponential distributions, or an Erlang 2 distribution. Letting h represent the number of meioses since the MRCA of the carriers, the probability of observing a shared haplotype length L is therefore

$$P\left(L=l|\text{Γ}\right)=\text{Erlang}\left(2,h\right).$$

We can then incorporate the probability of observing L into our Monte Carlo estimates, as we did with the global allele frequency in Equation 6. The expression for the most likely ancestor becomes

$$P\left(S,F=f,L=l|A=a\right)\simeq \frac{1}{M}\sum _{j=1}^M{\mathrm{1}}_a\left({\text{Γ}}_j\right)\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}P\left(F=f|{\text{Γ}}_j\right)P\left(L=l|{\text{Γ}}_j\right).$$ (Equation 7)

We can then refine the posterior probability that ancestor a was the origin of the allele within the genealogy by conditioning on L as well as S and F:

$$P\left(A=a|S,F=f,L=l\right)=\frac{P\left(S,F=f,L=l|A=a\right)}{{\sum }_{a^{\text{'}}\in \mathcal{A}}P\left(S,F=f,L=l|A=a^{\prime }\right)}.$$ (Equation 8)

Regional and Individual Carrier Rate Estimation

Obtaining individual and regional carrier rates is useful for both clinical and public health reasons. In a population such as Quebec with an extensive known genealogy, the known relatedness between individuals can be used to estimate such carrier rates. The posterior probability that individual I carries the minor allele is the proportion of transmission histories for which I is a carrier, among all transmission histories consistent with observations.

We again use importance sampling to simulate ascending histories consistent with the observations, and then descending simulations to estimate the probability that an individual is a carrier, conditional on the ascending genealogy. Appendix D shows that we can similarly estimate expected prevalences R_m of the minor allele for arbitrary regions:

$$E\left[R_m|S,F=f\right]\simeq \frac{{\sum }_{j=1}^M\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}P\left(F=f|{\text{Γ}}_j\right)E\left[R_m|{\text{Γ}}_j,F=f,S\right]}{{\sum }_{j=1}^M\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}P\left(F=f|{\text{Γ}}_j,S\right)}.$$ (Equation 9)

We compute $E\left[R_m|{\text{Γ}}_j,F=f,S\right]$ using the “boundary approximation” described above: R_m is taken to be a sum of independent contributions from individuals in $\partial \text{Γ}$.

Importance Tuning for Faster Convergence

While the straightforward importance sampling scheme presented above provides a large gain in efficiency compared to unweighted Monte Carlo (on the order of 2¹⁰⁰≈10³⁰ times more efficient), there are natural ways to improve and generalize it further. In this section, we describe a more complex scheme that results in faster convergence. The choice of a scheme affects only the convergence speed of the algorithm and has no effect on the converged results.

For example, while our scheme guarantees that every simulated inheritance path coalesces within the genealogy, it does not seek to favor maternal or paternal inheritance as long as both have nonzero coalescence likelihood. This is suboptimal when the two choices lead to different coalescence likelihoods.

To encourage alleles of a given type to converge toward each other within the genealogy, we implemented an importance sampling scheme that generates an effective attraction among alleles of the same type by sending messages up and down the genealogy. First, we define $t_k\left(i,j\right)$ as the length, in generations, of each genealogical route k connecting individual i with their genealogical ancestor j. The probability of an allele in i having independently been inherited from j is therefore the kinship coefficient

$$P\left(j\to i\right)=\sum _k{2}^{-t_k\left(i,j\right)}.$$ (Equation 10)

Each ancestor in the genealogy then gets a score which is the sum of these probabilities of each observed minor allele copy. An ancestor with a large score is therefore a plausible coalescence point for several carriers.

When choosing a parent to climb to, we want to favor parents with high-scoring ancestors. Specifically, we compute a parental score as the sum of the scores its own ancestor, weighted by kinship coefficient linking the parent to its ancestors. Parents are then sampled proportionately to these weighted scores.

Even though it requires many more computations per iteration, the faster convergence can still lead to much lower computational times. In our simulations and inferences, sampling parents by kinship score reduced the overall compute time by roughly a factor of 4. Comparison of convergence rates are shown in Figures S1 and S2: the mean standard deviation of likelihood estimates across all ancestor is reduced by an order of magnitude.

Validation

We first use forward simulations (allele dropping) for validation in the single locus setting. Motivated by the CAID example, we assumed a recessive trait. By dropping alleles through the genealogy from each founder, we generate sets of simulated homozygous patients, as well as an associated allele frequency in the rest of the population. We then evaluate how often the importance sampling method correctly re-identifies the generating founder of each patient panel and whether the posterior probabilities are well-calibrated.

We performed the simulations in the BALSAC Population Register genealogy described above. Because validation of posterior probability calibration is computationally intensive, requiring hundreds of individual inferences, we performed it within a subset of the entire genealogy. This subset had been generated by selecting 140 individuals from the most recent generation and including their complete ascending genealogies up to the founders. The 140 individuals included 12 individuals identified in the CAID study and 128 randomly selected individuals from the most recent generation (The CAID study membership is not used for this validation step, and all 140 individuals are treated equally in this simulation.) This gave a total of 41,523 individuals in a single genealogy with a maximum depth of 17 generations and a median maximum depth across individuals of 15. We then performed forward simulations, selecting forward simulations for which we had between 5 and 30 homozygous affected individuals, giving 470 simulated case subject panels for which we knew the ancestral origin of the shared allele.

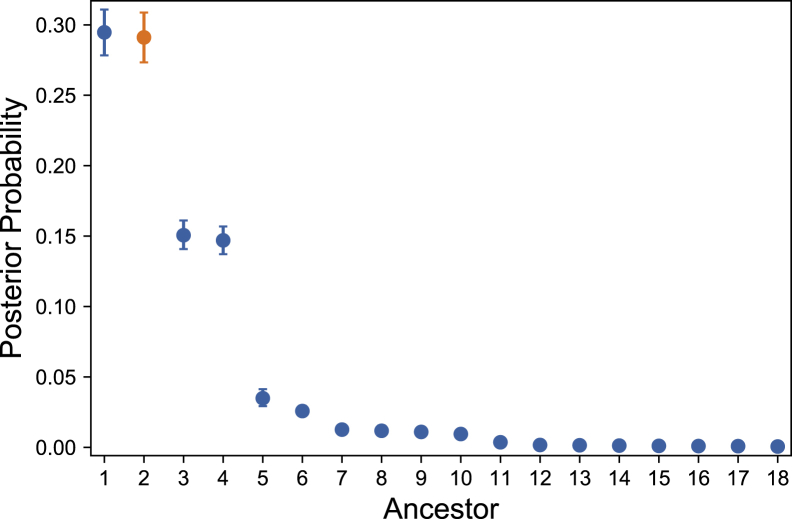
We then performed 300K importance sampling climbing simulations on each of these simulated panels. Each simulation estimates posterior probabilities for all common ancestors of the simulated homozygous patients (904 unique founders across all panels). In many cases, only a few ancestors have a high probability and the remaining probabilities are quite low. An example is shown in Figure 4.

Figure 4.

Ancestor Posterior Probabilities for a Simulated Patient Panel

The ancestor generating the panel is shown in orange. Ancestors 1 and 2, as well as 3 and 4, are genealogically indistinguishable founder couples and are expected to have identical probabilities. Error bars represent uncertainty due to the finite sample size (i.e., the finite number of iterations) in importance sampling. 95% confidence intervals were obtained from bootstrapping over iterations. This source of uncertainty could be further reduced by increasing the number of iterations. Only ancestors with nonzero posterior probability are displayed, and ancestor labels represent ordering by posterior probability for a given simulation. A representative set of simulation results is shown in Figure S5.

Some ancestors are statistically indistinguishable due to symmetries in the genealogy. Monogamous founder couples and grandparent groups connected to the genealogy through a single grandchild are examples. Calculating probabilities for these individuals separately gives no extra information on the likelihood of our simulated inheritance paths, so we sum their probabilities to get a total for the group.

Most ancestors have low posterior probabilities of being the initial carrier. Because we are especially interested in validating posteriors for fairly plausible events, we further group individuals in relatedness clusters, so that we report posterior probabilities that the founder originated in a given relatedness cluster rather than in a given individual (most relatedness clusters are composed of a single founder couple; see Appendix E for details of cluster composition).

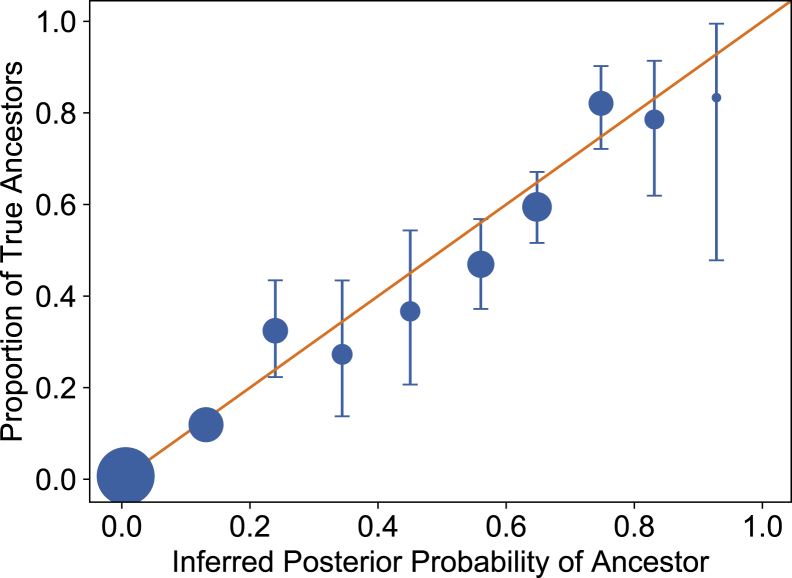
The posterior probability of each relatedness cluster, calculated using Equation 6, gives an estimate of how often we expect an ancestor from this cluster to be the generating ancestor of that particular patient panel. Figure 5 shows how often a relatedness cluster in a given posterior probability bin contains the true generating ancestor. The means and 95% confidence intervals of this distribution for each bin are obtained under a binomial model (see Appendix E for statistical details).

Figure 5.

Proportion of Ancestor Clusters that Contain the True Founding Ancestors as a Function of Cluster Posterior Probability of Containing the True Founding Ancestor

Error bars represent 95% confidence intervals based on the finite number of observations in each bin. Dot diameter corresponds to the logarithm of this bin count.

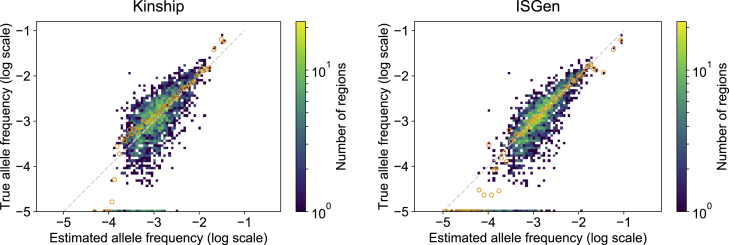
To validate regional allele frequencies, we used the full BALSAC genealogy. Again performing forward simulations to generate 100 panels of homozygous patients sharing an allele inherited from a single founder, we also recorded the associated allele frequencies in 23 geographic regions of Quebec. We then choose a random sample of 1,000 individuals to obtain an estimate f of the global allele frequency. We then use these subject panels S and global allele frequencies f together with Equation 9 to compute regional allele frequencies. We then compare the inferred results to the true simulated values, shown in Figure 6 and Table S3.

Figure 6.

Kinship and ISGen

Comparison of regional allele frequency estimates based on kinship with known patients and carriers (left column) to those based on inferred allele histories within the full BALSAC genealogical database (right column). We simulated 100 patient panels and corresponding regional allele frequencies. Simulated regional allele frequencies are compared to inference results based on case subject panels and estimated global allele frequency. Regions with zero allele frequency in the simulations appear here with frequency 10⁻⁵. The asymmetry of the heatmap is due to the logarithmic scale. Orange circles denote the mean true frequency for each estimated frequency bin. Spearman correlation of inference results with simulated allele frequencies is 0.673 (kinship) and 0.797 (ISGen).

We also compare the importance sampling method to a natural alternative, based on kinship scores. When a genealogy is available, pairwise kinship scores give the probability that two individuals are identical-by-descent (IBD) at any given locus. Calculating the average kinship of probands in a given region to all known carriers of an allele would give a (potentially biased) estimate of the allele frequency in that region. More details of how we calculated the kinship-based estimates are shown in Appendix D.1, and a comparison of the performance of each method is shown in Figure 6 and Table S3. The importance sampling method performed significantly better than the kinship method, with a Spearman correlation of 0.797 with the true allele frequencies, versus 0.673 using kinship.

Application to a Rare Recessive Disease

BALSAC Database and Genotype Data

We apply the importance sampling approach to reconstruct the transmission history and expected distribution of the rare recessive mutation causing chronic atrial and intestinal dysrhythmia (CAID) in Quebec, Canada, using the population-scale BALSAC genealogy (see Web Resources). Constructed from 3 million historical birth, death, and marriage records, we use here a single fully-connected genealogy of approximately 3.4 million individuals, of which approximately 2.7 million have an associated geographical region. The genealogy has a maximum depth of 17 generations, with most present-day individuals having at least one lineage measuring more than 12 generations. A breakdown of the number of historical records per region is shown in Figure S5. Despite its size, the proportion of incorrect links in the BALSAC Quebec genealogies is low, with approximately 1% false paternity.^{25, 26} All data were acquired and analyzed in accordance with IRB approval at McGill University under IRB Study No. A01-M48-15A.

In total, 11 affected individuals and 4 heterozygous carriers of the CAID allele have been identified in Quebec and used in this study, based on genotyping of case subjects using the Illumina HumanOmni5-Quad chip²⁷ and on population-based samples as part of the Quebec Regional Population Sample (see Web Resources). Of these, all 11 case subjects and 1 carrier have been linked to the BALSAC genealogy. The remaining 3 carriers were collected as part of a global screening effort, during which genealogical information was not obtained. See Appendix F for more details on the screening program.

We assume for this analysis that the minor allele was introduced into the Quebec population by a single European founder. All CAID-affected subjects share a 2.9 Mb homozygous segment on chromosome 3, where the causal mutation is located in SGO1 (previously named SGOL1 [MIM: 609168]), with an estimated haplotype age of 30 generations, or 900 years.²⁷ Because the same CAID mutation was also found in a Swedish patient who shares about 700 kb with the Quebec 2.9 Mb CAID haplotype, we assume that the mutation was not a de novo Quebec mutation.²⁷ The Genome Aggregation Database²⁸ gives a present-day frequency of the CAID allele (dbSNP rs199815268) of 0.000237 in Europeans. Thus the single founder assumption, while reasonable, cannot be held with absolute confidence. An approach to extend the present model to multiple founder introductions is outlined in the discussion below. See Appendix F for details on the identification of shared haplotypes among carriers of the CAID allele.

Finally, since CAID is associated with a severe reduction in fecundity, even with modern medical assistance,²⁷ we assume that no homozygote individuals are present in the ascending genealogy and assign zero likelihood to inheritance histories which contain them.

Estimating the Ascending Allele History

Using ISGen, we then constructed 20 million inheritance paths consistent with the 11 CAID-affected individuals and 1 carrier, avoid simulating inheritance paths that do not coalesce to a single ancestor, or which contain ancestral homozygotes for the CAID allele. We calculated the population allele frequency using 3 observed carriers among 900 individuals,²⁹ using Equations 7 and 8 to integrate this information with the importance sampling likelihoods.

Among 60,104 distinct ancestors identified in these genealogies, only 31 are founders and common to all CAID carriers. These include 13 founder couples and 5 individual founders who married with non-founders, thus leaving 18 possibly distinguishable genealogical routes for the CAID mutation to enter Quebec.

Two families (given anonymized labels 1 and 2 in Table 1) are most likely to have introduced the CAID mutation in the population. Posterior probabilities are shown in Table 1, along with confidence intervals from 1,000 bootstraps of the simulated inheritance paths and corresponding likelihoods. The combined posterior probability of founder families 1 and 2 is 98.8% (95% confidence interval 0.983–0.991). The two families in total contain 5 founders: family 1 consists of a single monogamous founder couple and family 2 contains a monogamous founder couple with a single child in the genealogy, who forms a monogamous couple with another founder.

Table 1.

Posterior Probabilities of the Two Families Most Likely to Have Introduced the CAID Allele into Quebec, along with 95% Confidence Intervals

Family	Posterior Probability	95% Confidence Interval
1	0.676	(0.599, 0.752)
2	0.312	(0.235, 0.389)
All Others	0.0123	(0.00894, 0.0171)

In the case of the CAID allele, the modeling of shared haplotype length has little effect on our estimates of the posterior probabilities of each ancestor, since most common ancestors were at comparable distances in the genealogy. Figure S4A shows that the difference between the most-favored and least-favored inheritance path is only a factor of 2, and the resulting change to the posterior probabilities of each ancestor by less than 1%, as shown in Figure S4B. A more detailed haplotype sharing analysis may lead to stronger corrections, especially in genealogies with a combination of very recent and older common ancestors.

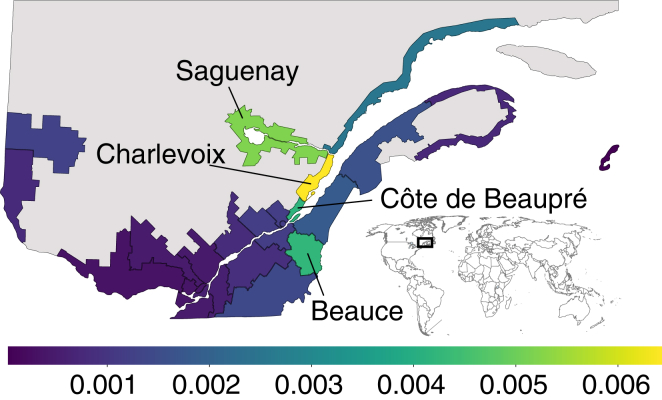
Figure 7 and Table S2 show regional allele frequencies estimated using 1 million simulated inheritance paths, with confidence intervals in Table S2 estimated from bootstrapping over inheritance paths. Using the Quebec-wide population frequency estimate of 1/600 for the CAID allele, random mating suggests one affected individual in 360,000 births roughly. However, we find considerable regional heterogeneity, as expected given that the population of Quebec is not genetically homogeneous,³⁰ but formed through a series of regional founder effects.^{31, 32} ISGen estimates the CAID allele frequency in Charlevoix to be approximately 1/155, giving a much higher estimated incidence of one affected individual per 24,025 births, assuming random mating.

Figure 7.

Regional Expected CAID Mutation Frequency within the Province of Quebec

Grey indicates low-population areas. For fully labeled regions, see Figure S6.

The full analysis, from simulating inheritance paths to estimating regional prevalences, was performed on a compute cluster in batches of 100K Monte Carlo iterations. Estimating the ascending allele history was the most computationally costly step, with each batch taking 35 hr to complete on an Intel 3.5GHz Core i7-3770K processor with 16 GB of DDR3 RAM. This gives a sizeable total compute time of approximately 280 days, although it is trivial to parallelize.

Regional allele frequencies can be estimated much more efficiently because convergence of estimates is much faster. Estimating regional frequencies took an extra 5 hr per 100K Monte Carlo iterations, giving a total of 40 hr per batch and 16.6 days for the full 1 million iterations. For those without academic access to such resources, the CAID regional frequency estimates could be completed in a single day on the Google Cloud Platform for CAN$49.58 (40 machines with 2 cores and 7.5 GB of memory, 10 hr usage).

Discussion

Current screening programs do not detect the majority of known rare genetic disorders,³³ which cumulatively are estimated to affect up to 2% of couples.³⁴ Screening programs for such disorders are already in place in regions where case subjects are found at relatively higher prevalence.³⁵ Extending these screening efforts to other regions requires a cost-benefit analysis based on incomplete information: genetic risk remains difficult to assess in regions with small population sizes (where the number of affected individuals is low) or with substantial recent migration.

By identifying regions with high predicted carrier rate, ISGen provides useful information for the most efficient extension of screening programs. Where genealogies are available, the importance sampling scheme presented here represents a simple way to estimate regional carrier rates, without going through the time- and resource-consuming process of recruiting and genotyping individuals in each region. For example, ISGen predicts the highest allele frequency in Quebec for the CAID mutation at 0.64% in the Charlevoix region, even though no case subjects or carriers have been reported in that area. This is 24% more than in the more populated Saguenay region where most case subjects have been identified and screening programs are already in place.

The model considered still has limitations. For example, it assumes that the genealogy is specified exactly. However, in some cases, the model defined by Equations 5 or 7 can be sensitive to genealogical errors. Allowing for adoption or false paternity is conceptually straightforward, but there are enough statistical and computational subtleties that we will leave this for future work. In short, even though it is straightforward to allow for adoption, missed paternities, or incorrect genealogical links while simulating inheritance histories, the importance sampling scheme that we have used above must be modified, as any ancestor now has a small but nonzero probability of contributing the minor allele. The same argument holds for multiple founding ancestors: it is straightforward to allow for multiple ancestors to have contributed an allele (this would happen naturally if we did not use importance sampling!), but allowing for multiple founders while ensuring rapid convergence requires more careful tuning of the importance sampling scheme.

We presented and implemented ISGen for neutral and lethal recessive alleles because the simple relationship between carrier fitness and genealogical structure simplifies the formulation and implementation. We leave for future work the analysis of alleles with more general modes of inheritance and fitness effects. In particular, estimates of fitness have been performed within the BALSAC genealogy using the effective family size, or number of married children.¹⁰ Family sizes can be influenced by geographic and cultural factors as well as by selection, and their modeling requires more careful discussion.

More generally, we have shown that inferring population-scale allele transmission histories is computationally feasible, even in genealogies containing millions of individuals. We have also made the corresponding software package ISGen open-source and freely available at the URL indicated below. Understanding the relative roles of drift and selection in shaping the distribution of disease variants has applications for both medical and evolutionary genetics. Demographic events such as serial founder effects, range expansions, and assortative mating can dramatically alter variant distributions and the effect of natural selection.^{10, 31} The increasing availability of large-scale genealogical data, together with statistical tools to infer allele transmissions over time, provides an opportunity to study autosomal inheritance with an unprecedented level of detail.

Declaration of Interests

The authors declare no conflict of interest.

Published: December 6, 2018

Appendix A: Symbol Glossary

ω: Minor allele frequency in ancestral source population

N_founders: Number of founders in the genealogy

a: Ancestral (founder) origin of minor allele

$\mathcal{A}$: Set of all founders in the genealogy

c: The set of haplotypes within genealogically connected individuals that have been observed to be minor

S: The (observed) event that haplotypes c carry the minor allele

$\text{Γ}$: A simulated inheritance path ascending from the minor alleles within c

A: A random variable representing the founder who carried the minor allele

${\mathrm{1}}_a\left(\text{Γ}\right)$_: Indicator function denoting whether $\text{Γ}$ coalesces to ancestor a

M: Number of Monte Carlo iterations

p: Original (unbiased) probability distribution of inheritance paths

q: Importance sampling (biased) probability distribution of inheritance paths

α: Number of allele transmissions in path $\text{Γ}$

β: Number of allele transmissions in path $\text{Γ}$ with only one valid maternal/paternal path consistent with coalescence

γ: Number of times a homozygote inconsistent with coalescence could have been created during the climbing process

F: Random variable representing the minor allele frequency in the population, independent of genealogical information

f: Observed value of the minor allele frequency in the population

$\partial \text{Γ}$: Boundary of $\text{Γ}$ (first-generation descendants who do not carry a minor allele)

${\varphi }_k$: Binomial success probability of ancestors in probability bin i being the true generating ancestors

${\tau }_k$_: Total number of ancestors in bin i

x_k: Number of true generating ancestors in bin i

$E_{\text{Γ}}$: Expectation summed over inheritance paths ${\text{Γ}}_j$

$B_i\sim b_i\left(t_i\right)$_: The contribution of individual i to global minor allele frequency given they have a single parent simulated to carry t_i alleles

$Y_i\sim y_i\left(t_i\right)$: The contribution of individual i to global minor allele frequency given they carry $t_i$ alleles themselves

${\delta }_{i,j}$: Kronecker delta function

K: True number of carriers in population

N: True number of individuals in the population

n: Size of sample taken from population (of size N)

k: Number of observed carriers in sample n

$H\left(k;N,n,K\right)$: Hypergeometric distribution

${\nu }_{i,self}$: Number of alleles carried by individual i

${\nu }_{i,parent}$: Number of alleles carried by the parent (who is simulated to have carried an allele) of individual i

$\text{Λ}$: Event that all minor allele lineages coalesce in the genealogy

${\mathrm{1}}_{\text{Λ}}\left(\text{Γ}\right)$: Indicator function denoting whether $\text{Γ}$ coalesces to a single ancestor

R_m: Random variable representing minor allele frequency in an arbitrary region m

$r_m$: Realized value of R_m

${\hat{r}}_{m,\text{kin}}$: Kinship-based estimate of regional allele frequency r_m

${\hat{r}}_{m,\text{kin},\text{ corrected}}$: Kinship-based estimate of regional allele frequency $r_m$, corrected to be conditional on global frequency of minor allele

h: Number of meioses since the most recent common ancestor (MRCA) of the carriers

L: Length in Morgans of longest haplotype shared among all carriers of the minor allele

l: Observed value of L

Appendix B: Jointly Modeling Individuals Inside and Outside of the Genealogy

We explained in the main text how to compute the posterior probability $P\left(a|S\right)$ of ancestor a being the ancestral carrier given the observed event S that the observed carriers received the minor alleles. We want to use the refined posterior $P\left(a|S,F=f\right),$ where F is the random variable denoting the minor allele frequency in individuals not linked to the genealogy. As before, this will be computed from the likelihood using Bayes theorem and a flat prior on all ancestors $P\left(a\right)=1/\left|\mathcal{A}\right|$. Letting $\mathcal{A}$ represent the set of all founding individuals.

$$P\left(a|S,F=f\right)=\frac{P\left(S,F=f|a\right)P\left(a\right)}{{\sum }_{a^{\prime }\in \mathcal{A}}P\left(S,F=f|a^{\prime }\right)P\left(a^{\prime }\right)}$$ (Equation B1)

$$=\frac{P\left(S,F=f|a\right)}{{\sum }_{a^{\prime }\in \mathcal{A}}P\left(S,F=f|a^{\prime }\right)}.$$ (Equation B2)

Now recall that ${\mathrm{1}}_a\left(\text{Γ}\right)$ indicates whether a simulated inheritance path $\text{Γ}$ coalesces to founding ancestor a, so that $P\left(S|\text{Γ},a\right)={\mathrm{1}}_a\left(\text{Γ}\right)$, and the probability $P\left(\text{Γ}\right)$ of an inheritance path is independent of a, that is, $P\left(\text{Γ}|a\right)=P\left(\text{Γ}\right)$. We then have

$$\begin{array}{c}P\left(S,F=f|a\right)=\sum _{\text{Γ}}P\left(S,F=f|\text{Γ},a\right)P\left(\text{Γ}|a\right)\\ =\sum _{\text{Γ}}P\left(F=f|\text{Γ},S,a\right)P\left(S|\text{Γ},a\right)P\left(\text{Γ}|a\right)\\ =\sum _{\text{Γ}}P\left(F=f|\text{Γ},S,a\right){\mathrm{1}}_a\left(\text{Γ}\right)P\left(\text{Γ}\right).\end{array}$$ (Equation B3)

Under the importance sampling scheme described in the main text, we can rewrite this estimate as

$$\begin{array}{c}P\left(S,F=f|a\right)=E_{\text{Γ}}\left[P\left(F=f|\text{Γ},S,a\right){\mathrm{1}}_a\left(\text{Γ}\right)\right]\\ \simeq \frac{1}{M}\sum _{j=1}^M{\mathrm{1}}_a\left({\text{Γ}}_j\right)\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}P\left(F=f|{\text{Γ}}_j,S,a\right).\end{array}$$ (Equation B4)

This expression can then be substituted into Equation B2 to provide an importance sampling estimate of $P\left(a|S,F=f\right)$.

Appendix C: Efficiently Estimating the Probability of the Observed Allele Frequency

In the main text and Figure 3, we argued that the probability distribution of the population allele frequency $P\left(F|\text{Γ}\right)$ can be estimated by performing a sum over the contributions of individuals in the path boundary $\partial \text{Γ}$, if individuals within $\text{Γ}$ all carry the minor allele.

Because the alleles of individuals in $\partial \text{Γ}$ are left unassigned during the climbing process that generated $\text{Γ}$, their contributions to the number of minor alleles in the population first depends on whether or not they received minor alleles from individuals in $\text{Γ}$. For simplicity of exposition we assume that each boundary individual has only one parent in the tree, although similar derivations can be made when both parents are in $\text{Γ}$. Since this is a rare occurrence, ISGen currently treats each individual in the boundary of the tree as if it had a single parent in $\text{Γ}$.

For each individual i in $\partial \text{Γ}$, we first denote by ${\nu }_{i,parent}$ the number of copies of the minor allele their parent in $\text{Γ}$ was simulated to have carried, and by ${\nu }_{i,self}$ the number of copies of the minor allele they may carry themselves. Let Y_i be the number of copies of the minor allele that i contributes to the present-day population, and $y_i\left[{\nu }_{i,self}\right]$ the distribution of Y_i given that i carried ${\nu }_{i,self}$ copies of the minor alleles:

$$Y_i|{\nu }_{i,self}\sim y_i\left[{\nu }_{i,self}\right].$$

We estimate this distribution using a single set of genealogy-wide allele-dropping simulations.

Then, assuming that $i\in \partial \text{Γ}$, let B_i denote the number of minor alleles that i contributes to the present-day population. Given the single-founder assumption, the minor allele frequency in a population of size N (excluding alleles inherited through $\text{Γ}$) is

$$F\simeq \frac{1}{N}\sum _{i\in \partial \text{Γ}}{B}_i.$$ (Equation C1)

We estimate the expected B_i by conditioning on the possible transmissions. Let $b_i\left[{\nu }_{i,parent}\right]$ be the conditional distribution of B_i given that the parent of i in $\text{Γ}$ carries ${\nu }_{i,parent}$ alleles:

$$B_i|{\nu }_{i,parent}\sim b_i\left[{\nu }_{i,parent}\right].$$

If we neglect the probability of inheriting a minor allele from the parent outside $\text{Γ},$ the conditional distributions $b_i\left[{\nu }_{i,parent}\right]$ and $y_i\left[{\nu }_{i,self}\right]$ follow:

$$\begin{array}{c}{b}_i\left[0\right]\left(B_i\right)\simeq {\delta }_{0,B_i}\\ b_i\left[1\right]\left(B_i\right)\simeq \frac{1}{2}{\delta }_{0,B_i}+\frac{1}{2}{y}_i\left[1\right]\left(B_i\right)\\ b_i\left[2\right]\left(B_i\right)\simeq y_i\left[1\right]\left(B_i\right).\end{array}$$

The distribution of F can be then calculated using Equation C1 via the convolution of the corresponding $b_i\left[{\nu }_{i,parent}\right]$. In this way, once we have simulated y_i for all individuals i in the genealogy, we can quickly estimate the distribution of F for any $\text{Γ}$ encountered in our Monte Carlo simulations, giving a huge gain in efficiency over a large number of simulated inheritance paths. A comparison of this method to allele-dropping simulations is shown in Figure S3.

Finite Sample Estimates of the Allele Frequency

In practice, the population allele frequency in individuals not connected to the genealogy is estimated from a sample of the population. We first denote the population size by N and let the total number of minor alleles (observed and unobserved) in the population be represented by K.

In the main text, a trajectory $\text{Γ}$ only contributes to the likelihood if it coalesces to the contributing founder, an event we label as $\text{Λ}$ in this section to simplify notation. Given $\text{Λ}$, the likelihood of an inheritance path $\text{Γ}$ giving rise to the observed number of carriers k = fN in a population sample of size n is given by summing over all values of K to get

$$P\left(F=f|\text{Γ},\text{Λ}\right)=P\left(k|n,\text{Γ},\text{Λ}\right)=\sum _{K=0}^{N}P\left(k|n,K,\text{Γ},\text{Λ}\right)P\left(K|n,\text{Γ},\text{Λ}\right).$$ (Equation C2)

Assuming that the subsample of n individuals was taken at random, then the number of observed carriers k given the total number of carriers K is independent of the particular inheritance path $\text{Γ}$, and follows the hypergeometric distribution:

$$P\left(k|n,K,\text{Γ},\text{Λ}\right)=P\left(k|n,K\right)=H\left(k;N,n,K\right)$$

and similarly the true number of carriers is independent of the sampling:

$$P\left(K|n,\text{Γ},\text{Λ}\right)=P\left(K|\text{Γ},\text{Λ}\right)$$

giving

$$P\left(F=f|\text{Γ},\text{Λ}\right)=P\left(k|n,\text{Γ},\text{Λ}\right)=\sum _{K=0}^{N}H\left(k;N,n,K\right)P\left(K|\text{Γ},\text{Λ}\right)$$ (Equation C3)

which we use in the calculation of Equation 5 in the main text.

Appendix D: Regional Allele Frequency Estimates

We can use the simulated inheritance paths to estimate regional allele frequencies given the observed event S that the set of haplotypes c in the carrier individuals do indeed carry the minor allele, and the event that we observe f carriers unconnected to the genealogy, under the assumption $\text{Λ}$ that $\text{Γ}$ climbs from carriers of the minor allele and coalesces to a single individual within the genealogy. Letting R_m be the number of carriers in some subset of individuals m (usually defined as a geographic region), we have

$$E\left[R_m|F=f,\text{Λ},S\right]=\sum _{r_m}{r}_{m}P\left(R_m=r_m|F=f,\text{Λ},S\right).$$ (Equation D1)

Summing over all inheritance paths $\text{Γ}$, the chain rule gives

$$\begin{array}{c}P\left(R_m=r_m|F=f,\text{Λ},S\right)=\sum _{\text{Γ}}P\left(R_m=r_m,\text{Γ}|F=f,\text{Λ},S\right)\\ =\frac{{\sum }_{\text{Γ}}P\left(\text{Λ},R_m=r_m,\text{Γ},F=f|S\right)}{P\left(F=f,\text{Λ}|S\right)}\\ =\frac{{\sum }_{\text{Γ}}P\left(\text{Λ}|R_m=r_m,\text{Γ},F=f,S\right)P\left(R_m=r_m|\text{Γ},F=f,S\right)P\left(F=f|\text{Γ},S\right)P\left(\text{Γ}\right)}{P\left(F=f,\text{Λ}|S\right)},\end{array}$$ (Equation D2)

where the last line uses the fact that $P\left(\text{Γ}|S\right)=P\left(\text{Γ}\right).$ Because the coalescence condition $\text{Λ}$ is fully determined by $\text{Γ}$ and S, we can write $P\left(\text{Λ}|\text{Γ},S,\cdot \right)=P\left(\text{Λ}|\text{Γ}\right)={\mathrm{1}}_{\text{Λ}}\left(\text{Γ}\right)$, where ${\mathrm{1}}_{\text{Λ}}\left(\text{Γ}\right)$ indicates whether $\text{Γ}$ coalesces to a single lineage. Using the law of total probability and the chain rule on the denominator as well, we can write

$$P\left(R_m=r_m|F=f,\text{Λ},S\right)=\frac{{\sum }_{\text{Γ}}{\mathrm{1}}_{\text{Λ}}\left(\text{Γ}\right)P\left(R_m=r_m|\text{Γ},F=f,S\right)P\left(F=f|\text{Γ},S\right)P\left(\text{Γ}\right)}{{\sum }_{{\text{Γ}}^{\text{'}}}{1}_{\text{Λ}}\left({\text{Γ}}^{\text{'}}\right)P\left(F=f|{\text{Γ}}^{\text{'}},S\right)P\left({\text{Γ}}^{\text{'}}\right)}.$$ (Equation D3)

We can now write Equation D1 as

$$E\left[R_m|F=f,\text{Λ},S\right]=\sum _{r_m}{r}_m\frac{{\sum }_{\text{Γ}}{\mathrm{1}}_{\text{Λ}}\left(\text{Γ}\right)P\left(R_m=r_m|\text{Γ},F=f,S\right)P\left(F=f|\text{Γ},S\right)P\left(\text{Γ}\right)}{{\sum }_{{\text{Γ}}^{\text{'}}}{\mathrm{1}}_{\text{Λ}}\left({\text{Γ}}^{\text{'}}\right)P\left(F=f|{\text{Γ}}^{\text{'}},S\right)P\left({\text{Γ}}^{\text{'}}\right)}$$ (Equation D4)

$$=\frac{E_{\text{Γ}}\left[1_{\text{Λ}}\left(\text{Γ}\right)E\left[R_m|\text{Γ},F=f,S\right]P\left(F=f|\text{Γ},S\right)\right]}{E_{\text{Γ}}\left[1_{\text{Λ}}\left(\text{Γ}\right)P\left(F=f|\text{Γ},S\right)\right]}.$$ (Equation D5)

We then estimate $P\left(F=f|\text{Γ},S\right)$ using the methods described in the main text and Appendix C.

Computing $E\left[R_m|\text{Γ},F=f,S\right]$ is challenging, because we do not have an expression for the distribution of R_m conditioning on F. We do have an expression for $E\left[R_m|\text{Γ},S\right]$, but R_m is not independent of f: when performing allele dropping from $\text{Γ}$, each transmission of the minor allele increases both the expectations of f and R_m.

To account for this correlation, we wish to simply scale the distribution based on the difference between the observed and expected global allele frequency. This is especially justified in a growing population, where an early success in allele transmission has a much larger effect on the variance of F and R_m than a later transmission. For example, if the founder individual transmits the minor allele to eight out of eight offspring, the expected descendant allele frequency among descendants is double its naive expectation. By contrast, the same information about a recent individual who is only one among hundreds of carriers will only have a marginal effect on the expected frequency. We can therefore consider that the global allele frequency is a random variable that is primarily determined by the proportion σ of individuals in $\partial \text{Γ}$ who receive the minor allele, and neglect the subsequent variation. If the sample size n is large enough, the allele frequency F drawn from a given inheritance path $\text{Γ}$ is approximately $2\sigma e_{\text{Γ}},$ where $e_{\text{Γ}}$ is the expected allele frequency generated from $\text{Γ}$.

Under this simplified model, we can compute

$$\begin{array}{c}E\left[R_m|\text{Γ},F=f,S\right]=\sum _{r_m}{r}_{m}P\left(R_m=r_m|\text{Γ},F=f,S\right)\\ =\sum _{r_m}{r}_m\sum _{\sigma }P\left(R_m=r_m,\sigma |\text{Γ},F=f,S\right)\\ =\sum _{r_m}{r}_m\sum _{\sigma }P\left(R_m=r_m|\sigma ,\text{Γ},F=f,S\right)P\left(\sigma |\text{Γ},F=f,S\right)\\ =\sum _{r_m}{r}_m\sum _{\sigma }P\left(R_m=r_m|\sigma ,\text{Γ},F=f,S\right){\delta }_{\sigma -\frac{F}{2e_{\text{Γ}}}}\\ =\sum _{r_m}{r}_{m}P\left(R_m=r_m|\sigma =\frac{F}{2e_{\text{Γ}}},\text{Γ},F=f,S\right)\\ =\sum _{r_m}{r}_{m}P\left(R_m=r_m|\sigma =\frac{f}{2e_{\text{Γ}}},\text{Γ},S\right)\\ =E\left[R_m|\sigma =\frac{f}{2e_{\text{Γ}}},\text{Γ},S\right].\end{array}$$ (Equation D6)

Since $R_m\simeq \sum _{i\in \partial \text{Γ}}{B}_{m,i},$ where $B_{m,i}$ is the number of minor alleles inherited, in population m, from boundary individual i, we find $E\left[R_m|\sigma ,\text{Γ},S\right]\simeq \sum _{i\in \partial \text{Γ}}E\left[B_{m,i}\right]=\sum _{i\in \partial \text{Γ}}\sigma E\left[C_{m,i}\right],$ where $C_{m,i}$ is the number of minor alleles inherited, in population m, from boundary individual $i,$ conditional on i carrying a minor allele. Since $E\left[R_m|\text{Γ},S\right]\simeq \sum _{i\in \partial \text{Γ}}1/2E\left[C_{m,i}\right],$ we conclude $E\left[R_m|\sigma \right]\simeq 2\sigma E\left[R_m\right]$, and

$$E\left[R_m|\text{Γ},F=f,S\right]\simeq \frac{f}{e_{\text{Γ}}}E\left[R_m|\text{Γ},S\right].$$ (Equation D7)

In other words, we rescale the expected allele regional frequencies by the ratio of predicted to observed global allele frequencies.

Using the importance sampling scheme described in the main text to simulate only those ${\text{Γ}}_j$ which coalesce to a single founder, implying that $1_{\text{Λ}}\left({\text{Γ}}_j\right)=1$ for all $i=1,\dots ,M$, the expected regional allele frequency estimate becomes:

$$E\left[R_m|F=f,\text{Λ},S\right]\simeq \frac{f}{e_{\text{Γ}}}\frac{{\sum }_{j=1}^M\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}E\left[R_m|\text{Γ},S\right]P\left(F=f|\text{Γ},S\right)}{{\sum }_{j=1}^M\frac{p\left({\text{Γ}}_j\right)}{q\left({\text{Γ}}_j\right)}P\left(F=f|\text{Γ},S\right)}.$$ (Equation D8)

Kinship-Based Regional Allele Frequency Estimates

Since calculating all pairwise kinship scores for probands of the BALSAC genealogy would require generating a matrix with the order of 10¹² entries, we take a random sample of 100 probands from each of 23 geographic regions of Quebec. Then for each simulated patient panel, we calculate the average kinship of these groups of 100 individuals with all patients.

Note that the approximation in Equation D7 guarantees that our estimate of the global allele frequency is always exactly equal to the observed allele frequency. To ensure a fair comparison when evaluating the accuracy of importance sampling versus kinship-based methods, we use a similar scaling factor to incorporate the global allele frequency information into kinship estimates. Denoting regional mean kinship estimates by ${\hat{r}}_{m,kin}$ and the global mean kinship estimate by ${\hat{f}}_{kin}$, we use the estimator

$${\hat{r}}_{m,\text{kin},\text{ corrected}}={\hat{r}}_{m,\text{kin}}\frac{f}{{\hat{f}}_{\text{kin}}}$$

to calculate our kinship-based regional estimates.

Appendix E: Validating the Calibration of Ancestor Posterior Probabilities

As described in the main text, we validate the posterior probabilities of groups of ancestors within relatedness clusters. Relatedness clusters are defined as groups of ancestors who together have only a single shared path to all carriers of the affected alleles. Each nuclear family group within such a cluster may have a single extra path to some carriers, as long as they have only a single path to all of them. Probabilities for cluster J are then given by:

$$P\left(A\in J|S\right)=\sum _{a_i\in J}P\left(A=a_i|S\right).$$

After generating validation panels and calculating the posterior probabilities for each relatedness cluster, we bin clusters by their posterior probability and model the number of true generating ancestors in bin i as a binomial process with success probability ${\varphi }_k$. To generate confidence interval on ${\varphi }_k$, we let ${\tau }_k$ represent the total number of ancestors bin i and x_k the number of true generating ancestors. Assuming a flat prior for all ${\varphi }_k$,

$$P\left({\hat{\varphi }}_k|{\tau }_k,x_k\right)\sim \text{Beta}\left(x_k+1,{\tau }_k-x_k+1\right).$$ (Equation E1)

Appendix F: CAID Data and IBD Computation

11 homozygous patients were previously diagnosed and genetically characterized using the Illumina HumanOmni5-Quad chip.²⁷ We also used genotypes³⁶, ³⁷, ³⁸ from the Quebec Regional Population Sample (QRS) (see Web Resources) as a control group. Among the 229 genealogically connected control subjects, we found one heterozygous carrier of the CAID mutation, based on genotype and confirmed by Sanger sequencing. The observation of 3 carriers in a cohort of 900 genotyped French Canadians from CARTaGENE²⁹ gave us our estimate of the CAID allele frequency.

Our assumption of a single origin for the CAID allele within the BALSAC genealogy is based on the sharing of a 2.9 Mb homozygous segment on chromosome 3, described in the Applications section of the main text. This segment was discovered by analyzing segments within the patients which were identical-by-descent (IBD). The 11 affected individuals and 229 control individuals gave 240 genotypes with which to evaluate the extent of pairwise IBD sharing. IBD was inferred by the analysis of more than 300,000 genotyped SNPs common to the case subject and QRS control subjects, using BEAGLE 4 software.³⁹

Web Resources

• ISGen, https://github.com/DomNelson/ISGen

• BALSAC Project, http://balsac.uqac.ca/

• gnomAD Browser, http://gnomad.broadinstitute.org/

• OMIM, http://www.omim.org/

• Quebec Reference Sample, http://www.quebecgenpop.ca/