Secondary pool boiling effects

Abstract

A pool boiling phenomenon referred to as secondary boiling effects is discussed. Based on the experimental trends, a mechanism is proposed that identifies the parameters that lead to this phenomenon. Secondary boiling effects refer to a distinct decrease in the wall superheat temperature near the critical heat flux due to a significant increase in the heat transfer coefficient. Recent pool boiling heat transfer experiments using femtosecond laser processed Inconel, stainless steel, and copper multiscale surfaces consistently displayed secondary boiling effects, which were found to be a result of both temperature drop along the microstructures and nucleation characteristic length scales. The temperature drop is a function of microstructure height and thermal conductivity. An increased microstructure height and a decreased thermal conductivity result in a significant temperature drop along the microstructures. This temperature drop becomes more pronounced at higher heat fluxes and along with the right nucleation characteristic length scales results in a change of the boiling dynamics. Nucleation spreads from the bottom of the microstructure valleys to the top of the microstructures, resulting in a decreased surface superheat with an increasing heat flux. This decrease in the wall superheat at higher heat fluxes is reflected by a “hook back” of the traditional boiling curve and is thus referred to as secondary boiling effects. In addition, a boiling hysteresis during increasing and decreasing heat flux develops due to the secondary boiling effects. This hysteresis further validates the existence of secondary boiling effects.

Enhancement of pool boiling heat transfer with the use of functionalized micro/nanostructured surfaces is currently a very popular research area. Surface functionalization of two-phase heat transfer surfaces can be accomplished through a wide range of fabrication techniques ranging from complex microfabrication to simple etching and deposition techniques.¹ This functionalization of the boiling surface is used to increase micro/nanoscale roughness, capillary wicking, and porosity which lead to increased critical heat fluxes and heat transfer coefficients. With silicon as the base substrate, significant enhancement of the critical heat flux and heat transfer coefficients is accomplished with the fabrication of microposts, nanowires, and nanostructuring.^2–8 These methods resulted in maximum critical heat fluxes around 250 W/cm² (Ref. 6) with maximum feature sizes of about 100 μm.² With the use of highly conductive copper and aluminum surfaces, functionalization is typically achieved with chemical etching processes or deposition techniques which result in maximum feature sizes of only a few microns,^9–18 and a moderate increase in critical heat flux and heat transfer coefficient. However, limited research on surface functionalization has been conducted on lower thermal conductivity metallic materials. This is largely due to the limited current state-of-the-art technologies for functionalizing such surfaces. Functionalization of Zircaloy surfaces has been accomplished with the use of an anodization process and was shown to result in critical heat fluxes up to about 200 W/cm^2,19,20 however with relatively low microstructures height. Surface enhancement techniques for stainless steel and similar metals are limited to coatings and deposition techniques.^21–23

In this paper, a phenomenon referred to as “secondary boiling effects” is explored. Secondary boiling effects correspond to a decrease in wall superheat near the critical heat flux and are reflected by a “hook back” on the boiling curve. Throughout the literature, only a few examples of secondary boiling effects can be found.^6,21,24,25 Secondary boiling effects can be seen on 10 μm silicon nanowire surfaces, stainless steel surfaces with 200 μm aluminum porous coatings,²¹ 35 μm tall stainless steel mound structures with a nanoporous layer,²⁴ and 400 μm tall copper microchannels with a porous coating.²⁵ An attempt to explain secondary boiling effects has been given by Chen et al.⁶ and Patil et al.²⁵ In the work conducted by Chen et al., secondary boiling effects were seen on 10 μm tall silicon nanowires. It was assumed that this was a result of submicron nucleation sites activating at higher wall superheat temperatures. Copper nanowires were also studied and secondary boiling effects were not seen, presumably because of a lack of submicron potential nucleation sites. Patil et al. observed secondary boiling effects with copper microchannel structures with a height of 400 μm or more.²⁵ It was assumed that this was a result of increased nucleation and liquid motion between channels and no further explanation was given.

In the present experiment, we use functionalized 304 stainless steel, Inconel 740 H, and copper surfaces created with the use of Femtosecond Laser Surface Processing (FLSP) to illustrate secondary boiling effects. The FLSP uses a complex dynamic of laser ablation to create self-organized mound-like microstructures on the metallic surfaces. During processing, a porous nanoparticle layer is also uniformly deposited on top of the mound-like surface micro-structures. These unique functionalized surfaces are studied for their two-phase heat transfer performance in a controlled pool boiling experimental setup. The sample surface consists of a thin, 1.0 in. diameter stainless steel or Inconel disk (thickness of 0.010 in. for stainless steel and 0.020 in. for Inconel) brazed to a thick copper heating block. Heat flux is measured via embedded thermocouples and surface temperature is calculated. A more in depth description of the FLSP technique and the pool boiling experimental setup is given by Kruse et al.^24,26

Five unique surfaces are analyzed in this work, two Inconel, two stainless steel, and one copper. Their surface characteristics have been obtained using a Keyence Laser Confocal Microscope and are tabulated in Table I. The two Inconel samples (Tall and Short Inconel) were designed to be extreme cases of each other representing the upper and lower microstructure size limits. A stainless steel was processed in order to have a structure height in between the two Inconel samples. An additional stainless steel surface of also medium height (Hysteresis SS) was created to specifically study hysteresis effects resulting from secondary boiling effects. Finally, a copper FLSP surface of medium height was fabricated to illustrate the role of thermal conductivity.

TABLE I.

Geometric and heat transfer characterization for each of the FLSP test surfaces.

Sample	Peak-to-valley height (μm)	Surface roughness (μm)	Surface area ratio	Biot number
Tall Inconel	55.2	12.2	8.1	0.21
Short Inconel	9.1	1.8	2.1	0.03
Medium SS	35.8	7.4	4.7	0.14
Medium copper	37.5	8.6	3.1	0.006
Hysteresis SS	27.1	5.1	5.1	0.1

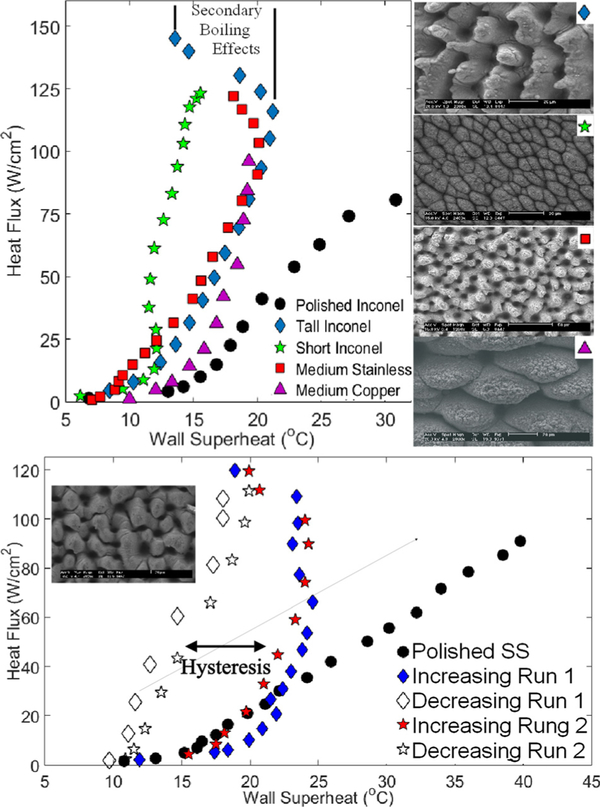
The top part of Figure 1 illustrates the traditional boiling curve, with the corresponding SEM images, for each of the first four samples given in Table I. Using deionized water as the working fluid, these curves were obtained at steady state for each point and in an increasing heat flux direction. The steady state was determined with a LabVIEW program and after about 20 min of boiling at each heat flux. The heat flux was continually increased until the critical heat flux (CHF) was reached. A polished Inconel reference sample was also included for comparison. The maximum CHF value and heat transfer coefficient (HTC) were seen with the tall Inconel sample and were 145 W/cm² and 107 000 W/m²-K, respectively. As seen with the tall Inconel and the medium stainless steel samples, the wall superheat temperature reaches a maximum and then decreases with a further increase in the heat flux until the CHF is reached. This shift in the boiling curve corresponds to a dramatic increase in the heat transfer coefficient. This phenomenon is what we refer to as the secondary pool boiling effects. This phenomenon is not seen with the copper surface or the short Inconel surface. As the micro-structure height increases, the degree of secondary boiling effects (degree of temperature change) also increases. With the tall Inconel surface, a 7.7° temperature change was seen. The medium stainless steel sample also follows this trend while the copper surface with similar height microstructures does not.

FIG. 1.

Top: Pool boiling curves illustrating the “hook back” associated with secondary boiling effects. Bottom: Hysteresis effect seen with increasing and decreasing heat fluxes due to secondary boiling effects.

The bottom part of Figure 1 shows a hysteresis that develops due to the secondary boiling effects. All data (except that for the polished sample) were obtained with the stainless steel hysteresis sample described in Table I. In this figure, the heat flux is increased up to 120 W/cm² in the method previously described and secondary boiling effects can be observed but the CHF was not reached. After 120 W/cm² is reached, the heat flux is then decreased and data are collected at steady state. Heat flux was decreased until nucleation stopped. This change in the boiling curve with respect to increasing and decreasing heat fluxes is referred to as the boiling curve hysteresis. After the completion of the first run, the system was allowed to completely cool down and the process was repeated. Similar results were observed and indicated as “Run2.” This eliminates the possibilities that secondary boiling effects could be caused by initial effects, chemical or physical changes, or experimental errors.

Typically, increases in the heat transfer coefficient are associated with the enhanced nucleation dynamics on the micro/nanostructure, although this is not the only factor that can alter boiling efficiency. In the case of the boiling surfaces created with the FLSP process, a unique combination is created that results in the secondary boiling effects. This combination consists of tall mound-like microstructures that are coated in a porous nanoparticle layer that exhibits a wide range of potential nucleation cavity sizes. The characterization of a tall structure depends on the Biot number,$Bi=\frac{h*Lc}{k},$ where h is the heat transfer coefficient, L_c is the characteristic length scale (i.e., height of microstructure), and k is the thermal conductivity of the solid material. Temperature gradients along the microsctructures are negligible for Biot numbers substantially less than 0.1. Using a typical heat transfer coefficient of 60 000 W/m²-K, and the corresponding microstructure heights, the corresponding Biot number was calculated for each of the test surfaces and presented in Table I. All of the surfaces that displayed secondary boiling effects had a Biot number greater than 0.1 and thus signifi-cant temperature variation along their microstructures.

In order to estimate the temperature range along the microstructures, a simple 1D conduction model was used. This was done for both the tall and short microstructure heights and two steady state conditions. A constant heat flux was applied to the bottom of the microstructure and a constant surface temperature was applied to the top of the micro-structures with values corresponding to Figure 1. The sides of the microstructures were considered to be insulated due to the thermal boundary layer thickness and heating from adjacent microstructures. Near the onset of secondary boiling effects, boundary conditions of 115 W/cm² and 121.1 °C were used. The maximum temperature at the base of the tall Inconel structure was predicted to be 128.6 °C, a temperature drop of 7.5 °C. The short Inconel structure was not included in this scenario because secondary boiling effects were not observed. As secondary boiling effects progress, the surface temperature begins to decrease. The second simulation scenario corresponds to the critical heat flux for both the short and tall Inconel structures. The simple 1D conduction model resulted in a temperature drop of 9.4 °C (122.8 to 113.4 °C) for the tall Inconel structure and 2.4 °C (117.8 to 115.4 °C) for the short Inconel structure. A copper microstructure was also simulated using the identical boundary conditions as the tall Inconel surface. This resulted in a maximum temperature drop of about 0.3 °C for the higher heat flux conditions and thus a nearly uniform temperature profile as predicted by the Biot number.

Using these temperature ranges, potentially active nucleation cavity sizes can be calculated. Using the model proposed by Hsu,²⁷ a minimum and maximum cavity diameters of around. 5 μm and 10 μm, respectively, could be active at the maximum (128.6 °C) surface temperature. At temperatures near the onset of nucleate boiling (110 °C), the active nucleation cavity size range is between 1.5 and 10 μm. The nucleation cavity model is as follows:

$$Dmax,Dmin=\frac{{\delta }_t{C}_2}{C_1}\frac{\Delta T_w}{\Delta T_w+\Delta T_{sub}}\times \left[1\pm \sqrt{1-\frac{8C_1\sigma T_{sat}\left(\Delta T_w+\Delta T_{sub}\right)}{{\rho }_v{h}_{fg}{\delta }_t{\left(\Delta T_w\right)}^2}}\right],$$ (1)

where C₁ = 1 + cosθ, C₂ = sinh, δ_t is the thermal boundary layer thickness, ΔT_w corresponds to the wall superheat, and ΔT_sub is the liquid subcooling. The remaining parameters θ, σ, P_v, and h_{f g}, correspond to the contact angle, the surface tension of the liquid, vapor density, and heat of vaporization of the liquid. Additional information related to the calculation of cavity sizes and the results are given in the supplementary material.²⁸

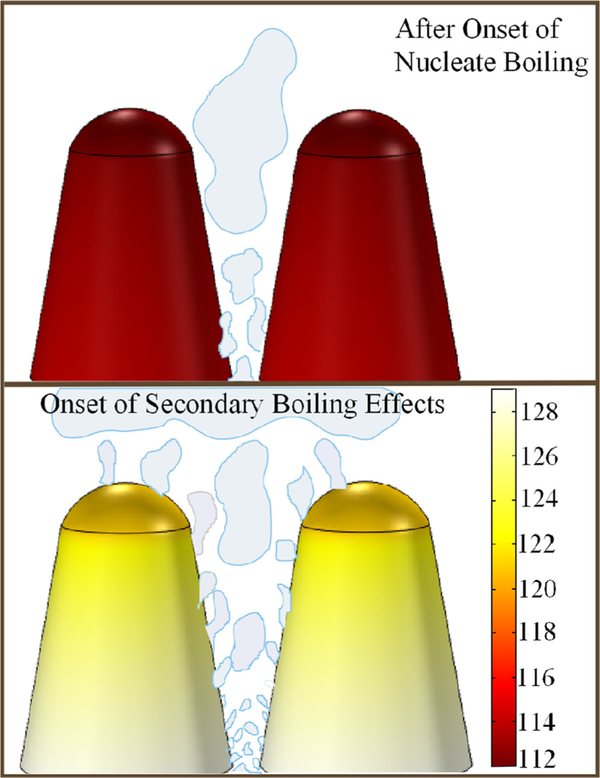
In order for secondary boiling effects to be present, it is ideal that a surface has a wide size range of potential nucleation cavities with significantly large temperature gradients. With the FLSP surfaces, a multiscale highly wetting surface is created regardless of the material composition. Although these surfaces have large sized cavities in between the micro-structures (10–20 μm), vapor will not be trapped in these cavities due to the highly wetting and wicking properties of the surface and the results from (Eq. (1)). Vapor can be trapped in the smaller nucleation cavities found on the sides and valleys of the microstructures. Thus, nucleation will occur from these smaller cavities and not the larger cavities between microstructures. Figure 2 describes the change in the nucleation dynamic that occurs during secondary boiling effects. Nucleation first starts from larger cavities located in the valleys of the microstructures where the temperatures are the highest. At low heat fluxes, the surface temperatures are relatively low and thus only larger nucleation cavities are active. In addition, minimal temperature drop in the tall and short structures occurs which results in a uniform distribution of active nucleation sites. As the heat flux is increased, the temperature drop along the tall structures with lower thermal conductivity increases allowing the nucleation to progress along the length of the microstructure. Because the relative temperature is elevated everywhere along the microstructures, activation of smaller submicron cavities will occur near the base of the microstructure. The increased temperature drop results in an uneven distribution of active nucleation cavities, where the density is greater near the bottom of the valleys. Secondary boiling effects are the result of this addition of new nucleation sites on the upper portion of the microstructure and smaller newly activated nucleation sites near the bottom. The changing nucleation characteristic length scale results in a nonlinear increase in the heat transfer coefficient and decreased wall superheat, and is reflected in the characteristic “hook back” seen on the boiling curve. In the case of the short structures and higher thermal conductivity materials, the microstructures have nearly uniform temperatures, as indicated by the Biot number. The size range of potentially active nucleation sites remains constant across the entire height of the microstructure and thus secondary boiling effects were not observed with the short Inconel and copper surfaces.

FIG. 2.

Schematic that describes how nucleation evolves and extends from the bottom of the valleys to the peaks of the microstructures.

The SEM images in Figure 3 highlight the multiscale nature of the FLSP surfaces and the range of potential nucleation cavity sizes. These images correspond to the tall Inconel, medium stainless steel, and copper surfaces. The large valleys in between the microstructures are in the range of 10–20 μm or larger while smaller submicron to 5 μm cavities are located on the sides of the microstructures. In the case of the tall Inconel microstructure surface, submicron cavities located on the tops and sides of the microstructures are more abundant. These smaller nucleation cavities are also located at different heights along the microstructures as well as inside the deep valleys. The copper microstructure surface actually has the most submicron potential nucleation sites and yet secondary boiling effects were not seen due to the higher thermal conductivity. Additional SEM images of these surfaces are included in the supplementary material.²⁸

FIG. 3.

SEM images of the medium SS, tall Inconel, and medium copper sample highlighting the range of sizes and vertical locations of potential nucleation cavities.

As the surface temperature decreases due to secondary boiling effects, it might be expected that the submicron nucleation cavities will deactivate due to unfavorable temperatures. However, this is not the case. Once the secondary boiling effects begin, these additional nucleation sites remain active at the lower wall superheat temperatures. This is validated by the hysteresis curves shown in Figure 1. If these additional nucleation sites are easily deactivated at the cooler superheat temperatures, then this significant hysteresis would not be seen and the decreasing heat flux curve would follow the increasing curve.

Secondary boiling effects refer to a unique shift (“hook back”) in the boiling curve near the critical heat flux which corresponds to an increased heat transfer coefficient. Through an experimental study, it has been determined that secondary boiling effects are due to a combination of temperature drop and nucleation length scales resulting in a changing boiling dynamics. The temperature drop is dependent on the microstructure thermal conductivity and micro-structure height. Nucleation starts at the bottom of the microstructure valleys and extends to the microstructure peaks as the heat flux increases. This creates a nonlinear increase in the heat transfer coefficient which results in the characteristic “hook back” in the boiling curve. Secondary boiling effects result in a boiling hysteresis which further validates its existence. Because of the significant impact that secondary boiling effects can have in many heat transfer applications, we suggest that additional studies can be conducted by the heat transfer community to further shed light into this important phenomenon.