Going with the Flow: Multiscale Insights into the Composite Nature of Water Transport in Roots^,

A bio-physical model of the ”root hydraulic anatomy“ allows testing hypotheses related to radial water transport down to the cell level and proves complementary to current experimental approaches.

Abstract

As water often limits crop production, a more complete understanding of plant water capture and transport is necessary. Here, we developed MECHA, a mathematical model that computes the flow of water across the root at the scale of walls, membranes, and plasmodesmata of individual cells, and used it to test hypotheses related to root water transport in maize (Zea mays). The model uses detailed root anatomical descriptions and a minimal set of experimental cell properties, including the conductivity of plasma membranes, cell walls, and plasmodesmata, which yield quantitative and scale-consistent estimations of water pathways and root radial hydraulic conductivity (k_r). MECHA revealed that the mainstream hydraulic theories derived independently at the cell and root segment scales are compatible only if osmotic potentials within the apoplastic domains are uniform. The results suggested that the convection-diffusion of apoplastic solutes explained most of the offset between estimated k_r in pressure clamp and osmotic experiments, while the contribution of water-filled intercellular spaces was limited. Furthermore, sensitivity analyses quantified the relative impact of cortex and endodermis cell conductivity of plasma membranes on root k_r and suggested that only the latter contributed substantially to k_r due to the composite nature of water flow across roots. The explicit root hydraulic anatomy framework brings insights into contradictory interpretations of experiments from the literature and suggests experiments to efficiently address questions pertaining to root water relations. Its scale consistency opens avenues for cross-scale communication in the world of root hydraulics.

Worldwide crop production is frequently limited by situations where the water supply is lower than the crop evaporative demand (Cattivelli et al., 2008). To develop crops and crop management systems that maintain high yields under water-limited conditions, we need a clear understanding of the variables and processes that control root water capture and plant water use. Root water uptake is influenced largely by the hydraulic properties of the soil-root network (Sperry et al., 2002; Draye et al., 2010; Schoppach et al., 2014). Among these properties, the root radial conductivity (k_r) stands out as a central feature (Parent et al., 2009; Draye et al., 2010). It reportedly responds within hours to its hydric environment (Hachez et al., 2012; Caldeira et al., 2014), allowing rapid adjustments of xylem water status and flow rates between soil and roots (Meunier et al., 2018).

There is growing evidence that subcellular components, such as water channels (aquaporins) and plasmodesmata, contribute to the regulation of k_r (Steudle and Peterson, 1998; Parent et al., 2009). On the one hand, the abundance and conformation of aquaporins control transmembrane elements of water pathways via cell membrane permeability (L_p; Maurel and Chrispeels, 2001; Chaumont and Tyerman, 2014). The gating of aquaporins provokes k_r reductions of −60% to −70% (Ye and Steudle, 2006; Boursiac et al., 2008; Parent et al., 2009). On the other hand, the aperture and frequency of plasmodesmata, which connect the protoplasts of adjacent cells (Maule, 2008; Sevilem et al., 2013; Brunkard and Zambryski, 2017), regulate symplastic elements of water pathways. Additionally, hydrophobic substances such as lignin (e.g. in radial walls forming a Casparian strip) or suberin (e.g. in the walls of cells forming a suberin lamella; Enstone and Peterson, 2005; von Wangenheim et al., 2017) may obstruct apoplastic elements of water pathways around specific cell protoplasts. For brevity, a local element of a water pathway will be referred to as apoplastic, symplastic, or a transmembrane pathway, depending on its nature. Pathways that connect the root surface to xylem vessels will be referred to as radial pathways.

A major specificity of water flow principles across plasma membranes is membrane semipermeability. Membranes exclude specific solutes, thus generating cell turgor through the principle of osmosis (Katchalsky and Curran, 1967). The impact of solute selectivity on water flow across a membrane is formulated via a reflection coefficient (σ; dimensionless). The coefficient typically ranges between 1 (which applies to water flowing through a perfectly selective membrane) and 0 (which applies to water flowing through a medium completely permeable to solute [e.g. cell primary wall and plasmodesmata]), although negative values have been reported for strong basic anion-exchange membranes (Pusch and Woermann, 1970). In case σ is null, the water pressure difference (Δψ_p; MPa) alone drives the water flow. Otherwise, the osmotic potential difference (Δψ_o; MPa) contributes as an additional driver in the water potential difference. Each piece of the water pathway also is characterized by its hydraulic conductance (K; m³ MPa⁻¹ s⁻¹), resulting from its pore size distribution and geometry. Because water flow across roots is laminar (the Reynolds number is orders of magnitude too low to generate turbulence at this scale; see Gunning [1976]), local water flow rates (Q; m³ s⁻¹) are proportional to the associated K. Using appropriate values for σ, the following general equation describes water flow through plasmodesmata, membranes, and walls at the subcellular scale:

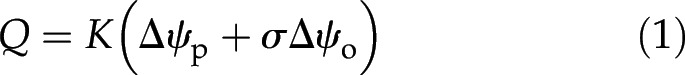Different approaches are used to estimate the intrinsic conductivities of each of the three types of pathway. First, L_p (i.e. conductance per membrane surface unit) is the most accessible of these properties. It can be measured with a cell pressure probe (Steudle and Jeschke, 1983). The foremost contribution of aquaporins to L_p can be quantified by repeating the measurement after acid loading, which provokes the closure of aquaporins due to their protonation (Tournaire-Roux et al., 2003). Second, the hydraulic conductance of individual plasmodesmata (K_PD) cannot be measured experimentally with the techniques currently available. However, their aperture can be estimated from the permeability of plasmodesmata to dyes (Lee et al., 2011). Recent studies still estimate K_PD with the Poiseuille-Hagen law (Foster and Miklavcic, 2017) and account for the partial occlusion of plasmodesmata by a desmotubular structure, leaving water pathways that are only 1 order of magnitude wider (2 × 10⁻⁹ m) than the aperture of an aquaporin (Terry and Robards, 1987; Törnroth-Horsefield et al., 2006). Then, scaling K_PD to the cell level requires data on plasmodesmata frequency (Ma and Peterson, 2001). Third, estimations of the hydraulic conductivity of cellulosic walls (i.e. conductance per ratio of wall cross section to wall length; k_w) remain highly uncertain, with reported values spreading over 3 orders of magnitude (Steudle and Boyer, 1985; Zhu and Steudle, 1991).

Our understanding of the quantitative impact of cell walls, aquaporins, and plasmodesmata on root radial permeability is hindered by their highly organized distribution in the root hydraulic network. However, according to Fiscus and Kramer (1975), capturing this level of complexity is not necessary to predict the bulk radial flow of water. One may simply represent the root as a single semipermeable membrane:

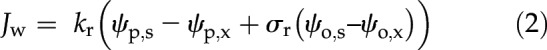where J_w is the water flux at the root surface (m³ m⁻² s⁻¹), k_r is the root radial conductivity (m³ m⁻² s⁻¹ MPa⁻¹; note that here conductivity stands for conductance per root surface area), ψ_p,s and ψ_p,x correspond to the water pressure potential at the root surface and in xylem vessels, respectively, relative to the atmospheric pressure (MPa), σ_r is the effective root reflection coefficient (dimensionless; not to be confused with the reflection coefficient of a cell membrane), and ψ_o,s and ψ_o,x correspond to the osmotic potential at the root surface and xylem vessels, respectively (MPa).

Equation 2 is an effective equation, as it merges indirectly root anatomical and cell-scale hydraulic properties into simple effective parameters (k_r and σ_r). Whether this equation remains accurate for any combination of hydraulic properties, anatomy, and environment is still unclear. Remarkably, k_r values measured with the root pressure probe (Steudle and Jeschke, 1983) by varying the xylem pressure potential (i.e. hydrostatic experiment; either as a pulse followed by pressure relaxation or as a steady-state pressure clamp) systematically differ from values measured by varying the osmotic potential of the root bathing solution (i.e. osmotic experiment; Steudle and Frensch, 1989). Two main hypotheses have been proposed to explain such k_r differences. First, water flow across the semipermeable endodermis generates the accumulation of solutes on the upstream side of the endodermis. This so-called sweep-away effect results in a bias in the estimated osmotic component of water potential, although it would not have time to form in the short pressure relaxation experiments (Knipfer et al., 2007). Due to the small volume of water involved and the transient nature of the experiment, the pressure relaxation method might suffer from interferences with the capacitance of the system, leading to an overestimation of k_r (Bramley et al., 2007). The second hypothesis is that the water filling of intercellular spaces in hydrostatic experiments may offer an increased area with low friction for radial water flow (Steudle and Peterson, 1998), resulting in a more conductive apoplastic radial pathway from the root surface to xylem vessels. In order to account for the separate contributions of purely apoplastic and other parallel radial pathways (cell to cell), Steudle and Boyer (1985) propose calculating k_r as the average of cell wall and membrane conductivities weighted by their respective transverse surfaces. A similar approach has been used to determine the parameter σ_r of Equation 2 for the composite transport model (Steudle and Frensch, 1989).

Although widely accepted, this simple model of radial water flow fails to explain several experimental results. For instance, cortex cell L_p may not correlate with k_r (Hachez et al., 2012), in contradiction with predictions of the composite transport model. Furthermore, the mere possibility of a substantial purely apoplastic radial pathway was questioned recently (Knipfer and Fricke, 2010). Approaches combining experiments and functional-structural models constitute an asset to understand such complex systems (Band et al., 2014; Postma et al., 2017), so that a consistent framework from the cell to the root scale has become central to investigate questions of root radial transport. A two-dimensional radial-axial version of such a framework was proposed recently by Foster and Miklavcic (2016, 2017) to investigate the role of apoplastic barriers in the salt stress response of Arabidopsis (Arabidopsis thaliana) roots. Addressing the complexity of radially asymmetric anatomical features in water transport questions, however, would necessitate the development of a complementary tool.

In this study, we developed a two-dimensional transverse model of the root hydraulic anatomy (MECHA) built on the scientific community’s understanding of cell hydraulics. The model is meant to address questions pertaining to the impact of root anatomy and subcellular hydraulics on water transport in the transverse plane. However, its insight may be extended to three-dimensional root segments as long as their anatomy, hydraulic properties, and environment do not vary substantially in the longitudinal direction.

In the following, we first introduce the model. Second, we conduct a meta-analysis comparing maize (Zea mays) k_r experimental values reported in the literature with predictions of MECHA using anatomical and subcellular hydraulic data from the literature. Third, through simulations of pressure clamp and osmotic experiments, we investigate whether the observed differences in k_r might arise from the water filling of intercellular spaces or from the solute sweep-away effect of apoplastic barriers. Finally, we estimate the contribution of plasmodesmatal conductance and L_p to root k_r, with a focus on specific tissues.

RESULTS

Overview of the New Model of Transverse Root Water Flow

Information on root anatomy and cell hydraulics was combined to build a finite difference model (MECHA) explicitly solving the equations of steady-state water flow (Eq. 1; Supplemental Note S1; Supplemental Fig. S1) across the network of individual cells. The model accommodates several plant species and root types, as shown in our Shiny application (https://plantmodelling.shinyapps.io/mecha/) for Arabidopsis and pearl millet (Pennisetum glaucum). Here, we report the case of maize.

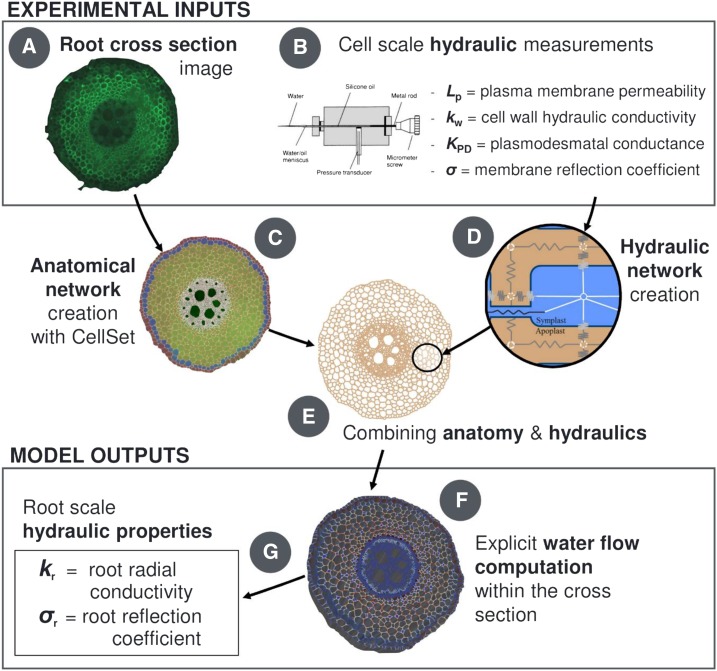
From the anatomical perspective, the model uses cell geometry and connectivity information collected from a cross-section image of the primary root of maize (Fig. 1A) and vectorized with the CellSet program (Pound et al., 2012; Fig. 1C). From the hydraulic perspective, the information includes maize literature data (Fig. 1B; Tables 1 and 2) of cell primary wall hydraulic conductivity (k_w; an intrinsic conductivity in units of m² s⁻¹ MPa⁻¹), cell plasma membrane permeability (L_p; m s⁻¹ MPa⁻¹), hydraulic conductance of individual plasmodesmata (K_PD; m³ s⁻¹ MPa⁻¹), their frequency in each root tissue, and membrane reflection coefficients (σ; dimensionless). These conductivities are combined in a scheme analog to electric circuits (Fig. 1D) over the root anatomical layout to constitute the explicit root hydraulic anatomy (Fig. 1E).

Figure 1.

Overview scheme of the root cross-section hydraulic anatomy approach. A transverse root microscope image (A) is treated through CellSet (C) to create the anatomical layout for cell-scale hydraulic principles (D). When coupled to cell-scale hydraulic properties (B), they form the root hydraulic anatomy (E). The computed water flow rates across individual cells (F) also yield the root radial conductivity and reflection coefficient (G).

Table 1. Plasmodesmata frequencies within and at transitions between maize root tissue types from Ma and Peterson (2001).

The missing frequency information was set at the average value by default.

Tissue Type or Transition between Tissue Types	Plasmodesmata Frequency
	μm−2
Epidermis to exodermis	0.54
Exodermis to cortex	1.14
Cortex	0.43
Cortex to endodermis	0.44
Endodermis	0.32
Endodermis to pericycle	0.48
Pericycle	0.35
Pericycle to stele parenchyma	0.53
Stele parenchyma	0.32
Default	0.4

Table 2. Summary of cell-scale properties used in the analyses.

Note that L_p and D variations were considered in the sensitivity analysis through variations around the default value. Solute reflection coefficients of cell walls and plasmodesmata were assumed to be null, while those of cell membranes equal 1 by default.

Parameter	Adjective	Value	Units	Sources or Comment
Cell membrane Lp	Default	5.3 × 10−7	m s−1 MPa−1	Estimated from Ehlert et al. (2009) and Bret-Harte and Silk (1994)
Cell primary wall kw	High	7.7 × 10−8	m2 s−1 MPa−1	Steudle and Boyer (1985)
	Low	1.4 × 10−10	m2 s−1 MPa−1	Tyree (1968)
Lignified/suberized cell wall kw,barrier	High	1.0 × 10−11	m2 s−1 MPa−1	Poiseuille law
	Low	Zero	m2 s−1 MPa−1	Ensures water impermeability
Plasmodesmata KPD	High	3.5 × 10−18	m3 s−1 MPa−1	Ginsburg and Ginzburg (1970)
	Low	6.1 × 10−19	m3 s−1 MPa−1	Geometrical average of range from Bret-Harte and Silk (1994)
Apoplastic solute D	Infinite	Infinity	m2 s−1	Ensures solute perfect mixing
	Default	4.0 × 10−11	m2 s−1	Knipfer et al. (2007)

The model simulates solute radial convection-diffusion in the apoplast at steady state (the solute diffusivity parameter in Table 2). According to pressure clamp experiments and modeling analyses (Knipfer et al., 2007), the solute distribution reaches such a steady state within a few seconds of alterations of the water flow rate. Because the focus of the current study is on water flow, we assumed solute homeostasis in the symplast and solved solute transport only in the apoplast. The assumption of symplastic homeostasis does not exclude the transfer of major solutes through plasmodesmata with the mass flow of water. Indeed, solutes leaving the protoplast symplastically may largely be replaced by the transmembrane transport at rates reported in the literature (Supplemental Note S2).

The computation of flow equations in the transverse hydraulic network yields steady-state water flow rates across each individual piece of the hydraulic pathways (Fig. 1F; Supplemental Note S3; Supplemental Fig. S2) and the hydrostatic water pressure in cell walls and protoplasts. Furthermore, effective metrics such as root k_r and σ_r are extracted from the simulations (Fig. 1G).

Experimental k_r Values Are Best Predicted Using High Values of k_w and Low Values of K_PD from the Literature

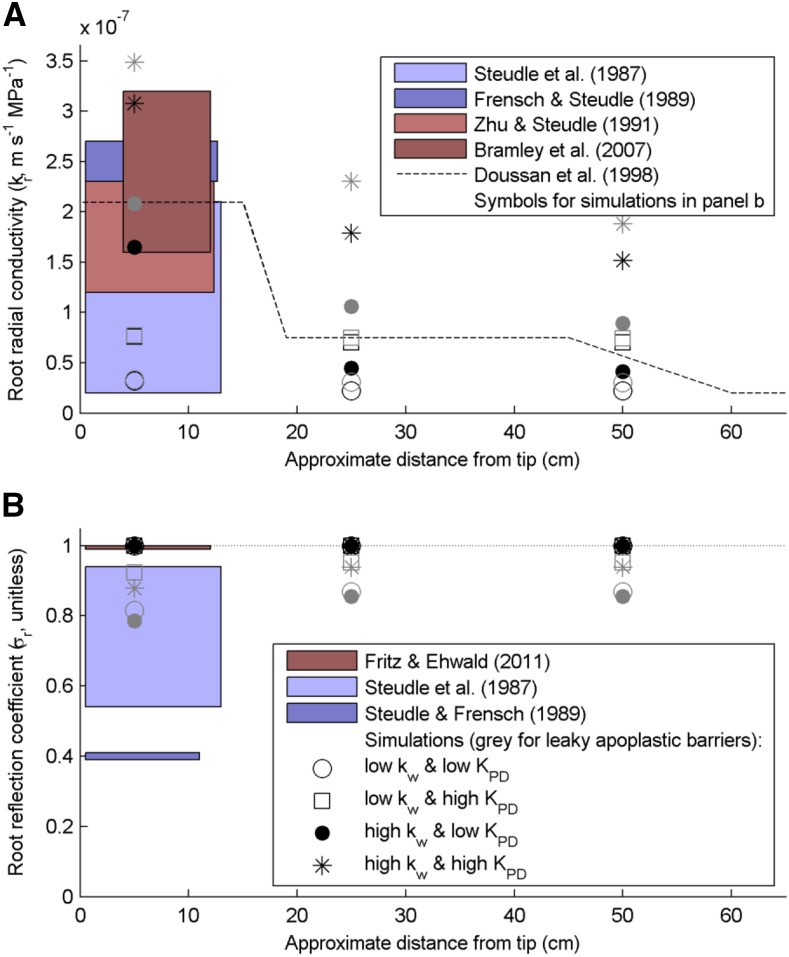
MECHA parameterized with experimental cell-scale hydraulic properties (Table 2) yielded radial conductivities that fall in the range of measured maize root k_r (measurements: colored boxes in Fig. 2A; simulations: symbols with legend from Fig. 2B, water-permeable and impermeable apoplastic barriers in gray and black, respectively).

Figure 2.

Comparison of root radial hydraulic properties measured and simulated for various cell-scale hydraulic properties along a root. The three simulated distances from the tip correspond to different levels of apoplastic barrier development: endodermal Casparian strip (5 cm), suberized endodermis with passage cells (25 cm), and suberized endodermis and exodermal Casparian strip (50 cm). A, Comparison between experimental k_r ranges in maize primary roots (colored rectangles and dashed line) and k_r simulated from the cell scale in the maize hydraulic anatomy (consistent symbols across legends with impermeable and leaky apoplastic barriers in black and gray, respectively). B, Comparison between experimental mannitol σ_r ranges in maize principal roots (colored rectangles) and root segment σ_r arising from the cell scale in the maize hydraulic anatomy (σ_r values lower than 1 were obtained with the water-permeable apoplastic barrier).

The combination of high cell k_w and low K_PD generated the best match with the experimental range of young maize root k_r and reproduced qualitatively the longitudinal trend estimated by Doussan et al. (1998b); Fig. 2A). A systematic mapping of the L_p-k_w-K_PD parametric space with 10³ sets of parameter values confirmed that this parameterization is in the direct vicinity of the overall best fit (Supplemental Note S4; Supplemental Fig. S3).

When increasing the water permeability of lignified and suberized cell walls from zero to their upper possible limit (Table 2), k_r increased by 36% ± 46% (n = 12, maximum +136%; black versus gray symbols in Fig. 2A) and σ_r decreased from 1 to 0.88 ± 0.05 (n = 12, minimum 0.79; Fig. 2B). Furthermore, the predicted fraction of fully apoplastic radial flow went from 0% to 9.9% ± 5.5% (n = 12, maximum 21%) and was highly negatively correlated to σ_r (r = −0.98; Supplemental Data Set S1).

The impact of aquaporin gating (reducing k_AQP by 95%) on k_r was less pronounced in the case of low k_w (−37% ± 3%, n = 12, minimum −45%) than high k_w (−57% ± 9%, n = 12, minimum −74%). The latter is closer to the values of −60% to −70% reported experimentally (Ye and Steudle, 2006; Boursiac et al., 2008; Parent et al., 2009).

The simulations also confirmed the limited impact of the geometrical positioning of transverse cell walls on k_r. On the one hand, hydraulic anatomies A with aligned transversal cell walls overestimated the value of k_r as compared with more realistic nonaligned systems B, which had longer apoplastic pathways. On the other hand, the latter system had higher k_r than system C with obstructed transversal walls. Considering that, in our results, the difference between k_r values in systems A and C was always less than 2.5% (Supplemental Data Set S2), we conclude that the difference between k_r values in systems A and B may not be substantial.

The Water Filling of Cortex Intercellular Spaces May Not Be Responsible for Experimental Differences between Osmotic and Hydrostatic k_r

The relative difference between k_r in hydraulic anatomies with air- and water-filled intercellular spaces (representative of hydrostatic and osmotic experiments, respectively) was only 1.3% ± 0.1% under high k_w (n = 12, maximum 2.8%), including scenarios with water-permeable apoplastic barriers, and was 92% ± 6% under low k_w (n = 12, maximum 158%; Supplemental Data Set S1). This impact is lower than hypothesized by Steudle and Peterson (1998), even though we intentionally overestimated k_r in the case of water-filled intercellular spaces to obtain an upper possible bound.

The Casparian Strip Solute Sweep-Away Effect Biases the Estimation of k_r in Osmotic Experiments More Than in Pressure Clamp Experiments

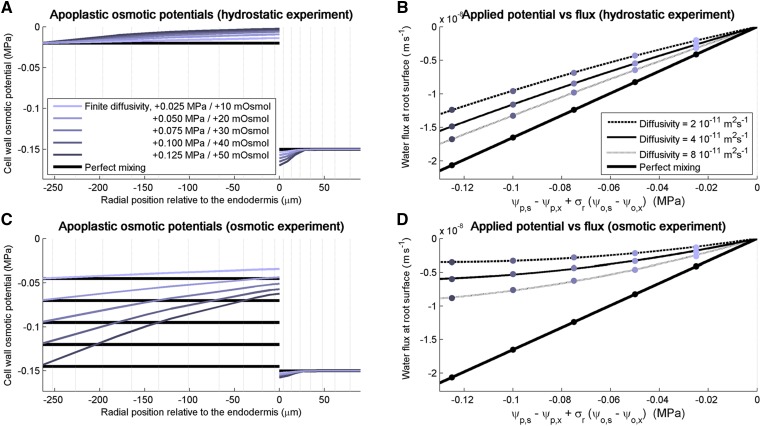
In conditions of perfect mixing of apoplastic solutes (i.e. infinite apoplastic solute diffusivity), the simulated fluxes yielded unique k_r and σ_r, regardless of xylem pressure and bathing solution osmotic potential. In consequence, the water flux-versus-Δψ relation was linear (thick black lines in Fig. 3, B and D), in compliance with the model of the root as a semipermeable membrane (Eq. 2; Fiscus and Kramer, 1975).

Figure 3.

Impact of solute radial convection-diffusion in the apoplast on the estimations of maize root radial conductivity in simulated osmotic and pressure clamp experiments for high k_w and low K_PD. A, Steady-state apoplastic osmotic potentials simulated when increasing the xylem pressure by incremental pressure clamps of 0.025 MPa for a solute diffusivity of 4 × 10⁻¹¹ m² s⁻¹ (colored curves) and an infinite diffusivity (black curves). B, Steady-state radial water fluxes simulated in response to the incremental pressure clamps of 0.025 MPa for four levels of solute diffusivity. C, Steady-state apoplastic osmotic potentials simulated after adding mannitol in the root bathing solution by increments of 10 mosmol for a solute diffusivity of 4 × 10⁻¹¹ m² s⁻¹ (colored curves) and an infinite diffusivity (black curves). D, Steady-state radial water fluxes simulated in response to the increments of 10 mosmol in the bathing solution for four levels of solute diffusivity.

When assuming finite solute diffusivity, apoplastic solute convection-diffusion affected the estimation of k_r in virtual pressure probe experiments. We first investigated the case of the hydraulic anatomy with high k_w and low K_PD. In virtual pressure clamp experiments with increasing pressure clamps, the outward water flow provoked the accumulation of solutes on the stele side of the endodermis and their depletion on the cortex side (Fig. 3A, light and darkest blue for xylem pressure increased by 0.025 and 0.125 MPa, respectively). These alterations of the osmotic potential partly countered the outward-driving pressure of water, thus reducing the absolute radial flow rates (light to dark blue dots in Fig. 3B) as compared with the case of perfect solute mixing (black dots in Fig. 3B). Because the water potentials at the root surface and in the xylem vessels are used in the estimation of k_r (Eq. 3; see “Materials and Methods”) instead of the full profile of water potentials, the driving force of water flow was overestimated and k_r was underestimated by a factor 1.2 to 1.6 (for higher and lower limits of solute diffusivity, respectively). Another consequence was that the water flux-versus-Δψ relationship, the slope of which corresponds to k_r, became slightly nonlinear. These features were exacerbated in the osmotic experiment (Fig. 3C), in which k_r was underestimated by a factor 2.7 to 7.5 (Fig. 3D).

It is particularly interesting that, for a hydraulic anatomy with low k_w (Table 2), k_r values estimated in the same experiments were barely underestimated and did not differ substantially between pressure clamp and osmotic experiments. The biases reached 1.02 to 1.08 and 1.1 to 1.3 in pressure clamp and osmotic experiments, respectively.

In Supplemental Note S5, we demonstrate that our results were not affected by spatial variations of osmotic potential in the symplast (see also Supplemental Fig. S5).

Endodermis L_p and Plasmodesmatal Conductance Are the Most Limiting Elements of the Water Pathway before and after the Suberization of the Endodermis, Respectively

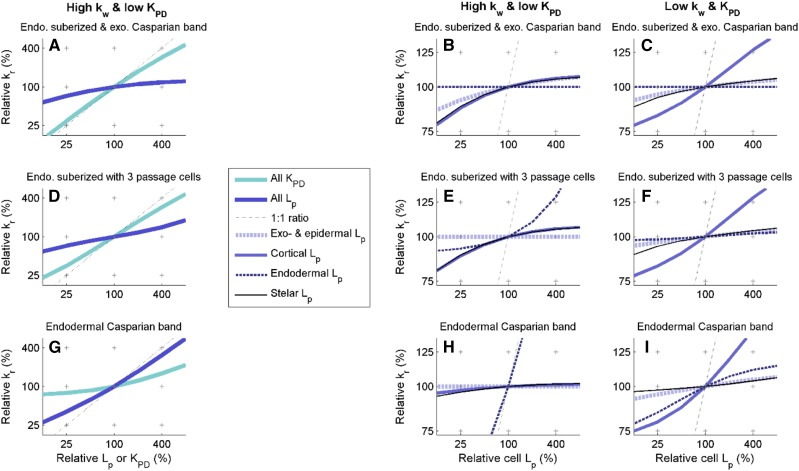
In the distal region of the root that has an endodermal Casparian strip but no suberized walls, the impact of L_p on k_r peaked in the scenario with high k_w and low K_PD. The increase of k_r per unit increase of L_p (hereafter referred to as sensitivity; Eq. 6; see “Materials and Methods”) was 72% (slope of the dark blue curve in Fig. 4G). This value is particularly high, considering that the sum of sensitivities to all individual pieces of pathways (also including plasmodesmata and cell walls) sums up to 100% by definition. Furthermore, the endodermis L_p alone accounted for 69% of the overall sensitivity (Fig. 4H). In other words, the permeability of endodermis plasma membranes was the bottleneck controlling k_r except when endodermal suberization was complete (Fig. 4B).

Figure 4.

Relative radial hydraulic conductivity as a function of specific relative cell hydraulic conductivities. Relationships are shown for the fully suberized endodermis with an extra exodermal Casparian band (A–C), the suberized endodermis with three passage cells (D–F), and the simple endodermal Casparian band stage (G–I). In A, D, and G, cell properties (L_p in blue or K_PD in cyan) were altered simultaneously in all tissue types, while in other graphs, L_p was modified in specific tissue types (in epidermis and exodermis in dashed light blue, cortex in solid blue, endodermis in dashed dark blue, and stele cells in solid black). Graphs B, E, and H and C, F, and I have high and low cell wall hydraulic conductivities, respectively, and low K_PD (Table 2).

As a matter of comparison, the cortex L_p accounted for less than 1% of the overall sensitivity (i.e. k_r was essentially independent from cortex L_p; Fig. 4H). The latter independence may explain the absence of correlation between k_r and cortex L_p reported in the literature (Hachez et al., 2012). The systematic exploration of the parametric space revealed that such a low sensitivity to cortex L_p occurs when the composite nature of the root allows the bypass of cortex membranes by flowing across the cortex along either the apoplastic or the symplastic pathway. This symplastic bypass occurred when low k_w and high K_PD were combined (Supplemental Note S4; Supplemental Fig. S4), with 51% of the overall sensitivity controlled by K_PD. Conversely, if both k_w and K_PD were low, water would not bypass cortex membranes and k_r would be systematically more sensitive to cortex L_p than to endodermis L_p (Fig. 4 C, F, and I).

The sensitivity of k_r to plasmodesmatal conductance evolved with the maturation of apoplastic barriers in the scenario with high k_w and low K_PD. It was as high as 23% before endodermal suberization (cyan curve in Fig. 4G) and reached 73% at maturity (cyan curve in Fig. 4A), thus becoming the new bottleneck for radial water flow. As a matter of comparison, the sensitivity of k_r to k_w was lower than 5% in this scenario.

DISCUSSION

Models of Water Flow across Root Tissues Are Not Functionally Equivalent

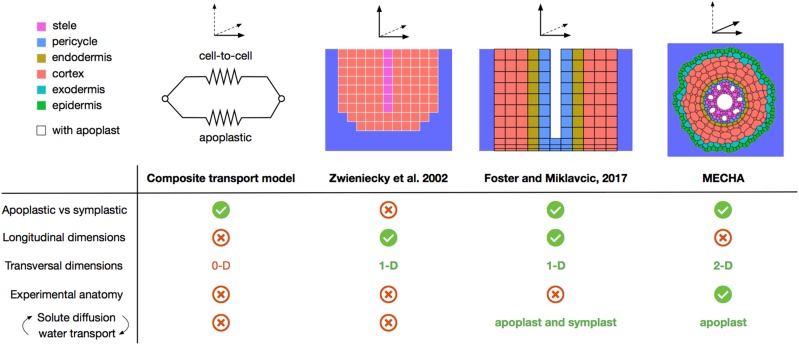
Models of water flow across root tissues (see overview of the major approaches in Fig. 5) have been elaborated with the purpose of addressing specific scientific questions. In the composite transport model (Steudle and Boyer, 1985; Steudle and Frensch, 1989), water flow is partitioned between two parallel radial pathways (apoplastic versus cell to cell), each with specific conductivities and reflection coefficients. This simple representation assumes uniform cell properties and no substantial variations of osmotic potential in each root compartment. However, its major interest lies in the generalization of Equation 2, explicitly separating apoplastic and cell-to-cell pathways while being compatible with root system-scale hydraulic models (Doussan et al., 1998a).

Figure 5.

Scheme comparing major approaches to simulate water flow across root tissues. The nonexhaustive criteria listed are the separation of apoplastic and symplastic pathways, the number of dimensions attributed to the representation of longitudinally and transversely varying root properties, the compatibility with experimental anatomical layouts, and the tight coupling between solute radial distribution and water flow.

The two-dimensional discretization of the root tissue hydraulic network proposed by Zwieniecki et al. (2002) allowed analyzing the impact of radial and longitudinal variations of tissue properties on water flow across roots. It was lately completed by Foster and Miklavcic (2017), who separated apoplastic and symplastic domains at the cell scale in order to precisely address interactions between the transport of major solutes (K⁺, Na⁺, H⁺, and Cl⁻) and water flow across cell walls, membranes, and plasmodesmata.

The MECHA model relaxes the constraint of radial symmetry present in all previous models by allocating two spatial dimensions to the transverse domain, thereby allowing the proper inclusion of complex anatomical features (e.g. xylem poles, passage cells, etc.) and a more realistic description of root anatomy from microscopic images. Unlike Foster and Miklavcic (2017), the subcellular discretization accommodates the presence of intercellular spaces, variations of water pressure along the walls of the same cell, and the localization of Casparian strips in radial walls. The current version of MECHA is suitable to address questions of water flow in root segments with little variation along the longitudinal axis in terms of hydraulic properties (e.g. distal differentiated 10 cm of maize roots grown in hydroponics, excluding the elongation zone) and in terms of environment (e.g. root in a bathing solution), as in the root pressure probe experiments simulated in this study. Longitudinal variations of hydraulic properties or root environment might be accounted for by coupling MECHA with a one-dimensional root architectural model such as that of Meunier et al. (2017b).

Hydraulic Properties Are Not Always Transferable between Cell and Root Scales

The k_r has frequently been measured on the distal portion of maize primary roots (up to 14 cm long) using a root pressure probe. Data from Steudle et al. (1987), Zhu and Steudle (1991), Frensch and Steudle (1989), and Bramley et al. (2007) cover 1 order of magnitude but mostly meet around 2 × 10⁻⁷ m s⁻¹ MPa⁻¹ (colored areas in Fig. 2A). Similar data in mature root zones are rare, likely due to the presence of lateral roots that complicate the attachment of the probe. Doussan et al. (1998b) estimated a whole profile of root k_r along the maturation gradient by combining inverse modeling and cumulative flow data from Varney and Canny (1993); dashed line in Fig. 2A, with the endodermal suberization between 15 and 19 cm from the tip and exodermis development between 45 and 60 cm from the tip). The similarity between k_r measured and predicted from the cell scale strengthens the hydraulic anatomy approach, particularly when considering that the experimental k_r range for maize (overall 2 × 10⁻⁸ to 3 × 10⁻⁷ m s⁻¹ MPa⁻¹; boxes in Fig. 2A) appears relatively narrow in view of values reported in the literature for other plants. For instance, McElrone et al. (2007) measured k_r values from 10⁻⁵ to 10⁻⁴ m s⁻¹ MPa⁻¹ with an ultra-low flowmeter in deep fine roots of live oak (Quercus fusiformis) and gum bumelia (Sideroxylon lanuginosa), while Zarebanadkouki et al. (2016) obtained k_r values of 10⁻⁶ m s⁻¹ MPa⁻¹ in undisturbed white lupine (Lupinus albus) primary roots by combining deuterium tracing, inverse modeling, and analytical hydraulic functions developed by Meunier et al. (2017a).

Our results support the simplification of the root as a semipermeable membrane, which perfectly captures the process of transverse water flow in the absence of variations of osmotic potential within the symplast and apoplastic domains. It also captures it reasonably well when these variations are small (Fig. 3, A and B), thereby allowing the transfer of hydraulic properties from the cell to the root scale. However, in particular conditions (e.g. osmotic experiments), the solute sweep-away effect due to the Casparian strip may generate a substantially nonlinear response of water flow to water potential difference between root surface and xylem vessels (Fig. 3, C and D), so that Equation 2 (Fiscus and Kramer, 1975) is no longer accurate. Water flow models are generally not fully compatible across scales, as found in root water uptake models (Feddes et al., 1978; Javaux et al., 2013; Couvreur et al., 2014) or in hydrological models (Pokhrel and Gupta, 2010; Brynjarsdóttir and OʼHagan, 2014; Couvreur et al., 2016), which is reason for introducing effective principles. Key structures or processes (e.g. solute diffusion-convection) too complex to be represented with simple physical equations at larger scales may explain such incompatibilities. Thus, an effective osmotic k_r might inform reasonably well on expected water flow rates in conditions similar to those in the osmotic experiment while being disconnected from actual cell-scale hydraulic properties.

The Estimation of k_r Is More Biased in Osmotic Experiments Due to a Solute Sweep-Away Effect Than in Hydrostatic Experiments Due to the Water Filling of Intercellular Spaces

In this study, we report changes of k_r between hydraulic anatomies with air-filled versus water-filled intercellular spaces that are far lower than 1 order of magnitude. This suggests that the intercellular space water-filling hypothesis proposed by Steudle and Peterson (1998) may not explain the 10-fold increase of k_r between osmotic and hydrostatic experiments (Steudle et al., 1987; Steudle and Frensch, 1989). Despite their high hydraulic conductivity and simulated three-dimensional connectivity when water filled, intercellular spaces are in series with less conductive pieces of the pathway that limit variations of k_r (e.g. at the endodermis, even when the Casparian strip is water permeable). Note that this interpretation applies to root regions that developed at least a Casparian strip and, thus, does not deny interpretations on the dominant role of intercellular spaces in water flow across slices of potato (Solanum tuberosum) storage organs (Michael et al., 1997).

The hydraulic anatomy approach, therefore, suggests that features other than water-filled intercellular spaces likely generated the systematic differences between k_r measured in osmotic and hydrostatic experiments. In this study, we hypothesize, and support with simulations, that most of the reported k_r differences between pressure clamp and osmotic experiments may stem from the erroneous estimation of the osmotic driving pressure (Fig. 3, C and D), as argued by Knipfer and Fricke (2010). Substantial biases in the estimation of k_r (factor 2.7–7.5) were simulated when the majority of the transmembrane flow was located near the Casparian strip (i.e. for parameter sets with high k_w). Interestingly, this bias did not appear in our simulations when using low k_w, which may be a critical property explaining that hydrostatic and osmotic k_r do not differ in wheat (Triticum aestivum; Bramley et al., 2007).

While the biased estimation of maize k_r in osmotic experiments is likely, it may be combined with actual alterations of the root radial conductivity, for instance due to changing cell L_p in response to osmotic stress. However, while a decrease of L_p may entail a reduction of k_r in an osmotic experiment, the literature reports increasing L_p with decreasing root medium water potential (from −0.075 to −0.34 MPa; Hachez et al., 2012). The plasmodesmatal aperture also responds to the root osmotic environment (Roberts and Oparka, 2003), but quantitative data are lacking so far.

Simulation Results Suggest Testing Whether Endodermis L_p or Plasmodesmatal Conductance Vary with k_r in Response to Osmotic Stress

The experimental observation that maize cortex L_p varies independently of the hydrostatic k_r (Hachez et al., 2012) was reproduced in our simulations whenever the water stream bypassed cortex membranes via the apoplast (for combined high k_w and low K_PD) or via the symplast (for combined low k_w and high K_PD). In the former case, 69% of the variability of k_r was controlled by the endodermis L_p, while in the latter case, plasmodesmatal conductance controlled 51% of variability. Identifying which property (endodermis L_p or K_PD) varies in coordination with k_r before and after osmotic stress may indicate whether the bypass of cortex plasma membranes is apoplastic or symplastic. These hypotheses could be tested indirectly by using immunocytochemistry to quantify maize plasma membrane intrinsic protein (ZmPIP; aquaporin) expression in the endodermis (Hachez et al., 2006) and callose distribution across the root (Baluška et al., 1999).

While the modeling approach alone could not explain the precise reason why maize cortex L_p varies independently of the hydrostatic k_r, it may narrow the number of hypotheses down to those few compatible with the physics of water flow. This inexpensive mathematical tool needs to be integrated in an iterative loop combining experimental and modeling approaches to express its full potential.

High Cell Wall Hydraulic Conductivity Values Are Necessary to Reproduce Four Root Responses Reported Experimentally

Estimated values of k_w reported in the literature vary by orders of magnitude. In this study, most illustrations depict root properties resulting from either the low k_w value estimated by Tyree (1968) or the high k_w values measured by Steudle and Boyer (1985); 3 orders of magnitude apart); 3 orders of magnitude apart) and are completed by systematic investigations of the multidimensional parametric space spanning 6 orders of magnitude. While this parameter is hardly measurable, the modeling approach demonstrated that the value of k_w needs to be high in order to reproduce four types of experimental observations.

First, high k_w was necessary to generate the significant longitudinal variations of k_r (stars and closed circles in Fig. 2A) assumed to result from apoplastic barrier deposition (Sanderson, 1983; Doussan et al., 1998b; Barrowclough et al., 2000). Such observed changes also could be the result of longitudinal differences in cell membrane properties, but this is unlikely, as differentiated cell L_p was reported to be longitudinally uniform in maize and onion (Allium cepa; Barrowclough et al., 2000; Zimmermann et al., 2000).

Second, the simulated response of k_r to the gating of aquaporins was close to changes observed experimentally (Ye and Steudle, 2006; Boursiac et al., 2008; Parent et al., 2009), with the condition that the value of k_w in the parameter set was high.

Third, effective k_r values obtained from simulated osmotic and pressure clamp experiments only differed significantly in the case of high k_w, reproducing the observation of effectively different osmotic and hydrostatic k_r (Steudle et al., 1987).

Finally, high k_w also was necessary to reproduce the absence of correlation between cortex L_p and k_r reported experimentally (Hachez et al., 2012), except when the plasmodesmatal conductance was high.

CONCLUSION

MECHA is a hydraulic model that computes the flow of water through the walls, membranes, and plasmodesmata of each individual cell throughout a complete root cross section. From this fine scale, the model predicts σ_r and k_r for the root cylinder approach used in plant-scale models. Hence, it connects hydraulic theories across scales based on detailed anatomical descriptions and experimental data on k_w, L_p, and K_PD. Its two transverse spatial dimensions allow accounting for radially asymmetric features, such as intercellular spaces and the locations of xylem poles or passage cells, on water flow rates across the root.

Using the anatomical structure of a maize root with cell hydraulic properties from the literature, MECHA simulated root k_r values that fit the range of measurements from the literature and the k_r response to aquaporin gating. In particular, a relatively high cell k_w (Steudle and Boyer, 1985) and low K_PD (Bret-Harte and Silk, 1994) yielded the best fit. The water filling of intercellular spaces did not affect k_r enough to explain the 10-fold difference between k_r estimations in hydrostatic and osmotic experiments, unlike that hypothesized by Steudle and Peterson (1998), but variations of the osmotic potential in radial walls, not accounted for in root radial flow models, might explain a major part of these differences. In the case of high cell k_w, the simulated root k_r did not correlate with cortex cell L_p, as observed experimentally (Hachez et al., 2012). The model also suggested that root k_r might be very sensitive to the aperture of plasmodesmata, despite their low conductance.

The proposed enrichment of the composite transport model sheds new light on the field of plant water relations. Cutting-edge research on hydropatterning (Bao et al., 2014), hydrotropism (Dietrich et al., 2017), and apoplastic barriers (Barberon et al., 2016; Doblas et al., 2017) recently highlighted the need for a quantitative hydraulic framework to address questions related to pressure distribution and water flow direction at the cell scale. The model compatibility with a root anatomical software (Pound et al., 2012) and functional-structural plant models (Javaux et al., 2008) may open avenues to investigate the relationships between root architecture, anatomy, and water availability.

Future developments of the model will focus on the integration of an explicit third spatial dimension, as proposed in a simpler scheme by Zwieniecki et al. (2002), to investigate axial variations of water pressure and flow along roots. While MECHA can be used with the roots of virtually any plant species, as illustrated in the online visualization interface (http://plantmodelling.shinyapps.io/mecha) with Arabidopsis and pearl millet, the collection of cell hydraulic data for these species is a future challenge. Presumably, the methods used by Hachez et al. (2012) in maize could be transferred to other plants with no major issue. Furthermore, recently developed techniques, such as serial block face scanning, offer great potential to estimate plasmodesmata frequency throughout organs (Ross-Elliott et al., 2017). Finally, with the proposed modeling approach, we offer possibilities to estimate cell hydraulic properties by inverse methods as illustrated in this study.

MATERIALS AND METHODS

Cell Level Hydraulic Parameterization

While the illustrations provided in this study focus on a limited number of default, high, and low parameter values from the literature, a wide range of cell hydraulic parameter values (10³ triples in the L_p-k_w-K_PD parametric space) were tested in order to finely explore the impact of parameterization on responses of the maize (Zea mays) root hydraulic anatomy.

The K_PD was evaluated from their geometry by Bret-Harte and Silk (1994) in maize, accounting for its partial occlusion by the desmotubule and increased viscosity of water in channels at the nanometer scale (3.4 mPa s⁻¹). The obtained K_PD values ranged from 3.05 × 10⁻¹⁹ to 1.22 × 10⁻¹⁸ m³ s⁻¹ MPa⁻¹ (geometrical average, 6.1 × 10⁻¹⁹ m³ s⁻¹ MPa⁻¹, here referred to as low K_PD). Their estimation was 1 order of magnitude less than estimated by Ginsburg and Ginzburg (1970) in maize (3.54 × 10⁻¹⁸ m³ s⁻¹ MPa⁻¹, here referred to as high K_PD), assuming a plasmodesmata frequency of 0.48 μm⁻² (Ma and Peterson, 2001) to turn the conductivity into a conductance per plasmodesmata. For the systematic exploration of the parametric space, we used 10 K_PD values ranging from 7.2 × 10⁻²⁰ to 3.7 × 10⁻¹⁷ m³ s⁻¹ MPa⁻¹.

Plasmodesmatal conductances were scaled to the cell level through multiplications by plasmodesmata frequency (μm⁻²) and shared wall surface (μm²) of neighboring cells. Plasmodesmata frequency data in maize roots after cell elongation were obtained from Warmbrodt (1985) and Clarkson et al. (1987) as reported by Ma and Peterson (2001); Table 1). Shared wall surface estimations were based on the discretized root cross-section anatomy for 200-μm-long cells. An effective K_PD of 2.4 × 10⁻⁷ m s⁻¹ MPa⁻¹ was estimated from the low K_PD and average plasmodesmata frequency (0.4 μm⁻²).

The default cell L_p value was obtained from the cell pressure probe estimation of Ehlert et al. (2009); 5.3 × 10⁻⁷ m s⁻¹ MPa⁻¹ after removal of K_PD). From the reported difference between hydraulic conductivities of control and acid-load treatments, the contributions of aquaporins (k_AQP) and the phospholipid bilayer (k_m) were estimated as 5 × 10⁻⁷ m s⁻¹ MPa⁻¹ and 2.6 × 10⁻⁸ m s⁻¹ MPa⁻¹, respectively. For the systematic exploration of the parametric space, 10 k_AQP values were used, ranging from 1.4 × 10⁻⁸ to 7.4 × 10⁻⁶ m s⁻¹ MPa⁻¹.

Pressure probe estimations of cellulosic wall hydraulic conductivity were taken from Steudle and Boyer (1985), who measured in soybean (Glycine max) a value of 7.7 × 10⁻⁸ m² s⁻¹ MPa⁻¹ (here referred to as high k_w), and Tyree (1968), who reported a value of 1.4 × 10⁻¹⁰ m² s⁻¹ MPa⁻¹ in nitella (Nitella flexilis; here referred to as low k_w). Note that Zhu and Steudle (1991) observed intermediate values of 2.5 × 10⁻¹⁰ to 6.1 × 10⁻⁹ m² s⁻¹ MPa⁻¹ in maize. For the systematic exploration of the parametric space, 10 k_w values were used, ranging from 1.8 × 10⁻¹³ to 1.4 × 10⁻⁷ m² s⁻¹ MPa⁻¹.

The hydrophobic Casparian strips and suberin lamellae were attributed null hydraulic conductivities, except in scenarios investigating the hypothesis of water-permeable apoplastic barriers. In this case, from the Poiseuille-Hagen law, the hydraulic conductivity of lignified cell walls, whose pores are 1 nm wide (Deng et al., 2016), was estimated as no more than 10⁻¹¹ m² s⁻¹ MPa⁻¹, which was used as a leaky upper limit.

As plasmodesmata and primary cell walls are not selective for cell solutes, they were attributed null σ. For simplicity, membranes were assumed to be fully selective (σ = 1), which is particularly representative of experiments using mannitol (Fritz and Ehwald, 2011). Finally, the bulk solute diffusivity value in cell walls (4 × 10⁻¹¹ m² s⁻¹) was obtained from the experimental estimations of Knipfer et al. (2007). A summary of cell-scale hydraulic properties is displayed in Table 2.

Cross-Section Geometry and Cell Typology

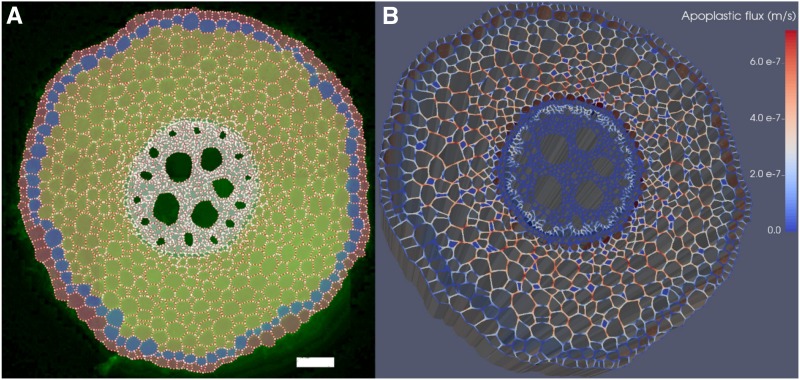
The hydraulic network geometry reproduced the anatomy of an aeroponically grown maize primary root (0.9 mm diameter), 5 cm proximal to the tip. A cross section stained by immunocytochemistry for the cellular distribution of ZmPIP2;1 and ZmPIP2;2, two plasma membrane aquaporins, was observed with an epifluorescence Leica DMR microscope as described by Hachez et al. (2006). The captured image was segmented with the program CellSet (Pound et al., 2012), and individual cells and structures were labeled manually (xylem, epidermis, exodermis, cortex, endodermis, pericycle, and stele parenchyma) based on their shapes and positions in the cross section (Fig. 6A). Phloem elements and their companion cells could not be identified at that resolution. However, as they do not bear apoplastic barriers and represent a relatively small fraction of the cross section, we assumed that their specific properties did not significantly impact root k_r and labeled them as their neighbor stele parenchyma cells. Cortex intercellular spaces (204 in total in this cross section) were recognized based on their relatively small size as compared with the surrounding cells.

Figure 6.

From anatomical segmentation to water flow simulation with CellSet and MECHA. A, Maize root cross section with exodermis after segmentation in CellSet. Successive cellular tissue types from the periphery are epidermis, exodermis, cortex, endodermis, pericycle, and other stele cells. Water potential boundary conditions were set at the epidermis surface and in xylem vessels (dark green). Bar = 100 µm. B, Simulated water fluxes in cell walls, in m s⁻¹, combining impermeable apoplastic barriers with high k_w, low K_PD hydraulic properties, and 0.5 MPa water potential difference between the root surface and xylem, generating an average uptake flux at the root surface of 2 × 10⁻⁸ m s⁻¹. Note that cell wall thickness is exaggerated to improve the visualization.

Three stages of apoplastic barrier development in the transverse plane (structured deposition of hydrophobic material in cell walls) were selected for this study: (1) presence of Casparian bands between endodermis cells, (2) presence of suberin lamellae covering the endodermis, except for three passage cells located in front of early metaxylem vessels, and (3) presence of suberin lamellae covering the whole endodermis combined with an exodermal Casparian strip (null apoplastic fluxes in both apoplastic barriers in Fig. 6B). To isolate the impact of apoplastic barrier deposition on root k_r and water pathways, the same network geometry was used for all simulations, and cell wall hydraulic properties were adjusted at apoplastic barrier locations.

The cross section was given a pseudo-three-dimensional representation by attributing a height of 200 μm (the typical length of maize elongated root cells) to the system. Transverse cell walls were thus included on the top and at the bottom of the cross section. In consequence, the top and bottom of cells were aligned in our model.

Calculation of the Theoretical k_r and Reflection Coefficient from the Cell Scale

The k_r is defined as the root water uptake rate (Q_w; m³ s⁻¹, positive inward) per unit of root surface under a unit pressure difference between root surface and xylem, where the pressure difference is ψ_p,s − ψ_p,x + σ_r (ψ_o,s – ψ_o,x; Fiscus and Kramer, 1975). As σ_r was unknown at first, k_r was obtained by running MECHA (the method for solving water flow equations detailed in Supplemental Note S1) under uniform osmotic potential throughout the cross section for nonnull pressure differences. Any pressure difference (ψ_p,s − ψ_p,x), in principle, should yield the same value of k_r, which was verified with the following equation for pressure differences of 0.025 to 0.125 MPa by increments of 0.025 MPa:

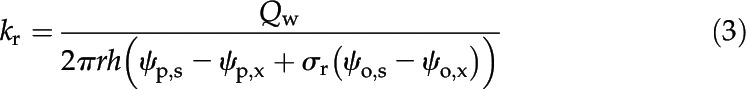where r (m) is the root radius, h (m) is the height of the cross section, and osmotic potentials canceled out. Note that the variable Q_w was calculated by summing up water flow rates at the root surface.

The effective parameter σ_r was calculated by running MECHA under no-flow conditions with ψ_o,s different from ψ_o,x (see default boundary conditions in Table 3):

Table 3. Summary of boundary conditions used for the calculation of the root reflection coefficients and for the virtual osmotic and pressure clamp experiments.

Boundary	ψp,s	ψo,s	ψp,x	ψo,x	ψo,c
	MPa	MPa	MPa	MPa	MPa
Default boundary condition (no flow)	0.0	−0.02	Equilibrium pressure (Pr 0)	−0.15	−0.7
Various ψo,s	0.0	−0.045 to −0.170 by −0.025 increments	Pr 0	−0.15	−0.7
Various ψp,x	0.0	−0.02	Pr 0 + 0.025 to Pr 0 + 0.125 by 0.025 increments	−0.15	−0.7

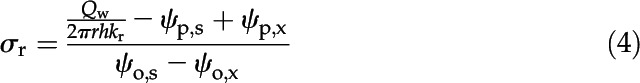where Q_w was set to 0 and the xylem pressure at equilibrium was an output of the model. The model also was run for various osmotic potentials at the root surface in order to verify the unicity of σ_r (see Various ψ_o,s in Table 3) for known k_r and ψ_p,x (Q_w then being an output of the model).

Note that, in this section, solutes were assumed to be perfectly mixed on either side of apoplastic barriers (i.e. the osmotic potential of all cell walls in the stele equals ψ_o,x, and the osmotic potential of all other walls equals ψ_o,s).

The comparison of simulated k_r with measured values from the literature was carried out for the 10³ combinations of k_AQP, k_w, and K_PD parameter sets reported in “Cell Level Hydraulic Parameterization” above. After comparing the overall ranges of measured and simulated values of k_r and σ_r, the cell hydraulic parameter set P* that minimized the square differences with k_r from the literature was obtained. The combination of default, high, and low cell hydraulic parameters (Table 2) that was closest to P* also was identified.

Furthermore, statistics on the impact of (1) the maximum possible water permeability of apoplastic barriers (Table 2) and (2) the gating of aquaporins (k_AQP reduced by 95%) on k_r were evaluated for partitions of 24 parametric sets (i.e. combinations of high or low K_PD, high or low k_w, water-permeable or impermeable apoplastic barriers, and three stages of apoplastic barrier development). The cell parameter sets that best reproduced literature data on the k_r response to aquaporin gating were identified.

Finally, whether the alignment of transverse walls in the virtual root provoked a significant overestimation of k_r, as compared with a more realistic tortuous apoplastic domain, was investigated. Root hydraulic anatomies with null transverse wall conductivities were used to estimate an upper bound to the difference between aligned and tortuous apoplastic domains.

Quantification of the Impact of Water-Filling Intercellular Spaces on k_r

The root radial conductivity was calculated for hydraulic anatomies including air-filled intercellular spaces and then with water-filled intercellular spaces. In the hydraulic network, intercellular spaces were considered as pseudo-cells with particular properties: (1) K_PD was null (i.e. no plasmodesmata) and (2) L_p depended on whether they were filled with air or water (i.e. mathematically allows access to the center of the intercellular space or not). If they were filled with air, there was no water pathway across the intercellular spaces, and L_p was set to zero (blue intercellular polygons [i.e. null apoplastic fluxes] in Fig. 6B). If they were filled with water, water may move freely from the cell wall to the center of intercellular spaces, and L_p was set to infinity. In the water-filled case, cortex cell wall hydraulic conductivities also were set to infinity to account for the possible three-dimensional connections between these spaces. In consequence, (1) all water-filled intercellular spaces were virtually connected and (2) the difference between k_r in the air- and water-filled cases was overestimated, due to neglected frictions in the cortex apoplast in the water-filled case. This set an upper limit to the possible impact of water-filled intercellular spaces on the estimation of k_r in hydrostatic experiments.

The relative difference of k_r was characterized for all 24 combinations of apoplastic barrier development stages and cell hydraulic properties reported in Table 2.

Quantification of the Impact of Solute Convection-Diffusion on the Estimation of k_r

An analytical solution of solute diffusion-convection in radial cell walls was implemented in MECHA to account for the feedback between solute distribution and water flow. Hydraulic anatomy with an impermeable endodermal Casparian strip, high k_w values, and low K_PD values (Table 2) was the main focus, which had fairly well-conserved water velocities across the cortex and transmembrane flow concentrated in the direct vicinity of the endodermis. To a first approximation, the endodermis was considered a semipermeable structure with unit reflection coefficient, as described by Knipfer et al. (2007).

For a constant solute concentration at the root surface [C(0); mosmol L⁻¹], full solute exclusion at the interface with endodermis membranes, and a uniform radial velocity of water in the cortex apoplast (u; m s⁻¹, positive inward), the solution of solute distribution was:

where r (m) is the radial position along the apoplast between the root surface (r = 0) and the endodermis and D (m² s⁻¹) is the solute diffusivity in the apoplast. Note that the radial velocity of water in the apoplast is obtained by dividing the simulated total radial flow rate (Q_w; m³ s⁻¹) by the average radial cell wall cross-section area (m²), which is very similar on either side of the endodermis. On the stele side of the endodermis, an analogous solution was used to estimate solute diffusion-convection between xylem vessels and the surface of the endodermis.

Boundary conditions representative of exosmotic (i.e. water flowing from the stele toward the root surface) pressure clamp and osmotic experiments were applied (Table 3), both starting with a bathing solution osmotic potential (ψ_o,s) of −0.02 MPa (Johnson solution) and a xylem pressure (ψ_p,x) at equilibrium (P_{r 0}; generating no water flow across the root). Cell cytosol and xylem osmotic potentials (ψ_o,c and ψ_o,x, respectively) were set to the average values measured in maize cortex (−0.7 MPa) and xylem vessels (−0.15 MPa) by Enns et al. (2000). For the pressure clamp experiments, ψ_p,x was increased sequentially by steps of 0.025 MPa up to a total of P_{r 0} + 0.125 MPa. In osmotic gradient experiments, decreasing bathing solution osmotic potentials were applied by steps of −0.025 MPa, down to −0.145 MPa (i.e. Johnson solution + 50 mosmol mannitol, using Van’t Hoff’s law to convert solute concentrations into osmotic potentials and vice versa). To offer a direct point of comparison with the pressure clamp experiment, the xylem pressure was maintained constant in this second type of experiment. Note that the current version of the model should not be used to simulate hydrostatic pressure relaxation experiments due to the steady-state flow assumption.

Because the water flux and solute distribution affected each other simultaneously, the problems of water flow and solute distribution needed to be solved iteratively until convergence, starting from uniform solute concentrations on either side of the endodermis. After convergence, k_r was calculated with Equation 3, and the relative bias was compared with the perfect mixing case.

To evaluate the sensitivity of the results with the selected value of solute diffusivity, the osmotic and pressure clamp virtual experiments were run with values of diffusivity divided or multiplied by 2 as compared with the default value estimated experimentally by Knipfer et al. (2007); 4 × 10⁻¹¹ m² s⁻¹).

Finally, the same virtual experiments were repeated on a hydraulic anatomy with low k_w (Table 2) to investigate the impact of cell wall hydraulic properties on the generality of the results

Sensitivity Analysis of Root k_r to Cell Hydraulic Properties

The sensitivity (L_s; %) of root k_r to cell-scale properties was quantified as the ratio of two quantities: (1) the relative change of 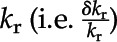resulting from a 1% change in a cell-scale hydraulic property (e.g. L_p or K_PD) and (2) the relative change of the latter cell-scale property, denoted L (i.e. 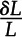; here equal to 1.01), in percentage units:

By definition, the sensitivity cannot exceed 100% (1:1 ratio). Furthermore, it can be demonstrated that the sensitivities of k_r to nonoverlapping elements of the hydraulic network must comprise between 0% and 100% and sum up to 100% when exhaustive.

On the one hand, a sensitivity analysis of k_r to an extensive list of cell-scale properties (K_PD and tissue-specific L_p) was conducted for a limited number of hydraulic anatomies (three stages of maturation of impermeable apoplastic barriers, low K_PD, and high or low k_w). On the other hand, a sensitivity analysis of k_r to a single cell-scale property (cortex cell L_p) was conducted for a wide number of hydraulic anatomies (10³ combinations of k_AQP, k_w, and K_PD parameter sets).

Accession Numbers

All information about the model, including the source code, is available at https://mecharoot.github.io/. We also developed a Web application to visualize typical outputs of our model. It was developed using the R Shiny framework and uses the following packages: ggplot2, ddply, and reshape2. The Web application is accessible at https://plantmodelling.shinyapps.io/mecha/. MECHA was released under the GPL.2 open-source license.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Scheme of the cell-level hydraulic network.

• Supplemental Figure S2. Cell-scale visualization of water fluxes at different stages of apoplastic barrier development for impermeable apoplastic barriers

• Supplemental Figure S3. Mapping of root mean square differences of root hydraulic conductivity profiles between a reference (Doussan et al., 1998b) and simulations for sets of cell hydraulic properties widely covering the parametric space.

• Supplemental Figure S4. Mapping of simulated sensitivities of root radial conductivity to cortex cell L_p for sets of cell hydraulic properties covering the full parametric space.

• Supplemental Figure S5. Impact of spatial variations of the osmotic potential in the symplast on the estimations of root hydraulic conductivity in simulated pressure clamp experiments for perfect solute mixing in the apoplast.

• Supplemental Note S1. Detailed solution of the water flow equations at the cell level.

• Supplemental Note S2. On the treatment of solutes in MECHA.

• Supplemental Note S3. Visualization of cell-scale composite water flow patterns at different maturity levels.

• Supplemental Note S4. Systematic exploration of the parametric space to search for parameter sets reproducing experimental observations.

• Supplemental Note S5. Impact of nonuniform symplastic solute concentrations on radial water fluxes.

• Supplemental Data Set S1. Impact of cell-scale hydraulic properties on simulated root radial conductivity, root reflection coefficient, and percentage of fully apoplastic radial water flow.

• Supplemental Data Set S2. Impact of transverse walls presence or absence on simulated root radial conductivity.