Self-Interaction of Human Serum Albumin: A Formulation Perspective

Abstract

In the present study, small-angle X-ray scattering (SAXS) and static light scattering (SLS) have been used to study the solution properties and self-interaction of recombinant human serum albumin (rHSA) molecules in three pharmaceutically relevant buffer systems. Measurements are carried out up to high protein concentrations and as a function of ionic strength by adding sodium chloride to probe the role of electrostatic interactions. The effective structure factors (S_eff) as a function of the scattering vector magnitude q have been extracted from the scattering profiles and fit to the solution of the Ornstein–Zernike equation using a screened Yukawa potential to describe the double-layer force. Although only a limited q range is used, accurate fits required including an electrostatic repulsion element in the model at low ionic strength, while only a hard sphere model with a tunable diameter is necessary for fitting to high-ionic-strength data. The fit values of net charge agree with available data from potentiometric titrations. Osmotic compressibility data obtained by extrapolating the SAXS profiles or directly from SLS measurements has been fit to a 10-term virial expansion for hard spheres and an equation of state for hard biaxial ellipsoids. We show that modeling rHSA as an ellipsoid, rather than a sphere, provides a much more accurate fit for the thermodynamic data over the entire concentration range. Osmotic virial coefficient data, derived at low protein concentration, can be used to parameterize the model for predicting the behavior up to concentrations as high as 450 g/L. The findings are especially important for the biopharmaceutical sector, which require approaches for predicting concentrated protein solution behavior using minimal sample consumption.

Introduction

In formulation of proteinaceous drugs, one of the main concerns is the physical stability of the drug molecule. Proteins at high concentrations tend to self-associate, potentially leading to high-viscosity solutions or aggregation. Modifications such as oxidation or adsorption to the vial are additional concerns in formulation strategies. If the three-dimensional structure of a protein is not conserved, this could lead to degradation, loss of activity, and the formation of new epitopes, which could induce an immunological response. Finally, the formulation of course needs to be compatible with the route of administration. All of these challenges generate issues during production, for ensuring prolonged shelf-life of a biopharmaceutical, and in administration, which all set high demands on the formulation.¹

Human serum albumin (HSA) is, with a blood concentration of 35–50 mg/mL, the most abundant plasma protein comprising more than half the amount of proteins in the blood plasma. HSA has many important physiological functions and, for instance, regulates the colloidal osmotic pressure and transports endogenous physiological metabolites and exogenous ligands, such as fatty acids, hormones, bile acids, and drugs.²⁻⁴ These properties have drawn much interest from the pharmaceutical industry and particularly in clinical applications.⁵ HSA’s pharmacokinetic properties are utilized in drug-delivery systems, and HSA’s ability to increase the solution stability of other proteins is used in drug formulations.

In formulations, HSA is used as a stabilizer, preventing aggregation, as an antiadsorption agent, or as an antioxidant^6,7 and was traditionally widely used in pharmaceutical products such as Avonex and Epogen. However, due to severe safety issues associated with infection of patients with human immunodeficiency virus from plasma-derived constituents in medicine in the 1980s and the 1990s and later with the occurrence of Creutzfeldt–Jakob disease transferred from infected cows, it became increasingly difficult to get regulatory approval of drugs containing constituents of mammalian origin. The use of serum-derived HSA was therefore limited. With the development of recombinant HSA (rHSA) derived from yeast (Recombumin, Albumedix Ltd.), the interest has resurfaced in the last decade and an increasing number of modern pharmaceuticals containing rHSA like the trivalent subunit vaccine M-M-R_II and the tetravalent subunit vaccine ProQuad have been marketed.

The use of albumin to stabilize protein-based drugs at low concentration was established decades ago and is expected to function via competitive inhibition of the protein-based drug adsorption to other materials.⁸ At protein-based drug concentrations less than 0.1 mg/mL, adsorption of protein-based drugs to the available air–liquid and solid–liquid surfaces in the primary packaging material will result in depletion and/or lead to surface-induced degradation of the active component. Hence, prevention of drug adsorption is thus essential and can be mitigated by addition of a nonionic detergent or by addition of HSA.

In contrast to this, the mechanism of action for preventing aggregation is speculative for formulations with protein-based drug concentrations above 1 mg/mL. Here, rHSA is used in concentrations ranging from a few mg/mL to all the way up to around 50 mg/mL. At these higher concentrations, the aggregation of proteins is a complex process. One commonly recognized mechanism is the nonspecific effects of steric exclusion, where the protein molecules in question are excluded from the volume occupied by other protein species. With increasing concentration, the volume of the solution available to proteins is restricted. In terms of thermodynamics, the entropy of a crowded solution is significantly reduced and hence the free energy of the proteins increases. The system reacts to this by association of proteins to reduce the exclusion of volume.^9,10 However, steric exclusion is not entirely nonspecific, and in many cases, the aggregation propensity of proteins depends on their specific structures and local environments.^11,12 It has been shown for solutions of monoclonal antibodies at relatively high concentrations that HSA prevents liquid–liquid phase separation, which is often preempted by aggregation or crystallization.¹³ Understanding the stabilizing ability of rHSA requires first elucidating the thermodynamic behavior in rHSA-only solutions from low to high protein concentrations. In dilute protein solutions, the osmotic pressure (or osmotic compressibility) of the solution is determined by the osmotic second virial coefficient B₂₂, which is commonly obtained by static light scattering (SLS).¹⁴⁻²⁰ The pH and ionic strength dependence of B₂₂ provides an insight into the intermolecular forces underpinning the solution behavior.^{16−18,21−25} Measurements for solutions of either rHSA or bovine serum albumin (BSA) have been rationalized in terms of potential of mean force models that describe the protein–protein interaction using an excluded volume potential and the electric double-layer force from the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory and, in some cases, an additional short-ranged protein–protein attraction.²⁶⁻²⁹

Early studies by Tardieu et al.³⁰⁻³⁴ on α-crystallin found in the eye lens showed how small-angle X-ray scattering (SAXS) could be used for examination of the interaction of proteins in highly concentrated solutions. The α-crystallin interaction was modeled using the renormalized mean spherical approximation with the electric double-layer potential from the DLVO theory and a hard core potential (the excluded volume effect).³¹

Due to its high solubility in aqueous solutions, serum albumin has been used as a model system to study high protein concentrations (up to 500 mg/mL) in buffer-free solution with and without salts.³⁵⁻⁴¹ SAXS experiments indicate that monovalent salts such as NaCl in general have a screening effect. Under low-ionic-strength conditions, measured structure factors were fit to the mean spherical approximation, which is based on a spherical model using only the electric double-layer potential from the DLVO theory, whereas at higher salt concentrations (greater than 1 M), the structure factors reflected the presence of a short-ranged attraction between proteins.⁴¹ The authors postulated the existence of a repulsive hydration force to prevent phase separation, which would ordinarily occur in the presence of an attractive interaction. Small-angle neutron scattering studies of HSA interacting in D₂O with and without NaCl (1.08 M) were fit by Sjöberg and Mortensen to Monte Carlo simulations using an ellipsoidal shape to describe the protein.^42,43 The fitting required including an additional square well repulsive potential at low salt conditions and a short-ranged repulsive Yukawa potential at high salt concentration, but there was no evidence for a short-ranged protein–protein attraction.

In the present study, to shed more insight into the observed stabilizing effect, we have used SAXS and SLS to study the solution properties and self-interaction of rHSA molecules in three pharmaceutically relevant buffer systems with different ionic strengths. The mean spherical approximation has been used to fit structure factor curves measured by SAXS and we have compared a hard sphere versus ellipsoidal model for reproducing osmotic compressibility curves up to 315 g/L obtained from SLS and SAXS. We show that rHSA behavior in solutions at NaCl concentrations up to 500 mM can be adequately explained without invoking the existence of any short-ranged attraction, where the excluded volume effects are more accurately captured using an ellipsoidal model rather than a spherical one. We find the only effect of changing the formulation buffer is to alter the strength of electrostatic interactions due to differences in the solution pH and ionic strength.

Theory

The next section provides an overview of the protein–protein interaction model, focusing on how the model is characterized from measurement of the osmotic second virial coefficient, and its relationship to the structure factor at high protein concentrations. Furthermore, we provide the relationships between the SLS and SAXS measurements and the osmotic compressibility in terms of the measured structure factor and emphasize the limitations of using SAXS to probe the behavior of anisotropic shaped particles such as rHSA.

Protein–Protein Interaction Theory

The two-body potential of mean force, w(r), where r is the center-to-center separation between proteins, provides the input into models for predicting thermodynamic properties and the equilibrium solution microstructure. w(r) corresponds to an interaction free energy averaged over the relative orientations between a pair of proteins as well as the solvent degrees of freedom. Previous studies on BSA and HSA under low- to moderate-ionic-strength conditions indicate that the protein–protein interaction is well described using a hard sphere repulsion in combination with an electrostatic contribution.^41,44 A theoretical model for the electrostatic terms is given by the electric double-layer potential derived within the DLVO theory, which treats the protein as a uniformly charged sphere immersed in a dielectric continuum containing point charges (e.g., salt ions). For low surface potentials, a reasonable approximation for the two-body interaction free energy is given by eq 1

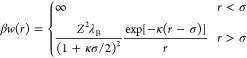1

where Z corresponds to the protein valency, σ is an effective hard sphere diameter, and β is the dimensionless inverse temperature 1/k_bT, where k_b is the Boltzmann constant. The excluded volume contribution to the interaction potential is controlled by the parameter σ, which controls the distance of closest approach between a pair of proteins. The range of the electrostatic interactions is controlled by κ, the inverse Debye–Hückel screening length

2

where I is the ionic strength of the solution, e is the electronic charge, ε₀ is the vacuum permittivity, ε is the dielectric constant of water, and N_A is Avogadro’s number. λ_B corresponds to the Bjerrum length 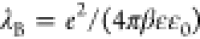, which is the separation between a pair of ions when the Coulomb energy is equal to thermal energy.

A commonly used method for characterizing simplified models for w(r) is through measurements of the osmotic second virial coefficient, B₂₂^v, obtained here through static light scattering. B₂₂ is related to w(r) through an average over r given by

3

Equation 3 can be further simplified by carrying out the integration over r between 0 and σ to give

4

where B₂₂^hs corresponds to the excluded volume interaction of a hard sphere of diameter σ, which is equal to 4 times the sphere volume (2πσ³/3). The integral on the right-hand side of eq 4 includes the contributions of all forces except for excluded volume, which are collectively referred to as soft potentials.

SAXS experiments provide information about the spatial protein density distribution in terms of the static structure factor. For an isotropic system, S(q) is related to the Fourier transform of the pair distribution function g(r) by

5

where ρ is the protein molecular density and q is the momentum transfer vector magnitude q = 4π sin θ/λ, where λ is the wavelength of the X-rays and 2θ is the scattering angle. The pair distribution function corresponds to the normalized density for the centers of protein molecules in a spherical shell located at r with thickness Δr and volume 4πr²Δr about a protein molecule fixed at the origin. The Ornstein–Zernike (OZ) equation, when combined with an appropriate closure relation, can be used to determine g(r) or equivalently S(q) in terms of the interaction potential, w(r). In this work, we have used an analytical solution for the OZ equation based on the mean spherical approximation for the Yukawa interaction model, which has the same mathematical form as the electric double-layer potential given in eq 1.²⁷

SLS Theory and Analysis

The measured quantity in an SLS experiment termed the excess Rayleigh ratio R̅_θ is equal to the light scattered by the protein sample minus the scattering from the solvent mixture at the same chemical potential as the protein solution. The relationship to the osmotic compressibility of the solution for a single solute in a mixed solvent is given by⁴⁵⁻⁴⁷

6

where c is the protein mass concentration, M_w is the protein molecular weight, and S(0) is the static structure factor evaluated in the limit of q → 0, which is related to the osmotic compressibility of the protein solution. K is an optical constant equal to 2π²n₀²/(N_Aλ⁴), where n₀ is the refractive index of the solvent. The refractive index increment (∂n/∂c) is at constant temperature and chemical potential of solvent components, which is obtainable through dialysis equilibrium experiments. We use a literature value approximately equal to 0.185 mL/g measured for BSA in solutions at low to moderate tonicities.⁴⁸Equation 6 is only valid when there is no angle dependence of the scattered light, which is a good approximation when the characteristic correlation length scale is less than 1/20th the wavelength of the incident light.

The experimental osmotic second virial coefficient, denoted here as B₂₂ = N_AB₂₂^v/M_w, is determined from SLS using only low-protein-concentration data. In this case, the osmotic compressibility is expanded in a virial expansion, which gives in the low-protein-concentration limit

7

B₂₂ is determined from a linear fit to eq 7 from 10 measurements with protein concentration varying between 2 and 20 g/L. The regressed slope is equal to 2B₂₂, and the inverse of the y-intercept is equal to M_w. In the Results and Discussion section, the reported error bars correspond to the standard error in the slope estimation.

SAXS Theory

A SAXS experiment is used to measure the scattering intensity per unit volume, I(q), as a function of the scattering vector q. The total scattering intensity is given by⁴⁹

8

where P(q) is the form factor defined as P(q) = ⟨|F_j(q,Ω_j)|²⟩_Ωj/(Δρ)²V_p², Δρ is the excess scattering length density of the protein, and ϕ is the protein volume fraction. For a particle with a homogeneous electron density distribution, the scattering length F_j(q,Ω_j) is given by an integral over the particle volume V_p

9

where R_j corresponds to the spatial coordinate within the particle relative to the particle center of mass and Ωj defines the particle orientation in the coordinate system of the laboratory reference frame.

The profile S_eff(q) can be obtained either by using an analytical expression for the form factor or by normalizing the X-ray scattering profile with data obtained at low protein concentration, which is the approach used here. At low protein concentration, there are no orientational or intermolecular correlations between particles and S_eff(q) = 1 so that⁵⁰

10

where the subscript low denotes a low concentration property. As such, the structure factor profile can be obtained by normalizing the intensity profile by the low-concentration data according to

11

Using eq 11 requires that there are no protein conformational changes as a function of protein concentration. Conformational changes would be reflected by differences in the normalized I(q)/c profiles over a range, where S_eff(q) ∼ 1 corresponding to q > 1.0 nm^–1, which is not observed for rHSA solutions studied here.

For nonspherical particles, S_eff(q) is given by an ensemble average over all possible orientations and separations between particles i and j

12

where N is particle number. The main purpose of measuring S_eff is to obtain information about the solution structure as characterized in terms of the true structure factor, which is defined in terms of an ensemble average over center-of-mass positions between particles

13

For spherical particles, the apparent and true structure factors are equal to each other because there is no orientational dependence of the scattering factor, F_j. For anisotropic particles, the measured structure factor can be related to the true structure factor, S(q), using the decoupling approximation, which assumes that there are no orientational correlations between particles. The approximation is given by

14

where the decoupling parameter is defined as β^DA = ⟨|F_j(q)|⟩_Ωj²/⟨|F_j(q)|²⟩_Ωj.

The limitations of fitting SAXS data with the decoupling approximation or using spherical models have been examined using molecular simulations of ellipsoids with aspect ratios ranging from 0.333 to 3.⁵¹ For aspect ratios less than 0.5 or greater than 2, the simulated S_eff(q) profile only equals the true structure factor for the ellipsoids in the range q(ab²)^1/3 ≲ 2, where a and b correspond to the radii along and perpendicular to the symmetry axis, respectively. The deviations between the structure factor profiles at larger q grow with increasing volume fraction, leading to a shift in the major peak in S_eff(q) to a higher q value than that occurring in S(q). Because the peak location is inversely related to the averaged particle center-to-center separation, matching the peak position can lead to underestimating key length scales in intermolecular correlations. In addition, for ellipsoids with aspect ratios less than 0.5, there is an occurrence of a second peak at higher q in S_eff(q) that does not reflect any characteristic length scale observable from S. For these particles, the decoupling approximation does not provide any additional accuracy due to strong orientational couplings at close center-to-center separation. Fitting form factor models to experimentally derived SAXS data indicates that HSA has a similar shape to an oblate ellipsoid with dimensions equal to 17 × 42 × 42 ų,⁴¹ which corresponds to an aspect ratio of approximately 0.4. To avoid any artifacts of these assumptions, only the region in the S_eff(q) profile corresponding to q(ab²)^1/3 ≲ 2 or equivalently q < 0.06 Å is used in our fitting.

SAXS Analysis

All calibrations and corrections of the SAXS data were done using the in-house software Bli911-4.⁵² Buffer averaging and subsequent subtraction prior to data analyses were done in Primus.⁵³ The ATSAS program package version 2.4⁵⁴ was used for further data analysis. Evaluation of the Guinier region was performed within Primus. The form factor for each buffer condition, P(q), was derived from merging data at low and high protein concentrations in the same buffer conditions. The pair distribution function, p(r), was evaluated using the interactive program GNOM.⁵⁵ An overview of the samples measured by SAXS, the SAXS scattering data, and the data treatment parameters are provided in Tables S1–S4 and Figure S1, Supporting Information.

The effective structure factors, S_eff(q), were derived by dividing the scattering intensity by the experimentally derived form factor for the corresponding buffer condition following the procedure defined by eq 11.

Results and Discussion

Protein–Protein Interactions Probed by SLS Scattering Indicate that the High Salt Behavior Is Only due to Excluded Volume Forces

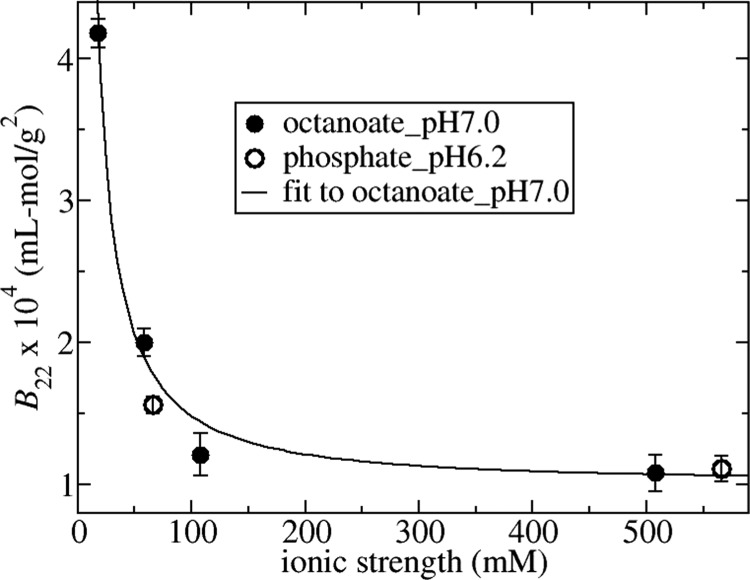
The SLS data were used for determination of the osmotic second virial coefficient, B₂₂, and the molecular weight. All measurements of molecular weight were on the order of 70.0 ± 3.5 kDa, indicating monodisperse samples. B₂₂ values plotted as a function of ionic strength are shown in Figure 1 for solutions either in octanoate_pH7.0 or in phosphate_pH6.2 along with a line of best fit to the octanoate_pH7.0 data. The main effect of increasing ionic strength up to 100 mM is to screen electrostatic repulsion, which leads to the decrease in B₂₂ values. Over this range, the ionic strength dependence of protein–protein interactions in terms of B₂₂ can be rationalized in terms of an electric double-layer force.^16,17,21,22 The line of best fit shown in Figure 1 has been obtained by fitting the octanoate_pH7.0 data to eq 4 using the double-layer potential for w as given by eq 1. The fit parameters are the limiting value for B₂₂ at high ionic strength given by the hard sphere value B₂₂^hs = 10.5 × 10^–5 mL mol/g² and a net charge value Z equal to −16.3e. The latter is in good agreement with the experimental value equal to −14e obtained from potentiometric titration data at pH 7⁵⁶ (Tanford and Buzzell,⁵⁷ obtained −13e at pH 7.3) indicating that the DLVO potential provides an adequate representation of the electrostatic contribution to the protein–protein interactions.

Figure 1.

B₂₂ values plotted vs ionic strength for solutions in octanoate_pH7.0 (closed circles) and phosphate_pH6.2 (open circles). The solid line is the best fit of octanoate_pH7.0 data corresponding to Z = −16.3e and B₂₂^hs = 10.5 × 10^–5 mL mol/g².

In modeling the protein–protein interactions, we neglected any contributions from a short-ranged protein–protein attraction so that the contribution to B₂₂ at high salt concentration is only from excluded volume forces. This assumption can be checked by comparing the fit value for B₂₂^hs versus a theoretical estimation of the parameter. The excluded volume for anisotropic-shaped proteins can be approximated by the excluded volume for a hypothetical sphere with the same hydrodynamic diameter as the protein.⁵⁸ The literature value for the hydrodynamic diameter of BSA is approximately 74 Å,⁵⁹ which corresponds to an excluded volume contribution in experimental units equal to 11.1 × 10^–5 mL mol/g². A similar value was reported independently³⁶ through calculating the excluded volume for an ellipsoid that gives the best fit to the form factor data for BSA. The theoretical value is indeed very close to our results for B₂₂ at 500 mM sodium chloride concentration equal to 10.8 ± 0.7 × 10^–5 and 11.1 ± 0.5 × 10^–5 mL mol/g² for octanoate_pH7.0 and phosphate_pH6.2, respectively, which, in turn, are similar to the fit value of B₂₂ because electrostatic interactions are sufficiently screened under these conditions. The close agreement between the theoretical estimate and the high ionic strength data for B₂₂ indicates that there is a negligible contribution from the short-ranged attraction. This deduction is consistent with SAXS studies of BSA and HSA under low- to moderate-ionic-strength conditions, which do not require any short-ranged protein–protein attraction in models for fitting to structure factor profiles.^35,41,44 This behavior is in direct contrast to SAXS studies of lysozyme, which require including a short-ranged attraction in models for capturing SAXS data even under conditions where the net protein–protein interaction is repulsive and S(0) is less than 1.^44,60

The measured values for the osmotic compressibility (or equivalent S(0)⁻¹) obtained from SLS are compared in Figure 2 for the same solution conditions used to measure the B₂₂ values. For the octanoate_pH7.0, there is a decrease in osmotic compressibility with increasing ionic strength due to screening the electrostatic repulsion. However, there is very little change between the curves with 145 mM NaCl versus 500 mM NaCl as the electrostatic forces have been sufficiently screened. The runs in phosphate_pH6.2 also follow the trends expected from considering the B₂₂ values and the effect of electrostatic interactions, which indicate that the protein–protein repulsion is greater than that at pH 7, 145 mM NaCl, but less than that at 50 mM NaCl and pH 7. The osmotic compressibility is bounded by the corresponding curves for these solution conditions. The high salt concentration run at pH 6.2 agrees very well with the high salt run at pH 7.0 as the electrostatic interactions have been screened and there is very little effect of changing the net charge on the protein due to reducing the pH from 7.0 to 6.2. This is also expected from the B₂₂ studies shown in Figure 1, which are similar under the high salt conditions.

Figure 2.

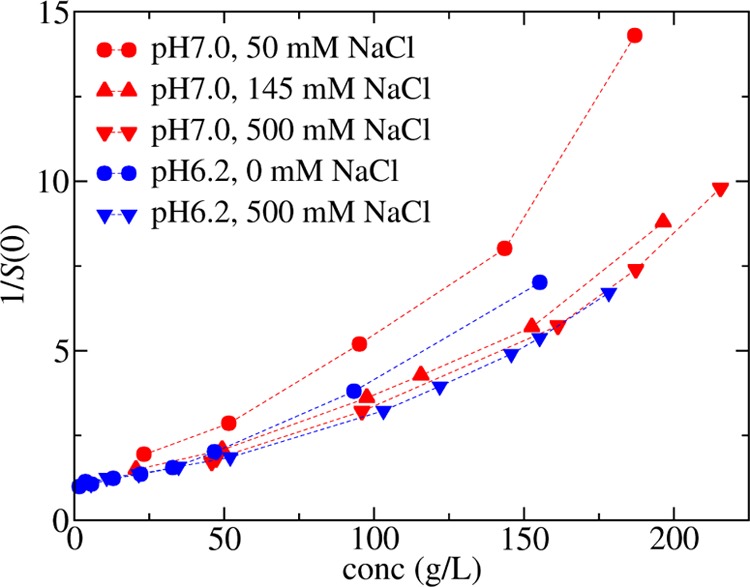
Osmotic compressibility measured using SLS in octanoate_pH7.0 (red symbols) or phosphate_pH6.2 (blue symbols) at different sodium chloride concentrations as denoted in the legend. The lines are drawn as a guide to the eye.

Decoupling Excluded Volume and Electrostatic Forces from Fitting to Low-q Region of S(q)

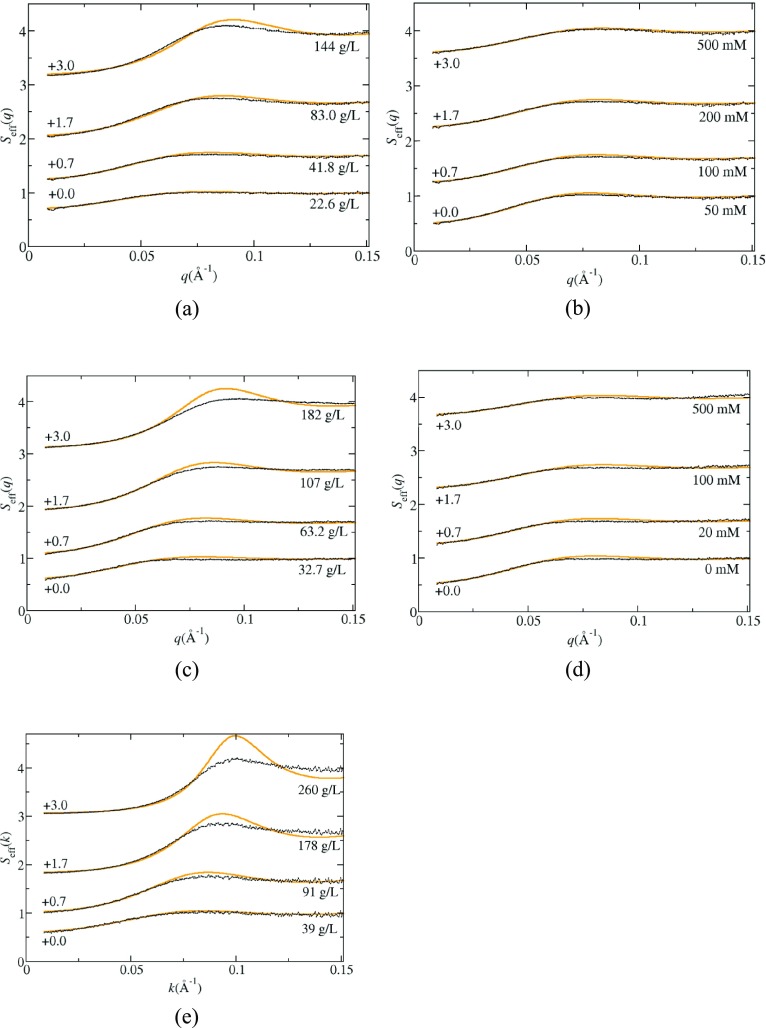
In Figure 3a–e are shown the measured static structure factor profiles S_eff(q) for rHSA as a function of salt concentration in octanoate_pH7.0 (Figure 3b) and in phosphate_pH6.2 (Figure 3d) with a nominal protein concentration of ∼40 g/L, and as a function of protein concentration in octanoate_pH7.0_I153 (Figure 3a), phosphate_pH6.2_I66 (Figure 3c), and citrate_pH6.5_I274 (Figure 3e). In all cases, the extrapolated values S_eff(0) are less than 1, indicating the presence of net repulsive protein–protein interactions. The effect of the electrostatic repulsion is apparent from the increase in S(0) values with increasing ionic strength as shown in Figures 2 and 3. The effect is much more dramatic in octanoate_pH7.0 because the initial ionic strength is 18 mM, whereas in citrate_pH6.5, the lowest ionic strength curve corresponds to 66 mM. With increasing protein concentration, the S(0) values decrease, which is expected for a system that exhibits only repulsive interactions.

Figure 3.

Selected structure factor profiles S_eff(q) obtained from SAXS measurements for solutions in octanoate_pH7.0 (a) 145 mM NaCl, ∼20 to ∼150 g/L rHSA, (b) 40 g/L rHSA, 50–500 mM NaCl; in phosphate_pH6.2 (c) no added salt, ∼30 to ∼180 g/L rHSA, (d) 0–500 mM NaCl, 40 g/L rHSA; and (e) in citrate_pH6.5, 40–260 g/L rHSA. The orange lines correspond to the electrostatic fitting in phosphate_pH6.2 and octanoate_pH7.0, and to the hard sphere fitting for the runs in citrate_pH6.5_I274.

The solid lines shown in Figure 3 are obtained from fitting data for q values less than 0.06 Å^–1, which is the region where S_eff(q) is equal to the true structure factor S(q).⁵¹ We have included only a small q range to avoid any artifacts that arise from including effects from orientational correlations on S_eff(q), but this limits the certainty in the estimates of fitting parameters. As such, we only consider fitting one parameter to the data using two different approaches. First, the fitting includes the hard sphere potential and the double-layer force, where the protein charge is treated as a fitting parameter and the hard sphere diameter is constrained to a value of 67 Å, which has been shown previously to provide a good fit to SAXS data for BSA at high protein concentration.⁴¹ The screening length is determined from eq 2 using the experimental ionic strength. This approach is referred to as the electrostatic model. The second approach only uses a hard sphere potential and does not include any long-ranged repulsive interactions. As such, the diameter is treated as a fitting parameter. The results of the fitting are shown in Tables 12–3 along with the reduced χ² values.

Table 1. Parameters Obtained from Fitting to S_eff(q) in Octanoate_pH7.0.

ionic strength (mM)	[NaCl] (mM)	[rHSA] (g/L)	Z (e)a	χ2 a	σ (Å)b	χ2 b
153	145	22.6	16.0 ± 0.2	2.14	73.5 ± 0.2	3.09
153	145	41.8	14.9 ± 0.1	3.64	72.2 ± 0.1	6.4
153	145	83.0	15.5 ± 0.2	11.0	71.6 ± 0.1	19.5
153	145	143.8	15.5 ± 0.2	17.9	70.5 ± 0.1	26.4
163	10	45.8	10.2 ± 0.1	33.2
173	20	44.7	11.7 ± 0.1	23.4
203	50	45.6	13.5 ± 0.1	9.43	78.8 ± 0.2	32.4
253	100	44.5	15.4 ± 0.1	4.27	75.1 ± 0.1	10.0
298	145	41.8	14.9 ± 0.1	3.64	72.2 ± 0.1	6.41
353	200	42.3	17.1 ± 0.2	2.83	71.6 ± 0.1	4.27
653	500	38.4	27.5 ± 0.3	1.59	70.7 ± 0.1	1.84

^aIndicates that the DLVO potential is included in the model where Z is the fit parameter.

^bIndicates fitting with only a hard sphere potential, where σ is the fitting parameter.

Table 2. Parameters Obtained from Fitting to S_eff(q) in Phosphate_pH6.2.

ionic strength (mM)	[NaCl] (mM)	[rHSA] (g/L)	Z (e)a	χ2 a	σ (Å)b	χ2 b
66	0	23.8	5.54 ± 0.4	23.8
66	0	32.7	9.4 ± 0.1	2.98	72.8 ± 0.2	6.15
66	0	41.1	10.0 ± 0.1	3.29	73.3 ± 0.2	7.98
66	0	63.2	10.1 ± 0.1	4.46	72.7 ± 0.2	12.5
66	0	107.4	9.4 ± 0.1	6.36	71.1 ± 0.1	16.2
66	0	181.8	8.4 ± 0.2	8.23	68.3 ± 0.1	28.5
76	10	39.9	9.7 ± 0.1	2.22	72.2 ± 0.2	4.74
86	20	38.9	10.1 ± 0.1	2.42	71.9 ± 0.2	4.53
116	50	39.3	8.3 ± 0.3	2.77	69.4 ± 0.2	3.59
166	100	38.2	10.5 ± 0.3	1.58	69.5 ± 0.1	1.97
216	150	34.2	10.0 ± 0.4	1.68	68.6 ± 0.1	1.87
266	200	35.1	10.9 ± 0.4	1.49	68.5 ± 0.1	1.65
566	500	30.7	23.4 ± 0.5	0.97	69.4 ± 0.1	1.01

^aIndicates that the DLVO potential is included in the model, where Z is the fit parameter.

^bIndicates fitting with only a hard sphere potential, where σ is the fitting parameter.

Table 3. Parameters Obtained from Fitting to S_eff(q) in Citrate_pH6.5.

ionic strength (mM)	[NaCl] (mM)	[rHSA] (g/L)	Z (e)a	χ2 a	σ (Å)b	χ2 b
274	0	28.6	17.7 ± 0.4	0.96	70.6 ± 0.2	0.89
274	0	38.8	16.6 ± 0.3	0.89	70.0 ± 0.1	0.89
274	0	49.7	17.7 ± 0.3	1.39	69.9 ± 0.1	1.05
274	0	91.5	17.5 ± 0.2	1.20	69.5 ± 0.1	1.55
274	0	129.5	10.2 ± 0.6	7.27	67.6 ± 0.1	8.88
274	0	177.9			66.6 ± 0.1	15.7
274	0	259.8			65.0 ± 0.1	24.1
274	0	315.1			64.1 ± 0.1	18.0

^aIndicates that the DLVO potential is included in the model, where Z is the fit parameter.

^bIndicates fitting with only a hard sphere potential, where σ is the fitting parameter.

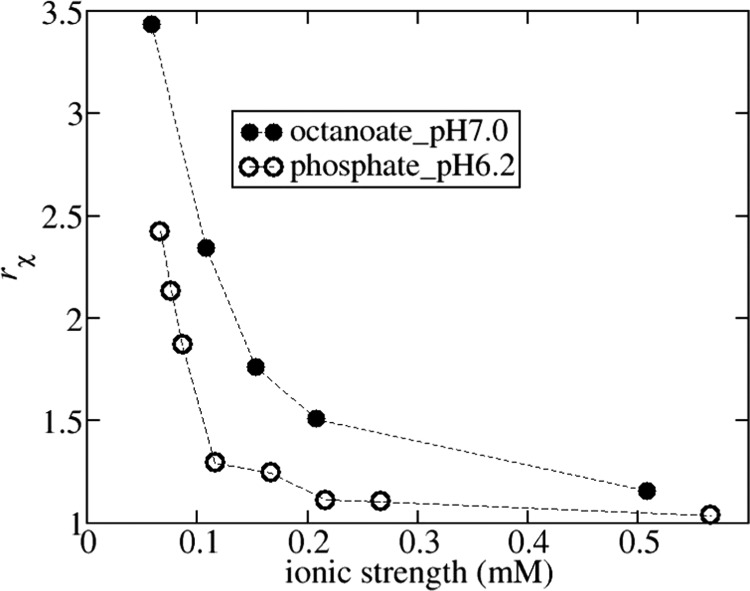
The results as a function of ionic strength can be used to examine the role of repulsive electrostatic interactions in the fitting. Previous studies of BSA have shown that thermodynamic properties (e.g., osmotic pressure, osmotic compressibility) can be accurately reproduced up to high protein concentrations using only a hard sphere model, where the diameter is tuned to account for any electrostatic repulsion.^28,61 Similarly, phase diagrams of protein solutions can be accurately reproduced using an effective diameter chosen to account for all repulsive contributions to the interaction potential.^62,63 As such, a key question is whether our fitting can discriminate a model including the electric double-layer force from a model including only hard sphere interactions. The relative accuracy of our fitting approaches can be ascertained from the ratio of χ² values obtained from fitting data to the hard sphere model versus the electrostatic model, r_χ = χ_hs²/χ_el. This ratio is plotted versus ionic strength in Figure 4 for the runs in phosphate_pH6.2 and octanoate_pH7.0. At low-ionic-strength conditions, the electrostatic model provides a much more accurate fit, but with increasing ionic strength above 200 mM, the accuracies become similar as the ratio approaches 1 due to sufficient screening of the electrostatic interactions. This is reflected by the B₂₂ measurements at 500 mM ionic strength, which are equal to the hard sphere value within the experimental certainty, whereas the measured B₂₂ value in octanoate_pH7.0 with 200 mM sodium chloride is only 10% larger in magnitude. Fitting the S_eff(q) profiles taken with 500 mM NaCl to the hard sphere model gives a diameter equal to 71 and 69 Å in octanoate_pH7.0 and phosphate_pH6.2, respectively. Both these values are slightly below the hard sphere diameter equal to 74 Å deduced from the B₂₂ measurements. We argue below that this discrepancy in part arises due to assuming that HSA is a sphere when fitting the structure factor at higher protein concentrations.

Figure 4.

Ratio of χ² values obtained from fitting data to the hard sphere model and the electrostatic model: r_χ = χ_hs²/χ_el. Solid sphere: octanoate_pH7.0; open sphere: phosphate_pH6.2.

The fitting also provides realistic values for the net charge of rHSA as a function of ionic strength. The values obtained in octanoate_pH7.0 are only slightly larger than the ones obtained in phosphate_pH6.2 reflecting an expected decrease in net negative charge. The absolute values in phosphate_pH6.2 remain relatively constant and approximately equal to −9e, whereas in octanoate_pH7.0, there is a slight increase from −10e to −17e when increasing ionic strength from 20 to 200 mM. The increase has been previously observed by fitting the model to SAXS data using the same hard sphere diameter and attributed to an increase in chloride-ion binding.^41,64 At high ionic strengths of 500 mM, the fit value of charge is much larger, but the electrostatic contribution to the interaction potential is very small due to the ionic screening. This condition corresponds to the case when the fitting cannot discriminate between the electrostatic model or a hard sphere model with a slightly larger diameter.

The experiments in citrate_pH6.5_I274 were pushed to much higher protein concentrations with a total ionic strength equal to 274 mM. At this ionic strength, the effect of electrostatic interactions is expected to be small so that the hard sphere model should provide an adequate fitting. This indeed is the case as χ² values are similar for both fittings for the runs at lower protein concentration. At protein concentrations less than 100 g/L, the fitting is similar to what was found in octanoate_pH7.0_I153, where the fit charge is similar to −17e when using the electrostatic model or the diameter is near to 70 Å for the hard sphere model. With further increasing protein concentration, the fit diameter steadily decreases to a value of 64 Å at a protein concentration of 315 g/L. At this limit, fits to the electrostatic model are not possible when fixing the diameter to 67 Å because the osmotic compressibility predicted by the hard sphere model is greater than the measured value for 1/S(0). Matching the experimental data requires either reducing the diameter below 67 Å or introducing a short-ranged protein–protein attraction. This discrepancy likely arises due to fitting the structure factor of an anisotropic-shaped protein with a spherical model. The spherical assumption was examined in a computational study for a monoclonal antibody by comparing the structure factor profiles and osmotic compressibility of a three-bead model for the protein to that of an equivalent hard sphere with the same osmotic second virial coefficient.⁶⁵ For excluded volume systems, the osmotic compressibility is proportional to the fraction of overlapping particle configurations. Because the three-bead model and the sphere have the same osmotic second virial coefficient, the osmotic compressibility is similar at low protein concentrations, where only two-body interactions are significant. With further increasing protein concentration, the osmotic compressibility for the sphere is always greater than that for the bead model because there are more n-particle nonoverlapping configurations available to the anisotropic model versus the sphere of the same excluded volume. Because the three-bead model has a similar flattened geometry to an oblate ellipsoid, it is likely that a similar argument applies to albumin. Indeed, in the study by Greene et al.,⁵¹ the sphere that best matches the oblate ellipsoidal structure factor at high packing fractions (e.g. greater than 20%) is smaller than the equivalent sphere with the same excluded volume. Our finding that a smaller sphere is needed to model HSA at high protein concentrations is also consistent with a molecular simulation study, indicating that the best-fit diameter to SAXS data is 63.6 Å, which is much less than the excluded volume diameter.³⁵

Osmotic Compressibility Curves Measured by SAXS and SLS Are Similar

SLS and SAXS provide complementary techniques for estimating S(0) as both approaches rely on assumptions about the angle dependence of the scattered light. For the SAXS data, fitting is required to extrapolate the S_eff(q) profile to the long-wavelength limit from data obtained for q-values greater than 0.01 Å^–1, whereas the SLS experiment assumes no q-dependence of scattered light for q less than approximately 0.001 Å^–1. As a check of the assumptions, Figure 5 shows a comparison of the measured values of 1/S_eff(0) by SLS to those obtained from the fits to the SAXS data in octanoate_pH7.0_I153 and in phosphate_pH6.2_I66. We find a very good agreement between the methods for both solutions. The general rule of thumb is that the wavelength should be greater than 20 times the characteristic correlation length in the protein solution for neglecting the angle dependence of scattered light. If the main contribution to protein–protein interactions is only from excluded volume interactions, the correlation length is expected to be on the order of the size of a protein molecule, about 70 Å, which is much less than the wavelength of laser light equal to 658 nm. The effects of electrostatic interactions on the correlation length are expected to be negligible even at the lower ionic strength conditions in phosphate_pH6.2_I66, where the screening length is on the order of 1.2 nm.

Figure 5.

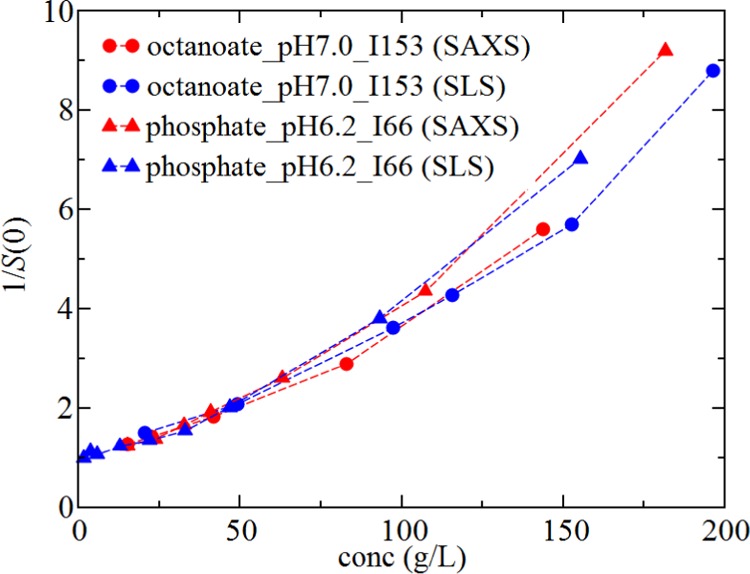
Comparison of osmotic compressibility profiles as a function of rHSA concentration obtained from SAXS (red symbols) to those obtained by SLS (blue symbols) for phosphate_pH6.2_I66 (triangles) or octanoate_pH7.0_I153 (circles).

Oblate Ellipsoidal Model Is More Accurate at Describing the Osmotic Compressibility from Low to High Protein Concentration

In Figure 6, S(0)⁻¹ curves obtained from SLS in solutions with 500 mM NaCl in phosphate_pH6.2 or octanoate_pH7.0 are compared against the values obtained for citrate_pH6.5_I274 from SAXS. Because the data agree very well with the behavior in the other buffers with 500 mM NaCl, we expect that an excluded volume model should be capable of describing the data obtained for citrate_pH6.5_I274. As such, these can be used to test the accuracies of using an ellipsoidal versus spherical model. We use the virial equation including the first 10 terms in the expansion for the hard sphere equation of state, given by

15

where B_i^v corresponds to the ith virial coefficient (noting that B₂₂ ≡ B₂^v). The calculated pressure from the 10-term virial expansion agrees with simulated data for hard spheres with a precision of ΔZ < 0.003 compared to molecular simulations up to a packing fraction η ≡ πρσ³/6 < 0.35.

Figure 6.

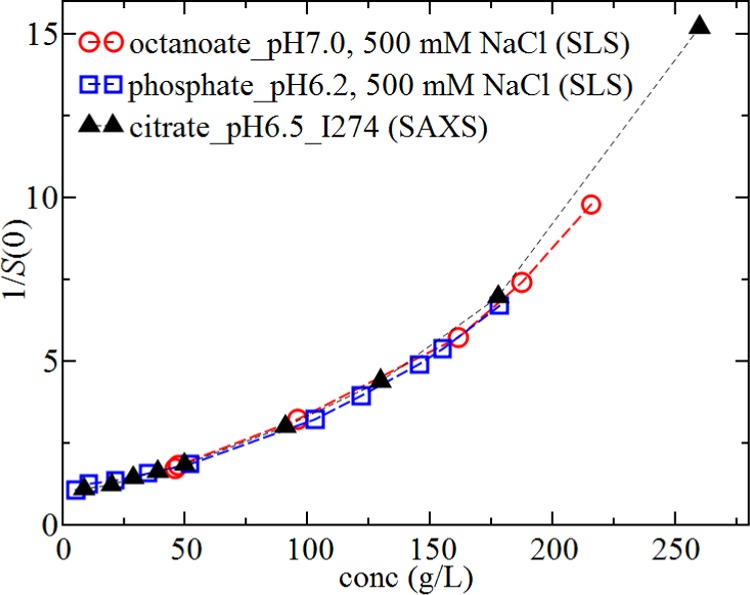
Measured values for S(0)⁻¹ as a function of rHSA concentration obtained from SLS for samples at high salt conditions in phosphate_pH6.2 (blue squares) and octanoate_pH7.0 (red circles) and from SAXS for samples in citrate_pH6.5_I274 (black triangles).

The ellipsoidal model is based on the equation of state derived by Vega.⁶⁶ For oblate ellipsoids with relative dimensions given by 1 × 2.5 × 2.5, the analytical calculations agree with simulation data up to packing fractions equal to 0.45.⁶⁷ The Vega equation of state is

16

where the nth dimensionless virial coefficient is given by B_n^* = B_n/V^n–1, V is the volume of the ellipsoid, and the packing fraction is given by η = ρV. The dimensionless virial coefficients are functions of the mean radius of curvature for the ellipsoid R and the ellipsoid surface area S and volume V. The mathematical expressions to calculate the geometric properties, R, S, and V, and the virial coefficients are given in ref (67).

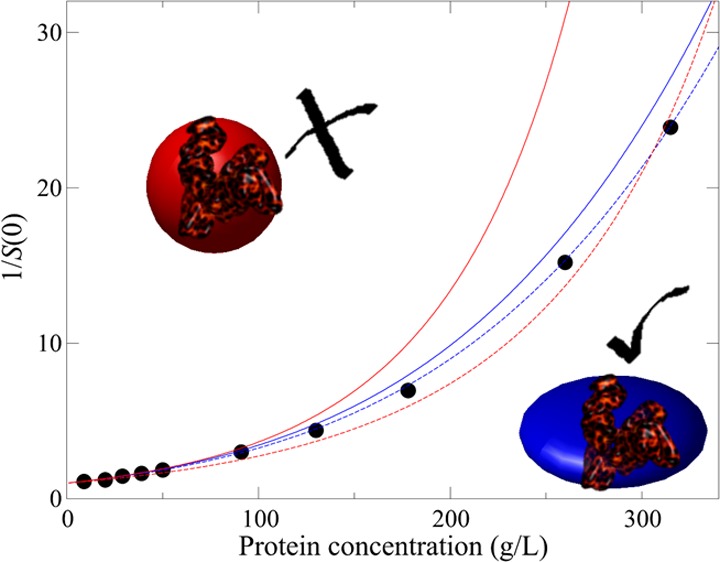
In Figure 7, the best fits of the spherical and the ellipsoidal model to the experimental data in citrate_pH6.5_I274 are shown. For the spherical model, the only fitting parameter is the hard sphere diameter σ equal to 64.7 Å. In the ellipsoidal model, we rely on the geometric structure determined from fitting to the form factor of albumin, which is an oblate ellipsoid with dimensions of 17 × 42 × 42 ų.⁴¹ In the fitting, each of the dimensions are multiplied by a constant factor f, which is necessary to account for the effect of surface roughness on the excluded volume calculation. The form factor should correspond to the actual volume of albumin including a hydration layer. However, the excluded volume is also increased due to the surface roughness over a smooth shape with the same actual volume.⁶⁸ As it is not possible to exactly quantify this effect, f is treated as a fitting parameter. The best fit to the ellipsoidal model is shown by the solid curve in Figure 7. The ellipsoidal model appears to provide a better representation of the data as the best-fit line corresponding to the 10-term virial equation has too much curvature, and as a consequence, underestimates the osmotic compressibility at moderate protein concentrations.

Figure 7.

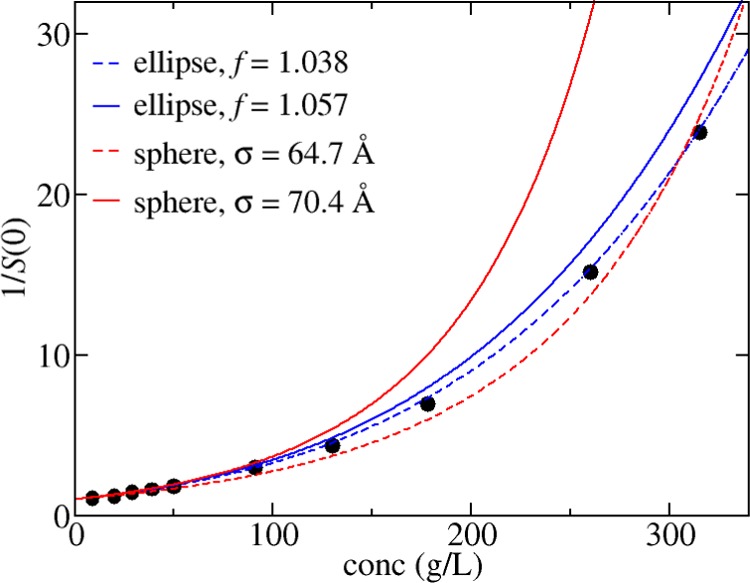
S(0)⁻¹ values from SAXS experiments in citrate_pH6.5_I274 corresponding to the filled circles have been fitted to the 10-term virial expansion (dashed red line) and the ellipsoid model (dashed blue line). Predictions based on using parameters derived from matching B₂₂ = 10.5 × 10^–5 mL mol/g² are shown for the 10-term virial expansion (solid red line) and the ellipsoid model (solid blue line). Fit parameters are shown in the legend.

The improved accuracy of the ellipsoidal model becomes more evident when also considering the dilute solution behavior. The second virial coefficient calculated for the best-fit spherical model is equal to 7.8 × 10^–5 mL mol/g², whereas the corresponding value for the ellipsoidal model is equal to 9.6 × 10^–5 mL mol/g². The latter is much closer to the excluded volume contribution to B₂₂ estimated from the SLS experiments equal to 10.5 × 10^–5 mL mol/g². Figure 7 also contains the curves for either model when the fitting parameters are chosen to match the excluded volume contribution to B₂₂. The ellipsoidal model prediction, as expected, is much more accurate; the close agreement to the experimental data indicates that the thermodynamic properties for albumin in concentrated solutions can be predicted using the oblate model when parameterized against a dilute solution parameter, B₂₂.

Previous studies have shown that the hard sphere model provides accurate fits to osmotic pressure data up to BSA concentrations of 450–500 g/L in solutions containing 150 mM NaCl for a range of pH values between 4.5 and 7.4.^61,69 Of most relevance to the work here is the pH 7.4 data, which were reproduced using a diameter of 69 Å by fitting the data to a six-term virial equation. These data are reproduced in Figure 8 including the best fits using the ellipsoidal model and the virial equation including 6 or 10 terms. A similar pattern to the structure factor data is observed, where the spherical model has more curvature than the ellipsoidal model, which leads to an underprediction for the compressibility at intermediate protein concentrations. This effect is more pronounced by increasing the precision of the virial expansion from using 6 versus 10 terms. The calculated virial coefficients for the best fits are 12.1 and 8.2 × 10^–5 mL mol/g² for the ellipsoidal and spherical models, respectively. While we have not measured the B₂₂ value at the pH 7.4 solution condition, which only included NaCl at a concentration of 150 mM with no buffer ions, the value should be similar to our experiment in octanotate_pH7.0_I154. According to the potentiometric titration curve measured by Tanford et al.,⁷⁰ there is an increase of net negative charge of ∼4e for this pH change (7.0–7.4). The corresponding value of B₂₂, as calculated by using the DLVO potential, is of the order 13.0 × 10^–5 mL mol/g², which provides a close agreement to the ellipsoidal model fit.

Figure 8.

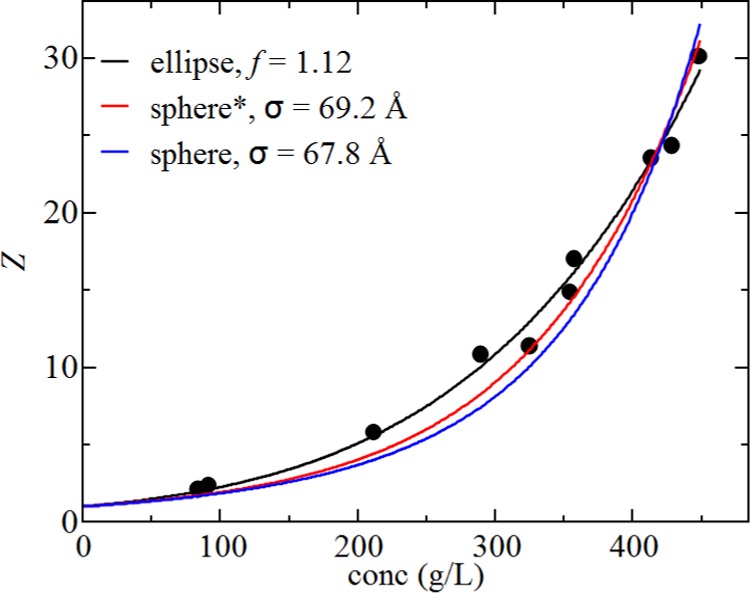
Compressibility factor obtained from the experimental data taken by Vilker et al.⁶⁹ along with the fits for the ellipsoidal model (black line) and the virial equation of state with either 6 terms (red line, denoted by *) or 10 terms (blue line). Fit parameters are shown in the legend.

Conclusions

The key finding from our work is that the thermodynamic properties of HSA (as well as BSA) are more accurately reproduced with an ellipsoidal versus spherical equation of state, which initially became evident from the decrease in hard sphere diameter values obtained from fitting the S_eff(q) profiles in citrate_pH6.5_I274. The spherical model, when parameterized on the dilute solution measurement, overpredicts the osmotic compressibility for excluded volume systems, an effect that grows with increasing protein concentration when higher-order virial terms contribute more to the thermodynamic properties. The ellipsoidal model, on the other hand, provides a more accurate extrapolation of the dilute solution data. This study has only been possible because there are no observable effects of short-ranged attractions on HSA so that the behavior at moderate ionic strengths reflects only excluded volume interactions. Nevertheless, the work is still significant for systems that exhibit short-ranged attraction. For instance, if an osmotic compressibility curve, or an effective structure factor profile, is fitted to a spherical interaction model, the fitted value of the short-ranged attraction will likely be larger than the true value to compensate for overpredicting the excluded volume contribution.

A key motivation for this work was to establish if there are any effects of typically used formulation conditions on the stability of HSA, in particular, slight changes in pH and the effect of adding trehalose. When comparing the runs in phosphate_pH6.2 and in octanoate_pH7.0, the differences can be rationalized in terms of changed electrostatic interactions due to changing the net charge of the protein. The fit values for the net charge are 10e in phosphate_pH6.2 versus 15e in octanoate_pH7.0 over the ionic strength range of 50–200 mM consistent with the expected change in the protonation state of the protein as measured by Tanford et al.⁷⁰ In both cases, there is a large increase at 500 mM NaCl, which, although not evident from the B₂₂ measurements, might reflect a slight increase in protein–protein repulsion. As such, it does not appear that the excipients, trehalose and polysorbate, used in the buffer impact the protein–protein interactions for HSA. This is partly because the rHSA we use is saturated with octanoate and polysorbate-defatted rHSA will behave differently.⁷¹ Indeed, osmotic second virial coefficient studies for lysozyme solutions in sodium chloride indicate that trehalose weakens short-ranged protein–protein attractive forces.⁷² However, our study indicates that these forces are absent, which might be why rHSA, saturated with octanoate and polysorbate, behavior is insensitive to the nonionic components of the formulation buffer.

It is clear that HSA is repulsive due to its large net charge. We speculate that this could be the physical reason for the stabilizing effect of HSA on other proteins. HSA is screening itself and thereby creating a network, making it possible for other proteins to distribute themselves among the HSA molecules, preventing aggregation.

Methods

Yeast-derived rHSA in the form of 100 mg/mL Recombumin supplied by Albumedix Ltd. was used.

Solvent Systems

Three distinct pharmaceutically relevant solvent systems were used (for an overview, see Table 4). The ionic strength of the buffer is determined from summing over all of the ionic components according to ionic strength = ∑_ic_iz_i², where c_i and z_i are the molar concentration and valency of ion i, respectively. Citrate_pH6.5_I274 is mimicking to the buffer of rituximab in MabThera. This buffer has a high ionic strength. Octanoate_pH7.0_I153 is mimicking the Recombumin buffer, and phosphate_pH6.2_I66 is similar to the buffer of bevacizumab in Avastin where the ionic strength is quite low compared to the other two buffers. Concentration series were measured in all three buffers, and additionally, the effect of varying ionic strength was studied in octanoate_pH7.0 and phosphate_pH6.2, where the ionic strength was adjusted by varying the concentration of NaCl.

Table 4. Solvent Systems.

buffer	constituents	pH	IS (mM)
citrate_pH6.5_I274	154 mM NaCl, 25 mM Na3C6H5O7·2H2O, 0.07% Tween 80	6.5	274
octanoate_pH7.0_I153	145 mM NaCl, 8 mM octanoate, 0.05 g/L Tween 80	7.0	153
phosphate_pH6.2_I66	42 mM NaH2PO4·2H2O, 8 mM Na2HPO4, 159 mM α,α-trehalose·2H2O, 0.4 g/L Tween 20	6.2	66

Preparation of Protein Samples and Buffers

Buffers were exchanged by dialysis in three shifts over 3 days at 4 °C applying gentle stirring. The dialysis was performed with Slide-A-Lyzer Dialysis G2 Cassettes from Thermo Scientific with the appropriate molecular mass cutoff value. The individual samples were prepared by diluting or concentrating the dialyzed sample. Samples with varying salt concentrations were prepared from buffer stock solutions with a high NaCl content by adding an appropriate amount of buffer to the individual samples. Importantly, buffers for buffer subtraction were also prepared to match the difference in NaCl content. Further concentration after dialysis was done using Pall Nanosep centrifugal device with Omega membrane 10 K cutoff. Concentration determinations were performed with the NanoDrop 1000 Spectrophotometer from Thermo Scientific at 280 nm. The extinction coefficient was calculated to be 34 445 cm^–1 M^–1, with the ProtParam⁷³ tool from ExPASy.org⁷⁴ using the primary sequences of HSA.

SAXS Data Collection

SAXS data collection was performed at the MAX II synchrotron, MAX IV laboratories at beamline I911-SAXS, Sweden.⁵² The sample detector distance and the direct beam position were calibrated using silver behenate. Measurements on pure water were used to get the data on an absolute scale. Buffers were measured both before and after each sample and averaged before subtraction. The sample size was approximately 50 μL injected manually in a flow cell.

Measurements were performed on a series of rHSA samples at various concentrations prepared as described above. The protein concentrations measured in the individual buffers are listed in Tables S1 and S2 with respect to, respectively, rHSA and NaCl concentrations at fixed albumin concentration. Data collection parameters are listed in Table S3.

SLS Data Collection

A Wyatt miniDAWN TREOS 3 angle detector was used for the SLS experiments. Samples were injected using a syringe pump through an in-line 0.1 mm filter, followed by the SLS flow cell connected in series to a UV Waters 2487 absorbance detector. We used a variable path length UV flow cell for accurate determination of protein concentration. The path length was set to 0.05 cm such that the absorbance of all protein solutions falls within the range where the Beer–Lambert law is valid. SLS measurements at high protein concentration were carried out using a Wyatt NanoStar cuvette-based system with a low-volume quartz cuvette. Both instruments use a 60 mW GaAs diode laser with vertically polarized light at a wavelength of 658 nm.

Glossary

Abbreviations

SAXS

small-angle X-ray scattering

SLS

static light scattering

rHSA

recombinant human serum albumin

OZ

Ornstein–Zernike

BSA

bovine serum albumin

DLVO

Derjaguin–Landau–Verwey–Overbeek

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02245.

• Experimental details for SAXS measurements (Tables S1–S3); SAXS scattering curves (Figure S1); sample parameters from SAXS data treatment (Table S4) (PDF)

Author Present Address

^∥ CMC Assist ApS, DK-2500 Copenhagen, Denmark (J.T.B.).

The authors declare no competing financial interest.