Regimes of Complex Lipid Bilayer Phases Induced by Cholesterol Concentration in MD Simulation

Abstract

Cholesterol is essential to the formation of phase-separated lipid domains in membranes. Lipid domains can exist in different thermodynamic phases depending on the molecular composition and play significant roles in determining structure and function of membrane proteins. We investigate the role of cholesterol in the structure and dynamics of ternary lipid mixtures displaying phase separation using molecular dynamics simulations, employing a physiologically relevant span of cholesterol concentration. We find that cholesterol can induce formation of three regimes of phase behavior: 1) miscible liquid-disordered bulk, 2) phase-separated, domain-registered coexistence of liquid-disordered and liquid-ordered domains, and 3) phase-separated, domain-antiregistered coexistence of liquid-disordered and newly identified nanoscopic gel domains composed of cholesterol threads we name “cholesterolic gel” domains. These findings are validated and discussed in the context of current experimental knowledge, models of cholesterol spatial distributions, and models of ternary lipid-mixture phase separation.

Introduction

Certain mixtures of lipids, sterols, and proteins in lipid bilayers laterally separate to two or more domains of unique composition, divided by macroscopically distinguishable interfaces (1). Eukaryotic membrane lipid bilayers can be composed of thousands of unique lipids and proteins, and of the many sterols that can exist in membranes, cholesterol (Chol) is ubiquitous (2).

Mammalian plasma membranes tend to contain 1:3–1:1 ratios of Chol to phospholipids (2, 3), though phospholipid membranes can accommodate ∼66 mol% Chol (4, 5, 6, 7), and this upper limit is approached in the plasma membranes of astrocyte cells in Alzheimer’s disease patients (8, 9).

Mixtures of lipid and Chol have been used to understand the phase behavior of complex lipid membranes since the late 1960s. The main lipid phase transition, from gel (S_o) to liquid crystalline (L_α) phase, was first characterized through observation of a large peak in heat capacity at the melting temperature (T_m) in differential scanning calorimetry (DSC) experiments (10). From the 1970s to 1990, several works using DSC and NMR found that mixtures of Chol with phospholipids lowered T_m (11). These investigations also built evidence for existence of two polymorphs of the L_α phase in binary mixtures of di-C 16:0 PC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine, DPPC) and Chol, finding there to be a phase of low Chol content and a more ordered, high-Chol-content phase using DSC and NMR. These low- and high-Chol-content L_α polymorphs have come to be known as liquid-disordered (L_d) and liquid-ordered (L_o) phases, respectively (12). This work culminated in the seminal study by Vist and Davis, who determined the phase diagram of DPPC:Chol mixtures, describing a pure L_d phase from 0 to 10 mol% Chol, an L_o + L_d coexistence from 10 to 22.5 mol% Chol, and a pure L_o phase beyond 22.5 mol% Chol at physiological temperature using NMR and DSC (13). Coexistence of spatially separated L_o and L_d domains on membrane surfaces are evidenced to be central to protein structure, interaction, and function because many proteins have different affinities for domains (14, 15).

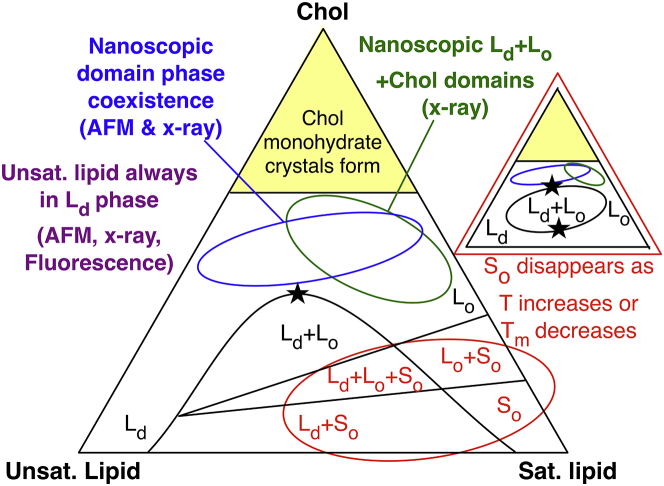
Formation of domains of lipids in bilayers has been called “lipid phase separation,” “lipid domain formation,” or “lipid raft formation,” each of which has a distinct meaning (1). In general, these terms are used to describe the binary liquid-liquid phase separation that features coexistence of L_d and L_o phases in the membrane. Over the past 15 years, many investigations have focused on ternary mixtures of Chol with one high- and one low-T_m lipid species (16). Multiple points on phase diagrams of macroscopically observable lipid bilayer phase separations resulting from mixtures of saturated lipids, unsaturated lipids, and Chol have been observed using fluorescence spectroscopy, (17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34) x-ray scattering (20, 35, 36, 37, 38, 39, 40), atomic force microscopy (AFM) (18, 37, 41, 42), NMR (24, 30, 32, 43, 44), interferometric scattering (45), and Raman spectroscopy (46, 47), allowing us to achieve a general concept of ternary lipid mixture phase diagrams (Fig. 1).

Figure 1.

General phase diagram of phase coexistence in ternary lipid bilayers of saturated lipids, unsaturated lipids, and cholesterol (Chol) forming liquid-disordered (L_d), liquid-ordered (L_o), gel (S_o), and pure Chol domains. Black phase boundaries are based on macroscopically observable phase separations in experiments. S_o phase is not present if temperature (T) or main phase-transition temperature of saturated lipid (T_m) are high enough. Regions where nanoscopic lipid domain coexistence have been experimentally observed are noted. Stars indicate where critical lateral mixing is observed in these phase diagrams. To see this figure in color, go online.

In Fig. 1, we briefly summarize the current picture of ternary phase diagrams. At relatively lower T (or higher T_m), the S_o phase is evidenced to exist as a macroscopic phase-separated state via fluorescence experiments, AFM, and NMR. The S_o phase can disappear at physiological temperatures because of the presence of Chol (11, 48, 49, 50, 51) or unsaturated lipids (52, 53, 54, 55), which lower the T_m of saturated lipids. At high (≳40 mol%) Chol concentrations, macroscopic phase separations disappear. Critical fluctuations in domain mixing manifest at one or two points in ternary phase diagrams, depending on whether the immiscible region is open or closed because of the lack or presence of the S_o phase (27, 30, 56, 57, 58, 59). Modern fluorescence (34, 60), x-ray (39, 61), and AFM experiments (41, 42) have shown that nanoscopic ordered and disordered domains coexist outside of the miscibility gap centered around 1:1:1-ratio mixtures because Chol appears to never truly induce the L_o phase in unsaturated lipids. X-ray scattering experiments have revealed that ∼60 nm diameter domains of pure Chol domains can coexist with domains of saturated and unsaturated lipids at these high mol% Chol compositions (37, 50, 62, 63). Beyond the ∼66 mol% solubility limit of Chol in bilayers (4, 5, 6, 7), Chol forms anhydrous crystals in solution (50, 64). Additionally, though the main phase transition (S_o to L_α) is first order, phase transitions from L_d to L_o and L_o to Chol domains seem to be continuous.

Spatially resolved knowledge of domain both composition and phase in both membrane leaflets is currently limited. Strong registration of domains between lipid leaflets has been experimentally quantified (65); however, this registration is only confirmed for macroscopic phase separations of symmetric bilayers and likely does not occur in mixtures in which smaller domains are observed because of complicated surface energies and interleaflet interactions.

Many theoretical works have considered the interleaflet coupling of lipids and domains, and arguments in favor of interleaflet registration or antiregistration of domains have been presented. Preference of domains for local curvature of the membrane surface as well as interleaflet interaction between domains can significantly impact the free energy of the membrane. Small, microscopic domains can form that preferably register or antiregister with domains of the opposing leaflet depending on the relative degree of local curvature (66, 67, 68, 69, 70, 71, 72, 73).

Typically, experimental approaches cannot discern the thermodynamic phase and degree of mixing of both lipid leaflets in bilayers of symmetric leaflet composition. Much work has been done to consider interleaflet interactions of domains using bilayers of strictly asymmetric leaflet composition in which interleaflet domain registration has been observed (65, 74, 75, 76). However, the methods employed, such as use of supported lipid bilayers, may limit the generality of the conclusions of these studies. It is known that Chol strongly prefers to partition to regions of concave curvature (77). That preferential partitioning may play a role in domain formation and registration that cannot be observed using supported bilayers.

MD simulations employing the MARTINI coarse-grained (CG) model, capable of producing various thermodynamic phases of lipids (78, 79) and lipid phase separation (80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92), have provided structural insight to interleaflet domain interaction. Perlmutter et al. observed the enhanced local curvature of membranes in the presence of antiregistered domains (90), and Fowler et al. found that domain registration may occur via a two-step kinetic process of antiregistered domain formation preceding the formation of registered domains (82). Additionally, Yesylevskyy et al. demonstrated the preferential partitioning of Chol to regions of locally higher curvature using simulations employing the MARTINI model (93).

It should be noted that a particular CG lipid may behave differently from its atomistic equivalent (87). As such, the MARTINI model may be considered as an advanced toy model suitable for understanding general concepts in lipid biophysics, though atomistic models have been shown to reasonably reproduce ternary phase diagrams (94). With this caveat in mind, CG simulation has contributed to our current understanding of complex membrane phase behavior, though no detailed investigation of the dependence of phase separation and liquid L_d + L_o phase coexistence in ternary mixtures on Chol has been performed.

Here, we investigate complex phase coexistence as a function of Chol concentration in ternary mixtures with DPPC and di-C 18:2/18:2 PC (1,2-dilinoleoyl-sn-glycero-3-phosphocholine, DIPC) lipids, maintained at DPPC:DIPC 1:1 molar ratios, using CG molecular dynamics (MD) simulation employing the MARTINI model. Performing simulations at 0, 3, 7, 13, 22, 30, 42, 53, and 61 mol% Chol, we observe that Chol induces three regimes of domain structure at varying concentrations, denoted 1) miscible, L_d phase; 2) domain-registered, macroscopically phase-separated L_o + L_d domain coexistence; and 3) domain-antiregistered, microscopically phase-separated coexistence of L_d domains with domains of a newly identified “cholesterolic gel” (S_oc) phase featuring “threads” of Chol.

Gradual transitions between the three identified phases are observed to be dependent on Chol composition, with compositionally unstable mixtures separating regimes sampled at 7 and 42 mol% Chol. The mol% of Chol in DPPC:Chol and DIPC:Chol domains are inferred from the number of lipid-Chol contacts out of all contacts. We find DPPC:Chol domains to rapidly become saturated with Chol, achieving 30% DPPC-Chol contacts by 13 mol% Chol in the membrane, before any substantial association of Chol with DIPC. The structure of DPPC, DIPC, and Chol as a function of the percentage of DPPC-Chol and DIPC-Chol contacts is reported in systems at each mol% Chol composition.

This work provides new insight into the role of Chol concentration in complex phase behavior observed and predicted in the past and provides evidence for a new gel phase that may be thermodynamically stable in membranes of typical Chol concentration.

Methods

All analysis methods described here were enabled through use of NumPy+SciPy (95, 96) and the MDAnalysis python library (97, 98), which is built on NumPy+SciPy and Cython (99). All figures were created using Matplotlib (100), Omnigraffle, and VMD 1.9.4 (101, 102). All simulations were performed with Gromacs 5.0.4 (103).

MD system construction

The mixture of DPPC, DIPC, and Chol in the MARTINI CG model is able to form macroscopic phase separations, as observed in past investigations of domain formation (80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92). The Chol model of Melo et al. was used (104), and all other molecules employed the MARTINI v2.0 force field (105). The insane.py script developed by the Marrink group was used to form three unique initial conditions for 0, 3, 7, 13, 22, 30, 42, 53, and 61 mol% Chol random bilayer mixtures, keeping DPPC and DIPC equimolar (106). Effectively 38 waters per lipid were used, and 10% of these used MARTINI antifreeze parameters to prevent spontaneous nucleation of ice droplets. NaCl at 150 mM concentration was used to approximate physiological salt conditions.

We previously found that the MARTINI mixture of DPPC, DIPC, and Chol at 35:35:30 mol% needs to be modeled with more than 1480 lipids to observe stable macroscopic domain formation (81). Arguments based on a Flory-Huggins model suggest the need for similarly large systems to observe macroscopic domain formation in other phase-separating mixtures. In this work, we construct all systems with 3040 lipids, substantially larger than the critical size, such that the periodic boundary conditions will not prevent the observation of domain formation and phase coexistence.

MD simulation

Each initial configuration was minimized using the Gromacs steepest-descent minimizer. Simulation parameters largely corresponded to the “common” parameter set described by De Jong et al. (107), and simulations were performed with the same protocol as our previous work (81). Nonbonded interactions used the Gromacs shifting function applied from 0.9 to 1.2 nm for Lennard-Jones and from 0.0 to 1.2 nm for Coulomb interactions. The velocity rescaling thermostat of Bussi et al. was used with a coupling time of 1 ps and a reference temperature of 295 K (108), as applied in many past studies of phase separation with this lipid mixture (81, 83, 85, 86, 87, 90, 91). The semi-isotropic Berendsen barostat was used with 1 atm reference pressure, a coupling time of 1 ps, and 3 × 10⁴ bar⁻¹ compressibility, coupling the x and y dimensions. The leapfrog integrator was used with a 20 fs time step, employing a “group” neighbor list with a 1.2 nm cutoff, updated every 200 fs. Three replicates of each system were simulated for 11 μs. One set of replicates representing each system condition used San Diego Supercomputer Center Comet resources via the Extreme Science and Engineering Discovery Environment through startup allocation TG-MCB150142 (109). The other two sets of replicas used the Shared Computing Cluster administered by Boston University’s Research Computing Services.

Atom selections

To analyze the coordinates of lipid headgroups in the MARTINI model, we define headgroups as the PO4 bead of DPPC and DIPC and the ROH bead of Chol. Lipid tail groups are defined as C2A and C2B for DPPC; D2A and D2B for DIPC; and the centroid of R1, R2, R3, R4, and R5 for Chol.

Chol flip-flops between lipid leaflets were observed in the MARTINI model over the course of simulation. Because several of the methods we apply here rely on discrimination between leaflets, we assign Chol to leaflets on a per-frame basis. For each Chol molecule, we find the shortest Chol-lipid headgroup distance within 1.5 nm and assign Chol to the leaflet of that lipid.

Order parameter analysis

We describe the local concentration of Chol in the membrane in reference to DPPC and DIPC, such that we can infer the content of Chol in lipid domains. We use xy-plane Voronoi tessellations of DPPC, DIPC, and Chol headgroups to determine the nearest neighbors, counting the number of DPPC-Chol and DIPC-Chol contacts in the membrane. At equilibrium, we infer the Chol composition of L_o (L_d) domains as the percentage of all DPPC-Chol (DIPC-Chol) contacts out of all DPPC-lipid (DIPC-lipid) contacts, noted as <%Chol-DPPC cont.>^eq (<%Chol-DIPC cont.>^eq).

The extent of lateral mixing of DPPC and DIPC in membrane, which is typically used to define phase separation, is described with a binary lateral mixing entropy

$$S_{mix}=-p_1{\log }_2{p}_1-p_2{\log }_2{p}_2,$$ (1)

where p₁ is the likelihood of contacts between lipids of the same type and p₂ is the likelihood of contacts between lipids of opposite type. This mixing entropy was evaluated by counting the number of DPPC-DPPC, DIPC-DIPC, and DPPC-DIPC headgroup nearest neighbors determined with Voronoi tessellation (Fig. S1 A).

Many experimental works infer the transition point between miscible and phase-separated states by the inflection point in some order parameter of mixing as a function of concentration or temperature, such as fluorescence intensity. Such inflection points are believed to correspond to points at which saturated and unsaturated lipids are 50% miscible. We develop a definition of the 50% miscibility point in S_mix $\left(S_{mix}^{50\%}\right)$ given a binary, periodic two-dimensional (2D) system exhibiting a stripe-shaped phase separation, similar to the Flory-Huggins model used in our previous work (81). We describe this as a binary mixture in which two pure domains coexist with an ideal mixture that takes up 50% of the system area. The probabilities determining $S_{mix}^{50\%}$ are

$$p_1=\left(\frac{3}{4}{N}_D+\frac{2}{3}\sqrt{N}+2\frac{7}{10}\sqrt{N}\right)/N$$ (2)

and

$$p_2=\left(\frac{1}{4}{N}_D+\frac{1}{3}\sqrt{N}+2\frac{3}{10}\sqrt{N}\right)/N,$$ (3)

where N_D = N − 3√N, as explained in the Supporting Materials and Methods and Figs. S2 and S3. For N = 1520, the number of lipids within each leaflet of our simulated systems, we find $S_{mix}^{50\%}$ = 0.8186.

The registration of lipid domains (Λ) was evaluated by computing the overlapping area of Voronoi tessels centered on lipid tails in each leaflet via Monte Carlo (MC) integration using N = 10⁵ points per frame. This was done by evaluating the sum

$$\mathit{\Lambda }=\frac{1}{N}\sum _{n=1}^{N}H{\left(x,y\right)}_i,H=\{\begin{array}{c}0,x,y\notin T_{DPPC+Chol}^{upper}orx,y\notin T_{DPPC+Chol}^{lower}\\ 1,x,y\in T_{DPPC+Chol}^{upper}andx,y\in T_{DPPC+Chol}^{lower}\end{array},$$ (4)

where Λ is counted as number of MC points (x,y) that fall within tessels of DPPC or Chol in the xy-plane of upper and lower leaflets ($T_{DPPC+CHOL}^{upper}$and $T_{DPPC+CHOL}^{lower}$) out of the total N MC test points (Fig S1 B). To compute the domain overlap describing a random mixture given the same coordinates, we randomly shuffle the chemical identity of lipids in both leaflets before calculation, finding Λ_random.

The order of lipid tails parallel to the membrane normal was evaluated using the liquid crystal order parameter (P₂) of each lipid tail

$$P_2^k=0.5\left(3{\cos }^2{\theta }_{kj}-1\right),$$ (5)

where k is the index of the vector representing a lipid tail, j is the index of the director vector, and θ_kj is the angle between them.

Because the membrane becomes substantially undulated at higher Chol concentrations, using the z-axis as the director vector would not be informative because the structural order of lipid tails is correlated with the membrane surface undulation. In measuring order parameters, we use a plane of best fit for each k-th lipid tail with its six nearest neighbors (indexed by l), found using the singular value decomposition of these coordinates (Fig. S1 C). P₂^k is measured using the vector from the GL1 (GL2) to C4A (C4B) beads and the normal vector of this plane of best fit for the k-th lipid (Fig. S1 D). Here, we investigate the average (P₂) for some selection of a number of lipid tails. Only DPPC and DIPC were considered for this analysis because Chol is rigid.

To quantify the order of lipids parallel to the membrane surface, we used the sixfold Nelson-Halperin 2D bond-orientational order parameter

$${\mathrm{\Psi }}_6^k=\frac{1}{6}\sum _{l\in nn\left(k\right)}^6{e}^{i6{\theta }_{kl}},$$ (6)

measured using the projections of the k-th lipid tail and its six nearest-neighbor lipid tails $\left(l\in nn\left(k\right)\right)$ to its plane of best fit to measure θ_kl, the angle between the vector from the k-th to the l-th lipid tail and an arbitrary reference vector, chosen as the projection of the positive x-axis to the plane of best fit of the k-th lipid tail.

The absolute value of this order parameter measures how well packed a lipid tail is with its nearest neighbors, with a maximum at 1 (ideal packing). The complex vector of this order parameter describes the bond orientation of each lipid tail, showing how an ideal hexagon centered on a tail is oriented (Fig. S1 E). We use the angle of the complex vector measured against the reference vector to describe the orientation of each lipid tail in terms of ${\mathit{\Psi }}_6^k$ (degrees). We use the average of the absolute value (|Ψ₆|) for some selection of a number of lipid tails of which DPPC, DIPC, and Chol were considered.

Transleaflet clustering

We evaluated the sizes of domains of DPPC and Chol lipid tails by both number of intra- (n) and interleaflet (m) lipid tails in the domain, using the same hierarchical clustering technique employed in our past work (81). Interleaflet spanning domains of DPPC and Chol were identified by first using hierarchical distance-based clustering of DPPC and Chol tails in one leaflet using a 5.8 Å distance cutoff, assigning the n lipid tails discovered using this clustering to the domain. After this, DPPC and Chol in the opposing leaflet were assigned to the interleaflet part of this domain if the C4A or C4B (DPPC) or C2 (Chol) beads were within 7.0 Å of the tail of any of the n lipid tails discovered in the domain. As such, we describe the size of each domain by the number of n lipids in one leaflet of the domain and the m lipids in the other leaflet of the domain that were discovered to be in contact with the n lipids.

Results and Discussion

Spatial and structural equilibration

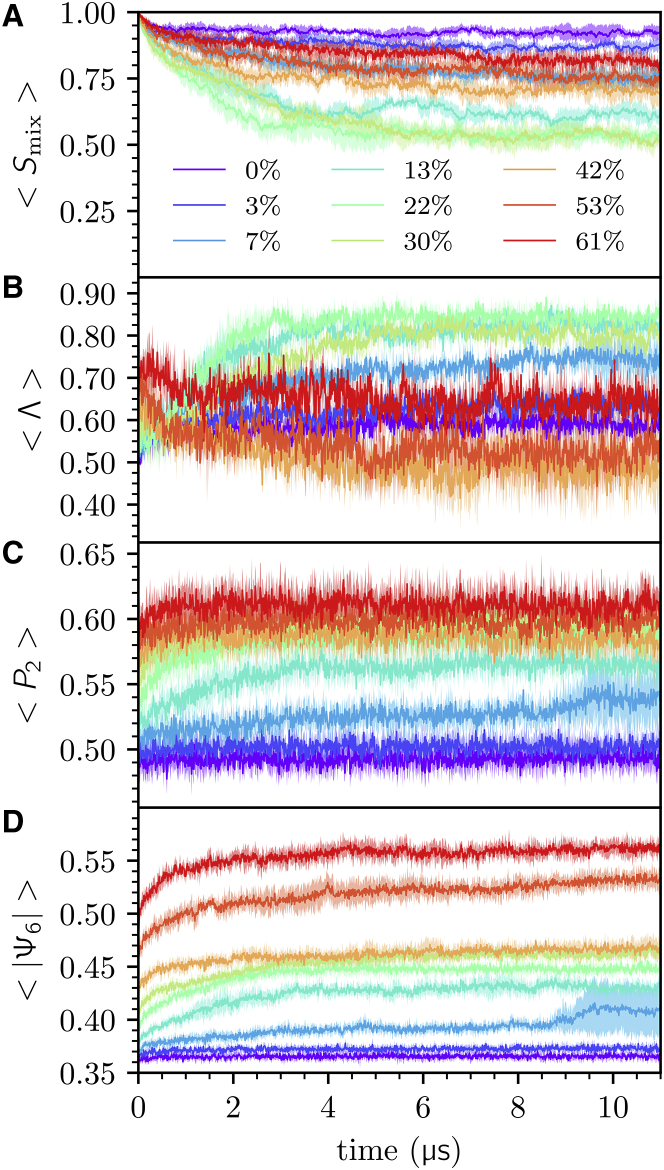
The impact of Chol concentration on the structure and dynamics associated with liquid phase behavior in lipid bilayers was investigated using a CG ternary lipid mixture observed to achieve macroscopic phase separation in MD simulation. Simulations of DPPC, DIPC, and Chol lipids at 0, 3, 7, 13, 22, 30, 42, 53, and 61 mol% Chol, maintaining DPPC and DIPC at equimolar ratios, were performed. Three 11 μs replicate trajectories of each system were sampled, representing a total of 3 × 9 × 11 μs = 297 μs of simulation. By evaluation of four order parameters—S_mix, Λ, P₂, and |Ψ₆| (see Methods)—we find most systems reach a stationary state by 3 μs. We hereafter refer to the timescale past 6 μs as equilibrium (Fig. 2).

Figure 2.

Time series averages of (A) mixing entropy, (B) interleaflet domain registration, (C) plane-fitted DPPC P₂ order parameter, and (D) absolute value of plane-fitted DPPC bond-orientational order parameter in nine mol% Chol systems. To see this figure in color, go online

Three regimes of phase behavior

We observe that the membrane becomes demixed at intermediate Chol concentrations (7–42 mol%) and that domains become registered in the phase-separated state, which has previously been confirmed experimentally (65). Additionally, we observe the well-known phenomenon that the membrane becomes more ordered as Chol concentration increases.

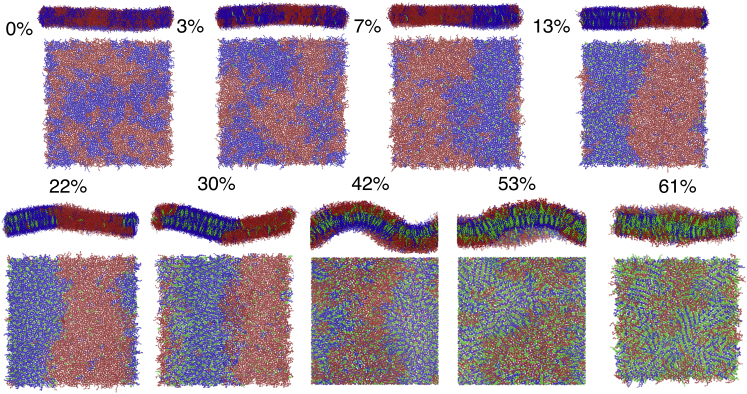
Structures drawn from the end of each simulation show a general trend of increasing local curvature as the concentration of Chol increases, ranging from a flat surface (0–13 mol%) to a standing wave (13–42 mol%) to a rough surface (42–61 mol%) (see Fig. 3). These changes in morphology appear to be directly related to the partitioning of Chol to regions of concave local curvatures (77, 110). Local Chol concentration is observed to be spatially correlated with antiregistration of lipid domains at high mol% Chol, and this is implied by the high % of DPPC-Chol contacts accompanying the antiregistration of lipid domains (Fig. 4, A and B). The standing wave observed in our simulations spans the unit cell, which is commensurate with the size of the phase-separated lipid domains. This was observed in other system sizes at 30 mol% Chol over a range of system sizes in past simulation work (81). These phase-separated domain-spanning undulations have been directly observed in experiment as well (111), demonstrating that lipid domains each effect their own local curvature on the membrane surface.

Figure 3.

Renderings over the top and the side of the final frame of simulation for a trajectory corresponding to each mol% Chol system. DPPC, DIPC, and Chol are rendered blue, red, and green, respectively, using VMD 1.9.4. Bonds are drawn using cg_bonds.tcl from the MARTINI developers. The xy-plane is rotated in some frames to better view the axis of phase separation.

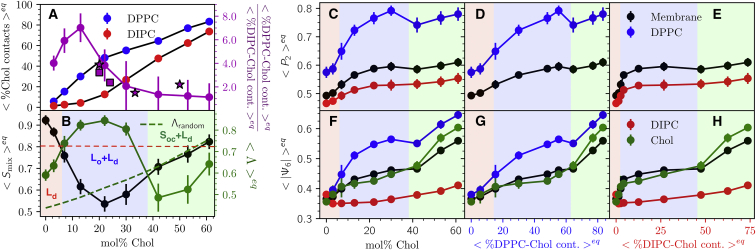
Figure 4.

(A) Number of Chol-lipid contacts with DPPC and DIPC as % of total lipid-lipid contacts. Stars indicate the DPPC:DOPC:Chol monolayer Raman spectra observations of Donaldson and Aguiar (46). Squares indicate x-ray inferences by Chen et al. (40) and Belička et al. (61) (B) The mixing entropy and interleaflet domain registration ratio of %Chol-DPPC to %Chol-DIPC contacts. Shading represents the regimes presenting unique phase behavior labeled I (red), II (blue), and III (green). The dashed red line is the mixing entropy at 50% domain miscibility, $S_{mix}^{50\%}$. The dashed green line is the equilibrium average domain registration determined from random permutation of chemical identities in these trajectories. Equilibrium DPPC, DIPC, and Chol order parameters as a function of (C and F) mol% Chol, (D and G) %Chol-DPPC contacts, and (E and H) %Chol-DIPC contacts are shown. All contacts are between headgroups.

Chol is observed to preferentially interact with DPPC. Counting the number of DPPC-Chol and DIPC-Chol contacts based on Voronoi tessellations of headgroups demonstrate that Chol almost exclusively aggregates with DPPC up to 13 mol% Chol (Fig. 4 A). This colocalization of DPPC and Chol supports L_o domain formation, ensuring complete formation of L_o phase at only 13 mol% Chol, at which 30% of all DPPC contacts are made with Chol (13). Near 20, 33, and 55 mol% Chol, the ratio of DPPC-Chol contacts to DIPC-Chol contacts agrees well with recent label-free Raman spectroscopy measurements of Chol partitioning in DPPC:DOPC:Chol monolayers (46), as well as with x-ray experiments by Chen et al. (40) and Belička et al. at 20 and 24 mol% Chol (61). The increase of DPPC order parameters as the percentage of DPPC-Chol contacts increase from 0 to 50% is similar to that observed recently by Wang et al. in MARTINI (see Fig. 3, D and G) (112). At Chol concentrations surpassing 50%, we see that DPPC-Chol contacts exceed the 66% solubility limit of Chol for a bulk membrane (4, 5, 6, 7).

At these high Chol concentrations, we observe the formation of antiregistered ordered domains that feature linear aggregates of DPPC and Chol (Fig. 3). This structure features repeating face-to-back linear aggregates of Chol separated by a single layer of DPPC tails, such that each Chol forms contacts with exactly two other Chol in these domains. This structure is supported by the Chol “umbrella model,” in which lipids associate with Chol to prevent solvation of Chol headgroups by water. The particular lamellar arrangement of lipids and Chol we observe was previously predicted by umbrella-model-inspired lattice simulations developed by Huang and Feigenson (5). In their simulation model, an energetic penalty to Chol-Chol contacts effectively modeled the umbrella effect, and at ∼66 mol%, aggregates of Chol, in which each Chol made contact with exactly two other Chol, formed a “maze”-like structure that minimizes the number of Chol-Chol contacts. Later, off-lattice simulations by Mouritsen and co-workers also observed these linear Chol aggregates and referred to them as “threads,” the term that we adopt to describe these aggregates (48). Förster resonance energy transfer (FRET) experiments by Parker et al. found that there is a global minimum in Chol-Chol contacts around ∼66 mol% Chol, with minima in the range of 45–70 mol%, just below concentrations that would form Chol monohydrate crystals in solution (6). Parker et al. argued these results support the existence of these Chol threads, which minimize the cluster size of Chol.

These Chol threads are much like our observed structures above 50 mol% Chol, in which we observe ≳66% of DPPC contacts to be with Chol (Fig. 4 A). We recently performed atomistic simulations to study Chol dimerization structures and found that Chol forms the face-to-back dimers (which we observe here) with high propensity, suggesting Chol threads form not only because of the umbrella effect but also because of some preference for dimerization (113). Additionally, AFM experiments in ternary mixtures of similar mol% Chol observe the persistence of nanoscopic domains of unknown phase, which may be the domains containing Chol threads we report here (37, 50, 62, 63).

These highly ordered domains also exhibit bond-orientational order at the domain length scale (Structure of Regimes of Phase Behavior), similar to the gel phase (84). As such, we refer this phase as a “cholesterolic gel” (S_oc)—a lipid gel phase that includes (and is induced by) Chol. We summarize these observations into three apparent regimes of phase behavior, denoted regime I, miscible L_d; regime II, domain-registered L_d + L_o coexistence; and regime III, domain antiregistered L_d + S_oc coexistence. The transition points between these regimes are discussed in Miscibility Transitions Between Regimes of Phase Behavior.

Structure of regimes of phase behavior

At low (0–7 mol%) Chol concentration, the whole membrane is in the L_d phase. This may be surprising because our simulations are at 295 K, and the T_m of pure DPPC is 314.5 ± 1.8 K (10). However, in the MARTINI model, the T_m of DPPC has been determined to be as low as 292.4 K—as determined via the generalized replica-exchange MD method (78)—and 296 K as determined via conventional replica-exchange MD (79). Additionally, binary mixtures of DPPC with other lipids are known to both substantially decrease T_m and broaden the corresponding peak in the heat capacity (52, 53, 54). For example, in an equimolar DPPC:DOPA mixture, T_m decreases to ∼294.45 ± 0.2 K (54). Because DIPC has more unsaturated bonds than DOPA, it is possible that mixtures of DPPC with DIPC would exhibit an even lower T_m than mixtures of DPPC with DOPA.

At equilibrium, the P₂ and |Ψ₆| order parameters increase up to a “dip” marking the apparent transition between L_o to S_oc phases at 42 mol% Chol, at which 66% of DPPC contacts are shared with Chol (Fig. 4, A, C, and F). The S_oc phase becomes yet more ordered with higher mol% Chol. The structure of DIPC is generally insensitive to Chol concentrations, and the P₂ of DIPC increases only slightly because the L_o phase is formed by DPPC and Chol (Fig. 4 E).

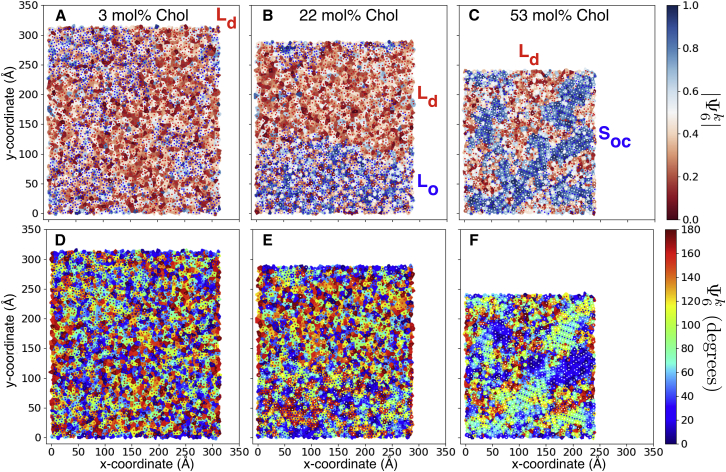
The S_oc phase is structurally distinct from the L_o phase because of the unique lamellar structures formed by DPPC and Chol, manifest in the bond-orientational order of DPPC and Chol. The 3, 22, and 52 mol% Chol systems, representative of regimes I, II, and III, are distinct as characterized by the $\left|{\mathit{\Psi }}_6^k\right|$ and ${\mathit{\Psi }}_6^k$ order parameter (Fig. 5).

Figure 5.

Voronoi tessellations of lipid and Chol tails in upper leaflets of simulated membranes at the last frame of each trajectory. DPPC (blue), DIPC (red), and Chol (white) dots represent tails. Voronoi cells are colored according to the absolute and untransformed value of lipid tail bond-orientational order parameters at (A and D) 3 mol% Chol, (B and E) 22 mol% Chol, and (C and F) 52 mol% Chol.

Inspection of ${\mathit{\Psi }}_6^k$ reveals that the L_d, L_o, and S_oc phases are analogous to the liquid, hexatic, and solid phases of 2D systems (114). In regime I (0–7 mol% Chol), there is no significant orientational order as measured by ${\mathit{\Psi }}_6^k$ or $\left|{\mathit{\Psi }}_6^k\right|$ over any length scale in the system. In regime II (7–42 mol% Chol), $\left|{\mathit{\Psi }}_6^k\right|$ is ordered and correlated over the L_o domain length. In regime III (42–61 mol% Chol), $\left|{\mathit{\Psi }}_6^k\right|$ is ordered, and $\left|{\mathit{\Psi }}_6^k\right|$ and ${\mathit{\Psi }}_6^k$ are correlated over the length scale of all S_oc domains (Figs. 5, S4, and S5).

The S_oc phase observed in this study is similar to a gel phase. Although gel phases showing “hexatic” order have recently been reported in terms of the Ψ₆ order parameters (115, 116), the S_oc phase is distinct because of the presence of Chol threads and the effects of Chol threads on the membrane surface that drive domain antiregistration.

Chol, DIPC, and DPPC are evidenced to strongly prefer concave, weakly prefer concave, and weakly prefer convex local curvature on the membrane surface, respectively, as determined via x-ray measurements on monolayers supported by inverted hexagonal phases (77). Because S_oc domains contain Chol in higher concentration, S_oc domains may induce concave curvature overall. This would explain the preference of S_oc domains for registration with L_d domains in the opposing leaflet, which are more fluid and contain less Chol. This important difference in domain preferences for local curvature may be accounted for by the theoretical model of Shlomovitz and Schick (67, 72). However, our results demonstrate that these quantities are sensitive to the concentration of Chol in the membrane and particularly in each domain, which has not been considered in these models.

Miscibility transitions between regimes of phase behavior

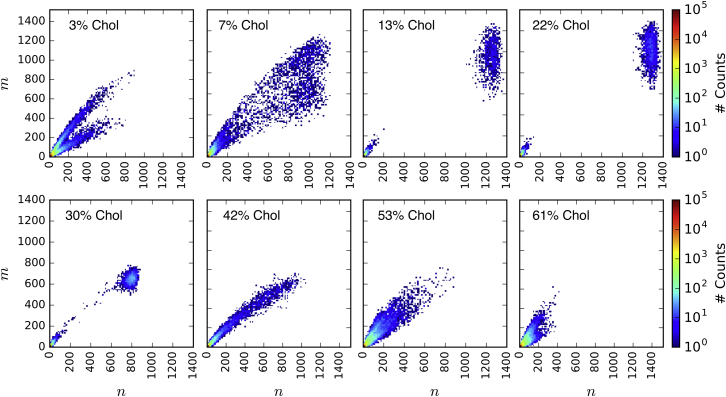
In undergoing the miscibility transition between these regimes of phase behavior, we expect the system to present fluctuations in local lipid compositions with a disperse distribution of domain sizes. To explore the miscibility transitions, we identified transleaflet clusters of DPPC and Chol tails, defining aggregates of n intra- and m interleaflet tails at equilibrium (Fig. 6, explanation in Methods, and illustration in Fig. S6). We find that the structural order of domains is largely insensitive to domain size (Fig. S6 A), as previously identified in 30 mol% Chol (81).

Figure 6.

Occurrences of intra- (n) and interleaflet (m) lipid tails in transleaflet DPPC-Chol domains at equilibrium in each mol% Chol system. To see this figure in color, go online.

Examination of transleaflet aggregate sizes in regimes I and III show a bifurcation of slopes of m(n) ≈ 2/3 and m(n) ≈ 1/3, corresponding to a ∼2/3 domain overlap similar to Λ in Fig. 4 B. A polydispersity in domain sizes is observed at 7 and 42 mol% Chol. The transition from regimes I to II seems to be well described by the 50% miscibility point because the 7 mol% Chol system S_mix is marginally lower than $S_{mix}^{50\%}$ (Fig. 4 B). Additionally, order parameters at 7 mol% Chol show larger fluctuations at equilibrium than other system compositions (Fig. 2). The transition observed at 42 mol% Chol is apparently not well described by $S_{mix}^{50\%}$. However, the transition of domain overlap, Λ, to below Λ_random indicates the onset of antiregistration at 42 mol% Chol (Fig. 3 B), and there is a clear signature of this transition in P₂ and |Ψ₆| (Fig. 4, C–H). It may be possible to identify the transition to regime III by measurement of domain overlap via a method analogous to our computation of Λ spectroscopically using leaflet-selective deuteration (74). The transition from nanoscopic domain coexistence to macroscopic phase separation near 7 and vice-versa at 42 mol% Chol approximately fits the DPPC:DOPC:Chol phase diagrams of Veatch et al. and Davis et al., which measure these transitions to occur at ∼10 and 45 mol% Chol (33) and 10 and 35 mol% Chol, respectively (43).

Conclusions

Via MD simulation, we have performed a detailed investigation of Chol concentration on phase separation in bilayers formed of ternary lipid mixtures. We observed three regimes of phase behavior, denoted 1) miscible L_d phase, 2) macroscopically phase-separated L_d + L_o coexistence featuring registered domains, and 3) microscopically phase-separated antiregistered domains of L_d coexistent with the newly identified liquid cholesterolic gel (S_oc) phase. These structures were validated by comparison to experimental determinations of Chol partitioning in lipid domains (40, 46, 61), theoretical expectations of Chol-lipid complex structures at high mol% Chol invoking the umbrella model (5) supported by FRET experiments (6), and the miscibility phase diagrams of DPPC:DIPC:Chol mixtures (33, 43). We demonstrate the structural difference between these three regimes via order parameters characterizing mixing, domain registration, structural order along the bilayer normal, structural order within the membrane plane, and transleaflet domain sizes. We find regimes I, II, and III to manifest distinct differences in bond-orientational order. The S_oc phase is found to exhibit 2D bond-orientational order over the length scale of the lipid domains, characterized by face-to-back threads of Chol and DPPC.

There may be biological implications of the S_oc phase for determination of protein structure and function because proteins can preferentially partition to particular lipid domains. For examples, amyloid precursor processing (APP) is known to change structure because of binding Chol (117, 118, 119, 120) or changes in membrane thickness (121, 122, 123), which depend on lipid domain composition and structure. APP is processed by α- or β-secretase, which reside in different lipid domains (124, 125, 126, 127). If APP is processed by α-secretase, occurring at low mol% Chol, the amyloid cascade will not proceed, and production of toxic amyloid β (associated with Alzhimer’s disease) will not occur. The complex phase behavior induced by Chol effects the structure, function, and processing of proteins in Alzheimer’s and other diseases and will therefore continue to be relevant to our understanding of these disease mechanisms. The S_oc phase may need to be considered in addition to the L_d and L_o phases when considering protein structures in such disease pathways.

These collected observations substantially enhance our understanding of the role of Chol in complex phase behavior in ternary lipid mixtures and provide a framework for exploring structure and dynamics of domain formation in future computational, theoretical, and experimental investigations.

Author Contributions

G.A.P. designed the research, performed the research, and analyzed the data. G.A.P. and J.E.S. wrote the manuscript.

Editor: D. Peter Tieleman.