Microtubule Feedback and LET-99-Dependent Control of Pulling Forces Ensure Robust Spindle Position

Abstract

During asymmetric division of the Caenorhabditis elegans zygote, to properly distribute cell fate determinants, the mitotic spindle is asymmetrically localized by a combination of centering and cortical-pulling microtubule-mediated forces, the dynamics of the latter being regulated by mitotic progression. Here, we show a, to our knowledge, novel and additional regulation of these forces by spindle position itself. For that, we observed the onset of transverse spindle oscillations, which reflects the burst of anaphase pulling forces. After delaying anaphase onset, we found that the position at which the spindle starts to oscillate was unchanged compared to control embryos and uncorrelated to anaphase onset. In mapping the cortical microtubule dynamics, we measured a steep increase in microtubule contact density after the posterior centrosome reached the critical position of 70% of embryo length, strongly suggesting the presence of a positional switch for spindle oscillations. Expanding a previous model based on a force-generator temporal control, we implemented this positional switch and observed that the large increase in microtubule density accounted for the pulling force burst. Thus, we propose that the spindle position influences the cortical availability of microtubules on which the active force generators, controlled by cell cycle progression, can pull. Importantly, we found that this positional control relies on the polarity-dependent LET-99 cortical band, the boundary of which could be probed by microtubules. This dual positional and temporal control well accounted for our observation that the oscillation onset position resists changes in cellular geometry and moderate variations in the active force generator number. Finally, our model suggests that spindle position at mitosis end is more sensitive to the polarity factor LET-99, which restricts the region of active force generators to a posterior-most region, than to microtubule number or force generator number/activity. Overall, we show that robustness in spindle positioning originates in cell mechanics rather than biochemical networks.

Introduction

Asymmetric cell divisions, with their differing daughter cell sizes, contents, and fates, are essential to achieve cellular diversity during development (1, 2). In the nematode Caenorhabditis elegans—as in many other species—during the first embryonic division, the mitotic spindle is oriented along the polarity axis and displaced out of the cell center (3, 4), where it helps position the cytokinesis cleavage furrow (5, 6, 7, 8). Most asymmetric divisions include pulling forces from the cell cortex that are exerted on the astral microtubule plus ends, and these forces are key in positioning and orienting the mitotic spindle (3, 4, 9). In the one-cell nematode embryo, cortical forces are generated by a well-conserved trimeric complex that pulls on astral microtubules. The complex is made up of a dynein/dynactin complex, a LIN-5 protein (homolog of NuMA), and the G-protein regulators GPR-1/2, which are mammalian LGN homologs (10). In an asymmetric division, GPR-1/2 proteins reflect polarity cues (11) through their asymmetric locations at the cortex (11, 12, 13), increasing the number of active force generators at the embryo posterior-most side (11, 14, 15). An active force generator is defined as a complex either currently pulling from the cortex or ready to do so upon meeting a microtubule (10, 16, 17).

In our initial “tug-of-war” physical model, we focused on the spindle oscillation and posterior displacement. We found that along the anaphase course, an embryo-wide decrease in the force generator detachment rate from astral microtubules accounted for the oscillation buildup and die down and for the increase in the pulling force imbalance, thus causing posterior spindle displacement (16). The suggested temporal regulation was reinforced by the proposed link between spindle displacement timing and the cell cycle (18). In our initial model, we assumed that astral microtubules were abundant at the cortex during anaphase and that the only limiting factor was the binding/unbinding dynamics of the force generators from the microtubules. Since then, Kozlowski et al. proposed a model that accounted for spindle oscillation by the limited access of the astral microtubules to the cortex (19). Furthermore, some studies showed that perturbations to microtubule dynamics, although mild enough to prevent catastrophic phenotypes, resulted in an alteration to final spindle position (20, 21). These results call for a re-examining of the role of astral microtubules in spindle positioning. In addition, we recently observed that the position of the posterior centrosome at which oscillation begins, hereafter called oscillation onset position, was not synchronized with mitotic progression in the cousin species C. briggsae (13), indicating that some other mechanism(s) contribute to regulating the cortical pulling forces.

Interestingly, the same machinery controlling spindle position and rocking at anaphase also accounts for the final spindle position. Furthermore, the mechanism connecting cortical polarity cues to the forces that set the final spindle position, and how this mechanism ensures a robust positioning of the mitotic spindle remains an open question. The LET-99 Disheveled, Egl-10, and Pleckstrin (DEP) domain containing protein is an important part of this mechanism (22) and acts downstream to PAR polarity proteins (23). Indeed, a band of LET-99 located at the cortex, spanning from 45 to 70% of embryo length, is devoid of force generation (24). To account for how LET-99 contributes to spindle positioning, two possible, nonexclusive mechanisms were proposed. Firstly, LET-99 could relocalize all GPR-1/2 proteins found at the posterior cortex to the posterior-most crescent, increasing their concentration and in turn creating an imbalance in the number of active force generators at the cortex (15). Posterior displacement of the spindle after LET-99 depletion, however, puts this mechanism into question (24). Secondly, LET-99 could act by inhibiting the GPR-1/2 proteins located in the 45–70% cortical band (termed posterolateral) and thus only constraining the cortical location at which forces can be generated, a so-called spatial restriction mechanism. In this case, the higher concentration of GPR-1/2 in the embryo’s posterior half (12, 13) would then be caused by another mechanism, still linked to polarity. Although this second possibility is attractive, the spatial restriction mechanism is still unknown. One proposed mechanism was the contribution of the orientation of the pulled astral microtubules (25), in which LET-99 could inhibit forces oriented backward with respect to spindle displacement. This nevertheless does not account for LET-99 depletion resulting in a strong anterior shift in the final spindle position (22, 23, 24). Overall, how the LET-99 cortical band contributes to final spindle positioning remains to be understood. Using a modeling approach, including cell geometry and microtubule roles, we here offer a mechanism that acts through microtubule dynamics.

We hypothesized that microtubule dynamics would be at the core of this, to our knowledge, novel regulation of cortical pulling forces, which would depend on spindle position. Delaying anaphase onset confirmed the existence of this positional control in C. elegans, and we subsequently directly observed astral microtubule availability at the cortex, especially in the posterior-most crescent. Combining the positional control of microtubule density with the posterior restriction of active force generators by the LET-99 band, we expanded the modeling of spindle rocking and positioning. We obtained and validated the dual control—temporal and positional—of pulling forces and took advantage of this so-called full-expanded model to dig into the robustness of the final spindle position, key for correct organism development. Interestingly, time simulations based on this model and our experiments suggest that spatial restriction of active force generators by the polarity factor LET-99 combined with microtubule dynamic instability limiting their contacts at the posterior-most cortex not only accounts for the final spindle position but also suggests that details of microtubule number and motor number/dynamics contribute more modestly, ensuring a robust final spindle position.

Materials and Methods

Culturing C. elegans

C. elegans nematodes were cultured as described in (26) and dissected to obtain embryos. All strains were maintained at 25°C, handled on nematode medium plates, and fed with OP50 bacteria.

Strains

TH65 C. elegans (Ce) YFP::TBA-2 (α-tubulin) (27) and ANA020 C. briggsae (Cb) GFP::β-tubulin strains with a microtubule fluorescent labeling were used for the “landing” assay. TH27 C. elegans GFP::TBG-1 (γ-tubulin) (28) and C. briggsae ANA022 (GFP::TBG-1;GFP::HIS-11^H2B) strains (13) displaying a centrosomal fluorescent labeling were the standards for the “centrosome-tracking” assay except for event timing. In that case, the control was the C. elegans TH231 (SPD-2::GFP) strain with centrosome labeling crossed with OD56 (mCherry::HIS-58^H2B) histone labeling, which generated the JEP15 strain. This was then crossed with the KR4012 such-1(h1960) mutant strain (29) to create JEP16.

Gene silencing by RNA interference

RNA interference (RNAi) experiments were performed by feeding, using bacterial clones from the Ahringer library (30) or ordered from Source BioScience (Nottingham, UK). let-99 exon3 was amplified from HT1593 genomic DNA and cloned into the L4440 plasmid. The feedings were performed at 25°C for various durations according to the experimental goals. When targeting proteins whose depletion led to changes in embryo size (cid-1(RNAi), c27d9.1(RNAi), ani-2(RNAi), and ima-3(RNAi)), we aimed for strong phenotypes and used a duration of 48 h, except for ima-3(RNAi), which was treated for 34 h. For the other depletions by RNAi imaged at the spindle plane, we performed durations large enough to deplete the proteins and observe a phenotype still having oscillations that could be quantified: the treatment lasted 6 h for spd-2 and gpr-1/2 and 24 h for par-3 and let-99. When investigating the residence time of the microtubules at the cortex, gpr-1/2(RNAi) and par-3(RNAi) were applied during 48 h, spd-2(RNAi) for 6 h, and let-99(RNAi) for 24 h. We did not notice any phenotype suggesting that the meiosis was impaired during these various depletion experiments. When we aimed to change the embryo size by RNAi, we observed oscillation amplitudes similar to the untreated embryos except after ima-3(RNAi), for which we found that the oscillation amplitudes were very variable between embryos, with amplitudes of the anterior centrosome similar to the posterior centrosome’s ones. The control embryos for the RNAi experiments were fed with bacteria carrying the empty plasmid L4440.

Quantitative Western blotting

For measuring the expression level of SPD-2, 50 adult gravid hermaphrodites were picked into 10 μL of M9 buffer and snap frozen in liquid nitrogen, then thawed, mixed with 10 μL sample buffer (180 mM Tris (pH 6.8), 7.2% sodium dodecyl sulfate w/v, 36% glycerol vol/vol, 100 mM dithiothreitol (DTT)), and loaded onto a Mini Protean TGX 4–20% Tris-Glicine gel from Bio-Rad (Hercules, CA). Immunoblots were probed using the primary anti-SPD-2 antibody MO750, kindly given by Prof. A. A. Hyman, at 1 mg/mL and detected using a horseradish-peroxidase (HRP)-conjugated secondary antibody (1:5000; Jackson ImmunoResearch, West Grove, PA) as described in (31). Quantification was performed using ImageJ after imaging the blot using an Amersham Imager 680 (GeHealthcare, Chicago, IL)

Preparation of the embryos for imaging

Embryos were dissected in M9 buffer and mounted on a pad (2% w/v agarose, 0.6% w/v NaCl, 4% w/v sucrose) between a slide and a coverslip. Depending on the assay, they were observed using different microscopic setups. To confirm the absence of phototoxicity and photodamage, we first checked for the normal rates of subsequent divisions before proceeding with further experimentation (32, 33).

Centrosome imaging

For the “centrosome-tracking” and the “event-timing” assays, embryos were observed at the spindle plane using a Zeiss Axio Imager upright microscope (Zeiss, Oberkochen, Germany) modified for long-term time lapse. First, extra antiheat and ultraviolet filters were added to the mercury lamp light path. Secondly, to decrease the bleaching and obtain optimal excitation, we used an enhanced transmission 12-nm bandpass excitation filter centered on 485 nm (AHF analysentechnik, Tübingen, Germany). We used a Plan Apochromat 100×/1.45 NA (numerical aperture) oil objective. Images were acquired with an Andor iXon3 EMCCD (electron multiplying charge-coupled device) 512 × 512 camera (Andor, Belfast, Northern Ireland) at 33 frames per second and using Solis software. Embryos were imaged at 23°C. The beginning of the spindle’s abrupt elongation (Fig. S4 A) was used as the marker for anaphase onset (34), and the centrosome tracks of individual embryos were aligned using this time reference for averaging purposes or for overlay on the “landing” assay. An exemplary event timing extraction is reproduced in Fig. S4 C. Timings are summarized in Fig. S4 D.

“Landing” assay

To measure the spatial distribution of microtubule cortical contact densities, fluorescent tubulin labeling of entire microtubules was used to observe both polymerizing and depolymerizing microtubules at the cortex of one-cell embryos at 23°C (Fig. 1 D), using a spinning disk microscope (Leica DMI6000/Yokogawa CSU-X1 M1; Leica Microsystems, Wetzlar, Germany/Yokogawa Electric, Tokyo, Japan) equipped with an HCX Plan Apochromat 100×/1.4 NA oil objective. Illumination was performed by a white-light Fianium laser filtered around 514 nm using a homemade setup (35), sold by Leukos (Limoges, France). We subsequently denoised the images by Kalman filtering (36) and detected microtubule contacts by applying u-track (37) (Fig. 1, A–C). The recovered lifetimes of the microtubule contacts followed an exponential distribution, as expected from a first-order stochastic process (Fig. 1 E) (19). To spatially map the microtubule contacts with a reasonable accuracy, for each embryo, we divided the cortex into 10 regions of equal width along the anteroposterior (AP) axis and counted the number of contacts in each region along mitosis. The densities were computed by dividing these counts with the respective cortical region areas, which were precisely measured using the active contour algorithm (38). To gain certainty, we then performed averaging over 10-s blocks because we observed minor changes of the microtubule contact density at that timescale. The final density map was obtained by averaging over embryos after the density maps were aligned temporally according to the onset of cytokinesis furrow ingression. This temporal cue was set when the embryo shape decreases its convexity, as reported by the ratio of convex area to active contour area (Fig. S4 B). The landing assay is further detailed in the Supporting Materials and Methods.

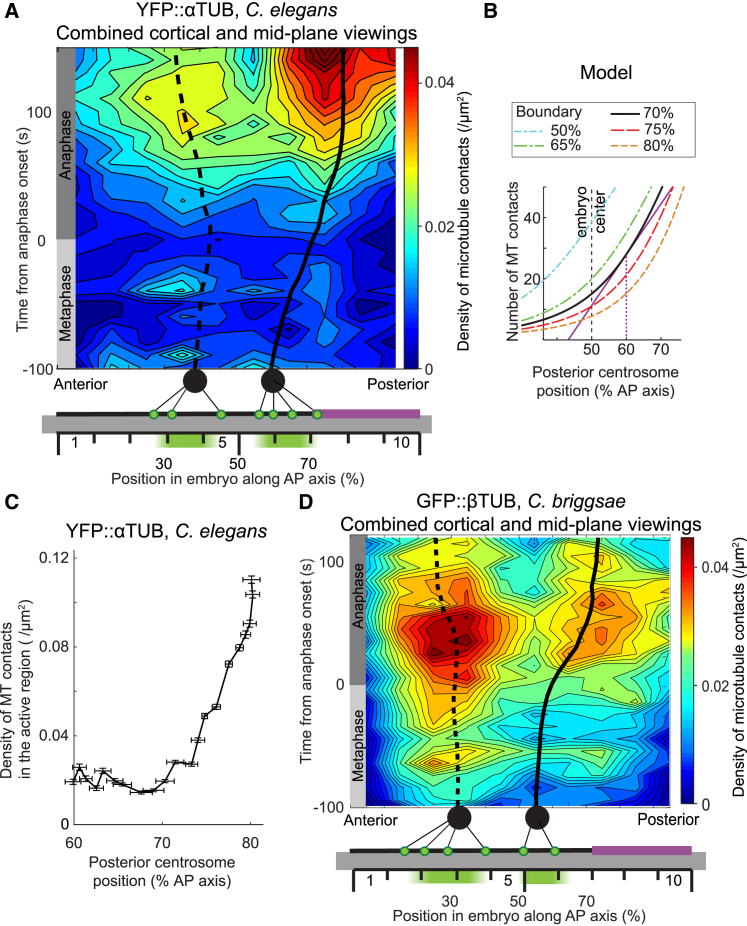
Figure 1.

Microtubule contact density at the cell cortex. (A–C) Exemplar spinning disk micrographs of C. elegans at the cortical plane with YFP::α-tubulin labeling of microtubules, viewed at 10 frames per second. The posterior tip of the embryo is on the right side of the pictures. The raw image (A) was denoised (B) using the Kalman filter, and microtubule contacts were tracked (C, green lines) using the u-track algorithm with the parameters listed in Table S3. The scale bar represents 10 μm. (D) The experimental setup for viewing microtubule contact density at the cell cortex. The scale represents the 10 regions along the anteroposterior (AP) axis used for analysis (Materials and Methods). Red and blue disks represent the anterior and posterior centrosomes, respectively, and the light blue clouds are the chromosomes. Microtubules emanating from the centrosomes are exemplified using thin black lines. The posterior-most crescent where the active force generators are located (the so-called active region) corresponds to the purple cortical region. (E) A semi-log plot of the histogram of the microtubule contact durations at the cortex during metaphase and anaphase for a single embryo (black dots), fitted with an exponential decay (gray line) corresponding to a characteristic time of 0.95 ± 0.03 s (N = 3832 microtubule contacts). (F and G) Microtubule contact densities at the cortex obtained by analyzing spinning disk microscopy images of (F) the YFP::α-tubulin-labeled microtubule strain in N = 12 C. elegans embryos and (G) the GFP::β-tubulin-labeled microtubule strain in N = 8 C. briggsae embryos. Microtubule contact densities measured at 23°C for each embryo were then averaged along the AP axis within 10 regions of equal width and over a 10-s running time window, and finally the average over embryos was computed (Materials and Methods).

Robustness plot

To assess the robustness of the position and timing of the posterior centrosomal oscillation onset against embryo length variations, we calculated dimensionless quantities (Fig. 4). For the timing, we used the reference duration T as being equal to the delay between two mitotic events independent of cell mechanics for control embryos. We chose the nuclear envelope breakdown and the anaphase onset as these events. For each experiment, we computed t₀, the shift of the oscillation onset time with respect to the anaphase onset. The normalized shift $\overline{\delta t_0}$ was thus obtained by subtracting the corresponding mean value for control $t_0^{ctrl}$ from the current value t₀ and by dividing the result by the reference duration: $\overline{\delta t_0}=\left(t_0-t_0^{ctrl}\right)/T$. We repeated this calculation for the positional quantities using the mean embryo length L in control as a reference for normalization. For each experiment, we computed the shift of the position of oscillation onset, P₀, with respect to the corresponding control mean position $p_o^{ctrl}$. Normalization yielded the normalized shift of the oscillation onset position $\overline{\delta p_0}=\left(p_o-p_o^{ctrl}\right)/L$. We used a Student’s t-test to see whether the linear fit slope was significantly different from 0. In doing so, we were able to determine whether, e.g., embryo length had an impact on the position or timing being studied.

Figure 4.

Embryo length has less effect on oscillation onset position than on its timing. (A) The modeled number of engaged force generators versus the posterior displacement of the centrosome along the AP axis as a percentage of embryo length. The line colors indicate the embryo length: untreated embryos are black; the shorter embryos corresponding to those produced by cid-1(RNAi), ima-3(RNAi), or ani-2(RNAi) are shown in blue and green; and the longer embryos from c27d9.1(RNAi) are shown in red and orange. The parameters used are listed in Table S1. Gray shading indicates when the number of engaged force generators was too low to permit oscillation. (B) Embryo lengths in control embryos and those treated by RNAi to vary their lengths. Error bars indicate SD, and asterisks indicate significant differences (Materials and Methods). (C) The shift in the posterior centrosome position at oscillation onset as compared to the control (normalized by the average embryo length in control, see Materials and Methods) and (D) the shift in oscillation onset timing normalized by the control’s average pro-metaphase and metaphase duration, both versus the variations in embryo lengths as compared to the control, are shown. The solid black lines indicate the linear least square fits, with slopes of −0.09 ± 0.03 (p = 8 × 10⁻⁴ compared to null slope) and 0.51 ± 0.06 (p = 1 × 10⁻¹¹), respectively. We measured N = 9 cid-1(RNAi), N = 6 c27d9.1(RNAi), N = 12 ani-2(RNAi), N = 6 ima-3(RNAi), and N = 49 control embryos with GFP::γ-tubulin-labeled centrosomes. The dashed black lines are the standard errors. Dots indicate individual embryos, and the average control values (0 shift) are thin black lines.

Simulation of the posterior displacement using the full-expanded model

We simulated the posterior displacement of the spindle using our full-expanded model with the TR-BDF2 algorithm (39). To ensure the proper force balance on the spindle poles, we also included the anterior centrosome in the full-expanded model and restricted the anterior active force generators’ location to between 0 and 40% of the AP axis (15). We also kept the anterior centrosome at a fixed position for the sake of simplicity, making the spindle position dependent only on that of its posterior pole. On the anterior side, we used a twofold lower force generator on-rate (14), resulting in half the number of active force generators compared to the posterior-most side (15). We assumed that force applied to the posterior centrosome and originating in the anterior side was halved after anaphase onset because sister chromatids separated. We modeled the centering force with a spring (34) and used the processivity to control the progression of mitosis (16). Finally, because the model was linearized, it was limited to considering modest variations in parameters around their nominal values. This simulation is further detailed in the Supporting Materials and Methods.

Statistics

Averaged values were compared using a two-tailed Student’s t-test with Welch Satterthwaite correction for unequal variance, except when otherwise stated. For the sake of simplicity, we recorded confidence levels using a diamond or asterisks (⋄ when p ≤ 0.05, ^∗p ≤ 0.01; ^∗∗p ≤ 0.001; ^∗∗∗p ≤ 0.0001; ^∗∗∗∗p ≤ 0.00001) and nonsignificant (ns for p > 0.05; sometimes omitted to save room).

Data processing, modeling, and simulation

All data analysis was developed using MATLAB (The MathWorks, Natick, MA). Modeling was performed using Wolfram Mathematica formal calculus software. Numerical simulations were performed using MATLAB and Simulink (The MathWorks).

Results

Astral microtubule contacts at the cortex depend upon centrosome position in C. elegans, enabling the spindle to sense its position

To establish the nematode C. elegans as a suitable model, we first aimed to confirm that a positional control, i.e., a mechanism relating the cortical pulling force regulation to the spindle position, exists in this organism. Indeed, we previously reported that the position of the spindle posterior pole controlled the onset of spindle oscillation in C. briggsae (13). In contrast with that nematode species, in which anaphase onset preceded oscillation by 30 s, in C. elegans these onsets were simultaneous. This could be coincidental, thus we tested whether a positional control exists in this latter by delaying anaphase. We used a such-1^ANAPC5(h1960) mutant of the anaphase-promoting complex/cyclosome (APC/C) (29), labeling centrosomes and chromosomes using SPD-2^CEP192::GFP; mCherry::HIS-58^H2B. We tracked the centrosomes (16, 34), and observed oscillations that started largely before anaphase in the mutant (Table 1) but occurred when the posterior centrosome was at 70.5% of embryo length, similar to the control (70.0%). In contrast, for both strains, the die down of oscillations occurred just short of 2 min after anaphase onset regardless of when oscillations started up, thus leading to different durations of the oscillation phase (Table 1). We conclude that a positional control of anaphase oscillation onset exists in the C. elegans embryos, similarly to C. briggsae.

Table 1.

Timing and Position of Metaphase and Anaphase Events in Delayed-Anaphase Mutants and in Reduced-Microtubule-Nucleation Embryos

Characteristic measured (mean ± SD)	Control #1 (N = 10)	such-1(h1960) (N = 13)	Control #2 (N = 10)	spd-2(RNAi) (N = 12)
Oscillation onset T1 (s)	−9.54 ± 8.04	−80.56 ± 37	−5.14 ± 20.19	9.49 ± 17.44
		p = 1 × 10−5		p = 0.043
Posterior centrosome (CS) reaching 70% of the AP axis T2 (s)	−9.19 ± 8.42	−89.78 ± 45.10	−5.24 ± 21.18	−0.53 ± 14.81
		p = 3 × 10−5		p = 0.43
Maximal oscillation amplitude (posterior) (%)	23.90 ± 3.39	21.88 ± 3.56	16.10 ± 3.45	14.64 ± 4.73
		p = 0.18		p = 0.39
Nuclear envelope breakdown time (s)	−150.1 ± 31.2	−284.9 ± 38.7	−194.83 ± 26.60	−170.0 ± 15.51
		p = 2 × 10−8		p = 0.04
Oscillation die down T3 (s)	114.90 ± 22.63	109.69 ± 16.23	111.50 ± 15.52	114.4 ± 23.8
		p = 0.55		p = 0.74
Oscillation duration T3–T1 (s)	124.44 ± 18.93	190.25 ± 30.13	116.64 ± 20.01	104.9 ± 18.9
		p = 3 × 10−6		p = 0.096
Posterior centrosome position at oscillation onset (%)	70.03 ± 1.73	70.48 ± 1.85	70.12 ± 1.23	72.46 ± 1.76
		p = 0.56		p = 0.0016
Posterior centrosome position at oscillation die down (%)	80.31 ± 2.04	80.72 ± 1.99	79.69 ± 1.94	81.46 ± 1.33
		p = 0.63		p = 0.025
Embryo length (μm)	49.23 ± 2.34	47.26 ± 3.34	50.33 ± 3.18	51.08 ± 2.78
		p = 0.11		p = 0.56
Embryo width (μm)	33.10 ± 2.36	31.85 ± 1.94	30.60 ± 1.80	30.49 ± 1.56
		p = 0.19		p = 0.88

Embryos with labeled centrosomes were imaged at 23°C, and spindle poles were tracked. We first compared labeled SPD-2^CEP192::GFP;mCherry::HIS-58^H2B embryos with (N = 13) and without (N = 10) non-null mutation such-1^ANAPC5(h1960). This gene codes for an anaphase promoting complex/cyclosome component (29). We also compared embryos whose centrosomes were labeled using GFP::γ-tubulin and that were treated with spd-2(RNAi) (N = 12) or L4440 empty vector (N = 10). Times were measured from the onset of anaphase, determined from the onset of spindle elongation (34). Peak-to-peak oscillation amplitude is shown as a percentage of embryo width. Positions along the AP axis are shown as a percentage of embryo length. Error bars indicate SDs. p values are reported for Student’s t-test, Welch-Satterthwaite corrected. Succession of the key timing events, i.e., nuclear envelope breakdown, T1, T2, and T3, are schematized in Fig. S4D and explained in Materials and Methods.

Previous studies have emphasized the key role of microtubules in the positioning of the microtubule-organizing center (MTOC). Indeed, they can “sense” cell geometry, for example to bring the MTOC to the cell center (40, 41) or to orient the nucleus by exerting pulling forces that scale with microtubule length (42). To challenge our hypothesis that the microtubule network provides a positional regulation of pulling forces, we decreased the microtubule nucleation rate through a mild spd-2^CEP192(RNAi) (27) (Fig. S2 E; Videos S1 and S2). The efficiency of this partial depletion was confirmed by Western blot (Fig. S2 D), with the loss of SPD-2 equal to 59.4 ± 6.4% (N = 3 replicates) of the quantity measured in control conditions. By measuring the centrosome trajectories along cell division, we found that the posterior centrosome position at oscillation onset was significantly displaced posteriorly in SPD-2-depleted embryos, reaching 72.5% of embryo length compared to 70.1% in the control (Table 1). We checked that this change could not be attributed to a difference in the dynamics of the microtubules at the cortex and found no significant difference (Fig. S1 C). We thus confirmed that astral microtubules, and likely the number of them contacting the cortex, play a role in regulating the centrosomal position at which oscillation begins.

Video S1. Spindle Positioning in a C. elegans Control Embryo

Video of a Caenorhabditis elegans one-cell embryo imaged at the spindle plane upon RNAi using the empty L4440 vector. Centrosomes are labeled by GFP::γ-tubulin and embryo radii are equal to 48.7 μm and 31.3 μm. The video was accelerated to 10x real-time. Anaphase onset was measured at 26.05 seconds. Stills extracted from this video are reproduced in Fig. S2 E, top row.

Video S2. Spindle Positioning in a Reduced-Microtubule-Nucleation Embryo

Video of a C. elegans one-cell embryo imaged at the spindle plane during mitosis upon spd-2(RNAi) treatment. Centrosomes are labeled by GFP::γ-tubulin and embryo radii are equal to 49.0 μm and 31.9 μm. The video was accelerated to 10x real-time. Anaphase onset was measured at 22.15 seconds. Stills extracted from this video are reproduced in Fig. S2 E, bottom row.

Kozlowski and co-workers have reported that microtubules are not always abundant at any place at the cortex (19). We therefore hypothesized that the distribution of microtubule cortical contacts might depend on MTOC proximity, i.e., on centrosome position. We tested this by directly measuring microtubule distribution at the cortex (“landing” assay, Materials and Methods; Fig. 1 D). We used α-tubulin labeling to view microtubules in both growing and shrinking states, the latter being present when microtubules are pulling from the cortex and not tracked by ending binding proteins. Because α-tubulin YFP::TBA-2 construct was added up to the endogenous copy and overexpressed because of the strong pie-1 promoter (19), we checked that this labeling led to no phenotype with respect to the modeled traits. We compared the spindle pole trajectories as well as the oscillation amplitudes and timings of this entire-microtubule-labeled strain with those of the GFP::γ-tubulin centrosome-labeled strain (Fig. S1, A and B; Supporting Materials and Methods). We did not observe any significant difference in these features, and thus the model could be safely grounded on data measured in these two different strains. Because the microtubule dynamics are so fast, we viewed the cortical contacts at a speed of 10 frames per second. This labeling combined with the fast acquisition led to images with a low signal-to-noise ratio, which required a powerful denoising and adequate tracking (Fig. 1, A–C; Supporting Materials and Methods). We validated our image-processing analysis pipeline using simulated data (Fig. S1, D–F; Supporting Materials and Methods). We measured a histogram of microtubule contacting times at the cortex displaying an exponential distribution (Fig. 1 E), characteristic of a first-order process, with a lifetime consistent with previously published values (19). We then calculated the spatial distribution of microtubule cortical contacts along the AP axis. To reduce uncertainty, we block-averaged the distribution in 10 regions of equal width along the AP axis (Fig. 1 D) and then performed a 10-s running average over the obtained density. The latter is possible because of the slower timescale associated with spindle displacement and microtubule dynamics regulation. The final density map was obtained by averaging the result over the embryos (Materials and Methods). Consistently, the associated standard errors of the mean were below 6% of the values themselves, except in the tip regions along the AP axis (#1 and #10, Fig. 1 D) at early metaphase, where they could reach 20% because of a low count of microtubule contacts. We observed spatial heterogeneity with two high-density ridgelines and an overall increase in contacts between metaphase and anaphase, the latter being consistent with the increasing nucleation rate previously described (27) (Fig. 1 F).

To test whether the high-density ridgelines could correspond to the centrosomal positions, we used a wide-field microscope to view the spindle plane in the same strain and at the same temperature and tracked the centrosomes. We then combined the results from both experiments and aligned them temporally with anaphase onset (Materials and Methods; Supporting Materials and Methods). We found that centrosome positioning coincides with the ridgelines (Fig. 2 A). Because we had initially observed the positional switch on cortical pulling forces in one-cell C. briggsae embryos (13), we thus considered whether it could rely on a similar modulation of microtubule cortical contacts in space and time. We performed the same experiments in this species and obtained similar results (Figs. 1 G and 2 D). We conclude that the distance from the centrosome to the cortex strongly controls the number of microtubules contacting the cortex in both species.

Figure 2.

Astral microtubules preferentially contact the cortex in the area closest to the centrosomes. (A) Microtubule contact density at the cell cortex in C. elegans with superposed centrosome trajectories obtained by combining two data sets. First, the densities, shown here as an interpolated heat map, were measured in the microtubule-labeled strain at the cortex and obtained by averaging the densities along the AP axis within 10 regions of equal width and over a 10-s running time window, finally taking the mean over embryos (Materials and Methods). Data are the same as in Fig. 1F. Second, the average trajectories of the centrosomes were obtained by imaging the same strain at the spindle plane (N = 8 embryos) and superposing the results on the microtubule-contact-density map. The dashed line represents the anterior centrosome trajectory, and the solid line indicates the posterior one. At the bottom is a schematic of the experimental setup in which centrosomes are shown as black disks, with thin black lines depicting the astral microtubules. Microtubule contacts at the cortex are shown as green dots. The active region, which is used to compute (C), corresponds to the purple cortical horizontal line. (B) The modeled number of microtubules contacting the cortex in the active region versus the posterior displacement of the centrosome along the AP axis, with the active region boundary expressed as a percentage of embryo length. The thick black line corresponds to a boundary at 70%, mimicking the untreated embryo. In this case, the number of contacts started to increase steeply at a position above 60% (purple line). Blue and green curves model let-99(RNAi) or par-3(RNAi) experiments in which the boundary was displaced anteriorly. Red and orange curves show the cases of posteriorly displaced boundaries. (C) The density of microtubule contacts versus the position of the posterior centrosome in a region ranging from 70 to 100% of the AP axis, computed from the data shown in (A). (D) The microtubule contact density at the cortex in C. briggsae with superposed centrosome trajectories represented similarly to (A). Microtubule contact densities at the cortex were obtained by viewing a GFP::β-tubulin-labeled microtubule strain. The data are the same as in Fig. 1 G. Centrosome trajectories were obtained in a second experiment by imaging a GFP::γ-tubulin;GFP::HIS-11-labeled centrosome and histone strain (N = 7 C. briggsae embryos) at the spindle plane.

In the posterior cortex, only the force generators localized in the posterior-most crescent (the so-called active region) are able to exert a pulling force on an astral microtubule. It is due to LET-99 inhibiting the force-generator pulling activity in the posterolateral region (distributed between 45 and 70% of the AP axis) (24) while preserving the twice larger number of active force generators on the posterior-most side of the embryo (11, 15). We propose that the displacement of the area where microtubule contacts are concentrated toward the posterior along the course of mitosis could increase the number of microtubule contacts in the active region—a means to regulate cortical forces. Could such a phenomenon create a positional switch? To address this question, we modeled the microtubule contacts at the cortex (Supporting Materials and Methods). While doing so, we included the dynamic instability of microtubules (43) and assumed for now that the force dependence of the catastrophe rate was negligible (25). We also assumed that catastrophes happened only at the cortex (no free-end catastrophe) and that microtubules fully depolymerized upon shrinking (negligible rescue rate) (19, 27, 44). We set a constant number of microtubule nucleation sites at the centrosomes, neglecting the modest increase in nucleation rate observed during anaphase compared to metaphase (27). Furthermore, these nucleation sites were never empty (25), and the microtubules emanated from there in an isotropic angular distribution (27, 45). We computed the number of microtubules that reached the cortex in the active region as a function of the position of the posterior centrosome (Fig. 2 B, black curve). This highlighted a limited number of microtubule cortical contacts when the centrosome position was close to cell center, with an initial slow increase in this number upon posterior displacement followed by a steeper increase so that a high level was reached at close to 70% of embryo length, consistent with the onset of oscillation observed at that position. To confirm, we sought to measure microtubule contacts in the active region experimentally, counting them in our “landing” assay and obtaining a consistent measurement (Fig. 2 C). We propose that microtubule dynamics are at the core of the experimentally observed positional switch by regulating the number of microtubules available to force generators, making it dependent on centrosome position. Furthermore, the large number of microtubules that reach the active region during mid- and late anaphase is consistent with the initial model’s assumption that microtubules saturate a limited number of cortical force generators during this phase (16, 17). The restriction of active force generators to a posterior crescent smaller than the embryo half, probably by LET-99, is key to this modeling result. Overall, it paves the way toward understanding the positional regulation of the cortical pulling forces involved in spindle rocking, posterior displacement, and elongation.

Microtubule cortical contact modulation exerts a positional control on the number of engaged force generators

To quantitatively investigate how varying microtubule cortical contact density interacts with spindle position to regulate cortical pulling forces and to further study the subsequent impact on final spindle position, we further developed the physical modeling and extended our initial model (16). We propose that two modules combine to regulate the pulling forces (Fig. 3 A). In the first module, the position of the posterior centrosome is linked to the number of microtubule cortical contacts in the active region, which is in turn able to limit the number of engaged force generators, as modeled in the previous section. The second module provides a temporal/mitotic progression control of the pulling forces through the dynamics of the force generators (16, 18, 46). Up to now, only the latter was accounted for in the initial model, and we envisioned that combining with the former would unravel novel robustness in the regulation of pulling forces and in doing so would reveal the mechanism linking cortical polarity and final spindle position.

Figure 3.

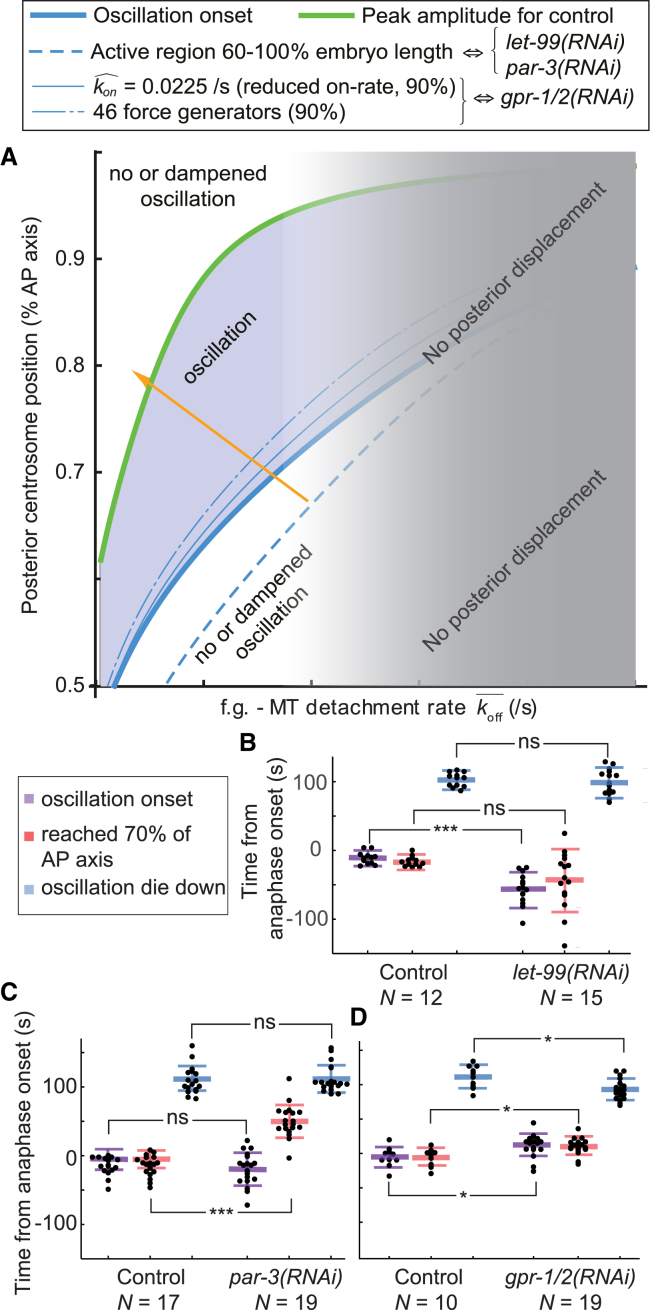
Expanded model accounts for positional and temporal regulations of cortical forces. (A) Schematics of the expanded model highlighting the players (top row), the quantity they regulate (second row), how they control forces (module, third row), and some related phenotypes (bottom row). Pink/yellow colors correspond to the positional control involving astral microtubule dynamics and the active region created by LET-99, and blue depicts the time control involving force generator dynamics. Although both controls participate in oscillation onset (purple), final spindle position mostly depends on active region extent (yellow) and oscillation die down on time control (blue). (B) The modeled number of engaged force generators versus the posterior displacement of the centrosome along the AP axis, with the active region boundary expressed as a percentage of embryo length. The thick black line represents the case in which active region boundary is located at 70% of the AP axis, mimicking the control embryo. Blue and green curves model let-99(RNAi) and par-3(RNAi) experiments in which the boundary was displaced anteriorly. Red and orange curves show cases of posteriorly displaced boundaries. Gray shading indicates when the number of engaged force generators is too low to permit oscillation. The parameters used are listed in Table S1. (C and D) Positions of the posterior centrosome at oscillation onset (C) in let-99(RNAi) (N = 15) and control (N = 12) embryos and (D) in par-3(RNAi) (N = 19) and control (N = 17) embryos, with centrosomes labeled by GFP::γ-tubulin. Bee swarm plots report values obtained for each embryo. Large thick horizontal bars depict the mean, whereas error bars indicate SD and asterisks indicate significant differences (Materials and Methods).

We created a first version of this two-module model, termed “expanded model,” in which we continued to neglect the temporal evolution of force generator processivity (Fig. 3 A). We modeled the binding of microtubule and dynein as a first-order chemical reaction using the law of mass action, assuming no cooperative binding between force generators (47), and estimated the association constant from the binding and unbinding rates used in the initial model (16) (Supporting Materials and Methods). This enabled us to compute the number of engaged force generators versus the posterior centrosome position (Fig. 3 B, black line). We found that when the centrosome was far from the posterior tip, we observed a scarcity of astral microtubules contacting the cortex in its active region, which limited the number of engaged force generators to below the previously described threshold for oscillating (16). Upon posterior displacement of the centrosome, beyond 60% of the AP axis, we observed a steep increase in engaged force generator count, similar to the one found in the number of microtubule cortical contacts (compare the black curves in Figs. 2 B and 3 B). This was followed by a saturation starting from 70% of the AP axis because of the limited number of active force generators. These two successive regime changes created a switch, which was consistent with our positional control hypothesis. In conclusion, our expanded model predicts that oscillation onset—a readout of pulling force increase—is regulated by posterior displacement of the posterior centrosome.

We experimentally challenged the expanded model in three ways related to each biological player (Fig. 3 A, top line) through measuring the timing of oscillation onset with respect to anaphase onset and the posterior centrosomal position when oscillation starts. Firstly, we varied the extent of the active force generator region in the expanded model and could predict that the precise position at which oscillations start correlates with the boundary of the active region (Fig. 3 B). The extent of this region inversely reflects the LET-99 cortical band (24). We thus increased this extent toward the anterior side, still in the embryo’s posterior half, by partially depleting LET-99. We observed that as compared to the control, the position of the posterior centrosome at which oscillations began was significantly displaced toward the anterior (Fig. 3 C), in agreement with the expanded model’s predictions (Fig. 3 B, blue and green curves). We checked for no change in microtubule residence time at the cortex (Fig. S1 C), consistent with the model assumptions. To gain certainty, we impaired the cortical domain boundary in a different manner: upon par-3(RNAi), we expected the PAR-1 domain to extend more toward the anterior pole so that the LET-99 band would be more anterior (48). We observed that in such a condition, the posterior centrosome started oscillation much more anteriorly than in control embryos (Fig. 3 D). This change could not be the consequence of the increased microtubule lifetime at the cortex upon par-3(RNAi) (Fig. S1 C) because it would result in an opposite effect (Fig. S8 E). Based on these two experiments in which the active region extended more anteriorly than in the untreated embryos, we conclude that the position of the active region boundary controls the position where oscillation onset occurs.

In a second prediction-challenging experiment, we focused on microtubules and predicted that a decrease in their total number emanating from either centrosome would posteriorly displace the position of oscillation onset (Fig. S2 A, blue and green curves). Experimental depletion of the protein SPD-2 by RNAi decreased microtubule nucleation at the centrosomes (27) and resulted, as predicted, in a posteriorly shifted position of the posterior centrosome at oscillation onset (Table 1).

Thirdly, we varied the number of active force generators, which is predicted to have a reduced impact on the oscillation onset (Fig. S2 B, green curve) provided that it was above the needed threshold (16). We previously observed that the oscillation onset position was not significantly changed in gpr-1(ok2126) or gpr-2(ok1179) mutants (13). We set out to reproduce this result in this work using a partial gpr-1/2(RNAi). To estimate the remaining level of force generation, we observed the posterior centrosome oscillations and noted a reduction of their amplitude to 11.4 ± 6.3% of embryo width (mean ± SD, N = 19 embryos, p = 9.7 × 10⁻³) compared to 16.1 ± 3.5% (N = 10), as expected (11). Under that condition, the position at which the oscillations began was not significantly altered (Fig. S2 C). Importantly, the residence time of the microtubules at the cortex was not affected in this condition (Fig. S1 C). Overall, these three results support our model: microtubule dynamics sense centrosome position and the extent of the active region, which in turn controls the position triggering oscillation onset.

The position at which pulling forces burst is resistant to variations in embryo length

Because the astral microtubules can sense the distance from the centrosomes to the cortex, the proposed mechanism may also make the positional regulation of the cortical pulling forces dependent on the cell geometry. In this respect, it could be reminiscent of the yeast positional check point (49), as well as the adaptation of cell division plane positioning to variations in cell shape observed in other contexts and organisms (42, 50, 51). Our expanded model suggested that the posterior centrosome position at oscillation onset is only weakly dependent upon the length of the embryo (Fig. 4 A). To experimentally investigate this prediction, we depleted C27D9.1 by RNAi to obtain longer embryos, and performed cid-1(RNAi), ima-3(RNAi), or ani-2(RNAi) to yield shorter ones (Fig. 4 B). In all cases, the imaged embryos were viable. Embryos with depleted IMA-3 displayed an altered oscillation phenotype, with a large variability in the centrosome oscillation amplitudes between embryos and with anterior and posterior centrosomes displaying similar amplitudes. We measured normalized variations in the timing and positioning of oscillation onset with respect to the variations in embryo length and computed the shifts from control averages (Materials and Methods). For both temporal and positional analyses, we fitted a linear regression, measuring oscillation onset timing slope 5.6 times larger than that of the oscillation onset position (Fig. 4, C and D). It was indicative that the positional switch at ∼70% of the AP axis was conserved despite variations in embryo length. Consistently, the position shift spread around the fitted line was narrower in comparison to normalized oscillation onset time shift. This was expected because the position of oscillation onset is regulated and thus constrained—as suggested by the proposed model—and depends on quantities mostly independent of embryo length, whereas its timing is unconstrained and could thus vary in a broader range. The very low slope of the linear regression in Fig. 4 C suggested that the positional control could make the position at which cortical force bursts resistant to changes in embryo length. Interestingly, Farhadifar et al. showed that both the final spindle length and the division plane position scale linearly with embryo length within different C. elegans natural isolates and beyond within several nematode species (52). These correlations may be either enforced by natural selection or because of some robustness mechanisms, two nonexclusive possibilities. Because the cortical pulling forces play an important role in setting the spindle length and positioning the division plane, the positional regulation exhibited here may be one of the mechanisms accounting for such a robustness. In contrast, we showed that the timing of oscillation onset displayed a positive correlation with embryo length, with a larger linear regression slope than the one measured for the position. This is consistent with longer embryos requiring a larger duration of posterior displacement to reach the critical 70% of the AP axis position for oscillation onset (13). Overall, it also supports the idea that the positioning and timing of oscillation initiation are not connected at anaphase onset.

Centrosome position and time/mitotic progression both contribute to oscillation and pulling force regulation

We found that the oscillation onset is controlled by the position of the posterior centrosome, whereas its die-down timing is dependent on the time control (mitotic progression). Beyond these dominant effects, however, we also noticed that oscillations might start while the centrosome was close to 70% of the AP axis rather than when it reached this position (Table 1). We suspected that a combination of both temporal and positional controls was at work. We set to recapitulate this regulation by completing our model and validating it. We included the temporal control within the expanded model as previously done in the initial model, i.e., through the decrease of microtubule force-generator detachment rate (off-rate), which is the inverse of processivity (16). Doing so, we made the microtubule-force-generator equilibrium constant dependent on time through the decreasing off-rate. We will from now refer to this model as the “full-expanded model” (Supporting Materials and Methods). In contrast to the initial model, the force generator on-rate is no longer constant and instead depends on the number of microtubules available at the cortex for binding a force generator and on the extent of the active region. It also depends on the on-rate imbalance reflecting polarity (14). Using the full-expanded model, we computed the stability diagram corresponding to centrosome oscillation, which depended on both temporal and positional control parameters: the force generator processivity and the position of the posterior centrosome, respectively. The nonstable region (Fig. 5 A, blue region) corresponded to model parameter sets in which oscillation developed. In contrast, in stable regions (Fig. 5 A, white regions), the system was overdamped, causing pre-existing oscillations to die down. This diagram suggested that to enable oscillation, in addition to a large enough force generator processivity (16), the posterior centrosome needed to be close enough to the posterior tip of the embryo, which supported our positional switch hypothesis investigated above (Fig. 5 A, thick blue curve), leading to a dual control of the pulling force outburst. Although this model offered a clear view about oscillation onset, we could only infer predictions of oscillation die down from the return-to-stability curve, which corresponded to when the system starts dampening out oscillation (Fig. 5 A, green curve). This was because no detailed model relates mitotic progression/time to processivity. Interestingly, the steeper slope of this return-to-stability curve compared to the oscillation onset curve suggested that the posterior centrosome position was likely to more strongly influence oscillation onset than die down (Fig. 5 A). This was consistent with the equal anaphase onset to oscillation die-down duration observed in such-1(h1960) mutant and its control (Table 1).

Figure 5.

Two independent controls both contribute to oscillations. (A) A stability diagram of the full-expanded model as a function of the detachment rate (off-rate $\overline{k_{off}}$, inverse of the processivity, x axis) and of the position of the centrosome as a percentage of embryo length (y axis). The unstable region (blue) corresponds to the values of off-rate and posterior-centrosomal position enabling oscillation development. The critical values are marked by the thick blue and green lines for parameters corresponding to control condition. Thin blue lines with various dashing patterns correspond to the oscillation onset’s critical curves for parameters distinct from the control, indicated by their raw values and their relative values in % of control condition and corresponding to experimental perturbations. The orange arrow indicates the typical “phase” trajectory during mitosis based on the parameters used in this study. The grayed-out area shows that above a detachment rate threshold, the posterior displacement of the spindle/posterior centrosome no longer occurs (orange curve in Fig. 6G). The centrosome needs to reach a position that is posterior enough to enable oscillations, whereas force generators must display a high enough processivity (measured to 1–2 s⁻¹ in metaphase (14)). The parameters used are listed in Table S1. (B–D) Timings of oscillation onset, oscillation die down, and posterior centrosome arrival at 70% of embryo length (B and C) when the size of the active region is changed in let-99(RNAi) (N = 15) compared to control (N = 12) embryos or in par-3(RNAi) (N = 19) compared to control (N = 17) embryos and (D) upon depletion of active force generators (f.g.) in gpr-1/2(RNAi) (N = 19) compared to control (N = 10) embryos. All embryos display GFP::γ-tubulin labeling of the centrosomes. Bee swarm plots report values obtained for each embryo. Large thick horizontal bars depict the mean, whereas error bars indicate SD and asterisks indicate significant differences (Materials and Methods).

To challenge this full-expanded model, we again experimentally investigated the role of players in each regulation (Fig. 3 A). We first observed that an anterior shift of the boundary position of the active region by let-99(RNAi) or par-3(RNAi) did not alter the oscillation die-down timing significantly with respect to the control, whereas oscillation onset happened not only earlier (Fig. 5, B and C) but more importantly when the posterior centrosome was positioned more anteriorly (Fig. 3, C and D). This was consistent with model predictions (Fig. 5 A, dashed blue line) and expected because oscillation die down depended on time control (Fig. 3 A). Secondly and in contrast, we decreased the number of active force generators at the cortex by gpr-1/2(RNAi) and measured a precocious oscillation die down (Fig. 5 D), whereas oscillation onset position was unchanged (Fig. S2 C). This result was predicted by the model, disregarding whether we modeled the decrease in active force generators through their number (11, 15) or their on-rate binding to microtubules (14) (Fig. 5 A, chain and continuous thin blue lines, respectively). Overall, the full-expanded model correctly accounted for phenotypes resulting from perturbations affecting a player either related to the positional module or the time module (Fig. 3 A). Interestingly, the resulting phenotype was affecting mostly either the posterior centrosome position at oscillation onset or the timing of oscillation die down but not both, suggesting some independence of the two pathways, likely caused by the different players involved in each regulation. This dual regulation calls for a re-examining of how the final position of the spindle is set, superseding the initial model, in which we proposed that only the force generator number and dynamics contributed (16).

LET-99 spatial restriction of active force generators sets the final spindle position

Equipped with the full-expanded model grounded on the analysis of oscillation onset, we used it to investigate the mechanism connecting the cortical polarity through its downstream effector LET-99 to the final centrosome positions. Indeed, the final positions of both the spindle poles and center set the position of the cytokinesis furrow (8). Their positions depend upon cortical pulling forces, and therefore the positional and temporal controls over these forces were expected to contribute to the robustness of the final spindle position. In contrast, in our initial model, we suggested that the final posterior centrosome position resulted from a balance between the cortical pulling forces and centering forces, the latter being modeled by a spring (16, 34). In a broader take, this is the current paradigm, disregarding the detail of the centering mechanism (9, 53). To investigate final spindle positioning, we simulated the posterior displacement using our full-expanded model (Materials and Methods). We could reproduce the global kinematics of posterior displacement: slow before anaphase, then accelerating afterward (Fig. S3 E), as we previously observed experimentally (34).

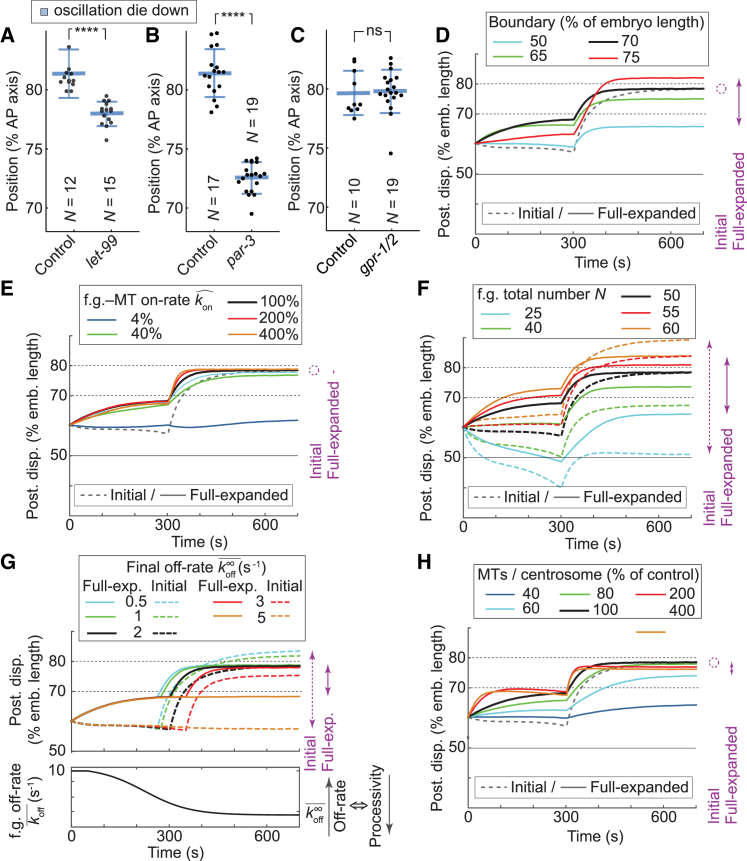
The polarity factor LET-99 sets the boundary of the active region and was proposed to set the final spindle position downstream of polarity (23, 24). We foresaw that the full-expanded model proposed here could recapitulate the mechanism of this control. To test this, we simulated posterior centrosome displacements during mitosis with different boundary positions of the active region and observed that the final position of the posterior centrosome was displaced anteriorly when the boundary of the posterior active crescent moved anteriorly, so long as the region was large enough to initiate posterior displacement in the first place (Fig. 6 D, solid lines). This result was confirmed experimentally in let-99(RNAi)- or par-3(RNAi)-treated embryos (Fig. 6, A and B) and is consistent with previous observations (24). This prediction and our experimental observations differed from the initial model ones, which stated that under similar cortical forces, the posterior displacement would be the same disregarding the cortical distribution of the force generators (Fig. 6 D, dashed line).

Figure 6.

Active region boundary position sets the final spindle position. (A–C) Posterior centrosome position at oscillation die down (A and B) upon anteriorly extending the active region (A) by let-99(RNAi) (N = 15 embryos) compared to control (N = 12 embryos) or (B) by par-3(RNAi) (N = 19) compared to control (N = 17) and (C) upon decreasing cortical force generation by gpr-1/2(RNAi) (N = 19) compared to control (N = 10) embryos. In all cases, centrosomes were labeled by GFP::γ-tubulin. Bee swarm plots report values obtained for each embryo. Large thick horizontal bars depict the mean, whereas error bars indicate SD and asterisks indicate significant differences (Materials and Methods). (D–H) Posterior displacement of the posterior centrosome averaged over 25 simulation runs with parameters varied as follows: (D) the position of the boundary of the active region; (E) the binding rate (on-rate) of the force generators to the microtubules $\widehat{k_{on}}$, whose asymmetry may encode the polarity (14); (F) the total number of active force generators available at the posterior active region N (active, i.e., currently pulling or ready to do so when meeting a microtubule); (G) the force generator final detachment rate (off-rate, the inverse of the processivity) $\overline{k_{off}^{\infty }}$; and (H) the number of microtubules emanating from each centrosome (in % of control, which has M = 3000 microtubules per centrosome). When it does not depend on the parameter considered, the initial model is shown by a dashed gray line. In all cases, the control values are black, lower values are blue and green, and the higher values are red and orange. The dispersions of the final values for each case are represented on the right side of the plots by purple arrows in dashed or solid lines according to the model used. There, a large span reveals a lack of robustness to parameter variations, whereas a circle is used when the parameter has no effect on the final value.

LET-99 may act either by concentrating force generators in the posterior active region or by spatially restricting them to a posterior-most crescent. To decide between these mechanisms, we tested how sensitive the centrosome final position was with respect to the precise final count or dynamics of the force generators. In particular, we investigated the impact of the total number of force generators available (Fig. 6 F), of their final detachment rate (off-rate) that reflected the time/mitotic progression control (Fig. 6 G), and of their binding rate to microtubules (on-rate), which was recently suggested to reflect polarity (14) (Fig. 6 E). In this latter case, we scaled the on-rate up or down in similar ways on both the anterior and posterior. Our time simulations of posterior centrosome displacement suggested a reduced dependency on force generator characteristics, in contrast with the initial model, provided that a threshold force was reached to enable posterior displacement. Experimentally, we observed that a hypomorphic gpr1/-2(RNAi) induced a partial reduction of the cortical forces (11, 15) and caused no significant shift in final spindle position (Fig. 6 C). This robustness of the full-expanded model was attributed to a smaller increase in cortical pulling forces after crossing the boundary position of the active region (Fig. S3 D) because the increasing processivity was tempered by a saturation of microtubule contact count in mid-anaphase. Along the same line, the force generator final processivity was likely disturbed in such-1(h1960), the mutant with delayed anaphase onset (18), and as predicted, the final position of the posterior centrosome was conserved (Table 1).

Microtubules are key players in our positional mechanism and are proposed to contribute to anaphase oscillation through a modulation of their cortical contact counts (19). We thus wondered how important the total number of microtubules was in setting the final spindle position. We simulated posterior centrosome displacements with a scaling down of microtubule number and observed that above a microtubule count threshold needed for posterior displacement, their precise number was again unimportant (Fig. 6 H). Consistently, we found no strong alteration of posterior centrosome final position upon partially depleting SPD-2 when compared to the shift measured in its position at oscillation onset (Table 1). Interestingly, we also observed an optimal value in microtubule count to maximize the posterior displacement (Fig. 6 H, red and green curves below the black one). We overall conclude that the proposed mechanism, in which the distribution of force generators is spatially restricted to the posterior-most crescent, perfectly accounts for the connection between the LET-99 band and the final position of the posterior centrosome and consequently of the spindle (Fig. 3 A, yellow). Furthermore, it also suggests that this position is resistant to modest changes in the parameters related to microtubules or force generators as long as they reach threshold values needed for posterior displacement of the spindle.

Discussion

We measured the spatial distribution of microtubule contacts at the cell cortex and found it uneven, with higher concentrations of microtubule contacts in the regions closest to the centrosomes. As a direct consequence and in combination with the restriction of cortical pulling force generation to a posterior-most crescent (24), the number of microtubules available to cortical force generators displayed a strong increase linked to the posterior spindle displacement, with a switch-like behavior. This in turn made the cortical pulling forces dependent on the position of the centrosomes. Thus, astral microtubule dynamics create a positional control over pulling forces, especially over their burst at anaphase onset, revealed by spindle oscillations. We quantitatively recapitulated this, to our knowledge, novel regulation into an expanding of our initial model of spindle oscillation and posterior displacement (16). This positional regulation superimposes firstly to the force imbalance, reflecting polarity and essential for the spindle to be displaced posteriorly (11, 15, 54), and secondly to the temporal control related to mitotic progression (18), which sets the velocity of displacement and consequently its duration. In this respect, in C. briggsae, we observed lower amplitude oscillation and a 30-s delay in posterior centrosome reaching 70% of embryo length (13).

The various aspects of the regulation of pulling forces during the first division of the C. elegans embryo—namely, temporal, positional, and polarity related—have been investigated independently using modeling, whereas here, in contrast, we have recapitulated these regulations in a single model. Although built on these previous results, our proposed model displays differences, and we discuss these with respect to four important aspects. 1) Our model is an expansion of our previous temporal regulation focused model (16). In both cases, the positive feedback needed to permit oscillations was due to the load-dependent detachment rate and force-velocity relation undergone by the force generators. It results in a larger persistence of force generator pulling on the microtubule as the centrosome gets closer to the “winning side” of the cortex. In contrast, Kozlowski et al. suggested a positive feedback mostly due to the inability of the microtubules to reach the “losing side” of the cortex (19). Both mechanisms may supplement each other, although we did not observe a variation of the microtubule contacts on the timescale of oscillations and therefore favored the positive feedback due to force generator dynamics. 2) In our model, the limited accessibility of microtubules to the cortex rather contributes to the positional regulation. Importantly, although we share a similar law for microtubule accessibility to the cortex with Kozlowski’s model, we supplemented this regulation with the temporal one—a novel feature. We showed in particular that both temporal and positional aspects play an independent role in regulation. This is also a distinctive feature from the model proposed by Kimura and Onami, in which the release of the repression of half of the posterior force generators needed to ensure the imbalance of the number of active force generators is suggested to be under mitotic progression, i.e., time control (55). In our case, the limit of the number of engaged force generators is released by the posterior displacement of the spindle making more microtubules contact the cortex, thus exerting a positional control. By doing so, our model well accounts for the delayed oscillation when the embryos are larger, as seen, e.g., in C. briggsae. A temporal regulation would instead produce oscillations at the same time as in normal-length embryos and therefore more anteriorly. 3) In contrast with the proposed model in which the final position of the spindle mainly reflects the extent of the region devoid from LET-99, it was previously proposed to result from the balance of centering forces modeled in various fashions and cortical pulling. This latter case requires precise tuning of these forces to ensure a correct and reproducible final position of the spindle (9). This means that the mechanism centering the spindle and the related cell geometry contribute substantially to determining the final spindle position. In particular, a dependence of pulling forces on the spindle eccentricity was previously proposed (56) combining similar aspects to ours, namely the three-dimensional modeling of astral microtubules isotopically emanating from the centrosome and contacting the cortex in which a limited number of active force generators are present. However, because Grill and co-workers assumed that microtubules are always abundant at the cortex, contrasting with our density measurements during metaphase, it creates a force contributing to center the spindle (53, 56). Interestingly, such a phenomenon is present in our model and likely contributes to limiting the posterior displacement when the spindle is posterior enough, thus microtubules being abundant at the cortex. It may account for the robust final positioning despite modest variations in the number of microtubules or force generators. But beyond that, we here propose an original robust mechanism ensuring a faithful positioning with respect to cortical polarity cues through LET-99 (24), requiring a minimal number of active forces generators but no tight regulation beyond that threshold. As a result, it accounts for a reduced dependency on the centering force (Fig. S9 B). 4) Finally, in our modeling, we have assumed an end-on attachment of the microtubules at the cortex as it corresponded to our and previous observations (19, 57). Indeed, side-on attachment was proposed to contribute to pronuclei centering before mitosis (58) and was also observed during telophase. However, the spindle displacement ends earlier than this switch in microtubule attachment. In conclusion, our model stands on and expands previous ones, altering the assumptions when experiments suggest to.

The identified dual regulation of the cortical pulling forces perfectly accounts for the robustness of the final spindle positioning. We prove that restricting spatially force generation to a posterior-most crescent is key, whereas the precise level of active force generators or microtubule contacts at the cortex is of lower importance. By precise level, we mean that minimal numbers of microtubules and active force generators are required to ensure posterior displacement, but beyond that constraint, the values do not need to be finely tuned, and modest variations can be buffered. Understanding robustness by accounting for a spatial distribution and regulation of force generation is in its principle similar to the contribution of both the asymmetric microtubule array and a LET-99 band to force regulation during centration and orientation of the pronuclei-centrosome complex (59). Indeed, we propose here that the mechanism linking the LET-99 domain and final spindle position relies on spatial restriction of active force generators to a posterior-most crescent. In contrast, and because the final spindle position is robust to modest variations of active force generator count, it is unlikely that LET-99 acts by concentrating the force generators in the posterior-most crescent. The imbalance in force generator number, reflecting GPR-1/2 posterior concentration (12, 13), is likely unrelated to the LET-99 band. Consistently, an extra shift of final spindle positioning toward the anterior pole was observed previously upon treating a let-99(or81) mutant with gpr-1/2(RNAi) (60).

The positional control of cortical pulling forces also contributes to ensuring the correct positioning of the cytokinesis cleavage furrow, essential for the correct distribution of cell fate determinants (1, 2, 5). Indeed, in late mitosis, furrow position is signaled by two parallel pathways: firstly, by the spindle poles through astral microtubules, and secondly by the central spindle (61). For the latter, the signaling comes from the central spindle position when the spindle has reached its full elongation, which is controlled by the microtubule pulling forces (62). Overall, by regulating the position of the posterior centrosome and where the pulling-force-burst that causes elongation occurs, the proposed mechanism, based on microtubule network sensing cell geometry, contributes to robustness in the cleavage furrow positioning.

Quantitative genetic studies in C. elegans have found an approximately threefold lower persistence of new mutations on the phenotypic trait positioning the division plane compared to the trait displaying the time between first oscillation peak and mid-elongation (52). We here measured the related parameter, duration of oscillations. As explained above, peak amplitude corresponds to the return-to-stability in our diagram (Fig. 5 A) and behaves similarly to oscillation die down. We found final spindle position with a reduced dependency on variations in force generator number and dynamics compared to oscillation timings, as reported by, e.g., oscillation duration. This is consistent with the proposed robustness mechanism de-correlating the final spindle position, likely essential to viability, from timings that appear less evolutionarily constrained. Along the same line, we recently performed a comparative study between two nematode cousins (C. elegans and C. briggsae) (13). Because of a duplication of the regulators of force generators in C. elegans—GPR-1 and GPR-2—whereas C. briggsae only displays GPR-2, the pulling force regulation is altered, leading to a delay in posterior displacement in the latter species. Here, the posterior centrosome arriving at 70% of the AP axis is delayed by 30 s and so is the oscillation onset, both with respect to anaphase onset. In contrast, the oscillation die-down timing is correlated with that of anaphase onset in both species. Our dual controls, position and time, perfectly account for the buffering of timing differences in centrosome kinematics to ensure robust oscillation-onset positions and similar final spindle positioning in both species. The evolution of the essential gpr genes between C. elegans and C. briggsae was likely made possible by the positional control and the resulting resistance to variations in force generator quantity and dynamics. Interestingly, cross-species insertion of gpr genes modulates oscillation amplitude but preserves the positional control, which is consistent with our gpr-1/2(RNAi) experiment (13). The robustness of final spindle positioning is therefore likely to be true in more than just these two species.

Finally, the observed positional switch is caused by astral microtubules and more precisely by the number of microtubule cortical contacts, which reflects the distance between the centrosome and the cortex. Indeed, said distance is measured in “units of microtubule dynamics.” Astral microtubules provide feedback about the posterior centrosome position to the cortical pulling forces, which suggests the existence of a mechanosensing pathway. Such a property already enables classic mechanisms for creating centering (41, 63) or other shape-dependent regulation (42, 64, 65). However, such mechanisms were mostly inferred from cell-level measurements. In contrast, here the distribution of the microtubule-end contacts located at the cortex was obtained from microscopic measurements. We observed a density ratio of approximately two between the regions with the most and least microtubule contacts at a given time, and this ratio represents the sensitivity to centrosomal position. From a theoretical point of view, considering the ellipsoidal shape of the C. elegans embryo and the microtubule dynamics measurements performed elsewhere, the predicted maximal ratio is 1.64 (Supporting Materials and Methods). Our experimental result is close to this prediction, suggesting that the microtubule dynamics parameters are optimal for the positional control that we discussed here.

Conclusions

This study of pulling force regulation by the mitotic spindle position was grounded in modeling and experimentally studying the microtubules at microscopic and cell scales. This was supplemented by investigating the precise timing of transverse oscillation onset with respect to anaphase onset and posterior centrosome positioning at that moment in the C. elegans embryo. It has highlighted the key role of microtubule dynamics in probing the boundary of the active force generator region. In particular, microtubules create a positional control on spindle oscillations, which acts in addition to the previously described regulation by pulling force generator dynamics (temporal control). Both controls contribute independently to the switch to prevent premature pulling force burst. The finding of this supplementary positional control paves the way to a novel understanding of the mitosis choreography mechanism, supplementing the regulation by the cell cycle.

In particular, our proposed positional control connects the final spindle position to cortical polarity cues. Indeed, LET-99 spatially restricts the force generators to a posterior-most crescent, and in turn, microtubule dynamics read out the boundary of this region to properly position the centrosomes and thus the spindle at the end of mitosis. Interestingly, it also makes this position resistant to modest variations in microtubule quantity or in force generator dynamics or number provided that these are above the required thresholds, guaranteeing correct cytokinesis furrow positioning and consequently a proper distribution of cell fate determinants (3, 4). Such robustness buffered changes in cortical pulling force levels and timings between the C. elegans and C. briggsae nematodes and permitted substantial modifications in the essential gpr-1/2^LGN genes, whose proteins are part of the complex that generates cortical pulling forces (13). Finally, the observed positional switch is caused by astral microtubules. They provide feedback about the posterior centrosome position with respect to the posterior-most crescent boundary through the cortical pulling forces, suggesting the existence of a mechanosensing pathway. This finding is a novel example of a microfilament-based system that controls essential aspects of cell division. In contrast with robustness resulting from classic biochemical signaling pathways (66, 67), this mechanism is based solely on cell mechanics and component dynamics.

Author Contributions

Conceptualization, J.P., H.B., and M.D.; methodology, H.B., L.C., and J.P.; software, J.P. and H.B.; validation/formal analysis, H.B., J.P., S.P., and L.C.; investigations/data curation, H.B., S.P., L.C., D.F., and J.P.; writing—original draft, H.B. and J.P.; writing—review and editing, H.B., L.C., M.D., D.F., and J.P.; supervision, J.P.

Editor: Jason Swedlow.

Supporting Citations

References (68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84) appear in the Supporting Material.