Abstract
Transcriptome measurements of individual cells reflect unexplored biological diversity, but are also affected by technical noise and bias. This raises the need to model and account for the resulting uncertainty in any downstream analysis. Here, we introduce Single-cell Variational Inference (scVI), a scalable framework for probabilistic representation and analysis of gene expression in single cells. scVI uses stochastic optimization and deep neural networks to aggregate information across similar cells and genes and approximate the distributions that underlie the observed expression values, while accounting for batch effects and limited sensitivity. We utilize scVI for a range of fundamental analysis tasks – including batch correction, visualization, clustering and differential expression – and demonstrate its accuracy and scalability in comparison to the state-of-the-art in each task. scVI is publicly available and can be readily used as a principled and inclusive solution for analyzing single-cell transcriptomes.
Introduction
The ability to map single cell transcriptomes en-mass with single-cell RNA sequencing (scRNA-seq) provides a powerful tool, which is beginning to make important contributions to diverse research areas such as development [1], autoimmunity [2], and cancer [3]. Interpreting scRNA-seq remains challenging, however, as the data is confounded by nuisance factors such as limited [4] and variable [5] sensitivity, batch effects [6] and transcriptional noise [7].
The challenge of modeling bias and uncertainty in single-cell data has been explored in several recent studies, where a common theme is treating each data point (cell × gene) as a random variable for which a probabilistic model is fit [8, 9, 10]. The parameters of these models are determined by a combination of cell- and gene-level coefficients (and in some cases additional metadata such as library depth [10]), thus providing a representation of the data in a lower and potentially less noisy dimension. Once these models have been fit, they can then in principle be used for various tasks such as clustering [11], imputation [12] or differential expression [13]. A complementary line of studies focuses on only one of these tasks, in some cases without explicit probabilistic modeling.
While these methods helped gain new insights into the meaning of biological variation between cells, several limitations remain. First, the existing distributional modeling methods assume that a low-dimensional manifold underlies the data, and that the mapping into this manifold can be captured by a generalized linear model. While the notion of a restricted dimensionality is plausible (e.g., reflecting common regulatory mechanisms among genes or common states among cells), it is difficult to justify the assumption of linearity. Second, different existing methods utilize their models to perform different subsets of tasks (e.g., imputation and clustering, but not differential expression [8]). Ideally, one would have a single distributional model that can be used for a range of downstream tasks, thus help ensuring consistency and interpretability. Finally, computational scalability is increasingly important. While most existing methods can be applied to no more than tens of thousands of cells, the next generation of tools must scale to the size of recent data sets that consist of hundreds of thousands of cells or more [14].
To address these limitations, we developed a fully probabilistic approach for normalization and downstream analysis of scRNA-seq data, which we refer to as Single-cell Variational Inference (scVI). scVI is based on a hierarchical Bayesian model [15] with conditional distributions specified by deep neural networks, which can be trained very efficiently even for very large datasets. The transcriptome of each cell is encoded through a non-linear transformation into a low-dimensional latent vector of normal random variables. This latent representation is then decoded by another non-linear transformation to generate a posterior estimate of the distributional parameters of each gene in each cell, assuming a zero-inflated negative binomial distribution, which accounts for the observed over-dispersion and limited sensitivity [10, 16, 17]. Independent of our work, several recent manuscripts have also demonstrated the utility of using neural networks to embed scRNA-seq datasets in a scalable manner [18, 19, 20, 21]. scVI stands out from these methods in two important ways (Online Methods, Supplementary Note 1, Supplementary Table 1). First, it is the only method that explicitly models the two key nuisance factors in scRNA-seq data, namely library size [8, 22] and batch effects [10, 23]. Second, scVI is the only method that offers readily available solutions for a range of analysis tasks using the same generative model. In the following, we demonstrate this property, focusing on batch removal and normalization, dimensionality reduction and clustering, and differential expression. For each of these tasks, we show that scVI compares favorably to the current state-of-the-art methods.
Results
The scVI model: definition and preliminary evaluation
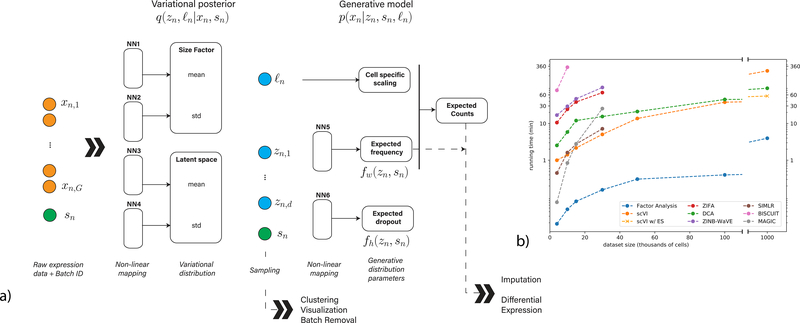
We model the observed expression xng of each gene g in each cell n as a sample drawn from a conditional distribution that has a zero-inflated negative binomial (ZINB) form [10, 16, 17] (Online Methods). The distribution is conditioned on the batch annotation bn of each cell (if available), as well as two additional, unobserved random variables. The first variable ℓn is a one-dimensional Gaussian that represents nuisance variation due to differences in capture efficiency and sequencing depth, serving as a cell-specific scaling factor. The second variable zn is a low dimensional vector of Gaussians (set here to 10 dimensions; see Supplementary Figure 1) representing the remaining variation, which should better reflect biological differences between cells [24]. We use it to represent each cell as a point in a low dimensional latent space, serving for visualization and clustering. We learn the distribution of these latent variables q(zn,logℓn|xn,sn), by training a neural network that approximates their posterior using variational inference and a scalable stochastic optimization procedure [25, 26, 27] (Figure 1a, NN1–4). The second part of our model consists of another neural network that generates a posterior ZINB distribution of the data p(xng|zn,sn,ℓn) from the latent variables (Figure 1a, NN5–6). This generative scheme consists of intermediate values , which provide a batch-corrected, normalized estimate of the percentage of transcripts in each cell n that originate from each gene g. We use the matrix ρ for differential expression analysis and its scaled version (multiplying by the estimated library size ℓn) for imputation. In the following sections we evaluate scVI using a collection of published datasets, spanning a range of technical and biological characteristics. These datasets are listed in Supplementary Table 2 and described in the Online Methods section.
Figure 1:
Overview of scVI. Given a gene-expression matrix with batch annotations as input, scVI learns a non-linear embedding of the cells that can be used for multiple analysis tasks. (a) The computational trees (neural networks) used to compute the embedding as well as the distribution of gene expression. (b) Comparison of running times (y-axis) on the BRAIN-LARGE data with a limited set of 720 genes, and with increasing input sizes (x-axis; cells in each input set are sampled randomly from the complete dataset). All the algorithms were tested on a machine with one eight-core Intel i7–6820HQ CPU addressing 32 GB RAM, and one NVIDIA Tesla K80 (GK210GL) GPU addressing 24 GB RAM. scVI is compared against existing methods for dimensionality reduction in the scRNA-seq literature. As a control, we also add basic matrix factorization with factor analysis (FA). For the one-million-cell dataset only, we report the result of scVI with and without early stopping (ES).
To evaluate the scalability of our training procedure, we use a data set of 1.3 million mouse brain cells provided by 10x [28] (BRAIN-LARGE) and record the time required to fit the model for increasing numbers of randomly sampled cells. To facilitate comparison to state-of-the-art algorithms for probabilistic modeling and dimensionality reduction of single cell data [8, 9, 10, 11, 12] which may be less scalable, we limited this analysis to the 720 genes with largest standard deviation across all cells and report results in Figure 1b. We find that most methods are capable of processing up to 50K cells before running out of memory (using 32Gb RAM). Conversely, we find that scVI is generally faster and capable of scaling to the full range of our tests (1M cells), thanks to its reliance on iterative stochastic optimization, where one only uses a fixed number of cells at each iteration (Online Methods). We also observe similar levels of scalability with DCA [20] a denoising auto-encoder, which also uses stochastic optimization. Notably, as the dataset size reaches one million cells, fewer training iterations (or epochs) are needed and heuristics for stopping the learning process may save time. Indeed, we observe that the standard scVI (which uses a fixed number of epochs) is slower than DCA (which uses the stopping heuristic by default) in this case, however, turning the early- stopping option on makes scVI substantially faster (trained in less than an hour), and fit the data as well a run with no early stopping (Supplementary Figure 2).
Next, we evaluated the extent to which scVI and the benchmark methods fit the data by assessing their ability to accurately impute missing data. We used five data sets of different sizes (3– 27k cells; see Supplementary Table 2; [28, 29, 30, 31, 32]; BRAIN-LARGE, CORTEX, PBMC, RETINA, HEMATO), where in each case we set 9% of the non-zero entries (chosen entirely randomly in Supplementary Figures 3 and 4, or preferring low values in Supplementary Figures 5 and 6) to zero and then test the ability of each benchmark method to recapitulate their values. Overall, we observe that in most cases methods that are based on a ZINB distribution, namely scVI, DCA and ZINB-WaVE (when it scales to the dataset size) perform better than ones that use alternative strategies [8, 12] (e.g., log normal [9] in ZIFA), thus supporting the notion that ZINB is appropriate for current scRNA-seq datasets. One important exception where MAGIC [12] (which imputes using propagation in a cell-cell similarity graph) outperformed scVI occurred with a dataset of hematopoietic differentiation [32] (HEMATO), in which the number of cells (4,016) is smaller than the number of genes (7,397). In such cases, scVI is expected to under-fit the data, potentially leading to worse imputation accuracy. However, additional gene filtering (to the top 700 variable genes) helped regaining a more accurate imputation (Supplementary Figure 3c). An alternative way to evaluate model fit is by testing the likelihood of data that was held-out during training. Using this procedure yields consistent results as above (Supplementary Figure 7, Supplementary Table 3). Furthermore, scVI, like ZIFA and FA, can also be used to generate unseen data by sampling from the latent space. As evidence of the validity of this procedure, we sampled from the posterior distribution given the perturbed training data and observed that the samples are largely consistent with the unperturbed data (Supplementary Figure 8).
Capturing biological structure in a latent low-dimensional space
We next turned to evaluate the extent to which the latent space inferred by scVI reflects biological variability between cells. One way to assess this is to rely on prior stratification of the cells into biologically meaningful sub-populations, which is normally done by unsupervised clustering followed by manual inspection and annotation [29, 30]. We evaluate the accuracy with respect to these stratifications (available in two of our reference data sets [29, 30]; CORTEX, PBMC) by either applying k-means clustering on the latent space and testing for the overlap with the annotated sub-populations (using the same k as in the annotated data), or by comparing between the proximity of cells in the same sub-population to the proximity of cells from different sub-populations (Online Methods). A data set provided by Stoeckius et al. [33] (CBMC), which includes single- cell protein measurements in addition to mRNA provides an alternative way for using computationally- derived annotations as a gold standard. Here, we evaluate the extent to which the similarity between cells in the mRNA latent space resembles their similarity at the protein level (Online Methods).
Overall in these tests, we find that scVI is capable of grouping together cells that are from the same annotated sub-population or that express similar proteins and that it compares favorably to other methods that aim to infer a biologically meaningful latent space (namely, ZIFA [9], ZINB-WaVE [10], DCA [20] and factor analysis; Supplementary Figure 9). Notably, we also included in this test a simpler version of scVI that does not explicitly models the library size. We observed that this simpler variant does not perform as well as the standard scVI, thus supporting our modeling choice.
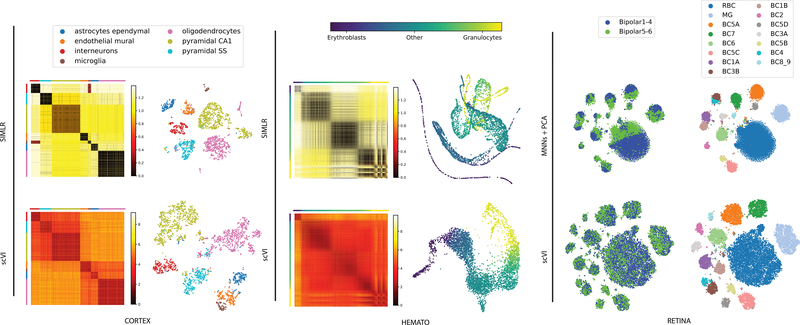
Next, we benchmark scVI with SIMLR [11], a method that couples clustering with learning a cell-cell similarity matrix and a respective low dimensional (latent) representation. We observed that SIMLR provides a tighter representation of the computationally annotated subpopulations and that it outperforms scVI in this test. This result is expected since SIMLR explicitly aims to produce a tight representation of the data in a target number of clusters. However, as a consequence, SIMLR may not capture structural properties of the cell-cell similarity map that are of higher resolution. Indeed, in the protein vs. mRNA metric similarity test, scVI and DCA are the best performing methods, albeit by a small margin (Supplementary Figure 9c). Another example is the possibility of a hierarchical structure among cell subsets, such as the one reported for cortical cells by Zeisel and colleagues [29] (CORTEX). In this case, we find that overall scVI captures this hierarchy more accurately, whereby cells from related sub-populations tend to be closer to each other in its latent space (Supplementary Figure 9efg). An additional important case occurs when the variation between cells has a continuous, rather than discrete, form. An example for this case was studied by Tusi and colleagues who profiled a set of hematopoietic cells, spanning various stages of differentiation [32] (HEMATO). Here we find that SIMLR identifies several discrete clusters, and does not reflect the continuous nature of this system as well as scVI or PCA (Figure 2, Supplementary Figure 10). Finally, there may be the case of lack of structure, where the data is almost entirely dominated by noise. To explore this scenario, we generated a noise dataset, sampled at random from a vector of zero-inflated negative binomial distributions. In this case, SIMLR erroneously reports eleven distinct clusters, which are not perceived by other methods (Supplementary Figure 11). Altogether, these results suggest that the latent space of scVI is flexible and describes the data well, either as a hierarchy of discrete clusters, as a continuum between cell state, or as structureless noise and is therefore better suited than SIMLR in scenarios where the data does not necessarily fit with a simple structure of discrete cell states.
Figure 2:
Biological signal retained by the latent space of scVI. scVI is applied to three datasets (from right to left: CORTEX n = 3,005 cells, HEMATO n = 4,016 cells and RETINA n = 27,499 cells). For CORTEX and HEMATO, we compare scVI with SIMLR and show a distance matrix in the latent space, as well as a two-dimensional embedding of the cells. Distance matrices: the scales are in relative units from low to high similarity (over the range of values in the entire matrix). Cells in the matrices are grouped by their pre-annotated labels, provided by the original studies (for the CORTEX dataset, cell subsets were ordered using hierarchical clustering as in the original study). Embedding plots: each point represents a cell and the layout is determined either by tSNE for CORTEX or by a 5-nearest neighbors graph visualized using a Fruchterman-Reingold force-directed algorithm for HEMATO; see Supplementary Figure 10d for the original embedding for SIMLR. Color scheme in the embeddings is the same as in the distance matrices. For the RETINA dataset, we compare scVI with MNNs followed by PCA. Embedding plots were generated by applying tSNE on the respective latent space. On the left, the cells are colored by batch. On the right, cells are colored by the annotation of subpopulations, provided in the original study [31].
Accounting for technical variability
scVI provides a parametric distribution designed to decouple the biological signal from the effects of sample- level categorial nuisance factors (e.g., representing batch annotations) and variation in sequencing depth. To evaluate the capacity of scVI to correct batch effects, we used a dataset of mouse retinal bipolar neurons that consists of two batches [31] (RETINA). We defined an entropy measure to evaluate the mixing of cells from different batches in any local neighborhood of the latent space (abstracted using k-nearest neighbor graph; see Online Methods). We compare our method to ComBat [34] - a standard pipeline of batch correction relying on linear models and empirical Bayes shrinkage, and a recent method based on matching mutual nearest neighbors [35] (Online Methods).
Our results (Figure 2, Supplementary Figures 9d and 12) demonstrate that in this dataset scVI aligns the batches significantly better than ComBat and MNNs, while still maintaining a tight representation of pre-annotated subpopulations. Considering algorithms that do not account for batch effects in their models we find, as expected, that the resulting mixing of the batches is poor. Specifically, while SIMLR and DCA are capable of clustering the cells well within each batch, the respective clusters from each batch remain largely separated. Similar results were obtained when applying a simplified version of scVI with no batch variable, thus supporting our modeling choice.
Turning to confounding due to variation in sequencing depth, we find as expected, that in relatively homogenous populations (taking sub-populations of cortical cells [28], BRAIN-SMALL or PBMC [30]) the library size factor inferred by scVI (ℓn) strongly correlates with the observed depth per cell (Supplementary Figure 13a). A related technical issue that can distort the simmilarity between cells in these sub-populations is the lack of sensitivity, due to limitations in mRNA capture efficiency and to a leser extent sequencing depth, resulting in an exacerbated amount of zero entries. Interestingly, we find that most of the zero entires in the data can be explained by the negative binomial component (Supplementary Figure 14ab) rather than the “inflation” of unexplained zeros added to it with a Bernoulli distribution. Consistently, we find that the occurence of zeros entries in is largely consistent with a random process of sampling genes from each cell in manner proportional to their expected frequency (as inferred in the the matrix ρ of our model, which is proportional to the negative binomial mean) and with no additional bias (Supplementary Figure 13b and Supplementary Note 2). Indeed, we show that the zero probability from the negative binomial distribution correlates more with cell-specific quality factors that are related to library size (e.g., number of reads per UMI) while the zero probabilities from the Bernouilli correlates more with quality factors indicative of alignment errors (Supplementary Figure 13cd and 14cd) , possibly indicative of contamination or mRNA degradation. Taken together, these results corroborate the idea that most zeros, at least in the datasets explored here, can be explained by low (or zero) “biological” abundance of the respective transcript, exacerbated by limited sampling.
Differential expression
With its probabilistic representation of the data, scVI provides a natural way of performing various types of hypotheses testing, while intrinsically controlling for nuisance factors. In the case of differential expression between two sets of cells, we can use the model to approximate the posterior probability of the alternative hypotheses (genes are different) and that of the null hypotheses by repeated sampling from our variational distribution, thus obtaining a low variance estimate of their ratio (i.e., Bayes factor [36, 37]; see Online Methods).
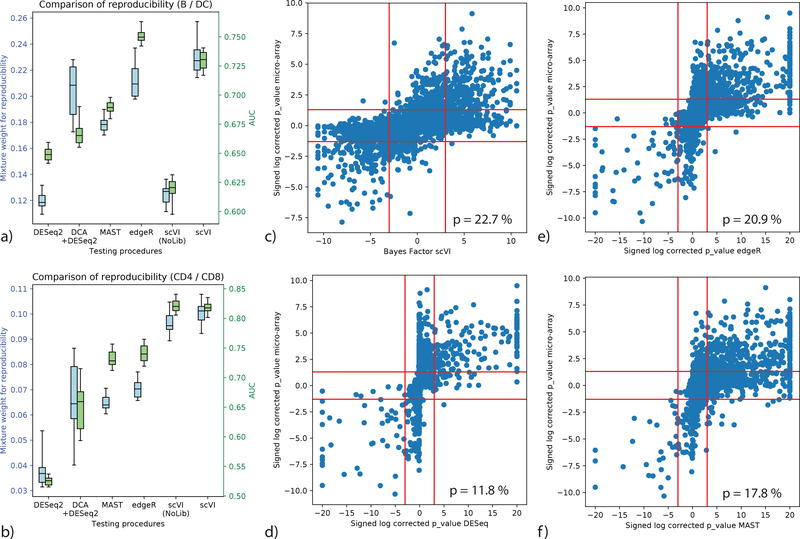
To evaluate scVI against other methods [13, 17, 20, 38] for differential expression, we used a dataset of 12,039 PBMCs from a healthy human donor [30] (PBMC) and looked for differentially expressed genes in two settings: comparing the clusters of B cells vs. dendritic cells, and similarly for the CD4+ vs. CD8+ T cell clusters. As ground truth, we used published bulk- level comparative analysis of similar cell subsets [39, 40]. For evaluation, we first defined genes as true positives if their BH-adjusted p-values in the bulk data was under 0.05 and then calculated the area under the ROC curve (AUROC) based on the Bayes factor (for scVI) or BH-corrected p-value (for the benchmark methods). Since defining true positives requires a somewhat arbitrary threshold, we also used a second score that evaluates the reproducibility of gene ranking (bulk reference vs. single cell; considering all genes), using the irreproducible discovery rate (IDR) [41]. Considering the AUROC metric, scVI is the best performing method in the T cell comparison, while edgeR outperforms scVI by a smaller margin in the B vs. dendritic cell comparison. Considering the proportion of genes with reproducible rank as fitted by IDR, scVI is the best performing method in both comparisons (Figure 3, Supplementary Figure 15a-e). Interestingly, we see that the hybrid method of DCA followed by DESeq2 constitutes a solid improvement over a direct application of DESeq2, which was designed with bulk data in mind, thus supporting the need of using models adapted for single cell data. Furthermore, a simpler variant of scVI that does not include the library size factor shows extremely poor performance on the B vs. dendritic cell comparison, being the only model that does not explicitly handle normalization. This is evidence of the usefulness of explicitly including library size normalization in the scVI model.
Figure 3:
Benchmark of differential expression analysis using the PBMC dataset (n = 12,039 cells), based on consistency with published bulk data. (a, b) Evaluation of consistency with the irreproducible discovery rate (IDR) [41] framework (blue) and using AUROC (green) is shown for comparisons of B cells vs Dendritic cells (a) and CD4 vs CD8 T cells (b). Error bars are obtained by sub-sampling a hundred cell from each clusters n = 20 times to show robustness. Box plots indicate the median (center lines), interquantile range (hinges) and 5–95th percentiles (whiskers). (c,d,e,f): correlation of significance levels of differential expression of B cells vs Dendritic cells, comparing bulk data and single cell. Points are individual genes (n = 3,346). Bayes factors or BH-corrected p-values on scRNA-seq data are presented on the x-axis; microarray-based BH-corrected p-values are depicted on the y-axis. Horizontal bars denote significance threshold of 0.05 for corrected p-values. Vertical bars denote significance threshold for the Bayes factor of scVI (c) or 0.05 for corrected p-values for DESeq2 (d), edgeR (e), and MAST (f). We also report the median mixture weight for reproducibility p (higher is better).
Discussion
scVI was designed to address an important need in the rapidly evolving field of single cell transcriptomics – namely, accounting for measurement uncertainty and bias in tertiary analysis tasks through a common, scalable statistical model. As such, it provides a computationally efficient and “all-inclusive” tool that couples low-dimensional probabilistic representation of gene expression data with downstream analysis capabilities, comparing favorably to the state-of-the-art methods in each of a range of tasks, including batch-effect correction, imputation, clustering, and differential expression.
scVI takes raw count data as input and includes an effective normalization procedure that is integrated into its model. First, it learns a cell-specific scaling factor as a hidden variable, with the objective of maximizing the likelihood of the data [8, 10, 22], which is more justifiable than a posteriori correction of the observed counts [5]. Second, scVI explicitly accounts for batch annotations, via a mild assumption of conditional independence. We demonstrated that both of these components are essential for the method’s performance. Additional discussion, explaining these and other modeling choices is provided in the Online Methods section.
The deep learning architecture used in scVI is built on several canonical building blocks such as non-linearities, regularization and mean-field approximation to the posterior [25] (Online Methods). Exploring other, possibly better, architectures [42] and procedures for parameter and hyper-parameter tuning [43] may in some instances provide a better model fit and more suitable approximate inference. Notably, since our procedure has a random component, and since it optimizes a non-convex objective function, it may give alternative results with different initializations. To address this, we demonstrate the stability of scVI in terms of its objective function, as well as imputation and clustering (Supplementary Figure 1). Another related issue is that, if there are few observations (cells) for each gene, the prior and the inductive bias of the neural network may keep us from fitting the data closely. Indeed, in cases where the number of cells is smaller than the number of genes, some procedure to pre-filter the genes may be warranted. A complementary approach would make use of techniques such as Bayesian shrinkage [17] or regularization and second order optimization [10]. We do however show that for a range of datasets of varying sizes, scVI is able to fit the data well and capture relevant biological diversity between cells.
Looking ahead, scVI provides a general probabilistic representation of gene expression in single cells and can therefore enable other forms of scRNA-seq analysis that were not explored in this manuscript, such as lineage inference [1] or cell-state annotation [7, 44]. Furthermore, since it only requires the latent space and the specification of the model (which both have a low memory footprint) to generate any data point (cell × gene) of interest, scVI can be used as an effective baseline for scalable and interactive visualization tools [45, 46, 47]. Finally, scVI can be extended to merge multiple datasets from a given tissue while integrating prior biological annotations of cell types. We therefore expect this work to be of immediate interest, especially in cases where dataset harmonization has to be done in a manner that is scalable and conducive to various forms of downstream analysis [14].
Online Methods
The scVI probabilistic model
First, we present in more detail the generative process for scVI. Altogether, each expression value xng is drawn independently through the following process:
A standard multivariate normal prior for z is commonly used in variational autoencoders since it can be reparametrized in a differentiable way into any arbitrary multivariate Gaussian random variable [25], which turns out to be extremely convenient in the inference process.
B denotes the number of batches and parameterize the prior for the scaling factor (on a log scale). ℓμ,ℓσ are set to be the empirical mean and variance of the log-library size per each batch. Let us note that the random variable ℓn is not the log-library size (scaling the sampled observation) itself but a scaling factor that is expected to correlate strongly with log-library size (hence the choice of the parameters). The parameter denotes a gene-specific inverse dispersion, estimated via variational Bayesian inference.
fw and fh are neural networks that map the latent space and batch annotation back to the full dimension of all genes: ℝd × {0,1}B → ℝG. We use superscript annotation (e.g., ) to refer to a single entry that corresponds to a specific gene g. Neural network fw is constrained during the inference to encode the mean proportion of transcripts expressed across all genes by using a softmax activation at the last layer. Namely, for each cell n the sum of values over all genes g is one. Neural network fh encodes whether a particular entry has been dropped out due to technical effects [9, 10]. These intermediate vectors can therefore be interpreted as expected frequencies. Importantly, let us note that neural networks allows us to go beyond the generalized linear model framework and provide a more flexible model of gene expression. All neural networks use dropout regularization and batch normalization. Each network has 1, 2, or 3 fully connected-layers, with 128 or 256 nodes each. The activation functions between two hidden layers are all ReLU. We use a standard link function to parametrize the distribution parameters (exponential, logarithmic or softmax). Weights for some layers are shared between fw and fh.
Fast inference via stochastic optimization
The posterior distribution combines the prior knowledge with information acquired from the data matrix X. We cannot directly apply Bayes rule to determine the posterior because the denominator (the marginal distribution) p(xn|sn) is intractable. Making inference over the whole graphical model is not needed. We can integrate out the latent variables wng,hng and yng since p(xng|zn,ℓn,sn) has a closed-form density. Notably, the distribution p(xng|zn,sn,ℓn) is zero-inflated negative binomial (ZINB) [16] with mean , gene-specific dispersion θg and zero-inflation probability (see Supplementary Note 3). We discuss numerical stability and parametrization of the ZINB distribution in Supplementary Note 4. Having simplified our model, we use variational inference [26] to approximate the posterior p(zn,ℓn|xn,sn). Our variational distribution q(zn,ℓn|xn,sn) is mean-field:
The variational distribution q(zn|xn,sn) is chosen to be Gaussian with a diagonal covariance matrix, mean and covariance given by an encoder network applied to (xn,sn), as in [25]. The variational distribution q(ℓn|xn,sn) is chosen to be log-normal with the scalar mean and variance also given by an encoder network applied to (xn,sn). The variational lower bound is
| (2) |
In this objective function, the dispersion parameters θg for each gene are treated as global variables to optimize in a Variational Bayesian inference fashion.
To optimize the lower bound, we use the analytic expression for p(x|z,l,s) and use analytic expressions for the Kullback-Leibler divergences. We use the reparametrization trick to compute low-variance Monte-Carlo estimates of the expectations’ gradients. Analytic closed-form for the Kullback-Leibler divergence and the reparametrization trick are only possible on certain distributions which multivariate Gaussians are a part of [25]. The reparametrization trick is a specific sampling scheme from the variational distribution which makes our objective function stochastic. Remarkably, this sampling step coupled with neural networks approximation to the posterior is what makes possible to go beyond restrictive “conditional conjugacy” properties often needed to perform sampling or variational inference. This allows us to efficiently perform inference with arbitrary models, including those with conditional distributions specified by neural networks [25].
A second level of stochasticity comes from sub-sampling from the training set (possible since the cells are identically independently distributed when conditioned on the latent variables). We then have an online optimization procedure that can handle massive datasets — used by scVI as well as other methods that exploit neural networks [18, 19, 20, 21]. At each iteration, we focus only on a small subset of the data randomly sampled (M = 128 data points) and do not need to go through the entire dataset. Therefore, there is no need to store the entire dataset in memory. Because the number of genes is in practice limited to a few tens of thousands, these mini-batches of cells fit easily into a GPU. Now, our objective function is continuous and end-to-end differentiable, which allows us to use automatic differentiation operators.
Throughout the paper, we use Adam (a first order stochastic optimizer) with ε = 0.01. As indicated in [27], we use deterministic warmup and batch normalization during learning to learn an expressive model. A complete list of hyperparameters is provided in Supplementary Table2. The hyperparameters were chosen using a small grid search that maximized held-out log likelihood—a common practice for training deep generative models. One of the strengths of scVI is that we have only three dataset-specific hyperparameters to set (learning rate, number of layers, and layer width). We optimize the objective function until convergence –usually between 120 and 250 epochs, where each epoch is a complete pass through the dataset (let us note that bigger datasets require fewer epochs). For the larger subset of the BRAIN-LARGE dataset, we also ran with the early stopping criterion: the algorithm stops after 12 consecutive epochs with no improvement on the validation loss.
Since the encoder network q(z|x,s) might still produce output correlated with the bath s, one could use in principle a Maximum Mean Discrepancy (MMD) based penalty as in [24] to correct the variational distribution. For this paper, however, we did not explicitly enforce the MMD penalty and simply retained the conditional independence property, which has shown to be sufficiently efficient. This may be useful on other datasets though it explicitly assumes the exact same biological signal is present in the datasets.
Bayesian differential expression
For each gene g and pair of cells (za,zb) with observed gene expression (xa,xb) and batch ID (sa,sb), we can formulate two mutually exclusive hypotheses:
where the expectation is taken with the empirical frequencies. Notably, we propose a hypothesis testing that do not to calibrate the data to one batch but will find genes that are consistently differentially expressed. Evaluating which hypothesis is more probable amounts to evaluating a Bayes factor [37] (Bayesian generalization of the p-value). Its sign indicates which of and is more likely. Its magnitude is a significance level and throughout the paper, we consider a Bayes factor as strong evidence in favor of a hypothesis if |K| > 3 [36] (equivalent to an odds ratio of exp(3) ≈ 20).
where the posterior of these models can be approximated via the variational distribution
where p(s) designated the relative abundance of cells in batch s and all of the measures are low-dimensional, so we can use naive Monte Carlo to compute these integrals. We can then use a Bayes factor for the test.
Since we assume that the cells are i.i.d., we can average the Bayes factors across a large set of randomly sampled cell pairs, one from each subpopulation. The average factor will provide an estimate of whether cells from one subpopulation tend to express g at a higher frequency.
We demonstrate the robustness of our method by repeating the entire evaluation process and comparing the results (Figure 3ab). We also ensure that our Bayes factor are well calibrated by running the differential expression analysis across cells from the same cluster and making sure no genes reach the significance threshold (Supplementary Figure 15f).
Modeling choices
In this section, we consider the extent to which each of a sequence of modeling choices in the design of scVI contributes to its performance. As a baseline approach, consider normalizing single-cell RNA sequencing data as in previous literature [9] and reducing the dimensionality of the data using a variational autoencoder with a Gaussian prior and a Gaussian conditional probability.
One way in which a model can be enhanced is by changing the Gaussian conditional probability to one of the many available count distributions, such as zero-inflated negative binomial (ZINB), negative binomial (NB), Poisson or others. Recent work by Eraslan and colleagues using simulated data shows that when the dropout effect drives the signal-to-noise ratio to a less favorable regime, a denoising autoencoder with mean squared error (i.e., Gaussian conditional likelihood) cannot recover cell-types from expression data while an autoencoder with ZINB conditional likelihood can [20]. This results points to the importance of at least modeling the sparsity of the data and is consistent with previous contributions [9, 10].
The next question is which count distribution to use. In scVI we have chosen to use the zero-inflated negative binomial, a choice motivated by previous literature (e.g., [10]). First, the choice of negative binomial is common in RNA-sequencing data, as it is over dispersed [17]. Furthermore, under some assumption this distribution captures the steady state form of the canonical two-state promoter activation model [16]. Finally, recent work by Grønbech and colleagues [21] proposes an analysis based on Bayesian model selection (held-out log-likelihood as in this manuscript). In that analysis, the NB and ZINB distribution stand out with similarly high scores. We demonstrate that the addition of a zero-inflation (Bernoulli) component is important for explaining a subset of the zero values in the data (Supplementary Figure 14) and that it captures important aspects of technical variability which are not captured by the NB component (Supplementary Figure 13).
To enhance the model further, we added terms to account for library-size as a nuisance factor, which can be considered as a Bayesian approach to normalization as in [8, 22]. We showed how this contributes to our model by increasing clustering scores and differential expression analysis accuracy on the PBMC dataset.
As a further enhancement, we designed the generative model to explain data from different experimental batches. This is not a trivial task as there may exist a significant covariate shift between the observed transcript measurements. We showed how this modification to our model is crucial when dealing with batch effects in subsection on the RETINA dataset.
Datasets and preprocessing
Below we describe all of the datasets and the preprocessing steps used in the paper. We focus on relatively large datasets (3k cells and more) with unique molecular identifiers (UMIs), thus providing enough information during training and avoiding the problem of over- counting due to amplification. A star after the dataset name indicates we used it as an auxiliary dataset; these datasets were not used for general benchmarking, but rather to support specific points presented in the paper. The only case where we subsampled the data multiple times was the BRAIN-LARGE dataset. However, we simply used one instance of it to report all possible scores (further details in Supplementary Table 2).
CORTEX
The Mouse Cortex Cells dataset from [29] contains 3005 mouse cortex cells and gold-standard labels for seven distinct cell types. Each cell type corresponds to a cluster to recover (see Supplementary Table 4). We retain the top 558 genes ordered by variance as in [8].
PBMC
We considered scRNA-seq data from two batches of peripheral blood mononuclear cells (PBMCs) from a healthy donor (4K PBMCs and 8K PBMCs) [30]. We derived quality control metrics using the cellrangerRkit R package (v. 1.1.0). Quality metrics were extracted from CellRanger throughout the molecule-specific information file. After filtering as in [23], we extract 12,039 cells with 10,310 sampled genes and generate biologically meaningful clusters with the software Seurat (see Supplementary Table 5). We then filter genes that we could not match with the bulk data used for differential expression to be left with g = 3346.
BRAIN LARGE
This dataset contains 1.3 million brain cells from 10x Genomics [28]. We randomly shuffle the data to get a 1M subset of cells and order genes by variance to retain first 10,000 and then 720 sampled variable genes. This dataset is then sampled multiple times in cells for the runtime and goodness-of-fit analysis. We report imputation scores on the 10k cells and 720 gene samples only.
RETINA
After their original pipeline for filtering, the dataset of bipolar cells from [31] contains 27,499 cells and 13,166 genes from two batches. We use the cluster annotation from 15 cell-types from the author. We also extract their normalized data with Combat and use it for benchmarking.
HEMATO
This dataset with continuous gene expression variations from hematopoeitic progenitor cells [32] contains 4,016 cells and 7,397 genes. We removed the library basal-bm1, which was of poor quality, based on authors recommendation. We use their population balance analysis result as a potential function for differentiation.
CBMC*
This dataset includes 8,617 cord blood mononuclear cells [33] profiled using 10x along with 13 well-characterized mononuclear antibodies for each cell. We kept the top 600 genes by variance.
BRAIN SMALL*
This dataset, which consists of 9,128 mouse brain cells profiled using 10x [28], is used as a complement to PBMC for our study of zero abundance and quality control metric correlation with our generative posterior parameters. We derived quality control metrics using the cellrangerRkit R package (v. 1.1.0). Quality metrics were extracted from CellRanger throughout the molecule-specific information file. We kept the top 3000 genes by variance. We used the clusters provided by cellRanger for the correlation analysis of zero probabilities.
Statistics
Differential expression for bulk datasets
Specifically, we assembled a set of genes that are differentially expressed between human B cells and dendritic cells (microarrays, n = 10 in each group [39], GSE29618) and between CD4+ and CD8+ T cells (microarrays, n = 12 in each group [40], GSE8835). For GSE29618, we first loaded bulk human expression array data using the GEOquery package, selecting all B cell and myeloid dendritic cell (mDC) samples from the baseline (“Day0”) timepoint. We retained all expression features described by exactly one Gene Symbol, and regressed the expression of these expression measures on cell type covariate (B cell vs mDC) using lmFit linear modeling in limma. p-values were derived from empirical Bayes moderated t-tests for difference between the two cell types, using eBayes in limma. We conducted a identical study on GSE8835 for the CD4+ and CD8+ T cells comparison. These p-values are then corrected using the standard Benjamini & Hochberg procedure.
Differential expression for scRNA-seq datasets
We used the packages as detailed in the Methods section. These p-values are then corrected using the standard Benjamini & Hochberg procedure.
Capturing technical variability
We compute the average probability of zero from the negative binomial distribution and from the Bernouilli across all gene for a particular cell. We test for a correlation between these cell-specific zero probabilities and cell-specific quality control metrics using a Pearson-correlation test.
Evaluation
We describe below how we compute the metrics used in the manuscript. For a further details of the algorithms used for benchmarking in this study, refer to the Supplementary Note 5.
Log-likelihood on held-out data
We provide a multi-variate metric of goodness of fit on the data in Supplementary Note 6.
Corrupting the datasets for imputation benchmarking
In this paper we use two different approaches to measure the robustness of algorithms to noise in the data:
Uniform zero introduction: We randomly select ten percent of the non-zero entries and multiply the entry n with a Ber(0.9) random variable.
Binomial data corruption: We randomly select 10% of the matrix and replace an entry n with a Bin(n,0.2) random variable.
Accuracy of imputing missing data
As imputation tantamount to replace missing data by its mean conditioned on being observed, we use the median distance between the original dataset and the imputed values for corrupted entries only. We now define what the imputed values are. For MAGIC, we use the output of their algorithm. For BISCUIT, we use the imputed counts. For ZIFA, we use the mean of the generative distribution conditioned on the non-zero event (mean of the factor analysis part) that we project back into count space. For scVI and ZINB-WaVE, we use the mean of the Negative Binomial distribution.
Silhouette width
The silhouette width requires either a similarity matrix or a latent space. We can define a silhouette score for each sample i with
where a(i) is the average distance of i to all data points in the same cluster ci and b(i) is the lowest average distance of i to all data points in the same cluster c among all clusters c. Clusters can be replaced with batches if we are estimating the silhouette width for assessing batch effects [23].
Clustering metrics
The following metrics require a clustering and not simply a similarity matrix. For these, we will use a k-means clustering on the given latent space of dimension 10 with T = 200 random initializations to achieve a stable score.
Adjusted Rand Index
This index requires a clustering. Most
where nij,ai,bj are values from the contingency table.
Normalized Mutual Information
where P,T designates empirical categorical distributions for the predicted and real clustering. I is the mutual entropy and is the Shannon entropy.
Entropy of batch mixing
Fix a similarity matrix for the cells and take U to be a uniform random variable on the population of cells. Take BU the empirical frequencies for the 50 nearest neighbors of cell U being a in batch b. Report the entropy of this categorical variable and average over T = 100 values of U.
Protein abundance / mRNA expression
Take the similarity matrix for the normalized protein abundance (centered log-ratio transformation, see [33]). Compute a 100 nearest neighbors graph. Fix a similarity matrix for the cells and compute a 100 nearest neighbors graph. Report the Spearman correlation of the flattened matrices and the fold enrichment.
Let A be the set of edges in the protein NN graph, B the set of edges in the cell NN graph and C the entire set of possible edges. The fold enrichment is defined as
Differential expression metrics
We used 100 cells from each cluster. In scVI, we draw 200 samples from the variational posterior; subsampling ensures that our results are stable.
Area under the curve
We assign each gene with a label of DE or non-DE based on their p-values from the reference data (genes with a BH corrected p-values under 0.05 are positive and the rest are negative); then these labels to compute AUROC
Irreproducible Discovery Rate
The IDR is computed using the corresponding R package. We adjust the prior for the mixture weight to be the fraction of genes detected in the micro-array data.
Software Availability
An open-source software implementation of scVI is available on Github (https://github.com/YosefLab/scVI). All code for reproducing results and figures in this manuscript is deposited at https://zenodo.org/badge/latestdoi/125294792 and included as Supplementary Software.
Reporting Summary
Further information on experimental design is available in the Nature Research Reporting Summary.
Data availability
All of the datasets analyzed in this manuscript are public and referenced at https://github.com/romain-lopez/scVI-reproducibility.
Supplementary Material
Acknowledgments
NY and RL were supported by grant U19 AI090023 from NIH-NIAID. We thank Allon Klein, Sandrine Dudoit and Jennifer Listgarten for helpful discussions.
Footnotes
Competing interests
The authors declare no competing interests.
References
- [1].Semrau S et al. Dynamics of lineage commitment revealed by single-cell transcriptomics of differentiating embryonic stem cells. Nature Communications 8, 1096 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Gaublomme JT, Yosef N, Lee Y, Gertner RS et al. Single-cell genomics unveils critical regulators of Th17 cell pathogenicity. Cell 163, 1400–1412 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Patel AP et al. Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma. Science 344, 1396–1401 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Kharchenko PV, Silberstein L & Scadden DT Bayesian approach to single-cell differential expression analysis. Nature Methods 11, 740–742 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Vallejos CA, Risso D, Scialdone A, Dudoit S & Marioni JC Normalizing single-cell RNA sequencing data: challenges and opportunities. Nature Methods 565–571 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Shaham U et al. Removal of batch effects using distribution-matching residual networks. Bioinformatics 33, 2539–2546 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Wagner A, Regev A & Yosef N Revealing the vectors of cellular identity with single-cell genomics. Nature Biotechnology 34, 1145–1160 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Prabhakaran S, Azizi E & Pe’er D Dirichlet process mixture model for correcting technical variation in single-cell gene expression data. In International Conference on Machine Learning (2016). [PMC free article] [PubMed] [Google Scholar]
- [9].Pierson E & Yau C ZIFA: Dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biology 16, 241 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Risso D, Perraudeau F, Gribkova S, Dudoit S & Vert J-P A general and flexible method for signal extraction from single-cell RNA-seq data. Nature Communications 9, 284 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wang B, Zhu J, Pierson E, Ramazzotti D & Batzoglou S Visual- ization and analysis of single-cell RNA-seq data by kernel-based similarity learning. Nature Methods 14, 414–416 (2017). [DOI] [PubMed] [Google Scholar]
- [12].van Dijk D, Nainys J et al. MAGIC: A diffusion-based imputation method reveals gene-gene interactions in single-cell RNA-sequencing data. bioRxiv (2017). URL https://www.biorxiv.org/content/early/2017/02/25/111591.
- [13].Finak G et al. MAST: A flexible statistical framework for assessing tran- scriptional changes and characterizing heterogeneity in single-cell RNA se- quencing data. Genome Biology 16, 278 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Regev A et al. The human cell atlas. eLife 6, e27041 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Gelman A & Hill J Data analysis using regression and multi- level/hierarchical models, vol Analytical methods for social research (Cambridge University Press, New York, 2007). [Google Scholar]
- [16].Grun D, Kester L & van Oudenaarden A Validation of noise models for single-cell transcriptomics. Nature Methods 11, 637–640 (2014). [DOI] [PubMed] [Google Scholar]
- [17].Love MI, Huber W & Anders S Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biology 15, 550 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ding J, Condon A & Shah SP Interpretable dimensionality reduction of single cell transcriptome data with deep generative models. Nature Communications 9, 2002 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Wang D & Gu J VASC: Dimension reduction and visualization of single cell RNA sequencing data by deep variational autoencoder. bioRxiv (2017). URL https://www.biorxiv.org/content/early/2017/10/06/199315. [DOI] [PMC free article] [PubMed]
- [20].Eraslan G, Simon LM, Mircea M, Mueller NS & Theis FJ Single cell RNA-seq denoising using a deep count autoencoder. bioRxiv (2018). URL https://www.biorxiv.org/content/early/2018/04/13/300681. [DOI] [PMC free article] [PubMed]
- [21].Grønbech CH et al. scVAE: Variational auto-encoders for single-cell gene expression data. bioRxiv (2018). URL https://www.biorxiv.org/content/early/2018/05/16/318295. [DOI] [PubMed]
- [22].Vallejos CA, Marioni JC & Richardson S BASiCS: Bayesian analysis of single-cell sequencing data. PLoS Computational Biology 11, 1–18 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Cole MB et al. Performance assessment and selection of normalization procedures for single-cell RNA-seq. bioRxiv (2017). URL https://www.biorxiv.org/content/early/2018/05/18/235382. [DOI] [PMC free article] [PubMed]
- [24].Louizos C, Swersky K, Li Y, Welling M & Zemel R The variational fair autoencoder. In International Conference on Learning Representations (2016). [Google Scholar]
- [25].Kingma DP & Welling M Auto-encoding variational Bayes. In The International Conference on Learning Representations (2014). [Google Scholar]
- [26].Blei DM, Kucukelbir A & McAuliffe JD Variational inference: A review for statisticians. Journal of the American Statistical Association 112, 859–877 (2017). [Google Scholar]
- [27].Sønderby CK, Raiko T, Maaløe L, Sønderby SK & Winther O Ladder variational autoencoders. In Advances in Neural Information Pro- cessing Systems (2016). [Google Scholar]
- [28].10x genomics (2017). URL https://support.10xgenomics.com/single-cell-gene-expression/datasets.
- [29].Zeisel A, Muñoz-Manchado AB, Codeluppi S et al. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347, 1138–1142 (2015). [DOI] [PubMed] [Google Scholar]
- [30].Zheng GXY, Terry JM, Belgrader P, Ryvkin P et al. Massively parallel digital transcriptional profiling of single cells. Nature Communications 8, 14049 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Shekhar K, Lapan SW, Whitney IE, Tran NM et al. Comprehensive classification of retinal bipolar neurons by single-cell transcriptomics. Cell 166, 1308–1323 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Tusi BK et al. Population snapshots predict early haematopoietic and erythroid hierarchies. Nature 555, 54–60 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Stoeckius M et al. Simultaneous epitope and transcriptome measurement in single cells. Nature Methods 14, 865–868 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Johnson WE, Li C & Rabinovic A Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 8, 118–127 (2007). [DOI] [PubMed] [Google Scholar]
- [35].Haghverdi L, Lun ATL, Morgan MD & Marioni JC Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nature Biotechnology 36, 421–427 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Kass RE, Raftery AE, Association S & Jun N Bayes factors. Journal of the American Statistical Association 90, 773–795 (1995). [Google Scholar]
- [37].Held L & Ott M On p-values and Bayes factors. Annual Review of Statistics and Its Application 5, 393–419 (2018). [Google Scholar]
- [38].Robinson MD, McCarthy DJ & Smyth GK edgeR: A bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26, 139–140 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Nakaya HI, Wrammert J, Lee EK, Racioppi L et al. Systems biology of vaccination for seasonal influenza in humans. Nature Immunology 12, 786–795 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Görgün G, Holderried TAW, Zahrieh D, Neuberg D & Gribben JG Chronic lymphocytic leukemia cells induce changes in gene expression of CD4 and CD8 T cells. The Journal of Clinical Investigation 115, 1797–805 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Li Q, Brown JB, Huang H & Bickel PJ Measuring reproducibility of high-throughput experiments. Annals of Applied Statistics 5, 1752–1779 (2011). [Google Scholar]
- [42].Zoph B & Le Q Neural architecture search with reinforcement learning. In International Conference on Learning Representations (2017). [Google Scholar]
- [43].Bergstra J, Bardenet R, Bengio Y & Kégl B Algorithms for hyper- parameter optimization. In Advances in Neural Information Processing Systems (2011). [Google Scholar]
- [44].Tanay A & Regev A Scaling single-cell genomics from phenomenology to mechanism. Nature 541, 331–338 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].DeTomaso D & Yosef N FastProject: A tool for low-dimensional analysis of single-cell RNA-seq data. BMC Bioinformatics 315 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Fan J et al. Characterizing transcriptional heterogeneity through pathway and gene set overdispersion analysis. Nature Methods 13, 241–244 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wolf FA, Angerer P & Theis FJ SCANPY: Large-scale single-cell gene expression data analysis. Genome Biology 19, 15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All of the datasets analyzed in this manuscript are public and referenced at https://github.com/romain-lopez/scVI-reproducibility.