Unraveling the Control of Cell Cycle Periods during Intestinal Stem Cell Differentiation

Abstract

During differentiation, intestinal stem cells (ISCs), a prototypical adult stem cell pool, become either secretory transit-amplifying cells, which give rise to all secretory cell types, or absorptive transit-amplifying cells, which give rise to enterocytes. These cells exhibit distinct cell cycle dynamics: ISCs cycle with a period of 24 h and absorptive transit-amplifying cells cycle with a period of ∼12 h, whereas secretory transit-amplifying cells arrest their cycle. The cell cycle dynamics of ISCs and their progeny are a systems-level property that emerges from interactions between the cell cycle control machinery and multiple regulatory pathways. Although many mathematical models have been developed to study the details of the cell cycle and related regulatory pathways, few models have been constructed to unravel the dynamic consequences of their interactions. To fill this gap, we present a simplified model focusing on the interaction between four key regulatory pathways (STAT, Wnt, Notch, and MAPK) and cell cycle control. After experimentally validating a model prediction, which showed that the Notch pathway can fine-tune the cell cycle period, we perform further model analysis that reveals that the change of cell cycle period accompanying ISC differentiation may be controlled by a design principle that has been well studied in dynamical systems theory—a saddle node on invariant circle bifurcation. Given that the mechanisms that control the cell cycle are conserved in most eukaryotic cell types, this general principle potentially controls the interplay between proliferation and differentiation for a broad range of stem cells.

Introduction

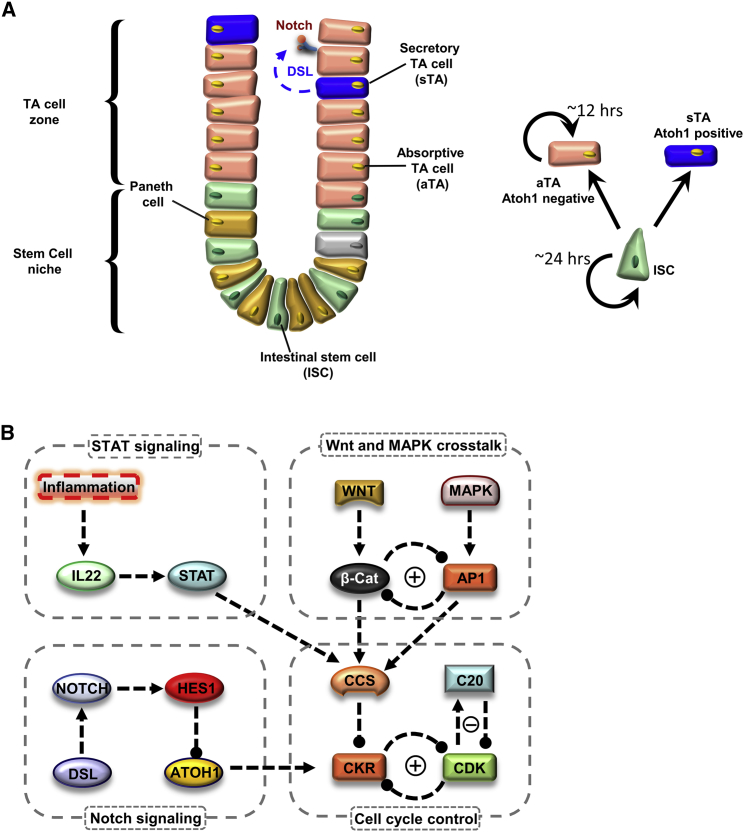
Stem cells are characterized by their distinct ability to both proliferate and differentiate and can be broadly classified into two types: embryonic stem cells, which give rise to the three germ layers during embryonic development, and adult (somatic) stem cells, which reside in a number of adult tissues where they serve as a lifelong source of cells that can regenerate damaged tissues and replenish dying cells (1, 2). Intestinal stem cells (ISCs) represent a prototypical adult stem cell pool that resides in niches at the base of intestinal crypts (2) (Fig. 1 A, left panel). The differentiation of these cells and their progenitors continuously repopulate the epithelial layer of the intestine, whereas the active proliferation of ISCs allows for the prolonged maintenance of the stem cell pool (2).

Figure 1.

The proliferative dynamics of intestinal stem cells (ISCs) and transit-amplifying (TA) cells. (A) A schematic illustration of the intestinal crypt, which is divided into two regions: the stem cell niche and TA zone. ISCs reside in a niche at the base of the crypt where they are supported by Paneth cells. The TA cells reside above the ISCs in the TA zone, which comprises a heterogeneous population of TA cells: absorptive TA cells (aTAs) proliferate, whereas secretory TA cells (sTAs), do not proliferate. Different TA cells can be marked by their expression of ATOH1, with sTAs expressing high levels of ATOH1 and aTAs expressing low ATOH1. Both cell types are derived from ISCs. (B) The influence diagram of the current model. Solid shapes with names represent the model components; arrows indicate activation; solid circle heads indicate repression. The model consists of four interacting modules. To see this figure in color, go online.

Differentiation of ISCs is associated with a change in their proliferation dynamics (Fig. 1 A, right panel). When they differentiate, ISCs make a binary fate decision to become either absorptive transit-amplifying cells (aTAs) or secretory transit-amplifying cells (sTAs) (3). ISCs have been estimated to proliferate with a period of ∼24 h (4, 5), whereas their daughter cells either cycle with a shorter period of 12 h (aTAs) (4) or exit the cell cycle (sTAs) (6). Such experimental observations trigger an intriguing question: how do these stem cells alter their proliferation rates during the differentiation process?

To uncover the dynamical control of proliferation during ISC differentiation, we have developed a simple mathematical model that includes a number of key signaling pathways (Wnt, Notch, and MAPK [mitogen-activated protein kinases]), which have been shown experimentally to be critical regulators of proliferation and differentiation in ISCs (2). These regulatory pathways were then coupled to the cell-cycle control network to gain insights into how their interplay influences the cell cycle (Fig. 1). Using this simplified model, we are able to recapture the experimentally observed proliferation dynamics of ISCs and their progenitors that arise during the differentiation process. Rigorous analysis of the model with a diverse set of tools revealed that a simple dynamic scenario, in terms of a well-defined saddle node of invariant circle (SNIC) bifurcation, might underlie the dramatic changes of cell proliferation during the differentiation of ISCs. In addition, the model also predicts how the proliferation of ISCs is disrupted by alterations in the STAT (signal transducers and activators of transcription) signaling pathway that are present in inflammatory bowel disease (7).

This work illustrates that simplified theoretical models can be used to unravel complex biological control mechanisms. The cell cycle dynamics of eukaryotic cells are controlled by conserved cell cycle regulators (Cdks [cyclin dependent kinase], Cyclins, Cdk inhibitors, etc.) and the feedback between them (8). Hence, we believe that this simplified model could be used to study a host of other types of stem cells, such as embryonic or hematopoietic stem cells, which alter their proliferation rates during differentiation (9, 10).

Methods

Modeling approach

When developing our mathematical model, we adopt a generic approach in which the dynamics of a particular model component, X_i, are determined by the following ordinary differential equation:

$$\frac{d{X}_i}{dt}={\tau }_i\left(F_i-X_i\right),$$

$$\text{where}{F}_i=\frac{1}{1+e^{-\sigma W_i}}\text{and}{W}_i=R_0^i+\sum _j{R}_j^i·X_j.$$

Briefly, each model component (X_i) reaches its desired steady state (F_i) over timescale τ_i. The steady state of each model component (F_i) is a nonlinear function of a weighted sum (W_i) over all model components X_j $\left(j\ne i\right)$. Positive weights $\left(R_j^i>0\right)$ promote X_i, whereas negative weights $\left(R_j^i<0\right)$ inhibit X_i. Weights of zero $\left(R_j^i=0\right)$ correspond to model components which have no effect on X_i. A more detailed description of the approach can be found in the literature (11, 12) as well as in our previous publications (13) and (14).

Existing experimental observations suggest that the cell cycle periods are controlled by the signaling gradients in the crypt. For example, WNT proteins are believed to form a gradient with the highest levels in the crypt base (in the stem cell niche) and lowest levels near the top of the crypt (15); a MAPK gradient is thought to run in the opposite direction (16). ISCs reside near the crypt base, where they receive high levels of WNT and lower levels of MAPK. As such, cells in this environment should cycle with a period of ∼24 h. As cells move up the crypt and into the transit-amplifying (TA) zone, they should begin to cycle faster with a period of ∼12 h (4). To recapture these biological observations, we first manually estimated a single set of parameters that could recapture these dynamics, and this served as the basal parameter set. The governing equations and the basal parameter values for the current models are shown in Tables S1 and S2. The differential equations were simulated using X-Windows Phase Plan Plus Auto (http://www.math.pitt.edu/∼bard/xpp/xpp.html) and plotted using Python (https://www.python.org/).

To produce a population of models, parameters for each model were randomly chosen from a uniform distribution that ranged between 70 and 130% of their basal values. Because of the simplifications of the cell cycle control module, the parameters controlling the interactions between CDK and C20 were not allowed to vary nor were the strengths of the interactions between CCS, CKR, and CDK. For the environmental variables (WNT, MAPK, and DSL), a value was chosen randomly from a uniform distribution over the range [0,2].

An approximate Bayesian computation rejection scheme (17) was used to identify feasible parameter sets. For a given model (i.e., a given parameter set), if simulation of the parameter set satisfied any of our preset criteria (CCT > 20 h, CCT < 18 h, or cell cycle arrest), then the parameter set was saved. If the parameter set did not meet any of these criteria, then the parameter set was rejected. This process continued until a desired number of parameter sets was amassed for each of the three cell types.

Some parameter sets produced cells that arrest with high levels of CDK. Because these do not resemble any known intestinal cells, the corresponding models were not used in any further analyses.

To simulate the cellular response to inflammation, representative cells were first chosen and simulated. Then, an addition of interleukin-22 was mimicked at hour 40 of the temporal simulation by changing the environment variable interleukin-22 from 0 to 1.

Bifurcation analysis

To perform the one parameter bifurcation analysis, the differential equations for CDK, CKR, and C20 were solved with CCS as a control parameter. For the two-parameter bifurcation analysis, both CCS and ATOH1 were viewed as control parameters, and the position of the threshold between the oscillatory and the nonoscillatory regions was tracked with Oscill8 (http://oscill8.sourceforge.net). All bifurcation diagrams were plotted with Python (https://www.python.org/).

Classification tree analysis

Each simulation was binned into one of three groups based on its cell cycle time (CCT): fast (CCT < 18 h), slow (CCT > 20 h), or arrested (CCT = 0). These groups were then used as classifiers for tree analyses. Tree models were run using the model parameters in addition to the steady-state values for model components, which were not shown to oscillate. Trees were computed in R (https://www.r-project.org/) using the rpart2 algorithm within the caret package (18).

Random forest analysis

Groups (as defined above) were used as classifiers for the random forest (RF) analysis. Computation was done in R using the randomForest algorithm (19) within the caret package (18). Default settings were used along with 10-fold cross validation. The most accurate model, defined as the model with the lowest misclassification rate, was chosen to calculate variable importance, which is a measure of the reduction in the accuracy of the statistical model when each of the predictors is permuted. This is done by permuting the value of each parameter and calculating the difference between the out-of-bag error for the initial model and the permuted model. This difference is then averaged over all trees within the forest and normalized by the standard error. The resulting error values are scaled to the maximal error value so that predictors with a value of 100 are the most important predictors within the statistical model, and predictors with a value of 0 have no importance in the model (18).

Both the number of models and the parameter variations included in the models influence the results of the CART and RF analyses. To address these effects, we performed additional simulations in which either the number of models increased (12,000 total models) or decreased (3000 total models). We also carried out simulations in which the parameter ranges were varied. See Fig. S2, A–D (CART analysis) and Fig. S3, A–D (RF analysis).

Confocal imaging and analysis

The imaging data from control and Atoh1-deficient enteroids (Matsu-Ura et al. (20)) were processed using ZEN (Zeiss, Thornwood, NY) or NIS elements (Nikon, Melville, NY). Three-dimensional (3D) images were reconstructed and analyzed using IMARIS (Bitplane, Zurich, Switzerland) to quantify the duration of fluorescent intensity in crypt structures.

Histogram distributions and Student’s t-tests (significance level: p = 0.05) were conducted using Prism 6 (GraphPad Software, La Jolla, CA) and SigmaPlot (Systat Software, San Jose, CA).

Results

Diverse parameter sets allow a single model structure to recapture the proliferation dynamics of ISC, aTA, and sTA cells

Our mathematical model comprises four interacting modules representing the STAT signaling pathway, the WNT/MAPK pathways, the Notch signaling pathway, and the cell cycle (Fig. 1 B). The cell cycle module has been reduced to its core components. CDK levels are controlled via two interactions: a negative feedback formed by CDK and its repressor APC/CDC20 (C20), and a mutually antagonistic positive feedback that exists between CDK and a generic class of cell cycle repressors (CKRs), which represent the action of many repressors of the cell cycle (i.e., p21, p27, p57). CKRs are also inhibited by cell cycle starters (CCSs), which represent the net effect of cell cycle promoters (i.e., CyclinD, cMyc), which are activated by upstream signaling pathways such as the Wnt or MAPK pathways. Both WNT and MAPK can promote cell proliferation (21), and the downstream transcriptional activities of these two pathways are hypothesized to repress each other in a mutually antagonistic feedback (22, 23). The STAT signaling pathway, which plays a significant role in the pathogenesis of inflammatory bowel disease, is assumed to activate CCSs through inflammatory signals (24, 25). The Notch signaling pathway represses CDK inhibitors through its inhibition of ATOH1, thus promoting cell proliferation in response to DSL (26). A detailed description of these modules is available in Supporting Materials and Methods.

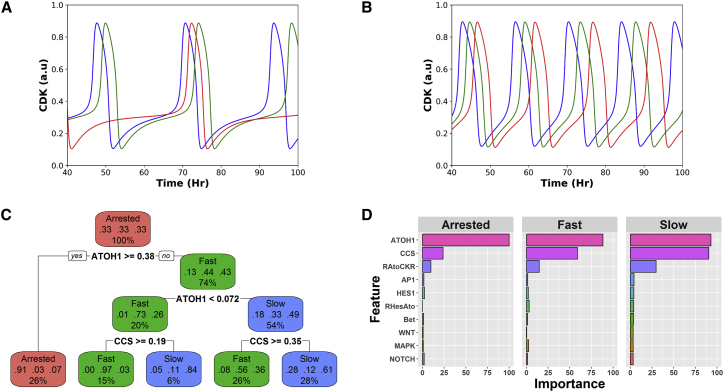
The molecular interactions contained within the modules were translated into a system of ordinary differential equations (Table S1) and parameter sets (which yielded experimentally observed cell cycle periods) were chosen at random (elaborated in Methods). With differing parameter sets, the model structure could reproduce the characteristic proliferation dynamics of ISCs, aTAs, and sTAs. Some parameter sets mimic ISC dynamics with a 24 h period of proliferation (see Fig. 2 A for three examples); others exhibit a 12 h proliferation rate similar to aTAs (see Fig. 2 B). A third group of models do not exhibit proliferative (oscillatory) dynamics and instead reach a stable steady state with low CDK, which is characteristic of sTAs (simulations not shown). Because the population of models recapitulate the proliferation dynamics of stem and TA cells, we intend to use them as functional “in silico” representations of the cell types of interest. However, before we use them for such a purpose, we must first understand how the molecular network can give rise to such drastic differences in proliferation rates of intestinal cells, and second, we must investigate whether these models show similar properties when compared to their experimental counterparts.

Figure 2.

The simplified models suggest that ATOH1 might contribute significantly to the control of cell proliferation. (A) Representative CDK activities of three slowly-cycling cells. (B) Representative CDK activities of three rapidly cycling cells. (C) A classification tree. Nodes in which slowly cycling cells dominate are labeled as Slow; those in which rapidly dividing cells dominate are labeled Fast; nodes associated with arrested nodes are labeled Arrested. (D) A variable-importance calculation with a random forest (RF) analysis. Values are scaled from 0 to 100, for which predictors with a value of 0 are dispensable for classification and values of 100 indicate the most important model components or parameters. To see this figure in color, go online.

The simplified models indicate that ATOH1 contributes significantly to the control of cell proliferation

As an initial test of model quality, we subject our population of models to a classification and regression tree (CART) (27) analysis to understand how individual elements of the molecular control network in our model might contribute to cell cycle periods. Bearing the same structure but different parameter values, our models are characterized by three different types of cell cycle dynamics: fast (<18 h period), slow (>20 h period), or arrested. Meanwhile, six model components (ATOH1, CCS, β-catenin, HES1, NOTCH, and AP1) reach nonoscillatory steady states. For a comprehensive analysis, all 35 model parameters and the six model components that reach nonoscillatory steady states are analyzed using the CART algorithm.

With recursive partitioning (27), the algorithm finds optimal predictors (parameter values or steady-state values) that can classify models. The models are then split into leaves (nodes or clusters) with similar identities. The resulting classification tree divides 6000 models in a binary fashion (Fig. 2 C). All models are included in the root node (Fig. 2 C, first red node on the top). It comprises 33% arrested cells, 33% rapidly cycling cells, and 33% slowly cycling cells and is labeled as “arrested” by the software. Then, at a threshold level of Atoh1 (ATOH1 ≥ 0.38), the root node is divided into two daughter nodes. All models with ATOH1 ≥ 0.38 are binned into a node that is characterized by a high percentage (91%) of arrested cells (Fig. 2 C, red node). In contrast, models with ATOH1 < 0.38 are incorporated into a second node with a high percentage (45%) of fast-cycling cells. These two nodes are also labeled on the basis of the dominant cell type. The algorithm continues to divide the resulting nodes in a similar manner until a preset threshold is met. This single tree has a classification accuracy of more than 70%, meaning that given the steady-state values of CCS and ATOH1, the tree can correctly classify the cell cycle dynamics of more than 70% of cells.

In theory, splitting can continue until leaves contain only models of homogeneous behaviors (example tree, Fig. S1). Growing a tree in this way comes with a number of costs; the trees can be difficult to visualize and hard to interpret and are vastly overfitted. So for practical purposes, trees are pruned to a smaller size to aid with visualization and to prevent overfitting (Fig. 2 C).

To overcome the limitations brought on by a single classification tree, the RF algorithm was used to achieve collective results from an ensemble of randomly modified trees (i.e., forest) (28). By computing and averaging the consequential error when a single model parameter or component is permuted, the RF algorithm was used to calculate the relative importance of each model parameter or component (Fig. 2 D). The RF analysis revealed that ATOH1 and CCS, the two model components used for the initial splitting in the classification tree, play critical roles in classifying cell cycle periods. Given the data-driven nature of the CART and RF methods, the results they generate are sensitive to the number of the models analyzed and the parameter variations included in these models (Fig. S2, A–D, CART analysis and Fig. S3, A–D, RF analysis). Despite such variation, these analyses consistently reveal that Atoh1 and CCS play significant roles in regulating the length of cell cycle periods in intestinal cells. In other words, the CART and RF analyses essentially examined the sensitivity of cell cycle dynamics to all changing model components (parameters and variables) and revealed that the cell cycle period is most sensitive to ATOH1 and CCS.

It is reasonable that ATOH1 and CCS were revealed to be the most significant regulators of cell cycle because CCS is the model component that summarizes the relative abundance of classical cell cycle promoters, and ATOH1 directly promotes the transcription of cell cycle inhibitors (elaboration and references in Supporting Materials and Methods). On the other hand, variation in parameters associated with upstream regulators of the cell cycle (e.g., HES1) have less of an effect on the cell cycle.

Given that CCS promotes the activation of CDK, it is expected that CCS significantly contributes to the regulation of cell cycle periods. Therefore, we focused on understanding the role of ATOH1 in controlling ISC proliferation in vitro.

Single cell cycle dynamics of enteroids reveal a significant role for ATOH1 in controlling cell proliferation rates

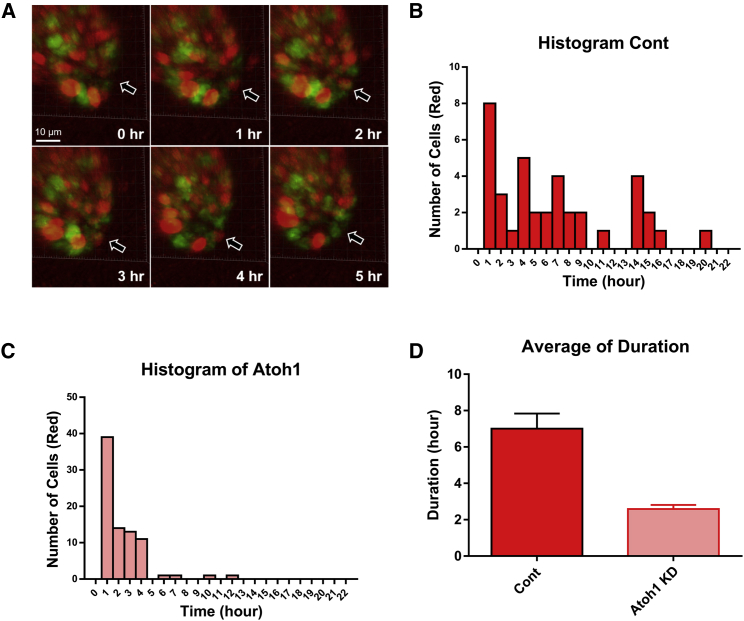
Traditionally, the CCTs of intestinal crypt cells have been estimated by pulse chase staining with tritiated thymidine, bromodeoxyuridine, or 5-ethynyl-2′-deoxyuridine (4, 5). These methods have low precision (because it is difficult to measure single cells) and can have poor temporal resolution (cells not sampled often enough). 3D intestinal enteroids represent a suitable experimental system to study crypt cell dynamics because their in vitro nature allows for increased precision and resolution of cellular measurements. Formed by the self-organization of intestinal epithelial cells into “mini guts,” enteroids contain the different cell types seen within the in vivo crypt (ISCs, TAs, and differentiated cell types) (29). By combining this 3D culture system with the fluorescent ubiquitination-based cell cycle indicator (FUCCI) system (30), we have developed a framework that allows for measurements of cell cycle periods with high temporal resolution in single crypt cells (20). In previous work, we have used this technique to show that the duration of the Gap 1 (G1) phase of the cell cycle has a strong positive correlation with the CCT of intestinal stem and progenitor cells (20). Based on this strong correlation, we measured the duration of the G1 phase in control versus Atoh1-knocked-down (KD) enteroids to evaluate the contribution of ATOH1 to cell cycle dynamics, as proposed by our CART and RF analyses (Fig. 2, C and D). Our experimental results show marked differences in the duration of G1 phases between control and Atoh1-KD enteroids (Fig. 3, B and C). The average duration of the G1 phase in Atoh1-KD enteroids (2.284 ± 0.213 h (average ± standard error); n = 81) is significantly reduced when compared to control enteroids (6.684 ± 0.856 h; n = 38; p < 0.0001) (Fig. 3 D). These findings are consistent with separate studies, which show that the induction of ATOH1 in skin cancer cell lines increases their doubling time (31).

Figure 3.

Experimental observations confirm the significant role of ATOH1 in controlling cell proliferation. (A) Representative crypt images from time-course confocal microscopy of an FUCCI2 (fluorescent ubiquitination-based cell cycle indicator)-derived enteroid. The arrow indicates a single cell that is traced to estimate the duration of the G1 phase of the cell cycle. Scale bar represents 10 μm. (B) The distribution of G1 phase durations obtained from FUCCI2 cells in control enteroids. (C) The distribution of G1 phase durations obtained from cells in Atoh1-KD enteroids. (D) Cells from control enteroids have a significantly longer G1 phase than Atoh1-deficient FUCCI enteroids (p < 0.0001). Error bars represent standard error. To see this figure in color, go online.

Given the consistency between the experimental results and the theoretically predicted significance of ATOH1, we conclude that the theoretical models can serve as in silico representations of the intestinal cells of interest and can be used for further investigation.

A SNIC bifurcation controls cell cycle period in differentiating ISCs

Although ATOH1 and CCS are “model components” in the full model, they rapidly attain steady states in time-dependent simulations. Hence, their effect on CCT can be understood by treating them as “control parameters” of the CDK control system.

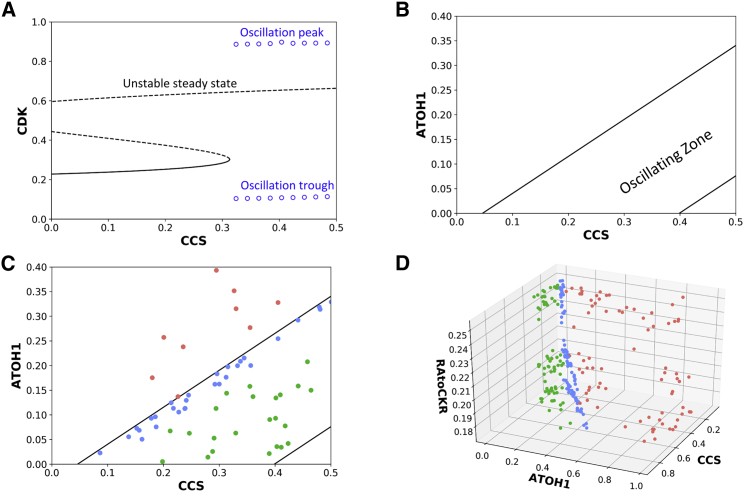
To investigate how cell proliferation is controlled by CCS, we performed a one-parameter bifurcation analysis using CDK as the representative variable and CCS as the control parameter. CDK was chosen as the representative variable because its oscillatory dynamics give rise to the cell cycle. At low levels of CCS, the cell cycle control system is attracted to a G1-like stable steady state with low levels of CDK. When CCS levels increase above a threshold (∼0.3, Fig. 4 A), the stable steady state collides with an unstable saddle point and disappears. For levels of CCS above the threshold, the cell cycle module evolves to a stable oscillation (Fig. 4 A).

Figure 4.

Bifurcation analysis revealed that a SNIC bifurcation controls ISC proliferation (A). A one-parameter bifurcation analysis showing the control of CDK by CCS. The solid curve indicates stable steady-state solutions, whereas the dashed curve indicates unstable steady states. Circles indicate the minimal and maximal amplitudes in oscillatory solutions of CDK. (B) A two-parameter bifurcation diagram showing how CCS and ATOH1 control the dynamics of CDK. The plane is separated into three distinct regions: one oscillatory and two nonoscillatory regions. The positions of different cells on this map determine their proliferative dynamics. (C) ISCs, aTAs, and arrested cells plotted on a two-parameter bifurcation diagram. ISCs and aTAs reside within the oscillatory region, whereas the arrested cells lie outside this region. (D) A three-dimensional (3D) plot of ISCs, aTAs, and arrested cells, with a third parameter, $R_{Ato}^{CKR}$. To see this figure in color, go online.

This particular transition from a stable steady state to oscillation is defined as a SNIC bifurcation (32). Such bifurcations arise when a stable node disappears by colliding with an unstable saddle point, generating an oscillatory solution with a very large period (hence the term invariant “circle”). As the level of CCS further increases, the system moves away from the SNIC transition and the oscillation period decreases (Fig. S4 A). The observed change of period with sustained amplitude distinguishes a SNIC bifurcation from the more widely studied Hopf bifurcation that controls the transition out of the oscillatory region (Fig. S4 B) (32).

The level of CCS needed to generate oscillatory behavior is regulated by other model components. Given the significant contribution of ATOH1 in our computational analyses and experimental observations, we performed a two-parameter bifurcation analysis and tracked the position of the SNIC bifurcation and Hopf bifurcation in response to continuous changes in both CCS and ATOH1. In this way, we identified a pair of lines that decompose the two-dimensional (2D) parameter plane into three distinct regions: a central region associated with oscillatory solutions, which is surrounded by two regions characterized by nonoscillatory solutions (Fig. 4 B).

The SNIC bifurcation explains the altered proliferation dynamics that occur during differentiation

We plotted model solutions that correspond to slow-cycling ISCs, fast-cycling aTAs, and arrested sTAs on the 2D plane spanned by CCS and ATOH1 (Fig. 4 C). Each model resides at a different position on this 2D plane, and the relationship between the positions of these models and the SNIC bifurcation line (Fig. 4 C, left line) readily explains both the quantitative and qualitative differences between their proliferation dynamics. Quantitatively, the ISCs reside near the threshold and proliferate with a large period of ∼24 h (Fig. 4 C, blue circles), whereas the aTAs reside far from the threshold and proliferate with a short period of ∼12 h (Fig. 4 C, green circles); qualitatively, the sTAs reside outside the oscillatory region (Fig. 4 C, red circles) and do not proliferate.

The RF analysis (Fig. 2 D) indicated that cell cycle dynamics are also controlled by the parameter, $R_{Ato}^{CKR}$, which specifies the extent to which ATOH1 promotes CKR production.

Different values of $R_{Ato}^{CKR}$ within individual cells result in different locations of their SNIC bifurcation lines, and the relationship between the SNIC bifurcation lines and the cellular position is what determines the cell cycle period for each cell. To visualize this control, we have plotted a series of SNIC bifurcation curves for different values of $R_{Ato}^{CKR}$ (Fig. S5). As the level of $R_{Ato}^{CKR}$ varies, so too do the slopes of the bifurcation curves (Fig. S5). This indicates that not only are the levels of individual model components (e.g., ATOH1) important in determining the dynamics of the system, but so too are the parameters that control their respective functions (e.g., $R_{Ato}^{CKR}$). When plotted in three dimensions (Fig. 4 D), we see that CCS, ATOH1, and $R_{Ato}^{CKR}$ are sufficient to separate the three cell populations. Collectively, these plots reveal how the positions of individual cells relative to the SNIC boundary can explain their different dynamic behaviors.

The model predicts three types of proliferation changes in response to STAT activation

In response to inflammatory signals, innate immune cells secrete cytokines that activate the STAT signaling pathway within ISCs and consequently enhance their proliferation (25). Consistent with this observation, overexpression of STAT has been shown to increase the pool of actively proliferating ISCs, whereas its deletion decreased this pool (24).

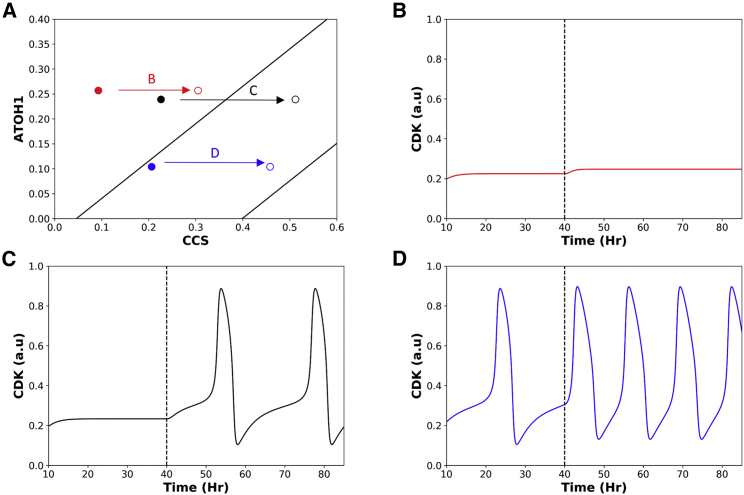
Given that the STAT pathway promotes the transcription of CyclinD (24), a component of CCS, STAT activation results in a rightward shift of cells on the ATOH1-CCS plane (indicated by arrows in Fig. 5 A).

Figure 5.

The model predicts three types of proliferation changes in response to STAT pathway activation. (A) The change in intestinal stem cells (ISCs) in response to activation of the STAT pathway. By elevating CCS, activation of the STAT pathway moves the ISCs rightward. Solid circles show the ISCs before STAT activation; open circles of identical colors show these ISCs after activation of the STAT pathway. Each arrow represents the trajectory of an individual cell following STAT activation. (B–D) Time series simulations of cells before and after STAT activation (dotted line); a cell that remains arrested after activation (B), a cell that begins to proliferate upon activation (C), and a third cell that proliferates faster after activation (D). To see this figure in color, go online.

Increasing CCS causes different effects within individual cells. A stem cell that was quiescent before STAT activation may be pushed into the oscillatory region and start to proliferate (black arrow in Fig. 5 A; the corresponding dynamic simulation is shown in Fig. 5 C). Alternatively, if STAT activation is insufficient to drive a quiescent stem cell into the oscillatory region, then the cell remains quiescent (red arrow in Fig. 5 A; the corresponding dynamic simulation is shown in Fig. 5 B). Such heterogeneous responses may explain why, in the experimental setting, only some but not all arrested cells resume cycling upon STAT5 activation (24). Cells that are already slowly proliferating are predicted to respond to STAT activation by relocating into the middle of the oscillatory region and cycling more rapidly (blue arrow in Fig. 5 B; corresponding temporal simulation in Fig. 5 D). After STAT activation, some cycling cells are arrested with high CDK activity (data not shown); these do not resemble any known intestinal cells and are not analyzed further.

STAT activation has been shown to increase the number of total cycling cells (24, 25). In addition, the overall crypt length is shown to be increased and is accompanied by an increase in the size of the TA zone (25). Shorter cell cycle periods after STAT in ISCs represent, to our knowledge, a novel and testable prediction of our mathematical model.

Discussion

We have shown how a simple mathematical model can be used to understand complex biological control mechanisms and, in doing so, highlighted how mathematical modeling can be used as a powerful tool in biology (33). Like a microscope, a mathematical model has to strike a balance between its field of view (how many pathways should be included) and its magnification (what level of molecular detail should be included). Finding this balance between field of view and magnification is essential and depends on the model’s purpose.

Our current model is designed to understand how the proliferation dynamics of ISCs change during differentiation. Accordingly, our model focuses on interactions between four simple functional modules rather than detailed mechanistic descriptions of each module.

There are, however, many detailed mathematical models of ISCs, some of which have been developed and validated against experimental data (34, 35, 36, 37). Additional models can be found in the reviews by Kershaw et al. (38), Fletcher et al. (39), Carulli et al. (40), and Lloyd-Lewis et al. (41). Compared with these models, our model is purposely simplified to unravel the complex dynamics that govern cell proliferation during differentiation. In future work, it would be interesting to assemble these existing models into multiscale models and to test whether the predictions generated by our simplified model are preserved as we vary the level of detail used to describe each module.

All stem cells undergo proliferation and differentiation. To date, Waddington’s Valley has been widely used as the dominant metaphor to describe stem cell differentiation. In mathematical terms, Waddington’s Valley represents a pitchfork bifurcation (42). Here, we propose that a SNIC bifurcation may explain the change in the proliferation rates of ISCs during differentiation. As discussed above, this SNIC bifurcation is sufficient to explain many of the experimentally observed differences between ISCs and TA cells. Qualitatively, presence inside or outside of the oscillatory region distinguishes the cycling cells of the crypt (ISCs and aTAs) from the noncycling sTA cells; quantitatively, the distance between an oscillatory cell and the SNIC boundary (Fig. 4 B, left line) can provide insight into the differences between ISCs (slow cell cycle period) and aTA cells (fast cell cycle period). Meanwhile, it helps us to understand the effect of STAT pathway activation on ISCs and was able to predict a shorter cell cycle period in these cells, which has not been experimentally observed. Previous models have used SNIC bifurcations to explain how cellular mass controls cell cycle oscillations (43). Here, we demonstrate that the same SNIC bifurcation may explain how ISC cell cycle dynamics are controlled by multiple regulatory pathways during differentiation. As the mechanisms that control the cell cycle are highly conserved among eukaryotes (8), we anticipate that our model could be tailored to study the interplay between proliferation and differentiation in other stem cell types.

Author Contributions

C.I.H. and T.Z. designed the study. S.L. carried out the experimental work. R.B., S.L., X.H., C.I.H., and T.Z. analyzed and interpreted the data. R.B., P.K.M., H.B., and T.Z. analyzed and interpreted the results from the computational modeling. All authors contributed to writing the manuscript and read and approved the final manuscript.

Editor: James Keener.