Quokka: a comprehensive tool for rapid and accurate prediction of kinase family-specific phosphorylation sites in the human proteome

Abstract

Motivation

Kinase-regulated phosphorylation is a ubiquitous type of post-translational modification (PTM) in both eukaryotic and prokaryotic cells. Phosphorylation plays fundamental roles in many signalling pathways and biological processes, such as protein degradation and protein-protein interactions. Experimental studies have revealed that signalling defects caused by aberrant phosphorylation are highly associated with a variety of human diseases, especially cancers. In light of this, a number of computational methods aiming to accurately predict protein kinase family-specific or kinase-specific phosphorylation sites have been established, thereby facilitating phosphoproteomic data analysis.

Results

In this work, we present Quokka, a novel bioinformatics tool that allows users to rapidly and accurately identify human kinase family-regulated phosphorylation sites. Quokka was developed by using a variety of sequence scoring functions combined with an optimized logistic regression algorithm. We evaluated Quokka based on well-prepared up-to-date benchmark and independent test datasets, curated from the Phospho.ELM and UniProt databases, respectively. The independent test demonstrates that Quokka improves the prediction performance compared with state-of-the-art computational tools for phosphorylation prediction. In summary, our tool provides users with high-quality predicted human phosphorylation sites for hypothesis generation and biological validation.

Availability and implementation

The Quokka webserver and datasets are freely available at http://quokka.erc.monash.edu/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein phosphorylation is a major post-translational modification (PTM), occurring when a phosphate group bonds with specific amino acids (such as serine, threonine and tyrosine) (Johnson and Barford, 1993). Numerous experimental studies have demonstrated that phosphorylation is involved in regulation of a variety of fundamental cellular processes, such as protein-protein interaction (Nishi et al., 2011), protein degradation (Swaney et al., 2013), signal transduction (McCubrey et al., 2000) and signalling pathways (Duan and Walther, 2015). On the other hand, aberrant phosphorylation, usually introduced by mutations, is frequently causative of human diseases, including cancers (Fleuren et al., 2016; Karaca et al., 2015). Therefore, it is crucial to accurately identify human phosphorylation sites and to further characterise their biological functions.

Recent technical advances in mass spectrometry have significantly facilitated high-throughput analysis of entire proteomes and identification of specific types of PTMs; however, determining specific kinase(s) that are associated with PTM sites still remains a challenging task (Horn et al., 2014). Kinases acting on phosphorylation sites are often unknown, making experimental validation of kinase-specific phosphorylation events even more challenging. In addition, a portion of phosphorylation sites cannot be identified as these modifications occur at very low levels in the cell (Boersema et al., 2009). Therefore, development of computational methods that are capable of predicting kinase family-specific or kinase-specific phosphorylation sites is urgently needed. Such methods can assist biologists by providing high-quality predicted phosphorylation sites, guiding experimental design and complementing experimental efforts validating uncharacterized phosphorylation events.

To date, a number of computational methods have been established for this purpose. These tools can be classified into two groups: (i) Sequence-scoring function based methods, including PhoScan (Li et al., 2007), GPS 2.0 (Xue et al., 2008) and GPS 3.0 (http://gps.biocuckoo.org/). PhoScan is a statistical scoring function-based method, which uses the log-odds ratio to predict potential phosphorylation sites. GPS 2.0 is another statistical scoring function-based method that employs the Group-based Phosphorylation Scoring (GPS) approach to predict phosphorylation sites for a number of kinases from different groups/families/subfamilies. GPS 3.0 (i.e. the latest version of GPS; http://gps.biocuckoo.org/) is currently online available for academic use; (ii) Machine-learning based methods, including NetPhos 3.1 (Blom et al., 2004), KinasePhos 2.0 (Wong et al., 2007), Musite (Gao et al., 2010), PhosphoPICK (Patrick et al., 2015) and PhosphoPredict (Song et al., 2017). NetPhos 3.1 is the most up-to-date version of the well-established NetPhos program. Benefiting from the artificial neural network (ANN) algorithm, NetPhos 3.1 can predict phosphorylation sites of 17 kinases in total. KinasePhos 2.0 is another machine-learning based method, developed based on a support vector machine (SVM) trained with a combination of sequence-derived features and solvent accessibility. Musite is an SVM-based bioinformatics tool that can predict both generic and kinase-specific phosphorylation sites (covering 13 kinase families) by integrating sequence similarities, protein disordered score and amino acid frequencies as the input features. PhosphoPICK utilizes cellular context and protein sequence information for phosphorylation site prediction trained by information extracted from three species: human (107 kinases), mouse (24 kinases) and yeast (26 kinases). PhosphoPredict is a random forest-based tool, which combines protein sequence-derived and functional features to predict kinase-specific phosphorylation sites for 12 human kinases and kinase families.

There has been outstanding progress in the development of useful methods for kinase family-specific or kinase-specific phosphorylation sites prediction; however, several issues still remain in most of the current methods that need to be addressed: (i) The datasets used for training are relatively out of date. For example, the methods aforementioned, including PhoScan, NetPhos 3.1, GPS 2.0, KinasePhos 2.0 and Musite, were all trained using the data extracted from older versions of the Phospho.ELM database (i.e. versions 3.0, 6.0 and 8.2). Since then, a larger number of experimentally verified novel kinase-specific phosphorylation sites have been identified and therefore should be incorporated into the training datasets to enhance the predictive power of the constructed models; (ii) The statistical techniques applied in the sequence-scoring function based methods are usually straightforward and prompt; however, as the performance of statistical scoring-based methods mainly depends on consensus patterns derived from the training data, the performance of these methods is usually less accurate than that of advanced machine learning-based methods (Miller and Blom, 2009; Song et al., 2017) and (iii) Machine learning based methods usually require considerable computation time and resources to calculate heterogeneous and high-dimensional biological features for model training, although they generally outperform the sequence-scoring function based methods. Therefore, such machine learning-based methods are not practically suitable for high-throughput post translational modification (PTM) prediction. Based on these shortcomings, it becomes necessary to develop a novel computational method that is capable of predicting kinase family-specific phosphorylation sites both rapidly and accurately, allowing high-throughput and cost-effective kinase family-specific phosphorylation site prediction at the proteomic scale. This have strongly motivated us to develop the Quokka tool.

In this study, we introduce Quokka (Quantitative predictor of kinase family-specific kinome and phosphorylation sites), to fill the above gaps and improve the performance of kinase family-specific phosphorylation sites prediction. Quokka includes a variety of sequence scoring functions for high-throughput phosphorylation prediction. Importantly, we built a logistic regression (LR) model by integrating the outcomes of sequence scoring functions for each kinase family. Experimental studies on phosphorylation sites of 11 kinase families using both benchmark and independent test datasets illustrate that Quokka’s LR models performed best amongst all. When compared with the prediction performance of currently available predictors mentioned above, Quokka achieved highest AUC values for phosphorylation sites regulated by nine (out of 11) kinase families. Therefore, we subsequently built LR models for all 65 kinase families, which we also collected in this study to expand the predictive capacity of Quokka.

2 Materials and methods

2.1 Overall framework

We applied the Chou’s 5-step rule (Chou, 2011) to construct and evaluate Quokka, as shown in Figure 1. These steps include data collection and pre-processing, sequence scoring, model construction and optimization, performance comparison and webserver construction. In the first step, the benchmark and independent tests datasets were collected from Phospho.ELM (version 9.0) (Dinkel et al., 2011) and UniProt database (release June 07, 2017) (Pundir et al., 2017) separately. In the second step, a variety of sequence scoring functions and their combinations were utilized to calculate scores for each protein, which were then used as the input features of the LR model. An optimization algorithm was performed in the third step, based on the benchmark datasets to train the optimal LR for each kinase family. These optimized LR models were subsequently used for five-fold cross-validation test. In the fourth step, the optimized LR models were validated using the independent test datasets and the performance comparison with other existing methods was conducted. Using the optimized LR models, we further performed human proteome-wide prediction of phosphorylation sites. The Quokka server, based on the optimized LR models, was constructed in the final step, to facilitate public high-throughput prediction of phosphorylation sites.

Fig. 1.

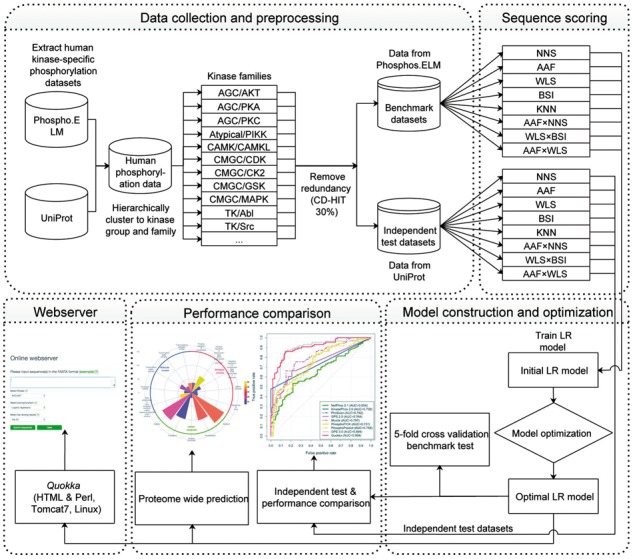
Schematic framework of Quokka

2.2 Dataset collection and protein kinase classification

We extracted experimentally verified human kinase-specific phosphorylation sites from Phospho.ELM (Version 9.0) (Dinkel et al., 2011) and UniProt (release June 07, 2017) (Pundir et al., 2017), which are two well-curated public databases for protein post-translational modifications. The two resulting datasets were utilized as the benchmark and independent test datasets, respectively. To further expand the coverage of our curated datasets for human kinase-specific phosphorylation, we investigated the PhosphoSitePlus database and identified some novel kinase-specific phosphorylation sites using CD-HIT, which we added into the benchmark and independent test datasets. The statistics of augmented benchmark and independent test datasets are shown in Supplementary Table S1, respectively. All substrate proteins with experimentally validated phosphorylation sites were subsequently hierarchically clustered, according to the corresponding kinase group and family, adopting the same kinase nomenclature that links commonly used kinase names to a unified naming scheme (Eid et al., 2017). We did not further sub-categorize kinase families down into kinase subfamilies and kinases, due to the relatively lower numbers of experimentally validated substrates within each subfamily and kinase.

To build accurate models and objectively assess the prediction performance, we removed sequence redundancy from all collected proteins using CD-HIT (Fu et al., 2012) with a stringent sequence identity threshold of 30% for each kinase family. This ensured that any two protein sequences in the benchmark dataset and independent test dataset had a sequence identity of less than 30%. Finally, we collected a total of 43 serine/threonine and 22 tyrosine kinase families (each kinase family contained at least 5 phosphorylation sites) for training the Quokka models. Among this, nine serine/threonine kinase families and two tyrosine kinase families (each kinase family contained at least 20 phosphorylation sites) were selected for performance evaluation.

2.3 Sequence scoring functions

Quokka provides five sequence scoring functions, four combinations of individual scoring functions and an optimized logistic regression model for kinase family-specific phosphorylation prediction. The scoring functions used by Quokka are described as follows.

2.3.1 Nearest neighbour similarity (NNS)

NNS describes the similarity between two motifs A(m, n) and B(m, n) and is defined as:

$$\mathrm{S}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}\left(\mathrm{A},\mathrm{B}\right)=\sum _{i=1,\mathrm{ }m+n+1}\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\left(\mathrm{A}\left[\mathrm{i}\right],\mathrm{B}\left[\mathrm{i}\right]\right)$$ (1)

where m and n denote the numbers of amino acids flanking both upstream and downstream of the centred phosphorylation site, respectively, while $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\left(\mathrm{A}\left[\mathrm{i}\right],\mathrm{ }\mathrm{B}\left[\mathrm{i}\right]\right)$ denotes the substitution score between amino acids $\mathrm{A}\left[\mathrm{i}\right]$ and $\mathrm{B}\left[\mathrm{i}\right]$ in the BLOSUM62 matrix (Henikoff and Henikoff, 1992). Therefore, (m + n + 1) denotes the total length of the sequence segment of a potential phosphorylation site, which was set to 15 (i.e. m = n = 7) in our study.

2.3.2 Amino acid frequency (AAF)

The AAF score of a sequence segment with the centered phosphorylation site is calculated as:

$${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_{\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}}=\sum _{i=\mathrm{P}\left(-7\right),\mathrm{ }\mathrm{P}(+7)}\mathrm{N}{\mathrm{F}}_{\mathrm{i}}$$ (2)

where $\mathrm{N}{\mathrm{F}}_{\mathrm{i}}$ is the normalized relative amino acid frequency, and P denotes the amino acid position surrounding the potential phosphorylation site (i.e. P =[−7, 7]). $\mathrm{N}{\mathrm{F}}_{\mathrm{i}}$ is defined as:

$$\mathrm{N}{\mathrm{F}}_{\mathrm{i}}=\frac{{\mathrm{f}}_{\mathrm{i}}}{{\mathrm{f}}_{\mathrm{i},\mathrm{m}\mathrm{a}\mathrm{x}}}$$ (3)

Here ${\mathrm{f}}_{\mathrm{i}}={\mathrm{n}}_{\mathrm{i}}/\mathrm{N}$ represents the frequency value of the amino acid at position i, while ${\mathrm{f}}_{\mathrm{i},\mathrm{m}\mathrm{a}\mathrm{x}}$ denotes the frequency value of the most common amino acid at the same position.

2.3.3 WebLogo-based sequence conservation (WLS)

WebLogo (Crooks et al., 2004) is a widely-applied sequence logo generation tool based on the calculation of the sequence conservation score (W). Here, we used the conservation score generated by WebLogo to rank all the potential phosphorylation sites. The conservation score of a sequence segment can be calculated as:

$${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_{\mathrm{w}\mathrm{e}\mathrm{b}\mathrm{L}\mathrm{o}\mathrm{g}\mathrm{o}}=\sum _{\mathrm{i}=\mathrm{P}\left(-7\right),\mathrm{P}(+7)}{\mathrm{W}}_{\mathrm{i}}$$ (4)

2.3.4 BLOSUM62 substitution Index (BSI)

The BLOSUM62 substitution matrix has been employed to predict phosphorylation sites in previous studies [such as GPS2.0 (Xue et al., 2008) and Musite (Gao et al., 2010)]. Given a testing sequence segment Test, its BSI score can be calculated as:

$${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_{\mathrm{B}\mathrm{L}\mathrm{O}\mathrm{S}\mathrm{U}\mathrm{M}62}=\frac{{\sum }_{\mathrm{P}(+7)}^{\mathrm{P}(-7)}\mathrm{B}\left(\mathrm{T}\mathrm{e}\mathrm{s}\mathrm{t}\right)}{{\sum }_{\mathrm{P}(+7)}^{\mathrm{P}(-7)}\mathrm{B}\left(\mathrm{K}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}\right)}.$$ (5)

${\sum }_{\mathrm{P}(+7)}^{\mathrm{P}(-7)}\mathrm{B}\left(\mathrm{T}\mathrm{e}\mathrm{s}\mathrm{t}\right)$ sums up the substitution score of the sequence segment Test against all known phosphorylation sequence segments for a given kinase family; ${\sum }_{\mathrm{P}(+7)}^{\mathrm{P}(-7)}\mathrm{B}\left(\mathrm{K}\mathrm{n}\mathrm{o}\mathrm{w}\mathrm{n}\right)$ sums up the substitution score of all know phosphorylation segments. Note that the value of ${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_{\mathrm{B}\mathrm{L}\mathrm{O}\mathrm{S}\mathrm{U}\mathrm{M}62}$ ranges from 0 to 1, and a higher value indicates that the sequence segment Test has a higher similarity to known phosphorylation sites. Finally, the highest ${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_{\mathrm{B}\mathrm{L}\mathrm{O}\mathrm{S}\mathrm{U}\mathrm{M}62}$ is selected as the BSI score.

2.3.5 K-nearest neighbours (KNN)

KNN (Altman, 1992; Chen et al., 2018) was previously used for scoring phosphorylation sites by Gao et al. (Gao et al., 2010). KNN aims to find the k nearest neighbours of a potential phosphorylation site by calculating the distance between the testing site and those known phosphorylation sites in the datasets. The distance between two sequence segments A(m, n) and B(m, n) is defined as:

$$\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\left(\mathrm{A},\mathrm{B}\right)=1-\frac{{\sum }_{i=1}^{m+n+1}\mathrm{S}\mathrm{i}\mathrm{m}\left(\mathrm{A}\left[\mathrm{i}\right],\mathrm{B}\left[\mathrm{i}\right]\right)}{m+n+1},$$ (6)

where m and n denote the numbers of amino acids flanking both upstream and downstream of the centred phosphorylation site, respectively. Moreover, if the length of sequence fragment in the upstream or downstream is shorter than m or n, ‘*’ (representing gaps in the BLOSUM62 matrix) will be used and added to the corresponding position upstream or downstream. In the equation (6), the $\mathrm{S}\mathrm{i}\mathrm{m}\left(\right)$ function calculates the similarity between two amino acids, defined as:

$$\mathrm{S}\mathrm{i}\mathrm{m}\left(\mathrm{a},\mathrm{b}\right)=\frac{\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\left(\mathrm{a},\mathrm{b}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left\{\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\right\}}{\mathrm{m}\mathrm{a}\mathrm{x}\left\{\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\right\}-\mathrm{m}\mathrm{i}\mathrm{n}\left\{\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\right\}},$$ (7)

where a and b denote amino acids from the sequence segments A and B, respectively. In Equation (7), the $\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}$ function denotes the BLOSUM62 substitution matrix; while $\mathrm{m}\mathrm{a}\mathrm{x}$ and $\mathrm{m}\mathrm{i}\mathrm{n}$ present the largest and smallest value of the element in the $\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}$, respectively.

The KNN function describes the average distance of a given sequence segment with a potential phosphorylation site to the segments of all the positive/negative phosphorylation sites. The calculated distance values are subsequently sorted and the k nearest neighbours selected. Finally, the KNN score (the percentage of positive neighbours among the k nearest neighbours) is calculated. In this study, k was as 0.5% of the total number of positive and negative sites in the training dataset for calculating the KNN score in Quokka, and the value of k varied depending on the particular kinase family.

2.3.6 Combinations of individual scoring functions

In addition to the five scoring functions mentioned above, Quokka also provides four combinations of individual scoring functions for kinase-specific phosphorylation sites prediction. These include AAF×NNS, WLS×BSI, NNS×WLS and AAF×WLS.

2.4 Model training and evaluation

2.4.1 Logistic regression (LR)

The LR algorithm is designed to estimate the distribution P(Y|X) from the training data, where Y is a discrete value and X=<X₁, …, X_d> represents any feature vector containing discrete or continuous variables. In this study, given the prediction of a phosphorylation site is a binary classification task, we only considered Y∈{0, 1}, where Y = 1 and Y = 0 indicate a positive (phosphorylation site) and negative sample (non-phosphorylation site), respectively. The LR model can be defined as:

$$\mathrm{p}\left(\mathrm{Y}=1|\mathrm{X}\right)=\mathrm{g}\left({\theta }^{\mathrm{T}}\mathrm{X}\right)=\frac{1}{1+{\mathrm{e}}^{-{\theta }^{\mathrm{T}}\mathrm{X}}},$$ (8)

where $\mathrm{g}\left(\mathrm{z}\right)=\frac{1}{1+{\mathrm{e}}^{-\mathrm{z}}}$ denotes the logistic function and ${\theta }^{\mathrm{T}}\mathrm{X}={\theta }_0+{\sum }_{\mathrm{i}=1}^{\mathrm{d}}{\theta }_{\mathrm{i}}\mathrm{ }{\mathrm{X}}_{\mathrm{i}}$. Both values of $\mathrm{g}\left({\theta }^{\mathrm{T}}\mathrm{X}\right)$ and p(Y|X) range from 0 to 1. Therefore, p(Y = 0|X) can be estimated using the following equation, given that the sum of the probabilities must be equal to 1:

$$\mathrm{p}\left(\mathrm{Y}=0|\mathrm{X}\right)=1-\mathrm{g}\left({\theta }^{\mathrm{T}}\mathrm{X}\right)=\frac{{\mathrm{e}}^{-{\theta }^{\mathrm{T}}\mathrm{X}}}{1+{\mathrm{e}}^{-{\theta }^{\mathrm{T}}\mathrm{X}}}.$$ (9)

Algorithm 1 Optimization procedure of the Logistic Regression models

Input:

 Training feature set, T;

Output:

 Optimal Logistic Regression model, optimisedLR.

1: initialLR = trainLR(T);

2: initialSummary = summary(initialLR);

3: T` = T;

4: initialAUC = getAUC(initialLR);

5: for each i∈[1, n] do

6:  Pvalues[i] = getCoefficientsPvalues(initialSummary, i);

7:  if Pvalues[i] >0.05

8:   T` = removeFeature(i, T`);

9:  end if;

10: end for;

11: reducedLR = trainLR(T`);

12: reducedAUC = getAUC(reducedLR);

13: chiSquareValue = chisqTest(initialLR, reducedLR);

14: if (reducedAUC≧initialAUC) && (chiSquareValue > 0.05)

15:  optimisedLR = reducedLR;

16: end if;

17: else

18:  optimisedLR = initialLR;

19: end else;

20: return optimisedLR;

In this study, the LR models were implemented using the R package and trained using the individual scoring functions and their combinations as the inputs. We also used an optimization algorithm to optimize the LR models for each kinase families. Algorithm 1 describes the detailed procedure of our optimization approach for the LR model. In the first step, an initial LR model initialLR is trained by using the training dataset T. In the second step, summary(initialLR) obtains the detailed model measures information of the initialLR. The information contains the P-values of each feature based on hypothesis test for the model. These P-values indicate whether the corresponding feature makes a significant contribution to the model. For example, if the P-value of a feature is equal or lower than 0.05, it makes a significant contribution to the model, and vice versa. In step 3 a copy of the training feature set T, T`, is created for the next optimization procedure. In step 4, getAUC(initialLR) extracted the AUC score, initailAUC, of the initial model. Steps 5–10 in Algorithm 1 describe our optimization strategy. For each feature i of feature set T`, if the P-value of feature i is insignificant (i.e. >0.05), this feature will be removed from T` (step 7). Here in step 5, n denotes the dimension of the T and in the step 6, the P-value of feature i is extracted by the function getCoefficientsPvalues(initialSummary, i). This procedure will be halted till all the features in F has been evaluated. Afterwards, a new LR model (i.e. reducedLR) will be trained using optimized feature set F` in step 11. Then, the AUC score, reducedAUC, of the reducedLR is obtained (step 12) and compared with the initialLR model (steps 13–15). A chi-square test was applied for testing whether the reducedLR model fits as well as the initialLR model. If the chi-square test result is bigger than 0.05 (not statistically significant), it means the reducedLR model fits as well as the initialLR model and vice versa. Therefore, the reducedLR model will be returned as the optimisedLR model if the chi-square test result is insignificant and the AUC score of the new model (reducedLR) is higher than the initial model (initialLR); otherwise, the initial LR model initialLR will be returned.

2.4.2 Performance evaluation

Throughout the literature, a set of four metrics directly taken from mathematics books are often used to quantitatively evaluate the prediction quality of a statistical predictor. They are (Chen et al., 2007): Sn (sensitivity), Sp (specificity), ACC (overall accuracy) and MCC (Mathew’s Correlation Coefficient) (Matthews, 1975). These metrics are not intuitive and hence biologists often find them difficult to understand. However, based on the Chou’s symbols, originally introduced to study protein signal peptides (Chou, 2001a,b), a set of four very intuitive metrics were defined as given below (Chen et al., 2013; Xu et al., 2013):

$$\left\{\begin{array}{l} \\ \begin{array}{l}\mathrm{S}\mathrm{n}=1-\frac{{\mathrm{N}}_{-}^{+}}{{\mathrm{N}}^{+}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{ }\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{0.17em}}0\le \mathrm{S}\mathrm{n}\le 1\mathrm{ }\\ \begin{array}{ll}\begin{array}{ll}\mathrm{S}\mathrm{p}=1-\frac{{\mathrm{N}}_{+}^{-}}{{\mathrm{N}}^{-}}& \mathrm{ }\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}0\le \mathrm{S}\mathrm{p}\le 1\end{array}\mathrm{ }& \mathrm{ }\end{array}\end{array}\\ \begin{array}{l}\begin{array}{l}\begin{array}{ll}\mathrm{A}\mathrm{c}\mathrm{c}=\mathrm{ }\mathrm{\Lambda }=1-\frac{{\mathrm{N}}_{-}^{+}+{\mathrm{N}}_{+}^{-}}{{\mathrm{N}}^{+}+{\mathrm{N}}^{-}}& \mathrm{ }\mathrm{ }\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\mathrm{ }\mathrm{ }0\le \mathrm{A}\mathrm{c}\mathrm{c}\le 1\mathrm{ }\end{array}\end{array}\mathrm{ }\\ \begin{array}{ll}\mathrm{ }\mathrm{M}\mathrm{C}\mathrm{C}=\mathrm{ }\frac{1-\left(\frac{{\mathrm{N}}_{-}^{+}}{{\mathrm{N}}^{+}}+\frac{{\mathrm{N}}_{+}^{-}}{{\mathrm{N}}^{-}}\right)}{\sqrt{\left(1+\frac{{\mathrm{N}}_{+}^{-}-{\mathrm{N}}_{-}^{+}}{{\mathrm{N}}^{+}}\right)\mathrm{ }\left(1+\frac{{\mathrm{N}}_{-}^{+}-{\mathrm{N}}_{+}^{-}}{{\mathrm{N}}^{-}}\right)}}\mathrm{ }& -1\le \mathrm{M}\mathrm{C}\mathrm{C}\le 1\mathrm{ }\end{array}\end{array}\end{array}\right.$$ (10)

where ${\mathrm{N}}^{+}$ represents the total number of positive samples investigated, while ${\mathrm{N}}_{-}^{+}$ is the number of positive samples incorrectly predicted to be negative; ${\mathrm{N}}^{-}$ is the total number of negative samples investigated, while ${\mathrm{N}}_{+}^{-}$ is the number of the negative samples incorrectly predicted to be positive. With the set of formulations in Eq. 10, the meanings of Sn, Sp, Acc and MCC have become much clearer and easier to understand, as discussed in a series of recent studies in various biological areas (Ehsan et al., 2018; Feng et al., 2017, 2018; Lin et al., 2014; Liu et al., 2017a,b,c, 2018).

Moreover, we also plotted the Receiver-Operating Characteristic (ROC) curves and calculated the Area Under the Curve (AUC) values, as the primary measures to evaluate the predictive performance of Quokka and all the compared methods.

3 Results and discussion

3.1 Amino acid specification and preference of phosphorylation in 11 kinase families

Based on the benchmark and independent test datasets, we analyzed the site specificity of 11 kinase-specific phosphorylation sites. Figure 2 and Supplementary Figure S1 show the sequence logos of the occurrences of amino acid residues located in both the upstream and downstream regions surrounding known phosphorylation sites for 11 kinase families (Only kinase families with more than 20 experimentally validated phosphorylation sites in the benchmark datasets were included in this analysis; see Supplementary Table S1 for more details). Not surprisingly, Figure 2 and Supplementary Figure S1 suggest that phosphorylation sites regulated by different kinases show different preferences in terms of the occurrences of flanking amino acids.

Fig. 2.

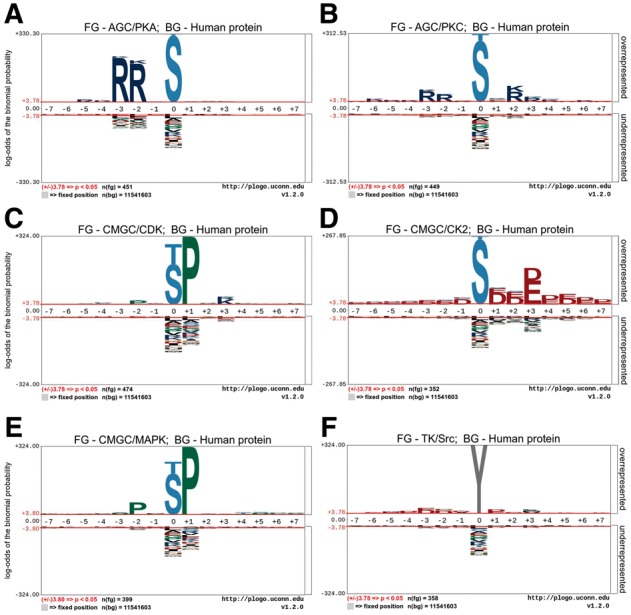
Sequence logos showing the occurrences of amino acid residue types surrounding the kinase-specific phosphorylation sites for the six kinase families investigated in this study: (A) AGC/PKA; (B) AGC/PKC; (C) CMGC/CDK; (D) CMGC/CK2; (E) CMGC/MAPK and (F) TK/Src. FG, Foreground dataset; BG, Background dataset

As expected, threonine (T) and serine (S) are the only two residue types occurring at the central position of sequence segments of phosphorylation sites of the serine/threonine kinases. Likewise, for phosphorylation sites of tyrosine kinases, the central position is predominated by tyrosine (Y). Nevertheless, other residue types at different positions also showed different amino acid preferences. For instance, a hallmark of the AGC/AKT kinase family is the requirement for a S or T residue at the central position with two arginine (R) in the upstream (-5 and -3 positions), as shown in Supplementary Figure S1A, i.e. the RXR phosphorylation site motif (Rust and Thompson, 2011).

3.2 Performance comparison among different scoring functions, combinations and the optimized LR model

We evaluated and compared the prediction performance of different individual scoring functions, combinations of individual scoring functions and the second-layer logistic regression models used by Quokka based on the kinase-specific phosphorylation site datasets for 11 kinase families. Each kinase family had at least 20 kinase-specific phosphorylation sites in both benchmark and independent test datasets (refer to Supplementary Table S1 for details). After applying this criterion, there were nine serine/threonine kinase families (AGC/AKT, AGC/PKA, AGC/PKC, Atypical/PIKK, CAMK/CAMKL, CMGC/CDK, CMGC/CK2, CMGC/GSK, CMGC/MAPK), and two tyrosine kinase families (TK/Abl and TK/Src) included in this analysis.

The percentages of true positives (TP) in the top 1, 3, 5, 10 and 20 ranking lists (Verspurten et al., 2009) of predicted phosphorylation sites and the AUC, MCC, ACC, Sn and Sp are provided in Supplementary Table S2. As can be seen, the LR models performed best among all the compared scoring functions and their combinations in terms of AUC for all the 11 examined kinase families. In terms of the percentages of TP in the top N ranking lists, the LR models also performed best, except for CMGC/CDK [for which BSI performed best when predicting the True Positives (TP) in the Top 20 ranking list], CMGC/GSK (for which WLS×BSI performed best when predicting TPs in the Top 20 ranking list) and Atypical/PIKK (for which WLS performed best when predicting TPs in the Top 10 ranking list). In addition, BSI outperformed all other four scoring functions, except for the prediction of phosphorylation regulated by Atypical/PIKK. As for the three combinations of scoring functions, WLS×BSI outperformed the other two except for the AGC/AKT kinase family. In summary, BSI is the best scoring function among all five individual scoring functions, while the second-layer logistic regression model achieved the overall best performance. Accordingly, we used the LR model as the final model for performing phosphorylation site prediction in Quokka.

3.3 Performance comparison between Quokka and other prediction tools

In this section, we compared the prediction performance of Quokka against eight existing tools on the independent test datasets. Specifically, we compared Quokka against NetPhos 3.1 (Blom et al., 2004), KinasePhos 2.0 (Wong et al., 2007), PhoScan (Li et al., 2007), GPS 2.0 (Xue et al., 2008), Musite (Gao et al., 2010), PhosphoPICK (Patrick et al., 2015), PhosphoPredict (Song et al., 2017) and GPS 3.0. To evaluate and compare the prediction performance, the protein sequences in FASTA format from the independent test datasets were submitted to each of these servers with default/recommended settings described by respective works. It is worth noting that some tools were specifically designed for certain kinases, indicating that they could be only used to predict the phosphorylation sites of the specific kinases they were designed for. As Quokka is designed for kinase family-specific phosphorylation prediction, we conducted performance comparisons of all the predictors at the kinase family level. To do so, for a given kinase family, we predicted the phosphorylation sites regulated by the kinase family. Then, the prediction result that received the best prediction score for each phosphorylation site was used to represent the final prediction outcome for this kinase family. For example, there are a number of kinases in the CMGC/CDK family, including CDK1, CDK2, CDK3, etc. PhosphoPICK is a computational tool that can predict phosphorylation sites regulated by eight types of CDK kinases (i.e. CDK1, CDK2, CDK3, CDK4, CDK5, CDK6, CDK7 and CDK9). To assess the performance of PhosphoPICK, we submitted the substrate sequences of the CMGC/CDK family to its webserver and selected all these eight CDK kinases to perform the prediction. For each protein sequence, PhosphoPICK calculated a score for each potential phosphorylation site (S/T). As a result, eight prediction scores of each S/T(/Y) site for eight kinases were generated. Then, for the sites which were labelled as positive samples in the independent test datasets, the best prediction score among these eight values was selected to represent the prediction outcome for such phosphorylation site regulated by the CMGC/CDK family. In contrast, for the sites which were labelled as negative samples, the minimum scores were selected as the prediction results to calculated the performance metrics. We summarize the performance comparison results between these methods for the 11 kinase-family-specific phosphorylation sites in Supplementary Table S3 and also present the ROC curves in Figure 3 and Supplementary Figure S2.

Fig. 3.

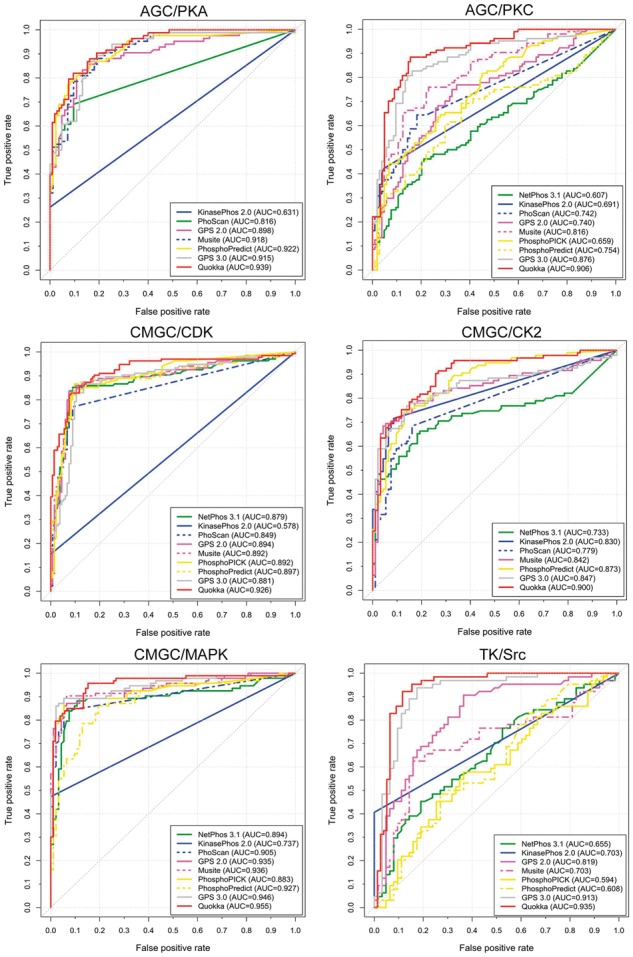
Performance comparison results between different kinase-specific phosphorylation site predictors in terms of the AUC value, for AGC/PKA, AGC/PKC, CMGC/CDK, CMGC/CK2, CMGC/MAPK and TK/Src. The following phosphorylation site prediction tools were included and compared: Quokka (based on the logistic regression model), NetPhos 3.1, KinasePhos 2.0, PhoScan, GPS 2.0, Musite, PhosphoPICK, PhosphoPredict and GPS 3.0

Figure 3 and Supplementary Figure S2 show the ROC curves of Quokka and other existing methods on the independent test datasets. As can be seen, Quokka (red line) outperformed the existing tools on nine out of 11 kinase families, with an exception of Atypical/PIKK and CMGC/GSK, for which GPS 3.0 performed best in terms of the AUC score (GPS 3.0, AUC = 0.925 versus Quokka, AUC = 0.921 for Atypical/PIKK and GPS 3.0, AUC = 0.886 versus Quokka, AUC = 0.870 for CMGC/GSK). The complete performance comparison results (as evaluated using AUC, MCC, ACC, Sn and Sp measures) on the independent tests are shown in Supplementary Table S3. Altogether, these results indicate Quokka is a powerful bioinformatics tool that provides a favourable prediction performance of kinase-specific phosphorylation prediction.

In addition, to investigate if Quokka is able to provide kinase-specific phosphorylation prediction, we selected eight kinases according to the numbers of available phosphorylation sites specific for these kinases (each kinase has more than 30 specific phosphorylation sites) from the independent test datasets, including AGC/AKT/AKT1, AGC/PKA/PKACA, AGC/PKC/PKCA, Atypical/PIKK/ATM, CMGC/CDK/CDK1, CMGC/CK2/CK2A1, TK/Abl/Abl1 and TK/Src/Src. We then conducted experiments to compare the performance of Quokka with existing methods at the kinase-specific level. The performance comparison results (in terms of AUC, MCC, ACC, Sn and Sp) are shown in Supplementary Table S4. We can see that Quokka outperformed the other eight tools on six out of eight tested kinases in terms of AUC, with the exception of AGC/AKT/AKT1 for which PhosphoPICK achieved the best performance (PhosphoPICK, AUC = 0.944 versus Quokka, AUC = 0.936) and CMGC/CK2/CK2A1 for which Musite achieved the best performance (Musite, AUC = 0.918 versus Quokka, AUC = 0.906).

3.4 Web server implementation

We constructed an open-access web server for Quokka using HTML and Perl programming languages, which we have made available at http://quokka.erc.monash.edu/. The Quokka web server is managed by Tomcat7 and resides on a Linux server, equipped with an 8-core CPU, 4 TB hard disk and 16 GB memory. Several steps need to be conducted to perform kinase-regulated phosphorylation prediction using Quokka. First, users need to provide Quokka proteins of interest in the FASTA format. An ‘Example’ link has been provided to assist users with the acceptable input format. Note that, to guarantee the prediction efficiency, we allow users to submit no more than 1000 sequences simultaneously. In the second step, users will need to select a specific kinase family for phosphorylation prediction. In total, Quokka provides prediction for 43 serine/threonine and 22 tyrosine kinase families. In the third step, a scoring function/model will be selected for Quokka to employ, overall, Quokka is able to conduct prediction for phosphorylation sites using nine functions/models. Based on our experimental results, the logistic regression models performed best amongst all scoring functions. However, the sequence scoring functions usually return the prediction result more rapidly than the logistic regression model. Therefore, the selection of appropriate scoring functions is left at the users’ discretion, based on their computational requirement and the complexity of the question at hand. In the last step, users can choose the number of top-ranking predicted phosphorylation sites (N; N = 1, 3, 5, 10 and 20) to be displayed in the result webpage. An example of a typical input for Quokka is demonstrated in Supplementary Figure S3, and an online instruction explaining the input, prediction parameters and result interpretation are detailed on the Quokka website.

A strength of Quokka is that it can rapidly return the prediction result, thus facilitating high-throughput prediction. Our test suggested that, on average, it takes eight minutes to finish processing 1000 sequences and to return the prediction results. This efficiency is a result of Quokka not calculating high-dimensional feature sets for the input, unlike most other machine-learning based methods. After Quokka completes the prediction, the outcomes of all submitted sequences are returned to the result webpage. Each result table contains the prediction scores for each protein (Supplementary Fig. S3). To comprehensively demonstrate the prediction results, six sortable columns, including ‘Rank’, ‘Position’, ‘Site’, ‘Motif’, ‘Score’, ‘Phosphorylation site?’ and ‘Kinase family’, are provided within each table. All the prediction results can be easily exported to widely used file formats, including CSV, Excel^® spreadsheet and PDF. In addition, there are two buttons ‘Phosphorylation Sites Distribution’ and ‘Visualize’ at the top of each result table for prediction results visualization. The corresponding results are shown in Supplementary Figures S5 and S6.

3.5 Proteome-wide prediction of kinase-specific phosphorylation sites

We further applied Quokka to perform proteome-wide prediction of kinase family-specific phosphorylation sites in the human proteome (containing 20 198 proteins extracted from the UniProt database; release June 07, 2017) for the 11 kinase families. We briefly summarize the results in this section. To obtain high-confidence predicted phosphorylation sites, we applied the prediction threshold at the 99% specificity (Gao et al., 2010; Li et al., 2015, 2016; Song et al., 2018a,b,c). The statistical summary of the predicted phosphorylated proteins and phosphorylation sites for the 11 kinase families are shown in Supplementary Table S5. A complete list of the predicted phosphorylated proteins and their phosphorylation sites are available on the Quokka, and can be downloaded and analyzed on a local computer (http://quokka.erc.monash.edu/#proteome).

3.6 Gene ontology enrichment analysis

Furthermore, we performed an in-depth analysis of enriched gene ontology (GO) terms including cellular component (CC), biological process (BP), molecular function (MF) and pathways of predicted phosphorylated proteins at the proteome-scale, in an effort to provide an insight into biological annotations and functional roles of those predicted phosphorylated proteins. For this purpose, we carried out two-sided hypergeometric tests, to identify significantly enriched (P-value ≤ 0.05) GO terms and pathways against the background protein dataset composed by the entire human proteome. The P-value of a given term t can be defined as:

$$\mathrm{P}-\text{value}={\mathrm{F}}_{\mathrm{h}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{m}}\left(m,n,N,M\right),$$ (15)

where m is the number of predicted phosphorylated proteins annotated by the term t, n denotes the number of human proteins annotated by term t, N is the number of human proteins annotated by at least one term, while M is the number of phosphorylated proteins annotated by at least one term. All the statistical results of GO term and pathway analysis are listed in Supplementary Tables S5 and S6, respectively. Figure 4 and Supplementary Figure S4 highlights the top five significantly over-represented BP, CC and MF terms of the predicted phosphorylated proteins for the 11 kinase families at the proteome-scale.

Fig. 4.

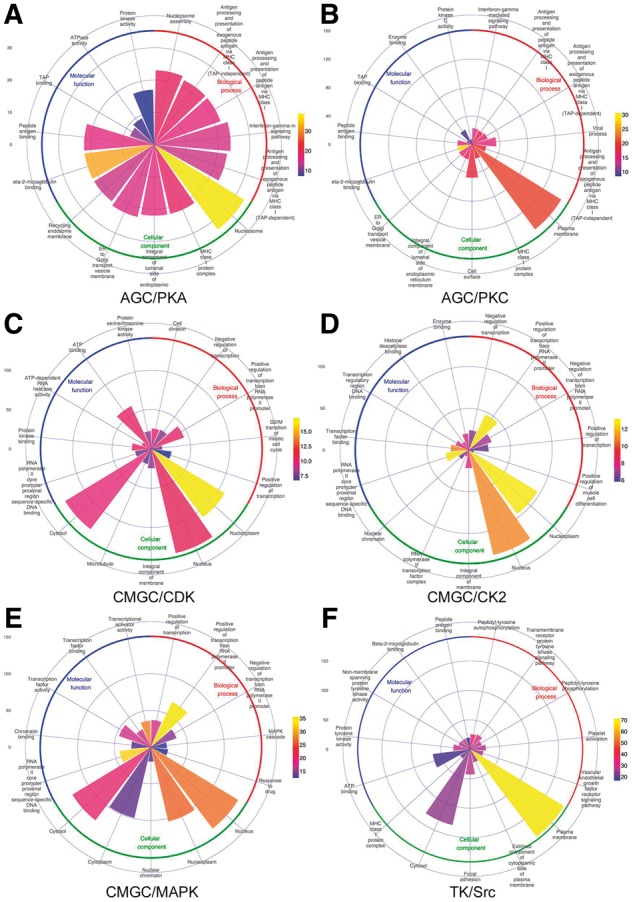
The GO term distributions of predicted phosphorylated proteins regulated by 6 kinase families, including (A) AGC/PKA; (B) AGC/PKC; (C) CMGC/CDK; (D) CMGC/CK2; (E) CMGC/MAPK and (F) TK/Src. The enrichment analyses of GO terms, including biological process, molecular functions and cellular components for phosphorylated proteins were performed with the hypergeometric distribution

Importantly, as shown by Figure 4 and Supplementary Figure S4, phosphorylated proteins by different kinase families are associated with different GO terms. The sectorial area for a GO term indicates the number of human proteins annotated by this term (n) while the different colors of the sectorial area represents the P-value for the corresponding GO term.

However, some similar GO terms can be found not only in the same kinase group but are shared by different families. For instance, in the AGC group (kinase families AGC/AKT, AGC/PKA and AGC/PKC), the phosphorylated proteins of both AGC/PKA and AGC/PKC families were found to be enriched with the GO BP terms ‘Interferon-gamma-mediated signalling pathway (GO: 0002479)’ and certain immune/anti-viral terms including ‘Antigen processing and presentation of exogenous peptide antigen via MHC class I (TAP-dependent) (GO: 0002479)’, ‘Antigen processing and presentation of exogenous peptide antigen via MHC class I (TAP-independent) (GO: 0002480)’, ‘Antigen processing and presentation of peptide antigen via MHC class I (GO: 0002474)’. This observation is consistent with previous experimental studies of the activities of these two kinase families (Burke et al., 1989; David-Watine and Yaniv, 1996; Kirshner, 2000; Lv et al., 2015). The GO_MF term ‘Protein kinase activity (GO: 0004672)’ was over-represented in phosphorylated proteins of AGC/AKT and AGC/PKA families, and ‘Enzyme binding (GO: 0019899)’ was over-represented in phosphorylated proteins of AGC/AKT and AGC/PKC families. In the case of the CMGC group (family CMGC/CDK, CMGC/CK2, CMGC/GSK and CMGC/MAPK), the GO_CC term ‘Nucleus (GO: 0005634)’ and the GO_BF term ‘Positive regulation of transcription from RNA polymerase II promoter (GO: 0045944)’ were over-represented in phosphorylated proteins for all these four kinase families.

In addition, our analysis also identified significantly enriched GO terms which were in good agreement with several previous experimental studies. For instance, the phosphorylated substrate of the Atypical/PIKK family was found to be enriched in the biological process of ‘Cellular response to DNA damage stimulus’. This is not surprising considering the fact that ATM and ATR have been identified as important members of this family due to their key roles in DNA damage response (Cortez et al., 1999; Zhou and Elledge, 2000). Similarly, the CMGC/CDK kinase family was characterized to be significantly enriched in the biological process of ‘cell division’. For example, the cyclin-dependent kinases (CDKs) from the CMGC/CDK family, have been previously demonstrated to be strongly associated with the process of cell division (Ortega et al., 2003; Wang et al., 2000). In addition, our analysis identified that the GO CC term ‘Focal adhesion’ was enriched for the TK/Src, consistent with the known regulatory role for Src at this subcellular location (Frame, 2004). Overall, the GO term enrichment analysis suggests that kinase-specific phosphorylated proteins play multi-faceted and fundamentally important roles in a variety of biological processes.

4 Conclusion

In this study, we present Quokka, a novel computational tool for rapid and accurate prediction of kinase family-specific phosphorylation sites in the human proteome. Quokka combines various sequence-scoring functions, and a logistic regression optimization algorithm is used to train the optimal model for each kinase family. Our empirical studies, based on cross-validation and independent tests, demonstrate Quokka logistic regression models’ competitiveness by outperforming existing tools, including NetPhos 3.1, KinasePhos 2.0, PhoScan, GPS 2.0, Musite, PhosphoPICK, PhosphoPredict and GPS 3.0. The improved performance of Quokka can be attributed to three major factors: i) Extraction of the most-recent experimental datasets that provide up-to-date knowledge on kinase-specific phosphorylation; ii) Inclusion of a variety of sequence-scoring functions and their combinations for calculating scores for each phosphorylation site, which were subsequently used as input features of the logistic regression models. These scoring functions themselves can be used as phosphorylation site prediction methods. Thus, Quokka is a two-level prediction system. The sequence-scoring functions are the first-level, while the subsequent logistic regression models are the second-level of this predictive system; iii) Use of an optimization algorithm to build the optimized logistic regression models which showed robust predictive power for each kinase family. The Quokka web server further provides a user-friendly interface and allows customizable prediction of kinase family-specific phosphorylation sites. The predicted human phosphoproteomic data by Quokka is also provided for further biological validation and analysis. We anticipate Quokka will be a valuable addition to efforts in developing next-generation bioinformatics tools for phosphorylation site identification and phosphoproteomic data analysis. We intend to apply this two-level prediction system to the prediction of kinase-specific phosphorylation sites of other species in our future work.

Funding

This work was supported by grants from the Australian Research Council (ARC) (LP110200333 and DP120104460), National Health and Medical Research Council of Australia (NHMRC) (490989), the National Institute of Allergy and Infectious Diseases of the National Institutes of Health (R01 AI111965) and a Major Inter-Disciplinary Research (IDR) Grant Awarded by Monash University. CL is currently supported by an NHMRC CJ Martin Early Career Fellowship (1143366). AL and TML were partially supported by Informatics start-up packages through the UAB School of Medicine. TL is an ARC Australia Laureate Fellow (130100038). RJD is an NHMRC Principal Research Fellow (1058540).

Conflict of Interest: none declared.