Data Analysis in Emission Tomography Using Emission–Count Posteriors

Abstract

A novel approach to analysis of emission tomography data using the posterior probability of the numbers of emissions per voxel (emission–count) conditioned on acquired tomographic data is explored. The posterior is derived from the prior and the Poisson likelihood of the emission–count data by marginalizing voxel activities. Based on emission–count posteriors, examples of Bayesian analysis including estimation and classification tasks in emission tomography are provided. The application of the method to computer simulations of 2D tomography is demonstrated. In particular, the minimum–mean–square–error (MMSE) point estimator of the emission–count is demonstrated. The process of finding this estimator can be considered as a tomographic image reconstruction technique since the estimates of the numbers of emissions per voxel divided by voxel sensitivities and acquisition time are the estimates of the voxel activities. As an example of a classification task, a hypothesis stating that some region of interest (ROI) emitted at least or at most r–times the number of events in some other ROI is tested. The ROIs are specified by the user. The analysis described in this work provides new quantitative statistical measures that can be used in decision making in diagnostic imaging using emission tomography.

1. Introduction

In emission tomography (ET) we are faced with a task of obtaining information about scanned object from tomographic data. The data consist of a list of events registered by a tomographic camera. In this work we investigate a conditional statistical approach to analyze data acquired in ET. The conditional approach to statistical inference is frequently referred to as conditional Bayesian analysis. Our method extends the algorithms investigated in the past [1, 2] providing statistical significance to the results of these algorithms and based on the statistical theory developed in this work introduces a set of new algorithms that can be used for drawing inferences about ET data.

We define an event as a nuclear decay in an imaged volume that directly or indirectly creates photons which later are detected by the camera. We assume each detected event corresponds to a single nuclear decay that occurred in the imaged volume. As an example of the emission tomographic imaging modality in Figure 1, a schematic of the positron emission tomography (PET) scanner is depicted with and without time–of–flight (TOF) capability. For PET, the positron is created by β⁺ decay from the commonly used medical–imaging agent, ¹⁸Fluorine. A pair of photons is created after annihilation of positrons with electrons from the body. The annihilation photons propagate in opposite directions (180° apart in the center–of–mass system) and are detected in coincidence by two detector crystals (Figure 1 A B and C D). The difference of arrival times for these two photons can be measured and recorded for TOF–PET. In 3D PET scanners (multiple rings of detectors) the number of crystals is of the order of 20–30 thousand. Assuming a rough estimate of the scanner radius as 90 cm, and a difference in arrival time measured with a precision of 1 ps this gives approximately 10⁹ different ways in which an event can be registered by the scanner. This is typically much larger than the actual number of events detected, since the number of detected events is restricted by the amount of radioactive material that is administered to patients and by the limited sensitivity of the camera. Usually, the number of detected events is no more than 10⁹ and typically much less than this number. In the reminder of this paper we will refer to the set of parameters that describes a possible way of detecting the event as a projection element. The number of projection elements is the number of ways an event can be detected by the camera. For the example presented in Figure 1, the projection element is specified by the two crystals in which the interaction occurred (A B or C D) and the difference in the time–of–arrival.

Figure 1.

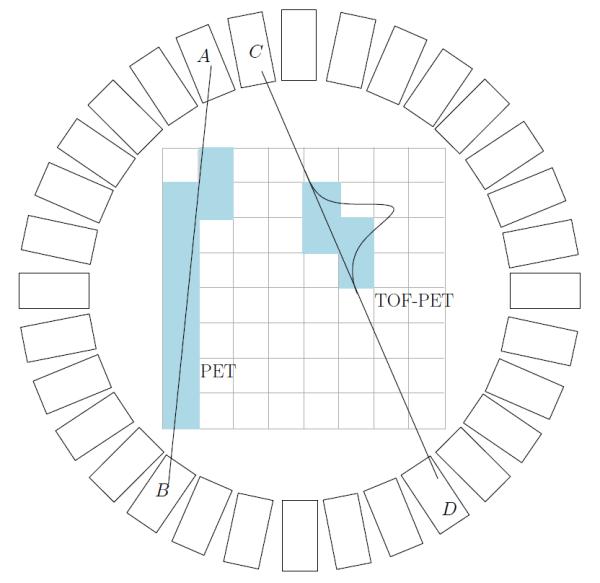
Schematic drawing of a PET scanner. Rectangles represent detector crystals. For standard PET, coincidence event detected in A and B define a line along which the origin of the event is located. For time–of–flight PET the difference in time of arrival is measured and location of the origin is assumed to be located in some section of the line joining detectors C and D. Shaded pixels represent possible pixels that contain the origin of the event. Note that for the TOF the number of these pixels is substantially smaller indicating more precise localization.

The approach described here is expected to provide information that is valuable in practical applications. For example, in amyloid imaging a quantitative value is used to indicate abnormal amyloid deposition i.e. a high (larger than predefined threshold) ratio of concentrations of the tracer between regions in the gray matter and reference regions usually placed on the cerebellum. The method presented in this paper can provide not only the ratio but also the probability that the ratio is larger than some threshold. In a decision theoretic setting, this information, combined with the loss function defined for false positive and false negative findings, provides the decision support for calling the study normal or abnormal.

Another interesting example of the application of information provided by the method presented in this work is the calculation of standardized uptake values (SUV) that is a common task in PET imaging. The confidence sets (Bayesian version of classical confidence intervals) for SUV values can easily be obtained. In longitudinal studies that look at SUVs our method provides the means for sound decision making about an increase or decrease in SUV over time i.e., the probability that SUV increased/decreased by some amount can be determined simply. These calculations can be done for modalities such list–mode TOF–PET for which the assessment of the precision of SUV estimate is very difficult using classical methods based on variance estimation.

2. Statistical Analysis

2.1. Preliminaries

It is assumed that during the scan N events were detected and, in principle, each event may or may not have been detected in a different projection element. Therefore, the method is general and works for either binned or list–mode (unbinned) data. In practice, N will vary from 20,000 for some 2D problems to hundreds of millions for 3D PET scanners. We assume that the imaged volume is divided into voxels (2D version depicted in Figure 1) and there are a total of I voxels. Typically, the 3D volume is divided into cubes of size around 4 mm and 128 × 128 × 128 voxels are used. The geometry of the scanner, photon attenuation, Compton scatter, efficiency of the detectors etc. are factored in into a single large matrix that will be referred to in this article as a system matrix. The element of the system matrix α_ki describes the probability that the event emitted in the voxel i is detected in the projection element k. By K we indicate the total number of projection elements. In this formulation, the number of events registered in projection element k will be denoted by g_k. For scanners with a large number of detector elements the g_k will usually be either zero or one, but in this work we keep it general and g_k can be any non–negative integer number.

The typical goal of the tomographic data reconstruction in ET is to determine emission intensities for voxels based on a list of events detected by the scanner. The units of emission intensities are the number of events divided by the unit of volume divided by the unit of time. We assume that the acquisition time is 1 and the volumes of all voxels are the same and equal to 1. In this case, the emission intensities are in units of numbers of events. The vector f of size I signify the voxel activities with element f_i denoting the emission intensity of voxel i.

2.2. Classical Statistical Analysis in ET

An overwhelming majority of the analyses of the ET data today is based on the classical approach to statistics, in which the values of unknown parameters (eg. voxel activities) are deterministic. When analyzing imaging systems or reconstruction methods this approach involves averaging over all possible data sets assuming the values of parameters are constant. In practice the use of multiple noise realizations (multiple data sets, MDS) which approximates averaging over all possible outcomes, is common. The typical result of MDS approach, estimates of biases, variances, and covariances, are important and useful indicators used in medical imaging to characterize performance of inverse tomographic methods for a given imaging system and assumed object. The MDS are demanding in terms of computing time and approaches have been developed to approximate MDS calculation of the biases and variances of the quantities of interest. Obviously the MDS are more difficult to realize when only a single data set is available (a typical clinical scenario). Statistical analysis when only a single sample of the data is available can be performed assuming the variance of the data is known and the propagation of variance in the image reconstruction process can be studied. When data variance is unknown it can be approximated for Poisson statistics by assuming that it is equal to the data. The quality of this approximation drops as the g_k become smaller.

To determine the statistical properties of the linear estimator Huesman 1984 [3] calculated the covariances of the parameters in the reconstruction image for filtered backprojection (FBP) exploiting linearity of the FBP operation. For non–linear estimation methods such expectation maximization (EM) [4, 5, 6] and general iterative methods that maximize penalized likelihoods [7] covariance of the estimate can be approximated without relying on MDS [8, 9, 10, 11, 12]. The computational cost for approximate methods for non–linear estimations is high and the methods have so far not found wide applications.

2.3. Conditional Analysis in ET

The conditional approach to statistics shifts the modeling of randomness from the data to the unknown parameters. In the conditional approach, the data are assumed constant and equal to the actual measurement. We will refer to this approach as the conditional Bayesian approach [13]. The word ‘conditional’ is used because of the fact that the analysis does not use the classical concept of averaging over all possible data sets; i.e. relies solely on the single dataset that was actually observed. This approach seems better suited than classical methods for analysis of just a single ET data set acquired in the clinical setting as knowledge of data variance is not necessary to perform the statistical analysis.

The description of conditional statistics is fully described by the posterior probability (or simply the posterior). In this paper we do not make a distinction in notation between probability and probability density, and always refer to distributions as probabilities. Whether probability or probability density is being considered should be obvious from the context.

In the past, some applications of Bayesian analysis have been investigated in the standard setting where voxel activities were considered as unknown parameters. In our approach we analyze emission counts. A high computational cost associated with evaluating the posterior $\mathcal{P}(\mathbf{f}\mid \mathbf{g})\propto \mathcal{P}(\mathbf{g}\mid \mathbf{f})\mathcal{P}\left(\mathbf{f}\right)$ is an obstacle even with today’s powerful computers to the widespread utilization of methods based on analysis of the posterior. The first work published by Geman and McClure [14] developed two Bayesian estimators of the image activities f for single photon emission computed tomography (SPECT). The maximum a posteriori (MAP) and minimum–mean–square-error (MMSE) estimators corresponding to the posterior mean were developed. The estimators were determined by using Monte Carlo methods and Gibbs sampling [15]. Monte Carlo methods based on Metropolis–Hastings sampling were used by Higdon [16] and Weir [17] who determined the posterior nodes and means and used hierarchical approaches in order to implement the priors. Credible sets for the estimators were also determined.

Most of the work done so far in terms of statistical analysis applies to binned data (sinograms) and in most cases it is not applicable to list–mode (unbinned) data. Our conditional approach does not make a distinction between these two types of acquisitions and applies the same to binned and list–mode data.

We depart from the standard formulation of the conditional inverse tomography investigated in the past in which the posterior of voxel activities was analyzed. In conditional Bayesian approach formulated here, we derive the posterior probability of the number of events emitted per voxel (emission count) and draw inferences from it. The inferences are drawn by means of the Origin Ensemble (OE) algorithm that is used to obtain samples of the posterior. By averaging the samples, the expectations over the posterior of various quantities can be determined.

Algorithms for image reconstruction based on origin ensemble were derived and used by us and others in the past [1, 18, 2, 19, 20]. In previous studies the origin ensemble algorithms were used but no statistical significance of the results were provided. In the first paper in which the algorithm was given [1], the algorithm was derived by assuming that the voxel activity can be estimated by dividing the number of emissions per voxel by sensitivity and acquisition time. This algorithm was investigated thoroughly in [2] and shown to provide reconstructions that approximate standard ML estimates of voxel activities for a high number of acquired counts. Slight ad hoc modifications of the algorithm derived in [1] were used for problems of the reconstruction of Compton Camera data in [18, 19, 20] and have shown to provide reconstructions comparable with ML approaches. This lack of statistical theory underlying the algorithm prevented investigators from making statistical inferences about the results and only point estimates of EC were provided in work published up–to–date as the statistical significance of the results of this method were unavailable.

In this work we provide the complete statistical theory of the approach. The understanding of the theory allows us to not only use point estimates of the EC but also to draw other inferences from the data and to understand the significance of modifications of the algorithm used in previous published work.

3. Derivation of Emission–Count Posterior

We will use the concept of the unobservable complete–data random variable Y with a vector y being a realization from Y. The complete data was introduced to emission tomography by Shepp and Vardi [5] who used it to derive the expectation–maximization (EM) algorithm [4] for estimation of emission intensities from tomographic projection data. y is defined as a vector with elements y_ki which describes the unobservable number of counts emitted in the voxel i and detected in the detector element k. Although double indexes are used, the y is a vector with K × I elements. The y will be refereed to as emission counts.

The goal of this section is to derive the posterior of the emission counts per voxel, conditioned on the acquired data $\mathcal{P}(\mathbf{y}\mid \mathbf{g})$. It is clear that this posterior is discrete since y is discrete. First, the following conditional is defined which can be interpreted as data likelihood

$$\mathcal{P}(\mathbf{g}\mid \mathbf{y})=\{\begin{array}{cc}1\hfill & \text{if}{\sum }_{i=1}^I{y}_{\mathit{ki}}=g_k\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (1)

Using Bayes theorem the posterior becomes a ratio of marginals of y and g multiplied by $\mathcal{P}(\mathbf{g}\mid \mathbf{y})$:

$$\mathcal{P}(\mathbf{y}\mid \mathbf{g})=\frac{\mathcal{P}\left(\mathbf{y}\right)}{\mathcal{P}\left(\mathbf{g}\right)}\mathcal{P}(\mathbf{g}\mid \mathbf{y})=\frac{{\int }_{\mathbf{f}}\mathcal{P}(\mathbf{y}\mid \mathbf{f})\mathcal{P}\left(\mathbf{f}\right)}{\mathcal{P}\left(\mathbf{g}\right)}\mathcal{P}(\mathbf{g}\mid \mathbf{y}).$$ (2)

The posterior is non–zero only for the subspace (Y_g) of Y corresponding to the observed data g which comes from the definition of likelihood in eq. 1. To keep the notation clear we will indicate the posterior by $\mathcal{P}(\mathbf{y}\mid \mathbf{g})$ keeping in mind that it is equal to zero if y ∉ Y_g. We use simplified notation such ${\int }_{\mathbf{f}}={\int }_0^{\infty }{\mathit{df}}_{1\cdots }{\int }_0^{\infty }{\mathit{df}}_I$. We implicitly assumed that since the f_i represent physical quantities the values cannot be negative. This is equivalent to requirement that the prior on $\mathcal{P}\left(\mathbf{f}\right)$ is 0 for f_i < 0. It should be pointed out that even though we are calculating the posterior on y, the prior is specified on f.

The denominator of the above equation is independent of y and therefore it is factored in the constant Z. In all sections constants are denoted as Z although they will have different values depending on the context.

Since the emission of counts from voxels is a Poisson process the conditional probability of y conditioned on f can be specified using Poisson distribution

$$\mathcal{P}(\mathbf{y}\mid \mathbf{f})=\prod _{i=1}^I\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}{f}_i\right)}^{y_{\mathit{ki}}}{e}^{-{\alpha }_{\mathit{ki}}{f}_i}}{y_{\mathit{ki}}!}=\prod _{i=1}^I{\left(f_i\right)}^{c_i}{e}^{-{∊}_i{f}_i}\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}$$ (3)

where ${∊}_i={\sum }_{k=1}^K{\alpha }_{\mathit{ki}}$ is the detection sensitivity of voxel i i.e. the probability that if a count is emitted in voxel i it is detected by the camera. The $c_i={\sum }_{k=1}^K{y}_{\mathit{ki}}$ is the total number of emitted and detected counts from voxel i. In the above equation the functional dependence on f is described by the gamma distribution.

In the following three sections we derive the explicit form of the posterior $\mathcal{P}(\mathbf{y}\mid \mathbf{g})$ by marginalizing f using different priors.

3.1. Flat Prior

The most straightforward prior $\mathcal{P}\left(\mathbf{f}\right)$ to implement here is the non–informative flat prior which assumes that the prior probability of all values of the activity per voxel are equally likely for f_i ≥ 0 and zero otherwise. This can be summarized by

$${\mathcal{P}}_F\left(\mathbf{f}\right)\propto 1$$ (4)

The posterior that is independent of f is obtained from Eqs. 2 and 3 by integrating out (see Appendix B) the voxel activities f_i which leads to

$${\mathcal{P}}_F(\mathbf{y}\mid \mathbf{g})\propto \prod _{i=1}^I\frac{\Gamma (c_i+1)}{{\left({∊}_i\right)}^{c_i}}\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}\text{for}\mathbf{y}\in Y_{\mathbf{g}}$$ (5)

and zero for y ∉ Y_g. The symbol Γ(A) is a Gamma function equal to ${\int }_0^{\infty }{t}^{A-1}{e}^{-t}\mathrm{d}t$.

3.2. Truncated Flat Prior

The assumption made in section 3.1 of a flat prior is simplistic. A probability of the voxel activity being infinite cannot be the same as the probability that the activity is close to zero since it is known that, due to the limited radioactive dose, f_i < ∞. Therefore it is more reasonable to assume that activities have probabilities between zero and some maximum Φ_i and zero otherwise. This is a generalization of the flat prior since for Φ_i → ∞ the flat prior is obtained. Truncation of the flat prior makes it proper. The truncated flat prior can be expressed by the following:

$${\mathcal{P}}_T\left(\mathbf{f}\right)=\frac{1}{{\prod }_{i=1}^I{\Phi }_i}\prod _{i=1}^I{\chi }_{[0,{\Phi }_i]}\left(f_i\right)$$ (6)

where χ_[0,Φi](f_i) is an indicator function equal to 1 for f_i ∈ [0, Φ_i] and 0 otherwise. This leads to the following posterior

$${\mathcal{P}}_T(\mathbf{y}\mid \mathbf{g})=\frac{1}{Z}\prod _{i=1}^I\frac{\gamma (c_i+1,{∊}_i{\Phi }_i)}{{\left({∊}_i\right)}^{c_i}}\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}\text{for}\mathbf{y}\in Y_{\mathbf{g}}$$ (7)

where γ(A, B) is a lower incomplete Gamma function equal to ${\int }_0^B{t}^{A-1}{e}^{-t}\mathrm{d}t$

3.3. Conjugate Prior

Suppose the mean of voxel activity ϕ_i is specified a priori. The conjugate prior is postulated as follows:

$${\mathcal{P}}_C\left(\mathbf{f}\right)=\frac{1}{Z}\prod _{i=1}^I{\left(f_i\right)}^{{\beta }_i{\varphi }_i-1}{e}^{-{\beta }_i{f}_i}.$$ (8)

where Z is a normalization constant. The prior distribution is designed such that the mean is at f_i = ϕ_i for all i. Parameter β_i (rate parameter of the Gamma distribution) can be interpreted as the confidence in the knowledge of ϕ_i. For large values of β_i the prior distribution is strongly peaked around ϕ_i (high confidence). We require that a priori specified values of ϕ_i and β_i are such that ϕ_iβ_i ≥ 1. This guarantees that the integral of the prior probability is finite and can be normalized to 1. For β_i → 0 and β_iϕ_i = 1 the conjugate prior is reduced to flat prior. See section 6 for more discussion on the conjugate prior postulated here.

Using Eqs. 2, 3, and 8 and integrating out f the resulting posterior is

$${\mathcal{P}}_C(\mathbf{y}\mid \mathbf{g})=\frac{1}{Z}\prod _{i=1}^I\frac{\Gamma (c_i+{\beta }_i{\varphi }_i)}{{({∊}_i+{\beta }_i)}^{c_i}}\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}\text{for}\mathbf{y}\in Y_{\mathbf{g}}$$ (9)

and zero for y ∉ Y_g.

4. Numerical Evaluation of the Posteriors

A very popular Bayesian approach for finding point estimates of voxel activities is based on maximum a posteriori (MAP) estimation. The MAP estimate corresponds to node of the posterior. It is computationally the easiest Bayesian analysis that can be performed in medical imaging when parameters are continuous. However, calculation of the expectations needed to perform other types of Bayesian analysis is much more difficult and computationally intensive. Interestingly, for EC posterior the situation is the opposite. Finding the maximum of the posterior is very difficult because the posterior has high–dimensionality and it is discrete. On the other hand, sampling the emission–count posterior and evaluating expectations is relatively straightforward as will be shown in the following section.

The factor y_ki! in equations 5, 7, and 9 is problematic from the computational point of view. Even taking into account the sparsity, this vector is typically too large to store in the computer memory. As we will show below this factor disappears when the emission–count posterior is considered in the Origin Ensemble [1] space. We first introduce a new discrete random variable s that we will refer to as a state from Origin Ensemble (OE) of states. The element of this discrete random vector s_in is either 0 or 1 and indicate if the origin of the detected event n is located in voxel i for state s. It follows that s_ni equal to 1 indicates that the origin of the event n is in voxel i and 0 that is not. For a given y there are m(y) corresponding OE states. If locations of two events detected in the same detector element k are interchanged it is the same y but corresponds to two different OE states, before and after interchanging. This reasoning can easily be generalized and using combinatorics we obtain:

$$m\left(\mathbf{y}\right)=\prod _{k=1}^K\frac{g_k!}{{\prod }_{i=1}^I{y}_{\mathit{ki}}!}\text{for}\mathbf{y}\in Y_{\mathbf{g}}$$ (10)

For list mode data for which g_k is either 0 or 1 it is obvious that OE space and Y space are the same. Since there is no reason to say otherwise, we assume that all OE states that correspond to the same y are equally probable which leads to:

$$\mathcal{P}(\mathbf{s}\mid \mathbf{g})=\frac{\mathcal{P}(\mathbf{y}\mid \mathbf{g})}{m\left(\mathbf{y}\right)}=\frac{1}{Z}\mathcal{P}(\mathbf{y}\mid \mathbf{g})\prod _{i=1}^I\prod _{k=1}^K{y}_{\mathit{ki}}!$$ (11)

subject to ${\sum }_i^I{\sum }_n^N{s}_{\mathit{ni}}{1}_k\left(n\right)={\sum }_i^I{y}_{\mathit{ki}}=g_k$ where 1_k(n) is an indicator function equal to 1 if the event n was detected in the detector element k and zero otherwise. For the posteriors Eqs. 5, 7, and 9 considered in OE space the problematic term y_ki! cancels.

Even without the y_ki! term, the posteriors seem difficult to evaluate. It can be noticed by considering two states from the OE that differ just by the location of a single event and considering the ratios of posterior probabilities of two such states, the formulas for the ratios become quite simple. Without losing generality, we assume that the event n detected in projection element k in OE state s is located in voxel i, and in OE state s’ in voxel i’. Note that α_ki must be larger than 0. In this case, the ratios of posteriors for OE states s and s’ assuming $\mathcal{P}(\mathbf{s}\mid \mathbf{g})>0$ can be derived from Eqs. 5, 7, and 9 and have the following simple forms for the priors that were considered:

$$\frac{{\mathcal{P}}_F({\mathbf{s}}^{\prime }\mid \mathbf{g})}{{\mathcal{P}}_F(\mathbf{s}\mid \mathbf{g})}=\frac{{\alpha }_{{\mathit{ki}}^{\prime }}{∊}_i(c_{i^{\prime }}+1)}{{\alpha }_{\mathit{ki}}{∊}_{i^{\prime }}{c}_i},$$ (12)

$$\frac{{\mathcal{P}}_T({\mathbf{s}}^{\prime }\mid \mathbf{g})}{{\mathcal{P}}_T(\mathbf{s}\mid \mathbf{g})}=\frac{{\alpha }_{{\mathit{ki}}^{\prime }}{∊}_i(c_{i^{\prime }}+1-\zeta (c_{i^{\prime }}+1,{∊}_{i^{\prime }}{\Phi }_{i^{\prime }}\left)\right)}{{\alpha }_{\mathit{ki}}{∊}_{i^{\prime }}(c_i-\zeta (c_i,{∊}_i{\Phi }_i\left)\right)}$$ (13)

where ζ(A, B) is $\frac{B^A{e}^{-B}}{\gamma (A,B)}$, and

$$\frac{{\mathcal{P}}_C({\mathbf{s}}^{\prime }\mid \mathbf{g})}{{\mathcal{P}}_C(\mathbf{s}\mid \mathbf{g})}=\frac{{\alpha }_{{\mathit{ki}}^{\prime }}({∊}_i+{\beta }_i)(c_{i^{\prime }}+{\beta }_{i^{\prime }}{\varphi }_{i^{\prime }})}{{\alpha }_{\mathit{ki}}({∊}_{i^{\prime }}+{\beta }_{i^{\prime }})(c_i+{\beta }_i{\varphi }_i-1)}$$ (14)

where the values of c_i and c_i’ are ones for OE state s from the definition, $c_i={\sum }_{n=1}^N{s}_{\mathit{ni}}$ and $c_{i^{\prime }}={\sum }_{n=1}^N{s}_{{\mathit{ni}}^{\prime }}$. The explicit dependence of c_i on s was dropped for clarity. See appendix Appendix C for derivation of the above ratios from posteriors given in Eqs. 5, 7, and 9. The above ratios can be used to construct a Markov Chain in which subsequent states in the chain differ by just the location of a single event.

Whichever Bayesian analysis technique is chosen the posterior probabilities need to be sampled in some computationally efficient way. The simplicity of equations 12, 13, and 14 makes the algorithm an attractive approach from the point of view of computational efficiency. It depends only on the total number of events in each voxel for a given state s and no calculation is done in projection space; therefore, expensive computation of the likelihood in projection space, needed for standard approaches, is not necessary. We used the Metropolis approach [21] to sample the space s:

• (i) Select starting state s₀. This can be done by randomly selecting for each event detected in projection element k a voxel for which α_ki > 0 i.e. assign the origin of the event to this voxel.

• (ii) Randomly select an event n, note the voxel i in which the origin of n is located for s.

• (iii) Randomly select a candidate new voxel i’ for event n with α_ki’ > 0.

• (iv) Move event n to candidate voxel with a chance equal to

  $$\min \left(1,\frac{\mathcal{P}({\mathbf{s}}^{\prime }\mid \mathbf{g})}{\mathcal{P}(\mathbf{s}\mid \mathbf{g})}\right)$$ (15)

  where s indicates a state with the event n in i and s’ a state with the event n in i’. The ratio of probabilities $\frac{\mathcal{P}({\mathbf{s}}^{\prime }\mid \mathbf{g})}{\mathcal{P}(\mathbf{s}\mid \mathbf{g})}$ can be one of ones defined by Eqs. 12, 13, or 14.

• (v) Repeat last 3 steps

One iteration of the algorithm is defined as repetition of the algorithm above N times. For the reminder of this paper we refer to the above algorithm as the OE algorithm.

4.1. MMSE Estimator

The OE algorithm described above is a reversible Markov Chain with Metropolis sampling. The algorithm will reach a steady state regardless of the starting point. Once in the steady state, future states are drawn with a chance proportional to the posterior. Effectively then, the expectation value over the posterior $E^{\mathcal{P}(\mathbf{y}\mid \mathbf{g})}\left[F\right(\mathbf{y}\left)\right]$ of any other function F(y) can be estimated. For example, the minimum mean square error (MMSE) estimator of the number of emitted counts per voxel $c_i={\sum }_{k=1}^K{y}_{\mathit{ki}}$ can be calculated as:

$${\widehat{c}}_i=\sum _{\mathbf{y}\in {\mathbf{Y}}_{\mathbf{g}}}{c}_i\mathcal{P}(\mathbf{y}\mid \mathbf{g})=\sum _{\mathbf{s}}{c}_i\mathcal{P}(\mathbf{s}\mid \mathbf{g})\approx \frac{1}{T}\sum _{t=1}^T{c}_i\left({\mathbf{y}}_{{\mathbf{s}}_t}\right)$$ (16)

where T indicates the number of samples taken from the chain while in steady state, and y_st indicates a vector y corresponding to OE state s_t.

4.2. Hypothesis Testing Using Emission–Count Posteriors

Binary and multiple hypothesis testing with Bayesian emission–count posteriors can also be done relatively easily. For the hypothesis testing in a conditional Bayesian setting used in this work, a loss function L(y, D_m) is specified which describes a penalty incurred when a decision D_m is made in favor of hypothesis H_m. Index m = 1…M indicates the hypothesis number; for a binary test, m = {1, 2}. We assume that the loss is zero for correct decisions. A decision–theoretic selection of D_m is made based on the smallest posterior expected loss, i.e. we seek to minimize the expectation ρ(D_m) of the loss for decision m.:

$$\rho \left(D_m\right)=E^{\mathcal{P}(\mathbf{y}\mid \mathbf{g})}\left[L\right(\mathbf{y},D_m\left)\right].$$ (17)

One of the simplest forms of the loss function that can be used is a 0 – K_m loss.

$$L(\mathbf{y},D_m)=\{\begin{array}{cc}0\hfill & \text{if}\mathbf{y}\in {\mathbf{Y}}_m\hfill \\ K_m\hfill & \text{if}\mathbf{y}\notin {\mathbf{Y}}_m\hfill \end{array}\phantom{\}}$$ (18)

where K_m is positive. By Y_m we indicate a subspace of Y for which hypothesis m is true.

For the special case of a binary hypothesis with 0 – K loss, the posterior expected losses are $\rho \left(D_1\right)=K_2\mathcal{P}({\mathbf{Y}}_1\mid \mathbf{g})$ and $\rho \left(D_2\right)=K_1\mathcal{P}({\mathbf{Y}}_2\mid \mathbf{g})$. Where Y₁ and Y₂ indicate subspaces of Y for which H₁ and H₂ are true. For notational convenience we used the following definitions $\mathcal{P}({\mathbf{Y}}_1\mid \mathbf{g})={\sum }_{\mathbf{y}\in {\mathbf{Y}}_1}\mathcal{P}(\mathbf{y}\mid \mathbf{g})$ and $\mathcal{P}({\mathbf{Y}}_2\mid \mathbf{g})={\sum }_{\mathbf{y}\in {\mathbf{Y}}_2}\mathcal{P}(\mathbf{y}\mid \mathbf{g})$.

5. Application to computer simulated tomography data

We used computer simulations of a 2D tomographic system. The reconstruction area consisted of 64×64 pixels with pixel size equal to 1 – the total number of image elements was I = 4096. We simulated 60 projections over 180°, each with 64 bins (K = 3840). The size of each projection bin was 1. The element of the system matrix α_ki was defined as the area of pixel i inside the parallel strip defined by projection bin k. This resulted in ∊_i equal to 60 for each pixel i.e. an area of 1 was projected onto 60 projections. Next, the activity for each voxel f_i was simulated as shown in Fig. 2, and noiseless data $\tilde{g}$ were generated as ${\tilde{g}}_k={\sum }_i^I{\alpha }_{\mathit{ki}}{f}_i$. The noiseless data were scaled such that the sum of all 3840 projection bins was equal to the desired number of detected counts. Three levels of total counts were simulated 20k (low), 100k (normal), and 2M (high). The Poisson distributed noise deviates were determined from the noiseless projection data. Figure 2 shows the noiseless sinogram and examples of noisy sinograms for a total of 20k and 2M counts. Since we aimed to investigate statistical properties in this work, the idealized tomographic system was used in which no attenuation, Compton scatter, finite spatial and energy resolutions of the detectors were simulated. This was done so the effects due to inaccuracies in system modeling were avoided.

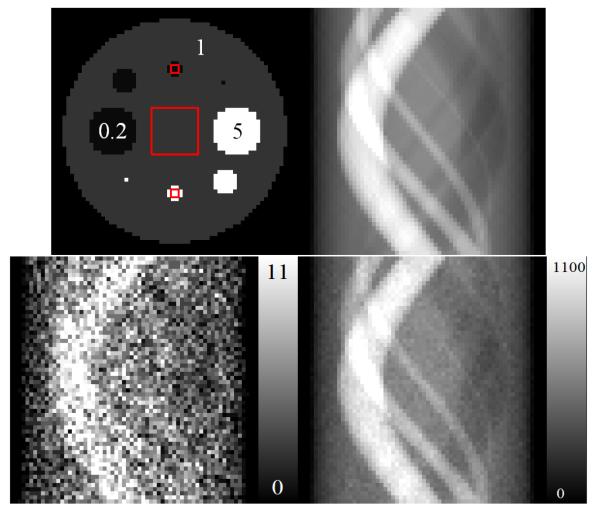
Figure 2.

Test image used in this work (upper–left). Three ROIs are marked as red squares. The numbers correspond to relative activities per pixel. The upper–right image is the noiseless sinogram of the test image. The bottom row shows two sinograms corresponding to noisy data with Poisson distributed noise with a total of 20k and 2M counts, respectively.

The object consisted of a large background circle with eight smaller circles representing lesions. The activity of the lesions was simulated to achieve a 5:1 ratio between hot lesions and the background, and a 0.2:1 ratio between cold lesions and the background. Three ROIs were identified (Fig. 2), one 12×12 pixels in size, positioned in the center of the object, and two 2×2–pixels in size, positioned on high– and low–intensity regions.

Calculations of the posterior expectations and marginalized distributions were done using 5000 iterations of the OE algorithm as a burn–in period (required for the algorithm to reach equilibrium) followed by 5 million iterations for low, 100 thousand iterations for normal, and 20 thousand iterations for high count cases. To make sure that system reaches equilibrium we observed the number of iteration at which number of counts in ROIs does not change significantly (which was around 1000 iterations) and then multiplied it by 5 to make sure equilibration is reached. We assumed that correlations between y in subsequent iterations can be ignored because assuming similar correlation times they average out in the long run (more than 20 thousand iterations). This assumption was verified by comparing results when samples were obtained in every iteration and in every hundred iterations and we found resulting images and distributions indistinguishably close. For current implementation using code not optimized for speed, the computing time for 1 iteration for 100k counts was 0.8 seconds on Xeon E5520 @ 2.27 GHz CPU and scaled linearly with number of counts. For analysis with the truncated flat prior, we assumed that Φ_i was the same for each pixel and equal to 1.1 times the maximum value of simulated activity per pixel.

We used the maximum–likelihood (ML) expectation–maximization (EM) algorithm [5] to obtain ML estimates of pixel activities (f). This was done by performing 10,000 iterations of the EM algorithm [5] so the ML solution was determined within the limits of the double–precision numerical accuracy.

5.1. Estimation of Emission–Count Images

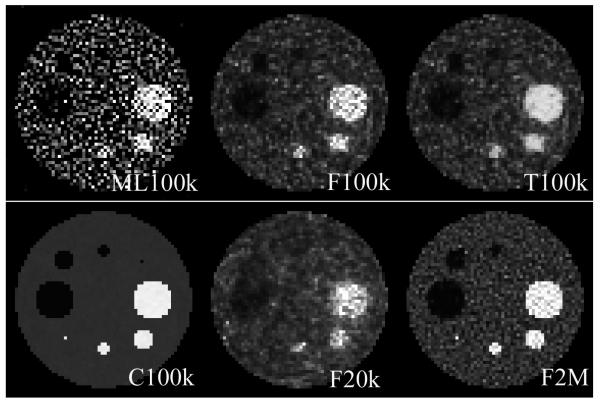
Images of the MMSE estimators of the number of emission counts per pixel using a flat prior are shown in Figure 3. The pixel values were determined using equation 16. Note that with an increasing number of acquired counts, the resulting images appear less noisy and resemble the original image more closely. For a high number of counts (2M), the one–pixel high intensity object can clearly be identified. For low–count images low–intensity regions are very difficult to identify. We see that the use of a truncated flat prior affects the uniformity of the high–intensity objects, but low–intensity regions and background seem unaffected.

Figure 3.

Estimates of f using ML method, and MMSE estimates of the emission–count for different priors (F–flat, T–truncated flat, C–conjugate with perfect knowledge of the mean) and different total number of counts in the sinogram. We show ML image to demonstrate that noise structure is identical in ML and emission–count MMSE estimates. We are not trying to show the superiority of one method over the other.

Figure 3(second row first column) shows reconstruction with gamma prior with ϕ equal to the true simulated values of f. The values of β were equal to 0.1. This experiment was done to demonstrate the stability of the OE algorithm. It shows that if an accurate prior is used, the OE estimate is very accurate. The lack of accurate prior information when non–informative priors were used for the reconstructions (Figure 3) leads to images that are similar to the ML reconstruction (see Figure 3). Note that although the ML image is much more noisy, artifacts due to noise correlations (artificially increased/deceased relative reconstructed value) are in the same locations in the image compared to MMSE estimates of the emission counts.

5.2. Hypothesis Testing/Detection

One task performed frequently in medical imaging is to determine whether apparent hot lesions (spots of increased uptake of the tracer) are significantly higher than the background region. Another similar task could be to determine if the apparent cold lesion are significantly lower than the background. If we define a signal as an increase (or decrease) of activity in some specified region compared to the background, this can be considered as a detection task.

To simulate such a task, we define two ROIs in the image, one corresponding to the lesion (ROI 1) and one corresponding to the background (ROI 2). Then, we for hot lesions we test if the average number of emissions per pixel in ROI 1 is r or more times higher than the average number of emissions in the ROI 2. For cold lesions we test if the average number of emissions per pixel in ROI 1 is r or more times smaller than the average number of emissions in the background ROI 2. These tasks would correspond to detection of hot and cold spots in the image. For hot lesion detection task we define hypothesis H₁ as the average number of emissions per pixel in ROI 1 being r–times or more higher than in ROI 2 and alternative hypothesis H₂ that it is not. In other words, the signal is defined as an r–times increased emission –count value compared to the background. For the cold lesion, hypothesis H₁ is defied as the average number of emissions per pixel in ROI 1 being r–times or more smaller than in the background ROI 2 and alternative hypothesis H₂ that it is not. Although not investigated in this paper, it is also straightforward to define a signal in terms of an absolute number of emissions.

Using definitions in section 4.2 the expected losses for D₁ and D₂ (decisions in favor of H₁ and H₂) are $\rho \left(D_1\right)=K_2\mathcal{P}({\mathbf{Y}}_1\mid \mathbf{g})$ and $\rho \left(D_2\right)=K_1\mathcal{P}({\mathbf{Y}}_2\mid \mathbf{g})$. Since, for the binary hypothesis $\mathcal{P}({\mathbf{Y}}_1\mid \mathbf{g})+\mathcal{P}({\mathbf{Y}}_2\mid \mathbf{g})=1$, H₁ will be accepted for ρ(D₁) < ρ(D₂), which leads to:

$$\mathcal{P}({\mathbf{Y}}_1\mid \mathbf{g})>\frac{K_1}{K_1+K_2}=\lambda$$ (19)

Decisions are made based on a decision threshold, λ, which is a function of K₁ and K₂. The value $\mathcal{P}({\mathbf{Y}}_1\mid \mathbf{g})$ has an intuitive interpretation as the probability of the hypothesis H₁.

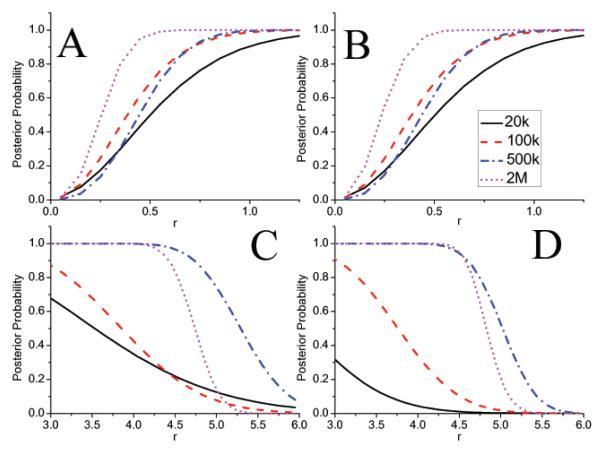
Figure 4 presents the value of the posterior probability of the hypotheses as a function of r. The graphs can be used for the hypothesis testing. For example from figure 4(A) the posterior of the hypothesis for r = 0.5 for 20k counts is about 0.4. Therefore the hypothesis is accepted if λ (see eq. 19) is less than 0.4. We note that use of the truncated prior does not effect the hypothesis about the low–intensity region, but it influences significantly the hypothesis about the high–intensity ROI. This can be appreciated in figure 4 (A) and (B) which shows that the posteriors are almost identical and therefore decisions made based on the posteriors will also be identical. On the contrary for hot lesions (Figure 4(C) and (D)) if decision to be made for 500k counts about lesion emitting at least 5.25 times counts as the background we see that posterior probability of this is 0.54 for flat prior (Figure 4(C)) and 0.24 for truncated flat prior (Figure 4(D)). If the decision threshold λ is assumed to be 0.5 than hypothesis is accepted for flat and rejected for truncated flat prior, respectively. This illustrates the effect of the prior on decision making.

Figure 4.

(A) and (B): values of the posterior probability for the hypothesis the the low–intensity ROI on average emitted r–times or fewer events than the background ROI and, (C) and (D), of the hypothesis that the high–intensity ROI emitted on average r–times or more than the background ROI. Graphs (A) and (C) correspond to the flat prior, and (B) and (D) to the truncated flat prior.

6. Discussion

One of the frequent criticisms of conditional Bayesian methods is concentrated on the issue of the subjectivity introduced by the prior, and relying only on observed data. In general, this issue is a core of the dispute between frequentist (classical) and Bayesian statisticians and is a long–standing problem. We do not wish to enter this discussion here, as it is beyond the scope of this work; however, it should be pointed out that classical methods used in imaging are not without flaws either. The most prominent flaw is that the classical measures used in imaging, such bias and variance, are object dependent. Therefore, if methods are shown to be valid for the assumed object, there is usually no effort expended to provide convincing arguments that the same methods would work for other objects as well. On the other hand, object variability is explicitly addressed in conditional Bayesian methods through the use of priors.

This paper is concerned with theoretical aspects of the novel approach to analysis of the data based on a conditional Bayesian approach for analysis of emission–count posteriors. One of the next steps would be to compare this approach with classical methods. The best procedure to achieve this comparison is far from obvious. One way of proceeding would be to compare the estimates obtained by the standard tomographic reconstruction with the emission–count posterior approach presented in this paper. From the decision–theoretic perspective the most reasonable measure that can be used is Bayes Risk. By using the Bayes risk, the same loss functions and the same priors can be utilized for both classical and conditional Bayesian approaches and averaged over the the objects and data variability. This procedure would provide a fair comparison in the decision theoretic setting between the methods. Unfortunately, for inverse problems in medical imaging the Bayes risk is computationally difficult to calculate especially for classical methods. A straightforward approach to compare point estimates obtained by classical and conditional Bayesian methods can be to use purely frequentist methods as bias/variance (quadratic loss in a decision theoretic setting) or task–specific methods [22, 23] without the use of priors. This in our view is disadvantageous to the conditional Bayesian approach as the method presented in this paper provides much more information over a simple point estimate.

An important aspect of analysis of the tomographic data that was not covered in this paper is the incorporation of attenuation, scatter, normalization, and randoms in the analysis. The attenuation effect is trivial as, for the method presented here it is contained in the system matrix, α, and sensitivity vector, ∊. Inclusion of other effects requires methods specific to the origin ensemble algorithm that we covered in our previous publication [24].

For the particular example presented in this paper, it is quite clear that for the low–count studies (20k and 100k), non–informative priors are not so useful. This is clearly reflected in Figures 4(C)(D), which indicate that the hypothesis that r > 4.5 (true simulated of activities r was 5) would be rejected for most loss functions. The reason for this is the limited information contained in the data. In other words the “strength” of the data is not sufficient to overcome the “strength” of the non–informative prior.

This initial study provides the groundwork for the development of better priors as well as for investigation of limits of quantitation achievable in emission tomography in the conditional Bayesian setting. An interesting continuation of this work is to use the conjugate prior with a good guess for ϕ_i and the hierarchical prior on β. For example a “good guess” can be obtained by performing a simple analytic reconstruction of the image using FBP. Although such a step violates the independence of the data and the prior, it brings into the problem the principles of analytic tomography that constitutes new a priori knowledge. Although not discussed in the paper the objective Jeffreys prior [25] can be easily implemented within our methods as well.

In summary, a novel approach to analysis of emission tomography data using the posterior probability of emission–count is explored. The EC posterior is derived by marginalizing voxel activities. Based on EC posteriors, examples of Bayesian analysis including estimation and classification tasks in emission tomography are provided using computer simulated data. The analysis described in this work provides new quantitative statistical measures that can be used in decision making in diagnostic imaging using emission tomography.

Appendix A. List of symbols used in paper

Table A1.

Glossary

Symbol	Meaning
α	System matrix with size K by I that defines the imaging system
αik	Element of the system matrix that corresponds to i–th voxel and k–th projection element
βi	Rate parameter of Gamma distribution for voxel i used as conjugate prior
c	Vector of size I of the number emissions per voxel
ci	Element of the vector c from the definition equal to ${\sum }_{k=1}^K{y}_{\mathit{ki}}$
${\widehat{c}}_i$	Estimate of ci
Dm	Decision in favor of the hypothesis Hm
∊i	Sensitivity of voxel i equal to ${\sum }_{k=1}^K{\alpha }_{\mathit{ki}}$
f	Vector of size I of voxel activities. Realization of the random variable (RV)
fi	Element i of the vector f
Γ(A)	Gamma function equal to ${\int }_0^{\infty }{t}^{A-1}{e}^{-t}\mathit{dt}$
γ(A, B)	Lower–Incomplete Gamma function equal to ${\int }_0^B{t}^{A-1}{e}^{-t}\mathit{dt}$
g	Data vector of size K. Realization of RV but considered constant for conditional analysis
gk	Element k of the vector g
Hm	Hypothesis m
I	Total number of voxels
K	Total number of projection elements
Km	Value of the constant loss (0 – Km) incurred when wrong decision m is made
λ	Binary decision threshold
L(y, Dm)	Loss function incurred when decision Dm is made assuming y is the true emission count vector
m(y)	Number of OE states that correspond to vector y
N	Total number of acquired counts
$\mathcal{P}\left(A\right)$	Probability or probability density distribution of RV A
$\mathcal{P}(A\mid B)$	Conditional probability or probability density distribution of RV A conditioned on RV B
Φi	Maximum value of activity for voxel i used for definition of truncated flat prior
ϕi	Product of ϕi and βi defines shape parameter of gamma distribution for voxel i used as conjugate prior
r	Ratio of average EC values in ROIs
ρ(Dm)	Expected loss corresponding to decision Dm
s	Vector from the OE space
sni	Element of the vector s equal to 0 or 1 indicating the event n located in voxel i (1 for yes 0 for no)
T	Number of samples used in Markov Chain Monte Carlo to approximate the posterior expectations.
Y	A set of of all possible y’s.
Yg	Subset of Y for which ${\sum }_{i=1}^I{y}_{\mathit{ki}}=g_k$
Ym	Subset of Y for which hypothesis m is true
y	Vector of size K × I of emission counts (a.k.a complete data). A realization of RV Y.
yki	Element of vector y which indicates the number of counts emitted in voxel i and detected in projection element k.

Appendix B. Derivation of the posterior by marginalization of voxel activities

Using Eq. 1 and 2 the posterior for the flat prior is of the form

$$\mathcal{P}(\mathbf{y}\mid \mathbf{g})=\frac{1}{\mathcal{P}\left(\mathbf{g}\right)}{\int }_0^{\infty }{\mathit{df}}_{1\cdots }{\int }_0^{\infty }{\mathit{df}}_I\prod _{i=1}^I{\left(f_i\right)}^{c_i}{e}^{-{∊}_i{f}_i}\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}$$ (B.1)

Pulling constant terms in the front of the integrals and interchanging the order of summation and integration the above equation becomes:

$$\begin{array}{cc}\hfill & \mathcal{P}(\mathbf{y}\mid \mathbf{g})=\frac{1}{\mathcal{P}\left(\mathbf{g}\right)}\left[\prod _{i=1}^I\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}\right]\left[\prod _{i=1}^I{\int }_0^{\infty }{\mathit{df}}_i{\left(f_i\right)}^{c_i}{e}^{-{∊}_i{f}_i}\right]\hfill \\ \hfill & =\frac{1}{\mathcal{P}\left(\mathbf{g}\right)}\left[\prod _{i=1}^I\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}\right]\prod _{i=1}^I\frac{\Gamma (c_i+1)}{{\left({∊}_i\right)}^{c_i+1}}\hfill \\ \hfill & =\frac{1}{\underset{=Z}{\underbrace{\mathcal{P}\left(\mathbf{g}\right)\prod _{i=1}^i{∊}_i}}}\left[\prod _{i=1}^I\prod _{k=1}^K\frac{{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}}{y_{\mathit{ki}}!}\right]\prod _{i=1}^I\frac{\Gamma (c_i+1)}{{\left({∊}_i\right)}^{c_i}}\hfill \end{array}$$ (B.2)

For the case of the flat prior c_i represents integer value and Γ(c_i + 1) = c_i!. In general however this will not be true if the argument of the gamma function in not an integer.

Marginalizations of f for posteriors derived using other priors were done in a similar manner.

Appendix C. Derivation of the ratio of the posteriors

Posterior ratios in section 4 were calculated directly from derived posteriors. For example, for the flat prior in the OE state s event n detected in projection element k is located in voxel i. In OE state s’ the same event is located in voxel i’. The ratio of the flat–prior posteriors corresponding to these two states using Eqs. 5 and 10 is:

$$\frac{{\mathcal{P}}_F({\mathbf{s}}^{\prime }\mid \mathbf{g})}{{\mathcal{P}}_F(\mathbf{s}\mid \mathbf{g})}=\left[\frac{\frac{1}{Z}\prod _{j=1,j\ne i,j\ne i^{\prime }}^I\frac{\Gamma (c_j+1)}{{\left({∊}_j\right)}^{c_j}}\prod _{l=1}^K{\left({\alpha }_{\mathit{lj}}\right)}^{y_{\mathit{lj}}}}{\frac{1}{Z}\prod _{j=1,j\ne i,j\ne i^{\prime }}^I\frac{\Gamma (c_j+1)}{{\left({∊}_j\right)}^{c_j}}\prod _{l=1}^K{\left({\alpha }_{\mathit{lj}}\right)}^{y_{\mathit{lj}}}}\right]\times \times \frac{\left[\frac{\Gamma \left(c_i\right)}{{\left({∊}_j\right)}^{c_i-1}}{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}-1}\prod _{l=1,l\ne k}^K{\left({\alpha }_{\mathit{li}}\right)}^{y_{\mathit{li}}}\right]\left[\frac{\Gamma (c_{i^{\prime }}+2)}{{\left({∊}_j\right)}^{c_{i^{\prime }}+1}}{\left({\alpha }_{{\mathit{ki}}^{\prime }}\right)}^{y_{{\mathit{ki}}^{\prime }}+1}\prod _{l=1,l\ne k}^K\left({\alpha }_{{\mathit{li}}^{\prime }}\right)y_{{\mathit{li}}^{\prime }}\right]}{\left[\frac{\Gamma (c_i+1)}{{\left({∊}_j\right)}^{c_i}}{\left({\alpha }_{\mathit{ki}}\right)}^{y_{\mathit{ki}}}\prod _{l=1,l\ne k}^K{\left({\alpha }_{\mathit{li}}\right)}^{y_{\mathit{li}}}\right]\left[\frac{\Gamma (c_{i^{\prime }}+1)}{{\left({∊}_j\right)}^{c_{i^{\prime }}}}{\left({\alpha }_{{\mathit{ki}}^{\prime }}\right)}^{y_{{\mathit{ki}}^{\prime }}}\prod _{k=1,l\ne k}^K{\left({\alpha }_{{\mathit{li}}^{\prime }}\right)}^{y_{{\mathit{li}}^{\prime }}}\right]}$$ (C.1)

The first square bracket in the equation above contains identical numerator and denominator and will be canceled. Expressions under the product symbol ∏ in numerator and denominator of the second part of the equation are identical and will be canceled as well. Using the property of the gamma function AΓ(A) = Γ(A + 1) and simplifying remaining terms we arrive to Eq. 12 repeated here for convenience:

$$\frac{{\mathcal{P}}_F({\mathbf{s}}^{\prime }\mid \mathbf{g})}{{\mathcal{P}}_F(\mathbf{s}\mid \mathbf{g})}=\frac{{\alpha }_{{\mathit{ki}}^{\prime }}{∊}_i(c_{i^{\prime }}+1)}{{\alpha }_{\mathit{ki}}{∊}_{i^{\prime }}{c}_i}.$$ (C.2)

Almost identical calculations can be used to derive Eq. 14. To derive Eq. 13 the property of the lower–incomplete Gamma function Aγ(A, B) – B^Ae^−B = γ(A + 1, B) is used. Values of ζ(A, B) can be precalculated, or a very good approximation can be used such that ζ(A, B) = 0 for A ≤ B and ζ(A, B) = A – B for A > B.