Small Networks Encode Decision-Making in Primary Auditory Cortex

SUMMARY

Sensory detection tasks enhance representations of behaviorally meaningful stimuli in primary auditory cortex (A1). However, it remains unclear how A1 encodes decision-making. Neurons in A1 layer 2/3 (L2/3) show heterogeneous stimulus selectivity, complex anatomical connectivity, and receive input from prefrontal cortex. Thus, task-related modulation of activity in A1 L2/3 might differ across subpopulations. To study the neural coding of decision-making, we used 2-photon imaging in A1 L2/3 of mice performing a tone detection task. Neural responses to targets showed attentional gain and encoded behavioral choice. To characterize network representation of behavioral choice, we analyzed functional connectivity using Granger causality, pairwise noise correlations, and neural decoding. During task performance, small groups of 4–5 neurons became sparsely linked, locally clustered, and spatially oriented, while noise correlations both increased and decreased. Our results suggest that sensory-based decision-making involves small neural networks driven by the sum of sensory input, attentional gain, and behavioral choice.

eTOC Blurb

Francis et al studied the neural coding of decision-making in auditory cortex using 2-photon imaging. Neural activity showed attentional gain and encoded behavioral-choice. Small neuronal networks predicted behavioral-choice. Functional connectivity became sparse, rostro-caudally oriented, and locally clustered during target recognition.

INTRODUCTION

The detection of sound is essential for communication and survival in natural environments. Auditory attention enhances the neural representation of behaviorally meaningful sound in primary auditory cortex (A1) by suppression or facilitation of target tone responses (Kuchibhotla et al., 2017, Kato et al., 2015, David et al., 2012, Fritz et al., 2003, Atiani et al., 2009). Task-related enhancement of cortical responsiveness (i.e., “attentional gain”) depends on task difficulty (i.e., acoustic signal-to-noise ratio), motivation, and how well the task is performed (Atiani et al., 2009, Fritz et al., 2003). While attentional gain has described how the task-engaged state differs from passive sensory perception, task performance requires decision-making, and it remains unclear how the neural correlates of auditory attention in A1 relate to behavioral choice (Zhang et al., 2012, Bizley et al., 2013, Tsunada et al., 2016).

In A1 layer 2/3 (L2/3), neighboring neurons can differ in their pure-tone frequency selectivity (i.e., “tuning”), and many neurons do not respond to sounds, or respond infrequently (Bandyopadhyay et al., 2010, Rothschild et al., 2010, Kanold et al., 2014, Maor et al., 2016, Winkowski et al., 2013, Sakata and Harris, 2009, Winkowski and Kanold, 2013). This local tuning diversity is likely due to the varied and complex intra- and inter-laminar connections to L2/3 (Meng et al., 2015, Atencio and Schreiner, 2010, Atzori et al., 2001, Oviedo et al., 2010, Meng et al., 2017). Given the diversity of local tuning and intracortical connectivity, subsets of neurons in A1 might process auditory and task-related information differently, and might therefore uniquely contribute to auditory-based decision-making.

To investigate how neurons represent task-related and sensory information in A1 L2/3, we used in vivo 2-photon imaging to record the activity of many individual neurons simultaneously in mice during the performance of a tone detection task. We found that most neurons had increased responses to target tones when the mouse correctly detected the target, while a minority of neurons showed decreased activity during correct detections. This neural correlate of attentional gain was similar across neurons tuned near or far from the target frequency. Granger causality (GC) and noise correlation analysis revealed that functional connectivity in small neural networks is modulated by auditory task performance. Small populations of 4–5 neurons in A1 formed sparsely connected and locally clustered subnetworks with enhanced encoding of behavioral choice. Our data suggest that in A1 L2/3, the activity of large neuronal populations is modulated by attentional gain, yet only small neuronal networks are necessary to encode behavioral choice.

RESULTS

Auditory task performance was reliable and characterized by well-controlled behavioral responses

To study the neural coding of decision-making, we designed a simple tone detection task that used behavioral response-timing rules to induce well-controlled behavioral responses in mice (Fig. 1). We trained 10 head-fixed CBA mice, then imaged in A1 using in vivo 2-photon (2P) Ca²⁺-imaging while the mice performed the tone detection task (Fig. 1A).

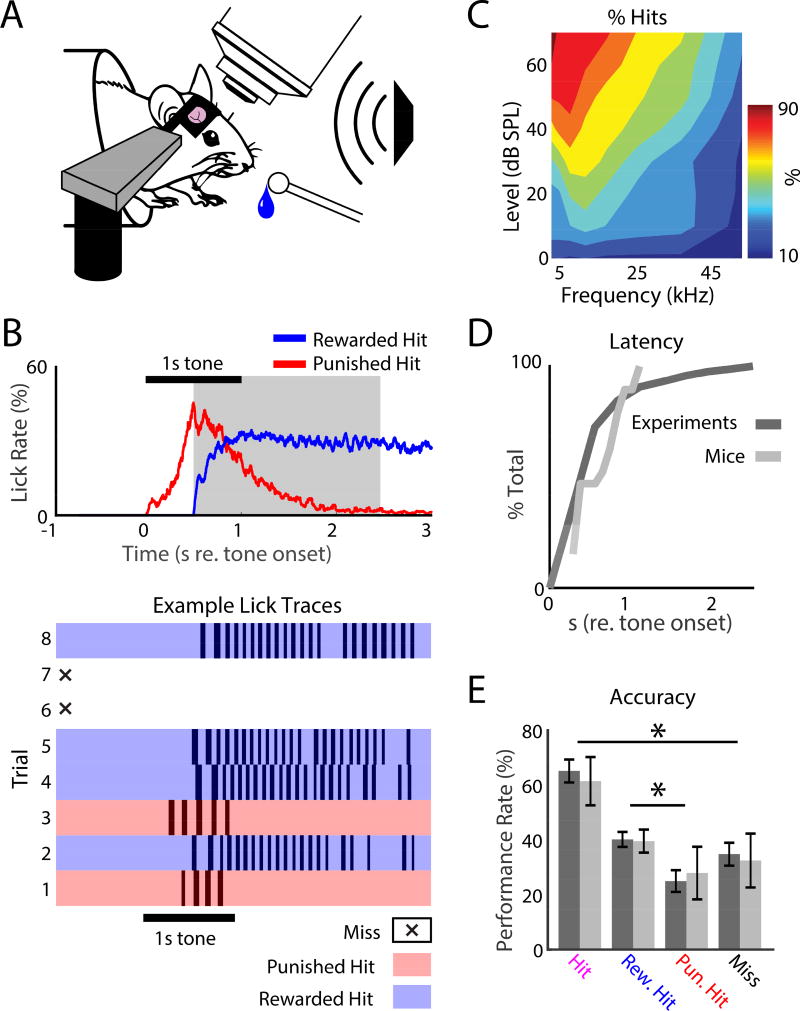
Figure 1.

2-Photon (2P) imaging in awake behaving mice. A. Head-fixed mice were trained to detect a 55 dB SPL, 1 s pure-tone presented from a free-field speaker, while neurons in A1 were imaged. Mice responded to tone detection by licking a waterspout. B. Tone detection behavior. Top: Average lick rate during task performance. Horizontal black bar shows when the target tone was presented. Red trace shows the average lick rate for punished hits, i.e., when the first lick occurred before the reward time-window (gray shaded region). No water was delivered after the first lick during punished hits, so the mice stopped licking. The blue trace shows the lick rate for rewarded hits indicating robust licking after receiving water. Bottom: example lick traces for 8 sequential trials during task performance. White regions with an X show miss trials, when the mouse did not respond. Blue and red regions show rewarded and punished hit trials respectively. C. Head-fixed task performance for roved tone levels to find the level (55 dB SPL) that produced a ~60–70% hit rate in the target frequency range (4–32 kHz). D. Cumulative distribution function (CDFs) for response latency (dark: total set of experiments; light: mice). E. Performance rates for each behavioral response-type for experiments (dark) and animals (light), respectively. Error bars show 2 standard errors of the mean (SEMs). Total hit rate: 65.2% ± 18.8% and 61.5% ± 13.9%, across experiments and animals, respectively. Rewarded hit rate: 40.2% ± 12.2% and 39.6% ± 6.7% across experiments and animals, respectively. Punished hit rate: 25% ± 17.7% and 28% ± 15.2% across experiments and animals, respectively. Miss rates: 35% ± 18.8% and 32.5% ± 15.5% across experiments and animals, respectively. Stars indicate significant differences between pairs of groups indicated by the bars: hits vs. misses (bootstrap t-test, experiments: p<0.001; animals: p=0.0011) and punished hits vs. rewarded hits (bootstrap t-test, experiments: p<0.001; animals: p=0.04).

Each trial of the task began with a 1 s pre-stimulus silence, followed by a 1 s, 55 dB SPL target tone with 8 Hz amplitude modulation (Fig. 1B), and then a 2.5 s silent interval. We chose 55 dB SPL, since at this sound level the mice performed consistently above chance (50%) for a wide range of tones (Fig. 1C). Inter-trial intervals (ITIs) were randomized between 5–9 s.

Mice were trained to lick a waterspout only after detecting the target tone. When the first lick on a trial occurred during the reward time-window (i.e., a rewarded hit; 0.5–2.5 s after the tone onset; gray shading, Fig. 1B, top panel), water was delivered for 2 s. If the mouse licked before the 0.5 s delay during a trial (i.e., a punished hit), no water was delivered for subsequent licks during that trial, and 8 s were added to the ITI. On miss trials, the mouse did not lick the waterspout. The mice typically ceased licking the waterspout quickly after making a punished hit, which is not surprising since no water was delivered (Fig. 1B). In contrast, the mice licked robustly after the water was delivered on rewarded hits (Fig. 1B).

In individual trials (Fig. 1B, lower panel), and on average across experiments and mice (Fig. 1D), behavioral response latencies (τ) tended to be longer than the 0.5 s wait period (experiments: τ = 0.67s ± 0.42s; mice: τ = 0.61s ± 0.28s), which indicates that licking was not random, and was well timed to tone presentation. Across the presented tones, task performance was reliable, yet with high enough error rates to allow investigation on the neural correlates of behavioral choice (Fig. 1E). While both punished and rewarded hits indicated tone detection (i.e. the first lick on a trial occurred after tone onset), tone detections occurred more often during rewarded hits (bootstrap t-test, experiments: p<0.001; mice: p=0.04). Thus, to increase the likelihood that hit trials occurred when the mice were actively listening, we only used the rewarded hit (i.e., active) trials for most of our main analysis of neural data (except Fig. 4).

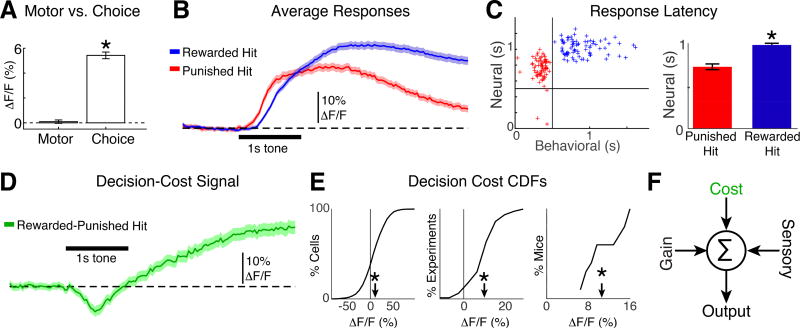
Figure 4.

Neurons in A1 encode decision timing and cost. A. Left: Time averaged activity aligned to licks during the silent period is similar to 0 (bootstrap t-test, p=0.5). Right: The time-averaged difference in activity of lick-aligned hit-miss trials (i.e., attentional gain, or “choice”) is positive (bootstrap t-test, p<0.001). B. Population average time-course of neural responses to tones during rewarded (blue) and punished (red) hits. Mice were trained to withhold licking for 0.5 s after the tone onset. Shading indicates 2 SEMs. C. Left: Average behavioral vs. neural response latencies for each experiment. Vertical and horizontal lines mark 0.5 s wait period. Right: Average neural response latency for punished and rewarded hits. ‘*” indicates p<0.001 (bootstrap t-test). Error bars show 2 SEMs. D. The time-course of the difference trace from panel B shows the dynamics of decision-cost (green; rewarded hit – punished hit). E. CDFs for decision-cost signaling for all cells (left), experiments (middle) and mice (right). Arrowheads indicate the means (9.5% +/− 0.78%, 9.1% +/− 1.7%, and 10.2% +/− 3.1% ΔF/F). ‘*’ indicate means different than 0 (bootstrap t-test, p<0.001). F. Model of A1 activity that is modulated by attentional gain, the cost of behavioral choice and sensory input.

Tone-evoked neuronal responses imaged in A1 L2/3 show pure-tone frequency selectivity

We injected AAV1.hSyn1.mRuby2.GSG.P2A.GCaMP6s.WPRE.SV40 (Rose et al., 2016) into A1 (Figs. 2, S1, S2) of CBA mice (~postnatal day 42–50) allowing the simultaneous observation of Ca²⁺ dependent fluorescence, as well Ca²⁺ independent visualization of cell bodies (Meng et al., 2017). For both wide-field (WF) and 2P imaging, neuronal activity was quantified by comparing fluorescence during the stimulus vs. the silent pre-stimulus baseline, resulting in a response amplitude (ΔF/F). To localize 2P imaging fields for each experiment to A1, we first mapped the frequency organization of auditory cortex in each mouse (Fig. 2A, S1) (Meng et al., 2017).

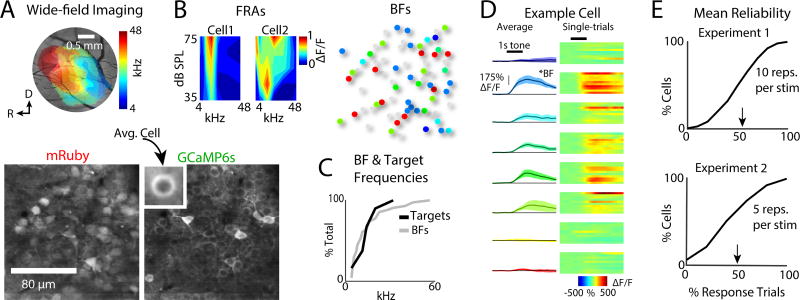
Figure 2.

Tone-evoked neuronal responses imaged in primary auditory cortex (A1) layer 2/3 show pure-tone frequency selectivity. A. Top left: Wide-field imaging used to localize A1, as indicated by a rostro-caudal gradient of high to low frequencies in the 4–48 kHz range (Fig. S1). Bottom: mRuby labeled cell bodies and GCaMP6s labeled cell membranes. B. Left: Two examples of frequency response areas (FRAs) generated by measuring responses to pure-tones presented at 35–75 dB SPL. Cells could show a narrow V-shape FRAs monotonic with level or show a wider FRA non-monotonic with level. Right: Best frequency (BF) of each cell for tones presented at 55 dB SPL. Gray cells were either too dim (see Fig. S3) or did not respond to pure-tones during passive trials. Color-coding same as A. C. CDFs of the set of pure-tone targets for each experiment (N=80 experiments), and BFs from all neurons (N=4316). D. Exemplar fluorescence traces from an A1 neuron in response to tones of different frequencies. Left column shows average of 10 repetitions of each frequency. Each row shows the data for a single tone frequency. Right column shows a heat-map for individual trial responses to each tone. E. Exemplar mean response reliability distributions from two experiments. Arrowheads indicate the mean. Response reliability was defined as the fraction of trials with significant responses in each cell, for the set of tones presented during Passive trials (Bandyopadhyay et al., 2010, Rothschild et al., 2010, Kanold et al., 2014, Maor et al., 2016, Winkowski et al., 2013). Reliability was similar for blocks of 5 or 10 trials per frequency.

To identify cellular responses, we performed 2P imaging. For each 2P imaging field, we first determined the frequency selectivity (Best frequency, BF) of individual neurons (Fig. 2B) during passive trials, i.e., when the mouse sat quiescently hearing tones. Cells showed different neighboring BFs (Fig. 2C right) and trial-to-trial response variability (Fig. 2D, E), consistent with previous findings (Bandyopadhyay et al., 2010, Rothschild et al., 2010, Kanold et al., 2014, Maor et al., 2016, Winkowski et al., 2013, Winkowski and Kanold, 2013). We imaged cells with BFs spanning 1–50 kHz, thus including cells both within and outside the range of our target frequencies (Fig. 2C).

Tone-evoked activity in A1 is modulated by attentional gain

We imaged 7879 neurons in 80 experiments, of which 4316 neurons were included in the analysis (Fig. S3). Figure 3A shows the average fluorescence response time-courses for the entire population of individual neurons, during target tone presentations on passive, hit, and miss trials. Most neurons (3762/4316, 87%) showed an increase in tone evoked response amplitudes during hit vs. passive trials (p<0.001, KS-tests). However, since the encoding of task-related information may still occur in the absence of tone-evoked neural responses, we included all 4316 neurons in our analysis. Most neurons (3302/4316, 77%) showed increased fluorescence relative to baseline (i.e., facilitative responses; average ΔF/F = 24.3% ± 0.7%; Fig. 3A). A minority of neurons (1014/4316, 23%) showed decreased fluorescence relative to baseline activity (i.e., suppressive responses; average ΔF/F = −22.1% ± 1.5%; Fig. 3A).

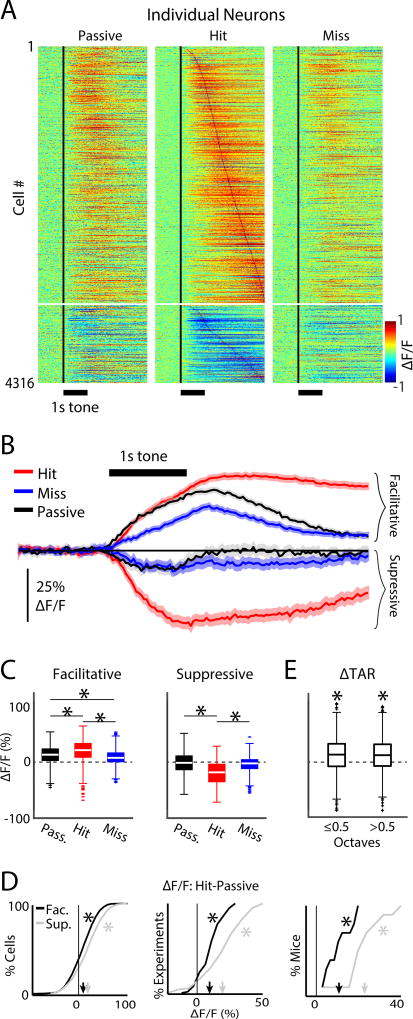
Figure 3.

Tone-evoked activity in A1 is modulated by behavioral choice. A. Heat-map of individual neuronal responses. Each row shows a neuron’s average response across repetitions of the same pure-tone frequency during passive (left), hit (middle) miss (right) trials. Facilitative and suppressive responses are shown as positive (warm colors) and negative (cool colors) values, respectively. The vertical black line shows the tone onset time. Neurons in all three panels were sorted by peak response latency during hit trials. B. Population average response time-courses for both facilitative and suppressive hit trials (red), miss trials (blue), and passive trials (black). Shading shows 2 SEMs. C. Box plots for the distribution of population responses, after collapsing the time-course for each cell into an average value across time after the tone onset. Conditions are color coded as in B. ‘*’ indicate p<0.001, KW-test. The average facilitative ΔF/F response for passive, hit and miss trials were 14.8% ± 0.62%, 24% ± 0.71%, and 10% ± 0.5%, respectively. The average suppressive ΔF/F response for passive, hit and miss trials were −2.9% ± 1.4%, −22.1% ± 1.4%, and −5.4% ± 1.04%, respectively. D. CDFs for attentional gain, measured as the differences in ΔF/F between hit and passive conditions. CDFs were computed by taking the cumulative sum of the histogram of attentional gain values separately across each population of experiments and mice. Left, middle and right panels show the CDFs for the total population of cells, experiments, and mice, respectively. CDFs for facilitative and suppressive responses in black and gray, respectively. The mean attentional gain for facilitative responses was 9.9% ± 0.93%, 9.9% ± 2.0%, and 9.9% ± 3.7%, across cells, experiments, and mice, respectively. The mean attentional gain for suppressive responses was 19.9% ± 2%, 20.7% ± 3.5%, and 23.8% ± 5.0%, across cells, experiments, and mice, respectively. Arrowheads indicate mean values. ‘*’ indicate a significant difference from 0 (bootstrap t-test, p<0.001). The magnitude of attentional gain in suppressive responses across individual cells, experiments, and mice was significantly greater than the attentional gain for enhanced responses (bootstrap t-test, p<0.001). E. Attentional gain for groups of cells according to their BF octave difference. Attentional gain was positive for both groups (ΔTAR≤0.5: 12.8% ± 0.6%; ΔTAR>0.5: 11.4% ± 0.6%, bootstrap t-test, p<0.001) but similar (bootstrap t-test, p=0.11).

Facilitative responses were largest during hit trials and smallest during miss trials (Kruskal-Wallis test (KW-test); p<0.001; Fig. 3B, C). Similarly, suppressive responses were largest for hit trials (KW-test, p<0.001). We also observed that facilitative responses during miss trials were smaller than passive response to target tones (bootstrap t-test, p<0.001; Fig. 3B, 3C). Together, we find that neural responses to target tones were generally enhanced during target detection.

We quantified the effect of tone detection for each neuron by calculating the difference in response magnitude between hit and passive trials. We then averaged over time after the tone onset resulting in a single value for each neuron that we interpreted as attentional gain, for both facilitative and suppressive responses (Fig. 3D). 1036/4316 cells (24%) had positive attentional gain across trials (KS-test, p<0.05). The 1036 neurons were distributed across all mice and experiments. Indeed, positive attentional gain was present in each mouse (Fig. 3D, right panel). Thus, attentional gain during hit trials was a robust phenomenon, and tended to be twice as large for suppressive responses compared to facilitative responses (~20% vs. ~10%). Together, our results indicate that tone detection increases the magnitude of both facilitative and suppressive auditory evoked responses in A1.

Attentional gain in A1 does not depend on neuronal frequency preference, relative to target tone frequency

Because of local heterogeneity in neuronal BFs (Fig. 2B), any given target tone frequency may not be close to each neuron’s BF. This allowed us to probe if the amount of attentional gain could depend on the relationship between target frequency and neuronal BF. To increase the likelihood of target frequencies falling near a given neuron’s BF, for each experiment we selected one frequency from a set of target frequencies between 4–32 kHz.

We separated neurons into two groups according to the octave difference between BF and the target frequency for a given experiment (ΔTAR≤0.5, and ΔTAR>0.5), while pooling across neurons showing facilitative and suppressive responses, since both populations showed positive attentional gain (Fig. 3D). Individual cells in both ΔTAR groups had positive (KS-test, p<0.05; Fig. 3E), but similar (bootstrap t-test, p=0.12) attentional gain. Thus, attentional gain was common, and largely independent of frequency tuning.

Neural responses in A1 reflect perceptual recognition, not motor-related signals

Behavioral choice involves at least two distinct processes: perceptual recognition and motor control (i.e., licking) to indicate choice. Since auditory cortex can exhibit motor related activity (Nelson and Mooney, 2016) we sought to delineate which part of the modulation is due to perceptual vs motor-related signals. To identify potential motor signals in A1, we compared lick-triggered averages of neural responses during silence vs tones. We averaged the response amplitude (ΔF/F) during the time following licks made during the pre-stimulus silence. We did not observe any significant lick-related activity (Fig. 4A, ΔF/F = 0.6% +/− 0.13%, bootstrap t-test, p=0.42). Since both hit and miss trials contained tone responses, but only hit trials contained licks, analysis of the difference between hit and miss trials describes the neural activity during licks with perceptual recognition of the target. The activity difference between hit and miss trials was positive (Fig. 4A, ΔF/F = 5% +/− 0.52%; bootstrap t-test, p<0.001). This indicates that while motor signals during licking did not appear to cause activity in A1 L2/3 neurons, task-related modulations of neural activity in A1 reflect perceptual recognition during behavioral choice.

A1 neurons encode decision-timing

Single-units in the primary visual cortex have been shown to encode the timing of behavioral choice during a visual detection task that incorporated delayed behavioral responsetiming rules (Levy et al., 2017). In our task, the mice were required to delay behavioral responses until 0.5 s after the tone onset to receive a reward. Thus, neuronal responses in A1 might encode the timing of behavioral choice during our task. We thus compared neuronal responses during punished vs rewarded hits (Fig. 4B). Neural response latencies (τ=time to half-peak response) in each experiment appear to cluster by response type, mainly because of the task’s response-timing rules that defined punished vs. rewarded hits (Fig, 4C, left). On average, neural response latencies during rewarded hits were longer than for punished hits (Fig. 4C; right) (bootstrap t-test, p<0.001; τ = 0.75 ± 0.14 vs. 1.01 ± 0.014, punished vs. rewarded hits, respectively). Since we did not detect lick related motor signals in A1, our data suggest that the difference in neural response latencies reflects a perceptual, rather than motor-related, decision-timing.

A1 neurons show a decision-cost analysis of behavioral choice

Non-auditory information, such as reward size and outcome, and the use of punishment vs. reward during operant conditioning, may also influence the suppression or facilitation of activity in A1 (Brosch et al., 2011, David et al., 2012, Weis et al., 2013), which suggests that in addition to attentional gain, the outcome of behavioral choice (i.e., “decision cost”) may be represented in the auditory cortex. In our task design, both punished and rewarded hits indicated that the animal correctly detected the target tone (i.e. the first lick in a trial occurred after the tone onset). However, the cost of punished hits was the removal of the reward and a time-out. Thus, the difference between neural activity during rewarded vs. punished hits describes how a cost analysis of behavioral choice (i.e. evaluating the outcome of choice in terms of punishment vs. reward) may be represented in neural populations. The difference in activity between punished hits and rewarded hits (decision-cost signal) was negative (Fig. 4D) during the behavioral response delay period, most likely reflecting either behavioral error recognition (i.e., impending punishment), and/or the difference in neural response latencies related to decision-timing. The decision-cost signal then increased to positive values representing reward. 20% of individual neurons had significant decision cost signals (KS-test, p<0.05) and neurons with decision-cost signals were present in 9/10 mice, indicating that like attentional gain, decision-cost signaling is common across A1 L2/3. The average decision-cost signal amplitude was ~10% (bootstrap t-test, p<0.001; Fig. 4E) and thus similar in amplitude to the attentional gain signal (Fig. 3). Together, our data suggest that neural populations in A1 are driven by the sum of sensory input, attentional gain, and a cost function of behavioral choice (Fig. 4F).

Auditory attention modulates pairwise noise correlations

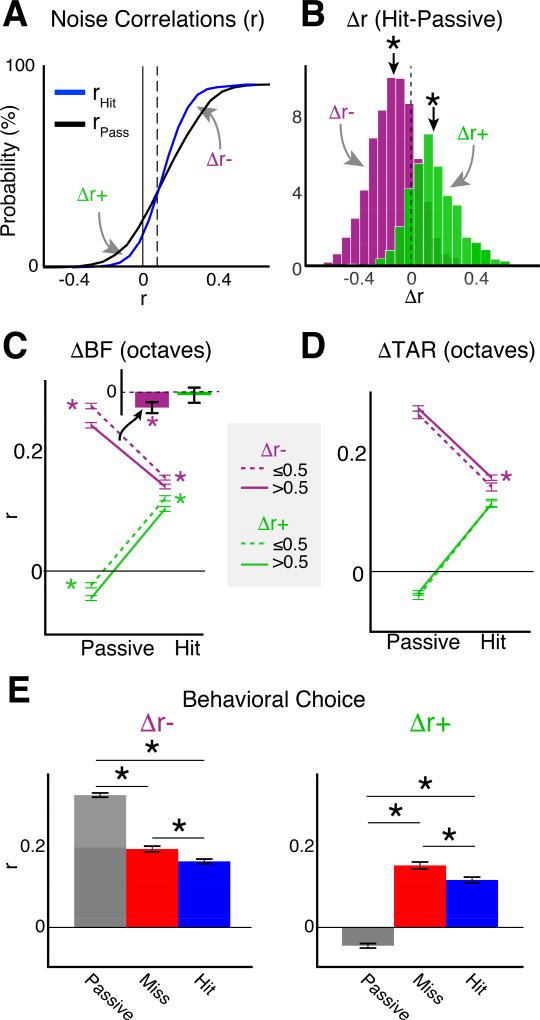
A1 contains neuronal subpopulations whose interactivity can be characterized by pairwise noise correlations (Rothschild et al., 2010, Winkowski et al., 2013, Averbeck et al., 2006). Pairwise noise correlations serve as a proxy for neuronal functional connectivity (Cohen and Maunsell, 2009, Nandy et al., 2017, Downer et al., 2015, Downer et al., 2017, Ruff and Cohen, 2014). Attention can either increase or decrease noise correlations, depending on the task design and neuronal tuning properties (Downer et al., 2015, Downer et al., 2017, Ruff and Cohen, 2014). We compared the noise correlations during passive vs hit trials (Fig. 5A). The average noise correlation during passive trials was 0.155 ± 0.006, consistent with previous findings (Rothschild et al., 2010, Winkowski et al., 2013, Downer et al., 2017, Downer et al., 2015). Noise correlations decreased during hit trials to 0.135 ± 0.004 (decrease of −0.02 ± 0.006, bootstrap t-test, p<0.001). However, comparison of the noise correlation CDFs during passive vs. hit trials (Fig. 5A) revealed an inflection point (r=0.09, vertical dotted line in Fig. 5A). Above the inflection point, noise correlations decreased during tone detection (Δr− = −0.12 ± 0.006, bootstrap t-test, p<0.001; Fig. 5B), whereas below the inflection point, noise correlations increased during tone detection (Δr+ = 0.15 ± 0.008, bootstrap t-test, p<0.001; Fig. 5B). Furthermore, the magnitude of the change in noise correlations for Δr+ cells was greater than that for Δr−cells (bootstrap t-test, p<0.001). 2756/4316 (64%) and 1560/4316 (36%) of neurons fell within the Δr− and Δr+ groups, respectively. We find that despite the larger population of cells that had decreased noise correlations during task performance, the dominant effect of attention, in terms of effect size, was to increased noise correlations, and thus by interpretation, increased functional connectivity in A1.

Figure 5.

Auditory attention modulates pairwise noise correlations in A1 L2/3. A. CDF of average pairwise neuronal noise correlations (r) for each neuron in the study (N=4316) during passive (black) and hit (blue) trials. The vertical dotted line shows the inflection point (r=0.09) where the sign of r_HIT-r_PASSIVE (i.e., Δr) reverses. Δr values indicated by the gray arrows pointing below (Δr+) and above (Δr−) the inflection point were separated for subsequent panels. B. Probability density functions (PDFs) for Δr+ and Δr−. ‘*’ indicate means different than 0 (bootstrap t-test, p<0.001). C. r values for cells grouped by the octave distance between best frequencies (ΔBF). The mean values for Δr+ for hit vs passive were ΔBF≤0.5: 0.12 ± 0.007 vs. −0.02 ± 0.007; ΔBF>0.5: 0.1 ± 0.007 vs. −0.05 ± 0.007. The mean values for Δr− for hit vs passive were ΔBF≤0.5: 0.16 ± 0.005 vs. 0.27 ± 0.006; ΔBF>0.5: 0.14 ± 0.005 vs. 0.24 ± 0.006. ‘*’ indicate differences between BF groups in Δr−group for both active and passive (bootstrap t-test, p<0.001). Error bars show 2 SEMs. Inset shows differences in Δr between BF groups (Δr (ΔBF≤0.5) - Δr (ΔBF>0.5)) and indicate that for Δr−cells with ΔBF<0.5 showed the largest reduction in r. D. Noise correlations as function of BF relative to the target frequency (ΔTAR). The average noise correlations for Δr− in hit vs passive trials were: ΔTAR≤0.5: 0.14 ± 0.008 vs. 0.26 ± 0.008; ΔTAR>0.5: 0.15 ± 0.006 vs. 0.27 ± 0.006. The average noise correlations for Δr+ in hit vs passive trials were: ΔTAR≤0.5: 0.11 ± 0.01 vs. −0.04 ± 0.009; ΔTAR>0.5: 0.11 ± 0.008 vs. −0.04 ± 0.006. E. Attentional effect on noise correlations across all neurons. ‘*’ indicate p<0.001, KW-test.

Cells with similar tuning have a higher chance of being connected (Ko et al., 2011). Thus, the change in noise correlations could depend on the relative tuning preferences of neurons. For both Δr− and Δr+ groups, neurons with similar BFs (ΔBF≤0.5) showed greater noise correlations than those with different BF’s (ΔBF>0.5), for both hit and passive trials (Figs. 5C, S4; bootstrap t-test, p<0.001 for both groups). Δr− neurons with similar BFs showed a greater decrease in noise correlations than those with different BFs during hit vs passive trials (bootstrap t-test, p<0.001). Δr+ neurons showed an increase in noise correlations that changed from being negative during passive trials to positive during hit trials. The increase in Δr+ noise correlations during tone detection (bootstrap t-test, p<0.001) was independent of BF relationships (bootstrap t-test, p=0.58). Our results indicate that tone detection modulates noise correlations toward the average noise correlation during hit trials (r=0.135), by reducing the amplitude of positive noise correlations, while increasing negative noise correlations to positive values.

Because we imaged neurons with a wide range of BFs (Fig. 2B), we next investigated if the change in noise correlation during tone detection depends on the relative frequency of the target tone to the BF of a given cell (Fig. 5D, S4). Noise correlations for Δr− cells with BFs near the target (ΔTAR≤0.5) had smaller noise correlations during hit trials than Δr− cells with BFs far from the target (ΔTAR>0.5) (bootstrap t-test, p=0.008). However, both Δr− and Δr+ cells showed changes in noise correlations during hit vs passive trials (bootstrap t-test, p<0.001) that were not different for cells with BFs near or far from the target (bootstrap t-test, Δr−: p=0.52, Δr+: p=0.51). Thus, consistent with prior results in both visual and auditory cortex (Downer et al., 2015, Downer et al., 2017, Ruff and Cohen, 2014) our results suggest that functional connectivity between pairs of neurons in mouse A1 are modulated (i.e., increased or decreased) by tone detection. In addition, we find that the modulation of noise correlations may be stronger for Δr− neurons with similar BFs, or BFs near the target frequency.

Behavioral choice decreases pairwise noise correlations

We showed that neuronal response magnitudes during miss trials were similar or often less than during passive trials (Fig. 3), suggesting that miss trials do not necessarily represent the equivalent attentional state as during passive trials. We thus tested if noise correlations also vary with behavioral choice (i.e., hit vs miss trials). For Δr− cells, noise correlation values were greatest during passive trials (0.26 ± 0.005), smaller during miss trials (0.17 ± 0.006), and smallest during hit trials (0.15 ± 0.005) (Fig. 5E, left panel; KW-test; p<0.001). For Δr+ cells, noise correlation values were smallest and negative during passive trials (−0.04 ± 0.005). During task performance, the sign of noise correlations reversed, and the magnitude increased for both miss trials (0.15 ± 0.008), and hit trials (0.11 ± 0.006), though, like the Δr− cells, noise correlations were significantly less during hit trials than in miss trials (Fig. 5E, right panel; KW-test; p<0.001). Together, these results indicate that not only is neuronal functional connectivity modulated by attentional state (i.e., passive vs active task engagement), but also by behavioral choice.

Granger causality analysis of effective network connectivity

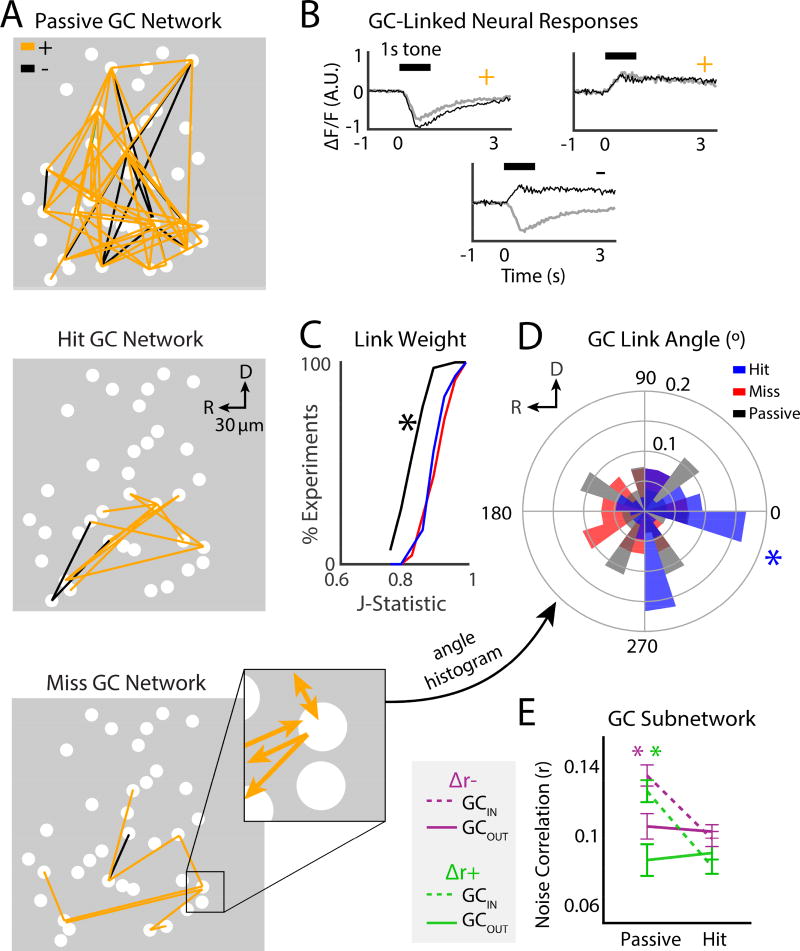
So far, our results show that the tone-evoked responses of neurons are driven by the sum of sensory input, attentional gain, and a cost function of behavioral choice. In addition, pairwise functional connectivity is modulated during task performance, and depends on behavioral choice. Since tones evoke activity in many A1 neurons simultaneously, we sought to investigate how not only pairs, but networks of neurons, are engaged during tasks. To gain insight on the spatial neuronal networks that encode task-related information in A1, we used Granger causality (GC) analysis (Granger, 1969, Sheikhattar and Babadi, 2016, Oya et al., 2007, Friston et al., 2013) to quantify effective connectivity between neurons, and then applied graph theory to describe the topology of GC networks. GC analysis estimates significant causal interactions between neurons, by statistically testing if the recent history of a neuron can improve the prediction of another neuron’s activity (Granger, 1969, Sheikhattar and Babadi, 2016) (Methods and Fig. S5). Since we are simultaneously imaging many neurons, we can thus evaluate the contribution of many neurons to the activity of individual neurons. Moreover, 2-photon imaging allows us to precisely identify the spatial location of each neuron, and thereby the spatial structure of the GC networks. Figure 6A shows an example of GC connectivity in an imaged field in A1. The causal interactions (i.e., GC “links”) are either positive or negative, which occur when the ΔF/F traces for linked neurons have the same or opposite sign, respectively (Fig. 6B). We examined 7 GC network characteristics and tested for significant differences across experiments between the network statistics for passive, hit, and miss trials (Supplementary Table S1).

Figure 6.

Granger causality (GC) subnetwork structure was modulated by task performance. A. GC analysis was used to find directional links (i.e., effective connections) between neurons. Example GC networks during passive (top), hit (middle), and miss (bottom) trials. Positive (+) and Negative (−) links are shown in orange and black, respectively. Magnification shows example of directionality for individual GC-links. B. Example traces of pairs of + or − GC-linked neurons. C. CDF of GC link weight. ‘*’ indicates difference between the passive and hit trials (bootstrap t-test, p<0.001). Trends were similar across mice (see Supp Table 1). D. GC link angle. ‘*’ indicates the significant rostro-caudal directionality of links during hit trials (Rayleigh test, p=0.03). E. Pairwise noise correlations for cells inside a GC subnetwork (GC_IN) and cells outside of a subnetwork (GC_OUT). Average Δr− noise correlations for GC_IN cells for hit vs. passive trials: 0.098 ± 0.006 vs. 0.135 ± 0.008. Average Δr− noise correlations for GC_OUT cells: 0.103 ± 0.005 vs. 0.11 ± 0.011. GC Average Δr+ noise correlations for GC_IN cells for hit vs. passive trials: 0.08 ± 0.007 vs. 0.13 ± 0.01. Average Δr+ noise correlations for GC_OUT cells for hit vs. passive trials: 0.09 ± 0.006 vs. 0.09 ± 0.02. For both Δr− and Δr+ groups, GC_IN cells had larger noise correlations during passive trials compared to GC_OUT cells, and significantly decreased noise correlations during hit trials (green and purple ‘*’ bootstrap t-test, p<0.001). Noise correlations in GC_OUT cells were similar for hit and passive trials (bootstrap t-test, Δr−: p=0.62, Δr+: p=0.66).

Auditory task performance strengthens effective network connectivity

Since noise correlations are believed to reflect the strength of functional connectivity, we first tested if GC link weight (i.e. the statistical strength of the estimated link, as measured by the J Statistic) changed during task performance. Link weight was less during passive trials compared to hit trials (Fig. 6C, 0.84 ± 0.005 vs. 0.91 ± 0.005, bootstrap t-test, p<0.001), but not different for hit trials vs miss trials (hit-miss: 0.91 ± 0.006, bootstrap t-test, p=0.52). Thus, we find that for both noise correlations and GC network analysis, the dominant effect of auditory task performance is to increase functional connection strength within networked neurons.

Tone detection occurs when effective network connectivity orients along the rostrocaudal axis

A1 has an anisotropic functional topology, in that sound frequency is represented roughly in a rostro-caudal direction (Fig. 2A), and this functional anisotropy is reflected in the underlying connectivity (Oviedo et al., 2010, Watkins et al., 2014). We thus speculated that subnetworks engaged in hit and miss trials might differ in their spatial organization, specifically, in the angle of their connections with respect to the tonotopic axis of A1 (rostro-causal). We calculated the average link angle for each experiment as the vector average of link angles, where 0° referenced the caudal direction. GC links with weights greater than 0.9 during hit trials had significant directionality along the rostro-caudal axis (Fig. 6D: −0.27° ± 0.18°, Rayleigh test, p=0.033). Significant directionality was absent for passive and miss trials (Rayleigh test, p>0.05). Thus, strong links are preferentially organized across the tonotopic axis during hit trials.

GC subnetwork membership depends on pairwise noise correlations

GC subnetworks could consist of neurons with similar or different pairwise correlations. Thus, after identifying subnetworks, we quantified the noise correlations for cells within a subnetwork (GC_IN) vs. outside a GC subnetwork (GC_OUT) (Fig. 6E). We found that both the absolute noise correlation values, and the task-driven changes were similar for both Δr− and Δr+ cells. In both groups, noise correlations during passive trials for GC_IN cells were greater than GC_OUT cells (bootstrap t-test, p<0.001), while noise correlations during hit trials significantly decreased, but only for GC_IN cells (bootstrap t-test, p<0.001, GC_IN).

Thus, we find that the modulation of noise correlations during task performance exists within GC subnetworks. However, both the noise correlation amplitude, and the magnitude of the task-dependent modulation depend on whether a neuron exists within or outside of a GC subnetwork. Indeed, significant changes in noise correlations during tone detection only occurred inside GC subnetworks. Thus, our results indicate a specific network control of functional connectivity during task performance.

Auditory task performance prunes effective network connectivity in A1

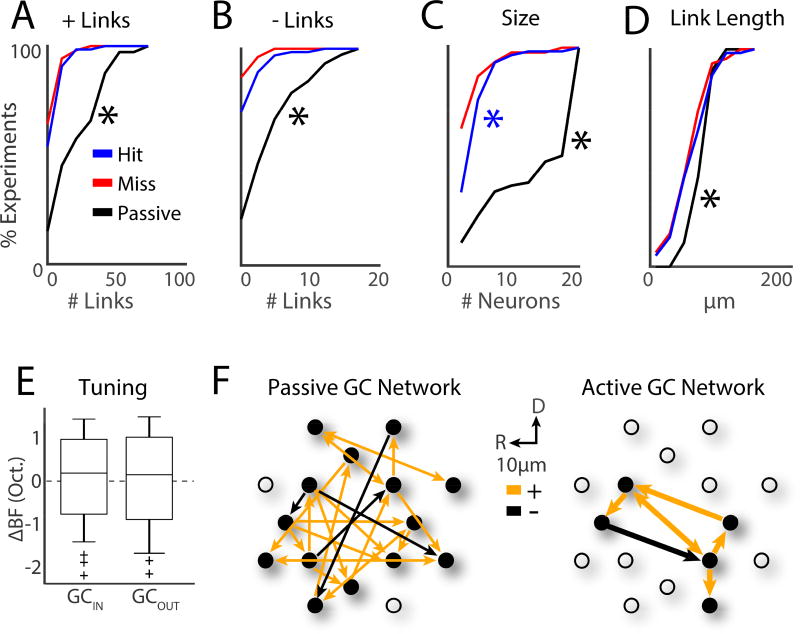
We next analyzed the size of the GC linked networks. We find that a predominant effect of task performance was to decrease the number of both excitatory and suppressive GC links. The average number of positive links was largest for passive trials (Fig. 7A, hit: 6.8 ± 0.84, miss: 5.3 ± 0.78, passive 24.7 ± 2.2; bootstrap t-test, p<0.001 for both hit and miss) while the number of links between hit and miss trials was similar (bootstrap t-test, p=0.14). Similarly, for negative links, more GC links were present in passive trials (Fig. 7B, hit: 1.3 ± 0.26, miss: 0.62 ± 0.15, passive 5.3 ± 0.51; bootstrap t-test, p<0.001 for both hit and miss) and the average number of links was similar between hit and miss trials (bootstrap t-test, p=0.27).

Figure 7.

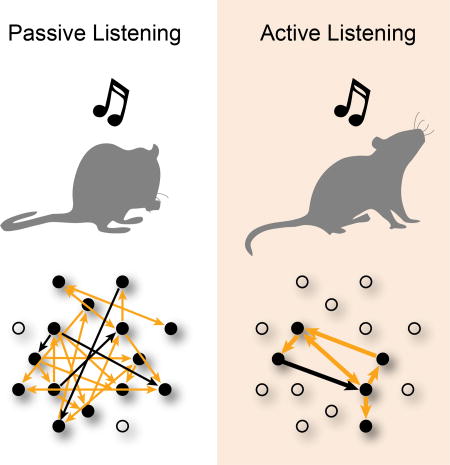
Tone detection drives GC subnetworks into small and localized clusters of 4–5 neurons with diverse frequency tuning. A. CDF for number of +links. ‘*’ indicates differences between passive and hit trials (bootstrap t-test, p<0.001). B. CDF for number of −links. C. CDF for GC subnetwork size. Blue ‘*’ indicates a significant difference between the hit and miss trials (bootstrap t-test, p=0.019). D. CDF for GC link length. E. BF differences (ΔBF) between pairs of cells for GC_IN and GC_OUT cells. Populations were similarly distributed, and means similar to 0 (bootstrap t-test, p>0.05). F. Illustration of passive and active (i.e., hit) GC networks.

Visual inspection of the GC networks suggested that groups of neurons formed isolated subnetworks within the larger GC network. We found that the number of neurons within each isolated GC subnetwork (Fig. 7C) was larger in hit than miss trials (4.6 ± 0.4 vs. 3.7 ± 0.41, bootstrap t-test, p=0.019). However, passive trials tended to have the greatest number of neurons per subnetwork (13.6 ± 0.8; bootstrap t-test, p<0.001).

Since 2P imaging enables us to determine the locations of GC linked cells we also analyzed the length of GC links (Fig. 7D). We found that not only did the number of links decrease during tone detection, but so did the length of links (hit: 66.9µm ± 3.6µm, miss: 62.8µm ± 4.03µm, passive 79.4µm ± 1.8µm; bootstrap t-test: hit vs miss trials p=0.58; hit or miss vs passive trials p<0.001) indicating that during hit trials, nearby cells were GC linked. Thus, together we find that tone detection reduces the area occupied by active neural networks in A1 L2/3.

Our GC network analysis indicates that auditory target recognition correlates with the transient formation of small and localized subnetworks, having both excitatory and suppressive causal interactions that move primarily across the rostro-caudal tonotopic axis of A1 during tone detection.

Effective network connectivity does not depend on the BF vs. target frequency difference

GC subnetworks could consist of neurons with similar or different auditory response properties. Thus, we quantified the similarity of BFs in GC_IN vs. GC_OUT cells. We found that BF differences (ΔBF) between pairs of cells were similar for both GC_IN and GC_OUT cells, tended to be within 2 semi-tones (i.e., 1/6 octave), and spanned a range >2 octaves (Fig. 7E). Thus, passive GC networks inherit the underlying heterogeneous local frequency preference of individual neurons, and, spectral integration inside GC networks may often be broadband.

Neural activity in subpopulations of A1 is predictive of behavioral choice

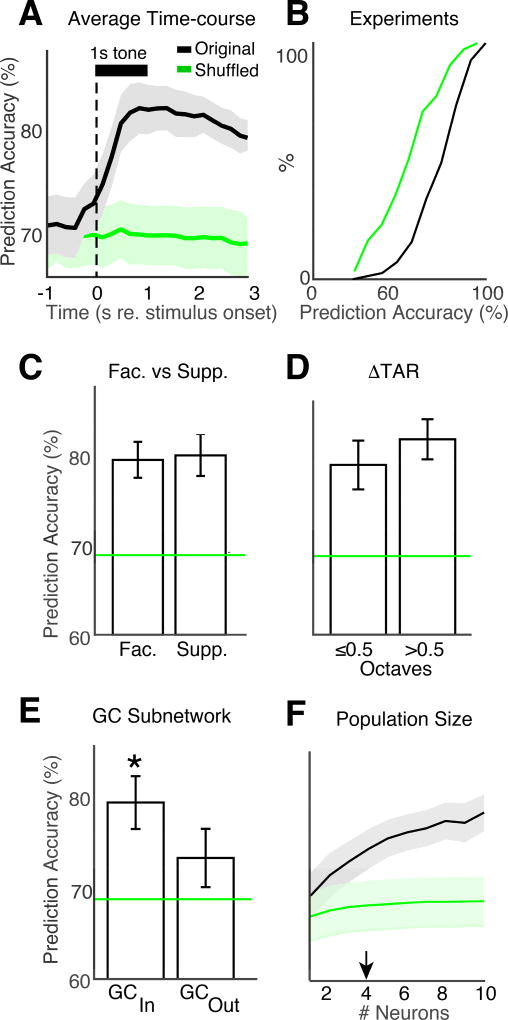
Since population response magnitudes were correlated with behavioral choice, we sought to test if behavioral choice could be decoded from trial-by-trial activity in neural populations, and to find which subpopulations of A1 neurons were best at encoding behavioral choice. We used a linear neural decoder (support vector machines, SVMs) to classify behavioral responses using population activity in each experiment. Trial-by-trial neural activity was labeled as belonging to hit or miss trials, and then concatenated into matrices with dimension size corresponding to the neural population size. Using “leave-one-out” cross-validation, SVMs use a hyperplane for binary trial-wise classification of population activity into hits or misses. Figure 8A shows the time-course of SVM prediction accuracy (PA) measured as the percent of correct trial classifications as hit or miss. Shuffled data indicate chance PA (69.5% ± 3%), given the underlying proportion of hit trials across experiments (65.2% ± 18.8%) as designed into our task. On average across experiments, PA for unshuffled data significantly increased from chance (bootstrap t-test, p<0.001), beginning ~300 ms after tone onset, peaking at ~82% by ~700 ms after tone onset, before beginning to decay. PA was greater than chance in most experiments (Fig. 8B). Given that behavioral response latencies were also ~700 ms after tone onset (Figs. 1D, 4C), these results indicate that neural activity is predictive of behavioral response, and that this information is present before the onset of behavioral choice (e.g. licking).

Figure 8.

GC subnetworks have enhanced encoding of behavioral choice. A. Prediction accuracy (PA) of decoded neural activity plotted as a function of time. The black curve shows the PA averaged across experiments. The green line shows the PA for shuffled data. Shading shows 2 SEMs. B. PA CDF is shown for all 80 experiments. C. Both facilitative and suppressive cells (see Fig. 3A, B) had PA greater than chance (bootstrap t-test, p<0.001), but were not different (bootstrap t-test, p=0.74). D. Cells with BF near and far from the target frequency had PA greater than chance (bootstrap t-test, p<0.001), but were not different (bootstrap t-test, p=0.1). E. GC subnetwork membership enhances PA. Both GC_IN and GC_OUT cells had PA greater than chance (bootstrap t-test, GC_IN: p<0.001, GC_OUT: p=0.008). ’*’ indicates that PA of GC_IN cells was larger than GC_OUT cells (bootstrap t-test, p=0.012). F. PA during each experiment was tested against the number of neurons used for prediction. Arrowhead: 4 neurons are sufficient to predict behavior above chance.

To gain insight into the role of different neuronal subpopulations in encoding behavioral choice, we compared the PA of different subpopulations. The mean PA for facilitative and suppressive groups were above chance (bootstrap t-test, p<0.001) but similar (Fig. 8C, 81% ± 2% and 82% ± 2.5%, respectively; bootstrap t-test, p=0.74). Similarly, the mean PA for ΔTAR≤0.5 and ΔTAR>0.5 groups (Fig. 8D, 79% ± 3% and 82% ± 2.3%, respectively) were both above chance (bootstrap t-test, p<0.001), but similar (bootstrap t-test, p=0.1).

In contrast, the mean PA for GC_IN and GC_OUT groups (79% ± 3% and 73% ± 3.2%, respectively) were both above chance (bootstrap t-test, p<0.001 and p=0.007, respectively), and different from each other (bootstrap t-test, p=0.013) (Fig. 8E). Thus, we find that the identified GC subnetworks have enhanced encoding of behavioral choice.

Neural decoding of behavioral choice requires only a small population of 4 neurons

Since target tones activated many neurons, we next sought to identify how many neurons were sufficient to predict behavioral choice above chance levels. We subsampled the neuronal population at increasing population sizes and performed SVM analysis for each size. Prediction accuracy started at chance for a single neuron, increased above chance for greater than 4 neurons (bootstrap t-test, p<0.001), and asymptotes at ~7 neurons. These results indicate that small neuronal populations may underlie behavioral choice (Fig. 8F).

Together, our results show that during tone detection, small and localized populations of neurons (4–5) in A1 L2/3 form sparsely linked subnetworks that have enhanced encoding of behavioral choice (Fig. 7F).

No effect of sex on encoding in A1

Since we imaged both male and female mice, we separated our data by sex. Separate analysis of data from males and females showed similar results in each group, indicating no effect of sex in our study (Fig. S6).

DISCUSSION

We used 2P imaging in the auditory cortex of awake behaving mice to study the neural correlates of decision-making in A1 L2/3. We find that on the single cell level, tone evoked responses are modulated by auditory task performance. To identify task-dependent effective connectivity in local neural networks, we employed a novel variant of GC analysis at the single cell level. Using this neuronal network analysis, we found that during passive presentation of tones, neurons were densely interconnected across ~80 µm, and formed large clusters of subnetworks (~13 neurons) with weak links. In contrast, tone detection drove the same neuronal populations into smaller and more sparsely connected subnetworks of 4–5 neurons, spaced ~65 µm apart, that tended to have stronger rostro-caudal oriented links. Thus, the encoding of task-related information in individual neurons may directly depend on the activity of neighboring neurons.

Pairwise noise correlations are a proxy to describe functional neuronal connectivity (Cohen and Maunsell, 2009, Nandy et al., 2017, Downer et al., 2015, Downer et al., 2017, Ruff and Cohen, 2014). GC analysis is a related, yet more powerful tool for studying functional connectivity, because (1) we test all neurons simultaneously, rather than only pairwise, and (2) GC analysis estimates effective, not only correlated, activity between neurons. Moreover, since we know the spatial location of imaged neurons we derive the spatial characteristics of effective connectivity. Our data indicate a complex but systematic relationship between noise correlations and GC networks. The attentional effect of modulated noise correlations during tone detection is believed to describe a modulation in connection strength between neurons, or of shared input to pairs of neurons. We revealed two opposing populations of neurons that had either increased or decreased noise correlation magnitudes during tone detection, largely depending on the sign of the noise correlation during passive trials. Thus, we find that the overall effect of tone detection on noise correlations may be described as a bias toward an optimal positive noise correlation value.

The dominant effect of tone detection was to increase both noise correlation values and GC link weights. Thus, the strength of connectivity, as described by noise correlations and GC links, may share a common underlying mechanism. Furthermore, decreases in noise correlations may separately reflect the task-driven sparsity of GC links, the decreased number of GC links, and the smaller GC subnetwork sizes.

SVM analysis showed that the activity of small subpopulations (4 neurons) was predictive of trial-by-trial behavioral choice. This was quite similar to the average number of 4.6 neurons per GC subnetwork, which suggested that the GC subnetworks we identified might be important for behavioral choice. Indeed, using SVMs, we found that the detected GC subnetworks had enhanced encoding of behavioral choice.

Our study describes attentional gain as commonplace across neurons during tone detection behavior, regardless of the BF of a given neuron relative to the target. Such non-specific effect might be reflective of neuromodulatory inputs suggested to be involved in attention (Kilgard and Merzenich, 1998, Kuchibhotla et al., 2017, Harris and Thiele, 2011, Ji and Suga, 2007). Moreover, pure-tone frequencies were varied across experiments for each mouse, thus the exact target frequency was not behaviorally meaningful, which might explain the lack of frequency specificity in attentional gain. By describing attentional gain through a comparison of passive vs. hit trials during task performance, we find positive attentional gain in both facilitative and suppressive responses, extending results of studies in both auditory and visual cortex (Kuchibhotla et al., 2017, Nandy et al., 2017, O'Connell et al., 2014, Atiani et al., 2014). Finally, our study is consistent with work in monkey A1, where individual neurons encoded reward outcome (Brosch et al., 2011). Here, we found that while attentional gain may increase neural responses to tones, recognition of a behavioral error may subsequently reduce neural responsiveness in A1. These cost signals may arise, in part, from inputs originating in the orbitofrontal cortex (Simon et al., 2015, Winkowski et al., 2013, Winkowski et al., 2017), the ventral tegmental area (Lou et al., 2014), or the basal forebrain (Miasnikov et al., 2008). We find that most neurons show attentional gain, but nevertheless GC linked populations are smaller during hit trials. This, suggests that despite global increases in activity, A1 subnetworks can separately be modulated.

In summary, our results show that activity in A1 L2/3 is not solely determined by the nature of the sensory signal but also by population coding of task-related information such as attentional gain and behavioral choice.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Patrick O. Kanold (pkanold@umd.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All procedures were approved by the University of Maryland Institutional Animal Care and Use Committee. We used N=10 mice (4 female, 6 male), CBA strain (The Jackson Laboratory; stock #000654), 8–24 weeks old, in 80 total experiments. We used CBA mice because they have good hearing into adulthood (Pharm and Willott, 1988). Each mouse was tested once per day over multiple days. The mice were trained to perform the task before collecting 2P data during task performance, since we were primarily interested in studying the neural correlates of attention and decision-making, rather than learning, per se. Mice were housed under a reversed 12 h-light/12 h-dark light cycle, and trained during the dark cycle. In total, we successfully implanted ~25 mice with a cranial window. Mice were rejected from the study due to poor visualization of cells, caused by cloudy windows or weak GCaMP6s expression. This eliminated ~40% of mice from the study. An inability to learn the behavioral task eliminated another ~20% of mice, leaving 10 mice in our study.

Separate analysis of data from males and females showed similar results in each group indicating no effect of sex (Fig. S6).

METHOD DETAILS

Auditory task

To study the neural coding of decision-making, we designed a simple tone detection task that used behavioral response-timing rules to induce well controlled behavioral responses in mice. Each mouse was trained on a positive reinforcement tone detection task, with water used as a rewarding stimulus. The mice were water restricted to motivate task engagement. Health was monitored daily by a skin Turgor test and checking that their body weight remained above 80% of their initial off-study weight.

Mice were initially trained away from the 2P microscope in sound attenuating boxes. Training began by habituating the mice to the head-fixing holder. Mice were placed on the holder and allowed to explore for ~60 min per day, for 2 days. We then habituated the mice to head-fixed waterspout licking by placing the water restricted, head-fixed mice in front of the waterspout and releasing water droplets at random time intervals, for roughly 45 minutes per day, for 2–5 days. Following waterspout habituation, we began training on the tone detection task twice a day. On each behavioral session, we initiated the task by briefly allowing water to drip until the mouse licked the waterspout. Each trial began with a 1 second silence, followed by a 55 dB SPL AM (8 Hz) tone presented for 1 s. The target tone frequency was selected between 4–32 kHz, and was different for each experiment in each mouse. The tone was followed by 2.5 s of silence, and a 5–9 s inter-trial interval (ITI). The tone was presented during every trial of task-performance, and the mice were trained to lick a waterspout after detecting the tone. During initial training, the mice received a water droplet for any lick made after the tone onset, and water was automatically delivered on 20% of trials, 2.5 s after the tone onset if the mouse did not lick. This was done to facilitate a reward association with hearing pure-tones. This phase of training lasted 2–3 days. Finally, the automatically delivered water was removed, and we instantiated strict response-timing rules described below. This phase of training typically lasted 2–5 days until the mice showed expertise. Once the mice learned the task, we then moved training to under the 2P microscope objective. Mice typically did poorly upon first doing the task under the objective, but performance usually recovered within 1–2 days. The mice tended to do 60 ± 22 trials per experiment.

Correct detections during task performance were classified as either “punished hits” or “rewarded hits.” Rewarded hits occurred when the first lick happened 0.5–2.5 s after the tone onset, and were reinforced with a water droplet being delivered after the first lick. When the first lick of a trial occurred after the tone onset, but before the 0.5 s delay, the trial was labeled a punished hit, which resulted in the water droplet being withheld, and an 8 s time-out added to the ITI. Licks made during the 1 s pre-stimulus silence (i.e., early licks) were punished in the same way. Misses occurred when the mouse did not lick during a trial. Response latencies were taken as the time of the first lick from the trial onset.

Virus injection and chronic window implantation

Mice were given a subcutaneous injection of dexamethasone (5mg/kg) at least 2 hours prior to surgery to prevent inflammation and edema. Mice were deeply anesthetized using isoflurane (44% induction, 2% for maintenance) and given subcutaneous injections of atropine (0.2mg/kg) and cefazolin (500mg/kg). Internal body temperature was maintained at 37.5 C using a feedback controlled heating blanket. The scalp fur was trimmed using scissors and any remaining fur was removed using Nair. The scalp was disinfected with alternating swabs of 70% ethanol and betadine. A patch of skin was removed and the underlying bone cleared of connective tissue using a bone curette. The temporal muscle was detached from the skull and pushed aside, and the skull was thoroughly cleaned and dried. A thin layer of cyanoacrylate glue (VetBond) adhesive was applied to the exposed skull surface and a 3D printed stainless steel head-plate, based on the design described in Guo et al. (2014), was affixed to the skull overlying the auditory cortex using a flow composite (Flow-It ALC) on the inner perimeter of the head-plate and dental cement (C&B Metabond) on the outer perimeter. A circular craniotomy (~3mm diameter) was made in the center opening of the head-plate and the patch of bone was removed.

Virus (AAV1.hSyn1.mRuby2.GSG.P2A.GCaMP6s.WPRE.SV40, titer: 3×10¹³; UPenn Vector Core) (Rose et al., 2016) was loaded into beveled glass pipettes and injected slowly (Nanoject II) into the areas corresponding to auditory cortex in 3 sites (~30 nL/site; ~450um from the surface; ~2–3 minutes/each injection site). Pipettes were left in place for at least 5 minutes after completion of each injection to prevent backflow. After virus injections, a chronic imaging window was implanted. The window consisted of a stack of 2 – 3mm diameter coverslips glued with optical adhesive (Norland 71, Edmund Optics) to a 5 mm diameter coverslip; the edges of the window between the glass and the skull were sealed with a silicone elastomer (Kwik-Sil). The edges of the glass and the skull were sealed with dental cement. The entire implant except for the imaging window was then coated with black dental cement created by mixing methyl methacrylate with iron oxide powder (AlphaChemical) (Goldey et al., 2014) to reduced reflections. Meloxicam (0.5mg/kg) and supplemental doses of dexamethasone were provided subcutaneously as a post-operative analgesic. Animals were allowed to recover for at least 2 weeks prior to the beginning of experiments.

Wide-field imaging

Awake mice were placed into a plastic tube and head restraint system, which was designed based on the system described by Guo et al. (2014). Blue excitation light was provided by an LED (470nm, Thorlabs) equipped with an excitation filter (470nm CWL, 40nm FWHM; Chroma ET470/40×) and directed toward the cranial window. Emitted light was collected through a tandem lens combination (Ratzlaff and Grinvald, 1991) consisting of a 55 mm lens and 85mm lens affixed to the camera and passed through a long-pass filter (cutoff: 495nm, Chroma Q495lp) followed by a bandpass emission filter (525nm CWL, 50nm FWHM; Chroma HQ525/50). Images were acquired using ThorCam software (Thorlabs) controlling a Thorlabs DCC3240M CMOS camera. After acquiring an image of the surface vasculature, the focal plane was advanced to a depth corresponding to ~500 µm below the brain surface.

To visualize tonotopic maps across the cranial window above auditory cortex, amplitude modulated (AM; 8 Hz) tones (4–48 kHz; 2 tones per octave, 5 or 10 repetitions per frequency) were presented from free field speakers at 55 dB SPL. Each trial consisted of a 1 s baseline silence followed by a 1 s tone and then a 2.5 s silence. Inter-trial intervals (ITIs) were 5 s. Wide-field images were acquired at a 4 Hz rate and 512×512 pixels. Images were downsampled to 256×256 and Gaussian filtered. Image sequences for each tone frequency were averaged and processed with a homomorphic filter to extract reflectance. For each pixel, ΔF/F traces were calculated by finding the average F taken from the silent baseline period, subtracting that value from subsequent time-points, then dividing all time-points by the baseline F. To visualize tonotopy, we kept only the set traces with ΔF/F within 75% of the maximum response in the pixel-wise grand-average of ΔF/F (i.e., ΔF/F₇₅). Pixel-wise tonotopic frequencies were taken as the median frequency of the set of tones corresponding to the ΔF/F₇₅ traces.

2-photon imaging

After visualizing wide-field tonotopic maps, a site was selected for 2-photon (2P) imaging in primary auditory cortex for each mouse. Our 2P recording sites were chosen at various regions across the rostro-caudal tonotopic gradient that was clearly identifiable in the wide-field images from our mice (Fig. 2A, S1) (Meng et al., 2017). This indicates that we most likely imaged neurons in primary auditory cortex (A1) L2/3. We used a scanning microscope (Bergamo II series, B248, Thorlabs) coupled to a pulsed femtosecond Ti:Sapphire 2-photon laser with dispersion compensation (Vision S, Coherent). The microscope was controlled by ThorImageLS software. The laser was tuned to λ = 940 nm in order to simultaneously excite GCaMP6s and mRuby2. Red and green signals were collected through a 16× 0.8 NA microscope objective (Nikon). Emitted photons were directed through 525/50-25 (green) and 607/70-25 (red) band pass filters onto GaAsP photomultiplier tubes. The field of view was 185 × 185 µm. Imaging frames of 512×512 pixels (pixel size 0.36 µm) were acquired at 30 Hz by bidirectional scanning of an 8 KHz resonant scanner. Beam turnarounds at the edges of the image were blanked with a Pockels cell. We typically limit the laser power to <70 mW, measured at the objective. mRuby and GCaMP6s fluorescence were imaged simultaneously on separate red and green channels, respectively. During experiments, the objective’s focal plane was lowered into layer 2/3 (150–250 µm below the surface). A different set of neurons was imaged for each experiment. Each experiment began with a Passive condition to characterize pure-tone frequency tuning between 4–48 kHz, and to find the baseline response to tone frequencies later used as targets during the task. We then found the tone frequency for each cell that elicited the biggest response, i.e., the best frequency (BF). After tuning estimations, the behavioral session was initiated.

After 2P experiments, all images were processed using Matlab (The Mathworks). Image motion was corrected by DFT registration. Frame-by-frame translation coordinates were found using mRuby image registration, and applied to the GcaMP6s images. Figure 2A (bottom panels) show the average of over 5000 registered images for both mRuby and GCaMP6s images. After semi-automatically selecting the centers of cell bodies (Cell Finder: https://github.com/KanoldLab/CellFinder), a ring-like region of interest (ROI) was cropped around the cell center using the method described in Chen et al. (2013). Overlapping ROI pixels (due to closely juxtaposed neurons) were excluded from analysis. For each labeled neuron, a raw fluorescence signal over time was extracted from somatic ROIs. Pixels within the ROI were averaged to create individual neuron fluorescence traces, F_C(t), for each trial of the experiment. Neuropil fluorescence was estimated for each cellular ROI using an additional ring-shaped ROI, which began 3 pixels from the somatic ROI. Pixels from the new ROI were averaged to obtain neuropil fluorescence traces, F_N(t), for the same time-period as the individual neuron fluorescence traces. Pixels from regions with overlapping neuropil and cellular ROIs were removed from neuropil ROIs. Neuropil-corrected cellular fluorescence was calculated as F̂_C(t) = F_C(t) – 0.7F_N(t). Only cells with positive values obtained from averaging F̂_C(t) across time were kept for analysis, since negative values may indicate the dominance of neuropil contamination (Fig. S3). ΔF/F was calculated from F̂_C(t), for each neuron, by finding the average F taken from the silent baseline period, subtracting that value from subsequent time-points, then dividing all time-points by the baseline F. Neuronal pairwise noise correlations were taken as the correlation coefficient between mean-subtracted ΔF/F responses to individual tone presentations. In order to account for differences in absolute response amplitudes from individual neurons in different cortical regions as the target frequency varied across experiments, the average ΔF/F trace from each experiment was normalized to unity magnitude before comparison with other experiments, and similarly normalized across cells for within population comparisons.

Support Vector Machine Analysis

We performed support vector machine (SVM) analysis (Cristianini and Shawe-Taylor, 2000) using the Matlab function, fitcsvm, on the neurons imaged within each experiment to predict behavioral choice (hit or miss) during the tone detection task. Prediction accuracy was calculated using leave one out cross-validation for each trial during an experiment, computed on a 250 ms sliding window (100 ms steps) across the length of a trial. To determine chance prediction accuracy, we performed SVM on data sets with shuffled trial labels. Error bars on shuffled data were obtained from 15 iterations of shuffled SVM analysis.

Granger Causality Analysis

We present a method for modeling, estimation and inference of the functional neuronal networks underlying two different task conditions, hit versus miss, in the sense of Granger. The notion of causality proposed by Granger (Granger, 1969), aims at capturing the two fundamental principles of temporal predictability and the precedence of cause over effect.

In order to capture the functional dependencies within a neuronal network, and the sparsity of interactions thereof, we employ sparse multivariate autoregressive models. We introduce a novel measure of Granger causality (GC) which accounts for sparse interactions, estimate the model parameters using fast optimization methods, and perform statistical tests to assess the significance of possible GC interactions, while controlling the false discovery rate (FDR) to avoid spurious detection of GC links.

Modeling

Consider a sequence of calcium indicator fluorescence measurements from a set of C neurons indexed by c = 1,2, …, C within a slice, denoted by ${\{{\mathrm{y}}_{r,n}^{(c)}\}}_{r=1:R,n=1:N}^{c=1:C}$ over time bins n = 1, …, N, and across R trial repetitions indexed by r = 1, …, R. We adopt a sparse vector autoregressive (VAR) framework (Valdés-Sosa et al., 2005) for modeling the slow-decaying and transient dynamics of the calcium fluorescence signals as well as the cross-dependencies among the neurons.

Suppose that the fluorescence observation vector of neuron (c) at the r-th repetition is represented by ${\mathbf{y}}_r^{(c)}≔[y_{r,1}^{(c)},\dots ,y_{r,N}^{(c)}]\prime$, and let ${\overline{\mathbf{y}}}^{(c)}≔[{\mathbf{y}}_1^{(c)\prime },{\mathbf{y}}_2^{(c)\prime },\dots ,{\mathbf{y}}_R^{(c)\prime }]\prime$ denote the zero-mean total observation vector, containing the set of all observation vectors ${\mathbf{y}}_r^{(c)}$ from all trials r = 1,…, R.

The effective neural covariates taken into account in our models are each neuron's self-history of activity and the history of activities of other neurons in the network. We consider a lag of L samples within which the possible neuronal interactions may occur. Then, we segment L into M windows of lengths W₁, W₂, …, W_M such that ${\sum }_{i=1}^M{W}_i=L$. Let $b_m≔{\sum }_{\ell =1}^m{W}_{\ell }$ for m = 1, …, M, and b₀ = 0. Let

$${\mathit{h}}_{\mathit{r}\mathbf{,}\mathit{n}\mathbf{,}\mathit{m}}^{(\mathit{c})}≔\frac{\mathbf{1}}{{\mathit{W}}_{\mathit{m}}}{\mathbf{\sum }}_{\mathit{k}=\mathit{n}-\mathbf{1}-{\mathit{b}}_{\mathit{m}}}^{\mathit{n}-\mathbf{1}-{\mathit{b}}_{\mathit{m}-\mathbf{1}}}{\mathbf{y}}_{\mathit{r}\mathbf{,}\mathit{k}}^{(\mathit{c})}\mathbf{,}$$ (1)

represent the average activity of neuron (c) within the m-th window lag of length W_m with respect to time n and at trial r. We can then define the vector of history covariates from neuron(c), effective at time n and trial r as ${\mathbf{h}}_{r,n}^{(c)}≔[h_{r,n,1}^{(c)},h_{r,n,2}^{(c)},\dots ,h_{r,n,M}^{(c)}]\prime$. Next, let ${\mathbf{x}}_{r,n}≔[{\mathbf{h}}_{r,n}^{(c)\prime },{\mathbf{h}}_{r,n}^{(c)\prime },\dots ,{\mathbf{h}}_{r,n}^{(c)\prime }]\prime$ denote the vector of covariates from all neurons at time n and trial r.

In order to represent the covariates in a more compact form, we consider the X_r≔ [x_r,1, x_r,2, …, x_r,N]′ which contains in its rows the covariate vectors at all times n = 1, …, N within trial r. Finally, let X̅≔ [X₁′, X₂′, …, X_R′]′ represent the matrix of all covariates with standardized columns (i.e., zero-mean columns with unit norm), capturing the covariates X_r for all the trials r = 1, …, R

The VAR model can then be expressed as:

$${\overline{\mathbf{y}}}^{(\mathit{c})}=\overline{\mathbf{X}}{\mathit{\omega }}^{(\mathit{c})}+{\overline{\mathit{\epsilon }}}^{(\mathit{c})}\mathbf{,}$$ (2)

where ${\overline{\mathit{\epsilon }}}^{(c)}≔[{\mathit{\epsilon }}_1^{(c)\prime },{\mathit{\epsilon }}_2^{(c)\prime },\dots ,{\mathit{\epsilon }}_R^{(c)\prime }]\prime ~𝒩(\mathbf{0},{\sigma }^{(c)2}\mathbf{I})$ is a zero-mean Gaussian noise vector of size RN with variance σ^(c)2, and ω^(c) is a parameter vector accounting for the interactions in the network, for c = 1,2,…, C.

In agreement with the parsing of the covariates in the matrix X̅, the parameter vector ω^(c)≔ [ω^(c,1)′, ω^(c,2)′, …, ω^(c,C)′]′ in Eq. (2) is composed of a collection of cross-history dependence vectors {ω^(c,c̃)}^c̃=1:C, where ω^(c,c̃) represents the contribution of the history of neuron (c̃) to the activity of neuron (c) via the corresponding covariate vector ${\mathbf{h}}_{r,n}^{(c)}$ encoded in matrix X̅. In particular the component ω^(c,c) is important in capturing the slow calcium florescence decay in an autoregressive fashion, and thereby excluding the transient effects of florescence decay from the GC analysis.

Next, we invoke the hypothesis of sparsity in the interactions among the neurons in the network. This hypothesis is grounded in a body of well-accepted evidence from theoretical and experimental studies (Rehn and Sommer, 2007, Babadi and Sompolinsky, 2014, Olshausen and Field, 1997, Druckmann et al., 2012, Song et al., 2005, Sporns and Zwi, 2004). In our model, the sparsity of the interactions can be captured through the sparsity of the parameter vector ω^(c): when only very few components of ω^(c) are non-zero, neuron (c) is only affected by the activity history of a few neurons in the network. In addition, as the dimension of the parameter vector given by MC scales with the network size C, the hypothesis of sparsity enables the detection of salient interactions within a large network, and thereby mitigates overfitting, especially when the observations are noisy and trials are limited in number.

Parameter Estimation

In order to define a framework for inferring a possible GC link (c̃ ↦ c, two nested models are taken into account: 1) the VAR model in Eq. (2), where the contributing covariates from all the neurons are taken into account, referred to as the full model, and 2) the same model in which the covariates and parameters of a single neuron (c̃) on neuron(c), c̃ ≠ c are excluded, to which we refer as the reduced model. The parameters and covariates associated with the reduced model are denoted by ω^(c\c̃) and X̅^\c̃, respectively.

The sparse parameter vector associated with either of the two models can be estimated by solving an ℓ₁-regularized maximum likelihood (ML) problem for each neuron as follows:

$$\hat{\mathit{\omega }}=\underset{\mathit{\omega }}{\mathbf{\text{argmin}}}(\frac{\mathbf{1}}{\mathbf{2}}{\Vert {\overline{\mathbf{y}}}^{(\mathit{c})}-\mathbf{X}\mathit{\omega }\Vert }_{\mathbf{2}}^{\mathbf{2}}+\mathit{\gamma }{\Vert \mathit{\omega }\Vert }_{\mathbf{1}})\mathbf{,}$$ (3)

where X takes the two values of X̅ and X̅^\c̃ for the full and reduced models, respectively, the ℓ₁ - norm is defined as ${\Vert \mathit{\omega }\Vert }_1≔{\sum }_{m=1}^M|{\omega }_m|$, and γ ≥ 0 is a regularization parameter tuning the sparsity level, which can be selected based on analytical results on ℓ₁-regularized ML problems (Van de Geer et al., 2014) or via cross-validation. This ℓ₁-regularized ML problem can be solved efficiently using proximal algorithms (Parikh and Boyd, 2014, Bruckstein et al., 2009). Given the parameter estimate ω̂, the corresponding variance associated with the model can be computed as ${\hat{\sigma }}^2=\frac{1}{\mathit{\text{NR}}}{\Vert \overline{\mathbf{y}}-\overline{\mathbf{X}}\hat{\mathit{\omega }}\Vert }_2^2$.

Inference

The conventional measures of GC are based on ML estimates of the VAR parameters, and not the regularized ML as in our case. Hence, we need to modify the GC measure and the corresponding deviance statistics, to account for the estimation bias incurred due to ℓ₁-regularization. This new measure is the static VAR-based counterpart of a similar measure presented in our earlier studies in the context of dynamic sparse point process models (Sheikhattar and Babadi, 2016).

To this end, we modify the deviance difference statistic corresponding to the full and reduced models to compensate for the bias incurred due to sparse regularization. Building on recent results from high dimensional statistics (Van de Geer et al., 2014), and our previous work in the context of point processes (Sheikhattar and Babadi, 2016), the bias can be computed for the full model as B^(c)≔ g^(c)′H^(c)−1g^(c), where g^(c)≔ X̅′(y̅^(c) − X̅ω̂^(c))/σ̂^(c)2 and H^(c)≔ −X̅′X̅/σ̂^(c)2 are the gradient and Hessian of the log-likelihood function for the Gaussian VAR model of Eq. (2), respectively. Similarly, the bias B^(c\c̃) for the reduced model can be computed by replacing the matrix of covariates and parameter estimate by X̅^\c̃ and ω̂^(c\c̃), respectively.

The deviance difference statistic associated with the two nested full and reduced models can be expressed as:

$${\mathit{D}}^{(\stackrel{\sim }{\mathit{c}}\mapsto \mathit{c})}≔\mathit{\text{NR}}\mathbf{\text{log}}\frac{{\hat{\mathit{\sigma }}}^{(\mathit{c}\backslash \stackrel{\sim }{\mathit{c}})\mathbf{2}}}{{\hat{\mathit{\sigma }}}^{(\mathit{c})\mathbf{2}}}-{\mathit{B}}^{(\stackrel{\sim }{\mathit{c}}\mapsto \mathit{c})}\mathbf{,}$$ (4)

where B^(c̃↦c)≔ B^(c) − B^(c\c̃) denotes the difference of bias terms corresponding to the full and reduced models. Note that the first term coincides with the log-likelihood ratio statistic for Gaussian data (Bressler and Seth, 2011), and captures the prediction improvement of the full model over the reduced model.

We finally employ the inference framework presented in (Sheikhattar and Babadi, 2016, Kim et al., 2011) to simultaneously test the statistical significance of all possible GC interactions and to control the FDR at a given significance level α. This inference framework integrates an extension of classical results on analysis of deviance, and a multiple hypothesis testing procedure based on the Benjamini-Yekutieli FDR control (Benjamini and Yekutieli, 2001). The weights of the detected links are further characterized using the Youden's J-statistic, which is a summary statistic for quantifying the strength of hypothesis tests. The excitatory or suppressive nature of GC links are determined by the effective sign of estimated cross-history parameters associated with shorter latencies.

Validation of Granger Causality (GC) Inference: Sparse Estimation & Bias Correction

To validate the proposed GC inference technique, and particularly the roles of sparse estimation and bias correction, we provide an illustrative simulation study with known ground truth causal links. To this end, we compare the performance of our proposed method with the conventional ML-based GC inference technique, as well as GC inference from sparse estimates with no bias correction.

We consider a network of C = 8 neurons, causally inter-connected based on the pattern shown in Fig. S5B (the leftmost panel). For each neuron, we simulate a sequence of fluorescence measurements of length N = 150 samples, across R = 10 trial repetitions, based on the VAR model in (2), driven by a zero-mean Gaussian sequence of variance σ² = 0.002. Fig. S5A shows one simulated trial for all 8 neurons. In order to model the fluorescence traces, we consider a random sequence of discrete events uniformly distributed over time with a low probability of p = 0.33 event/trial, to represent spikes. We select a sparse parameter vector θ of length M_h= 20 with a support set of S = {1,5, 15,20} of sparsity s = 4, and respective values of θ_{1,5,15,20} = {0.3, 0.05, 0.05, −0.05} to model the self and cross-history dependencies among neurons. The cross-history parameters are chosen to be the same for all the existing G-causal links, i.e., ω^(c,c̃) = θ, and have a positive or negative sign for the excitatory or suppressive GC links, respectively. In addition to the cross-history effects, we assume self-history dependence of excitatory nature, ω^(c,c̃) = θ, and a scalar fluorescence baseline parameter, μ^(c) = 0.01, consistent across all neurons. The underlying ground truth functional pattern is unknown to the estimator, and is to be inferred from the simulated fluorescence traces. For estimation of GC links, we consider $M_h^{\mathit{\text{Cross}}}=M_h^{\mathit{\text{Self}}}=50$ history components associated with the lag of L = 50 samples (with W_m = 1). For sparse estimation, the regularization parameter γ is separately tuned for each neuron via cross-validation across trials. The FDR is controlled at a rate of α = 0.05, for simultaneous testing of 56 possible GC links.

Fig. S5B and S5C show the comparison of our proposed method (2^nd panel) with: 1) sparse estimation without bias correction (3^rd panels), and 2) the conventional GC inference based on ML estimates (4^th panel), in graphical and matrix forms, respectively. The GC maps of Fig. S5C represent 8 × 8 color-coded arrays, where red, blue, and green show excitatory, suppressive, and no link, respectively. The first method (3^rd panels) is the biased variant of our proposed GC inference framework, where we adopt a similar estimation procedure and inference, but disregard the bias correction term incurred by the sparse regularization in (4). In the second method, the sparsity of the parameters is not taken into account, and the parameter estimation and deviance computation are performed based on ML estimates.

Fig. S5B and S5C reveal that our presented method outperforms the two other compared methods in terms of both identification of the true GC links and avoiding false discoveries: while our proposed method matches the ground truth, removing the bias correction step results in low hit rate, and not accounting for sparsity results in high false alarm rate. This illustrative example highlights the crucial role of bias correction for the deviance difference statistics in our proposed statistical inference procedure. In addition, it shows that ML-based approaches that do not account for sparsity overfit the parameters when applied to limited data, and hence result in significant false discoveries.

GC Network Analysis

After finding the matrix of link weights, GC networks were analyzed as directed graphs in Matlab. The GC link weights, lengths, angles and sign were indexed to each link, then stored separately. The square GC matrix was then converted to an unweighted adjacency matrix by taking its absolute value, and then changing all non-zero values to 1. The adjacency matrix was then input to the Matlab function, digraph, to produce a directed graph for each experiment. Each graph was then analyzed using the Matlab function, conncomp, to find connected nodes, i.e., “subnetworks.”

Immunohistochemistry

Following in vivo imaging, mice were anesthetized with 4% Isoflurane (Fluriso, VetOne) and transcardially perfused with 1× PBS (Sigma Aldrich) followed by 4% paraformaldehyde (Electron Microscopy Sciences) in 1× PBS. Brain tissue was extracted and drop-fixed in 4% paraformaldehyde in 1× PBS overnight at 4°C. Fixed brains were then dehydrated in 30% sucrose (Sigma Aldrich) in 1× PBS and sectioned into 60 µm coronal slices using a freezing microtome. Slices were rinsed in 1× PBS for 10 minutes, blocked with normal goat serum (Kirkegaard & Perry Laboratories) and Trion X-100 (Sigma-Aldrich) for one hour on a shaker, and incubated at room temperature overnight on a shaker with primary antibodies against GFP (pChicken; 1:500; Aves Lab) to enhance cytosolic GCaMP signal, GFAP (pRabbit; 1:1000; Life Technologies) to stain astrocytes, and NeuN (mMouse; 1:50; EMD Millipore) to stain neuronal cell bodies. Slices were then rinsed three times in 1× PBS and incubated for two hours with secondary antibodies raised in goat: Alexa Fluor 488 (anti-chicken; 1:200; Life Technologies), Alexa Fluor 546 (anti-mouse; 1:200; Life Technologies), and Dylight 594 (anti-rabbit; 1:100; Vector Laboratories). After mounting slices on glass slides with Fluoromount-G with DAPI (Southern Biotech), images were acquired with a Leica SP5 × Confocal Microscope (UMD Imaging Core Facility). Sections were stained for GFP (to enhance GCaMP6 cytosolic signal), GFAP (astrocytes), NeunN (neuronal cell bodies), and DAPI (all cell nuclei) (Fig. S4).

In order to estimate the percentages of excitatory vs. inhibitory neurons expressing GcaMP6s in CBA mice injected with AAV1 using the synapsin promoter, Gad2-tdTomato mice were generated by crossing homozygous Gad2-IRES-Cre mice (Jax no. 010802) to homozygous Ai9 mice (Jax no. 007909). Offspring were injected at 3 sites (30nL/site) with AAV1.Syn.GCaMP6s.WPRE.SV40 (Penn Vector AV-1-PV2824) in left auditory cortex at 450 µm depth. Following 2 weeks incubation, brain tissue was extracted and drop-fixed in 4% paraformaldehyde in 1X PBS overnight at 4°C. Fixed brains were then dehydrated in 30% sucrose (Sigma Aldrich) in 1× PBS and sectioned into 60 µm coronal slices using a freezing microtome. After mounting slices on glass slides with Fluoromount-G with DAPI (Southern Biotech), images were acquired with a Leica SP5 × Confocal Microscope. GFP and co-labeled GFP/RFP positive cells up to a depth of 300 µm from pia were counted with the Cell Counter plugin within the FIJI software. See Supplementary figure S2 for detailed images.

Quantification and statistical analysis

Unless noted otherwise, statistical comparisons were performed using a bootstrap t-test with 10000 iterations or a Kolmogorov–Smirnov test (KS-test), for both one- and paired-sample tests. Kruskal-Wallis tests were used when there were >2 groups being compared. We used a Bonferroni correction for multiple comparisons. All mean values are reported with 2 standard errors of the mean, unless noted differently.

Data and software availability

The dataset and software are available upon request.

Highlights.

• -A1 L2/3 neural responses to target sounds were enhanced during task performance
• -Sensory input, attentional gain, and behavioral-choice modulated A1 neural activity
• -Behavioral-choice modulated functional connectivity in neuronal populations
• -Neural decoding of behavioral-choice was best within small neuronal networks