Abstract
We experimentally demonstrate the use of continuous, time-delayed, feedback stimulation for controlling the synchronization of neuron action potentials. Phase-based models were experimentally constructed from a single synaptically isolated cultured hippocampal neuron. These models were used to determine the stimulation parameters necessary to produce the desired synchronization behavior in the action potentials of a pair of neurons coupled through a global time-delayed interaction. Measurements made using a dynamic clamp system confirm the generation of the synchronized states predicted by the experimentally constructed phase model. This model was then utilized to extrapolate the feedback stimulation parameters necessary to disrupt the action potential synchronization of a large population of globally interacting neurons.
I. INTRODUCTION
Abnormal synchronization of neural activity can be seen in many neurological diseases, including epilepsy, Parkinson’s disease, and essential tremors [1–4]. Neurostimulation therapy can be used to alleviate the symptoms of these diseases [5,6]; it typically involves applying a pulse-train stimulation signal to an electrode which has been surgically implanted into the brain of the patient [7–9]. This electrical stimulation signal modulates the extracellular potential of all of the neurons within the targeted area, which is thought to alter their collective behavior. One main challenge is to determine the necessary stimulation parameters in order to obtain the desired collective firing behavior. While electrical stimulation has been shown to modulate the activity of individual neurons, its effect on the synchronization behavior of a group of neurons is currently under investigation [10,11]. Theoretical models have been developed which illustrate how electrical stimulation can be utilized to alter the firing patterns of simulated populations of neurons [12,13].
Time-delayed feedback has been shown to desynchronize groups of model neurons [12,14–18], and can be employed in place of pulse-train stimulation. The feedback can be used to design a therapeutic state of synchronization [19,20]. The application of locally addressable stimulation has been shown to synchronize the action potentials of neurons [21].
Here, we experimentally demonstrate the use of time-delayed feedback stimulation for engineering the synchronization of the action potentials of cultured neurons. Phase models have been shown to have sufficient accuracy to allow precise control over synchronization states of complex oscillatory systems [21–29]. The standard approach for the construction of a phase model involves the measurement of the phase response of a system to a set of discrete pulses applied at specific times in the cycle of the element [21,24,30–35]. However, precise measurements of phase shift are difficult to obtain, particularly when, for example, the period is nonstationary. In this paper, an experimental method was used to construct phase-based models using continuous stimulation of a single patch clamped neuron. We believe that this method overcomes some of the limitations inherent in standard pulse-based approaches. The mean period of the neuron was measured with and without applied feedback. The change in the mean period of the action potentials as a result of the application of feedback was determined as a function of feedback delay. This allowed for the construction of a phase model of the dynamical behavior of the neuron. The experimentally constructed model was then used to determine the feedback parameters necessary to produce in-phase and antiphase synchronization states within a two-neuron system using global stimulation. The parameters were applied to an experimental system of two patch clamped neurons, and the desired synchronization states were observed. The validated model was then used to determine feedback parameters which may disrupt the synchronization of a large population of globally coupled neurons.
II. THEORY
A phase-based model can be constructed to represent the dynamical behavior of a population of coupled oscillatory elements:
| (1) |
where ϕi is the phase of the element, K is the interaction strength, ωi is the natural frequency, and H(Δϕ) is the interaction function [36,37]. The interaction function can be determined from macroscopic physical quantities:
| (2) |
where Z(ϕ) is the response function and h(ϕ) is the stimulation function [37]. The response function quantifies the sensitivity of the neuron to perturbations as a function of phase, while the stimulation function quantifies the amount of stimulation applied to the neuron at a given phase.
The construction of the model proceeds by experimental determination of the response function of the neuron. Standard methods for determining the response function of an oscillatory element often require large pulses [38] or access to multiple coupled elements [39], making them difficult to apply in experimental systems. As a result, a method was developed which utilized weak delayed self-feedback stimulation applied to a single oscillator [40]. A phase model can be defined for a system composed of one element as
| (3) |
where is the phase of the stimulation signal applied to the element. For delayed self-feedback stimulation, the phase of the stimulation is related to the phase of the physical element by
| (4) |
where τ is the feedback delay.
The phase of an oscillator can be integrated over one cycle and expressed as a function of the period of the oscillation:
| (5) |
where Pi is the intrinsic mean period of the oscillator (2π/ωi), and ΔPi is the change in the period of the oscillator due to external stimulations, such that Pi + ΔPi is the observed period of the element [39,41]. By substituting Eqs. (3) and (4) into (5), H(Δϕ) can be analytically approximated as
| (6) |
Equation (6) allows for the determination of the interaction function directly from experimental measurements of the period of an oscillatory element stimulated using delayed self-feedback. A similar method using a synaptic stimulation function was developed by Cui et al. [42].
Z(ϕ) can be analytically determined from Eq. (2) given an experimentally measured interaction function obtained under a known stimulation. Each function in Eq. (2) can be expanded in a Fourier series,
| (7) |
| (8) |
| (9) |
Substitution of these Fourier series into Eq. (2) and integration yields a linear system of equations in terms of their Fourier coefficients:
| (10) |
which can be solved using standard matrix techniques.
Once the response function is known, Eqs. (1) and (2) can be used to determine how the the parameters of the stimulation function affect the collective phase behavior of a set of two or more neurons. For a system of two neurons, we construct a phase model of the form
| (11) |
which by subtraction yields
| (12) |
Stationary solutions to this equation will occur at phase differences which satisfy
| (13) |
where H−(Δϕ) is the odd part of the interaction function. A linear stability analysis indicates that these stationary states will be stable when
| (14) |
Synchronization states can therefore be generated by selecting feedback stimulation parameters such that the interaction function has the necessary properties Eqs. (13) and (14) to stabilize the desired states.
III. EXPERIMENTAL METHODS AND APPARATUS
Rat hippocampal cells were cultured using methods modified from the literature [43,44]. Cultures were prepared from P0-P1 Sprague-Dawley newborn rats. The newborn rats were decapitated, and their brains were removed and placed in cold HEPES-buffered Hank’s balanced salt solution 4- (2-Hydroxyethyl)piperazine-1-ethanesulfonic acid (HEPES)- HBSS. The hippocampi were removed under a dissecting microscope and collected in a small petri dish containing HEPES-HBSS. Tissues were incubated in 0.125% trypsin for 15 min at 37 °C. The trypsin solution was replaced with 5 ml HEPES-HBSS and the cells were rinsed twice more with HEPES-HBSS at 5 min intervals. The hippocampi were triturated until no fragments of tissue remained. Neurons were collected by centrifugation and resuspended in 5 ml of Dulbeccos modified Eagles medium and F-12 supplement (1:1) (Invitrogen) with 10% fetal bovine serum (heat inactivated, Invitrogen), 2 mM L-glutamine (Invitrogen), and penicillin (100 U/ml)-streptomycin (100 U/ml).
Culture dishes were coated with polylysine and filled with 2 ml of culture medium. Cells were plated at a minimum density of 50 000 per 35 mm2 dish and kept at 37 °C in a 5% CO2 incubator. After 24 h, the culture medium was changed to serum-free medium containing 2% B27 and 2 mmol/l glutamine. The medium was replaced with fresh medium every 2–3 days. The cultures used for the experiments were between 9 and 15 days old. Cells were placed in external media consisting of (in mM) 146 NaCl, 3 KCl, 2 CaCl2, 3 MgCl2, 11 glucose, and 10 HEPES, pH 7.4, osmolarity 310–315 mOsm. The neurons were synaptically isolated by adding 50 μM DL-2-Amino-5-phosphonopentanoic acid (DL-AP5), 50 μM bicuculline methiodide, and 20 μM 6,7-Dinitroquinoxaline-2,3-dione (DNQX). In order to create periodic spiking, 50 μM of 4-aminopyridine, a common agent used to induce seizurelike activity, was added to the external solution.
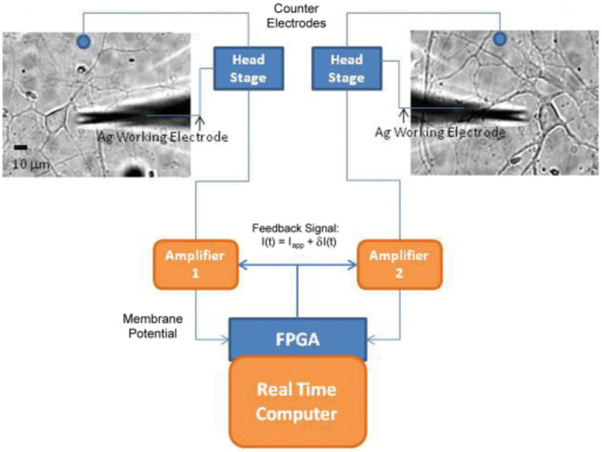
Cells were patched using a micropipette with a resistance of 6–9 MΩ and filled with a solution of (in mM) 145 K-gluconate, 0.6 Ethylene glycol-bis(2-aminoethylether)-N,N,N’,N’-tetraacetic acid (EGTA), 11 HEPES, 8 KCl, 3 NaCl, and 4 MgATP, pH 7.3, osmolarity 295–300 mOsm. A silver counterelectrode was placed into the external solution. The membrane potentials of the cells were recorded using two Axopatch amplifiers. The amplified membrane potential measurements were digitized using a 16-bit data acquisition system. A Xilinx FPGA processor was programmed to calculate a stimulation signal from the membrane potential measurements of the neurons. The stimulation was of the form
| (15) |
| (16) |
| (17) |
where I(t) is the injected current stimulation signal, Iapp is the baseline injected current, is the mean value of the neuron membrane potential, K is the feedback gain, τ is the feedback delay, and V is the measured neuron membrane potential. The loop rate of the controller was 25 kHz. A schematic of the dynamic clamp apparatus is in Fig. 1. Other similar dynamic clamp apparatuses have been discussed in the literature [45,46].
FIG. 1.
(Color online) Schematic of the patch clamp apparatus setup. For one-cell experiments only one patch clamp apparatus was used and for the two-neuron experiments both patch clamp apparatuses were used.
After the cells were successfully patched, they were hyperpolarized to −70 mV and allowed to rest for 120 s to ensure the formation of a 1 GΩ seal. A baseline current of 40 pA was injected into the neurons, causing repetitive spiking. After allowing 1 s for accommodation, feedback stimulation was applied to the neuron. The feedback signal was applied for approximately 10 s, after which time the current stimulation was removed and the neuron was allowed to rest for a period of approximately 20–30 s, before the next depolarization.
1V. EXPERIMENTAL RESULTS
Experiments were conducted to illustrate the use of global feedback stimulation for controlling the synchronization behavior of neurons. The interaction function of a single, synaptically isolated neuron to delayed feedback stimulation was experimentally measured. A single neuron was patch clamped and its membrane potential was recorded over time [Fig. 2(a)]. Delayed feedback stimulation was then applied to the neuron. Figures 2(b)–2(d) illustrate the firing period of the neuron as a function of feedback delay. Baseline observations of the natural firing rate of the neuron (without applied stimulation) were taken before and after each experiment (left and right panels). The natural period distribution of the neuron was observed to be approximately the same before and after the application of feedback stimulation, indicating that the stimulation did not disrupt the intrinsic behavior of the neuron. Experiments were repeated using three different neurons.
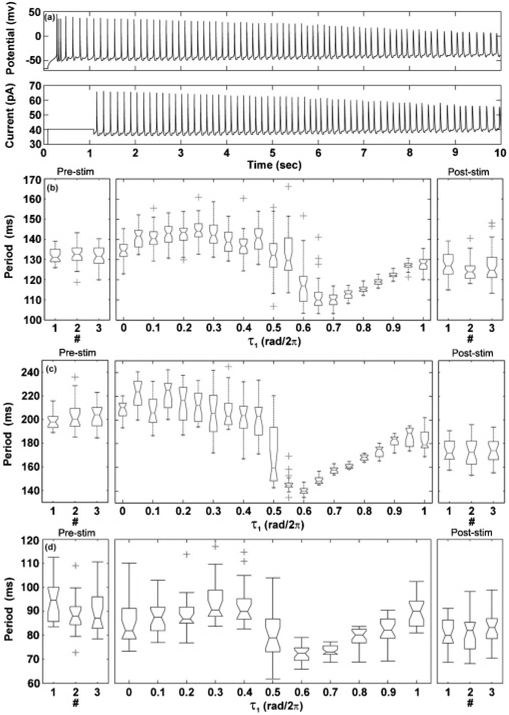
FIG. 2.
(a) The membrane potential of a single neuron (top) and the applied stimulation signal (bottom) as functions of time (K0 = 13 mV, K1 = 350, τ = 0.5 rad/2π). (b), (c), (d) Period distributions for three separate cells. Middle panel shows the period distribution as the feedback stimulation delay was increased from from 0 to 1 rad/2π. Left and right panels illustrate the period distribution of the neuron action potentials before and after application of stimulation.
The period of the neuron action potentials was observed to change as the feedback delay was increased [middle panels, Figs. 2(b)–2(d)]. The maximum firing period was achieved with a feedback delay of approximately τ = 0.25 rad/2π, while the minimum firing period was obtained at approximately τ = 0.7 rad/2π. The firing period of the neuron with τ = rad/2π was close to the firing period when τ = 0 rad/2π. Drift in the natural period of the action potentials occurred but was small compared to the mean period of the action potentials, except for the case of the second cell [Fig. 2(c)]. For this cell, the mean period was adjusted linearly from the initial prestimulation mean period to the poststimulation mean period. The qualitative frequency response was found to be similar for each neuron.
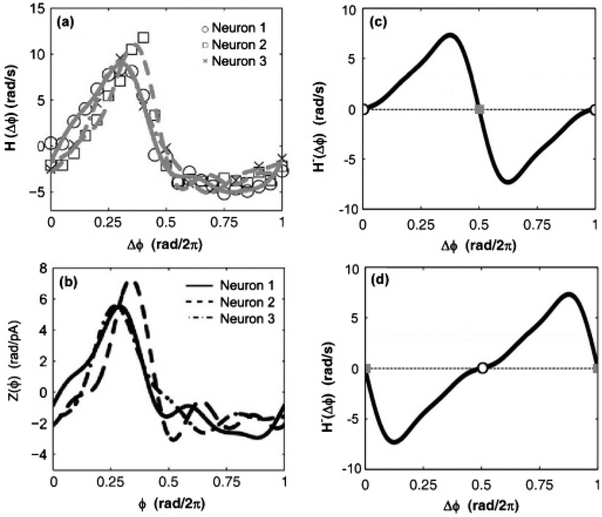
Equation (6) was applied to the experimental observations in Figs. 2(b)–2(d); the resulting interaction functions are illustrated in Fig. 3(a). The period of the neuron action potentials was taken to be the median period of the observed action potentials. Once the interaction functions were determined for each of the neurons, their corresponding response functions were calculated using Eq. (2). For this calculation, the stimulation function was set to Eq. (17) and the neuron wave form x(ϕ) was set to the mean cycle of the neuron action potential. The resulting response functions for each of the neurons are illustrated in Fig. 3(b). Qualitative agreement was seen between these three functions, indicating that their sensitivities to electrical stimulation are approximately equal.
FIG. 3.
(a) Calculated interaction function data and Fourier fit for three neurons. (b) Calculated response functions for three isolated neurons. (c) Odd part of the interaction function for the experimental system with applied global feedback (K0 = 13 mV, K1 = 350, and τ = 0 rad/2π). (d) Odd part of the interaction function for the experimental system with applied global feedback (K0 = 13 mV, K1 = 350, and τ = 0.5 rad/2π). In (c) and (d) the open circles are stable states and the gray squares are unstable states.
The experimentally constructed phase model was used to determine the values of feedback delay which would produce in-phase and antiphase synchronization states in a system of two neurons. As indicated by Eqs. (12) and (14), a system of two neurons will exhibit a stable phase-locked state when the odd part of the interaction function equals the value Δω/K with positive slope. Assuming the ratio of Δω/K is small, the stationary states of the system can be found as the roots of H−(Δϕ). The roots of H−(Δϕ) for the experimental system were determined as a function of the feedback delay. It was observed that feedback delays less than 0.2 rad/2π produced a unique and stable in-phase synchronization state while feedback delays between 0.4 and 0.6 rad/2π produced a unique and stable antiphase synchronized state. Figures 3(c) and 3(d) illustrate the odd part of the interaction function for feedback delays of 0 and 0.5 rad/2π, respectively.
The identified feedback delays were applied to the two-neuron system in order to produce the expected in-phase and antiphase synchronization states. To ensure that the neurons were connected only through the feedback stimulation, they were synaptically isolated and placed in separate cultures. Both neurons were patch clamped using standard methods. The recorded membrane potentials for both cells under different experimental conditions can be seen in Figs. 4(a1)–4(a3); the applied stimulation signal is illustrated in Figs. 4(b1)–4(b3). The neurons were observed to experience accommodation for the first three seconds of each experiment; these data were not considered as part of the analysis.
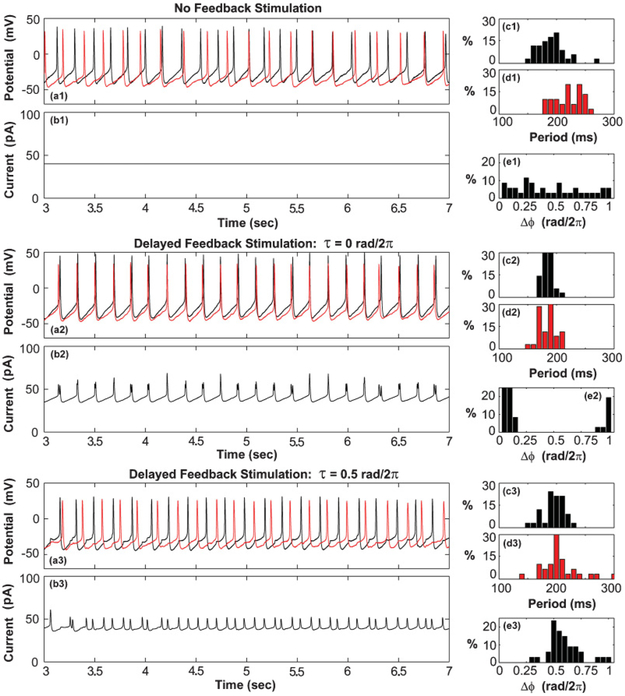
FIG. 4.
(Color online) (a) Membrane potential recording of two neurons. (b) Applied stimulation current (K0 = 13 mV, K = 400). (c), (d) Period distribution of neuron action potentials of neurons 1 and 2, respectively. (e) Observed distribution of phase differences between the action potentials of the two neurons.
Without feedback stimulation, the phases of the action potentials of the two neurons were found to be uncorrelated [Figs. 4(a1)–4(e1)]. The mean periods of the cells were not observed to lock and no preferred phase orientation was found [Fig. 4(e1)]. Application of the global feedback stimulation with a delay of τ = 0 rad/2π caused the mean period of the two cells to lock with a period of approximately 180 ms [Figs. 4(c2) and 4(d2)]. The mean phase difference between the neuron action potentials was observed to be approximately 0.05 rad/2π, indicating the presence of a nearly in-phase synchronized state [Fig. 4(e2)]. This observation was consistent with theoretical expectations [Fig. 3(c)]. The in-phase synchronized state persisted until the feedback stimulation was removed (not shown). Increase in the feedback delay to τ = 0.5 rad/2π caused the action potentials of the two neurons to synchronize in an antiphase configuration [Figs. 4(a3)–4(e3)]. This was consistent with expectations [Fig. 3(d)].
V. DISCUSSION
Current research has explored the synchronization behavior of neurons as a function of inhibitory and excitatory synaptic connections [47–49]. Here we demonstrate that the phase model can also be used to generate global electrical stimulation parameters which can potentially overcome natural behaviors of a neural system. Phase-based models have proven to be a valuable tool for characterizing the individual and collective dynamical behavior of neurons [30,31,35,50,51]. Such models are advantageous since no detailed knowledge of the biochemistry of neurons is required; only macroscopic measurements of membrane potential are necessary for model construction. Typically, models are generated from experimental measurements on a single neuron and subsequently used to infer the synchronization behavior of a population of interacting neurons. We reverse the process by using the phase model to determine the stimulation required to produce a desired synchronization behavior.
Models constructed from experimental measurements on single neurons have proved effective for estimating stimulation parameters for controlling the action potential synchronization of two neurons. However, the ultimate goal is the creation (or disruption) of synchronization in large-scale systems. To demonstrate this application, the experimentally constructed phase model was utilized to estimate stimulation parameters which would disrupt the collective synchronization of a large population of globally coupled neurons. The dynamical behavior of such a system is governed by the superposition of all interactions (internal and external) between elements:
| (18) |
Typically the intrinsic interactions (Hint) of such a system are unknown. The application of an external stimulation is utilized to overwhelm the unknown intrinsic coupling between elements, allowing new dynamical behaviors to be artificially created. The challenge is in picking the stimulation parameters which will produce the desired effect on the collective behavior of the target system.
To create a desynchronized state, all stationary states of the system must be simultaneously destabilized. The stability of synchronized states can be determined by calculating the eigenvalues associated with these states. Assuming that only balanced phase cluster states are possible, the associated eigenvalues can be determined from the Fourier coefficients of the net interaction function [52,53]. To actively disrupt phase synchronized states in a rhythmic population, a set of feedback parameters must be selected such that all phase cluster states have at least one eigenvalue with positive real part.
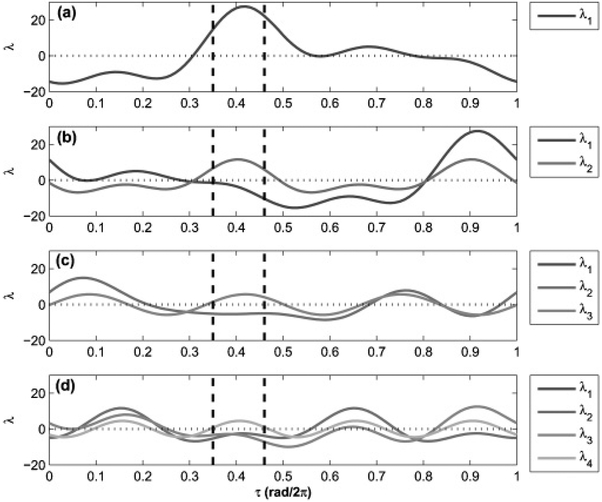
Having experimentally obtained the response function of the experimental neuron system, the stability of balanced phase cluster states can be determined as a function of the stimulation parameters. Only linear feedback will be considered for this analysis. By adjusting the feedback delay parameter, the stability of the synchronized states can be externally influenced; the amplitude of the feedback signal does not affect the stability of such states. The eigenvalues of cluster states 1–4 were calculated as a function of feedback delay for the experimental neuron system under first-order feedback (Fig. 5). The eigenvalues indicate that the external feedback signal will desynchronize a population of globally coupled neuron when the feedback delay is between 0.35 and 0.45 rad/2π. In this parameter range each cluster state will have at least one eignevalue with a positive real part. This parameter range is believed to be large enough to provide a robust starting point for future experiments.
FIG. 5.
Eigenvalues calculated for balanced cluster states as a function of feedback stimulation delay. (a) One-, (b) two-, (c) three-, and (d) four-cluster state. Dashed lines indicate region of possible desynchronization. In the three-cluster state λ1 = λ2, and in the four-cluster state λ1 = λ3.
The use of model-derived feedback signals for controlling the synchronization behavior of neurons may represent an improvement over the ad hoc methods of parameter estimation for current neurostimulation therapies. We have previously demonstrated that phase models can be used to engineer global feedback stimulations for controlling the collective behavior of large populations of complex rhythmic elements in nonlinear electrochemical systems [22]. This work demonstrates a proof of concept for the application of our engineering framework to control the synchronization behavior of biological neurons. As seen in Fig. 4, both in-phase and antiphase configurations were successfully generated using global delayed feedback. In both cases, a single common stimulation signal was applied equally to the neurons. Such global stimulation is required for clinical neurostimulation applications. Previous work has demonstrated the use of addressable electrical stimulation for influencing the synchronization of neurons [54].
The effect of synaptic connections on the synchronization of neurons was not considered due to experimental limitations. However, past work has shown that synaptic connectivity and interactions may be directly incorporated into the phase model [49,55]. Previous work has also demonstrated that stimulation signals can be created to overwhelm intrinsic interactions between elements and guide the target system toward the desired state [22]. The use of nonlinear stimulation for controlling populations of neurons has been previously demonstrated in numerical simulations [56].
The use of a phase model for estimating neurostimulation parameters is subjected to limitations. As derived, the phase model requires the use of relatively periodic elements. Since neurons under physiological conditions have long quiescent periods, describing their natural behavior by such a model may not be possible. However, neurological events such as seizures have long episodes of roughly periodic neuronal activation which may be described using such models [57].
Additionally, the use of phase models requires that the stimulation signal remains small such that the amplitude of the action potential remains undisturbed. However, weak feedback stimulation is desirable since it minimizes disruption of the natural rhythmic behavior of the neurons. This can be seen in Fig. 2, where upon the removal of the feedback stimulation, the period distributions of the action potentials of the neurons return to their prestimulation baseline distribution. No permanent changes to the neuron were observed.
VI. CONCLUSIONS
A method of constructing a phase model, using time-delayed self-feedback, has been developed; this method requires experimental access to only a single representative rhythmic unit. After construction of the phase model from observations of the action potential of a single neuron, it was used to predict the synchronization states of a two neuron system. Experiments were conducted to observe the phase behavior of the action potentials of two neurons under linear time-delayed feedback. The predictions of the phase model were confirmed by the experimental observations. This method provides an additional approach for the construction of dynamical models of complex rhythmic systems.
ACKNOWLEDGMENTS
This work was supported in part by the National Science Foundation under Grant No. CBET-0730597, the National Institutes of Health under Grant Nos. RO1 NS040337, RO1 NS044370, UO1 NS58204, and T32 GM08715 (Biotechnology Training Program), and the Biomedical Innovation Fund of the University of Virginia.
References
- [1].Schnitzler A and Gross J, Nat. Rev. Neurosci 6, 285 (2005). [DOI] [PubMed] [Google Scholar]
- [2].Uhlhaas PJ and Singer W, Neuron 52, 155 (2006). [DOI] [PubMed] [Google Scholar]
- [3].Artieda J, Alegre M, Valencia M, Urrestarazu E, Perez-Alcazar M, Nicolas MJ, Azcarate JL, and Iriarte J, An. Sist. Sanitario Navarra 32(suppl. 3), 45 (2009). [DOI] [PubMed] [Google Scholar]
- [4].Pogosyan A, Yoshida F, Chen CC, Martinez-Torres I, Foltynie T, Limousin P, Zrinzo L, Hariz MI, and Brown P, Neuroscience 171, 245 (2010). [DOI] [PubMed] [Google Scholar]
- [5].Coffey RJ, Artif. Organs 33, 208 (2009). [DOI] [PubMed] [Google Scholar]
- [6].Fisher R, Salanova V, Witt T, Worth R, Henry T, Gross R, Oommen K, Osorio I, Nazzaro J, Labar D, Kaplitt M, Sperling M, Sandok E, Neal J, Handforth A, Stern J, DeSalles A, Chung S, Shetter A, Bergen D, Bakay R, Henderson J, French J, Baltuch G, Rosenfeld W, Youkilis A, Marks W, Garcia P, Barbaro N, Fountain N, Bazil C, Goodman R, McKhann G, Krishnamurthy KB, Papavassiliou S, Epstein C, Pollard J, Tonder L, Grebin J, Coffey R, and Graves N, Epilepsia 51, 899 (2010).20331461 [Google Scholar]
- [7].Albert GC, Cook CM, Prato FS, and Thomas AW, Neurosci. Biobehav. Rev 33, 1042 (2009). [DOI] [PubMed] [Google Scholar]
- [8].Hodaie M, Wennberg RA, Dostrovsky JO, and Lozano AM, Epilepsia 43, 603 (2002). [DOI] [PubMed] [Google Scholar]
- [9].Lee KH, Blaha CD, Garris PA, Mohseni P, Horne AE, Bennet KE, Agnesi F, Bledsoe JM, Lester DB, Kimble C, Min HK, Kim YB, and Cho ZH, Neuromodulation 12, 85 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Wagenaar DA, Madhavan R, Pine J, and Potter SM, J. Neurosci. 25, 680 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Gluckman BJ, Nguyen H, Weinstein SL, and Schiff SJ, J. Neurosci 21,590 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Hauptmann C, Popovych O, and Tass PA, Biol. Cybern 93, 463 (2005). [DOI] [PubMed] [Google Scholar]
- [13].Franaszczuk PJ, Kudela P, and Bergey GK, Epilepsy Res. 53, 65 (2003). [DOI] [PubMed] [Google Scholar]
- [14].Scholl E, Hiller G, Hovel P, and Dahlem MA, Philos. Trans. R. Soc. London, Ser. A 367, 1079 (2009). [DOI] [PubMed] [Google Scholar]
- [15].Batista CA, Lopes SR, Viana RL, and Batista AM, Neural Netw. 23, 114(2010). [DOI] [PubMed] [Google Scholar]
- [16].Hauptmann C, Popovych O, and Tass PA, Neurocomputing 65–66, 759 (2005). [Google Scholar]
- [17].Popovych OV, Hauptmann C, and Tass PA, Phys. Rev. Lett 94, 164102 (2005). [DOI] [PubMed] [Google Scholar]
- [18].Popovych OV, Hauptmann C, and Tass PA, Biol. Cybern 95, 69 (2006). [DOI] [PubMed] [Google Scholar]
- [19].Santaniello S, Fiengo G, Glielmo L, and Grill WM, IEEE Trans. Neural Syst. Rehabil. Eng 19, 15 (2011). [DOI] [PubMed] [Google Scholar]
- [20].Andrews RJ, Ann. N.Y. Acad. Sci 1199, 204 (2010). [DOI] [PubMed] [Google Scholar]
- [21].Netoff TI, Banks MI, Dorval AD, Acker CD, Haas JS, Kopell N, and White JA, J. Neurophysiol 93, 1197 (2005). [DOI] [PubMed] [Google Scholar]
- [22].Kiss IZ, Rusin CG, Kori H, and Hudson JL, Science 316, 1886 (2007). [DOI] [PubMed] [Google Scholar]
- [23].Rusin CG, Kiss IZ, Kori H, and Hudson JL, Ind. Eng. Chem. Res 48, 9416 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Galan RF, Ermentrout GB, and Urban NN, Phys. Rev. Lett 94, 158101 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Goldberg JA, Deister CA, and Wilson CJ, J. Neurophysiol 97, 208 (2007). [DOI] [PubMed] [Google Scholar]
- [26].Sieling FH, Canavier CC, and Prinz AA, J. Neurophysiol 102, 69 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Tateno I and Robinson HPC, Biosystems 89, 110 (2007). [DOI] [PubMed] [Google Scholar]
- [28].Pikovsky AS, Rosenblum MG, and Kurths J, Synchronization: A Universal Concept in Nonlinear Science (Cambridge University Press, Cambridge, 2001). [Google Scholar]
- [29].Manirubia SC, Mikhailov AS, and Zanette DH, Emergence of Dynamical Order: Synchronization Phenomena in Complex Systems, World Scientific Lecture Notes in Complex Systems, Vol. 2 (World Scientific, River Edge, NJ, 2004). [Google Scholar]
- [30].Acker CD, Kopell N, and White JA, J. Comput. Neurosci 15, 71 (2003). [DOI] [PubMed] [Google Scholar]
- [31].Gutkin BS, Ermentrout GB, and Reyes AD, J. Neurophysiol 94, 1623 (2005). [DOI] [PubMed] [Google Scholar]
- [32].Netoff TI, Acker CD, Bettencourt JC, and White JA, J. Comput. Neurosci 18, 287 (2005). [DOI] [PubMed] [Google Scholar]
- [33].Preyer AJ and Butera RJ, Phys. Rev. Lett 95, 138103 (2005). [DOI] [PubMed] [Google Scholar]
- [34].Tateno T and Robinson HPC, Biophys. J 92, 683 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Tsubo Y, Takada M, Reyes AD, and Fukai T, Eur. J. Neurosci 25, 3429 (2007). [DOI] [PubMed] [Google Scholar]
- [36].Winfree AT, The Geometry of Biological Time (Springer, New York, 1980). [Google Scholar]
- [37].Kuramoto Y, Chemical Oscillations, Waves and Turbulence (Springer, New York, 1984). [Google Scholar]
- [38].Kiss IZ, Zhai Y, and Hudson JL, Phys. Rev. Lett 94, 248301 (2005). [DOI] [PubMed] [Google Scholar]
- [39].Miyazaki J and Kinoshita S, Phys. Rev. Lett 96,194101 (2006). [DOI] [PubMed] [Google Scholar]
- [40].Rusin CG, Tokuda I, Kiss IZ, and Hudson JL, Angew. Chem 50, 10212(2011). [DOI] [PubMed] [Google Scholar]
- [41].Miyazaki J and Kinoshita S, Phys. Rev. E 74, 5 (2006). [DOI] [PubMed] [Google Scholar]
- [42].Cui JX, Canavier CC, and Butera RJ, J. Neurophysiol 102, 387 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Culturing Nerve Cells, edited by Banker G and Goslin K, 2nd ed. (MIT Press, Cambridge, MA, 1998). [Google Scholar]
- [44].Nunez J, J. Vis. Exp 19, e895 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Dorval AD, Christini DJ, and White JA, Ann. Biomed. Eng 29, 897 (2001). [DOI] [PubMed] [Google Scholar]
- [46].Nowotny T, Szucs A, Pinto RD, and Selverston AI, J. Neurosci. Methods 158, 287 (2006). [DOI] [PubMed] [Google Scholar]
- [47].Nowotny T, Zhigulin VP, Selverston AI, Abarbanel HDI, and Rabinovich MI, J. Neurosci 23, 9776 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Kopell N and Ermentrout B, Proc. Natl. Acad. Sci. USA 101, 15482 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Mancilla JG, Lewis TJ, Pinto DJ, Rinzel J, and Connors BW, J. Neurosci 27, 2058 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Galan RF, Ermentrout GB, and Urban NN, Neurocomputing 69, 1112 (2006). [Google Scholar]
- [51].Izhikevich EM, Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (MIT Press, Cambridge, MA, 2007). [Google Scholar]
- [52].Okuda K, Physica D 63, 424 (1993). [Google Scholar]
- [53].Manrubia SC, Mikhailov AS, and Zanette DH, Emergence of Dynamical Order: Synchronization Phenomena in Complex Systems (World Scientific, Singapore, 2004). [Google Scholar]
- [54].Suzurikawa J, Nakao M, Jimbo Y, Kanzaki R, and Takahashi H, IEEE Trans. Biomed. Eng 56, 2660 (2009). [DOI] [PubMed] [Google Scholar]
- [55].Hansel D, Mato G, and Meunier C, Europhys. Lett 23, 367 (1993). [Google Scholar]
- [56].Wang J, Deng B, and Fei XY, Chaos Solitons Fractals 27, 1272 (2006). [Google Scholar]
- [57].Velazquez JLP, Galan RF, Dominguez LG, Leshchenko Y, Lo S, Belkas J, and Erra RG, Phys. Rev. E 76, 6 (2007). [DOI] [PubMed] [Google Scholar]