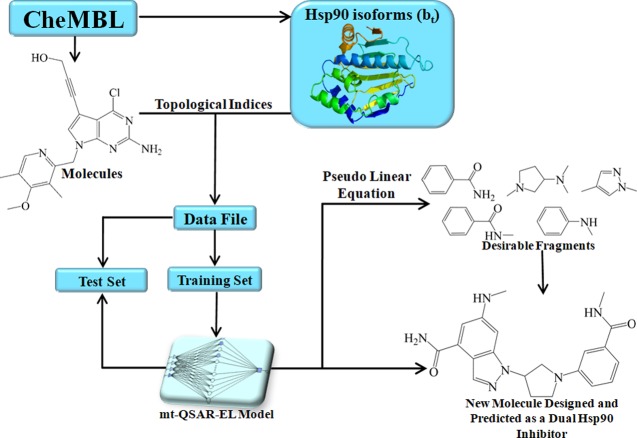
Abstract
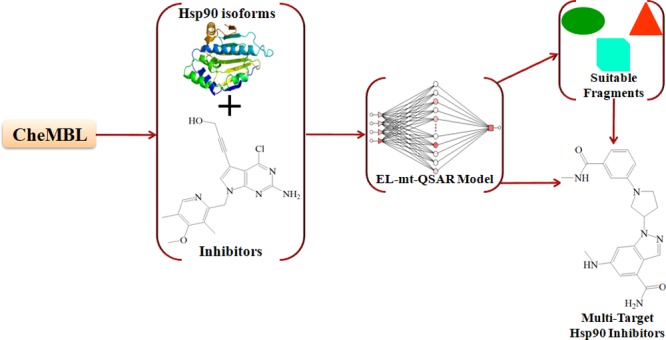
Machine learning methods have revolutionized modern science, providing fast and accurate solutions to multiple problems. However, they are commonly treated as “black boxes”. Therefore, in important scientific fields such as medicinal chemistry and drug discovery, machine learning methods are restricted almost exclusively to the task of performing predictions of large and heterogeneous data sets of chemicals. The lack of interpretability prevents the full exploitation of the machine learning models as generators of new chemical knowledge. This work focuses on the development of an ensemble learning model for the prediction and design of potent dual heat shock protein 90 (Hsp90) inhibitors. The model displays accuracy higher than 80% in both training and test sets. To use the ensemble model as a generator of new chemical knowledge, three steps were followed. First, a physicochemical and/or structural interpretation was provided for each molecular descriptor present in the ensemble learning model. Second, the term “pseudolinear equation” was introduced within the context of machine learning to calculate the relative quantitative contributions of different molecular fragments to the inhibitory activity against the two Hsp90 isoforms studied here. Finally, by assembling the fragments with positive contributions, new molecules were designed, being predicted as potent Hsp90 inhibitors. According to Lipinski’s rule of five, the designed molecules were found to exhibit potentially good oral bioavailability, a primordial property that chemicals must have to pass early stages in drug discovery. The present approach based on the combination of ensemble learning and fragment-based topological design holds great promise in drug discovery, and it can be adapted and applied to many different scientific disciplines.
1. Introduction
Machine learning (ML) methods have revolutionized modern science, providing deeper insights into the understanding of multiple phenomena and generating plausible solutions to different problems. In medicinal chemistry and drug discovery, ML methods have played an essential role in areas such as data mining and virtual screening.1−3 However, with the use of ML methods, several issues emerge. From one side, there is a tendency of the ML models to overfitting the data, a detrimental property where the ML models unknowingly extract certain residual information (i.e., the noise), assuming that such information represents the underlying model structure. An accepted solution to this situation (among some potential options that exist) is to use ensemble learning, a process focused on generating multiple ML models that are strategically combined to solve a particular problem by providing a consensus response. It is also known that the models based on ensemble learning can provide better prediction results than single ML models.4−10
On the other hand, the greatest concern is that, to date, the ML models are frequently treated as black boxes regardless of the ML method employed, the purpose for their creation, and the approaches used to assess the reliability of the predictions. Consequently, this prevents the use of the ML models as generators of new chemical knowledge in medicinal chemistry and drug discovery. Some successful attempts have been made in the sense of applying programming/codification approaches and rules within the ML models, which allow the generation of new chemical structures that are accurately predicted to exhibit desired properties.11−14 However, it can take too much time to master the necessary programming skills, and in the end, the lack of a phenomenological interpretation in the ML models remains; most of the ML models are not capable of providing an interpretation of the physicochemical and/or structural features of the chemicals in the databases, which they intend to analyze and predict.
In an attempt to solve all of the aforementioned restrictions, this work reports a multitarget ensemble learning model for quantitative structure–activity relationships (mt-QSAR-EL), which is applied in combination with a fragment-based topological approach for the de novo design and prediction of inhibitors of the α and β isoforms of the heat shock protein 90, namely, Hsp90α and Hsp90β, respectively. These biomolecular targets have been used as cases of study due to their direct implication in genetic and epigenetic variations,15 which are associated with high mortality causing diseases such as cancers.16 Here, plausible physicochemical/structural interpretations of the variables (molecular descriptors) of the mt-QSAR-EL model are given. In addition, the term “pseudolinear equation” is introduced within the context of ML methods. By using this pseudolinear equation derived from the mt-QSAR-EL model, the relative quantitative contributions of different molecular fragments to the inhibitory activity against the Hsp90 isoforms are calculated. It is shown that from the joint use of the fragments with positive contributions and the physicochemical/structural interpretation of the mt-QSAR-EL model, completely new molecules can be designed as potentially dual Hsp90 inhibitors.
2. Results and Discussion
2.1. Mt-QSAR-EL Model
The mt-QSAR-EL model was built by considering both sets of molecular descriptors. The notation of the best mt-QSAR-EL model found is Output 5:[5]:1, meaning that the ensemble model is composed of five molecular descriptors used as inputs, five artificial neural networks (ANNs) based on the radial basis function (RBF) architecture, and one output that is the predicted value of the categorical variable of inhibitory activity [Pred_APi(bt)]. All of the chemical and assay data used in this study are reported in the Supporting Information 1. The molecular descriptors used to develop the mt-QSAR-EL model are reported in Table 1, including their corresponding definitions.
Table 1. Molecular Descriptors Present in the mt-QSAR-EL Model and Their Corresponding Definitions.
| molecular descriptor | concept |
|---|---|
| D[TnsAq3(E)_MX]bt | deviation of the total nonstochastic atom-based quadratic index of order 3 weighted by the electronegativity, modified by the maximum value as mathematical operator, depending on the chemical structure and the target |
| D[TmpAq7(E)_MN]bt | deviation of the total mutual probability atom-based quadratic index of order 7 weighted by the electronegativity, modified by the minimum value as mathematical operator, depending on the chemical structure and the target |
| D[TmpAq0(PSA)_AM]bt | deviation of the total mutual probability atom-based quadratic index of order 0 weighted by the polar surface area, modified by the arithmetic mean as mathematical operator, depending on the chemical structure and the target |
| D[TmpAq3(PSA)_MX]bt | deviation of the total mutual probability atom-based quadratic index of order 3 weighted by the polar surface area, modified by the maximum value as mathematical operator, depending on the chemical structure and the target |
| D[Xv(C)5]bt | deviation of the atom-based valence connectivity index of type cluster and order 5, depending on the chemical structure and the target |
In terms of the internal quality and predictive power, the mt-QSAR-EL model exhibited accuracy [Ac(%)] values of 83.07 and 83.2% for the training and test sets, respectively. In Table 2, the statistics sensitivity [Sn(%)] and specificity [Sp(%)] define the percentages of correct classification for active and inactive compounds, respectively. In this sense, both Sn(%) and Sp(%) surpass the value of 80%, and therefore, the mt-QSAR-EL model has a very good performance in classifying/predicting active and inactive molecules. Also, the local counterparts of Sn(%) and Sp(%) were calculated. Such statistics are [Sn(%)]bt and [Sp(%)]bt, and they depend only on those compounds assayed against a specific Hsp90 isoform. According to the Supporting Information 2, these percentage-based statistics display values in the interval 75–93% in the training set, while in the test set, the range 76–90% is reported.
Table 2. Performance of the mt-QSAR-EL Model.
| symbolsa | training set | test set |
|---|---|---|
| Nactive | 373 | 121 |
| CCactive | 312 | 104 |
| Sn(%) | 83.65 | 85.95 |
| Ninactive | 401 | 134 |
| CCinactive | 331 | 109 |
| Sp(%) | 82.54 | 81.34 |
| MCC | 0.662 | 0.672 |
Nactive: total number of active molecules; Ninactive: total number of inactive molecules; CCactive: molecules correctly classified as active; CCinactive: molecules correctly classified as inactive; Sn(%): sensitivity expressed as the percentage of molecules correctly classified as active; Sp(%): specificity expressed as the percentage of molecules correctly classified as inactive; MCC: Matthews correlation coefficient.
Finally, in Table 2, the Matthews correlation coefficient (MCC) is higher than 0.66. This statistical index can have values from −1 (total divergence between prediction and observation) to 1 (perfect prediction/classification), while 0 indicates the performance of a random predictor. As the MCC values are closer to 1 than to 0, then it is fair to say that the MCC values reported for the mt-QSAR-EL model reflect a strong correlation between the observed and predicted values of the categorical variable of activity APi(bt).
In any computational model exhibiting potential predictive capabilities, it is very important to assess the reliability of the predictions. In this sense, the applicability domain is a well-known concept, which defines an interpolation region where a model is thought to perform the most reliable predictions. Thus, many applicability domain approaches have been reported in the scientific literature.17 In the present study, a consensus approach is used to exploit the potentialities of the mt-QSAR-EL model in predicting chemicals. Consensus approaches have also been studied, and in contrast to the applicability domain concept, they can be used for both interpolation and extrapolation.17 Here, a consensus approach has been applied. The mt-QSAR-EL model is based on an ensemble of ANNs, and when classifying/predicting chemicals, each ANN in the ensemble gives a classification response, and then, the different responses of the ANNs are combined to yield the final output classification. At its essence, an ensemble of ANNs works very similarly to the ML method known as random forests.17 In addition, the applicability domain based on the descriptor space was assessed; all of the chemicals whose values of their molecular descriptors fell beyond the maximum and minimum values in the training set composed of the compounds correctly classified by the mt-QSAR-EL model were considered to be outside the applicability domain (Supporting Information 3). We note that the maximum and minimum values of each molecular descriptor define the upper and lower boundaries in the descriptor space. To provide a better explanation of the applicability domain employed here, the information of the maximum and minimum values of each molecular descriptor was used to calculate local scores. If a defined descriptor value of a new molecule was between the aforementioned boundaries, the local score took the value of 1; otherwise, the local score took the value of 0. Consequently, for the mt-QSAR-EL model, as it was constructed from five variables, the total score (sum of the local scores) must have a value of 5 to ensure the complete agreement with the applicability domain.
2.2. Physicochemical Interpretation of the Molecular Descriptors in the mt-QSAR-EL Model
Currently, most of the chemoinformatic models (including those based on mt-QSAR approaches) are focused on predicting large and heterogeneous databases of drugs/chemicals. Consequently, the phenomenological information that the predictive models may provide is often neglected and underestimated.18 Here, the different molecular descriptors present in the mt-QSAR-EL model will be interpreted from a physicochemical and/or structural point of view. Such interpretations will provide deeper insights into the features that a molecule should have to inhibit the two Hsp90 isoforms. While analyzing the different molecular descriptors in a physicochemical/structural context, the interpretations will be elucidated on the basis of their importance values SV (also known as sensitivity values), which are depicted in Figure 1. The higher the SV of a molecular descriptor, the greater will be its significance in the mt-QSAR-EL model.
Figure 1.

Relative importance of each molecular descriptor in the mt-QSAR-EL model.
To give a reasonable physicochemical/structural interpretation of the molecular descriptors, it is important to know how their values should vary to increase the inhibitory activity against the Hsp90 isoforms. However, ML models are very difficult to interpret due to their nonlinear nature. For this reason, Speck-Planche and co-workers proposed an approach to interpret the molecular descriptors of an ML model.19 This approach will be used here to explain the information content of the molecular descriptors present in the mt-QSAR-EL model. The approach focuses on the calculation of the class-based mean values (Table 3), and it is applied only to those molecules in the training set that were correctly predicted/classified. This indicates that for each molecular descriptor, two mean values will be calculated, one for the class of molecules annotated and correctly predicted as active and the other for those molecules assigned and correctly predicted as inactive.
Table 3. Relative Tendency of the Molecular Descriptors in the mt-QSAR-EL Model Expressed through to the Class-Based Means.
| means |
|||
|---|---|---|---|
| descriptors | active | inactive | relative tendencya |
| D[TnsAq3(E)_MX]bt | –8.133 × 10–3 | 0.022 | decrease |
| D[TmpAq7(E)_MN]bt | –7.866 × 10–3 | 0.102 | decrease |
| D[TmpAq0(PSA)_AM]bt | –1.14 × 10–3 | 0.044 | decrease |
| D[TmpAq3(PSA)_MX]bt | –4.502 × 10–3 | 0.023 | decrease |
| D[Xv(C)5]bt | 2.388 × 10–3 | –0.057 | increase |
Relative tendency indicates the type of variation (increase or diminution) that a descriptor should undergo.
As separated classes, active and inactive molecules correctly predicted by the mt-QSAR-EL model display different physicochemical properties and structural characteristics, which will be reflected in some way in the mean values of each molecular descriptor for each category/class. The comparison between the mean values of the two classes for a defined molecular descriptor permits to establish a tendency, indicating how the physicochemical properties and the structural features should be modified to improve the inhibitory potency against the Hsp90 isoforms. Of course, such a tendency is relative due to the nonlinearity of the mt-QSAR-EL model, but it is rigorous enough to ensure a correct interpretation of the molecular descriptors.19
It should be noted that all of the molecular descriptors used in this work consider the bond order; the higher the value of this bond property, the higher will be the values of these molecular descriptors. There are two molecular descriptors with electronic information in the mt-QSAR-EL model. One of them is D[TnsAq3(E)_MX]bt. Being the most significant descriptor in the model, D[TnsAq3(E)_MX]bt characterizes the diminution of the electronegativity of the atoms that are separated at a topological distance equal to 3. This means that the electronegative atoms should be dispersed throughout the entire molecule, preferably at topological distances larger than 3. Substituted aromatic and aliphatic rings and their corresponding heteroatom-based counterparts, as well as linear and ramified aliphatic portions, can contribute to the diminution of the aforementioned molecular descriptor. The other molecular descriptor embodying electronic information is D[TmpAq7(E)_MN]bt, which indicates the decrease of the electronegativity of the atoms that are separated at a topological distance equal to 7. This descriptor has the second highest importance in the mt-QSAR-EL, and its value can be diminished by placing polysubstituted aromatic and heteroaromatic rings in the periphery of the molecules, while aliphatic and heteroaliphatic portions (rings included) should be placed between any two rings (if possible) regardless of whether the rings are aromatic or aliphatic. In addition, D[TmpAq7(E)_MN]bt also considers the frequency with which the electronegative atoms appear in the molecules at the topological distance equal to 7; the lower the frequency of appearance of a defined electronegative atom, the lower the value of D[TmpAq7(E)_MN]bt. It should be emphasized that fused rings can contribute to the diminution of both D[TnsAq3(E)_MX]bt and D[TmpAq7(E)_MN]bt.
There are two other molecular descriptors, which account for the hydrophilic aspects of the molecules. In this sense, D[TmpAq0(PSA)_AM]bt describes the decrease of the total polar surface area. Therefore, the number of atoms able to form hydrogen bonds should be diminished. In convergence with D[TmpAq0(PSA)_AM]bt, the descriptor D[TmpAq3(PSA)_MX]bt also characterizes the decrease of the polar surface area, but only in regions where any two atoms are placed at a topological distance equal to 3. Consequently, atoms able to form hydrogen bonds should be placed at a topological distance different from 3. One should note that D[TmpAq0(PSA)_AM]bt and D[TmpAq3(PSA)_MX]bt contain information regarding the frequency of appearance of specific types of atoms able to form hydrogen bonds; the lower the frequency, the lower the values of both molecular descriptors. It should be pointed out that D[TmpAq0(PSA)_AM]bt is the fourth most influent descriptor in the mt-QSAR-EL model, while D[TmpAq3(PSA)_MX]bt has the lowest significance.
Finally, D[Xv(C)5]bt is the third most influent descriptor in the mt-QSAR-EL model. This descriptor accounts for the steric factor known as molecular accessibility, which defines the regions in a molecule that are available to interact with the surrounding medium (in this case, the protein). More specifically, D[Xv(C)5]bt contains information regarding the increment of the number of fragments composed of five bonds, where each bond of the fragment act as a ramification. Consequently, in all of the molecules containing regions that topologically resemble 2,3-dimethylbutane, the value of D[Xv(C)5]bt will increase.
2.3. Relative Quantitative Contributions of the Fragments to the Inhibitory Activity
When inhibiting a target, a molecule acts as a whole. Nevertheless, due to their structural characteristics and physicochemical properties, certain regions of a molecule will be more suited than others to interact with the target in an effective manner. Such regions or fragments will have a higher influence in the interaction and consequently a higher contribution to the inhibition against a target. Therefore, it is very important to quantify how much a fragment can contribute to the inhibitory activity.
It has been established that any topological (graph-based) index of a molecule can be represented as a linear combination of the frequency with which diverse fragments (connected and disconnected) appear in the molecule.20 Therefore, if we have a linear QSAR equation (e.g., as those obtained from multiple linear regression or linear discriminant analysis) involving several topological indices, it is possible to calculate these indices for a fragment of interest and substitute them in the linear equation, yielding an activity score for the fragment. There are many examples in the scientific literature that have employed this idea to calculate the quantitative contributions of the molecular fragments to multiple biological effects, such as activity, toxicity, and ADME properties.18,21−25 In this study, to calculate the quantitative contributions of the different fragments to the inhibitory activity against the Hsp90 isoforms, the data set used to generate the mt-QSAR-EL model was manually inspected, and 35 molecular fragments were selected by considering the activity values of the molecules to which they belong, as well as their frequency in the data set (Figure 2). Then, the molecular descriptors present in the mt-QSAR-EL model were calculated for these fragments.
Figure 2.
Molecular fragments extracted from the data set.
In this work, however, an ML-based model has been developed instead of one focused on linear regression methods. Consequently, a “pure linear equation” cannot be generated. In ideal conditions, an equation derived from linear regression methods will have standardized independent variables (molecular descriptors), so the coefficients accompanying these independent variables will express in some degree the relative importance of each variable. In addition, it is always possible to know the sign of the coefficients, and therefore, how the value of a defined independent variable should change to increase the value of the response variable. In the case of the mt-QSAR-EL model, we have the importance/sensitivity values (Figure 1), which express the significance of the molecular descriptors, and therefore, they can serve as coefficients. At the same time, in Table 3, the relative tendency gives us information regarding the direction (positive or negative) with which each molecular descriptor should vary to increase the biological activity. Thus, a pseudolinear equation can be written in the following form:
| 1 |
In eq 1, SAPi(bt) defines the activity score of a fragment depending on the Hsp90 isoform against which the analysis is realized. Now, the molecular descriptors calculated for the different fragments can be substituted in eq 1, yielding the corresponding activity scores as reported by the previous works.18,21−25 We note that now, one can in principle compare the molecular fragments according to their quantitative contributions estimated by using eq 1, or any other linear equation. However, the local physicochemical and structural information will be diluted within the global activity scores. So, it becomes more difficult to know the position in which a fragment should be placed in a molecule to effectively contribute to the increase of the biological activity. Here, local activity scores have been calculated according to the following procedure.
First, a defined descriptor (e.g., D[TnsAq3(E)_MX]bt) and its coefficient and the corresponding sign in eq 1 were considered as a local physicochemical/structural component. The substitution of the values of D[TnsAq3(E)_MX]bt for the 35 fragments depicted in Figure 2 in this component yielded 35 local activity scores for each of the two Hsp90 isoforms. Therefore, in total, 70 local activity scores were calculated. Second, each local activity score was divided by the total number of atoms that constituted each fragment, and as a result, 70 normalized local activity scores were generated. The purpose here was to eliminate the effect of the size of the fragments. Third, the mean and the standard deviation of the 70 normalized local activity scores were calculated. Finally, the normalized local activity scores were standardized; from each normalized local activity score, the mean was subtracted, and the result was divided by the standard deviation. The standardized local activity scores represent the relative quantitative contributions of the molecular fragments to the inhibitory activity against the two Hsp90 isoforms (Table 4). All of these steps were applied to the other molecular descriptors in eq 1.
Table 4. Local Quantitative Contributions (LQCs) of the Molecular Fragments Depending on Each Molecular Descriptor and the Hsp90 Isoforms.
| LQC_C1 |
LQC_C2 |
LQC_C3 |
LQC_C4 |
LQC_C5 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDa,b | Hsp90α | Hsp90β | Hsp90α | Hsp90β | Hsp90α | Hsp90β | Hsp90α | Hsp90β | Hsp90α | Hsp90β |
| F1 | 0.378 | 0.938 | –1.868 | –2.771 | 0.988 | 0.969 | 0.318 | 1.007 | –0.73 | –0.612 |
| F2 | –0.515 | –0.145 | 0.439 | 0.183 | 0.926 | 0.911 | 0.275 | 0.827 | –0.73 | –0.612 |
| F3 | –1.183 | –1.021 | 1.177 | 1.135 | 0.644 | 0.680 | –0.143 | –0.197 | 1.552 | 1.551 |
| F4 | –0.689 | –0.255 | –0.508 | –1.033 | 0.988 | 0.969 | 0.318 | 1.007 | –0.73 | –0.612 |
| F5 | –0.822 | –0.403 | –0.110 | –0.524 | –2.752 | –1.872 | –1.852 | –3.601 | –0.73 | –0.612 |
| F6 | –0.383 | –0.055 | 0.494 | 0.258 | –0.193 | 0.053 | 0.247 | 0.707 | 1.492 | 1.495 |
| F7 | –1.224 | –0.960 | 0.738 | 0.567 | –0.718 | –0.341 | 0.265 | 0.782 | 1.411 | 1.42 |
| F8 | –0.890 | –0.540 | 0.368 | 0.091 | –0.132 | 0.110 | –0.647 | –1.105 | –0.73 | –0.612 |
| F9 | –0.566 | –0.179 | 0.166 | –0.167 | –1.207 | –0.706 | –0.252 | –0.268 | –0.73 | –0.612 |
| F10 | 0.586 | 0.977 | 0.456 | 0.212 | 0.825 | 0.820 | 0.222 | 0.597 | –0.73 | –0.612 |
| F11 | –0.211 | 0.280 | 0.292 | –0.010 | 0.028 | 0.240 | 0.148 | 0.647 | –0.73 | –0.612 |
| F12 | 0.283 | 0.611 | 0.782 | 0.631 | 0.804 | 0.800 | 0.198 | 0.518 | 1.555 | 1.552 |
| F13 | 0.742 | 1.204 | 0.156 | –0.175 | 0.648 | 0.692 | 0.134 | 0.466 | –0.73 | –0.612 |
| F14 | 0.814 | 1.269 | –0.066 | –0.457 | –0.084 | 0.134 | 0.240 | 0.675 | –0.73 | –0.612 |
| F15 | –0.760 | –0.460 | 1.060 | 0.980 | 0.607 | 0.663 | 0.166 | 0.552 | –0.73 | –0.612 |
| F16 | –0.292 | 0.229 | –2.253 | –3.265 | 0.102 | 0.301 | –1.040 | –1.836 | –0.73 | –0.612 |
| F17 | –1.018 | –0.827 | 1.144 | 1.092 | 0.198 | 0.342 | 0.079 | 0.284 | 1.54 | 1.539 |
| F18 | –0.662 | –0.310 | 0.647 | 0.449 | 0.361 | 0.482 | –0.121 | –0.014 | –0.73 | –0.612 |
| F19 | –0.553 | –0.307 | 0.936 | 0.826 | 0.498 | 0.570 | 0.217 | 0.576 | –0.73 | –0.612 |
| F20 | –1.215 | –1.001 | 1.163 | 1.114 | 0.373 | 0.481 | 0.240 | 0.675 | 1.389 | 1.399 |
| F21 | 1.119 | 1.682 | –0.688 | –1.257 | –1.753 | –1.124 | –0.922 | –1.717 | 1.472 | 1.477 |
| F22 | 0.254 | 0.767 | 0.416 | 0.150 | 0.851 | 0.861 | 0.301 | 0.938 | –0.73 | –0.612 |
| F23 | 1.844 | 2.493 | –0.584 | –1.124 | –1.452 | –0.896 | 0.275 | 0.827 | –0.73 | –0.612 |
| F24 | –0.513 | –0.164 | 0.865 | 0.729 | –2.018 | –1.328 | 0.265 | 0.782 | –0.73 | –0.612 |
| F25 | –1.269 | –0.989 | 0.610 | 0.402 | –0.331 | –0.044 | 0.275 | 0.827 | 1.387 | 1.387 |
| F26 | 1.609 | 2.530 | –2.214 | –3.226 | 1.144 | 1.115 | 0.423 | 1.457 | –0.73 | –0.612 |
| F27 | –0.416 | –0.075 | 0.467 | 0.222 | –2.816 | –1.937 | –1.017 | –1.960 | 1.443 | 1.45 |
| F28 | –0.555 | –0.105 | –0.079 | –0.485 | 0.988 | 0.969 | 0.318 | 1.007 | –0.73 | –0.612 |
| F29 | 1.314 | 1.844 | 0.085 | –0.265 | 0.598 | 0.654 | 0.247 | 0.707 | –0.73 | –0.612 |
| F30 | –1.182 | –0.932 | 0.868 | 0.734 | 0.436 | 0.533 | 0.255 | 0.742 | 1.441 | 1.447 |
| F31 | –1.597 | –1.396 | 0.295 | 0.001 | 0.684 | 0.721 | –0.169 | –0.160 | 1.395 | 1.404 |
| F32 | –0.761 | –0.396 | 0.407 | 0.141 | –2.117 | –1.398 | –0.382 | –0.543 | –0.73 | –0.612 |
| F33 | 0.952 | 1.496 | –0.584 | –1.124 | –1.452 | –0.896 | 0.275 | 0.827 | –0.73 | –0.612 |
| F34 | 1.189 | 1.689 | 0.148 | –0.184 | 0.412 | 0.511 | 0.240 | 0.675 | –0.73 | –0.612 |
| F35 | –0.827 | –0.471 | 0.570 | 0.350 | –0.189 | 0.067 | –2.039 | –4.062 | –0.73 | –0.612 |
The terminology “LQC_” stands for the “local quantitative contribution”.
C1: descriptor D[TnsAq3(E)_MX]bt; C2: descriptor D[TmpAq7(E)_MN]bt; C3: descriptor D[TmpAq0(PSA)_AM]bt; C4: descriptor D[TmpAq3(PSA)_MX]bt; C5: descriptor D[Xv(C)5]bt.
One should note that in the specific case of the descriptor D[Xv(C)5]bt, instead of dividing the local activity scores by the total number of atoms in a fragment, they were divided by the denominator (nC + 1), nC being the total number of those atoms (including the hydrogen atoms attached to them) involved in the formation of clusters of order 5. That is because while the other molecular descriptors account for the distribution of physicochemical properties, D[Xv(C)5]bt is more focused on indicating the presence or absence of a very specific kind of fragment. Consequently, if the clusters of order 5 are absent in a fragment, then the local activity score of the fragment will have the same constant negative value; otherwise, the local activity score will have a positive value, being this proportional to the number of cluster of order 5 and the chemical environment of each atom in the aforementioned clusters.
It is very important to point out that the fragments with positive contributions can be present in molecules annotated and correctly classified as inactive, while the fragments with negative contributions can be present in molecules assigned and correctly predicted as active. The presence of a given fragment is not a sufficient condition for the enhancement of the biological activity. Therefore, the local quantitative contributions depicted in Table 4 reflect the relative tendency of the fragments to influence the activity of the fragments to influence the activity of a molecule according to its intrinsic physicochemical properties when properly connected to other fragments; the suitability with which a fragment should be connected strongly depends on the physicochemical/structural interpretations of the molecular descriptors in the mt-QSAR-EL model, which have been explained in the previous section.
In addition, even though these local contributions will be restricted to the chemico-biological space defined by the molecules in the data set, they can guide medicinal chemists toward the detection of two-dimensional (2D) pharmacophores.21,23
A careful inspection of Table 4 suggests that the molecular fragments with positive local quantitative contributions with respect to three or more physicochemical/structural components (or with six or more positive values) are desirable for the future design of highly active molecules against both Hsp90 isoforms. Such contributions are represented with bold values. Therefore, they may appear in different positions in the molecules, favorably contributing to enhancing the inhibitory activity. This desirability of some of these fragments is reflected in the molecules depicted in Figure 3, which are among the most active in the database used in this study, and they contain more than one of these positive fragments. For instance, fragments F3 and F22 appear in the first three molecules, which are structurally related. Regardless of the other fragments present in these molecules, it is clear that F3 and F22 play an important role in the inhibitory potency of the molecules to which they belong. Other important fragments present in the molecules illustrated in Figure 3 are F1, F2, F7, F12, F17, and F19. Special attention must be paid to the fragment F12, which is present in the molecule CHEMBL3234777. This is the only molecular fragment with positive local contributions against all of the physicochemical/structural components. Because of that, when properly connected, F12 can be used in any region of a molecule because it will always contribute positively to the increment of the inhibitory activity. Of course, all of the ideas explained here converge with the interpretations of the molecular descriptors present in the mt-QSAR-EL model, which allow the aforementioned fragments to be properly connected to the others. We note that if one considers only the intrinsic physicochemical properties of the different fragments while neglecting how properly they should be connected, a huge amount of random molecules can be generated, and they may not be active.
Figure 3.
Molecules containing some of the most desirable fragments associated with the increment of the inhibitory activity against the Hps90 isoforms.
On the other hand, fragments with negative local quantitative contributions with respect to three or more physicochemical/structural components can be detrimental to the inhibitory activity. Some of these fragments are F5, F8, F9, F16, F32, and F35, and a similar analysis to that performed for the positive fragments can be made. For example, it can be deduced that if these fragments have negative local contributions with respect to the physicochemical components C1 and C2 depicted in Table 4, then, if present in a molecule, they should be kept isolated (preferably in the central region of the molecule) from other fragments with electronegative atoms in such a way that the topological distance between electronegative atoms is different from 3 and 7. In any case, the most interesting aspect is that according to Table 4, the molecular fragment F5 is the most undesirable of all due to its negative contribution against all of the physicochemical/structural components regardless of the Hsp90 isoform. And yet, F5 appears in the most active molecules of the data set (Figure 3). This has an explanation, and once again, everything obeys the physicochemical/structural interpretations of the molecular descriptors in the mt-QSAR-EL model. We note that despite having negative contributions against all of the components, F5 is placed in the periphery of the first three molecules represented in Figure 3, and according to the physicochemical interpretation of the molecular descriptor D[TmpAq7(E)_MN]bt, that is a desirable aspect. At the same time, in most of the cases, the electronegative atoms of F5 are placed at topological distances different from 3 with respect to atoms belonging to other fragments. This favors the diminution of the descriptor D[TnsAq3(E)_MX]bt, contributing to increasing the activity. Finally, F5 has an atom (specifically a halogen) attached to an aromatic carbon adjacent to one of the pyridinic nitrogens. In addition, F5 is fused with another ring. These two aspects generate two clusters of order 5 increasing the value of D[Xv(C)5]bt, which is also required for the enhancement of the inhibitory activity against the Hsp90 isoforms. With F5, a similar situation happens in the case of the compounds CHEMBL3675258, CHEMBL3675272, and CHEMBL3360305, which are not shown in Figure 3 but are present in the Supporting Information 1, having been correctly classified by the mt-QSAR-EL model.
Another example is the molecular fragment F18, which, being seemingly negative, appears in the molecule CHEMBL560895 (Figure 3). In F18, its pyridinic nitrogen is placed at a topological distance equal to 3 with respect to the fluorine atoms (increasing D[TnsAq3(E)_MX]bt), which is detrimental to the inhibitory activity. Nevertheless, by being connected to F7 while fused with F19 (both of them predominantly positive fragments), F18 is involved in the formation of four clusters of order 5, which are very favorable for the enhancement of the inhibitory activity against the Hsp90 isoforms.
In the end, it can be seen that the application of the approach involving the calculation of class-based mean values for each molecular descriptor and the subsequent generation of a pseudolinear equation for the calculation of fragment contributions have pros and cons. From one side, a clear advantage of using this approach is that the pseudolinear equation allows the rapid calculation of quantitative contributions, enabling the comparison between fragments to select those that are more suitable for the design of virtually potent dual Hsp90 inhibitors. Thus, by combining the analysis of the different quantitative contributions of the fragments and the physicochemical interpretations of the molecular descriptors in the mt-QSR-EL model, it is possible to establish a set of rules to define steric and electronic features responsible for the enhancement of the inhibitory activity. A second advantage is that a pseudolinear equation can in principle be generated from any ML model as long as the molecular descriptors will be somehow normalized and the software used to develop the ML model will yield the values indicating the significance of the different descriptors. For instance, as shown in the present study, the program STATISTICA v6.0 calculates sensitivity values, which serve as weights of the pseudolinear equation, indicating the influence of the molecular descriptors in the mt-QSAR-EL model. If other techniques such as random forest or support vector machine were used by the same program, then, the so-called “importance values” would be calculated, also serving as weights for the pseudolinear equation; as in the present study, the means of the different classes/categories for each molecular descriptor would also be compared to determine its tendency (increment of diminution) in the model.
On the other hand, an important limitation in the use of the pseudolinear equation is that this will strongly depend on the performance of the mt-QSAR model-EL. The approach based on the generation of a pseudolinear equation is only valid because the model developed in this work shows a very good performance; the percentages of correct classification for active and inactive molecules are higher than 70%. With a poorer performance, it would not make any sense at all to generate an equation based on the tendencies of variation in the means of the molecular descriptors in the mt-QSAR-EL model. A second disadvantage is that because of the nonlinear nature of the mt-QSAR-EL model, the pseudolinear equation may be useful in a seemingly restricted region of the chemical space covered by this model. Nevertheless, the physicochemical properties and structural features needed to inhibit the Hsp90 isoforms is plausibly explained by the analysis of the molecular fragments and their local quantitative contributions as depicted in Figures 2 and 3 and Table 4.
2.4. In Silico Design of Dual Hsp90 Inhibitors
Currently, most of the QSAR models and related chemoinformatic tools constructed from heterogeneous data sets of compounds are mainly employed with the aim of performing virtual screening of large libraries of chemicals. Nevertheless, most of the time, the experimental data used to develop the models can have a great uncertainty because they come from different laboratories. Additionally, it should be considered that the molecular descriptors used to construct the models can characterize only a limited fraction of the diversity and complexity codified within the molecules.
When a model performs predictions of a certain property/activity, it does that according to predetermined values of the molecular descriptors used to construct it. When predicted, many molecules may not follow the rules under which the model has been developed. Here, it is not about how well a model will perform according to any applicability domain approach or method focused on determining the reliability of the predictions. This is based on the fact that in any model, there is a degree of hierarchy among the molecular descriptors, which embody a phenomenological meaning in the sense of describing the physicochemical and structural features needed for the improvement of the biological effect under study (in this particular case, the inhibitory activity). Therefore, compounds whose molecular descriptors follow such degree of hierarchy (as shown in Figure 1) will be predicted with better accuracy, where the prediction will be expected to converge to a greater extent with the experimental results. All of this is usually neglected by the current models devoted to screening vast chemical databases, but it was considered here when generating new molecules.
To properly design new molecules, a series of steps were followed. First, in most of the cases, only those fragments with local quantitative contributions against three or more physicochemical components were selected. Second, the new molecules were assembled by connecting and/or fusing different fragments. Third, when needed, certain atoms and/or bioisosteric replacements were added to the structure of the molecule. Last and most important, all of these chemical modifications mentioned in the three previous aspects strictly obeyed the physicochemical and structural interpretations of the molecular descriptors in the mt-QSAR-EL model. In addition, the predominantly negative fragment F18 was added to different positions in the structure of the designed molecules with the aim of analyzing the effect of the position and the connectivity on the potential inhibitory activity.
Eight molecules were designed (Figure 4), and all of them fell within the applicability domain (Supporting Information 4). By considering the cutoff value of inhibitory activity employed in this work (half-maximal inhibitory concentration (IC50) ≤230 nM), six of these molecules (IP-01 to IP-05 and IP-07) were predicted by the mt-QSAR-EL model as inhibitors of both Hsp90 isoforms, while the molecules IP-06 and IP-08 were predicted as active against Hsp90α but inactive with respect to Hsp90β (Supporting Information 4). We note that the presence of the fragment F18 does not define if a molecule will be active against the Hsp90 isoforms. However, the fragment F18 has been fused with positive fragments such as F3 and F17 in the way of minimizing as much as possible the number of electronegative atoms placed at the topological distances equal to three and seven (diminution of the descriptors D[TnsAq3(E)_MX]bt and D[TmpAq7(E)_MN]bt). This fusion also increases the number of clusters of order 5 (increasing the value of descriptor D[Xv(C)5]bt).
Figure 4.
New molecules designed by using the mt-QSAR-EL model.
If one compares IP-05 with IP-06, it is easy to see that they are similar molecules. Nevertheless, they have two differences. One of them is the replacement of fragment F11 in IP-05 by a fragment similar to F18 in the molecule IP-06. In this sense, the fragment F18 has been correctly placed in the molecule IP-06 according to its positive contribution to the physicochemical component C2 while favoring the physicochemical component C5. Still, this is not enough for the molecule IP-05 to be predicted as an inhibitor of both Hsp90 isoforms. The second divergent aspect is the key because a fragment similar to F17 is present in the two aforementioned molecules, but while there is an additional substitution between the two hydroxyl groups in the molecule IP-05, such substitution is absent in IP-06. This simple additional substitution dramatically favors the physicochemical component C5, resulting in the difference of potential inhibitory activity between IP-05 and IP-06. In terms of additional substitutions present in an aromatic ring, a similar situation to that involving IP-05 and IP-06 can be explained for the case of the molecules IP-07 and IP-08.
Finally, it should be noted that the eight designed molecules were not reported in the data set used to develop the mt-QSAR-EL model. In this sense, ChEMBL and ZINC26 were used to search for chemical similarities. The search did not produce any exact match, and even when the similarity cutoff was set to be ≥0.8, no results were found.
2.5. Assessing the Druglikeness
An essential stage in any drug discovery campaign is the estimation of the druglikeness of a molecule, i.e., how desirable is a chemical in terms of its bioavailability. In this sense, Lipinski’s rule of five is a classically accepted approach for the assessment of the bioavailability of the organic compounds.27 According to this rule, a chemical will have good oral bioavailability if it simultaneously complies with all of the following properties: molecular weight (MW) less than 500 Da, logarithm of the octanol–water partition coefficient (C log P) lower than 5, no more than five hydrogen bond donors (HBDs), and no more than 10 hydrogen bond acceptors (HBAs). However, Lipinski’s rule of five has received some criticism regarding the cutoff value of MW, and according to Veber and co-workers, the polar surface area (PSA) and the number of rotatable bonds (RBNs) have been found to better discriminate between compounds that are orally active from those that are not.28 In this sense, it has been established that the molecules with RBN ≤ 10 and PSA < 140 Å2 are expected to have good oral availability.
All of these physicochemical properties were estimated for the eight designed molecules (Table 5). The properties HBD and HBA were calculated manually; fluorine atoms were considered as hydrogen bond acceptors while pyrrolic nitrogens were not. The C log P was calculated by the program ChemDraw Ultra v8.0,29 and the other properties were calculated by the software Marvin Sketch v15.11.16.0 from ChemAxon.30 The eight molecules comply with Lipinski’s rule of five as well as with the Veber’s guidelines.
Table 5. Physicochemical Properties of the Designed Molecules.
| IDa,b | MW (Da) | HBD | HBA | C log P | PSA (Å2) | RBN |
|---|---|---|---|---|---|---|
| IP-01 | 452.55 | 3 | 7 | 2.37 | 109.5 | 7 |
| IP-02 | 411.5 | 3 | 7 | 1.754 | 95.67 | 7 |
| IP-03 | 392.45 | 4 | 7 | 0.698 | 105.28 | 5 |
| IP-04 | 393.44 | 3 | 7 | 1.92 | 99.49 | 5 |
| IP-05 | 436.5 | 3 | 7 | 2.509 | 99.85 | 6 |
| IP-06 | 422.48 | 3 | 7 | 2.38 | 99.85 | 6 |
| IP-07 | 410.46 | 4 | 7 | 2.466 | 118.72 | 8 |
| IP-08 | 410.46 | 4 | 7 | 2.806 | 118.72 | 8 |
Hydrogen bond donors (HBDs) and hydrogen bond acceptors (HBAs) were calculated manually. In addition, pyrrolic nitrogen was not considered as a hydrogen bond acceptor.
RBN stands for the number of rotatable bonds.
3. Conclusions
The Hsp90 family has become a focus of attention in drug discovery. Particularly, the search for inhibitors simultaneously targeting several Hsp90 isoforms is of great interest because it opens new horizons toward the discovery of new chemicals capable of therapeutically modulating many biochemical pathways involved in the emergence and development of complex diseases. In this work, the present approach focused on multitarget modeling represents a promising alternative toward the discovery of dual Hsp90 inhibitors. By combining the good performance of the mt-QSAR-EL model with the clear physicochemical/structural interpretations of the molecular descriptors, it has been possible to estimate the quantitative contributions of the fragments to the inhibitory activity. This has permitted the guided design of eight new molecules, six of them being predicted as potential dual Hsp90 inhibitors, and all of them displaying very good druglikeness. The multitarget modeling methodology focused on the joint use of an ML model with a fragment-based topological design approach can serve as a powerful alternative to speed up early drug discovery by considering important biomolecular targets such as the Hsp90 isoforms, whose roles have been linked to genetic and epigenetic variations.
4. Materials and Methods
4.1. Generation of the Database and Calculation of the Molecular Descriptors
The methodology involved in the development of the mt-QSAR models has been reported in detail in the scientific literature.31−33 So, only the principal aspects will be discussed here. All of the chemical and biological data reported in this work were retrieved from ChEBML,34 an online source containing more than 15 million assay endpoints against more than 1.8 million compounds. The data set used here was formed by 983 molecules experimentally tested against at least one of the two Hsp90 isoforms. In each assay, the in vitro potency against the proteins was measured as IC50, i.e., the inhibitory concentration causing 50% inhibition. When a molecule was assayed more than one time against the same Hsp90 isoform, its IC50 values were averaged. It should be pointed out that not all of the molecules present in the data set were assayed against both Hsp90 isoforms. Nevertheless, some molecules were tested against the two Hsp90 isoforms. Consequently, the data set employed here contains 1030 statistical cases.
Each statistical case was assigned as active [APi(bt) = 1] or inactive [APi(bt) = −1], with APi(bt) being a binary categorical variable that described the inhibitory activity of the ith case/molecule with respect to a defined biological target (in this case, an Hsp90 isoform). Such annotations were realized by considering IC50 ≤ 230 nM as the cutoff value. Thus, regardless of the Hsp90 isoform used in the assay, a molecule was annotated as active if its activity was IC50 ≤ 230 nM; otherwise, the molecule was assigned as inactive. It is important to note that in medicinal chemistry and drug discovery campaigns, the search for hit compounds starts at the micromolar range (depending on the target under analysis).35 As one can see, the selected cutoff value appears in the medium nanomolar range, which will improve the strictness of the model in the sense of rapidly searching for (or designing) more potent inhibitors. Also, from a statistical point of view, the cutoff value selected here avoids any excessive imbalance between the number of molecules annotated as active and those labeled as inactive.
All of the chemical information was stored as SMILES codes in a *.txt file, which was manually changed to *.smi. Then, to get information regarding the 2D connectivity of the molecules, the program Standardizer v15.11.16.0 was employed to convert the *.smi file to *.sdf.36 Two sets of molecular descriptors were calculated. From one side, the software QUBILs-MAS v1.0 was used to calculate the molecular descriptors known as nonstochastic and mutual probability atom-based quadratic indices.37 In general terms, quadratic indices have been used in different fields of research associated with drug discovery,37−40 and currently, more advanced versions of these descriptors can be calculated according to the following equations:
| 2 |
In eq 2, Li[qk(x)] represents the local nonstochastic quadratic index of order k, which considers an atom i and its chemical environment (formed by their jth neighbors) at the topological distance d = k. The element x refers to any atomic physicochemical property such as hydrophobicity (HYD), electronegativity (E), atomic weight, polar surface area (PSA), and atomic refractivity (AR), among others. At the same time, the element kaij characterizes the adjacency between any two atoms of the molecule. It should be emphasized that eq 2 is applied always to each atom of a molecule. Then, the total nonstochastic atom-based quadratic indices [TnsAqk(x)_MO] for a molecule having n atoms can be calculated by applying different mathematical/statistical operators (MO) to the set of local quadratic indices Li[qk(x)]. Some examples are shown in the following equations:
| 3 |
| 4 |
| 5 |
| 6 |
In eqs 3–6, the symbol Tnsqk(x) represents the total nonstochastic quadratic index, while the MOs include (but are not limited to) the Manhattan distance (N1), the Euclidean distance (N2), the geometric mean (GM), and the range (RA), the latter considering the maximum (MX) and minimum (MN) values. For the calculation of the mutual probability counterparts of the nonstochastic quadratic indices, the same equations can be used; the only difference is that in eq 2, the element kaij of a nonstochastic matrix is replaced by the element kpij of the mutual probability matrix.24,41 Thus, while the general symbology of the total nonstochastic atom-based quadratic indices is TnsAqk(x)_MO, the corresponding total mutual probability atom-based quadratic indices will have the symbol TmpAqk(x)_MO. It should be pointed out that the local atom-type quadratic indices have also been reported in the literature to account for the substructural patterns contained within the chemicals’ databases.42−44 However, in this study, only the total quadratic indices have been used because, as depicted in eqs 3–6, through the application of the diverse MOs, new classes of topological indices are created; such hybrid molecular descriptors have an enhanced ability to characterize local features in the molecules such as atom, bonds, and fragments. Also, although seemingly simpler than their global counterparts, the local atom-type quadratic indices may add complexity to the models from a statistical point of view because a greater number of molecular descriptors may be needed to develop the models.
Traditional molecular descriptors such as the atom- and bond-based connectivity indices, shape descriptors, and others widely reported in the literature constituted the second set of molecular descriptors used in this study;45 they were calculated by the program ModesLab v1.5 using the SMILES codes stored in the *.txt file.46 One should note that the molecular descriptors reported in eqs 3 – 6 characterize only the chemical structure of the molecules, being incapable of discriminating the effect of the chemical structure of a molecule when this is assayed against more than one target. In this context, the Box–Jenkins approach can solve this inconvenience.47 In time series, Box–Jenkins operators involve the calculation of successive average values of a given property of a system determined at different intervals of time.48 In the mt-QSAR methodology, the Box–Jenkins operators are not based on the time domain. Instead, in a first step, the average of any molecular descriptor is calculated according to the following mathematical formalism:49−51
| 7 |
In eq 7, TIa refers to any of the topological indices mentioned above, including those calculated via eqs 3–6, while avgTI(bt) is the average of a topological index for all of the drugs/chemicals that were assayed against the same protein and annotated as active. Consequently, n(bt) represents the number of molecules assayed against the same Hsp90 isoform and annotated as active. After, in a second step, the following formula is applied
| 8 |
In eq 8, DTIa(bt) is a deviation topological index, measuring how much a drug/chemical structurally deviates from a set of compounds annotated as active and assayed against the same Hsp90 isoform.52−56 On the other hand, TI(MX)(bt) and TI(MN)(bt) are the maximum and minimum values for a defined molecular descriptor, respectively. In this case, TI(MX)(bt) and TI(MN)(bt) depend on the Hsp90 isoform against which the molecules were tested. We note that DTIa(bt) is also a normalized descriptor due to the presence of an average in the numerator, and a subtraction between maximum and minimum values in the denominator. In addition, DTIa(bt) is a multitarget descriptor because it considers both the chemical structure and the Hsp90 isoform against which a molecule was tested. It should be pointed out that eq 8 unifies the calculation of the Box–Jenkins operators with the mean-based normalization procedure.
4.2. Development of the mt-QSAR-EL Model
The diverse steps involved in the development of the mt-QSAR-EL model are summarized in Figure 5. The data set composed of 1030 statistical cases was randomly divided into training and test sets. The training set was employed to find the best model, and it contained 774 cases (75.14%), 373 annotated as active and 401 assigned as inactive. The test set was used to validate the model, with the purpose of demonstrating its predictive power. The test set contained 256 cases (24.86%), 121 considered active and 134 annotated as inactive. The ML method focused on ANNs was used to generate the mt-QSAR-EL model. Particularly, the model was based on an ensemble of ANNs.
Figure 5.
Steps leading to the development of the mt-QSAR-EL model.
Finding the best mt-QSAR-EL model was subjected to finding the collection of ANNs that cooperate in performing predictions in a consensus voting manner. Several ANNs architectures were used in the search for the single models: linear neural networks (LNN), radial basis function (RBF), and multilayer perceptron (MLP).
The task of generating the best mt-QSAR-EL model was performed by the Intelligent Problem Solver of the ANNs package of the program STATISTICA v6.0.57 The first run was used to determine the most important ANNs architectures and the number of ANNs forming the ensembles, rank the most significant molecular descriptors, and estimate the correlations between them. The diversity among the ANNs models forming the ensemble was considered. In this sense, all of the ANNs models forming the ensemble were inspected in the sense that they obligatorily needed to have different number of neurons in their hidden layers, as well as different training and test errors (as low as possible) while having different values (but as high as possible) of the statistical indices Sn(%), and Sp(%), Ac(%), and MCC.58 These statistical indices were used to assess the internal quality (training set) and the predictive power (test set) of the mt-QSAR-EL model.
On the other hand, the most significant molecular descriptors were ranked according to the importance analysis (also known as sensitivity analysis) available in the Intelligent Problem Solver of the ANNs package of the program STATISTICA v6.0. This procedure attempts to quantify the effect of a defined molecular descriptor by calculating a ratio of the error generated in the ANN when estimating the value of the molecular descriptor using a missing value procedure, and the error generated in the ANN by using the real value of a molecular descriptor. The most influential molecular descriptors are those with importance values (SV) higher than 1; only these descriptors were chosen to enter the final model. Consequently, the importance analysis served as a variable selection strategy.
Finally, the correlations between the molecular descriptors were estimated, and the cutoff interval −0.7 < PCC < 0.7 was used as the criterion to determine the lack of redundancy, PCC being the Pearson’s correlation coefficient.59 Those descriptors that fell outside the aforementioned interval were not used in the search for the best mt-QSAR-EL model.
Acknowledgments
A.S.-P. acknowledges the Spanish Juan de la Cierva program (Grant: FJCI-2015-25572) for the financial support.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02419.
Chemical and biological data, average and related measures, input data, and classification results (Supporting Information 1) (XLSX)
Local measures of the statistical quality and performance of the mt-QSAR-EL model (Supporting Information 2) (PDF)
Applicability domain of the mt-QSAR-EL model (Supporting Information 3) (XLSX)
New molecules designed by the mt-QSAR-EL model: prediction results and assessment of the applicability domain (Supporting Information 4) (XLSX)
The author declares no competing financial interest.
Supplementary Material
References
- Lo Y.-C.; Rensi S. E.; Torng W.; Altman R. B. Machine learning in chemoinformatics and drug discovery. Drug Discovery Today 2018, 23, 1538–1546. 10.1016/j.drudis.2018.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.; Tan J.; Han D.; Zhu H. From machine learning to deep learning: progress in machine intelligence for rational drug discovery. Drug Discovery Today 2017, 22, 1680–1685. 10.1016/j.drudis.2017.08.010. [DOI] [PubMed] [Google Scholar]
- Lavecchia A. Machine-learning approaches in drug discovery: methods and applications. Drug Discovery Today 2015, 20, 318–331. 10.1016/j.drudis.2014.10.012. [DOI] [PubMed] [Google Scholar]
- Zhang L.; Ai H.; Chen W.; Yin Z.; Hu H.; Zhu J.; Zhao J.; Zhao Q.; Liu H. CarcinoPred-EL: Novel models for predicting the carcinogenicity of chemicals using molecular fingerprints and ensemble learning methods. Sci. Rep. 2017, 7, 2118 10.1038/s41598-017-02365-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchese Robinson R. L.; Palczewska A.; Palczewski J.; Kidley N. Comparison of the Predictive Performance and Interpretability of Random Forest and Linear Models on Benchmark Data Sets. J. Chem. Inf. Model. 2017, 57, 1773–1792. 10.1021/acs.jcim.6b00753. [DOI] [PubMed] [Google Scholar]
- Lei T.; Li Y.; Song Y.; Li D.; Sun H.; Hou T. ADMET evaluation in drug discovery: 15. Accurate prediction of rat oral acute toxicity using relevance vector machine and consensus modeling. J. Cheminf. 2016, 8, 6. 10.1186/s13321-016-0117-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaneko H. Discussion on Regression Methods Based on Ensemble Learning and Applicability Domains of Linear Submodels. J. Chem. Inf. Model. 2018, 58, 480–489. 10.1021/acs.jcim.7b00649. [DOI] [PubMed] [Google Scholar]
- Ezzat A.; Wu M.; Li X. L.; Kwoh C. K. Drug-target interaction prediction using ensemble learning and dimensionality reduction. Methods 2017, 129, 81–88. 10.1016/j.ymeth.2017.05.016. [DOI] [PubMed] [Google Scholar]
- Lee K.; Lee M.; Kim D. Utilizing random Forest QSAR models with optimized parameters for target identification and its application to target-fishing server. BMC Bioinf. 2017, 18, 567. 10.1186/s12859-017-1960-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moon H.; Ahn H.; Kodell R. L.; Baek S.; Lin C. J.; Chen J. J. Ensemble methods for classification of patients for personalized medicine with high-dimensional data. Artif. Intell. Med. 2007, 41, 197–207. 10.1016/j.artmed.2007.07.003. [DOI] [PubMed] [Google Scholar]
- Putin E.; Asadulaev A.; Ivanenkov Y.; Aladinskiy V.; Sanchez-Lengeling B.; Aspuru-Guzik A.; Zhavoronkov A. Reinforced Adversarial Neural Computer for de Novo Molecular Design. J. Chem. Inf. Model. 2018, 58, 1194–1204. 10.1021/acs.jcim.7b00690. [DOI] [PubMed] [Google Scholar]
- Gómez-Bombarelli R.; Wei J. N.; Duvenaud D.; Hernández-Lobato J. M.; Sánchez-Lengeling B.; Sheberla D.; Aguilera-Iparraguirre J.; Hirzel T. D.; Adams R. P.; Aspuru-Guzik A. Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules. ACS Cent. Sci. 2018, 4, 268–276. 10.1021/acscentsci.7b00572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segler M. H. S.; Kogej T.; Tyrchan C.; Waller M. P. Generating Focused Molecule Libraries for Drug Discovery with Recurrent Neural Networks. ACS Cent. Sci. 2018, 4, 120–131. 10.1021/acscentsci.7b00512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadurin A.; Nikolenko S.; Khrabrov K.; Aliper A.; Zhavoronkov A. druGAN: An Advanced Generative Adversarial Autoencoder Model for de Novo Generation of New Molecules with Desired Molecular Properties in Silico. Mol. Pharmaceutics 2017, 14, 3098–3104. 10.1021/acs.molpharmaceut.7b00346. [DOI] [PubMed] [Google Scholar]
- Zabinsky R. A.; Mason G. A.; Queitsch C.; Jarosz D. F. It’s not magic - Hsp90 and its effects on genetic and epigenetic variation. Semin. Cell Dev. Biol. 2018, 10.1016/j.semcdb.2018.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calderwood S. K.; Khaleque M. A.; Sawyer D. B.; Ciocca D. R. Heat shock proteins in cancer: chaperones of tumorigenesis. Trends Biochem. Sci. 2006, 31, 164–172. 10.1016/j.tibs.2006.01.006. [DOI] [PubMed] [Google Scholar]
- Sahigara F.; Mansouri K.; Ballabio D.; Mauri A.; Consonni V.; Todeschini R. Comparison of different approaches to define the applicability domain of QSAR models. Molecules 2012, 17, 4791–4810. 10.3390/molecules17054791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speck-Planche A.; Cordeiro M. N. D. S. Speeding up Early Drug Discovery in Antiviral Research: A Fragment-Based in Silico Approach for the Design of Virtual Anti-Hepatitis C Leads. ACS Comb. Sci. 2017, 19, 501–512. 10.1021/acscombsci.7b00039. [DOI] [PubMed] [Google Scholar]
- Speck-Planche A.; Kleandrova V. V. QSAR and molecular docking techniques for the discovery of potent monoamine oxidase B inhibitors: Computer-aided generation of new rasagiline bioisosteres. Curr. Top. Med. Chem. 2012, 12, 1734–1747. 10.2174/1568026611209061734. [DOI] [PubMed] [Google Scholar]
- Baskin I. I.; Skvortsova M. I.; Stankevich I. V.; Zefirov N. S. On the basis of invariants of labeled molecular graphs. J. Chem. Inf. Model. 1995, 35, 527–531. 10.1021/ci00025a021. [DOI] [Google Scholar]
- Prado-Prado F. J.; Garcia-Mera X.; Gonzalez-Diaz H. Multi-target spectral moment QSAR versus ANN for antiparasitic drugs against different parasite species. Bioorg. Med. Chem. 2010, 18, 2225–2231. 10.1016/j.bmc.2010.01.068. [DOI] [PubMed] [Google Scholar]
- Speck-Planche A.; Cordeiro M. N. D. S. Chemoinformatics for medicinal chemistry: in silico model to enable the discovery of potent and safer anti-cocci agents. Future Med. Chem. 2014, 6, 2013–2028. 10.4155/fmc.14.136. [DOI] [PubMed] [Google Scholar]
- Speck-Planche A.; Cordeiro M. N. D. S. Fragment-based in silico modeling of multi-target inhibitors against breast cancer-related proteins. Mol. Diversity 2017, 21, 511–523. 10.1007/s11030-017-9731-1. [DOI] [PubMed] [Google Scholar]
- Speck-Planche A.; Cordeiro M. N. D. S. De novo computational design of compounds virtually displaying potent antibacterial activity and desirable in vitro ADMET profiles. Med. Chem. Res. 2017, 26, 2345–2356. 10.1007/s00044-017-1936-4. [DOI] [Google Scholar]
- Kleandrova V. V.; Ruso J. M.; Speck-Planche A.; Cordeiro M. N. D. S. Enabling the Discovery and Virtual Screening of Potent and Safe Antimicrobial Peptides. Simultaneous Prediction of Antibacterial Activity and Cytotoxicity. ACS Comb. Sci. 2016, 18, 490–498. 10.1021/acscombsci.6b00063. [DOI] [PubMed] [Google Scholar]
- Irwin J. J.; Shoichet B. K. ZINC--a free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 2005, 45, 177–182. 10.1021/ci049714+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipinski C. A.; Lombardo F.; Dominy B. W.; Feeney P. J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Delivery Rev. 2001, 46, 3–26. 10.1016/S0169-409X(00)00129-0. [DOI] [PubMed] [Google Scholar]
- Veber D. F.; Johnson S. R.; Cheng H. Y.; Smith B. R.; Ward K. W.; Kopple K. D. Molecular properties that influence the oral bioavailability of drug candidates. J. Med. Chem. 2002, 45, 2615–2623. 10.1021/jm020017n. [DOI] [PubMed] [Google Scholar]
- CambridgeSoft . ChemDraw Ultra, version 8.0; CambridgeSoft: Cambridge, MA, 2003.
- ChemAxon . Marvin Sketch, JChem, version 15.11.16.0; ChemAxon: Budapest, Hungary, 1998–2016.
- Romero-Durán F. J.; Alonso N.; Yañez M.; Caamaño O.; García-Mera X.; González-Díaz H. Brain-inspired cheminformatics of drug-target brain interactome, synthesis, and assay of TVP1022 derivatives. Neuropharmacology 2016, 103, 270–278. 10.1016/j.neuropharm.2015.12.019. [DOI] [PubMed] [Google Scholar]
- Tenorio-Borroto E.; Penuelas-Rivas C. G.; Vasquez-Chagoyan J. C.; Castanedo N.; Prado-Prado F. J.; Garcia-Mera X.; Gonzalez-Diaz H. Model for high-throughput screening of drug immunotoxicity - Study of the anti-microbial G1 over peritoneal macrophages using flow cytometry. Eur. J. Med. Chem. 2014, 72, 206–220. 10.1016/j.ejmech.2013.08.035. [DOI] [PubMed] [Google Scholar]
- Speck-Planche A.; Cordeiro M. N. D. S. Simultaneous virtual prediction of anti-Escherichia coli activities and ADMET profiles: A chemoinformatic complementary approach for high-throughput screening. ACS Comb. Sci. 2014, 16, 78–84. 10.1021/co400115s. [DOI] [PubMed] [Google Scholar]
- Gaulton A.; Bellis L. J.; Bento A. P.; Chambers J.; Davies M.; Hersey A.; Light Y.; McGlinchey S.; Michalovich D.; Al-Lazikani B.; Overington J. P. ChEMBL: a large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012, 40, D1100–D1107. 10.1093/nar/gkr777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson A. C. The process of structure-based drug design. Chem. Biol. 2003, 10, 787–797. 10.1016/j.chembiol.2003.09.002. [DOI] [PubMed] [Google Scholar]
- ChemAxon. Standardizer (Tool for Structure Canonicalization and Transformation), JChem, version 15.11.16.0; ChemAxon: Budapest, Hungary, 1998–2016.
- Valdés-Martiní J. R.; Marrero-Ponce Y.; García-Jacas C. R.; Martinez-Mayorga K.; Barigye S. J.; Vaz d’Almeida Y. S.; Pham-The H.; Pérez-Giménez F.; Morell C. A. QuBiLS-MAS, open source multi-platform software for atom- and bond-based topological (2D) and chiral (2.5D) algebraic molecular descriptors computations. J. Cheminf. 2017, 9, 35. 10.1186/s13321-017-0211-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medina Marrero R.; Marrero-Ponce Y.; Barigye S. J.; Echeverria Diaz Y.; Acevedo-Barrios R.; Casanola-Martin G. M.; Garcia Bernal M.; Torrens F.; Perez-Gimenez F. QuBiLs-MAS method in early drug discovery and rational drug identification of antifungal agents. SAR QSAR Environ. Res. 2015, 26, 943–958. 10.1080/1062936X.2015.1104517. [DOI] [PubMed] [Google Scholar]
- Marrero-Ponce Y.; Siverio-Mota D.; Galvez-Llompart M.; Recio M. C.; Giner R. M.; Garcia-Domenech R.; Torrens F.; Aran V. J.; Cordero-Maldonado M. L.; Esguera C. V.; de Witte P. A.; Crawford A. D. Discovery of novel anti-inflammatory drug-like compounds by aligning in silico and in vivo screening: the nitroindazolinone chemotype. Eur. J. Med. Chem. 2011, 46, 5736–5753. 10.1016/j.ejmech.2011.07.053. [DOI] [PubMed] [Google Scholar]
- Casañola-Martin G. M.; Marrero-Ponce Y.; Khan M. T.; Khan S. B.; Torrens F.; Perez-Jimenez F.; Rescigno A.; Abad C. Bond-based 2D quadratic fingerprints in QSAR studies: virtual and in vitro tyrosinase inhibitory activity elucidation. Chem. Biol. Drug Des. 2010, 76, 538–545. 10.1111/j.1747-0285.2010.01032.x. [DOI] [PubMed] [Google Scholar]
- Speck-Planche A.; Cordeiro M. N. D. S. Multi-target QSAR approaches for modeling protein inhibitors. Simultaneous prediction of activities against biomacromolecules present in gram-negative bacteria. Curr. Top. Med. Chem. 2015, 15, 1801–1813. 10.2174/1568026615666150506144814. [DOI] [PubMed] [Google Scholar]
- Marrero-Ponce Y.; Medina-Marrero R.; Torrens F.; Martinez Y.; Romero-Zaldivar V.; Castro E. A. Atom, atom-type, and total nonstochastic and stochastic quadratic fingerprints: a promising approach for modeling of antibacterial activity. Bioorg. Med. Chem. 2005, 13, 2881–2899. 10.1016/j.bmc.2005.02.015. [DOI] [PubMed] [Google Scholar]
- Casañola-Martín G. M.; Marrero-Ponce Y.; Khan M. T. H.; Torrens F.; Pérez-Giménez F.; Rescigno A. Atom- and bond-based 2D TOMOCOMD-CARDD approach and ligand-based virtual screening for the drug discovery of new tyrosinase inhibitors. J. Biomol. Screen. 2008, 13, 1014–1024. 10.1177/1087057108326078. [DOI] [PubMed] [Google Scholar]
- Ponce Y.; Pérez M.; Zaldivar V.; Ofori E.; Montero L. Total and Local Quadratic Indices of the “Molecular Pseudograph’s Atom Adjacency Matrix”. Application to Prediction of Caco-2 Permeability of Drugs. Int. J. Mol. Sci. 2003, 4, 512–536. 10.3390/i4080512. [DOI] [Google Scholar]
- Todeschini R.; Consonni V.. Molecular Descriptors for Chemoinformatics; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2009. [Google Scholar]
- Estrada E.; Gutiérrez Y.. MODESLAB, version 1.5; MOlecular DEScriptors LABoratory: Santiago de Compostela, 2002–2004.
- Gonzalez-Diaz H.; Arrasate S.; Gomez-SanJuan A.; Sotomayor N.; Lete E.; Besada-Porto L.; Ruso J. M. General theory for multiple input-output perturbations in complex molecular systems. 1. Linear QSPR electronegativity models in physical, organic, and medicinal chemistry. Curr. Top. Med. Chem. 2013, 13, 1713–1741. 10.2174/1568026611313140011. [DOI] [PubMed] [Google Scholar]
- González-Díaz H.; Herrera-Ibatá D. M.; Duardo-Sánchez A.; Munteanu C. R.; Orbegozo-Medina R. A.; Pazos A. ANN multiscale model of anti-HIV drugs activity vs AIDS prevalence in the US at county level based on information indices of molecular graphs and social networks. J. Chem. Inf. Model. 2014, 54, 744–755. 10.1021/ci400716y. [DOI] [PubMed] [Google Scholar]
- Alonso N.; Caamaño O.; Romero-Duran F. J.; Luan F.; Cordeiro M. N. D. S.; Yañez M.; González-Díaz H.; García-Mera X. Model for high-throughput screening of multitarget drugs in chemical neurosciences: synthesis, assay, and theoretic study of rasagiline carbamates. ACS Chem. Neurosci. 2013, 4, 1393–1403. 10.1021/cn400111n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marzaro G.; Chilin A.; Guiotto A.; Uriarte E.; Brun P.; Castagliuolo I.; Tonus F.; González-Díaz H. Using the TOPS-MODE approach to fit multi-target QSAR models for tyrosine kinases inhibitors. Eur. J. Med. Chem. 2011, 46, 2185–2192. 10.1016/j.ejmech.2011.02.072. [DOI] [PubMed] [Google Scholar]
- Speck-Planche A.; Kleandrova V. V.; Scotti M. T. Fragment-based approach for the in silico discovery of multi-target insecticides. Chemom. Intell. Lab. Syst. 2012, 111, 39–45. 10.1016/j.chemolab.2011.11.010. [DOI] [Google Scholar]
- Bediaga H.; Arrasate S.; González-Díaz H. PTML Combinatorial Model of ChEMBL Compounds Assays for Multiple Types of Cancer. ACS Comb. Sci. 2018, 10.1021/acscombsci.8b00090. [DOI] [PubMed] [Google Scholar]
- Blay V.; Yokoi T.; González-Díaz H. Perturbation Theory-Machine Learning Study of Zeolite Materials Desilication. J. Chem. Inf. Model. 2018, 10.1021/acs.jcim.8b00383. [DOI] [PubMed] [Google Scholar]
- Simón-Vidal L.; García-Calvo O.; Oteo U.; Arrasate S.; Lete E.; Sotomayor N.; González-Díaz H. Perturbation-Theory and Machine Learning (PTML) Model for High-Throughput Screening of Parham Reactions: Experimental and Theoretical Studies. J. Chem. Inf. Model. 2018, 58, 1384–1396. 10.1021/acs.jcim.8b00286. [DOI] [PubMed] [Google Scholar]
- Ferreira da Costa J.; Silva D.; Caamaño O.; Brea J. M.; Loza M. I.; Munteanu C. R.; Pazos A.; García-Mera X.; González-Díaz H. Perturbation Theory/Machine Learning Model of ChEMBL Data for Dopamine Targets: Docking, Synthesis, and Assay of New l-Prolyl-l-leucyl-glycinamide Peptidomimetics. ACS Chem. Neurosci. 2018, 10.1021/acschemneuro.8b00083. [DOI] [PubMed] [Google Scholar]
- Martínez-Arzate S. G.; Tenorio-Borroto E.; Pliego A. B.; Díaz-Albiter H. M.; Vázquez-Chagoyán J. C.; González-Díaz H. PTML Model for Proteome Mining of B-Cell Epitopes and Theoretical-Experimental Study of Bm86 Protein Sequences from Colima, Mexico. J. Proteome Res. 2017, 16, 4093–4103. 10.1021/acs.jproteome.7b00477. [DOI] [PubMed] [Google Scholar]
- StatSoft-Team. STATISTICA, Data Analysis Software System, version 6.0; StatSoft, Inc.: Tulsa, 2001.
- Matthews B. W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta 1975, 405, 442–451. 10.1016/0005-2795(75)90109-9. [DOI] [PubMed] [Google Scholar]
- Pearson K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. London 1895, 58, 240–242. 10.1098/rspl.1895.0041. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.