THE MULTIVARIATE A/C/E MODEL AND THE GENETICS OF FIBER ARCHITECTURE

Abstract

We present a new algorithm to compute the voxel-wise genetic contribution to brain fiber microstructure using diffusion tensor imaging (DTI) in a dataset of 25 pairs of monozygotic (MZ) twins and 25 pairs of dizygotic (DZ) twins. First, the structural and DT scans were linearly co-registered. The structural MR scans were nonlinear mapped via a 3D fluid transformation to a geometrically centered mean template, and the deformation fields were applied to the DTI volumes. After tensor re-orientation to realign them to the anatomy, we computed several scalar and multivariate DT-derived measures including the geodesic anisotropy (GA), the tensor eigenvalues and the full diffusion tensors. A covariance-weighted distance was found between twins in the Log-Euclidean framework [2], and used as input to a maximum-likelihood based algorithm to compute the contributions from genetics (A), common environmental factors (C) and unique environmental ones (E) to fiber architecture. Quantitative genetic studies can make use of the full information in the diffusion tensor, using covariance weighted distances and statistics on the tensor manifold.

1. INTRODUCTION

Twin studies are popular in the neurosciences and medical imaging as a means to understand the genetic control on brain structure and function. Of particular importance in these works is the search for specific genes implicated in brain development and disease.

Much work has previously been performed to understand the influence of genetic factors on various aspects of brain anatomy such as cortical thickness [20], regional gray and white matter volumes [4], and fiber structure [5, 11]. In large-scale studies of pediatric twins [19], the corpus callosum, cerebrum, cerebellum, thalamus and basal ganglia were found to be strongly influenced by a single genetic factor. Even so, few studies have analyzed genetic influences on signals that are inherently multidimensional, such as diffusion tensors.

Several models have been established to estimate the genetic and environmental contributions to a phenotype, by comparing correlations in monozygotic twins (MZs, who share 100% of their genes) to those found between dizygotic twins (DZs, who share 50% of their genes on average). Among these, the A/C/E structural equation model uses information from both types of twins to distinguish between sources of variance that are attributable to additive genetic factors (A), common environment (C) and environmental factors unique to each individual (E) [15].

The ACE model was first introduced to the brain imaging community through the popular Mx software [15]. Mx uses a maximum-likelihood approach to estimate the relative contribution of each of the A/C/E components. Though Mx was designed for the analysis of single traits such as total brain volume, we recently extended it to compute maps of genetic parameters at each voxel in a brain image [5], revealing the profiles of genetic influences in 3D.

One means to understand the genetics of brain fiber architecture is through diffusion weighted MR imaging, which measures the multidirectional profile of water diffusion in tissue. When used to analyze brain tissue, the method provides vital information on brain architecture and composition, and estimates of fiber integrity that are correlated with intellectual performance [5]. In most studies of diffusion weighted images, a diffusion tensor (DT) is computed at each voxel whose eigenvectors represent the three orthogonal principal directions of the diffusion, and its eigenvalues represent the magnitude of diffusion along these axes. Fiber directions can be inferred from the principal eigenvector direction, and several tractography methods have been developed to estimate white matter connectivity [13].

Several measures, both scalar and multivariate, can be derived from the DTs to better understand the fiber structure in the brain. Common measures include the fractional anisotropy (FA), mean diffusivity (MD) and the eigenvalues. More recently, a few more sophisticated quantities have been used such as the geodesic anisotropy (GA) [3, 14], which measures the geodesic distance between tensors on the symmetric positive-definite tensor manifold. In [11], we found that a multivariate statistical analysis of the full diffusion tensor outperformed derived scalar signals in detecting group differences in the blind.

Here we present a new multivariate A/C/E model that can estimate genetic influences on multidimensional signals such as DTI. As diffusion tensors lie in a non-Euclidean manifold, we use a covariance-weighted distance to map the genetic/environmental contributions to the full multivariate DT. As the matrices are positive-definite and symmetric, they do not form a vector subspace of the vector space of matrices with the usual matrix addition and scalar multiplication. To account for this, we performed all statistical computations in the Log-Euclidean framework [2], which allows for simple computations on the DT manifold. This method enables us to assess genetic influences in brain architecture by computing variances within and between members of twin pairs, with distances computed on the diffusion tensor manifold.

We implemented a version of our model by expanding on the multi-voxel univariate A/C/E algorithm in [5]. Our method is used to compute 3D maps of the genetic and environmental influences on FA, GA and the full DT in 100 healthy young adult twins. We also compared the DTI-derived measures to determine which one is most heritable. The search for heritable measures in images is typically the first step in identifying specific genes that affect aspects of brain structure and function [8].

2. METHODS

2.1. Statistical analysis of structural equation models for twins

To understand how genetic and environmental effects are estimated for a scalar DTI-derived measure, such as the GA, we note that such a measure can be computed in a range of MZ pairs and DZ pairs, and the covariance between twin 1 and twin 2 for these measures can be computed. These empirically estimated covariance matrices can be computed for any observed variable (Z), and a structural equation model (SEM) can be fitted to the covariances to infer how much of the population variance is attributable to additive gene effects (A), environmental factors that are shared, or common, between twins (C), and unique environmental factors coupled with measurement errors (E). Measurement errors or inter-subject registration errors will both be classified as part of the E component of variance. Z for one twin pair may be modeled as:

$$Z=aA+cC+eE$$ (1)

where A/C/E are latent variables and a, c, e are the weights of each parameter to be estimated. A maximum-likelihood estimate (MLE) [15] is used to estimate the proportion of the voxel-based intersubject variance that is attributable to each of the 3 free model parameters. The 3 variance components combine to create the total observed inter-individual variance, so that a² + c² + e² = 1. The weights Θ = (a, c, e) are estimated by comparing the covariance matrix implied by the model, Σ(Θ), and the sample covariance matrix of the observed variables, S, using maximum-likelihood fitting:

$$F_{L,M,\beta }=\mathit{log}|\sum (\mathrm{\Theta })|+\mathit{trace}({\sum }^{-1}(\mathrm{\Theta })S)-\mathit{log}|S|-p$$ (2)

where p = 2 is the number of observed variables. Under the null hypothesis that Z is multivariate normal (i.e., each of A, C and E are normally distributed), the MLE model follows a χ² distribution with p(p + 1) − t degrees of freedom, where t is number of model parameters (3 in our case). We used the Broyden-Fletcher-Goldfarb-Shannomethod [17] to obtain the minimum F_LM,β

2.2. Multivariate Statistics in Log-Euclidean Space

In the case of the 3-component vector whose elements are the eigenvalues, or the full DT, there are either 3 or 6 parameters per voxel, all containing potentially useful information for genetic analysis. The covariance matrices can no longer be computed using the previous general formula. Here we propose to use a new covariance-weighted distance in the Log-Euclidean formalism using twin pairs (Fig. 1). We first compute the matrix logarithms of the tensors in the Log-Euclidean space. In the Log-Euclidean framework, the distance d(S₁, S₂) between two tensors S1 and S2 is defined as

$$d(S_1,S_2)=\Vert \mathit{log}{S}_1-\mathit{log}S2\Vert$$ (3)

where ||.|| is the norm. Here we use [2]

$$d(S_1-S_2)={(\mathit{Trace}{(\mathit{log}{S}_1-\mathit{log}S2)}^2)}^{\frac{1}{2}}$$ (4)

We built on equation 4 to design a distance that measures the deviation from each subject to the mean of the population, weighted by the component-wise covariance of the 6D tensors in the sample:

$$M=\frac{1}{N_p}{\displaystyle \sum _{i=1}^{N_p}(\mathit{log}{T}_1^i-\mathit{log}\overline{T})}Co{v}^{-1}{(\mathit{log}{T}_2^i-\mathit{log}\overline{T})}^T$$ (5)

where $\overline{T}$ is the mean of a set of vectors Tⁱ, i = 1, …, m; T₁ and T₂ represent each subject of the twin pair; $\overline{T}=\text{exp}(\frac{1}{N}{\displaystyle {\sum }_{i=1}\mathit{log}{T}^i})$ where N_p is number of twin pairs and the component-wise covariance, Cov, is the 6×6 matrix. This distance is illustrated in Figure 1, where each twins tensors are represented as ellipsoids on the curved manifold. This distance on the Lie group may be thought of as a bilinear form that takes two tensors as arguments and returns their discrepancy, taking into account the naturally occurring (and perhaps genetically mediated) correlations between the tensor component i in twin 1 and tensor component j in twin 2. This defines the covariance among samples of tensors, and the variances of twin 1 and twin 2 are computed by making a sample consisting of one twin from each pair, i.e., Var[T_i¹] = Cov[T_i¹, T_i¹] and Var[T_i²] = Cov[T_i², T_i²]. The 3 variance/covariance terms, Var[T_i¹], Var[T_i²], Cov[T_i¹, T_i²] are computed separately for both MZ and DZ twins, yielding 6 scalars per voxel that are used as an input to form matrices Σ(Θ) in (2).

Fig. 1.

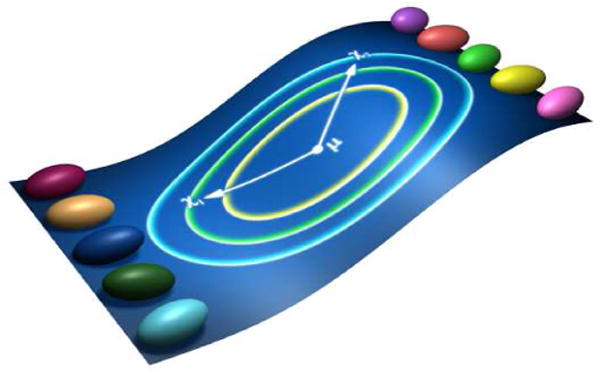
Statistical distance on tensors. Here we define a statistical distance between two tensors as (x₁ −μ)Σ⁻¹(x₂ – μ)^T, where Σ is the 6×6 matrix whose i, j^th element is the covariance between tensor component i in twin 1 (x₁) with tensor component j in twin 2 (x₂), and μ is the mean tensor of all the twins in log-Euclidean space. The green and blue 2D concentric ellipses on the center show isovalues of the Mahalanobis metric associated with this covariance matrix

2.3. Data and Preprocessing

2.3.1. Subject description and image acquisition

To test our analysis methods, we acquired 3D structural brain MRI scans and DT-MRI scans from 100 subjects: 25 pairs of MZ twins (25.1 ± 1.5SD years old) and 25 pairs of DZ twins (23.08 ± 2.1 years) on a 4T Bruker Medspec MRI scanner with an optimized diffusion tensor sequence [6]. Imaging parameters were: 21 axial slices (5 mm thick), FOV = 23 cm, TR/TE 6090/91.7 ms, 0.5mm gap, with a 128 ∗ 100 acquisition matrix. 30 directional gradients were applied: three scans with no diffusion sensitization (i.e., T2-weighted images) and 27 diffusion-weighted images for which gradient directions were evenly distributed on the hemisphere [10]. The reconstruction matrix was 128 ∗ 128, yielding a 1.8 ∗ 1.8 mm² in-plane resolution. Total scan time was 3.05 minutes.

2.3.2. Image Preprocessing and Registration

3D structural MR images were automatically skull-stripped using the Brain Surface Extraction software (BSE) [18] followed by manual editing. Each masked image was registered via 12-parameter affine transformation to a high resolution single-subject brain template image, the Colin27 template, using the FLIRT software [9]. 3D structural images were registered to a Mean Deformation Template (MDT; created from the dataset) using a 3D fluid registration [6]. Jacobian matrices were obtained from the resulting deformation fields.

Diffusion Tensors (3×3 positive symmetric matrices) were computed from DICOM DT-MR images and smoothed using Log-Euclidean tensor denoising to eliminate singular, negative definite, or rank-deficient tensors, using MedINRIA (http://www.sop.inria.fr/asclepios/software/MedINRIA). To eliminate extracerebral tissues, non brain tissues were manually deleted from one of the diagonal component images (D_xx), yielding a binary brain extraction mask (cerebellum included). Masked images were registered by 9-parameter transformation to the corresponding 3D structural images in the standard template space using FLIRT software [9].

Transformation parameters from affine and nonlinear registrations were used to rotationally reorient the tensors at each voxel [1] to ensure that the multidimensional tensor orientations remained consistent with the anatomy after image transformation [1, 21]. We used two separate algorithms to compute the tensor rotations: the finite Strain (FS) and the preservation of principal direction (PPD) algorithms (see [1] and [21]).

2.4. Scalar Statistics in the Log-Euclidean space

As a scalar statistic to compare to our multivariate measures, we used the GA, which is the manifold equivalent of the FA computed in the Log-Euclidean framework [2, 12]:

$$GA(S)=\sqrt{(}\mathit{Trace}{(\mathit{log}S-<\mathit{log}S>I)}^2)$$ (6)

with $<\mathit{log}S>=\frac{\mathit{Trace}(\mathit{log}S)}{3}$ We renormalized GA by applying the hyperbolic tangent transformation to the GA values (tGA) as in [3], to create maps with a comparable range to the F A.

2.5. Statistical analysis for twins

We computed GA and tGA values as well as the logarithms of the eigenvalues and the matrix logarithms of the full diffusion tensors for each subject. Two sets of voxel-wise covariance matrices for the MZ pairs and DZ pairs were computed for all the univariate and multivariate measures detailed above. We estimated the genetic (A) and non-genetic (C/E) contribution to DT-derived measures at each voxel using the methods described in section 2.1 and 2.2. We also computed permutation-based p values to evaluate the goodness-of-fit.

3. RESULTS

Figure 2 shows the probability values mapped for GA (univariate) and 3 eigenvalues (multivariate) measures. Note that in A/C/E model, a probability of less than 0.05 indicates that the model is not trustworthy. We only mapped the voxels where had probability values greater than 0.05. Higher probabilities are seen in the 3 eigenvalues maps indicating the multivariate measures do have more genetic information than scalar measures.

Fig. 2.

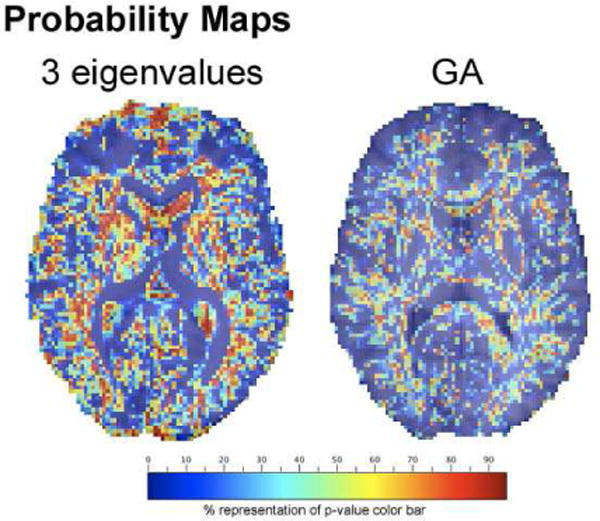
Probability maps for the A/C/E model with 3 eigenvalue (left) and GA (right). Only voxels with p¿0.05 are shown.

4. DISCUSSION

Here we showed how to estimate genetic contributions to the multidimensional signals in diffusion tensor images by transforming the diffusion tensors to the log-Euclidean domain via the matrix logarithm transformation. In the resulting space, the component-wise correlations in the diffusion tensor components were incorporated into a 6×6 covariance matrix, which was used as an inverse distance metric on the Lie group to weight the contributions of each component to the overall distance between two tensors. These covariances were computed to generate 6 scalar covariance values per voxel, as needed to fit a conventional structural equation model of the A/C/E type, which is widely used in quantitative genetics. This automated voxel-wise SEM based A/C/E algorithm can also be applied to any other multidimensional neuroimaging measures in twin studies. For example, the Jacobian determinants in a tensor based morphometry are only a scalar summary of the full deformation tensor, and as in [13], one could replace the covariance definitions among twins to use a log-Euclidean distance on the associated Lie group of strain tensors. These multivariate tactics may be beneficial for identifying heritable measures in high-dimensional brain images, such as HARDI [5] or diffusion spectrum images.