Abstract
In this paper, we ask whether variation in preference anomalies is related to variation in cognitive ability. Evidence from a new laboratory study of Chilean high-school students with similar schooling backgrounds shows that small-stakes risk aversion and short-run discounting are less common among those with higher standardized test scores. The relationship with test scores survives controls for parental education and wealth. We find some evidence that elementary-school GPA is predictive of preferences measured at the end of high school. Two laboratory interventions provide suggestive evidence of a possible causal impact of cognitive resources on expressed preferences. (JEL: J24, D14, C91)
1. Introduction
High discount rates over short time horizons (Laibson 1997; Strotz 1955) and substantial risk aversion over small-stakes gambles (Rabin 2000; Kahneman and Tversky 1979) are major ‘behavioral’ deviations from neoclassical assumptions about preferences that may help explain a wide range of field behaviors (DellaVigna 2009). The normative benchmark of expected utility theory with exponential time discounting implies that non-negligible discounting over short time horizons and risk aversion over small stakes are mistakes (Rabin 2000; Rabin 2002; Shapiro 2005). We therefore define ‘normative’ choices as perfectly patient, expected-wealth maximization. We ask whether ‘anomalous preferences’, as measured by discounting over short time horizons and risk aversion over small stakes, are related to cognitive ability.
The possibility that higher cognitive ability is correlated with less biased behavior is important for at least two reasons. First, heterogeneity in behavioral biases affects how these biases will ‘aggregate up’ in market outcomes, and may be relevant for targeting public policies designed to mitigate their effects. Second, such evidence is relevant for testing theories that may predict such an association, such as ‘two-systems’ theories of behavior that posit a within-person game between a long-run, patient self and a short-run, impulsive self (e.g., Bernheim and Rangel 2004; Loewenstein and O’Donoghue 2005; Fudenberg and Levine 2006; Brocas and Carrillo 2008).
Our evidence comes from three laboratory studies conducted on students in a Chilean high school during the 2004–2005 and 2005–2006 academic years. Most of the students had been in the same school for their entire schooling careers, allowing us to hold constant many schooling-related factors that might otherwise confound our analysis.
In our first two studies, both conducted with high-school seniors, we measure the cross-sectional relationship between cognitive skills and discounting and risk attitudes. In our first study we find consistent evidence that higher cognitive skills, as proxied by scores on a standardized math test, are associated with less short-run discounting and less small-stakes risk aversion. The coefficients on standardized test scores are economically nontrivial in magnitude. In our second study we find more mixed evidence on risk attitudes, but we continue to find a strong effect on short-run discounting.
As a contrast with choices that are likely to be ‘mistakes’, we also study fair-minded giving in a dictator game, a behavior that is not likely to be a mistake. We do not find evidence of an association between test scores and this behavior.
In both studies, results are robust to controls for proxies for socioeconomic status and family background. A more detailed analysis using siblings to control for family background shows a statistically significant effect on one measure of risk aversion, but the sample is too small to draw sharp conclusions in general.
After presenting our cross-sectional analysis we turn to a discussion of possible causal mechanisms. Evidence from a simple calculation task shows that essentially all participants are capable of performing the arithmetic operations necessary to maximize expected value. This allows us to rule out a purely mechanical correlation due to ability to perform arithmetic operations, though it leaves open the possibility that higherability individuals are more likely to perform these calculations spontaneously. We next consider the possibility that our results—particularly those on time preference—may be due to reverse causality from preferences to skill accumulation. We provide some evidence that ability measured in elementary school predicts short-run time preference measured at the end of high school. This complements prior evidence that self-control ability measured in preschool predicts cognitive skills in adolescence (Mischel, Shoda, and Rodriguez 1989; Shoda, Mischel, and Peake 1990).
Our third study involves two interventions drawn from the social psychology literature, and is intended to experimentally manipulate the cognitive resources available for evaluating choices. These interventions were conducted on a small sample of high-school juniors. The first manipulation involved subjecting participants to a distracting task. The second involved asking them to explain the reasons for their decisions. The cognitive load intervention increases one measure of small-stakes risk aversion and has no statistically detectable effect on other outcomes. The reasoning task decreases both small-stakes risk aversion and short-run discounting, though only the latter effect is statistically significant.
Our findings provide some tentative support for ‘two-system’ theories, which posit a causal relationship between the application of cognitive resources and the expression of behavioral biases. According to these theories, decision-making results from the interaction of a deliberative system, which is patient and risk neutral, and an emotional system, which is impulsive and risk averse (e.g., Bernheim and Rangel 2004; Loewenstein and O’Donoghue 2005; Fudenberg and Levine 2006; Brocas and Carrillo 2008). Since cognitive ability is highly correlated with working memory capacity (Colom et al. 2004; Gray, Chabris, and Braver 2003) and involves overlapping brain regions (Gray and Thompson 2004; Kane and Engle 2002), and since cognitive ability and working memory capacity relate to time discounting through shared neural processes (Shamosh et al. 2008), in evaluating the theory we consider cognitive ability to be an empirical proxy for the long-run player’s cognitive resources. Under that interpretation, the theory predicts that higher cognitive ability will be correlated with greater small-stakes risk aversion, correlated with greater short-term impatience, and uncorrelated with impatience between two delayed rewards, the pattern of results that is most consistent with our evidence. In the concluding section of the paper, we discuss other interpretations of our findings.
This paper was first circulated in 2005, and our working paper is Benjamin, Brown, and Shapiro (2006). There is now a small literature finding results that are consistent with a relationship between higher cognitive ability and less biased risk-taking and time discounting behavior. Contemporaneously with our work, Frederick (2005) finds that performance on a range of cognitive tests correlates negatively with impatience and risk aversion. Dohmen et al. (2010) find these relationships in a large, representative sample. Burks et al. (2009) find the same relationships in a large sample from the lower end of the cognitive ability distribution. Beauchamp, Cesarini, and Johannesson (2011) find that the estimated association between cognitive ability and risk aversion is much stronger once the measurement error in risk aversion has been corrected for. Shamosh and Gray (2008) conduct a literature review and meta-analysis and conclude that higher cognitive ability is associated with less impatience. There is some evidence that the complexity of a choice problem influences expressed risk preferences, suggesting that cognitive limitations may play a role in risk-taking behavior (Huck and Weizsäcker 1999). Brandstätter and Güth (2002) find little evidence for a relationship between cognitive ability and dictator game or ultimatum game choices.1
Our paper is complementary with this published work. That work leaves open the possibility that differences in educational environment could drive cognitive skills, risk-taking, and time discounting behavior. By studying a population with fairly homogeneous schooling experiences, our paper focuses on a relatively narrow population but rules out differences in educational environment as the sole driver of the relationship between cognitive ability and preferences.
Our study of the effects of a cognitive load manipulation relate most closely to the prior work of Hinson, Jameson, and Whitney (2003) and Shiv and Fedorikhin (1999), who find that cognitive load increases impulsive behavior, and the subsequent work of Whitney, Rinehart, and Hinson (2008), who find that cognitive load increases risk aversion.
The remainder of the paper is organized as follows. Section 2 discusses the methods and data for our three laboratory studies. Section 3 presents our main findings from studies 1 and 2. Section 4 discusses evidence on causal mechanisms including the experimental interventions in study 3. Section 5 discusses some alternative interpretations and implications of the results and concludes. The Online Appendix contains robustness checks as well as description and analysis of our pilot experiment with Harvard undergraduate participants.
2. Methods and Data
2.1. Study 1: Chilean High-School Seniors
2.1.1. Participants
Participants were students at a semi-private high school in Santiago, Chile. The participants were the 92 out of 160 members of the senior class (during academic year 2004–2005) who submitted the parental consent forms necessary for participation in the study. Most participants entered the school for kindergarten at age 4 or 5. Some students were admitted because older siblings had attended, but most were admitted on the basis of adequate performance on an entry exam. Most students (more than 80%) had received their entire formal education at the school. Therefore, these participants had had a similar schooling experience. None had received any formal schooling in economics. We held a single, 30-minute experimental session on 24 August 2004, with participants sitting in widely-separated desks in the school gym.
2.1.2. Measured Cognitive Ability
In all of our studies, we measure cognitive ability with standardized test scores and school grades. Existing evidence indicates that elementary-school grades and performance on standardized exams such as the SAT are highly correlated with general cognitive ability (Jensen 1998; Frey and Detterman 2004).
Our standardized test score measure comes from practice exams for the Prueba de Selección Universitaria (PSU). The PSU is a national exam taken at the end of senior year. For many Chilean universities, the PSU score together with GPA are the sole determinants of admission. Because performance on the exam is so important, seniors at this school take monthly practice tests. We obtained five practice test scores (for April through August, 2004) from the school for each participant. We use scores from the Math and Verbal sections. The math section is very much like the SAT I Math Section, while the verbal section covers literary concepts, reading comprehension, logical paragraph organization, and vocabulary.
Our primary measure of cognitive ability for these students is the average of the five practice exam scores, standardized by the sample standard deviation. In cases where one or more exam scores were missing, we used the mean of the nonmissing values. In all, 9 of the 92 students were missing one mathematics score, and one student was missing two mathematics scores. Seven of the 92 students were missing one verbal exam score, and no students were missing more than one verbal score. The students’ mathematics scores range from the 32nd percentile to the 99th percentile of the test-taking population distribution (Universidad de Chile, 2004).2
Because verbal exam scores are less correlated with general cognitive ability than mathematics exam scores (Frey and Detterman 2004), we focus on math scores in our main analysis and present results for verbal scores in the Online Appendix. In the case of study 1, correlations between preferences and ability are generally weaker for verbal scores; in the case of study 2, they are somewhat stronger for verbal scores. The only qualitative difference in findings between the two scores is a sign reversal in the relationship with fairness preferences as measured by dictator-game giving in study 2.
The school also gave us grade point averages for grades 1 through 11 for all students participating in our study for whom such data were available.
2.1.3. Procedures
We wrote a questionnaire in English. The questionnaire was translated into Spanish by a native Spanish speaker and then back-translated into English by a different native Spanish speaker. The back-translated version closely matched the original. We administered the Spanish-language translation, but in the discussion that follows we quote from the original English-language version. We present payment amounts in pesos (and dollar-equivalents at the then-current exchange rate of 632 pesos per dollar in brackets).
After handing out a questionnaire booklet to each participant, an experimenter guided participants through the questionnaire in unison by reading instructions aloud. The questionnaire was divided into sections (with neutral labels such as ‘Choices’ and ‘More Choices’), each of which elicited a type of preference. The questionnaire contained a section that elicited small-stakes risk preferences, followed by a section that elicited short-term time preferences, then a small-stakes risk preferences section that allowed for the possibility of losses, and finally a section that asked a few demographic questions.
To discourage participants from thinking of the preference measures as a test of computation skill, we told participants that “there are no right or wrong answers … Which choice you make is a matter of personal preference.”
Small-Stakes Risk Preference
The section of the questionnaire that elicited risk attitudes comprised exactly five questions of the following form:
Please circle either Choice A or Choice B.
You get 250 pesos [$0.40] for sure.
If the die comes up 1, 2, or 3, you get X. If the die comes up 4, 5, or 6, you get nothing.
where X was 400, 550, 700, 850, and 1,000 pesos [$0.63, $0.87, $1.11, $1.34, and $1.58]. In each case, (A) is the safe bet, and (B) is the risky bet.
To make sure that participants understood the choices they were making, we gave them an example question in the instructions for these sections. We also informed participants that they would answer five questions of the same form. Finally, we gave participants the opportunity to ask any questions about the instructions. There was no stated time limit for answering the questions, but we waited about 6 minutes for all participants to finish before moving on. We then rolled a die five times to determine their payment.
The questionnaire contained all five questions on the same page, with the risk reward X in ascending order. This presentation made salient to participants the strategy of choosing (A) (the safe bet) for small X and (B) (the risky bet) for large X. In fact, 70 out of 92 gave monotonic responses, choosing (A) below some threshold value of X and (B) above it. We use data from all respondents in our main analysis. In the Online Appendix we present results for the subset of respondents whose choices are monotonic. Most point estimates are similar, but estimated effects for risk tend to fall when we restrict to monotonic choices.
Small-Stakes Risk Preference With Possibility of Loss
This section was the same as the small-stakes risk preference section, except that each outcome paid 250 pesos less in this section. That is, option (A) paid 0 pesos, and option (B) gave a 50% chance of losing 250 pesos [$0.40] and a 50% chance of winning X, where X was 150, 300, 450, 600, and 850 pesos [$0.23, $0.47, $0.71, $0.94, and $1.18].
Short-Term Time Preference
We measured discounting with six questions of the form,
Please circle either Choice A or Choice B.
You get 500 pesos [$0.79] right now.
You get X a week from now.
For the six questions, X was 450, 550, 650, 750, 850, and 950 pesos [$0.71, $0.87, $1.03, $1.19, $1.34, and $1.50].
For each question, the participant chose between 500 pesos today and X a week from today. All six questions were on the same page, with the delayed reward X in ascending order. In the instructions for this section, the experimenter gave participants an example question, told them that a die roll would select the question to be implemented, and gave them a chance to ask questions. Participants took about 6 minutes to answer the six questions. The instructions explained that participants would receive cash to pay them for this section. The cash would be paid at lunchtime the next day if the participant had chosen (A) for the relevant question, or at lunchtime in a week if the participant had chosen (B).
We ordered the questions with the delayed reward X in ascending order to make obvious to participants the strategy of choosing (A) (the immediate payoff) for small X and (B) (the delayed payoff) for large X. 87 out of 92 participants chose (A) below some threshold value of X and (B) above it.
Demographics
Participants recorded their age, sex, course of study, and municipality of residence. We measure the income in each participant’s municipality of residence using the 2000 Chilean Census.
2.1.4. Payment
Participants were paid in cash for their choices in the risk-preferences sections, as well as paid a participation fee of 1,250 pesos [$2.00], during lunch break the following day. Participants who chose to be paid “now” in the time-preference section were also paid in cash for that section at the same time. Participants who chose to be paid “a week from now” in the time-preference section were paid in cash during lunch break one week after the experiment.3
To address concerns about the credibility of delayed delivery of payment, at the end of the experiment we asked participants, “Did you believe that you would actually get paid in a week if you chose to take the money in a week?” Of our 92 participants, 90 said they believed they would get paid in a week. Additionally, the two participants who did not believe they would receive the money in a week actually had higher-than-average mathematical ability, suggesting that heterogeneity in trust is not likely to bias our results toward finding that more able individuals are more patient.
2.2. Study 2: Chilean High-School Seniors and Their Siblings
2.2.1. Participants
We returned to the same Chilean high school the year after study 1 to conduct study 2. Participants in study 2 were the 81 out of 103 members of the senior class (during academic year 2005–2006) who turned in parental consent forms. We then identified all siblings of these participants who were also students at the school. 22 out of 27 siblings turned in parental consent forms and participated. For the seniors, we held a single 60-minute session in the school gym on 3 November. We held two sessions for the siblings, on 10 December (14 participants) and 11 December (8 participants).
2.2.2. Measured Cognitive Ability
We obtained eleven PSU practice test scores (for March through November, 2005) from the school for each participant. The school also gave us grade point averages for grades 1 through 11 for all students participating in our study for whom such data were available.
Because we do not have information on practice exam scores for students below their senior year, for our sibling analysis we rely on a student’s average mathematics GPA over her entire tenure in the school as our measure of cognitive ability. This variable has a correlation of 0.8724 (p < 0.0001) with average practice PSU mathematics score among the 21 seniors for whom we have data on siblings, suggesting that it is a reasonable proxy for mathematical ability.
2.2.3. Procedure
The procedure closely paralleled study 1, except that the questionnaire contained more sections and did not contain a risk section with possibility of loss. The questionnaire presented the sections in the following order: small-stakes risk preferences, short-term time preferences, fairness preferences, small-stakes risk preferences with equalized complexity, calculating expected values, and demographics. We distinguish between the two risk preferences sections by referring to the earlier one as ‘safe versus risky options’ and the later one, with equalized complexity, as ‘risky versus risky options’. As in study 1, in addition to what they earned during the study, we paid a participation fee of 1,200 pesos (about $2.35 at the then-exchange rate of 510 pesos/$).
Small-Stakes Risk Preference: Safe versus Risky Options
This section is like the risk preference section from study 1, having choices between option (A) (the safe bet) 250 pesos [$0.49], and option (B) (the risky bet) 0 pesos with probability 50% and X with probability 50%. The only difference is that the values of X differed from those in study 1: 200, 350, 500, 650, and 800 pesos [$0.39, $0.69, $0.98, $1.27, and $1.57] (in ascending order for half the participants, descending for the other half). Out of the 81 participants, 65 chose (A) below some threshold value of X and (B) above it. For each question, a die roll determined the payment for participants who chose option (B).
Small-Stakes Risk Preference: Risky versus Risky Options
This section was the same as the previous small-stakes risk preferences section, except that we replaced the sure thing option (A) of 250 pesos with a low-risk gamble that has the same expected value: “If the die comes up 1, 2, or 3, you get 200 pesos [$0.39]. If the die comes up 4, 5, or 6, you get 300 pesos [$0.59].” Option (B) remained the same. As a result, option (A) is parallel to option (B) in complexity; both make the payoff depend on the outcome of a die roll.
Calculating Expected Values
In this section, we presented participants with five questions of the form,
Please circle whichever number is larger.
250
(X × (1/2)) + (0 × (1/2))
where X took values 200, 350, 500, 650, and 800. These values exactly match those in the risk preference section. Participants were told they would be paid 50 pesos [$0.10] for each correct answer. (Although we included X = 500 in the questionnaire for parallelism, we exclude it from the analysis because there is no correct answer.)
Short-Term Time Preference
We measured time preferences exactly as in study 1. All but one participant made ‘monotonic’ choices, choosing the immediate reward for values of the delayed reward below some threshold and the delayed reward for values above it.
Long-Term Time Preference
This section gave choices between (A) 500 pesos [$0.98] to be received “four weeks from now,” and (B) X to be received “five weeks from now”, where X took the values 450, 550, 650, 750, 850, and 950 pesos [$0.88, $1.08, $1.27, $1.47, $1.67, $1.86]. Hence the payoffs were exactly the same as in the short-term time preference section, except that they all occurred four further weeks in the future. A die roll determined which of the six choices was played out. An experimenter returned to the school four weeks and five weeks after each session to pay the participants for their choices.
Fairness Preferences
While there are arguments for why small-stakes risk aversion (Rabin 2000) and discounting over short time horizons (Rabin 2002; Shapiro 2005) are deviations from normative decision-making, there is no such clear argument for fairness preferences. Hence, we did not have an ex-ante hypothesis regarding the relationship between cognitive ability and fairness preferences. Nonetheless, to compare with risk aversion and discounting, we measured selfish versus fair-minded preferences with an anonymous dictator game. The experimenter informed participants that we had randomly assigned each of them to one other participant at the session, but no one would ever find out who had been assigned to whom. The questionnaire explained that the participant was given a total of 200 pesos and could choose how much to ‘give away’ to the assigned other participant: 0, 50, 100, 150, or 200 pesos (presented to half the participants in ascending order, half in descending order). As is typical in dictator game experiments, a majority of participants (60.5%) chose either to give away nothing (behaving ‘selfishly’) or to give away half of the total (behaving ‘fairly’).
Demographics
As in study 1, we asked participants their age, sex, course of study, and municipality of residence. We also asked each participant to tell us the highest level of schooling completed by her parents, which we translate into the number of years of completed schooling. All but one participant chose to answer these questions. The measures of father’s and mother’s schooling years have correlations of 0.77 (p = 0.0011) and 0.67 (p = 0.0001), respectively, with the average report of the students’ siblings (in cases where the student’s sibling participated in our study), suggesting a reasonable amount of reliability in these measures.
In addition, on the parent permission form, we asked parents several questions to proxy for family background and socioeconomic status. First, we asked the parent to indicate the household’s monthly income in terms of a set of income categories, from which we imputed (at the midpoint of each category) the household’s monthly income in pesos. We standardized this variable to have a mean of zero and a standard deviation of one. Second, we asked the parent to list the year, make, and model of all of the household’s automobiles. We used the Tasación Fiscal de Vehículos,4 a Chilean analogue to the Kelley Blue Book, to estimate the value of each car, from which we computed the household’s total automobile wealth. We requested the list of automobiles because we expected it to generate a higher response rate than direct questions about the household’s financial wealth. When we were unable to estimate the value of an automobile, we imputed its value as the average value of the other automobiles that the household reported. We computed total automobile wealth and standardized this variable to have a mean of zero and a standard deviation of one within the sample.
The parents of 19 participants did not answer the income question. The parents of 20 participants did not provide information on their automobiles. We impute all missing data at the sample mean of the nonmissing observations. In the Online Appendix we show that the results are qualitatively similar, though estimated less precisely, when we exclude observations with missing demographics instead of imputing the missing data.
2.3. Study 3: Chilean High-School Juniors
2.3.1. Participants
We returned to the same Chilean high school the year after study 1 to conduct study 3 (the same year we conducted study 2). Participants in study 3 were the 37 out of 108 members of the junior class (during academic year 2005–2006) who turned in parental consent forms. We held seven sessions in the school gym that lasted between 60 and 75 minutes: 14 December (fifteen participants), 15 December (six participants), 16 December (five participants), 17 December (two participants), 20 December (four participants), 21 December (four participants), and 22 December (one participant).
2.3.2. Measured Cognitive Ability
Because the participants were juniors, they had not taken PSU practice tests. We use grade point averages for grades 1 through 10 provided by the school.
2.3.3. Procedure
The procedure mirrored study 2, except that we added several new sections to the end of the questionnaire (in this order): reasons for small-stakes risk preference, reasons for short-term time preference, and math quiz. Moreover, during half of the sections, participants were put under cognitive load, as described in what follows. In addition to what they earned during the study, we paid a participation fee of 1200 pesos, as before. Here we describe only the sections that are new in study 3.
Reasons for Small-Stakes Risk Preference
In this section, we told participants they would face the same questions they had answered previously (in the small-stakes risk preferences section). The difference was that, in each question, immediately after choosing the safe option (A) or the risky option (B), participants were required to fill in a blank with reasons for why they made their choice. For example, a respondent who chose the safe option of 250 pesos instead of a 50% chance of winning 650 pesos wrote, “It seems safer to me”.
As before, a die roll for each question determined the payoff to choosing the risky option.
Reasons for Short-Term Time Preference
Participants answered the same questions as in the short-term time preference elicitation but were required to give reasons for why they made their choice. For example, a respondent who chose to receive 500 pesos immediately instead of receiving 650 pesos in one week wrote that it was “very little silver to wait one week”. We adapted our reasoning task from Wilson and Schooler’s (1991) study, which finds that such reasoning tasks can inhibit instinctive judgment.
We rolled a die to pick which of the six questions would be carried out.
Math Quiz
We administered to participants two 10-minute, six-question quizzes that contained SAT-like math problems (arithmetic, algebra, geometry, and probability). Participants were told we would pay them 50 pesos [$0.10] for each correct answer. Half of the participants were under cognitive load during one of the math quizzes, and the other half during the other math quiz.
Cognitive Load Manipulation
Requiring participants to remember a string of seven numbers while they are engaged in the task of interest is a common “cognitive load” manipulation in the psychology literature (e.g., Shiv and Fedorikhin 1999; Hinson, Jameson, and Whitney 2003) designed to inhibit working memory. Working memory capacity is strongly correlated with general cognitive ability (Colom et al. 2004; Gray, Chabris, and Braverman 2003).
Although we put half the participants under cognitive load in each section, the instructions for each section had to be identical across participants because an experimenter led them through the experiment in unison. To achieve this, participants were told at the beginning of the experiment that immediately prior to every section, there would be a page in the instruction booklet with “YOUR NUMBERS ARE:” followed by either a sequence of seven numbers or a blank space. Immediately after the section, they would be asked to fill in the blank for the question “WHAT ARE YOUR NUMBERS?” If the participant had seen seven numbers, the correct answer was to recall the sequence in the correct order, and if the participant had seen a blank space, the correct answer was to leave the line blank. To incentivize participants to remember the numbers, participants were paid for their responses in a section only if they correctly answered the “WHAT ARE YOUR NUMBERS?” question for that section. Across all participants and modules, 65% of the digit sequences supplied by participants were correct.
There were four versions of the instruction booklet that differed in which sections cognitive load was applied (i.e., a seven-digit number was shown instead of a blank space). No participant was ever under cognitive load during the two reasons sections of the experiment, but every participant was under cognitive load during four of the other eight sections. Every participant was under cognitive load during exactly one of the two math quiz sections. We counterbalanced the cognitive load manipulation by designing the second and fourth versions of the questionnaire to apply cognitive load during the reverse set of four sections as the first and third versions, respectively. Consequently, while answering each of the sections (except for the two reasons sections), about half of the participants were under cognitive load.5 We implemented a counterbalanced design for two reasons: to minimize confounds from fatigue effects by ensuring that all participants had a similar amount of time under load during the experiment; and to allow us to separate the effect of load from any possible difference in math quiz difficulty.
A few participants failed to answer all of the preference elicitation questions (three did not answer one of the risk questions, and one did not answer one of the discounting questions). We conduct our analysis on the sample who answered all the questions. In the Online Appendix we present evidence using the full sample and making the conservative assumption that missing choices are normative under load and non-normative otherwise. Doing so does not affect the main result we report in what follows for the ‘risky versus risky’ measure because there were no missing choices in that section. For other outcomes, the bounds are meaningfully different from the point estimates we report in what follows.
3. Results
Following Rabin (2000), the normative benchmark of expected utility theory implies that participants should make risk-neutral choices over stakes as small as those in our experiment. A similar argument implies that participants should be patient over the time horizons that we consider (Rabin 2002; Shapiro 2005). Because we are interested in whether cognitive ability predicts behavior that matches normative decision theory, for each type of preference we use as our primary dependent measure the number of “normative” choices, which we define as choices consistent with perfectly patient, expected-wealth maximization.
For each type of preference, we estimate an ordered probit model relating the number of normative choices to one or more measures of cognitive ability. We report model parameters as well as the estimated marginal effect of the variable on the probability that all choices are normative. The marginal effect serves as a useful statistic for evaluating magnitudes.
3.1. Study 1
Table 1 reports results from study 1.
Table 1.
Preferences and cognitive ability: Study 1. Dependent variable: Number of normative (risk neutral, patient) choices.
| Preference type | Risk (gains)
|
Risk (gain/loss)
|
Time preference (now vs. one week)
|
|||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Standardized math score | 0.3059 | 0.3361 | 0.2393 | 0.2486 | 0.2125 | 0.2797 |
| (0.1192) | (0.1330) | (0.1172) | (0.1295) | (0.1147) | (0.1268) | |
| [0.0535] | [0.0585] | [0.0432] | [0.0447] | [0.0703] | [0.0911] | |
| Demographic controls? | X | X | X | |||
| Share making all normative choices | 0.1087 | 0.1087 | 0.1087 | 0.1087 | 0.2826 | 0.2826 |
| Pseudo-R2 | 0.0268 | 0.0282 | 0.0200 | 0.0231 | 0.0120 | 0.0198 |
| N | 92 | 92 | 92 | 92 | 92 | 92 |
Notes: Results are from ordered probit models, with standard errors in parentheses and estimated marginal effect on the probability of all normative choices (evaluated at the sample mean of the independent variables) in brackets. Dependent variable is the number of normative choices made in the given preference elicitation. See Section 2 for details of preference elicitation. Demographic controls are gender and the mean income in the participant’s municipality of residence.
The first set of results in columns (1), (3), and (5) shows the effect of math score with no controls. The second set of results in columns (2), (4), and (6) shows the effect of math score after controlling for gender and mean income in the neighborhood (a crude proxy for socioeconomic status).
In all cases the coefficient on the math score is positive and at least marginally statistically significant. (In the case of time preference, it is statistically significant at the 10% level without controls and at the 5% level with controls.) In all cases the inclusion of controls strengthens the coefficient on the math score.
The magnitude of the estimated coefficient is economically large. In our final models with controls, for risky choices, a one-standard-deviation increase in the math score increases the probability of making fully normative choices by about one-half of the sample mean probability. For time preference, the effect is about one-third of the sample mean.
3.2. Study 2
Table 2 reports results from study 2.
Table 2.
Preferences and cognitive ability: Study 2. Dependent variable: Number of normative (risk neutral, patient, selfish) choices.
| Preference type | Risk (safe vs. risky)
|
Risk (risky vs. risky)
|
Time preference (now vs. one week)
|
Time preference (four vs. five weeks)
|
Selfishness
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
| Standardized math score | 0.1502 | 0.0684 | 0.1656 | 0.1464 | 0.3887 | 0.4059 | 0.1726 | 0.1524 | −0.1298 | −0.1454 |
| (0.1257) | (0.1333) | (0.1297) | (0.1365) | (0.1267) | (0.1323) | (0.1232) | (0.1277) | (0.1228) | (0.1278) | |
| [0.0539] | [0.0224] | [0.0643] | [0.0541] | [0.1074] | [0.1103] | [0.0588] | [0.0511] | [−0.0204] | [−0.0223] | |
| Demographic controls? | X | X | X | X | X | |||||
| Share making all normative choices | 0.3333 | 0.3333 | 0.4321 | 0.4321 | 0.2222 | 0.2222 | 0.2963 | 0.2963 | 0.0864 | 0.0864 |
| Pseudo-R2 | 0.0081 | 0.0841 | 0.0095 | 0.0497 | 0.0428 | 0.0548 | 0.0094 | 0.0206 | 0.0047 | 0.0190 |
| N | 81 | 81 | 81 | 81 | 81 | 81 | 81 | 81 | 81 | 81 |
Notes: Results are from ordered probit models, with standard errors in parentheses and estimated marginal effect on the probability of all normative choices (evaluated at the sample mean of the independent variables) in brackets. Dependent variable is the number of normative choices made in the given preference elicitation. See Section 2 for details of preference elicitation. Demographic controls are gender, father’s years of schooling, mother’s years of schooling, household monthly income, and the total market value of the family’s automobiles.
For each type of preference we report estimates of the effect of math score with and without demographic controls. These demographic controls are much richer than those available in study 1, but their inclusion does not meaningfully affect our coefficients in most cases.
The effect of math score on risk preference is weaker than in study 1, although the coefficients are still positive. We investigated the possibility that this difference, along with the greater share of normative choices in study 2, is due to the small difference in the payoffs we offered, but we find similar results on the subset of choices for which payoffs are most comparable between the two studies.6
The effect on short-run time preference persists in study 2 as in study 1 and remains large in magnitude. Study 2 also allows us to estimate the effect on long-run time preference. Here we find no statistically significant relationship with the math score. Although we cannot distinguish the short-run and long-run effects statistically, this is an intriguing result in light of recent findings that suggest that neural systems associated with working memory capacity may be involved in self-control (Hare, Camerer, and Rangel 2009; see also McClure et al. 2004). In an analysis presented in the Online Appendix, we estimate a statistically insignificant negative relationship between the math score and the number of present-biased choices, defined as behaving patiently when trading off rewards at four and five weeks but impatiently when trading off rewards between the present and one week.
We find a statistically insignificant negative effect of math score on selfishness as expressed in dictator games. As we report in the Online Appendix, however, we find the opposite relationship, which is also statistically insignificant, when we measure cognitive ability using verbal scores instead of math scores. Overall then, we do not find clear evidence of any relationship between cognitive ability and selfishness.
In the Online Appendix we present additional findings using sibling groups to control for family background. The sample size is too small to draw precise conclusions, but in general the point estimates are directionally consistent with those we report here.
3.3. Pooled Estimates
Table 3 presents results using pooled data from studies 1 and 2 on risk preferences and short-run time preferences. (In the case of risk preference, we use as the dependent variable the number of normative choices across our two elicitations.) For each preference we report results with and without demographic controls.
Table 3.
Preferences and cognitive ability: Studies 1 and 2. Dependent variable: Number of normative (risk neutral, patient) choices.
| Preference type | Risk (all)
|
Time preferences (now vs. one week)
|
||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Standardized math score | 0.2805 | 0.2580 | 0.2808 | 0.3273 |
| (0.0816) | (0.0866) | (0.0845) | (0.0899) | |
| [0.0338] | [0.0291] | [0.0864] | [0.0990] | |
| Demographic controls? | X | X | ||
| Share making all normative choices | 0.0751 | 0.0751 | 0.2543 | 0.2543 |
| Pseudo-R2 | 0.0806 | 0.1062 | 0.0223 | 0.0317 |
| N | 173 | 173 | 173 | 173 |
Notes: Results are from ordered probit models, with standard errors in parentheses and estimated marginal effect on the probability of all normative choices (evaluated at the sample mean of the independent variables) in brackets. All models include study fixed effects. Dependent variable is the number of normative choices made in the given category of preference elicitation. Data are from studies 1 and 2. Risk elicitations are: gains (study 1), gain/loss (study 1), safe vs. risky (study 2), risky vs. risky (study 2). Time preference elicitations are now vs. one week, studies 1 and 2. Demographic controls are gender, mean income in the participant’s municipality of residence (study 1) and father’s years of schooling, mother’s years of schooling, household monthly income, and the total market value of the family’s automobiles (study 2). Demographics not available for a given study are imputed at an arbitrary value and ‘dummied out’. See Section 2 for details of preference elicitations.
We find a statistically significant positive relationship between math score and both risk and time preference. The results should be taken with caution as the elicitations differ between studies.
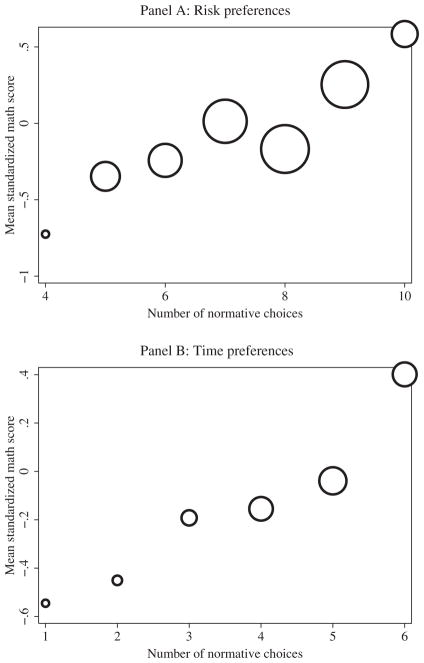
Figure 1 provides a graphical representation of the pooled data. We compute, separately for risk and time preference, the mean math score as a function of the number of normative choices made. The figure shows an upward-sloping relationship for both risk and time preference, consistent with the estimates in Table 3.
Figure 1.
Preferences and cognitive ability: Studies 1 and 2. Each figure shows the mean standardized math score for participants grouped by the number of normative choices made in all preference elicitations in a given category. The area of each marker is proportional to the number of observations in the category. Data are from studies 1 and 2. Risk elicitations are: gains (study 1), gain/loss (study 1), safe vs. risky (study 2), risky vs. risky (study 2). Time preference elicitations are now vs. one week, studies 1 and 2. See Section 2 for details of preference elicitations. [Correction added after publication on 20 November 2013: panel titles were added for clarity.]
4. Evidence on Causal Mechanisms
4.1. Pure Computation
One possible explanation for our results is that every participant tried to make the risk-neutral or patient choice, but that some were unable to perform the computations necessary to determine which option was ‘correct’. On this view, our estimates merely show that one measure of mathematical ability is correlated with another. Several pieces of evidence argue against such an interpretation. First, the computations necessary to make patient choices in the time preference tasks involve only ordinal comparisons (greater than, less than, or equal to), which the students in our sample are clearly capable of making. Of the 81 seniors who participated in study 2, only three chose the ‘dominated’ option of 450 pesos in one week rather than 500 today in the first intertemporal choice questionnaire, and only three made the analogous choice in the second intertemporal choice questionnaire.
The computation of expected values is slightly more cumbersome, so to check whether participants’ inability to calculate expected values drives risk-averse behavior, we also asked each participant to make comparisons that involved calculations equivalent to those necessary to compute the expected values in our risk questionnaires, such as comparing 250 to (200 × (1/2)) + (0 × (1/2)). Only five participants made even one error in the set of five questions of this form. Additionally, only three students chose the stochastically dominated gambles in either of our two risk questionnaires. These facts seem difficult to reconcile with the hypothesis that the students in our sample who made choices inconsistent with patience and risk-neutrality were merely unable to make the necessary calculations. However, these facts leave open the possibility that, even though all participants were able to do the computations, the higher-ability participants were more likely to do them spontaneously when presented with the preference measures.
4.2. Predicting Adolescent Preferences from Elementary-School Cognitive Ability
Existing work has reported that self-control ability measured in preschool predicts cognitive skills in adolescence, as measured by standardized test scores (Mischel, Shoda, and Rodriguez 1989; Shoda, Mischel, and Peake 1990). That finding is sometimes interpreted as indicating that self-control ability is the more fundamental individual attribute and that there is a one-way causal effect of self-control ability on accumulation of cognitive skills. Because elementary-school grades are available to us for those who attended the school in elementary grades, we can investigate whether cognitive ability in childhood, as measured by elementary-school grades, predicts short-run time preference at the end of high school.
Table 4 presents results using as a cognitive ability measure the standardized average math GPA from elementary school for those students whose elementary-school grades are available. We focus on the short-run time preference measure, the time preference measure for which we find a correlation with contemporaneous skill. Our findings are mixed. We find a positive and statistically and economically significant relationship in study 1, and we find a small, barely positive and statistically insignificant relationship in study 2. The confidence interval for study 2 includes the point estimate from study 1. In the Online Appendix, we present results for the full set of preference measures, and we find that the risk preference measures are positively associated with average math GPA from elementary school in study 1, while none of the preference measures are associated with math GPA in study 2.
Table 4.
Time preference and elementary-school performance. Dependent variable: Number of normative (patient) choices.
| Time preference (now vs. one week)
|
||
|---|---|---|
| Study 1 (5) |
Study 2 (6) |
|
| Standardized elementary-school math GPA | 0.2431 | 0.0041 |
| (0.1158) | (0.1276) | |
| [0.0801] | [0.0012] | |
| Share making all normative choices | 0.2824 | 0.2267 |
| Pseudo-R2 | 0.0163 | 0.0000 |
| N | 85 | 75 |
Notes: Results are from ordered probit models, with standard errors in parentheses and estimated marginal effect on the probability of all normative choices (evaluated at the sample mean of the independent variables) in brackets. Dependent variable is the number of normative choices made in the given preference elicitation. See Section 2 for details of preference elicitation. Elementary school is defined as grades 1–6.
It is difficult, if not impossible, to establish the direction of causation between cognitive ability and time preference. Nonetheless, our findings may suggest that the direction of predictability is not uniquely from early-life self-control ability to adolescent cognitive ability, but also from early-life cognitive ability to adolescent time discounting.
4.3. Causal Effects of Cognitive Resources
We conducted two experimental manipulations designed to manipulate the extent to which participants deploy cognitive resources when evaluating their choices.
Table 5 presents the results of our first manipulation in which we subjected participants to cognitive load. As in our other analysis, we use ordered probits to estimate the effect of cognitive load. In the Online Appendix, we present results using Fisher exact p-values, which do not rely on distributional assumptions, and find the same pattern of statistical significance.
Table 5.
The effect of cognitive load: study 3. Dependent variable: Number of normative (risk neutral, patient, selfish, mathematically correct) choices.
| Preference type | Risk (safe vs. risky) (1) |
Risk (risky vs. risky) (2) |
Time preference (now vs. one week) (3) |
Time preference (four vs. five weeks) (4) |
Selfishness (5) |
Math quiz 1 (6) |
Math quiz 2 (7) |
|---|---|---|---|---|---|---|---|
| Cognitive load | −0.3684 | −0.9694 | −0.0364 | 0.1581 | 0.0640 | 0.2930 | −0.3598 |
| (0.3785) | (0.3829) | (0.3543) | (0.3587) | (0.3512) | (0.3523) | (0.3533) | |
| [−0.1035] | [−0.3285] | [−0.0108] | [0.0567] | [0.0070] | [0.0540] | [−0.1171] | |
| Share making all normative choices | 0.2059 | 0.3784 | 0.2222 | 0.3243 | 0.0541 | 0.1081 | 0.2703 |
| Pseudo-R2 | 0.0102 | 0.0736 | 0.0001 | 0.0021 | 0.0003 | 0.0062 | 0.0083 |
| N | 34 | 37 | 36 | 37 | 37 | 37 | 37 |
Notes: Results are from ordered probit models, with standard errors in parentheses and estimated marginal effect on the probability of all normative choices (evaluated at the sample mean of the independent variables) in brackets. Dependent variable is the number of normative choices made in the given preference elicitation. See Section 2 for details of preference elicitation and math quizzes.
For both risk preferences the point estimates indicate that cognitive load reduces normative behavior. In the case of comparisons of risky gambles, the effect is statistically significant, and in both cases the point estimates are economically large. Cognitive load slightly increases non-normative behavior in short-run time preference, though the effect is not statistically significant. There is a statistically insignificant effect on long-term time preference that does not have the expected sign. Cognitive load slightly (and statistically insignificantly) increases selfish behavior.
Importantly, we find no consistent evidence that cognitive load reduces performance on the math quizzes that we administered. Because it seems very likely that the quiz required cognitive resources (there was significant heterogeneity in performance), we take this finding to indicate that we do not have much power to detect effects of cognitive load, and therefore our cognitive load findings should be interpreted cautiously.
In the Online Appendix we present evidence on the interaction between the effect of cognitive load and baseline cognitive ability, as measured by high-school math GPA. We find no consistent evidence of such an interaction, although in the case of the second math quiz, we find some evidence that the effect of cognitive load is greater for those with greater cognitive ability.
Table 6 presents the results of our reasoning task. For each type of preference we present the mean number of normative choices at baseline and in the reasoning task. We restrict attention to those not under cognitive load at baseline. We present p-values from a within-subject Wilcoxon signed-rank test.
Table 6.
The effect of explicit reasoning: study 3. Dependent variable: Number of normative (risk neutral, patient) choices.
| Preference type | Risk (safe vs. risky) (1) |
Time preference (now vs. one week) (2) |
|---|---|---|
| Mean at Baseline | 3.7692 | 4.2500 |
| Mean in reasoning task | 4.1538 | 5.0500 |
| No. of observations | 13 | 20 |
| Wilcoxon sign-rank p-value | 0.2043 | 0.0063 |
Notes: Reasoning task indicates that the participant was asked to think about and express the reasons for her choice. Dependent variable is the number of normative choices made in the given preference elicitation. See Section 2 for details of preference elicitation. Sample consists of participants who were not under cognitive load at baseline.
Reasoning caused a statistically insignificant increase in the number of risk-neutral choices and a statistically significant increase in the number of patient choices. In the Online Appendix we present some suggestive evidence that the effect of the reasoning manipulation is weaker for individuals with higher cognitive ability.
Our samples are too small to draw firm conclusions, but they suggest that the application of cognitive resources may causally impact discounting and risk attitudes. This hypothesis fits naturally with ‘two-system’ models of individual decision making (e.g., Bernheim and Rangel 2004; Loewenstein and O’Donoghue 2005; Fudenberg and Levine 2006; Brocas and Carrillo 2008). These models treat decision making as a result of a strategic interplay between an impulsive, myopic player and a rational, forward-looking player who can reduce the influence of the impulsive player only by drawing down a limited budget of cognitive resources.
5. Conclusions
In a series of laboratory studies of high-school students we find that short-term discounting and small-stakes risk aversion are more prevalent among students with lower measured cognitive ability. To the extent that measured cognitive ability can be taken as a proxy for available cognitive resources, our findings are consistent with ‘two-system’ theories that posit that these preference anomalies result from a conflict between a patient, deliberative long-run self and an impulsive short-run self. Evidence from experimental interventions designed to manipulate the application of cognitive resources to decision making also appears consistent with such models, though our samples are too small to permit strong conclusions.
While we have emphasized the consistency of our findings with ‘two-system’ models, there are other possible explanations for our results as well. For example, individuals with greater measured cognitive ability may be more likely to ‘broadly bracket’ their choices, assessing the consequences of the lab choices in the context of broader lifetime decisions (Rabin and Weizsacker 2009). Such recognition that the experimental choices are a small piece of a much longer stream of related choices would generate more patient and risk-neutral behavior (Read, Loewenstein, and Rabin 1999; Barberis, Huang, and Thaler 2006).
Because our laboratory preference measures are based on stylized, quantitative frames that do not closely reflect the framing of market decisions, a potential concern is that our findings may not generalize to market decisions. For example, a possible explanation for the correlation between cognitive ability and time-preference measures based on monetary tradeoffs is that higher-ability individuals are more likely to recognize that money earned in the experiment is fungible with money earned outside the experiment. Participants who understand this fungibility will behave more patiently (Frederick, Loewenstein, and O’Donoghue 2002). If this explains our findings, then the association between cognitive ability and patient behavior would extend to field behaviors involving monetary tradeoffs but not other intertemporal choices.
However, an emerging literature suggests that there is a correlation between cognitive ability and market behaviors related to time and risk preference. Our working paper, Benjamin, Brown, and Shapiro (2006), reports evidence from the National Longitudinal Survey of Youth (NLSY) that individuals who score higher on the AFQT, a commonly used measure of cognitive ability, exhibit higher rates of financial market participation and asset accumulation and lower rates of obesity and smoking. A growing body of work documents a relationship between cognitive ability and portfolio allocations and wealth accumulation (e.g., Kézdi and Willis, 2003; Banks and Oldfield 2007; Christelis, Jappelli, and Padula 2010).
These findings suggest that market outcomes (e.g., aggregate savings) that depend more on the behaviors of the highly skilled will tend to be less sensitive to short-run time preference and small-scale risk preference than outcomes (e.g., payday loan borrowing) that depend more on the behaviors of the less skilled. This, in turn, may suggest that policymakers target some interventions toward lower-ability individuals. Indeed, Gaurav, Cole, and Tobacman (2011) find that lower-ability individuals are more responsive to interventions designed to encourage take-up of rainfall insurance in India.
We note, however, that biases in preference and judgment have been documented even among very skilled individuals. For example, in our pilot study of Harvard undergraduates (described in the Online Appendix to this paper), only 36% of those scoring a perfect 800 on the Math SAT are risk-neutral, and only 67% are perfectly patient.
Supplementary Material
Acknowledgments
A previous version of this paper circulated under the title “Does Cognitive Ability Reduce Psychological Bias?” We are grateful to the editor, three anonymous referees, Nick Barberis, Gary Becker, Colin Camerer, Andrew Caplin, David Cesarini, Chris Chabris, Keith Chen, Judy Chevalier, Steve Cicala, Stefano DellaVigna, Erik Eyster, Ray Fair, Shane Frederick, Ezra Friedman, Sean Gailmard, Dan Gilbert, Ed Glaeser, Josh Gottlieb, Dean Karlan, Lisa Kahn, Emir Kamenica, Shachar Kariv, Larry Katz, Miles Kimball, Botond Köszegi, David Laibson, Dan Levin, Steve Levitt, John List, Barry Nalebuff, Emily Oster, Sharon Oster, Matthew Rabin, Al Roth, Andrei Shleifer, Richard Thaler, Jeremy Tobacman, Georg Weizsäcker, Leeat Yariv, Richard Zeckhauser and seminar participants at Harvard University, UC Berkeley, Yale University, the ENABLE European Symposium on Behavioral Economics, Harvard Business School, the University of Michigan, Dartmouth College, and the People and Money Conference at the Driehaus Center for Behavioral Finance for helpful comments. We thank the Russell Sage Foundation Small Grants Program, the Harvard University Economics Department, the Chiles Foundation, the National Science Foundation, the Institute for Humane Studies, and the Institute for Quantitative Social Science. Benjamin acknowledges financial assistance from the Program on Negotiation, Center for Justice, Welfare, and Economics, and the National Institute on Aging, through Grant Number T32-AG00186 to the NBER. We are grateful to Felipe Brown, Nicolás Brown, Julia Goorin, Shih En Lu, Dina Mishra, and David Sokoler for outstanding research assistance. Benjamin and Shapiro are Research Associates at the NBER.
Footnotes
The finding that cognitive ability is correlated with some measured preferences (and associated behavioral outcomes) also relates to a large and wide-ranging literature in cognitive science on the correlates of cognitive ability (see Jensen 1998, for a review). Most pertinently, Stanovich (1999) and Stanovich and West (1998) find that individuals with greater cognitive skills display fewer biases in judgment and decision making (such as the sunk-cost fallacy, gain–loss framing, and the conjunction fallacy) in hypothetical choice scenarios. Recently in the economics literature, studies find that individuals with greater cognitive skills are less likely to exhibit the winner’s curse (Casari, Ham, and Kagel 2007), conservatism in updating probabilities and overconfidence (Oechssler, Roider, and Schmitz 2009; Hoppe and Kusterer 2011), and anchoring bias (Bergman et al. 2010).
Among all seniors enrolled in nonvocational schools, 31.5% take the PSU exam (see www.demre.cl/estadisticas.htm).
Participants were told that if they missed school on the payment day, their homeroom teacher would hold their payment envelope until they came to school. Two participants who chose the immediate reward were absent in school the next day and received their payment the following day. All participants who chose the delayed reward were present in school when they were paid the next week.
Due to an error by the local Kinko’s, a page was omitted from some of the copies of two of our questionnaire versions. Consequently, there was a slight imbalance in the number of each version we used, resulting in a slightly uneven number of participants in the different cognitive load conditions.
In study 1, across the five questions, the risky option has a 50% chance of paying 400, 550, 700, 850, and 1,000 pesos. In study 2, these payoffs are 200, 350, 500, 650, and 800 pesos. If we drop the 1,000-peso question in study 1 and the 200-peso question in study 2, then the remaining four questions have a similar range of payoffs in the two studies. When we analyze the data after dropping these questions, the results look similar to those we report.
Additional Supporting Information may be found in the online version of this article at the publisher’s website:
Online Appendix: Code and Data for Replication
Contributor Information
Daniel J. Benjamin, Cornell University
Sebastian A. Brown, Barclays Capital
Jesse M. Shapiro, University of Chicago, Booth School of Business
References
- Banks James, Oldfield Zoë. Understanding Pensions: Cognitive Function, Numerical Ability and Retirement Saving. Fiscal Studies. 2007;28:143–170. [Google Scholar]
- Barberis Nicholas, Huang Ming, Thaler Richard. Individual Preferences, Monetary Gambles, and Stock Market Participation: A Case for Narrow Framing. American Economic Review. 2006;96:1069–1090. [Google Scholar]
- Beauchamp Jonathan P, Cesarini David, Johannesson Magnus. Working paper. Harvard University; 2001. The Psychometric Properties of Measures of Economic Risk Preferences. [Google Scholar]
- Benjamin Daniel J, Brown Sebastian A, Shapiro Jesse M. Who is ‘Behavioral’? Cognitive Ability and Anomalous Preferences. 2006 doi: 10.1111/jeea.12055. Available at SSRN: http://ssrn.com/abstract=675264. [DOI] [PMC free article] [PubMed]
- Bergman Oscar, Ellingsen Tore, Johannesson Magnus, Svensson Cicek. Anchoring and Cognitive Ability. Economic Letters. 2010;107:66–68. [Google Scholar]
- Bernheim B Douglas, Rangel Antonio. Addiction and Cue-triggered Decision Processes. American Economic Review. 2004;94:1558–1590. doi: 10.1257/0002828043052222. [DOI] [PubMed] [Google Scholar]
- Brandstätter Hermann, Güth Werner. Personality in Dictator and Ultimatum Games. Central European Journal of Operations Research. 2002;10:191–215. [Google Scholar]
- Brocas Isabelle, Carrillo Juan D. The Brain as a Hierarchical Organization. American Economic Review. 2008;98:1312–1346. [Google Scholar]
- Burks Stephen V, Carpenter Jeffrey P, Goette Lorenz, Rustichini Aldo. Cognitive Skills Affect Economic Preferences, Strategic Behavior, and Job Attachment. PNAS. 2009;106:7745–7750. doi: 10.1073/pnas.0812360106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casari Marco, Ham John C, Kagel John H. Selection Bias, Demographic Effects, and Ability Effects in Common Value Auction Experiments. American Economic Review. 2007;97:1278–1304. [Google Scholar]
- Christelis Dimitris, Jappelli Tullio, Padula Mario. Cognitive Abilities and Portfolio Choice. European Economic Review. 2010;54:18–38. [Google Scholar]
- Colom Roberto, Rebollo Irene, Palacios Antonio, Juan-Espinosa Manuel, Kyllonen Patrick C. Working Memory is (Almost) Perfectly Predicted by g. Intelligence. 2004;32:277–296. [Google Scholar]
- DellaVigna Stefano. Psychology and Economics: Evidence from the Field. Journal of Economic Literature. 2009;47:315–372. [Google Scholar]
- Dohmen Thomas, Falk Armin, Huffman David, Sunde Uwe. Are Risk Aversion and Impatience Related to Cognitive Ability? American Economic Review. 2010;100:1238–1260. [Google Scholar]
- Frederick Shane. On the Ball: Cognitive Reflection and Decision-making. Journal of Economic Perspectives. 2005;19:25–42. [Google Scholar]
- Frederick Shane, Loewenstein George, O’Donoghue Ted. Time Discounting and Time Preference: A Critical Review. Journal of Economic Literature. 2002;40:351–401. [Google Scholar]
- Frey Meredith C, Detterman Douglas K. Scholastic Assessment or g? The Relationship Between the Scholastic Assessment Test and General Cognitive Ability. Psychological Science. 2004;15:373–378. doi: 10.1111/j.0956-7976.2004.00687.x. [DOI] [PubMed] [Google Scholar]
- Fudenberg Drew, Levine David K. A Dual-self Model of Impulse Control. American Economic Review. 2006;96:1449–1476. doi: 10.1257/aer.96.5.1449. [DOI] [PubMed] [Google Scholar]
- Gaurav Sarthik, Cole Shawn, Tobacman Jeremy. Marketing Complex Financial Products in Emerging Markets: Evidence from Rainfall Insurance in India. Journal of Marketing Research. 2011;48:S150–S162. [Google Scholar]
- Gray Jeremy R, Chabris Christopher F, Braver Todd S. Neural Mechanisms of General Fluid Intelligence. Nature Neuroscience. 2003;6:316–322. doi: 10.1038/nn1014. [DOI] [PubMed] [Google Scholar]
- Gray Jeremy R, Thompson Paul M. Neurobiology of Intelligence: Science and Ethics. Nature Reviews Neuroscience. 2004;5:471–482. doi: 10.1038/nrn1405. [DOI] [PubMed] [Google Scholar]
- Hare Todd A, Camerer Colin F, Rangel Antonio. Self-control in Decision-making Involves Modulation of the vmPFC Valuation System. Science. 2009;324:646–648. doi: 10.1126/science.1168450. [DOI] [PubMed] [Google Scholar]
- Hinson JM, Jameson TJ, Whitney P. Impulsive Decision Making and Working Memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:298–306. doi: 10.1037/0278-7393.29.2.298. [DOI] [PubMed] [Google Scholar]
- Hoppe Eva I, Kusterer David J. Behavioral Biases and Cognitive Reflection. Economic Letters. 2011;110:97–100. [Google Scholar]
- Huck Steffen, Weizsäcker Georg. Risk, Complexity, and Deviations from Expected-value Maximization: Results of a Lottery Choice Experiment. Journal of Economic Psychology. 1999;20:699–715. [Google Scholar]
- Jensen Arthur R. The g factor: The Science of Mental Ability. Praeger; Westport, CT: 1998. [Google Scholar]
- Kane Michael J, Engle Randall W. The Role of Prefrontal Cortex in Working-memory Capacity, Executive Attention, and General Fluid Intelligence: An Individual-Differences Perspective. Psychonomic Bulletin and Review. 2002;9:637–671. doi: 10.3758/bf03196323. [DOI] [PubMed] [Google Scholar]
- Kahneman Daniel, Tversky Amos. Prospect Theory: An Analysis of Decision Under Risk. Econometrica. 1979;47:263–291. [Google Scholar]
- Kézdi Gábor, Willis Robert J. Working paper. University of Michigan; 2003. Who Becomes a Stockholder? Expectations, Subjective Uncertainty, and Asset Allocation. [Google Scholar]
- Laibson David. Golden Eggs and Hyperbolic Discounting. Quarterly Journal of Economics. 1997;112:443–477. [Google Scholar]
- Loewenstein George, O’Donoghue Ted. Working paper. Cornell University; 2005. Animal Spirits: Affective and Deliberative Processes in Economic Behavior. [Google Scholar]
- McClure Samuel M, Laibson David I, Loewenstein George, Cohen Jonathan D. Separate Neural Systems Value Immediate and Delayed Monetary Rewards. Science. 2004;306:503–507. doi: 10.1126/science.1100907. [DOI] [PubMed] [Google Scholar]
- Mischel Walter, Shoda Yuishi, Rodriguez Monica L. Delay of Gratification in Children. Science. 1989;244:933–938. doi: 10.1126/science.2658056. [DOI] [PubMed] [Google Scholar]
- Oechssler Jôrg, Roider Andreas, Schmitz Patrick W. Cognitive Abilities and Behavioral Biases. Journal of Economic Behavior and Organization. 2009;72:147–152. [Google Scholar]
- Rabin Matthew. Risk Aversion and Expected-Utility Theory: A Calibration Theorem. Econometrica. 2000;68:1281–1292. [Google Scholar]
- Rabin Matthew. A Perspective on Psychology and Economics. European Economic Review. 2002;46:657–685. [Google Scholar]
- Rabin Matthew, Weizsacker Georg. Narrow Bracketing and Dominated Choices. American Economic Review. 2009;99:1508–1543. [Google Scholar]
- Read Daniel, Loewenstein George, Rabin Matthew. Choice Bracketing. Journal of Risk and Uncertainty. 1999;19:171–197. [Google Scholar]
- Shamosh Noah A, DeYoung Colin G, Green Adam E, Reis Deidre L, Johnson Matthew R, Conway Andrew RA, Engle Randall W, Braver Todd S, Gray Jeremy R. Individual Differences in Delay Discounting: Relation to Intelligence, Working Memory, and Anterior Prefrontal Cortex. Psychological Science. 2008;19:904–911. doi: 10.1111/j.1467-9280.2008.02175.x. [DOI] [PubMed] [Google Scholar]
- Shamosh Noah A, Gray Jeremy R. Delay Discounting and Intelligence: A Meta-analysis. Intelligence. 2008;36:289–305. [Google Scholar]
- Shapiro Jesse M. Is There a Daily Discount Rate? Evidence from the Food Stamp Nutrition Cycle. Journal of Public Economics. 2005;89:303–325. [Google Scholar]
- Shiv Baba, Fedorikhin Alexander. Heart and Mind in Conflict: The Interplay of Affect and Cognition in Consumer Decision Making. Journal of Consumer Research. 1999;26:278–292. [Google Scholar]
- Shoda Yuichi, Mischel Walter, Peake Philip K. Predicting Adolescent Cognitive and Self-regulatory Competencies from Preschool Delay of Gratification: Identifying Diagnostic Conditions. Developmental Psychology. 1990;26:978–986. [Google Scholar]
- Stanovich Keith E. Who is Rational? Studies of Individual Differences in Reasoning. Lawrence Erlbaum Associates; 1999. [Google Scholar]
- Stanovich Keith E, West Richard F. Individual Differences in Rational Thought. Journal of Experimental Psychology: General. 1998;127:161–188. [Google Scholar]
- Strotz RH. Myopia and Inconsistency in Dynamic Utility Maximization. Review of Economic Studies. 1955;23:165–180. [Google Scholar]
- Universidad de Chile. Compendio Estadìstico: Proceso de Admisiûn. Vicerrectora de Asuntos Acadèmicos, Departamento de Evaluaciûn, Medicina y Registro Educacional; Santiago, Chile: 2004. [Google Scholar]
- Whitney Paul, Rinehart Christa A, Hinson John M. Framing Effects Under Cognitive Load: The Role of Working Memory in Risky Decisions. Psychonomic Bulletin and Review. 2008;15:1179–1184. doi: 10.3758/PBR.15.6.1179. [DOI] [PubMed] [Google Scholar]
- Wilson Timothy D, Schooler Jonathan W. Thinking Too Much: Introspection can Reduce the Quality of Preferences and Decisions. Journal of Personality and Social Psychology. 1991;60:181–192. doi: 10.1037//0022-3514.60.2.181. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.