Abstract
Fluid registration is widely used in medical imaging to track anatomical changes, to correct image distortions, and to integrate multi-modality data. Fluid mappings guarantee that the template image deforms smoothly into the target, without tearing or folding, even when large deformations are required for accurate matching.
Here we implemented an intensity-based fluid registration algorithm,7 accelerated by using a filter designed by Bro-Nielsen and Gramkow.3 We validated the algorithm on 2D and 3D geometric phantoms using the mean square difference between the final registered image and target as a measure of the accuracy of the registration. In tests on phantom images with different levels of overlap, varying amounts of Gaussian noise, and different intensity gradients, the fluid method outperformed a more commonly used elastic registration method, both in terms of accuracy and in avoiding topological errors during deformation. We also studied the effect of varying the viscosity coefficients in the viscous fluid equation, to optimize registration accuracy. Finally, we applied the fluid registration algorithm to a dataset of 2D binary corpus callosum images and 3D volumetric brain MRIs from 14 healthy individuals to assess its accuracy and robustness.
Keywords: structural MRI, registration, brain imaging
1. INTRODUCTION
Non-linear registration involves the matching of a template image T to a study S, typically by applying a deformation vector field to T so that its features are geometrically aligned with those in S. Its numerous applications in medical image analysis include the alignment of images from different subjects, time-points and modalities, and the study of deformations to understand morphometric differences, such as brain development or degeneration.
To register a pair of 2D or 3D images, a displacement vector field is found such that corresponds with . Here denotes the voxel location. Anatomical correspondence between the images is found based on features such as common anatomical landmarks between the two image datasets, or, more commonly, from intensity-based cost functions such as the mean square intensity difference between images, cross-correlation, or information-theoretic measures such as normalized mutual information or the Jensen-Rényi divergence.5
In the commonly used elastic registration,8 the image is treated as an elastic medium. A force is applied at each voxel that drives the template image towards increased anatomical similarity to the study image, against the restoring forces of the medium. The deformation fields are generated by the elastic registration equation:
| (1) |
Here is the image-derived force that drives the transformation, and µ and λ are the Lamé coefficients. This method works well for small deformations. However, as distances increase between the initial and final images, so do the restoring forces, so that large deformations can not be generated without shearing or tearing of the image medium.
For viscous fluid registration, a continuum mechanical law is again applied to the registration. In this case the image is treated as a viscous fluid and the velocity field is computed at each time step along the path to obtain the final deformation field, using the Navier-Stokes equation for v that was derived by Christensen7 as
| (2) |
This equation is solved using sliding boundary conditions.6 The Lamé coefficients µ and λ are chosen by the user. The force field F is the gradient of the cost function, selected here as the mean square difference between the registered template and study intensities, that is
| (3) |
In both the fluid and elastic cases, the mechanical equations regularize the deformation, enforcing the smoothness of the mapping. Though the elastic regularization breaks down at large distances, the fluid registration generates smooth maps even for large deformations.
Other velocity-based approaches exist such as the Large Deformation Diffeomorphic Metric Mapping10 and symmetric normalization,2 for which the full path between images is optimized to generate the deformation. In,4 the viscous fluid regularizer was replaced by a Log-Euclidean1 regularizer which is sensitive to local directional or anisotropic deformations of the image.
Computational speed is an issue in finding a numerical solution of the viscous equation, as the local velocity depends on the force field over the entire volume. A filter solution to this equation based on the Green’s function solution of the fluid equation was originally derived by Bro-Nielsen and Gramkow,3 and significantly decreases computational time.
Here, sets of 2D and 3D phantom images with varying shapes, levels of Gaussian noise, intensity gradients and overlap were created in order to assess the validity and robustness of the viscous fluid algorithm, and optimize its free parameters. We also compared its performance to that of the more commonly used elastic registration method. To assess the algorithm’s ability to recover morphometric differences in real data, we also tested our algorithm on a 3D MRI dataset from 14 healthy individuals. To examine the 2D case, we used binary corpus callosum images, while whole-brain volumetric MRIs were used for the 3D experiments.
2. METHOD
The viscous fluid registration algorithm was implemented using a multi-resolution scheme.9 The free parameters of the algorithm are the Lamé coefficients µ and λ, as well as the number of iterations at each resolution, the time step and filter size. These parameters were set for each registration problem in order to optimize the final result.
2D disk and C-shaped phantoms and 3D rectangular phantoms were created under various conditions of Gaussian noise, overlap and intensities (see Figures 2 to 6). To test the algorithm on 2D and 3D brain MRI data, we used a group of 14 healthy controls who received 3D spoiled gradient recovery (SPGR) anatomical brain MRI scans (256×256×124 matrix, TR = 25 ms, TE = 5ms; 24-cm field of view; 1.5-mm slices, zero gap; flip angle = 40°). Extracerebral tissues (e.g., scalp, meninges, brainstem and cerebellum) were removed using the software BrainSuite.11 The corpus callosum for each subject was hand-traced according to previously published criteria,12 using interactive segmentation software.
Figure 2.
The moving image is a disk and the fixed image is a C with added Gaussian noise of different standard deviations σ (from top to bottom: σ = 0.05, 0.1, 0.2, 0.3, 0.5). The central column shows the registered images and the difference images are shown in the right column. Initial MSD values from top to bottom are: 2204.2, 2175.8, 2137.9, 2081.6, 1981.6. Final ones are: 469.9, 980.0, 1890.7, 2762.2, 4481.4; registration performance only degrades substantially with high amplitude additive noise.
Figure 6.
This figure shows the results of viscous fluid registration applied to 3D binary phantoms (64x64x64) with levels of intensities varying from 0 to 255, and µ = 0.1, λ = 0.7. The columns correspond to x, y and z slices, respectively. The moving image consisted of a cubic shown in the first row (x slice, y slice and z slice). The fixed image is shown in the second row and the registered image is shown in the third row. The 4th row shows the difference image of the fixed image and the moving image. The 5th row is the difference image of the registered image and the fixed image.
Here throughout we use the mean square difference (MSD) as a measure of the residual registration error between the registered template and target image intensities:
| (4) |
3. RESULTS
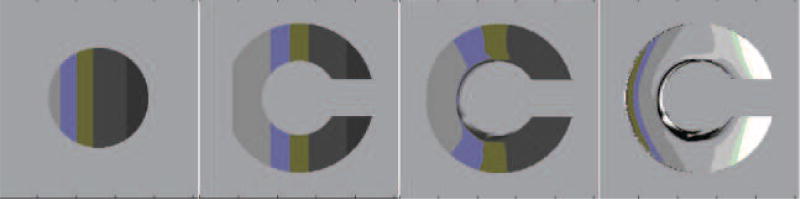
In Figure 1, we show the result of using the viscous fluid code compared to the more commonly used elastic registration method for 2D phantoms. Since the two phantoms differ greatly in shape, we expect the elastic registration to be unable to produce the required deformation. As expected, the elastic registration fails completely in this example. By contrast, the fluid registration performs quite well. This is because the elastic regularizer penalizes large displacements, while the fluid regularizer only penalizes the gradients of the velocity field, so that arbitrarily large displacements can be recovered. This suggests that the latter method should be used whenever large anatomical differences are expected.
Figure 1.
Top left: the moving image. Top right: the fixed image. Bottom left: registered image using the viscous fluid transformation model with viscosity coefficients µ = 1.7, λ = 0.1. Bottom right: registered image using the elastic model, which performs much worse than the fluid model in matching the target image.
We also examined how adding Gaussian noise to one of the images affects registration performance, for values of the noise variance σ ranging from 0.05 to 0.5 (see Figure 2). The noise only significantly affects registration quality for the highest value of σ = 0.5. This is reasonable because the force driving the registration depends on spatial gradients in the image, and the magnitude and direction of these gradients is stable unless the noise is relatively high.
Figure 3 shows the results of varying the level of overlap between the initial images. The code performs well, even when the initial overlap is as small as 10%, though it becomes much worse when the images do not overlap at all.
Figure 3.
2D registration of objects with different level of overlap. Column 1 through 4 show the moving images, fixed images, registered images and difference images, respectively. Levels of overlap from top to bottom are taken at 10% intervals from 90% to 10%. The initial MSDs are, from top to bottom: 2613, 2413.72279.7, 2315.3, 2323.2, and the final ones are: 2585.7, 1307.4, 246.9, 96.0, 36.4.
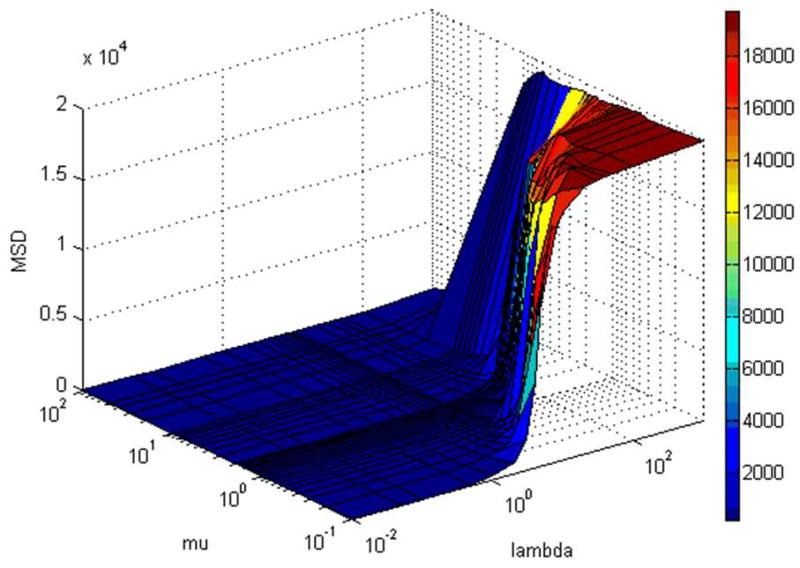
In Figure 4, we varied the viscosity coefficients λ and µ in the fluid equation. The fluid viscosity increases with µ and λ, and it becomes increasingly hard for the the forces to drive the flow. The MSD increases dramatically for large viscosity coeffcients. However, for the lower values of the viscosity coefficients, registration quality varies little with the choice of these parameters over a wide range. Thus, the registration is not very sensitive to the particular choice of λ and µ, so long as these values are not set too high.
Figure 4.
Values of image dissimilarity (MSD), after registration of C to O, as a function of the viscosity coefficients λ (0.01, 0.05, 0.1, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 100, 1000) and µ (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 20.0, 30.0, 40.0, 50.0, 100.0).
Figure 5 and 6 show the results of varying the level of intensity between the initial images on 2D and 3D phantoms. Though the overall shape is preserved, the final MSD is much higher than for the binary images, and there is quite a bit of distortion in the intensity distribution in the registered images.
Figure 5.
Registration using different phantoms with gradations (0 to 255) in intensity. The moving image consisted of a circle (leftmost image) and the fixed image consisted of a C (second image to the left). The third image is the result of deforming the circle into the C with the viscosity coefficient λ = 0.1; µ = 1.7 and the value of image dis-similarity between the registered image and the fixed image is 156.6 using MSD. Next is the difference image between the registered and fixed images.
Examples of registration on a pair of 2D corpus callosum images and volumetric 3D whole-brain images are shown in Figures 7 and 8. For both the 2D and 3D examples, the registered image is in good agreement with the target image.
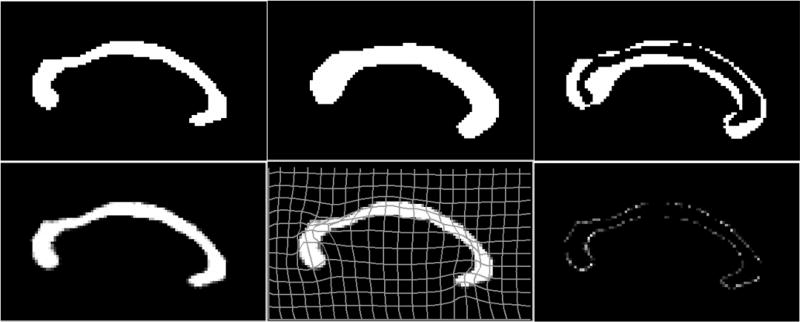
Figure 7.
2D registration of binary traces of the corpus callosum, a midline structure in the brain: Top left: Fixed image. Top middle: Moving image, from a different subject. Top right: Difference image before registration. Bottom left: Registered image. Bottom middle: Deformation grid. Bottom middle: Difference image after registration.
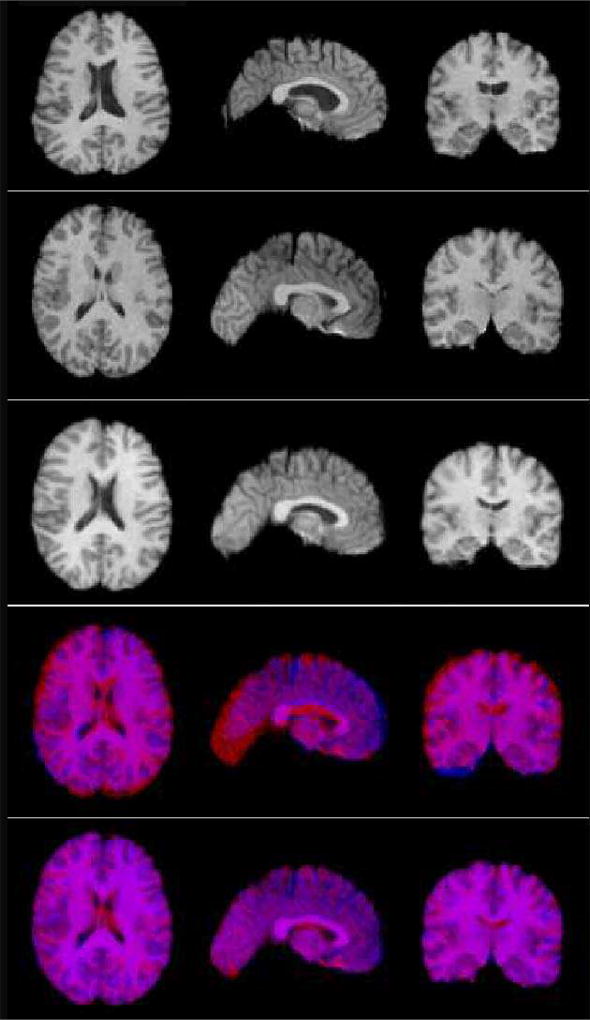
Figure 8.
3D registration of pairs of brain MRIs from several randomly selected control subjects. Images were downsampled by a factor of 2 along each axis, to a resolution of 128x128x128. Parameters for the code were λ = 1, µ = 1, and the filter size was D = 30, with 30 iterations. From top to bottom: moving image, fixed image, registered image, overlap (red: fixed image, blue: moving image), overlap (red: fixed image, blue: registered image).
4. CONCLUSIONS
Here we studied the performance of a viscous fluid registration algorithm on different types of geometric phantoms in 2D and 3D, and on medical data from 2D binarized corpus callosum images and 3D brain MRIs. The fluid algorithm performs well for all levels of noise and overlap tested, as well as for images with varying intensities. We also showed that registration performance was stable for a wide range of choices of the viscosity coefficients. For phantoms of widely different shapes, as in the C to disk example, we obtained a reasonable agreement from the fluid registration, while the elastic registration failed completely. The registration was also shown to be relatively independent of the Lamé coefficients for a wide range of values of these parameters.
The performance of the viscous fluid algorithm may depend on the cost function used to drive the registration. In a future study, it would be interesting to compare differences in performance from various cost functions such as the Jensen-Rényi divergence5 using the different tests presented here. Furthermore, the viscous registration algorithm described here is not sensitive to the directionality of the deformation. It would be interesting to compare its performance to the registration from algorithms such as the one described in Brun et al. (2007),4 where the regularization was done in the Log-Euclidean space to account for anisotropic deformations.
References
- 1.Arsigny V, Fillard P, Pennec X, Ayache N. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magnetic Resonance in Medicine. 2006;56:411–421. doi: 10.1002/mrm.20965. [DOI] [PubMed] [Google Scholar]
- 2.Avants B, Gee JC. Geodesic estimation for large deformation anatomical shape averaging and interpolation. Neuroimage. 2004;23(Suppl 1):139–150. doi: 10.1016/j.neuroimage.2004.07.010. [DOI] [PubMed] [Google Scholar]
- 3.Bro-Nielsen M, Gramkow C. Fast fluid registration of medical images. Proceedings of the 4th International Conference on Visualization in Biomedical Computing; Hamburg, Germany. September 22–25; 1996. pp. 267–276. [Google Scholar]
- 4.Brun C, Leporé N, Pennec X, Chou Y-Y, Lopez OL, Aizenstein HJ, Toga AW, Becker JT, Thompson PM. Comparison of Standard and Riemannian Fluid Registration for Tensor-Based Morphometry in HIV/AIDS. Proceedings, MICCAI 2007 Workshop on Statistical Registration: Pair-wise and Group-wise Alignment and Atlas Formation; Brisbane, Australia. Nov 2 (2007). [Google Scholar]
- 5.Chiang MC, Dutton RA, Hayashi KM, Lopez OL, Aizenstein HJ, Toga AW, Becker JT, Thompson PM. 3D pattern of brain atrophy in HIV/AIDS visualized using tensor-based morphometry. NeuroImage. 2007;34:44–60. doi: 10.1016/j.neuroimage.2006.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Christensen GE. Electrical Engineering D.Sc. Dissertation. Washington University; St. Louis, Missouri: 1994. Deformable shape models for anatomy. [Google Scholar]
- 7.Christensen GE, Rabbitt RD, Miller MI. Deformable templates using large deformation kinematics. IEEE Trans. Image Process. 1996;5:1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
- 8.Davatzikos C, Vaillant M, Resnick S, Prince JL, Letovsky S, Bryan RN. A computerized approach for morphological analysis of the corpus callosum. Journal of Computer Assisted Tomography. 1996;20:88–97. doi: 10.1097/00004728-199601000-00017. [DOI] [PubMed] [Google Scholar]
- 9.Gramkow C. Master’s thesis. Danish Technical University; Copenhagen, Denmark: 1996. Registration of 2D and 3D medical images. [Google Scholar]
- 10.Miller MI. Computational anatomy: shape, growth and atrophy comparison via diffeomorphisms. 2004;23(Suppl 1):19–33. doi: 10.1016/j.neuroimage.2004.07.021. [DOI] [PubMed] [Google Scholar]
- 11.Shattuck DW, Leahy RM. BrainSuite: an automated cortical surface identification tool. Medical Image Analysis. 2002;8:129–141. doi: 10.1016/s1361-8415(02)00054-3. [DOI] [PubMed] [Google Scholar]
- 12.Thompson PM, Dutton RA, Hayashi KM, Lu A, Lee SE, Lee JY, Lopez OL, Aizenstein HJ, Toga AW, Becker JT. 3D mapping of ventricular and corpus callosum abnormalities in HIV/AIDS. Neuroimage. 2006;31:12–23. doi: 10.1016/j.neuroimage.2005.11.043. [DOI] [PubMed] [Google Scholar]