Motion robust reconstruction of multi-shot diffusion-weighted images without phase estimation through locally low-rank regularization

Abstract

Purpose:

The goal of this work is to propose a motion robust reconstruction method for diffusion-weighted MRI that resolves shot-to-shot phase mismatches without using phase estimation.

Methods:

Assuming shot-to-shot phase variations are slowly varying, spatial-shot matrices can be formed using a local group of pixels to form columns, where each column is from a different shot (excitation). A convex model with a locally low-rank constraint on the spatial-shot matrices is proposed. In-vivo brain and breast experiments were performed to evaluate the performance of the proposed method.

Results:

The proposed method shows significant benefits when the motion is severe, e.g. for breast imaging. Further, the resulting images can be used for reliable phase estimation in the context of phase-estimation-based methods to achieve even higher image quality.

Conclusion:

We introduced shot-LLR, a reconstruction method for multi-shot diffusion-weighted MRI without explicit phase estimation. In addition, its motion robustness can be beneficial to neuroimaging and body imaging.

Introduction

As a non-invasive imaging method, diffusion-weighted MRI has been widely used in clinical applications (1–7) and neuroscience applications (8,9). Single-shot echo planar imaging (EPI) is the most commonly used method because of its fast acquisition speed and immunity to motion. It is, however, limited by image blurring and distortion due to the long readout window (10). Multi-shot EPI can provide high-resolution diffusion-weighted images (DWIs) with reduced distortion (10). Unfortunately, significant aliasing artifacts and signal cancellation may exist due to the mismatch of the motion-induced phase between different shots (10). The reconstruction becomes non-convex and intractable to solve when this phase is included in the forward model.

Many methods have been developed to estimate the motion-induced phase. These methods can be classified into two categories. One uses self-navigators or extra-navigators to estimate the phase of each individual shot (11–22). Unfortunately, acquisition of the navigator data increases scan time. Furthermore, there might be a mismatch between the extra-navigator and the data to be reconstructed. The other category uses parallel imaging to reconstruct each shot separately, and the low-resolution results are used as phase estimation (23–28). Guo et al. further developed this approach to jointly estimate the phase and the image (29,30). The phase estimation with these methods becomes very challenging when the number of shots is high and performance tends to depend on the geometry of the array coil used for signal reception. The phase estimation might fail in case of high-frequency phase variations due to large motion.

In this work, we propose a locally low-rank reconstruction approach to reconstruct multi-shot DWI. Our method bypasses the challenging phase estimation step by using a relaxed model while still exploiting inter-shot dependencies. The proposed method is evaluated in vivo in both the brain and breast. We also apply this method as a more reliable phase estimation method to improve the conventional phase-estimation-based methods when the number of shots is as high as 8.

Theory

Locally low-rank regularization and shot-LLR

Locally low-rank (LLR) regularization takes advantages of the smoothness of sensitivity maps for calibrationless parallel imaging reconstruction (31), or similarities between images at different time points for dynamic imaging (32–37). Here, we use locally low-rank regularization to reconstruct multi-shot DWI based on the assumption that the motion-induced phase is spatially smooth in most regions. We parameterize the image by multiple images (from each shot) rather than motion-induced phase and one single image, so that the phase estimation is not necessary. This enables the reconstruction to be formulated as a convex optimization problem which is easy to solve and guaranteed to converge to the global minimum.

The construction of spatial-shot LLR matrix is illustrated in Supporting Information Figure S1. With images from all shots, we define an operator R_b, similar to that introduced by Trzasko, Joshua et al. (31), which extracts one small spatial block at pixel index b in the image domain, reshapes it into a vector, and concatenates vectors from all shots into one matrix. With n pixels in one block, and N_s shots, an n-by-N_s spatial-shot matrix is constructed, in which ${R_b\left\{x_{1, \dots ,N_s}\right\}}_{i,j}$ represents the image at the i^th pixel and j^th shot. The spatial-shot matrix can be decomposed into the product of two matrices (Eq. 1). Each element of the diagonal matrix I represents the target complex image without motion-induced phase. Matrix φ contains the motion-induced phase θ of each shot.

$$R_b\left\{x_{1,\dots ,N_s}\right\}=\underset{I}{\underbrace{\left[\begin{array}{ccc}\hfill I_1\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill I_n\hfill \end{array}\right]}}\underset{\phi }{\underbrace{\left[\begin{array}{ccc}\hfill e^{i{\theta }_{1,1}}\hfill & \hfill \cdots \hfill & \hfill e^{i{\theta }_1,N_s}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill e^{i{\theta }_{n,1}}\hfill & \hfill \cdots \hfill & \hfill e^{i{\theta }_{n,N_s}}\hfill \end{array}\right]}}$$ (1)

If the motion-induced phase θ is spatially smooth, the rank of matrix φ is low. Consequently, $R_b\left\{x_{1, \dots ,N_s}\right\}$, which is the product of a diagonal matrix and a low-rank matrix, is also low-rank. Intuitively, we can combine the forward encoding model with a constraint on the rank of $R_b\left\{x_{1, \dots ,N_s}\right\}$. We reduce the high computational complexity of the non-convex rank penalty by replacing the rank constraint with its convex envelope, the nuclear norm, to make the optimization problem convex (38,39). We formulate the reconstruction as the following optimization problem,

$$P1:\underset{x_{1,\dots ,N_s}}{\text{min}}{\Sigma }_{i=1}^{N_s}{\Vert D_i{\mathit{FSx}}_i-y_i\Vert }_2^2+\lambda {\Sigma }_{b\in \Omega }{\Vert R_b\left\{x_{1,\dots ,N_s}\right\}\Vert }_{\ast }$$ (2)

where D_i and y_i are the sampling operator, image to be reconstructed, acquired multi-channel data of the i^th shot, F is Fourier transform, S is the multi-channel sensitivity map, λ is a regularization parameter, and Ω is the set of all non-overlapping blocks which uniformly tile the image domain.

This formulation mirrors the approach of CLEAR (31), except that coil sensitivity information is used to combine multi-channel images within one shot before forming the low-rank matrices, and the difference between different coil-combined images comes from the motion-induced phase instead of coil sensitivity encoding. Equation 2 is solved using an iterative thresholding algorithm (40). The estimated images from all shots can be then combined using complex averaging or root sum of square.

Virtual Conjugate Shots for shot-LLR with Partial Fourier

Partial Fourier is commonly used in EPI to accelerate the acquisition or to acquire the central k-space earlier in the echo train. Partial Fourier reconstruction methods can be used to fill in the missing phase encoding lines after the shot-LLR reconstruction by employing the conjugate symmetric property of the k-space. Similar to the idea of virtual conjugate coils (41,42), which is an alternative way of exploiting this property, we generate virtual conjugate shots (VCS) by flipping and conjugating the acquired data, and treat them as additional shots to avoid the estimation of the low-resolution phase from the central k-space data. The decomposition of the LLR matrices with VCS is provided in the appendix.

Methods

With approval from the institutional review board and written informed consent, data were acquired on a 3 Tesla (T) MRI system (Discovery MR750, GE Healthcare) using a 2D single-refocused Stejskal-Tanner diffusion-weighted spin-echo EPI sequence.

Brain Image Acquisition

Axial brain images were acquired on five healthy volunteers using a 32-channel head receive coil (Nova Medical) with the following parameters: TE/TR = 46/2000 ms, 16 consecutive slices covering the corpus callosum, field-of-view (FOV) = 21 × 21 cm², matrix size = 248 × 244, slice thickness = 3 mm, BW = +/−250 kHz, number of shots = 4 and 8, b-value = 1000 s/mm², number of averages (nex) = 4. Partial Fourier acquisition was used (14 extra ky lines) and the corresponding partial Fourier factor was about 0.557. The readout direction was left-right.

To further evaluate the performance of the proposed method, a diffusion tensor imaging (DTI) scan was performed on one volunteer with 30 diffusion encoding directions uniformly distributed on a sphere, nex = 2 and all other parameters identical.

To evaluate the motion robustness of different methods, we performed two additional experiments with nex = 6 and all other parameters identical. The volunteer was asked to breathe normally the first time, and deeply the second time to simulate severe respiratory motion. Each time one non-diffusion-weighted image was acquired first, then six 4-shot data were acquired.

Breast Image Acquisition

Axial breast images were acquired on two healthy volunteers and one patient using a 16-channel Sentinelle breast coil (Invivo, Gainsville, FL).

In the first experiment, two volunteers were scanned with the following parameters: TE/TR = 51.5/2000 ms, FOV = 36 × 36 cm², matrix size = 256 × 244, slice thickness = 4 mm, BW = +/−250 kHz, number of shots = 4 and 8, b-value = 600 s/mm², nex = 2, and 14 extra ky lines for partial Fourier acquisition. The readout direction was anterior-posterior so that cardiac pulsation artifacts interfered minimally with the breast.

For the second experiment, we collected an 8-shot dataset from a ductal carcinoma in situ (DCIS) patient, using the following parameters: FOV = 36 × 36 cm², matrix size = 360 × 360, slice thickness = 4 mm, BW = +/−250 kHz, b value = 600 s/mm², nex = 2, number of extra ky lines = 20. For comparison, the single-shot data were also collected: reduction factor = 4, matrix size = 256 × 256, nex = 16 (to match the scan time of 8-shot scans), and all other parameters identical.

Image Reconstruction and Processing

Sensitivity maps were calculated from the multi-shot non-diffusion-weighted data using ESPIRiT (43). POCS-MUSE and POCS-ICE, which solved the following problem, were implemented in Matlab for comparison (25,29):

$$\underset{x,P_{1,\dots ,N_s}}{\text{min}}\sum _i^{N_s}{\Vert D_i{\mathit{FSP}}_{i}x-y_i\Vert }_2^2$$ (3)

where P_i is the phase of the i^th shot, and x is the final image to be reconstructed. The proposed method was implemented based on the open-source Berkeley Advanced Reconstruction Toolbox (BART) with a block size of 8 × 8 (44). Homodyne was used for partial Fourier reconstruction after proposed method, POCS-MUSE, and POCS-ICE (45). The number of iterations was 200 for all methods if not specified. The k-space data were normalized first. The regularization parameter for the normalized data was 0.0008 for shot-LLR and 0.0004 for shot-LLR with VCS.

DTI data were corrected for eddy current distortions and bulk motion and co-registered using the “eddy” function from the FMRIB Software Library (FSL, http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) (46). The diffusion tensor model was then fitted using FSL’s “dtifit” function to derive the fractional anisotropy (FA) and the primary eigenvector (V1). The image quality was evaluated visually based on the existence of aliasing artifacts, shading artifacts, and our knowledge of brain anatomy.

Results

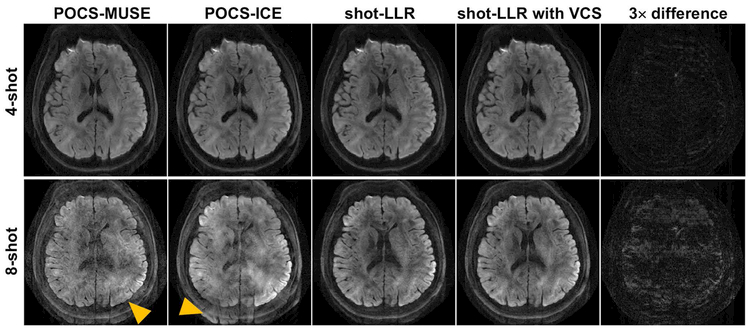
In all five brain volunteers, shot-LLR and shot-LLR with VCS provided comparable image quality to POCS-MUSE and POCS-ICE for 4-shot acquisitions and markedly reduced aliasing artifact in comparison to POCS-MUSE and POCS-ICE for 8-shot acquisitions. Figure 1 shows a representative slice reconstructed by different methods from 4-shot and 8-shot data. All methods work similarly on 4-shot data (Fig. 1, first row, Supporting Information Figure S2), and this demonstrates the capability of shot-LLR to solve the motion-induced phase mismatch problem without phase estimation. For 8-shot data, shot-LLR and shot-LLR with VCS significantly reduce aliasing artifacts compared with POCS-MUSE and POCS-ICE (Fig. 1, second row), despite the presence of areas of signal loss in shot-LLR and shot-LLR with VCS.

Fig. 1.

4-shot and 8-shot diffusion-weighted images (resolution = 0.85 × 0.85 × 3 mm³, b-value = 1000 s/mm², nex = 4) reconstructed by different methods, and the difference between shot-LLR images without and with using VCS (3× difference). For 8-shot results (second row), the arrowheads highlight aliasing artifacts in POCS-MUSE and POCS-ICE, while shading artifacts exist in shot-LLR with/without VCS.

The difference between shot-LLR and shot-LLR with VCS for 4-shot acquisition is minor (Fig. 1, first row, last column), which indicates that virtual conjugate shots can be also used for partial Fourier reconstruction as homodyne. Using virtual conjugate shots may have some advantages, similar to the virtual conjugate coil approach, but the discussion of this is beyond the scope of this article.

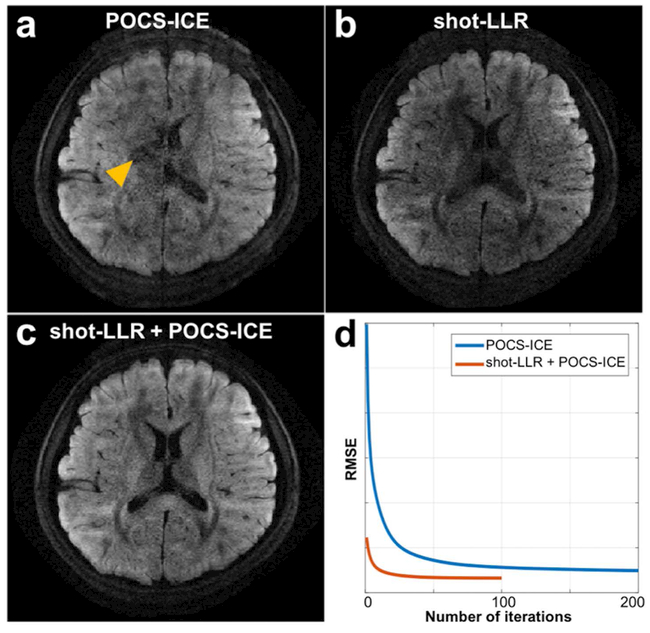
Shot-LLR can be used as a reliable phase estimator for POCS-ICE to achieve improved image quality for numbers of shots as high as 8 (Fig. 2). For 8 shots, conventional POCS-ICE suffers from aliasing artifacts (Fig. 2a). Shot-LLR performs better in terms of aliasing, but there are regions suffering signal loss (Fig. 2b). Using the phase of each shot and the averaged amplitude image of the shot-LLR approach as the initialization of POCS-ICE (rather than 0 as in the original paper) results in reduced aliasing artifacts and improvement over the image from shot-LLR (Fig. 2c). This illustrates that POCS-ICE can achieve a faster and better convergence by initializing with shot-LLR (Fig. 2d). Even with under-sampled 8-shot data by a factor of 2, initializing POCS-ICE with shot-LLR still achieves the best results (Supporting Information Figure S3), but the results are too noisy to use.

Fig. 2.

8-shot brain diffusion-weighted images (resolution = 0.85 × 0.85 × 3 mm³, b-value = 1000 s/mm², nex = 1) reconstructed by POCS-ICE (a), shot-LLR (b) and POCS-ICE with shot-LLR as initialization (c). Figure 2a, 2b and 2c have the same window level. The yellow arrow shows aliasing artifacts in POCS-ICE. The curve (d) shows values of the cost function used in POCS-ICE and the horizontal axis is the iteration axis. Using shot-LLR as initialization makes the algorithm converge much faster and to a better local minimum.

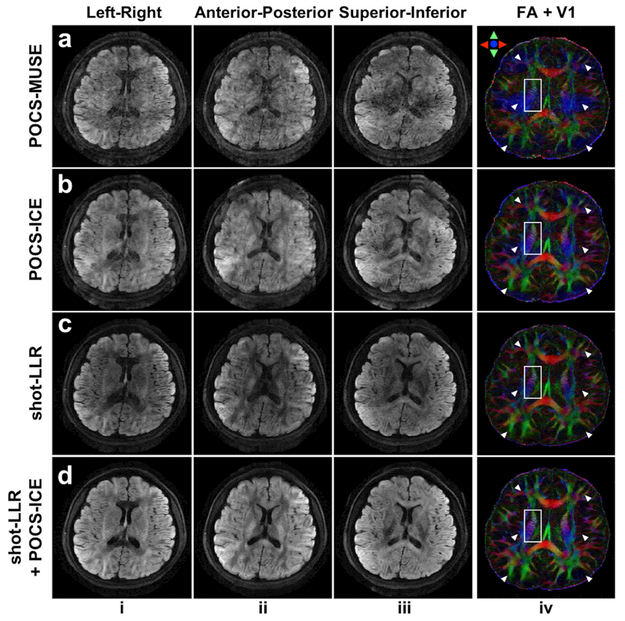
Figure 3 further demonstrates that 8-shot DTI results can be improved by initializing POCS-ICE with shot-LLR. Severe signal cancellation and aliasing artifacts are shown in POCS-MUSE (Fig. 3a), because parallel imaging works poorly on one of the eight shots of data, giving an inaccurate phase estimation. POCS-ICE reduces the signal cancellation problem by phase updating, but the aliasing artifacts are still present (Fig. 3b). These artifacts lead to erroneously estimated DTI V1 (Fig. 3ab, column iv, blue regions highlighted by arrows) and a loss of structural details (Fig. 3ab, column iv white boxes). Shot-LLR shows some advantages for resolving aliasing artifacts (Fig. 3c). Initializing POCS-ICE with shot-LLR achieves the best performance in terms of aliasing and SNR, as demonstrated by the V1-encoded FA (note how detailed anatomical structures are retained in the white box).

Fig. 3.

3 out of 30 directions 8-shot diffusion-weighted images (columns i-iii, resolution = 0.85 × 0.85 × 3 mm³, b-value = 1000 s/mm², nex = 2), and corresponding fractional anisotropy (FA) maps color-encoded by the principal diffusion tensor eigenvector (V1) (column iv) of different methods. Inaccurate phase estimation leads to erroneously estimated DTI V1 (Fig. 3ab, column iv, blue regions highlighted by arrows) and a loss of structural details (Fig. 3ab, column iv white boxes). Shot-LLR initialized POCS-ICE reduces artifacts in POCS-ICE, and also removes shading from shot-LLR.

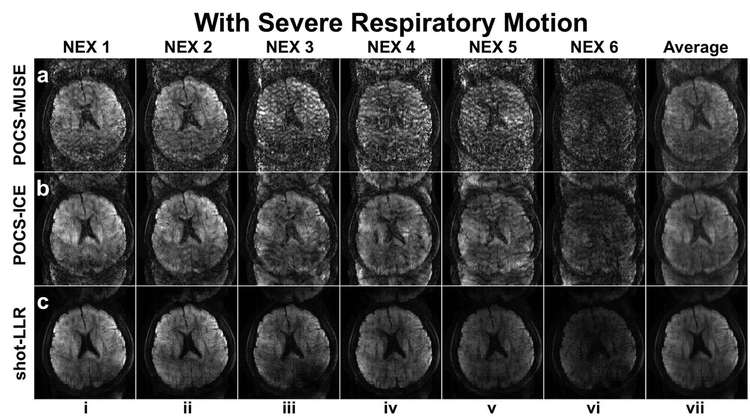
Figure 4 demonstrates that the proposed method is more motion robust compared to POCS-MUSE and POCS-ICE. If the subject’s motion is not significant, all these methods work well and images from different acquisitions look consistent (Supporting Information Figure S4). There are obvious aliasing artifacts due to severe respiratory motion, especially in POCS-MUSE (Fig. 4, row a) and POCS-ICE (Fig. 4, row b). Shot-LLR has significantly fewer artifacts (Fig. 4, row c, columns i-vi), especially after averaging the resultant image from six acquisitions (Fig. 4, row c, column vii), which implies that it can handle more complicated phase variations between shots.

Fig. 4.

4-shot images reconstructed by different methods with severe (rows a-c) respiratory motion. Columns i-vi show images from different acquisitions and column vii shows the averaged images of columns i-vi. Shot-LLR significantly reduced the aliasing artifacts compared with POCS-MUSE and POCS-ICE in the case of severe motion.

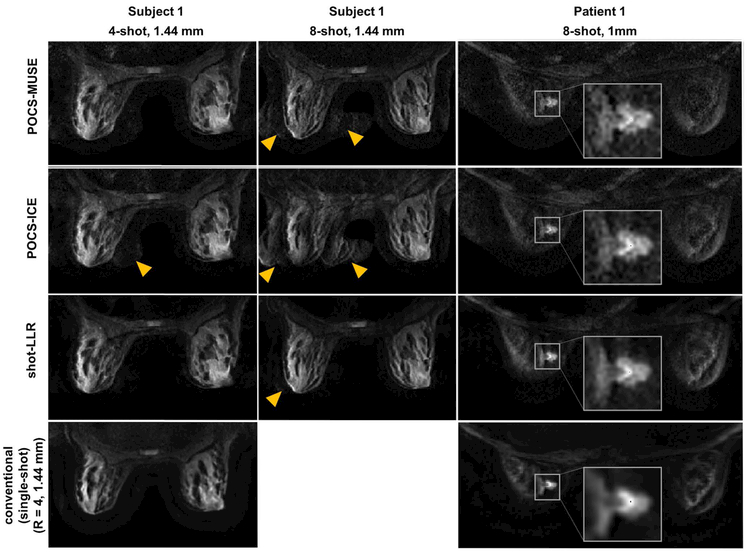
Shot-LLR achieves superior performance in breast diffusion-weighted MRI, which is susceptible to motion artifacts due to the proximity to the lungs and heart. For a 4-shot acquisition, results from all three methods look consistent with the image from the conventional single-shot method, except there is some signal outside of the breast in POCS-ICE as indicated by the yellow arrowheads (Fig. 5, column 1). The increased SNR and reduced aliasing artifact achieved with shot-LLR are pronounced in the 8-shot images (Fig. 5, column 2). There are similar improvements in the 2^nd volunteer. The diagnostic impact of improved image quality and respective higher resolution achieved with shot-LLR is demonstrated in the improved depiction of lesion morphology in the patient (Fig. 5, column 3): shot-LLR shows decreased ghost artifacts versus POCS-MUSE and POCS-ICE, and compared with the single-shot image, the 8-shot acquisition and shot-LLR reconstruction together provide higher in-plane resolution (1mm) and sharper boundaries for clinical evaluation.

Fig. 5.

Breast images of a volunteer (1st and 2nd columns) and a patient (3rd column) (slice thickness = 4 mm, b-value = 600 s/mm², nex = 2) reconstructed by different methods under different numbers of shots and different in-plane resolutions. The last row shows the results using the conventional method, in which single-shot and parallel imaging were used, and the reduction factor was 4. Yellow arrows highlight aliasing artifacts. In the 3rd column, an enlarged view of the tumor is provided in the white boxes. Note the improved depiction of the lesion detail in shot-LLR vs conventional single-shot DWI, with reduced artifacts compared to POCS-ICE and POCS-MUSE.

Discussion

We propose a new method for multi-shot diffusion-weighted MRI reconstruction. Spatial-shot matrices are constructed, and a convex model with a low-rank constraint on these matrices is used to avoid the challenging phase-estimation step. The proposed method is shown to have the capability to reconstruct data from acquisitions with relatively high numbers of shots, especially in the breast.

For 8-shot brain data, results of proposed method start to have some regions of signal loss in comparison to 4-shot results. The reason for this is that the proposed method treats each shot as a separate image, and if some shot lacks central k-space data, then the recovery of that shot may fail, and this can even influence the reconstruction of other shots. For EPI, when the number of shots is high, there are always some shots which don’t have central k-space lines. The reconstruction of the 8-shot brain images without using navigator is also very challenging for the current state-of-the-art methods and there are even evident aliasing artifacts, but we have found that using the results of proposed method as phase estimation can improve the reconstruction accuracy as shown in Figure 2. Using shot-LLR as initialization can also improve POCS-MUSE, but the improvement is not as significant as that of POCS-ICE, since the phase update in POCS-ICE can refine phase estimation.

The proposed method shows superior unaliasing capabilities when the physiologic motion is severe, and phase-estimation-based methods may fail because in these cases phase can vary significantly in some regions. The inaccurate phase estimation can lead to severe artifacts in the image, and may accumulate for POCS-ICE during repeated iterations. This motion robustness property of shot-LLR benefits from the fact that we use a relaxed model with a low-rank constraint, and no explicit phase estimation is needed. Since the constraint is on the sum of the ranks, some blocks can still have high-frequency phase variations. Data rejection (47,48) and external phase information can be also incorporated into this method, and it is expected that this can further improve the performance.

For partial Fourier reconstruction, the common homodyne approach estimates the low-resolution phase from ACS data and reconstructs the amplitude image by exploiting the Hermitian symmetric property of the k-space data. However, this may be error-prone where localized phase variations exist in the image domain. Inspired by the idea of real-valued CLEAR in which the low-rank matrices are formed with the real and imaginary parts of the image, we propose the virtual conjugate shot concept, in which flipped and conjugated k-space data are treated as additional shots. Use of virtual conjugate shots tends to make the reconstructed image have a smooth phase, thus the un-acquired half of k-space will be also filled. This idea can be also applied to other multi-shot DWI reconstruction methods. The major limitation of using this concept is the increase of reconstruction time due to doubling of the number of shots. The reconstruction time for a matrix size 248 × 244, 4-shot, 32-channel dataset on a Linux work station with 2.3 GHz CPU with 256 GB RAM is about 60 seconds, and is doubled if using VCS. The regularization parameter was selected empirically, which was found working well for different slices and subjects. Using region-specific regularization factors, perhaps based on initial reconstruction results, could improve overall performance of the shot-LLR reconstruction. Block size was set to 8 as in (31), and it did not make a big difference by changing it to 6 or 10.

Several papers have been published to solve the phase mismatch problem by k-space-based block-Hankel low-rank matrix completion (49,50). The proposed method has a computational advantage compared with these methods since the spatial-shot matrices are small and non-overlapping. However, the performance of proposed method compared with these k-space domain methods needs to be further assessed in future studies.

Conclusion

We proposed a motion-robust reconstruction method for multi-shot DWI without phase estimation, named shot-LLR. Several in vivo experiments have been done to demonstrate the capability of solving phase variations between shots as well as robustness to motion.

Appendix

Decomposition of the spatial-shot matrix with VCS

With virtual shots, the total number of shots is doubled, and the new low-rank matrix can be formed and decomposed as follows:

$$R_b\left\{x_{1,\dots ,2N_s}\right\}=\left[\begin{array}{ccc}\hfill \mid I_1\mid \hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill \mid I_n\mid \hfill \end{array}\right]\left[\begin{array}{ccc}\hfill e^{i({\theta }_{1,1}+{\beta }_{1,1})}\hfill & \hfill \cdots \hfill & \hfill e^{i({\theta }_{1,2\mathit{Ns}}+{\beta }_{1,2N_s})}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill e^{i({\theta }_{n,1}+{\beta }_{n,1})}\hfill & \hfill \cdots \hfill & \hfill e^{i({\theta }_{n,2\mathit{Ns}}+{\beta }_{n,2N_s})}\hfill \end{array}\right]$$

Where θ and β represent the motion-induced phase during diffusion encoding and the phase induced from B0 inhomogeneity and other factors, respectively. Under the assumption that β is also spatially smooth, the low-rank property of $R_b\left\{x_{1,\dots ,2N_s}\right\}$ which includes both real and virtual shots still holds. This way the final results will tend to have a smooth phase by adding a constraint on the rank of these matrices, and no other partial Fourier reconstruction is needed.

Using VCS, our problem is formulated as follows:

$$P2:\underset{x_{1,\dots ,2N_s}}{\text{min}}{\Sigma }_{i=1}^{2N_s}{\Vert D_i{\mathit{FS}}_i{x}_i-y_i\Vert }_2^2+\lambda {\Sigma }_{b\in \Omega }{\Vert R_b\left(x_{1,\dots ,2N_s}\right)\Vert }_{\ast }$$

Note that in this formulation there are 2N_s shots in total, including N_s original shots and N_s virtual conjugate shots. Sensitivity maps of real shots are the same as in P1, and for virtual shots, the maps are calculated from the flipped and conjugated reference data.

Supplementary Material

Figure S1

Construction of the “spatial-shot” matrix containing a block of pixels from each of the shots. Because the motion-induced phase is slowly varying in the image domain, the spatial-shot matrices are low-rank. Therefore, constraints on the rank of these matrices can be used to remove the phase inconsistency.

Figure S2

3 out of 30 directions 4-shot diffusion-weighted images (resolution = 0.85 × 0.85 × 3 mm³, b-value = 1000 s/mm², nex = 2), and corresponding V1-encoded FA maps with different methods. No visible difference exists among POCS-MUSE (a), POCS-ICE (b) and shot-LLR (c). This further indicates that shot-LLR can be used as a multi-shot DWI reconstruction method.

Figure S3

8-shot DW images reconstructed by different methods using 2, 4 and 8 out of 8 shots (res: 0.85 × 0.85 × 3 mm³, b-value = 1000 s/mm², nex = 1). Aliasing artifacts exist in POCS-MUSE (column i) and POCS-ICE (column ii) even when using all 8 shots as indicated by the yellow arrows. Regions of signal loss exist in shot-LLR (column iii) as indicated by the white arrows. Initializing POCS-ICE with shot-LLR gives best results (column iv, row a), while decreasing the amount of data used for reconstruction tends to make the results noisier, and harder for POCS-ICE to recover signal loss from shot-LLR (column iv). In the case of 2 shots, there is not enough information to recover the signal loss (column iv).

Figure S4

4-shot images reconstructed by different methods with normal (rows a-c) respiratory motion. Columns i-vi show images from different acquisitions and column vii shows the averaged images of columns i-vi.