Whole Heart Spiral Simultaneous Multi-Slice First-Pass Myocardial Perfusion Imaging

Abstract

Purpose

To develop and evaluate a simultaneous multi-slice (SMS) spiral perfusion pulse sequence with whole heart coverage.

Methods

An orthogonal set of phase cycling angles following a Hadamard pattern was incorporated into a golden-angle (GA) variable density spiral perfusion sequence to perform SMS imaging at different multiband (MB) factors. Images were reconstructed using an SMS extension of L1-SPIRiT that we have termed SMS-L1-SPIRiT. The proposed sequence was evaluated in 40 subjects (10 each for MB factors of 1, 2, 3 and 4). Images were blindly graded by two cardiologists on a 5-point scale (5, excellent). To quantitatively evaluate the reconstruction performance against images acquired without SMS, the MB=1 data was used to retrospectively simulate data acquired at MB factors of 2–4.

Results

Analysis of the SMS point-spread function for the desired slice showed that the proposed sampling strategy significantly cancelled the main-lobe energy of the other slices and has low side-lobe energy resulting in an incoherent temporal aliasing pattern when rotated by the GA. Retrospective experiments demonstrated the SMS-L1-SPIRiT method removed aliasing from the interfering slices and showed excellent agreement with the ground-truth MB=1 images. Clinical evaluation demonstrated high quality perfusion images with average image quality scores of 4.3±0.5 (MB=2), 4.2±0.5 (MB=3) and 4.4±0.4 (MB=4) with no significant quality difference in image quality between MB factors (p=0.38).

Conclusion

The SMS spiral perfusion at MB factors 2, 3 and 4 produces high quality perfusion images with whole heart coverage in a clinical setting with high sampling efficiency.

Introduction

First-pass contrast-enhanced myocardial perfusion using cardiac magnetic resonance imaging (CMR) is a valuable method to access patients with suspected coronary artery disease (CAD) providing important diagnostic and prognostic information^1–4. However, most clinically available techniques have limited spatial-temporal resolution and ventricular coverage. Recent advances in parallel imaging^5–7 and compressed sensing^{8; 9} have greatly improved the spatial coverage while maintaining spatial-temporal resolution^{10; 11}. Non-Cartesian techniques using radial^{12; 13} or spiral^14–16 techniques have demonstrated good image quality with minimal dark rim artifacts¹⁷, and have demonstrated accurate detection of CAD in preliminary studies¹⁸. Over the last few years, there has been increased interest in obtaining full heart coverage using 3D imaging techniques, and multi-center trials have demonstrated excellent diagnostic utility¹⁹. However, 3D perfusion techniques^{20; 21} have limited temporal and spatial resolution, typically around 200 ms per volume, with an in-plane spatial resolution of 2–2.3mm.

Recently, we have demonstrated a rapid multi-slice spiral-perfusion pulse sequence which can image 8 slices with an isotropic 2 mm in-plane spatial resolution with a temporal resolution of 35 ms per slice using a motion-compensated L1-SPIRiT¹⁴ reconstruction. We have demonstrated accuracy of this technique for detecting obstructive CAD in a preliminary study²². However, this approach involves significantly reducing the amount of data that is acquired for each slice position, which has signal-to-noise implications.

An alternative way to achieve whole-heart coverage is to obtain multiple slices at the same time using simultaneous multi-slice imaging techniques (SMS)²³. SMS has found significant applications in neurological MRI, and more recently has been used for cardiac applications^24–26. The performance of SMS techniques can be enhanced using the CAIPIRINHA²⁷ (controlled aliasing in parallel imaging results in higher acceleration) technique, which utilizes phase modulation of the RF excitation pulses of multiple simultaneously acquired slices to shift the aliasing between slices to improve image reconstruction. The application of Cartesian CAIPIRINHA to myocardial perfusion imaging has been shown at a multiband (MB) factor of 2, enabling acquisition of 6 slices every heartbeat with 2 mm in plane resolution²⁵. CAIPIRINHA has been extended to radial trajectories, where it has been shown to have a lower g-factor penalty at high acceleration rates²⁸. Recently, a radial CAIPIRINHA myocardial perfusion imaging technique has been developed, enabling perfusion imaging with MB factors of 2 to 3 using a constrained iterative reconstruction²⁴.

We have previously demonstrated a variable density spiral perfusion technique with 3-slice coverage, which has demonstrated high image quality and diagnostic utility in patients with known or suspected CAD¹⁸. Spiral trajectories, which are inherently highly efficient, may be advantageous for SMS imaging as they can be designed to significantly cancel signal between simultaneously excited slices. To date, there has been limited application of SMS for spiral trajectories²⁹. We propose a novel spiral SMS acquisition strategy and CS reconstruction to achieve multi-slice whole heart coverage (6–9 slices) which utilizes simultaneous excitation of 2–4 slices to maximize the data sampling time for each slice, improving SNR efficiency as compared to our prior interleaved highly-accelerated approach¹⁴.

Methods

Theory

When multiple slices are excited simultaneously, the raw k-space signal can be expressed in a generalized form as:

$${\mathit{S}}_{mb}=\sum _{j=1}^{\mathit{nSlc}}{\mathit{S}}_j\ast e^{i{\mathbf{\Phi }}_j}$$

Where the S_mb is the vector representing multiple slices excitation raw k-space signal, S_j is raw k-space signal of the j^th slice, nSlc is the total number of slices excited and e^iΦ_j is the phase modulation for the k-space of the j^th slice.

Without phase modulation (Φ_j = 0), the resulted MB signal would be the superposition of the signals from all slices. Typically, a SENSE or GRAPPA approach is used to separate the images by directly or indirectly exploring variation in coil sensitivities in the through-slice direction. However, the direct overlap of the images results in a high g-factor for high MB factors^{23; 30}. To reduce the g-factor, the concept of CAIPIRINHA was introduced. This technique modulates the phase of the RF excitation (Φ_j = [0 π 0 π …]) of each slice to induce a linear phase shift along the phase encoding direction to prevent direct overlap of the reconstructed images from each slice²⁷. This linear phase shift in the k-space data results in a position shift in the image domain, reducing direct overlap between slices resulting in lower g-factors and improving image reconstruction quality.

For non-Cartesian data acquisition, the phase-shifting approach does not provide a linear position shift, but rather enables cancellation of data from different slices. By carefully choosing a sampling strategy and excitation phase modulation scheme, signals from the desired slice add coherently, while signals from other slices destructively interfere resulting in an aliasing pattern, which can be removed by parallel imaging and/or compressed sensing reconstruction. For spiral trajectories, the density can be modified to fully-sample or over-sample the k-space center, enabling a trade-off between sampling efficiency and signal cancellation for each slice. Higher MB factors need a phase cycling strategy for each slice such that the contribution from the other slices is minimized when a single slice is reconstructed. We propose that an orthogonal set of phase cycling angles following a Hadamard pattern,³¹ which is orthonormal, would achieve this desired signal cancellation. This strategy would require 2^(MB-1) interleaves. For an 8 spiral interleaved design, the phase modulation for each slice up to MB factor of 4 is given as follows:

$$\begin{gathered} {\mathbf{\Phi }}_1=[00000000] \\ {\mathbf{\Phi }}_2=[0\pi 0\pi 0\pi 0\pi ] \\ {\mathbf{\Phi }}_3=[00\pi \pi 00\pi \pi ] \\ {\mathbf{\Phi }}_4=[0000\pi \pi \pi \pi ] \end{gathered}$$

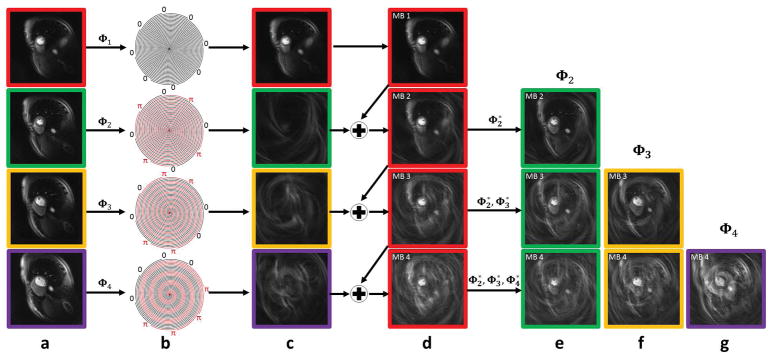
Figure 1 shows the effect of the phase modulation scheme on the signal from each slice for an example of phase modulation of 8 spiral interleaves at MB = 1, 2, 3 and 4. Figure 1(a) shows images from the 4 different slice locations. After phase modulation (b) the contribution of the phase modulated signal for the images for each slice is shown in column (c). Slice 1 (red) has no phase modulation and is thus unchanged from column (a). The images from the slices 2–4 following excitation phase modulation show minimal signal from the heart, and demonstrate a characteristic aliasing pattern depending of the phase modulation pattern for each slice. Columns (d) shows the effect for slice 1 of adding the data from the modulated slices for MB factors 2–4. Columns (e) to (g) show the raw image data from slices 2–4 at the various multiband factors. In all cases the residual signal from the modulated slices appears as an incoherent noise artifact with an increasing amount of residual aliasing artifacts as the MB factor is increased. Without any temporal variation of the sampling pattern, this aliasing pattern would be coherent and could be reconstructed using a “slice-GRAPPA” like approach³⁰. However, by varying the sampling pattern for each heart beat by the golden-angle as shown in Figure 2b, the residual aliasing pattern becomes incoherent in time and amenable to reconstruction using CS. For an 8-interleaf spiral acquisition, the Hadamard strategy was chosen over the standard CAIPIRINHA approach as it achieves better suppression of signal from the phase modulated slices for all MB factors between 1 and 4. We propose to jointly reconstruct the multiple-slices across the time series using an SMS-parallel imaging and CS approach that we have named non-Cartesian SMS-L1-SPIRiT as described below.

Figure 1.

Demonstration of the phase modulation strategy for 8 spiral interleaves at MB = 1,2,3 and 4. (a) Spiral perfusion images acquired separately from 4 slice positions. (b) Hadamard excitation RF phase modulation pattern as applied to each slice position for MB factors of 1–4. (c) For slices 2–4 there is nearly complete suppression of image with an incoherent residual aliasing artifact that varies by slice position. (d) The combined SMS images for MB factors 1–4 show the image at slice position 1 with superposition of the aliasing patterns from the other slices as shown in (c). By applying phase demodulation, the images from the other slice locations can be generated through phase demodulation as shown in (e, f and g). Images at each slice location have a different aliasing pattern in time due to golden angle rotation of the trajectory, and the residual aliasing can be removed using an SMS-L1-SPIRiT reconstruction.

Figure 2.

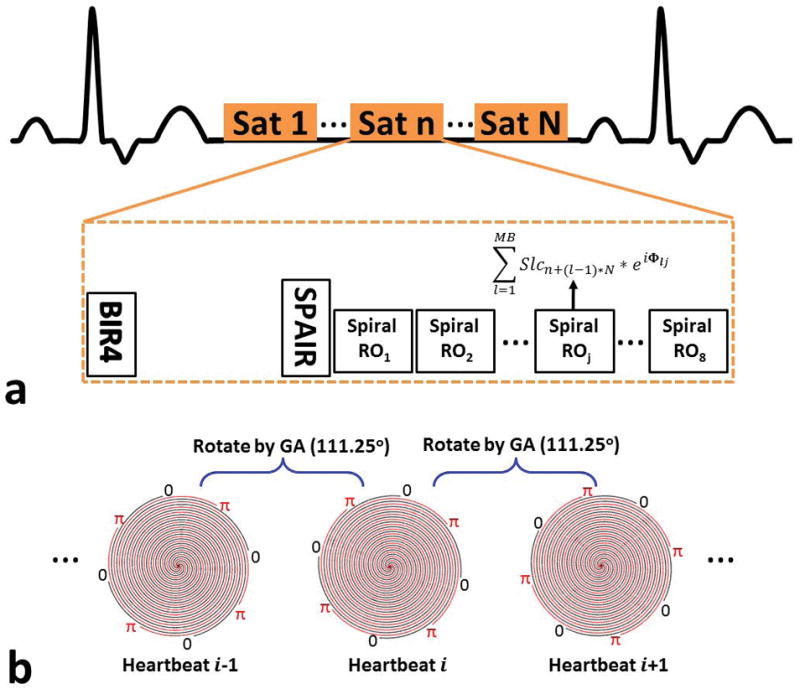
Schematic of the SMS spiral perfusion pulse sequence. (a) A non-selective saturation with an adiabatic BIR-4 pulse is used for T1-weighted preparation. Before data acquisition, a spectrally selective adiabatic fat-inversion pulse (SPAIR) is applied for fat saturation. An 8 interleaved spiral trajectory is used with the following design parameters: 6 ms readout per spiral interleave with linear variable density starting density of 1.2× Nyquist to ending density of 0.4× Nyquist. The excitation phase of each slice in the SMS acquisition is modulated using a Hadamard phase cycling scheme, as described in the text, to achieve MB factors of 1–4. Full heart coverage may be achieved with MB factor 2, 3, and 4 with 4, 3, or 2 saturation blocks respectively. (b) Excitation phase modulation angle was rotated by the golden-angle between heartbeats using MB factor of 2 as an example.

Pulse Sequence

The SMS spiral perfusion pulse sequence is shown schematically in Figure 2 (a). A non-selective saturation with an adiabatic BIR-4 pulse is used for T1-weighted preparation. As we described previously, a spectrally selective adiabatic fat-saturation pulse is applied before data acquisition³². An 8 interleaved spiral trajectory was used with the following design parameters: 6 ms readout per spiral interleave with linear variable density starting density of 1.2× Nyquist to ending density of 0.4× Nyquist.³³ Given the nature of variable density spirals where the acceleration rate varies during the trajectory by design, we define the effective acceleration rate as the corresponding constant acceleration factor required for a uniform density spiral trajectory to achieve the same desired FOV and maximum k-space radius (nominal spatial resolution) with the same number of interleaves and readout duration per interleave. Therefore, the effective acceleration rate for this VD spiral is 1.25 fold. Other sequence parameters included: FOV 340mm, TE 1.0ms, TR 8ms, SRT 80ms, FA 26°, with 10mm thickness, 2 mm in-plane resolution, and MB factors from 1–4.

The multiband RF pulse was designed by the summation of single band RF pulse with different phase modulation for each slice. The single band RF pulse is a 1ms sinc-shaped pulse with time band product of 5.6. The peak amplitude of the multiband RF pulse and the total power in the pulse was confirmed to not exceed specific absorption rate (SAR) limits. The excitation phase of each slice in the SMS acquisition was modulated using the previously described Hadamard phase cycling scheme to achieve MB factors of 1–4. One to 4 slices are acquired in each saturation recovery (SR) block, and SR blocks are repeated until all the slices are imaged. To achieve temporal incoherence, the excitation phase modulation angle was incremented by the golden-angle between heartbeats as shown in Figure 2 (b) using MB factor of 2 as an example. Full heart coverage could be achieved with MB factor 2, 3, and 4 with 4, 3, or 2 SR blocks respectively.

A pre-scan, consisting of images acquired at each slice location (i.e. without SMS) without magnetization preparation, was acquired during a separate 10 heart-beat breath hold to derive the calibration kernel for SMS reconstruction. The k-space trajectory was the same as that used for acquisition of the perfusion data. The sequence parameters included: FOV 340mm, TE 1.0 ms, TR 8 ms, FA 10°, with 10 mm thickness, 2 mm in-plane resolution.

Reconstruction

The perfusion images were reconstructed using the following SMS-L1-SPIRiT technique:

$$\underset{x}{\text{argmin}}{\Vert \mathit{\Phi }{F}_{u}x-y\Vert }^2+{\lambda }_1{\Vert (G-I)x\Vert }^2+{\lambda }_2{\Vert {\mathrm{\Psi }}_{t}x\Vert }_1$$

where F_u is a Non-uniform Fourier operator which transfers the data from the image domain to the spiral k-space domain, G is an image-space SPIRiT operator that represents the k-space self-consistency convolutions in the image domain, ψ_t is the finite time difference transform that operates on each individual coil separately to achieve sparsity in the temporal domain of image time series, Φis the operator describing the phase modulation pattern needed to coherently select the signal from each slice from the SMS data, and λ₁ and λ₂ are parameters that balance the data acquisition consistency with calibration consistency and sparsity. The calibration kernel is derived from the pre-scan proton density images described in the pulse sequence section.

Human Studies

Forty patients undergoing clinically ordered CMR studies with gadolinium (Gd)-based contrast agents were included in this study. The indications for the clinical CMR studies included evaluation of myocardial viability (N=8), myocardial infarction (N=5), non-ischemic cardiomyopathy (N=5), myocarditis (N=1), pre-atrial fibrillation ablation (N=1), pericardial disease (N=2), arrhythmias (premature ventricular contractions/ventricular tachycardia) (N=3), cardiac sarcoid (N=3), hypertrophic cardiomyopathy (N=11) and right ventricular enlargement (N=1). Written informed consent was obtained from all subjects, and imaging studies were performed using a protocol approved by the University of Virginia Health Research Institutional Review Board. Imaging was performed on a 1.5T MRI scanner (MAGNETOM Aera, Siemens Healthineers, Erlangen, Germany). Perfusion imaging was performed using 0.075mmol/kg of Gd-DTPA (Bayer AG, Leverkusen, Germany) injected intravenously at a rate of 4mL/s followed by 25 mL of saline flush at 4mL/s. The subjects were asked to hold their breath as long as possible followed by shallow breathing during the acquisition of perfusion images over 50–60 heart beats. A 34-channel cardiac phased-array receiver coil was used for signal reception. 10 studies were performed at each MB factor. 4 slices, 6 slices, 9 slices, and 8 slices were acquired for MB factors of 1–4 respectively. All patients underwent late gadolinium enhancement imaging with phase-sensitive inversion recovery (PSIR) as part of the standard clinical CMR protocol. The sequence parameters of PSIR included: FOV 320–380 by 260–300 mm with 75% phase resolution, matrix size 256×156, in-plane spatial resolution between 1.25 and 1.5 mm, inversion time in the range of 320 to 400 ms, slice thickness 8 mm, TE 3.2 ms, FA 25o, breath-hold and ECG-trigged for 16 heart beats.

Image Analysis

To validate the reconstruction performance, we used data acquired with MB = 1 to retrospectively simulate acquisition and reconstruction for MB factors of 2–4. The retrospectively reconstructed images were assessed quantitatively as compared to the MB = 1 images as a gold-standard using normalized root mean square error (NRMSE) and the structural similarity index³⁴ (SSIM) measured in a manually drawn region of interest only containing the heart. Additionally we performed quantitative analysis of the apparent CNR. The NRMSE and SSIM was analyzed by two-way analysis of variance (ANOVA) with subject as the blocking factor factorial and a P-value<0.05 was considered significant.

Perfusion images for MB factors of 1, 2, 3 and 4 were first reconstructed by SMS-L1-SPIRiT. The reconstruction parameters λ₁ = 0.02 and λ₂ = 0.05 were chosen based on the L-curve analysis, and the parameters were fixed for all datasets. The details of the L-curve analysis were presented in the Supporting Information. Next, dynamic perfusion images from 3 slice locations (basal, mid, and apical) were randomly selected from each patient study for blind grading on a 5-point scale (5 = excellent, 1 = poor) by two cardiologists for image quality assessment. Image quality scores between MB factors were analyzed using the Kruskal-Wallis test.

Results

Figure 3 shows the point spread function (PSF) of the MB = 1, and the interference pattern added by the additional excited slices for MB = 2, 3 and 4 acquisition. The majority of the main lobe energy was cancelled for MB slices 2–4 due the phase sampling scheme, and the side lobe amplitude were 6% of the MB1 main lobe amplitude of MB1 with an incoherent pattern suitable for SMS-L1-SPIRiT reconstruction.

Figure 3.

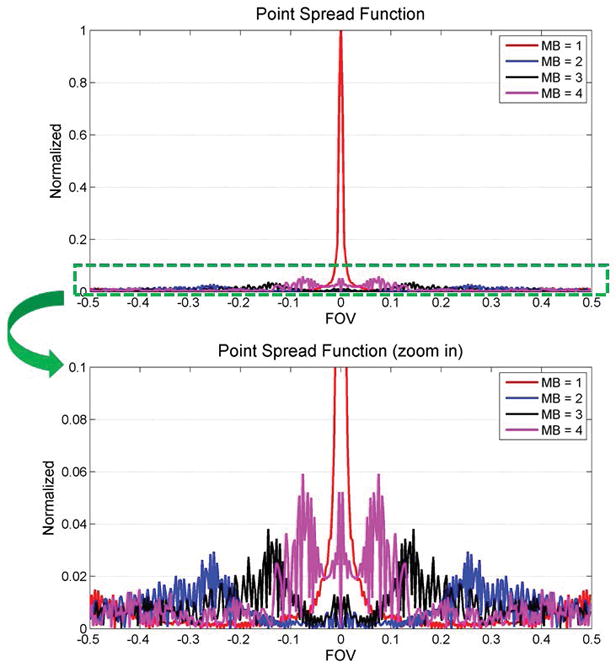
Point spread function (PSF) analysis of the MB = 1, and the interference pattern added by the additional excited slices for MB = 2, 3 and 4 acquisition. The majority of the main lobe energy is cancelled for MB slices 2–4 due the phase sampling scheme. The side lobe amplitude is only 6% of the main lobe amplitude for the MB1 PSF, and has an incoherent pattern suitable for SMS-L1-SPIRiT reconstruction.

Figure 4 demonstrates example perfusion images from one case from the retrospective experiment. The images in the top row were collected without SMS (i.e MB = 1) and reconstructed with L1-SPIRiT to serve as the “gold-standard”. The subsequent rows show images with simulated MB factors of 2 to 4 reconstructed with the proposed SMS-L1-SPIRiT pipeline. This reconstruction technique had minimal residual aliasing artifacts even at the highest MB factor of 4. The perfusion images simulated at MB 2 to 4 visually have image quality comparable to the ground truth MB 1 reconstruction. Figure 5 shows the NRMSE maps from the same subject showing the corresponding residual error as compared with gold-standard images for MB factors of 2 to 4.

Figure 4.

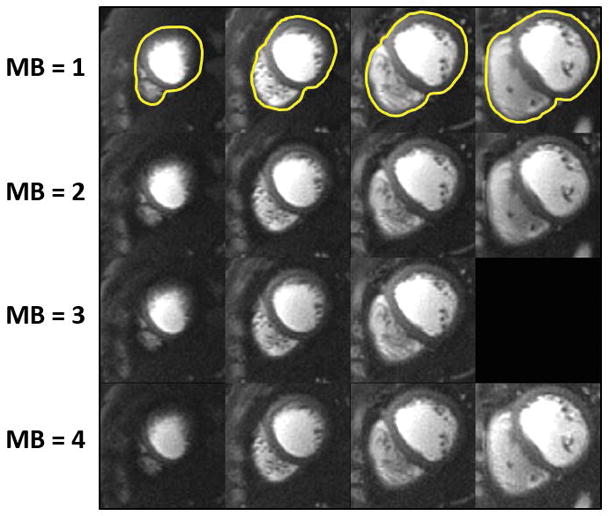
Retrospective SMS reconstruction. The perfusion images in the top row are collected without SMS (i.e MB = 1) and reconstructed with L1-SPIRiT to serve as the “gold-standard”. The subsequent rows show images with simulated MB factors of 2 to 4 reconstructed using the proposed SMS-L1-SPIRiT pipeline. This reconstruction technique has minimal residual aliasing artifacts, even at MB = 4. The perfusion images simulated at MB 2 to 4 visually have image quality comparable to the ground truth MB 1 reconstruction.

Figure 5.

Retrospective NRMSE maps from one subject showing the corresponding residual error as compared with gold-standard images.

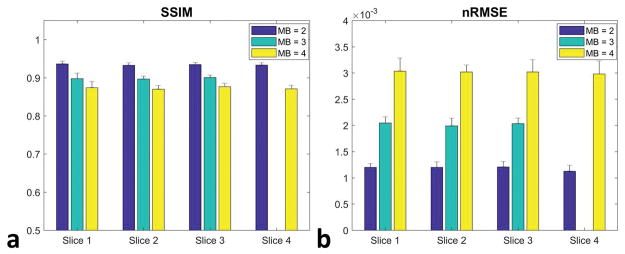
Figure 6 shows the quantitative analysis of NRMSE and SSIM from the retrospective experiments of different MB factors at all slice locations. Increasing the MB factor results in significantly higher NRMSE and lower SSIM values. However, the NRMSE from MB factors 2 to 4 at all slice locations is smaller than 0.5% of the ground truth signal, implying good reconstruction performance.

Figure 6.

Quantitative analysis of SSIM (a) and NRMSE (b) from the retrospective experiments of different MB factors at all slice locations. Increasing the MB factor raised NRMSE while lowering SSIM values. However, the NRMSE from MB factors 2 to 4 at all slice locations is smaller than 0.5% of the ground truth signal, implying good reconstruction performance.

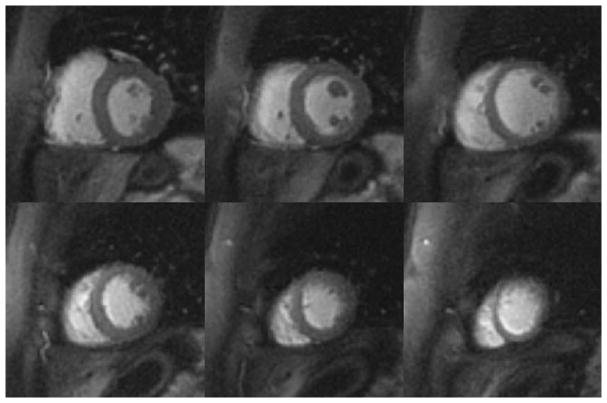
Figure 7 shows perfusion images from a patient (female, 48 years old, evaluated for hypertrophic cardiomyopathy) acquired with MB = 2 and 6 slices per heartbeat at a single time point during first-pass of contrast. Figure 8 shows perfusion images acquired from a patient (female, 40 years old, evaluated for non-ischemic cardiomyopathy) with MB = 3 and 9 slices per heartbeat. Images acquired with both MB = 2 and MB = 3 demonstrate high image quality while maintaining the same spatial-temporal resolution as the single-excitation technique. Corresponding movies for these two subjects are shown in the Supporting Movies S1 and S2.

Figure 7.

Perfusion images from a patient (female, 48 years old, evaluated for hypertrophic cardiomyopathy) acquired with MB = 2 and 6 slices per heartbeat at a single time point during first-pass of contrast.

Figure 8.

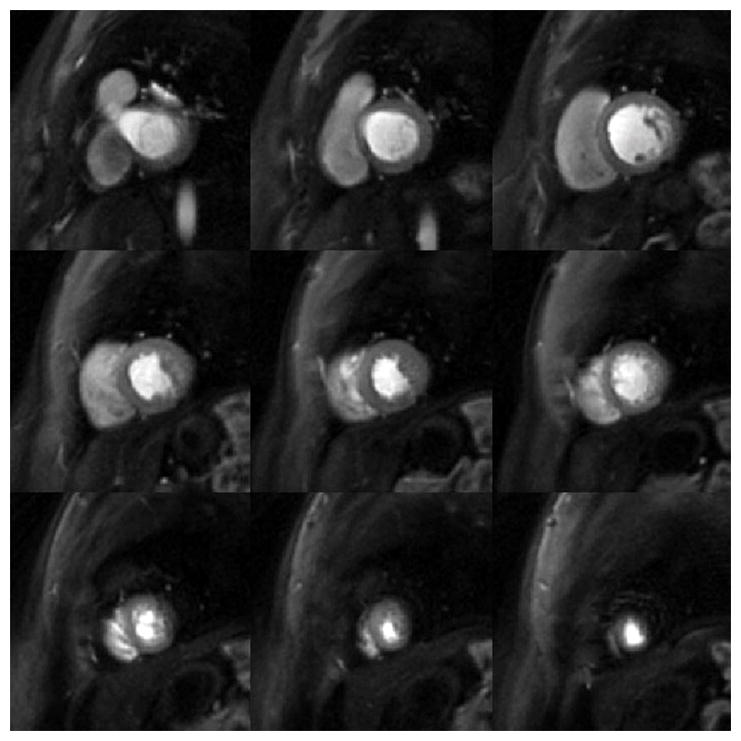
Perfusion images from a patient (female, 40 years old, evaluated for non-ischemic cardiomyopathy) acquired with MB = 3 and 9 slices per heartbeat at a single time point during first-pass of contrast.

Figure 9 demonstrates perfusion images from an ST-elevation myocardial infarction (STEMI) patient (female, 48 years old) at an MB = 4 with 8 slices per heartbeat. Even at this high MB factor, the images (a) clearly delineated a perfusion abnormality with a location corresponding to the infarction on the late gadolinium enhanced images (b).

Figure 9.

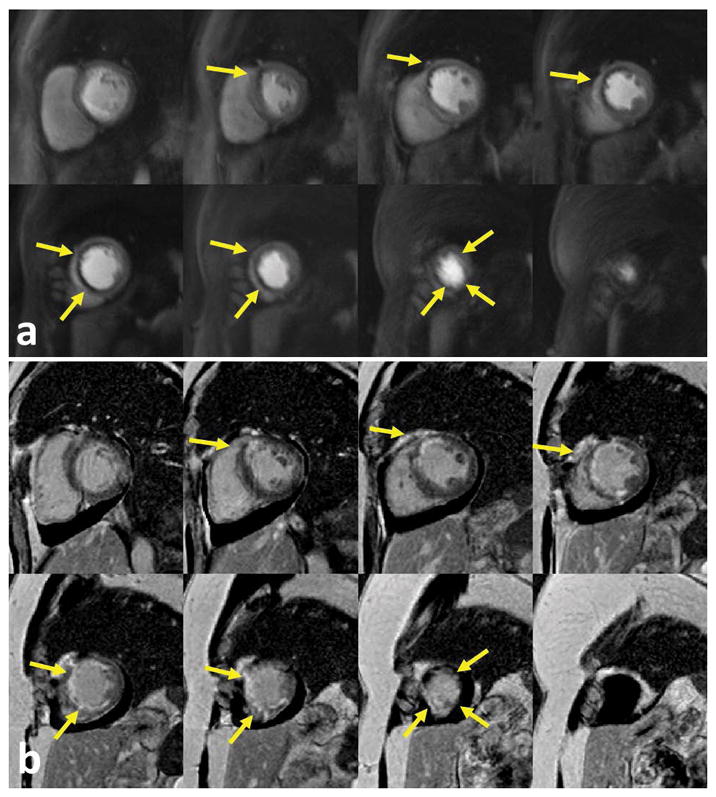
Perfusion images from an ST-elevation myocardial infarction (STEMI) patient (female, 48 years old) at an MB = 4 with 8 slices per heartbeat. Even at a higher MB factor, the perfusion images (a) clearly delineated a perfusion abnormality corresponding with the infarction on the late gadolinium enhanced images (b).

The image quality scores are 4.2±0.5 (MB = 2), 4.3±0.5(MB = 3) and 4.5±0.3 (MB = 4) from cardiologist one, 4.4±0.5 (MB = 2), 4.2±0.5(MB = 3) and 4.2±0.8 (MB = 4) from cardiologist two, with no significant quality difference in image quality between MB factors (p=0.40 for cardiologist one and p=0.58 for cardiologist two).

Discussion

The SMS spiral perfusion sequence with MB factors 2 to 4 enabled high quality and high spatial-temporal resolution perfusion images with whole heart coverage without additional scan time. In Cartesian SMS perfusion imaging using CAIPIRINHA and a parallel imaging reconstruction, phase modulation is used to shift the spatial location of the images from the different slice locations. At higher MB factors, there is significant reduction in g-factor, resulting in reconstructed images with reduced image quality and spatially varying noise amplification. For our non-Cartesian SMS approach using a phase modulation scheme to cancel signal from other slices, the aliasing pattern from the different slice locations appear as an incoherent swirling artifact. By rotating the spiral sampling pattern in time by the golden angle, temporal incoherence of the aliasing artifacts is also achieved. These two factors favor a CS reconstruction such as our proposed SMS-L1-SPIRiT approach. Blinded visual analysis showed high image quality across MB factors 2–4 likely due to the absence of coherent aliasing artifacts. From the quantitative analysis, it is clear that the image degradation at higher MB factors for this approach appears as noise enhancement. The high SNR efficiency of the spiral acquisition combined with the incoherent spatial and temporal aliasing artifacts likely explain the differences between our results and the prior Cartesian SMS results for imaging at high MB factors. We chose finite-difference in time as the sparsity constrained term, as artifacts due to respiratory motion, which usually occur near the end of the breath-hold, tend to be localized to only this portion of the data acquisition. We have recently demonstrated a technique based on a simple rigid-registration of the heart region which further improves robustness of the CS reconstruction to motion³⁵ and have previously applied this technique for spiral perfusion imaging³⁶. This technique is used to correct respiratory motion in the supplemental movie.

Retrospective reconstruction experiments based on MB = 1 clinical datasets showed that as the MB factor increased, the NRMSE also increased. This is due to the fact that more aliasing energy was added from the additional slices, and the constrained reconstruction did not fully recover the images from high MB factors. However, the average NRMSE from all the datasets at all MB factors was still below 0.5% in the heart ROI, with the majority of the increased NRMSE in the lung region resulting in visually similar image quality. The retrospective experiments also demonstrated that the chest wall and body fat contribute to the majority of high-energy aliasing artifacts, which are not completely removed by the phase-modulation strategy. Improved fat suppression or spectral-spatial water-excitation pulses³⁷ may more effectively suppress the signal from chest fat, improving the performance of the SMS spiral perfusion technique. In addition, outer volume suppression³², which we have demonstrated previously for spiral perfusion imaging, can be incorporated into this SMS spiral perfusion sequence to further suppress the signals outside the heart to achieve more benign and incoherent aliasing pattern.

In vivo evaluation in patients undergoing CMR studies demonstrated that our spiral SMS perfusion technique resulted in high quality images at MB factors of 2–4, which had similar image quality to single band variable density spiral perfusion images. The scan efficiency is greatly improved by SMS, which enabled whole heart coverage with the same temporal footprint as our previously validated 3-slice perfusion technique. The proposed SMS spiral perfusion sequence can support heart rates up to 100 BPM (MB=2), 133 BPM (MB=3) and 200 BPM (MB=4) with minimal 8 slice locations to cover the whole ventricle. Despite the similar image qualities from the in vivo cases among different MB factors, the retrospective study still demonstrated that with the higher MB factor, the potential image quality would be reduced. The recommendation for practical selection of MB factors in clinical cases should really base on patient’s heart rate to choose the lower MB factor with the desired ventricle coverage. Our group has previously demonstrated whole heart coverage by utilizing higher in-plane accelerated spirals with a slice-interleaved acquisition¹⁴. In the slice interleaved approach, spiral interleaves are collected by alternating the slice location which is selectively excited. Disadvantages of this approach are that data is only being acquired from each location for half of the total acquisition time for the two slices. Without other changes in the sequence this results in a 30% loss of SNR for each slice position due to the reduction in sampling time. Furthermore, the slice interleaved approach requires a higher in-plane acceleration factor (5x) to achieve the same resolution as the SMS acquisition with a MB factor of 2 which only requires a 1.25× in-plane acceleration factor. The reduction of in-plane acceleration may improve L1-SPIRiT reconstruction, and the longer acquisition time for each slice improves the underlying SNR of the raw data. If we consider the MB factor as an additional acceleration factor, the total acceleration for SMS acquisition with MB 2 to 4 are 2.5, 3.75 and 5× respectively. The above factors create a practical limitation of about 2 slices per saturation for a slice interleaved spiral acquisition, whereas with SMS, 3–4 slices can be acquired simultaneously following a single saturation pulse. Furthermore, the slice interleaved approach required a higher in-plane acceleration factor (5x) to achieve the same resolution as the SMS MB=2 acquisition which only required a 1.25× in-plane acceleration factor. The reduction of in-plane acceleration may improve L1-SPIRiT reconstruction, and the longer acquisition time for each slice improves the underlying SNR of the raw data. If we consider the MB factor as an additional acceleration factor, the total acceleration for SMS acquisition with MB 2 to 4 are 2.5, 3.75 and 5× respectively. While we have evaluated MB factors from 2–4 for myocardial perfusion imaging, the limit on the multi-band factor is likely a function of the intrinsic SNR of the raw data, the incoherence of the PSF, the g-factor of the coil array, and the amount of residual aliasing artifact, as manifested by an increase in nRMSE, which results in clinically acceptable images. As compared to Cartesian SMS imaging, non-Cartesian imaging should be less sensitive to the inherent g-factor related to the coil array configuration, and may explain improved performance at higher under-sampling factors as has been shown for radial imaging²⁸. For myocardial perfusion imaging we typically need about 8–10 slices to cover the whole heart. Given that we typically separate the slices by one slice dimension to avoid cross-talk between slices, practically MB factors above 4 (to perhaps 5) are probably not necessary for this application to achieve whole heart coverage.

The proposed spiral SMS perfusion pulse sequence can be further extended to 3T to achieve higher in-plane spatial resolution with good image quality, which might provide a tool to assess regional difference in the perfusion of the subendo and subepi myocardium. Potential technical challenges for 3T spiral SMS imaging include increased SAR and worse off-resonance artifacts for the same spiral interleaf duration. We have recently demonstrated the feasibility of high resolution spiral perfusion imaging at 3T using both slice interleaved and SMS techniques.

This study has some limitations. Since the patient studies were acquired during a routine clinical examination, we were only able to obtain resting perfusion. Further evaluation of the performance of these techniques with stress imaging in patients with suspected CAD will be necessary for clinical validation. Our spiral design was based on our prior perfusion clinical experience with linear variable density spiral trajectories¹⁸, which have benign undersampling aliasing artifacts. Additional optimization of the spiral trajectories and temporal sampling pattern may further improve the performance of this technique. Our goal in this study was to evaluate whether directly accelerating the acquisition of spiral perfusion imaging is feasible with SMS MB factors of 2–4. We previously evaluated the golden angle rotation of spiral trajectories through time to generate incoherence temporal sampling¹⁴. We chose this temporal sampling strategy so that the residual aliasing artifacts resulting from our Hadamard phase-cycling strategy would be incoherent in time and amenable to a temporal CS constraint. Further optimization of the temporal sampling pattern and phase cycling strategy may also improve image reconstruction.

In conclusion, we demonstrated the successful application of an SMS spiral perfusion at MB factor 2, 3 and 4 in a clinical setting. Due to the increased sampling efficiency of SMS, whole heart coverage was achieved with high image quality without the need for interleaving slices or significantly shortening the readout time for each slice. Further validation will be required in patients undergoing vasodilator stress CMR.

Supplementary Material

Supp VideoS1

Supporting Movie S1: Perfusion movie from a patient (female, 48years old, evaluated for hypertrophic cardiomyopathy) acquired with MB = 2 and 6 slices per heartbeat.

Supp VideoS2

Supporting Movie S2: Perfusion movie from a patient (female, 40 years old, evaluated for LV dysfunction) acquired with MB = 3 and 9 slices per heartbeat.

Supp info

Supporting Table T1. Apparent CNR analysis from retrospective and prospective experiments.

Supporting Figure F1: L-curve analysis for MB factor of 2 from 10 retrospective cases to demonstrate the selection of reconstruction parameters.

Supporting Figure F2: L-curve analysis for MB factor of 3 from 10 retrospective cases to demonstrate the selection of reconstruction parameters.

Supporting Figure F3: L-curve analysis for MB factor of 4 from 10 retrospective cases to demonstrate the selection of reconstruction parameters.