Design and Validation of a Semi-Active Variable Stiffness Foot Prosthesis

Abstract

This paper presents the design and validation of a novel lower-limb prosthesis called the Variable-Stiffness Foot (VSF), designed to vary its forefoot stiffness in response to user activity. The VSF is designed as a semi-active device that adjusts its stiffness once per stride during swing phases, in order to minimize size, mass and power consumption. The forefoot keel is designed as an overhung composite beam, whose stiffness is varied by moving a support fulcrum to change the length of the overhang. Stiffness modulation is programmed in response to gait characteristics detected through foot trajectory reconstruction based on an embedded inertial sensor. The prototype VSF has mass of only 649 g including the battery, and build height of 87 mm. Mechanical testing demonstrated a forefoot stiffness range of 10–32 N/mm for the prototype, a threefold range of stiffness variation. The stiffness range can be altered by changing the keel material or geometry. Actuation testing showed that the VSF can make a full-scale stiffness adjustment within three strides, and tracks moderate speed-driven variations within one swing phase. Human subjects testing demonstrated greater energy storage and return with lower stiffness settings. This capability may be useful for modulating prosthesis energy return to better mimic human ankle function. Subjective feedback indicated clear perception by subjects of contrasts among the stiffness settings, including interpretation of scenarios for which different settings may be beneficial. Future applications of the VSF include adapting stiffness to optimize stairs, ramps, turns, and standing.

I. Introduction

THE standard high-performance prosthesis for persons with lower-limb amputation is an Energy Storage and Return (ESR) foot. ESR prostheses store and return energy to the user through deflection of compliant leaf springs, bumpers or other elastic elements. The driving mechanical factor in the performance of ESR feet is the stiffness of the compliant elements. The type of foot and stiffness category is usually chosen by a prosthetist based on the user’s weight and activity level. Since the stiffness of the foot is fixed, it cannot adapt to different conditions during daily life including walking up and down stairs and ramps, walking faster or slower than normal, or transitioning between standing and walking. This fixed behavior contrasts with the behavior of a healthy ankle, which modulates its performance to match conditions, such as increasing push-off work or plantarflexion angle with walking speed or slope [1], [2].

Recent advances have produced several prostheses that actively vary their behavior under microprocessor control. The most aggressive approach is to use a fully actuated robotic ankle that provides mechanical power during the gait cycle, such as the Ottobock Empower [3]. This and other powered prostheses [4]–[10] may provide superior function to ESR feet, but their cost, height, weight, and power consumption are substantial challenges to wide adoption. An alternative can be found in the class of semi-active prostheses. These devices modulate their mechanical properties without applying human-scale power. Several examples use hydraulic elements to vary resistance, including the Endolite Elán [11], College Park OdysseyK2 [12] and OdysseyK3 [13], Fillauer Raize [14], Ottobock Meridium [15] and Triton Smart Ankle [16], and Freedom Innovations Kinnex [17]. These ankles adjust their resistance (damping) during certain portions of the gait cycle with the goal of adapting to different terrain. But, the hydraulic resistance can have adverse effects because adjusting resistance also affects the amount of power dissipated through ankle motion [18], [19]. The Össur Proprio Foot [20] uses another strategy, actively adapting ankle angle using robotic control. This is advantageous for slopes and stairs, but varying the angle still does not vary the energy storage and return that is analogous to healthy ankle push-off work.

Another approach to modulating properties is to vary prosthesis stiffness in the sagittal plane. Most such efforts use variable-stiffness actuators [21] capable of power input, such as pneumatic muscles [22], [23] or series elastic actuators [24]–[26]. Others modulate impedance, the dynamic version of stiffness, through active robotic emulation [27]–[29]. These solutions retain the advantages and drawbacks of robotic prostheses described above. Another approach uses discrete mode switching, e.g. to change between walking and standing stiffnesses [30] or shapes [31]. Recently, the Variable-Stiffness Prosthetic Ankle-Foot (VSPA Foot) has implemented a true semi-active mechanism for ankle stiffness modulation [32]. It uses an internal leaf spring with varying free length to modulate overall stiffness, shaped by a cam in the ankle designed to emulate a human’s varying ankle impedance.

This paper introduces an alternative variable-stiffness design called the Variable Stiffness Foot (VSF; Fig. 1). Rather than emulating a varying impedance within the gait cycle, the VSF retains the leaf-spring rollover structure of commercial ESR prostheses, and rapidly modulates overall stiffness on a stride-to-stride basis in response to changes in the user’s movement pattern. The VSF combines the energy-storing and stiffness-modulating components to achieve the design goals of very low mass and build height compared to other semi-active feet. Example intended use cases include: reducing stiffness with increasing speed to increase energy storage and return [33], [34]; setting very high stiffness for standing stability [30], [35]; and modulating stiffness on slopes and stairs to mimic the effects of ankle angle changes [36]–[44].

Fig. 1.

Variable Stiffness Foot (VSF) prototype. A composite leaf spring keel is supported by a moveable fulcrum, changing the free length to adjust the forefoot stiffness of the prosthesis. The semi-active design achieves nearly fourfold variation of stiffness while maintaining low weight, build height, and power consumption. An embedded sensor and controller provides real-time adaptation to changing demands of balance and locomotion.

II. Design Concept

The VSF aims to balance the simplicity of ESR feet and the adaptability of powered ankles to provide a significant benefit while minimizing weight, height, and power consumption. The VSF is a semi-active foot that acts like a traditional ESR foot during the stance phase of walking but during the swing phase, it can rapidly change its forefoot stiffness based on use conditions. It is outfitted with an inertial measurement unit (IMU) and microcontroller to estimate the foot’s trajectory in real time, identify key movement characteristics, and vary stiffness in response. For example, in our first study the VSF is programmed to change stiffness based on walking speed; other options include changing stiffness based on slope, stair ascent/descent, turning, and/or standing.

A. Variable Stiffness Keel

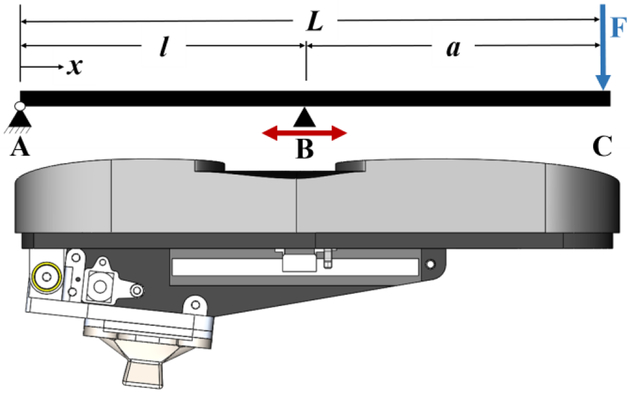
The forefoot keel of the VSF is an overhung beam that changes its endpoint stiffness by moving a support fulcrum to alter the length of the overhang (Fig. 2). Moving the fulcrum alters the deflection of the forefoot for a given load, and thereby varies the stiffness of the forefoot. Analytically, the VSF can be broken down into three main components analogous to the beam model: the composite leaf spring keel, the rotation joint, and support fulcrum (Fig. 3). Equations (1) and (2) are derived from the Euler-Bernoulli overhung beam model with a force F applied at the toe, where y_c is deflection at the toe (point C), k is stiffness at the toe, and keel parameters are shown in Fig. 2 and Table 1.

$$y_C=-\frac{FL{a}^2}{3EI}$$ (1)

$$k=\frac{F}{y_C}=\frac{3EI}{L{a}^2}$$ (2)

The materials and geometric parameters (Table 1) were designed to provide a fourfold range of stiffness, approximating that observed in humans and used in other prostheses [45]. Using the designed range of fulcrum positions (varying a and l, Table 1), the stiffness of the forefoot keel was predicted to vary from 9 to 40 N/mm.

Fig. 2.

Euler-Bernoulli overhung beam model showing the VSF upside-down to match the traditional model orientation. The keel is pinned at A and simply supported at B.

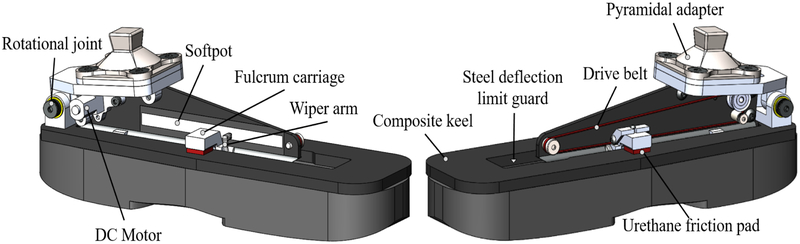
Fig. 3.

Variable Stiffness Foot (VSF) CAD Model identifying important design features.

Table 1.

Nominal parameters of the VSF forefoot keel

L	beam length	229 mm
a	overhung length (variable)	163 to 78 mm
l	supported length (l = L − a)	66 to 151 mm
I	moment of inertia (bh3/12)	992 mm4
b	cross section width	46.5 mm
h	cross section height	6.35 mm
E	flexural elastic modulus	18.6 GPa [38]

The deflection y_AB of the keel at any point x between the rotation joint A and the fulcrum B is given by:

$$y_{AB}(x)=\frac{Fax}{6EIl}(l^2-x^2)$$ (3)

The derivative of deflection gives the angle of the keel θ_AB (4). The angle at the rotation joint (x = 0) is given by (5).

$${\theta }_{AB}(x)=\frac{d{y}_{AB}}{dx}=\frac{Fal}{6EI}-\frac{Fa{x}^2}{2EIl}$$ (4)

$${\theta }_{AB}(0)=\frac{Fal}{6EI}=\frac{Fa(L-a)}{6EI}$$ (5)

Assuming a load F = 1200 N, the angle at the rotation joint was predicted to be between 6.7 and 8.1 degrees. Because this rotational angle is substantial, it was necessary to build a physical rotation joint instead of a simple bolt or bushing joint, to avoid over-constraining the system.

B. Drive Mechanism

The fulcrum carriage translates along the length of the composite keel, effectively varying the overhang length a. The carriage is attached to a belt driven by a small DC motor (Micro Metal Gearmotor HP 6V, Pololu, Las Vegas, NV, USA; mass 9 g) at the proximal end of the foot. Position feedback is given by a linear potentiometer (Softpot SP-L-0100-103-3%-MP, Spectra Symbol, Salt Lake City, UT, USA), contacted by a compliant wiper fixed to the carriage. Position is controlled with a bang-bang algorithm, allowing a sufficient dead zone to avoid wasting power to correct negligible errors. To minimize actuator mass and power consumption, the system is commanded to move only during the swing phase of walking when the forefoot is unloaded. This means that the stiffness setting is constant during each stance phase and no power is directly transferred to the user from the motor. Since the fulcrum carriage can only be driven during the swing phase of walking, the adjustment needs to be as fast as possible to maximize the effectiveness of the varying stiffness. The VSF achieves this using the belt system shown in Fig. 3. A timing belt passes over a motor pulley and two idler pulleys and is attached by screw clamps to the fulcrum carriage. A belt tension torsion spring (not shown) is used to prevent slipping. This belt system replaced an earlier power screw design, which was heavier, slower, and subject to over-constraint and misalignment problems. The belt driven design is lighter, faster, and much more robust to flexibility in the system.

C. Other Design Features

Since the belt provides no resistance to movement when the motor is unpowered, urethane friction pads (Fig. 3) are used to make the system non-backdrivable. This feature proved critical to enabling the belt system and to overall weight reduction efforts. In addition to establishing non-backdrivability, the urethane pads also act to reduce the stress concentrations that would otherwise be caused by the direct contact between the aluminum fulcrum carriage and composite keel.

The rail on which the fulcrum carriage rides was designed with a round profile to allow the fulcrum to rotate to compensate for uneven loading in the frontal plane. The rotation could also allow for future designs to use a split-toe keel similar to those found in many commercial prostheses.

D. Weight and Build Height

The current VSF has a total mass of 649 grams including battery and pyramid adapter. This is comparable to the mass of commercially available passive ESR prosthetic feet (e.g. Freedom Innovations’ Renegade, 625 g [46]; Ability Dynamics’ Rush LoPro, 639 g [47]) and much less than popular robotic feet (e.g. Ottobock Empower, 2200 g [48]; Össur Proprio, 1424 g [20]). The main components of the VSF mechanism (keel, frame, carriage, and controller) have a combined mass of 478 grams. The battery and support foam have masses of 65 and 106 grams, respectively. These components could be optimized to further reduce mass, especially the battery which is much larger than necessary.

The foot also has a lower build height (87 mm with support foam; 50 mm without support foam) than many commercially available feet, potentially allowing use by individuals with longer residual limbs. For comparison, the Rush LoPro that is specifically designed for users with long residual limbs has a build height of 114.3 mm [47]. The current support foam is thick for walking without a shoe, but in future versions it will be made thinner (and lighter) to fit inside a shoe.

E. Control of the VSF

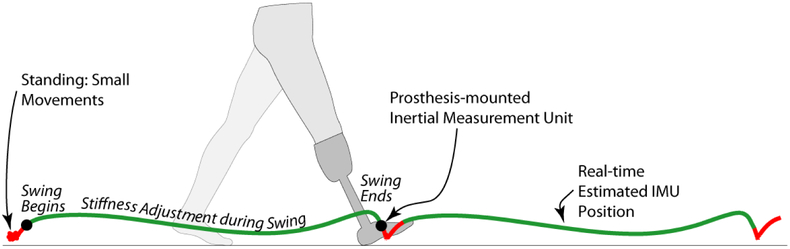
During all modes of operation, the VSF is controlled according to gait characteristics estimated using the onboard IMU (Fig. 4). The trajectory of the IMU is calculated using strapdown integration [49], [50], in real-time. Based on this reconstruction, gait characteristics are estimated, such as speed or stair ascent/descent. These gait characteristics determine the stiffness setting, which in turn determines the target fulcrum location, which is finally controlled by the motor.

Fig. 4.

Method of real-time stiffness changes using based on movement kinematics. Signals from the onboard IMU are numerically integrated to estimate gait parameters, which are mapped to desired adjustments in stiffness during swing phases.

One example use case is to vary the stiffness with walking speed. This program might be desirable, for example, to increase energy return at higher speed by reducing the forefoot stiffness [34]. In this case, foot position is recorded when the foot speed is below a pre-specified threshold during mid-stance. After another gait cycle, the new foot position is recorded at the next mid-stance. These mid-stance times and positions are used to calculate stride length and walking speed. Speed is then mapped to stiffness, corresponding to a specific analog value on the Softpot. The motor then drives the carriage to the desired position while the foot is unloaded in the next swing phase.

F. Drive Mechanism Performance

Fig. 5 shows an example of the stiffness changes in real time. In this example, the VSF was programmed to change stiffness linearly with walking speed, and the user intentionally varied speed to test this function. The inset shows the details of a typical adjustment: a slight overshoot (left uncorrected to minimize power consumption), followed by a slight settling movement when the forefoot is loaded. Any error that accrues due to such settling is corrected when it builds beyond the dead zone of the controller. The stiffness achieved by the foot matches the target stiffness as expected.

Fig. 5.

(left) Actual stiffness measured by the fulcrum position versus target stiffness mapped from walking speed. 1. Toe off, speed is updated, fulcrum can move. 2. Heel contact, fulcrum moves slightly under load. 3. Second toe off. (right) Fulcrum speed test demonstrating that the fulcrum can move through the entire range in three swing phases of normal walking.

The fulcrum can move through the full range of stiffness settings in less than 3 swing phases at a typical speed, as demonstrated in a contrived test at right (Fig. 5). This test represents the most extreme example. In real use, the subject would most likely not use the full range of stiffness during normal walking, and would seldom change speed so rapidly as to induce such a change. Therefore the fulcrum would rarely make such a full-scale adjustment, and the practical adjustment delay is likely 1–2 strides.

G. Variable Stiffness Performance

The achievable stiffness range was determined through static compression testing (Model 120-P-1000, TestResources, Shakopee, MN, USA). Load was applied at a constant speed (50 mm/min) to a point 30 mm proximal to the toe to maintain contact throughout the deflection (30 mm proximal to the toe = 200mm beam length L from the rotational joint, Figs. 2–3). Stiffness was computed as the slope of the force-displacement curve for points with greater than 200 N loading. This test was performed with the fulcrum set to five different positions. Forefoot stiffness was measured with and without the support foam. Heel stiffness was measured with the support foam using the same method, but only for one fulcrum position since the structures supporting the heel do not move with the fulcrum. Due to limitations in the compression testing machine, the maximum load used was 700 N and this was further limited when testing the softest settings due to large displacements. Also, it should be noted that the stiffness measurements are for a specific keel design; the stiffness range can be increased or decreased by changing the material or geometry of the keel or the support foam.

Fig. 6 (left) shows the measured forefoot force-displacement curves. With support foam (i.e., in the conditions experienced by a user), forefoot stiffness ranges from 10 to 32 N/mm (Fig. 6, right, blue circles). With only the structural keel (Fig. 6, right, red squares), forefoot stiffness ranges from 12 to 44 N/mm. Heel stiffness is 66 N/mm and is solely due to foam compression, as the mechanism is rigid on the heel side. The relationship between forefoot stiffness and fulcrum position follows a second-degree polynomial fit, which is used to compute intermediate stiffness settings for the fulcrum. The measured relationship is compared to the predictions of the beam model (2) using a beam length adjusted to account for the more proximal loading point in the compression tests (200 mm). This reduction affects both L and a, so the predicted stiffness range is dramatically increased relative to the full-length keel, to 15 to 115 N/mm. The much lower measured stiffness can be attributed to unmodeled deformations in the proximal support structures (urethane friction pads, fulcrum arms, frame, mounting brackets), which add series compliance.

Fig. 6.

(left) Force vs. displacement curves from mechanical testing of the VSF as worn (keel with support foam) for five fulcrum positions. Stiffness k is the slope of the least-squares linear fit to data above 200 N load; values are shown in the legend and plotted at right (blue circles). Keel-only data not shown. (right) Stiffness k vs. fulcrum position I with theoretical curves (dashed) and model fits to data (solid, Eq. 2) for the conditions of keel only (squares, model fit R2=0.9992) and keel plus foam (circles, model fit R²=0.9997). For the keel-plus-foam theoretical stiffness, the measured stiffness of the foam was added as a series spring to the model-predicted stiffness of the keel. Flexural modulus was taken to be the apparent modulus of the least stiff keel-only condition.

III. VSF Performance in Human Walking

We performed a pilot study to evaluate the ability of the VSF to control stiffness in real-time and to evaluate how the stiffness changes influenced energy storage and return. Three persons with unilateral transtibial amputation completed a preliminary set of trials to test these metrics. There were two males and one female, ages 34, 61, and 70 years, all 8+ years post amputation. Subjects gave their written informed consent to participate in the study according to IRB-approved procedures.

A. Subject Specific Stiffness Range

The VSF has a set stiffness range of 10 to 32 N/mm with the support foam attached and a 6.35 mm thick G10/FR4 keel. The deflection is limited by a hard stop in the support foam, which contacts the superstructure when the adjacent point on the keel deflects 30 mm. Deflecting the foot to this hard stop can cause undesired effects in the gait biomechanics, so we set a minimum stiffness for each subject based on his/her body mass.

We derived the value of this minimum stiffness using the same overhung beam model used to derive (1), scaled using the measured mechanical test results. We assumed a maximum force of 1.2 times body weight (typical for fast walking [51]) applied at the toe, and calculated the fulcrum location that would just prevent engagement of the hard stop. We converted this fulcrum location to a stiffness value, and applied a safety factor of 1.1. This procedure resulted in a quadratic relationship between body mass and the minimum stiffness setting for each user. The maximum stiffness was set to the maximum of the achievable range, or the maximum deemed tolerable for walking by the user in a preliminary test.

B. Data Collection and Analysis

Subjects completed nine over-ground walking trials (three at each stiffness: softest, medium, and stiffest) at 1.2 ± 0.1 m/s. We recorded body movement (Optitrack Prime 13, NaturalPoint, Inc., Corvallis, OR, USA) and ground reaction forces (Bertec, Inc., Columbus, OH, USA) under both feet. Recorded trials were preceded by a short acclimation period of hallway walking, stairs and ramps.

We computed lower-body joint kinematics and inverse dynamics using Visual 3D software (C-Motion, Inc., Germantown, MD, USA). We used a “functional joint centers” method using the Gilette algorithm [52] to calculate the location of each joint. We computed power absorption and return for the prosthesis using the unified deformable segment model (UD power, [53]). We computed energy stored and returned by the prosthesis by integrating UD power, excluding the initial heel impact.

We non-dimensionalized the data using subject specific body mass, M, and leg length, L, and the acceleration due to gravity, g. Work or energy was non-dimensionalized by M·g·L (redimensionalization value from mean subject parameters: 688 J) and stiffness by M·g/L (0.787 N/mm).

We hypothesized that energy stored and returned by the prosthesis would follow a hyperbolic trend with respect to stiffness, derived from Hooke’s law:

$$E=F^2/2k$$ (6)

Here F is peak force applied to the forefoot and k is the stiffness. Assuming F is constant across conditions, the relationship simplifies to a hyperbolic prediction:

$$E\text{ = }c\left(1/k\right)$$ (7)

We computed the fit coefficient c for energy stored and for energy returned using linear regression. To account for inter-subject variations, we allowed subject-specific offsets in the model fit, and averaged them. Accompanying r² values were computed without these offsets, to quantify only the variation explained by the independent variable rather than by the offsets.

IV. Results

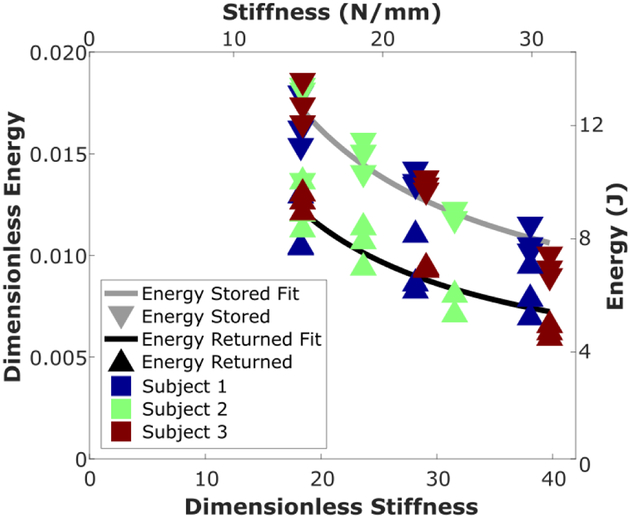
Example prosthetic side unified deformable segment power is shown in Fig. 7 for three stiffnesses spanning the possible range. The trend of higher peaks in power absorption and generation with lower stiffness settings was consistent across subjects. The curve fits (7) showed a statistically significant relationship (Fig. 8) between stiffness and energy stored in the prosthesis (P<0.001) and energy returned (P<0.001). The best fit for dimensionless stored energy ranged from 0.0106 at the highest stiffness (re-dimensionalized value: 7.30 J) to 0.0173 at the lowest stiffness (11.91 J). The data fit for dimensionless energy returned ranged from 0.0072 (4.96 J) to 0.0122 (8.40 J). Dimensionless stiffness ranged from 18.25 (14.37 N/mm) to 39.75 (31.29 N/mm) based on the subjects’ body parameters.

Fig. 7.

Example prosthetic side uniform deformable segment power delivered to the shank by the foot for a speed of 1.2±0.1 m/s. Energy storage and return increase with lower stiffness settings.

Fig. 8.

Energy stored (P<0.001, R²=0.8) and energy returned (P<0.001, R²=0.7), with hyperbolic model fit.

V. Discussion

A. Prosthesis Performance

The VSF performed mostly as hypothesized during this study. It was able to modulate its stiffness in real time based on a user’s walking speed. It was able to move through its full range of stiffness in about three swing phases (Fig. 5), meeting the initial goal for the speed of the design. It was also shown that increased forefoot stiffness led to decreased energy return to the user, which aligns with findings in past studies [33], [34].

Subject feedback indicated that different settings of the VSF affected user perception. One subject walking over level ground with the stiffest setting stated “It’s like you put a two-by-four [a rigid flat wooden board] on the bottom of my foot”. After descending a ramp with the same setting, the subject also said “I’m assuming this mode is for going down ramps.” For the softest setting the subject said it felt like “putting it in overdrive” and that “going up the ramp is so much easier.” Other subjects made similar comments contrasting different settings, indicating that changes in stiffness had a strong effect on how the foot felt to the user.

B. Hypothesized Use Cases for Active Control

Based on the VSF’s influence on energy storage and return and user perception, we propose some hypotheses about how the stiffness variations accomplished by the VSF could help address some documented shortcomings of prostheses and improve gait. First, we hypothesize that users would prefer to have a forefoot that decreases its stiffness (becomes more compliant) as walking speed increases. This trend would lead to increasing energy return at higher speeds, which is a well-known aspect of natural ankle performance. Second, we hypothesize that for walking up ramps users would prefer a more compliant forefoot, to allow for quicker center of mass progression over the ankle and larger range of motion that can be limited with a stiff foot [42]. For walking down ramps, we hypothesize that users would prefer a stiffer forefoot. In these cases, the user tends to fall forward as they progress down a ramp, and a stiffer foot may help to slow their center of mass [39]. Third, we hypothesize that for walking down stairs users would prefer a more compliant forefoot because healthy ankle dorsiflexion (corresponding to increased prosthetic foot deflection) is greater than when walking on level-ground [54]. Conversely we hypothesize that a stiffer forefoot would be preferred for ascending stairs because the goal is to gain elevation and increased deflection from a more compliant prosthesis would act against this goal [37], [55]. A stiffer forefoot would limit the deflection and therefore limit the elevation loss. Each of these hypotheses is a candidate for future testing of user preferences and biomechanical performance.

C. Limitations

This study was limited by the fact that the VSF has a fixed size and stiffness range. The length does not exactly match any of the subjects that have participated in the study thus far. This can make walking on the foot slightly unnatural especially when going up stairs. Ideally, the VSF length would be matched to the subject’s prescribed foot, but manufacturing a new keel for each subject was not practical at this stage.

The stiffness range could also be more finely tuned for each subject. In this study the minimum stiffness is set according to body mass and the maximum stiffness is the maximum setting of the prosthesis. These changes are defined by mechanical limitations of the VSF, and not what might be best for each subject. The results of this study should help inform future studies on how to better tune the stiffness for each subject.

The testing and foot control laws assume that the ground reaction forces will be relatively constant for all normal walking. However, this may not always be the case. Since the deflection of the foot is directly proportional to the force applied to it, the foot’s effect on the user can change from stride to stride depending on how much the forces change. This could account for some of the variation in the data between strides of the same setting and may need to be accounted for to fully understand the effects of the VSF on its user.

The delay of at least 1 stride in adjusting settings to match gait is also sub-optimal. In ideal circumstances, stiffness would be adjusted during the swing phase prior to the step when it is needed. It may prove possible to anticipate the desired settings based on classification of IMU signals during early and mid-swing phase, potentially enabling adjustments before the next footfall. Alternatively, intent-recognition techniques such as in-socket EMG could be used to give users feed-forward control of the stiffness, eliminating any perception of delay [56], [57].

Finally, the analysis up to this point is limited by the small number of participants. Acclimation periods were also shorter than ideal and should be extended in future studies if possible.

D. Future Work

The study will be expanded to include more participants to strengthen the statistical basis for the current outcomes and to analyze other biomechanical outcomes like proximal joint mechanics. The VSF’s effect on the user will be measured in level walking at constant and varying speed with the VSF set to vary stiffness based on walking speed. We will also collect and analyze data for walking up and down stairs and ramps for a variety of stiffness settings to determine which settings give preferable biomechanical outcomes. We will record user preference throughout all conditions with a standardized questionnaire to better understand how biomechanical variations translate to user perception. We will also investigate spontaneous behavioral adaptations, such as changes in preferred walking speed for different stiffness settings, or other unanticipated adaptations.

The VSF also provides a capable platform to test other phenomena discovered in previous literature but still not fully understood, such as the “drop-off effect” in prostheses that have a forefoot that is too compliant [58]. Tests with the VSF could explore the trade-off between maximizing energy return (minimizing stiffness) and supporting body weight to prevent the drop-off effect. VSF testing could also investigate the value of modulating stiffness for varying walking speed, in comparison to an optimal constant stiffness. Since the energy returned by conventional passive prostheses is only about 60–65% [59] of the push-off work provided by a healthy ankle, it is possible that the best strategy is simply to maximize the energy return for all walking speeds by using the most compliant foot possible, but this question can only be resolved by a direct comparison.

VI. Conclusion

The Variable Stiffness Foot allows real-time modulation of stiffness in a lightweight, low-power semi-active prosthesis. This stiffness variation allows modulation of energy storage and return and influences user perception. Real-time stiffness modulation could provide a means of beneficial adaptation to the different activities a person undertakes, including standing, walking at different speeds, and negotiating stairs and ramps. Initial hypotheses for how the VSF could be programmed to maximize benefit will be pursued in future work.