Quantifying and comparing bacterial growth dynamics in multiple metagenomic samples

Abstract

Accurately quantifying microbial growth dynamics for species without complete genome sequences is biologically important but computationally challenging in metagenomics. Here we present DEMIC, a new multi-sample algorithm based on contigs and coverage values, to infer relative distances of contigs from replication origin and to accurately compare bacterial growth rates between samples. We demonstrate robust performances of DEMIC for various sample sizes and assembly qualities using multiple synthetic and real datasets.

Reporting Summary

Further information on experimental design is available in the Nature Research Reporting Summary linked to this article.

The growth dynamics of microbial populations is an important feature that reflects their physiological status and drives variation of their compositions. Available approaches for estimating the growth dynamics of bacteria make use of phenotypic markers, sequencing tag or fluorescence dilution and involve additional experimental steps^1–4. Such methods are often limited by low stability, population complexity or aerobic environment. Recently, peak-to-trough ratio (PTR) was reported as a promising index for species with complete genome sequences⁵. PTR measures growth dynamics of a bacterial population by calculating sequencing coverage difference resulting from bidirectional replication from a fixed replication origin in the genome (Supplementary Fig. 1).

For species with only genome assemblies, the accurate locations of the assemblies on the original genome are unknown, making it infeasible to calculate peak-to-trough ratio of the coverages^5,6. In addition, the contigs assembled from metagenomic sequencing data are usually fragmented due to intraspecific variations, interspecific/intraspecific repeated sequences as well as limited sequencing depths^7,8. Moreover, binning algorithms sometimes fail to cluster all the contigs from the same species into one group, or erroneously include a fraction of contigs from other species^9–11. These noisy features complicate the estimation of growth dynamics for genome assemblies.

Here, we present Dynamic Estimator of Microbial Communities (DEMIC), which takes advantage of highly fragmented contigs assembled in multiple metagenomic samples such as different time points or host subjects to accurately compare growth dynamics of a given species observed in multiple samples. In DEMIC, for a given contig cluster, relative distances from the replication origin that contribute most to the variability of read coverages of different contigs are inferred via dimension reduction of contig coverage matrix (Fig. 1, Methods). This is combined with GC bias correction and contig/sample filtering to achieve the final estimates of the growth dynamics of different samples. The method can be applied to a wide range of bacterial communities with closely related species and is robust to sample sizes, contig contaminations and completeness of contig clusters.

Figure 1. Computational pipeline of DEMIC.

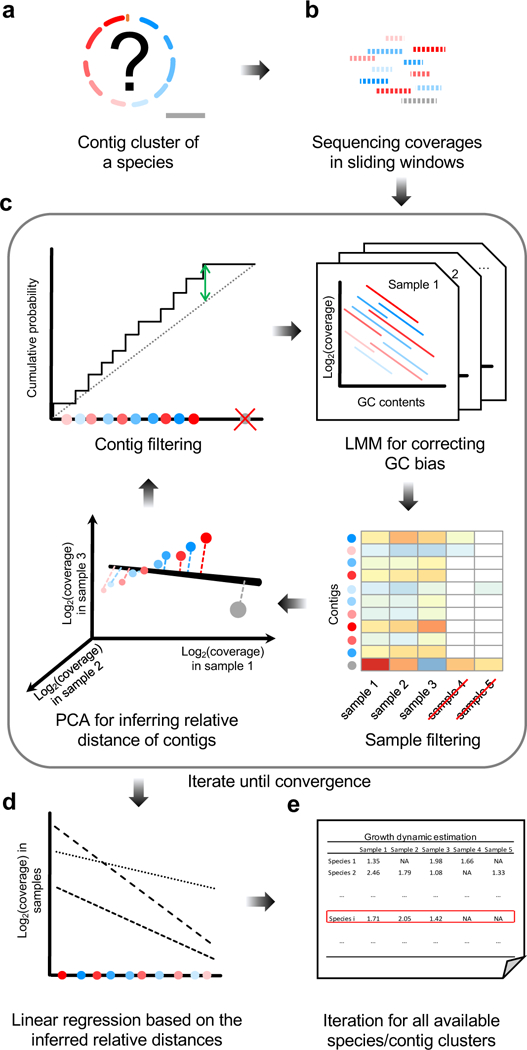
(a) In a contig cluster identified by the binning algorithm, the genomic locations and potential contamination of contigs represented by different colors are unknown. (b) The coverages (sequencing depths) of contigs in a cluster are first calculated for all sliding windows. (c) The inference is an iterative process that includes GC bias correction using LMM, identification of informative samples, relative distance inference using PCA and filtering of contaminated contigs. Colored dots represent different contigs in the cluster. (d) After convergence of both sample and contig sets, growth rates are estimated for the informative samples. Dashed lines represent linear regressions of log-transformed coverages of contigs in different samples and their inferred relative distances to the replication origin. (e) The same pipeline is applied to each of the contig clusters identified by the binning algorithm.

To evaluate the performance of DEMIC, we used multiple sequencing data sets from four bacterial species grown in different media, including 36, 36, 50 and 19 data sets of Lactobacillus gasseri, Enterococcus faecalis, Citrobacter rodentium and Escherichia coli, respectively (Supplementary Fig. 2, Methods). When applied to contig clusters of three species (L. gasseri, E. faecalis and C. rodentium with completeness and contamination shown in Supplementary Table 1) generated from the synthetic data sets by co-assembly and binning^12,13, DEMIC was able to estimate the growth rates in all 122 species-experiment combinations (Supplementary Fig. 3).

PTRC⁵, the method to calculate the PTR, relies on the availability of complete reference genomes and has been demonstrated experimentally to be accurate in estimating the growth dynamics for the data sets analyzed above. PTRs from PTRC were therefore chosen as the gold standard in our evaluations. As shown in Fig. 2a,b and Supplementary Fig. 4, estimates from DEMIC and PTRC were highly correlated for all 122 growth rates of all three species. In contrast, iRep⁶, the algorithm based on the draft genomes, had relatively low and unstable correlations with PTRC. For example, E. faecalis had a moderate growth rate in sample 24 based on the estimates from PTRC and DEMIC, but it was classified by iRep as fast growing (Fig. 2a). For C. rodentium, although contig contamination accounted for about 15% of the contig clusters (Supplementary Table 1), estimates from DEMIC still showed a correlation of 0.97 with PTRs (Fig. 2b).

Figure 2. Performance evaluation of DEMIC based on sequencing data sets of three species.

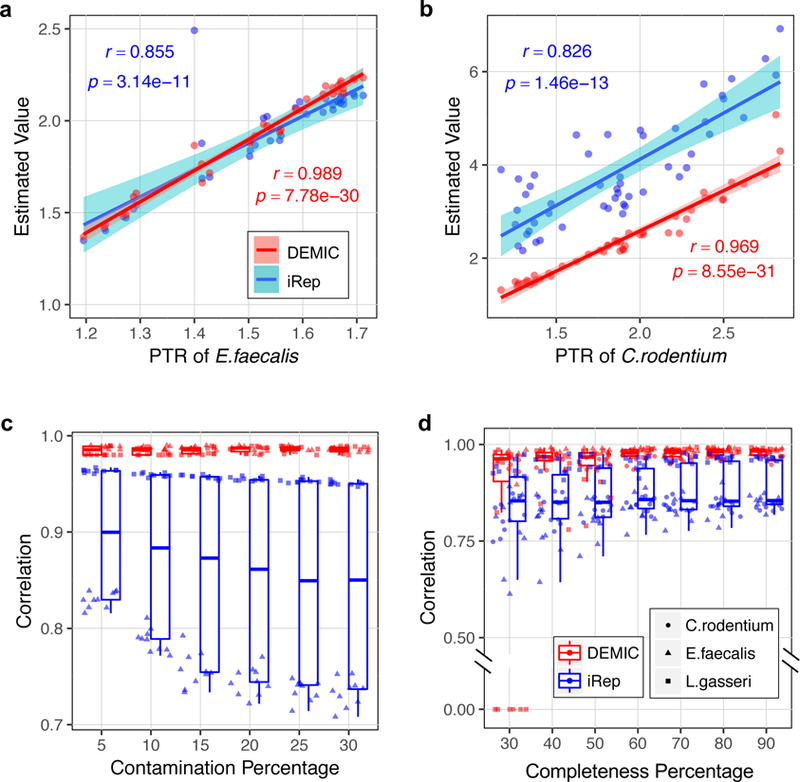
(a-b) Correlations of estimates from DEMIC and iRep with PTR values (Pearson’s r value) in 36 data sets of Enterococcus faecalis (a) and 50 data sets of Citrobacter rodentium (b). The shading areas indicate 99% level of confidence interval. (c-d) Evaluation of the effects of contig contamination (c) and completeness (d) of the contig cluster on the performances of DEMIC and iRep. Evaluations of the sample size and contig cluster completeness were based on L. gasseri, E. faecalis and C. rodentium (n = 10 for each), and evaluation of contig contaminations was based on L. gasseri and E. faecalis (n = 10 for each). Correlations of all evaluations were plotted, and the boxplots indicate the median (center line), first and third quartiles (box edges), and 1.5 times the interquartile range (whiskers).

For growth dynamic estimation, one of the keys steps is the inference of the relative distance of a contig to the replication origin. In DEMIC, this step is based on principal component analysis (PCA) of contig coverages in multiple samples (Methods). For all three species, the inferred relative distances based on multiple samples were more accurate than direct sorting of contigs based on their coverages in a single sample (Supplementary Table 2). For example, the inferred relative distances of C. rodentium contigs achieved a high correlation of 0.964 with the true distances, whereas direct sorting of the contigs by coverages only had a mean correlation of 0.756 in all 50 samples.

We next evaluated how assembly contamination, completeness and sample size affect the performance of DEMIC. First, to assess the effect of assembly contamination, we randomly added different fractions of assembled sequences from E. coli into the contig clusters of L. gasseri and E. faecalis, and used the mixed assemblies to compare the performance. Remarkably, all estimates from DEMIC still showed a high correlation of 0.98 even when as high as 30% of the contigs were from contamination (Fig. 2c), suggesting high effectiveness and robustness of the contig filtering steps adopted by DEMIC. Second, we observed that increasing the fraction of contigs led to an improved accuracy in estimating growth dynamics (Fig. 2d). In 93.3% of test cases with 40–50% completeness of the contigs, estimates from DEMIC showed a high correlation (r > 0.9) with the PTR values, and such a high correlation was observed in all 120 tests when the completeness was 60% or more. Finally, we observed more stable performances of DEMIC with an increase of sample size (Supplementary Fig. 5). DEMIC output highly consistent estimates with PTRs in 93.3% of the test cases with only three samples (r > 0.9), and in 99.3% of the test cases with six or more samples. In contrast, iRep showed clearly decreased performances with increased assembly contaminations and little improvement with increased assembly completeness (Fig. 2c,d).

To further assess the accuracy of DEMIC in estimating the growth dynamics from more complex and diverse bacterial communities, especially those composed of closely related species, we simulated a data set of 45 species with randomly assigned PTRs and average coverages in 50 samples. These 45 species were from 15 genera of five phyla including Actinobacteria, Bacterioidetes, Firmicutes, Proteobacteria and Spirochaetes (Supplementary Fig 6,7,8), and each genus included three species with an average nucleotide identity (ANI) ranging from 66.6% to 91.2% (Methods). The co-assembly and binning pipeline generated a total of 41 contig clusters with different completeness (48.4%−100%) and contamination (0–81.6%), and each was dominated by one species simulated. DEMIC successfully estimated almost all growth rates of these 41 species (1,220 out of 1,222, Fig. 3a) without estimating any spurious rate for species absent in a sample. Moreover, the mean of correlations between DEMIC estimates and the true PTRs (0.992) achieved a similar level with those from PTRC (0.995) based on complete genomes, and greatly outperformed iRep (0.888) (Fig. 3b, Supplementary Fig. 9).

Figure 3. Performance evaluation of DEMIC based on simulated data of 45 closely related species from five phyla.

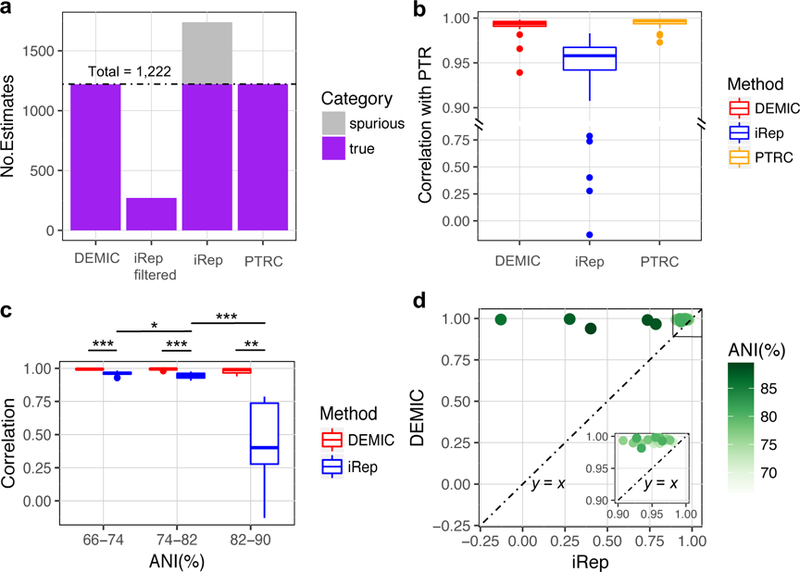
(a) DEMIC estimated 1,220 of a total of 1,222 simulated PTRs with no spurious estimates for all species whose contigs were dominant in the 41 contig clusters. (b) The correlation between DEMIC estimates for the 41 contig clusters and PTRs (Pearson’s r value) achieved a similar level with PTRC based on the 41 complete genomes, and outperformed iRep. (c) Significant difference in estimation accuracy of iRep was observed among different ANI groups of species (n = 19, 17 and 5 for ANI% group 66–74, 74–82 and 82–90, respectively), but not the accuracy of DEMIC estimates (two-sided Mann-Whitney U tests, * p value < 0.05, ** p value < 0.01, and *** p value < 0.001). For (b) and (c), the boxplots indicate the median (center line), first and third quartiles (box edges), and 1.5 times the interquartile range (whiskers). (d) Correlations (Pearson’s r value) between DEMIC estimates and PTRs were higher than those between iRep estimates and PTRs for all 41 species, and the difference was more pronounced in species sharing higher ANI with others. The inset graph shows species having correlations with PTRs greater than 0.9 by both methods.

Phylogenetically related species affect assembly and binning qualities due to their similar genome sequences, which not only resulted in failure of binning four species in the above simulated data sets, but also led to the mixture of their contigs in clusters dominated by other species. We evaluated the effects of these related species on performances of DEMIC by comparing results in different ANI groups. As shown in Fig. 3c,d, no significant change was observed between any two of the three ANI groups of species (p-value > 0.1 for all comparisons). In contrast, iRep was dramatically affected by increased ANI (p-value < 0.001 or 0.05). For example, since species Paenibacillus polymyxa and Paenibacillus terraes shared a high ANI (87.4%), bining algorithm output a mixed contig cluster with P. polymyxa as the dominant species (53.1%) but also containing contigs from P. terrae. Such a high proportion of contamination completely failed iRep, resulting in estimates that were inconsistent with either of the two species (r < 0.3, Supplementary Fig. 10a,b). However, by iteratively filtering contigs according to distribution of their PC1 of the stepwise PCA (Fig. 1d, Methods), DEMIC successfully improved the contig cluster (99.7% from P. polymyxa, Supplementary Fig. 10c) and thus accurately estimated the growth dynamic for P. polymyxa (r = 0.994, Supplementary Fig. 10d).

To compare PTR, DEMIC and iRep in real metagenomic data, we analyzed the sequencing data sets from seawater samples of eight Red Sea stations¹⁵ and fecal samples of 26 healthy subjects¹⁶. PTRs can be calculated using PTRC for 7 and 34 bacterial species with complete reference genomes for the two data sets, respectively (Supplementary Fig. 11a). In constrast, DEMIC can effectively estimate growth dynamics for 34 and 110 species with contig clusters, compared to 8 and 57 species by iRep, respectively, indicating that DEMIC can quantify the growth dynamics for a larger set of bacteria. DEMIC outperformed the other two methods by 133% to 437% (Supplementary Fig. 11b) in number of growth rates estimated. As DEMIC and iRep have the same input requirements, we also compared the computational resources needed. When using eight threads, DEMIC completed its estimation for these data sets (86 Gb and 74 Gb) in about two hours with 10 G RAM, about one fifth of time and one third of RAM needed by iRep (Supplementary Fig. 11c,d). When using different binning algorithms, we observed similar results (Supplementary Fig. 12).

Depth-dependent gradients of physicochemical properties explain the most variation in microbial compositions in Red Sea¹⁵. Using the estimates from DEMIC, we observed a strong association of bacterial growth dynamics and the sea depth (Supplementary Fig. 13a). For example, DEMIC estimated growth rates for a contig cluster, with about 60% completeness and an average identity of 92% to Marinobacter adhaerens, in 22 seawater samples from seven stations. At a depth of 500 m, the estimated growth rates were between 1.06 and 1.15 in all stations, significantly lower than those in 10 m and 100 m that ranged from 1.37 to 1.92 (p-value < 0.005; Supplementary Fig. 13b,c).

When applied to metagenomic data sets of fecal samples of 26 healthy and 86 Crohn’s disease children¹⁶, DEMIC estimated growth dynamics for 278 species with contig clusters in a wide range of completeness and contamination, of which more than 20% were estimated in 50 samples or more (Supplementary Fig. 14a,b). The high sensitivity of DEMIC made it possible to compare growth dynamics among different groups. For example, we found six (one) species (Supplementary Table 3) having significantly higher (lower) growth rates in healthy subjects compared to Crohn’s disease patients. Interestingly, after treatment by antiTNF or enteral diet for one to eight weeks, the corresponding growth dynamics of three out of the seven species above in Crohn’s disease subjects showed a significant shift towards the healthy subjects (Supplementary Fig. 14c; p-value < 0.05 after FDR correction).

Shotgun metagenomic sequencing data offer new insights into bacterial growth dynamics in microbiome studies. We have presented DEMIC, which effectively utilizes the data from multiple samples of each species in order to infer relative distances of contigs to the replication origin. Closely related organisms are one of the main factors that affect the completeness and contamination of a metagenomics pipeline including assembly and binning. DEMIC adopts a stepwise filtering strategy to iteratively update contig clusters, which provides an effective way of removing the high proportion of contig contaminations (Supplementary Fig. 10). Due to substantially lower fraction of the genomes recovered by assembly and binning methods for different strains of the same species^17,18, DEMIC, like other available PTR estimation methods, is currently not able to provide estimation of growth dynamics at strain level. As continuous efforts are being made on assembly, binning and other related methods^19,20, we expect that DEMIC may eventually be extended to strain level.

Methods

DEMIC implementation

This algorithm was implemented in Perl and R, and has been extensively tested on Linux and Mac OS X. No dependency is needed for running DEMIC except two non-default packages lme4 (ref. 21) and FactoMineR²² in R. Multithreading is available for processing both multiple metagenomic samples and multiple contig clusters in large data sets.

Calculation of contig coverages for sliding windows

DEMIC is designed to process sorted alignments of metagenomic shotgun sequencing reads against assembled contigs in SAM format (Fig. 1a). To estimate growth dynamics for a species, sequencing coverage values are first calculated from the read alignments of each sample, for all sliding windows of the same size within contigs (Fig. 1b). Thresholds for mapping length (≥ 50 bp by default), mapping quality (≥ 5 by default), and mismatch ratio (≤ 0.03 by default) are adopted during the following process to filter out spurious or ambiguous alignments.

Specifically, reads that are aligned to the jth contig with length $l_j\ge l^{\prime }\text{+}p\text{+2}{l}_r$ are used for coverage calculation using sliding windows, where $p$ is the sliding window step size (100 bp by default), $l\text{'}$ is the window size (5,000 bp by default, an integer multiple of p), and $l_r$ is the read length being excluded from each side of the contig. The total steps within a window is $q\text{=}\raisebox{1ex}{$l^{\prime }$}\!\left/ \!\raisebox{-1ex}{$p$}\right.$. For the ith sample, the average coverage of the kth window $Y_{ijk}$ is calculated as

$$Y_{ijk}\text{=}\raisebox{1ex}{$\left(T_{ijk\text{-1}}\text{+}{T^{\prime }}_{ijkq}\text{-}{T^{\prime }}_{ij\left(k\text{-1}\right)\text{1}}\right)$}\!\left/ \!\raisebox{-1ex}{$l^{\prime }$}\right.\text{,}$$

where $T_{ijk\text{-1}}$ represents the total base coverage for the previous (k-1)th window, ${T^{\prime }}_{ij\left(k\text{-1}\right)\text{1}}$represents the total base coverage in the first p bases of the previous (k-1)th window, and ${T^{\prime }}_{ijkq}$ represents the total read coverage of the last p bases of the current kth window. Using this calculation, the average coverages of all sliding windows in a contig except the first one can be efficiently calculated while the sorted alignments of a sample are being scanned, avoiding repetitively counting the aligned reads for the bases that are in the previous sliding windows. As another filter step to remove chimeric contigs, only contigs with coverages larger than 0 in all sliding windows are kept for a sample, and these coverage values are log-transformed for the subsequent analyses.

A linear mixed-effects model for correction of sequencing bias

GC content has been reported to result in bias in next-generation sequencing platforms such as Illumina²³. To detect and eliminate such biases, GC content in each window is first calculated during the scanning of contig sequences, in the same pattern as described above for the coverage calculation. For a given contig cluster, a linear mixed-effects model (LMM) is then fitted for the coverage values calculated above with GC contents as the fixed effect and sample- and contig-specific random intercept. Specifically,

$$lo{g}_{\text{2}}{Y}_{ijk}\text{=}{a}_{\text{0}}\text{+}\left(X_{jk}\text{-}\overline{X}\right)a\text{+}{Z}_{ij}\text{+}{e}_{ijk}$$

where $Y_{ijk}$ is the average sequencing coverage for the kth window of the jth contig of the ith sample, $a_{\text{0}}$ is the intercept, $X_{jk}$ is the GC content of the jth window of the kth contig, $\overline{X}$ is the average GC content of all the contigs, $a$ is the regression coefficient, $Z_{ij}$is the sample- and contig- specific random intercept and $e_{ijk}$ is the random error, respectively. This model is fitted for each contig cluster to estimate both the intercept, fixed effects $a$ of the GC content and random effects $Z_{ij}$ for contig j and sample i using the best linear unbiased predictor (BLUP). The resulting BLUP of $Z_{ij}$, denoted by ${\widehat{Z}}_{ij}$, corrects the average coverage of contig according to its GC content difference from the average GC content of all contigs and therefore eliminates sequencing bias. We define ${Y^{\prime }}_{ij}\text{=}{\widehat{a}}_{\text{0}}\text{+}{\widehat{Z}}_{ij}$ as the GC-adjusted log-transformed coverage of sample i and contig j and $Y^{\prime }$ as the final log-transformed coverage matrix, where ${\widehat{a}}_{\text{0}}$ is the estimate of $a_{\text{0}}$

Estimation of growth dynamics based on multiple samples

For an accurate inference of the relative distances between contigs and replication origin, samples with low coverage of the given species are excluded from the following steps. Specifically, since the majority of contigs in each cluster are expected to be from the same species, an informative sample should have coverage for more than half of the contigs. Samples with an average of coverages lower than 0 for all contigs are also excluded in this step for their relatively large variation. If two or more informative samples achieve the above thresholds, a preliminary filtering of the contigs is then employed to remove contigs with no coverages in any of the informative samples.

To infer relative distance of contigs from the replication origin, dimension reduction method is applied to the log-transformed coverage matrix $\left(Y^{\prime }\right)$ of the informative samples and contigs. Suppose that the log-transformed coverage matrix has a dimension of N_s × N_c, where N_c and N_s represent the number of contigs and informative samples, respectively. A principal component analysis (PCA) is performed to reduce the dimension to 1 × N_c so that the first principal component (PC1) accounts for the largest contribution to the variability of coverages among the N_c contigs across all N_s samples. This variability across different contigs is expected to result from different relative distances of the contigs to the replication origin. PC1 values of the N_c contigs, denoted as a vector U, are therefore expected to be highly correlated with the contig locations relative to the replication origin. We then sort the N_c contigs and determine their relative distances based on their PC1 values. These sorted values are used to estimate the PTR in the next step.

The contig group needs further filtering to make sure that the PCA is not affected by the contigs from other species. Specifically, the assembled contigs are expected to evenly distributed along a bacterial genome, and such a uniform distribution will be distorted if a few contigs from the other species are mixed into the group. Thus, the distribution of PC1 of all contigs U is examined against the putative uniform distribution, unif(min(U), max(U)), by a Kolmogorov–Smirnov test. If a difference is found between the current distribution and the uniform distribution at the significance level of 0.05, the two contigs with maximum/minimum PC1 values are compared with respect to their distance from the adjacent contig, and the one with a larger distance is regarded as the contamination and removed in this step (Fig. 1c).

All of the remaining contigs are then used to fit an ordinary linear regression model for each sample (Fig. 1d). Specifically, for the ith sample, we fit the following linear regression

$${Y^{\prime }}_{ij}\text{=}{b}_{\text{0}i}\text{+}{b}_i{U}_j\text{,}\hspace{0.17em}\hspace{0.17em}j\text{=1,2,}\mathrm{...}\text{,}{N}_c$$

where $b_{\text{0}i}$and $b_i$ are the intercept and slope parameters. Let ${\widehat{b}}_{\text{0}i}$and ${\widehat{b}}_i$ be the least squares estimates of the coefficients. From these models, the growth dynamics of the species in these samples are calculated as the ratio of exponential of model-fitted coverages of the two contigs with the maximum $\left(U_{\left(N_c\right)}\right)$ and minimum $\left(U_{\left(\text{1}\right)}\right)$ values of the PC1. We call this quantity as the estimated PTR (ePTR). Specifically, for the ith sample, its ePTR is defined as

$$\frac{\text{exp}\left({\widehat{b}}_{\text{0}i}\text{+}{\widehat{b}}_i{U}_{\left(N_c\right)}\right)}{\text{exp}\left({\widehat{b}}_{\text{0}i}\text{+}{\widehat{b}}_i{U}_{\left(\text{1}\right)}\right)}\text{,}\hspace{0.17em}\hspace{0.17em}i\text{=1,2,}\mathrm{...}\text{,}{N}_s$$

Iteration and random strategies

In the implementation of DEMIC, several iteration and random strategies are adopted to ensure robustness of the pipeline before the final estimation of PTR. First, the four steps in previous sections are repeated until convergence (Fig. 1c), including GC bias correction based on LMM, identification of informative samples, relative distance inference based on PCA and filtering of contigs. Both sets of contigs and samples are required to be the same between the current and the last iteration to achieve convergence of the four steps, which is designed to avoid potential influence of less informative samples or contig contaminations on LMM and PCA. Second, to eliminate potential local optimum of the iteration steps, one can test the consistency between two different subsets of the contigs. Briefly, after calculation of coverages for contigs within the sliding windows, two subsets are randomly selected so that each of them contains the same fraction (80% by default) of the total contigs and their union represents the total contigs. Each subset is independently used for relative distance inference by the four steps described above, and their consistency with each other is tested by the correlation of linear regression slopes $\left(b\right)$ in all remaining samples. Third, these linear regression slopes are used to estimate growth dynamics only when the correlation is above the designated threshold (0.98 by default), otherwise another two subsets are randomly selected and the above steps are iterated.

Data sets

Different types of data sets were downloaded or generated to evaluate the performance of DEMIC. We first used a synthetic data set composed of 141 real sequencing data sets generated in a previous study⁵. The sequencing data sets were downloaded from the European Nucleotide Archive (accession number PRJEB9718) with the corresponding metadata, and each of them was from Lactobacillus gasseri (ERR969426 - ERR969461), Enterococcus faecalis (ERR969335 - ERR969370), Citrobacter rodentium (ERR930224 - ERR930295, ERR969253 - ERR969278), and Escherichia coli (ERR969315 - ERR969334) grown in vitro separately. The synthetic data set contained 50 simulated samples, and each sample was set to randomly contain two to four of the above sequencing data sets from different species in order to mimic composition of microbiota (Supplementary Fig. 2). The synthetic data set contained 6.1 G base pairs in total, and each species present in a sample has a sequencing depth ranging from 0.17 to 96 folds.

A simulated sequencing data set was next generated to test the effects of phylogenetically related species on the performance. A list of species with RefSeq ID, taxonomy and replication origin recorded in a previous study²⁴ was downloaded. A total of 15 genera in the list with at least three species in each were randomly selected. Reference genome sequences of randomly selected three species in each genus were downloaded from NCBI to generate sequencing reads. According to the replication origin and genome size, for a given randomly assigned PTR (<3), we first generated read coverages along the genome based on an exponential distribution. A function of accumulative distribution of read coverages along the genome was then calculated. Sequencing reads were next generated one by one by using the above accumulative distribution function and a random number to determine the location of each read on the genome, until the total read number achieved a randomly assigned average coverage (between 0.5 and 10 folds) for the species in a sample. Sequencing errors including substitution, insertion and deletion were simulated in a position- and nucleotide-specific pattern according to a recent study on metagenomic sequencing error profiles of Illumina²⁵. The generated data set contained 45 species from 15 genera of five different phyla (Supplementary Fig. 6, generated by iTOL²⁶), and the ANI between species within each genus ranged from 66.6% to 91.2% according to Integrated Microbial Genomes & Microbiomes²⁷. The probability of one species existing in each of the 50 simulated samples was set as 0.6, and a total of 1,336 average coverages and the corresponding PTRs were randomly and independently assigned (Supplementary Fig. 7 and 8). The final simulated sequencing data set is about 18.9 Gbp.

The PLEASE data¹⁶ included sequencing data from the fecal samples of 26 healthy and 86 Crohn’s disease children. Healthy children were sequenced at one time point, and the Crohn’s disease patients were sequenced at four time points including baseline, one week, four weeks and eight weeks after antiTNF or enteral diet treatment. The reads were downloaded from NCBI short read archive (SRP057027) with the corresponding metadata. We used the subset of 26 healthy subjects (73.6 Gbp) to compare DEMIC, PTRC and iRep on bacterial growth dynamics estimation, and used the whole data sets (819 Gbp) to compare growth dynamics of the same species in different samples by DEMIC.

The RedSea data set¹⁵ included 45 metagenomic samples of seawater sampled from different depths at eight stations in the Red Sea. The reads were downloaded from NCBI short read archive (SRP061183) with the corresponding metadata. We used the whole data sets (85.6 Gbp) to compare DEMIC, PTRC and iRep on bacterial growth dynamics estimation, and also to compare growth dynamics of the same species in different samples by DEMIC.

Coassembly, binning and mapping

For both of synthetic and real data sets, coassembly was performed to facilitate binning as well as analysis of DEMIC and iRep. MEGAHIT¹³ version 1.1.1 was used as the assembler for its advantages on both total assembly length¹⁸ and controllable memory usage that is convenient for large metagenomic data sets. The default settings of MEGAHIT were used for all of the data sets.

After co-assembly, contigs were clustered into groups by using binning algorithms. MaxBin¹² version 2.2.4 was used for clustering contigs in the synthetic data sets, simulated data sets, all RedSea and 26 healthy PLEASE data sets for its outstanding performances in medium and low complexity data sets¹⁸. MetaBAT²⁸ version 2.12.1 was used for binning of the RedSea and PLEASE data sets for its overall performances and high speed to process high complexity data sets. CheckM¹⁴ was used to assess the contig completeness and contamination of the contig clusters using the default settings.

For all of the data sets above, Bowtie 2 (ref. 29) version 2.3.2 was used to align reads back to assembled contigs. The output alignment results were then sorted by samtools³⁰ version 0.1.19 and used as input of both DEMIC and iRep.

Evaluation based on the synthetic data sets and random tests

After coassembly and binning of the constructed contigs, contigs from three species were successfully clustered, including L. gasseri, E. faecalis, and C. rodentium. Neither MaxBin nor MetaBAT generated a contig cluster corresponding to E. coli, due to its relatively low sequencing depths compared with C. rodentium in the same family. The following evaluations are therefore based on contig clusters of L. gasseri, E. faecalis, and C. rodentium. Bacterial growth rates in the synthetic data sets were first estimated by PTRC, DEMIC and iRep using the respective default settings. For a total of 122 growth rates of the three species (36, 36 and 50, respectively), correlations between PTRC and DEMIC as well as between PTRC and iRep were calculated using Pearson’s r value.

To generalize our evaluation to diverse metagenomic data sets, three different types of random tests were performed to test the effects of sample counts, fraction of contig contaminations and completeness of contig clusters on the performance. Specifically, groups of 3, 6, 10, 15, 20, 25 samples, groups with 5%, 10%, 15%, 20%, 25% and 30% of contig contaminations and groups of 30%, 40%, 50%, 60%, 70%, 80% and 90% completeness of contig clusters were considered. For each random test, DEMIC was applied to the selected subset of samples or contig clusters that were randomly generated according to a given fraction, so that these random tests in the same group are independent of each other.

After coassembly and binning for the simulated data set of 45 species in 50 samples, contigs from 41 species were successfully clustered. Four species failed to be binned into separate clusters as dominant species, including Caldicellulosiruptor lactoaceticus, Paenibacillus terrae, Xanthomonas axonopodis and Xanthomonas oryzae. The subsequent evaluations are therefore all based on contig clusters of the 41 clusters and the corresponding 1,222 PTRs (Supplementary Fig. 9). A window size of 3,000 and a mismatch threshold of 0.02 were used in DEMIC with all other settings as default. PTRC were provided with complete reference genomes, and the default settings were used for both PTRC and iRep.