Fetal Brain Growth Portrayed by a Spatiotemporal Diffusion Tensor MRI Atlas Computed From In Utero Images

Abstract

Altered structural fetal brain development has been linked to neuro-developmental disorders. These structural alterations can be potentially detected in utero using diffusion tensor imaging (DTI). However, acquisition and reconstruction of in utero fetal brain DTI remains challenging. Until now, motion-robust DTI methods have been employed for reconstruction of in utero fetal DTIs. However, due to the unconstrained fetal motion and permissible in utero acquisition times, these methods yielded limited success and have typically resulted in noisy DTIs. Consequently, atlases and methods that could enable groupwise studies, multi-modality imaging, and computer-aided diagnosis from in utero DTIs have not yet been developed. This paper presents the first DTI atlas of the fetal brain computed from in utero diffusion-weighted images. For this purpose an algorithm for computing an unbiased spatiotemporal DTI atlas, which integrates kernel-regression in age with a diffeomorphic tensor-to-tensor registration of motion-corrected and reconstructed individual fetal brain DTIs, was developed. Our new algorithm was applied to a set of 67 fetal DTI scans acquired from healthy fetuses each scanned at a gestational age between 21 and 39 weeks. The neurodevelopmental trends in the fetal brain, characterized by the atlas, were qualitatively and quantitatively compared with the observations reported in prior ex vivo and in utero studies, and with results from imaging gestational-age equivalent preterm infants. Our major findings revealed early presence of limbic fiber bundles, followed by the appearance and maturation of projection pathways (characterized by an age related increase in FA) during late 2^nd and early 3^rd trimesters. During the 3^rd trimester association fiber bundles become evident. In parallel with the appearance and maturation of fiber bundles, from 21 to 39 gestational weeks gradual disappearance of the radial coherence of the telencephalic wall was qualitatively identified. These results and analyses show that our DTI atlas of the fetal brain is useful for reliable detection of major neuronal fiber bundle pathways and for characterization of the fetal brain reorganization that occurs in utero. The atlas can also serve as a useful resource for detection of normal and abnormal fetal brain development in utero.

INTRODUCTION

Diffusion Tensor Imaging (DTI), based on diffusion-weighted Magnetic Resonance Imaging (MRI), can be used to characterize anisotropic diffusion of water molecules within an imaging domain (Alexander et al., 2007). DTI is thus frequently used in neuroimaging to study brain microstructure and connectivity by inferring the organization of major axonal fiber pathways. DTI-derived parameters such as Fractional Anisotropy (FA), Mean Diffusivity (MD) and Apparent Diffusion Coefficient (ADC) are also employed to study impairment of brain structure and function in neurological disorders, among other applications (Garcia-Lazaro et al., 2016; Li et al., 2014). DTI requires acquisition of multiple diffusion-sensitive images through the application of magnetic field gradients along ≥ 6 non-collinear directions. To achieve acceptable signal-to-noise ratio (SNR), a much larger number of gradient directions are normally used. Despite using accelerated ultra-fast MRI sequences based on echo-planar imaging (EPI), this approach results in long DTI acquisition times that render DTI very susceptible to subject motion.

Neuroimaging researchers studying fetal and infant populations have used diffusion-weighted imaging (DWI) including DTI to characterize brain microstructural development in prenatal and postnatal periods when the brain undergoes significant structural and functional development (Dubois et al., 2014; Kunz et al., 2014; Qiu et al., 2015) and reorganization (Kostović et al., 2014). In utero DWI studies of the fetal brain, however, have been scarcely reported mainly because they have been challenged by unconstrained fetal motion, unintentional maternal motion and breathing, limited scan times for patient comfort, and thus limited SNR (Gholipour et al., 2014). These challenges have dramatically limited routine application of fetal DTI and the development of in utero DTI atlases. In the following paragraphs, we first review the literature on fetal DWI including DTI, and then review the atlas construction methods and literature that build the bases of our in utero fetal DTI atlas construction method.

Fetal DTI:

Imaging the fetal brain in utero is highly desired as it helps develop insights into neurodevelopmental disorders that emerge during pregnancy. In early works on fetal DWI, Righini et al. (2003) scanned 15 fetuses between gestational age (GA) 22w–35w under 20-second maternal breath hold with only 3 non-collinear gradient directions, and reported variations of ADC with age in the frontal and occipital white matter regions and also in the basal ganglia. Bui et al. (2006) imaged 24 fetuses under maternal sedation between GA 31w–37w and reported ADC and FA values in the centrum semiovale, corpus callosum and pyramidal tract. They dropped >50% of subject scans due to excessive motion. Kim et al. (2008) modified the conventional EPI sequences to accelerate image acquisition and scanned 14 fetuses within GA 22w–30w. They compared the ADC values obtained from their modified sequence to those from the conventional sequence and reported that DWIs acquired using their accelerated sequence without breath-hold were nearly equal in quality to the DWI acquired using conventional sequences under breath-hold. Further, Kasprian et al. (2008) scanned 40 unsedated fetuses within GA 18w–37w using a 2-minute axial EPI sequence with 32 directions. They reported imaging 90% of the fetuses in cephalic presentation which resulted in limited motion of the fetal head and successful visualization of sensorimotor and callosal tracts in ~40% of the subjects despite the relatively long scan time.

Jiang et al. (2009) developed the first slice-level motion correction based approach to compute DTI from multiple DWI scans and applied their technique to image 8 fetuses between GA 24w–34w. Only two of these fetuses were normal. They reported FA and ADC values over the gestational age in several fiber-rich regions. Zanin et al. (2011) scanned 141 fetal brains and selected 17 scans (out of 61 normal fetuses in their study) to evaluate FA and ADC values at cortico-spinal tracts, corpus callosum and optic radiations. In clinical evaluation, Jakab et al. (2015) and Kasprian et al. (2013) evaluated agenesis of corpus callosum in ~20 in utero fetuses based on a volume-to-volume registration approach for motion correction. Fogtmann et al. (2014) and Oubel et al. (2012) developed novel slice-level motion-correction strategies and showed the impact of motion-corrected DTI reconstruction in four fetuses, achieving tractography of corpus callosum and pyramidal tracts. Mitter et al. (2015a) and (2015b) used DTI in a large fetal cohort and successfully accomplished tractography reconstruction of fetal association fibers in 24 out of 120 fetal DTI subjects (80% drop rate). Marami et al. (2017) performed connectivity analysis in 21 healthy fetuses scanned in utero within GA 22w-38w via robust DTI reconstruction based on temporal slice registration.

The low success rates in aforementioned fetal DTI studies highlight the need for population-based atlases of normal growth that can be used as references for the evaluation of quality of image acquisition, reconstruction, and analysis. Despite the impressive progress, no DTI atlas of in utero fetal brain growth exists. In our view, motion artifacts, high drop rates, noisy anisotropic tensor maps, and lack of fetal subjects have been the main barriers in DTI atlas construction for in utero fetal brain growth analysis.

DTI Atlas Construction:

The DTI atlas construction methods presented in the literature can be broadly categorized into two groups. The first group computes an atlas by registering (linear and deformable) FA, b=0 s/mm², or other scalar images of the subjects, and then applies the resulting transforms to the tensor images in order to compute a diffusion tensor template (Brown et al., 2014; Calabrese et al., 2015; Geng et al., 2012; Kersbergen et al., 2014; Oishi et al., 2011). The second group directly registers tensor images using specialized tensor-registration methods to compute a diffusion tensor template (Adluru et al., 2012; Dean et al., 2017; Evangelou et al., 2014; Taquet et al., 2014; Wang et al., 2011). While both approaches have been used, a number of studies have reported that the methods in the 2^nd approach result in better overall alignment of white matter tracts by exploiting tensor-specific metrics in the registration process (Adluru et al., 2012; Barona-Garcia, 2014; Liu et al., 2015; Wang et al., 2011).

It is important to note that the fetal brain rapidly evolves in structure and function during gestation, while the ages of imaged subjects are often unevenly distributed over the GA range. For these reasons, in utero structural imaging studies (Gholipour et al., 2017; Serag et al., 2012) have embraced the kernel-regression approach proposed by (Davis et al., 2010) to compute an unbiased atlas that can be used to regress a representative template at any desired age. Even though fetal and neonatal structural atlases have adopted this idea, to the best of our knowledge, no reported DTI study has integrated kernel-regression in age within tensor-specific registration for atlas construction. This work aimed to fill the gaps in methods and resources for fetal DTI atlases and group analysis.

Contributions:

The main contribution of this work is, therefore, the development of a robust computational framework for the construction of the first DTI atlas of normal fetal brain development in-utero from noisy DTI scans of fetuses, and its use to portray microstructural growth and reorganization of the fetal brain. To qualitatively and quantitatively evaluate the use of the atlas in characterizing neurodevelopmental trends in utero we compare and discuss the findings with the results of previous in utero DTI studies, DTI studies of preterm infants, and, in particular, ex-vivo DTI and histological analysis studies of post-mortem fetal brains (Huang et al., 2009, 2006; Huang and Vasung, 2014; Kolasinski et al., 2013; Kostovic and Goldman Rakic, 1983; Kostovic and Vasung, 2009; Takahashi et al., 2012; Vasung et al., 2016, 2010; Xu et al., 2014).

Our proposed computational framework and the constructed spatiotemporal DTI atlas of in utero fetal brain growth can serve a number of needs, including: (a) computer-aided diagnosis, where a subject DTI can be compared to DTI from the normative atlas at the corresponding age; (b) represent spatiotemporal development of the brain through evaluation of tensors and DTI-derived parameters such as FA, MD and ADC; (c) computer-aided groupwise analysis, where comparison between healthy and abnormal fetal cohorts can be carried out to evaluate the region-specific impact of an abnormality on the structure and function of the brain; and (d) provide additional imaging information complementary to those obtained from T1w and T2w structural MRI atlases.

The materials and methods, including subjects, data acquisition and processing, DTI analysis, the DTI atlas construction method, and the analysis techniques including region-of-interest sampling are discussed in the next section. The atlas and its features are then presented in the Results section, where we also show quantitative trends of regional FA changes throughout the GA period of analysis. The results are discussed with respect to the previous work, and are followed by the Limitations and Usage, and the Conclusion sections.

MATERIALS AND METHODS

Subjects:

Data for this study was collected from in utero fetal MRI scans acquired as part of fetal MRI research studies conducted at Boston Children’s Hospital (BCH), Boston, MA. Data collection protocols were approved by the Institutional Review Board (IRB) committee at BCH, and written informed consent was obtained prior to imaging from each pregnant woman volunteer who participated in the studies. All women were imaged without sedation or breath-hold. Subject exclusion criteria were: (a) maternal contra-indication for MRI, (b) prior congenital infection in the fetus, (c) known or diagnosed brain or other physical abnormalities in the fetus, (d) any chromosomal abnormalities, (e) multiple-gestation pregnancy, and (f) known genetic disorders of siblings or parents.

The available scans were screened for the availability of at least two DWI scans without extreme motion-induced artifacts, distortion, and signal loss that prohibited successful motion correction and registration between DWI and structural T2w scans. For final analysis and atlas construction, we used data from 67 fetal scan sessions (60 unique subjects, data collected from 7 subjects imaged at two different stages of their pregnancy were included as well). The post-menstrual gestational age (GA) of fetuses ranged from 21 weeks 6 days to 38 weeks 3 days with a mean of 29.62 ± 4.64 weeks. Structural and diffusion MR images were acquired in all of these scans with the parameters described below.

MRI Data Acquisition Protocol:

The MRI scans were acquired using a 3 T Siemens Skyra MRI scanner with 16-channel body matrix and spine coils. A 3-plane localizer scan was obtained at the start of and during the imaging session (as needed) to ensure that images were being acquired in the desired orientation. Field of view (FOV) and number of slices were variable based on maternal and fetal dimensions.

1. Structural Imaging Protocol: Multiple T2-weighted (T2w) HASTE (Half-Fourier Single Shot Turbo Spin Echo) scans of the fetal brain in orthogonal planes were obtained with: TR = 1400–2000 ms, TE = 100–120 ms, 0.9–1.1 mm in-plane resolution, 2 mm slice thickness with no inter-slice space, acquisition matrix size = 256 × 204, 256 × 256, or 320 × 320 with 2- or 4-slice interleaved acquisition.

2. DTI Imaging Protocol: Each DTI session comprised 2–8 scans each along one of the orthogonal planes with respect to the fetal head. In each scan, 1 or 2 b = 0 s/mm² images, and 12 diffusion-sensitized images at b = 500s/mm² were acquired. Acquisition parameters were: TR = 3000–4000 ms, TE = 60 ms, in-plane resolution = 2 mm, slice thickness = 2–4 mm.

Total imaging time per subject per session was 30–45 min. DTI acquisition time was 3–10 min.

MRI Data Processing:

An overview of data processing pipeline has been shown in Fig. 1 and Fig. 2. Major processing blocks of the pipeline are discussed below. The reported execution times are based on a workstation with an nVidia Quadro K2200 GPU, and Intel Xeon E5–2640 processor with 64GB RAM.

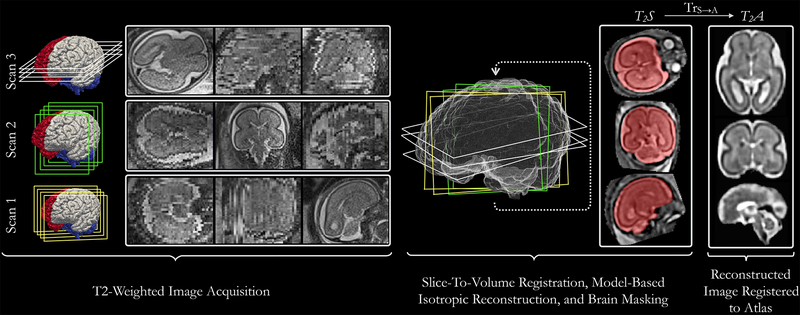
Fig. 1:

Block diagram representing the T2-weighted (T2w) structural image processing pipeline. Multiple anisotropic T2w images are acquired in orthogonal views. A slice-to-volume registration approach used within an iterative model-based super-resolution framework is employed to reconstruct an isotropic T2w image (T₂S). The reconstructed image is brain-extracted, registered with a preexisting image (at the corresponding age) from the fetal brain atlas to bring it into a standard space.

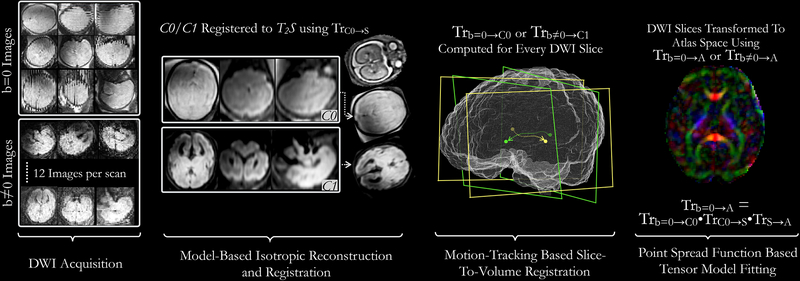
Fig. 2:

Block diagram representing diffusion-weighted imaging processing pipeline: For each DWI scan, 1 b=0 and 12 b≠0 images are acquired. All non-diffusion-sensitive images (b=0) from multiple scans are merged using a superresolution approach shown in Fig. 1 to construct a composite isotropic C0 image. C1 image is similarly computed using b≠0 images. C0 or C1 image is registered to the isotropic reconstructed T2-weighted image (T₂S) of the same fetus; the resulting transformation is stored as Tr_B0→S. Subsequently, all slices from b=0 and b≠0 images are registered to the C0 and C1 images respectively and the resulting transformations are stored as Tr_b=0→C0. Finally, all DWI slices are transformed using a composite Tr _b=0→A) transform and a pointspread-function (PSF) based tensor fitting approach is used to compute the DTI for the fetal subject.

Structural Image Processing Pipeline:

The structural image preprocessing pipeline is shown in Fig. 1. The workflow is as follows: A trained research assistant manually reviewed all acquired images and removed those with extreme motion from the preprocessing pipeline. Depending on the number of acquired images and the extent of motion present in them, typically 4–15 images were selected for further processing. Images were input to a deep neural network-based algorithm to compute corresponding brain masks (Salehi et al., 2017) (execution time: 1–3 s for a 3D image). Subsequently, each image was masked using a dilated version of its mask and cropped to the edges of a bounding box that enclosed the dilated mask. Cropped anisotropic images were input to an automatic motion-robust slice-to-volume registration based algorithm that harnesses GPUs for accelerated reconstruction of an isotropic T2w image in 3–5 iterations of super-resolution reconstruction (Kainz et al., 2015) (execution time: 3–15 min). Following the procedure described in (Gholipour et al., 2017), the reconstructed image was bias corrected (Tustison et al., 2010) and brain-extracted (Salehi et al., 2017). This image is referred to as T₂S, where T₂ signifies the type of image (T2w) and S represents the fact that the reconstructed image was in the scanner space. T₂S, was rigidly registered (using transformation Tr_s→A:Ω→Ω) with an existing spatiotemporal T2w image atlas (Gholipour et al., 2017) to bring it into a standard orientation. The domain of T2w images is defined as Ω, which exists in ${ℝ}^3$ (e.g. $T_{2}S(x):{ℝ}^3\to ℝ$), and all rigid transformations map points Ω to Ω. As an outcome of preprocessing, an isotropic bias-corrected T2w brain image of the fetus was achieved in anatomic space of the existing atlas (Fig. 1). This image is denoted as T₂S, where A represents the fact that the reconstructed image was in atlas space. The resolutions of both T₂S and T₂A is 0.75mm isotropic.

Following the reconstruction of atlas-space isotropic images for all fetal subjects, brain masks were manually refined using ITK-SNAP (Yushkevich et al., 2006). The refined masks were applied to T₂A images. Finally, an unbiased template construction procedure described in Gholipour et al. (2017) was used to compute 17 template T2w brain images of the fetal cohort at 1 week intervals in the 22–38 week GA range. The atlas of T2w images is denoted as ${\widehat{T}}_2(x,t):{ℝ}^3\to ℝ$.

Diffusion Tensor Computation:

In the discussion hereafter, images acquired at inactive gradient coil (b = 0 s/mm²) and active gradient coil (b = 500 s/mm²) are collectively referred to as b=0 images and b≠0 images, respectively. An overview of the DTI processing pipeline is shown in Fig. 2. Fetal head motion affects alignment of slices within an image as well as among b=0 and b≠0 images. To account for this, isotropic composites of b=0 and b≠0 images, referred to as C0 and C1 respectively ($C0(x),C1(x):{ℝ}^3\to ℝ$, ‘C’ represents ‘Composite image’), were first computed. Slices from individual b=0 and b≠0 images were registered (rigidly) to C0 and C1 images using a robust state-space motion trajectory estimation framework (Marami et al., 2017). These transformations are denoted as Tr_b=0→C0, or Tr_b≠0→C1. Composite C0 and C1 images were registered to subject’s T2w image (T₂S) using transformation Tr_C0→S, where the subscript C0 → S denotes the transformation from diffusion image space to the space of T₂S. C0 and C1 images are co-located. Finally, a compounded transformation for each slice in b=0 and b≠0 images was computed by combining transformation Tr_b=0→C0 or Tr_b≠0→C1 (computed for each slice) with Tr_C0→S and Tr_S→A. As an end result of this registration process, we obtained the transformations necessary to map each slice from b=0 and b≠0 image set to the atlas space; this allowed us to reconstruct the diffusion tensor image directly in the standard orientation of the atlas space, which was also in rigid alignment with the reconstructed T2w image in the atlas space (T₂A). The registration workflow applied to compute a diffusion tensor image for each subject is described in the following paragraphs.

Composite C0 and C1 Image Computation:

Similar to the isotropic reconstruction of T2w images (T₂S), composite C0 and C1 images were computed using an iterative slice-to-volume registration based algorithm (Kainz et al., 2015) in 2–3 iterations of super-resolution reconstruction. We used truncated-sinc as the point spread function (PSF) in super-resolution formulation for computing C0 and C1 images. The sinc PSF was truncated at its first zero crossings with a full width at half max (FWHM) set to 1.2 times in-plane resolution in the x-y direction equal to slice thickness in the out-of-plane (z) direction.

To compute the composite C0 image, a cropped b=0 s/mm² image was used as a reference for slice-to-volume registration. The C1 image was computed using the C0 image as a reference to initialize slice-to-volume registration in the 1^st iteration, subsequent iterations of slice-to-volume registration used a reference computed from b≠0 images. No brain masks were used for computing C0 and C1 images. We empirically found 2–3 iterations of motion-robust super-resolution reconstruction to be sufficient for computing composite C0 and C1 images. The resolution of C0 and C1 reconstructed images is 0.8 mm isotropic.

Registering Image Slices to Composite C0 and C1 Images:

Motion-corrupted image slices from b=0 and b≠0 images need to be co-registered to compute a diffusion tensor image. To accomplish this, a robust Kalman-filter based slice-to-volume (S2V) registration algorithm was used (Marami et al., 2017). Slice-to-volume registration parameters for each slice were initialized using volume-to-volume (V2V) rigid registration parameters between the fixed and the moving image. The final S2V registration was obtained through iterations of the aforementioned robust state estimation method that aimed to track the motion of the fetus through temporal slice registration. This process was repeated for each slice in the b=0 and b≠0 image set. As an outcome, a transformation (Tr_b=0→C0 or Tr_b≠0→C1) was obtained for each slice in b=0 and b≠0 images.

Computing Diffusion Tensors in Atlas Space:

Next, a transformation (Tr_C0→S) between the C0 image and T₂S was computed automatically through 1^st order geometric moments matching followed by multi-scale mutual information (MSMI) based rigid registration. In situations where this approach failed, Tr_C0→S was computed by registering C1 (as a surrogate of C0) to T₂S. In a few cases where fetal motion (translation and rotation) between the acquisition of T2w and diffusion-sensitized images was too large, automatic registration seeded through 1^st order geometric moments matching failed to compute an accurate transformation. For these instances, the MSMI-based rigid registration was initialized using a rigid transformation obtained by manually selecting corresponding points in the C0 (or C1) and T₂S images using Slicer (Fedorov et al., 2012). Tr_C0→S for 8 out of 67 cases was obtained in this manner. Finally, having computed Tr_b=0→C0, for each slice in b=0 images, and Tr_C0→S we computed a transformation (Tr_b=0→A) between each slice in the b=0 image and the reconstructed T2w image in the atlas space (T₂A) as follows:

$${\text{Tr}}_{b=0\to \text{A}}={\text{Tr}}_{b=0\to C0}\circ {\text{Tr}}_{C0\to S}\circ {\text{Tr}}_{S\to A},$$

where (∘) represents composition of two rigid transformations. Similarly, Tr_b≠0→A was computed for each slice in b≠0 images. Using Tr_b=0→A and Tr_b≠0→A each voxel in the b=0 and b≠0 image was projected to the atlas space, and a Gaussian PSF based formulation was used to estimate diffusion tensors from motion-corrected DWI data in atlas space using the Constrained Weighted Linear Least Squares (CWLLS) method (Koay et al., 2006; Marami et al., 2017; Veraart et al., 2013). The brain mask created for the corresponding T₂A image of each fetal subject was copied into a new mask file and refined for the reconstructed tensor image, I(x). I(x) was masked using the refined mask image. Using the computed tensors, derived parameters such as Fractional Anisotropy (FA) and Mean Diffusivity (MD) were also computed. The resolution of the estimated diffusion tensor image is 1.2 mm isotropic.

Unbiased Spatiotemporal Diffusion Tensor Atlas Construction:

A GA-dependent population-specific spatiotemporal diffusion tensor atlas that represents the microstructural variability of the healthy in utero fetal brain was constructed. The set of diffusion tensor images were treated as time-indexed data points in a Riemannian manifold M, and time-regressed templates at GA 22–38 weeks were computed at 1-week interval. We aimed to compute Fréchet expectation, given the distribution of manifold-valued images, using generalized Nadaraya-Watson kernel regression in order to compute representative templates at different GA points (Davis et al., 2010). To characterize the variations in shape over gestational age, a large deformation diffeomorphic model (LDDMM) of growth was applied to the diffusion tensor image set. This approach is described below.

We denote the set of time-indexed diffusion tensor image observations over gestational age as: ${\left\{t_i,I_i\right\}}_{i=1}^N$, where $t_i\in ℝ$ is the gestational age of fetus i, and I_i ∈ M is the diffusion tensor image computed for fetus i that is embedded in the 3D Euclidean space. To represent the non-linear anatomical geometric differences between any pair of these images, we use transformations (ϕ: M → M) that lie on an infinite dimensional space of diffeomorphism $\mathcal{H}$. A diffeomorphism (and its inverse) is a differentiable non-rigid transform (ϕ(x)) between two manifold-valued images embedded in the 3D Euclidean space that cannot be represented in the space of rigid (${ℝ}^6$) or affine (${ℝ}^{12}$) transforms. The atlas construction problem can now be posed as computing an atlas $\widehat{I}(t)$ that can be deformed using minimum deformation diffeomorphisms (ϕ(x,t)) to match any member of the input image set (Davis et al., 2010). Intuitively, ϕ(x) at some time t represents the voxel-wise deformation that can be applied to the moving image to warp it to the space of the reference image. Fig. 3 provides a schematic overview of this procedure. The ϕ(x) satisfies the following Lagrangian ordinary differential equation:

$$\frac{d}{ds}\varphi (x)=v_s(\varphi (x))$$ (1)

where v_s(x) represents the velocity fields that are integrated forward in time to compute the transformations, and s ∈[0,1] is a time parameter. We can now describe atlas computation $(\widehat{I}(t))$ as a manifold kernel regression problem:

$$\widehat{I}(t)={\text{argmin}}_{\forall I_i}\left(\frac{{\sum }_{i=1}^{N}K\left(t-t_i\right)d{\left(I,I_i\right)}^2}{{\sum }_{i=1}^{N}K\left(t-t_i\right)}\right)$$ (2)

where K(t) is a kernel that is used to calculate weight for a fetal brain image (I_i) at time t relative to the age of the fetus at scan (t_i). Further, d(I, I_i)² is a metric in M:

$$d{\left(I,I_i\right)}^2={\min }_v\left(\frac{1}{{\sigma }^2}{\Vert I\left({\varphi }_i\right)-I_i\Vert }^2+{\int }_0^1{\Vert v_S\Vert }_{\psi }^{2}ds\right)$$ (3)

where ${\int }_0^1{\Vert v_s\Vert }_{\psi }^{2}ds={\varphi }_i(x)$ represents the Sobolev norm of velocity fields (integration over the domain ψ), and $\frac{1}{{\sigma }^2}{\Vert I\left({\varphi }_i\right)-I_i\Vert }^2$ accounts for the dissimilarity between diffusion tensor images. Computer implementation of atlas construction algorithm is described ahead.

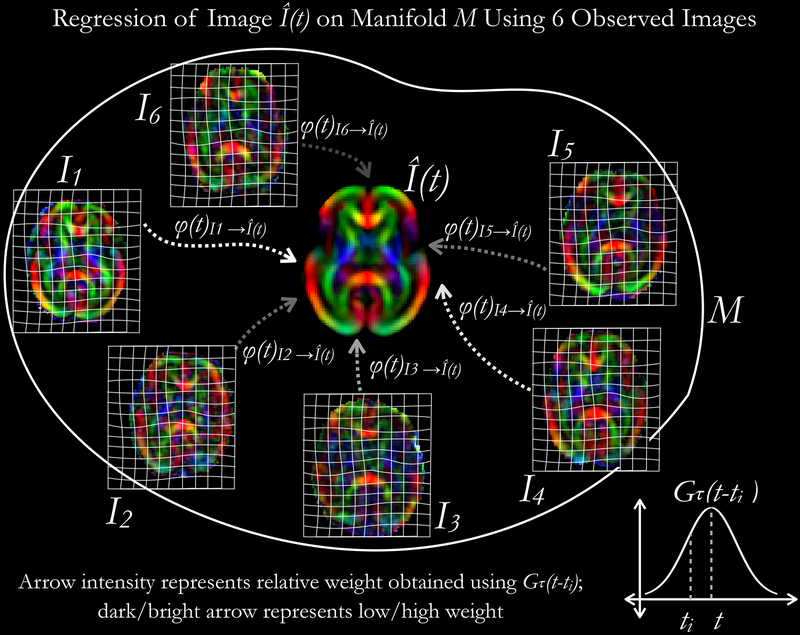
Fig. 3:

An illustration on regression of tensor-valued data on a manifold M using kernel-regression approach. Steps involved in the computation have been presented in Algorithm 1.

An iterative numerical approach that employs tensor-to-tensor rigid, affine, and diffeomorphic non-rigid registration was used to compute the atlas. We used a truncated-Gaussian kernel (G_τ) as shown below with a flexible bandwidth (τ: 1 week 0 days – 1 week 3 days):

$$G_{\tau }\left(t-t_i\right)=\{\begin{array}{rr}\hfill \frac{1}{\tau \sqrt{2\pi }}exp\left(-\frac{{\left(t-t_i\right)}^2}{2{\tau }^2}\right),& \hfill t\le \tau \\ \hfill 0,& \hfill t>\tau \end{array}$$ (4)

The bandwidth (τ) was kept flexible to select at least 5 images (empirically determined) within a window of time 2τ at time t for computing the atlas $\widehat{I}(t)$. The atlas estimate at time t was initialized with a weighted average of all I_i. In Algorithm 1 below, $\tilde{I}(t)$ is used to denote intermediate estimates of $\widehat{I}(t)$ during the atlas computation procedure.

Algorithm 1.

Compute $\widehat{I}(t)$ at t = [22:1:38] weeks

Input: $\tau ,{\left\{t_i,I_i\right\}}_{i=1}^N,$

Output: $\widehat{I}(t)$ at t = [22:1:38] weeks, ϕi(x): i ∈ [1,N], $\text{Tr}{(t)}_{I_i\to \widehat{I}(t)}$

1:   Compute Gτ(t – ti) at t = [22:1:38] weeks for all Ii.

2:   Compute $\tilde{I}(t)$ as a weighted average of all $I_i:\tilde{I}(t)=\frac{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)I_i}{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)}$

3:   for t = 22:1:38

DO TENSOR-TENSOR RIGID REGISTRATION AND INITIALIZE ATLAS

for i =1:1:N

3.1      $\text{Tr}{(t)}_{l_i\to \tilde{I}(t)}$ ← rigid transformation mapping Ii to $\tilde{I}(t)$

3.2      $\text{Tr}{(t)}_{I_i\to \tilde{I}(t)}$ ← affine transformation mapping Ii to $\tilde{I}(t)$ initialized using $\text{Tr}{(t)}_{I_i\to \tilde{I}(t)}$

3.3      $I_i^{Tr}(t)\leftarrow I_i$ transformed using $\text{Tr}{(t)}_{I_i\to \tilde{I}(t)}$

end for

3.4    $\tilde{I}(t)\leftarrow \frac{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)I_i^{Tr}(t)}{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)}$

DO 3 ITERATIONS OF TENSOR-TENSOR AFFINE REGISTRATION

for i = 1:1:3

for i = 1:1:N

3.5      $\text{Tr}{(t)}_{I_i\to \tilde{I}(t)}$ ← affine transformation mapping Ii to $\tilde{I}(t)$ initialized using $\text{Tr}{(t)}_{I_i\to \tilde{I}(t)}$

3.6      $I_i^{Tr}(t)\leftarrow I_i$ transformed using $\text{Tr }{(t)}_{I_i\to \tilde{I}(t)}$

end for

3.7    $\tilde{I}(t)\leftarrow \frac{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)I_i^{Tr}(t)}{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)}$

end for

DO 6 ITERATIONS OF TENSOR-TENSOR DIFFEOMORPHIC NON-RIGID REGISTRATION

for i =1:1:6

3.8    ϕ (t) ← 0

for i = 1:1:N

3.9     $\varphi {(t)}_{I_i^{Tr}(t)\to \tilde{I}(t)}$ ← non-rigid transformation mapping $I_i^{Tr}(t)$ to $\tilde{I}(t)$

3.10    $I_i^{\varphi }(t)\leftarrow I_i^{Tr}(t)$ deformed using $\varphi {(t)}_{I_i^{Tr}(t)\to \tilde{I}(t)}$

3.11    $\varphi (t)\leftarrow \varphi (t)+\varphi {(t)}_{I_i^{Tr}(t)\to \tilde{I}(t)}\times G_{\tau }\left(t-t_i\right)$

end for

3.12     $\tilde{I}(t)\leftarrow \frac{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)I_i^{\varphi }(t)}{{\sum }_{i=1}^N{G}_{\tau }\left(t-t_i\right)}$

3.13     $\tilde{I}(t)\leftarrow \tilde{I}(t)$ deformed using ϕ−1 (t)

end for

3.14  $\widehat{I}(t)\leftarrow \tilde{I}(t)$

end for

In Algorithm 1, all tensor-to-tensor rigid, affine, and diffeomorphic registrations were computed using DTI-TK (Zhang et al., 2007). This approach incorporated local orientation of diffusion tensors as a feature to influence the registration cost function and is thus ideal for aligning individual tracts where anisotropy is different than the neighboring regions. The minimization problem in eq. 3 was solved at step 3.9. Eq. 2 was used to estimate atlas at steps 3.4, 3.7. 3.12, the averaging was performed in log-Euclidean space (Arsigny et al., 2006). The registrations in 3.1 and 3.2 were performed using Normalized Mutual Information distance metric between tensor components, whereas step 3.5 used Euclidean Distance Squared metric between tensors. The diffeomorphic non-rigid registration step in 3.9 used Euclidean Distance Squared between Deviatoric tensors (DDS) as a metric to compute the deformation field. We refer to Zhang et al., 2006 for description of tensor metrics and their usage. The rigid, affine, and non-rigid transformations were applied to tensor maps using DTI-TK.

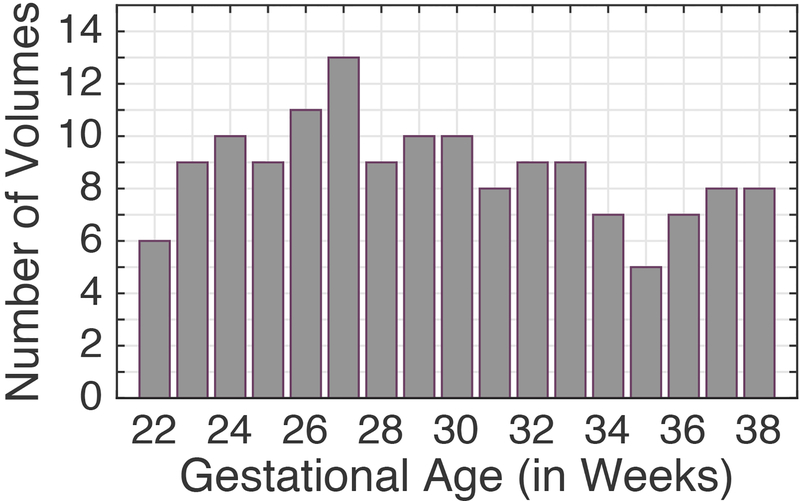
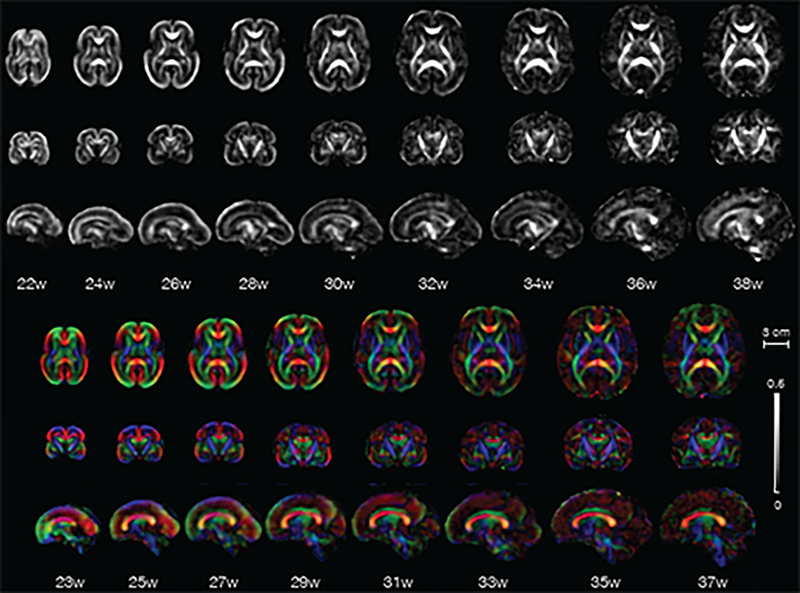
Following the processing steps described above, an unbiased spatiotemporal atlas was constructed using 67 fetal scans. The atlas consists of templates of scalar diffusion parameters and diffusion tensors at gestational age (GA) 22 weeks to 38 weeks at 1-week intervals as representative time points. The number of scans used to compute the template at each time point is shown in Fig. 4. The described algorithm allows construction of the atlas at any GA. All atlas templates were visually inspected. The resulting template tensors were used to compute the following template scalar properties: Fractional Anisotropy (FA), Axial Diffusivity (AD), Radial Diffusivity (RD), Mean Diffusivity (MD). Further, Color Fractional Anisotropy (CFA) maps were also computed where the color assignment at a voxel was based on the orientation of principal eigenvector of the diffusion tensor at that voxel. The standard red-green-blue (RGB) code (red for right-left, blue for inferior-superior, and green for anterior-posterior orientation of the principal eigenvector) was used for the color-coding in CFA.

Fig. 4:

Number of fetal scans used in atlas construction at different gestational age points.

Region-of-Interest Sampling for Fetal Brain Growth Analysis:

Abbreviations:

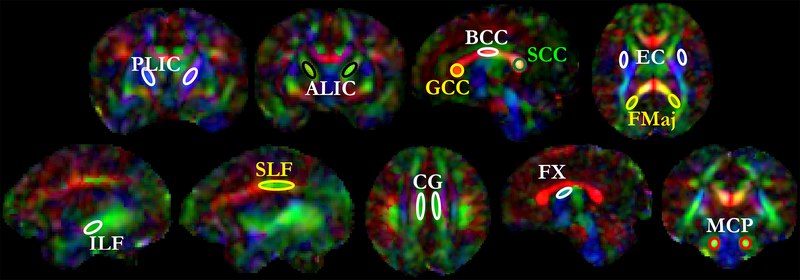
The following abbreviations are used for the regions-of-interest that were analyzed and discussed in this paper:

Cingulum (Cg), Fornix (Fx), Corpus Callosum (CC), Genu of Corpus Callosum (GCC), Splenium of Corpus Callosum (SCC), Body of Corpus Callosum (BCC), Anterior Limb of the Internal Capsule (ALIC), Posterior Limb of the Internal Capsule (PLIC), Retrolenticular Limb of the Internal Capsule (RLIC), External Capsule (EC), Forceps Major (Fmaj), Forceps Minor (Fmin), Anterior Thalamic Radiation (ATR), Posterior Thalamic Radiation (PTR), Superior Thalamic Radiation (STR), Inferior Longitudinal Fasciculus (ILF), Superior Longitudinal Fasciculus (SLF), Inferior Fronto Occipital Fasciculus (IFOF), Middle Cerebellar Peduncle (MCP), Corona Radiata (CR), Sagittal Stratum (SS), Corticospinal Tract (CST), Corticopontine Tract (CPT).

To study the regional trends in FA values over GA, we sampled 27 voxels (~46 mm³) with relatively high FA values in each region-of-interest (ROI), Fig. 5. ROIs were manually defined at each GA time point (22–38w) in the atlas using CFA images. The ALIC and PLIC were sampled in the coronal view and voxels close to the genu of the internal capsule were not included. The axial view was used for sampling Fmaj, where green-colored voxels from the CFA were chosen and yellow-colored voxels close to the Fmaj were avoided. The ILF and SLF were sampled in the sagittal view. While sampling SLF, red-colored voxels were avoided and green-colored voxels were chosen. Cingulum was only sampled in the axial view as a green strand. Fornix was sampled in the sagittal view in the superior region. MCP was sampled in the coronal view as green voxels.

Fig. 5:

Region-of-interest (ROI) selection for fractional anisotropy sampling: 27 voxels of relatively high intensity on FA images were chosen within each ROI. The ROIs are shown over a template from the atlas. Label descriptions are available in the ‘Abbreviations’ subsection under Methods.

Further, to study changes in FA in the cortical plate, the cortical plate was segmented on T2w atlas corresponding to the DTI atlas at each GA and propagated to the DTI atlas. This was done through deformable registration between T2w and DTI atlases at each GA, and labels were propagated using atlas-based segmentation (Gholipour et al., 2017). For quantitative analysis, FA values were averaged voxel-wise in each region-of-interest.

RESULTS

Fig. 6 shows the FA and CFA of the constructed atlas at representative GA points, each at 2-week intervals. In this section, we first discuss features of the atlas that are observed with increasing GA, including the appearance of prominent tracts and their course of development in the observed time period. Then we show regional quantitative changes in FA as a measure of fiber maturation, organized by major fiber bundles of interest. We also analyze FA changes in the cortical plate.

Fig. 6:

Axial, coronal, and sagittal views of fractional anisotropy (grayscale) and color fractional anisotropy templates from the in-utero DTI atlas. Gestational age in weeks is mentioned below the images.

Features of the Atlas:

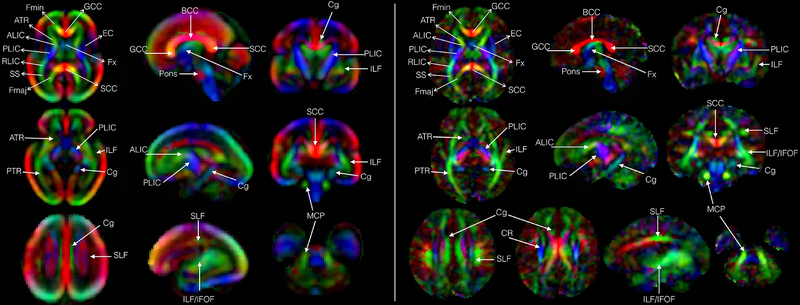
Fig. 7 shows various fiber bundles identified in two time points of the atlas (GA 27-week and GA 38-week) in axial, coronal, and sagittal planes. Several fiber pathways of interest could be observed, which are discussed here.

Fig. 7:

Color fractional anisotropy maps showing various fiber-rich structures labeled at the end of the 2^nd trimester at GA-27w (a), and at the end of the 3^rd trimester at GA-38w (b) respectively. Label descriptions are available in the ‘Abbreviations’ section.

Limbic Fibers:

we observed prominent limbic fibers (Cg and Fx) at all time points in the atlas. Cg and Fx bundles at GA-22w were observed in sagittal and coronal views (Fig. 7). However, Cg bundle, oriented in anterior-posterior direction, was identified as a continuous region in axial slices only around GA-26w. Limbic fibers continued to increase in volume and were identified throughout the 3^rd trimester. Both the superior and inferior regions of Cg could be visualized in their respective views (axial, sagittal, coronal).

Projection Fibers:

We identified a number of projection fibers at the earliest GA points of the atlas. At GA-22w ALIC was identified as a bright green region in axial, sagittal or coronal views. Similarly, at GA-22w the PLIC region was also detectable. However, it consisted of dark blue anterior regions, light blue middle regions, and green posterior regions indicating that it is composed from fiber pathways with different orientations. Projection fibers continued to develop through the 2^nd trimester. During the 3^rd trimester, all major white matter tracts and regions could be located. Projection fibers including the thalamo-cortical fibers as well as regions occupied by CST and CPT (seen as blue regions with superior-inferior orientation within PLIC) continued to increase in volume, and were easier to distinguish in the color FA maps throughout this period. The corona radiata which begin to develop in the 3^rd trimester were also observed towards the end of this period (Fig. 7).

Association fibers:

ILF was observed as a longitudinal band of green fibers in the parieto-occipital region and continued to grow in size throughout gestation. Moreover, the occipital regions containing ILF were more voluminous compared to anterior suggesting that these regions, having antero-posterior orientations, contained elements of IFOF. In contrast, SLF was not visualized in continuity as a green antero-posteriorly oriented band before GA-26w. We also noted that projections from SLF to cortical region began developing in late 3^rd trimester and could be observed in the sagittal view as shown in Fig. 7.

Corpus Callosum:

The SCC develops significantly during the 2^nd trimester. We found that by the end of the 3^rd trimester both the GCC and SCC regions appeared equally prominent. Fmaj and Fmin were visible in the axial views throughout this period and continued to grow in size. We noted that at GA-22w, the GCC appeared more compact (higher FA) but of the same thickness as SCC (Fig. 6). Towards the end of the 2^nd trimester (Fig. 6) CC appeared more uniform as seen in FA images. We also observed Fmaj and Fmin early on, although Fmin could not be clearly visualized in these images as a continuous green region (oriented antero-posterior) in the frontal lobe, connected to the GCC, until GA-25w. Fmaj was observed as a green band in the occipital regions and was in continuity with SCC in the axial view throughout the period of analysis.

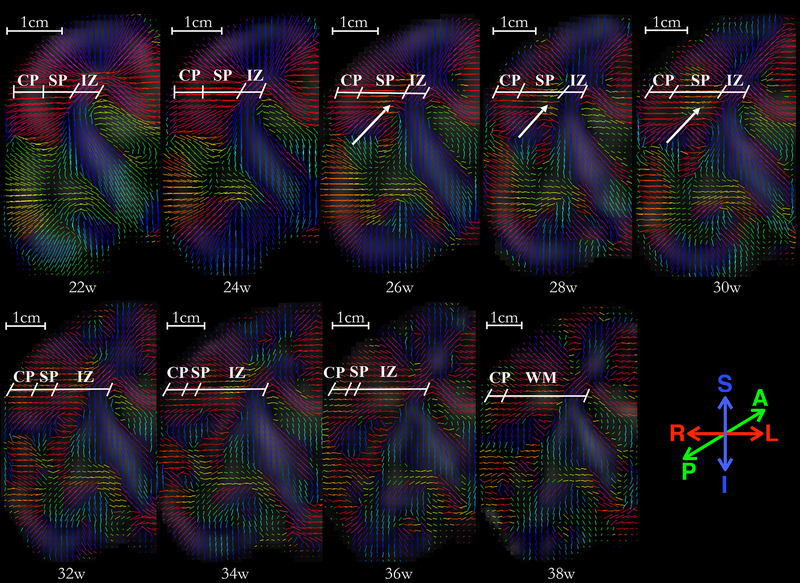
In addition to these observations, we noted the neuronal migration in the cortical region and gradual disappearance of radial coherence throughout the gestational age. These observations have been shown in Fig. 10 and discussed further in the next section.

Fig. 10:

A panel of primary eigenvectors of diffusion tensors projected on the right-half coronal plane located in the vicinity of genu of the internal capsule, with inferior section in the temporal lobe and superior section at the boundary of frontal and parietal lobe. Age in gestational weeks is shown below each image. Initial radial organization of cortical plate and subplate, indicated by the primary eigenvectors of the diffusion tensors directed towards the ventricles at 22w, gradually disappears with an increase in gestational age. The reduction in the radial coherence appears to affect various brain regions differently; reduction in inferior region (temporal lobe) appears near-complete at 36 weeks, as compared to the superior region (fronto-parietal lobe) which appears to have significantly reduced radial coherence at GA-34w. Moreover, note that the radial coherence of cortical plate and subplate in central regions, marked at 22w, starts to disappear in regions of deep subplate zone first (26–28w). The reduction in radial coherence parallels appearance of long association fibers (arrows). The borders between transient fetal zones (CP, SP, IZ) were identified in the underlying FA images, and are marked by an oblique line. Abbreviations: cortical plate (CP), subplate (SP), intermediate zone (IZ), and fetal white matter (WM). Borders are approximate and were identified visually on the underlying FA and T2 images by a neuro-anatomist (LV) with expertise in delineating transient fetal zones on MR and histology images.

Changes in Fractional Anisotropy and Mean Diffusivity over the Gestational Age Period:

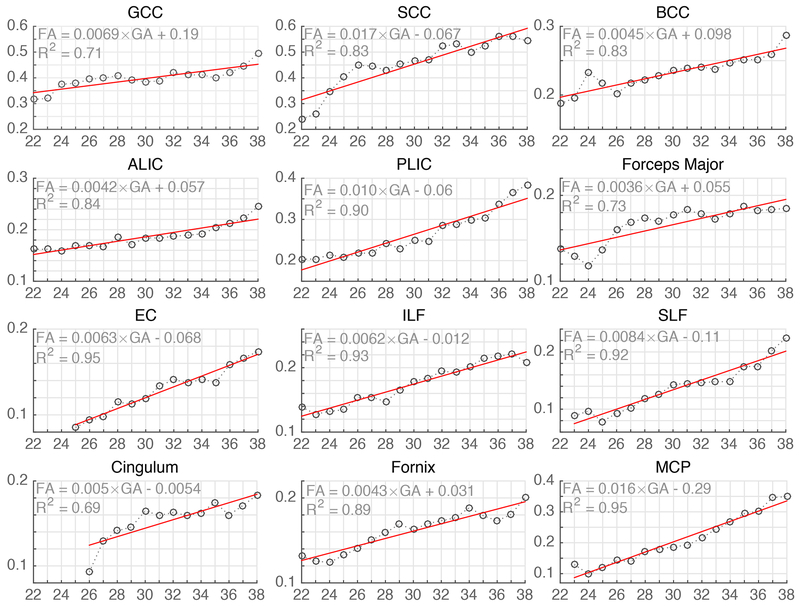
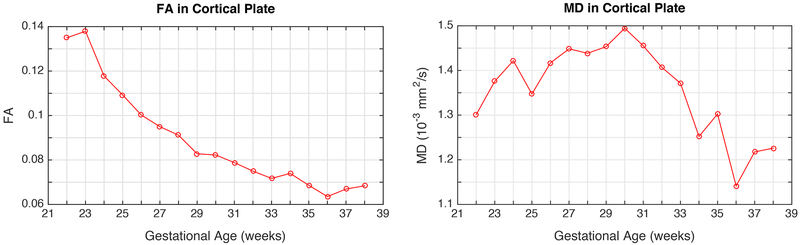
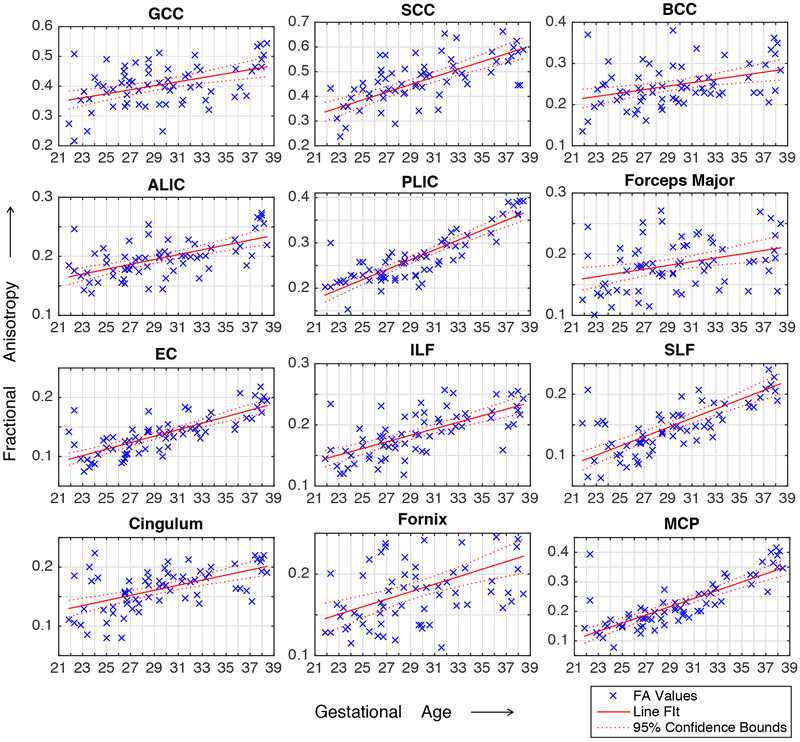
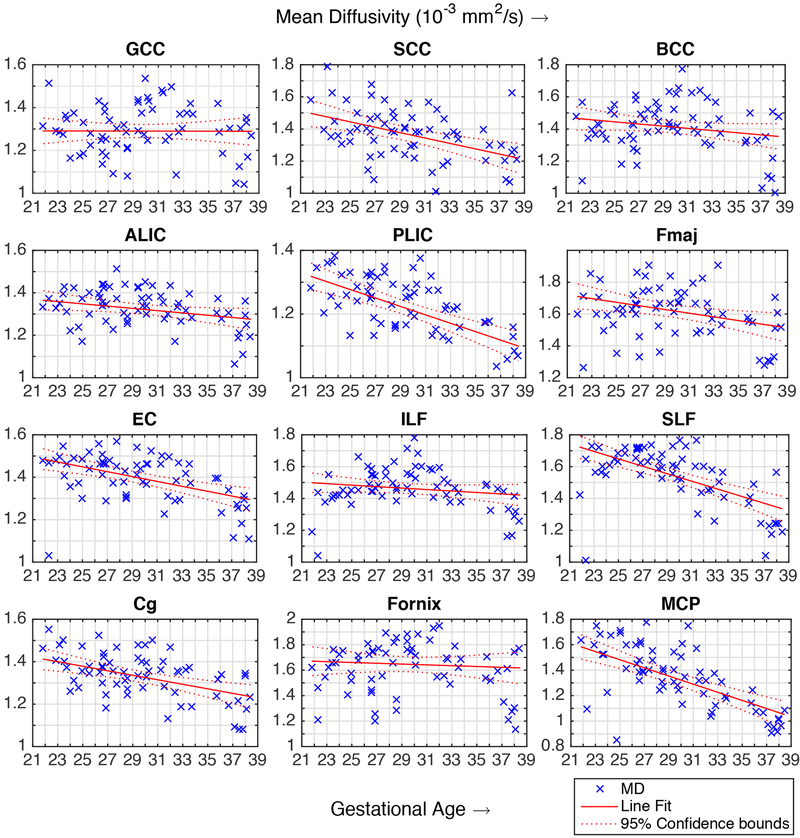
The variation of FA over the gestational age range of the atlas was quantitatively probed in the following fiber regions and structures: Fx, Cg, ALIC, PLIC, ILF, SLF, GCC, BCC, SCC, MCP, Fmaj, EC. The observed trends are shown in Fig. 8 along with linear regression fitted lines and the coefficient of determination (R²). FA values in these regions were also calculated for the images of individual subjects through projection of ROIs defined on the GA-matched atlas (mapped through computed deformable registrations). The plots of FA and MD values for individual subjects along with regression lines and confidence intervals are shown in the appendix. Further, changes in FA and MD in the cortical plate region were also studied throughout gestation. The average FA and MD values in the cortical plate are shown in Fig. 9. These results are discussed with respect to the previous ex vivo and preterm infant studies in the next section.

Fig. 8:

Fractional Anisotropy (FA) (y-axis, unitless) plotted against the gestational age (x-axis, in weeks) for major fiber pathway structures. The FA values and trends observed in our atlas are in agreement with previously published ex vivo, preterm infant and in utero studies. The abbreviation used in the figure for fiber structures have been described in the Methods section.

Fig. 9:

Fractional Anisotropy (FA) and mean diffusivity (MD) in the cortical plate, plotted against gestational age (in weeks). While FA shows decreasing trend with gestational age, MD reaches a peak between 28 and 32 gestational weeks.

DISCUSSION

In this section we discuss our qualitative and quantitative observations on the atlas in the context of previous ex vivo fetal, pre-term infant and newborn studies. We also discuss neuronal migration and loss of radial coherence with the progression of GA as a major transformative event of interest during gestation.

Development of Major Fiber Bundles:

Limbic Fibers:

Consistent with ex vivo based studies (Dubois et al., 2015; Huang et al., 2009; Huang and Vasung, 2014), we observed limbic fibers on the atlas throughout gestation. Limbic fibers sampled in this study (Cg, Fx) start developing in the 1^st trimester (Clowry, 2007; Kostovic and Vasung, 2009; Vasung et al., 2010) and continue developing throughout the gestation. FA in these regions rises from 0.1 at the beginning of late 2^nd trimester to 0.2 near the end of gestation. The estimated near-term FA values in Cg and Fx (Fig. 8) are comparable to the FA in these regions (~0.2) reported at birth (Hermoye et al., 2006; Kunz et al., 2014).

Projection Fibers:

Projection fibers (ATR, STR, PTR, CST, CPT, etc.) or regions containing mostly projection fibers (ALIC, PLIC, RLIC) start developing in the 1^st trimester of pregnancy (Clowry, 2007; Kostovic and Vasung, 2009; Vasung et al., 2010). The internal capsule (IC) undergoes complex microstructural changes due to intermingling of various fibers that start developing at different stages of gestation. In both the ALIC and PLIC regions, a general trend of increasing FA was observed throughout gestation. The FA near term in PLIC (~0.38) was found to be close to the reported FA value in the PLIC in neonates (~0.4) (Kunz et al., 2014; Oishi et al., 2013). Compared to the ALIC, higher FA values in the PLIC were observed across the GA range (Fig. 8), which is in agreement with previously reported FA trends in the IC in fetal (Jiang et al., 2009) and neonatal (Geng et al., 2012; Kunz et al., 2014; Sadeghi et al., 2013) studies.

The ALIC white matter region contains predominantly ATR fibers that connect the anterior and medial thalamic nuclei with prefrontal cortex, and frontopontine fibers. ATR fibers intermingle with the frontopontine fiber in the superior region of ALIC where ATR occupies central portion surrounded by frontopontine fibers. In contrast, ATR fibers are predominant in the inferior ALIC region close to the anterior commissure (Mamah et al., 2010). At GA-22w, this area shows a diffuse green band without sharp boundaries on our atlas (which are observed in the higher GA images). We hypothesize that the edges in ALIC region are not sharp because of the partial voluming effects which affects how small structures appear in these images (Counsell et al., 2014). Further, this indicates that ATR is still developing in the late 2^nd-trimester, which has also been reported in histology-based and ex vivo studies (Huang et al., 2016; Vasung et al., 2017). From adult studies it is known that PLIC is composed of parietopontine fibers, corticorubral tract, corticobulbar tract, STR, CST, and CPT fibers that develop very early during fetal brain development (Vasung et al., 2010). Therefore, our reconstructions are in agreement with prior knowledge and suggest that projection fibers to brainstem and spine, that are occupying PLIC, could be identified as a distinctly blue band as early as GA-23w.

Association Fibers:

These fibers begin developing in the 2^nd trimester (Vasung et al., 2010) and continue to grow throughout gestation. SLF in particular, grows rapidly during this period and continues to develop significantly even after birth (Huang and Vasung, 2014). SLF appeared most voluminous at GA-38w in our computed atlas. SLF was reliably visualized on our atlas at GA-26w, while ILF/IFOF could be located as early as GA-22w. In previous studies, the SLF was not observed at GA-19w (Huang et al., 2006), and ILF became apparent closer to GA-20w (Huang et al., 2009; Vasung et al., 2017). As expected, FA in ILF/SLF shows an upward trend with GA (Fig. 8). We found the FA values in these two regions to be comparable to each other. The FA at the end of gestation (~0.22) in ILF and SLF observed in this study is close to the FA at birth (~0.25) reported by Hermoye et al. (2006) and Oishi et al. (2013).

Corpus Callosum (CC):

Compared to SCC, we observed higher FA in the GCC region in the lower GAs up to 25 weeks (Fig. 8). FA continued to rise in all sampled areas of CC (SCC, GCC, BCC) throughout gestation, although the rate of change appeared to be lower near term. The initial disparity in FA values between GCC and SCC may be due to the fact that the anterior region of corpus callosum is more developed than the posterior region near GA-20w (Huang et al., 2006; LaMantia and Rakic, 1990). After GA-26w, FA in the SCC region exceeded the FA in the GCC region, and was close to previously reported FA in the SCC (Jiang et al., 2009) near term (approaching 0.55). Similarly, higher FA in SCC compared to GCC was reported by Kasprian et al. (2008) in a fetal-specific study and Geng et al. (2012) in a neonate study. Further, FA in the BCC was found to be lower than the FA in GCC and SCC, which is in agreement with previous studies (Kunz et al., 2014). These regional differences of FA in CC might be explained by differences in the density and number of axons as well as their pruning across development (Kunz et al., 2014; LaMantia and Rakic, 1990). Our observations were also in agreement with the prior findings in primates where LaMantia and Rakic (1990) observed higher number of axons in the anterior regions of CC compared to its posterior region in the early 2^nd trimester.

FMaj, EC, and MCP all showed an upward trend of increasing FA with gestational age (Fig. 8). The observed FA in FMaj in higher GA (~0.2) was lower than the reported FA (~0.32) in preterm neonates at birth (Kunz et al., 2014). This difference could have arisen due to the fact that we limited sampling to the green region of Fmaj. In the EC, FA near term (~0.18) is close to the FA in 2-week old normal neonates (~0.2) reported by Sadeghi et al. (2013) but is slightly lower than the FA at GA-38w (~0.22) reported in (Jiang et al., 2009). This discrepancy could be due to differences in FA sampling and the relatively lower SNR in Jiang et al. study, which has been shown to result in higher FA (Pierpaoli et al., 1996). The MCP is a fiber-rich bundle that starts developing early in gestation, and the FA observed in the MCP rose sharply to ~0.35 near term from ~0.1 at GA-22w.

Neuronal Migration and Gradual Disappearance of Radial Coherence:

During 2^nd trimester, neurons actively migrate from the ventricular zone to their final destination in cortical plate along the radial glial-cell scaffold (Rakic, 1988). The majority of these migratory neurons typically reach their destination by the end of GA20–21w (Bystron et al., 2008). A distinct radial arrangement of cortical neurons, apparent at this stage of gestation, has been suggested by visualizing radial coherence of the telencephalic wall in the prior ex vivo and preterm infant DTI studies.

In this study, we observed the radial coherence of the telencephalic wall (between ventricular/subventricular or intermediate zone and pial surface) at GA-22w (Fig. 10). This radial arrangement emanates most likely from the radial glial cells, glial migration streams (Takahashi et al., 2012), and abundant radially oriented callosal fibers (Vasung et al., 2017). With increase in gestational age, radial coherence of the telencephalic wall gradually disappears (Fig. 10). From the upper row in Fig. 10, it can be observed that the regional radial coherence of fronto-parietal operculum starts to disappear around GA 26w in the areas of the deep subplate zone. This regional loss of radial coherence coincides with the appearance of long association cortico-cortical tracts reported previously (Vasung et al., 2017). At this stage, it is unclear whether the retention of radial coherence, continuously stretching from the cortical plate to more superficially located subplate zone, reflects an abundant growth of efferent cortico-cortical connections (which gyrate and join association cortico-cortical bundle in the deep subplate zone) or remnants of transforming radial glia (Schmechel and Rakic, 1979). This could be resolved with more sophisticated ex vivo MRI. Approaches that rely on DTI-specific parameters to segment cortical plate (Maas et al., 2004) can also be explored.

Our results are in agreement with previously reported studies. Takahashi et al. (2012) reported the disparities in regression of radial coherence among different regions of the brain in a study of fetal brains aged GA 17w–40w. Xu et al. (2014) used High Angular Resolution Diffusion Imaging (HARDI) on ex vivo and preterm infant brains to demonstrate transient radial coherence in a study of fetuses (>GA-19w), preterm and term-born infants, toddlers, and adults. Kolasinski et al. (2013) studied the radial coherence originating in ventricular zone, and tangentio-radial coherence emanating in the ganglionic eminence in a cohort comprising fetal brains GA 19w–22w. Vasung et al. (2017) observed the changes in radial coherence in 9 fetal specimens aged GA 18–34w in a HARDI study. An observation of prominent radial coherence in mid-gestational period and subsequent decline is common among these studies, however, these studies suffer from limitations such as differences in post-mortem interval and tissue damage (Takahashi et al., 2012; Vasung et al., 2017, 2016; Xu et al., 2014), as well as the differences in MRI acquisition and voxel size between preterm infant and ex vivo MRIs (Xu et al., 2014).

Further, changes in FA and MD in the cortical plate region were also evaluated throughout gestation (Fig. 9). Fig. 9 showed a decreasing trend in average FA of the cortical plate with increase in GA, while average MD showed increase during early development, reached the peak between 28 and 32 GA, which was followed by the decline. Thus, our results resemble the ones reported by (McKinstry et al., 2002) with the main difference in reaching the peak MD values 2 weeks earlier. The decrease in cortical FA and bell shape curve of cortical MD throughout gestation has been associated with addition of neuropil (Bourgeois and Rakic, 1993), decrease in cell density due to apoptosis (Chan and Yew, 1998), disappearance of embryonic columns, parallel increase in dendritic arborization (Mrzljak et al., 1992), and cortical ingrowth of axons (Kostović and Jovanov-Milošević, 2006) as suggested by McKinstry et al., (2002) and Nossin-Manor et al. (2015). However, the two-week difference in reaching the peak cortical MD in in utero fetal brains that we observed, compared to the peaks described by McKinstry et al., 2002 might be explained by differences in sampling of cortical ROIs or by altered maturation of cortex described by Ball et al. (2013) and Bourgeois et al. (1989). We note that given the effective resolution of in utero imaging and the thickness of the developing cortical plate, we were not able to reliably and accurately delineate the transition areas between cortical plate and subplate in all areas across telencephalon. Therefore, we did not examine regional differences in FA or MD of the cortical plate, which may be influenced by regional existence of subplate and to a lesser extent by cytoarchitectonic variation of the cortical plate.

Lastly, we describe the presence of the medial migratory stream that is easily seen and identified on T2w MRI as previously reported (Paredes et al., 2016). In Fig. 11, these streams are situated below the gyrus rectus. The area 14 of the gyrus rectus has local connections (with areas 13, 11, and of the orbital proisocortex, with medial areas 10, 9, 32, 25, and 24, but it also has some connections with area 46) and long connections derived from agranular insula, temporal polar proisocortex, areas TS1 and TS2, hippocampus and the presubiculum (Petrides and Pandya, 2012). The direction and the shape of the encircled area in Fig. 11 does not correspond to any of the aforementioned connections, and therefore strongly suggests the presence of medial migratory stream. These migratory paths are used by young neurons to travel from the anterior tip of the lateral ventricle to the medial prefrontal cortex, after the peak migration period and up to few months postnatal. We observed the presence of medial migratory stream in the sagittal view of CFA maps in older fetuses (higher gestational ages) during 3^rd trimester. Fig. 11 shows the medial migratory stream observed in a template color FA map at GA-33w from the computed in utero DTI atlas.

Fig. 11:

Medial migratory steam of inhibitory neurons migrating from anterior tip of the lateral ventricle to the medial prefrontal cortex has been shown (on the right) on a color FA template computed at GA-33w. The zoomed in view on the left shows the projection of principal eigenvectors of the diffusion tensors in this area on the sagittal plane visualized in this figure. The red bounding line was hand drawn over the medial migratory stream.

LIMITATIONS AND USAGE

Imaging Resolution:

To construct an anatomic atlas from in vivo imaging, ideally the images would be acquired at an isotropic resolution that is consistent for visualizing structures of interest across subjects. This was not accomplished in our study due to practical limitations. Anisotropic acquisition leads to partial voluming artifacts in DTI, which are further exacerbated by the complex microstructural interaction of various fiber bundles that start developing at different stages of gestation and mature at their specific schedule. Imaging resolution also limits which structures can be visualized at a given gestational age, for example, we were unable to visualize Cingulum as a continuous antero-posteriorly oriented green fiber region in the axial view before GA-26w, even though it was visualized in an ex vivo study by (Huang et al., 2006) at GA-19w. This limitation stems from the anisotropic resolution imaging approach rather than the atlas construction process. In contrast, we were able to visualize the inferior portion of Cingulum even at the low end (GA-22w) of the gestational period observed in this study. Imaging resolution can also potentially affect quantitative measurements performed using DTI parameters as the neighboring regions can contribute to DWI signal arising at the voxels where two different structures are present. In our study, we restricted the FA sampling to regions fully within the tract of interest.

Our comparison with previously reported FA values in different regions of the fetal brain is qualitative. No statistical comparison could be done due to the lack of a DTI atlas of fetal brain. In addition, while making similar FA-based comparisons with previous in utero studies that typically suffer from low SNR, the previous reports of lower SNR resulting in higher FA (Pierpaoli et al., 1996) must be taken into consideration.

Sample Size:

The sample size used for computing templates at GA-22w to GA-38w was not evenly distributed. This is a common problem in fetal and infant imaging due to the challenges in recruiting subjects and imaging (Huang et al., 2009; Ou et al., 2017; Sadeghi et al., 2013; Sanchez et al., 2012). In this study, 13 out of 17 age bins included a sample size of 8 or higher, with only 2 out of 17 age bins with sample size higher than 10. In age bins with more than 6 volumes, removing or adding one sample did not appear to visually impact the computed template or the features that were observed. To-date this study builds upon and reports one of the largest sample sizes of its kind based on in utero fetal DTI; yet to reliably study the impact of biological variables on brain microstructural development and its characteristics such as hemispheric asymmetry, we aim to collect more samples.

Usage:

The DTI parameter atlas is available online (http://crl.med.harvard.edu/research/fetal_brain_atlas/) and can be useful in several important applications: 1) the atlas provides normative quantitative and qualitative data for in utero neurodevelopmental studies, 2) the atlas addresses a wider gestational age range and larger number of sampled areas than prior studies, 3) our atlas computation method represents the first comprehensive approach to compute motion-robust diffusion tensor maps from noisy in utero fetal measurements and combine individual DTI maps into a kernel-regressed template at any given gestational age; this new atlas building approach should enable statistical voxel-wise analysis, tract-based spatial statistics (TBSS), or tract-specific analysis (TSA) based on DTI data (Khan et al., 2018; Smith et al., 2013), 4) the atlas may be used by radiologists as a point of reference for clinically acquired DTI scans, and 5) the post-processing methods used in this study can also be used to analyze data from individual fetuses and the atlas can be used to compare the observations from an individual fetus with the previously imaged population.

CONCLUSION

We presented a comprehensive method and algorithms to compute a spatiotemporal DTI atlas from a motion-corrupted dataset. We applied these algorithms to a set of 67 fetal DWI scans acquired in utero from normal subjects. From oversampled, motion-corrupted noisy DWI data acquired from subjects in a normal fetal population, we computed diffusion tensor maps. Further boost in SNR was achieved during atlas construction by spatiotemporal averaging of the tensor maps across subjects that were scanned at different age points. This led to the computation of the first spatiotemporal DTI atlas of the fetal brain that depicts in utero development. The primary contributions of this study are the following: 1) We introduced a pipeline for kernel-regression based spatiotemporal diffusion tensor atlas construction which utilizes tensor-based registration for accurate alignment of white matter structures and produces an unbiased age-regressed template at any given age point. To the best of our knowledge, this is the first study integrating a kernel-regression approach within a diffusion tensor atlas construction pipeline that relies on tensor-based registration. 2) We applied this atlas construction technique to create the first DTI atlas of the in utero fetal brain from a relatively large fetal cohort. 3) We evaluated the atlas in terms of its ability to effectively capture and portray qualitative and quantitative developmental trends observed in the previously reported ex vivo, preterm infant, and in utero studies. The atlas was found to correctly portray the early presence of limbic fiber bundles as well as the appearance and maturation of projection and association fiber bundles throughout gestation. We also reported gradual disappearance of radial coherence of the telencephalic wall in agreement with prior ex vivo and preterm infant DTI studies. The constructed atlas can be used as a reference for DTI-based studies on in utero fetal brain development, and groupwise DTI studies to investigate normal and abnormal brain development.

Plot of individual subject FA at multiple ROIs.

Plot of individual subject MD at multiple ROIs.