Multicenter reproducibility of quantitative susceptibility mapping in a gadolinium phantom using MEDI+0 automatic zero referencing

Abstract

PURPOSE

To determine the reproducibility of quantitative susceptibility mapping at multiple sites on clinical and preclinical scanners (1.5, 3, 7 and 9.4 T) from different vendors (Siemens, GE, Philips and Bruker) for standardization of multicenter studies.

METHODS

Seven phantoms distributed from the core site, each containing five compartments with gadolinium solutions with fixed concentrations between 0.625 mM to 10 mM. Multi-echo gradient echo scans were performed at 1.5, 3, 7 and 9.4 Tesla on 12 clinical and 3 preclinical scanners. DICOM images from the scans were processed into quantitative susceptibility maps using the Laplacian Boundary Value (LBV) and MEDI+0 automatic uniform reference algorithm. Region of interest (ROI) analyses were performed by a physicist to determine agreement between results from all sites. Measurement reproducibility was assessed using regression, Bland-Altman plots and the intra-class correlation coefficient (ICC).

RESULTS

QSM maps from all scanners had similar, artifact-free visual appearance. Regression analysis showed a linear relationship between gadolinium concentrations and average QSM measurements for all phantoms (y = 350× − 0.0346, r² > 0.99). The standard deviation of measurements increased almost linearly from 32 ppb to 230 ppb as the measured susceptibility increased from 0.26 to 3.56 ppm. A Bland-Altman plot showed the bias, upper and lower limits of agreement for all comparisons were −10, −210 and 200 ppb respectively. The ICC was 0.991 with a 95% CI (0.973, 0.99).

CONCLUSIONS

QSM shows excellent multicenter reproducibility for a large range of susceptibility values encountered in cranial and extra-cranial applications on a diverse set of scanner platforms.

INTRODUCTION

From its initial applications to endogenous brain iron quantification, quantitative susceptibility mapping (QSM) has seen increasing applications to a wide range of quantitative research on disease conditions including intracerebral hemorrhage (1–4), liver iron overload (5,6), bone mineral quantification (7) and preclinical contrast agent toxicity studies (8). These applications require confidence in the reproducibility QSM for a wider range of susceptibility values, field strengths, and vendor platforms than has been previously reported by researchers (9–13).

An important tool used in MRI research including the QSM approach is a phantom that contains a set of compartments with different gadolinium concentrations that are fixed in agarose gel (14–17). Gadolinium solutions at known concentrations are regularly employed as tissue models of susceptibility for both healthy and diseased anatomical targets because their magnetic behavior can be designed to closely mimic that of each target tissue (18). The absolute susceptibility of 0.5 mM solution of a gadolinium-based contrast agent (formulated at a standard concentration of 0.5 M), is −8.859 ppm which is close to that of most biological tissues. QSM experiments on phantoms of gadolinium have been used useful starting points for obtaining insight into various physiological processes including urine concentration by kidneys (19), cardiac flow rate (20) and cerebral perfusion (21). Gadolinium solutions can reproducibly model QSM measurements of tissue iron, which are in the form of ferritin and hemosiderin, across all field strengths, unlike iron oxides which exhibit saturation of magnetization by 1 Tesla (22). Because of regular use of such gadolinium-based phantoms for both the development and validation of QSM acquisition and post-processing algorithms, the study of reproducibility of QSM measurements in gadolinium phantoms is important.

Previous investigations that examined the reproducibility of QSM by employing phantoms are now known to have two specific shortcomings. First, studies prior to 2015 utilized specific algorithms that performed a key dipole inversion step either without regularization (9,11), or by minimization of a linear data term with L1-regularization (9), which consistently yielded moderate to severe streaking artifacts in resultant images (9,11). Subsequently developed post-processing methods have been able to more effectively suppress these streaking artifacts, most notably by minimizing a nonlinear data fidelity term with L1-regularization (23). QSM measurements from different MRI scanners are only comparable with respect to a suitably chosen reference. Susceptibility sources are usually embedded in an aqueous gel which retains phase information for more accurate QSM reconstruction. Since it is reasonable to expect that susceptibility within the aqueous gel solution is uniform, this knowledge can be employed as a constraint during QSM reconstruction to potentially improve QSM image quality. A recently developed algorithm, MEDI+0, takes advantage of this constraint by adding another L2-regularization term to the optimization equation used in the iterative approach (23), to enforce homogeneity in specified regions (24).. MEDI+0 enables the use of the aqueous gel region as a consistent automatic zero-reference and eliminates the need for manual selection of an arbitrary reference region. This feature makes MEDI+0 highly suitable for performing multicenter QSM comparisons using agarose gel phantoms. In this study, we compare the QSM estimates derived using the MEDI+0 algorithm across a fixed range of susceptibility sources in a set of simultaneously synthesized gadolinium phantoms, distributed across at seven sites on multiple vendor systems, and imaged at four field strengths.

METHODS

A phantom was constructed by embedding five latex balloons (Imperial Kaos, Tie-Not, US), each filled with a specific concentration (10, 5, 2.5, 1.25 or 0.625 mmol/L) of gadolinium (Magnevist, Berlex Laboratories, Wayne, NJ), in a 1% agarose gel solution in a 500 mL plastic container. Images of the phantom were acquired on 1.5 and 3 Tesla scanners available at the primary study site (Site A, Table 1) in a head coil using a 3D multi-echo spoiled gradient recalled-echo (SPGR) sequence with the following parameters: voxel size = 0.6 × 0.6 × 0.6 mm³, flip angle = 15°, TR = 49 ms, number of echoes = 10, first TE = 3.7 ms, echo spacing = 4.1 ms. Four additional phantoms were constructed in an identical manner, scanned at Site A and shipped to Sites B to E (Table 1) for the multi-site imaging experiment. Imaging parameters across all sites were kept similar to parameters from Site A. For imaging on small bore preclinical scanners, two dedicated phantoms were designed and constructed by embedding five balloons with gadolinium concentrations ranging from 10 to 0.625 mmol/L in a 50 mL conical centrifuge tube (Falcon, Fisher-Scientific, USA) of 1% agarose gel. This phantom was scanned on a Bruker 7T scanner (BioSpin MRI GmbH) at Site 1 using the following parameters: voxel size = 0.5 × 0.5 × 0.5 mm³, flip angle = 15°, TR = 34 ms, number of echoes = 8, first TE = 3.4 ms, echo spacing = 3.8 ms. These phantoms were then shipped to Sites E and F for imaging on preclinical scanners. The phantoms scanned on the MR platforms available at each site are shown in Table 1. The range of imaging parameters used for all scans are displayed in Table 2. All DICOM images generated from the examined scanner hardware at each site were electronically transmitted to Site A. Derived MRI DICOMs required the complex dataset that consisted of the phase map information. These were imported into a custom MATLAB software (The Mathworks, Natick, MA). For each scan, the total magnetic field map was generated from the DICOM images using a nonlinear voxel-wise fit (23) with a correction to remove residual echo-to-echo phase inconsistencies in the readout direction when present (25). Phase processing was performed using quality guided field unwrapping (26) and Laplacian Boundary Value (LBV) background field removal (27), because these methods have been shown to produce the best performance in QSM processing (12,28). The QSM map was reconstructed from the local field map using the MEDI+0 method (24), which minimized variation in the agarose gel medium of the phantom according to the expression:

$${\chi }^{\ast }=\underset{\chi }{\text{argmin}}\frac{1}{2}{\Vert w\left(e^{-if}-e^{-i(d\ast \chi )}\right)\Vert }_2^2+{\lambda }_1{\Vert M_G\nabla \chi \Vert }_1+{\lambda }_2{\Vert M_{\mathit{AGAROSE}}(\chi -\overline{{\chi }_{\mathit{AGAROSE}}})\Vert }_2^2$$ (1)

where χ is the susceptibility map, * is the convolution operation, w is noise weighting, f is the measured local field, ∇ is the gradient operator, and M_G is a binary edge mask. The term, $\overline{{\chi }_{\mathit{AGAROSE}}}$, penalizes susceptibility variation within the agarose gel medium, which can be isolated using a mask, M_AGAROSE, obtained automatically by complementing a mask of the entire phantom with a mask of the gadolinium balloons defined as voxels with intensity greater than 40% of the maximum intensity of the magnitude image.. The optimal values for the regularization parameters, λ₁ and λ₂ were determined using L-curve plot analysis to be 10 and 1 respectively. The output of each step of the reconstruction procedure is shown in FIG 1. The mean voxel value in a 3-dimensional ROI covering the entire region of the gadolinium solution in each balloon was recorded.

Table 1.

Scanner specifications for all sites. The description in each cell is formatted as manufacturer model name (software version, coil name). The coils are 8 Channel Head (8 Ch HE), 20 Channel Head/Neck (20 Ch HE/NE), 32 Channel Head (32 Ch HE), 64 Channel Head/Neck (64 CH HE/NE) and linear transmit/receive body coil. Further details on the phantoms and scanners are shown in Supporting Information Table S1.

Site	1.5T scanners	3T scanners	7T Scanners	9.4 T scanners
A	Siemens Aera (VE11A, 64 Ch HE/NE)	Siemens Skyra (VE11A, 20 Ch HE/NE), Siemens Biograph mMR (VB20P, 32 Ch HE)	Bruker Biospin (Paravision 5.1, body coil)
B	Philips Achieva (5.1.7.2, 8 Ch HE)	Philips Achieva dStream (5.1.7.2, 32 Ch HE)
C	GE Signa HDxT (V23, 8 Ch HE)	GE Signa HDxT (V23, 8 Ch HE)
D	Siemens Aera (E11, 20 Ch HE/NE)	Siemens Prisma (E11, 20 Ch HE/NE)
E	GE Signa HDxT (V23, 8 Ch HE)	GE Discovery MR750 (V25, 8 Ch HE)
F			Philips Achieva (5.1.7.0, 32 Ch HE), Bruker Pharmascan (Paravision 6.0.1, body coil)
G				Bruker Biospin (ParaVision 6.0.1, body coil)

Table 2.

Range of MRI acquisition parameters

	1.5T	3T	7T	9.4 T
Number of echoes	6–10	6–10	8	7
Minimum echo (ms)	1.8 – 3.7	1.3 – 4.3	3.4	4.0
ΔTE (ms)	2.2 – 4.1	3.5 – 4.1	3.75	4.7
Slice thickness (mm)	0.6 – 0.7 mm	0.6 – 0.7 mm	0.47	0.39
Bandwidth (Hz/Pixel)	125 – 488	125 – 1116	334 – 842	500
Flip Angle	15	15	15	20
Scan time (mins)	6 – 8	6 – 8	5 – 12	20

FIG. 1.

Intermediate maps for generating QSM from the DICOM files exported from the MR scanner. A nonlinear least squares fitting algorithm is used to estimate frequency map (a) which is then unwrapped with quality-guided phase unwrapping to obtain (b) from which the background field is removed using LBV to obtain the local field map (c). A magnitude image (d) is generated from the DICOM files using sum-of-squares summation and its forward gradient is computed to obtain the weighting matrix (e). All these maps serve as input to the MEDI+0 algorithm which generates the final QSM map (f).

Statistical Analysis

Statistical analysis was performed using Predictive Analytics Software (PASW) Statistics 18 (SPSS, Chicago, IL). Summary statistics, including mean, (μ_x), and standard deviation, (σ_x), of the QSM measurements observed at each gadolinium concentration was recorded. These measurements were subsequently used to determine if there was any change in dispersion of measurements with changes in susceptibility. A regression of the susceptibility estimates against the gadolinium concentration in each phantom was performed to estimate the molar susceptibility of gadolinium. To assess the agreement of the measurements, Bland and Altman’s method for multiple measurements per object (phantom) was applied to measurements from pairs of scanners used for each phantom (29). This method involves plotting the differences between pairs of measurements on the y-axis against their averages on the x-axis. The limits of agreement for all measurement methods (scanners) are determined from the standard deviation of the data as follows: If we designate the error and true variances in the measurements of each gadolinium concentration by multiple scanners as ${\sigma }_e^2$ and ${\sigma }_t^2$ respectively, then, a one-way analysis of variance (ANOVA) gives the within-group mean square ( ${\text{MS}}_{\mathrm{W}}={\sigma }_e^2$) and the between-group mean square ( ${\text{MS}}_{\mathrm{B}}=\mathrm{k}{\sigma }_t^2+{\sigma }_e^2$), where k is the number of between-group degrees of freedom. The square root of the total variance, $\sqrt{{\sigma }_t^2+{\sigma }_e^2}$, is then used to estimate the limits of agreement for the Bland-Altman (BA) plot.

A coefficient of reliability of measurements can be defined as $\rho ={\sigma }_t^2/({\sigma }_t^2+{\sigma }_e^2)$. By arithmetic manipulation, this coefficient can be expressed in terms of ANOVA variables as

$$\rho =\frac{{MS}_B-{MS}_W}{{MS}_B+(k-1){MS}_W}$$ (2)

Eqn (2) is also known as intra-class correlation coefficient (ICC), which is a measure of both the correlation and agreement of measurements (30). In this study, the ICC for all measurements was computed using a one-way random effect, absolute agreement, multiple raters model in PASW Statistics 18.

Another useful statistical measure is the standard deviation of the sampling error also called the standard error of measurement (SEM) which gives an estimate of the precision of a single measurement. This can be determined from the definition of the coefficient of reliability provided above to be

$$\mathit{SEM}={\sigma }_e\sqrt{1-\mathit{ICC}}$$ (3)

and is useful for constructing confidence intervals for measurements.

RESULTS

Twenty-two QSM maps were reconstructed from GRE scans of seven synthesis-matched gadolinium phantoms performed on twelve clinical and three preclinical scanners at seven imaging sites. Individual measurements of the susceptibility in each gadolinium compartments are shown in Supporting Information Table S1. The MEDI+0 approach was employed for this study’s QSM reconstruction resulted in maps with no observable streaking artifacts and a uniform agarose gel region. Fig. 2 shows representative QSM maps generated for 3 clinical scanners at different field strengths, and for one preclinical scanner at 7T. The visual similarity of the susceptibility sources, and the uniformity of the surrounding agarose gel medium on the maps generated by MEDI+0 for all scanners can be appreciated.

FIG. 2.

Representative QSM maps of phantoms obtained (a) GE Signa Hdxt 1.5T, (b) Siemens Prisma 3T, (c) Philips Achieva 7T clinical scanners, and (d) Bruker Biospin 7T preclinical scanner. The phantoms were gadolinium-filled balloons immersed in 500 and 50 mL containers of 1% agarose for the clinical and preclinical scanners respectively. All maps were reconstructed using MEDI+0 with the same parameters.

The advantage of using MEDI+0 is visible for highly magnetized gadolinium samples; that is very high concentrations at high field strengths. In Supporting Information Figure S1, the magnitude and local field map are shown together with the QSM computed using MEDI+0 and the standard MEDI algorithms. Both MEDI+0 and MEDI use an SNR weighting term (w in Eqn (1)) derived from the magnitude image. The low SNR at highest gadolinium concentration (white arrow on magnitude image) propagates into a reconstruction artifact in the QSM image generated by MEDI. The additional constraint of a Dirichlet-like boundary condition in the MEDI+0 model results in a better QSM map as can been seen in Supporting Information Figure S1.

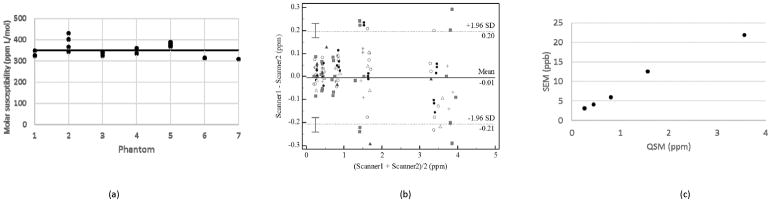
ROI-based estimates of susceptibility values showed a linear increase as the reference Gd concentration increased for all acquired MRI scans. A linear regression of QSM estimates of susceptibility against gadolinium concentration in each phantom was performed to obtain an estimate of the molar susceptibility of gadolinium from that phantom. Fig. 3a is a dot plot showing the molar susceptibility values recorded for each phantom by different scanners. The bold horizontal line indicates the average molar susceptibility of 350 ppm L/mol obtained for all molar susceptibility estimates. This value is in reasonable agreement with previous gadolinium susceptibility measurements using MRI (17,31). Except for Phantom 2, the estimated molar susceptibility values are closely clustered showing good agreement between estimates of the molar susceptibility from a given phantom by different scanners. Possible reasons for the large dispersion observed in the data for Phantom 2, such as temperature effects, are addressed in the discussion section. The ICC value calculated from all susceptibility measurements was 0.991 with a 95% confidence interval of 0.973 to 0.999. Using this ICC value and the standard deviation of the QSM measurement at each concentration, the standard error of measurement was calculated with Eq. [2] and displayed in Fig. 3b. It showed decreasing precision of QSM measurements with increasing susceptibility strength. Fig. 3c is a plot of the differences against the averages of pairs of QSM measurements obtained using different scanners. The solid and dotted lines are the bias and limits of agreement calculated using the Bland-Altman method of multiple measurements. The bias values are close to zero for all BA comparisons showing a lack of systematic error in QSM measurements. The limits of agreements are relatively large, about ±200 ppb, and are indicative of the large standard deviation in the measurements of the highest gadolinium concentration.

FIG. 3.

Summary statistics and comparisons of QSM data from all scanners. (a) Molar susceptibility estimates obtained as the slope of a linear regression of measured susceptibility values against prepared gadolinium concentrations in each of the seven phantoms. The straight line is the average of all the molar susceptibility values, which is 350 ppm L/mol. b) A Bland-Altman plot of measurements by pairs of scanners for each gadolinium concentration. The limits of agreement were obtained using the method of multiple measurements described by Bland and Altman. Each marker type designates measurements from the same phantom. The maximum difference between measurements can be seen to increase from less than 0.1 ppm for measurements for average measurements of 0.21 ppm to more than 0.2 ppm for average measurements of 3.36 ppm. (c) Plot of the standard error of measurement (SEM) against the QSM measurement. The SEM increases from 3.1 ppb to 21.9 ppb, as the gadolinium concentration increases.

DISCUSSION AND CONCLUSIONS

In this study, we analyzed 22 QSM datasets generated with the MEDI+0 automatic reference algorithm from scans of a gadolinium phantom on fifteen scanners at four field strengths and observed good reproducibility for a wide range of susceptibility values such as may be encountered in cerebral and extracranial applications of QSM. An excellent intra-class coefficient of 0.991 was obtained for all data with 95% confidence interval of 0.973 to 0.999. The standard error of measurement was estimated to increase from 3 ppb for an average measurement of 0.26 ppm to 21 ppb for an average measurement of 3.56 ppm. Bland-Altman analysis showed a bias of 10 ppb, and lower and upper limits of agreements of −210 and 200 ppb respectively.

Phantoms of gadolinium solution embedded in agarose gel are a useful starting point for the development and verification of QSM methods. As a result, investigations into the reproducibility of QSM measurements in gadolinium phantoms remain a useful area of study. However, previous studies have published maps that show streaking artifacts and lack a consistent reference. In this study, we demonstrate visual improvement in QSM images by using MEDI+0, an algorithm originally developed to enforce the homogeneity of the susceptibility map in the cerebrospinal fluid (CSF), resulting in the generation of a consistent reference and reduction of shadowing artifacts (24). MEDI+0 was used to enforce homogeneity in the region of the agarose gel to realize this improvement.

Despite good agreement in QSM measurements, the standard deviation of measurements was observed to increase with susceptibility strength resulting in decreasing precision (standard error of measurement) (Fig. 3b). This is because the standard deviation of QSM measurements is proportional to the phase noise, which is in turn inversely proportional to the SNR on the magnitude image. Increasing susceptibility values decrease the magnitude SNR from T2* loss, and consequently increase standard deviation of QSM measurements from 32.5 ppb at 0.26 ppm to 230 ppb at 3.56 ppm. From Eq. [3], the corresponding values of SEM are 3.08 to 21.9 ppb. The implication of this observation is that confidence intervals of QSM measurements widen as measured susceptibility increases. Fortuitously, the SEM is small even at a relatively high susceptibility. A possible remedy for this problem is the use of QSM algorithms developed specifically to deal with a wide range of susceptibility values (2,4).

Despite the good reproducibility of QSM obtained for the statistical measures considered in this study, critical examination of the QSM values (Supporting Information Table S1), does show there can be outlier values from certain scans. The sources of this variability are difficult to trace and may be due to variations in image processing tasks such as automated mask and ROI generation. The small differences in acquisition parameters between different sites that can be seen in Table 2 did not appear to be the dominant factor in producing observed differences between QSM estimates of gadolinium. Another possible source of variability in this study was the temperature of the phantom which may have affected the measured molar susceptibility values. The theoretical value for the molar susceptibility of Gd³⁺ is reported to be 7.88 cm³ K mol⁻¹(32), or 0.099 L K mol⁻¹. For example, the molar susceptibility for Gd-DTPA at 298 K is 0.0265 cm³/mol or 332.3 ppm L/mol as estimated in (31). The change in molar susceptibility with temperature can be determined from a regression to be −1.093 ppm/M/K. Therefore, a 1 degree change in temperature can significantly affect the measured molar susceptibility. Future multicenter comparisons of molar magnetic susceptibility measurements can ensure the phantoms are kept at the same temperature prior to and during scanning.

One limitation of this study was the use of phantom replicates instead of a single phantom. The former approach was adopted to reduce the time duration of the project, the possibility of damage to, or loss of, a single phantom that is repeatedly transported from one site to another. However, the use of replicates introduces the possibility of variation between concentrations of similar gadolinium compartments in different phantoms. The QSM estimates from Site A for the replicate phantoms are shown in bold in Supporting Information Table S1. The ICC from this dataset is 0.99, which does not differ greatly from that for the entire dataset, and suggests insignificant variation between the different gadolinium phantoms. Another limitation of the study was that only DICOM images was used for reconstructing QSM images. This limited the study to scanner platforms that are known to generate DICOM images without phase artifacts. The use of the raw k-space data can allow this study to be extended to other scanner platforms that are known generate DICOMs with unreliable phase information.

In conclusion, we show that high quality QSM maps can be generated using MEDI+0 for on both preclinical and clinical scanners at several field strengths for a wide range of susceptibility values. Compared to MEDI, MEDI+0 produced improved images of the high susceptibility values at even at high field strengths. An increasing dispersion in measurements at high susceptibilities was observed, and this appeared to be the result of decreased SNR in the magnitude image, which decreases the reliability of the derived noise weighting for the data fidelity term.

Supplementary Material

Supp info

Supporting Information Figure S1 - Improvement in QSM image quality obtained using MEDI+0 on a 7 Tesla clinical scanner. The magnitude and local field map (RDF) shown are obtained from the gradient-echo DICOM images of a gadolinium phantom with increasing concentrations of gadolinium. The image quality in the magnitude image for the first four gadolinium concentrations is enough to provide accurate SNR weighting for QSM reconstruction. However, the quality of the magnitude image for the highest gadolinium concentration (white arrow) is not enough to provide accurate SNR weighting for MEDI resulting in halo-like artifact (white arrow) around the susceptibility source reconstructed by MEDI. By using the additional constraint of enforcing homogeneity in the agarose gel medium, MEDI+0 eliminates this artifact.

Supporting Information Table S1. Susceptibility values (χ, ppm) and standard deviations within the measured ROI obtained for all QSM measurements of different compartments of gadolinium in phantoms scanned using different scanner platforms (first column). The table header has the prepared concentration of gadolinium in each compartment. The rows in bold has data from scanners at the primary site (Site A).